Definicje i twierdzenia na ustny egzamin maturalny z matematyki
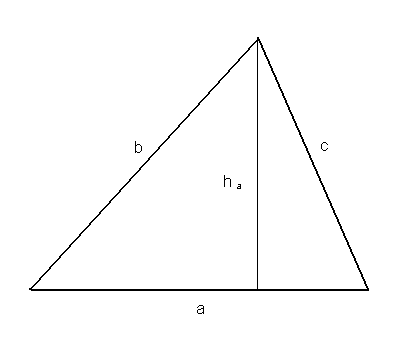
1. Twierdzenie sinusów (tw. Snelliusa)
Tw.
Dla dowolnego trójkąta stosunek długości boku do sinusa kąta leżącego naprzeciw jest stały i równa się podwojonej długości promienia okręgu opisanego na tym trójkącie.
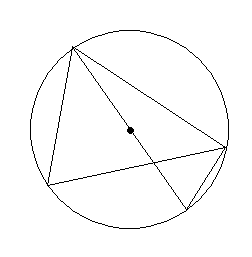
![]()
Dowód:
Z twierdzenia, że kąty wpisane oparte na tym samym łuku mają równe miary:
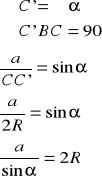
c.n.d.
2. Twierdzenie cosinusów (tw. Carnota, uogólnienie tw. Pitagorasa)
Tw.
W dowolnym trójkącie kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków pomniejszonej o podwojony iloczyn długości tych boków przez cosinus kąta zawartego między nimi.
a2 = b2 + c2 - 2bc*cosα
b2 = a2 + c2 - 2ac*cosβ
c2 = a2 + b2 - 2ab*cosγ
Dowód 1:
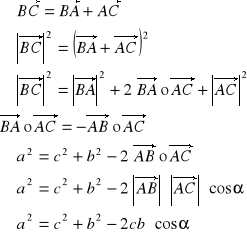
c.n.d.Dowód 2:
Na mocy twierdzenia sinusów boki a, b, c są proporcjonalne do odpowiednio sinα, sinβ, sinγ. Twierdzenie cosinusów przybierze zatem postać:
sin2α = sin2β + sin2γ - 2 sinβ sinγ cosα
Z twierdzenia o sumie kątów w trójkącie :
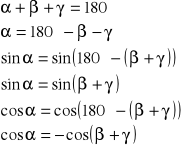
Lewa strona równania (I):
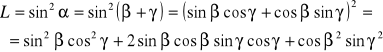
Prawa strona równania (I):
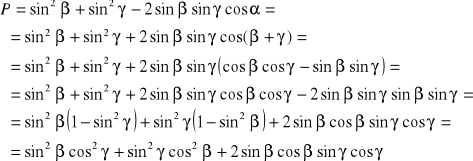
L = P c.n.d.
Wnioski z twierdzenia cosinusów:
1.
![]()
2. Twierdzenie Pitagorasa
![]()
3.
![]()
3. Twierdzenie o wysokości w trójkącie prostokątnym
Tw.
Wysokość poprowadzona z wierzchołka kąta prostego trójkąta jest średnią geometryczną długości odcinków na jakie dzieli przeciwprostokątną.
(W trójkącie prostokątnym kwadrat wysokości opuszczonej na przeciwprostokątną jest równy iloczynowi długości odcinków, na które dzieli tą przeciwprostokątną)
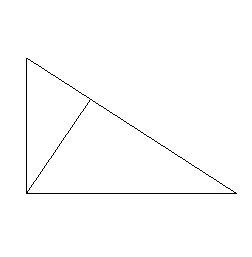
![]()
( h2 = pq )
Dowód:
Z podobieństwa trójkątów:
c.n.d.
4. Twierdzenie o czworokącie opisanym na okręgu
Tw.
Czworokąt wypukły można opisać na okręgu wtedy i tylko wtedy gdy sumy długości przeciwległych boków w tym czworokącie są równe.
Teza:
|BC| + |AD| = |AB| + |CD|
Dowód:
Zauważamy przystawanie par trójkątów:

Wtedy:
|AB| = u + x
|BC| = x + y
|CD| = y + z
|DA| = z + u
L = |BC| + |AD| = x + y + z + u
P = |AB| + |CD| = u + x + y + z
L = P
c.n.d.
5. Twierdzenie o czworokącie wpisanym w okrąg
Tw.
Czworokąt wypukły można wpisać w okrąg wtedy i tylko wtedy, gdy sumy miar przeciwległych kątów w tym czworokącie są równe i wynoszą 180° (π).
Teza:
α + β = γ + δ = 180° = π
Dowód:
Korzystając z twierdzenia o kącie środkowym i wpisanym w okrąg:
2α + 2β = 2π /:2
α + β = π
c.n.d.
6. Twierdzenie o odległości dwóch dowolnych punktów koła
Tw.
Odległość dwóch dowolnych punktów koła jest niewiększa od jego średnicy.
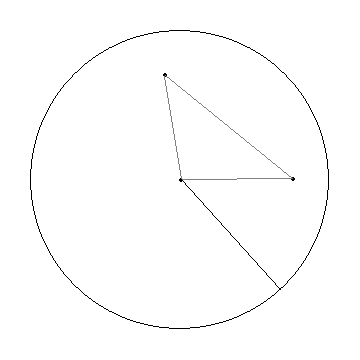
Teza:
![]()
Dowód:
Z definicji koła:
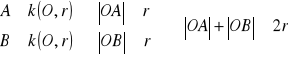
(po dodaniu nierówności stronami)
Z twierdzenia o długościach boków trójkątów:
![]()
Z własności nierówności:
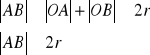
c.n.d.
7. Twierdzenie o dwusiecznej kąta wewnętrznego w trójkącie
Tw.
Rzuty dwóch boków trójkąta w kierunku dwusiecznej kąta wewnętrznego zawartego miedzy tymi dwoma bokami są proporcjonalne do długości tych boków.
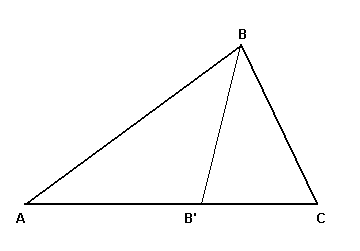
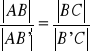
Dowód:
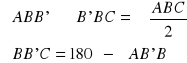
Z twierdzenia sinusów:
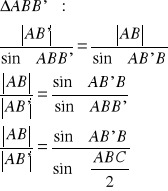
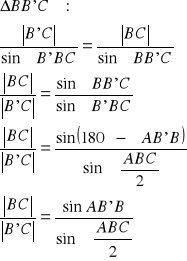
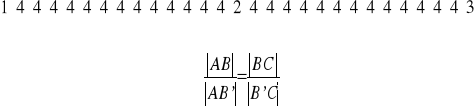
c.n.d.
8/9. Twierdzenie o kącie środkowym i wpisanym w okrąg
Tw.
Miara kąta środkowego jest dwa razy większa od miary kąta wpisanego opartego na tym samym łuku.
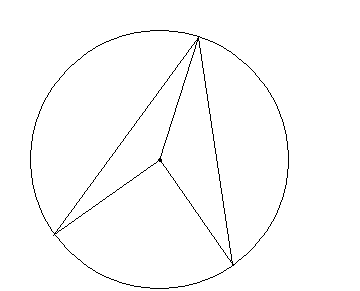
założenie:
β = γ + δ
teza:
α = 2β
dowód:

c.n.d.
10. Twierdzenie o symetralnych boków trójkąta
Tw.
W dowolnym trójkącie wszystkie trzy symetralne jego boków przecinają się w jednym punkcie, który jest środkiem okręgu opisanego na tym trójkącie.
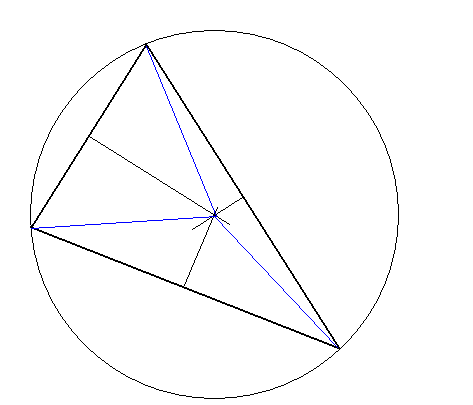
założenie:
ΔABC
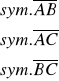
teza:
![]()
dowód:
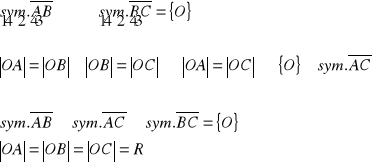
korzystając z def. symetralnej odcinka (zbiór punktów równo oddalonych od końców odcinka)
c.n.d.
11. Twierdzenie o dwusiecznych kąta
Tw.
W dowolnym trójkącie wszystkie trzy dwusieczne jego kątów przecinają się w jednym punkcie, który jest środkiem okręgu wpisanego w ten trójkąt.
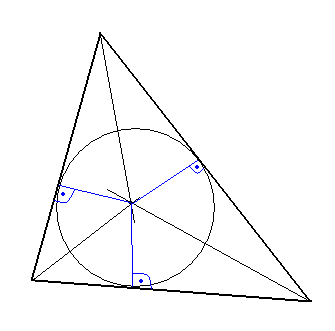
założenia:
teza:
![]()
dowód:
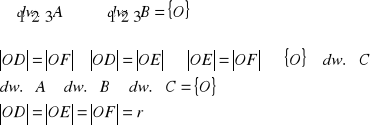
z def. dwusiecznej kąta (zbiór punktów równo oddalonych od prostych, w których zawierają się ramiona kąta)
c.n.d.
12. Twierdzenie Pitagorasa
Tw.
W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.
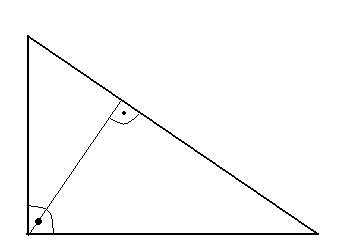
a2 + b2 = c2
założenie:
![]()
dowód 1:
dowód 2:
ΔBDC i ΔABC są podobne o skali podobieństwa ![]()
;
ΔADC i ΔABC są podobne o skali podobieństwa ![]()
.
Oznaczmy pole ΔABC przez P, pole ΔBDC przez P1 i pole ΔADC przez P2
Ponieważ stosunek pól figur podobnych jest równy kwadratowi skali prawdopodobieństwa otrzymujemy:
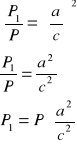
![]()
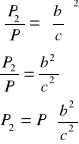
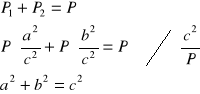
c.n.d.
dowód 3:
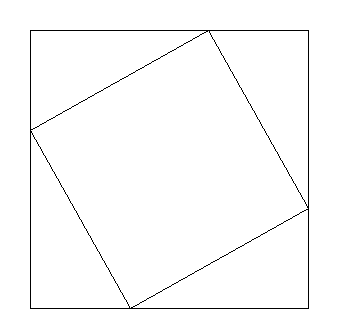
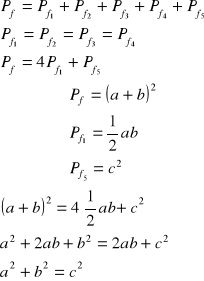
c.n.d.
13. Twierdzenie o środkowych boków trójkąta
Tw.
W dowolnym trójkącie wszystkie trzy środkowe jego boków przecinają się w jednym punkcie, który jest środkiem ciężkości tego trójkąta. Punkt ten dzieli każdą ze środkowych na odcinki o stosunku długości 2:1.
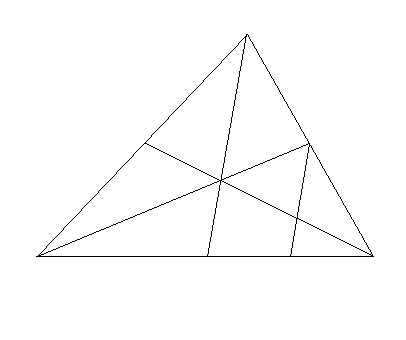
założenia:
środkowe ![]()
![]()
teza:
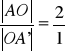
dowód:
z twierdzenia Talesa dla kąta ![]()
:
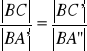
z założenia:
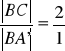
zatem:
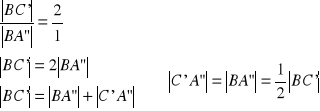
z twierdzenia Talesa dla kąta ![]()
:
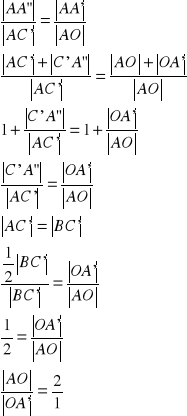
c.n.d.
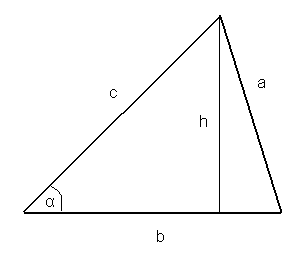
14. Wzory na pole trójkąta
![]()
dowód:

![]()
![]()
c.n.d.
II.
W trójkącie prostokątnym:
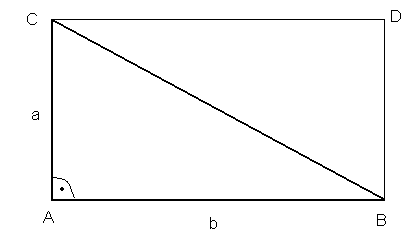
![]()
dowód:
c.n.d.
III.
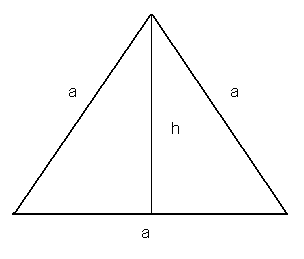
W trójkącie równobocznym:
![]()
dowód:
z twierdzenia Pitagorasa:
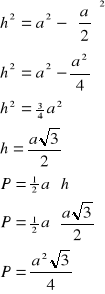
c.n.d.
IV.
![]()
dowód:
c.n.d.
(pozostałe dowodzi się analogicznie)
V.
![]()
dowód:
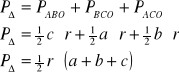
c.n.d.
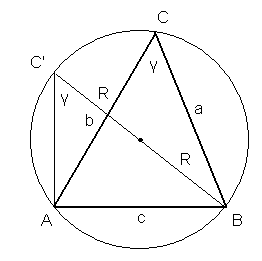
VI.
![]()
dowód:
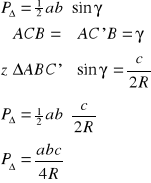
udowodnione wyżej
z twierdzenia o kątach opartych na tym samym łuku
z tw.o kątach wpisanym i środkowym ΔABC' jest
prostokątny
c.n.d.
VII.
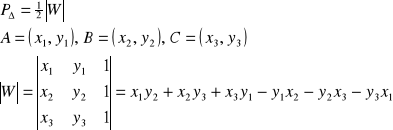
VIII.
Wzór Herona:
![]()
15. Twierdzenie o podzielności wielomianu przez dwumian (tw. Bezout)
Tw.
Wielomian W(x) dzieli się bez reszty przez dwumian x-p wtedy i tylko wtedy gdy p jest pierwiastkiem wielomianu W(x).
dowód:
Niech p będzie pierwiastkiem wielomianu W(x). Dzieląc z resztą wielomian W przez x-p otrzymujemy :
W(x)=(x-p)V(x)+R
gdzie V(x) to pewien wielomian, zaś R - liczba.
Podstawiając za x=p otrzymujemy:
0=W(p)=(p-p)V(p)+R
stąd R=0, czyli W(x) dzieli się przez x-p.
Niech teraz wielomian W(x) dzieli się przez x-p. Wtedy:
W(x)=(x-p)V(x)
Podstawiając x=p mamy:
W(p)=(p-p)V(p)=0
czyli p jest pierwiastkiem wielomianu W(x)
c.n.d.
16. Twierdzenie na wyraz ogólny ciągu arytmetycznego
Tw.
an=a1+(n-1)r
dowód:
Wykorzystujemy zasadę indukcji matematycznej:
I
sprawdzenie dla n=1:
L=a1
P= a1+(1-1)r= a1
L=P
II
założenie indukcyjne dla n=k :
ak= a1+(k-1)r
teza indukcyjna dla n=k+1 :
ak+1= a1+kr
dowód:
z def:
ak+1 - ak=r
ak+1= ak+r
zał.ind.
ak+1= a1+(k-1)r +r
ak+1= a1+kr-r +r= a1+kr c.n.d.
17. Twierdzenie na wyraz ogólny ciągu geometrycznego
Tw.
an=a1·qn-1
dowód:
Wykorzystujemy zasadę indukcji matematycznej:
I
sprawdzenie dla n=1:
L=a1
P= a1·q1-1= a1
L=P
II
założenie indukcyjne dla n=k :
ak= a1·qk-1
teza indukcyjna dla n=k+1 :
ak+1= a1·qk
dowód:
z def:
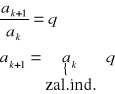
ak+1 = a1·qk-1·q = ak+1= a1·qk c.n.d.
18. Wzór na sumę n początkowych wyrazów ciągu arytmetycznego
Tw.
![]()
dowód:
Wykorzystujemy zasadę indukcji matematycznej:
I
sprawdzenie dla n=1:
L= S1= a1
![]()
L=P
sprawdzenie dla n=2:
L= S2= a1+ a2
![]()
L=P
II
założenie indukcyjne dla n=k :
![]()
teza indukcyjna dla n=k+1 :
![]()
dowód:
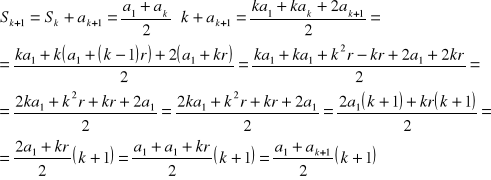
c.n.d.
19. Wzór na sumę n początkowych wyrazów ciągu geometrycznego
Tw.
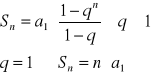
dowód:
Wykorzystujemy zasadę indukcji matematycznej:
I
sprawdzenie dla n=1:
L= S1= a1
![]()
L=P
sprawdzenie dla n=2:
L= S2= a1+ a2
![]()
L=P
II
założenie indukcyjne dla n=k :
![]()
teza indukcyjna dla n=k+1 :
![]()
dowód:
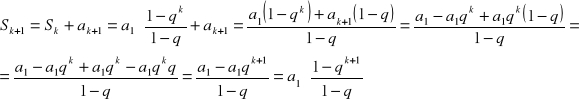
c.n.d.
20. Twierdzenia o działaniach na logarytmach
I.
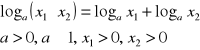
dowód:
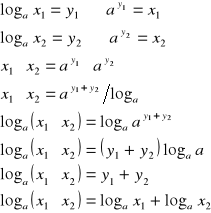
c.n.d.
II.
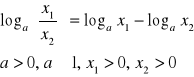
dowód:
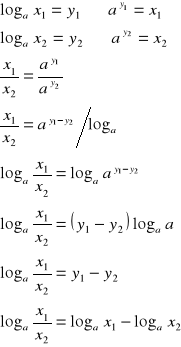
c.n.d.
III.
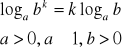
dowód:
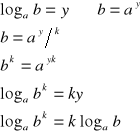
c.n.d.
IV.
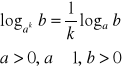
dowód:
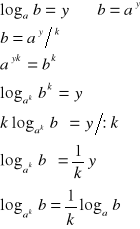
c.n.d.
V.
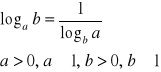
dowód:
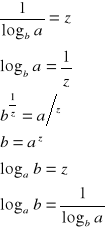
c.n.d.
VI.
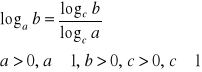
dowód:
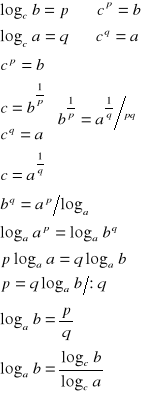
c.n.d.
VII.
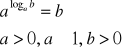
dowód: (niewprost)
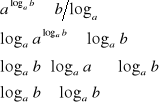
sprzeczność, zatem wzór jest prawdziwy c.n.d.
21. Twierdzenie o pochodnej iloczynu i ilorazu dwóch funkcji
Tw.
Pochodna iloczynu dwóch funkcji jest równa sumie iloczynów pochodnej pierwszej funkcji przez funkcję drugą oraz pierwszej funkcji przez pochodną drugiej funkcji.
![]()
dowód:
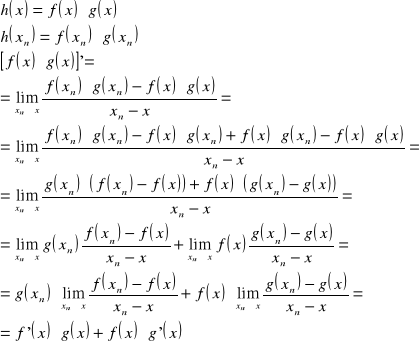
c.n.d.
Tw.
Pochodna ilorazu dwóch funkcji jest równa ilorazowi różnicy iloczynów pochodnej pierwszej funkcji przez funkcję drugą oraz pochodnej drugiej funkcji przez funkcję pierwszą, przez kwadrat funkcji drugiej.
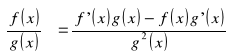
dowód:
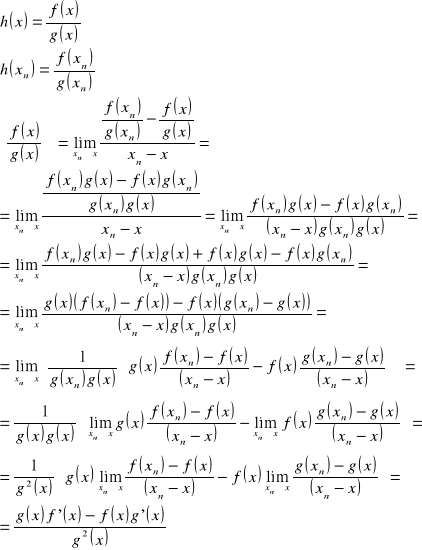
c.n.d.
22. Własności prawdopodobieństwa
Niech Ω będzie danym zbiorem zdarzeń elementarnych, niech P będzie prawdopodobieństwem określonym na zdarzeniach ![]()
. Wówczas:
I.
![]()
dowód:
korzystamy ze wzorów ![]()
na mocy warunku definicji prawdopodobieństwa, że![]()
otrzymujemy:
![]()
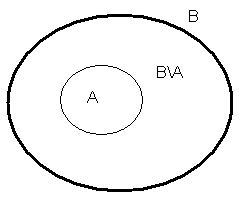
c.n.d.
II.
![]()
dowód:
![]()
zbiory A i B\A są rozłączne
na mocy warunku definicji prawdopodobieństwa, że ![]()
otrzymujemy:
![]()
c.n.d.
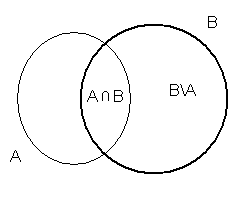
III.
![]()
dowód:
z udowodnionej własności II: ![]()
z warunku definicji prawdopodobieństwa, że ![]()
otrzymujemy:
![]()
c.n.d.
IV.
![]()
dowód:
korzystając ze wzoru ![]()
oraz warunków definicji prawdopodobieństwa, że
![]()
otrzymujemy:
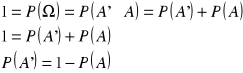
c.n.d.
V.
![]()
dowód:
korzystamy z tożsamości :
![]()
ponieważ
![]()
więc na mocy warunku definicji prawdopodobieństwa, że
![]()
otrzymujemy:
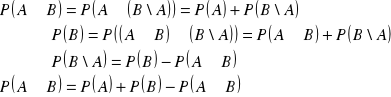
c.n.d.
23. Twierdzenie o prostej prostopadłej do płaszczyzny
Tw.
Jeżeli prosta jest prostopadła do dwóch przecinających się prostych to jest prostopadła do płaszczyzny w której się te dwie proste zawierają.
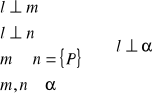
dowód:
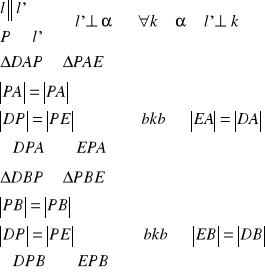

c.n.d.
24. Twierdzenie o trzech prostopadłych
Tw.
Jeżeli prosta l należąca do płaszczyzny α jest prostopadła do rzutu prostej pochyłej k względem tej płaszczyzny, to prosta l jest prostopadła do tej pochyłej.
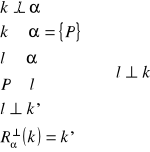
dowód:
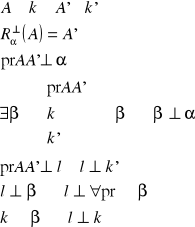
c.n.d.
25. Twierdzenie o pierwiastkach wymiernych wielomianu
Tw.
Jeżeli wszystkie współczynniki wielomianu a0, a1, a2,..., an są całkowite, a liczba wymierna zapisana w postaci ułamka nieskracalnego ![]()
jest pierwiastkiem równania
anxn+...+ a2x2+ a1x+ a0=0
to p jest dzielnikiem a0, natomiast q jest dzielnikiem an.
dowód:
z założenia mamy:
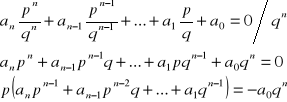
Lewa strona otrzymanej równości dzieli się przez p oraz p i q nie mają wspólnych dzielników więc p i qn również nie mają wspólnych dzielników zatem a0 dzieli się przez p.
Przez symetrię prawdziwa jest i druga teza twierdzenia.
c.n.d.
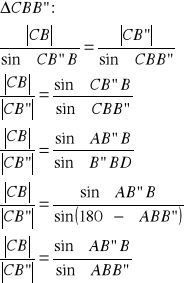
26. Twierdzenie o dwusiecznej kąta zewnętrznego w trójkącie
Tw.
Rzuty dwóch boków trójkąta w kierunku dwusiecznej kąta zewnętrznego przyległego do danego kąta są proporcjonalne do długości tych boków.
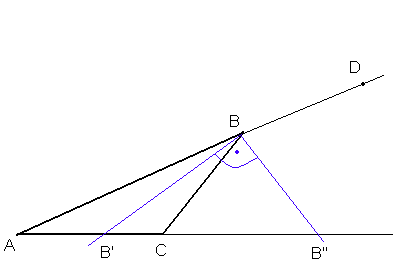
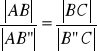
dowód:
![]()
z twierdzenia sinusów:
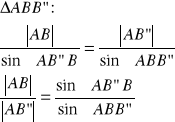
![]()
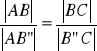
c.n.d.
C
γ
b a
R
O
β
B
α c
A α
C'
B
β
c a
γ
C
α
A b
B
q
D
h p
C A
D
z
G
z y
r C
H
r
O y
u r
F
r
A
x
u
E
x
B
α
δ
γ
2β
2α
β
A
O B
r
C
β
δ γ
O
α
δ
A γ
B
C
O
A
B
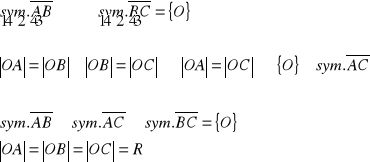
C
E
F
O
A
D B
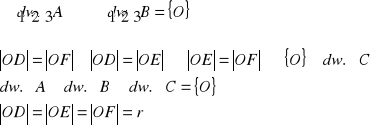
A
D
b c
C a B
a b
f1 f2
b c
a
c
f5
a c
f4 c
f3 b
b a
C
B' A'
O
A C' A” B
figura A figura B
1 2 4
h h h
3
a a a
są przystające
są przystające
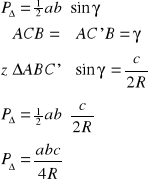
![]()
Wyszukiwarka
Podobne podstrony:
mat.matura, Definicje i twierdzenia na ustny egzamin maturalny z matematyki
USTNA97M, Zakres wymaga˙ na ustny egzamin maturalny z matematyki - technikum 5-letnie - maj 1996
USTNY EGZAMIN MATURALNY Z MATEMATYKI, szkoła, Matura, Matura - Matematyka, Zadania maturalne
Odpowiedzi na ustny egzamin z przedsiębiorczości
pytania na ustny[1], Egzamin specjalizacja ginekologia i położnictwo
ZESTAW TEMATOW NA WEWNETRZNY EGZAMIN MATURALNY Z JEZYKA POLSKIEGO W ZESPOLE SZKOL TECHNICZNYCH IM
Od 19 do 25
do pracy na ustny, Szkoła, przydatne w szkole
propozycje zabaw dydaktycznych w przedszkolu dla dzieci od 4 do 6 lat na podstawie?jki o kopciuszku
konkurs poż pytania na ustny, materiały do otwp - młodzierz zapobiega pożarom
od m. wiśniowej do wełnowca, Moje studia na SGGW - Ogrodnictwo, Entomologia
Zadania administracji publicznej w sferze ochrony środowiska, POS na ustny - definicje
Historia Od, Do, Wiosna Ludów na Węgrzech
Ustrój i prawo na ziemiach polskich od X do XX wieku, st. Administracja notatki
AMINOKWASY OD 13 DO 25, Studia, 1-stopień, inżynierka, Ochrona Środowiska, Od Agaty
Oblicznie skali, 1)Na mapie 1:200000 od A do B 3 cm a, ile w terenie
więcej podobnych podstron