1. Macierz, działania algebraiczne
Macierzą nazywamy tablicę liczb postaci:
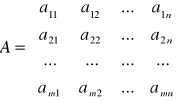
jest to macierz o m wierszach i n kolumnach
A=[ aij]mxn
Rodzaje macierzy:
1) diagonalna - (kw) pod i nad przekątna musza być same 0
2) skalarna - macierz diagonalna w której wszystkie elementy na gł. przekątnej są sobie równe
3) jednostkowa - macierz diagonalna i szczególny przyp. skalarnej z tym że na gł. przekątnej znajdują się same 1.
4) zerowa - wszystkie elementy są 0
5) trójkątna - rozróżniamy górno- i dolnotrójkątną (w macierzy kwadratowej!!!) poniżej lub powyżej przekątnej 0
Działania na macierzach:
1. TRANSPOZYCJA - zapisujemy kolumny jako wiersze lub wiersze jako kolumny
2. DODAWANIE - macierze muszą być jednakowych rozmiarów : A mxm+ B mxm = C mxm ⇔ cij = a ij + b ij
- jest przemienne
- jest łączne
Analogicznie wykonuje się odejmowanie.
3. MNOŻENIE PRZEZ SKALAR - mnożymy każdy element macierzy przez skalar
- α(β•A) = (α•β)A
- (α+β)A = αA+βA
- α(A+B) = αA+αB
4. MNOŻENIE MACIERZY - jeżeli liczba kolumn macierzy A = liczbie wierszy macierzy B, to iloczynem AB macierzy Amxp przez macierz Bpxn nazywamy taką macierz Cmxn której elementy są określone wzorem:
cij = ai1bi1+ ai2bi2+…+ aipbpj
Wiersze 1 macierzy mnożymy przez kolumny 2 macierzy.
- nie jest przemienne!!!
- αAB = AαB
- (A+B)C = AC + BC
- C(A+B) = CA + CB
- IEA = A
2. wyznacznik macierzy, obliczanie
Wyznacznikiem macierzy kwadratowej A=[aij] stopnia n nazywamy liczbę A lub det A.
Wyznacznik zależy od stopnia macierzy:
1) A=[a11] detA= a11
2) B= b11 b12 detB = b11 •b22 - b12 •b21
b21 b22
3) Macierze stopnia 3 - Metoda Sarrusa
1.przepisujemy 2 pierwsze wiersze pod wyznacznikiem
2.tworzymy 6 składników sumy
3.dodajemy 3 kolejne od drugie strony (z minusem)
4) Macierze stopnia 4 i wyższego - Rozwinięcie Laplace'a
Pojęcie MINORA: minorem nazywamy wyznacznik stopnia o 1 mniej otrzymany przez skreślenie dowolnie wybranej kolumny i dowolnego wiersza.
Wszystkie elementy wybranego wiersza mnożymy przez minory i (-1)i+j
3. macierz odwrotna, jej wyznaczenie
Macierzą odwrotną A-1 do macierzy kwadratowej A stopnia n nazywamy macierz, dla której prawdziwa jest równość :
A-1• A = A• A-1= IE
Gdzie IE jest macierzą jednostkową stopnia n.
1)Metoda operacji elementarnych na wierszach macierzy
[AIE] ∼ [IEB] - macierz B jest macierzą odwrotną macierzy A
2)Metoda dopełnień algebraicznych
Macierz odwrotna do danej macierzy jest równa transponowanej macierzy dopełnień algebraicznych pomnożonej przez odwrotność wyznacznika:
A-1= 1/ detA • (A*)T
Dopełnienie algebraiczne dowolnego el. macierzy (Aij) jest równe pomnożonemu minorowi Mij (-1)i+j
4. rząd macierzy i jego wyznaczanie
Rzędem macierzy nazywamy najwyższy stopień niezerowego wyznacznika wyjętego z tej macierzy.
Wyznaczenie rzędu macierzy odbywa się metodą operacji elementarnych na wierszach i kolumnach macierzy. Doprowadzamy macierz do postaci schodkowej.
Rząd macierzy jest równy liczbie wierszy niezerowych postaci schodkowej macierzy.
5. układy równań liniowych, metody rozwiązywania
1) Metoda macierzowa
A•X=B, gdzie A-macierz współczynników (macierz układu)
X- wektor niewiadomych
B- wektor wyrazów wolnych
2) Układ Cramera
Ukł. równań liniowych którego macierz współczynników A jest kwadratową macierzą nieosobliwą (det≠0) nazywamy układem Cramera.
Stosuje się wzory Cramera:
x1=W1/W
x2=W2/W
xj=Wj/W
3) Metoda eliminacji Gaussa
Opiera się na operacjach elementarnych na ukł. równań liniowych:
1.można przestawić ze soba dwa różne równania
2. można pomnożyć równanie obustronnie przez dowolną liczbę różną od 0
3.można dodać wielokrotność jednego równania do innego równania
4.można wykreślić równanie składające się z samych 0
A+ = [AB] ∼ IED , [ IED] , IE , [IE]
00 0
6. twierdzenie Kroneckera - Capellego
Orzeka o istnieniu i ewentualnej liczbie rozwiązań dowolnego układu równań.
Układ równań posiada jedno rozwiązanie jeśli R (A) = R(A+)=n, gdzie n= liczba niewiadomych (układ oznaczony)
Układ równań posiada nieskończenie wiele rozwiązań jeśli R (A) = R(A+)< n (układ nieoznaczony)
Układ równań nie posiada rozwiązań jeśli R(A) ≠ R(A+) (układ sprzeczny)
7. statyczny model przepływów międzygałęziowych
Gospodarka dzieli się na szereg gałęzi (np. hutnictwo, rolnictwo) których produkcje są powiązane między sobą. Każdy produkt wytworzony w jednej gałęzi jest w części przeznaczony na zużycie prod. Własnej gałęzi, jak tez na potrzeby prod. Innych gałęzi.. Zarządzanie całością gospodarki wymaga ułożenia bilansu gosp. narodowej , ile dana gałąź gosp. produkuje na rzecz pozostałych gałęzi itd.
Y1 ,Y2 , .…..Yn - produkcja globalna
xik - oznacza tę część produkcji globalnej i-tej gałęzi (Yi) która jest zużywana na potrzeby produkcyjne k-tej gałęzi - są to przepływy międzygałęziowe.
Nadwyżkę produkcji i-tej gałęzi która pozostaje na konsumpcję, eksport, czy na zwiększenie rezerw i zapasów nazywamy produktem końcowym i-tej gałęzi i oznaczamy yi.
x11 + x12 + x13 + y1 = Y1
x21 + x22 + x23 + y2 = Y2
x31 + x32 + x33 + y3 = Y3
Model LEONTIEFA
aik = xik / Yk - techniczny współczynnik produkcji
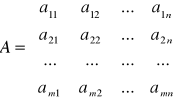
Macierz A nazywamy macierzą technicznych współczynników produkcji lub macierzą współczynników kosztów.
Przekształcając wzór mamy : xik = aik •Yk
Po podstawieniu do układu równań otrzymamy wzór :
MODEL LEONTIEFA
IE - A=L → (IE - A) • Y = y → L•Y=y
Macierz L nazywamy macierzą Leontiefa. Jest ona różnicą macierzy jednostkowej i macierzy technicznych współczynników produkcji.
8. Optymalne planowanie
Przypuśćmy, że funkcją celu zmiennych x1 i x2 jest :
z = c1 x1+ c2 x2 (c1>0 ; c2 >0)
a układ warunków ma postać:
a11 x1+ a12 x2 ≤ b1
a21 x1+ a22 x2 ≤ b2
gdzie aik >0 i b1 , b2 > 0 oraz x1≥ 0 , x2≥ 0
Chodzi o znalezienie wartości zmiennych decyzyjnych x1 i x2 takich aby spełniony był podany układ warunków i aby f. celu :
z = c1 x1+ c2 x2 przyjmowała wartość największą.
Oznaczając przez l1 i l2 proste o równaniach :
l1 : a11 x1+ a12 x2 = b1 , l2 : a21 x1+ a22 x2 = b2
to na płaszczyźnie O x1x2 nierówność a11 x1+ a12 x2 ≤ b1 spełniają współrzędne wszystkich punktów płaszczyzny znajdujących się na lub pod prostą l1.Analogicznie jest z drugą nierównością. Przyjmując jeszcze warunki brzegowe x1≥ 0 , x2≥ 0 otrzymujemy, że obszar rozwiązań dopuszczalnych tworzą punkty pierwszej ćwiartki układu współrzędnych leżące równocześnie pod prostymi l1 i l2 lub na nich. Jeśli w f. celu zmienia się z ,to równanie to przedstawia pęk prostych w postaci kierunkowej.
Im większe jest z tym wyżej położona jest odpowiednia prosta z pęku prostych równoległych. Najwyżej położona spośród nich prosta przedstawia rozwiązanie optymalne.
9. pojęcie funkcji i jej podstawowe właśności
Mówimy że f jest funkcją (odwzorowaniem) zbioru X w zbiór Y, jeżeli każdemu elementowi x zbioru X przyporządkowano dokładnie jeden element y ze zbioru Y.
Zbiór X- dziedzina funkcji : D f , a jego elementy x argumentami tej funkcji.
Przeciwdziedzina : R f
Jeśli R f =Y to jest to odwzorowanie f : X→Y(odwzorowanie „na”) f : R→R
Jeśli R f nie wyczerpuje całego zbioru Y to jest to odwzorowanie „w” (f : R→R)
1) f. różnowartościowa ⇔ ∀ x1 x2∈X zachodzi x1 ≠ x2⇒ f(x1) ≠ f(x2)
2) f. odwrotna f—1 - jest odwzorowaniem „na”
- jest różnowartościowa
np. f(x)=x2
3) f. złożona h(x)=g(f(x)) np. sin2x
Monotoniczność:
Rosnąca ⇔∀ x1 x2∈X : x1 < x2⇒ f(x1) < f(x2)
Malejąca ⇔∀ x1 x2∈X : x1 < x2⇒ f(x1) > f(x2)
Nierosnąca ⇔∀ x1 x2∈X : x1 < x2⇒ f(x1) ≥ f(x2)
Niemalejąca ⇔∀ x1 x2∈X : x1 < x2⇒ f(x1) ≤ f(x2)
Stała ⇔ ∀x∈X : f(x)=a ; ∀x1 x2∈X f(x1) = f(x2)
f (x) okresowa ⇔ ∃ T>0 ze dla każdego x∈X zachodzi: x+T∈X i f(x+T)= f(x)
f (x) parzysta ⇔ ∀x∈X zachodzi -x∈X i f (-x)= f (x) (symetryczne względem osi OY)
f (x) nieparzysta ⇔ ∀x∈X zachodzi -x∈X i f (-x)= - f (x) (symetryczne względem p.(0;0)
f (x) ograniczona z góry ⇔ ∃ M∈R ∀x∈X : f (x)≤ M
f (x) ograniczona z dołu ⇔ ∃ m∈R ∀x∈X : f (x)≥ m
Funkcja jest f. ograniczoną jeśli jest ograniczona z góry i z dołu.
10. Wielomiany
W (x)= an xn+ an-1 xn-1+…+ a1 x+a0, gdzie n∈N
n- stopień wielomianu; an współczynnik wielomianu; a0 wyraz wolny wielomianu
Może mieć nieograniczoną liczbę miejsc zerowych
11. Funkcja wymierna
Jest to iloraz wielomianów.
f(x)= W(x) / G(x), gdzie W(x) i G(x) wielomiany i G(x) ≠ 0
12. funkcja potęgowa
f(x) =xn
dziedzina f. potęgowej zależy od wykładnika
13. funkcja wykładnicza
f(x) =ax , a>0 i a≠1
jeśli a >1 t f. jest rosnąca w całej swej dziedzinie
jeśli a ∈ (0;1) to f. jest malejąca w całej swej dziedzinie
f. logarytmiczna jest różnowartościowa
14. Funkcja logarytmiczna
f(x) = loga x , a>0 a≠1
jeśli a >1 t f. jest rosnąca w całej swej dziedzinie
jeśli a ∈ (0;1) to f. jest malejąca w całej swej dziedzinie
f. logarytmiczna jest różnowartościowa
Odwrotną do funkcji logarytmicznej jest funkcja wykładnicza.
15. funkcje trygonometryczne
f(x)=sin x, f(x)=cos x → x∈R
f(x)=tg x → x ≠Π/2 + kΠ, gdzie k∈C
f(x)=ctg x → x ≠kΠ, gdzie k∈C
16. funkcje cyklometryczne
Są to funkcje odwrotne do trygonometrycznych.
1) f(x)= arc sin x X=<-Π/2; Π/2>
Y=<-1;1>
2) f(x)=arc cos x X=<0; Π>
Y=<-1;1>
3) f(x)=arc tg x X=<-Π/2; Π/2>
Y=<-∞;+∞>
4) f(x)=arc ctg x X=<0; Π>
Y=<-∞;+∞>
17. Ciągi liczbowe
Ciągiem nazywamy każdą funkcję określona na zbiorze liczb naturalnych N lub nieskończonym jego podzbiorze.
an= f(n)
Monotoniczność ciągów:
Rosnący ∀n∈N an+1 > an
Malejący ∀n∈N an+1 < an
Niemalejący ∀n∈N an+1 ≥ an
Nierosnący ∀n∈N an+1 ≤ an
18.Granica ciągu
Mówimy że ciąg liczbowy {an} ma właściwą granicę g, co zapisujemy : (n→∞ ) lim an = g
jeżeli: ∀ε>0 ∃ nε ∀n> nε : an∈U (g,ε)
19. Granica funkcji
Funkcja f(x) posiada granicę właściwą g przy x→ xo wtedy i tylko wtedy gdy dla każdego ciągu xn należącego do sąsiedztwa S(xo;δ) i zbieżnego do xo ciąg f(xn) jest zbieżny do g . (lim f(xn)=g)
20. ciągłość funkcji
Funkcja f(x) jest ciągła w p. xo wtedy i tylko wtedy gdy
(x→xo) lim f(x)=f(xo) i :
xo∈Df
(x→xo-) lim f(x)= (x→xo+) lim f(x)= f(xo)
Def. Punkt nieciągłości, nazywamy punktem nieciągłości pierwszego rodzaju jeżeli istnieje skończona granica jednostronna.
Def. Punkt nieciągłości, nazywamy punktem nieciągłości drugiego rodzaju jeżeli choć jedna z granic jednostronnych nie istnieje lub jest granicą niewłaściwą.
Usuwalne: granica lew. = gr. praw. ≠ f (xo)
Nieusuwalne: gr. lew. ≠ gr. praw. Bądź jedna lub obie są gr. niewłaściwymi.
21. pochodna funkcji i jej obliczanie
Jeśli istnieje granica ciągu ilorazów różnicowych przy h→0 g≠+- ∞ to jest to pochodna funkcji w p. xo
(h→0) lim f (xo+h) - f (xo)=g
h
Pochodna istnieje jeśli istnieje granica lewo- i prawostronna.
Można liczyć pochodną z definicji i z wzorów.
22. różniczka funkcji i jej zastosowanie
Różniczką funkcji w p. xo nazywamy iloczyn f ` (xo) • h i oznaczamy symbolem d f(xo):
d f(xo)= f ` (xo) • h
h=dx
d f(xo)= f ` (xo) • dx
d f(xo) = f ` (xo)
dx
Różniczka jest wykorzystywana do liczenia przybliżonych wartości funkcji.
f (xo)
f (xo+h)= f (xo)+ Δ f (xo)
f (xo+h)≈ f (xo)+d f (xo)]
23.Twierdzenie rolle'a i lagrange'a
Twierdzenie Rolle'a:
Jeżeli funkcja jest ciągła w <a,b>, różniczkowalna w (a,b), oraz f(a) = f(b), to istnieje c ∈ (a,b) taki, że f ` (c) = 0.
Twierdzenie Lagrange'a:
Jeżeli funkcja jest ciągła w <a,b>, różniczkowalna w (a,b), to istnieje c ∈ (a,b), taki, że:
![]()
24. twierdzenie de l'hospitala i przykłady zastosowań
Stosujemy tylko kiedy występuje symbol nieoznaczony
![]()
Tw. (Z: - założenie)
są określone i różniczkowalne w
sąsiedztwie punktu x0 (Sx0).
![]()
![]()
Teza (T) Istnieje
![]()
Przykład:
![]()
Przykład:
![]()
25. ekstremum
Warunkiem koniecznym istnienia ekstremum lokalnego f(x)w p. x0 jest zerowanie się pierwszej pochodnej: np. f(x)=x3 : f` (x)=2x2: f(0)=0
Warunkiem wystarczającym istnienia ekstremum lokalnego f(x)w p. x0 jest zmiana znaku pochodne w tym punkcie.
Jeśli 1 pochodna zmienia znak :+ → - posiada maximum
- →+ posiada minimum
26. wypukłość, wklęsłość i punkty przegięcia
Funkcja jest wypukła jeśli :
- jej wykres leży nad styczną
- 2 pochodna jest dodatnia (+)
Funkcja jest wklęsła jeśli:
- jej wykres leży pod styczną
- 2 pochodna jest ujemna (-)
Punkt przegięcia jest wtedy, gdy wykres przechodzi z wklęsłego na wypukły i odwrotnie.
Punkt x0 jest punktem przegięcia wtedy jeśli 2 pochodna zmienia znak.
27. asymptoty wykresu funkcji
![]()
Pionowe:
lewostronna
prawostronna
Poziome:
lewostronna (x→-∞) lim f(x)= g≠+- ∞
prawostronna (x→+∞) lim f(x)= g≠+- ∞
Ukośne:
Równanie asymptoty : (x→∞) lim [f(x) - (mx+b)]=0
Muszą być spełnione następujące warunki:
(x→+- ∞) lim f(x)/x = m≠+- ∞
(x→+- ∞) lim [f(x)-mx]=b≠+- ∞
28. funkcja pierwotna i całka nieoznaczona
Def: Funkcją pierwotną danej funkcji f(x) na przedziale X nazywamy każdą F(x)której pochodna F `(x)jest równa f(x)
Funkcja F(x) = sinx jest funkcją pierwotną funkcji f(x)=-cosx.
Każdą f(x) określoną na przedziale X posiadającą F(x)nazywamy funkcją całkowalną w sensie Newtona na tym przedziale.
Def: Jeśli mamy f(x) określoną na przedziale X to całką nieoznaczoną f(x) na przedziale X nazywamy zbiór wszystkich f. pierwotnych i tylko tych funkcji:
![]()
29. metody całkowania
Całkowanie przez podstawianie:
Jeżeli funkcja t=ϕ(x) jest różniczkowalna w przedziale (α,β) i odwzorowuje ten przedział na przedział (a,b), w którym funkcja f(t)jest całkowalna, to zachodzi wzór:
![]()
1) ∫ f[g(x)]•g'(x)dx= g(x)=t = ∫ f(
g'(x)dx=dt
2) ∫ f(x)dx= x=h(t) =∫ f [h(t)]h'(t)dt
dx= h'(t)dt
Całkowanie przez części:
∫ f(x) •g'(x)dx=f(x) •g(x) - ∫ f '(x)g(x)dx
30. całka oznaczona riemana
Def: Jeśli dla każdego normalnego ciągu podziałów {xn} (lim dn = 0) przedziału <a,b> istnieje skończona granica
n→∞
ciągu sum całkowych niezależna od wyboru punktów pośrednich, to granicę tę nazywamy całką oznaczoną w sensie Riemanna funkcji f(x)
![]()
Każda funkcja ciągła w przedziale <a,b> jest całkowalna, posiada całkę oznaczoną.
Każda f. ograniczona przedziałem <a,b> i posiadająca skończoną liczbę nieciągłości, jest również całkowalna.
Całka oznaczona jest polem powierzchni ograniczonym z jednej strony wykresem funkcji, a z drugiej osią OX.
Własności
31.obliczanie całek oznaczonych - twierdzenie newtona - leibnitza
Pozwala na obliczanie całek oznaczonych.
![]()
Jeśli F(x) jest dowolną f. pierwotną funkcji f(x) to całka oznaczona f(x) w przedziale <a,b> jest równa różnicy wartości f. pierwotnej w p. b i wart. f. pierwotnej w p. a: F (b) - F (a)
32. Całki niewłaściwe
Całką niewłaściwą rodzaju I nazywamy całkę oznaczoną w której jedna bądź dwie granice całkowania są niewłaściwe czyli równe +∞ lub -∞
![]()
Ta całka niewłaściwa jest zbieżna jeżeli ta granica istnieje i jest skończona. W pozostałych przypadkach ta całka jest rozbieżna.
Całki niewłaściwe rodzaju II - wartość funkcji może dążyć do ∞ .Jeśli w granicach całkowania (a,b) całka nie jest ograniczona, to całkę nazywamy całką niewłaściwą rodzaju II.
![]()
33.Funkcja dwóch zmiennych
Def: Zbiór wszystkich uporządkowanych par (a,b) : [(a,b)=(b,a)] ⇔ [a=b], których poprzednik należy do zbioru A, zaś następnik do zbioru B, nazywamy iloczynem kartezjańskim zbiorów A, B i oznaczamy AxB:
AxB:={(a,b) : a∈A i b∈B}
Iloczyn kartezjański nie jest przemienny : AxB ≠ BxA
Def: Zbiór punktów nazywamy zbiorem płaskim, jeżeli wszystkie jego punkty leżą na płaszczyźnie
Def: Funkcję f której dziedziną D f jest zbiór płaski a przeciwdziedziną R f podzbiór liczb rzeczywistych nazywamy funkcją dwóch zmiennych.
F : Df ⊆ R2→ Rf⊆ R
z = f (x, y), (x, y) ∈D f gdzie z - zmienna zależna, x, y - zmienne niezależne
Def: Obszarem geometrycznym lub wykresem funkcji z = f (x, y) określonym w zbiorze D f , nazywamy zbiór wszystkich punktów o współrzędnych (x, y, z), gdzie x, y, z są współrzędnymi punktów zbioru D f , a z = f (x, y).
34. granica funkcji dwóch zmiennych
Def: Definicja Heinego Jeżeli każdej liczbie naturalnej n został w sposób jednoznaczny przyporządkowany punkt (xn , yn) ∈D ⊂ R, to mówimy, że w zbiorze D został określony ciąg punktów {(xn , yn)}.
Def: Liczbę g nazywamy granicą funkcji f (x, y) w punkcie (x0 , y0) i piszemy:
lim f (x, y) = g lub lim f (x, y) = g
(x,y)→( x0 , y0) x→ x0 y→, y0
wtedy i tylko wtedy, gdy dla każdego ciągu punktów {( xn , yn)} o wyrazach należących do U(x0 , y0) i różnych od (x0 , y0) odpowiedni ciąg wartości funkcji {f(xn , yn)} dąży do liczby g.
Podobnie jest w przypadku granic niewłaściwych +∞ lub -∞:
Def: Jeżeli dla każdego ciągu {(xn , yn)} punktów spełniających warunki podane w def. Heinego granicy właściwej, odpowiadający mu ciąg wartości funkcji {f(xn , yn)} jest rozbieżny do +∞ (-∞), to mówimy, że rozważana funkcja ma w p. (x0 , y0) granicę niewłaściwą +∞ (-∞) i piszemy:
lim f (x, y) = +∞ (-∞)
(x,y)→( x0 , y0)
Def: Funkcję f (x, y) nazywamy ciągłą w punkcie (x0 , y0) jeżeli ma w tym punkcie granicą równą swojej wartości, tzn. jeśli : lim f (x, y) = f (x0, y0)
(x,y)→( x0 , y0)
35. pochodne cząstkowe funkcji dwóch zmiennych
Def: Jeżeli istnieje granica właściwa :
lim f(x0+Δx, y0) - f(x0 , y0)
Δx→0 Δx
to granicą nazywamy pochodną cząstkową rzędu pierwszego funkcji f(x, y) względem zmiennej x w p. (x0 , y0) i oznaczamy jednym z symboli:
f'x (x0 , y0) lub ∂f (x0 , y0)
∂x
Def: Jeżeli istnieje granica właściwa:
lim f(x0, y0+Δy) - f(x0 , y0)
Δy→0 Δy
to granicę tę nazywamy pochodną cząstkową rzędu pierwszego funkcji f(x, y) względem zmiennej y w p. (x0 , y0) i oznaczamy jednym z symboli:
f'y (x0 , y0) lub ∂f (x0 , y0)
∂y
Def: Pochodne cząstkowe pochodnych cząstkowych rzędu pierwszego funkcji f(x, y) nazywamy pochodnymi cząstkowymi rzędu drugiego tej funkcji:
36. Macierze operacje elementarne.
Operacją elementarną na macierzy nazywamy każde z następujących przekształceń:
-przestawienie (zamiana miejscami) dwóch dowolnych wierszy (kolumn)
-dodanie do wszystkich elementów dowolnego wiersza (kolumny) odpowiednich elementów innego wiersza (kolumny), pomnożonych przez dowolną liczbę
-pomnożenie wszystkich elementów dowolnego wiersza (kolumny) przez dowolną liczbę różną od zera
37. Rozwinięcie Laplace'a
Wartość wyznacznika macierzy kwadratowej A jest równa sumie iloczynów elementów pewnego wiersza pomnożonych przez dopełnienia algebraiczne tego wiersza czyli:
![]()
Gdzie i oznacza numer dowolnie wybranego wiesza. Rozwinięć dokonujemy względem linii zawierających jak najwięcej elementów zerowych.
38. Układ równań liniowych. Układ jednorodny i niejednorodny, zapis macierzowy układu. Macierz rozsz.
Układem m równań liniowych o n niewiadomych x1, x2…. , nazywamy układem równań o postaci:
Układ jednorodny
Układ równań liniowych nazywamy jednorodnym, gdy wszystkie wyrazy wolne tego układu są równe zero.
Zapis macierzowy
Macierz
nazywa się macierzą współczynników lub macierzą układu
Macierz rozszerzona
![]()
powstaje z macierzy głównej przez dołączenie do niej kolumny wyrazów wolnych
ciąg dalszy pkt. 16 Funkcje cyklometryczne
Ciąg dalszy pkt. 13 Funkcja wykładnicza
Ciąg dalszy pkt. 14 Funkcja logarytmiczna
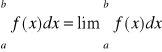
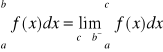
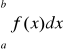
= F (b) - F (a)
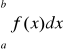
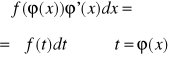
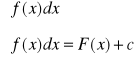
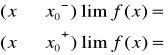
![]()
![]()
![]()
![]()
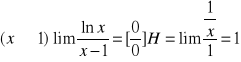
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
ściąga z matmy1 (zadania)
eco sciaga, 33. Keyness - glowne zasady teorii, Prawo popytu - wraz ze wzrostem ceny danego dobra, z
Ściąga 33
SCIAGA 33
SCIAGA 33
(33) Leki stosowane w niedokrwistościach megaloblastycznych oraz aplastycznych
33 Przebieg i regulacja procesu translacji
Image Processing with Matlab 33
1 sciaga ppt
6 Wielki kryzys 29 33 NSL
33 Postepowanie administracyjne
15 Wyposażenie Auta 1 33
od 33 do 46
33 sobota
MSR 33 KOREFERAT Zysk przypadający na jedną akcje
więcej podobnych podstron