Materiał dla studentów

Model statystyczny i jego własności

(studium przypadku)

Nazwa przedmiotu: Statystyka matematyczna I, Statystyka, Ekonometria

Kierunek studiów: MIESI

Studia I stopnia/studia II stopnia

Opracowała: dr Elżbieta Getka-Wilczyńska, Zakład Statystyki Matematycznej, Instytut Eko-

nometrii, KAE

Warszawa, 2010

2

I.

Informacje wstępne

(przedstawiające cele oraz kontekst dydaktyczny analizy przypadku, np. czy chodzi o po-
kazanie jak dokonywane są wybory, uświadomienie, co modeluje zachowanie osób w kon-
kretnych sytuacjach, czy też, jakie są możliwe strategie rozwiązywania problemów stoją-
cych przed osobą, grupa społeczną lub organizacją. Informacje powinny też uwzględniać
doświadczenie studentów, ich wiedzę z zakresu dyscypliny naukowej, z perspektywy, której
studium przypadku jest rozważane.)

Studium przypadku” Model statystyczny i jego własności” jest wprowadzeniem do przedmiotów statystyka, sta-
tystyka matematyczna i zawiera opis oraz zastosowanie podstawowych pojęć takich jak



model statystyczny



losowa próba statystyczna



statystyka i statystyka dostateczna (definicje, kryterium faktoryzacji)

niezbędnych do zrozumienia, konstruowania i wykorzystywania bardziej zaawansowanych metod statystycznych
i ekonometrycznych.

Najogólniej, statystyką nazywamy zbieranie danych liczbowych i wnioskowanie o nich. Wyróżniamy dwa
rodzaje sytuacji, w których zajmujemy się statystyką.

1. Sytuacja, w której nie posiadamy wiedzy a priori o badanym zjawisku (ekonomicznym, społecznym, medycz-
nym, itp.) i na podstawie zebranych danych chcemy dopiero sformułować wstępne teorie o badanym zjawisku.
Tym działem statystyki nazywanym statystyczną analizą danych (statystyką opisową) w studium przypadku nie
zajmujemy się.

2. Sytuacja, gdy posiadamy wiedzę a priori o badanym zjawisku w postaci pewnego modelu probabilistycznego ,
tzn. znamy tylko częściowo rozkład prawdopodobieństwa pewnej obserwowalnej (w pojedynczym doświadcze-
niu losowym lub serii doświadczeń) zmiennej losowej X i na podstawie wyników doświadczenia – obserwacji -
posiadaną wiedzę o rozkładzie uzupełniamy (teoria estymacji) lub weryfikujemy (testowanie hipotez statystycz-
nych). Obie teorie są szczególnymi przypadkami ogólnego problemu podejmowania decyzji w warunkach nie-
pewności, który jest rozwiązywany w ramach statystycznej teorii podejmowania decyzji. Tym właśnie działem
statystyki nazywanym statystyką matematyczną zajmujemy się w studium przypadku.

I – Model statystyczny

Podstawą wnioskowania statystycznego jest zbiór wyników doświadczenia dokonywanego w celu zbadania in-
teresującego nas zjawiska. Mogą to być dane opisujące zarówno cechy ilościowe jak i jakościowe badanego
zjawiska.

W statystyce matematycznej wyniki doświadczenia – obserwacje są interpretowane jako wartości zmiennych lo-
sowych

X

X

X

n

,...,

,

2

1

, których rozkłady prawdopodobieństwa są przynajmniej częściowo nieznane.

Obserwacja jest wartością zmiennej losowej X lub wektora losowego X=





X

X

X

n

,...,

,

2

1

, gdzie

X

X

X

n

,...,

,

2

1

są zmiennymi losowymi określonymi na pewnej przestrzeni probabilistycznej Ω.

Taką zmienną losową (także wektor losowy) nazywa się obserwowalną zmienna losową X, z tym jednak, że
określenie to ma charakter wyłącznie interpretacyjny. Obserwowalna zmienna losowa X jest punktem wyjścia w
konstrukcji modelu statystycznego.

Przestrzeń prób

Zbiór wartości jakie może przyjmować obserwowalna zmienna losowa X oznaczamy przez S i nazywamy prze-
strzenią prób. W studium przypadku przyjmujemy, że S jest zbiorem skończonym lub zbiorem przeliczalnym lub

podzbiorem przestrzeni

R

n

.

3

Rodzina rozkładów prawdopodobieństwa obserwowalnej zmiennej losowej X

Problemy statystyczne charakteryzują się tym, ze rozkład prawdopodobieństwa obserwowalnej zmiennej losowej
X jest przynajmniej częściowo nieznany, a posiadane informacje pozwalają jedynie wyróżnić pewną rodzinę
rozkładów prawdopodobieństwa P określoną na przestrzeni prób S, do której ten rozkład należy. Ponieważ ob-
serwowalna zmienna losowa stanowi element modelu matematycznego badanego zjawiska znajomość jej roz-
kładu prawdopodobieństwa jest w praktyce potrzebna do podejmowania właściwych decyzji.

Niech















:

P

P

będzie rodziną rozkładów prawdopodobieństwa na przestrzeni prób S indeksowaną

pewnym parametrem



przebiegającym zbiór



.

Dokładniej, P jest rodziną rozkładów prawdopodobieństwa na odpowiednim



-ciele zdarzeń losowych w zbio-

rze wartości S obserwowalnej zmiennej losowej X, ale wobec przyjętych ograniczeń o zbiorze S będzie to



-

ciało wszystkich podzbiorów S, albo



-ciało podzbiorów borelowskich i w dalszej części nie będziemy tego

specjalnie podkreślać.

W studium przypadku definiujemy wyłącznie parametryczną rodzinę rozkładów prawdopodobieństwa oraz pa-
rametryczny model statystyczny.

Definicja 1. Rodzinę rozkładów prawdopodobieństwa















:

P

P

indeksowaną parametrem



prze-

biegającym zbiór



nazywamy rodziną parametryczną wtedy i tylko wtedy, gdy

R

k





dla pewnego k cał-

kowitego i dodatniego i każdy rozkład

P



jest rozkładem znanym, gdy parametr



jest znany. Zbiór



nazy-

wamy przestrzenią parametrów, a liczbę k jej wymiarem.

Definicja 2. Przestrzeń prób S z rodziną rozkładów prawdopodobieństwa















:

P

P

nazywamy mode-

lem statystycznym (używa się również nazwy przestrzeń statystyczna) i zapisujemy



















:

,

P

P

S

.

Jeżeli rodzina rozkładów prawdopodobieństwa















:

P

P

jest rodziną parametryczną, to mówimy o

parametrycznym modelu statystycznym.

Statystyczna próba losowa

Zakładamy, że obserwujemy w pewnym doświadczeniu zmienne losowe

X

X

X

n

,...,

,

2

1

i przyjmujemy, że

wyniki doświadczenia – obserwacje maja postać skończonego ciągu liczb

x

x

x

n

,...,

,

2

1

i są realizacjami (war-

tościami) zmiennych losowych

X

X

X

n

,...,

,

2

1

tj.

 

 

 







n

n

X

x

X

x

X

x







,...,

,

2

2

1

1

dla







.

Generalnie dopuszczalne są dowolne zależności pomiędzy kolejnymi obserwacjami, ale w studium przypadku
zajmujemy się wyłącznie zmiennymi losowymi niezależnymi. W tym celu wprowadzamy pojęcie próby, nazy-
wanej też prostą próba losową.

Definicja 3. Wektor losowy X=





X

X

X

n

,...,

,

2

1

, gdzie

X

X

X

n

,...,

,

2

1

są niezależnymi zmiennymi loso-

wymi o jednakowym rozkładzie prawdopodobieństwa









,

P

nazywamy n- elementową próbą z rozkładu

P



i stosujemy zapis:

X=





X

X

X

n

,...,

,

2

1

jest próbą z rozkładu

P



Funkcję prawdopodobieństwa albo gęstości próby X oznaczamy przez





x

x

f

n

,...,

1



i na mocy niezależności

zmiennych losowych zachodzi wzór





   

 

x

f

x

f

x

f

x

x

f

n

n

















2

1

1

,...,

4

Przy tych oznaczeniach model statystyczny dla próby X zapisujemy w postaci n - krotnego produktu modelu sta-
tystycznego dla pojedynczej zmiennej losowej z definicji 2:









n

P

P

S











:

,

W każdym problemie praktycznym wybór i budowa modelu statystycznego jest pierwszym etapem analizy do-
świadczenia, którego ten problem dotyczy.

 Dla zdefiniowania modelu statystycznego w rozważanym doświadczeniu wystarczy podać
przestrzeń prób S,

rodzinę rozkładów prawdopodobieństwa















:

P

P

na przestrzeni prób S i

przestrzeń parametrów



.

Przykład 1.
W każdym tygodniu kierowca powoduje 1 wypadek z prawdopodobieństwem równym



.

Niech X będzie zmienną losową przyjmująca wartość 1, gdy kierowca miał wypadek w tygodniu i wartość 0,
gdy go nie miał.
W tym modelu statystycznym mamy do czynienia tylko z jedną obserwacją i zmienna losowa X przyjmuje dwie
wartości, 0 i 1, więc przestrzeń prób

 

1

,

0



S

.

Zmienna losowa X ma rozkład zero- jedynkowy z nieznanym parametrem











)

1

( X

P

,











1

)

0

(X

P

,

 

1

,

0





a gęstość jest postaci

 





x

x

x

f







1

1







,

 

 

1

,

0

,

1

,

0







x

. (1)

Rodziną rozkładów prawdopodobieństwa















:

)

,

1

(

Be

P

jest rodziną rozkładów Bernoulliego indek-

sowana parametrem

 

1

,

0





, a przestrzenią parametrów zbiór

 

1

,

0





.

Model statystyczny ma postać

 

 









,

:

,

1

,

1

,

0











Be

P

 

1

,

0





.

Rozważmy próbę X=





X

X

X

n

,...,

,

2

1

z rozkładu zero-jedynkowego o gęstości danej wzorem 1.

W tym modelu statystycznym przestrzeń prób S jest zbiorem wszystkich n –wyrazowych ciągów zer i jedynek,

więc

 

n

S

1

,

0



.

Łączna gęstość próby X jest postaci





 

























n

i

i

n

i

i

x

n

x

i

n

i

n

x

f

x

x

f

1

1

1

,...,

1

1









,

 

 

1

,

0

,

,...,

2

,

1

,

1

,

0









n

i

x

i

Model statystyczny dla n obserwacji jest dany wzorem

 

 









n

Be

P











:

,

1

,

1

,

0

, gdzie

 

1

,

0





.

Przykład 2.
Poborowy na strzelnicy oddaje 10 strzałów z prawdopodobieństwem trafienia równym



.

Model statystyczny dla liczby celnych trafień konstruujemy w następujący sposób.
Niech X będzie zmienną losową, której wartość jest równa liczbie celnych trafień.
Ponownie mamy czynienia tylko z jedną obserwacją, a zmienna losowa X przyjmuje wartości ze zbioru





10

,...

2

,

1

,

0



S

.

Zmienna losowa X ma rozkład dwumianowy z nieznanym parametrem







k

k

k

k

X

P





















10

1

10

)

(







,

 

1

,

0





,





10

,...

2

,

1

,

0



k

(2)

Przestrzenia prób jest zbiór





10

,...

2

,

1

,

0



S

.

Rodziną rozkładów prawdopodobieństwa















:

)

,

(n

Be

P

jest rodzina rozkładów dwumianowych

 



,

n

Be

indeksowana parametrem

 

1

,

0





, a przestrzenią parametrów zbiór

 

1

,

0





.

5

Przykład 3.
Liczba wypadków drogowych w ciągu tygodnia jest zmienną losową X o rozkładzie Poissona

!

)

(

k

e

k

X

P

x













,

.

2

,

1

,

0



k

..

Niech

X

X

X

n

,...,

,

2

1

oznaczają wypadki zdarzające się niezależnie w kolejnych tygodniach. Jeżeli sytuacja

jest stabilna (pogoda jest podobna i nie zaczyna się właśnie okres wakacyjny), to można przyjąć, że każda ze
zmiennych

X

X

X

n

,...,

,

2

1

ma taki sam rozkład jak zmienna losowa X.

W ten sposób otrzymujemy próbę losową X=





X

X

X

n

,...,

,

2

1

z rozkładu Poissona o funkcji prawdopodobień-

stwa





!

!...

!

2

2

1

1

2

1

1

,....,

,

x

x

x

n

n

n

n

n

i

xi

e

x

X

x

X

x

X

P





















.

Przestrzenią prób jest zbiór





n

S

,...

2

,

1

,

0



, rodziną rozkładów prawdopodobieństwa jest rodzina rozkładów

Poissona

 





0

:









Poiss

P

indeksowana parametrem







, a przestrzenią parametrów zbiór

 







,

0

.

Przykład 4. Ogólnie, przedmiotem badania jest zbiór składający się z N elementów i zawierający pewną liczbę
M elementów wyróżnionych. Interesuje nas przypadek, gdy N jest ustalone i znane, a M nie jest znane i chcemy
się dowiedzieć jaka jest wartość M.

Sondaż opinii publicznej.

Interesuje nas, jaki procent wyborców popiera partię A.
Zakładamy, ze spośród N wszystkich wyborców M popiera partię A, a N-M wyborców nie popiera partii. M i M
jest wielkością nieznaną.
Jeżeli liczba N wszystkich wyborców jest tak duża, że zbadanie każdego ze względu na preferencje partyjne i
ustalenie liczby M wyborców popierających partię A jest niemożliwe lub nieopłacalne postępuje się w następu-
jący sposób.
Spośród N elementowego zbioru wszystkich wyborców losujemy n- elementowy podzbiór i każdemu wyborcy z
tego podzbioru zadajemy pytanie „Czy popierasz partię A ?”
Przez X oznaczamy liczbę wyborców popierających partię A w wylosowanym n- elementowym podzbiorze. Je-
żeli losowanie jest wykonane w taki sposób, że każdy n –elementowy podzbiór może być wylosowany z jedna-

kowym prawdopodobieństwem













n

N

1

, to prawdopodobieństwo, że w wylosowanym podzbiorze znajdzie się x

wyborców popierających partię A jest równe

















































n

N

x

n

M

N

x

M

x

X

P

,









M

n

M

N

n

x

,

min

,...,

)

(

,

0

max







,

Zmienna losowa X ma rozkład hipergeometryczny z parametrem M.
W tym modelu statystycznym ustalonymi i znanymi wielkościami jest liczba N wszystkich wyborców i liczeb-
ność n losowanej próbki. Nieznanym parametrem jest





N

M

,...,

1

,

0



.

Przestrzenią prób jest zbiór





n

S

,...,

2

,

1

,

0



.

Rodziną rozkładów prawdopodobieństwa na przestrzeni prób jest rodzina rozkładów hipergeometrycznych in-
deksowana parametrem M,













N

n

N

N

M

n

M

N

H

P

,...,

2

,

1

,

,

,...,

1

,

0

:

)

,

,

(











.

O wyniku obserwacji, tzn. o zmiennej losowej X wiemy, ze ma pewien rozkład z tej rodziny, ale nie wiemy który
z nich.

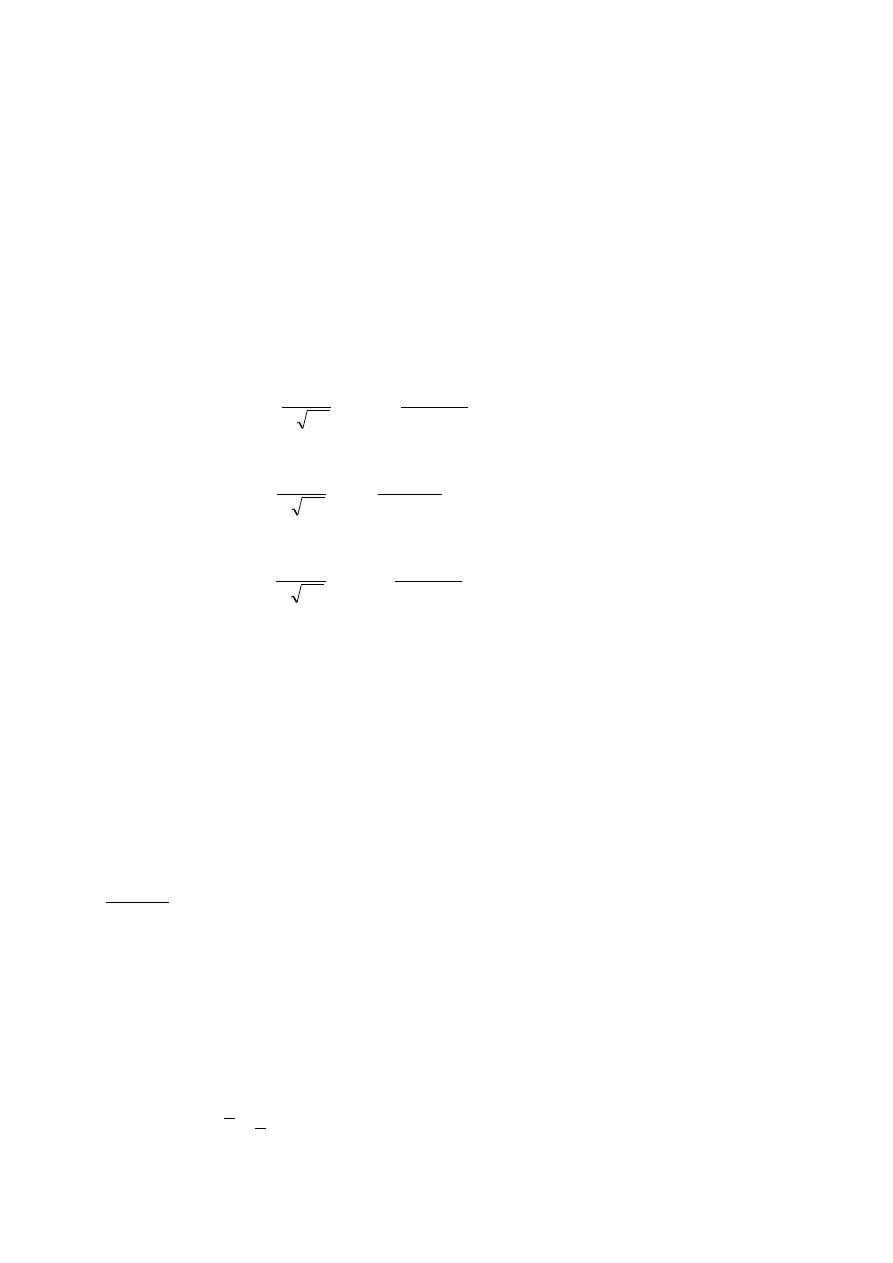
6

Przykład 5.
Dokonujemy pomiaru pewnej nieznanej wielkości



(np. długości, masy, wydajności procesu technologiczne-

go). Pomiar zwykle jest obarczony pewnym błędem- oznaczamy ten błąd przez



tak, że wynikiem pomiaru jest









X

.

Na

podstawie

wyniku

pomiaru

X

lub na podstawie serii takich pomiarów

n

i

X

i

i

,...,

2

,

1

,











należy udzielić informacji o nieznanej wielkości



.

Jeżeli przyjmujemy, ze błąd



jest wielkością losową, to mamy do czynienia ze statystyką matematyczną. Róż-

ne i coraz bardziej szczegółowe założenia o probabilistycznej naturze zmiennej losowej



prowadzą do różnych

i coraz węższych, statystycznych modeli pomiaru. Zwykle zakłada się, ze



jest zmienną losową, której rozkład

nie zależy od



.

Jeżeli wykonuje się serię pomiarów

n

X

X

X

...

,

2

1

, to najczęściej zakłada się, że

n







...

,

2

1

są niezależnymi

zmiennymi losowymi o jednakowym rozkładzie, np. normalnym

 

2

,

0



N

o wariancji

2



.

Wtedy gęstość łącznego rozkładu pomiarów

n

X

X

X

...

,

2

1

jest dana wzorem



































n

i

i

n

x

x

x

f

1

2

2

,...,

1

,

2

exp

2

1













.

W tym przykładzie model statystyczny dla pojedynczej obserwacji ma postać

 





n

i

R

x

x

f

R

























































0

,

:

2

exp

2

1

,

2

2

,

















,

a dla n obserwacji





































































0

,

:

2

exp

2

1

,

1

2

2

,...,

1

,

















R

x

x

x

f

R

n

i

i

n

n

,

gdzie przestrzenią prób jest zbiór

R

S



w przypadku pojedynczej obserwacji i zbiór

n

R

S



w przypadku n

obserwacji, rodziną rozkładów prawdopodobieństwa jest dwuparametryczna rodzina rozkładów normalnych

 





0

,

:

,

2















R

N

P

,

 













R

R

2

,







.

II – Statystyka i statystyka dostateczna

Aby wnioskować na podstawie danych należy zawarte w nich informacje przedstawiać w sposób bardziej zwar-
ty, czyli konstruować funkcje od danych. W tym celu wprowadzone są pojęcia takich funkcji jak statystyka i sta-
tystyka dostateczna. Pojęcie statystyki w statystyce matematycznej jest odpowiednikiem pojęcia zmiennej loso-
wej w rachunku prawdopodobieństwa. W praktyce statystyka służy do wyodrębnienia z danych doświadczalnych
pewnych istotnych charakterystyk tych danych.

Statystyka

Definicja 4. Funkcję próby X=





X

X

X

n

,...,

,

2

1

postaci





X

X

T

T

n

,...,

1



nazywamy statystyką, jeżeli jest

zmienną losową na





P

F

S

,

,

.

Statystyka jest funkcją

n

R

S

T



:

i nie zależy od nieznanego parametru



.

Na przykład, wyrażenie









X

X

T

n

,...,

1

nie jest statystyką, bo zależy od nieznanego parametru



i nie

można tego wyrażenia obliczyć na podstawie danych. Jeżeli jednak wybierzemy dowolną, ale ustaloną wartość

parametru



0

, to wyrażenie





0

1

,...,





X

X

T

n

jest statystyką.

Przykłady statystyk:

a) średnia z próby







n

i

i

X

n

X

1

1

7

b) wariancja z próby definiowana na trzy różne sposoby













n

i

i

X

n

S

1

2

2

1

ˆ



, gdy znana jest wartość oczekiwana





EX













n

i

i

X

X

n

S

1

2

2

1

lub















n

i

i

X

X

n

S

1

2

2

1

1

~

, gdy





EX

jest nieznane

Wiadomo, że próba X=





X

X

X

n

,...,

,

2

1

dostarcza pewnych informacji o nieznanym rozkładzie obserwowal-

nej zmiennej losowej. Ale okazuje się, że dla niektórych rodzin rozkładów















:

P

P

nie jest konieczna

znajomość informacji o nieznanym parametrze rozkładu z całej próby, lecz możliwa jest redukcja danych: cala
informacja o nieznanym rozkładzie jest zawarta w pewnej funkcji próby nazywanej statystyką dostateczną.
Pojęcie statystyki dostatecznej zostało wprowadzone przez R. A. Fishera i jest bardzo ważne w statystyce mate-
matycznej, gdyż statystyka dostateczna umożliwia redukcję danych bez straty informacji o nieznanym parame-
trze rozkładu. Cała informacja o nieznanym parametrze rozkładu jest zawarta w statystyce dostatecznej.

Statystyka dostateczna

Definicja 5. Statystykę

n

R

S

T



:

nazywamy dostateczną dla rodziny rozkładów















:

P

P

lub do-

stateczną dla parametru







, jeżeli dla każdej wartości t statystyki T rozkład warunkowy próby

X=





X

X

X

n

,...,

,

2

1

przy ustalonej wartości statystyki T= t nie zależy od parametru









Aby wyznaczyć statystykę dostateczną z definicji dla dowolnej rodziny rozkładów należy: wyznaczyć

łączną gęstość próby X, prawdopodobieństwa





t

T

x,

X







P

,





t

T





P

i sprawdzić, czy













t

T

t

T

x,

X

t

T

x

X



















P

P

P

rozkład warunkowy próby X =x przy ustalonej wartości statystyki T=t

nie zależy od nieznanego parametru







.

Przykład 6.

Niech X=





X

X

X

n

,...,

,

2

1

będzie próbą z rozkładu zero-jedynkowego o gęstości

 





x

x

x

f







1

1







,

 

 

1

,

0

,

1

,

0







x

.

Łączna gęstość próby X jest postaci























n

i

i

n

i

i

x

n

x

n

x

x

f

1

1

1

,...,

1







,

 

 

1

,

0

,

1

,

0







i

x

W tym modelu statystycznym przestrzenią prób jest zbiór wszystkich

n

2

n –wyrazowych ciągów zer i jedynek.

Dla ustalonego zdarzenia – ciągu zer i jedynek - próba X zawiera informację o liczbie sukcesów w n doświad-
czeniach Bernoulliego i numerach doświadczeń, w których te sukcesy nastąpiły.
Ze wzoru na łączną gęstość próby X wynika, że informacja o numerach doświadczeń, w których nastąpił sukces

jest nieistotna, gdyż tylko liczba sukcesów w n doświadczeniach równa





n

i

i

x

1

jest podstawą do wnioskowania o

wartości parametru



. Wiadomo również, że jeżeli

k

x

n

i

i







1

, to każdy z













k

n

możliwych układów k jedynek

w próbie ma to samo prawdopodobieństwa wystąpienia, niezależnie od wartości parametru



.

Definiujemy statystykę

 







n

i

i

X

T

1

X

.

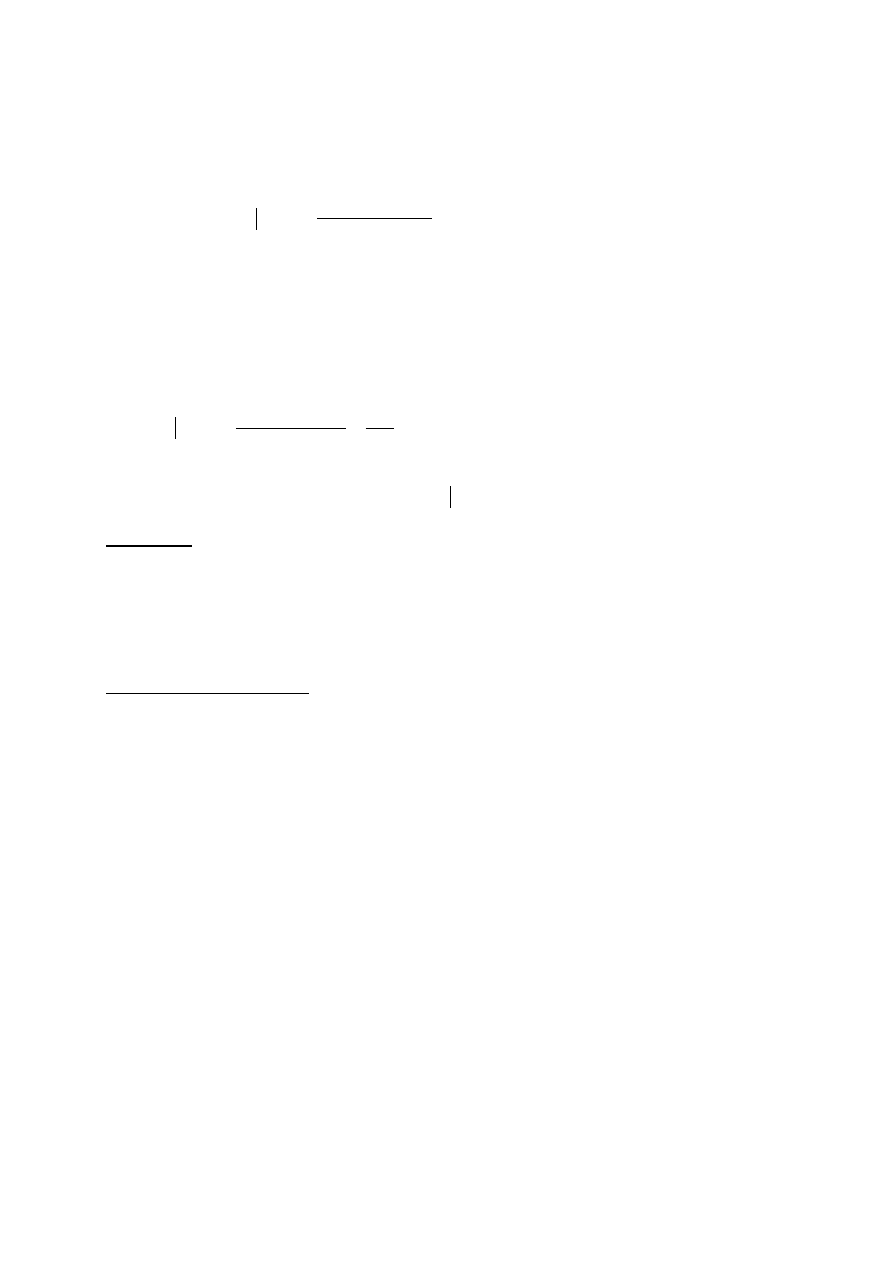
8

Jest to liczba sukcesów w n doświadczeniach Bernoulliego. Rozkład tej statystyki jest rozkładem dwumianowym
o gęstości





t

n

t

t

n

t

T

P



























1

)

(

,

 

1

,

0





,

n

t

,...,

1

,

0



Wyznaczamy













t

T

t

T

x,

X

t

T

x

X



















P

P

P

.

Prawdopodobieństwo w liczniku jest równe zeru z wyjątkiem przypadku, gdy

t

x

n

i

i







1

i każde

x

i

jest równe

zeru lub jedynce.
Wtedy





t

T

x,

X







P

=





x

X





P

=









t

n

t

x

n

x

n

i

i

n

i

i



























1

1

1

1

Stąd





















































t

n

t

n

P

t

n

t

t

n

t

1

1

1

t

T

x

X











.

Z tego wzoru wynika, że rozkład warunkowy





t

T

x

X







P

nie zależy od parametru



.

Interpretacja: gdy wiemy, że T= t, to informacja o tym, który z













t

n

punktów przestrzeni prób faktycznie się

zrealizował nie wnosi żadnej wiedzy parametrze



. To uzasadnia nazywanie statystyki T dostateczną.



Znalezienie statystyki dostatecznej bezpośrednio z definicji jest niekiedy trudne. Prosty sposób

rozpoznawania, czy dana statystyka jest dostateczna i konstruowania statystyk dostatecznych podaje poniższe
twierdzenie.

Kryterium faktoryzacji Neymana

Statystyka

n

R

S

T



:

jest dostateczna dla parametru







wtedy i tylko wtedy, gdy gęstość łącznego roz-

kładu prawdopodobieństwa próby X=





X

X

X

n

,...,

,

2

1

można przedstawić w postaci











 



x

x

h

x

x

T

g

x

x

f

n

n

n

,...,

,...,

,...,

1

1

1









,

gdzie





x

x

h

n

,...,

1

jest funkcją, która nie zależy od parametru







,









x

x

T

g

n

,...,

1



jest funkcją, która zależy od argumentu





T

n

x

,...,

x

x

1



poprzez wartość statystyki T

i jako funkcja zależy od parametru







.



Aby wyznaczyć statystykę dostateczną z kryterium o faktoryzacji dla dowolnej rodziny rozkładów

należy: wyznaczyć łączną gęstość próby X i sprawdzić, czy tę gęstość można przedstawić jako iloczyn dwóch

funkcji











 



x

x

h

x

x

T

g

x

x

f

n

n

n

,...,

,...,

,...,

1

1

1









spełniających warunki z twierdzenia.

Przykład 7.

Niech X=





X

X

X

n

,...,

,

2

1

będzie próbą z rozkładu zero-jedynkowego o gęstości

 





x

x

x

f







1

1







,

 

 

1

,

0

,

1

,

0







x

.

Łączna gęstość próby X jest postaci

9























n

i

i

n

i

i

x

n

x

n

x

x

f

1

1

1

,...,

1







,

 

 

1

,

0

,

1

,

0







i

x

Przyjmujemy





1

,...,

1



x

x

h

n

,













t

n

t

n

x

x

T

g













1

,...,

1

oraz

 







n

i

i

X

T

1

X

.

Wtedy na mocy kryterium statystyka T jest statystyką dostateczną dla parametru



w rozkładzie zero-

jedynkowym.



Z kryterium o faktoryzacji otrzymujemy następujący wniosek.

Wniosek 1. Statystyka

n

R

S

T



:

jest dostateczna dla parametru







wtedy i tylko wtedy, gdy dla do-

wolnych dwóch różnych wartości parametru





'

,





i



'





iloraz









x

x

f

x

x

f

n

n

,...,

,...,

1

'

1





jest funkcją statystyki

 

x

T

(zależy od x tylko poprzez

 

x

T

).



Aby wyznaczyć statystykę dostateczną z wniosku 1 dla dowolnej rodziny rozkładów należy: wyznaczyć

łączną gęstość próby X , obliczyć iloraz łącznych gęstości









x

x

f

x

x

f

n

n

,...,

,...,

1

'

1





dla

'







i sprawdzić czy zale-

ży od x tylko poprzez

 

x

T

.

Przykład 8.

Niech X=





X

X

X

n

,...,

,

2

1

będzie próbą z rozkładu zero-jedynkowego o gęstości

 





x

x

x

f







1

1







,

 

 

1

,

0

,

1

,

0







x

.

Łączna gęstość próby X jest postaci























n

i

i

n

i

i

x

n

x

n

x

x

f

1

1

1

,...,

1







,

 

 

1

,

0

,

1

,

0







i

x

oraz

















































n

i

xi

n

n

i

i

x

n

n

x

x

f

x

x

f

1

1

1

1

'

,...,

1

'

,...,

1













.

Stąd

 







n

i

i

X

T

1

X

jest statystyką dostateczną dla parametru



w rozkładzie zero-jedynkowym.

Najważniejsze statystyki w modelu z rodziną normalnych rozkładów prawdopodobieństwa

Twierdzenie 1. Jeżeli

n

X

X

X

...,

,

,

2

1

jest ciągiem niezależnych zmiennych losowych takich, że

X

k

~





2

,

k

k

m

N



dla k=1, 2, ...,n oraz

n

a

a

a

...,

,

,

2

1

, są pewnymi stałymi, to zmienna losowa

(1)



























n

k

k

k

n

k

k

k

n

k

k

k

a

m

a

N

X

a

Z

1

2

2

1

1

,

~



.

Z twierdzenia 1 można wyciągnąć dwa praktyczne wnioski.

Wniosek 2. Jeżeli





X

N m

~

,



2

, to

(2)





n

σ

m

N

X

2

,

~

,

gdzie







n

i

i

X

n

X

1

1

jest średnią z próby X.

10

Wniosek 3. Jeżeli X i Y są niezależnymi zmiennymi losowymi takimi, że





2

1

1

,

~

σ

m

N

X

oraz





2

2

2

,

~

σ

m

N

Y

, X=





1

...,

,

1

n

X

X

i Y=





2

...,

,

1

n

Y

Y

są próbami odpowiednio n1 oraz n2 elementowymi z

rozkładów zmiennych losowych X i Y, to:

(3)



















2

2

2

1

2

1

2

1

,

~

n

n

m

m

N

Y

X





,

(4)



















2

2

2

1

2

1

2

1

,

~

n

n

m

m

N

Y

X





,

gdzie







1

1

1

1

n

i

i

X

n

X

,







2

1

2

1

n

i

i

Y

n

Y

.

Definicja 6. (Rozkład chi-kwadrat) Niech X

1

, ..., X

k

będą niezależnymi zmiennymi losowymi, przy czym

 

1

,

0

~ N

X

i

dla i=1,...,k. Wtedy zmienna losowa







k

i

i

X

Y

1

2

ma rozkład chi-kwadrat o k stopniach swobo-

dy, co zapisujemy krótko

 

k

χ

Y

2

~

.

Rozkład

 

k

χ

2

jest szczególnym przypadkiem rozkładu gamma, w którym

2

k

p



oraz

2

1



b

. Po pod-

stawieniu tych wielkości do wzorów na wartość oczekiwaną i wariancję zmiennej losowej o rozkładzie gamma
dostajemy

(5)

 





k

k

χ

E



2

oraz

 





.

2

2

2

k

k

χ

D



Twierdzenie 2. (Fishera). Jeżeli





2

,

~



m

N

X

, to statystyki

X

i S są niezależne, a ponadto





n

m

N

X

2

,

~



(6)





nS

n

2

2

2

1





~



.

Twierdzenie odwrotne jest również prawdziwe. Jeżeli statystyki

X

i S są niezależne, to oznacza, że próba zo-

stała wylosowana z rozkładu normalnego.

Ze wzorów 5 i 6 wynika następujący wniosek.

Wniosek 4.

(7)

 

2

2

2

2

2

2

,

1

S

E

σ

n

σ

nS

E

n

σ

nS

E































i stąd

 

2

2

1 σ

n

n

S

E





.

Podobnie

(8)





,

1

2

2

2

2

















n

σ

nS

D

 

2

2

4

2

2

2

2

S

D

σ

n

σ

nS

D















i stąd

 





4

2

2

2

1

2

σ

n

n

S

D





Twierdzenie 3. Jeżeli

k

Y

Y ...,

,

1

są niezależnymi zmiennymi losowymi takimi, że

 

Y

v

i

i

~



2

dla i=1,...,k, to

wtedy

(9)























k

i

i

k

i

i

v

Y

Y

1

2

1

~



.

Twierdzenie odwrotne jest również prawdziwe.

Wniosek 5. Niech zmienne losowe X i Y będą niezależne oraz





2

1

1

,

~

σ

m

N

X





2

2

2

,

~

σ

m

N

Y

.

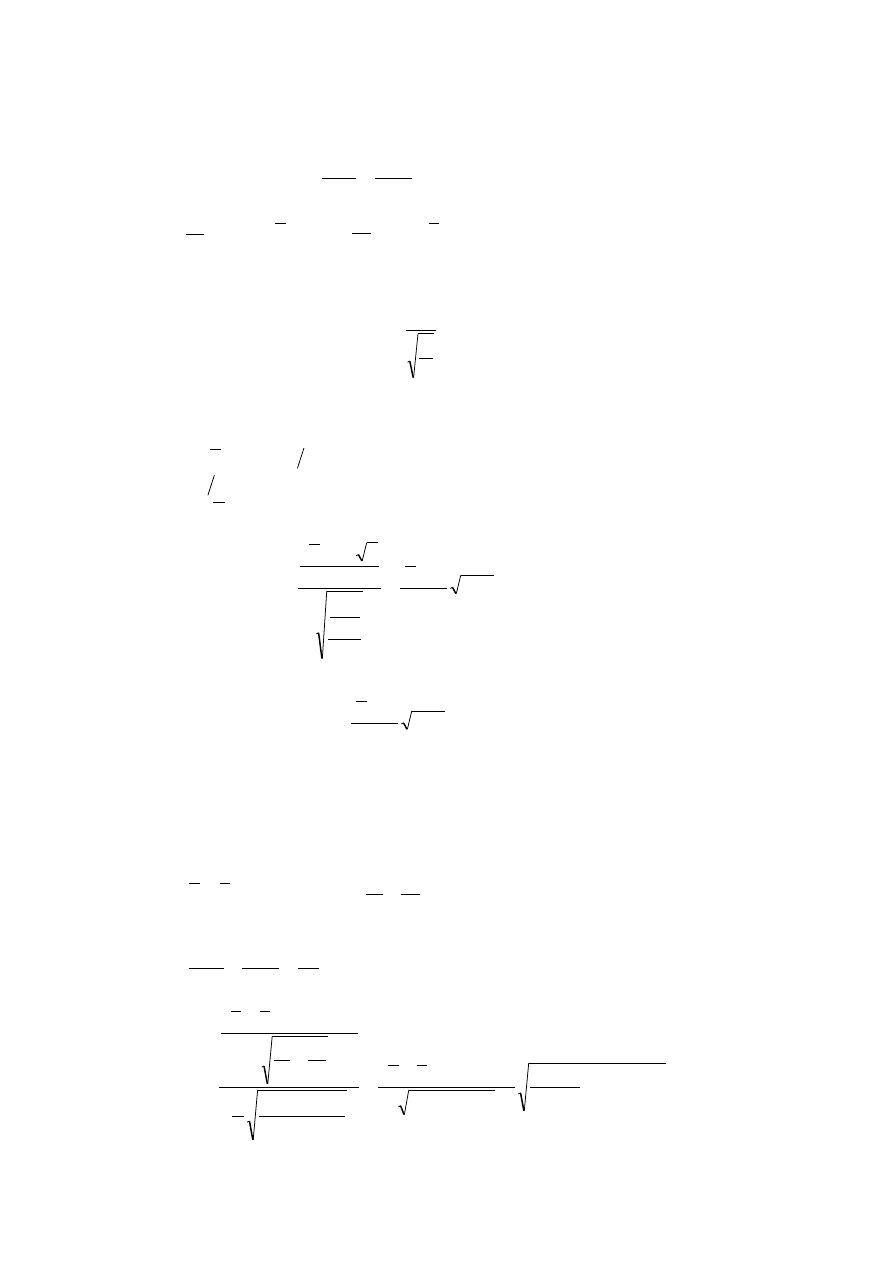
11

Niech X=





1

,...,

1

n

X

X

i Y=





2

,...,

1

n

Y

Y

będą niezależnymi próbami, odpowiednio n

1

oraz n

2

elementowymi.

Wtedy

(10)





2

~

2

1

2

2

2

2

2

2

2

1

2

1

1







n

n

χ

σ

S

n

σ

S

n

,

gdzie













1

1

2

1

2

1

1

n

i

i

X

X

n

S

,













2

1

2

2

2

2

1

n

i

i

Y

Y

n

S

.

Definicja 7. Jeżeli zmienne losowe X i Y są niezależne,

 

1

,

0

~ N

X

i

 

v

Y

2

~



, to zmienna losowa

(11)

v

Y

X

T



ma rozkład t-Studenta o v stopniach swobody (T~t(v)).

Wniosek 6. Jeżeli X=





n

X

X ...,

,

1

jest próbą prostą z rozkładu, w którym





2

,

~

σ

m

N

X

, to





n

σ

m

N

X

2

,

~

(wzór 2),





1

~

2

2

2



n

χ

σ

nS

(wzór 6),

zmienne losowe

X

i S są niezależne (twierdzenie 2) i wtedy

(12)









1

~

1

1

2

2















n

t

n

S

m

X

n

σ

nS

σ

n

m

X

T

.

Statystyka

(13)





1

~

1









n

t

n

S

m

X

T

ma rozkład t-Studenta o n-1 stopniach swobody i nie zależy od nieznanego odchylenia standardowego

.

σ

Fakt ten udowodnił w 1908 r. W.S. Gosset (publikujący pod pseudonimem Student).

Wniosek 7. Jeżeli zmienne losowe X i Y są, przy czym





2

1

,

~

σ

m

N

X

i





2

2

,

~

σ

m

N

Y

, to

(14)































2

1

2

2

1

1

1

,

~

n

n

m

m

N

Y

X



(wzór 4),

(15)









2

~

1

2

1

2

2

2

2

2

1

1

2

2

2

2

2

2

2

1

1











n

n

χ

S

n

S

n

σ

σ

S

n

σ

S

n

(wzór 4)

i stąd

(16)



















 



2

~

2

2

1

1

1

2

1

2

1

2

1

2

1

2

2

2

2

1

1

2

1

2

1

2

2

2

2

1

1

2

1

2

1





































n

n

t

n

n

n

n

n

n

S

n

S

n

m

m

Y

X

n

n

S

n

S

n

σ

n

n

σ

m

m

Y

X

T

.

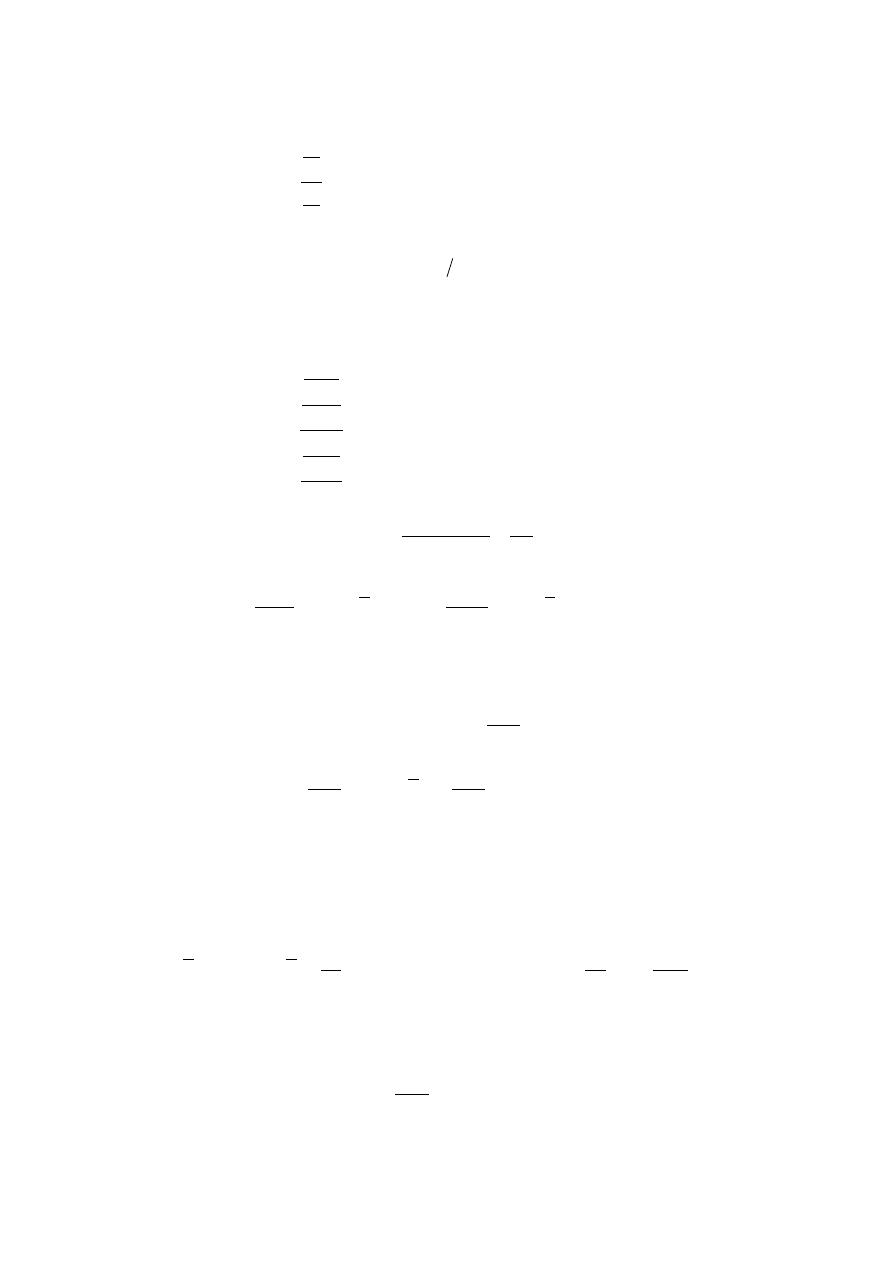
12

Definicja 8. Jeżeli zmienne losowe X i Y są niezależne oraz

 

1

2

~

v

χ

X

i

 

2

2

~

v

χ

Y

, to zmienna losowa

(17)





2

1

2

1

,

~

v

v

F

v

Y

v

X

F



ma rozkład F-Snedecora z v

1

i v

2

stopniami swobody.

Z powyższego wzoru wynika, że zmienna losowa





1

2

,

~

1





F

F

G



Wniosek 8. Jeżeli zmienne losowe X i Y są niezależne oraz





2

1

1

,

~



m

N

X

i





2

2

2

,

~



m

N

Y

, a ponadto

X=





1

...,

,

1

n

X

X

i Y=





2

...,

,

1

n

Y

Y

są próbami z rozkładów zmiennych losowych odpowiednio X i Y, to

(18)





.

1

,

1

~

1

1

2

1

2

2

2

2

2

2

1

2

1

2

1

1











n

n

F

n

σ

S

n

n

σ

S

n

F

W szczególności, gdy

2

2

2

2

1

σ

σ

σ





, to

,

~

~

)

1

(

)

1

(

2

2

2

1

2

2

1

2

2

1

2

1

S

S

S

n

n

S

n

n

F









gdzie

(19)





























2

1

1

2

2

2

2

1

2

1

2

1

1

1

~

,

1

1

~

n

i

i

n

i

i

Y

Y

n

S

X

X

n

S

.

Z wniosku 4 wynika następujący wniosek.

Wniosek 9. Jeżeli X=





n

X

X ...,

,

1

jest próbą z rozkładu, w którym





2

,

~



m

N

X

, to zachodzą równości

(20)

 

 

1

2

~

oraz

~

4

2

2

2

2







n

σ

S

D

σ

S

E

,

gdzie

(21)





2

1

2

2

1

1

1

~

S

n

n

X

X

n

S

n

i

i















.

Twierdzenie 4. Jeżeli X=





T

n

X

X

,

,

1



jest próbą prostą, przy czym zmienna losowa X ma dowolny rozkład o

skończonych momentach do czwartego rzędu włącznie i

(22)

 

 





4

4

2

2

2

oraz

,

μ

m

X

E

σ

μ

X

D

m

X

E











,

to

(23)

 

 

 

 

,

1

3

~

oraz

~

;

;

2

4

2

2

2

2

2

2



























n

n

β

n

σ

S

D

σ

S

E

n

σ

X

D

m

X

E

gdzie

4

4

2

/ σ

μ

β



.

Wniosek 10. Jeżeli





2

,

~



m

N

X

, to

4

4

3σ

μ



i stąd

3

2



β

. Zatem (por. wniosek 9)

(24)

 

1

2

~

4

2

2





n

σ

S

D

.

13

III –ARKUSZ TESTOWY

I. Definicje. Podkreśl właściwą odpowiedź:

A. Modelem statystycznym jest

a) przestrzeń zdarzeń elementarnych



b) rodzina rozkładów

















:

P

c) uporządkowana trójka







,

, F

S

B. Dziedziną funkcji nazywanej statystyką jest: a) przestrzeń zdarzeń elementarnych



b) przestrzeń prób

S

c) rodzina rozkładów

















:

P

C. Która z podanych funkcji nie jest statystyką: a)







n

k

k

X

T

1

1

b)







2

2

X

T

, c)

2

1

1

X

X

T



II. Budowa modelu statystycznego. Uzupełnij tabelę 1 dla 5 wybranych przykładów.

Tabela 1

Numer

przykła-

du

Przestrzeń prób S

Rodzina rozkładów prawdopodobień-

stwa















:

P

P

na przestrzeni

prób S

Przestrzeń

parame-

trów







,...

2

,

1

,

0



S















:

)

(

Ge

P

-rodzina

roz-

kładow geometrycznych

 

1

,

0





n

R

S



 





0

,

:

,

2















R

N

P









R

R

 

n

S

1

,

0

















:

)

,

1

(

Be

P

 

1

,

0









n

S

,...

2

,

1

,

0













m

m

NBe

P

:

)

,

(



-rodzina

rozkładów ujemnych dwumianowych

 

















R

0













M

M

S

,

10

min

,...,

50

10

,

0

max





















M

M

H

P

:

10

,

,

50





50

,...,

0





 





,

0

S















:

)

,

10

(

Gamma

P

 







,

0





n

S

,...

2

,

1

,

0



 





0

:









Poiss

P

 







,

0

 

R

O

S

,

















:

)

,

1

(

Be

P

 

1

,

0





 





,

0

S















:

)

(

E

P

-rodzina rozkła-

dów wykładniczych

 







,

0

14

Przykład 1. Statystyczna kontrola jakości.
Producent chce się dowiedzieć, jaki procent wywarzanych przez niego wyrobów jest wadliwych i bada n –
elementową partię wyrobów.
Niech

X

i

będzie zmienną losową przyjmująca wartość 1, gdy wyrób jest wadliwy i 0, gdy jest prawidłowy.

Zmienna losowa

X

i

ma rozkład zero- jedynkowy z nieznanym parametrem











)

1

( X

P

i

,











1

)

0

( X

P

i

.

Producenta interesuje procent sztuk wadliwych wśród wszystkich wyrobów.
W tej sytuacji obserwacje

X

X

X

n

,...,

,

2

1

badanej n-elementowej partii wyrobów mają postać ciągów zer i je-

dynek (wyrób prawidłowy lub wadliwy), a liczba wadliwych wyrobów jest zmienną losową







n

i

i

X

X

1

o roz-

kładzie Bernoulliego z nieznanym parametrem



,





n

k

k

n

k

X

P

k

n

k

,...,

2

,

1

,

1

)

(





























Na podstawie wyników doświadczenia (obserwacji

X

X

X

n

,...,

,

2

1

) producent chce sformułować pewne

wnioski o nieznanej wartości parametru



.

Przykład 2. Komis samochodowy „Jak nowy” oferuje w chwili obecnej 50 pojazdów, przy czym M spośród po-
chodzi z kradzieży. Policja sprawdza 10 losowo wybranych samochodów. Wielkością obserwowaną jest liczba
samochodów pochodzących z kradzieży wśród 10 sprawdzanych.

Przykład 3. Niech X oznacza liczbę roszczeń pojedynczego klienta w ciągu roku w firmie ubezpieczeniowej.
Zakładamy, ze X jest zmienną losową o rozkładzie Poissona z parametrem



o funkcji prawdopodobieństwa

!

)

Pr(

k

e

k

X

x











,

.

2

,

1

,

0



k

..

Ubezpieczyciel na podstawie historii klienta

n

X

X

X

...

,

2

1

(znane z poprzednich lat liczby roszczeń) chce wy-

znaczyć odpowiednią składkę, której wartość zależy od parametru



.

Przykład 4. Obserwujemy

n

X

X

X

...

,

2

1

- dzienne stopy zwrotu pewnego instrumentu finansowego. Dla ce-

lów modelowania przyjmujemy założenie, że pochodzą one z rozkładu normalnego









2

,

N

. Na podstawie

zaobserwowanych danych chcemy sprawdzić, czy założenie o rozkładzie normalnym można zaakceptować.

Przykład 5. Wykonujemy ciąg niezależnych doświadczeń, z których każde kończy się sukcesem z nieznanym
prawdopodobieństwem



lub porażką z prawdopodobieństwem





1

. Doświadczenia wykonujemy tak długo,

aż uzyskamy m sukcesów. Zakładamy, że wyniki poszczególnych eksperymentów są niezależnymi zmiennymi
losowymi.

Przykład 6. Jacek dysponujący niesymetryczną monetą gra n –krotnie gra z Pawłem. Pojedyncza gra polega na
1- krotnym rzucie monetą, przy czym jeśli wypadnie orzeł, to Jacek otrzymuje 100 PLM od Pawła, a jeśli wy-
padnie reszka, to Paweł otrzymuje 100 PLN od Jacka. Obserwowanymi zmiennymi losowymi są kolejne rzuty
monetą.

Przykład 7. Żółwiowi udaje się szczęśliwie przejść na drugą stronę szosy z prawdopodobieństwem



. W ciągu

swojego życia żółw przekroczy szosę X razy. Zakładamy, ze żółw, o ile nie zginie pod kolami samochodu, żyje
nieskończenie długo.

Przykład 8. W żyrandolu jest 10 żarówek. Czas życia każdej żarówki ma rozkład wykładniczy z nieznanym pa-

rametrem



o gęstości

 

 

x

x

f











exp

dla

0



x

. Skonstruować model statystyczny dla czasu do

przepalenia się pierwszej żarówki.

Przykład 9. Korytarz oświetlony jest przez jedną żarówkę. W zapasie mamy 10 żarówek i po przepaleniu się ak-
tualnie świecącej, wkręcamy kolejną. Czas życia każdej żarówki ma rozkład wykładniczy z nieznanym parame-
trem



. Skonstruować model statystyczny dla czasu do przepalenia się ostatniej żarówki.

15

III. Zastosowanie kryterium o faktoryzacji. Uzupełnij poniższe zdania.

A. Niech X=





X

X

X

n

,...,

,

2

1

będzie próbą z rozkładu normalnego









2

0

,

N

, gdy

R





, wariancja



2

0

jest znana.
Łączna gęstość próby X jest postaci









































































2

0

2

1

2

0

1

2

2

0

,...,

1

2

exp

2

1

exp

2

1

n

x

x

x

x

f

n

i

i

n

i

i

o

n

n

Korzystając z kryterium o faktoryzacji przyjmujemy, że funkcja





x

x

h

n

,...,

1

=

…………………………….

j

est funkcją, która nie zależy od parametru

R





, funkcja









x

x

T

g

n

,...,

1



=

…………………….…

jest funkcją, która zależy od argumentu





T

n

x

,...,

x

x

1



poprzez wartość statystyki T i jako funkcja jest zależ-

na od parametru

R





.

Wtedy statystyka







X

X

T

n

,...,

1

………………………………

jest statystyką dostateczną dla parametru

R





w rozkładzie normalnym









2

0

,

N

ze znaną wariancją



2

0

.

B. Niech X=





X

X

X

n

,...,

,

2

1

będzie próbą z rozkładu normalnego









2

0

,

N

, gdy wartość oczekiwana

o



jest znana, wariancja

0





. Łączna gęstość próby X jest postaci













































n

i

i

n

n

x

x

x

f

1

2

2

,...,

1

2

1

exp

2

1











Korzystając z kryterium o faktoryzacji przyjmujemy, że funkcja





x

x

h

n

,...,

1

=…………………………………..

jest funkcją, która nie zależy od parametru

0





, funkcja









x

x

T

g

n

,...,

1



=……………………………

jest funkcją, która zależy od argumentu





T

n

x

,...,

x

x

1



poprzez wartość statystyki T i jako funkcja jest zależ-

na od parametru

0





.

Wtedy statystyka







X

X

T

n

,...,

1

…………………………….

jest statystyką dostateczną dla parametru

0





w rozkładzie normalnym









2

0

,

N

ze znaną wartość ocze-

kiwana

o



.

C. Niech X=





X

X

X

n

,...,

,

2

1

będzie próbą z rozkładu normalnego

 





2

,

N

, gdy parametr











,



,

R





,

0





jest nieznany. Łączna gęstość próby X jest postaci





















































n

i

i

n

n

x

n

x

x

x

x

f

1

2

2

2

,...,

1

2

1

exp

2

1











Korzystając z kryterium o faktoryzacji przyjmujemy, że funkcja

16





x

x

h

n

,...,

1

=………………………………………….

jest funkcją, która nie zależy od parametru











,



, funkcja





t

t

g

2

1

,



=……………………………………………..,

..........

t

..........

2

1





t

jest funkcją, która zależy od argumentu





T

n

x

,...,

x

x

1



poprzez wartość statystyki T i jako funkcja jest zależ-

na od parametru











,



.

Wtedy statystyka





T

T

T

2

1

,



,

gdzie





........

..........

,...,

1

1



X

X

T

n





......

..........

,...,

1

2



X

X

T

n

jest statystyką dostateczną dla parametru











,



w rozkładzie normalnym









2

0

,

N

z nieznanym para-

metrem











,



.

IV. Rozkłady wybranych statystyk. Uzupełnij Tabelę 2.


Tabela 2

Próba

Rozkład prawdopodo-
bieństwa próby

Statystyka T

Rozkład prawdopodo-
bieństwa statystyki T

X=





X

X

X

n

,...,

,

2

1

 

1

,

0

N

 

X

X

T



X=





X

X

X

n

,...,

,

2

1

 

2

,





N

 

X

X

T



X=





X

X

X

n

,...,

,

2

1

 

1

,



N

 













n

i

i

X

X

X

T

1

2

X=





X

X

X

n

,...,

,

2

1

 

2

,





N

 

n

S

X

X

T







X=





X

X

X

m

,...,

,

2

1

Y=





Y

X

Y

n

,...,

,

2

1





2

,





x

N





2

,





y

N





S

S

Y

X

T

Y

X

2

2

,



X

Y

 

1

,

0

N

 





2







Y

X

Y

X

T



,

X





X

X

X

n

1

,...,

,

2

1

Y=





X

X

X

n

2

,...,

,

2

1





2

,

x

x

N









2

,

y

y

N









Y

X

Y

X

T





,

X

Y

 

1

2





 

2

2









2

1

,





Y

X

Y

X

T



17

V. Wyznaczanie statystyki dostatecznej. Uzupełnij Tabelę 3.

Tabela 3


Rozkład próby
X=





X

X

X

n

,...,

,

2

1





t

T

x

X







P



lub

   

 





x

T

x

x

g

h

f









lub

 

 

 

x

x

'

f

f





dla

'







Statystyka dostateczna T

rozkład Poissona Poiss

 



z parametrem



rozkład wykładniczy E

 



z parametrem



rozkład

dwumianowy

ujemny

 

p

r

NB ,

z parametrem p

rozkład gamma









,

G

z parametrami





,

18

II. Harmonogram/scenariusz realizacji/kolejność działań

1. Indywidualne zapoznanie się z opisem problemów/ zadań zawartych w częściach I-II

materiałów.

2. Praca w grupach nad rozwiązywaniem problemów/zadań z części III materiałów.

3. Dyskusja w grupach, a następnie na forum ogólnym nad odpowiedziami na postawio-

ne pytania.

4. Komentarz prowadzącego.

III. Opis przypadku/sytuacji

(w tym np. opis ról odgrywanych przez studentów; tło

przypadku – film, kroniki; materiały liczbowe: tabele z danymi, arkusze kalkulacyjne;, arku-
sze decyzyjne; oprogramowanie obliczeniowe, wyszukujące lub prezentujące, itd.)

W częściach I- II materiałów są opisane podstawowe pojęcia statystyki matematycznej:



losowa próba statystyczna



model statystyczny (przestrzeń statystyczna)



statystyka i statystyka dostateczna (definicje, kryterium faktoryzacji),

konieczne do rozwiązania problemów/zadań zawartych w części III (arkusze testowe)

Część III materiałów zawiera problemy/ zadania, które należy rozwiązać stosując pojęcia

wprowadzone w częściach I- II.

IV. Wymagane rezultaty pracy i ich forma

Rezultatem Twojej pracy, a następnie w grupach jest



skonstruowanie poprawnego modelu statystycznego dla podanych eksperymentów lo-

sowych



poprawne wyznaczanie statystyk dostatecznych dla rodzin rozkładów prawdopodo-
bieństwa w skonstruowanych modelach statystycznych



poprawne zastosowanie wprowadzonych statystyk w modelu z rodziną normalnych
rozkładów prawdopodobieństwa.