6

Liczba dróg pomi dzy wierzchołkami.

Je eli

M jest macierz grafu G (macierz s siedztwa) to element

]

,

[ j

i

M

tej macierzy

reprezentuje liczb kraw dzi wychodz cych z wierzchołka i do wierzchołka j. Ta
liczba kraw dzi jest zarazem liczb dróg o

długo ci 1 od wierzchołka v

1

do

v

2

.

Przykład

4.

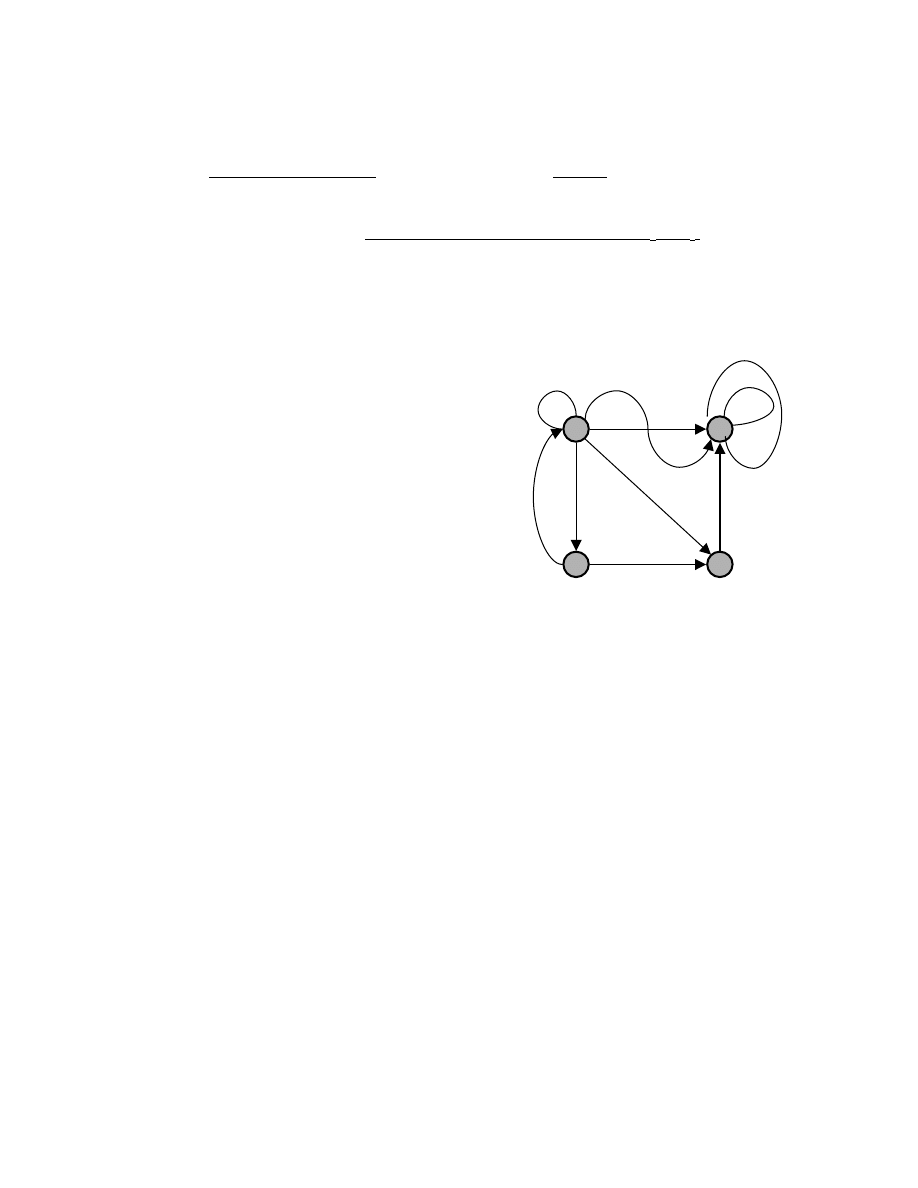
Rozwa my graf z Rysunku

4. Jego macierz

s siedztwa ma posta :

Łatwo zauwa y , e drogami o długo ci 2 z
wierzchołka

v

1

do wierzchołka

v

2

s drogi

ab, ac, bd, be, cd, ce i hj. Jest ich 7. W
podobny sposób mo na wyznaczy liczb
dróg o długo ci n pomi dzy wybranymi
wierzchołkami.
Metoda zliczania „na wprost” jest jednak mudna i łatwo o bł dy, szczególnie gdy
analizujemy grafy o du ej liczbie w złów i kraw dzi.
Zauwa my, e np. ka da droga o długo ci 2 z wierzchołka

v

1

do

v

2

w mi dzyczasie

przechodzi przez wierzchołki

v

1

,

v

2

,

v

3

oraz

v

4

. Tak wi c mo emy policzy drogi z v1

do

v

1

przechodz ce przez

v

1

, przez

v

2

itd. a nast pnie je doda . Je li np. chcemy

policzy drogi maj ce ci g wierzchołków

v

1

v

2

v

1

, zliczamy kraw dzie z

v

1

do

v

1

(p tle) i kraw dzie z

v

1

do

v

2

i otrzymane liczby mno ymy przez siebie:

2

2

1

=

⋅

.

Tymi drogami s

ab i ac. Liczby, które mno ymy, tzn. M[1,1] i M[1,2] s wzi te z

macierzy M. Podobnie jest z drogami maj cymi ci g wierzchołków

v

1

v

2

v

2

. Zliczamy

kraw dzie od

v

1

do

v

2

oraz od

v

2

do

v

2

a nast pnie te liczby mno ymy przez siebie:

4

2

2

]

2

,

2

[

]

2

,

1

[

=

⋅

=

⋅ M

M

. Tymi drogami s : bd, be, cd oraz ce. Liczba wszystkich

dróg od

v

1

do

v

2

o długo ci 2 wynosi:

=

0

0

1

0

1

0

0

1

0

0

2

0

1

1

2

1

M

d

f

g

h

k

j

v

3

v

4

v

1

v

2

a

b

c

e

Rysunek 4

7

.

7

1

0

4

2

]

2

,

4

[

]

4

,

1

[

]

2

,

3

[

]

3

,

1

[

]

2

,

2

[

]

2

,

1

[

]

1

,

1

[

]

1

,

1

[

=

+

+

+

=

⋅

+

⋅

+

⋅

+

⋅

M

M

M

M

M

M

M

M

Liczba, któr otrzymali my jest elementem [1,2] macierzy M

2

. Wyraz

]

,

[

2

j

i

M

jest

liczb dróg od

v

i

do

v

j

o długo ci k

Ogólnie:

=

]

,

[ j

i

M

k

liczba dróg

v

i

do

v

j

o długo ci

k.

Dla grafu z Rysunku 4 mamy:

Czyli, np. jest 3 drogi długo ci 3 od

v

3

do

v

2

.

Znajomo liczby dróg ró nej długo ci dla danego grafu jest wa na gdy analizujemy
relacj osi galno ci w zbiorze V(G) wierzchołków grafu G.

Dwa

wierzchołki v, w s osi galne je li istnieje w G droga od v do w

długo ci co najmniej 1.

Np. dla grafu z Rys. 4 wida , e chocia nie ma kraw dzi od

v

3

do

v

2

,

,

0

]

2

,

3

[

=

M

to

jednak

,

3

]

2

,

3

[

2

=

M

a zatem istniej 3 drogi o długo ci 2 od

v

3

do

v

2

, i wierzchołki te

s w relacji osi galno ci.

,

0

0

2

0

1

1

3

1

0

0

4

0

2

1

7

2

2

=

M

8

Izomorfizm grafów.

Cz sto zdarza si , e dwa grafy s „wła ciwie takie same”, pomimo, e ró ni si
nazwami wierzchołków i kraw dzi. Wa nym jest czy podobie stwo jest tylko
wizualne czy te strukturalnie dwa grafy s identyczne.

Ogólnie dwa zbiory wyposa one w pewne struktury matematyczne nazywamy
izomorficznymi, je li istnieje przekształcenie wzajemnie jednoznaczne pomi dzy
tymi zbiorami zachowuj ce ich struktury.

Izomorfizmem grafu G na graf H nazywamy przekształcenie wzajemnie jednoznaczne

)

(

)

(

:

H

V

G

V

→

α

takie, e

}

,

{ w

u

jest kraw dzi grafu G wtedy i tylko wtedy, gdy

)}

(

),

(

{

w

u

α

α

jest kraw dzi w grafie H. Zapisujemy to jako

.

H

G

≅

Uwaga:

powy sze okre lenie jest poprawne dla grafów bez kraw dzi

wielokrotnych. Je li graf ma jednak kraw dzie wielokrotne to sytuacja si komplikuje
w tym sensie, e wymagana jest jeszcze wzajemna jednoznaczno dodatkowego
przekształcenia

)

(

)

(

:

H

E

G

E

→

β

pomi dzy zbiorami kraw dzi grafów.

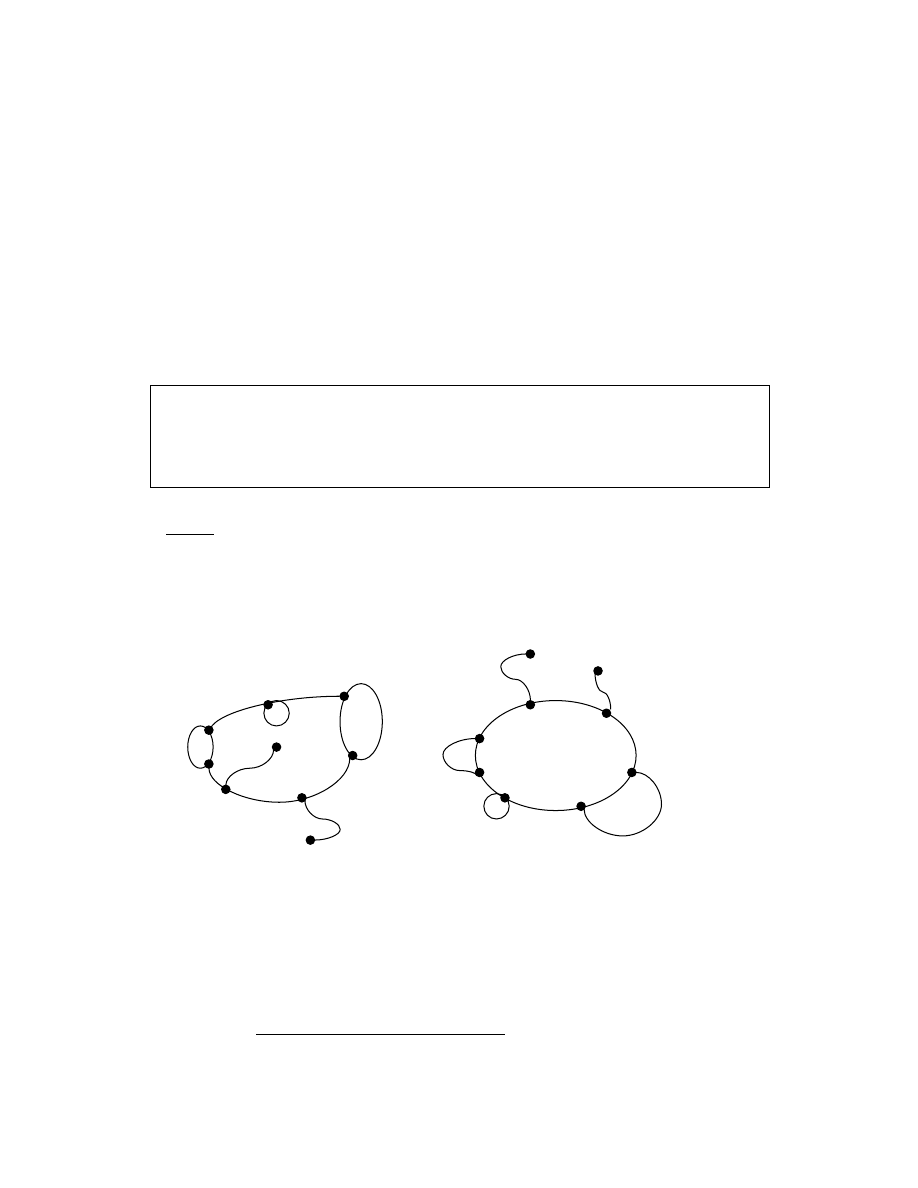
Czy grafy przedstawione na Rys. 5 s izomorficzne?

Istniej pewne cechy grafów, zwane

niezmiennikami izomorfizmu, które pozwalaj

oceni czy dwa grafy s to same w sensie strukturalnym.
Przykładami niezmienników izomorfizmu grafów s liczby: wierzchołków, kraw dzi,
p tli czy liczba dróg prostych o danej długo ci.

Rysunek 5

9

Innym przydatnym niezmiennikiem jest

stopie wierzchołka.

Stopie wierzchołka, oznaczany jako deg(w), jest to liczba dwuwierzchołkowych
kraw dzi z

w jako jednym z wierzchołków, plus podwojona liczba p tli o

wierzchołku

w.

Na przykład wierzchołek w na grafie z
Rysunku 6 ma stopie 4, gdy s dwie
kraw dzie

wychodz ce

z

tego

wierzchołka oraz jedna p tla,

Natomiast wierzchołek v ma stopie 1:

Niech

)

(G

D

k

oznacza liczb wierzchołków stopnia k w grafie G.

)

(G

D

k

jest

niezmiennikiem izomorfizmu.

Niezmiennikiem jest równie ci g liczb

wierzchołków kolejnych stopni

).

),

(

),

(

(

1

0

G

D

G

D

4

1

2

2

)

deg(

=

⋅

+

=

w

.

1

0

2

1

)

deg(

=

⋅

+

=

v

w

v

Rysunek 6