
Rachunek różniczkowy
funkcji jednej zmiennej
Definicja. Zał. że
,
. Ilorazem różnicowym funkcji w punkcie
nazywamy odwzorowanie
określone równaniem
( )
: ,
f
a b
→
: ,
ϕ
(
b
a
x
,
0
∈
( ) { }
0
\ x
→
)
f
0
x
)
a b
( )
( ) (
0
0
x
x
x
f
x
x
−
−
ϕ
f
=
.
( )
( )
( ) ( )
(
) ( )
h
x
f
h
x
x
f
x
x
0
0
0
lim
0
−
+
=
′
→
ϕ
x
0
f
x
h 0
0
lim
=
→
x
x
f
x
f
x
x
lim
0
−
−
=
→
nazywamy pochodną w punkcie
;
f
0
x
( )
( ) ( )
(
) ( )
h
x
f
h
x
f
x
x
x
f
x
f
x
f
h
x
x
0
0
0
0
0
0
lim
lim
0
−
+
=
−
−
=
′
−
−
→
→
−
nazywamy pochodną lewostronną w punkcie
;
0
x
( )
( ) ( )
(
) ( )
h
x
f
h
x
f
x
x
x
f
x
f
x
f
h
x
x
0
0
0
0
0
0
lim
lim
0
−
+
=
−
−
=
′
+
+
→
→
+
nazywamy pochodną prawostronną w punkcie
.
0
x
Mówimy, że funkcja jest różniczkowalna
, gdy
istnieje i jest skończona.
f
0
x
( )
x
f ′
Mówimy, że funkcja jest różniczkowalna na
, gdy
jest różniczkowalna w
.
f
(
b
a,
)
]
)
)
)
( )
b
a
x
,
∈
∀
f
0
x
Mówimy, że funkcja jest różniczkowalna na
[
, gdy jest różniczkowalna w
oraz
pochodne jednostronne w punktach
istnieją i są skończone.
f
,
a b
f
(
b
a
x
,
0
∈
b
a,
Definicja. Zał. że
jest różniczkowalna. Funkcję, która każdemu punktowi
przyporządkowuje
nazywamy pochodną funkcji .
( )
: ,
f
a b
→
( )
x
f ′
( )
b
a
x
,
∈
f
Mówimy, że
jest pochodną, jeśli istnieje
taka, że
.
( )
: ,
f
a b
→
( )
: ,
F a b
→
( )
( )
( )
x
F
x
f
b
a
x
′
=
∀
∈ ,
Twierdzenie. Jeżeli funkcja
jest różniczkowalna w
, to jest ciągła w
.
( )
: ,
f
a b
→
(
b
a
x
,
0
∈
f
0
x
Twierdzenie. Jeżeli
są różniczkowalne w
. Wtedy:
( )
, : ,
f g a b
→
(
b
a
x
,
0
∈
(1) h
jest funkcją różniczkowalną w
i
;
g
f
+
=
0
x
( )
( )
( )
0
0
0
x
g
x
f
x
h
′
+
′
=
′
(2) h
jest funkcją różniczkowalną w
i
;
g
f
−
=
0
x
( )
( )
( )
0
0
0
x
g
x
f
x
h
′
−
′
=
′
(3) h
jest funkcją różniczkowalną w
i
;
g
f
⋅
=
0
x
( )
( ) ( ) ( ) ( )
0
0
0
0
0
x
g
x
f
x
g
x
f
x
h
′
⋅
+
⋅
′
=
′
(4)
g
f
=
h
i
jest funkcją różniczkowalną w
i
( )
0
0
≠
x
g
0
x
( )
( ) ( ) ( ) ( )
( )
(
)
2
0
0
0
0
0
0
x
g
x
g
x
f
x
g
x
f
x
h
′
⋅
−
⋅
′
=
′
.
Twierdzenie. Funkcja
jest różniczkowalna w
i
istnieje
taka, że
i jest ciągła w oraz
.
( )
: ,
f
a b
→
x
0
x
(
f x
( )
c
x
f
=
′
(
)
0
0
c x x
+
−
⇔
ϕ
( )
: ,
a b
ϕ
→
)
0
x
−
( )
0
0
=
x
ϕ
ϕ
0
( )
( )
)
( )(
,
x a b
f x
x x
∈
∀
=
+
Twierdzenie. Zał. że
,
,
,
, jest
różniczkowalna w
, a w
. Wtedy
jest różniczkowalna w
oraz
.
( )
: ,
f
a b
→
g
(
0
f x
( )
(
)
0
f x
′
( )
b
a
x
,
0
∈
)
h
=
( ) (
d
c
b
a
f
,
,
⊂
f
g
)
( )
: ,
g c d
→
0
x
f
0
x
( )
( )
0
0
h x
f x
g
′
′
=
⋅
Twierdzenie. Zał. że
jest różnowartościowa, ciągła i różniczkowalna w
,
. Wtedy
jest różniczkowalna w
oraz
.
( )
: ,
f
a b
→
1
−
( )
b
a
x
,
0
∈
( )
0
0
≠
x
f
f
(
0
0
x
f
y
=
)
( )
(
)
( )
(
)
1
0
0
1
−
−
′
=
′
x
f
y
f
1
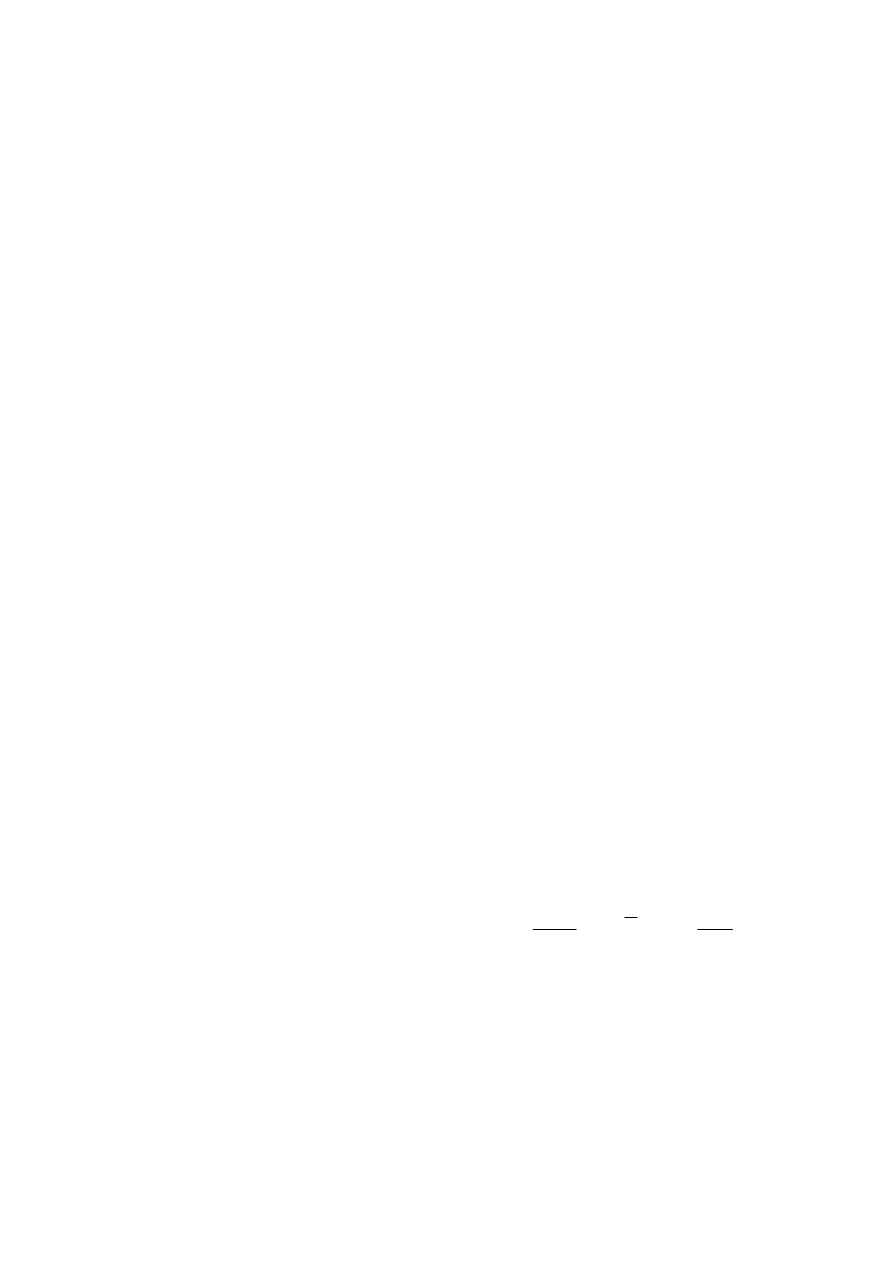
Definicja. Zał. że
. Wtedy:
0
:
,
f A
x
A
→
∈
(1) funkcja posiada maksimum lokalne w
, gdy
;
f
0
x
(
)
( )
( )
0
,
0
0
0
x
f
x
f
x
x
A
x
≤
∀
∃
+
−
∩
∈
>
δ
δ
δ
(2) funkcja ma ścisłe maksimum lokalne w
, gdy
;
f
0
x
(
) { }
( )
( )
0
\
,
0
0
0
0
x
f
x
f
x
x
x
A
x
<
∀
∃
+
−
∩
∈
>
δ
δ
δ
(3) funkcja posiada minimum lokalne w
, gdy
;
f
0
x
(
)
( )
( )
0
,
0
0
0
x
f
x
f
x
x
A
x
≥
∀
∃
+
−
∩
∈
>
δ
δ
δ
(4) funkcja ma ścisłe maksimum lokalne w
, gdy
.
f
0
x
(
) { }
( )
( )
0
\
,
0
0
0
0
x
f
x
f
x
x
x
A
x
>
∀
∃
+
−
∩
∈
>
δ
δ
δ
Twierdzenie. Zał. że
jest różniczkowalna na
. Wtedy, jeżeli przyjmuje
ekstremum lokalne w
, to
.
[ ]
: ,
f
a b
→
( )
b
a
x
,
0
∈
(
b
a,
)
)
)
)
)
)
)
)
f
( )
0
0
=
′ x
f
Twierdzenie Rolle’a. Zał. że
jest ciągła i różniczkowalna na
oraz
.
Wtedy
.
[ ]
: ,
f
a b
→
(
b
a,
( )
( )
b
f
a
f
=
( )
( )
0
0
,
0
=
′
∃
∈
x
f
b
a
x
Twierdzenie Lagrange’a. Zał. że
jest ciągła i różniczkowalna na
(
. Wtedy
.
[ ]
: ,
f
a b
→
b
a,
( )
( )(
)
( ) ( )
a
f
b
f
a
b
c
f
b
a
c
−
=
−
′
∃
∈ ,
Twierdzenie Cauchy’ego. Zał. że
są ciągłe i różniczkowalne na
. Wtedy
.
[ ]
, : ,
f g a b
→
) ( )
(
) ( )
c
f
a
′
(
b
a,
( )
( ) ( )
(
) ( )
(
g
b
g
c
g
a
f
b
f
b
a
c
−
=
′
−
∃
∈ ,
Twierdzenie. Zał. że
jest ciągła i różniczkowalna na
. Wtedy:
[ ]
: ,
f
a b
→
(
b
a,
(1) jest niemalejąca na
;
f
( )
( )
( )
0
,
.
≥
′
∀
⇔
∈
c
f
b
a
b
a
c
(2) jest rosnąca na
, gdy
;
f
(
,
a b
( )
( )
.
0
c a b
f c
∈
′
∀
>
(3) jest nierosnąca na
;
f
( )
( )
( )
0
,
.
≤
′
∀
⇔
∈
c
f
b
a
b
a
c
(4) jest malejąca na
, gdy
.
f
(
,
a b
( )
( )
.
0
c a b
f c
∈
′
∀
<
Twierdzenie. Jeżeli
jest różniczkowalna, to
ma własność Darobux, tzn.
.
( )
: ,
f
a b
→
(
)
( )
y
x
f
x
x
=
′
∃
2
1
,
f ′
( )
( ) ( )
(
)
x
x
f
x
f
y
b
a
x
x
∀
∀
∈
′
′
∈
∈
2
1
2
1
,
,
,
Reguła d’Hospitala. Zał. że
,
są różniczkowalne na
oraz
. Jeżeli
li
oraz
+∞
≤
<
≤
∞
−
b
a
( )
li
.
x
symbol
f x
nieozn
→
→
=
( )
, : ,
f g a b
→
( )
a
g x
=
(
b
a,
( )
( )
0
,
≠
′
∀
∈
x
g
b
a
x
m
m
x
a
( )
( )
li
, to
m
x a
→
f x
A
g x
′
= ∈
′
( )
( )
A
a
x
→
lim
x
g
x
f
= .
Twierdzenie. Zał. że
jest ciągiem funkcji różniczkowalnych,
,
oraz
. Jeżeli
jest funkcją ciągłą oraz
(
jest jednostajnie zbieżny do
,
to jest różniczkowalna oraz
.
( )
n
n
f
n
n
f
∈
′
∀
[ ]
: ,
n
f
a b
→
n
n
f
f
′
[ ]
: ,
f
a b
→
[ ]
: ,
g a b
→
f
f
n
→
)
n
n
f ′
lim
→∞
f
[ ]
( )
( )
,
x a b
f x
g x
∈
′
∀
=
(
)
lim
n
n
→∞
′
=
2

Wniosek. Zał. że
jest różniczkowalna
są ciągłe oraz
,
zbiega jednostajnie do u a
, to jest różniczkowalna oraz
[ ]
: ,
n
f
a b
→
[ ]
: ,
n
f
a b
′
→
( )
( )
1
n
n
n
s n
f x
=
=
∑
∑
∞
=
′
1
n
n
f
[ ]
: ,b
→
s
( )
( )
s x
u x
∀
=
,
x a b
∈
′
,
.
( )
∑
∞
=
=
′
1
n
x
( )
′
n
x
f
∑
∞
=
1
n
n
f
Twierdzenie. Szeregi
∑
,
∑
mają ten sam promień zbieżności , oraz
.
∞
=0
n
n
n
x
a
−1
n
n
x
na
∞
=
−
1
1
n
n
n
x
na
r
(
)
∑
∑
∞
=
∞
=
−
∈
=
′
∀
1
0
,
n
n
n
n
r
r
x
x
a
Definicja. Zał. że
jest różniczkowalna w
. Jeżeli
posiada pochodną w
, to
pochodną tę nazywamy pochodną drugiego rzędu w
i oznaczamy
( )
: ,
f
a b
→
( )
0
x
f ′
0
x
0
x
( )
( )
(
)
( )
0
0
0
0
x
x
f
x
f
′
′
′
=
′′
( )
b
a,
( )
f
b
a
x
∀
∈ ,
0
lim
x
x
f
x
f
x
x
−
−
′
=
→
( )
x
′′
. Mówimy, że funkcja jest dwukrotnie różniczkowalna na
, gdy
istnieje i jest skończona.
Zał. że
oraz jest n-krotnie różniczkowalna na
. Jeżeli
istnieje pochodna funkcji
w
, to pochodną tę nazywamy pochodną
rzędu w
, oraz
.
( )
: ,
,
f
a b
n
→
∈
(
n
f
( )
( )
( )
(
)
′
=
0
0
x
f
x
n
)
)
)
f
0
x
( )
(
0
, ,
,
a b x
a b
∈
(
)
1
+
n
)
0
x
(
)
+1
f
n
Definicja. Mówimy, że funkcja
jest klasy
na
(
, jeżeli
jest określona i
ciągła na
( )
.
( )
: ,
f
a b
→
n
C
b
a,
( )
n
f
b
a,
Mówimy, że funkcja
jest klasy
(jest „gładka”) na
(
, gdy
jest klasy
.
( )
: ,
f
a b
→
∞
C
b
a,
n
f
∈
∀
n
C
Twierdzenie Leibniza. Jeżeli
są funkcjami klasy
C
, to
oraz
,
(
)
.
( )
, : ,
f g a b
→
)
( )
( )
n
f g
x
⋅
=
n
( )
x
n
C
g
f
g
f
∈
⋅
+ ,
(
)
( )
( )
( )
( )
( )
(
x
g
x
f
x
g
f
n
n
n
+
=
+
( )
( )
( )
0
n
n
n
i
n
f
x g
i
=
⋅
∑
Twierdzenie Taylora. Zał. że
jest klasy
C
. Wtedy
(
)
:
,
f
α β
→
1
n
+
(
) ( )
( )
( )
(
)
( )( )
( )
( )( )
(
)
( )
(
) (
)
1
1
2
,
,
,
!
1
!
!
1
(
+
+
∈
∈
−
+
+
−
+
−
′
+
=
∃
∀
n
n
n
n
b
a
c
b
a
a
b
n
c
f
a
b
n
a
f
a
b
a
f
a
f
b
f
β
α
!
2
)
′′
+
−
a
f
a
b
+
…
.
Definicja. Ustalmy
. Wtedy
(
β
α,
∈
a
( )
)
(
) ( )
( )
(
)
( )
( ) ( )
( )
(
)
( )
(
) (
)
( )
1
1
,
,
,
( )
!
1 !
n
n
n
n
n
n
x
c a x
P x
R x a
f
a
f
c
f x
x a
x a
x a
n
n
α β
+
+
∈
∈
∀
∃
=
−
+ +
−
+
−
+
…
1!
f a
f a
′
+
.
n
R to n-ta reszta Taylora w postaci Lagrange’a. Wtedy
( )
(
)
0
,
lim
=
−
→
n
n
a
x
a
x
a
x
R
.
3

Jeżeli we wzorze Taylora podstawimy a
to otrzymamy wzór MacLaurina
0
=
( )
( )
( )
( )
( )
( )
0
,
!
2
0
0
0
2
x
R
x
f
x
f
f
x
f
n
+
+
+
′′
+
′
+
=
…
!
x
n
f
n
n
.
Twierdzenie. Jeżeli
oraz
i
, to
(
)
1
, :
,
n
f g
C
α β
+
→ ∈
( )
( )
( )
( )
( )
( )
( )
( )
a
g
a
g
a
f
a
f
n
n
=
=
=
=
=
=
…
…
0
(
)
( )
0
1
≠
+
a
g
n
( )
( )
( )
( )
1
1
n
n
f x
f
a
g x
g
a
+
+
=
lim
x a
→
.
Definicja. Zał. że
.
( )
( )
0
: ,
,
,
f
a b
C
x
a b
∞
→ ∈
∈
( )
( )(
)
( )
( )(
)
…
…
+
−
+
+
−
′
+
n
n
x
x
n
x
f
x
x
x
f
x
f
0
0
0
0
0
!
0
x
nazywamy szeregiem Taylora (dla funkcji względem środka
).
f
Twierdzenie. Jeżeli
, to
(
)
0
lim
,
0
n
n
R x x
→∞
=
( )
( )
( ) (
)
0
0
0
!
i
i
i
f
x
f x
x x
i
∞
=
=
−
∑
.
Definicja. Zał. że
. Mówimy, że jest funkcją analityczną, gdy jest
równa sumie swojego szeregu MacLaurina.
( )
(
: ,
, 0
,
f
a b
C
a b
∞
→ ∈
∈
)
)
f
f
Twierdzenie. Jeżeli
oraz
( )
(
: ,
, 0,
,
f
a b
C
x
a b
∞
→ ∈
∈
( )
( )
( )
0
0,
n
M
t
x n
f
t
M
> ∈
∈
∃ ∀ ∀
≤
, to jest funkcją
analityczną.
f
Twierdzenie. Jeżeli rozwija się w szereg MacLaurina, to istnieje tylko jedno takie rozwinięcie.
f
Twierdzenie. Jeżeli
jest różniczkowalna na
oraz
i
zmienia znak
przechodząc przez
, to posiada ekstremum lokalne w
.
( )
: ,
f
a b
→
0
f
(
b
a,
0
x
)
)
)
)
)
)
)
)
( )
b
a
x
,
0
∈
f ′
x
Definicja. Zał. że
. Mówimy, że ma punkt przegięcia w
, gdy
taka, że:
( )
(
2
0
: ,
,
,
f
a b
C x
a b
→ ∈
∈
f
0
x
0
>
∃
δ
(1) na przedziale
leży nad styczną do wykresu w punkcie
, a na przedziale
(
leży pod ;
(
0
0
, x
x
δ
−
( )(
0
0
x
x
x
−
′
f
)
(
)
f
)
0
x
( )
( )
0
f
x
f
x
g
+
=
δ
+
0
0
, x
x
f
g
(2) albo zachodzi sytuacja odwrotna.
Twierdzenie. Zał. że
oraz
. Wtedy:
( )
(
0
: ,
,
,
n
f
a b
C x
a b
→ ∈
∈
( )
( )
( )
1
0
0
0
n
f x
f
x
−
′
=
=
=
…
(1) jeżeli n
i
, to posiada maksimum lokalne w
;
k
2
=
( )
( )
0
0
<
x
f
n
f
0
x
(2) jeżeli n
i
, to posiada minimum lokalne w
;
k
2
=
( )
( )
0
0
>
x
f
n
f
0
x
(3) jeżeli n
i
dowolna, to posiada punkt przegięcia w
.
1
2
+
= k
(
0
x
f ′
f
0
x
Twierdzenie. Zał. że
. Wtedy:
( )
(
2
: ,
,
,
f
a b
C c
a b
→ ∈
∈
(1) jeżeli
, to krzywa
jest dla pewnego otoczenia punktu
c położona powyżej
stycznej do tej krzywej w punkcie
(a więc skierowana wypukłością w dół);
( )
0
>
′′ c
f
( )
x
f
y
=
(
c
f
c,
( )
(2) jeżeli
, to krzywa
jest dla pewnego otoczenia punktu
c położona poniżej
stycznej do tej krzywej w punkcie
(a więc skierowana wypukłością w górę).
( )
0
<
′′ c
f
( )
x
f
y
=
(
c
f
c,
( )
4
Wyszukiwarka
Podobne podstrony:
Rachunek różniczkowy funkcji jednej zmiennej, SZKOŁA, Matematyka, Matematyka
RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ 62, Geodezja i Kartografia, I rok, Matematyka
5 Rachunek różniczkowy funkcji jednej zmiennej
wykład, RACHUNEK ROZNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ 63, 1)
5 RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ
Rachunek rozniczkowy funkcji jednej zmiennej
5 Rachunek różniczkowy funkcji jednej zmiennej
Rachunek różniczkowy funkcji jednej zmiennej pochodne
2 - Rachunek całkowy funkcji jednej zmiennej. Metody całkowania, Analiza matematyczna
Matematyka III (Ćw) - Lista 05 - Rachunek rózniczkowy funkcji wielu zmiennych, Odpowiedzi
Wykłady z Matematyki, Wykłady - Rachunek Różniczkowy Funkcji Wielu Zmiennych, Dr Adam Ćmiel
Matematyka III (Ćw) - Lista 05 - Rachunek rózniczkowy funkcji wielu zmiennych, Zadania
Matematyka III (Ćw) Lista 05 Rachunek rózniczkowy funkcji wielu zmiennych Odpowiedzi
RACHUNEK CAŁKOWY FUNKCJI JEDNEJ ZMIENNEJ, SZKOŁA, Matematyka, Matematyka
więcej podobnych podstron