WYKŁAD OBIERALNY rok akademicki 2002/03
1
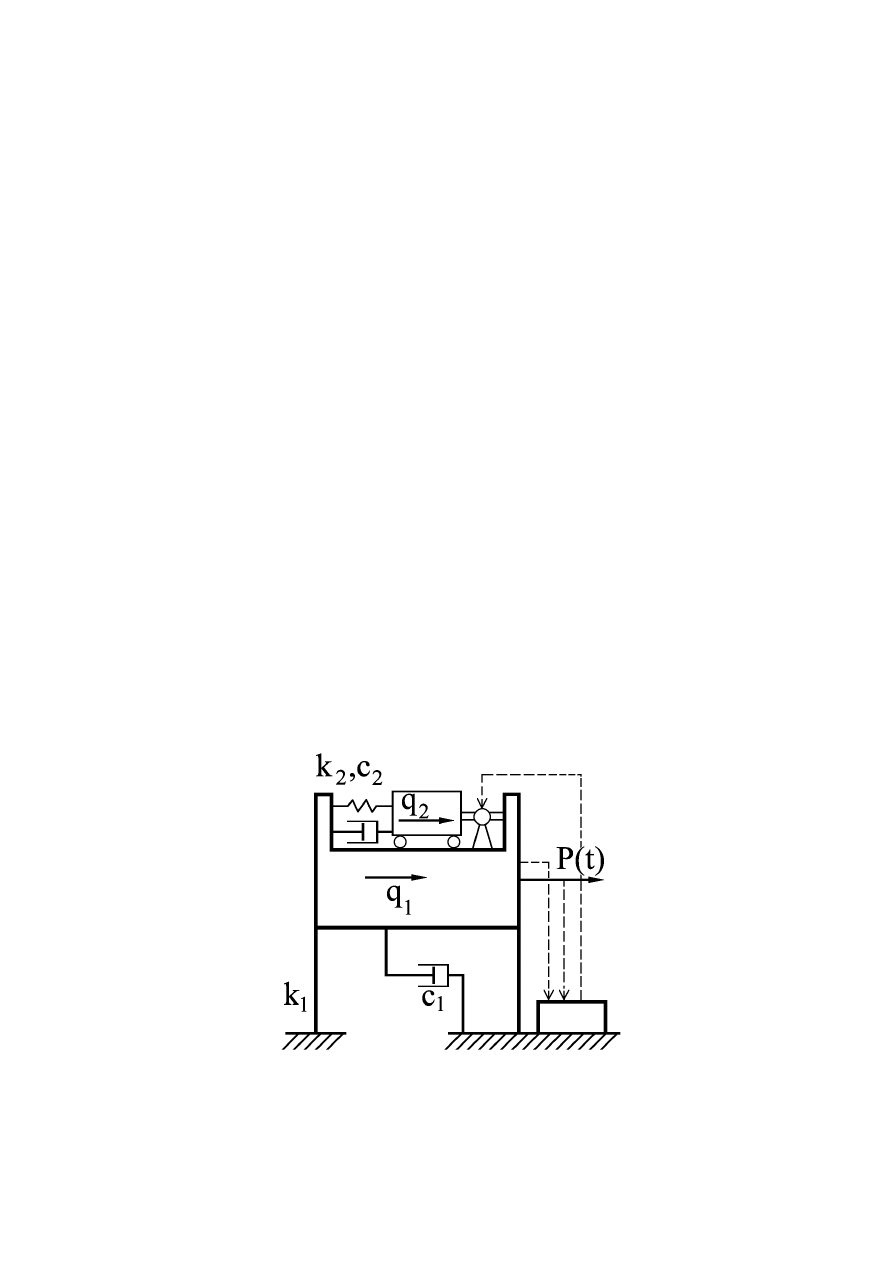
AKTYWNE ELIMINATORY DRGAŃ (1)
· Ogólny opis aktywnego tłumika drgań
Istota aktywnej regulacji drgań sprowadza się do pomysłu aby ge-
nerować dodatkowe siły działające na konstrukcję po to by prze-
ciwdziałały one obciążeniom dynamicznym.
Aktywny eliminator drgań to w istocie pewien układ automatycz-
nej regulacji zamontowany na konstrukcji. Główne elementy tego
układu to czujniki, komputer oraz siłowniki.
Czujniki rozmieszczone w różnych punktach konstrukcji mierzą jej
stan dynamiczny (tzn. mierzą przemieszczenia, prędkości lub/i
przyspieszenia). Informacje te są przesyłane do komputera, który
na tej podstawie określa pożądane wartości sił regulacji. Następnie
wysyłane są sygnały do siłowników które z kolei wzbudzają od-
powiednie siły regulacji i działają nimi na konstrukcję.
Proces monitorowania stanu konstrukcji, doboru i generowania sił
regulacji jest procesem dynamicznym.
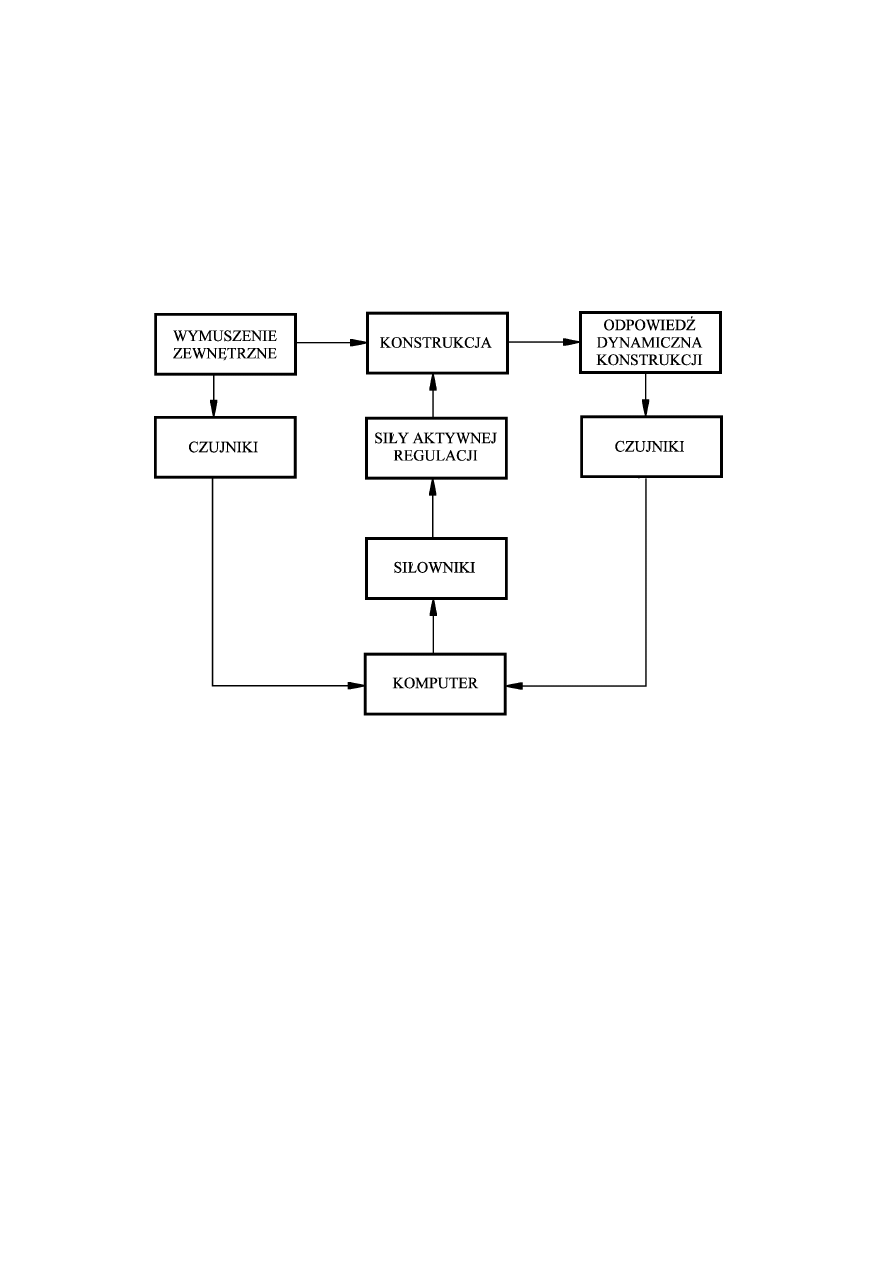
WYKŁAD OBIERALNY rok akademicki 2002/03
2
AKTYWNE ELIMINATORY DRGAŃ (2)
· Ogólny schemat działania układu automatycznej regulacji
Pomiar wymuszenia zewnetrznego jest trudny lub zgoła
niemożliwy do przeprowadzenia i dlatego wymuszenie zwykle nie
wpływa bezpośrednio na wielkość sił aktywnej regulacji.
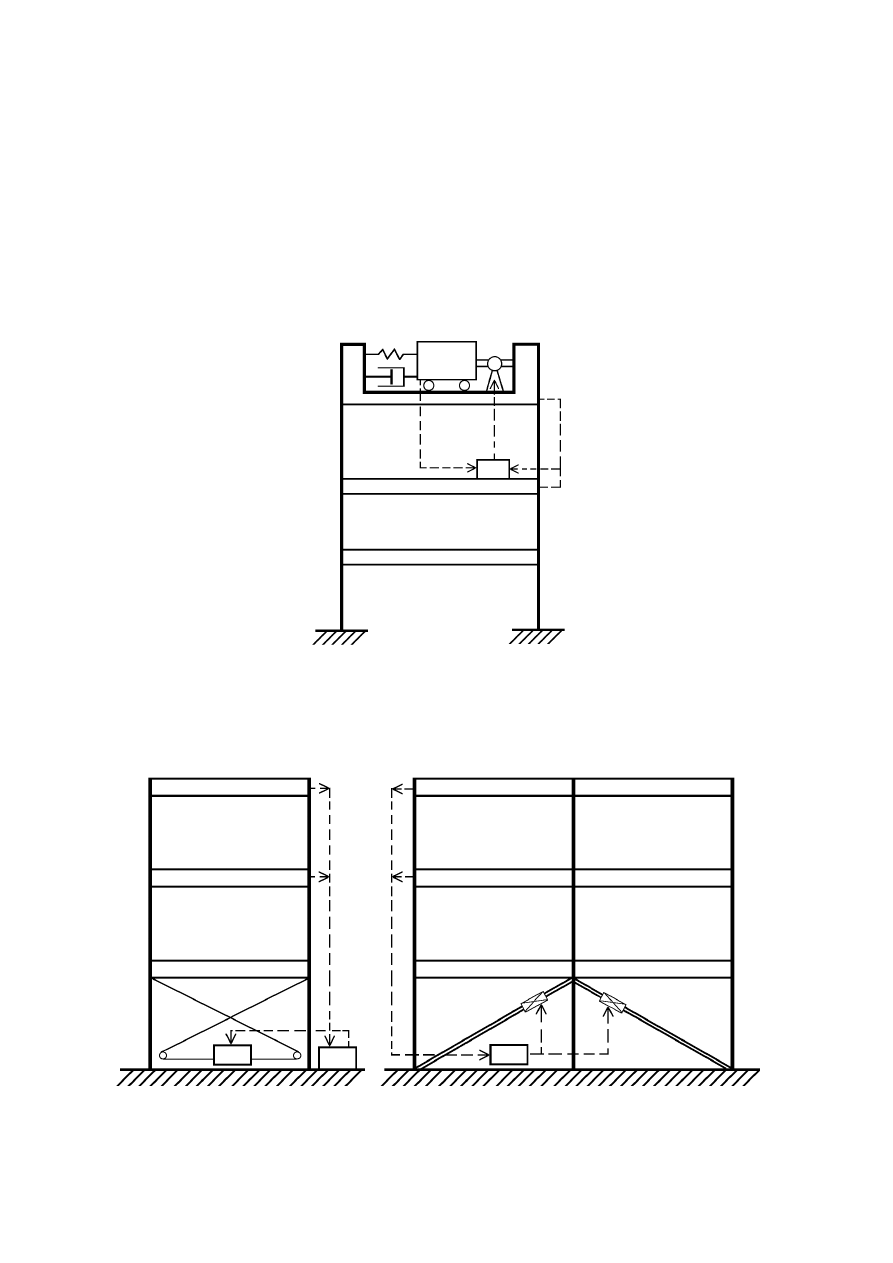
WYKŁAD OBIERALNY rok akademicki 2002/03
3
AKTYWNE ELIMINATORY DRGAŃ (3)
· Ogólny opis technicznej realizacji układu aktywnej regulacji drgań
•
Aktywny tłumik masowy
•
Aktywny układ cięgnowy (zastrzałowy)
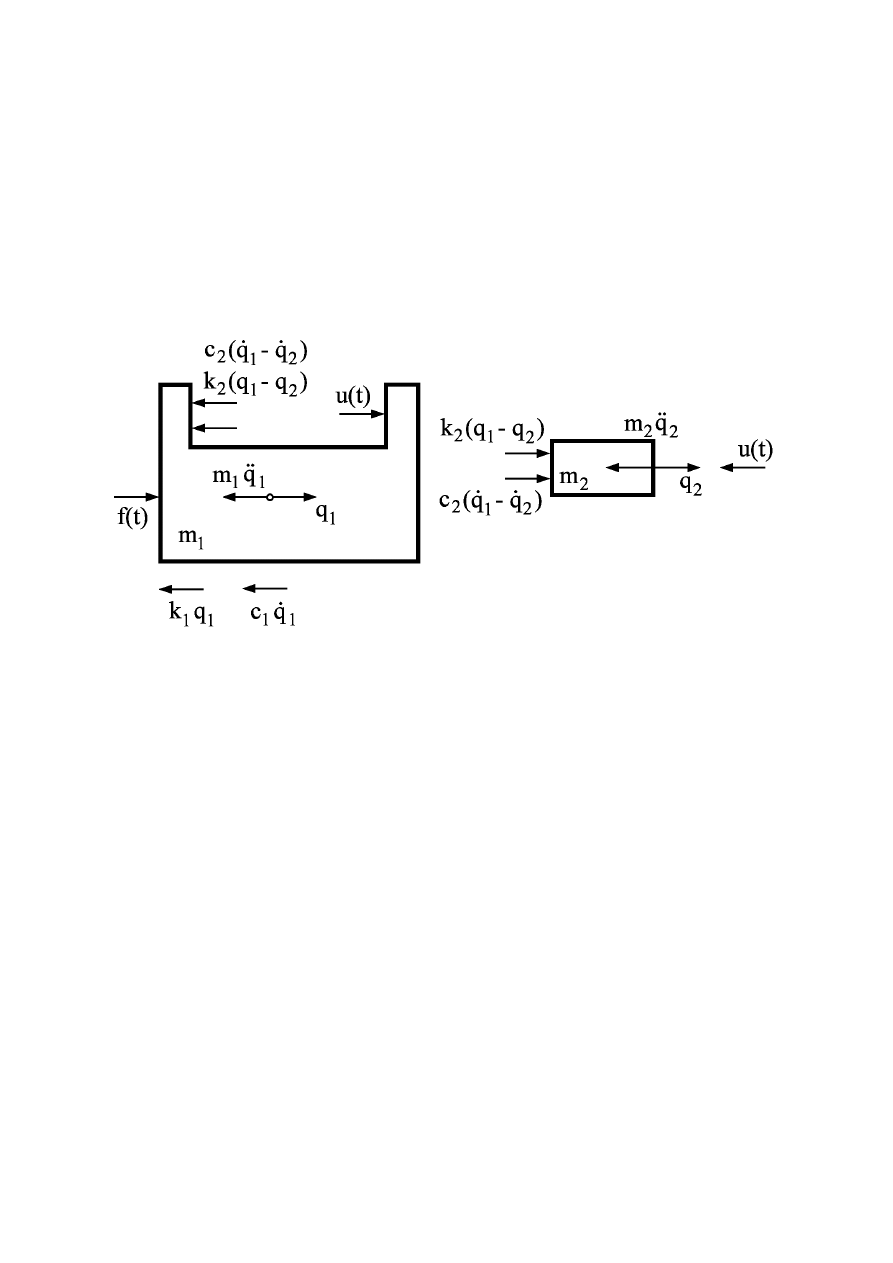
WYKŁAD OBIERALNY rok akademicki 2002/03
4
AKTYWNE ELIMINATORY DRGAŃ (4)
· Równania ruchu
•
Równania ruchu prostej konstrukcji i aktywnym (masowym)
tłumikiem drgań
m q
c
c q
c q
k
k q
k q
f t
u t
1 1
1
2
1
2
2
1
2
1
2
2
&& (
) &
&
(
)
( )
( )
+
+
−
+
+
−
=
−
,
m q
c q
c q
k q
k q
u t
2
2
2 1
2
2
2 1
2
2
&&
&
&
( )
−
+
−
+
=
,
•
Macierzowe równanie ruchu – równanie dowolnej konstrukcji
M
=
m
m
1
2
0
0
,
K
=
+
−
−
k
k
k
k
k
1
2
2
2
2
,
{ }
u( )
( )
t
u t
=
,
C
=
+
−
−
c
c
c
c
c
1
2
2
2
2
, E
=
−
1
1
, f ( )
( )
t
f t
=
0
Mq
Cq
Kq
f
Eu
&&( )
& ( )
( )
( )
( )
t
t
t
t
t
+
+
=
+

WYKŁAD OBIERALNY rok akademicki 2002/03
5
AKTYWNE ELIMINATORY DRGAŃ (5)
· Interpretacja matematyczna sposobu działania układu aktywnej
regulacji drgań
Mq
Cq
Kq
f
Eu
&&( )
& ( )
( )
( )
( )
t
t
t
t
t
+
+
=
+
u
K q
C q
M q
D f
( )
( )
& ( )
&&( )
( )
t
t
t
t
t
=
+
+
+
1
1
1
1
(
)&&( ) (
) &( ) (
) ( ) (
) ( )
M EM q
C EC q
K EK q
I D f
1
−
+
−
+
−
= +
t
t
t
t
1
1
1
Uwagi:
•
Z matematycznego punktu widzenia wprowadzenie układu aktyw-
nej regulacji może być rozumiane jako pewien sposób modyfikacji
własności tłumiących oraz charakterystyk dynamicznych konstruk-
cji poprzez modyfikację macierzy tłumienia, sztywności i bezwład-
ności.
•
Problem polega na tym w jaki sposób dobrać macierze
K C M D
1
1
1
1
, , ,
aby uzyskać możliwe duże zmniejszenie drgań i
osiągnąć ten cel możliwie małym kosztem tzn. za pomocą możliwie
małych sił aktywnej regulacji
u( )
t
.
•
Problem projektowania układu aktywnej regulacji drgań może być
wobec tego traktowany jako pewne zadanie optymalizacji.
•
W praktyce pomiar sił wymuszających może być bardzo trudny i
wobec tego zazwyczaj projektuje się układ aktywnej regulacji w ten
sposób, że przyjmuje się
D
0
1
=
.
•
Pomiar przyspieszeń konstrukcji jest stosunkowo prosty i dokładny.
Z tego punktu widzenia racjonalne byłoby rozpatrywanie układu
aktywnej regulacji jako układu z tzw. sprzężeniem bezwładnościo-
wym.

WYKŁAD OBIERALNY rok akademicki 2002/03
6
AKTYWNE ELIMINATORY DRGAŃ (5)
· Zapisanie równań ruchu za pomocą zmiennych stanu
•
Tradycyjny zapis równań ruchu
Mq
Cq
Kq
f
Eu
&&
( )
&
( )
( )
( )
( )
t
t
t
t
t
+
+
=
+
•
Zmienne stanu
z
q
q
( )
( )
& ( )
t
t
t
=
,
&( )
& ( )
&&( )
z
q
q
t
t
t
=
•
Zmodyfikowana postać równań ruchu
& ( ) & ( )
q
q
t
t
=
,
&&
( )
&
( )
( )
( )
( )
q
M Cq
M Kq
M f
M Eu
t
t
t
t
t
= −
−
+
+
−
−
−
−
1
1
1
1
,
•
Równania ruchu zapisane za pomocą zmiennych stanu
&( )
( )
( )
( )
z
Az
Hf
Bu
t
t
t
t
=
+
+
,
gdzie
A
0
I
M K
M C
=
−
−
−
−
1
1
,
H
0
M
=
−
1
,
B
0
M E
=
−
1
.

WYKŁAD OBIERALNY rok akademicki 2002/03
7
AKTYWNE ELIMINATORY DRGAŃ (6)
· Projektowanie regulatora drgań
K
C
M
D
1
1
1
1
=
=
=
=
?
?
?
?
,
,
,
· Metoda liniowej regulacji optymalnej (LQR) (1)
W metodzie tej wektor sił aktywnej regulacji jest określany w ten
sposób aby pewien funkcjonał nazywany funkcjonałem działania
osiągał wartość minimalną. W kategoriach teorii optymalizacji
funkcjonał ten należy traktować jako funkcję celu. Ma on postać:
[
]
∫
+
=
k
t
T
T
dt
t
t
t
t
J
0
)
(
)
(
)
(
)
(
Ru
u
Qz
z
Rolę ograniczeń spełniają równania stanu
&( )
( )
( )
( )
z
Az
Hf
Bu
t
t
t
t
=
+
+
Uwagi:
•
Występujące powyżej macierze
Q R
,
nazywamy macierzami
wagowymi. Wymaga się aby macierz
R
była dodatnio określo-
na, a macierz
Q
była półdodatnio określona.
•
Macierze
Q R
,
wyrażają do pewnego stopnia kompromis mię-
dzy efektami regulacji (zmniejszeniem amplitud drgań), a kosz-
tami regulacji (koniecznością doprowadzenia energii do układu
w celu wywołania sił regulacji
u( )
t
)
. Wybór dużych wartości
elementów macierzy
Q
w stosunku do elementów macierzy
R
oznacza, że bardziej zależy nam na zmniejszeniu drgań. Mniej
istotna jest natomiast wielkość doprowadzanej do układu energii.
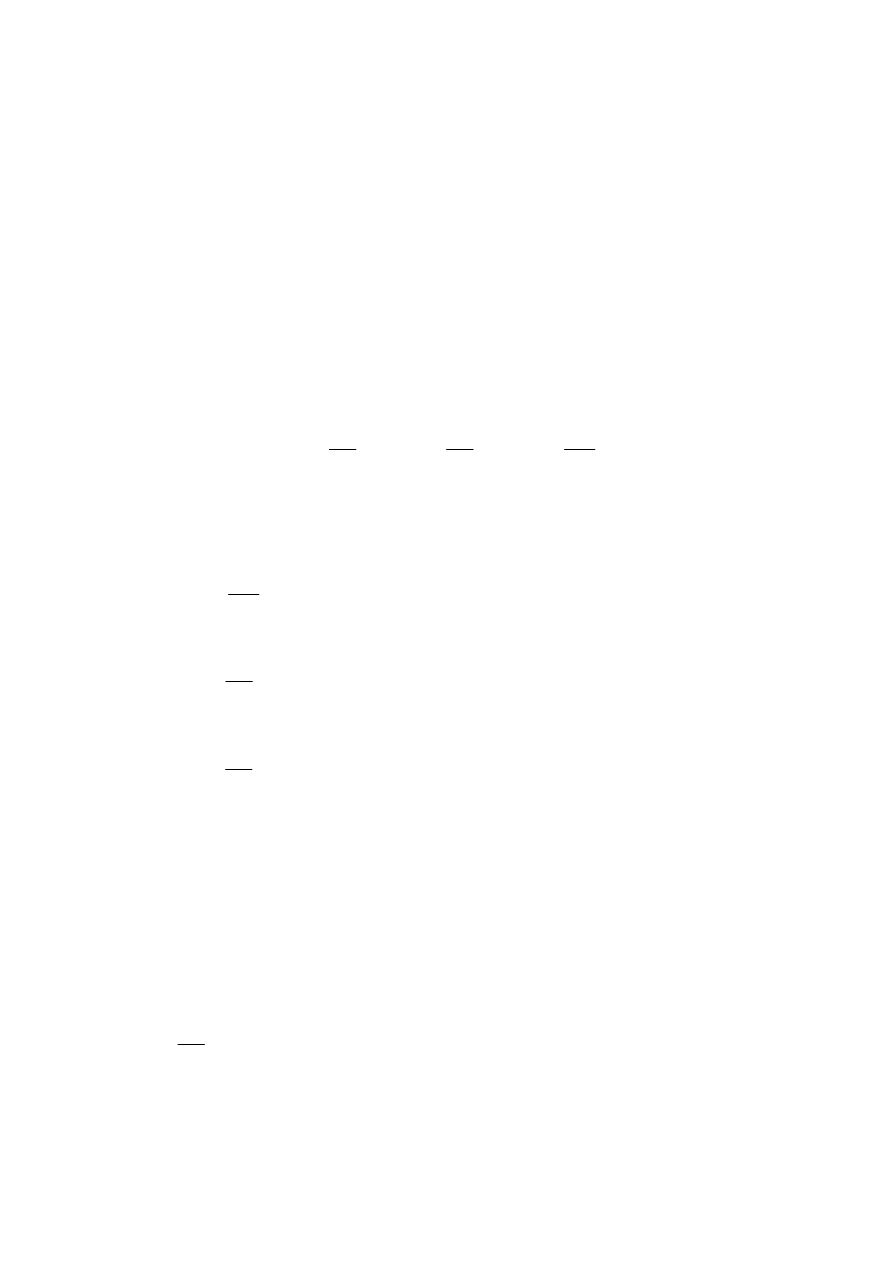
WYKŁAD OBIERALNY rok akademicki 2002/03
8
AKTYWNE ELIMINATORY DRGAŃ (7)
· Metoda liniowej regulacji optymalnej (LQR) (2)
•
Zmodyfikowany funkcjonał - dołączono równania stanu
[
]
{
}
∫
−
+
+
+
+
=
k
t
T
T
T
dt
t
t
t
t
t
t
t
t
L
0
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
z
Bu
Hf
Az
Ru
u
Qz
z
&
Λ
•
Warunek optymalności funkcjonału
))
(
),
(
),
(
(
t
t
t
L
Λ
u
z
0
)
(
)
(
)
(
=
∂
∂
+
∂
∂
+
∂
∂
=
Λ
Λ
L
t
L
t
L
t
L
T
T
T
δ
δ
δ
δ
u
u
z
z
•
Obliczenie wariacji
(
)
dt
L
t
f
t
T
T
∫
−
+
+
=
∂
∂
0
)
(
z
Hf
Bu
Az
&
Λ
Λ
Λ
δ
δ
(
)
(
)
dt
dt
L
t
f
f
t
T
T
t
T
T
T
∫
∫
Λ
+
=
Λ
+
=
∂
∂
0
0
2
2
)
(
B
Ru
u
u
B
Ru
u
u
u
δ
δ
δ
δ
(
)
[
]
dt
L
t
f
t
T
T
T
∫
−
Λ
+
=
∂
∂
0
2
)
(
z
z
A
Qz
z
z
z
&
δ
δ
δ
δ
dt
t
t
t
t
dt
t
t
f
f
t
T
f
f
T
T
t
T
)
(
)
(
)
(
)
(
)
0
(
)
0
(
)
(
)
(
0
0
∫
∫
+
+
−
=
−
z
z
z
z
δ
δ
δ
δ
Λ
Λ
Λ
Λ
&
&
)
(
)
(
t
t
T
T
v
=
Λ
,
dt
t
dt
t
)
(
)
(
w
z
&
&
=
δ
dt
t
dt
t
T
T
)
(
)
(
v&
&
=
Λ
,
)
(
)
(
t
t
w
z
=
δ
(
)
dt
t
t
L
f
t
T
T
T
f
f
T
T
∫
+
+
+
−
=
∂
∂
0
2
)
0
(
)
0
(
)
(
)
(
Λ
Λ
Λ
Λ
&
A
Qz
z
z
z
z
z
δ
δ
δ
δ

WYKŁAD OBIERALNY rok akademicki 2002/03
9
AKTYWNE ELIMINATORY DRGAŃ (8)
· Metoda liniowej regulacji optymalnej (LQR) (3)
•
Warunki optymalności funkcjonału
0
=
∂
∂
Λ
L
⇒
0
z
Hf
Bu
Az
=
−
+
+
)
(
)
(
)
(
)
(
t
t
t
t
&
,
(1)
0
u
=
∂
∂
L
⇒
0
B
Ru
=
+
Λ
T
2
,
(2)
0
z
=
∂
∂
L
⇒
0
A
Qz
=
+
+
Λ
Λ
&
T
2
,
(3)
Warunkami dodatkowymi są warunki początkowe ruchu o postaci:
0
=
t
0
)
0
(
z
z
=
⇒
0
z
=
)
0
(
δ
,
oraz warunek „początkowy” dla mnożników Lagrange’a o postaci:
f
t
t
=
0
=
)
(
f
T
t
Λ
bo
)
(
f
t
z
δ
jest dowolne.
Warunek (1) to równanie ruchu zapisane we współrzędnych stanu
&( )
( )
( )
( )
z
Az
Hf
Bu
t
t
t
t
=
+
+
,
Z warunku (2) możemy wyznaczyć wektor sił aktywnej regulacji
)
(
)
(
1
2
1
t
t
T
Λ
B
R
u
−
−
=
(4)
Siły regulacji są proporcjonalne do wektora mnożników Lagran-
ge’a.
Funkcję mnożników Lagrange’a wyznacza się z równania
)
(
)
(
2
)
(
t
t
t
T
Λ
Λ
A
Qz
+
=
−
&
(5)

WYKŁAD OBIERALNY rok akademicki 2002/03
10
AKTYWNE ELIMINATORY DRGAŃ (9)
· Metoda liniowej regulacji optymalnej (LQR) (4)
•
Rozwiązanie zadania optymalizacji (1)
Zakłada się, że wektor sił aktywnej regulacji jest określany na
podstawie stanu dynamicznego układu (sprzężenie przemiesz-
czeniowo - prędkościowe)
Λ
( )
( ) ( )
t
t
t
=
P
z
,
⇒
(
)
u
K q
C q
( )
( )
&( )
t
t
t
=
+
1
1
(6)
)
(
)
(
)
(
)
(
)
(
t
t
t
t
t
z
P
z
P
&
&
&
+
=
Λ
(7)
)
(t
P
- nieznana macierz sprzężenia zwrotnego
Podstawiamy
zależności (6) i (7) do (5) otrzymując
)
(
)
(
)
(
2
)
(
)
(
)
(
)
(
t
t
t
t
t
t
t
T
z
P
A
Qz
z
P
z
P
+
=
−
−
&
&
(8)
Uwzględniamy zależność (4) w równaniach ruchu
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
1
2
1
t
t
t
t
t
t
t
t
t
T
z
P
B
BR
P
Hf
Az
Bu
Hf
Az
z
−
−
+
=
+
+
=
&
Prawa stronę powyższego równania podstawiamy do (8) pomija-
jąc równocześnie wpływ wymuszenia
)
(
)
(
)
(
2
)
(
)
(
)
(
)
(
)
(
)
(
)
(
1
2
1
t
t
t
t
t
t
t
t
t
t
T
T
z
P
A
Qz
Az
P
z
P
B
BR
P
z
P
+
=
−
+
−
−
&
Po
uporządkowaniu otrzymuje się
[
]
0
z
Q
P
A
A
P
P
B
BR
P
P
=
−
−
−
+
−
−
)
(
2
)
(
)
(
)
(
)
(
)
(
1
2
1
t
t
t
t
t
t
T
T
&
WYKŁAD OBIERALNY rok akademicki 2002/03
11
AKTYWNE ELIMINATORY DRGAŃ (9)
· Metoda liniowej regulacji optymalnej (LQR) (4)
•
Rozwiązanie zadania optymalizacji (2)
Powyższe równanie będzie spełnione w dowolnej chwili jeżeli
Q
P
B
BR
P
P
A
A
P
P
2
)
(
)
(
)
(
)
(
)
(
1
2
1
+
−
+
=
−
−
t
t
t
t
t
T
T
&
(9)
Jest to macierzowe równanie różniczkowe 1 rzędu ze względu
na macierz
)
(t
P
. Równanie jest nieliniowe. Nazywa się równa-
niem różniczkowym Riccati’ego. Równanie to należy rozwiązać
z warunkiem „początkowym”
0
=
)
(
f
T
t
Λ
⇒
0
z
P
=
=
)
(
)
(
)
(
f
f
f
t
t
t
Λ
⇒
0
P
=
)
(
f
t
Można wykazać, że macierz
)
(t
P
jest symetryczna.
Typowy przebieg funkcji
)
(t
p
ij
(elementów macierzy
)
(t
P
) po-
kazano na rysunku
0
10
20
30
40
50
60
t
-3.0
-2.0
-1.0
0.0
1.0
2.0
3.0
P(t
)
P (t)
11
P (t)
12
Oznacza to, że jeżeli
∞
→
f
t
to
0
P
→
)
(t
&
i równanie (9) staje
się równaniem algebraicznym a ponadto P
P
( )
.
t
const
= =

WYKŁAD OBIERALNY rok akademicki 2002/03
12
AKTYWNE ELIMINATORY DRGAŃ (10)
· Metoda liniowej regulacji optymalnej (LQR) (5)
•
Uwagi o algebraicznym równaniu Riccati’ego
PA A P
PBR B P
Q 0
+
−
+
=
−
T
T
1
2
1
2
Równanie jest nieliniowe, algebraiczne i trudne do rozwiązania.
Macierz P jest symetryczna i rzeczywista.
Równnie można wyznaczyć np. metodą Pottera lub Kleinemana.
W Matlabie są dostępne biblioteczne procedury rozwiązujące
równanie Riccati’ego.
Kłopoty zaczynają się dla układów o dużej liczbie stopni swo-
body.
•
Ostateczny wzór na siłę regulacji
)
(
)
(
)
(
1
2
1
t
t
t
T
Gz
Pz
B
R
u
=
−
=
−
,
P
B
R
G
T
1
2
1
−
−
=
(10)
G - macierz sprzężenia zwrotnego
•
Uwagi końcowe
Macierz wzmocnienia G jest obliczana tylko raz.
W czasie rzeczywistym komputer oblicza siłę regulacji na pod-
stawie wzoru (10).
Rozwiązanie jest suboptymalne ponieważ w trakcie wyprowa-
dzania równania Riccati’ego pominięto wpływ wymuszenia.
Przedstawiono wersja metody LQR korzysta z założenia, że mie-
rzony jest cały wektor stanu. Należałoby jeszcze uwzględnić
fakt, że w rzeczywistości mierzymy tylko część wektora stanu.

WYKŁAD OBIERALNY rok akademicki 2002/03
13
AKTYWNE ELIMINATORY DRGAŃ (10a)
· Rozwiązanie równania Riccati’ego metodą Pottera (1)
•
Uwagi ogólne
PA A P
PBR B P
Q 0
+
−
+
=
−
T
T
1
2
1
2
(1)
Równanie jest nieliniowe, algebraiczne i trudne do rozwiązania.
Macierz
k
k
DP
A
A
−
=
jest symetryczna i rzeczywista.
•
Opis metody
Wprowadźmy macierz
A
P
B
BR
C
−
=
−
T
1
2
1
,
(2)
i oznaczmy symbolami
µ
i f jej wartości własne i wektory wła-
sne. Utwórzmy z wartości własnych
i
µ
(i=1,2,....,m) diagonalną
macierz
[
]
m
diag
µ
µ
µ
.........,
,
,
2
1
=
J
, a z wektorów własnych
macierz
[
]
m
f
f
f
F
.......,
,
,
2
1
=
. Jest więc spełnione równanie
(
)
FJ
CF
0
F
J
C
=
⇒
=
−
.
(3)
Mnożąc to równanie lewostronnie przez P otrzymuje się:
PFJ
PCF
=
.
(4)
Przekształćmy prawą stronę tego równania w sposób następując:
(
)
(
) (
)
F
Q
P
A
F
PA
P
B
PBR
F
A
P
B
BR
P
PCF
2
1
2
1
1
2
1
+
=
−
=
−
=
−
−
T
T
T
(5)
Można wobec tego napisać:
(
)
PFJ
F
Q
P
A
=
+
2
T
.
(6)

WYKŁAD OBIERALNY rok akademicki 2002/03
14
AKTYWNE ELIMINATORY DRGAŃ (10b)
· Rozwiązywanie równania Riccati’ego metodą Pottera (2)
Teraz bierzemy ponownie pod uwagę równanie
FJ
CF
=
.
Uwzględniając w tym równaniu definicję macierzy C mamy:
(
)
FJ
F
A
P
B
BR
=
−
−
1
2
1
T
.
(7)
Wprowadźmy transformację:
E
PF
=
.
(8)
Uwzględniając (8) w (6) i (7) możemy te dwa równania przepi-
sać w postaci:
(
)
EJ
QF
E
A
PFJ
F
Q
P
A
=
+
⇒
=
+
2
2
T
T
,
(9a)
(
)
FJ
AF
E
B
BR
FJ
F
A
P
B
BR
=
−
⇒
=
−
−
−
T
T
1
2
1
1
2
1
. (9b)
Równania (9a)i (9b) są równoważne równaniu (1). Aby to wyka-
zać należy podstawić lewą stronę równania (9b) do (9a) (1 wer-
sja) i zauważyć, że
0
F
≠
.
Równania (9a) i (9b) można zapisać w postaci 1 równania
J
F
E
F
E
M
=
, (10)
gdzie
−
=
−
2
1
2
1
A
B
BR
Q
A
M
T
T
.
(11)
Problem własny o wymiarze 2m i ma 2m wartości własnych. Jak
wynika z (10) nas interesuje tylko m wartości własnych. Które
wybrać?

WYKŁAD OBIERALNY rok akademicki 2002/03
15
AKTYWNE ELIMINATORY DRGAŃ (10c)
· Rozwiązywanie równania Riccati’ego metodą Pottera (3)
Aby ustalić które wartości własne nas interesują zauważmy że
PA
P
B
PBR
P
B
PBR
P
A
PC
P
C
−
+
+
−
=
+
−
−
T
T
T
T
1
2
1
1
2
1
, (12)
Q
P
B
PBR
PA
P
A
2
1
2
1
=
+
−
−
−
T
T
.
(13)
co pozwala na napisanie równania:
P
B
PBR
Q
PC
P
C
T
T
1
2
1
2
−
+
=
+
(14)
Jeżeli prawa strona równania (14) jest dodatnio określona to czę-
ści rzeczywiste wartości własnych macierzy C są dodatnie. Po-
nadto jeżeli macierze Q i
T
B
BR
1
−
są rzeczywiste i dodatnio
określone, a
λ
jest wartością własną macierzy
M
to
λ
-
jest
też wartością własną macierzy M . Wobec tego
M
ma m warto-
ści własnych z dodatnimi częściami rzeczywistymi. Te wartości
własne i odpowiadające im wektory własne są rozwiązaniem nas
interesującym. Górne i dolne części wektorów własnych tworzą
odpowiednio macierze E i F. Rozwiązanie równania Riccati’ego
otrzymamy mnożąc równanie
E
PF
=
prawostronnie przez
1
−
F
otrzymując:
1
−
=
EF
P
. (15)
Algorytm obliczeń składa się z następujących kroków:
•
budowa macierzy M ,
•
rozwiązanie problemu własnego (10),
•
obliczenie macierzy P ze wzoru (15).
Wektory własne tworzące macierze E i F są zazwyczaj wekto-
rami zespolonymi. Komplikuje to procedurę obliczeniową. Ze
względu na błędy numeryczne rozwiązanie uzyskane tą metodą
często prowadzi do niesymetrycznej macierzy P .

WYKŁAD OBIERALNY rok akademicki 2002/03
16
AKTYWNE ELIMINATORY DRGAŃ (10d)
· Rozwiązywanie równania Riccati’ego metodą Kleinmana (1)
Równanie Riccati’ego
0
Q
PDP
P
A
PA
=
+
−
+
2
T
(1)
gdzie
T
B
BR
D
1
2
1
−
−
=
.
Zakładamy, że znamy przybliżenie rozwiązania które oznaczamy
symbolem
k
P
. Możemy teraz napisać, że
(
)
k
k
k
k
P
P
P
P
P
P
−
+
≈
+
=
+
1
∆
.
(2)
Podstawiając (2) do (1) mamy
(
)
[
]
(
)
[
]
(
)
[
]
(
)
[
]
0
Q
P
P
P
D
P
P
P
P
P
P
A
A
P
P
P
=
+
−
+
−
+
−
−
+
+
−
+
+
+
+
+
2
1
1
1
1
k
k
k
k
k
k
k
k
k
T
k
k
k
(
)
(
)
(
) (
)
0
P
P
D
P
P
DP
P
Q
P
D
P
A
DP
A
P
=
−
−
+
+
+
−
+
−
+
+
+
+
k
k
k
k
k
k
k
k
T
k
k
1
1
1
1
2
Jeżeli założymy, że
(
) (
)
0
P
P
D
P
P
≈
−
−
+
+
k
k
k
k
1
1
to otrzymamy
(
)
(
)
0
DP
P
Q
P
D
P
A
DP
A
P
=
+
+
−
+
−
+
+
k
k
k
k
T
k
k
2
1
1
.
(3)
Uwagi o równaniu (3) i metodzie Kleinmana:
•
Równanie (3) jest liniowe ze względu na
1
+
k
P
i nosi nazwę
równania Lapunowa.
•
Można wykazać, że
P
P
=
+
∞
→
1
lim
k
k
jeżeli macierz
1
DP
A
−
jest
ujemnie określona.
•
Metoda Kleinmana jest odpowiednikiem metody Newtona
rozwiązywania układu nieliniowych równań algebraicznych.
WYKŁAD OBIERALNY rok akademicki 2002/03
17
AKTYWNE ELIMINATORY DRGAŃ (10e)
· Rozwiązywanie równania Riccati’ego metodą Kleinmana (2)
Proces iteracyjnego rozwiązywania równania Riccati’ego ma na-
stępujący przebieg:
•
przyjmujemy początkowe przybliżenie rozwiązania
1
P
tak aby
macierz
1
DP
A
−
była ujemnie określona - np. rozwiązując
równanie Lapunowa o postaci
0
Q
P
A
PA
=
+
+
2
T
,
następnie dla k=1,2,.....
•
znając macierz
k
P
obliczamy
k
k
DP
A
A
−
=
,
k
k
k
DP
P
Q
Q
+
=
2
,
•
rozwiązujemy równanie Lapunowa względem
1
+
k
P
0
Q
P
A
A
P
=
+
+
+
+
k
k
T
k
k
k
1
1
,
•
sprawdzamy warunki zbieżności procesu iteracyjnego
1
1
1
+
+
<
−
k
k
k
P
P
P
ε
,
Q
R
2
2
1
ε
<
+
k
,
gdzie
1
ε
i
2
ε
to założone dokładności obliczeń, a
Q
DP
P
P
A
A
P
R
2
1
1
1
1
1
+
−
+
=
+
+
+
+
+
k
k
k
T
k
k
•
jeżeli warunki iteracji są spełnione to ostatnio otrzymaną ma-
cierz
1
+
k
P
uważa się za rozwiązanie równania Riccati’ego. W
przeciwnym przypadku wykonujemy kolejną iterację,
Metoda Klienmana jest zbieżna jeżeli dysponujemy dobrym, po-
czątkowym przybliżeniem rozwiązania.

WYKŁAD OBIERALNY rok akademicki 2002/03
18
AKTYWNE ELIMINATORY DRGAŃ (10f)
· Rozwiązywanie równania Lapunowa (1)
Warunek istnienia i jednoznaczności rozwiązania
Równanie Lapunowa ma rozwiązanie i jest ono jednoznaczne je-
żeli suma dwóch dowolnych wartości własnych macierzy A jest
różna od zera (tzn. dla dowolnych i oraz j zachodzi
0
≠
+
j
i
λ
λ
)
W zagadnieniach dynamiki konstrukcji warunek ten jest spełniony
jeżeli w równaniach ruchu uwzględni się siły tłumienia.
Najprostsza metoda rozwiązania równania Lapunowa
Jeżeli wymiar macierzy
Q
A
P
i
,
jest równy 2 to równanie
0
Q
P
A
PA
=
+
+
T
,
może być przedstawione w postaci:
−
=
+
22
12
21
11
22
12
21
11
22
21
12
11
22
21
12
11
22
12
21
11
q
q
q
q
a
a
a
a
p
p
p
p
p
p
p
p
a
a
a
a
,
−
=
+
+
+
+
+
+
+
+
+
22
12
21
11
22
22
21
21
22
12
21
11
12
22
11
21
12
12
11
11
22
22
12
12
21
22
11
12
22
21
12
11
21
21
11
11
q
q
q
q
p
a
p
a
p
a
p
a
p
a
p
a
p
a
p
a
p
a
p
a
p
a
p
a
p
a
p
a
p
a
p
a
.
i
następnie zapisane w sposób tradycyjny (
12
21
p
p
=
,
12
21
q
q
=
)
(
)
11
12
12
21
11
11
2
q
p
a
a
p
a
−
=
+
+
,
(
)
21
22
21
12
22
11
11
21
q
p
a
p
a
a
p
a
−
=
+
+
+
,
(
)
22
22
22
12
21
12
2
q
p
a
p
a
a
−
=
+
+
.
Powyższe równania mogą być rozwiązane w tradycyjny sposób.

WYKŁAD OBIERALNY rok akademicki 2002/03
19
AKTYWNE ELIMINATORY DRGAŃ (10g)
· Rozwiązywanie równania Lapunowa (2)
Sposób omówiony powyżej prowadzi, przy większym wymiarze
zadania do bardzo dużego układu równań (o wymiarze
)
1
(
2
1
+
n
n
).
Ponadto, procedura rozwiązania takiego układu musi uwzględniać
możliwość pojawienia się zer na głównej przekątnej macierzy
współczynników.
Bardzo dobrą metodą rozwiązywania równania Lapunowa jest me-
toda opracowana przez Bartelsa i Stewarta. Opis tej metody jest
złożony i dlatego poprzestaniemy na opisie algorytmu obliczeń.
Algorytm metody Bartelsa-Stewarta (1)
Krok 1 - Nadać macierzy A postać trójkątnej macierzy rzeczy-
wistej Schura wykonując transformację opisaną wzorem
=
=
pp
p
p
T
A
0
0
A
A
0
A
A
A
AU
U
A
~
......
........
..........
..........
~
......
~
~
.......
~
~
~
2
22
1
12
11
W rezultacie powyższej transformacji określona zostanie macierz
U.
Krok 2 – Obliczyć macierz
Q
~
korzystając ze wzoru:
=
−
=
pp
p
T
p
T
Q
Q
Q
Q
QU
U
Q
~
.......
~
..........
..........
~
.........
~
~
1
1
11
.

WYKŁAD OBIERALNY rok akademicki 2002/03
20
AKTYWNE ELIMINATORY DRGAŃ (10h)
· Rozwiązywanie równania Lapunowa (3)
Algorytm metody Bartelsa-Stewarta (1)
Krok 3 – Dla l=1,2,...,p i k=l,l+1,...,p rozwiązać szereg układów
równań o maksymalnym wymiarze równym 4.
∑
∑
−
=
−
=
−
−
=
+
1
1
1
1
~
~
~
~
~
~
~
~
~
l
i
il
ki
k
j
jl
T
jk
kl
ll
kl
kl
T
kk
A
P
P
A
Q
A
P
P
A
W rezultacie otrzymujemy macierz P
~
.
=
pp
p
T
p
P
P
P
P
P
~
.......
~
..........
..........
~
.........
~
~
1
1
11
Krok 4 – Obliczyć macierz P korzystając ze wzoru
T
U
P
U
P
~
=
.
Tekst programu napisanego w FORTRANIE jest opublikowany w
czasopiśmie matematycznym. W Matlabie są procedury rozwiązu-
jące równania Riccati’ego i Lapunowa.

WYKŁAD OBIERALNY rok akademicki 2002/03
21
AKTYWNE ELIMINATORY DRGAŃ (11)
· Stabilność układu aktywnej regulacji
Układ regulacji może być przyczyną niestabilnego zachowania się
konstrukcji. Należy sprawdzić warunki stabilności ruchu.
Ruch układu jest niestabilny jeżeli jego przemieszczenia rosną do
nieskończoności.
Punktem wyjścia w analizie stabilności są równania ruchu w któ-
rych pominięto siły wymuszenia i wzór na siłę regulacji
)
(
)
(
)
(
t
t
t
Bu
Az
z
+
=
&
)
(
)
(
t
t
Gz
u
=
)
(
~
)
(
)
(
)
(
t
t
t
z
A
z
BG
A
z
=
+
=
&
Rozwiązanie macierzowego, liniowego i jednorodnego równania
różniczkowego o stałych współczynników ma postać:
c
z
)
exp(
)
(
t
t
λ
=
,
c
z
)
exp(
)
(
t
t
λ
λ
=
&
.
Podstawiając proponowaną postać rozwiązania do równania ruchu
otrzymuje się liniowy problem własny o postaci:
(
)
0
c
I
A
=
−
λ
~
Rozwiązaniem są wartości własne
j
j
j
i
η
µ
λ
+
=
(w ogólności
liczby zespolone) i wektory własne
j
c
, j=1,2,..,m. Rozwiązaniem
równania ruchu jest funkcja
i
m
i
i
t
t
c
z
∑
=
=
1
)
exp(
)
(
λ
.
Rozwiązanie rośnie do nieskończoności jeżeli
∞
→
)
exp( t
i
λ
dla
∞
→
t
. Zachodzi to gdy któraś z wartości własnych ma część rze-
czywistą dodatnią. Ruch jest wtedy niestabilny.
Ruch układu jest stabilny wtedy gdy dla każdego j
0
<
j
µ
.

WYKŁAD OBIERALNY rok akademicki 2002/03
22
AKTYWNE ELIMINATORY DRGAŃ (12)
· Oszacowanie efektywności układów regulacji
Równanie ruchu konstrukcji z zainstalowanym układem regulacji
(aktywnym, pasywnym lub bez tego układu) można zapisać w po-
staci:
)
(
~
)
(
t
t
z
A
z
=
&
Dla konstrukcji bez układu regulacji
A
A
=
~
.
Dla pasywnego układu regulacji (np. tłumiki lepko-sprężyste)
+
−
+
−
=
−
−
)
(
)
(
~
1
1
t
t
C
C
M
K
K
M
I
0
A
.
Dla układu aktywnej regulacji
BG
A
A
+
=
~
.
Rozwiązaniem równania ruchu jest
c
z
)
exp(
)
(
t
t
λ
=
,
c
z
)
exp(
)
(
t
t
λ
λ
=
&
.
Wartość własną
λ
należy wyznaczyć rozwiązując problem własny:
(
)
0
c
I
A
=
−
λ
~
Wartości własne
j
j
j
i
η
µ
λ
+
=
są w ogólności liczbami zespolo-
nymi. Częstość drgań własnych
j
ω
i bezwymiarowy współczynnik
tłumienia
j
ς
stowarzyszone z j-tą postacią związane są z wartością
własną
j
λ
w sposób następujący:
2
2
2
j
j
j
η
µ
ω
+
=
j
j
j
ω
µ
ς
/
−
=
.
Porównując modalne współczynniki tłumienia dla konstrukcji z za-
instalowanym układem regulacji i konstrukcji bez takiego układu
można ocenić efektywność zaproponowanego układu regulacji.

WYKŁAD OBIERALNY rok akademicki 2002/03
23
AKTYWNE ELIMINATORY DRGAŃ (13)
· Numeryczna symulacja zachowania układu aktywnej regulacji
Zachowanie konstrukcji z zainstalowanym układem aktywnej re-
gulacji można analizować rozwiązując równania ruchu o postaci:
)
(
)
(
~
)
(
t
t
t
Hf
z
A
z
+
=
&
Rozwiązanie powyższego równania da się przedstawić w postaci:
τ
τ
τ
d
t
t
t
t
)
(
)
(
)
(
)
(
0
0
Hf
z
z
∫
−
+
=
Φ
Φ
,
( )
m
m
m
t
t
t
t
t
t
A
A
A
A
I
A
~
!
......
~
!
3
~
!
2
~
~
exp
)
(
3
3
2
2
+
+
+
+
+
=
=
Φ
.
•
Realizacja numeryczna obliczeń
Przedział całkowania dzielimy na małe odcinki o długości h. Jeżeli
oznaczyć
1
1
)
(
+
+
≡
k
k
t
z
z
,
k
k
t
z
z
≡
)
(
a
h
t
t
k
k
+
=
+
1
to stan układu w
chwili czasu
1
+
k
t
można obliczyć ze wzoru:
τ
τ
τ
d
h
h
h
k
k
)
(
)
(
)
(
0
1
Hf
z
z
∫
−
+
=
+
Φ
Φ
Całkę w powyższym wzorze oblicza się zakładając, że w przedzia-
le czasu
)
,
(
1
+
k
k
t
t
wartość siły wymuszającej się nie zmienia. Wte-
dy
k
h
h
d
h
Hf
Hf
)
(
)
(
)
(
0
Γ
Φ
=
−
∫
τ
τ
τ
,
.....
~
~
~
)
(
3
4
!
4
1
2
3
!
3
1
2
!
2
1
+
+
+
+
=
A
A
A
I
h
h
h
h
h
Γ
,
a stan układu w kolejnych chwilach oblicza się ze wzoru:
k
k
k
h
h
Hf
z
z
)
(
)
(
1
Γ
Φ
+
=
+
.
WYKŁAD OBIERALNY rok akademicki 2002/03
24
AKTYWNE ELIMINATORY DRGAŃ (14)
· Wyniki przykładowej analizy numerycznej (1)
•
Budynek o konstrukcji szkieletowej, 15 kondygnacyjny
•
Schemat statyczny - rama płaska (rama ścinana, rama Paza)
•
Wysokość kondygnacji 4 m, masa stropu 56000,0 kg, sztywność
słupa na zginanie 135,0 MNm
2
, tłumienie modalne 1 i 2 postaci
drgań odpowiednio 1% i 2% tłumienia krytycznego
•
Masa tłumika 8400,0 kg, sztywność tłumika 74800,0 N/m,
współczynnik tłumienia 4200,0 Ns/m
•
Obciążeniem budynku jest parcie wiatru opisane widmem
Davenporta
V z t
V z
w z t
( , )
( )
( , )
=
+
0
20
40
60
80
100
120
140
t [s]
-20.0
-10.0
0.0
10.0
20.0
w(
t)
[m
/s
]
Symulacja fluktuacji prędkości wiatru w(z,t) na poziomie rygla 15 kondygnacji
Wybór macierzy
Q R
,
•
Macierz
R
jest tutaj skalarem; przyjęto r=0,5 10
-15
•
Macierz
Q
wyznaczono 2 sposobami:
1. Rozwiązując równanie Lapunova o postaci:
A Q AQ
D
T
+
= −
2. Metodą prób i błędów

WYKŁAD OBIERALNY rok akademicki 2002/03
25
AKTYWNE ELIMINATORY DRGAŃ (15)
· Wyniki przykładowej analizy numerycznej (2)
•
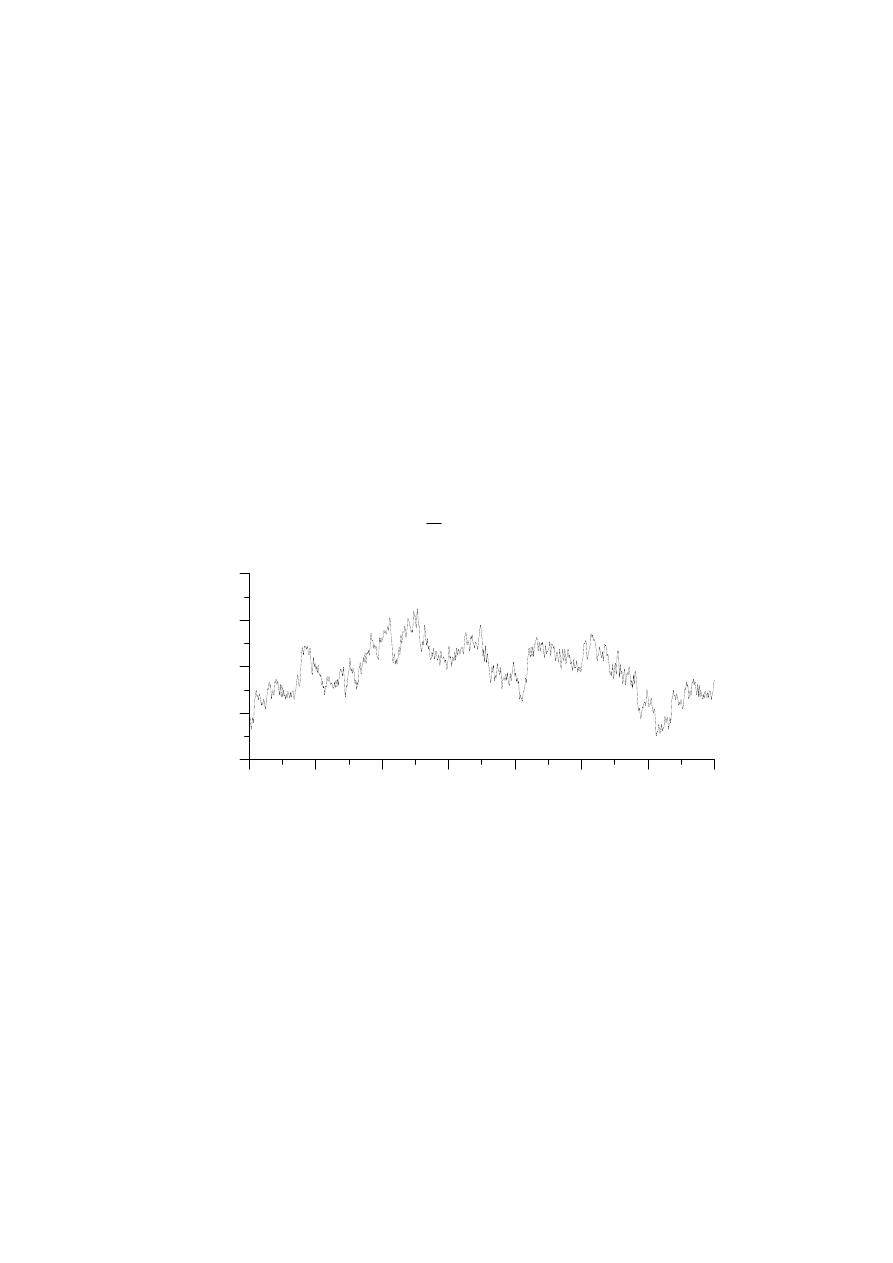
Odpowiedź dynamiczna ramy
0
20
40
60
80
100
120
140
czas t [s]
-0.04
-0.03
-0.02
-0.01
0.00
0.01
0.02
0.03
0.04
Prz
emiesz
cz
enie
1
5
kon
dy
gna
cji
[m]
Rys.2 Przemieszczenia poziome rygla 15 kondygnacji ramy
linia przerywana - rama bez tłumika drgań
linia ciągła - rama z aktywnym tłumikiem drgań
•
Wyniki obliczeń statystycznych
Tablica 1 Wartości średniokwadratowe dla 15 kondygnacji ramy
Wartość średniokwa-
dratowa
Rama bez
tłumika
drgań
Rama z bier-
nym tłumi-
kiem drgań
Rama z ak-
tywnym
układem re-
gulacji przy-
padek 1
Rama z aktyw-
nym układem
regulacji przy-
padek 2
Przemieszczenia [cm] 1,307
0,847
0,760
0,786
Prędkości [cm/s]
3,413
1,568
1,088
1,058

WYKŁAD OBIERALNY rok akademicki 2002/03
26
AKTYWNE ELIMINATORY DRGAŃ (16)
· Metoda wykorzystująca twierdzenie Lapunowa o stabilności ru-
chu – regulacja bang-bang (1)
•
Metoda wykorzystuje twierdzenie o stabilności ruchu układu
dynamicznego (stabilności ruchu według Lapunowa)
•
Definicja funkcji Lapunowa
Funkcją Lapunowa nazywamy każdą funkcję
)
(z
V
ciągłą, róż-
niczkowalną i lokalnie dodatnio określoną. Spełnia ona wobec
tego warunki:
0
)
(
=
0
V
,
0
)
(
>
z
V
dla każdego
0
z
≠
.
•
Twierdzenie Lapunowa
Rozważmy układ dynamiczny którego ruch jest opisany wekto-
rowym równaniem różniczkowym o postaci:
)
(z
f
z
=
&
.
Ponadto, niech
0
0
f
=
)
(
. Ruch układu jest stabilny (w sensie
Lapunowa) jeżeli można znaleźć taką funkcję Lapunowa
)
(z
V
,
że
0
)
(
≤
z
V&
,
dla wszystkich trajektorii
)
(t
z
w pewnym otoczeniu
0
z
=
.
•
Powyższe twierdzenie może być punktem wyjścia przy projek-
towaniu aktywnego regulatora drgań.

WYKŁAD OBIERALNY rok akademicki 2002/03
27
AKTYWNE ELIMINATORY DRGAŃ (17)
· Metoda wykorzystująca twierdzenie Lapunowa o stabilności ru-
chu – regulacja bang-bang (2)
•
Równanie stanu (bez składnika uwzględniającego wymuszenie)
)
(
)
(
)
(
t
t
t
Bu
Az
z
+
=
&
,
•
Funkcja Lapunowa
)
(
)
(
)
(
t
t
V
T
Qz
z
z
=
,
•
Pochodna funkcji Lapunowa
)
(
)
(
)
(
)
(
)
(
t
t
t
t
V
T
T
z
Q
z
Qz
z
z
&
&
&
+
=
,
)
(
)
(
2
)
(
)
)(
(
)
(
t
t
t
t
V
T
T
T
Qz
B
u
z
QA
Q
A
z
z
T
+
+
=
&
,
•
Uwagi:
Ruch układu będzie stabilny jeżeli macierz
QA
Q
A
T
+
będzie
ujemnie określona i równa na przykład macierzy
P
−
gdzie ma-
cierz
P
jest dowolną macierzą dodatnio określoną. Można więc
napisać równanie:
P
QA
Q
A
T
−
=
+
. (Równanie Lapunowa)
Siłę regulacji
)
(t
u
dobieramy tak aby
)
(z
V&
było możliwie małe.
Można wykazać, że będzie tak jeżeli
[
]
)
(
sgn
)
(
max
t
t
T
Qz
B
u
u
−
=
.
P
,
max
u
,
[ ]
•
sgn
?
Równanie Lapunowa jest zlinearyzowaną wersją równania Ric-
cati’ego. Można je rozwiązać metodą Bartelsa-Stewarta.

WYKŁAD OBIERALNY rok akademicki 2002/03
28
AKTYWNE ELIMINATORY DRGAŃ (17a)
· Metoda natychmiastowej regulacji optymalnej (1)
Instantaneous optimal control
Przybliżone rozwiązanie równania ruchu
&( )
( )
( )
( )
z
Az
Hf
Bu
t
t
t
t
=
+
+
,
(1)
( )
(
)
[
][
]
τ
τ
τ
τ
d
t
t
t
t
t
t
t
∫
+
−
+
=
0
)
(
)
(
exp
)
(
exp
)
(
0
Hf
Bu
A
z
A
z
.
(2)
Niech w chwili
0
0
=
t
1
0
)
(
−
=
k
t
z
z
, a stan układu w chwili
h
t
t
+
=
0
oznaczmy symbolem
k
t
z
z
=
)
(
. Rozwiązanie (2) moż-
na teraz przepisać w postaci:
( )
(
)
[
][
]
τ
τ
τ
τ
d
t
h
h
h
k
k
∫
+
−
+
=
−
0
1
)
(
)
(
exp
exp
Hf
Bu
A
z
A
z
.
(3)
Całkę występującą we wzorze (3) oblicza się w sposób przybli-
żony metodą trapezów. Wartość funkcji podcałkowej na końcach
przedziału całkowania tzn. dla
0
=
τ
i
h
=
τ
wynosi:
( )(
)
1
1
1
exp
−
−
−
+
=
k
k
k
h
Hf
Bu
A
s
,
k
k
k
Hf
Bu
s
+
=
.
(4)
We powyższych wzorach wielkości z indeksami k-1 i k odnoszą
się odpowiednio do chwil
0
0
=
t
i
h
t
t
+
=
0
. Po zastosowaniu
metody trapezów można rozwiązanie (3) przepisać w postaci:
(
)
k
k
k
k
h
Hf
Bu
d
z
+
+
=
−
2
1
,
(5)
gdzie
( )(
)
1
1
1
1
exp
−
−
−
−
+
+
=
k
k
k
k
h
Hf
Bu
z
A
d
.
Formuła rekurencyjna (5) pozwala na obliczanie stanu układu w
dyskretnych chwilach czasu. Może być rozumiana jako analogon
równania ruchu.

WYKŁAD OBIERALNY rok akademicki 2002/03
29
AKTYWNE ELIMINATORY DRGAŃ (17b)
· Metoda natychmiastowej regulacji optymalnej (2)
Wskaźnik jakości regulacji – funkcja celu
k
T
k
k
T
k
k
J
Ru
u
Qz
z
+
=
(6)
Wymaga się aby macierz
R
była dodatnio określona, a macierz
Q
była półdodatnio określona.
Funkcjonał (6) ma osiągnąć wartość minimalną przy czym powi-
nien być równocześnie spełniony warunek (5). Wprowadzamy
wobec tego funkcjonał rozszerzony o postaci:
(
)
+
−
−
+
+
=
−
k
k
k
k
T
k
k
T
k
k
T
k
k
h
L
Hf
Bu
d
z
Ru
u
Qz
z
2
1
Λ
. (7)
Warunki stacjonarności
W punkcie stacjonarności funkcjonału 1 wariacja jest równa ze-
ru.
0
=
∂
∂
+
∂
∂
+
∂
∂
=
k
k
T
k
k
k
T
k
k
k
T
k
k
L
L
L
L
Λ
Λ
δ
δ
δ
δ
u
u
z
z
,
(8)
0
Qz
z
=
+
=
∂
∂
k
k
k
k
L
Λ
2
,
(9)
0
B
Ru
u
=
−
=
∂
∂
k
T
k
k
k
h
L
Λ
2
2
,
(10)
(
)
0
Hf
Bu
d
z
=
+
−
−
=
∂
∂
−
k
k
k
k
k
k
h
L
2
1
Λ
. (11)
Teraz warunki stacjonarności są równaniami algebraicznymi
(warunki (9) i (10)) lub równaniami rekurencyjnymi (równanie
(11)).

WYKŁAD OBIERALNY rok akademicki 2002/03
30
AKTYWNE ELIMINATORY DRGAŃ (17c)
· Metoda natychmiastowej regulacji optymalnej (3)
Warunki sprzężenia zwrotnego i rozwiązanie problemu regulacji
Podobnie jak w przypadku metody LQR zakłada się, że
k
k
k
z
P
=
Λ
,
(12)
Po podstawieniu (12) do równania (9) otrzymuje się
Q
P
k
2
−
=
, a
po podstawieniu ostatniego rezultatu i (12) do równania (10)
mamy:
k
T
k
h
Qz
B
R
u
1
2
−
−
=
.
(13)
Zauważmy, że rolę macierzy Riccati’ego spełnia teraz macierz
Q
h
oraz, że nie zachodzi potrzeba rozwiązywania równania Ric-
cati’ego.
Należy jednak pamiętać, że o efektywności aktywnej regulacji i o
stabilności ruchu całego układu (konstrukcja + układ regulacji)
decyduje teraz omawiana macierz
Q
.
Wyznaczanie wektora stanu
Po podstawieniu (13) do (5) otrzymuje się
k
k
T
k
k
h
h
Hf
Qz
B
BR
d
z
2
4
1
2
1
+
−
=
−
−
,
a dalej po prostych przekształceniach
+
+
=
−
−
−
k
k
T
k
h
h
Hf
d
Q
B
BR
I
z
2
4
1
1
1
2
.
(14)

WYKŁAD OBIERALNY rok akademicki 2002/03
31
AKTYWNE ELIMINATORY DRGAŃ (17d)
· Metoda natychmiastowej regulacji optymalnej (4)
Określanie macierzy wagowej
Q
(1)
Dodatnio określoną macierz
Q
można wyznaczać metodą prób i
błędów. Dodatnią określoność można to sprawdzić obliczając
wartości własne tej macierzy. Metoda prób i błędów jest bardzo
uciążliwa w praktycznym stosowaniu.
Inna metoda polega na tym aby macierz
Q
dobierać w taki spo-
sób by ruch całego układu był stabilny. Do badania stabilności
ruchu można zastosować bezpośrednią metodę Lapunowa.
Ponieważ chodzi o określenie macierzy
Q
która byłaby dodatnio
określona można w zastępstwie problemu z czasem dyskretnym
rozpatrywać problem z czasem ciągłym. Wtedy po pominięciu
wymuszenia mamy
)
(
)
(
)
(
t
t
t
Bu
Az
z
+
=
&
,
)
(
)
(
1
2
1
t
t
T
Qz
B
R
u
−
−
=
, (15)
a po prostych przekształceniach:
(
)
)
(
)
(
1
2
1
t
t
T
z
Q
B
BR
A
z
−
−
=
&
.
(16)
Funkcję Lapunowa wybiera się w postaci:
)
(
)
(
)
(
t
t
t
V
Qz
z
=
.
(17)
Pochodną tej funkcji, po uwzględnieniu (16), można przedstawić
w postaci:
(
)
)
(
)
(
)
(
)
(
)
(
)
(
)
(
1
2
1
t
t
t
t
t
t
t
V
T
T
T
T
T
z
Q
B
QBR
QA
Q
A
z
z
Q
z
Qz
z
−
−
+
=
+
=
&
&
&
(18)

WYKŁAD OBIERALNY rok akademicki 2002/03
32
AKTYWNE ELIMINATORY DRGAŃ (17e)
· Metoda natychmiastowej regulacji optymalnej (5)
Określanie macierzy wagowej
Q
(2)
Ruch układu jest stabilny jeżeli
0
)
(
<
t
V&
. Będzie tak jeżeli w (18)
wyrażenie w nawiasie będzie równe pewnej ujemnie określonej
macierzy
D
−
. Powinno być wobec tego spełnione równanie Ric-
cati’ego o postaci:
D
Q
B
QBR
QA
Q
A
−
=
−
+
−
T
T
1
2
1
.
(19)
Ponieważ macierz
R
jest dodatnio określona więc macierz
T
B
BR
1
−
jest również dodatnio określona. W rezultacie macierz
Q
można wyznaczać z (19) po pominięciu składnika nieliniowe-
go. Mamy więc ostatecznie do rozwiązania równanie Lapunowa:
D
QA
Q
A
−
=
+
T
.
(20)
Równanie to jest łatwiejsze do rozwiązania.
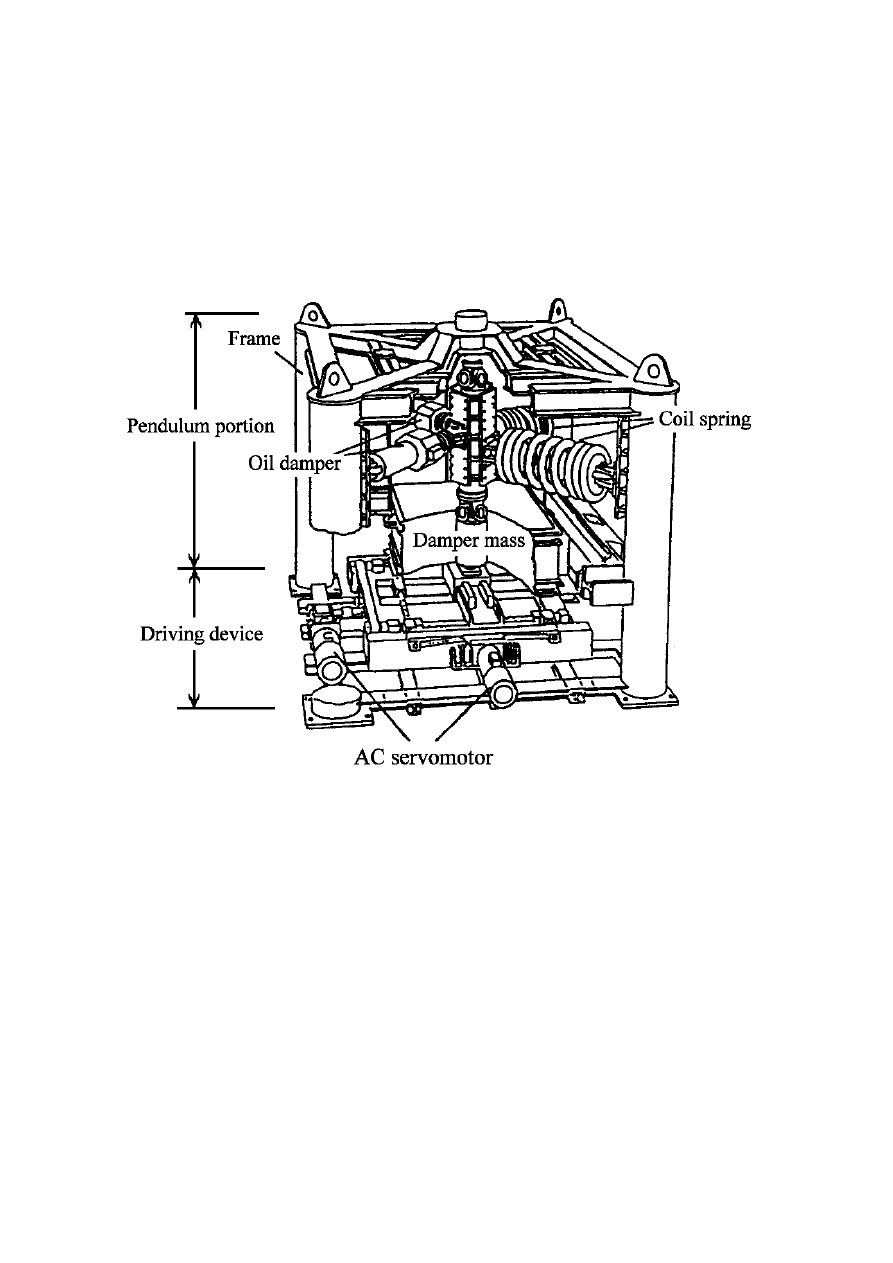
WYKŁAD OBIERALNY rok akademicki 2002/03
33
AKTYWNE ELIMINATORY DRGAŃ (18)
· Techniczna realizacja aktywnego eliminatora drgań
Wieża kontrolna portu lotniczego w Osace
•
budynek o wymiarach 12,9x12,9x86,0m
•
2 aktywne eliminatory drgań na poziomie 72,0 m
•
zmniejszenie drgań wywołanych działaniem wiatrem o 50%
•
tłumik masowy o masie 5000 kg (0,4% masy budynku)
•
tłumik dostrojony do 1 częstości drgań własnych budynku (0,8
Hz)
•
algorytm regulacji - liniowy regulator kwadratowy
•
współczynnik tłumienia wzrósł z około 0,4% do 7% tłumienia
krytycznego
•
w przypadku awarii zasilania układ działa jako pasywny elimi-
nator drgań lub zostaje całkowicie wyłączony.

WYKŁAD OBIERALNY rok akademicki 2002/03
34
AKTYWNE ELIMINATORY DRGAŃ (19)
· Zalety i wady aktywnych eliminatorów drgań
Najistotniejsze zalety
•
Możliwe jest znaczne zmniejszenie amplitud drgań.
•
Możliwe jest znaczne zmniejszenie przyspieszeń konstrukcji.
•
Można zmniejszyć przemieszczenia dynamiczne i przyspie-
szenia konstrukcji stowarzyszone z kilkoma postaciami drgań.
Najistotniejsze wady
•
Niezbędne są urządzenia wywołujące duże siły aktywnej regu-
lacji i wobec tego istnieje duże zapotrzebowanie na energię.
•
Układy aktywnej regulacji muszą pozostawać w stałej gotowo-
ści do działania pomimo, że trzęsienia ziemi i silne wiatry wy-
stępują sporadycznie.
Wyszukiwarka
Podobne podstrony:
zestaw podstawowych drgan id 58 Nieznany
200603autotrax drukowanie id 54 Nieznany (2)
eliminacja drgan cw1 id 160384 Nieznany
54 B 1984 1990 r id 41448 Nieznany
54 7 id 41444 Nieznany
54 3 id 41440 Nieznany (2)
filtry aktywne wemif id 171041 Nieznany
54 60 id 41458 Nieznany (2)
54 2 id 41438 Nieznany (2)
54 id 41434 Nieznany
aktywnosc fizyczna id 54384 Nieznany (2)
54 A 1984 1990 r id 41446 Nieznany
decyzja 54 id 132505 Nieznany
metoda aktywna id 294176 Nieznany
aktywnosc enzymoteczna id 54407 Nieznany
II 54 id 209782 Nieznany
54 B 1984 1990 r id 41448 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
więcej podobnych podstron