ALGEBRA LINIOWA 1
Specjalna lista zadań*
Uwaga. Lista zawiera zadania trudniejsze i jest ona przeznaczona dla studentów pragnących głębiej zastanowić się nad
tematyką kursu. Lista jest przygotowana również z myślą o tych osobach, które zamierzają ubiegać się w przyszłości o ocenę
celującą 5,5 z ALGEBRY LINIOWEJ 1, ALGEBRY Z GEOMETRIĄ ANALITCZNĄ oraz kursów pokrewnych. Prezen-
towane tu zadania pojawiły się na egzaminach na ocenę celującą organizowanych od roku 1995. Lista jest podzielona na cztery
części tematyczne, a zadania są ułożone w kolejności merytorycznej.
Oryginalne zestawy zadań z poprzednich egzaminów na
ocenę celującą wraz z odpowiedziami i wskazówkami znajdują się w zbiorze: M. Gewert, Z. Skoczylas (opr.), Algebra liniowa
1. Kolokwia i egzaminy
.
Specjalna lista zadań, standardowa lista zadań oraz inne materiały dotyczące tego kursu znajdują się
także na stronie
www.im.pwr.wroc.pl
/~tjurlew
Egzamin na ocenę celującą będzie się składał z czterech zadań o podobnym stopniu trudności ocenianych w skali od 0 do 5
punktów. Uzyskanie w czasie trzech godzin co najmniej 10 punktów będzie gwarancją sukcesu.
LITERATURA UZUPEŁNIAJĄCA
:
[1] P. R. Halmos, Linear Algebra Problem Book, Dolciani Mathematical Expositions, No 16, The Mathematical
Association of America, Washington 1995
[2] J. Klukowski, Algebra w zadaniach, Wydawnictwo Politechniki Warszawskiej, Warszawa 1991
[3] Pod red. A. I. Kostrikina, Zbiór zadań z algebry, PWN, Warszawa 1995
[4] S. Przybyło, A Szlachtowski, Algebra i geometria afiniczna w zadaniach, WNT Warszawa 1983
[5] I. V. Proskuryakov, Problems in Linear Algebra, Mir Publishers, Moscow 1978
[6] Fuzhen Zhang, Linear algebra, Challenging Problems for Students, The Johns Hopkins University Press, Baltimore and
London 1996.
Teresa Jurlewicz
, Zbigniew Skoczylas, luty 2007
ZADANIA
1. Liczby zespolone
1.1*
Liczby zespolone i spełniają warunki
. Czy
?
u
v
u
5
= v
5
, u
17
= v
17
u
= v
Odpowiedź uzasadnić.
(cel-05-1)
1.2*
Zbadać postać zbioru
w zależności od liczby zespo-
{ z ∈ C :
z
− z
0
= r }
lonej
i liczby dodatniej .
(cel-15-1)
z
0
r
1.3*
Wyrazić
w zależności od
i
wiedząc, że moduły
arg
( z
1
− z
2
)
arg z
1
arg z
2
liczb zespolonych
są jednakowe.
(cel-13-1)
z
1
, z
2
1.4*
Wyznaczyć wszystkie liczby zespolone
spełniające układ równań
z
1
, z
2
, z
3
.
(cel-06-4)
z
1
= z
2
= z
3
= 1
z
1
+ z
2
+ z
3
= 1
z
1
⋅ z
2
⋅ z
3
= 1
1.5*
Kąty ostre
są określone warunkami
.
α, β, γ
tg
α = 1, tg β =
1
2
, tg
γ =
1
3
Za pomocą działań na liczbach zespolonych obliczyć
.
(cel-11-1)
α + β + γ
1.6*
Zbadać, dla jakich liczb naturalnych oraz dla jakich kątów prawdziwy jest
n
α
"przekręcony wzór de Moivre'a"
.
(cel-17-1)
( sin α + i cos α )
n
= sin nα + i cos nα
1.7*
Zbadać, czy istnieje liczba naturalna taka, że
jest liczbą rzeczywistą.
n
( 2 + i )
n
(cel-07-3)
1.8*
W okrąg o promieniu wpisano siedmiokąt foremny o wierzchołkach
,
1
A
1
. Na okręgu wybrano punkt . Korzystając z liczb zespolonych udo-
A
2
,
…, A
7
P
wodnić, że suma
nie zależy od położenia
( PA
1
)
2
+ ( PA
2
)
2
+ … + ( PA
7
)
2
punktu .
(cel-02-3)
P
1.9*
Na wszystkich bokach równoległoboku zbudowano zewnętrzne kwadraty. Korzy-
stając z liczb zespolonych pokazać, że środki tych kwadratów tworzą kwadrat.
(cel-19-2)
1.10* Niech
oraz będą liczbami naturalnymi. Wykorzystując liczby zespolone
a
, b
n
udowodnić, że istnieją liczby całkowite
, dla których zachodzi równość
x
, y
.
(cel-01-4)
( a
2
+ b
2
)
n
= x
2
+ y
2
1.11* Liczba zespolona spełnia związek
. Obliczyć
z
z
+
1
z
= 2 cos
π
2000
.
(cel-10-1)
z
2000
+
1
z
2000
1.12* Znaleźć wszystkie pary
liczb całkowitych, dla których zachodzi równość
( p, q )
.
(cel-16-1)
1
2
+ i
3
2
p
=
2
2
− i
2
2
q
1.13* Niech
. Pokazać, że
2001
1
= { 1, z
1
, z
2
, ..., z
2000
}
.
(cel-12-1)
Π
k
= 1
2000
( 1 − z
k
) = 2001
1.14* Uzasadnić, że istnieją liczby naturalne
spełniające warunek
m
≠ n
.
(cel-18a-1)
e
im
− e
in
<
1
2006
2. Wielomiany
2.1*
Znaleźć wszystkie liczby całkowite , dla których wielomian
p
P
( x ) =
jest podzielny przez wielomian
.
(cel-02-4)
x
13
+ x + 90
Q
( x ) = x
2
− x + p
2.2*
Znaleźć liczby wymierne
, dla których liczba
jest
p
, q
x
1
= 3 + 2
pierwiastkiem wielomianu
.
(ce1-13-2)
W
( x ) = x
4
+ px
2
+ q
2.3*
Uzasadnić, że liczba
jest wymierna.
(cel-10-2)
3
2
+ 5 +
3
2
− 5
2.4*
Znaleźć resztę z dzielenia wielomianu
przez wielomian
x
2000
+ x
1999
+ 2001
.
(cel-09-1)
( x
2
+ 1 )
2
2.5*
Czy istnieje wielomian
stopnia
, który spełnia warunki
W
2002
oraz
,
W(
1)
= W(2) = W(3) = ... = W(2001) = 1
W(
2002)
= 2
. Odpowiedź uzasadnić.
(ce1-15-2)
W(
2003)
= 3
2.6*
Wielomian stopnia mniejszego od
spełnia warunek
2005
.
W
(1) = W (2) = ... = W (2005)
Podać wartość
(cel-17-2)
W
(2006) − W (0).
2.7*
Pokazać, że wielomiany
,
z
4
− z
3
+ z
2
+ 2z − 6 z
4
+ z
3
+ 3z
2
+ 4z + 6
mają wspólne pierwiastki zespolone.
(cel-16-2)
2.8*
Liczby zespolone
są pierwiastkami wielomianu
z
1
, z
2
,
…, z
9
. Obliczyć sumę
.
(cel-03-2)
W
( z ) = z
9
+ 13z
8
+ 5z − 2
Σ
i
= 1
9
z
i
2
2.9*
Prosta
przecina wykres funkcji
y
= mx + b
y
= 2x
5
− x
3
+ 4x
2
+ 3x − 7
w pięciu różnych punktach
. Pokazać,
( x
1
, y
1
), ( x
2
, y
2
), ..., ( x
5
, y
5
)
ż
e liczba
nie zależy od parametrów
i .
(cel-01-3)
x
1
+ x
2
+ … + x
5
5
m
b
2.10* Liczby zespolone
są pierwiastkami wielomianu
. Obliczyć
α, β, γ
x
3
+ x + 1
wartość wyrażenia
.
(cel-08-2)
1
α + i
+
1
β + i
+
1
γ + i
2.11* Liczby zespolone
są pierwiastkami wielomianu
α, β, γ
Uzasadnić, że
.
(cel-04-1)
W
( z ) = z
3
+ ( 1 − 2i ) z + 3 − 5i.
α
3
+ β
3
+ γ
3
= 3αβγ
2.12* Wielomian
ma współczynniki
W
( z ) = z
n
+ a
n
−1
z
n
−1
+ ... + a
1
z
+ a
0
rzeczywiste. Pierwiastkiem tego wielomianu jest liczba
, gdzie
z
0
= e
i
ϕ
. Uzasadnić równość
ϕ ∈ R
(cel-06-1)
a
n
−1
sin
ϕ + a
n
−2
sin 2
ϕ + ... + a
1
sin
[ (n − 1) ϕ ] + a
0
sin n
ϕ = 0.
2.13* Wielomian
rozłożyć na czynniki rzeczywiste.
(cel-11-2)
x
2001
+ x
2000
+ ... + x + 1
2.14* Wykorzystując rozkład wielomianu
na czynniki rzeczywiste uzasadnić
x
2n
− 1
równość:
.
(cel-18a-2)
sin
π
2n
⋅ sin
2
π
2n
⋅ sin
3
π
2n
⋅ ... ⋅ sin
( n−1 )π
2n
=
n
2
n
−1
2.15* Zbadać, czy istnieje wielomian zespolony
taki, że
W
.
(ce1-14-1)
W
2
( z ) = z
2002
+ z
2001
+ z
2000
+ ... + z + 1
2.16* Znaleźć niezerowy wielomian o współczynnikach całkowitych, możliwie naj-
niższego stopnia, którego pierwiastkami są liczby
, gdzie
.
(ce1-18-2)
e
4 k
π
101
i
k
= 1, 2, 3, ..., 50
2.17* Niech
. Znaleźć wszystkie pierwiastki zespolone równania
f
( x ) = x
2
+ 12x + 30
.
(ce1-14-3)
f
{ f [ f ( x ) ] } = 0
2.19* Adam napisał i ukrył wielomian
pewnego stopnia o nieujemnych współ-
W
( x )
czynnikach całkowitych. Bartek chce odgadnąć ten wielomian. Adam może mu
podać wartość wielomianu dla dowolnego argumentu wymiernego . Pokazać,
x
ż
e Bartek może odgadnąć wielomian zadając tylko dwa pytania, przy czym drugie
po uzyskaniu odpowiedzi na pierwsze z nich.
(cel-19-1)
3. Macierze i wyznaczniki
3.1*
Uzasadnić, że nie istnieją macierze
spełniające warunek
A
, B
,
AB
− BA = I
gdzie oznacza macierz jednostkową.
(cel-11-3)
I
3.2*
Znaleźć wszystkie macierze stopnia
, które spełniają równości
A
1998
.
A
1997
= I,
A
2000
= I
Odpowiedź uzasadnić.
(cel-6-2)
3.3*
Pokazać, że macierz
jest nieosobliwa.
102495 550429 873296 660697
370628 909093 127450 925601
835044 601178 624655 263392
663780 487252 292276 593107
Odpowiedź uzasadnić.
(cel-09-3 )
3.4*
Elementami macierzy kwadratowej stopnia są tylko liczby
oraz (dowol-
4
−2
1
nie ustawione). Pokazać, że wyznacznik tej macierzy jest podzielny przez
.
(cel-12-2)
27
3.5*
Pokazać, że istnieje macierz kwadratowa stopnia
, złożona tylko z liczb
12
, której wyznacznik jest równy
.
(cel-02-2)
−1, 0, 1
1995
3.6*
Obliczyć wyznacznik macierzy kwadratowej
stopnia
, gdzie
[a
ij
]
n
∈ N
dla
.
(cel-14-2)
a
ij
= min { i, j }
1
≤ i, j ≤ n
3.7*
Obliczyć wyznacznik macierzy
stopnia
, której elementy mają postać
[a
ij
]
n
≥ 3
.
(cel-15-3)
a
ij
=
2 dla i
= j,
1 dla
i
− j = 1,
0 dla
i
− j ≥ 2.
3.8*
Obliczyć
dla macierzy
stopnia
określonej następująco:
det A
A
= [a
ij
]
2005
dla
,
dla
,
a
i i
+1
= 2005
1
≤ i ≤ 2004 a
i i
+2
= −2004
1
≤ i ≤ 2003
dla
,
dla
,
a
ii
−1
= −2005
2
≤ i ≤ 2005 a
i i
−2
= 2004
3
≤ i ≤ 2005
w pozostałych przypadkach.
(cel-17-3)
a
ij
= 0
3.9*
Niech będzie antysymetryczną macierzą stopnia
. Obliczyć wyznacznik
A
1997
macierzy
.
(cel-05-2)
1996 A
− 1998 A
T
3.10*. Macierz spełnia warunek
. Pokazać, że wówczas
A
A
2007
= O
.
(cel-19-3)
det
( I + A + A
2
+ ... + A
2006
) ≠ 0
3.11* Elementami macierzy kwadratowej są liczby
. Każdy wiersz
0, 1, 2,
…, 9
tej macierzy czytany jako liczba w systemie dziesiętnym jest podzielny przez .
7
Udowodnić, że wyznacznik tej macierzy także jest podzielny przez .
(cel-03-1)
7
3.12* Miejscowości
położone są przy prostoliniowej drodze. Odleg-
M
1
, M
2
, ..., M
n
łość między miejscowościami
oraz
jest równa
, gdzie
.
M
i
M
j
d
ij
1
≤ i, j ≤ n
Udowodnić, że
.
(cel-01-1)
det
[d
ij
] ≠ 0
3.13* Pierwszy wiersz wyznacznika stopnia , gdzie
, tworzą kolejne liczby
n
n
≥ 2
pierwsze
. Pokazać, że w pozostałe wiersze wyznacznika
2, 3, 5, ..., p
n
można wpisać liczby naturalne tak, aby był on równy .
(cel-16-3)
1
3.14* Niech oznacza macierz jednostkową stopnia
. Ponadto niech
I
n
∈ N
oraz
będą liczbami rzeczywistymi.
a
1
, a
2
, ..., a
n
b
1
, b
2
, ..., b
n
Uzasadnić równość
(cel-08-4)
.
det
( I +
a
1
a
2
.
..
a
n
b
1
b
2
. .
. b
n
) = 1 + det ( b
1
b
2
. .
. b
n
a
1
a
2
.
..
a
n
)
3.15* Na płaszczyźnie zespolonej dane są trójkąty o wierzchołkach
oraz
z
1
, z
2
, z
3
. Pokazać, że te trójkąty są podobne wtedy i tylko wtedy, gdy
w
1
, w
2
, w
3
.
(cel-18-1)
det
z
1
z
2
z
3
w
1
w
2
w
3
1
1
1
= 0
3.16* Uzasadnić, że równanie macierzowe
2X
2
+ 2X =
−1
5
3
−2
1
2
0
−4 −3
nie ma rozwiązań w zbiorze macierzy rzeczywistych.
(cel-18-3)
3.17* Niech
oraz
. Macierze
X
1
= [ 1 1 1 ], X
2
= [ 1 −1 2 ]
X
3
= [ 2 2 1 ]
i wymiaru
spełniają równości:
A
B
3
× 1999
.
X
1
A
= X
1
B
,
X
2
A
= X
2
B
,
X
3
A
= X
3
B
Czy
? Odpowiedź uzasadnić.
(cel-08-3)
A
= B
3.18* Macierz jest odwracalna i ma następującą własność: wszystkie elementy
A
jej głównej przekątnej są jednakowe oraz wszystkie elementy spoza jej głównej
przekątnej są jednakowe. Zbadać, czy macierz
ma tę samą własność.
(cel-18a-3)
A
−1
3.19* Macierz spełnia warunek
. Obliczyć
.
(cel-07-1)
A
A
+ A
−1
=
1 3 5
0 2 4
0 0 3
A
3
+ A
−3
3.20* Macierz jest odwracalna. Obliczyć sumę wszystkich elementów głównej
P
przekątnej macierzy
.
(cel-10-3)
A
= P
−1
⋅
1 0 0 . .
.
0
0 2 0 . .
.
0
0 0 3 . .
.
0
.
..
.
..
.
..
.
.
.
.
..
0 0 0 . .
. 2000
⋅ P
3.21* Liczba zespolona
jest pierwiastkiem równania
. Uzupełnić zapis
z
≠ 1
z
5
= 1
.
(ce1-13-3)
1 1 1 1 1
1 z z
2
z
3
z
4
1 z
4
z
3
z
2
z
1 z
2
z
4
z
1
z
3
1 z
3
z
1
z
4
z
2
−1
=
1
5
1 1 1 1 1
1 . . . .
1 . . . .
1 . . . .
1 . . . .
4. Układy równań liniowych
4.1*
Wzór Eulera wyrażający zależność między liczbą ścian , liczbą krawędzi
S
K
oraz liczbą wierzchołków
dowolnego wielościanu wypukłego ma postać
W
,
αS + βK + γW + δ = 0
gdzie
są nieznanymi współczynnikami. Znaleźć ten wzór.
(ce1-10-2)
α, β, γ, δ
4.2*
Pokazać, że dla dowolnych liczb rzeczywistych
oraz
x
1
< x
2
y
1
, y
2
, y
1
, y
2
istnieje wielomian
stopnia
spełniający warunki
W
≤ 3
oraz
.
(ce1-12-3)
W
( x
1
) = y
1
, W
( x
2
) = y
2
W
( x
1
) = y
1
, W
( x
2
) = y
2
4.3*
Elementami macierzy kwadratowej
stopnia są liczby całkowite.
[a
ij
]
n
Udowodnić, że jedynym rozwiązaniem układu równań
x
1
2
= a
11
x
1
+ a
12
x
2
+ … + a
1n
x
n
x
2
2
= a
21
x
1
+ a
22
x
2
+ … + a
2n
x
n
.
..
.
..
.
..
.
.
.
.
..
x
n
2
= a
n
1
x
1
+ a
n
2
x
2
+ … + a
nn
x
n
jest
.
(cel-04-2)
x
1
= x
2
= … = x
n
= 0
5. Geometria przestrzeni
R
3
5.1* Korzystając z rachunku wektorowego uzasadnić, że środkowe trójkąta przecinają
się w jednym punkcie, który dzieli każdą z nich w stosunku
licząc od
2 : 1
wierzchołków.
(Ćw. 5.1.8e*)
5.2*
Ś
rodkiem ciężkości trójkąta nazywamy punkt, w którym przecinają się jego
ś
rodkowe. Uzasadnić, że odcinek łączący wierzchołki czworościanu ze środkami
ciężkości przeciwległych boków przecinają się w jednym punkcie, który dzieli te
odcinki w stosunku
licząc od wierzchołków.
(cel-18a-4a)
3 : 1
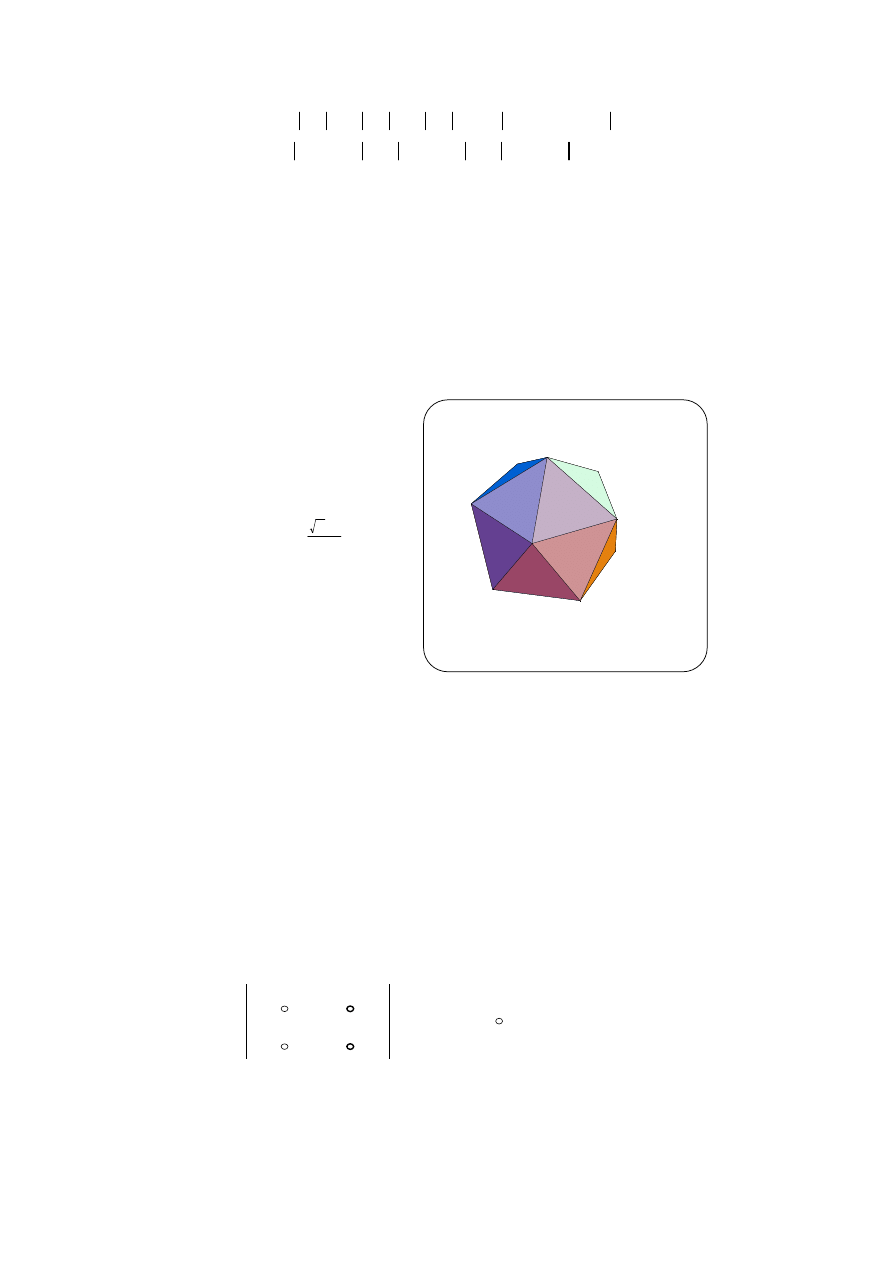
5.3*
Niech
będą dowolnymi wektorami w
. Uzasadnić tożsamość
→
u
,
→
v
,
→
w
R
3
3
(
→
u
2
+
→
v
2
+
→
w
2
) =
→
u
+
→
v
+
→
w
2
+
.
(cel-03-4)
→
u
−
→
w
2
+
→
v
−
→
w
2
+
→
w
−
→
u
2
5.4*
Na sferze o promieniu znajdują się punkty
.
1
P
1
, P
2
, ..., P
2002
Uzasadnić, że suma kwadratów odległości wszystkich par punktów
, dla
, nie przekracza liczby
.
P
i
, P
j
1
≤ i < j ≤ 2002
(2002)
2
Przy jakim rozmieszczeniu punktów wartość
jest osiągnięta?
(ce1-13-4)
(2002)
2
5.5*
Do każdej ściany dowolnego czworościanu wystawiono wektor prostopadły
o długości równej polu tej ściany, skierowany na zewnątrz. Udowodnić, że
suma tych wektorów jest wektorem zerowym.
(cel-02-1)
5.6*
Korzystając z rachunku wektorowego
wyznaczyć cosinus kąta dwuściennego
między sąsiednimi ścianami dwudzie-
stościanu foremnego.
Wskazówka. W rozwiązaniu można wyko-
rzystać równość
Jak
cos 72
o
=
5
−1
4
.
ją uzasadnić w oparciu o liczby zespolone?
Rysynek wykonano wykorzystując
pakiet Mathematica.
(ce1-7-4)
5.7*
Wektory
oraz
spełniają warunek
→
OA
,
→
OB
→
OC
.
→
OA
×
→
OB
+
→
OB
×
→
OC
+
→
OC
×
→
OA
=
→
O
Pokazać, że punkty
są współliniowe.
(ce1-12-4)
A
, B, C
5.8*
Określić liczbę rozwiązań układu równań
w zależności od
→
x
×
→
y
=
→
a
→
y
×
→
z
=
→
b
→
z
×
→
x
=
→
c
wektorów
.
(ce1-5-3)
→
a
,
→
b
,
→
c
∈ R
3
5.9*
Niech
będą dowolnymi wektorami w
. Uzasadnić tożsamość
→
a
,
→
b
,
→
c
,
→
d
R
3
.
(ce1-4-3)
→
a
→
c
→
a
→
d
→
b
→
c
→
b
→
d
= (
→
a
×
→
b
) (
→
c
×
→
d
)
5.10* Cztery punkty poruszają się w przestrzeni
po prostych ze stałymi pręd-
R
3
kościami. Znaleźć najmniejszą liczbę naturalną taką, że jeżeli w chwilach
n
,
punkty były współpłaszczyznowe, to w dowolnej
t
= 1, t = 2, ... t = n
chwili także będą współpłaszczyznowe.
(ce1-6-3)
5.11* Punkt porusza się w przestrzeni
w ten sposób, że współrzędne jego położenia
R
3
w chwili są wielomianami zmiennej stopnia nie większego niż . Pokazać,
t
t
2
ż
e tor punktu jest zawarty w pewnej płaszczyźnie.
(cel-19-4)
5.12* Równoległościan rozpięty na wektorach
ma objętość . Podać
→
u
,
→
v
,
→
w
V
objętość równoległościanu rozpiętego na wektorach
.
(ce1-11-4)
→
u
×
→
v
,
→
u
×
→
w
,
→
v
×
→
w
5.13* Wewnątrz czworościanu
wybrano punkt
. Udowodnić równość
ABCD
O
,
V
OBCD
⋅
→
OA
+ V
OCDA
⋅
→
OB
+V
OABD
⋅
→
OC
+ V
OABC
⋅
→
OD
=
→
0
gdzie
oznacza objętość czworościanu o wierzchołkach
.
(cel-16-4)
V
XYZT
X
, Y, Z, T
5.14* Napisać równanie prostej, która przecina trzy parami skośne proste
.
l
1
:
x
− 1
1
=
y
− 1
2
=
z
− 1
3
l
2
:
x
−1
=
y
1
=
z
2
l
3
:
x
+ 1
2
=
y
+ 1
1
=
z
− 2
−2
Ile jest takich prostych.
(ce1-4-4)
5.15* W
dane są proste skośne i . Znaleźć zbiór środków odcinków o końcach
R
3
k
l
i położonych odpowiednio na prostych i .
(cel-15-4)
K
L
k
l
5.16* W przestrzeni
dane są niewspółpłaszczyznowe wektory
.
R
3
→
p
,
→
q
,
→
r
Znaleźć wersor, który tworzy z nimi jednakowe kąty.
(ce1-10-4)
5.17* W przestrzeni
dany jest sześciokąt foremny
. Odległości
R
3
ABCDEF
wierzchołków
sześciokąta od pewnej płaszczyzny są równe
A
, B, C
odpowiednio
. Obliczyć odległości pozostałych wierzchołków
1, 2, 5
sześciokąta od tej płaszczyzny.
(cel-17-4)
5.18* Wiadomo, że punkty
,
są końcami jednej
A
= ( 0, 0, 0 ) C = ( 0, 0, 3 )
z przekątnych sześcianu
. Ponadto wiadomo, że wierzchołek
ABCDA B C D
sześcianu należy do płaszczyzny
. Wyznaczyć współrzędne pozostałych
B
xOz
wierzchołków tego sześcianu.
(cel-18-4)
5.19* Dane są proste
, gdzie
, przy czym
l
1
:
→
r
=
→
r
1
+ t
→
v
1
, l
2
:
→
r
=
→
r
2
+ t
→
v
2
t
∈ R
. Uzasadnić, że odległość między tymi prostymi wyraża się wzorem
→
v
1
×
→
v
2
≠
→
0
.
(ce1-9-4)
d
=
(
→
r
1
−
→
r
2
,
→
v
1
,
→
v
2
)
→
v
1
×
→
v
2
5.20* Snajper strzela z punktu
w kierunku wektora
.
P
= ( 5, 5, 5 )
→
v
= (−4, −3, −7 )
Zbadać, czy trafi on w czworościan o wierzchołkach
A
= ( 1, 6, 0 ), B = ( 0, 1, −2 ), C = ( 3, 2, −3 ), D = ( 0, 0, 0 ).
Odpowiedź uzasadnić.
(ce1-5-4)
5.21* Płaszczyzny pierwszego oktantu współrzędnych są zwierciadłami. Promień świetlny
wychodzi z punktu
i po odbiciu od zwierciadeł
,
A
= ( 2, 4, 8 )
x
= 0 y = 0
i
dociera do punktu
. Wyznaczyć punkty odbić promienia
z
= 0
B
= ( 4, 6, 2 )
od tych zwierciadeł.
(ce1-1-2)
5.22* Punkt
obrócono o kąt a)
; b)
wokół prostej
A
= ( 3, 8, 1 )
α =
2
π
3
α =
π
3
. Znaleźć obraz tego punktu.
(ce1-3-3)
l
: x
= y = z
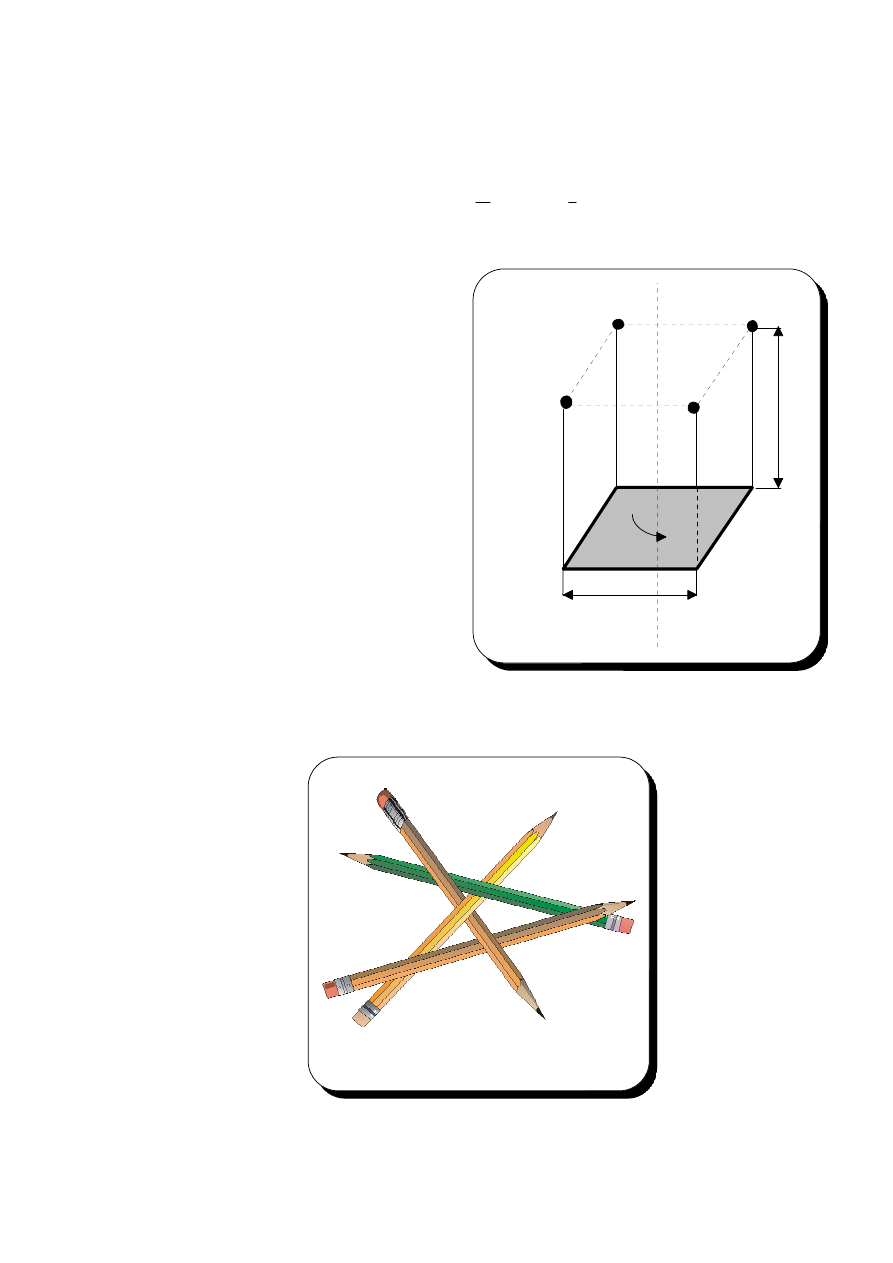
5.23* Kwadratowa płyta, której bok ma długość ,
a
jest zawieszona poziomo na czterech
pionowych linach o długości . Obliczyć,
l
o ile podniesie się płyta po jej obrocie o kąt
wokół pionowej osi symetrii.
0
< ϕ ≤ π
Jakie warunki powinny liczby i ,
a
l
aby taki obrót był możliwy?
(ce1-8-1)
Rysunek wykonała
Małgorzata Jurlewicz
IZ/INF/SI
2004/2005
5.24* Czy możliwe jest ułożenie ołówków przedstawione poniżej? Odpowiedź
uzasadnić korzystając z geometrii analitycznej w
.
(cel-14-4)
R
3
Rysunek wykonał
Michał Bryłka
IZ/INF/PPI
2003/2004
l
ϕ
.
a