Ćwiczenie 1 i 2 (wykład: 1)
Kinematyka punktu
Zadanie 1
Wyznaczyć równanie toru punktu, gdy: x = hcos2ωt, y = hcosωt. h[m], ω[1/s]
stałe,
t[s]
czas.
Ze wzoru trygonometrycznego: cos2
t = cos
2
t
sin
2
t
z „1
ki” trygonometrycznej: sin
2
t + cos
2
t = 1 → sin
2
t = 1
cos
2
t
czyli: cos2
t = cos
2
t
(1
cos
2
t) = 2cos
2
t
1 → x = h(2cos
2
t
1)
y = hcos
t → cos
t
h
y
→ cos
2
t
2
2
h
y
i podstawiamy do wzoru na x:
x = h(2
2
2
a
y
1)
równanie toru.
Zadanie 1a
Równanie ruchu punktu A ma postać: x(t) = t
3
2t
2
4t + 10; x[m], t[s]. Wyznaczyć położenie
punktu na osi x i jego przyspieszenie w chwili, gdy jego prędkość V = 0[m/s].
dt
dx
V
3t
2
4t
4
V = 0 → 3t
2
4t
4 = 0 , Δ = (
4)
2
4
3
(
4) = 64 →
8
[s]
3
2
6
8
4
t
lub
s]
[
2
6
8
4
t
Oczywiście przyjmujemy pierwszą odpowiedź i liczymy
2s
t
x
:
2s
t
x
= 2
3
2
2
2
4
2 + 10 = 2 [m].
Zadanie 2
Z danych równań ruchu punktu: x = (1/2)t
2
, y = (1/3)t
3
, wyprowadzić równanie toru i
narysować go oraz wyznaczyć równanie ruchu punktu po torze (równanie drogi), licząc drogę
od początku położenia punktu
.
Podnosimy obustronnie do potęgi trzeciej równanie x(t), a równanie y(t) do potęgi drugiej:
6
3
t
8
1
x
,
6
2
t
9
1
y
Dzieląc jedno równanie przez drugie, bądź wyliczając z jednego t
6
i podstawiając do drugiego
eliminujemy czas i otrzymujemy równanie toru
y(x):
3
2
x
9
8
y
→
2
3
x
3
2
2
y
y
x
2
8
3
2
3
x
3
2
2
y
Równanie ruchu punktu po torze (równanie drogi): s =
Vdt
+ C
V
prędkość punktu, C
stała zależna od położenia początkowego
2
y
2
x
V
V
V
,
t
dt
dx
V
x
,
2
y
t
dt
dy
V
→
2
4
2
t
1
t
t
t
V
[m/s]
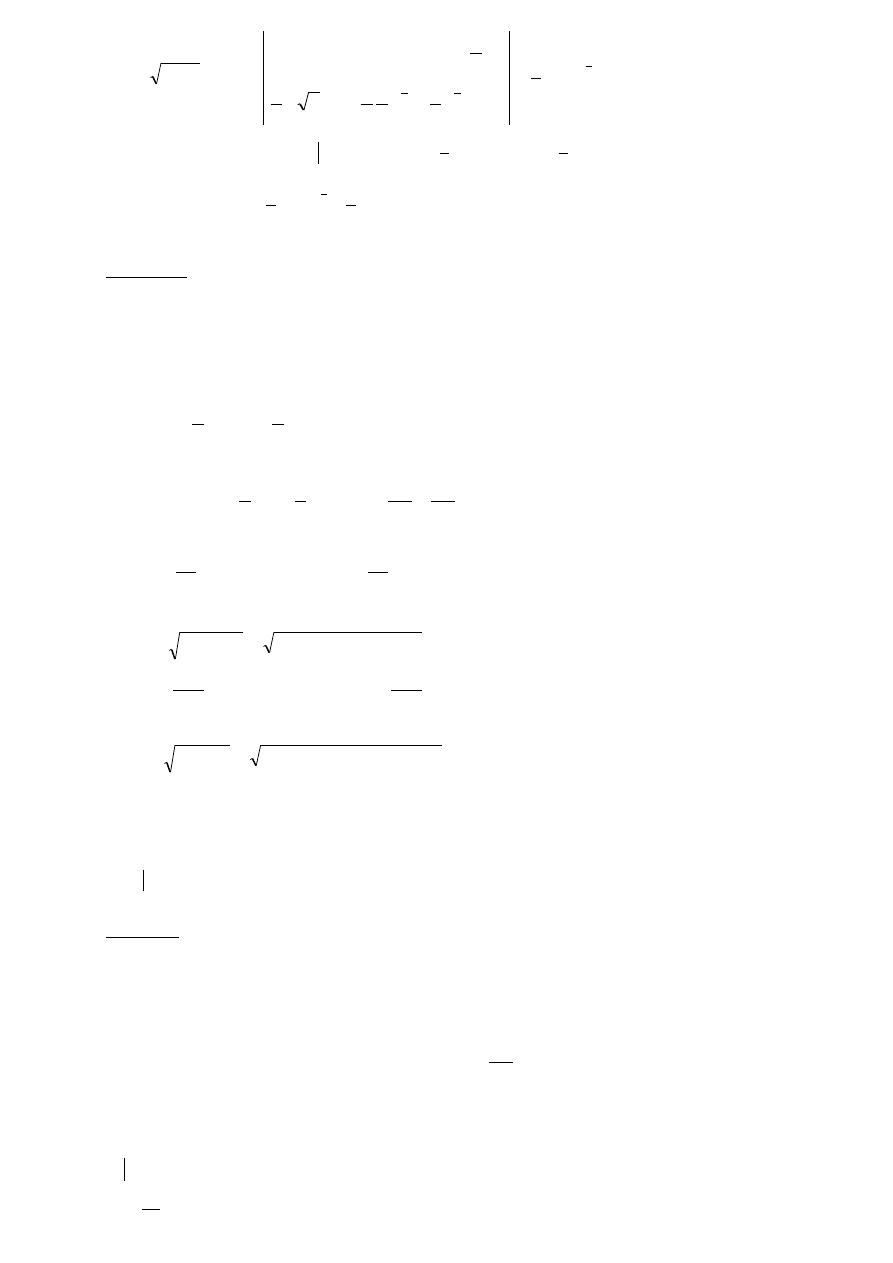
s =
dt
t
1
t
2
+ C =
2
3
2
3
2
z
3
1
z
3
2
2
1
dz
z
2
1
dz
2
1
tdt
,
dz
2tdt
,
z
t
1
2
3
t)
(1
3
1
+ C
W położeniu początkowym
0
t
s
= 0, czyli:
C
3
1
0
→
3
1
C
Równanie drogi:
3
1
t)
(1
3
1
s
2
3
[m].
Zadanie 2a
Ruch punktu A jest dany w postaci: x = 3cos2t, y = 3sin2t, x[m], y[m], t[s]. Wyznacz:
a) tor punktu,
b) współrzędne prędkości, wektor prędkości i moduł (wartość) prędkości.
c) współrzędne przyspieszenia, wektor przyspieszenia i moduł (wartość) przyspieszenia.
d) równanie ruchu po torze.
a)
3
y
sin2t
,
3
x
cos2t
korzystamy z „1
ki” trygonometrycznej, co daje równanie:
1
2t
sin
2t
cos
2
2
wobec tego:
1
3
y
3
x
2
2
→
1
9
y
9
x
2
2
→
9
y
x
2
2
torem jest okrąg o środku w punkcie (0,0) i promieniu r = 3.
b)
6sin2t
dt
dx
V
x
[m/s] ,
6cos2t
dt
dy
V
y
[m/s]
]
6cos2t
6sin2t,
[
]
V
,
V
[
V
y
x
[m/s]
6
2t
36cos
2t
36sin
V
V
V
2
2
2
y
2
x
c)
6cos2t
3
dt
dV
a
x
x
[m/s
2
],
6sin2t
3
dt
dV
a
y
y
[m/s
2
]
36sin2t]
6cos2t,
3
[
]
a
,
a
[
a
y
x
]
[m/s
6
3
2t
cos
296
1
2t
1296sin
a
a
a
2
2
2
2
y
2
x
d) Równanie ruchu punktu po torze (równanie drogi): s =
Vdt
+ C
C
stała zależna od położenia początkowego
podstawiamy: V = 6 [m/s] i otrzymujemy: s =
dt
6
+ C = 6t + C
0
t
s
= 0 → C = 0, stąd ostatecznie: s = 6t [m].
Zadanie 3
Prędkość lądowania samolotu wynosi V
o
= 144[km/h]. Obliczyć jego opóźnienie a w [m/s
2
]
przy zatrzymywaniu się oraz czas t
1
w [s], jaki upłynie od początku lądowania do zatrzymania
się, jeżeli jego droga lądowania jest równa s
1
= 200[m]. Zakładamy, że opóźnienie jest stałe.
Ruch jest jednostajnie opóźniony wobec tego:
dt
dV
a
czyli
C
adt
V
C
stała zależna od warunku początkowego,
a jest stałe (nie zależy od czasu) stąd:
C
dt
a
V
czyli:
C
at
V
0
t
V
=
V
o
→ C =
V
o
→
V
at
V
o
dt
ds
V
czyli
1
C
Vdt
s
, C
1
stała zależna od warunku początkowego,
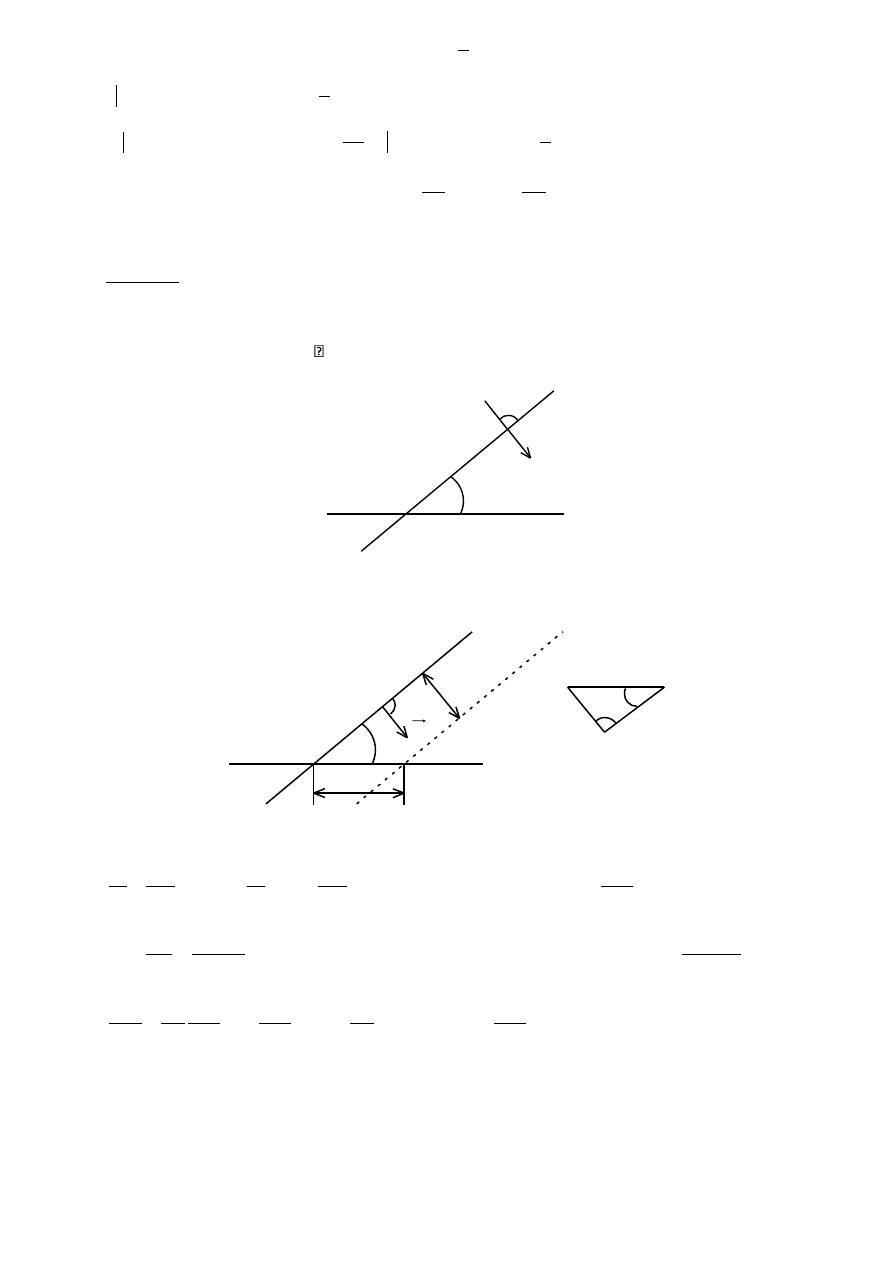
1
o
2
1
o
1
o
C
t
V
at
2
1
C
dt
V
tdt
a
C
)dt
V
at
(
s
0
t
s
= 0 → C
1
= 0 →
2
o
at
2
1
t
V
s
1
t
t
V
= 0 → 0 =
at
1
+ V
o
→
a
V
t
o
1
,
1
t
t
s
= s
1
→
2
1
1
o
1
at
2
1
t
V
s
Podstawiając t
1
do wzoru na s
1
mamy:
2a
V
s
2
o
1
stąd:
1
2
o
2s
V
a
(V
o
= 40 [m/s])
Podstawiając dane liczbowe otrzymujemy: a = 4 [m/s
2
] oraz t
1
= 10 [s].
Zadanie 4
Prosta m porusza się prostopadle do swego kierunku ze stałym przyspieszeniem a
o
, przy
czym jej prędkość w chwili początkowej wynosiła V
o
. Prosta ta przecina się z nieruchomą
prostą n pod stałym kątem . Wyznaczyć prędkość i przyspieszenie punktu A przecięcia się
prostych.
A
n
m
.
o
a
Oznaczmy przez s
A
drogę jaką przebędzie punkt A w pewnym czasie t, zaś przez s drogę jaką
przebył w tym samym czasie punkt znajdujący się na prostej m. Sytuację tą oraz związek
między drogami s
A
i s pokazuje poniższy rysunek.
A
n
m
V
s
A
s
.
.
s
s
A
s = s
A
sin
Różniczkujemy po czasie związek między drogami s
A
i s i otrzymujemy związek między
prędkościami V
A
i V:
A
A
A
V
dt
ds
i
V
dt
ds
ale
,
sinα
dt
ds
dt
ds
czyli: V = V
A
sinα , stąd:
sinα
V
V
A
(1)
Ruch prostej m jest jednostajnie przyspieszony z przyspieszeniem a
o
czyli:
t
V
V
t
ΔV
a
o
o
→ V = a
o
t + V
o
, podstawiając do równania (1) mamy:
sinα
V
t
a
V
o
o
A
Różniczkując po czasie równanie (1) otrzymujemy związek między przyspieszeniami a
A
i a
o
:
sinα
a
a
:
czyli
a
dt
dV
i
a
dt
dV
ale
,
sinα
1
dt
dV
dt
dV
o
A
o
A
A
A
.

Zadanie 5
Tulejka A jest przesuwana po pręcie za pomocą linki przerzuconej przez mały krążek B
odległy od pręta o wielkość OB = b. Wyznaczyć wzór na prędkość i przyspieszenie tulejki w
funkcji odległości OA = x, jeśli swobodny koniec linki jest ciągnięty ze stałą prędkością V
0
.
b
x
O
A
B
o
V
/2
V
o
V
x
b
x
x
V
(x)
V
b
x
x
α
cos
α
cos
V
V
2
2
o
x
2
2
o
x
x
x
x
x
x
x
V
dt
dx
bo
,
V
dx
dV
dt
dx
dx
dV
dx
dx
dt
dV
dt
dV
a
,
?
dx
dV
x
2
3
2
2
2
o
2
2
2
2
2
2
2
o
2
2
2
2
2
2
o
2
2
o
x
)
b
(x
b
V
b
x
)
b
(x
x
b
x
V
b
x
b
x
2
2x
x
b
x
V
b
x
x
dx
d
V
dx
dV
2
2
2
2
2
o
2
2
o
2
3
2
2
2
o
x
2
3
2
2
2
o
)
b
(x
x
b
V
b
x
x
V
)
b
(x
b
V
V
)
b
(x
b
V
a(x)
.
Zadanie 6
Ruch punktu określony jest równaniem x(V) = bV
2
c. Po jakim czasie prędkość punktu
będzie dwa razy większa od prędkości początkowej. W chwili początkowej punkt znajdował
się w położeniu x = 0.
V
dV
dx
a
V
dx
dV
dt
dx
dx
dV
dx
dx
dt
dV
dt
dV
a
2bV
dV
dx
→ a
2bV = V →
2b
1
a
dt
dV
a
→
2b
1
a
→
2b
1
dt
dV
→
dt
2b
1
dV
→
C
dt
2b
1
dV
→
C
t
2b
1
V
C
stała zależna od warunku początkowego,
0
t
V
=
V
o
→ C =
V
o
→
o
V
t
2b
1
V
z treści zadania: V = 2V
o
→
o
o
V
t
2b
1
2V
→
t
2b
1
V
o
→ t = 2bV
o
, V
o
= ?
o
V
V
x
= 0 → 0 = bV
o
2
c →
b
c
V
o
[m/s]
czyli czas, po którym prędkość wzrośnie dwukrotnie:
bc
2
b
c
2b
t
[s].
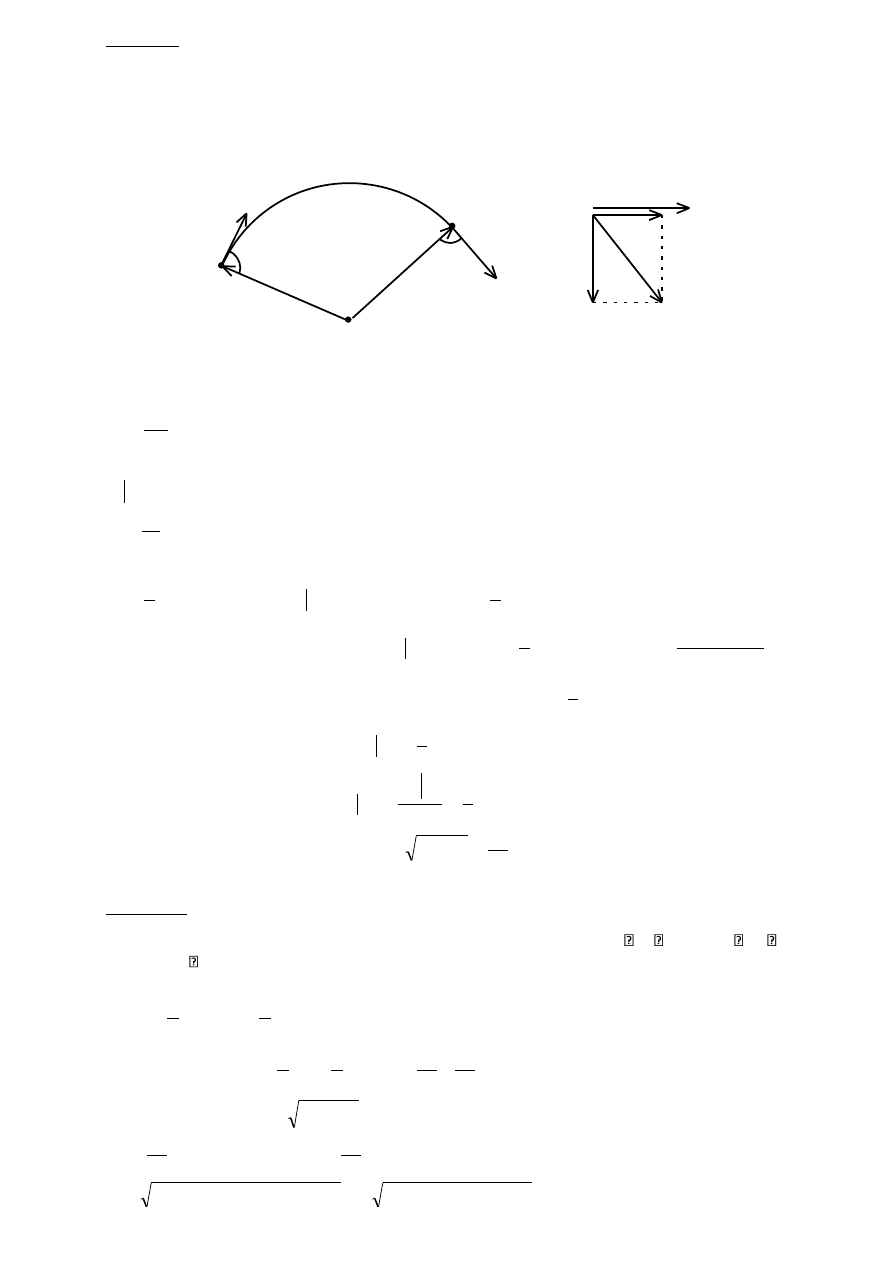
Zadanie 7
Pociąg mający prędkość początkową V
o
= 54[km/h], przejechał drogę s
1
= 600[m] w ciągu
czasu t
1
= 30[s]. Zakładając stałe przyspieszenie styczne pociągu, obliczyć jego prędkość i
przyspieszenie całkowite w końcu trzydziestej sekundy, jeżeli ruch odbywał się po łuku o
promieniu R=1[km].
R
o
V
1
V
R
s
1
V
a
t
a
n
a
.
.
a
t
przyspieszenie styczne,
a
n
przyspieszenie normalne,
a
przyspieszenie całkowite.
C
t
a
V
C
dt
a
dV
C
dt
a
dV
dt
a
dV
dt
dV
a
t
t
t
t
t
C
stała zależna od warunku początkowego,
0
t
V
=
V
o
→ C =
V
o
→ V = a
t
t + V
o
(1)
1
o
t
1
o
t
1
C
dt
V
tdt
a
s
C
)dt
V
t
(a
ds
C
Vdt
ds
Vdt
ds
dt
ds
V
C
1
stała zależna od warunku początkowego,
1
o
2
t
C
t
V
t
a
2
1
s
→
0
t
s
= 0 → C
1
= 0 →
t
V
t
a
2
1
s
o
2
t
Z ostatniego równania wyliczamy a
t
: →
1
t
t
s
= s
1
→
1
o
2
1
t
1
t
V
t
a
2
1
s
→
2
1
1
o
1
t
t
)
t
V
2(s
a
Podstawiając dane liczbowe (V
o
= 15 [m/s]) otrzymujemy:
]
[m/s
3
1
a
2
t
Liczymy V w chwili t
1
ze wzoru (1):
[m/s]
25
15
30
3
1
V
1
t
t
a
n
w chwili t
1
liczymy ze wzoru:
8
5
R
V
a
1
1
t
t
2
t
t
n
[m/s
2
]
całkowite przyspieszenie w chwili t
1
:
24
17
a
a
a
2
n
2
t
[m/s
2
].
Zadanie 7a
Punkt materialny A porusza się zgodnie z równaniami ruchu: x(t) = b sin t, y(t) = c cos t,
gdzie b, c i są stałymi. Wyznacz równanie toru punktu, jego całkowitą prędkość i całkowite
przyspieszenie oraz przyspieszenie styczne i normalne w dowolnej chwili czasu t.
b
x
t
sinω
,
c
y
t
ω
cos
i korzystamy z „1
ki” trygonometrycznej: sin
2
ωt + cos
2
ωt = 1
Równanie toru [y(x)]:
1
c
y
b
x
1
c
y
b
x
2
2
2
2
2
2
elipsa
Całkowita prędkość:
2
y
2
x
V
V
V
t
cosω
bω
dt
dx
V
x
[m/s] ,
t
sinω
cω
dt
dy
V
y
[m/s]
[m/s]
t
ω
sin
c
t
ω
cos
b
ω
t)
sinω
cω
(
t)
cosω
(bω
V
2
2
2
2
2
2
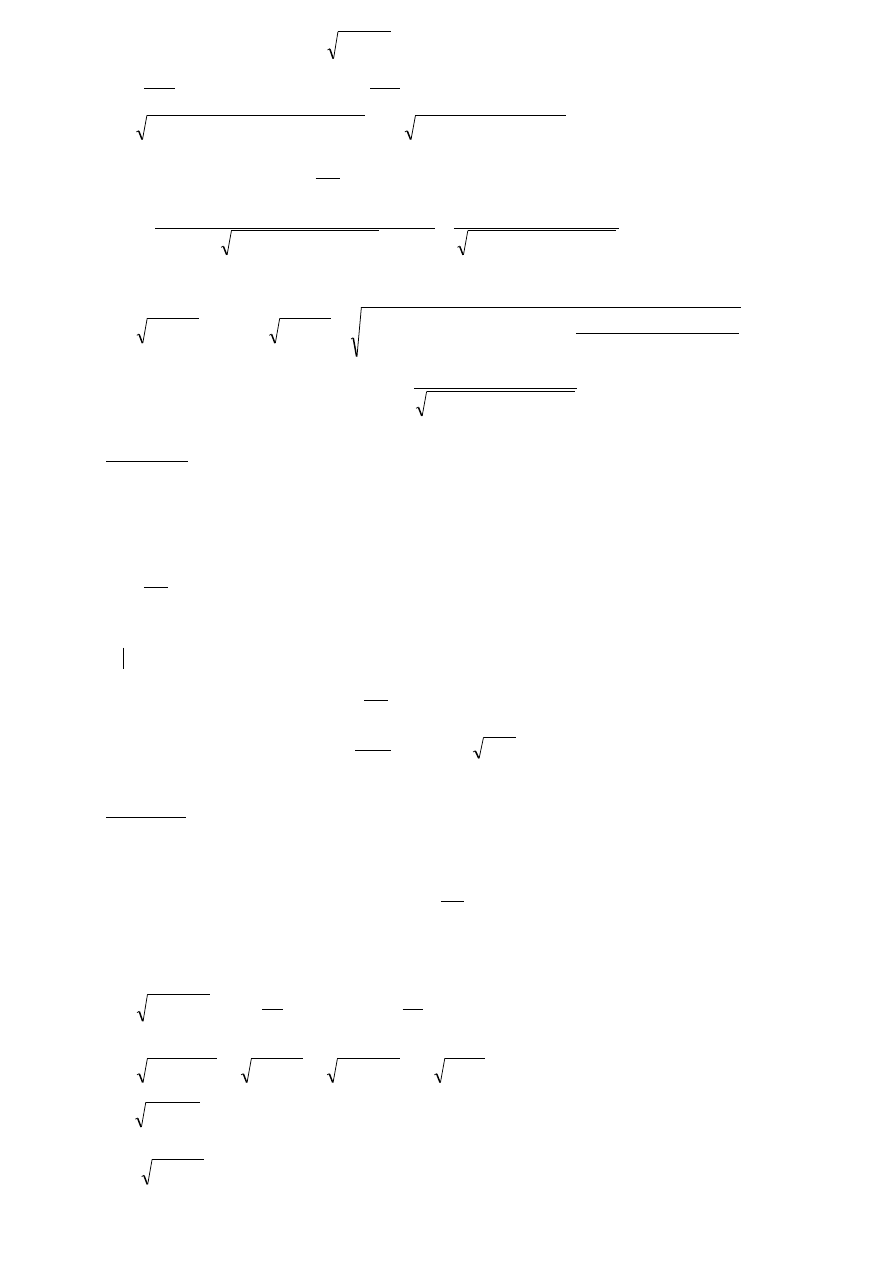
Całkowite przyspieszenie:
2
y
2
x
a
a
a
t
sinω
bω
dt
dV
a
2
x
x
[m/s
2
] ,
t
cosω
cω
dt
dV
a
2
y
y
[m/s
2
]
]
[m/s
t
ω
cos
c
t
ω
sin
b
ω
t)
cosω
cω
(
t)
sinω
bω
(
a
2
2
2
2
2
2
2
2
2
2
Przyspieszenie styczne:
dt
dV
a
t
t
ω
sin
c
t
ω
cos
b
t
cosω
t
)sinω
b
(c
ω
t
ω
sin
c
t
ω
cos
b
2
t
cosω
t
sinω
ω
2
c
t
sinω
t
cosω
ω
2)
(
b
ω
a
2
2
2
2
2
2
2
2
2
2
2
2
2
t
[m/s
2
]
Przyspieszenie normalne (a
n
) liczymy następująco:
t
ω
sin
c
t
ω
cos
b
]
t
cosω
t
)sinω
b
(c
[
ω
t)
ω
cos
c
t
ω
sin
(b
ω
a
a
a
a
a
a
2
2
2
2
2
2
2
4
2
2
2
2
4
2
t
2
n
2
n
2
t
i po przekształceniach otrzymujemy:
t
ω
sin
c
t
ω
cos
b
bc
ω
a
2
2
2
2
2
n
[m/s
2
].
Zadanie 7b
Punkt materialny A zaczął poruszać się po okręgu o promieniu r = 0.1[m] w ten sposób, że
jego przyspieszenie styczne (a
t
) jest stałe równe 2 [m/s
2
]. Po jakim czasie jego przyspieszenie
normalne będzie równe stycznemu?
C
t
a
V
C
dt
a
dV
C
dt
a
dV
dt
a
dV
dt
dV
a
t
t
t
t
t
C
stała zależna od warunku początkowego,
0
t
V
=
0
→ C =
0
→ V = a
t
t , podstawiając a
t
= 2[m/s
2
]: V = 2t [m/s]
Przyspieszenie normalne (a
n
):
r
V
a
2
n
Z treści zadania: a
n
= a
t
czyli:
0,1
(2t)
2
2
stąd:
0,22
0,05
t
[s].
Zadanie 7c
Obliczyć promień krzywizny toru środka kulki w początku ruchu, jeżeli równania ruchu mają
postać: x = 2t, y = t
2
; przy czym t [s], x i y [m].
Promień krzywizny (
) dany jest wzorem:
n
2
a
V
ρ
gdzie: V
prędkość punktu
a
n
przyspieszenie normalne punktu
V =
2
y
2
x
V
V
,
[m/s]
2
dt
dx
V
x
,
[m/s]
2t
dt
dy
V
y
V =
2
2
(2t)
2
=
2
4t
4
=
)
t
4(1
2
= 2
2
t
1
[m/s]
a =
2
n
2
t
a
a
gdzie: a
przyspieszenie całkowite punktu
a
t
przyspieszenie styczne punktu
a
n
=
2
t
2
a
a
, a = ?, a
t
= ?
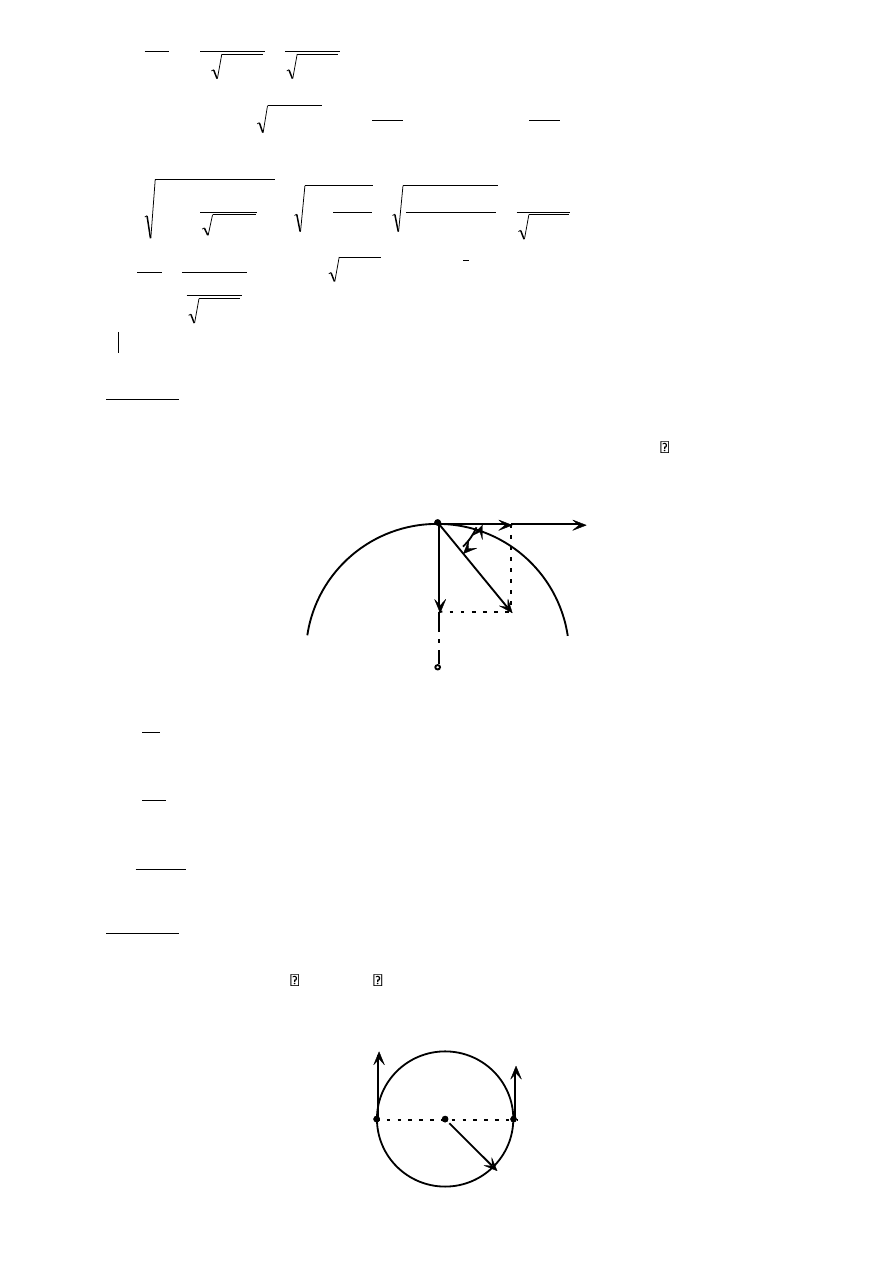
2
2
t
t
1
2t
t
1
2
2t
2
dt
dV
a
[m/s]
z drugiej strony: a =
2
y
2
x
a
a
,
0
dt
dV
a
x
x
[m/s
2
],
2
dt
dV
a
y
y
[m/s
2
]
a = a
y
= 2 [m/s
2
]
2
2
2
2
2
2
2
2
2
n
t
1
2
t
1
4t
4t
4
t
1
4t
4
t
1
2t
2
a
[m/s
2
]
)
t
2(1
t
1
)
t
2(1
t
1
2
)
t
1
4(
a
V
ρ
2
3
2
2
2
2
2
n
2
[m]
0
t
ρ
= 2 [m].
Zadanie 8
Punkt A porusza się po krzywej płaskiej zgodnie z równaniem s = b(e
kt
1), gdzie s w [m], b, k
są stałymi. Kąt między całkowitym przyspieszeniem, a prędkością wynosi = 60
o
. Obliczyć
prędkość i całkowite przyspieszenie punktu.
a
n
a
t
V
A
a
Prędkość punktu wyznaczamy ze wzoru:
kt
bke
dt
ds
V
[m/s]
Przyspieszenie styczne wynosi:
kt
2
t
e
bk
dt
dV
a
[m/s
2
]
Całkowite przyspieszenie jest równe:
kt
2
t
e
bk
2
cos60
a
a
[m/s
2
].
Zadanie 9
Dwa punkty A i B poruszają się po okręgu o promieniu R = 6[m] w przeciwne strony zgodnie z
równaniami drogi s
A
(t) = t
2
i s
B
(t) = t
4
, gdzie s
A
i s
B
w [m], t – czas w [s]. Punkty wyruszyły z
przeciwnych końców średnicy. Obliczyć normalne i styczne przyspieszenia punktów w
momencie ich spotkania.
V
A
V
B
A
B
R

Do chwili spotkania oba punkty przebyły w sumie drogę równą połowie obwodu okręgu,
wobec tego: s
A
+ s
B
= πR. Podstawiając dane wielkości s
A
i s
B
otrzymujemy równanie:
t
2
+ t
4
= πR → t
4
+ t
2
R = 0
Otrzymaliśmy równanie dwukwadratowe, z którego obliczymy czas, jaki upłynął do chwili
spotkania punktów. Podstawiając R = 6[m] mamy: t
4
+ t
2
6 = 0
2
2
5
1
t
5
25
6)
(
1
4
1
Δ
2
[s
2
] lub
3
2
5
1
t
2
sprzeczność
czyli:
2
t
[s]
Prędkości punktów A i B (odpowiednio V
A
i V
B
) wyznaczamy ze wzorów:
t
2π
dt
ds
V
A
A
[m/s],
3
B
B
t
4π
dt
ds
V
[m/s]
Przyspieszenia styczne punktów A i B (odpowiednio a
tA
i a
tB
) wyznaczamy ze wzorów:
2π
dt
dV
a
A
tA
[m/s
2
] ,
3
B
tB
t
2π
1
dt
dV
a
[m/s
2
]
Podstawiając
2
t
[s] otrzymujemy wartości liczbowe a
tA
i a
tB
:
a
tA
= 6,28 [m/s
2
],
]
[m/s
106,57
2
2π
1
a
2
3
tB
Przyspieszenia normalne punktów A i B (odpowiednio a
nA
i a
nB
) wyznaczamy ze wzorów:
R
t)
(2π
R
V
a
2
2
A
nA
[m/s
2
] ,
R
)
t
(4π
R
V
a
2
3
2
B
nB
[m/s
2
]
Podstawiając dane otrzymujemy wartości liczbowe a
nA
i a
nB
:
a
nA
= 13,15 [m/s
2
], a
nB
= 210,34 [m/s
2
].
Zadanie 10
Punkt porusza się po okręgu o promieniu r = 2[m] według równania s = 0,1 t
2
, (t[s], s[m]). Po
jakim czasie przyspieszenie normalne i styczne będą równe?
Prędkość punktu wyznaczamy ze wzoru:
t
2
,
0
dt
ds
V
[m/s]
Przyspieszenie styczne punktu wyznaczamy ze wzoru:
2
,
0
dt
dV
a
t
[m/s
2
]
Przyspieszenie normalne punktu wyznaczamy ze wzoru:
r
t)
2
,
(0
r
V
a
2
2
n
[m/s
2
]
Z treści zadania: a
t
= a
n
, czyli otrzymujemy równanie:
r
t)
2
,
(0
2
,
0
2
stąd otrzymujemy:
2
,
3
10
5r
t
[s].
Ćwiczenie 3 i 4 (wykład: 2)
Kinematyka ciała sztywnego
Zadanie 1
Dla układu przegubowo połączonych prętów jak na rysunku określić prędkość punktu C,
jeżeli prędkość punktu A wynosi 8[m/s] a prędkość punktu B 6[m/s].
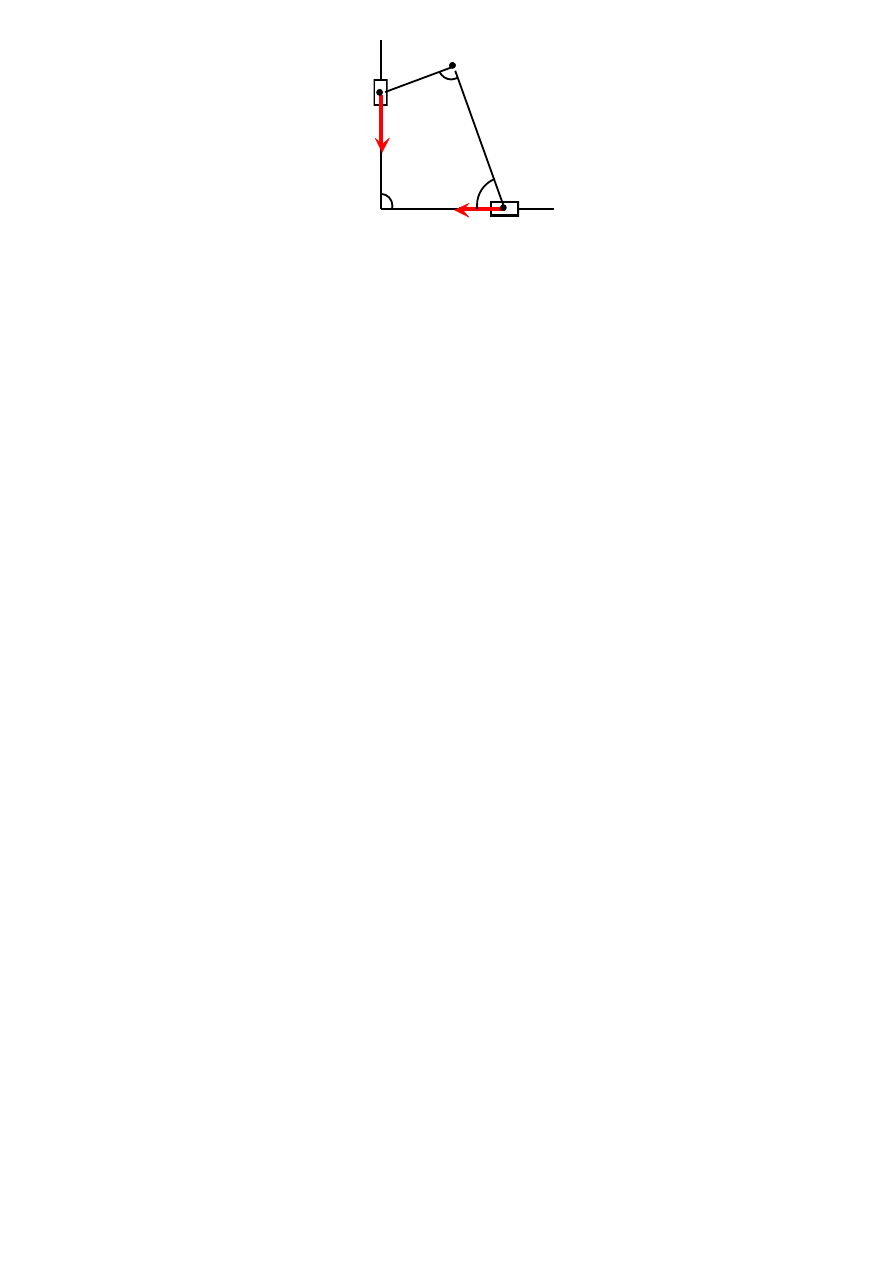
.
/2
.
/2
B
A
C
60
V
A
V
B

Rozpatrzmy pręt CA:
A
C
60
V
A
V
C
Na podstawie twierdzenia o rzutach predkości dwóch punktów
ciała sztywnego na prostą, która je łączy otrzymujemy równanie:
V
A
cos60
= V
C
cos
Rozpatrzmy pręt BC:
B
V
B
60
C
(90
)
V
C
Na podstawie twierdzenia o rzutach predkości dwóch punktów
ciała sztywnego na prostą, która je łączy otrzymujemy równanie:
V
B
cos60
= V
C
cos(90
) = V
C
sin
Wobec tego otrzymujemy układ równań:
C
B
C
B
C
A
C
A
2V
V
sinα
sinα
V
2
V
2V
V
cosα
cosα
V
2
V
Korzystamy z „1
ki” trygonometrycznej: cos
2
+ sin
2
= 1, co daje równanie:
2
B
2
A
2
C
2
C
B
2
C
A
V
V
4V
1
2V
V
2V
V
Stąd wyliczamy V
C
:
2
V
V
V
2
B
2
A
C
Podstawiając dane liczbowe (V
A
= 8 [m/s] i V
B
= 6 [m/s]) otrzymujemy: V
C
= 5 [m/s].
Zadanie 2
Koło mające nieruchomą oś otrzymało początkową prędkość kątową ω
o
= 2π[rad/s]. Po
wykonaniu 10 obrotów, wskutek tarcia w łożyskach, koło zatrzymało się. Obliczyć opóźnienie
kątowe ε tego koła uważając je za stałe.
Ruch jest jednostajnie opóźniony wobec tego:
dt
dω
ε
czyli
C
εdt
ω
C
stała zależna od warunku początkowego,
jest stałe (nie zależy od czasu) stąd:
C
dt
ε
ω
czyli
C
εt
ω
0
t
ω
=
ω
o
→ C =
ω
o
→
ω
εt
ω
o
dt
dφ
ω
czyli:
1
C
ωdt
φ
,
φ
kąt obrotu, C
1
stała zależna od warunku początkowego,
1
o
2
1
o
1
o
C
t
ω
εt
2
1
C
dt
ω
tdt
ε
C
)dt
ω
εt
(
φ
0
t
φ
= 0 → C
1
= 0 →
2
o
εt
2
1
t
ω
φ
, oznaczmy przez t
1
czas, po którym koło zatrzymało się:
1
t
t
ω
= 0 →
o
1
ω
εt
0
→
ε
ω
t
o
1
,
1
t
t
φ
=
φ
1
→
2
1
1
o
1
εt
2
1
t
ω
φ
podstawiając t
1
do wzoru na φ
1
mamy:
2ε
ω
φ
2
o
1
stąd:
1
2
o
2φ
ω
ε
(
φ
1
= 20π tj. 10 obrotów)

podstawiając dane liczbowe otrzymujemy:
10
π
ε
[rad/s
2
].
Zadanie 2a
Walec obraca się dokoła swej nieruchomej osi symetrii tak, że jego opóźnienie kątowe jest
proporcjonalne do jego prędkości kątowej ze współczynnikiem k. Prędkość początkowa
walca wynosiła
o
. Wyprowadzić równanie ruchu obrotowego walca φ(t).
Z treści zadania wynika równanie:
kω
dt
dω
ε
, znak minus oznacza, że mamy do
czynienia z ruchem opóźnionym. Rozdzielamy zmienne (ω,t) i całkujemy stronami:
C
dt
k
ω
dω
kdt
ω
dω
, C
stała zależna od warunku początkowego
o
o
o
0
t
lnω
kt
lnω
lnω
C
ω
ω
C,
kt
lnω
przekształcamy ostatni wzór:
e
ω
ω
kt
ω
ω
ln
kt
lnω
lnω
kt
o
o
o
z ostatniego wzoru wynika wzór na prędkość kątową:
e
ω
ω
kt
o
związek między kątem obrotu (φ)
i prędkością kątową:
kt
o
e
ω
dt
dφ
ω
rozdzielamy zmienne (φ,t) i całkujemy stronami:
1
kt
o
kt
o
C
dt
e
ω
dφ
dt
e
ω
dφ
, C
1
stała zależna od warunku początkowego
k
ω
C
C
k
ω
0
0
φ
,
C
e
k
ω
φ
o
1
1
o
0
t
1
kt
o
równanie ruchu obrotowego walca:
)
e
(1
k
ω
φ
k
ω
e
k
ω
φ
kt
o
o
kt
o
.
Zadanie 3
Tarcza kołowa obraca się dokoła nieruchomej osi z opóźnieniem kątowym
a
początkowa prędkość kątowa tarczy wynosiła . Znaleźć równanie ruchu tarczy φ(t).
Z treści zadania mamy równanie:
2
ηω
dt
dω
ε
, znak minus oznacza, że mamy do czynienia
z ruchem opóźnionym. Rozdzielamy zmienne (ω,t) i całkujemy stronami:
C
dt
η
ω
dω
ηdt
ω
dω
2
2
, C
stała zależna od warunku początkowego
o
o
o
0
t
ω
1
ηt
ω
1
ω
1
C
ω
ω
,
C
ηt
ω
1
z ostatniego wzoru wynika wzór na prędkość kątową:
1
t
ηω
ω
ω
o
o
związek między kątem obrotu φ
i prędkością kątową:
1
t
ηω
ω
dt
dφ
ω
o
o
rozdzielamy zmienne (φ,t) i całkujemy stronami:
1
o
o
o
o
C
1
t
ηω
dt
ω
dφ
dt
1
t
ηω
ω
dφ
, C
1
stała zależna od warunku początkowego
0
C
0
φ
,
C
1)
t
ω
ln(η
η
1
φ
1
0
t
1
o
równanie ruchu obrotowego tarczy:
1)
t
ω
ln(η
η
1
φ
o
.
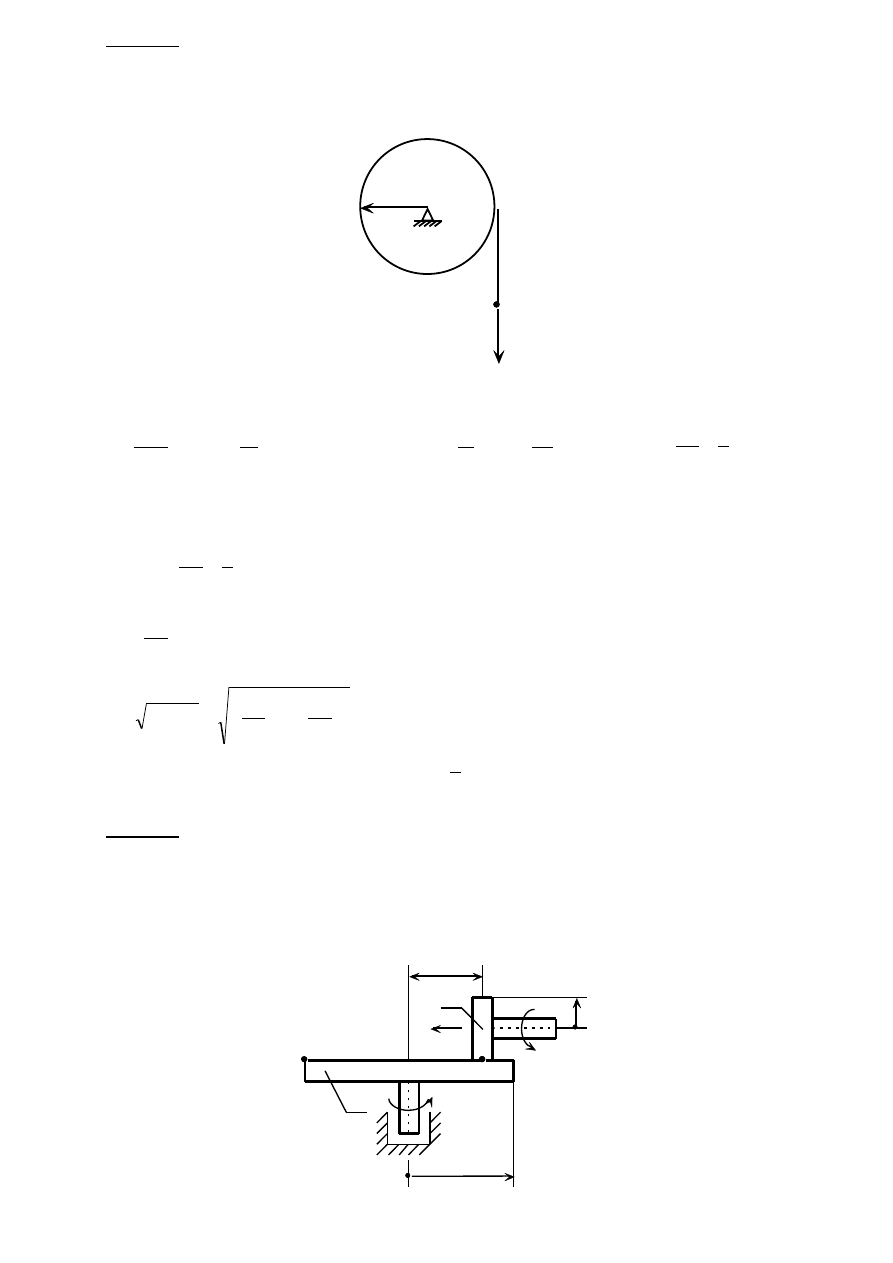
Zadanie 4
Na bęben o promieniu R = 0,5[m] nawinięto linę. Koniec liny A porusza się ze stałym
przyspieszeniem. Po przebyciu drogi s = (1/3)[m] koniec A osiągnął prędkość V = 1[m/s].
Znaleźć przyspieszenie dowolnego punktu leżącego na obwodzie bębna.
R
A
a
A
Ruch punktu A jest ruchem jednostajnie przyspieszonym (bez prędkości początkowej).
Przyspieszenie tego punktu znajdujemy ze wzoru:
2
A
2
A
t
2s
a
2
t
a
s
, ale z drugiej strony:
A
A
a
V
t
t
V
a
, tak więc:
]
[m/s
2
3
2s
V
a
2
2
A
Przyspieszenie punktu leżącego na obwodzie bębna jest sumą geometryczną składowej
stycznej (a
t
) i składowej normalnej (a
n
). Przyspieszenie styczne punktu leżącego na obwodzie
bębna jest równe przyspieszeniu punktu A.
]
[m/s
2
3
2s
V
a
a
2
2
A
t
przyspieszenie normalne znajdujemy ze wzoru:
]
[m/s
2
R
V
a
2
2
n
przyspieszenie całkowite (a) w rozważanej chwili:
2
2
2
2
2
n
2
t
R
V
2s
V
a
a
a
podstawiając dane liczbowe otrzymujemy:
]
[m/s
2
5
a
2
.
Zadanie 5
Koło 1 przekładni ciernej wykonuje f
1
= 600 [obr/min] i jednocześnie przesuwa się osiowo
według równania: u = (10
0,5t) gdzie: u[cm], t[s]. Obliczyć: a) przyspieszenie kątowe
2
koła
2 w funkcji przesunięcia u, tzn.
2
=
2
(u) b) całkowite przyspieszenie punktu B na obwodzie
koła 2 w chwili gdy u = r. Przyjąć: r = 5[cm], R = 15[cm].
u
r
1
2
2
1
B
A
R

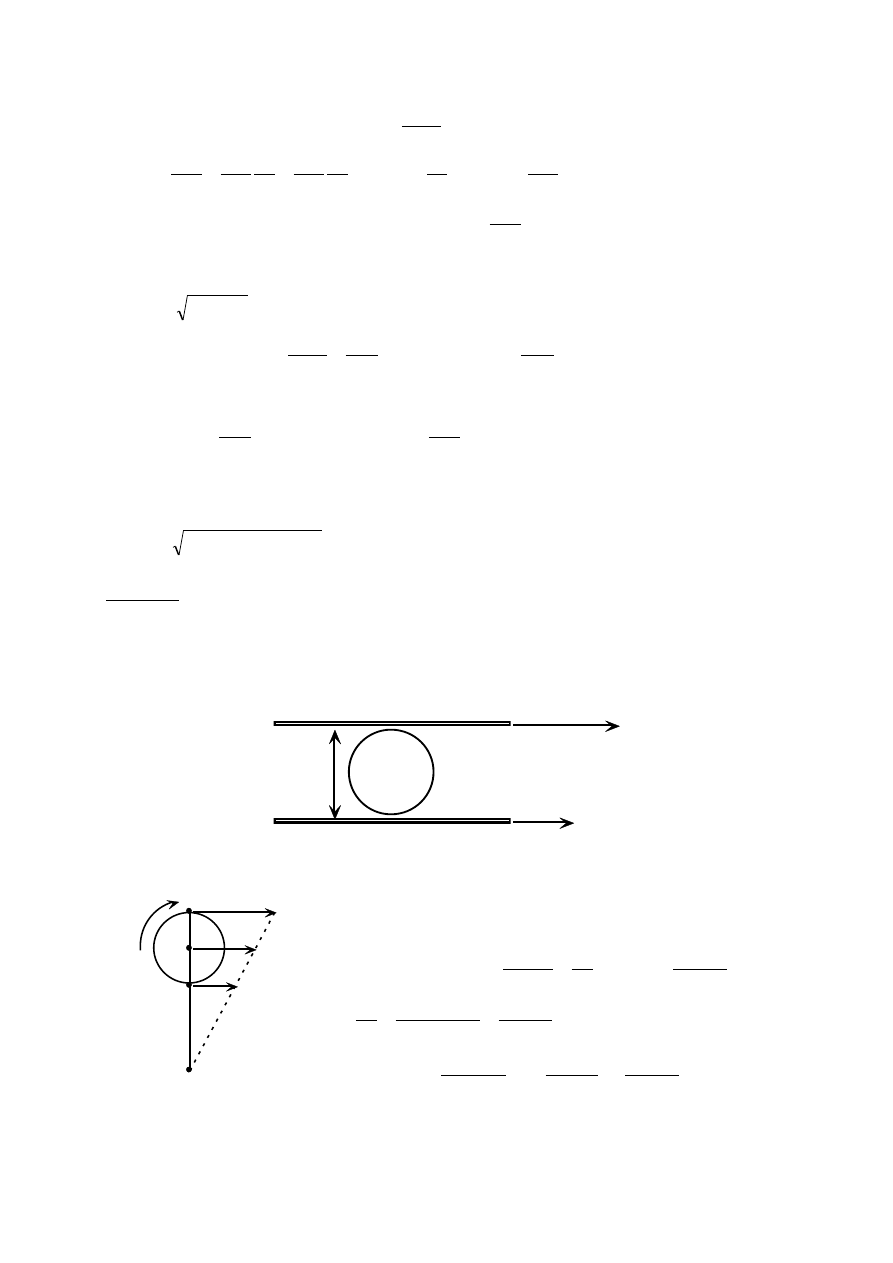
a) Prędkość liniowa punktu styczności A jest taka sama dla koła 1 i 2
oznaczmy:
)
1
(
A
V
prędkość punktu A dla koła 1
)
1
(
A
V
=
1
r = 2
f
1
r
)
2
(
A
V
prędkość punktu A dla koła 2
)
2
(
A
V
=
2
u
)
1
(
A
V
=
)
2
(
A
V
2
f
1
r =
2
u
u
r
f
2π
ω
1
2
2
1
2
1
2
2
2
2
u
r
f
π
0,5)
(
u
1
r
f
2π
dt
du
du
dω
du
du
dt
dω
dt
dω
ε
podstawiając dane liczbowe otrzymujemy:
]
[rad/s
u
1,57
ε
2
2
2
b) Przyspieszenie punktu B leżącego na obwodzie koła 2 jest sumą geometryczną składowej
stycznej (a
t
) i składowej normalnej (a
n
).
a
a
a
2
n
2
t
B
R
ω
a
2
2
n
ale:
[rad/s]
u
3,14
u
r
f
2π
ω
1
2
czyli:
R
u
3,14
a
2
n
podstawiając: u = r = 0,05 [m] oraz R = 0,15 [m] otrzymujemy: a
n
=
591,58 [m/s
2
]
R
u
1,57
R
ε
a
2
2
t
, ale u = r czyli:
R
r
1,57
a
2
t
podstawiając dane liczbowe otrzymujemy: a
t
= 94,2 [m/s
2
]
wobec tego przyspieszenie punktu B jest równe:
a
B
=
2
2
)
58
,
591
(
(94,2)
≈ 599 [m/s
2
].
Zadanie 6
Pomiędzy dwie równoległe odległe od siebie o 2R listwy wstawiono koło, które toczy się
względem nich bez poślizgu. Wyznaczyć prędkość środka koła i jego prędkość kątową, jeżeli
listwy poruszają się poziomo z prędkościami V
1
i V
2
.
V
1
V
2
2R
Przyjmujemy, że V
1
> V
2
V
1
V
2
V
o
O
A
B
C
Punkt C jest chwilowym środkiem obrotu, czyli V
C
= 0
Oznaczmy długość odcinka BC jako x.
R
R
x
2
1
2
2
1
V
V
2RV
x
x
V
x
2R
V
ω
stąd:
2R
V
V
2RV
)
V
(V
V
x
V
ω
2
1
2
2
1
2
2
.
2
V
V
V
V
2RV
R
2R
)
V
(V
x)
ω(R
V
2
1
2
1
2
2
1
o
Prędkość kątowa:
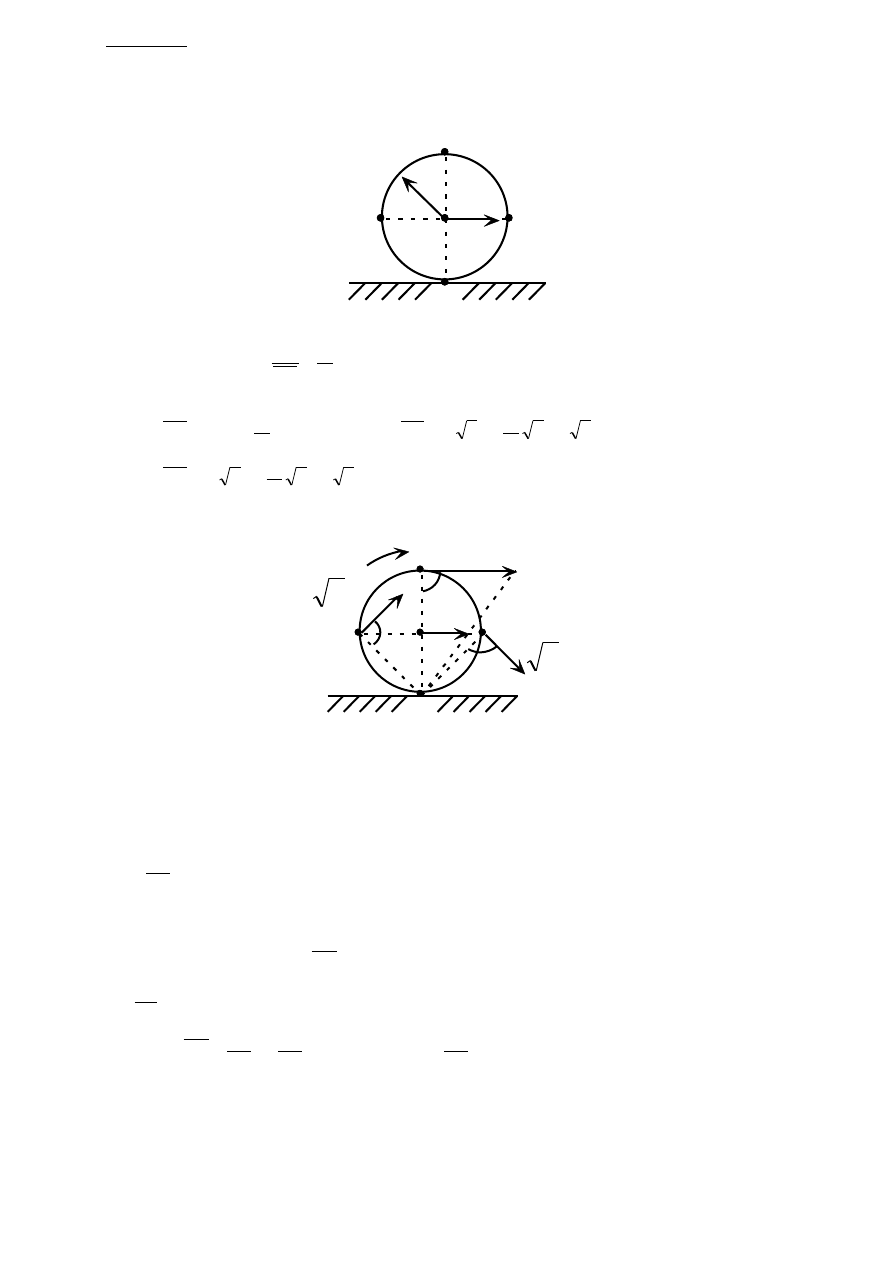
Zadanie 6a
Tarcza kołowa o promieniu r toczy się po prostej, przy czym środek tarczy O porusza się ze
stałą prędkością V. Wyznaczyć prędkości i przyspieszenia punktów A, B, C i D zaznaczonych
na rysunku.
A
C
B
D
V
r
O
Punkt C jest chwilowym środkiem obrotu, czyli: V
C
= 0
prędkość kątowa:
const
r
V
CO
V
ω
oznaczmy przez V
A
, V
B
, V
D
szukane prędkości punktów A, B, D
2V
2r
r
V
ω2r
CA
ω
V
A
,
V
2
r
2
r
V
r
2
ω
CB
ω
V
B
V
2
r
2
r
V
r
2
ω
CD
ω
V
D
Kierunki i zwroty prędkości pokazano na poniższym rysunku
A
C
B
D
V
2V
V
2
V
2
.
.
.
O
Oznaczmy przez a
A
, a
B
, a
C
, a
D
szukane przyspieszenia punktów A, B, C, D
Przyspieszenia tych punktów wyznaczymy w oparciu o sumę geometryczną przyspieszenia
bieguna (punktu, którego znamy przyspieszenie) oraz przyspieszenia danego punktu w ruchu
obrotowym wokół tego bieguna. W naszym przypadku biegunem będzie punkt O, a jego
przyspieszenie (a
o
) wyznaczamy ze wzoru:
0
dt
dV
a
O
ponieważ prędkość (V) środka tarczy jest stała
Przyspieszenie w ruchu obrotowym ma składową styczną (t) i normalną (n).
Dla punktu A:
A/O
O
A
a
a
a
,
n
t
A/O
A/O
A/O
a
a
a
czyli:
n
t
A/O
A/O
A
a
a
a
Wartości liczbowe:
εr
OA
ε
a
t
A/O
,
przyspieszenie kątowe
0
dt
dω
ε
ponieważ prędkość kątowa (ω) jest stała, czyli:
0
a
t
A/O
, a więc:
n
A/O
A
a
a
r
V
r
r
V
OA
ω
a
2
2
2
2
n
A/O
wobec tego:
r
V
a
2
A
Postępując analogicznie jak dla punktu A możemy wyznaczyć przyspieszenia pozostałych
trzech punktów, należy zamienić tylko literę A na B, C lub D.
Kierunki i zwroty przyspieszeń pokazano na poniższym rysunku
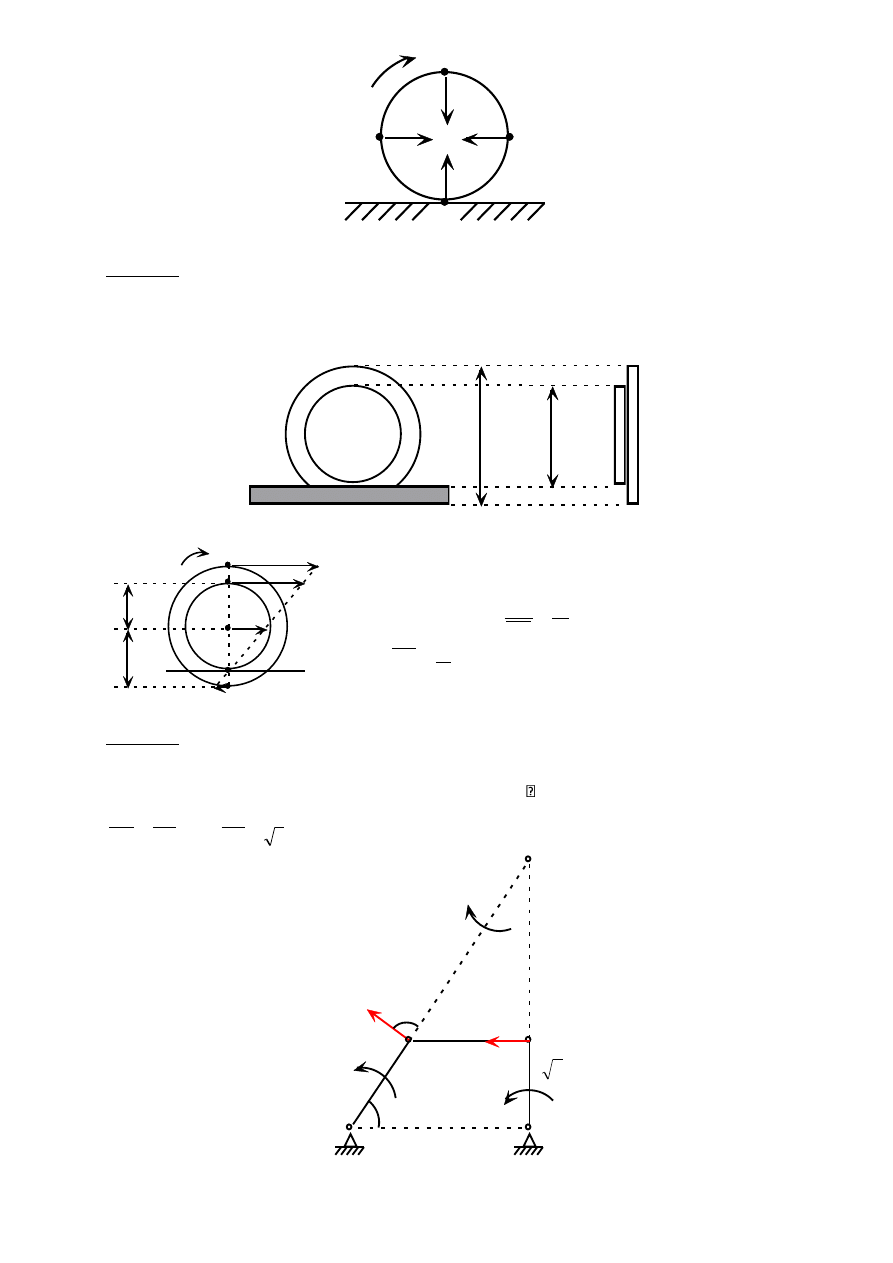
A
C
B
D
A
a
D
a
C
a
B
a
.
Zadanie 7
Koło zestawu kołowego toczy się bez poślizgu po prostej szynie ze stała prędkością V. Znaleźć
prędkość i przyspieszenie punktu A na obrzeżu koła.
2R
1
2R
A
.
C
A V
A
V
Punkt C jest chwilowym środkiem obrotu, czyli: V
C
= 0.
O
Prędkość kątowa:
R
V
CO
V
ω
R
1
R
).
R
R
(
R
V
CA
ω
V
1
A
Zadanie 8
Obliczyć prędkość punktu B mechanizmu oraz prędkości kątowe prętów AB i BD w położeniu
jak na rysunku. Korba OA obraca się z prędkością kątową
1
. Zaznaczone na rysunku wymiary
mechanizmu wynoszą:
60
φ
i
90
ABD
,
r
3
DB
,
2r
AB
OA
1
3
r
2r
2r
A
B
C
1
φ
1
ω
A
V
B
V
O
D
3
ω
2
ω
.
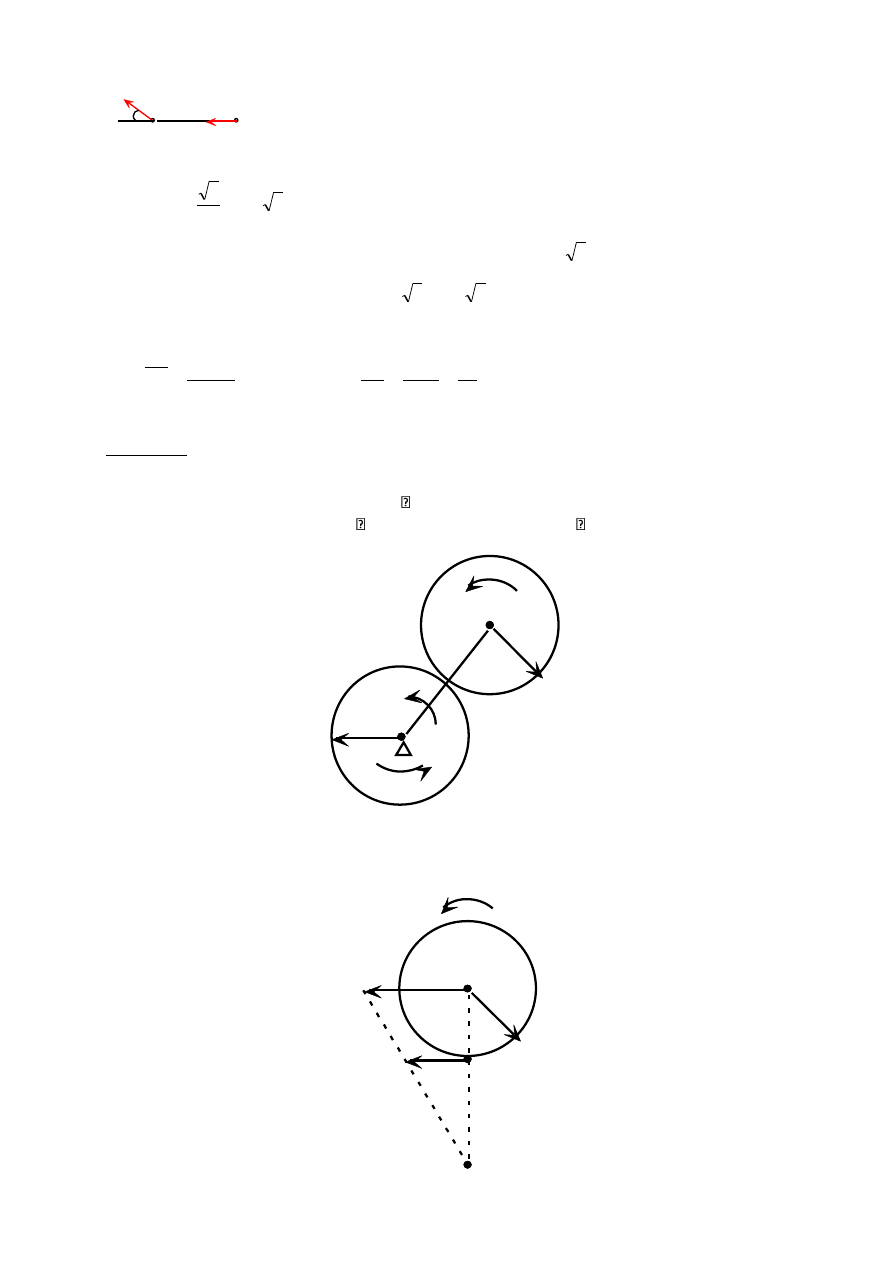
Pręt OA porusza się ruchem obrotowym, wobec tego: V
A
= ω
1
2r
Rozpatrzmy pręt AB:
A
B
A
V
B
V
30
Na podstawie twierdzenia o rzutach predkości dwóch punktów
ciała sztywnego na prostą, która je łączy otrzymujemy równanie:
V
B
= V
A
cos30
czy
li:
3
r
ω
2
3
2r
ω
V
1
1
B
Pręt DB porusza się ruchem obrotowym, wobec tego:
3
r
ω
V
3
B
wobec tego otrzymujemy równanie:
3
r
ω
3
r
ω
1
3
stąd ω
3
= ω
1
Dla pręta AB punkt C jest chwilowym środkiem obrotu,
30
ACB
stąd
4r
sin30
2r
AC
, czyli
2
ω
4r
2r
ω
4r
V
ω
1
1
A
2
.
Zadanie 8a
Dwie tarcze kołowe o średnicach D i d stykają się ze sobą. Tarcza I obraca się wokół swej
nieruchomej osi z prędkością kątową
0
. Tarcza II połączona jest z tarczą I korbą O
1
O
2
obracającą się ze stałą prędkością
1
. Wyznacz prędkość kątową
2
tarczy II.
O
2
O
1
1
o
2
r
R
I
II
Rozpatrujemy jedynie górną tarczę. Na rysunku pokazano prędkości środka górnej tarczy i
punktu styku obydwu tarcz.
O
2
2
r
II
A
C
2
O
V
A
V
x
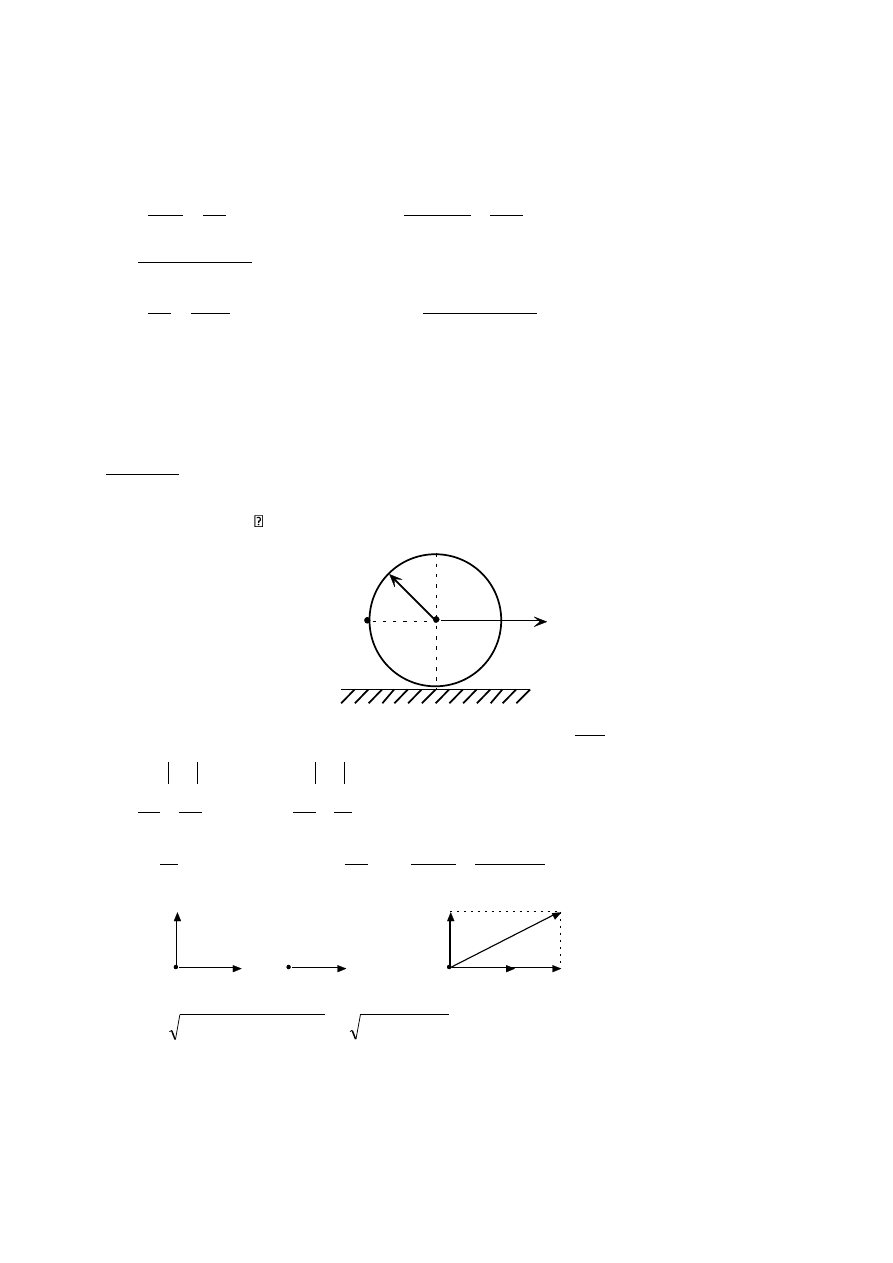
Dla górnej tarczy punkt C jest chwilowym środkiem obrotu (V
C
),
oznaczmy długość odcinka CA jako x.
Dla oznaczeń jak na rysunku możemy zapisać:
V
A
= ω
o
R
ponieważ tarcza dolna porusza się ruchem obrotowym,
r)
(R
ω
V
1
O
2
ponieważ korba O
1
O
2
porusza się ruchem obrotowym,
Wobec tego dla górnej tarczy prędkość kątowa spełnia zależność:
x
V
x
r
V
ω
A
O
2
2
czyli możemy zapisać:
x
R
ω
x
r
r)
(R
ω
o
1
i stąd wyliczamy wartość x:
R
ω
r)
(R
ω
Rr
ω
x
o
1
o
i możemy wyliczyć ω
2
:
R]
ω
r)
(R
ω
[
Rr
ω
R
ω
x
V
ω
o
1
o
o
A
2
→
r
R
ω
r)
(R
ω
ω
o
1
2
Uwaga! gdy ω
1
(R+r) = ω
o
R ruch tarczy górnej jest jedynie postępowy.
Ćwiczenie 5 i 6 (wykład: 3)
Kinematyka ciała sztywnego
ruch płaski c.d.
Zadanie 1
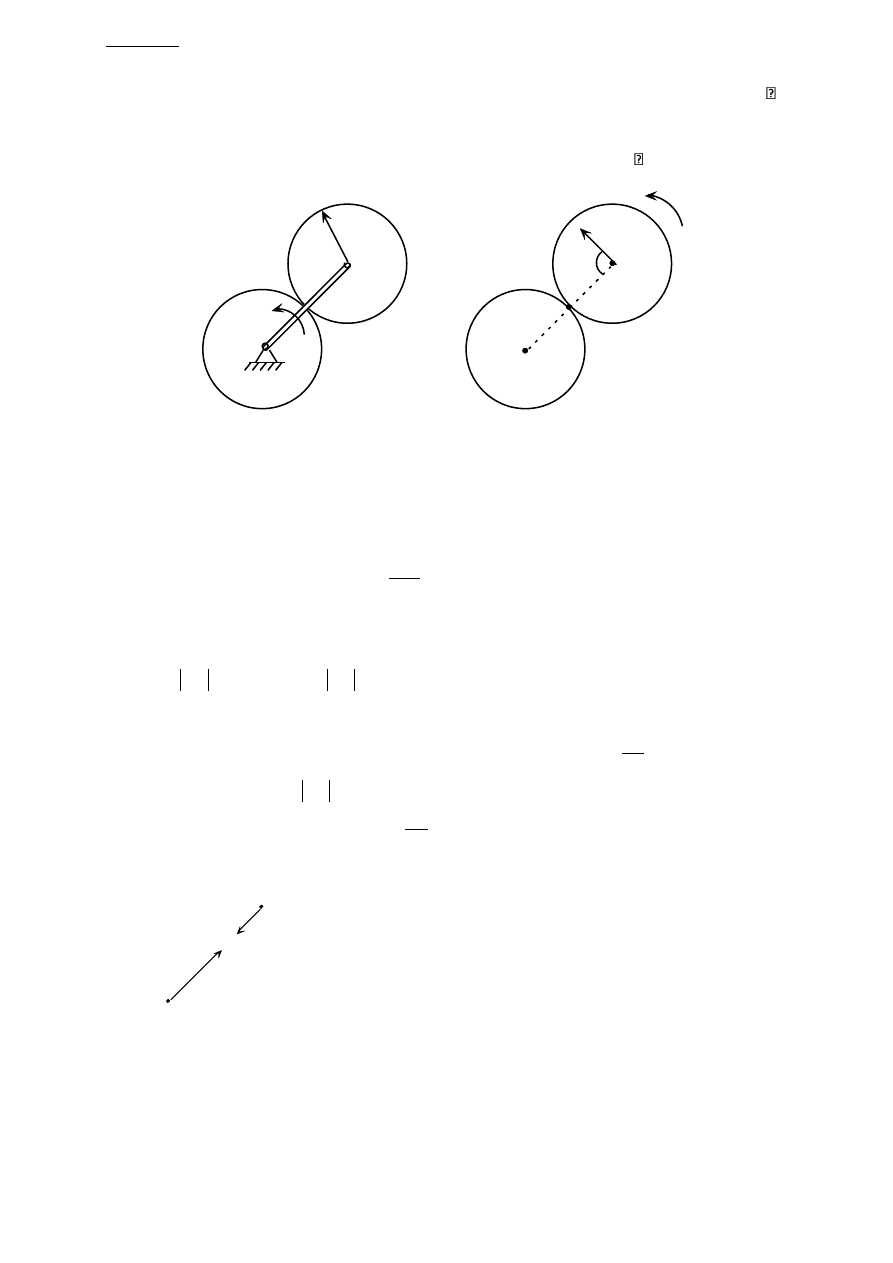
Koło toczy się bez poślizgu po prostej. Obliczyć przyspieszenie punktu A koła w chwili
t = 2[s], jeśli: V
o
= 12 t [m/s], r = 0,2[m].
O
A
V
o
r
A/O
O
A
a
a
a
,
A/On
A/Ot
A/O
a
a
a
,
A/On
A/Ot
O
A
a
a
a
a
,
dt
dV
a
o
o
12 [m/s
2
]
A/Ot
a
=
OA
=
r,
A/On
a
=
2
OA
=
2
r
r
12t
r
V
ω
o
[rad/s],
r
12
dt
dω
ε
[rad/s
2
]
r
r
12
a
A/Ot
12 [m/s
2
],
0,2
(2)
144
r
144t
r
r
12t
a
2
2
2
A/On
2880 [m/s
2
]
A
a
O
a
A/On
a
A/Ot
A
a
A
a
O
a
A/On
a
A/Ot
O
a
A
=
2
A/Os
2
O
A/On
a
)
a
(a
=
2
2
12
2892
= 2892,02 [m/s
2
].
Zadanie 2
Koło zębate o promieniu R jest uruchamiane korbą OA obracającą się dokoła osi O stałego
koła zębatego o tym samym promieniu. Korba obraca się z prędkością kątową stałą
o
.
Wyznaczyć przyspieszenie punktu koła ruchomego, który w danej chwili jest chwilowym
środkiem obrotu tego koła.
Po wyprowadzeniu wzoru ogólnego wykonać obliczenia dla: R = 12[cm],
o
= 2[rad/s].
O
A
R
o
O
A
C
V
A
.
prędkość kątowa koła ruchomego.
Chwilowym środkiem obrotu koła ruchomego jest punkt C
styku obydwu kół (V
C
= 0)
C/A
A
C
a
a
a
,
?
a
A
,
?
a
C/A
Punkt A porusza się po okręgu o promieniu 2R. Wobec tego:
An
At
A
a
a
a
,
At
a
=
o
R = 0, bo
o
dt
dω
o
0 (
o
jest stała),
An
a
=
2
o
ω
2R
czyli:
A
a
= 2
2
o
ω R
C/An
C/At
C/A
a
a
a
C/An
C/At
A
C
a
a
a
a
C/An
a
=
2
AC
=
2
R ,
C/At
a
=
AC
=
R ,
= ?,
= ?
Dla korby OA prędkość punktu A: V
A
=
o
2R
Chwilowym środkiem obrotu koła ruchomego jest punkt C, zatem:
R
V
o
Prędkość punktu A: V
A
=
AC
=
R
Wobec tego:
o
2R =
R
= 2
o
,
dt
dω
0, (bo
jest stała)
An
/
C
A
/
C
a
a
=
2
R = (2
o
)
2
R = 4
2
o
R
A
C
a
C/An
a
A
a
c
= a
C/A
a
A
= 4
2
o
R
2
2
o
R = 2
2
o
R, R = 12 [cm] = 0,12 [m],
o
= 2 [rad/s].
czyli: a
c
= 0,96 [m/s
2
].
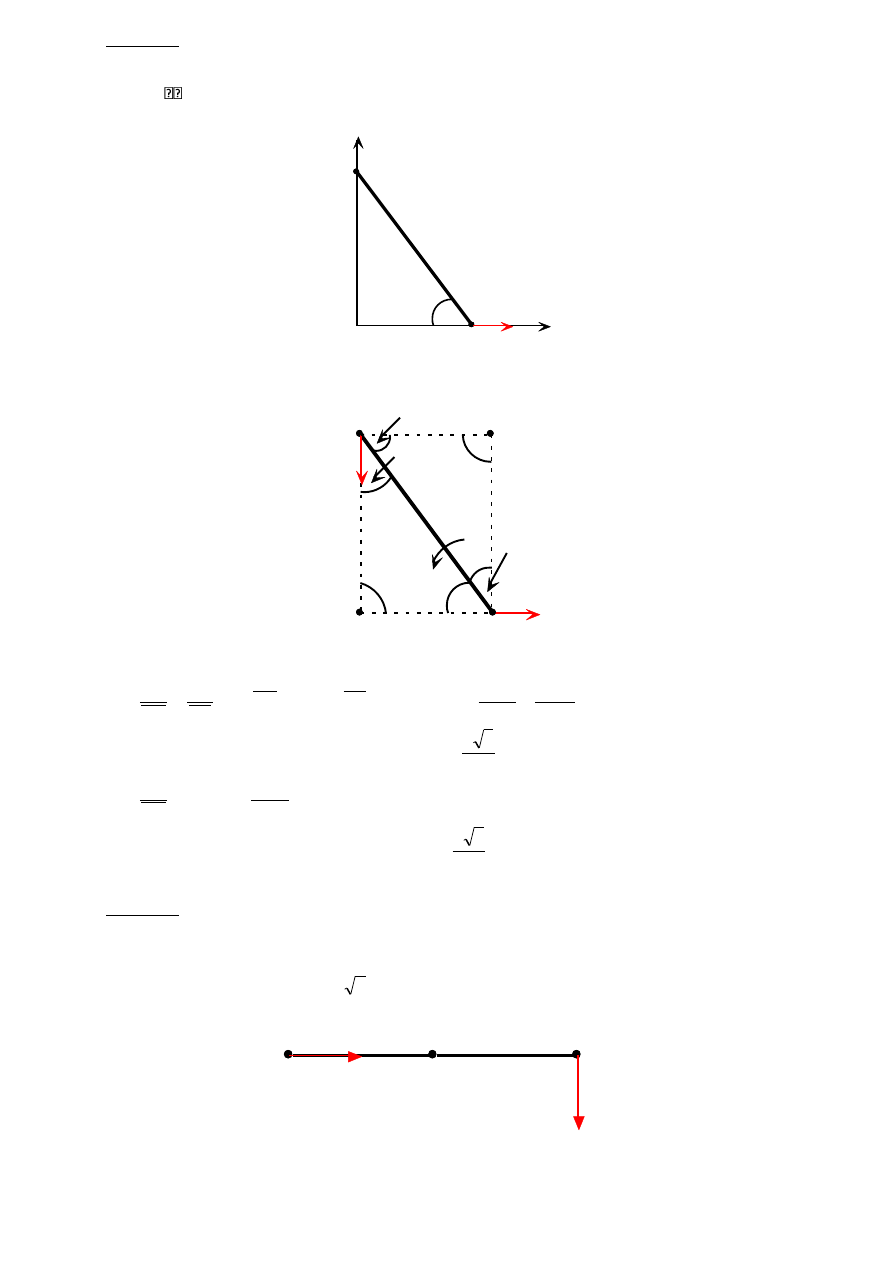
Zadanie 3
Pręt prosty AB ślizga się ruchem płaskim po osiach układu Oxy. W chwili, gdy tworzy on z osią
Ox kąt
= 60
o
, prędkość jego końca A wynosi V
A
= 2[m/s]. Wyznacz dla tego położenia
chwilowy środek obrotu, prędkość kątową pręta i prędkość końca B.
x
y
A
B
O
V
A
Oznaczmy długość pręta AB jako l i przyjmijmy jego długość l = 1[m]
będzie ona potrzebna
do obliczenia prędkości kątowej (ω) pręta.
A
B
O
V
A
90
-
V
B
.
C
.
90
-
l
Punkt C jest chwilowym środkiem obrotu pręta AB (V
C
= 0)
CB
V
CA
V
ω
B
A
, ale
lcosα
CB
,
lsinα
CA
, czyli:
lcosα
V
lsinα
V
B
A
→
ctgα
V
V
A
B
Podstawiając dane liczbowe otrzymujemy:
[m/s]
3
3
2
V
B
CA
V
ω
A
, stąd:
lsinα
V
ω
A
Podstawiając dane liczbowe otrzymujemy:
[rad/s]
3
3
4
ω
.
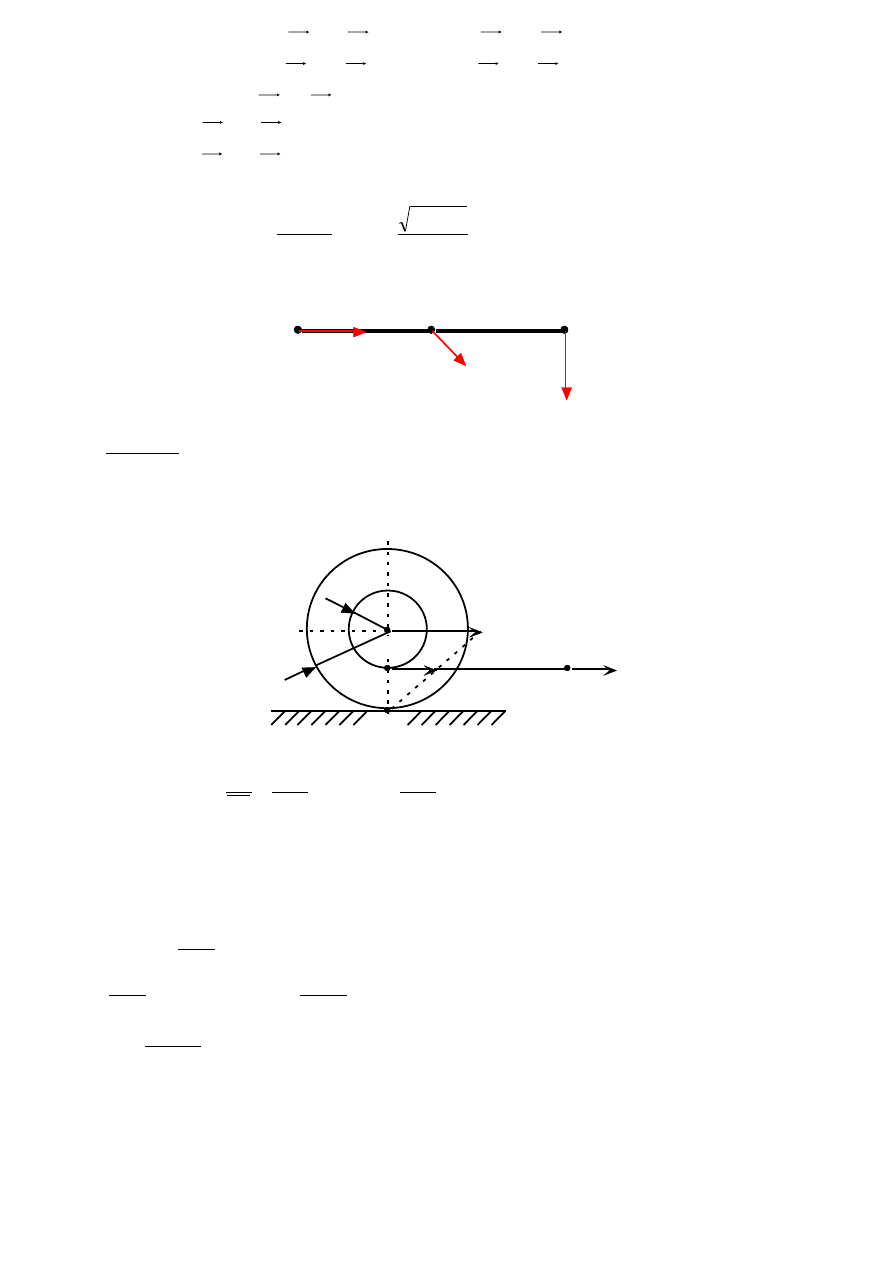
Zadanie 4
Przyspieszenia końców pewnego pręta prostego wynoszą a
A
i a
B
. Wyznaczyć przyspieszenie
a
S
środka S tego pręta, oznaczyć na rysunku jego kierunek i zwrot oraz obliczyć wartość
przyspieszenia a
S
, jeśli: a
A
= a
B
= 2 [m/s
2
].
S
a
B
B
A
a
A
S/A
A
S
a
a
a
,
AS
ω
AS
ε
a
2
S/A
,
AS
ω
AS
ε
a
a
2
A
S
S/B
B
S
a
a
a
,
BS
ω
BS
ε
a
2
S/B
,
BS
ω
BS
ε
a
a
2
B
S
z rysunku widać, że:
BS
AS
, czyli możemy zapisać:
BS
ω
BS
ε
a
a
2
A
S
BS
ω
BS
ε
a
a
2
B
S
dodając stronami dwa ostatnie równania otrzymujemy:
B
A
S
a
a
a
2
2
a
a
a
B
A
S
a
S
2
a
a
2
B
2
A
1 [m/s
2
]
kierunek i zwrot przyspieszenia a
s
pokazano na poniższym rysunku:
S
a
B
B
A
a
A
a
s
.
Zadanie 5
Na szpulę o promieniach a i b nawinięto nierozciągliwą nić, której koniec A ma prędkość
u = const. Obliczyć, jaką drogę s
A
przebędzie koniec A nici, gdy odcinek, AB = e tej liny
nawinie się na szpulę. Dane: a, b, e, u.
C
V
o
V
B
A
u
B
O
b
a
Punkt C jest chwilowym środkiem obrotu (V
C
= 0)
V
B
= V
A
= u,
b
a
u
BC
V
ω
B
,
b
a
au
ωa
V
o
W jednakowym czasie t droga środka szpuli (s
o
) O musi być o e większa od drogi punktów B
(s
A
) (leżących stale pod punktem O):
s
o
= s
B
+ e (1)
Oba punkty poruszają się ruchem jednostajnym, zatem ich drogi wynoszą:
s
o
= V
o
t , s
A
= ut
stąd
u
V
s
s
o
A
o
i po podstawieniu do wzoru (1) otrzymujemy
e
s
u
V
s
A
o
A
stąd:
u
V
eu
s
o
B
, a po uwzględnieniu wzoru na V
o
ostatecznie otrzymujemy:
b
b)
(a
e
s
A
.
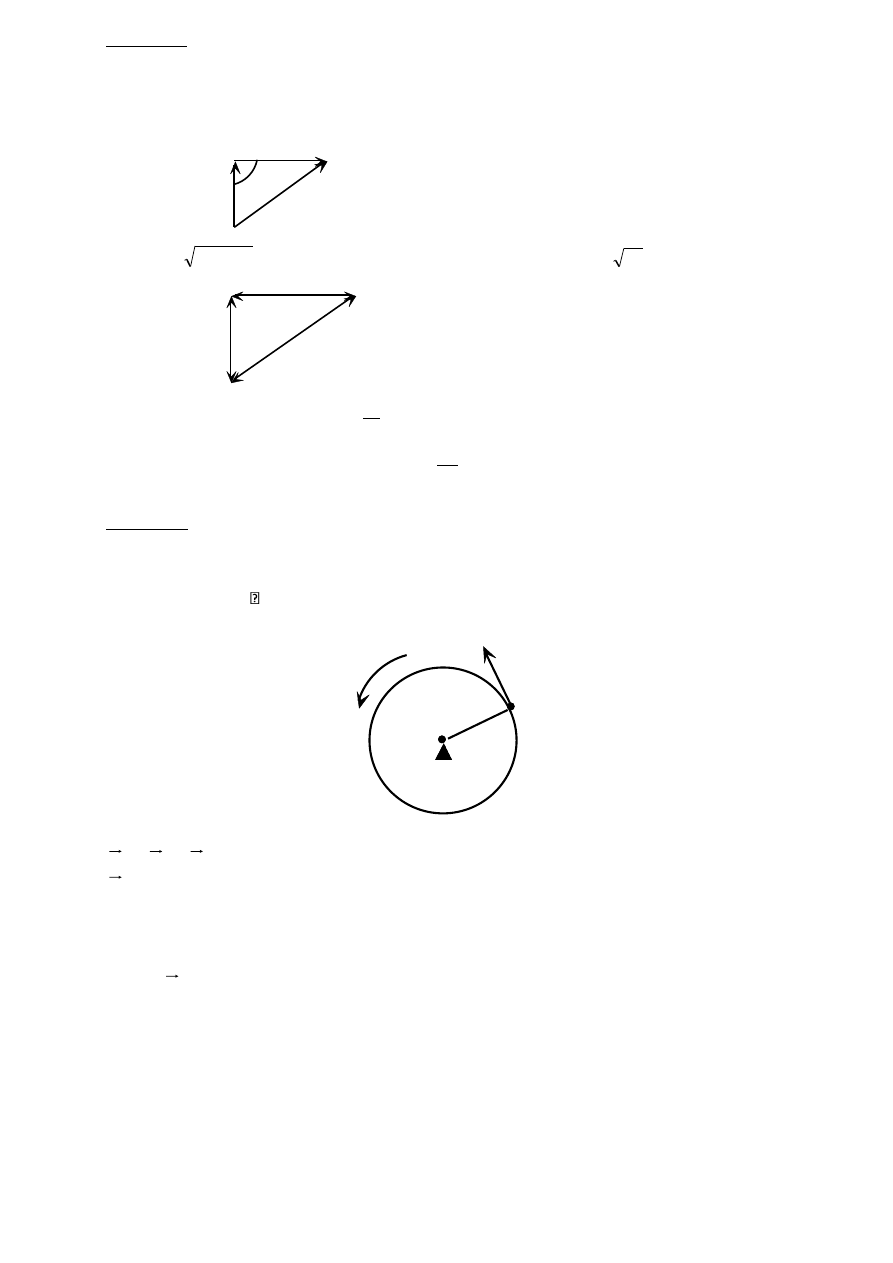
Zadanie 5a
Balon wznosi się pionowo z prędkością w = 5[m/s], zaś prędkość bocznego podmuchu wiatru
wynosi u = 8[m/s]. Jaka jest prędkość bezwzględna balonu? Oblicz wartość znoszenia
bocznego po uzyskaniu przez balon wysokości h = 1[km].
w
V
b
u
V
b
szukana bezwzględna prędkość balonu
V
b
= w + u
.
czyli:
2
2
B
u
w
V
i po wstawieniu danych liczbowych mamy:
[m/s]
9,4
89
V
B
h
x
x
szukana wartość znoszenia bocznego
t
czas ruchu balonu
h = wt, stąd czas ruchu balonu
w
h
t
x = ut i po podstawieniu t otrzymujemy:
w
uh
x
, a po podstawieniu danych liczbowych: x = 1,6 [km].
Zadanie 5b
Punkt A porusza się po obwodzie koła o promieniu r = 1[m] z prędkością względną
V
w
= 1[m/s]. Jednocześnie koło obraca się względem swego nieruchomego środka z
prędkością kątową = 1[rad/s]. Oblicz prędkość bezwzględną i przyspieszenie bezwzględne
punktu A. Wykonaj odpowiednie rysunki.
O
A
r
V
w
Prędkość bezwzględną (V
b
) punktu A wyznaczamy ze wzoru:
u
w
b
V
V
V
, gdzie: V
u
prędkość unoszenia
r
ω
V
u
gdzie:
r
jest wektorem poprowadzonym z punktu O do punktu A
)
r
,
ω
(
sin
r
ω
V
u
,
90
)
r
,
ω
(
ponieważ wektor
ω
jest prostopadły do płaszczyzny
kartki i skierowany „do nas”
czyli: V
u
= ωr = 1 [m/s]
wektor
u
V
ma kierunek (ustalony na podstawie reguły „śruby prawoskrętnej”) pokazany na
poniższym rysunku
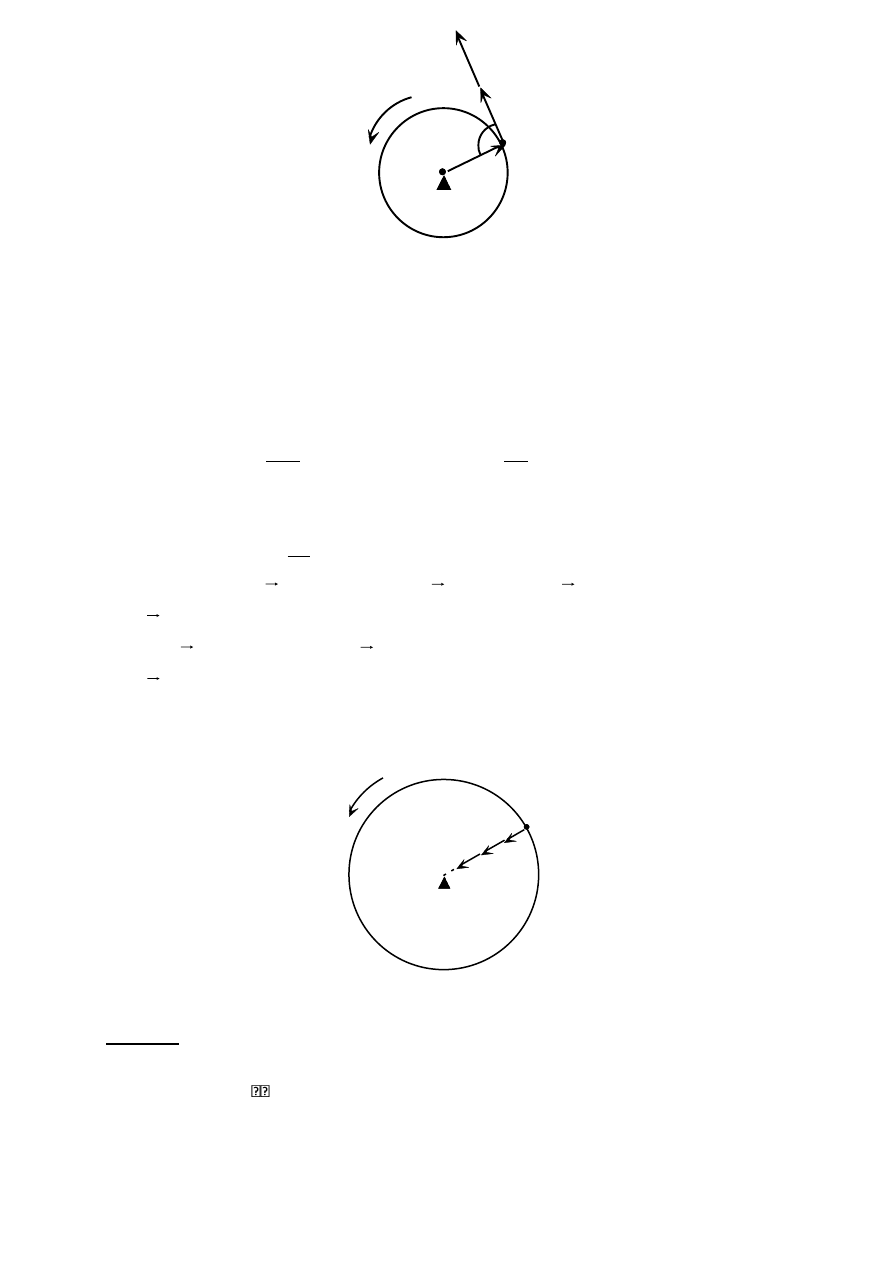
O
A
V
w
r
V
u
Wobec tego wartość prędkości bezwzględnej (V
b
): V
b
= V
w
+ V
u
= 2 [m/s]
Przyspieszenie bezwzględne (a
b
) punktu A wyznaczamy ze wzoru:
c
u
w
b
a
a
a
a
, gdzie:
a
w
przyspieszenie względne,
a
u
przyspieszenie unoszenia,
a
c
przyspieszenie Coriolisa,
W rozpatrywanym przypadku ruch względny jest ruchem po okręgu, wobec tego:
wn
wt
w
a
a
a
,
0
dt
dV
a
w
wt
, bo V
w
jest stała,
1
r
V
a
2
w
wn
[m/s
2
]
czyli: a
w
= a
wn
= 1 [m/s
2
] i jest skierowane do środka koła
un
ut
u
a
a
a
,
r
ε
a
ut
,
ε
wektor przyspieszenia kątowego, który ma ten sam kierunek i
zwrot jak wektor
ω
,
0
dt
dω
ε
, bo ω jest stała, czyli a
ut
= 0 i mamy
un
u
a
a
u
un
V
ω
)
r
ω
(
ω
a
,
)
V
,
ω
(
sin
r
ω
)
V
,
ω
(
sin
V
ω
a
u
2
u
u
un
90
)
V
,
ω
(
u
wobec tego:
1
r
ω
a
a
2
un
u
[m/s
2
]
w
c
V
ω
2
a
,
)
V
,
ω
(
sin
V
ω
2
a
w
w
c
90
)
V
,
ω
(
w
wobec tego:
2
V
ω
2
a
w
c
[m/s
2
]
Kierunki i zwroty przyspieszeń unoszenia i Coriolisa ustalamy na podstawie reguły „śruby
prawoskrętnej”. Kierunki i zwroty przyspieszeń pokazano na poniższym rysunku.
O
A
.
a
w
a
u
a
c
Wobec tego wartość przyspieszenia bezwzględnego (a
b
): a
b
= a
w
+ a
u
+ a
c
= 4 [m/s
2
].
Zadanie 6
Koło o promieniu R = 0,2[m] obraca się w swej płaszczyźnie wokół stałego punktu O ze stałą
prędkością kątową
= 5[rad/s]. Po obwodzie koła przesuwa się punkt ze stałą prędkością
V
w
= 1[m/s]. Obliczyć bezwzględne przyspieszenie punktu w położeniu A.

.
O
A
V
w
R
r
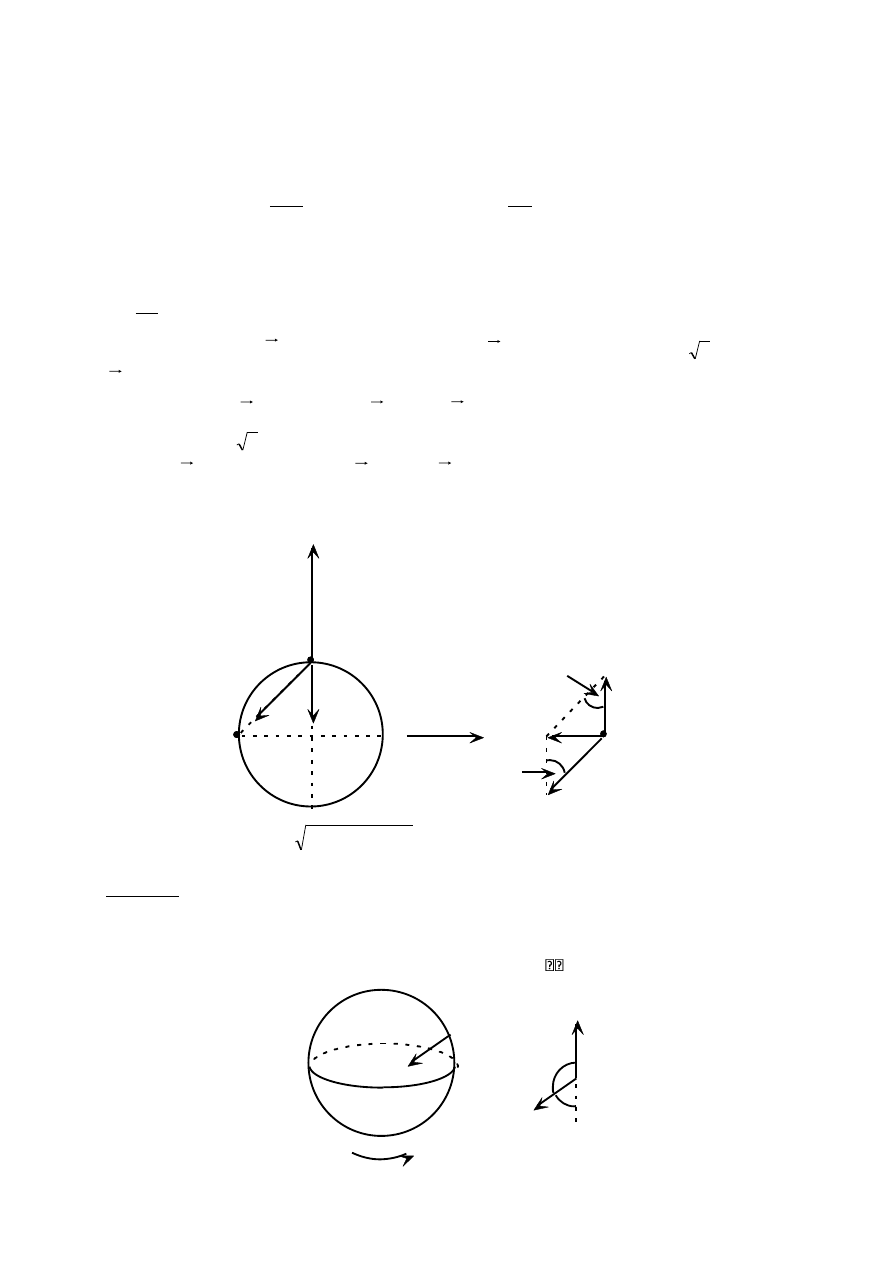
Przyspieszenie bezwzględne (a
b
) punktu A wyznaczamy ze wzoru:
c
u
w
b
a
a
a
a
, gdzie:
a
w
przyspieszenie względne,
a
u
przyspieszenie unoszenia,
a
c
przyspieszenie Coriolisa,
W rozpatrywanym przypadku ruch względny jest ruchem po okręgu, wobec tego:
wn
wt
w
a
a
a
,
0
dt
dV
a
w
wt
, bo V
w
jest stała,
]
[m/s
5
R
V
a
2
2
wn
w
czyli a
w
= a
wn
= 5 [m/s
2
] i jest skierowane do środka koła
un
ut
u
a
a
a
,
r
ε
a
ut
gdzie:
r
jest wektorem poprowadzonym z punktu O do punktu A
0
dt
dω
ε
, bo ω jest stała, czyli a
ut
= 0 i mamy
un
u
a
a
u
un
V
ω
)
r
ω
(
ω
a
, V
u
prędkość unoszenia,
r
ω
V
u
, oczywiście:
R
2
r
r
ω
V
u
,
)
r
,
ω
(
sin
r
ω
V
u
,
90
)
r
,
ω
(
, czyli: V
u
= ωr
)
V
,
ω
(
sin
r
ω
)
V
,
ω
(
sin
V
ω
a
u
2
u
u
un
,
90
)
V
,
ω
(
u
, wobec tego:
]
[m/s
2
5
r
ω
a
a
2
2
un
u
w
c
V
ω
2
a
,
)
V
,
ω
(
sin
V
ω
2
a
w
w
c
,
90
)
V
,
ω
(
w
, wobec tego:
0
1
V
ω
2
a
w
c
[m/s
2
]
Kierunki i zwroty przyspieszeń unoszenia i Coriolisa ustalamy na podstawie reguły „śruby
prawoskrętnej”. Kierunki i zwroty przyspieszeń pokazano na poniższym rysunku.
A
a
c
a
w
a
u
A
a
c
a
u
a
w
a
b
45
45
O
Z rysunku widać, że:
5
)
a
(a
a
a
2
w
c
2
u
b
[m/s
2
].
Zadanie 7
Linia kolejowa przebiega wzdłuż południka. Lokomotywa jedzie z prędkością
V = 180 [km/h] na południe. Obliczyć przyspieszenie Coriolisa lokomotywy w chwili, gdy jej
położenie jest określone szerokością geograficzną północną
= 60
o
.
V
V
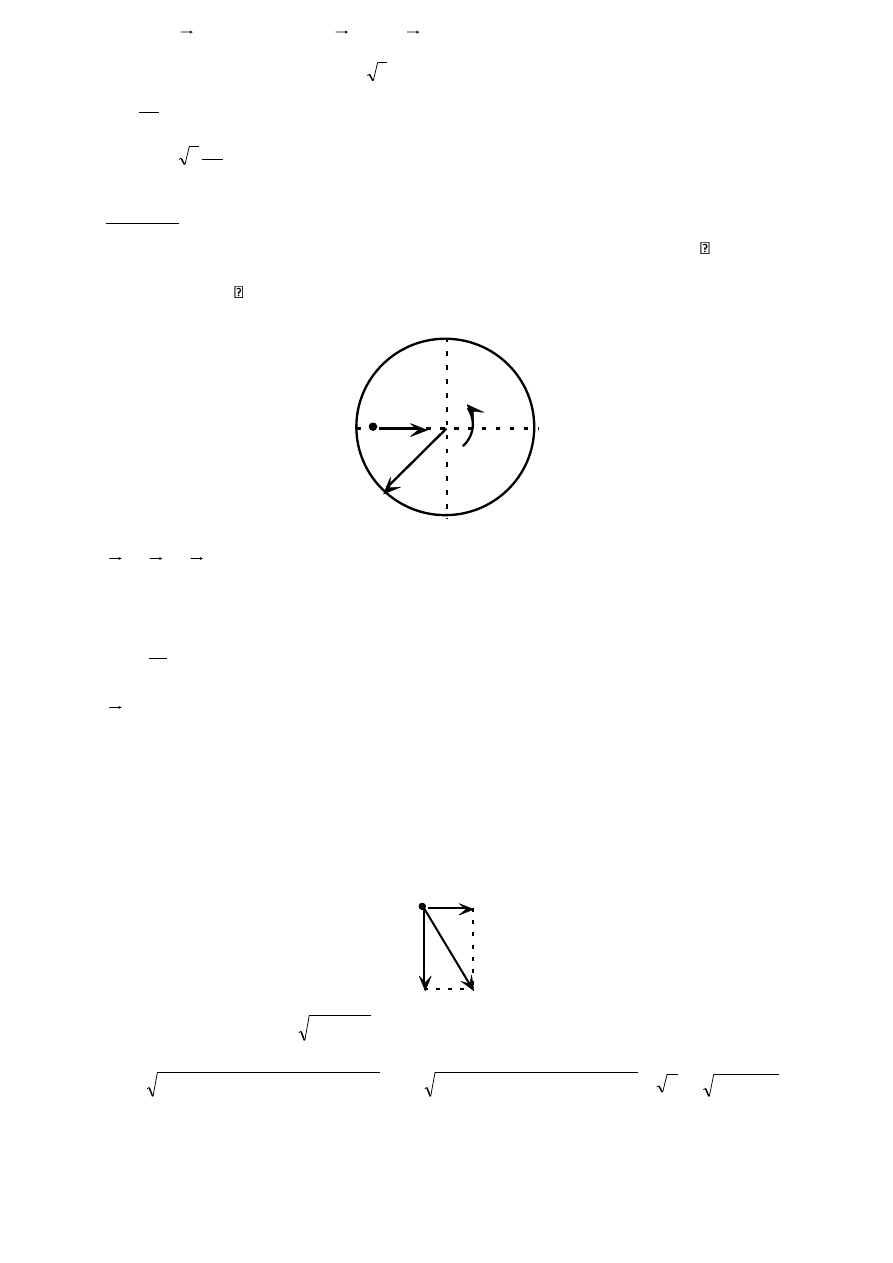
V
ω
2
a
c
,
)
V
,
ω
(
sin
V
ω
2
a
c
,
0
2
1
)
V
,
ω
(
wobec tego:
V
ω
3
0
6
sin
V
ω
2
20
1
sin
V
ω
2
a
c
, V = 50 [m/s]
T
2π
ω
, T
okres obrotu Ziemi dookoła własnej osi, T= 24 [h] = 86400 [s]
czyli
V
T
2π
3
a
c
, podstawiając dane liczbowe otrzymujemy: a
c
= 6,3
10
3
[m/s
2
].
Zadanie 8
Koło o promieniu R obraca się w swej płaszczyźnie ze stałą prędkością kątową wokół osi
przechodzącej przez jego środek. Po średnicy koła porusza się punkt zgodnie z równaniem
drogi s(t) = Rsin t. Punkt wystartował ze środka koła. Znaleźć prędkość bezwzględną i
przyspieszenie bezwzględne punktu w zależności od czasu.
.
V
w
R
A
Prędkość bezwzględną (V
b
) punktu (oznaczyliśmy go jako A) wyznaczamy ze wzoru:
u
w
b
V
V
V
, gdzie: V
w
prędkość względna, V
u
prędkość unoszenia
W rozpatrywanym przypadku ruch względny jest ruchem postępowym, prostoliniowym,
wobec tego prędkość względna punktu A dana jest wzorem:
t
ω
cos
ωR
dt
ds
V
w
Prędkość unoszenia wyznaczamy ze wzoru:
r
ω
V
u
gdzie
r
jest wektorem poprowadzonym ze środka koła do punktu A
Długość wektora
r
jest równa: |
r
|
t)
ω
sin
R(1
t
ω
sin
R
R
s
R
r
)
r
,
ω
(
sin
r
ω
V
u
,
90
)
r
,
ω
(
ponieważ wektor
ω
jest prostopadły do płaszczyzny
kartki i skierowany „do nas”, czyli: V
u
= ωr =
t)
ω
sin
ωR(1
Kierunek i zwrot prędkości unoszenia ustalamy na podstawie reguły „śruby prawoskrętnej”.
Kierunki i zwroty poszczególnych prędkości pokazano na poniższym rysunku.
V
w
V
u
V
b
A
Z rysunku widać, że:
2
w
2
u
b
V
V
V
Podstawiając wyliczone wartości V
w
i V
u
otrzymujemy:
t
ω
sin
1
ωR
2
t
ω
cos
t
ω
sin
t
ω
sin
2
1
ωR
t)
ω
cos
ωR
(
t)]
ω
sin
ωR(1
[
V
2
2
2
2
b
Przyspieszenie bezwzględne (a
b
) punktu A wyznaczamy ze wzoru:
c
u
w
b
a
a
a
a
, gdzie:
a
w
przyspieszenie względne
a
u
przyspieszenie unoszenia
a
c
przyspieszenie Coriolisa

Przyspieszenie względne (a
w
) punktu wyznaczamy ze wzoru:
t
sinω
R
ω
dt
dV
a
2
w
w
znak minus wskazuje, że wektor przyspieszenia względnego ma przeciwny zwrot do wektora
prędkości względnej.
un
ut
u
a
a
a
,
r
ε
a
ut
,
0
dt
dω
ε
, bo ω jest stała , czyli a
ut
= 0 i mamy
un
u
a
a
u
un
V
ω
)
r
ω
(
ω
a
)
V
,
ω
(
sin
t)
ω
sin
R(1
ω
)
V
,
ω
(
sin
V
ω
a
u
2
u
u
un
,
90
)
V
,
ω
(
u
, wobec tego:
t)
ω
sin
R(1
ω
a
a
2
un
u
w
c
V
ω
2
a
,
)
V
,
ω
(
sin
V
ω
2
a
w
w
c
,
90
)
V
,
ω
(
w
, wobec tego:
t
ω
cos
R
ω
2
a
2
c
Kierunki i zwroty przyspieszeń unoszenia i Coriolisa ustalamy na podstawie reguły „śruby
prawoskrętnej”. Kierunki i zwroty poszczególnych przyspieszeń pokazano na poniższym
rysunku.
a
w
a
u
a
c
A
a
b
z rysunku widać, że:
2
c
2
w
u
b
a
)
a
(a
a
Podstawiając wyliczone wartości poszczególnych przyspieszeń otrzymujemy:
2
2
2
2
2
2
c
2
w
u
b
t)
ω
cos
R
ω
2
(
t]
sinω
R
ω
t)
ω
sin
R(1
ω
[
a
)
a
(a
a
po przekształceniach otrzymujemy:
t
ω
sin
4
5
R
ω
a
2
b
[m/s
2
].
Ćwiczenie 7 i 8 (wykład: 4)
Równania ruchu punktu materialnego (PM).
Zadanie 1
Punkt materialny o masie m = 0,1[kg] porusza się pod działaniem sił: F
x
=
2sin3t [N],
F
y
=
2cos3t [N]. Określić tor tego punktu przy zerowych warunkach początkowych.
F
x
= ma
x
→
m
F
a
x
x
20sin3t [m/s
2
]
C
dt
a
V
x
x
, C
stała zależna od warunku początkowego
C
cos3t
3
20
C
sin3tdt
20
V
x
,
0
V
0
t
x
→
C
3
20
0
→
3
20
C
3
20
cos3t
3
20
V
x
[m/s]
1
x
C
dt
V
x
, C
1
stała zależna od warunku początkowego
1
1
1
C
t
3
20
sin3t
9
20
C
dt
3
20
cos3tdt
3
20
C
dt
3
20
cos3t
3
20
x
0
x
0
t
→ C
1
= 0
[m]
t
3
20
sin3t
x
(1)
F
y
= ma
y
→
m
F
a
y
y
20cos3t [m/s
2
]
2
y
y
C
dt
a
V
, C
2
stała zależna od warunku początkowego
2
2
y
C
sin3t
3
20
C
cos3tdt
20
V
0
V
0
t
y
→ C
2
= 0
sin3t
3
20
V
y
[m/s]
3
y
C
dt
V
y
, C
3
stała zależna od warunku początkowego
3
3
C
cos3t
9
20
C
sin3tdt
3
20
y
0
y
0
t
→
3
C
9
20
0
→
9
20
C
3
9
20
cos3t
9
20
y
[m] stąd:
1
y
20
9
arccos
3
1
t
i podstawiamy do równania (1) otrzymując równanie toru:
[m]
1
y
20
9
arccos
9
20
1
y
20
9
arccos
sin
x
.
Zadanie 2
Punkt materialny o masie m = 2[kg] porusza się zgodnie z równaniami x(t) = hcos t [m],
y(t) = hsin t [m]. Wyznacz: a) prędkość w chwili t
1
= / , b) przyspieszenie w chwili
t
2
= 2 / , c) siłę działającą na ten punkt w chwili t
2
. Przyjąć do obliczeń: h = 0,05[m],
= 10[rad/s].
a)
2
y
2
x
V
V
V
,
[m/s]
ωhsinωt
dt
dx
V
x
,
[m/s]
ωhcosωt
dt
dy
V
y
[m/s]
ωh
ωt
cos
ωt
sin
ωh
t)
hcosω
(ω
ωhsinωt)
(
V
2
2
2
2
[m/s]
0,5
ωh
V
1
t
t
b)
2
y
2
x
a
a
a
,
t
hcosω
ω
dt
dV
a
2
x
x
[m/s
2
] ,
t
hsinω
ω
dt
dV
a
2
y
y
[m/s
2
]
h
ω
ωt
sin
ωt
cos
h
ω
t)
hsinω
ω
(
t)
hcosω
ω
(
a
2
2
2
2
2
2
2
2
[m/s
2
]
5
h
ω
a
2
t
t
2
[m/s
2
]
c)
am
F
, F = ω
2
hm [N]
10
hm
ω
F
2
t
t
2
[N].
Zadanie 3
Suwak obrabiarki o masie m = 0,6[kg] będąc w stanie spoczynku, został wprawiony w ruch
wzdłuż prowadnicy za pomocą siły Q = 10[N], skierowanej do osi prowadnicy pod kątem
α = 30
o
. Jaką prędkość uzyska suwak po przesunięciu go na odległość s = 1[m], jeżeli
współczynnik tarcia suwak-prowadnica wynosi µ = 0,2?
m
Q
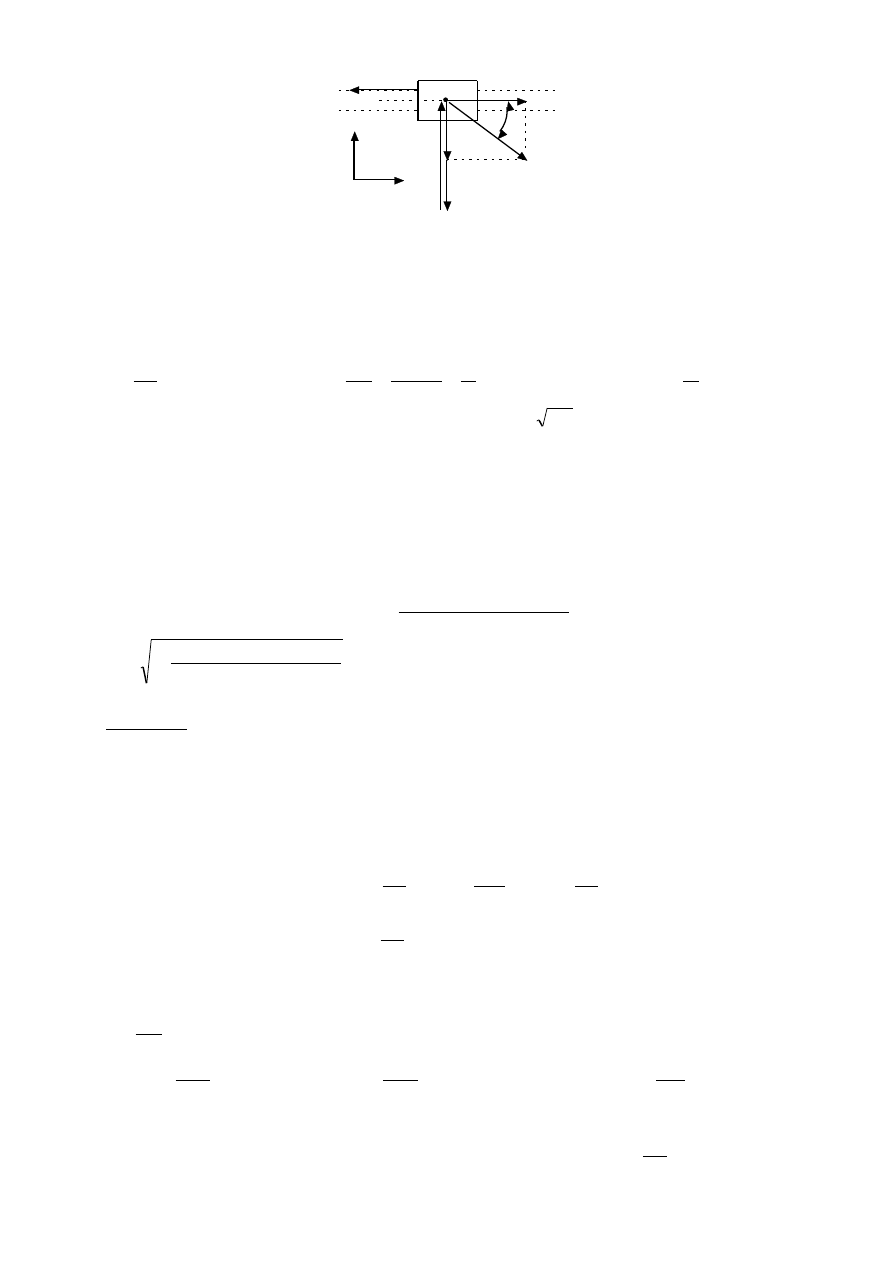
Poniższy rysunek przedstawia siły działające na suwak w trakcie ruchu:
Q
Q
x
Q
y
P
N
T
x
y
N
siła reakcji podłoża, T
siła tarcia, P
siła ciężkości
Q
x
, Q
y
składowe (pozioma i pionowa) siły Q
Pod wpływem działania siły Q suwak będzie poruszał się ruchem jednostajnie
przyspieszonym (bez prędkości początkowej) z przyspieszeniem a. Wobec tego przebyta
drogę s, jaką przebędzie suwak znajdujemy ze wzoru:
2
at
s
2
, ale z drugiej strony:
t
V
t
V
V
t
ΔV
a
o
, bo V
o
= 0, wyliczamy t:
a
V
t
i podstawiając do wzoru na s otrzymujemy wzór na V:
2as
V
(1)
czyli musimy znaleźć przyspieszenie z jakim będzie poruszać się suwak
piszemy dynamiczne równania ruchu suwaka w kierunku x i y:
x: a
x
m = Q
x
T, Q
x
= Qcos
, T = Nμ
y: a
y
m = N
P
Q
y
, Q
y
= Qsin
, P = mg
wobec tego, że ruch odbywa się tylko po współrzędnej x mamy a
y
= 0, czyli a
x
= a
am = Qcos
Nμ (2)
0 = N
mg
Qsin
→ N = mg + Qsin
i podstawiamy do (2)
am = Qcos
(mg + Qsin
)μ stąd:
m
μ
)
Qsinα
(mg
Qcosα
a
i podstawiamy do (1)
m
μ
)
Qsinα
(mg
Qcosα
2s
V
, podstawiając dane liczbowe mamy: V = 12,36 [m/s].
Zadanie 3a
Po jakim czasie i na jakim odcinku może zatrzymać się wskutek hamowania wagon
tramwajowy jadący po poziomym i prostym torze z prędkością V
o
= 36[km/h], jeśli opór
hamowania jest stały i wynosi 3[kN] na jedną tonę ciężaru wagonu.
Dynamiczne równanie ruchu:
op
F
am
, gdzie F
op
siła oporu
przekształcamy dane równanie:
m
F
a
op
→
mg
g
F
a
op
→
g
P
F
a
op
, P
ciężar wagonu
występujący po prawej stronie iloraz
P
F
op
jest danym w zadaniu oporem hamowania, który
oznaczymy F
m
(F
m
= 3 [kN/T]), 1 [T] = 10
3
[kG] = 9,81 [kN], czyli F
m
≈ 0,3)
wobec tego dynamiczne równanie ruchu ma postać:
g
F
a
m
(1)
t
V
a
,
o
k
V
V
ΔV
, V
k
prędkość końcowa, V
k
= 0
z treści zadania →
o
V
ΔV
czyli:
t
V
a
o
i podstawiamy do (1),
g
F
t
V
m
o
, stąd wyliczamy t →
g
F
V
t
m
o
podstawiając dane liczbowe (V
o
= 10 [m/s]) otrzymujemy: t = 3,4 [s]
odcinek (s) po jakim wagon zatrzyma się wyznaczamy ze wzoru:
2
at
t
V
s
2
o
podstawiając dane {ze wzoru (1)
2,94
a
[m/s
2
]} otrzymujemy: s
17 [m].

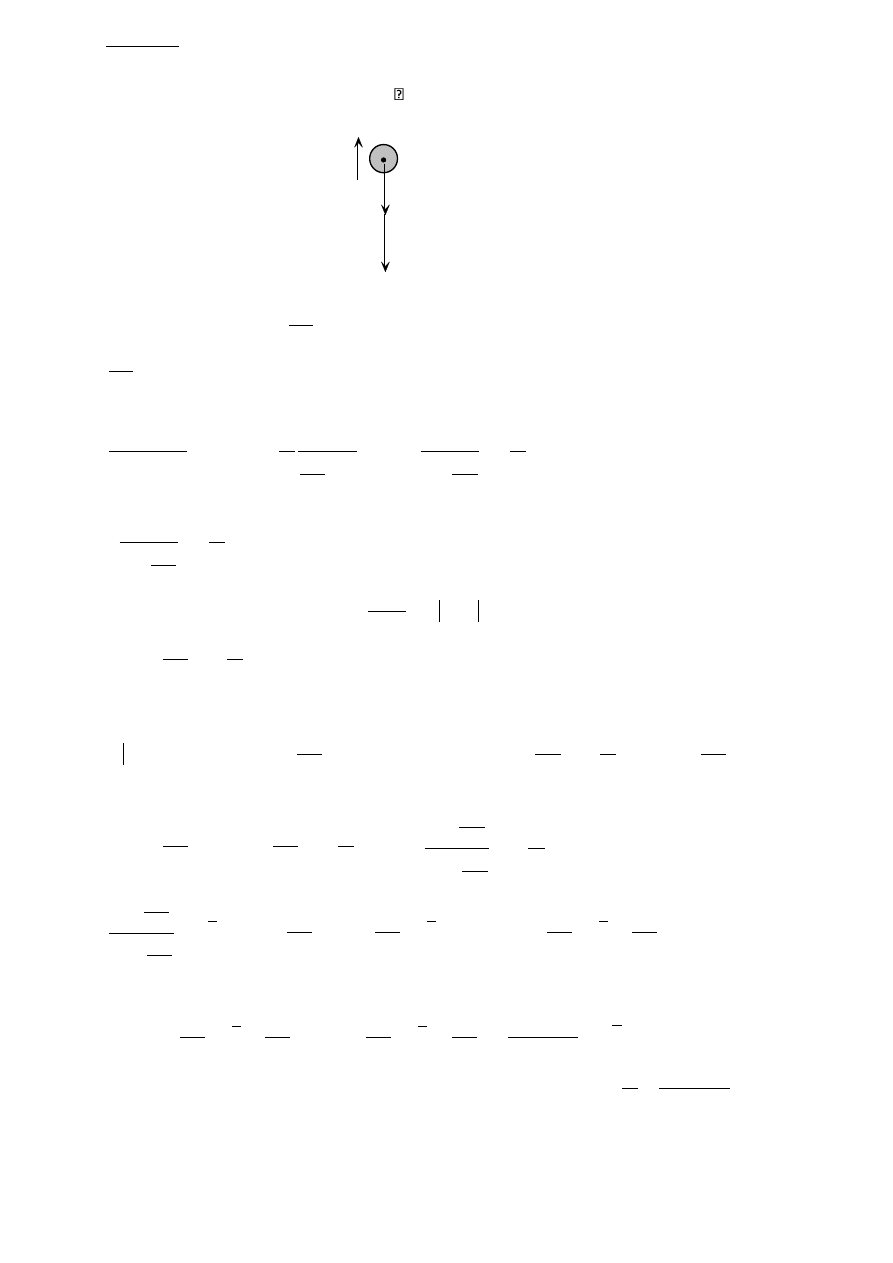
Zadanie 4
Pocisk o masie m wystrzelono pionowo w górę z prędkością początkową V
o
. Wiedząc, że siła
oporu powietrza jest w postaci R = k V (k
stały współczynnik, V
prędkość pocisku),
wyznaczyć czas, po którym pocisk osiągnie maksymalną wysokość.
V
P
R
P = mg , R = kV
Dynamiczne równanie ruchu:
R
P
am
, P = mg
kV
mg
am
, ale
dt
dV
a
kV
mg
m
dt
dV
, jest to równanie różniczkowe o zmiennych rozdzielonych
rozdzielamy zmienne (V,t) i przekształcamy równanie:
dt
m
kV
mg
dV
→
dt
V
k
mg
dV
k
m
→
dt
m
k
k
mg
V
dV
ostatnie równanie obustronnie całkujemy:
C
dt
m
k
k
mg
V
dV
C
stała zależna od warunku początkowego,
korzystamy z całki nieoznaczonej:
C
a
x
ln
a
x
dx
, a
pewna stała i otrzymujemy:
C
t
m
k
k
mg
V
ln
stałą C wyznaczamy z warunku początkowego: dla t = 0 → V = V
o
o
0
t
V
V
→
k
mg
V
ln
C
o
czyli otrzymujemy:
k
mg
V
ln
t
m
k
k
mg
V
ln
o
przekształcamy ostatnie równanie:
t
m
k
k
mg
V
ln
k
mg
V
ln
o
→
t
m
k
k
mg
V
k
mg
V
ln
o
t
m
k
o
e
k
mg
V
k
mg
V
→
t
m
k
o
e
k
mg
V
k
mg
V
→
k
mg
e
k
mg
V
V
t
m
k
o
Pocisk osiągnie maksymalną wysokość gdy V = 0
k
mg
e
k
mg
V
0
t
m
k
o
→
k
mg
e
k
mg
V
t
m
k
o
→
t
m
k
o
e
mg
kV
mg
po zlogarytmowaniu obu stron ostatniego równania otrzymujemy:
mg
kV
mg
ln
k
m
t
o
.
Zadanie 4a
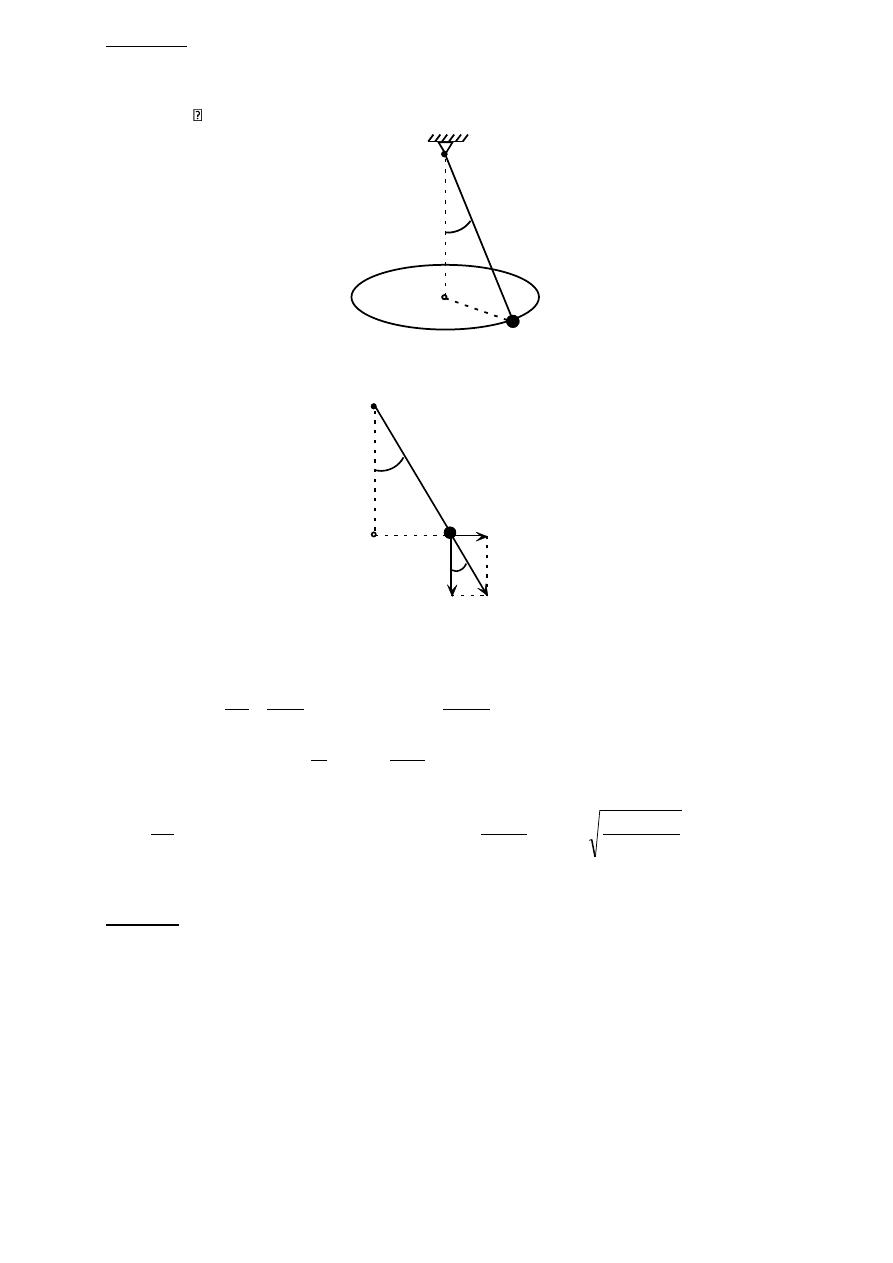
Mała kulka A o ciężarze Q = 10 [N] zawieszona w nieruchomym punkcie O na lince o długości
l = 30 [cm] tworzy wahadło stożkowe (zatacza okrąg w płaszczyźnie poziomej). Linka tworzy z
pionem kąt . Obliczyć prędkość kulki i naciąg linki.
A
O
Poniższy rysunek przedstawia siły działające na kulkę podczas ruchu
A
O
l
r
N
F
od
Q
gdzie: Q
siła ciężkości
N
siła naciągu linki
F
od
siła odśrodkowa
Q = mg,
lsinα
r
,
gr
QV
r
V
m
F
2
2
od
→
glsinα
QV
F
2
od
Z rysunku widać, że:
N
Q
cosα
→
cosα
Q
N
podstawiając dane (l = 0,3 [m] i przyjmując
= 30
) otrzymujemy: N = 11,55 [N]
Q
F
tgα
od
→ F
od
= Qtg
→ F
od
= 5,77 [N] →
glsinα
QV
77
,
5
2
→
Q
5,77glsin α
V
podstawiając dane otrzymujemy: V = 0,92 [m/s].
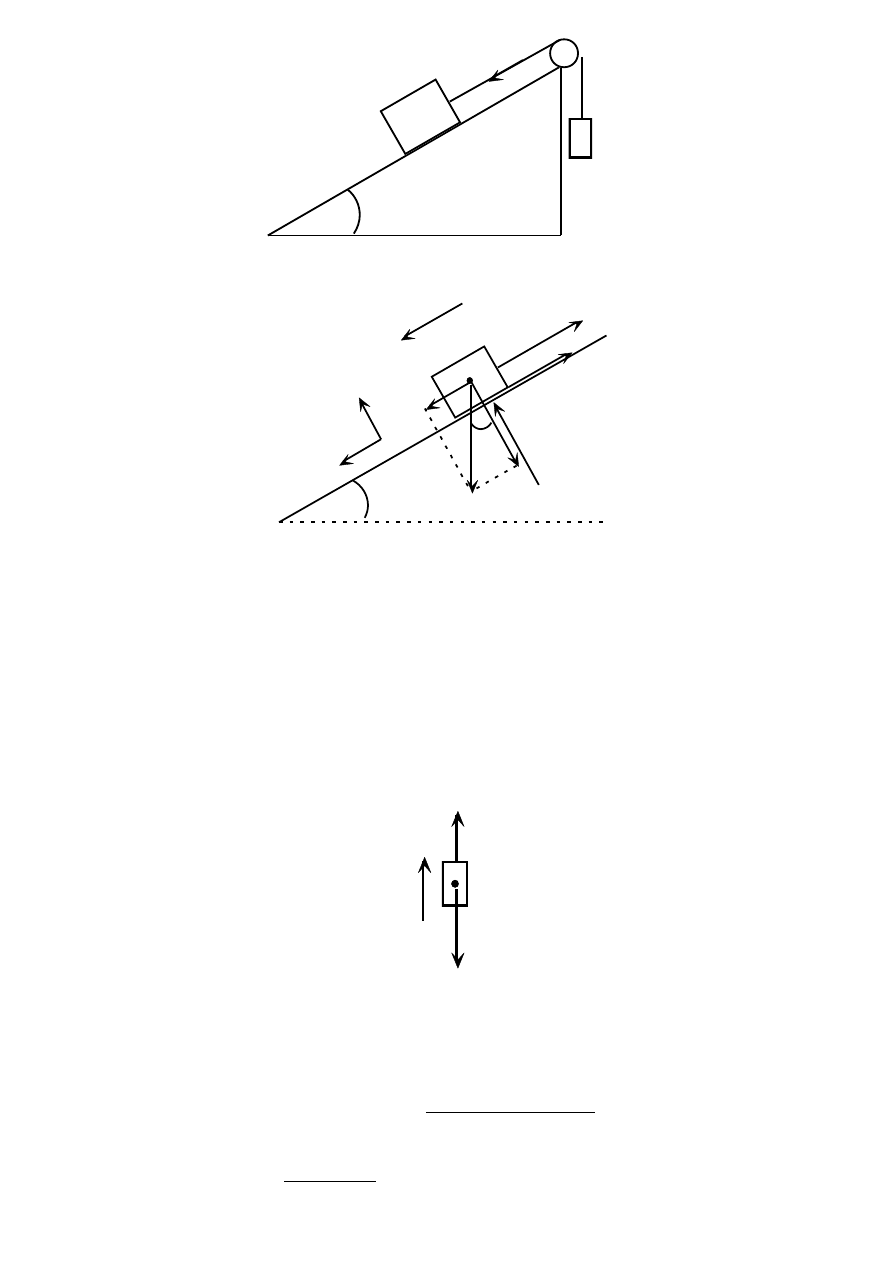
Zadanie 5
Dla układu dwóch mas M i m połączonych nierozciągliwą i lekką nicią wyznaczyć ich
przyspieszenie oraz naciąg nici. Ciało o masie M spoczywa na chropowatej równi pochyłej o
kącie nachylenia α, współczynnik tarcia o równię wynosi µ. Jaki warunek musi spełniać masa
M, aby jej ruch w dół równi był możliwy?
a
M
m
Rozpatrujemy ruch masy M:
M
F
2
S
F
1
P
T
a
x
y
gdzie: P
siła ciężkości, P = Mg, F
1
= Psin
= Mgsin
, F
2
= Pcos
= Mgcos
S
siła naciągu linki
N
siła nacisku
T
siła tarcia
Dynamiczne równania ruchu w kierunku osi x i y (obranych jak na rysunku)
x: aM = F
1
T
S
y: 0 = N
F
2
Uwzględniając, że: T = Nμ oraz podstawiając wartości F
1
i F
2
otrzymujemy:
aM = Mgsin
Nμ
S, N = Mgcos
→ aM = Mgsin
Mgμcos
S (1)
Rozpatrujemy ruch masy m:
S
Q
a
gdzie: Q
siła ciężkości, P = mg, S
j.w.
Dynamiczne równanie ruchu:
am = S
Q → am = S
mg (2)
dodając stronami równania (1) i (2) otrzymamy wzór na przyspieszenie układu:
aM + am = Mgsin
Mg
cos
mg →
m
M
mg
μcosα)
Mg(sinα
a
aby ruch masy M w dół równi był możliwy musi być: a > 0, czyli: Mg(sin
cos
)
mg > 0
stąd otrzymujemy:
μcosα
sinα
m
M
.
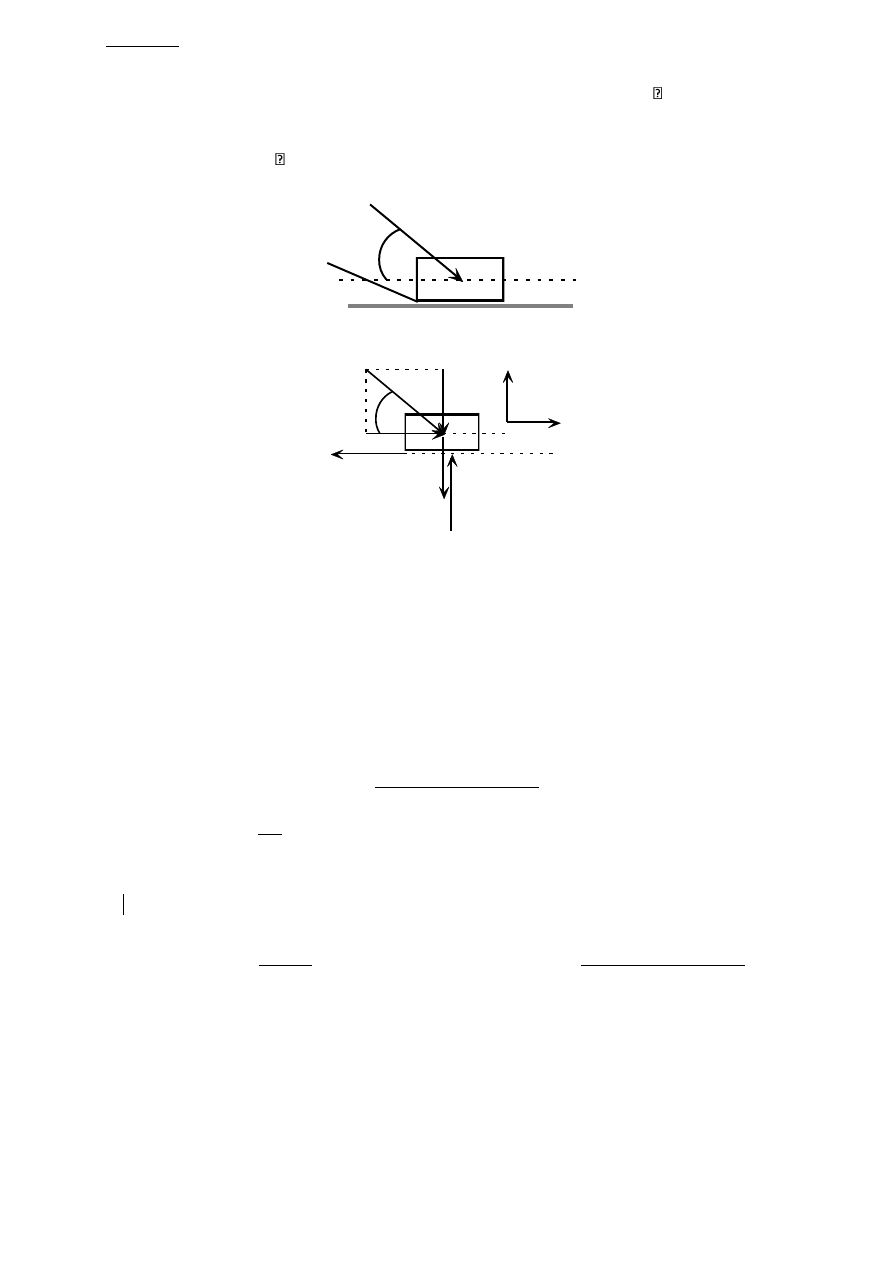
Zadanie 6
Do ciała o masie m, które może poruszać się prostoliniowym ruchem postępowym po
chropowatej poziomej płaszczyźnie, przyłożona została siła P tworząca kąt z tą płaszczyzną.
Wyznaczyć przyspieszenie, z którym zacznie poruszać się to ciało. Po jakim czasie uzyska ono
prędkość V
1
, jeśli na początku miało prędkość V
o
? Współczynnik tarcia między ciałem a
płaszczyzną jest równy .
P
m
Poniższy rysunek przedstawia siły działające na ciało w trakcie ruchu
P
P
x
P
y
Q
N
T
x
y
N
siła reakcji podłoża, T
siła tarcia, Q
siła ciężkości
P
x
, P
y
składowe (pozioma i pionowa) siły P
Pod wpływem działania siły P ciało będzie poruszało się ruchem jednostajnie przyspieszonym
(z prędkością początkową V
o
) z przyspieszeniem a.
dynamiczne równania ruchu suwaka w kierunku x i y:
x: a
x
m = P
x
T, P
x
= Pcos
, T = Nμ
y: a
y
m = N
Q
P
y
, P
y
= Psin
, Q = mg
wobec tego, że ruch odbywa się tylko po współrzędnej x mamy: a
y
= 0, czyli a
x
= a
am = Pcos
Nμ (1)
0 = N
mg
Psin
→ N = mg + Psin
i podstawiamy do (1)
am = Pcos
(mg + Psin
)μ →
m
)μ
Psinα
(mg
Pcosα
a
z drugiej strony:
dt
dV
a
czyli
C
adt
V
, C
stała zależna od warunku początkowego,
a jest stałe (nie zależy od czasu) stąd:
C
dt
a
V
czyli:
C
at
V
0
t
V
=
V
o
→ C =
V
o
→
V
at
V
o
Oznaczmy jako t
1
szukany czas, po którym prędkość ciała będzie równa V
1
, wobec tego:
V
at
V
o
1
1
→
a
V
V
t
o
1
1
i podstawiając a otrzymujemy:
)μ
Psinα
(mg
Pcosα
)
V
m(V
t
o
1
1
.
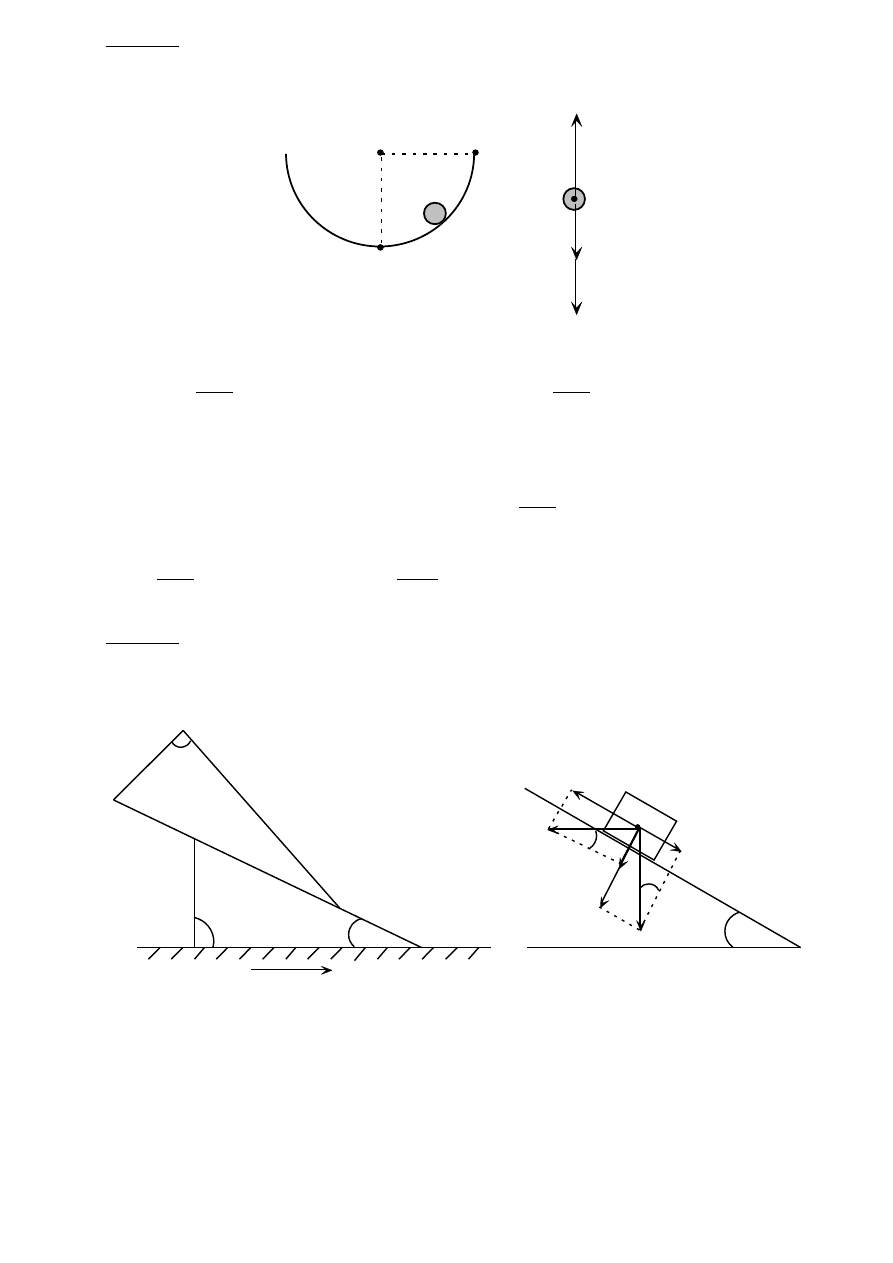
Zadanie 7
Kulka o masie m stacza się po rynnie kołowej o promieniu r bez prędkości początkowej z
punktu A. Znaleźć reakcję rynny, gdy kulka będzie mijała punkt B.
r
A
B
R
P
F
B
R
szukana reakcja, P
siła ciężkości, F
siła odśrodkowa
R
P
F = 0 → R = P + F
P = mg,
r
mV
F
2
, V
prędkość kulki w punkcie B,
r
mV
mg
R
2
, V = ?
V obliczymy z zasady zachowania energii (jako poziom odniesienia dla energii potencjalnej
przyjmujemy prosta poziomą przechodzącą przez punkt B)
Całkowita energia mechaniczna kulki w punkcie A: E
A
= mgr
Całkowita energia mechaniczna kulki w punkcie B:
2
mV
E
2
B
Z zasady zachowania energii wynika równanie: E
A
= E
B
2
mV
mgr
2
→ V
2
= 2gr czyli:
3mg
r
m2gr
mg
R
.
Zadanie 8
Z jakim przyśpieszeniem musi poruszać się klin dolny, aby klin górny nie zsuwał się względem
dolnego? Między powierzchniami styku klinów nie występuje tarcie, kąt pochylenia klina
dolnego wynosi α.
.
P
F
F
x
P
x
a
P = mg, F = ma
Z warunku równowagi wynika równanie: F
x
= P
x
, F
x
= Fcos
, P
x
= Psin
F
x
= macos
, P
x
= mgsin
macos
= mgsin
→ a = gtg
.
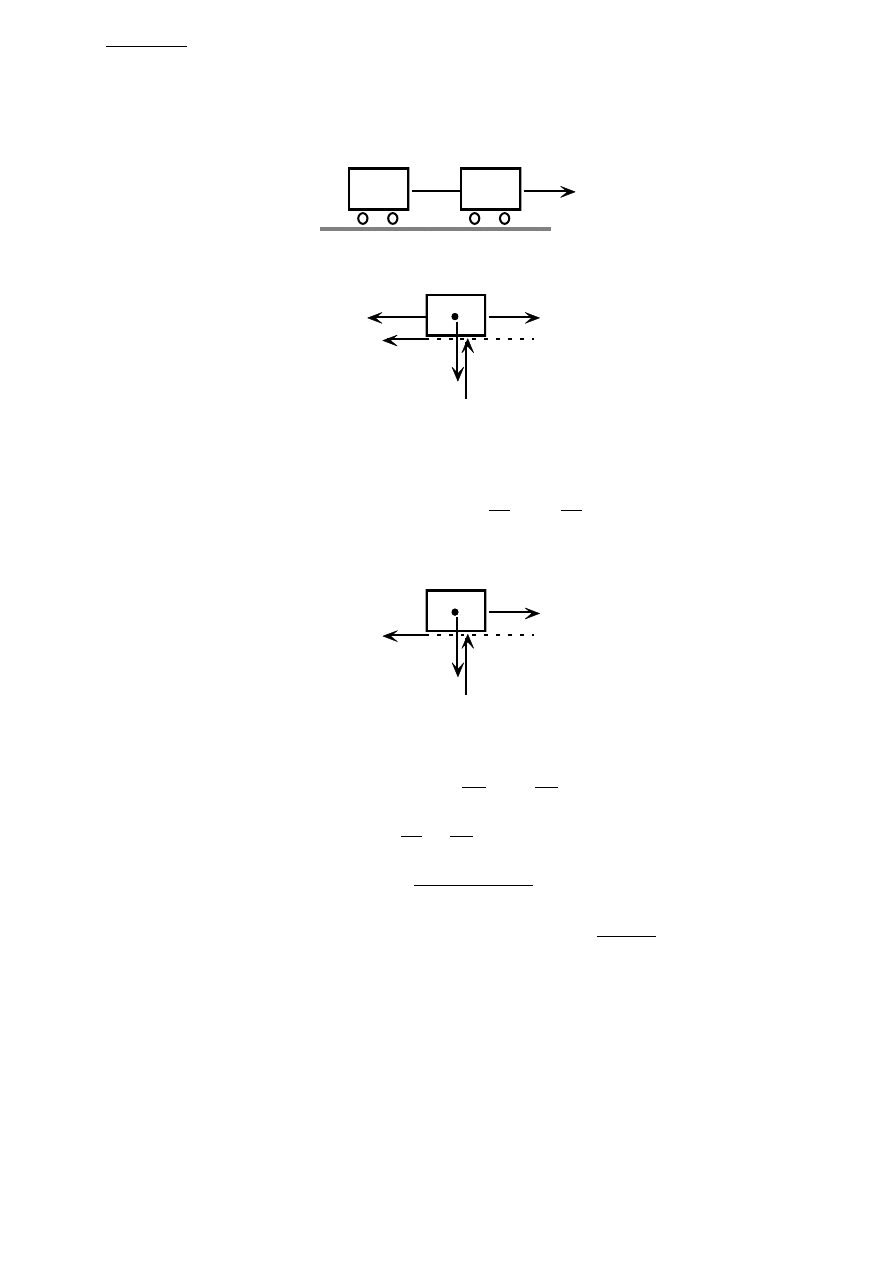
Zadanie 8a
Dwa wagoniki połączone nierozciągliwą liną poruszają się po torze prostym poziomym pod
działaniem stałej siły pociągowej P. Ciężary wagoników wynoszą odpowiednio G
1
i G
2
a siła
oporu ruchu każdego wagonika wynosi 0.1 jego ciężaru. Oblicz przyspieszenie wagoników i
naciąg liny między nimi.
P
G
1
G
2
Rozpatrujemy ruch wagonika o ciężarze G
1
P
G
1
S
T
1
N
1
gdzie: S
szukana siła naciągu liny
N
1
reakcja podłoża
T
1
siła oporu (z treści zadania T
1
= 0,1G
1
)
Dynamiczne równanie ruchu: am
1
= P
S
T
1
,
g
G
m
1
1
→
1
1
G
1
,
0
S
P
g
G
a
(1)
Rozpatrujemy ruch wagonika o ciężarze G
2
G
2
S
T
2
N
2
gdzie: N
2
reakcja podłoża
T
2
siła oporu (z treści zadania T
2
= 0,1G
2
)
dynamiczne równanie ruchu: am
2
= S
T
2
,
g
G
m
2
2
→
2
2
G
1
,
0
S
g
G
a
(2)
dodajemy stronami równania (1) i (2):
2
1
2
1
G
1
,
0
G
1
,
0
P
g
G
a
g
G
a
i wyliczamy szukane przyspieszenie:
2
1
2
1
G
G
)
G
0,1(G
P
g
a
podstawiając a do równania (2) wyliczamy szukany naciąg liny:
2
1
2
G
G
PG
S
.
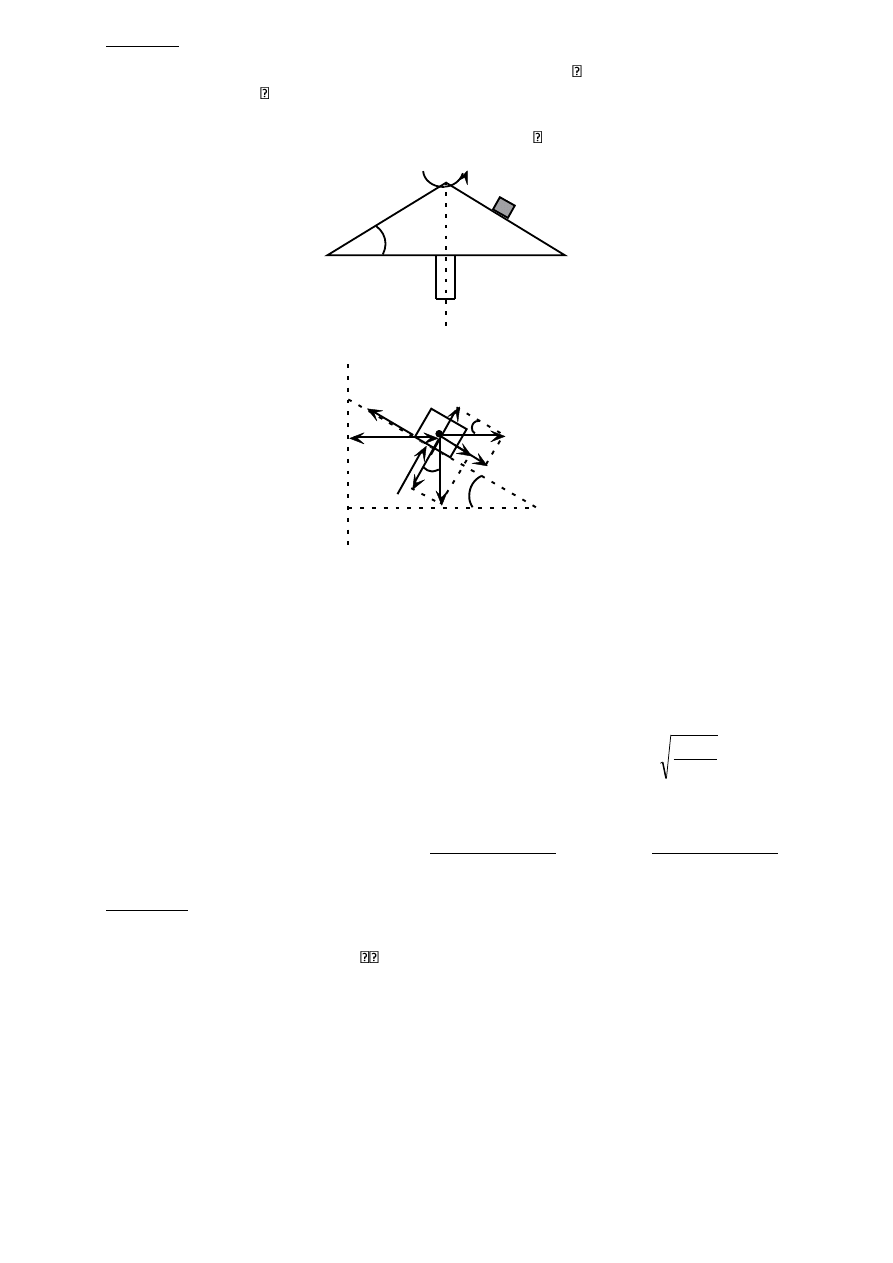
Zadanie 9
Na powierzchni ruchomego stożka o kącie przy podstawie obracającego się ze stałą
prędkością kątową znajduje się punkt materialny o masie m. W jakiej największej
odległości r od osi obrotu może pozostawać ten punkt aby nie nastąpił jego poślizg po
tworzącej stożka. Współczynnik tarcia statycznego wynosi .
Poniższy rysunek przedstawia siły działające na punkt materialny
T
P
F
od
N
r
gdzie: T
siła tarcia
P
siła ciężkości
F
od
siła odśrodkowa
N
siła reakcji podłoża
Poślizg nie zajdzie, gdy: F
od
cos
+ Psin
T (1), F
od
= mω
2
r, P = mg, T = Nμ (2)
N wyznaczamy z równowagi sił w kierunku pionowym: N + F
od
sin
Pcos
= 0
czyli: N = Pcos
F
od
sin
i podstawiamy do (2)
oczywiście musi być: Pcos
F
od
sin
0, stąd: mgcos
mω
2
rsin
→
r
ctgα
g
ω
T = (Pcos
F
od
sin
)μ i podstawiamy do (1), F
od
cos
+ Psin
(Pcos
F
od
sin
)μ
F
od
cos
+ Psin
(Pcos
F
od
sin
)μ → mω
2
rcos
+ mgsin
(mgcos
mω
2
rsin
)μ
stąd po przekształceniach otrzymujemy:
α)
cos
α
sin
(μ
ω
α)
sin
α
cos
g(μ
r
2
czyli:
α)
cos
α
sin
(μ
ω
α)
sin
α
cos
g(μ
r
2
max
.
Zadanie 10
Pozioma gładka rurka o długości 2b jest osadzona symetrycznie na pionowej osi obracającej
się ze stałą prędkością kątową
Wewnątrz rurki znajduje się kulka o masie m. W
początkowej chwili kulka znajdowała się w spoczynku w odległości a od osi obrotu.
Wyznaczyć poziomą reakcję rurki na kulkę w chwili, w której ta opuści rurkę.
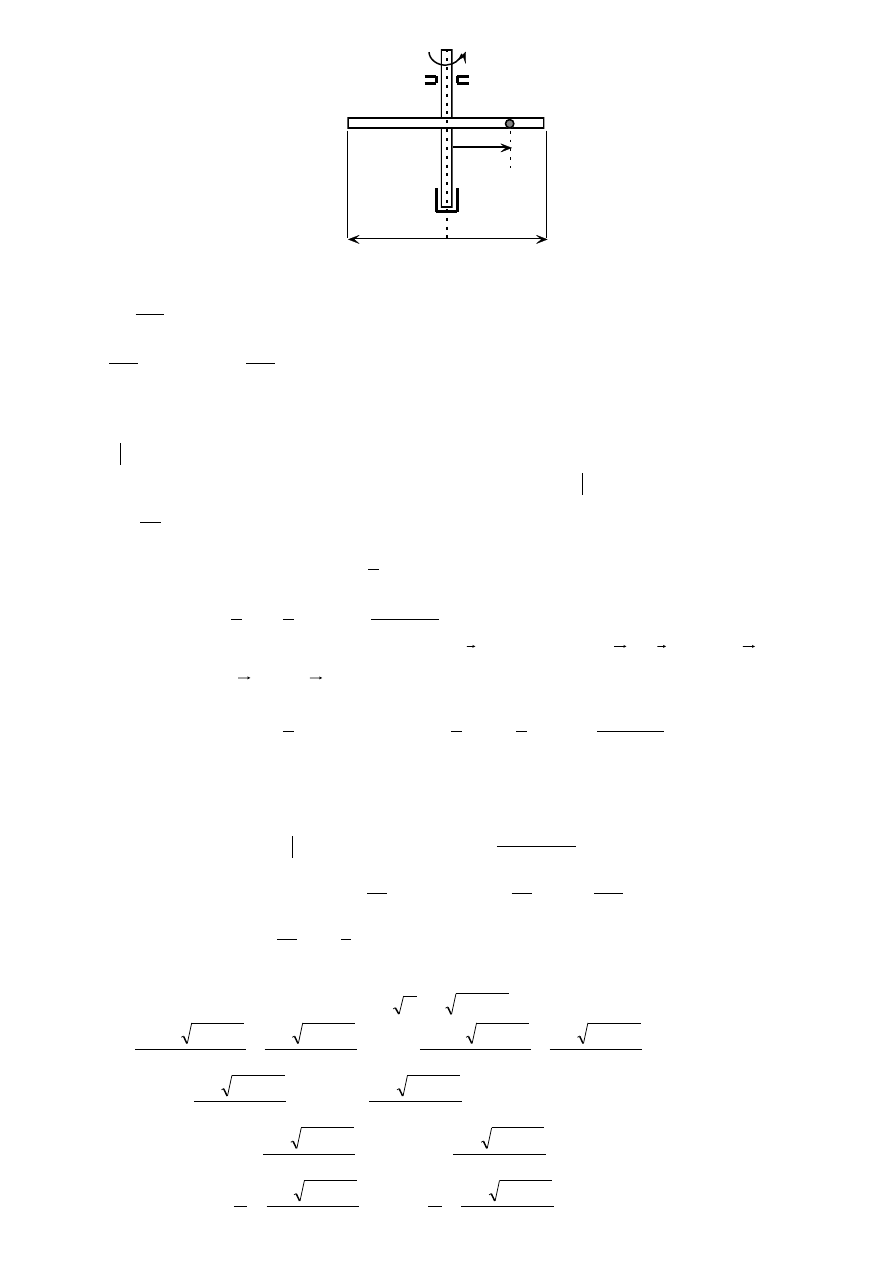
2b
a
Dynamiczne równanie ruchu kulki: am = F
od
, F
od
siła odśrodkowa
2
2
dt
x
d
a
, F
od
= mω
2
x, x
odległość od osi obrotu
x
mω
m
dt
x
d
2
2
2
→
0
x
ω
dt
x
d
2
2
2
równanie różniczkowe liniowe, drugiego rzędu
równanie charakterystyczne: r
2
ω
2
= 0 stąd:
ω
r
1
,
ω
r
2
t
r
2
t
r
1
2
1
e
C
e
C
x
→
ωt
2
ωt
1
e
C
e
C
x
, C
1
, C
2
stałe zależne od warunków początkowych
a
x
0
t
→
2
1
C
C
a
(1)
w początkowej chwili kulka znajdowała się w spoczynku, czyli:
0
V
0
t
,
ωt
2
ωt
1
e
ωC
e
ωC
dt
dx
V
(2) → 0 = ωC
1
ωC
2
→ C
1
= C
2
,
uwzględniając (1) mamy:
2
a
C
C
2
1
wobec tego:
t
acoshω
2
e
e
a
e
C
2
a
e
2
a
x
ωt
ωt
ωt
2
ωt
poziomą reakcją rurki na kulkę jest siła Coriolisa:
c
c
a
m
F
,
V
ω
2
a
c
→
V
ω
m
2
F
c
)
V
,
ω
(
sin
ωV
2
a
c
,
90
)
V
,
ω
(
, wobec tego: F
c
= 2mωV
podstawiając
2
a
C
C
2
1
do (2) mamy:
ωasinhωt
2
e
e
ωa
e
2
a
ω
e
2
a
ω
V
ωt
ωt
ωt
ωt
stąd: F
c
= 2mω
2
asinhωt
aby znaleźć poziomą reakcję rurki na kulkę w chwili, w której ta ją opuści należy wyznaczyć
czas, po jakim kulka opuści rurkę. Czas ten oznaczymy jako t
b
.
korzystamy z warunku:
b
x
b
t
t
→
2
e
e
a
t
acoshω
b
b
b
ωt
ωt
b
przekształcamy ostatnie równanie:
b
b
ωt
ωt
e
e
a
2b
→
b
b
ωt
ωt
e
1
e
a
2b
oznaczmy:
z
e
b
ωt
→
z
1
z
a
2b
→
0
a
2bz
az
2
)
a
4(b
4a
4b
4a
2b)
(
Δ
2
2
2
2
2
2
2
2
a
b
2
Δ
a
a
b
b
2a
a
b
2
2b
z
2
2
2
2
lub
a
a
b
b
2a
a
b
2
2b
z
2
2
2
2
czyli:
a
a
b
b
e
2
2
ωt
b
lub
a
a
b
b
e
2
2
ωt
b
wobec tego:
a
a
b
b
ln
ωt
2
2
b
lub
a
a
b
b
ln
ωt
2
2
b
ostatecznie:
a
a
b
b
ln
ω
1
t
2
2
b
lub
a
a
b
b
ln
ω
1
t
2
2
b
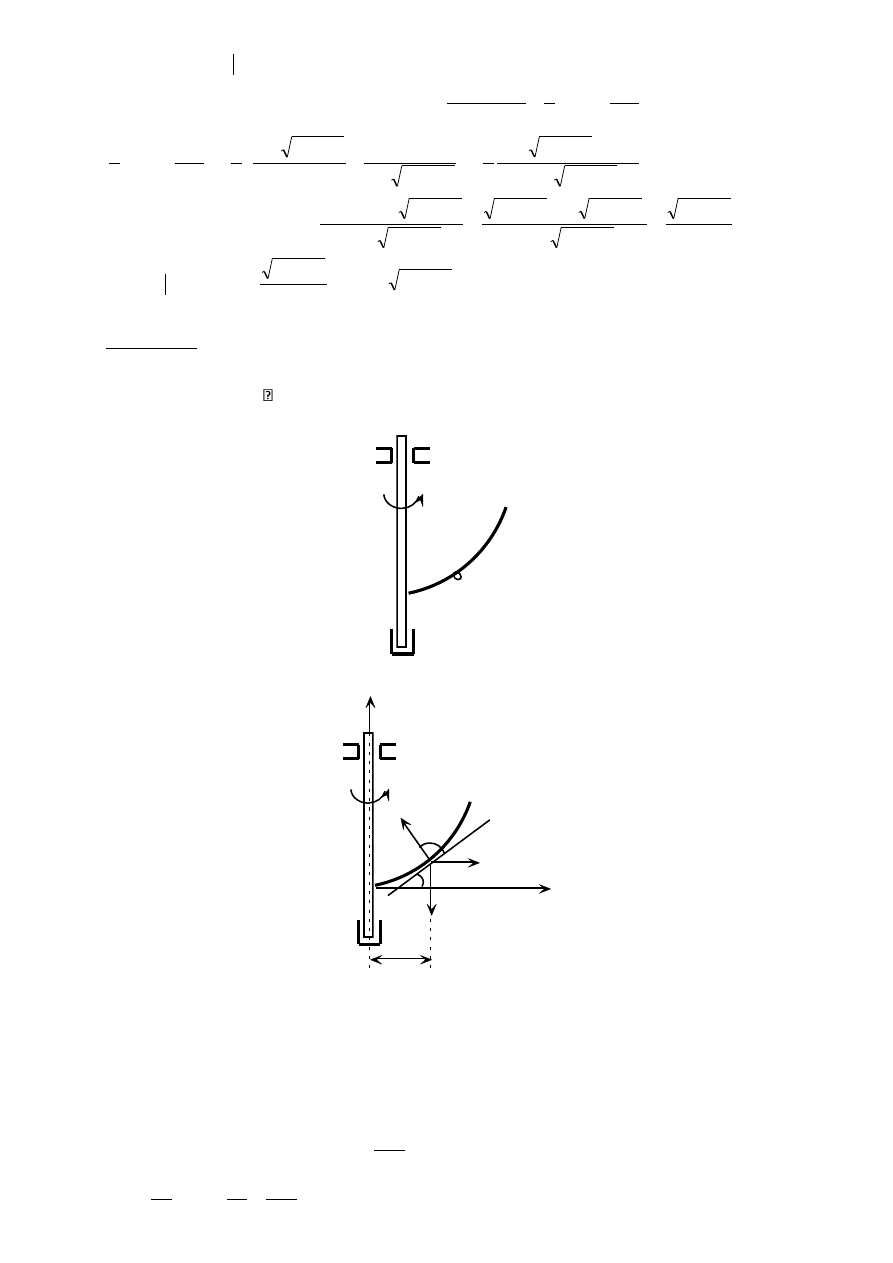
przyjmujemy drugą odpowiedź (autor pozostawia studiującemu rozważania dlaczego?)
i wyznaczamy:
b
t
t
c
F
musimy znaleźć wartość wyrażenia:
b
b
b
b
ωt
ωt
ωt
ωt
b
e
1
e
2
1
2
e
e
t
sinhω
, co daje:
2
2
2
2
2
2
2
2
2
2
ωt
ωt
a
b
b
a
a
a
b
b
2
1
a
b
b
a
a
a
b
b
2
1
e
1
e
2
1
b
b
po przekształceniach mamy:
a
a
b
a
b
b
a
a
b
b
a
b
a
b
b
a
a
b
b
a
b
2
2
2
2
2
2
2
2
2
2
2
2
2
2
czyli:
2
2
2
2
2
2
t
t
c
a
b
2mω
a
a
b
a
2mω
F
b
.
Zadanie 10a
Mały pierścień o masie m jest nasunięty na gładki drut OA obracający się wokół pionowej osi
z prędkością kątową
o
= const. Oś drutu jest krzywą płaską. Znaleźć równanie tej krzywej,
aby zachodziła równowaga względna dla dowolnego położenia pierścienia.
o
O
A
Rozpatrzymy siły działające na pierścień, znajdujący się w punkcie B
o
O
A
B
N
P
F
od
x
x
y
.
.
gdzie: N
reakcja drutu
F
od
siła odśrodkowa,
x
mω
F
2
o
od
P
siła ciężkości, P = mg
Warunek równowagi wynika z rzutów siły odśrodkowej i siły ciężkości na styczną do osi drutu
w punkcie B
0
mgsinα
xcosα
mω
2
o
stąd:
g
x
ω
tgα
2
o
dx
dy
tgα
czyli:
g
x
ω
dx
dy
2
o
jest to równanie różniczkowe o zmiennych rozdzielonych

rozdzielając zmienne (y,x) i całkując obustronnie otrzymujemy:
C
xdx
g
ω
dy
2
o
, C
stała zależna od warunku początkowego
C
x
2g
ω
y
2
2
o
, stałą C wyznaczamy z warunku:
0
y
0
x
, czyli C = 0
szukane równanie krzywej:
2
2
o
x
2g
ω
y
parabola przechodząca przez punkt (0,0).
Ćwiczenie 9 i 10 (wykład: 5)
Zasady zmienności w dynamice punktu materialnego
Zadanie 1
Lufa działa jest nachylona poziomo, a działo ma ciężar G = 11[kN]. Ciężar pocisku wynosi P =
5,5[N]. Prędkość pocisku u wylotu lufy wynosi V = 900[m/s]. O ile i w którą stronę przesunie
się działo, jeżeli opory jego ruchu są równe 0,1G?
Oczywiście działo przesunie się o szukaną wielkość s o zwrocie przeciwnym, niż zwrot
prędkości pocisku. Oznaczmy jako V
1
prędkość działa w chwili, gdy pocisk jest u wylotu lufy. Z
zasady zachowania energii wynika równanie:
E
k
= W
gdzie:
E
k
zmiana energii kinetycznej działa
W
praca oporów ruchu
2
mV
2
mV
ΔE
2
1
2
k
k
, V
k
prędkość końcowa działa, V
k
= 0, m
masa działa,
g
G
m
czyli:
2g
GV
ΔE
2
1
k
Ts
W
, T
siła oporu, z treści zadania: T = 0,1G, czyli
0,1Gs
W
0,1Gs
2g
GV
2
1
→
g
5V
s
2
1
(1) V
1
= ?
V
1
wyznaczamy z zasady zachowania pędu. W momencie, gdy pocisk jest u wylotu lufy pęd
pocisku (p
1
) i działa (p
2
) są sobie równe
p
1
= m
1
V, m
1
masa pocisku,
g
P
m
1
czyli:
V
g
P
p
1
1
2
V
g
G
p
, p
1
= p
2
→
1
V
g
G
V
g
P
→
V
G
P
V
1
i podstawiamy do równania (1)
2
2
2
gG
V
5P
s
, podstawiając dane liczbowe otrzymujemy: s
0,1 [m].
Zadanie 2
Pocisk artyleryjski o masie m = 30[kg] wylatuje z lufy armaty z prędkością V = 50[m/s]. Jaka
jest siła odrzutu działająca na armatę, jeśli lot pocisku w lufie trwał 0,1[s].
Korzystamy z zależności: F = am,
t
ΔV
a
, ∆V = V →
m
t
V
F
Podstawiając dane liczbowe otrzymujemy: F = 15000 [N].
Zadanie 3
Dwie kule, jedna o masie m
1
= 200[g], a druga o masie m
2
= 300[g] poruszają się do siebie
wzdłuż prostej z prędkościami odpowiednio V
1
= 0,5[m/s] i V
2
= 0,4[m/s] W pewnej chwili
zderzyły się i następnie zaczęły poruszać się razem. Znaleźć ich wspólną prędkość oraz
kierunek ruchu.
Pęd pierwszej kuli przed zderzeniem: p
1
= m
1
V
1
= 0,1 [kg
m/s]
Pęd drugiej kuli przed zderzeniem: p
2
= m
2
V
2
= 0,12 [kg
m/s]
Pęd drugiej kuli jest większy, wobec tego po zderzeniu kule będą poruszać się w tym
kierunku, w którym poruszała się druga kula.
Pęd kul po zderzeniu: p = (m
1
+ m
2
)V
Z zasady zachowania pędu wynika równanie: p
2
p
1
= p
m
2
V
2
m
1
V
1
= (m
1
+ m
2
)V
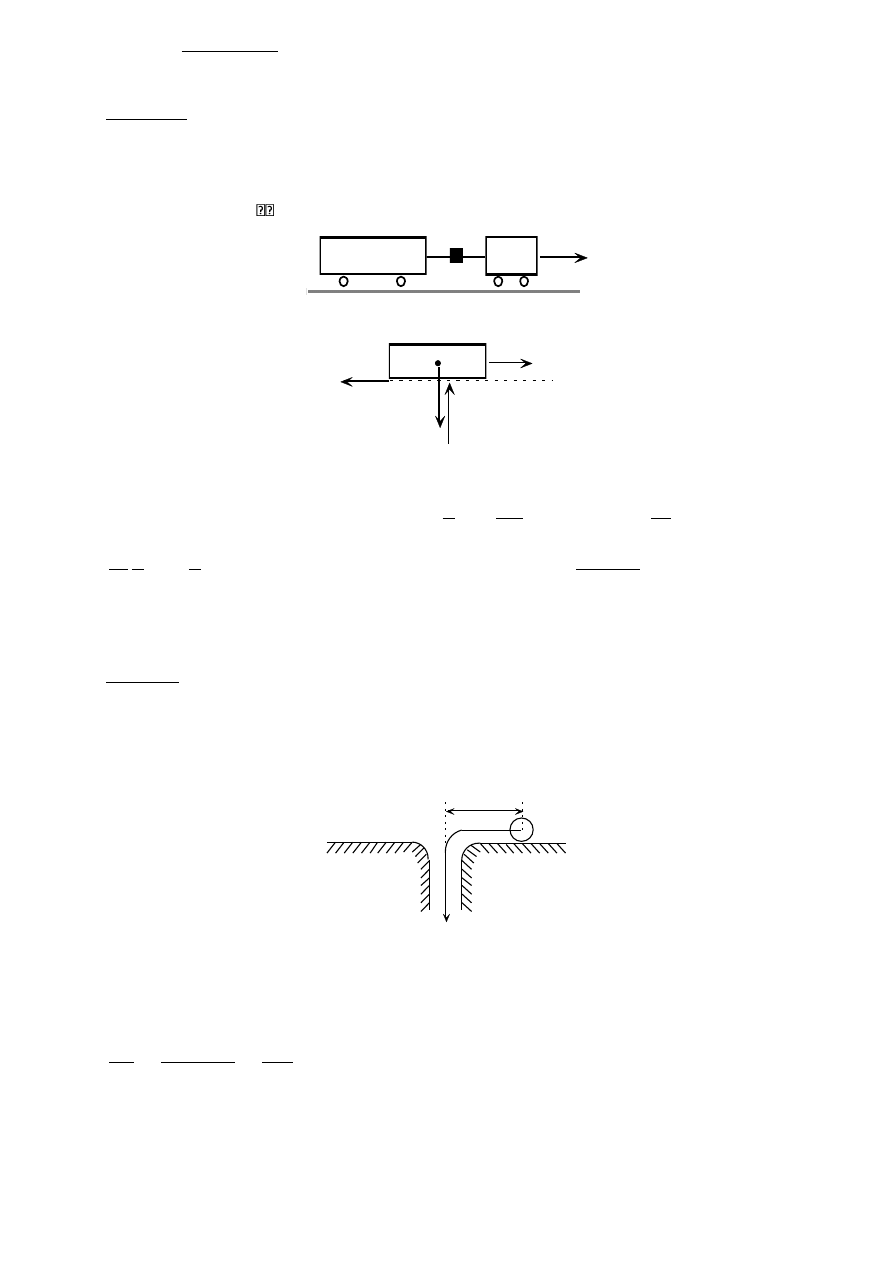
Stąd:
[m/s]
0,04
m
m
V
m
V
m
V
2
1
1
1
2
2
.
Zadanie 3a
W celu zmierzenia ciężaru zestawu wagonów wstawiono między lokomotywą a pierwszym
wagonem dynamometr. W ciągu czasu t
1
= 2[min] dynamometr wskazywał średnio siłę
F = 100,8[T]. W tym czasie pociąg ze stanu spoczynku nabrał prędkości V
1
= 57,6[km/h].
Współczynnik tarcia
= 0,02. Obliczyć ciężar zestawu wagonów.
V
Rozpatrzymy siły działające na zestaw wagonów w trakcie ruchu
F
T
P
N
P
ciężar zestawu wagonów (P = mg), N
siła reakcji podłoża (N = P = mg),
T
siła tarcia (T = Nμ = mgμ)
Dynamiczne równanie ruchu: am = F
T,
g
P
m
,
1
t
ΔV
a
, ∆V = V
1
→
1
1
t
V
a
gμ
g
P
F
g
P
t
V
1
1
, stąd wyliczamy ciężar zestawu wagonów:
μ
gt
V
Fgt
P
1
1
1
Podstawiając dane liczbowe (t
1
= 120[s], F = 988848 [N], V
1
= 16 [m/s])
Otrzymujemy: P = 29
10
6
[N].
Zadanie 4
Punkt o masie m jest zamocowany do nieważkiej i nierozciągliwej nici i porusza się po okręgu
o promieniu r
o
ze stałą prędkością kątową ω
o
. Następnie nić została wciągnięta do otworu i
punkt porusza się po okręgu o promieniu 0,5r
o
. Pomijając opory ruchu, obliczyć, w jakim
stopniu zmieni się naciąg nici.
r
o
O naciągu (N) nici stanowi siła odśrodkowa.
W pierwszym przypadku: N
1
= m
2
o
ω
r
o
Po wciągnięciu nici do otworu: N
2
= m
2
0,5r
o
= 0,5m
2
r
o
prędkość kątowa punktu po wciągnięciu nici do otworu
2
o
2
o
2
o
o
2
1
2
2
r
m
r
m
5
,
0
N
N
,
= ?
obliczymy z zasady zachowania krętu (momentu pędu)
Kręt w pierwszym przypadku: K
1
= mV
o
r
o
, V
o
=
o
r
o
K
1
= m
o
2
o
r
Po wciągnięciu nici do otworu: K
2
= 0,5mVr
o
, V = 0,5
r
o
K
1
= 0,25m
2
o
r
Z zasady zachowania krętu wynika równanie: K
1
= K
2
m
o
2
o
r
= 0,25m
2
o
r
→
= 4
o
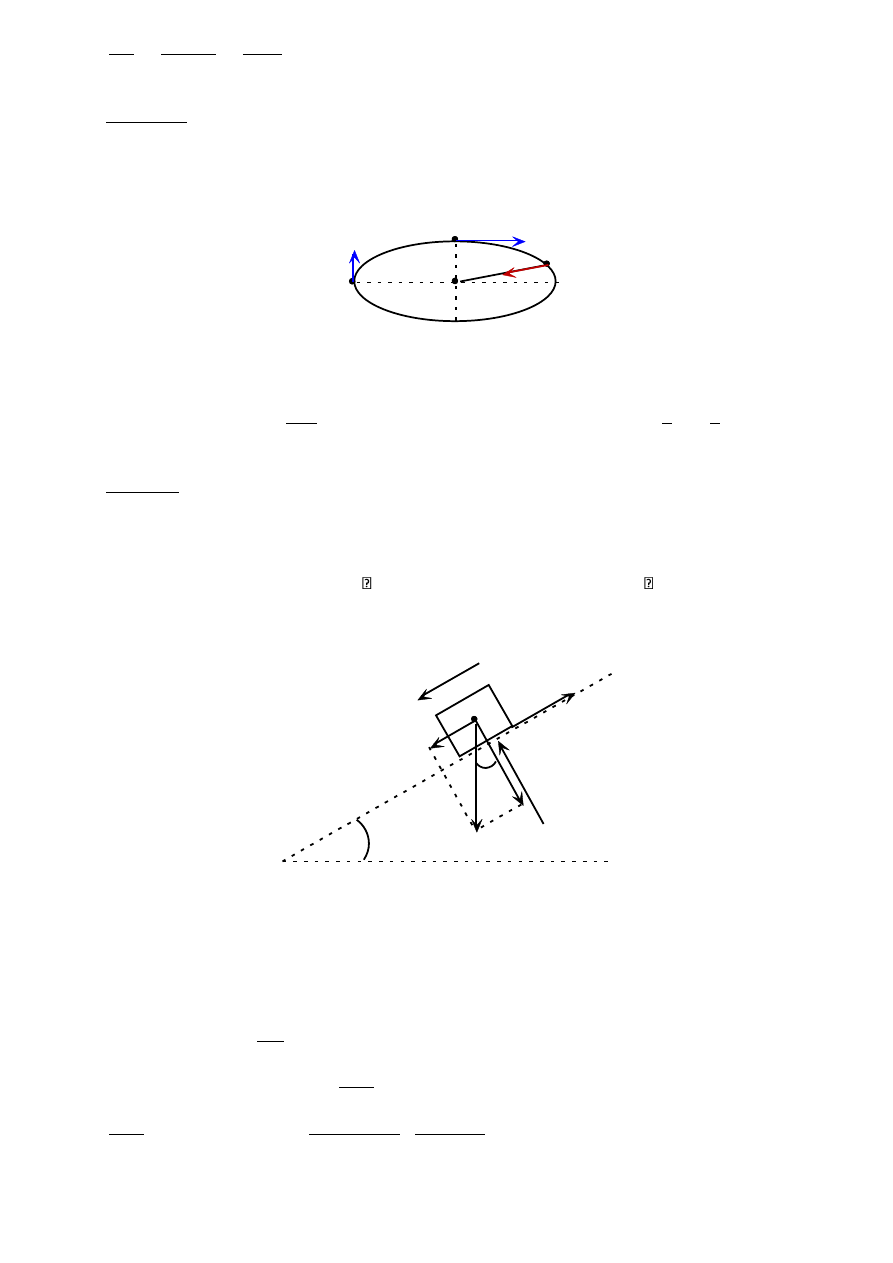
8
2ω
16ω
2ω
)
4ω
(
N
N
2
o
2
o
2
o
2
o
1
2
naciąg zwiększył się 8 razy.
Zadanie 4a
Punkt M porusza się dokoła nieruchomego środka pod działaniem siły przyciągającej do tego
środka. Znaleźć prędkość V
2
w punkcie toru najbardziej oddalonym od środka, jeżeli
prędkość punktu w miejscu najbliższym środka V
1
= 3[m/s], a promień r
2
= 5r
1
.
r
1
r
2
V
1
V
2
M
1
M
2
M
F
Kręt (K
1
) punktu M w miejscu najbliższym środka: K
1
= mV
1
r
1
(m
masa punktu M)
Kręt (K
2
) punktu M w punkcie toru najbardziej oddalonym od środka: K
2
= mV
2
r
2
Z zasady zachowania krętu wynika równanie: K
1
= K
2
→ mV
1
r
1
= mV
2
r
2
stąd wyliczamy V
2
:
2
1
1
2
r
r
V
V
, uwzględniając, że r
2
= 5r
1
otrzymujemy:
[m/s]
5
3
V
5
1
V
1
2
.
Zadanie 5
Samochód jedzie z prędkością V
o
= 108[km/h] w dół po stoku nachylonym do poziomu pod
kątem α = 0,008[rad]. W pewnej chwili kierowca zobaczywszy niebezpieczeństwo zaczyna
hamować. Opór całkowity hamowania jest stały i wynosi 0,1 ciężaru samochodu. Obliczyć, w
jakiej odległości d i po jakim czasie samochód zatrzyma się. Przyjąć sinα α.
Rozważymy siły działające na samochód podczas ruchu
m
F
2
F
1
P
T
V
gdzie: P
siła ciężkości, P = mg, F
1
= Psin
= mgsin
, F
2
= Pcos
= mgcos
N
siła nacisku
T
siła oporu hamowania (z treści zadania T = 0,1P = 0,1mg)
Dynamiczne równanie ruchu:
T
F
am
1
→
0,1mg
mgsin α
am
(1)
stąd opóźnienie z jakim porusza się samochód:
0,1)
g(sinα
a
z drugiej strony:
τ
ΔV
a
,
V = V
k
V
o
, V
k
prędkość końcowa,
szukany czas ruchu
V
k
= 0, czyli:
V =
V
o
stąd:
τ
V
a
o
(2), przyrównując do siebie wzory (1) i (2) mamy:
0,1)
g(sinα
τ
V
o
→
α)
g(0,1
V
)
sinα
g(0,1
V
τ
o
o
podstawiając dane liczbowe (V
o
= 30 [m/s]) otrzymujemy:
= 33,24 [s]
podstawiając wyliczony
do wzoru (2) obliczamy opóźnienie ruchu:
9
,
0
a
[m/s
2
]

szukana droga (d) dana jest wzorem:
2
aτ
τ
V
d
2
o
podstawiając dane liczbowe otrzymujemy: d
500 [m].
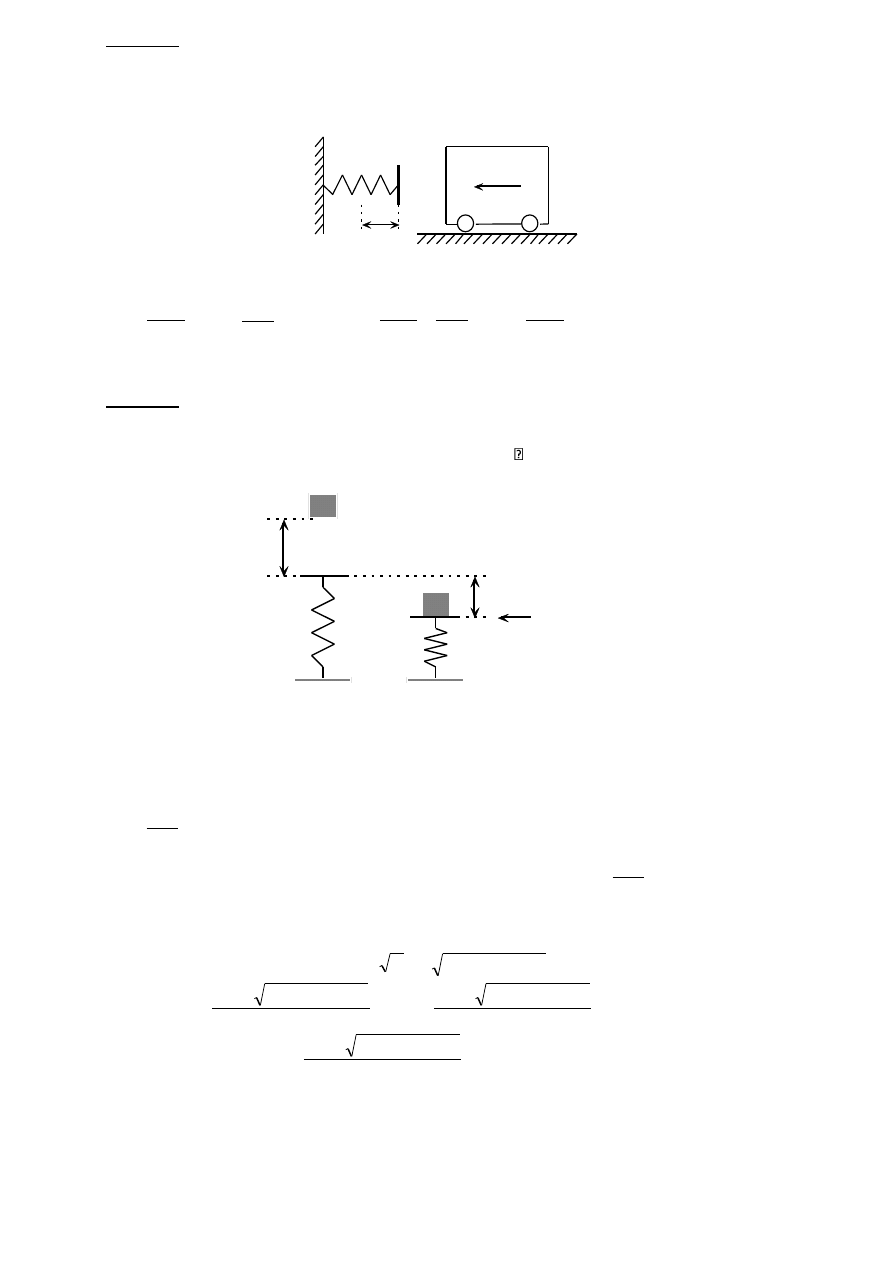
Zadanie 6
Wagonik o masie m = 10
3
[kg] jedzie z prędkością V = 36[km/h] po torze prostym poziomym i
uderza o zderzak. Jaka musi być sztywność sprężyny zderzaka aby jego ugięcie e = 0,5[m]?
Zakładamy liniową charakterystykę sprężyny i brak strat energii mechanicznej.
V
e
Energia kinetyczna (E
k
) wagonika jest zamieniana na energię potencjalną sprężystości (E
ps
)
sprężyny.
2
mV
E
2
k
,
2
ke
E
2
ps
→ E
k
= E
ps
→
2
ke
2
mV
2
2
→
2
2
e
mV
k
podstawiają dane liczbowe (V = 10 [m/s]) otrzymujemy: k = 40000 [N/m].
Zadanie 7
Ciężarek o masie m ze stanu spoczynku spada pionowo z wysokości h na nieważką sprężynę
śrubową o stałej sztywności równej k. Wyznacz ugięcie tej sprężyny zakładając, że ciężarek
po zetknięciu z górnym końcem sprężyny przykleił się do niej. Opory ruchu pomijamy.
h
k
poziom
odniesienia
Korzystamy z zasady zachowania energii. Energia kinetyczna ciężarka w chwili początkowej
jak i końcowej jest równa zero. Przyjęto poziom odniesienia dla energii potencjalnej
grawitacji jak pokazano na rysunku. Wobec tego całkowita energia (E
1
) w położeniu
początkowym: E
1
= mg(h +
)
całkowita energia (E
2
) w położeniu końcowym jest energią potencjalną sprężystości:
2
λ
k
E
2
2
Z zasady zachowania energii wynika równanie: E
1
= E
2
→
2
λ
k
λ)
h
mg(
2
Po przekształceniach otrzymujemy: k
2
2mg
2mgh = 0
2hk)
4mg(mg
2mgh)
4k(
2mg)
(
Δ
2
2hk)
mg(mg
2
Δ
k
2hk)
mg(mg
mg
λ
lub
0
k
2hk)
mg(mg
mg
λ
sprzeczne
czyli odpowiedzią jest:
k
2hk)
mg(mg
mg
λ
[m].

Zadanie 8
Mała kula o masie M = 1[kg] wykonuje ruch harmoniczny u(t) = 12 sin2t (gdzie: u
w
metrach, t
w sekundach). Obliczyć energię mechaniczną kuli, jeśli sztywność sprężyny, na
której jest oparta kula wynosi k = 4[N/m].
Całkowita energia (E) w ruchu harmonicznym dana jest wzorem:
2
kA
E
2
gdzie: A
amplituda drgań, w naszym przypadku: A = 12 [m]
podstawiając dodatkowo k = 4 [N/m] otrzymujemy: E = 288 [J].
Zadanie 9
Z wysokości h = 10[m] spada kamień o masie m = 5[kg]. Ile procent energii kinetycznej
zostało przez ten kamień stracone w wyniku oporu powietrza, jeśli przy zetknięciu z Ziemią
jego prędkość była równa V = 10[m/s].
100%
E
E
E
η
p
k
p
, gdzie:
szukany procent strat energii kinetycznej
E
p
energia potencjalna, E
p
= mgh
E
k
energia kinetyczna, E
k
2
mV
2
100%
mgh
2
mV
mgh
η
2
, podstawiając dane liczbowe otrzymujemy:
= 50%.
Zadanie 10
Kula o ciężarze Q = 2[kG] zawieszona na nieważkiej lince o długości l = 1[m] uzyskała wskutek
uderzenia prędkość V = 5[m/s]. Oblicz siłę w lince bezpośrednio po uderzeniu. Podaj wynik
obliczenia z dokładnością do 0.01[N].
V
Q
l
Q
F
od
N
gdzie: N
szukana siła w lince bezpośrednio po uderzeniu
F
od
siła odśrodkowa,
l
mV
F
2
od
,
g
Q
m
→
gl
QV
F
2
od
N
Q
F
od
= 0 → N = Q + F
od
→
gl
V
1
Q
gl
QV
Q
N
2
2
Podstawiając dane liczbowe (Q = 19,62 [N], g = 9,81 [m/s
2
]) otrzymujemy: N = 69,62 [N].
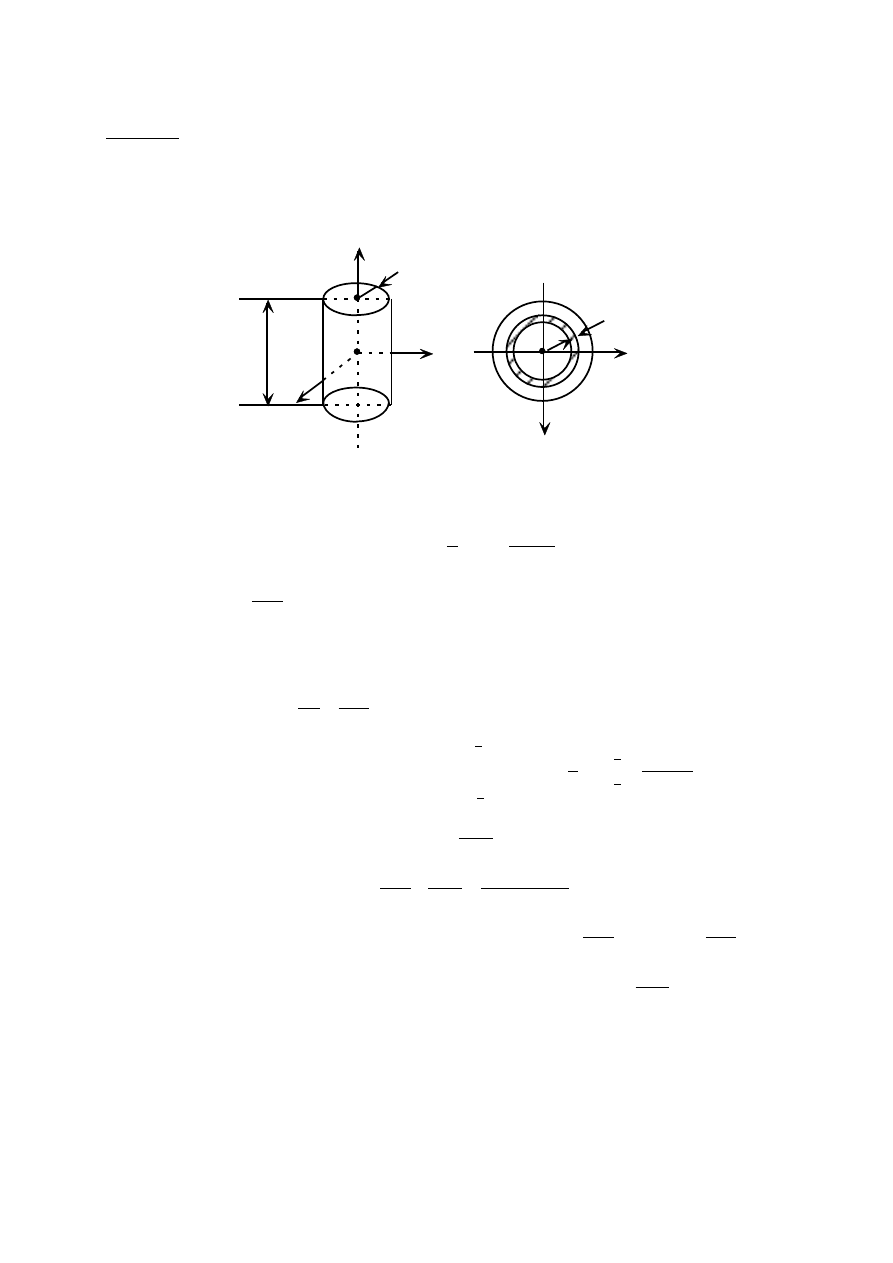
Ćwiczenie 11 i 12 (wykład: 5 cz.II i 6)
Zasady zmienności w dynamice układu punktów materialnych i ciała sztywnego.
Środek masy. Momenty bezwładności. Pęd i moment pędu. Praca siły i energia kinetyczna.
Zadanie 1
Wyprowadź wzory na główne centralne momenty bezwładności walca kołowego
jednorodnego o masie m, promieniu r i wysokości h. Dalej, korzystając z tych wzorów
wyznacz główne centralne momenty bezwładności dla jednorodnej cienkiej tarczy kołowej i
jednorodnego pręta prostego.
z
c
y
c
x
c
h
r
C
y
c
x
c
d
C
Moment bezwładności walca względem osi z
c
:
m
2
m
2
c
2
c
z
dm
η
dm
)
y
x
(
I
c
(1)
Masa (m) walca: m = V
, V =
r
2
h, czyli masa elementarna (dm): dm = 2
h
d
i podstawiamy do (1):
2
r
hρ
π
]
η
[
4
1
hρ
2π
dη
η
hρ
2π
I
4
r
0
4
r
0
3
z
c
, pamiętając, że: m =
r
2
h
,
otrzymujemy:
2
mr
I
2
z
c
c
c
c
c
c
z
x
y
x
x
I
I
I
, dla walca:
c
c
y
x
I
I
wiadomo, że:
c
c
c
c
c
z
y
z
x
z
I
I
I
, przy czym dla walca:
c
c
c
c
z
y
z
x
I
I
, czyli:
c
c
c
c
c
z
y
z
x
z
2I
I
2
I
wobec tego:
4
mr
2
I
I
I
2
z
z
y
z
x
c
c
c
c
c
m
2
y
x
dm
z
I
c
c
, gdzie: dm =
r
2
dz →
12
ρh
πr
]
[z
3
1
ρ
πr
dz
z
ρ
πr
I
3
2
2
h
2
h
3
2
2
h
2
h
2
2
y
x
c
c
pamiętając, że: m =
r
2
h
, otrzymujemy:
12
mh
I
2
y
x
c
c
wobec tego otrzymujemy:
12
)
h
3r
m(
12
mh
4
mr
I
I
2
2
2
2
y
x
c
c
Dla jednorodnej cienkiej tarczy kołowej mamy: h → 0, czyli:
2
mr
I
2
z
c
,
4
mr
I
I
2
y
x
c
c
Dla jednorodnego pręta prostego mamy: r → 0, czyli:
0
I
c
z
,
12
mh
I
I
2
y
x
c
c
.
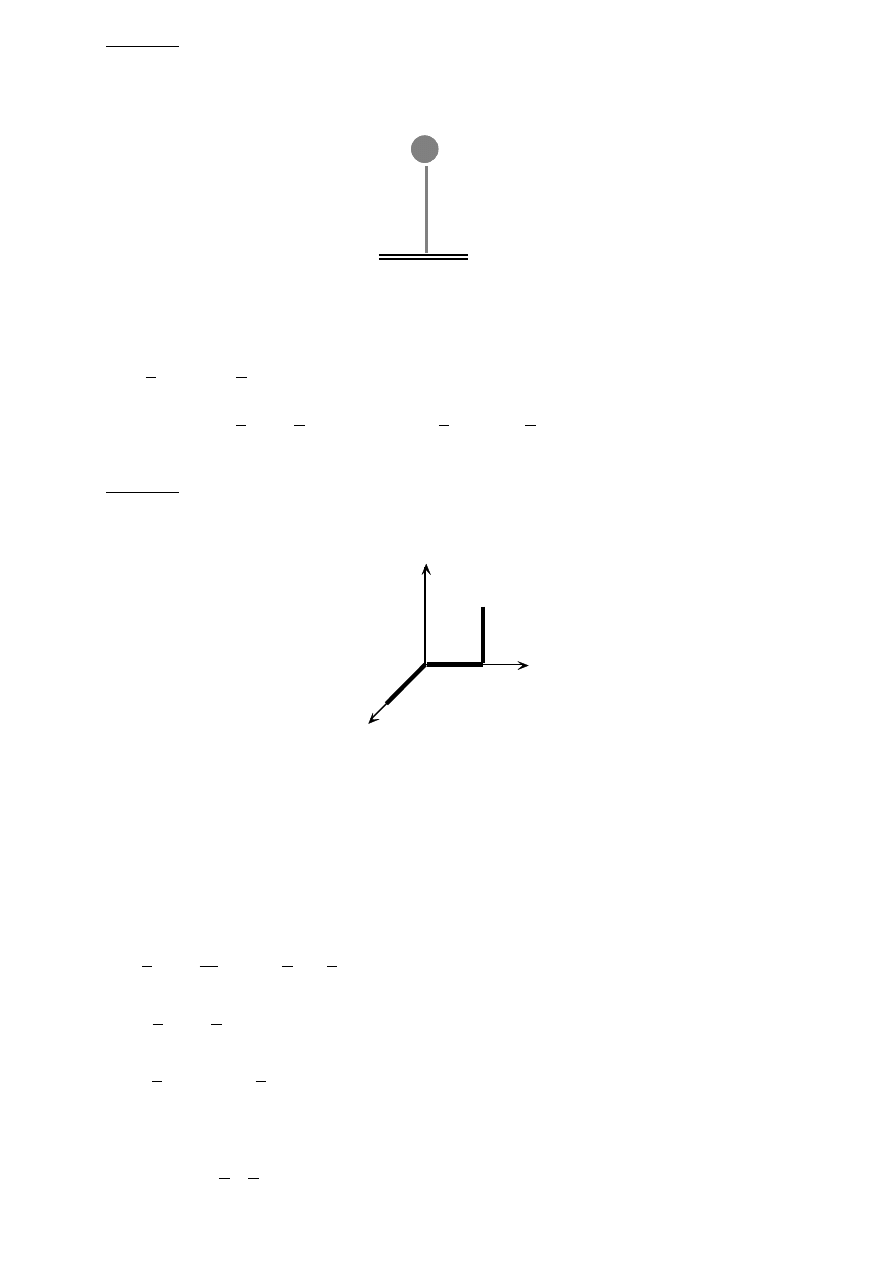
Zadanie 2
Obliczyć moment bezwładności drążka zmiany biegów samochodu względem jego osi x.
Zakładamy, że drążek składa się z jednorodnego pręta o masie m i długości l z osadzoną na
nim kulką o promieniu r i masie M.
m,l
M,r
x
Na moment bezwładności (I
x
) drążka względem osi x składa się moment bezwładności pręta
(I
x1
) i moment bezwładności kulki (I
x2
): I
x
= I
x1
+ I
x2
. Moment bezwładności pręta jest
momentem bezwładności względem jego własnego końca, natomiast moment bezwładności
kulki liczymy z twierdzenia Steinera:
2
x1
m
3
1
I
l
,
2
2
x2
)
M(r
M r
5
2
I
l
wobec tego:
2
2
2
2
2
2
x
)
(r
r
5
2
M
m
3
1
)
M(r
Mr
5
2
m
3
1
I
l
l
l
l
.
Zadanie 3
Znaleźć macierz bezwładności układu 3 jednorodnych prętów każdy o masie m i długości l
połączonych tak jak na rysunku.
y
x
z
O
Macierz (tensor) bezwładności układu wygląda następująco:
I
y
zy
zx
yz
y
yx
xz
xy
x
I
D
D
D
I
D
D
D
I
I
x
, I
y
, I
z
momenty bezwładności względem poszczególnych osi
D
xy
= D
yx
, D
yz
= D
zy
, D
zx
= D
xz
odpowiednie momenty dewiacji
2
2
2
2
x
m
3
5
4
5
m
m
12
1
m
3
1
I
l
l
l
l
2
2
y
m
3
2
m
3
1
2
I
l
l
2
2
2
z
m
3
5
m
m
3
1
2
I
l
l
l
0
D
D
yx
xy
2
zy
yz
m
2
1
2
m
D
D
l
l
l

0
D
D
xz
zx
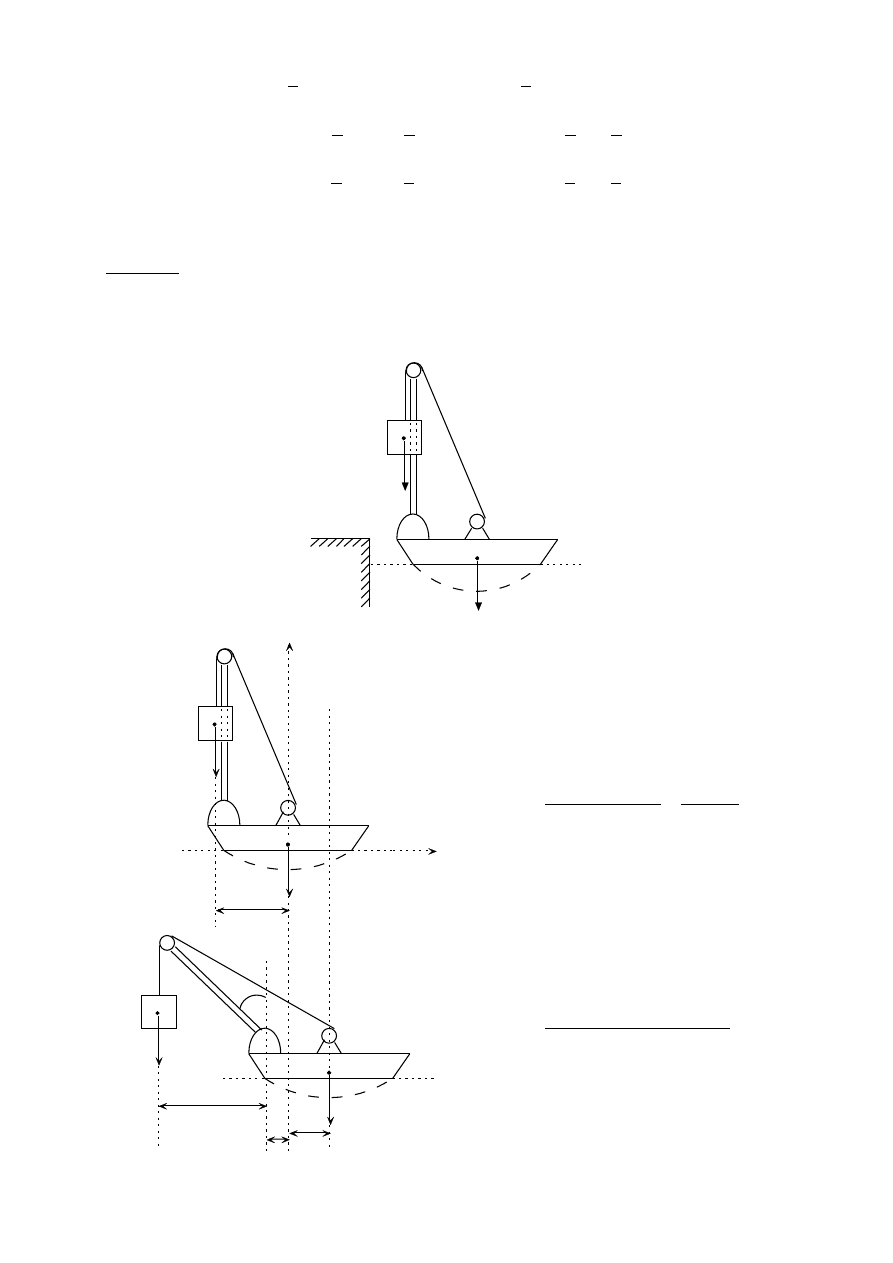
Wobec tego macierz (tensor) bezwładności układu wygląda następująco:
I
3
5
2
1
0
2
1
3
2
0
0
0
3
5
m
m
3
5
m
2
1
0
m
2
1
m
3
2
0
0
0
m
3
5
2
2
2
2
2
2
l
l
l
l
l
l
.
Zadanie 4
Obliczyć przesunięcie pływającego żurawia, przenoszącego ciężar P
1
= 2[T], jeśli wysięgnik z
pozycji pionowej obróci się o kąt α = 30
o
. Ciężar żurawia P
2
= 20[T]. Długość wysięgnika OA =
l = 8[m]. Opór wody i ciężar wysięgnika pominąć.
o
P
1
P
2
O
A
o
o
P
1
P
2
O
A
o
y
x
x
1
Współrzędna x (x
sm
) środka masy:
P
P
x
P
P
P
0
P
)
x
(
P
x
2
1
1
1
2
1
2
1
1
sm
o
P
2
o
Współrzędna x (x
sm
) środka masy:
P
1
O
A
lsin
-x
1
+ x
x
2
1
2
1
1
sm
P
P
x
P
x)
x
lsinα
(
P
x
l
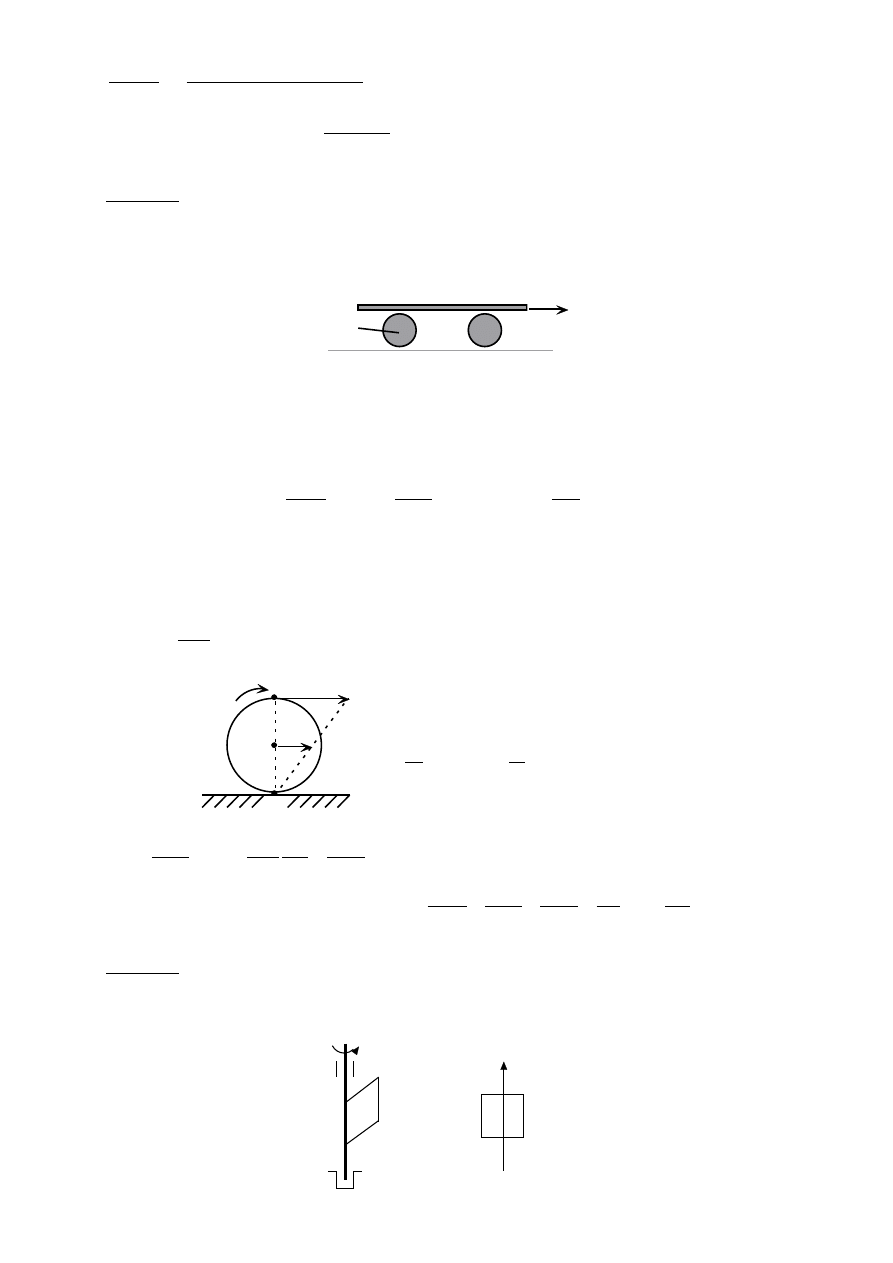
Współrzędna środka masy środka masy x pozostaje bez zmiany zatem:
2
1
2
1
1
2
1
1
1
P
P
x
P
x)
x
lsinα
(
P
P
P
x
P
→
P
1
x
1
P
1
lsin
P
1
x
1
+ P
1
x + P
2
x
(P
1
+ P
2
)x
P
1
lsin
→ x
2
1
1
P
P
sin
l
P
, po wstawieniu danych otrzymujemy: x = 0,36 [m].
Zadanie 5
Oblicz energię kinetyczną układu składającego się z jednorodnej belki o masie M i dwóch
jednakowych rolek o masie m i promieniu r. Belka jest przetaczana po rolkach ze stałą
prędkością V.
V
M
m,r
Belka porusza się ruchem postępowym, zaś obie rolki poruszają się ruchem płaskim.
Na energię kinetyczną układu (E
k
) składa się:
1. energia kinetyczna ruchu postępowego belki (E
k1
)
2. energia ruchu postępowego rolek (E
k2
)
3. energia ruchu obrotowego rolek (E
k3
)
E
k
= E
k1
+ E
k2
+ E
k3
,
2
M V
E
2
k1
,
2
o
2
o
k2
mV
2
mV
2
E
,
2
2
k3
ω
I
2
ω
I
2
E
gdzie: V
o
prędkość środka masy rolki
ω
prędkość kątowa rolki
I
moment bezwładności rolki względem osi przechodzącej przez środek masy,
2
r
m
I
2
C
V
o
V
O
C
chwilowy środek obrotu, V
c
= 0
r
r
2
V
ωr
V
,
2r
V
ω
o
4
mV
E
2
k2
,
8
mV
4r
V
2
mr
E
2
2
2
2
k3
Energia kinetyczna układu jest równa:
4
3m
M
2
V
8
mV
4
mV
2
M V
E
2
2
2
2
k
.
Zadanie 6
Ile wynosi energia kinetyczna i kręt płyty kwadratowej o boku a i masie m wirującej z
prędkością kątową ω
o
= const wokół swego nieruchomego boku?
a
a
o
a
a
y
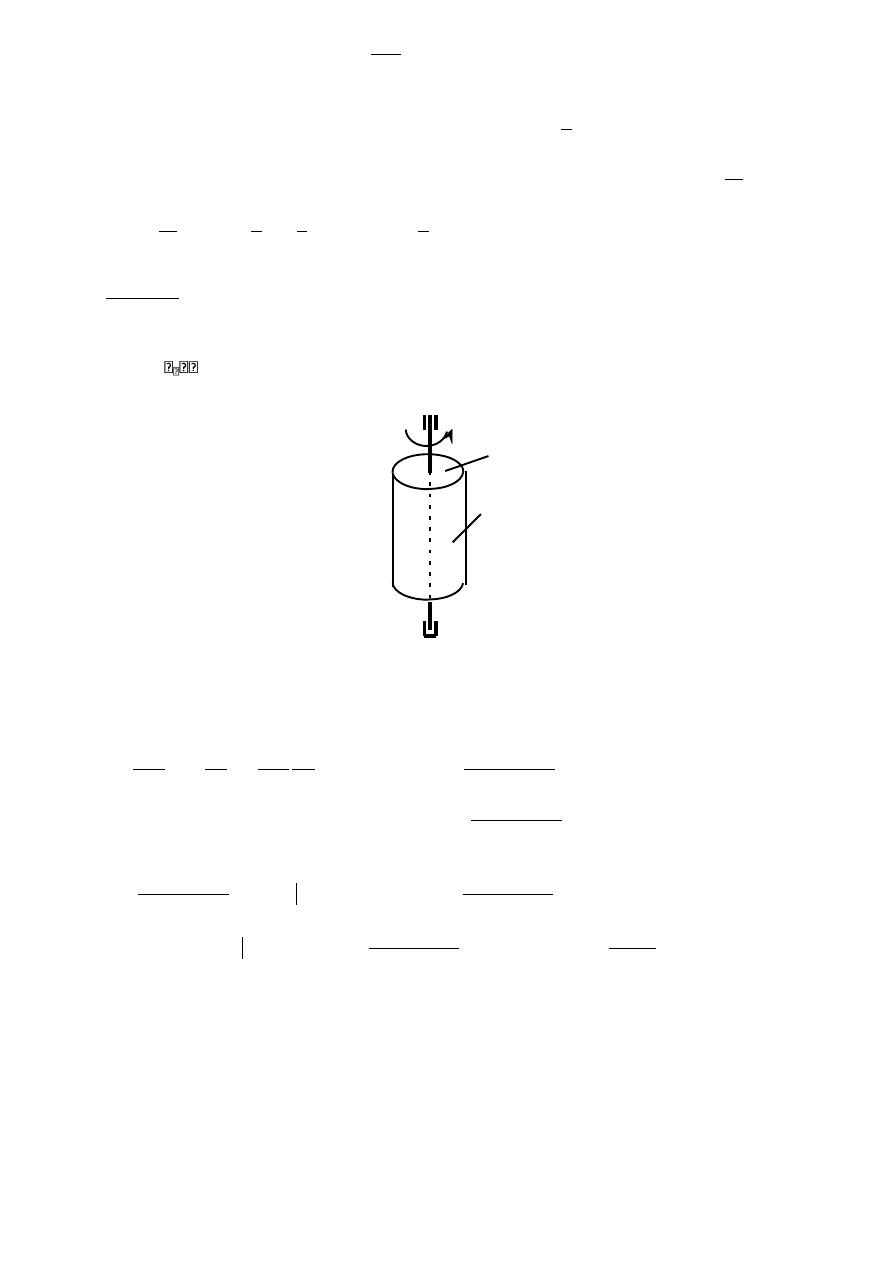
Szukana energia kinetyczna:
2
ω
I
E
2
o
I
moment bezwładności kwadratu względem jednego z boków
Moment I obliczamy na podstawie tw. Steinera: I = I
y
+ m
2
2
a
gdzie: I
y
moment bezwładności kwadratu względem osi y (rys. po prawej),
2
y
ma
12
1
I
I
2
ma
12
1
+ m
2
2
a
2
ma
3
1
stąd:
2
o
2
ω
ma
6
1
E
.
Zadanie 7
Jednorodny walec o masie m = 30[kg] i promieniu r = 0,1[m] został ze stanu spoczynku
wprawiony w ruch obrotowy wokół swej nieruchomej osi symetrii uzyskując prędkość
kątową
120[rad/s] w ciągu t
1
= 8[s]. Wiedząc, że moment oporowy ruchu M
t
= 0,2[Nm],
oblicz moment napędowy zakładając jego stałą wartość.
m
o
r
Dynamiczne równanie ruchu:
t
n
M
M
ε
I
gdzie: I
moment bezwładności walca względem osi obrotu
przyspieszenie kątowe
M
n
szukany moment napędowy
2
r
m
I
2
,
dt
dω
ε
→
t
n
2
M
M
dt
dω
2
r
m
→
dt
r
m
)
M
M
2(
dω
2
t
n
całkujemy obustronnie ostatnie równanie:
C
dt
r
m
)
M
M
2(
dω
2
t
n
C
stała zależna od warunku początkowego
C
t
r
m
)
M
M
2(
ω
2
t
n
,
0
ω
0
t
→ C = 0 →
t
r
m
)
M
M
2(
ω
2
t
n
z treści zadania:
1
t
t
ω
ω
1
→
1
2
t
n
1
t
r
m
)
M
M
2(
ω
stąd:
1
2
1
t
n
2t
mr
ω
M
M
podstawiając dane liczbowe otrzymujemy: M
n
= 2,45 [Nm].
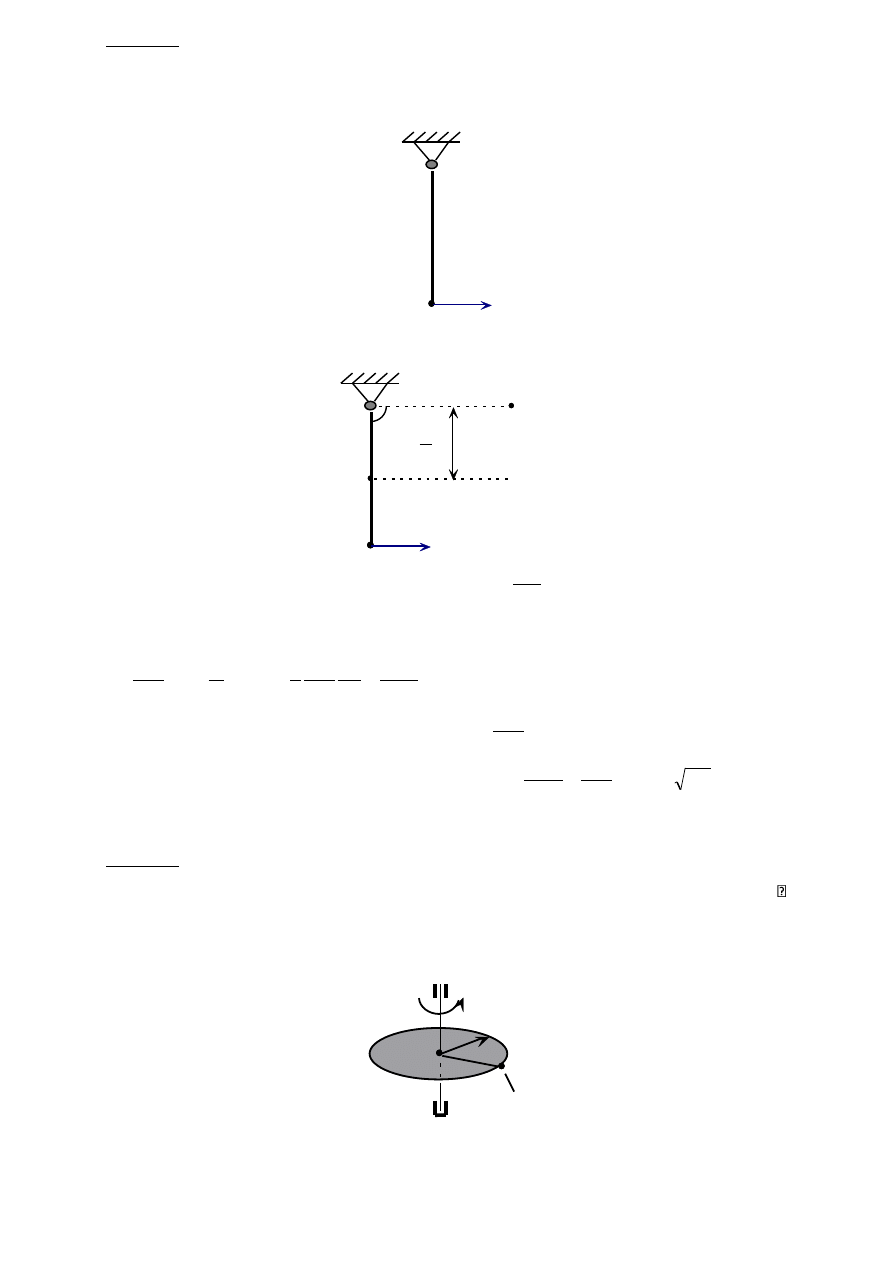
Zadanie 8
Prosty jednorodny pręt o długości l = 3,27 [m] osadzony jest swoim końcem O obrotowo na
osi i może wykonywać ruchy w płaszczyźnie pionowej, prostopadłej do tej osi. Jaką prędkość
trzeba nadać końcowi A, aby pręt z położenia równowagi wykonał pół obrotu?
V
l
O
A
Korzystamy z zasady zachowania energii. Na poniższym rysunku zaznaczono poziom
odniesienia dla energii potencjalnej (liczona jest względem środka masy)
V
l
O
A
A
.
V = 0
l
2
1
poziom
odniesienia
Całkowita energia (E
1
) w położeniu początkowym:
2
Iω
E
2
1
gdzie: I
moment bezwładności pręta względem własnego końca
ω
prędkość kątowa w chwili początkowej
3
m
I
2
l
,
l
V
ω
→
6
V
m
V
3
m
2
1
E
2
2
2
2
1
l
l
Całkowita energia (E
2
) w położeniu końcowym:
2
mg
E
2
l
Z zasady zachowania energii wynika równanie: E
1
= E
2
→
2
mg
6
V
m
2
l
→
l
3g
V
Podstawiając dane liczbowe otrzymujemy: V = 9,81 [m/s].
Zadanie 9
Jednorodna tarcza kołowa o masie M i promieniu r obraca się ze stałą prędkością kątową
wokół własnej pionowej i nieruchomej osi symetrii, przy czym na obwodzie tarczy spoczywa
punkt A o masie m. Co stanie się, jeśli po przesunięciu punkt A znajdzie się w środku tarczy?
Opory ruchu pomijamy.
M
r
A
m
Po przesunięciu punktu A na środek tarczy prędkość kątowa układu powinna ulec
zwiększeniu. Aby to wykazać skorzystamy z zasady zachowania krętu.
Kręt (K
1
) w położeniu początkowym jest sumą kretów tarczy (K
1M
) i krętu punktu A (K
1m
):
K
1
= K
1M
+ K
1m
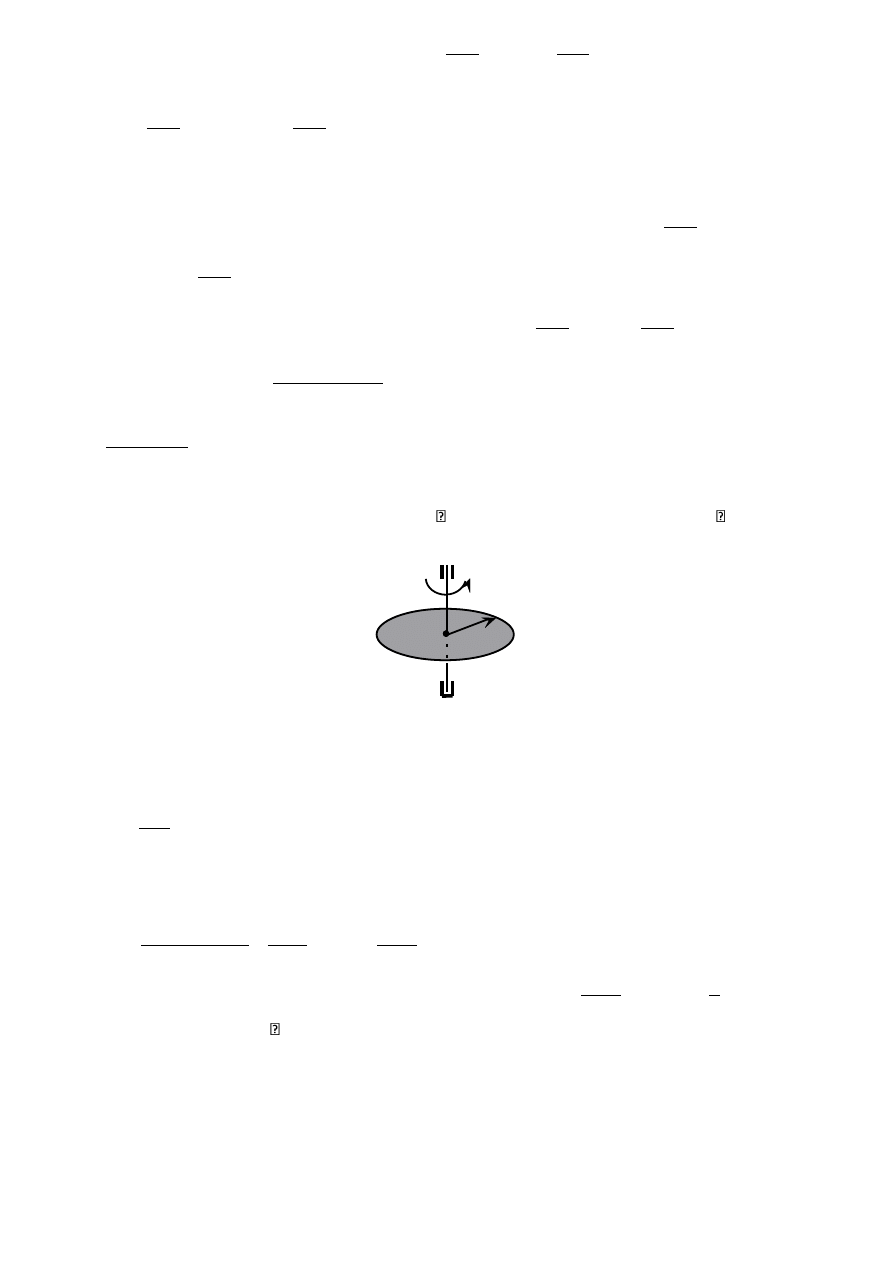
K
1M
= Iω, I
moment bezwładności tarczy,
2
M r
I
2
→
ω
2
M r
K
2
1M
K
1m
= mVr, V
prędkość liniowa punktu A, V = ωr → K
1m
= mωr
2
2
2
2
2
1
mr
2
M r
ω
r
mω
ω
2
M r
K
Kręt (K
2
) w położeniu końcowym jest tylko krętem tarczy (K
2M
), ponieważ punkt A znajduje
się na osi obrotu:
K
2M
= Iω
x
, ω
x
szukana prędkość kątowa w położeniu końcowym →
x
2
2M
ω
2
M r
K
x
2
2M
2
ω
2
M r
K
K
Z zasady zachowania krętu wynika równanie: K
1
= K
2
→
x
2
2
2
ω
2
M r
mr
2
M r
ω
Stąd szukana ω
x
:
2
2
2
x
M r
mr
2
M r
ω
ω
i łatwo dostrzec, że jest większa od ω.
Zadanie 10
Jednorodna tarcza kołowa o promieniu r = 0,3[m] i masie m = 2[kg] jest wykonana z
tworzywa nasączonego równomiernie cieczą. Tarcza obracała się na początku wokół własnej
osi symetrii ze stałą częstotliwością f
1
= 10/ [Hz]. Oblicz, jaką prędkość kątową
2
[rad/s]
osiągnęła tarcza, jeśli po osuszeniu jej masa zmniejszyła się o 20%. Opory ruchu pomijamy.
m
r
f
1
Korzystamy z zasady zachowania krętu.
Kręt (K
1
) tarczy przed osuszeniem: K
1
= I
1
ω
1
gdzie: I
1
moment bezwładności tarczy przed osuszeniem
ω
1
prędkość kątowa tarczy przed osuszeniem
2
mr
I
2
1
, ω
1
= 2
f
1
→ K
1
= mr
2
f
1
Kręt (K
2
) tarczy po osuszeniu: K
2
= I
2
ω
2
gdzie: I
2
moment bezwładności tarczy po osuszeniu
ω
2
szukana prędkość kątowa tarczy po osuszeniu
5
2mr
2
m)r
20%
(m
I
2
2
2
→
2
2
2
ω
5
2mr
K
Z zasady zachowania krętu wynika równanie: K
1
= K
2
→
2
2
1
2
ω
5
2mr
πf
mr
→
1
2
πf
2
5
ω
Po wstawieniu f
1
= 10/ [Hz] otrzymujemy: ω
2
= 25 [rad/s].
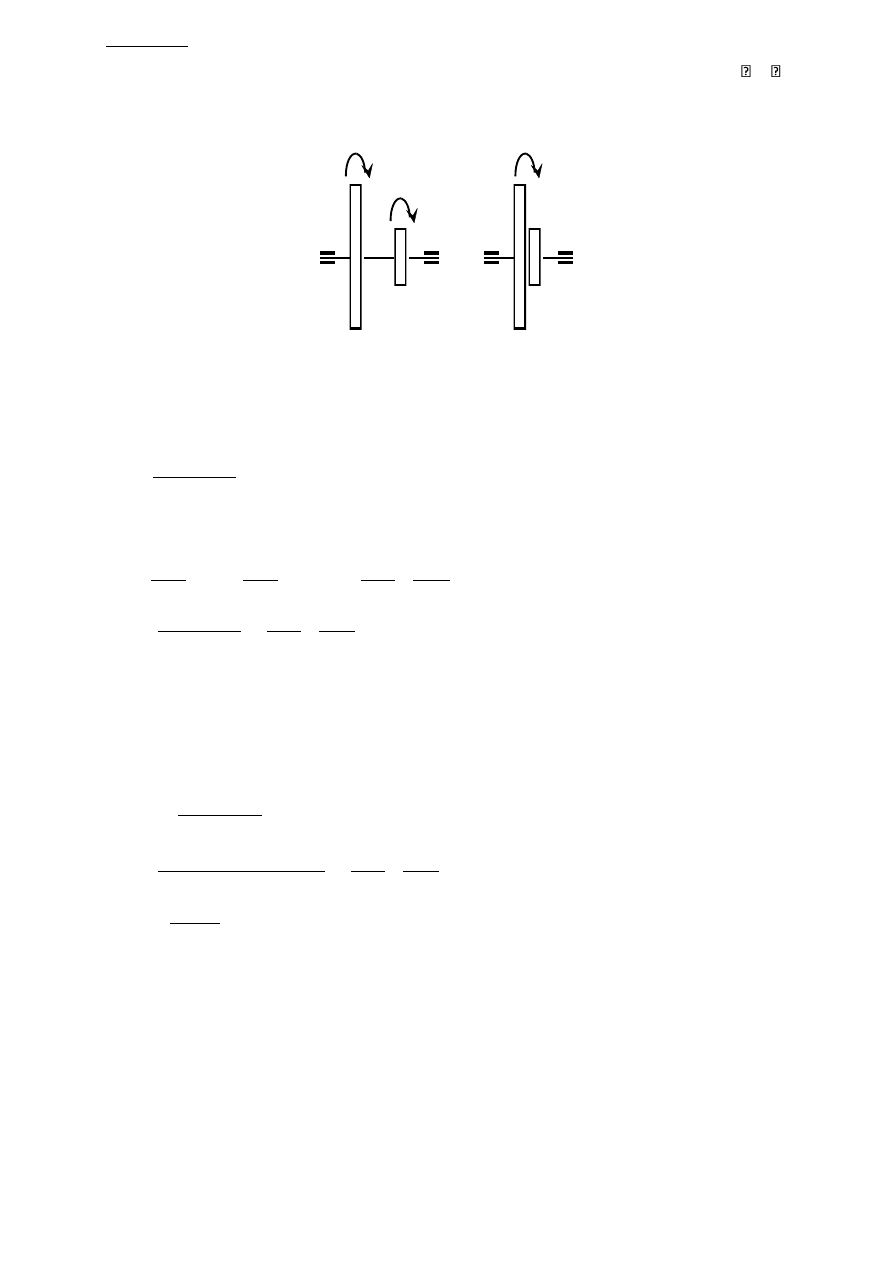
Zadanie 11
Dwie niezależnie wirujące na jednej nieruchomej osi tarcze z prędkościami kątowymi
1
i
2
zostały nagle połączone (sklejone). Jak zmieni się energia kinetyczna układu, jeśli momenty
bezwładności tych tarcz względem osi obrotu wynoszą odpowiednio J
1
i J
2
?
1
2
J
1
J
2
Zmiana
E
k
energii kinetycznej układu:
p
k
k
k
k
E
E
ΔE
gdzie:
k
k
E
końcowa energia kinetyczna układu
p
k
E
początkowa energia kinetyczna układu
2
ω
)
J
J
(
E
2
2
1
k
k
, ω
nieznana prędkość kątowa układu po połączeniu tarcz
k2
k1
k
E
E
E
p
E
k1
energia kinetyczna pierwszej tarczy, E
k2
energia kinetyczna drugiej tarczy
2
ω
J
E
2
1
1
k1
,
2
ω
J
E
2
2
2
k2
→
2
ω
J
2
ω
J
E
2
2
2
2
1
1
k
p
2
ω
J
2
ω
J
2
ω
)
J
J
(
E
2
2
2
2
1
1
2
2
1
k
(1)
ω liczymy z zasady zachowania krętu.
Kręt (K
1
) układu przed połączeniem tarcz:
K
1
= J
1
ω
1
+ J
2
ω
2
Kręt (K
2
) układu po połączeniu tarcz:
K
1
= (J
1
+ J
2
)ω
Z zasady zachowania krętu wynika równanie: K
1
= K
2
→ J
1
ω
1
+ J
2
ω
2
= (J
1
+ J
2
)ω
stąd:
2
1
2
2
1
1
J
J
ω
J
ω
J
ω
i podstawiamy do równania (1):
2
ω
J
2
ω
J
)
J
J
2(
)
ω
J
ω
J
(
)
J
J
(
E
2
2
2
2
1
1
2
2
1
2
2
2
1
1
2
1
k
i po przekształceniach otrzymujemy:
2
2
1
2
1
2
1
k
)
ω
ω
(
J
J
J
J
E
.
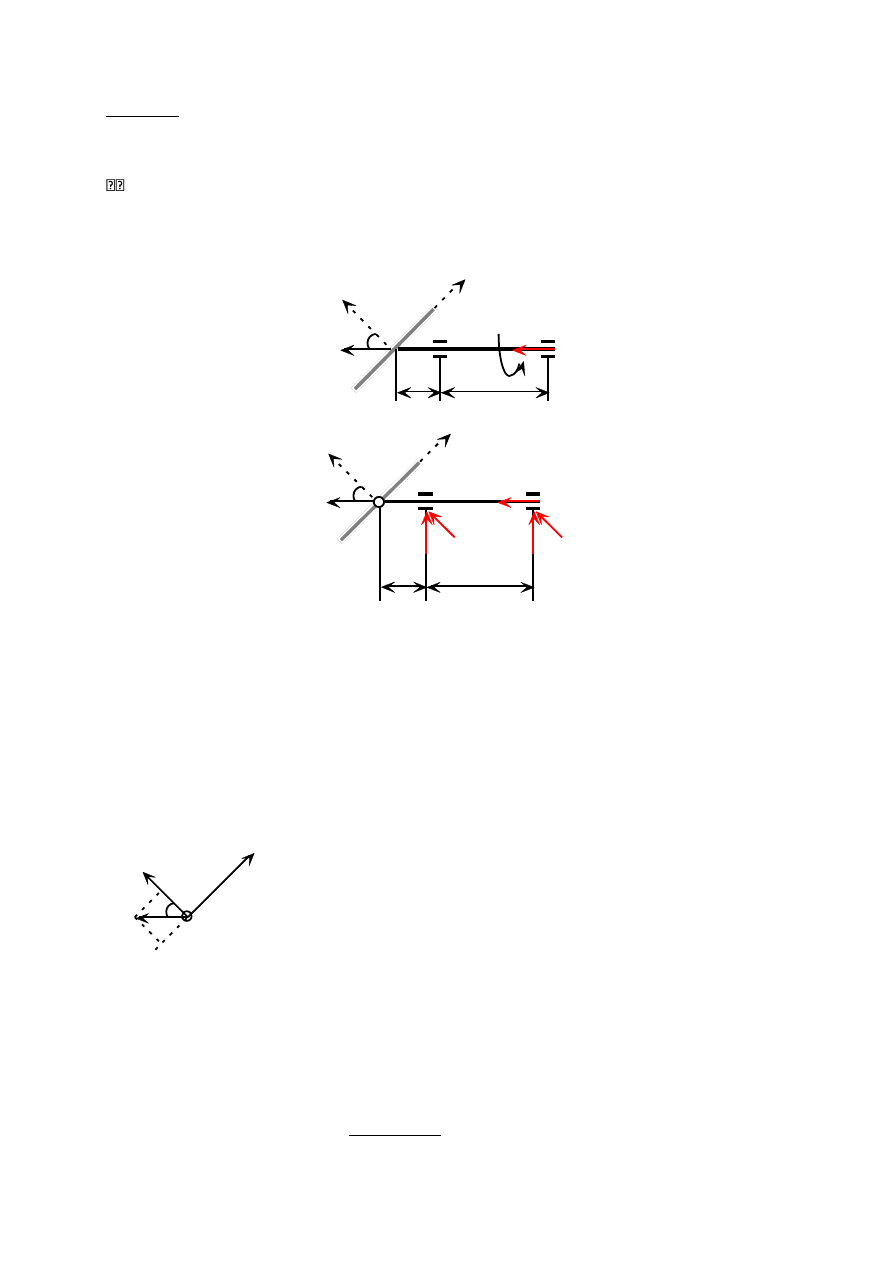
Ćwiczenie 13 i 14 (wykład: 7)
Dynamiczne równania ruchu ciała sztywnego
Zadanie 1
Oblicz reakcje dynamiczne w łożyskach A i B dwuramiennego śmigła samolotu w czasie jego
obrotu, jeśli wskutek złego wykonania oś symetrii śmigła jest odchylona od osi obrotu o kąt
= 0,015 [rad], a jego środek leży na osi obrotu. Śmigło należy traktować jako pręt prosty
jednorodny. Ciężar śmigła P = 147,15[N], jego moment bezwładności względem osi symetrii J
= 4.905 [kgm
2
], wymiary: h = 0,25[m], a = 0,15[m], a prędkość obrotowa jest stała i wynosi n
= 3000 [obr/min.].
A
B
h
a
z
3
2
A
B
h
a
z
3
2
R
AX
R
AY
R
BY
R
BX
1
Jeśli środek masy obracającej się bryły leży na osi obrotu (tak jest w tym przypadku), to
można do wyznaczenia reakcji dynamicznych zastosować dynamiczne równania Eulera.
Równania te są przedstawione w układzie głównych centralnych osi bezwładności:
1
3
2
3
2
1
1
M
ω
ω
)
I
I
(
ω
I
(a)
2
3
1
1
3
2
2
M
ω
ω
)
I
I
(
ω
I
(b)
3
2
1
2
1
3
3
M
ω
ω
)
I
I
(
ω
I
(c)
I
1
, I
2
, I
3
główne, centralne momenty bezwładności względem osi 1,2,3
I
1
= J, I
2
<< I
1
0, I
3
= J
]
ω
,
ω
,
[ω
ω
3
2
1
rzuty wektora
ω
na osie 1,2,3
3
2
1
0
ω
1
,
ωsinα
ω
2
,
ωcosα
ω
3
oczywiście
0
ω
1
,
0
ω
2
,
0
ω
3
, ponieważ
= const, wobec tego będziemy korzystać
tylko z równania (a), ponieważ w dwóch pozostałych mamy po lewej stronie 0.
M
1
, M
2
, M
3
momenty sił względem osi 1,2,3
M
1
= R
AY
a
R
BY
(a + h), w naszym zadaniu:
R
R
R
BY
AY
czyli:
Rh
h)
R(a
Ra
M
1
i podstawiamy (wraz z
2
i
3
) do równania (1)
Rh
)
sα
ωsinα)(ωco
J(
→
h
cosα
sinα
Jω
R
2
podstawiając dane liczbowe (
= 2
n = 100 [rad/s]) otrzymujemy: R = 2943000 [N]
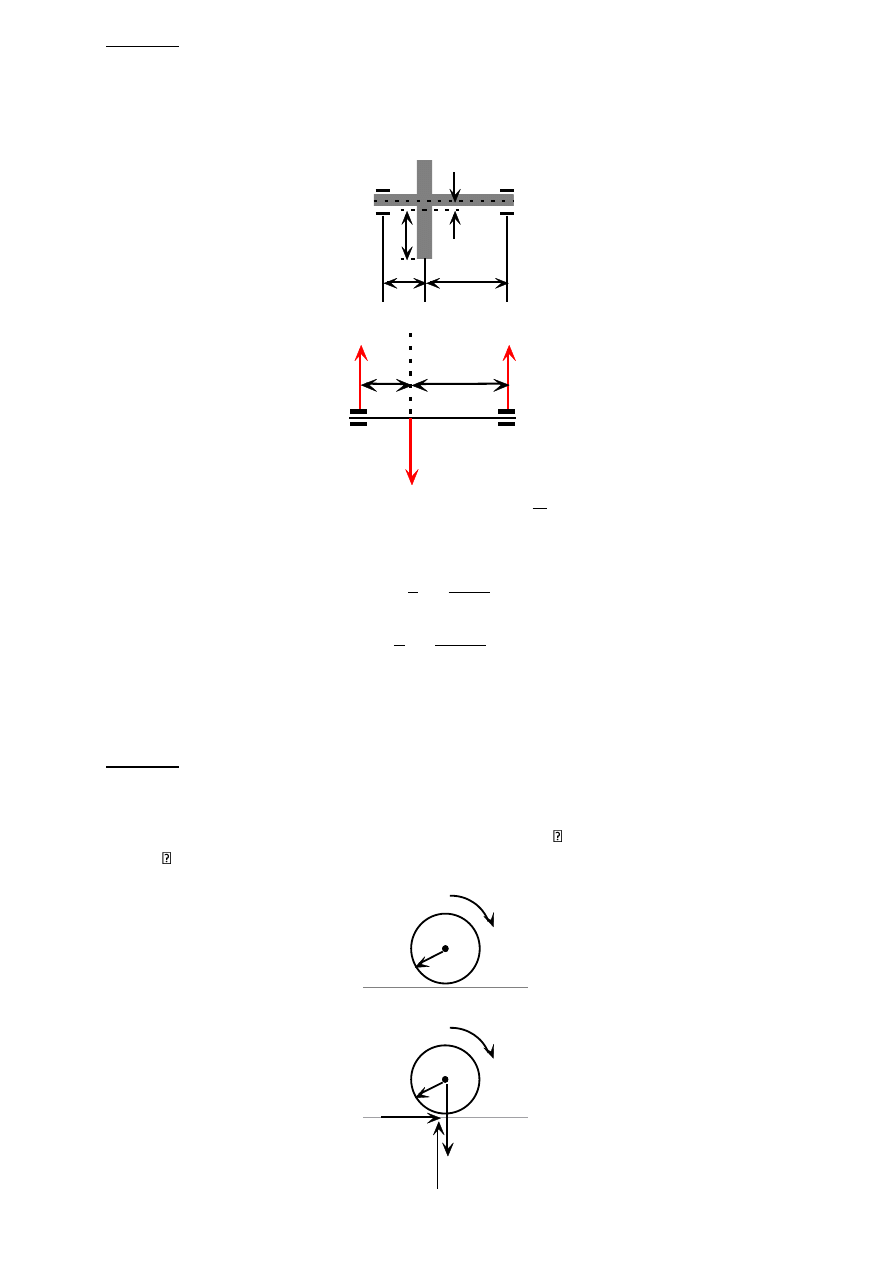
Zadanie 2
Jednorodne koło zamachowe o ciężarze Q = 1[T] i promieniu r = 0,6[m] jest osadzone na
ułożyskowanej osi AB i obraca się z prędkością n = 1200[obr/min.]. Geometryczna oś obrotu
jest przesunięta równolegle względem osi symetrii koła o wielkość e =1[mm]. Obliczyć
reakcje dynamiczne łożysk A i B, jeśli h = 0,4[m].
h
2h
.
A
B
C
e
r
A
B
R
A
F
h
2h
R
B
R
A
, R
B
szukane reakcje, F
siła odśrodkowa,
e
ω
g
Q
e
mω
F
2
2
Warunki równowagi:
0
R
F
R
F
B
A
y
,
0
3h
R
Fh
M
B
A
z drugiego równania otrzymujemy:
3g
e
Qω
F
3
1
R
2
B
z pierwszego równania:
3g
e
2Qω
F
3
2
R
F
R
2
B
A
podstawiając dane liczbowe (Q = 9810000 [N], n = 20 [obr/s], e = 0,001 [m]) otrzymujemy:
R
A
= 133333,33 [N], R
B
= 266666,66 [N].
Zadanie 3
Napędowe koło samochodu o promieniu tocznym r i ciężarze P porusza się po prostej
poziomej. Do koła jest przyłożony moment obrotowy M. Ramię bezwładności koła względem
jego osi centralnej, prostopadłej do jego płaszczyzny, wynosi . Współczynnik tarcia suwnego
wynosi . Jaki warunek musi spełniać moment obrotowy, aby koło toczyło się bez poślizgu?
Opory toczenia pomijamy.
M
r
Na poniższym rysunku pokazano siły działające na koło podczas ruchu.
M
r
T
P
N
O
P
siła ciężkości, N
siła reakcji podłoża (N = P), T
siła tarcia
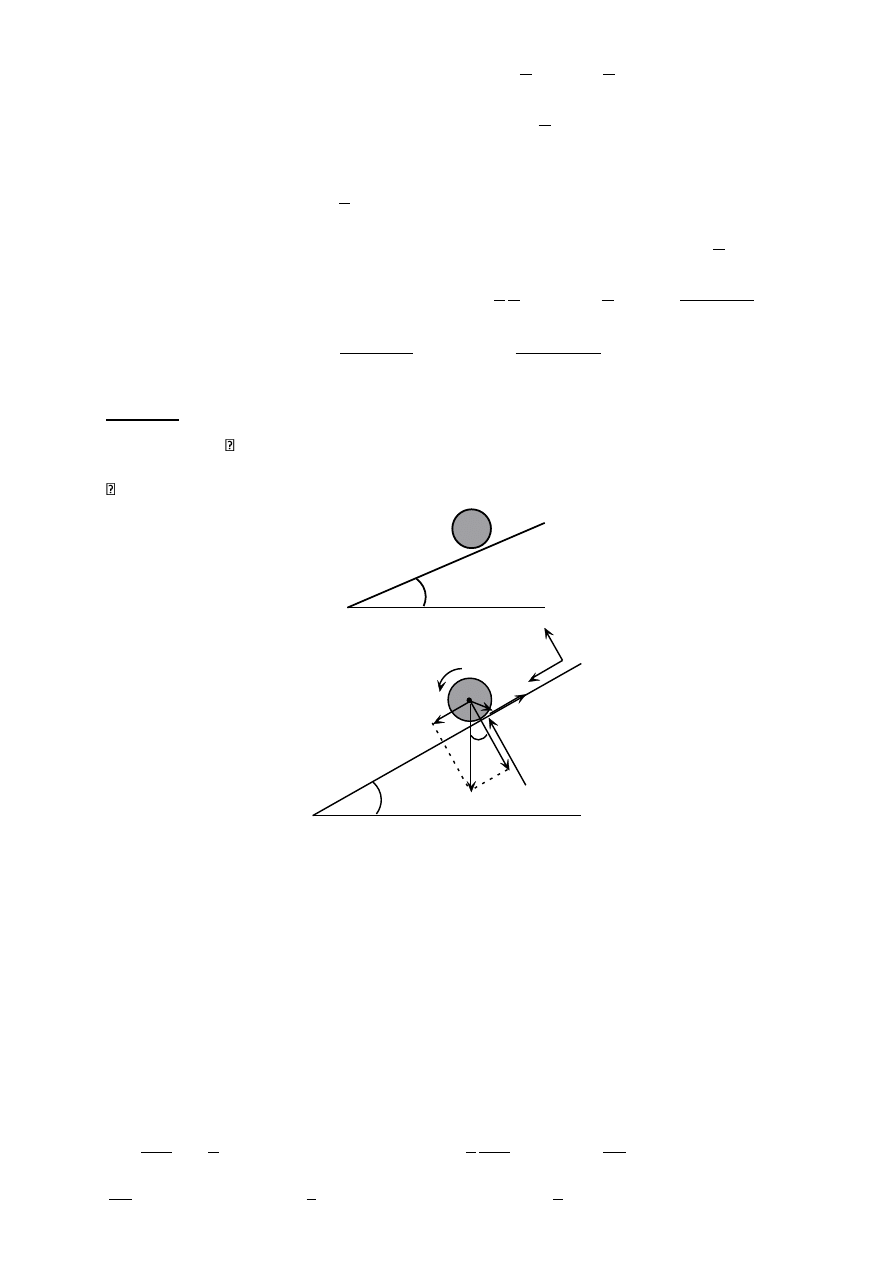
Aby koło toczyło się bez poślizgu musi być spełniony warunek: T
Nμ → T
Pμ (1)
Dynamiczne równanie ruchu postępowego: am = T,
g
P
m
→
g
P
a
T
(2)
Podstawiając równanie (2) do warunku (1) otrzymujemy:
Pμ
g
P
a
→ a
g
(3)
Dynamiczne równanie ruchu obrotowego względem punktu O:
Tr
M
I
ε
o
(4)
przyspieszenie kątowe,
r
a
ε
(5)
I
o
moment bezwładności względem osi przechodzącej przez punkt O,
2
2
o
ρ
g
P
mρ
I
(6)
podstawiamy równania (2), (5) i (6) do równania (4):
r
g
P
a
M
ρ
g
P
r
a
2
→
)
r
P(ρ
M gr
a
2
2
i podstawiamy do warunku (3):
gμ
)
r
P(ρ
M gr
2
2
→
r
)
ρ
r
(
Pμ
M
2
2
.
Zadanie 4
Oblicz, jaki kąt powinna tworzyć z poziomem płaszczyzna, po której ma się toczyć bez
poślizgu walec, jeżeli wiadomo, że współczynnik tarcia między walcem a płaszczyzną wynosi
.
F
2
F
1
P
T
o
x
y
r
gdzie: T
siła tarcia
P
siła ciężkości (P = mg)
N
siła reakcji podłoża
Aby walec mógł toczyć się bez poślizgu musi być spełniony warunek: T
Nμ (1)
Dynamiczne równania ruchu postępowego walca w kierunku osi x i y, obranych jak na
rysunku:
y: am = F
1
T
x: 0 = N
F
2
F
1
= Psin
= mg sin
, F
2
= Pcos
= mgcos
am = mg sin
T (2), N = mgcos
, czyli (1): T
mgμcos
(1a)
Dynamiczne równania ruchu obrotowego walca względem punktu O:
I
o
= Tr (3)
I
o
moment bezwładności walca względem osi przechodzącej względem punktu O
2
mr
I
2
o
,
r
a
ε
i podstawiamy do równania (3):
Tr
2
mr
r
a
2
→
m
2T
a
i podstawiamy do (2)
T
mgsin α
m
m
2T
→
mgsinα
3
1
T
i podstawiamy do (1a):
cosα
mgμ
mgsin α
3
1

stąd: tg
≤ 3μ →
arctg3μ.
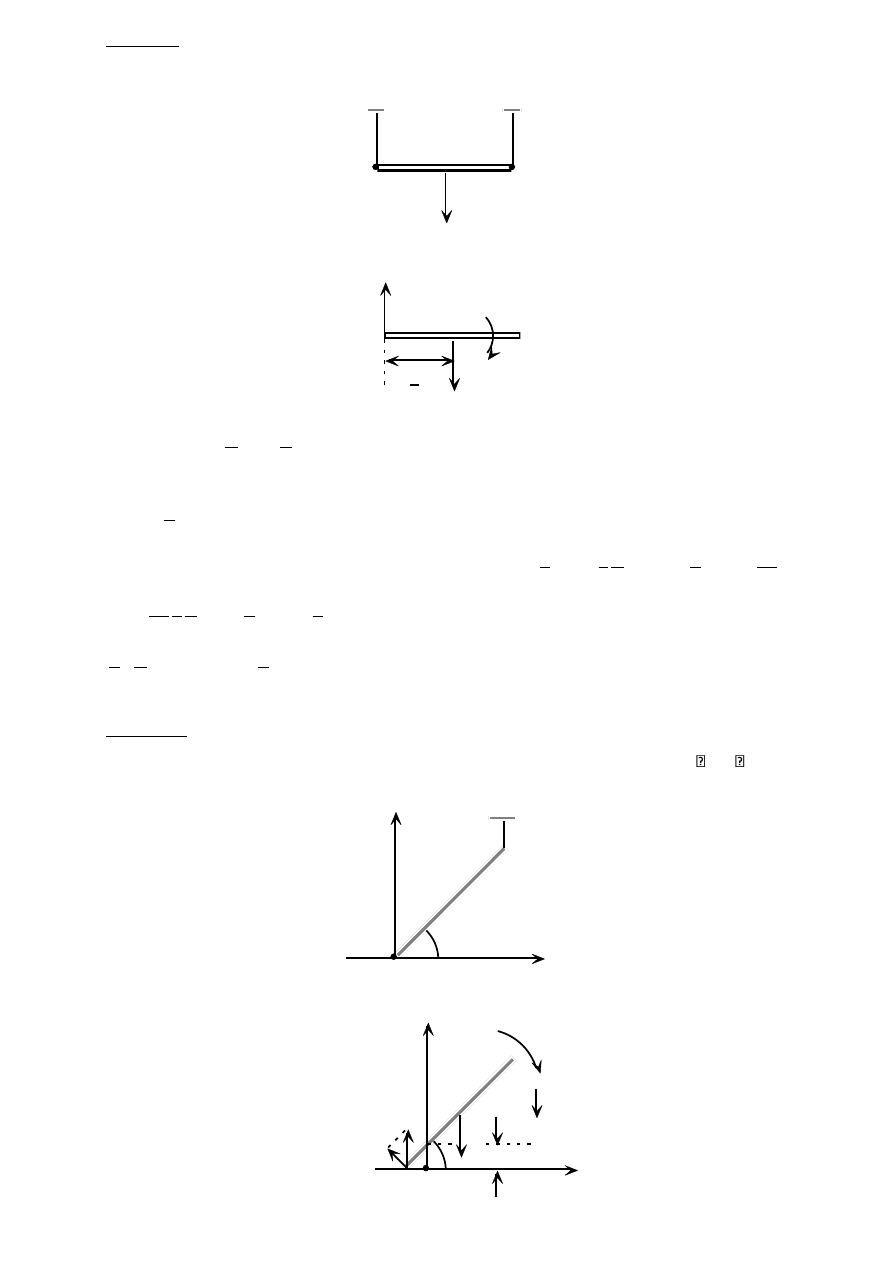
Zadanie 5
Prosty jednorodny pręt AB o ciężarze P jest zawieszony poziomo na dwóch pionowych
linkach przyczepionych do sufitu. Oblicz siłę naciągu jednej linki w chwili zerwania się drugiej.
P
l
B
A
Poniższy rysunek pokazuje siły działające na pręt w chwili zerwania się jednej z
podtrzymujących go linek, gdzie S
szukana siła naciągu linki, która nie uległa zerwaniu.
P
l
S
1
2
.
A
Dynamiczne równanie ruchu postępowego w kierunku pionowym:
am = P
S,
g
P
m
→
S
P
g
P
a
(1)
Dynamiczne równanie ruchu obrotowego względem punktu A:
2
P
εI
A
l
I
A
moment bezwładności pręta względem punktu A,
2
2
A
g
P
3
1
m
3
1
I
l
l
,
2
ε
a
l
→
l
2a
ε
stąd:
2
P
g
P
3
1
2a
2
l
l
l
→
g
4
3
a
i podstawiamy do równania (1)
S
P
g
P
g
4
3
→
P
4
1
S
.
Zadanie 5a
Jednorodna belka o ciężarze G i długości 2l jest podtrzymywana pod kątem
o
= /3 do
poziomu. Oblicz nacisk belki w momencie zerwania podtrzymującej ją linki.
x
y
o
.
O
C
Poniższy rysunek pokazuje siły działające na pręt w chwili zerwania podtrzymującej go linki,
gdzie N
szukana siła nacisku belki
x
y
.
O
P
N
C
l
y = l
N
1
N
1
= Ncos
a
sin
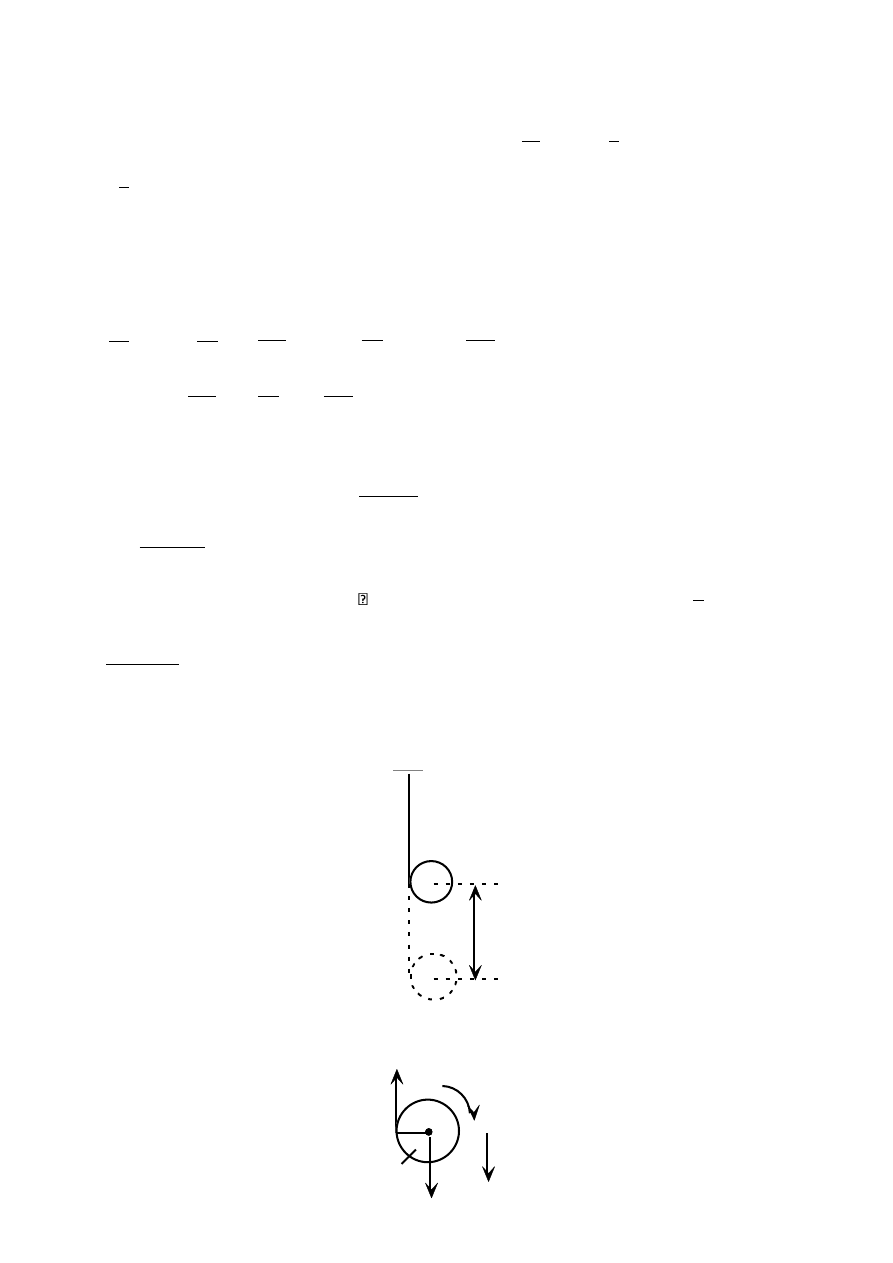
Dynamiczne równanie ruchu postępowego belki w kierunku pionowym:
am = P
N, P = mg → am = mg
N (1)
Dynamiczne równanie ruchu obrotowego belki względem środka masy (C):
I = (Ncos
)l
I
moment bezwładności belki względem jej środka,
2
2
m
3
1
)
m(2
12
1
I
l
l
cosφ
N
m
3
1
ε
2
l
l
(2)
przyspieszenie kątowe belki
Jak pokazano na ostatnim rysunku: y = l sin
Różniczkujemy dwukrotnie po czasie ostatnie równanie:
dt
dφ
cosφ
dt
dy
l
→
2
2
2
2
2
dt
φ
d
cosφ
dt
dφ
sinφ
dt
y
d
l
l
Ponieważ:
a
dt
y
d
2
2
,
ω
dt
dφ
,
ε
dt
φ
d
2
2
Otrzymujemy:
)
sinφ
ω
cosφ
ε
(
a
2
l
i podstawiamy do równania (1)
N
mg
)
sinφ
ω
cosφ
ε
(
m
2
l
(3)
Wyznaczamy z równania (2)
:
l
m
cosφ
N
3
ε
i podstawiamy do równania (3)
N
mg
sinφ
ω
m
φ
cos
N
3
m
2
2
l
l
W chwili uwolnienia belki
=
o
= /3, natomiast ω = 0, stąd otrzymujemy:
mg
7
4
N
.
Zadanie 6
Walec o masie m owinięto linką, której drugi koniec przymocowano do stałego punktu A. W
pewnej chwili walec zaczął swobodnie opadać, odwijając swobodnie się z linki. Obliczyć
prędkość V osi walca w chwili, gdy jego środek obniżył się o wysokość h oraz obliczyć siłę
naciągu linki.
h
Poniższy rysunek pokazuje siły działające na walec w trakcie ruchu, gdzie S
szukana siła
naciągu linki.
S
P
r
m
a
o
Dynamiczne równanie ruchu postępowego walca:
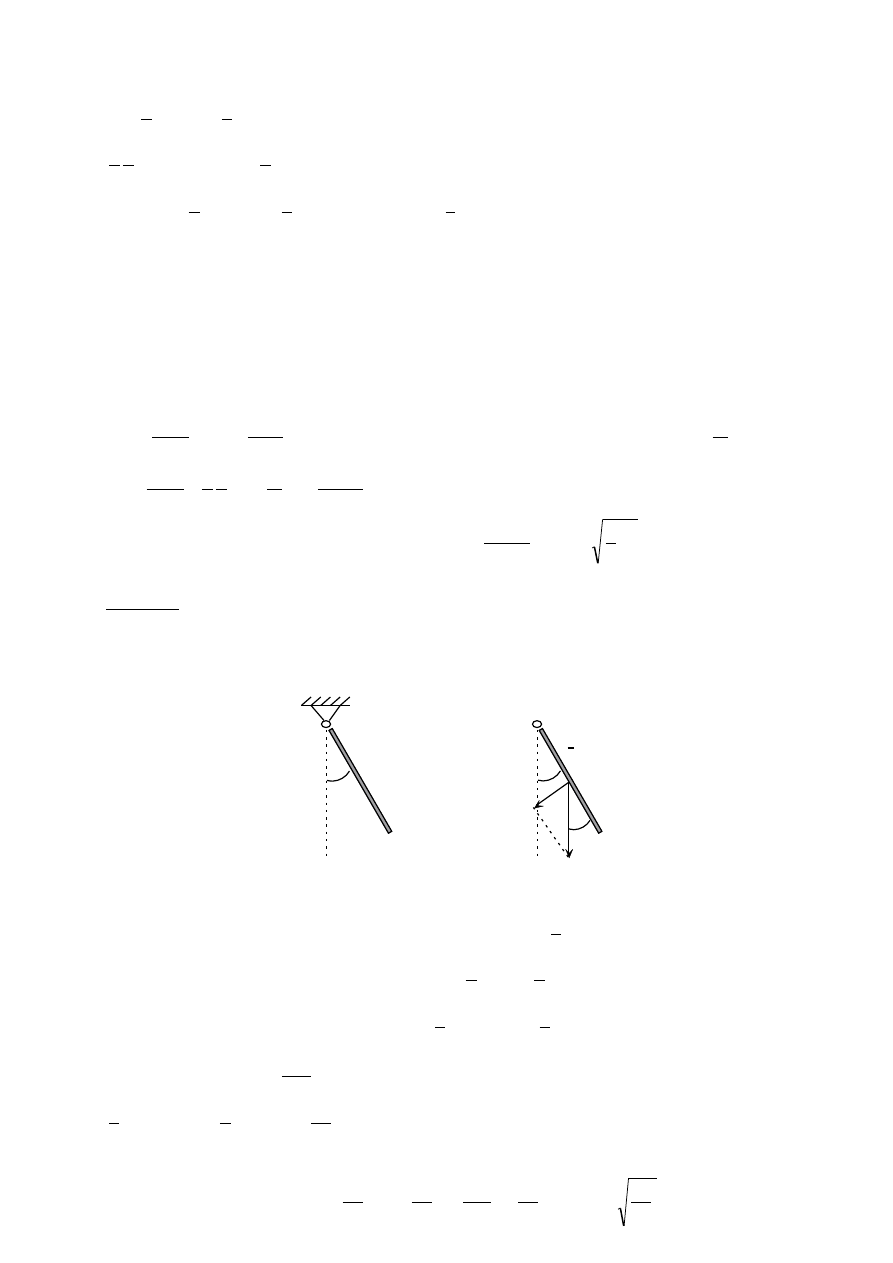
am = P
S, P = mg → am = mg
S (1)
Dynamiczne równanie ruchu obrotowego walca wokół punktu O:
I
o
= Sr (2), I
o
moment bezwładności walca względem punktu O
2
o
mr
2
1
I
,
r
a
ε
i podstawiamy do równania (2)
Sr
mr
2
1
r
a
2
→
am
2
1
S
i podstawiamy do równania (1)
am
2
1
mg
am
→
g
3
2
a
i wyliczamy S:
mg
3
1
S
Prędkość V osi walca w chwili, gdy jego środek obniżył się o wysokość h obliczymy z zasady
zachowania energii. Poziomem odniesienia dla energii potencjalnej będzie prosta
przechodząca przez punkt O i prostopadła do prostej zawierającej linkę w położeniu
końcowym walca.
Całkowita energia (E
1
) w położeniu początkowym: E
1
= mgh
Całkowita energia (E
2
) w położeniu końcowym jest sumą energii (E
kp
) ruchu postępowego i
energii (E
ko
) ruchu obrotowego:
E
2
= E
kp
+ E
ko
2
mV
E
2
kp
,
2
ω
I
E
2
o
ko
, ω
prędkość kątowa walca w położeniu końcowym,
r
V
ω
4
mV
3
r
V
mr
2
1
2
1
2
mV
E
2
2
2
2
2
Z zasady energii wynika równanie: E
1
= E
2
→
4
3mV
mgh
2
→
gh
3
4
V
.
Zadanie 7
Wyznacz równanie małych drgań swobodnych pręta jednorodnego o długości l = 1[m],
zamocowanego obrotowo w punkcie A i wykonującego ruch w płaszczyźnie pionowej. Oblicz
okres tych drgań z dokładnością do 0,01[s].
l
A
A
P
F
l
1
2
P = mg , F = Psin
= mgsin
Równanie ruchu: I
A
= M
A
I
A
moment bezwładności pręta względem punktu A,
2
A
m
3
1
I
l
M
A
moment siły względem punktu A,
sinφ
2
mg
2
F
M
A
l
l
podstawiając do równania (1) otrzymujemy:
sinφ
2
mg
ε
m
3
1
2
l
l
Uwzględniając, że:
φ
dt
φ
d
ε
2
2
oraz, że dla małych kątów sin
otrzymujemy:
φ
2
mg
φ
m
3
1
2
l
l
→
0
φ
2
3g
φ
l
równanie odpowiadające równaniu drgań
harmonicznych w postaci:
0
x
ω
x
2
o
, gdzie: ω
o
częstość drgań własnych układu
czyli w naszym przypadku:
l
2
3g
ω
2
o
,
T
2π
ω
o
→
l
2
3g
T
4π
2
2
→
3g
2
2π
T
l

po podstawieniu danych liczbowych (g = 9,81 [m/s
2
]) otrzymujemy: T = 1,64[s].
Wyszukiwarka
Podobne podstrony:
Lista zadań Mechanika Ogólna
I Lista zadan Mechanika Plynow
Fizyka lista zadań 1, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka
Metodyka rozw zadań z mechaniki J Nizioł
zestawy zadan mechanika techniczna
Niziol Metodyka rozwiazywania zadan z mechaniki
I Lista zadan Mechanika Plynow
Brojan,Mostowski,Wodkiewicz Zbiór Zadan z Mechaniki Kwantowej grayscale
Niziol Metodyka rozwiazywania zadan z mechaniki
J Nizioł Metodyka rozw zadań z mechaniki
Zbiór zadań z mechaniki budowli Metoda przemieszczeń i metoda elementów skończonych Tadeusz Chmiel
Sprawozdanie 81, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizy
wstep do zadan, BUDOWNICTWO polsl, sem IV, sem IV, Mechanika budowli, EGZ, egzam
MECHANIKA OGOLNA ZBIOR ZADAN
więcej podobnych podstron