´
Cwiczenie 5: Funkcja napr ¾
e·
ze´
n Airy’ego dla p÷
as-
kiego stanu napr ¾
e·
zenia (PN, PSN)
opracowa÷
a Ma÷
gorzata Stojek
Teoria dla metod odwrotnych w rozwi ¾
azywaniu PSN
metoda odwrotna
polega na:
1. za÷
o·
zeniu pewnej funkcji napr ¾
e·
ze´n lub wprost pewnego stanu napr ¾
e·
zenia
2. poszukiwaniu obci ¾
a·
ze´n wywo÷
uj ¾
acych ten stan
Zastosujemy j ¾
a do funkcji Airye’go, któr ¾
a zak÷
adamy w postaci wielomianu.
Mo·
zna te·
z wiele zagadnie´n rozwi ¾
aza´c za pomoc ¾
a funkcji napr ¾
e·
ze´n Airy’ego w
postaci wielomianów harmonicznych i biharmonicznych, ale zagadnienia
te wykraczaj ¾
a poza zakres czasowy naszych ´cwicze´n.
napr ¾
e·
zeniowe warunki brzegowe
wspó÷
rz ¾
edne tensora napr ¾
e·
zenia dla zadanej
funkcji Airy’ego F w przypadku braku si÷masowych s ¾
a równe
x
=
@
2
F
@y
2
;
y
=
@
2
F
@x
2
;
xy
=
@
2
F
@x@y
czyli tensor ma posta´c
T =
"
@
2
F
@y
2
@
2
F
@x@y
@
2
F
@x@y
@
2
F
@x
2
#
=
F
00
yy
F
00
xy
F
00
xy
F
00
xx
Wykorzystuj ¾
ac wzory (7.13) na wspó÷
rz ¾
edne normalnej i stycznej do konturu
n
x
n
y
=
cos '
sin '
otrzymujemy ogólne wzory na warunki brzegowe dla zadanych warto´sci obci ¾
a·
zenia
normalnego p
nn
p
nn
=
@
2
F
@x
2
(n
y
)
2
2
@
2
F
@x@y
n
y
n
x
+
@
2
F
@y
2
(n
x
)
2
(1)
i stycznego p
ns
p
ns
=
@
2
F
@x
2
@
2
F
@y
2
n
y
n
x
+
@
2
F
@x@y
(n
y
)
2
(n
x
)
2
(2)
do konturu obszaru. Mo·
zemy unikn ¾
a´c automatyzmu wzorów (1, 2) w przypadku
gdy kontur jest równoleg÷
y do osi uk÷
adu. Wówczas dla n = [n
x
; n
y
] ;
stosujemy
wprost wzory (7.28)
p
nx
p
ny
=
x
xy
xy
y
n
x
n
y
=
F
00
yy
F
00
xy
F
00
xy
F
00
xx
n
x
n
y
(3)
1
y
y
y
y
x
x
x
x
r
0
0
0
a
a
a
a
a
a
a
0
A
A
B
C
D
A
B
C
D
A
C
B
a)
b)
c)
d)
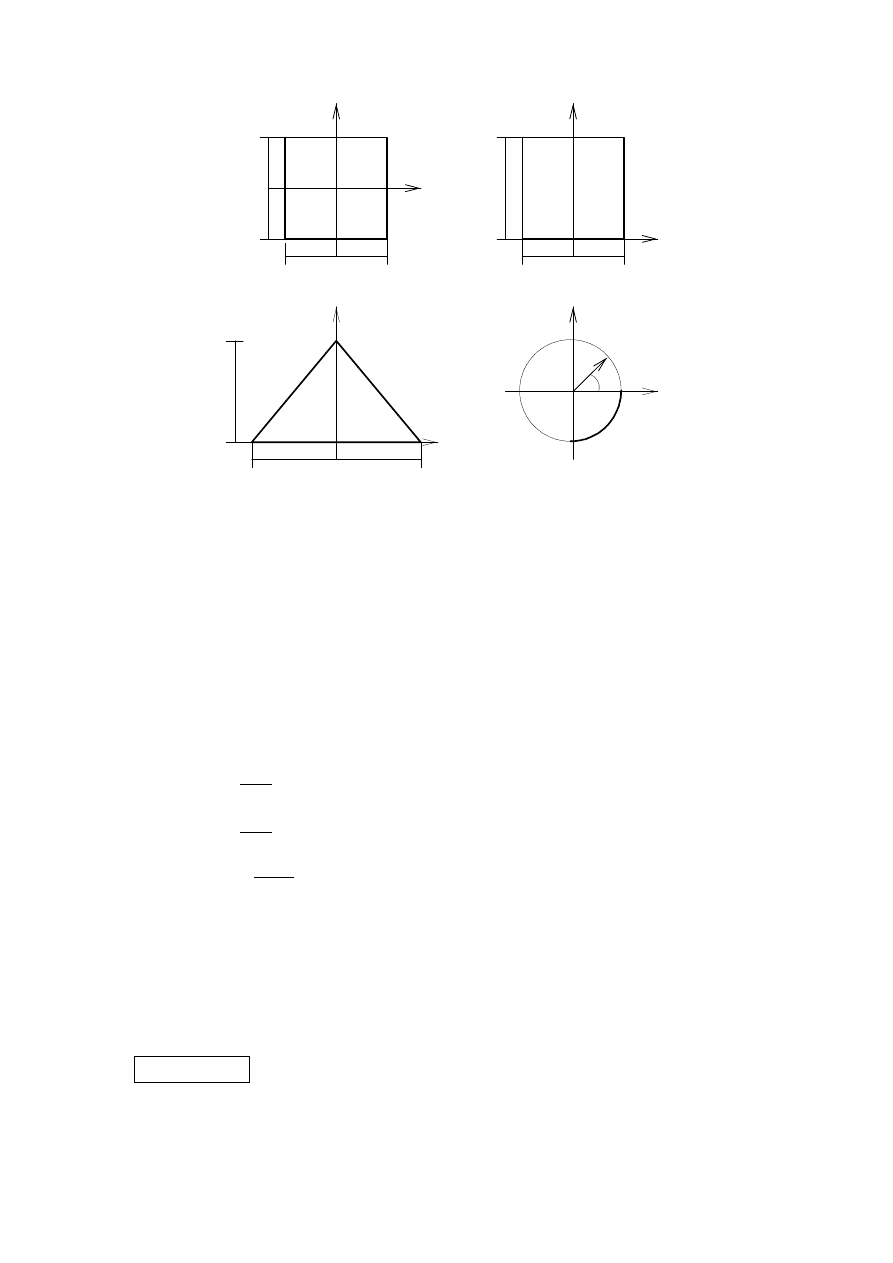
Figure 1: .
czyli
p
nx
p
ny
=
n
x
F
00
yy
n
y
F
00
xy
n
x
F
00
xy
+ n
y
F
00
xx
Przyk÷
ad 1
·
Zyczkowski–Krzy´s, strona 154
Jak nale·
zy obci ¾
a·
zy´c tarcze (Rys.1), aby biharmoniczna funkcja F (x; y) = A (x
3
+ y
2
x)
by÷
a dla nich funkcj ¾
a napr ¾
e·
ze´n Airy’ego?
Sk÷
adowe tensora napr ¾
e·
zenia wynosz ¾
a
x
=
@
2
F
@y
2
=
y
=
@
2
F
@x
2
=
xy
=
@
2
F
@x@y
=
czyli tensor ma posta´c
T =
(4)
ad a)
kraw ¾
ed´z AB Wektor normalnej zewn ¾
etrznej ma wspó÷
rz ¾
edne n = [
;
]
Wspó÷
rz ¾
edne wektora napr ¾
e·
zenia
na tym brzegu w uk÷
adzie global-
2

nym
wynosz ¾
a (3)
p
nx
p
ny
=
za´s po uwzgl ¾
ednieniu, ·
ze x =
a
2
mamy ostatecznie
p
nx
p
ny
=
kraw ¾
ed´z BC n = [
;
] ;
y =
a
2
p
nx
p
ny
=
kraw ¾
ed´z CD n = [
;
] ;
x =
a
2
p
nx
p
ny
=
kraw ¾
ed´z DA n = [
;
] ;
y =
a
2
p
nx
p
ny
=
Uwaga: Jak wida´c w tym przypadku nie ma potrzeby stosowania wzorów (1, 2).
Zwró´cmy uwag ¾
e, ·
ze na kraw¾
edziach równoleg÷
ych do osi y zachodzi
k p
nn
;
k p
ns
;
natomiast na kraw¾
edziach równoleg÷
ych do osi x
k p
ns
;
k p
nn
;
Znak
p
nn
; p
ns
jest okre´slony przez osie uk÷
adu w÷
asnego
, utworzonego przez
wektory normalnej zewn ¾
etrznej i stycznej do konturu. Kierunek stycznej jest taki,
·
ze przemieszczaj ¾
ac si ¾
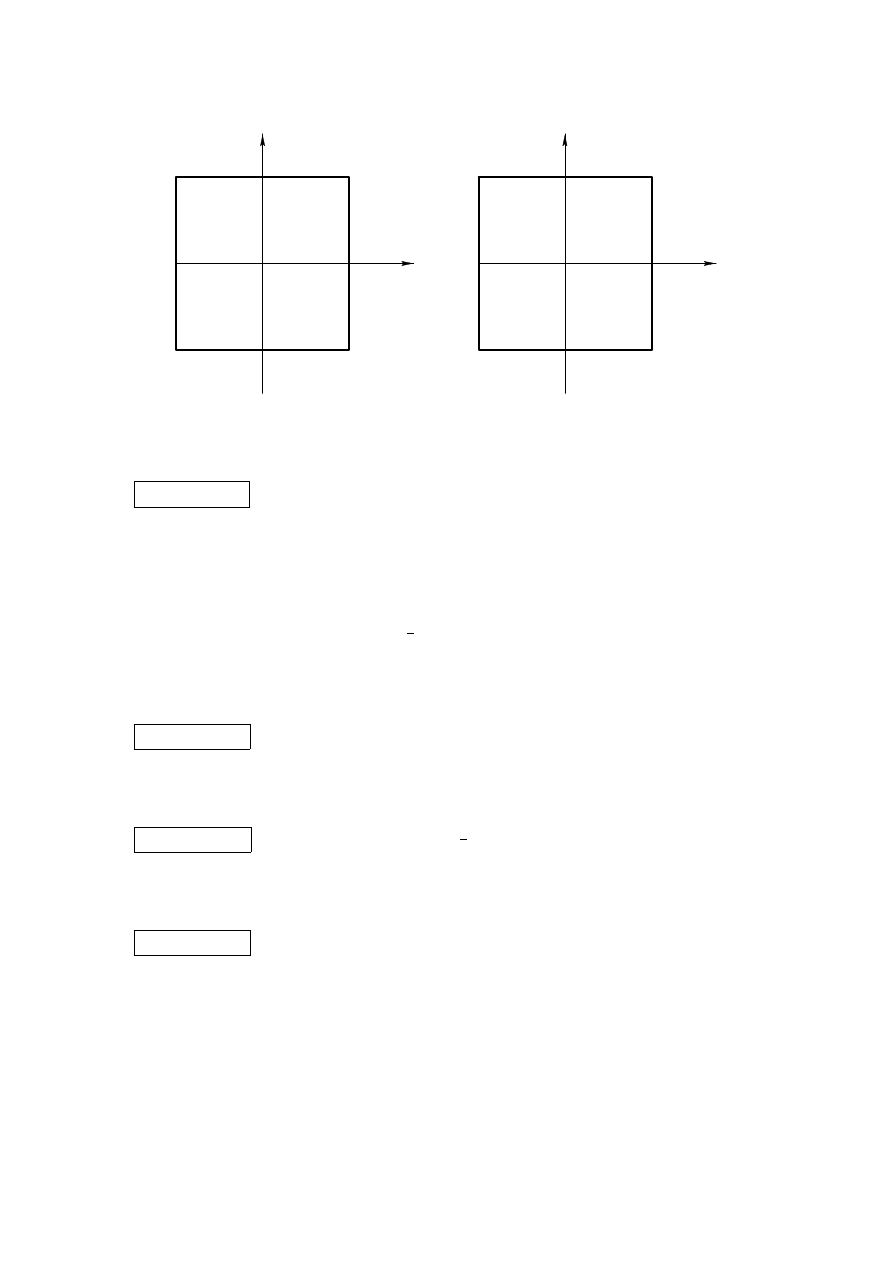
e w tym kierunku obszar mamy po lewej stronie. Rysunek
2 przedstawia gra…czn ¾
a interpretacj ¾
e powy·
zszych wyników i rzeczywiste wektory
obci ¾
a·
zenia normalnego i stycznego do kolejnych fragmentów konturu.
ad b)
Tym razem skorzystamy z gotowych wzorów (1, 2), które dla naszego
tensora (4)
T =
F
00
yy
F
00
xy
F
00
xy
F
00
xx
=
przyjmuj ¾
a posta´c
p
nn
= (
) n
2
y
2 (
) (n
y
) (n
x
) + (
) n
2
x
p
ns
= (
) (n
y
) (n
x
) + (
) n
2
y
n
2
x
3
y
y
x
x
(a)
(b)
p
p
nn
ns
Figure 2: .
kraw ¾
ed´z AB Wektor normalnej zewn ¾
etrznej ma wspó÷
rz ¾
edne n = [
;
] :
Wspó÷
rz ¾
edne wektora napr ¾
e·
zenia
na tym brzegu w uk÷
adzie lokalnym
wynosz ¾
a
p
nn
=
p
ns
=
za´s po uwzgl ¾
ednieniu, ·
ze x =
a
2
mamy ostatecznie
p
nn
=
p
ns
=
kraw ¾
ed´z BC n = [
;
] ;
y = a
p
nn
=
p
ns
=
kraw ¾
ed´z CD n = [
;
] ;
x =
a
2
p
nn
=
p
ns
=
kraw ¾
ed´z DA n = [
;
] ;
y = 0
p
nn
=
p
ns
=
Uwaga: Porównanie wyników dla kraw¾
edzi CD wykazuje, ·
ze
p
nn
= (
) p
nx
p
ns
= (
) p
ny
4
y
y
(a)
(b)
p
p
nn
ns
x
x
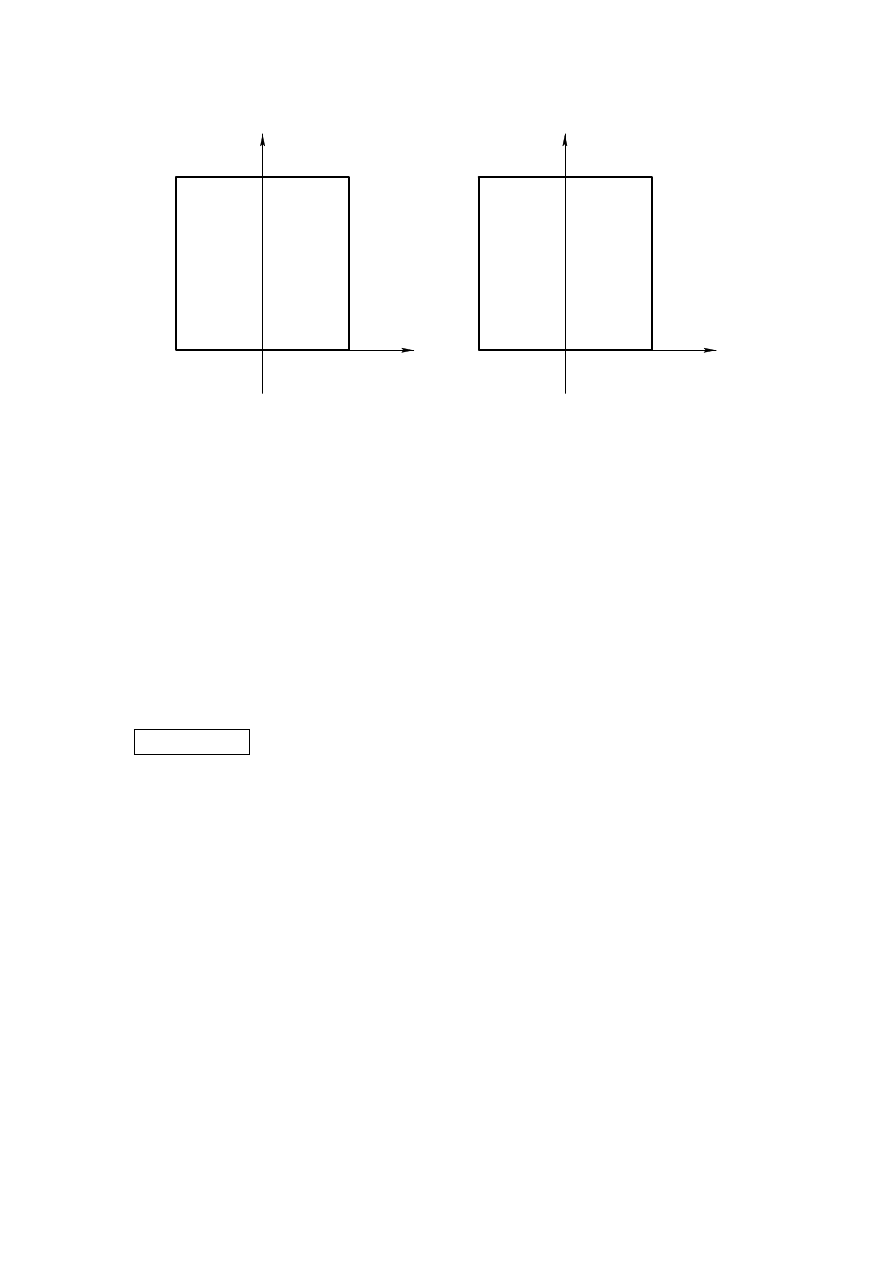
Figure 3: .
Jest to oczywisty wynik je·
zeli zauwa·
zymy, ·
ze lokalny uk÷
ad wspó÷
rz ¾
ednych zwi ¾
azany
z t ¾
a kraw¾
edzi ¾
a jest w stosunku do uk÷
adu globalnego obrócony o : Gra…czna in-
terpretacja rezultatów jest podana na rysunku 3.
ad c)
W tym przypadku skorzystamy od razu ze wzorów (1, 2), gdy·
z nor-
malne do kraw¾
edzi AB i BC nie s ¾
a równoleg÷
e do osi globalnego uk÷
adu wspó÷
rz ¾
ed-
nych.
p
nn
= (
) n
2
y
2 (
) (n
y
) (n
x
) + (
) n
2
x
p
ns
= (
) (n
y
) (n
x
) + (
) n
2
y
n
2
x
kraw ¾
ed´z AB Wektor normalnej zewn ¾
etrznej ma wspó÷
rz ¾
edne n = [
;
] :
Wspó÷
rz ¾
edne wektora napr ¾
e·
zenia
na tym brzegu w uk÷
adzie lokalnym
wynosz ¾
a
p
nn
=
p
ns
=
warto´sci w punktach
A(a; 0)
p
nn
=
p
ns
=
B(0; a)
p
nn
=
p
ns
=
5

p
nn
= 0
dla punktu D, w którym zachodzi
(
)
czyli y = (
) ;
sk ¾
ad po uwzgl ¾
ednieniu równania kraw¾
edzi
y = (
)
otrzymujemy
(
)
sk ¾
ad mamy D(
;
)
kraw ¾
ed´z BC n = [
;
]
p
nn
=
p
ns
=
warto´sci w punktach
B(0; a)
p
nn
=
p
ns
=
C( a; 0)
p
nn
=
p
ns
=
p
nn
= 0
dla punktu E, w którym zachodzi
(
)
czyli y = (
) ;
sk ¾
ad po uwzgl ¾
ednieniu równania kraw¾
edzi
y = (
)
otrzymujemy
(
)
sk ¾
ad mamy E(
;
)
kraw ¾
ed´z CA n = [
;
] ;
y = 0
p
nn
=
p
ns
=
czyli
p
ns
=
p
nn
(C) =
p
nn
(A) =
Gra…czna reprezentacja wyników jest przedstawiona na rysunku 4
6
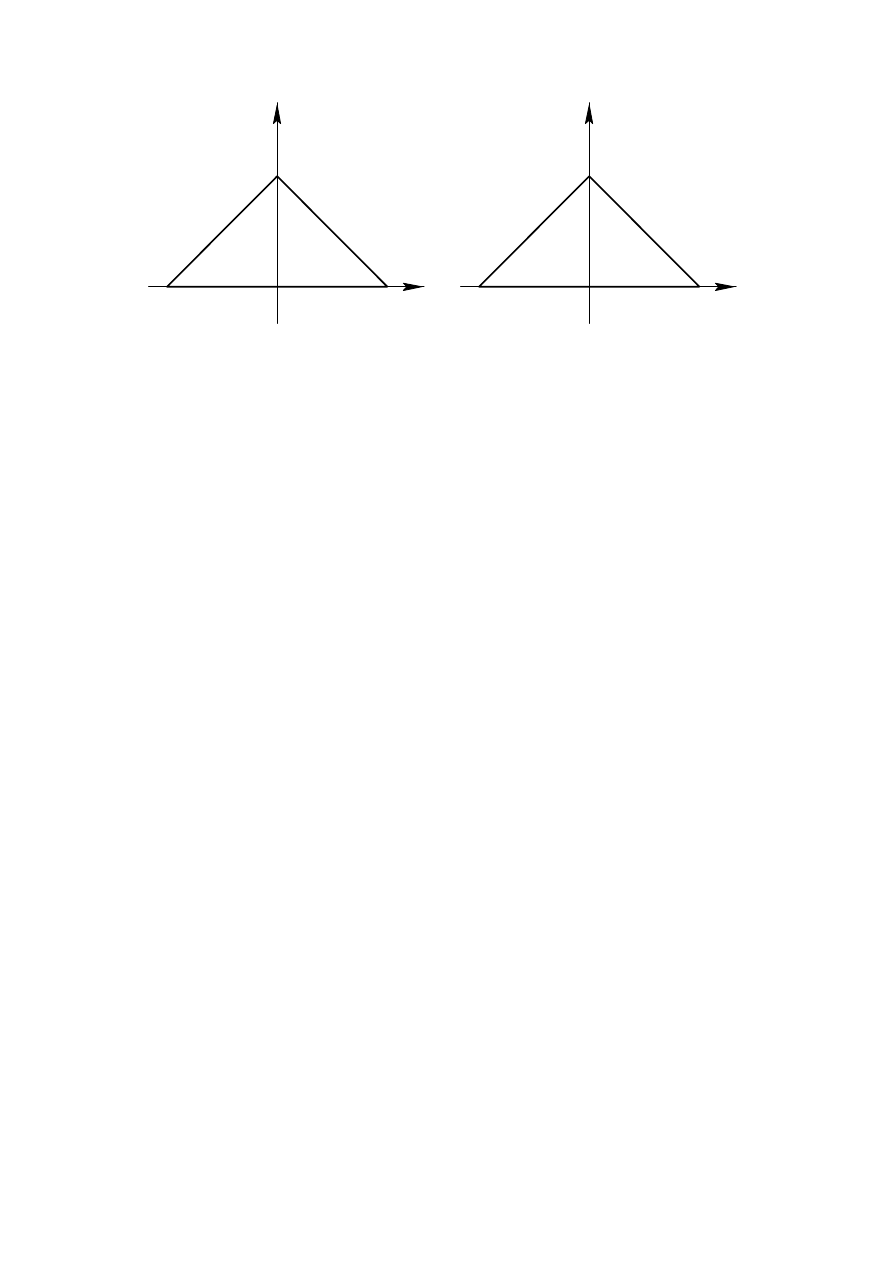
y
y
x
x
Figure 4: .
ad d)
W tym przypadku znowu skorzystamy od razu ze wzorów (1, 2),
p
nn
= (
) n
2
y
2 (
) (n
y
) (n
x
) + (
) n
2
x
(5)
p
ns
= (
) (n
y
) (n
x
) + (
) n
2
y
n
2
x
gdy·
z wspó÷
rz ¾
edne jednostkowego wektora normalnego do konturu i skierowanego
na zewn ¾
atrz obszaru, zmieniaj ¾
a si ¾
e wraz z punktem na konturze. Dla dowol-
nego punktu B(x; y) le·
z ¾
acego na okr ¾
egu o promieniu r; wprowadzamy wspó÷
rz ¾
edne
biegunowe (r; ') i otrzymujemy
n
= [
;
]
x =
y =
Wstawiaj ¾
ac te warto´sci do (5) otrzymujemy
p
nn
=
p
ns
=
Podsumowanie wyników
7

wspó÷
rz ¾
edne wektora w uk÷
adzie lokalnym zwi ¾
azanym z normaln ¾
a i styczn ¾
a
do zorientowanego konturu
p
nn
=
p
ns
=
d÷
ugo´s´c wektora jp
n
j
jp
n
j =
p
p
2
nn
+ p
2
ns
=
k ¾
at
mi ¾
edzy wektorem p
n
[p
nn
; p
ns
]
a normaln ¾
a do konturu n [1; 0]
cos
=
p
n
n
p
n
=
sk ¾
ad
=
Rysunek 5 przedstawia wektory napr ¾
e·
zenia p
n
dla wielokrotno´sci =4
' = k =4;
k = 0; 1; : : : ; 7
8
Wyszukiwarka
Podobne podstrony:
Ćwiczenie 3 Funkcje agregujące
cwiczenia funkcji percepcyjno-motorycznych
funkcjonowanie cwiczenia3, Funkcjonowanie Unii Europejskiej FUE
05 Analiza plaskiego stanu naprezenia
Zestaw ćwiczeń doskonalących umiejętności techniczne z koszykówki dla uczniów szkół podstawowych i g
Funkcjonowanie nerek i ich znaczenie dla ustroju, Medyczne, Studia pielęgniarstwo, Fizjologia
cwiczenia4 funkcje id 124969 Nieznany
Ćwiczenia pobudzające twórcze myślenie, Zabawy dla przedszkolaków
zestawy cwiczen logopedycznych, Szkoła- Porady pedagog, dla rodziców
04 Elementy plaskiego stanu naprezen i odksztalcen
cwiczenia wiek i tempo wzrostu wyslac dla v roku ochrony tryb zgodnosci
Analiza plaskiego stanu napreze Nieznany
więcej podobnych podstron