POGRUBIONYMI LITERAMI ZAZNACZAM TO CO MUSI ZNALEŚĆ SIĘ W
PRACY.
Zadanie 1.
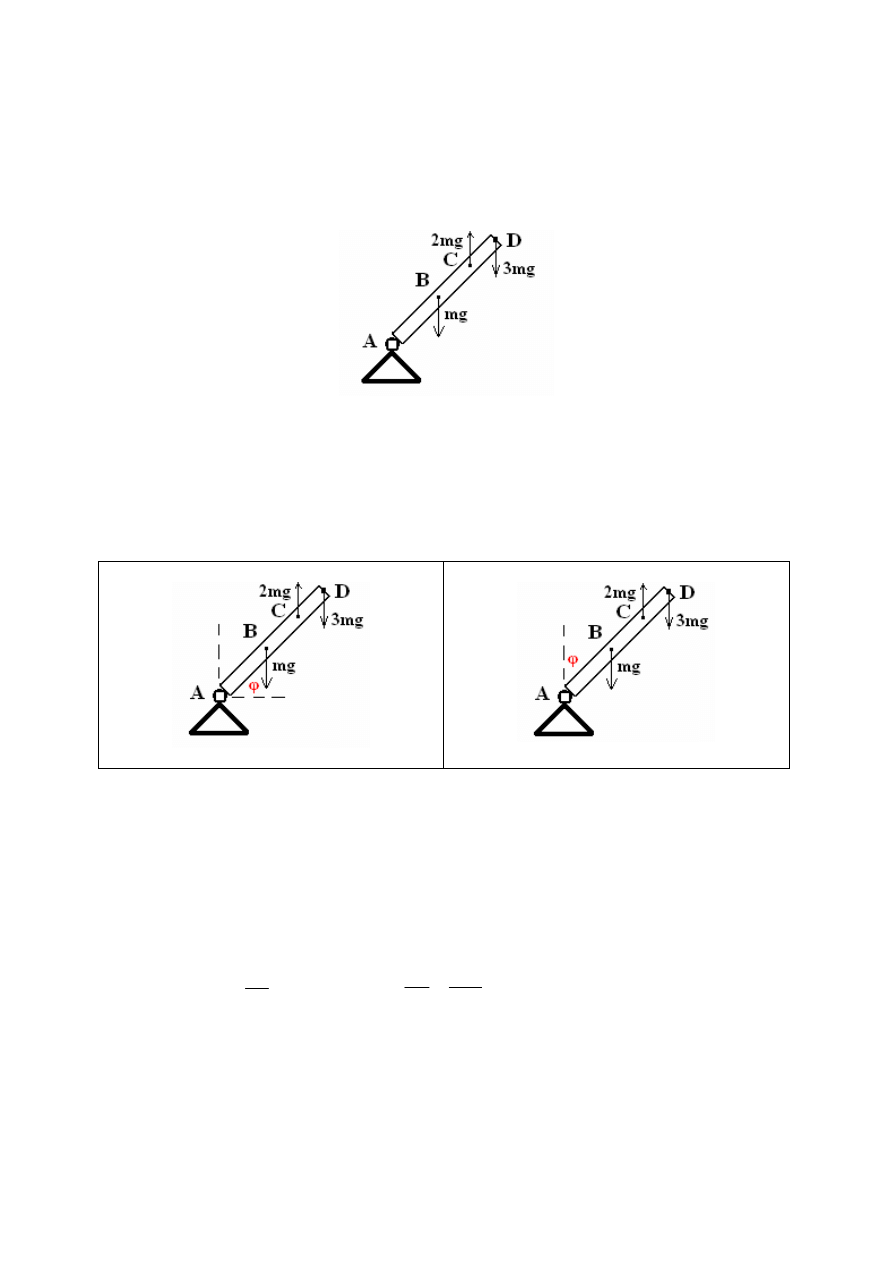
Oblicz przyspieszenie normalne i styczne w punkcie D belki o masie m jak na rysunku:
WARTOŚCI 2·mg i 3·mg są wymyślone dla przykładu,
SIŁA mg jest zawieszona w środku bełki tzn: punkt B jest dokładnie w połowie belki.
W jego zadaniach jeśli nie narysuje siły w środku belki o wartości: mg, należy tą siłę
naryswować samemu.
(jeszcze tego nie zrobił, ale gdyby zmienił, że belka ma mase inną niż m, np. 2m to
wtedy ta siła w punkcie B wynosiłaby 2mg).
Są dwie możliwości umieszczenia kąta φ:
1)
COS φ
2)
SIN φ
Rozwiązywanie tego zadania zaczynam od napisania obu wzorów:
Przyspieszenie styczne:
a
τ
= ω
2
· R
Przyspieszenie normalne: a
N
= ε · R
Dla niekumatych:
ϕ
ω
&
=
ϕ
ε
&&
=
Dla jeszcze bardziej niekumatych:
dt
d
ϕ
ϕ
=
&
2
2
dt
d
dt
d
ϕ
ω
ϕ
=
=
&&
Następnie piszemy:
Dynamiczne równanie ruchu obrotowego:
∑
=
A
A
M
I
ϕ
&&
I liczymy powyższe:
=
ϕ
&&
A
I
SUMA MOMENTÓW WZGLĘDEM PUNKTU A:
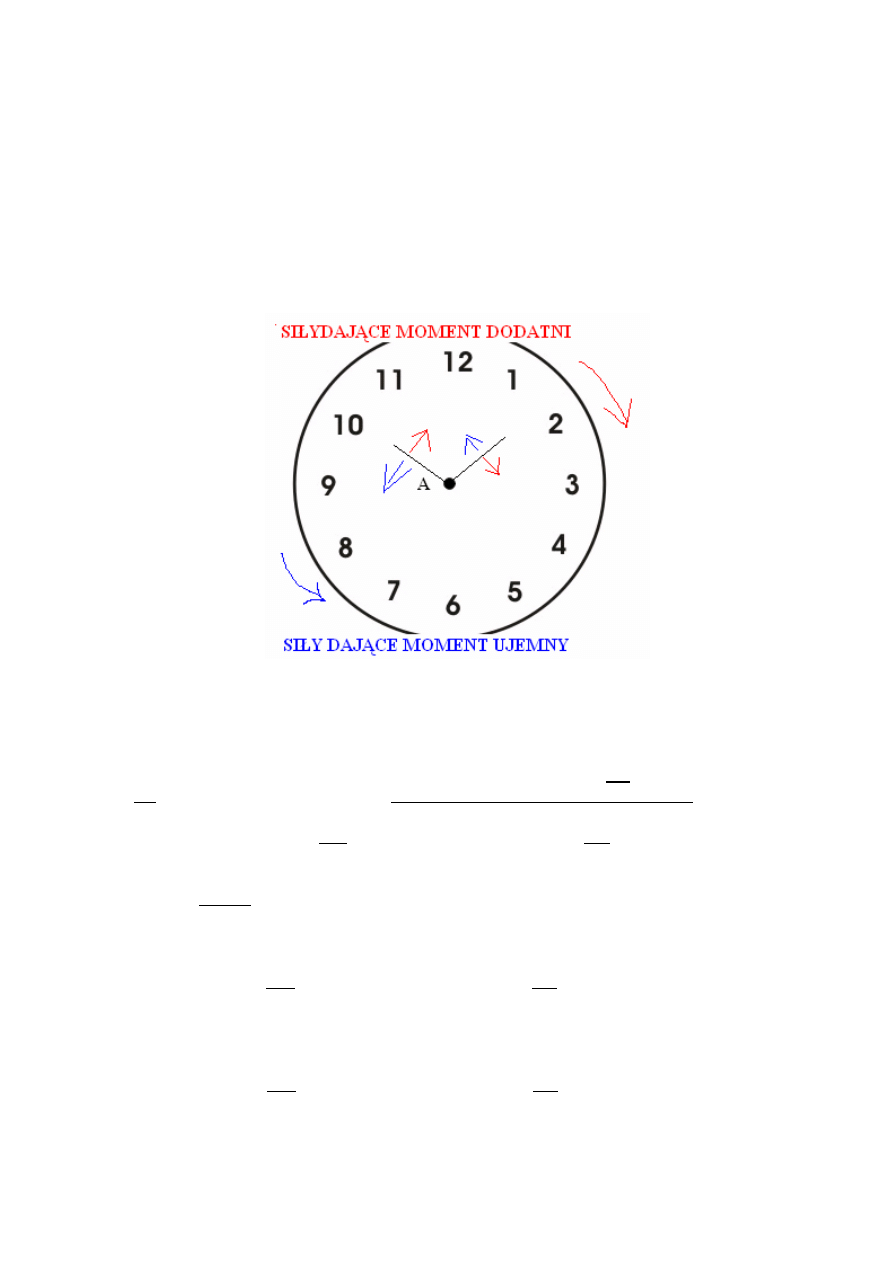
- Wszytkie siły w powyższym zadaniu i wszystkich, które on do tej pory dawał tworzą momenty
względem punktu A (punkt A to jest JEDYNY punkt, który w każdym tego typu zadaniu od
niego jest ten sam!)
- Czyli po kolei:
Siły skierowane w taki sposób, że pokazują kierunek ruchu wskazówek od zegara, dają
moment dodatni, skierowane odwrotnie dają moment ujemny:
Dla
niekumatych:
Moment pochodzący od siły z punktu B:
- jest dodatni ponieważ siła jest skierowana zgodnie z ruchem wskazówek zegara.
- ma wartość równą odległości punktu B od punktu A, czyli odległości AB (zazwyczaj
daje ją w TREŚCI zadania, jeśli nie to przypominam, ze punkt B jest w środku belki!)
pomnożoną przez siłę prostopadłą do belki (czyli siłę z punktu B: mg·cos(φ) w przypadku 1),
mg·sin(φ) w przypadku 2). Kto nie zna trygonometri niech to wykuje na pamięć.
- czyli moment pochodzący od siły z punktu B ma wartość:
1)
AB· mg·cos(φ)
lub
2)
AB· mg·sin(φ)
Moment pochodzący od sily z punktu C:
- jest ujemny ponieważ siła jest skierowana przeciwnie do ruchu wskazówek zegara!
( poza tym to, że ta siła jest skierowana do góry nie ma wpływu na dalszy sposób
rozwiązywania zadania!)
- wynosi:
1)
AC· mg·cos(φ)
lub
2)
AC· mg·sin(φ)
Moment pochodzący od sily z punktu D:
- jest dodatni ponieważ siła jest skierowana zgodnie z ruchem wskazówek zegara.
- wynosi:
1)
AD· mg·cos(φ)
lub
2)
AD· mg·sin(φ)
JEŚLI SIŁ JEST WIĘCEJ, MOMENTY TWORZYMY ANALOGICZNIE
Podsumowując:
Dla przypadku 1)
ϕ
ϕ
ϕ
ϕ
cos
3
cos
2
cos
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
mg
AD
mg
AC
mg
AB
I
A
&&
Dla przypadku 2)
ϕ
ϕ
ϕ
ϕ
sin
3
sin
2
sin
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
mg
AD
mg
AC
mg
AB
I
A
&&
Następnie rozwiązujemy:
)
3
2
(
sin
AD
AC
AB
mg
I
A
+
+
⋅
=
ϕ
ϕ
&&
Przypominam, że wartości 2, 3, i nazwy odcinków mogą się zmienić i są takie tylko dla tego
przypadku!
__________________________________________________________________________
Następnie obliczamy I
A
– gdyby ktoś nie wiedziałe jest to geometryczny moment
bezwładoności.
Zaczynamy od liczenia momentu bezwładności w środku belki, w celu podstawienia później
do Twierdzenia Steinera.
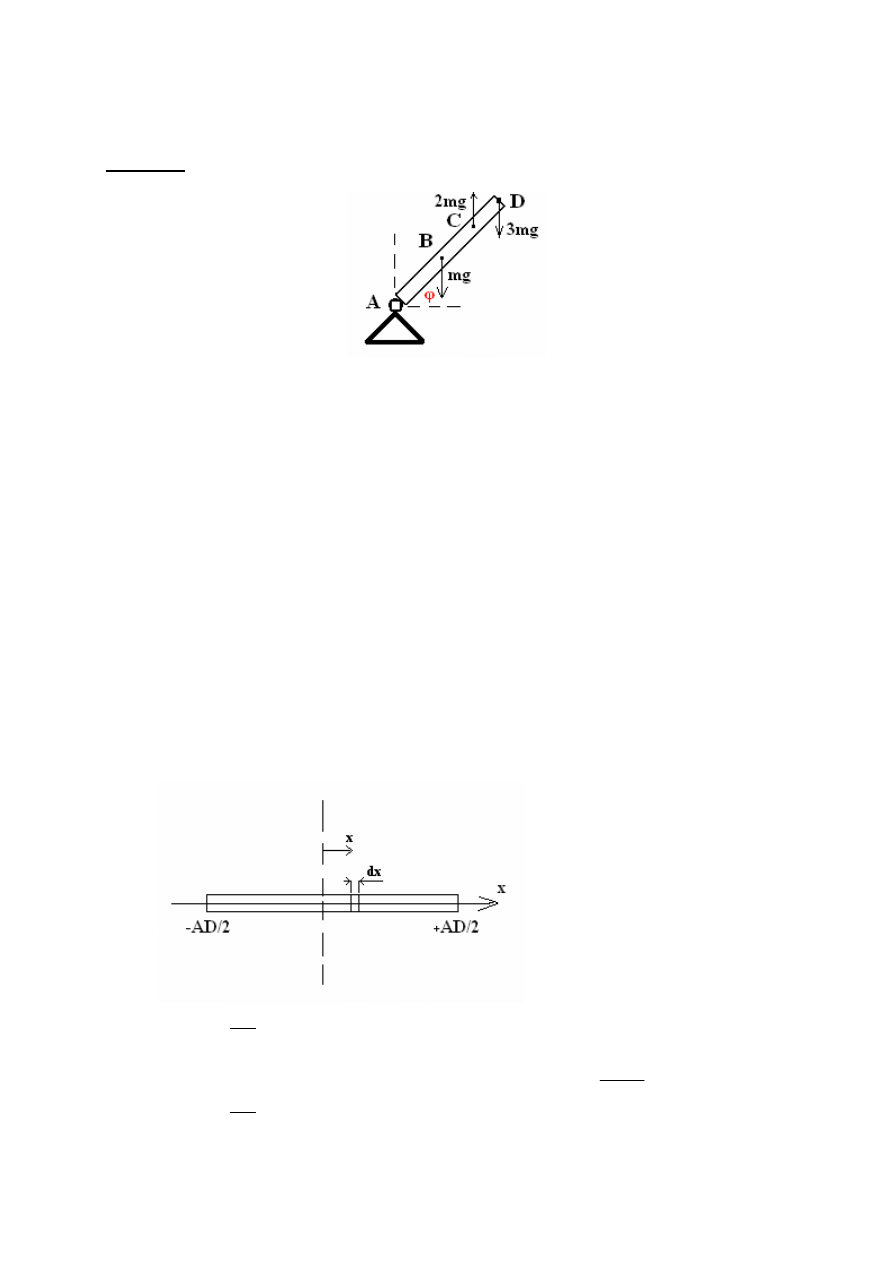
W granicach całkowania ustawiamy następująco:
Dolna
minus połowa długości belki
w powyższym przykładzie: -AD/2
Górna
plus połowa długości belki
w powyższym przykładzie: +AD/2
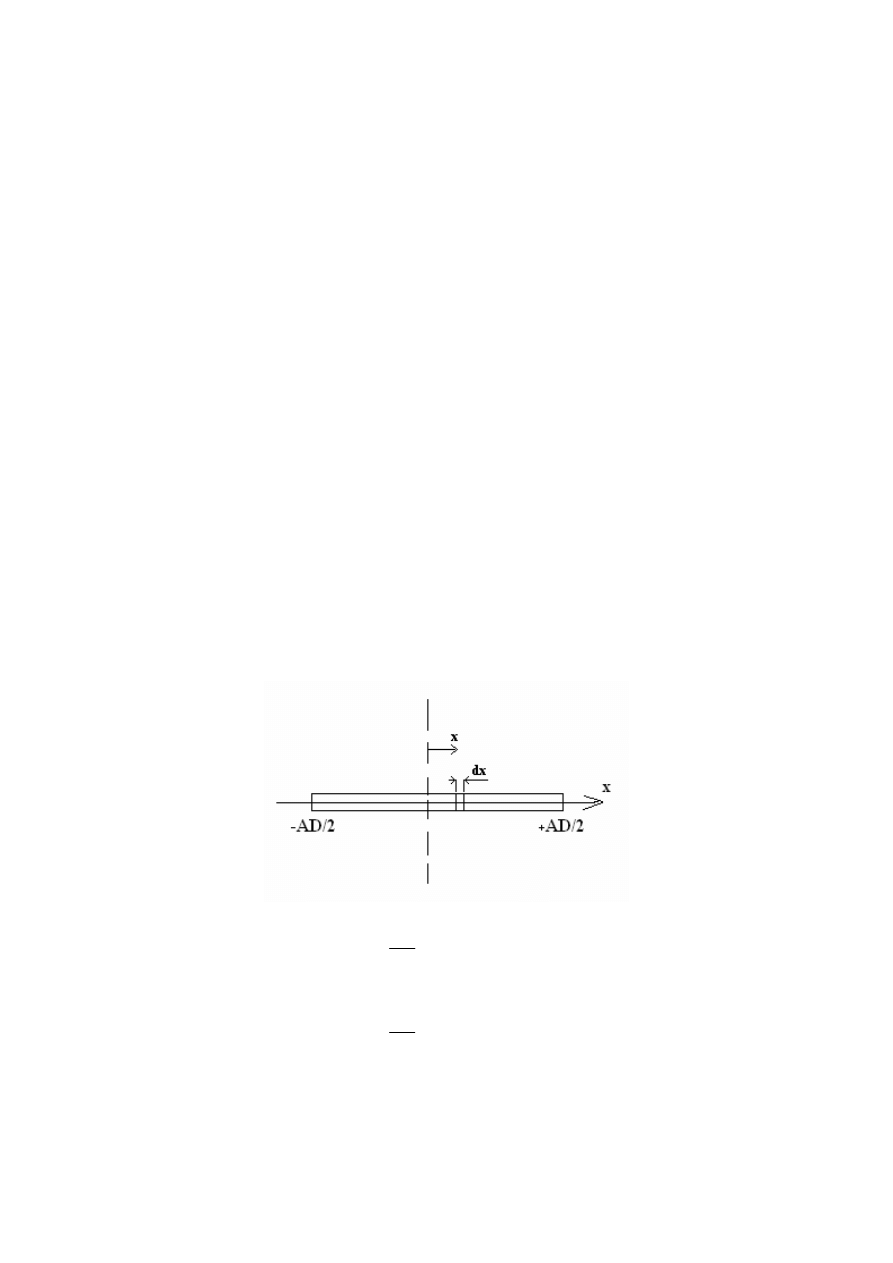
Rysujemy rysunek:
Następnie piszemy:
∫
+
−
=
2
2
2
AD
AD
B
dm
x
I
dm – jest to masa nieskończenie małej części belki:
a po ludzku: dm = gęstość_belki · dx
gęstość belki jest równa stosunkowi masy belki przez długość belki, czyli dla naszego
przykładu: m/AD
i to już piszemy:
dx
AD
m
dm
=
i
podstawiamy:
∫
+
−
=
=
2
2
2
...
AD
AD
B
dx
AD
m
x
I
Ponieważ
AD
m
jest wartością stałą wyciągamy ją przed znak całki:
...
...
2
2
2
=
=
∫
+
−
AD
AD
dx
x
AD
m
No tutaj jest zwykły całkowanie, czyli:
dla
przypomnienia
( )
(
)
3
3
3
2
3
1
3
1
a
b
x
dx
x
b
a
b
a
−
=
=
∫
( )
...
2
2
3
1
3
1
...
3
2
2
3
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
⋅
=
⋅
=
+
−
AD
AD
m
x
AD
m
AD
AD
Po skróceniu(matmy z gimnazjum nie będę tłumaczył)
2
12
1
AD
m
I
B
⋅
=
Następnie piszemy:
Z TWIERDZENIA STEINERA:
2
AB
m
I
I
B
A
⋅
+
=
2
2
12
1
AB
m
AD
m
I
A
⋅
+
⋅
=
Ta liczba po podstawieniu jego danych wygklądać powinna mniej-więcej tak:
2
l
m
ulamek
I
A
⋅
⋅
=
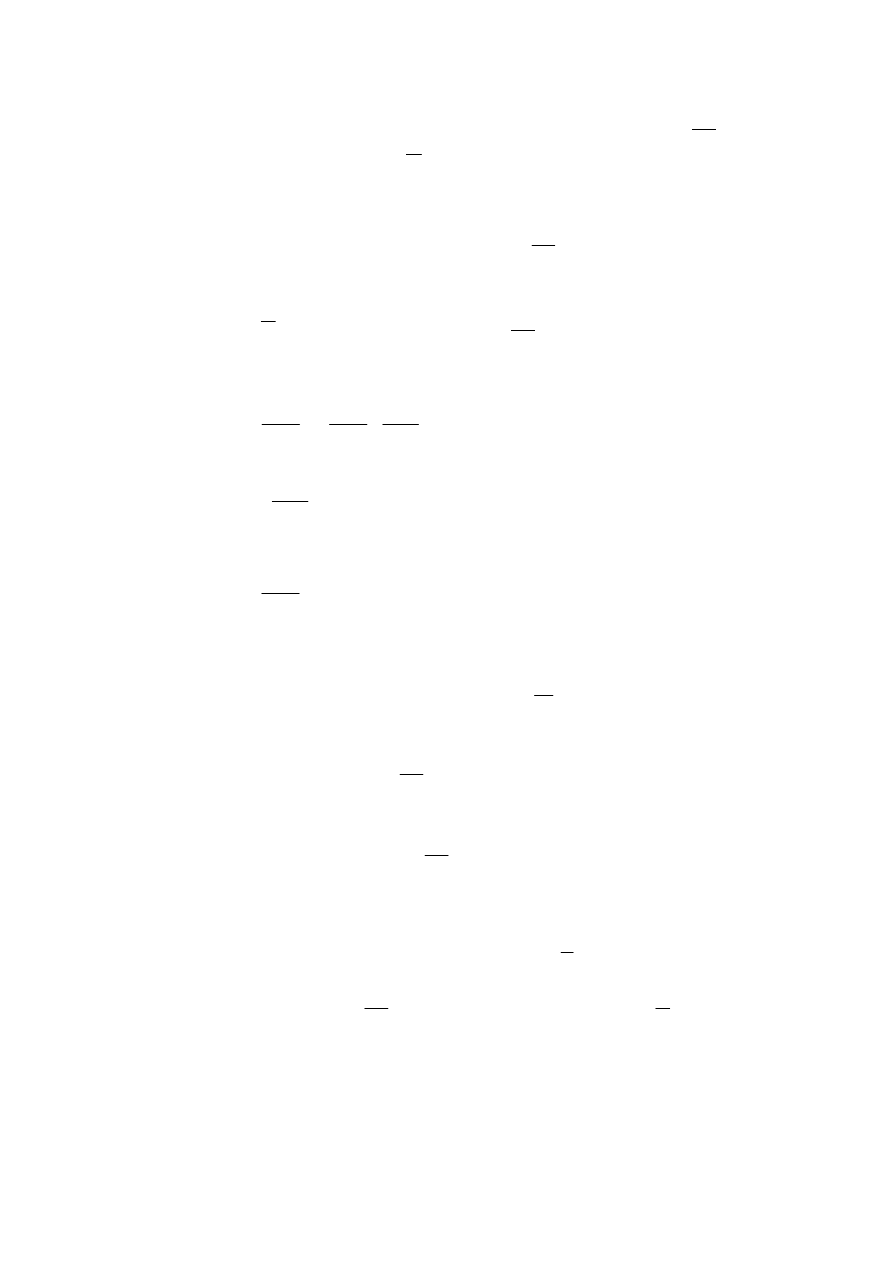
Ponieważ już mamy:
)
3
2
(
sin
AD
AC
AB
mg
I
A
+
+
⋅
=
ϕ
ϕ
&&
(lub cosφ)
Oraz:
2
2
12
1
AB
m
AD
m
I
A
⋅
+
⋅
=
Wyliczamy:
)
12
1
/(
)
3
2
(
sin
2
2
AB
m
AD
m
AD
AC
AB
mg
⋅
+
⋅
+
+
⋅
=
ϕ
ϕ
&&
Co po podstawieniu jego danych powinno wyglądać mniej-więcej tak:
ϕ
ϕ
sin
⋅
⋅
=
l
g
ulamek
&&
(lub cosφ)
Następnie piszemy coś takiego, (piszczie, jak nie rozumiecie od razu, nie pytajcie czemu):
dt
d
d
d
dt
d
ϕ
ϕ
ω
ω
ϕ
⋅
=
=
&&
Gdzie:
ω
ϕ
=
dt
d
Z
czego
wynika
że:
ω
ϕ
ω
ϕ
⋅
=
d
d
&&
ω
ω
ϕ
ϕ
d
d
⋅
=
⋅
&&
Teraz podstawiamy za
)
12
1
/(
)
3
2
(
sin
2
2
AB
m
AD
m
AD
AC
AB
mg
⋅
+
⋅
+
+
⋅
=
ϕ
ϕ
&&
, czyli:
(pomijam już przypadek z cos
ϕ , robi się analogicznie)
ω
ω
ϕ
ϕ
d
d
AB
m
AD
m
AD
AC
AB
mg
⋅
=
⋅
⋅
+
⋅
+
+
⋅
)]
12
1
/(
)
3
2
(
sin
[
2
2
Obustronnie całkujemy:
∫
∫
⋅
=
⋅
⋅
+
⋅
+
+
⋅
ω
ω
ϕ
ϕ
d
d
AB
m
AD
m
AD
AC
AB
mg
)]
12
1
/(
)
3
2
(
sin
[
2
2
I otrzymujemy:
Przypominam:
ϕ
ϕ
ϕ
cos
sin
−
=
⋅
∫
d
ϕ
ϕ
ϕ
sin
cos
=
⋅
∫
d
2
2
1
ω
ω
ω
=
⋅
∫
d
C
AB
m
AD
m
AD
AC
AB
mg
+
=
⋅
⋅
+
⋅
+
+
−
2
2
2
2
1
cos
)]
12
1
/(
)
3
2
(
[
ω
ϕ

I liczymy stałą C (zawsze tak samo):
Dla φ = 0, ω = 0:
Podstawiamy i wychodzi:
Przypominam: cos(0) = 1; sin(0) = 0;
cos(0) = 1
)]
12
1
/(
)
3
2
(
[
2
2
AB
m
AD
m
AD
AC
AB
mg
C
⋅
+
⋅
+
+
−
=
Dla drugiego przypadku C = 0!
Obliczamy ω
2
:
)
1
(cos
)]
12
1
/(
)
3
2
(
[
2
2
2
2
+
⋅
⋅
+
⋅
+
+
⋅
−
=
ϕ
ω
AB
m
AD
m
AD
AC
AB
mg
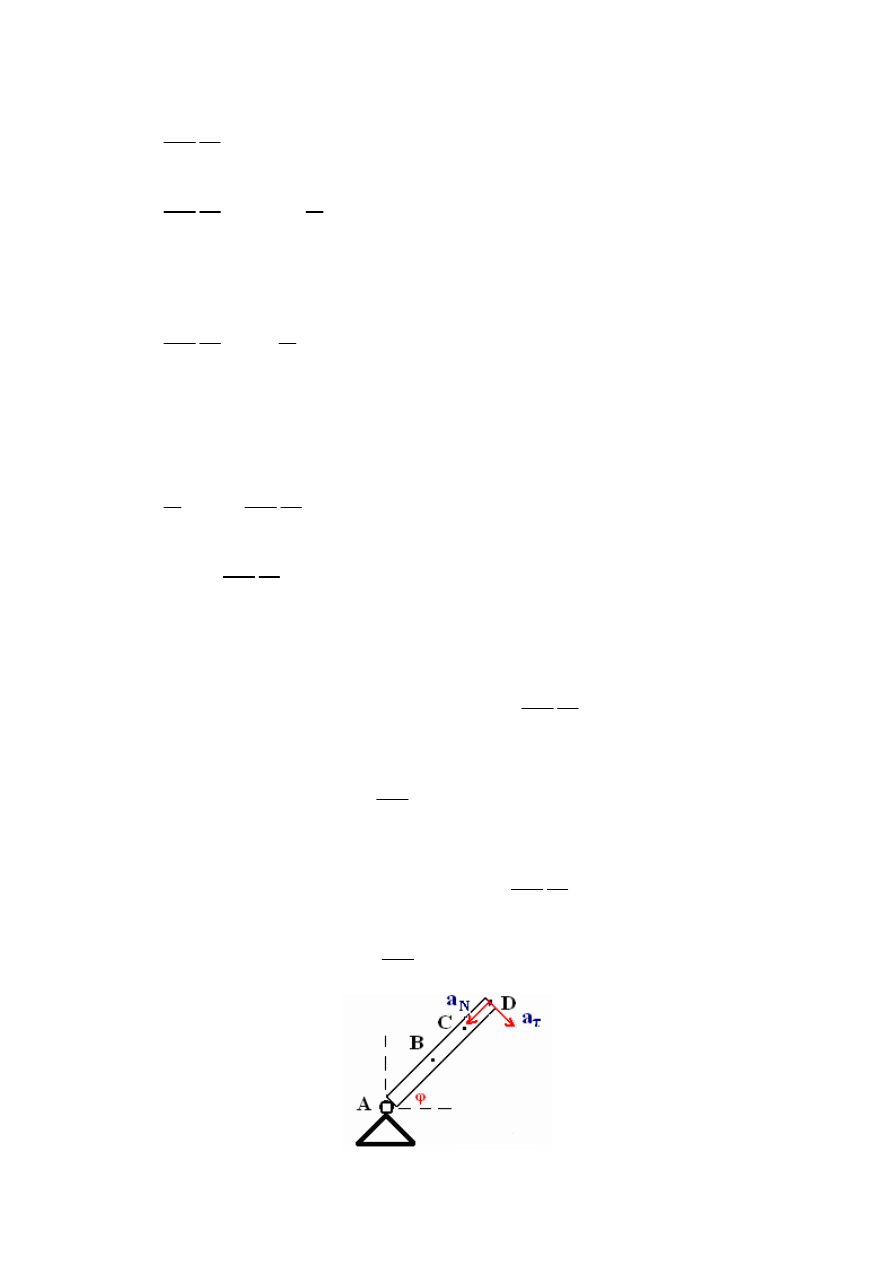
Została już tylko jedna rzecz podstawić do wzorów, które napisaliśmy jako pierwsze
R w tym wzorze jest to odległość między punktem A, a punktem w którym mamy obliczyć
przyspieszenie:
„Oblicz przyspieszenie normalne i styczne
w punkcie D
belki o masie m jak na rysunku:”
Zatem R = A
D
Przyspieszenie styczne:
a
τ
=
AD
AB
m
AD
m
AD
AC
AB
mg
⋅
+
⋅
⋅
+
⋅
+
+
⋅
−
)
1
(cos
)]
12
1
/(
)
3
2
(
[
2
2
2
ϕ
Przyspieszenie normalne:
a
N
= ε · R =
)
12
1
/(
)
3
2
(
sin
2
2
AB
m
AD
m
AD
AC
AB
mg
AD
⋅
+
⋅
+
+
⋅
⋅
ϕ
ZAPAMIĘTAJCIE JESZCZE JEDNO, JEŚLI W JEDNYM PRZYSPIESZENIU JEST
COSINUS TO W DRUGIM MUSI BYĆ SINUS!
ODPOWIEDŹ ZAWSZE JEST POSTACI:
ułamek * g * sin()/cos(),
Ułamek rozumiem jako liczbę wymierną.
CZYSTE ROZWIĄZANE DLA DWÓCH PRZYPADKÓW ZADAŃ
(Z RÓŻNIE UMIESZCZONYM KĄTEM
φ
)
Zadanie 1.
Oblicz przyspieszenie normalne i styczne w punkcie D belki o masie m jak na rysunku:
Dane:
AD = 4L
AC = 5/2L= 2.5L
Wartości sił zgodnie z rysunkiem.
AB = 2L
Rozwiązanie
Przyspieszenie styczne:
a
τ
= ω
2
· R
Przyspieszenie normalne: a
N
= ε · R
ϕ
ε
&&
=
Dynamiczne równanie ruchu obrotowego:
∑
=
A
A
M
I
ϕ
&&
=
⋅
⋅
⋅
+
⋅
⋅
⋅
−
⋅
⋅
=
ϕ
ϕ
ϕ
ϕ
cos
3
cos
2
cos
mg
AD
mg
AC
mg
AB
I
A
&&
=
⋅
⋅
⋅
+
⋅
⋅
⋅
−
⋅
⋅
=
ϕ
ϕ
ϕ
cos
3
4
cos
2
5
.
2
cos
2
mg
L
mg
L
mg
L
ϕ
ϕ
cos
9
)
3
4
2
5
.
2
2
(
cos
⋅
⋅
⋅
=
⋅
+
⋅
−
⋅
⋅
=
mg
L
mg
L
Moment bezwładności belki dla osi obortu prostopadłej do belki, przechodzącej
przez punkt B.
∫
+
−
=
2
2
2
AD
AD
B
dm
x
I
dx
AD
m
dm
=

...
4
4
2
2
2
2
2
2
∫
∫
+
−
+
−
=
=
=
L
L
L
L
B
dx
x
L
m
dx
L
m
x
I
( )
( )
3
2
2
3
2
2
3
1
4
3
1
4
...
L
L
m
x
L
m
L
L
⋅
⋅
⋅
=
⋅
=
+
−
2
3
4
L
m
I
B
⋅
=
Z TWIERDZENIA STEINERA:
2
AB
m
I
I
B
A
⋅
+
=
2
2
2
3
16
)
2
(
3
4
L
m
L
m
L
m
I
A
⋅
=
⋅
+
⋅
=
ϕ
ϕ
ϕ
cos
16
27
3
16
cos
9
2
L
g
L
m
g
m
L
=
⋅
/
⋅
/
⋅
/
⋅
=
/
&&
dt
d
d
d
dt
d
ϕ
ϕ
ω
ω
ϕ
⋅
=
=
&&
Gdzie:
ω
ϕ
=
dt
d
Z czego wynika że:
ω
ϕ
ω
ϕ
⋅
=
d
d
&&
ω
ω
ϕ
ϕ
d
d
⋅
=
⋅
&&
ω
ω
ϕ
ϕ
d
d
L
g
⋅
=
⋅
cos
16
27
Całkujemy obustronnie:
∫
∫
⋅
=
⋅
ω
ω
ϕ
ϕ
d
d
L
g
cos
16
27
∫
∫
⋅
=
⋅
ω
ω
ϕ
ϕ
d
d
L
g
cos
16
27
C
L
g
+
=
2
2
1
sin
16
27
ω
ϕ
Obliczamy stałą całkowania, podstawiając wartości φ oraz ω dla belki ustawionej
pionowo:
φ = 0, ω = 0:
C
L
g
+
⋅
=
⋅
0
2
1
0
16
27
0
=
C
Zatem:
ϕ
ω
sin
16
27
2
1
2
L
g
=
ϕ
ω
sin
8
27
2
L
g
=
Odpowiedź:
R = AD = 4L
Przyspieszenie styczne:
=
⋅
=
⋅
=
2
L
L
g
R
4
sin
8
27
a
ϕ
ω
τ
ϕ
τ
sin
2
27
a
g
=
Przyspieszenie normalne:
=
⋅
=
⋅
=
L
L
g
R
N
4
cos
16
27
a
ϕ
ε
ϕ
cos
4
27
a
g
N
=
CZYSTE ROZWIĄZANE DLA DWÓCH PRZYPADKÓW ZADAŃ
(Z RÓŻNIE UMIESZCZONYM KĄTEM
φ
)
Zadanie 2.
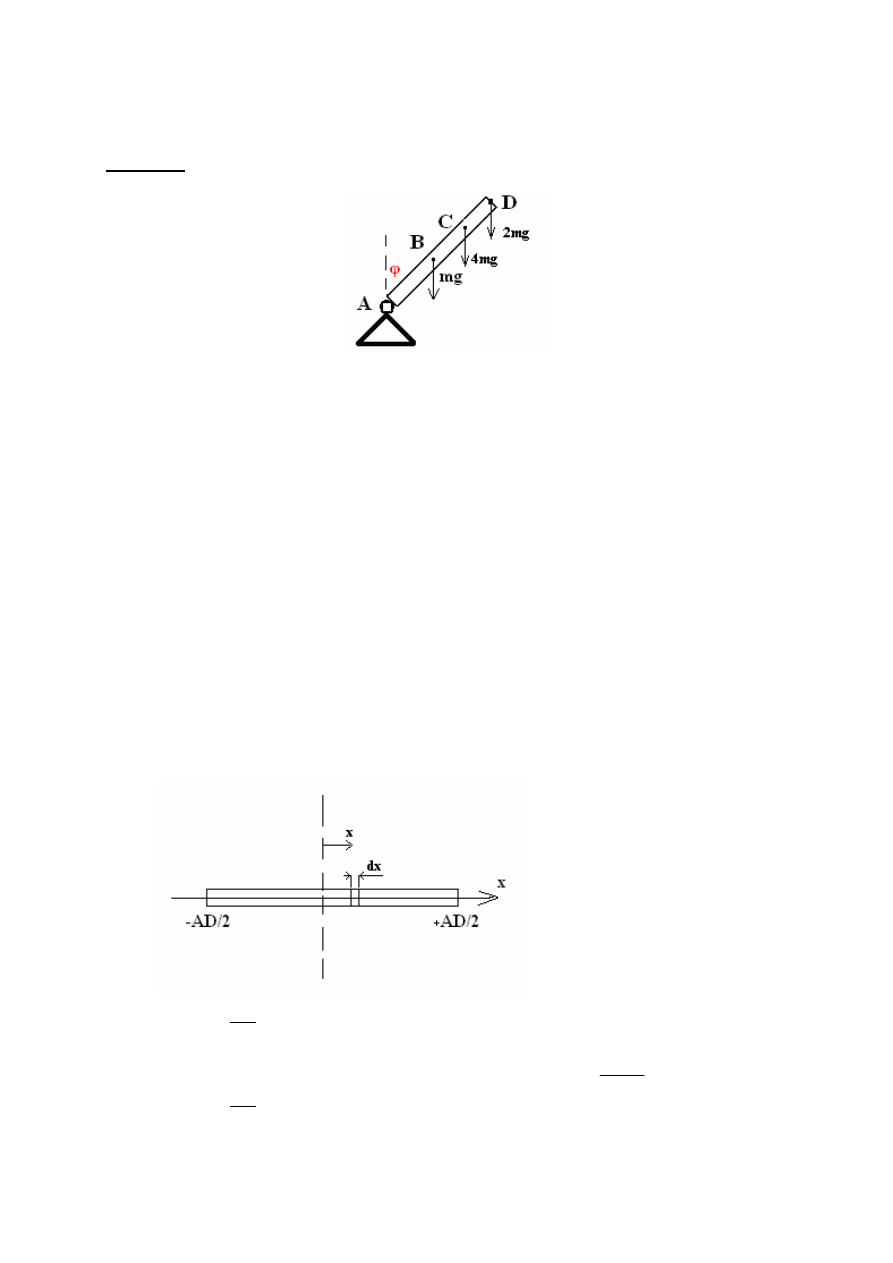
Oblicz przyspieszenie normalne i styczne w punkcie D belki o masie m jak na rysunku:
Dane:
AD = 5L
AC = 3L
Wartości sił zgodnie z rysunkiem.
AB = 5/2L = 2.5L
Rozwiązanie
Przyspieszenie styczne:
a
τ
= ω
2
· R
Przyspieszenie normalne: a
N
= ε · R
ϕ
ε
&&
=
Dynamiczne równanie ruchu obrotowego:
∑
=
A
A
M
I
ϕ
&&
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
ϕ
ϕ
ϕ
ϕ
sin
2
sin
4
sin
mg
AD
mg
AC
mg
AB
I
A
&&
=
⋅
⋅
⋅
+
⋅
⋅
⋅
+
⋅
⋅
=
ϕ
ϕ
ϕ
sin
2
5
sin
4
3
sin
5
.
2
mg
L
mg
L
mg
L
ϕ
ϕ
sin
5
.
24
)
2
5
4
3
5
.
2
(
sin
⋅
⋅
⋅
=
⋅
+
⋅
+
⋅
⋅
=
mg
L
mg
L
Moment bezwładności belki dla osi obortu prostopadłej do belki, przechodzącej
przez punkt B.
∫
+
−
=
2
2
2
AD
AD
B
dm
x
I
dx
AD
m
dm
=
...
5
5
5
.
2
5
.
2
5
.
2
5
.
2
2
2
∫
∫
+
−
+
−
=
=
=
L
L
L
L
B
dx
x
L
m
dx
L
m
x
I
( )
(
)
3
5
.
2
5
.
2
3
5
.
2
2
3
1
5
3
1
5
...
L
L
m
x
L
m
L
L
⋅
⋅
⋅
=
⋅
=
+
−
2
12
25
L
m
I
B
⋅
=
Z TWIERDZENIA STEINERA:
2
AB
m
I
I
B
A
⋅
+
=
2
2
2
3
25
)
5
.
2
(
12
25
L
m
L
m
L
m
I
A
⋅
=
⋅
+
⋅
=
ϕ
ϕ
ϕ
sin
50
147
3
25
sin
2
49
2
L
g
L
m
g
m
L
=
⋅
/
⋅
/
⋅
/
⋅
=
/
&&
dt
d
d
d
dt
d
ϕ
ϕ
ω
ω
ϕ
⋅
=
=
&&
Gdzie:
ω
ϕ
=
dt
d
Z czego wynika że:
ω
ϕ
ω
ϕ
⋅
=
d
d
&&
ω
ω
ϕ
ϕ
d
d
⋅
=
⋅
&&
ω
ω
ϕ
ϕ
d
d
L
g
⋅
=
⋅
sin
50
147
Całkujemy obustronnie:
∫
∫
⋅
=
⋅
ω
ω
ϕ
ϕ
d
d
L
g
sin
50
147

∫
∫
⋅
=
⋅
ω
ω
ϕ
ϕ
d
d
L
g
sin
50
147
C
L
g
+
=
−
2
2
1
cos
50
147
ω
ϕ
Obliczamy stałą całkowania, podstawiając wartości φ oraz ω dla belki ustawionej
pionowo:
φ = 0, ω = 0:
C
L
g
+
⋅
=
⋅
−
0
2
1
1
50
147
L
g
C
50
147
−
=
Zatem:
L
g
L
g
50
147
sin
50
147
2
1
2
+
−
=
ϕ
ω
)
sin
1
(
25
147
2
ϕ
ω
−
=
L
g
Odpowiedź:
R = AD = 5L
Przyspieszenie styczne:
=
⋅
−
=
⋅
=
2
L
L
g
R
5
)
sin
1
(
25
147
a
ϕ
ω
τ
)
sin
1
(
5
147
a
ϕ
τ
−
=
g
Przyspieszenie normalne:
=
⋅
=
⋅
=
L
L
g
R
N
5
sin
50
147
a
ϕ
ε
ϕ
sin
10
147
a
g
N
=
Wyszukiwarka
Podobne podstrony:
proj masz1 (2)
MASZ1, Studia, sprawozdania, sprawozdania od cewki 2, Dok 1, Dok 1, Dokumenty , Energo
MASZ1 2
MASZ1
MASZ1 ŚĆ DOC
więcej podobnych podstron