CAŁKI

POWIERZCHNIOWE

CAŁKI POWIERZCHNIOWE 2 / 25

C

AŁKA POWIERZCHNIOWA NIEZORIENTOWANA

Definicja 1

Gładkim płatem powierzchniowym

S

(wzgl. płaszczyzny xOy)

nazywamy wykres funkcji

)

,

(

y

x

g

z

=

,

D

y

x

∈

)

,

(

różniczkowalnej na obszarze regularnym

D

.

Analogicznie określamy gładki płat regularny względem płaszczyzn

xOz

i

yOz

.

Definicja 2

Powierzchnię stanowiącą zbiór spójny punktów, którą można
podzielić na skończoną liczbę gładkich płatów powierzchniowych,
nazywamy powierzchnią regularną.

CAŁKI POWIERZCHNIOWE 3 / 25

Rozważmy powierzchnię dwustronną regularną S o równaniu

)

,

(

y

x

g

z

=

, gdzie

D

y

x

∈

)

,

(

, oraz funkcję

)

,

,

(

z

y

x

f

określoną

i ograniczoną na tej powierzchni.
Powierzchnię

S

dzielimy na n dowolnych części

n

S

S

S

,

,

,

2

1

K

o polach

n

S

S

S

,

,

,

2

1

K

i z ka

ż

dej z tych cz

ęś

ci wybieramy po jednym

dowolnym punkcie

)

,

,

(

i

i

i

i

z

y

x

M

.

Wtedy istnieje granica sum

∑

=

n

i

i

i

i

i

S

z

y

x

f

1

)

,

,

(

, gdy średnice

i

∂

wszystkich części

i

S dążą do zera, niezależna od sposobu podziału

powierzchni S na części i od wyboru punktów

)

,

,

(

i

i

i

i

z

y

x

M

.

CAŁKI POWIERZCHNIOWE 4 / 25

Definicja 3 (całki powierzchniowej niezorientowanej)

Całką powierzchniową niezorientowaną nazywamy

∑

=

→

∂

n

i

i

i

i

i

S

z

y

x

f

n

1

0

)

,

,

(

lim

i oznaczamy

∫∫

S

dS

z

y

x

f

)

,

,

(

.

Czyli

∑

∫∫

=

→

∂

=

n

i

i

i

i

i

S

S

z

y

x

f

dS

z

y

x

f

n

1

0

)

,

,

(

lim

)

,

,

(

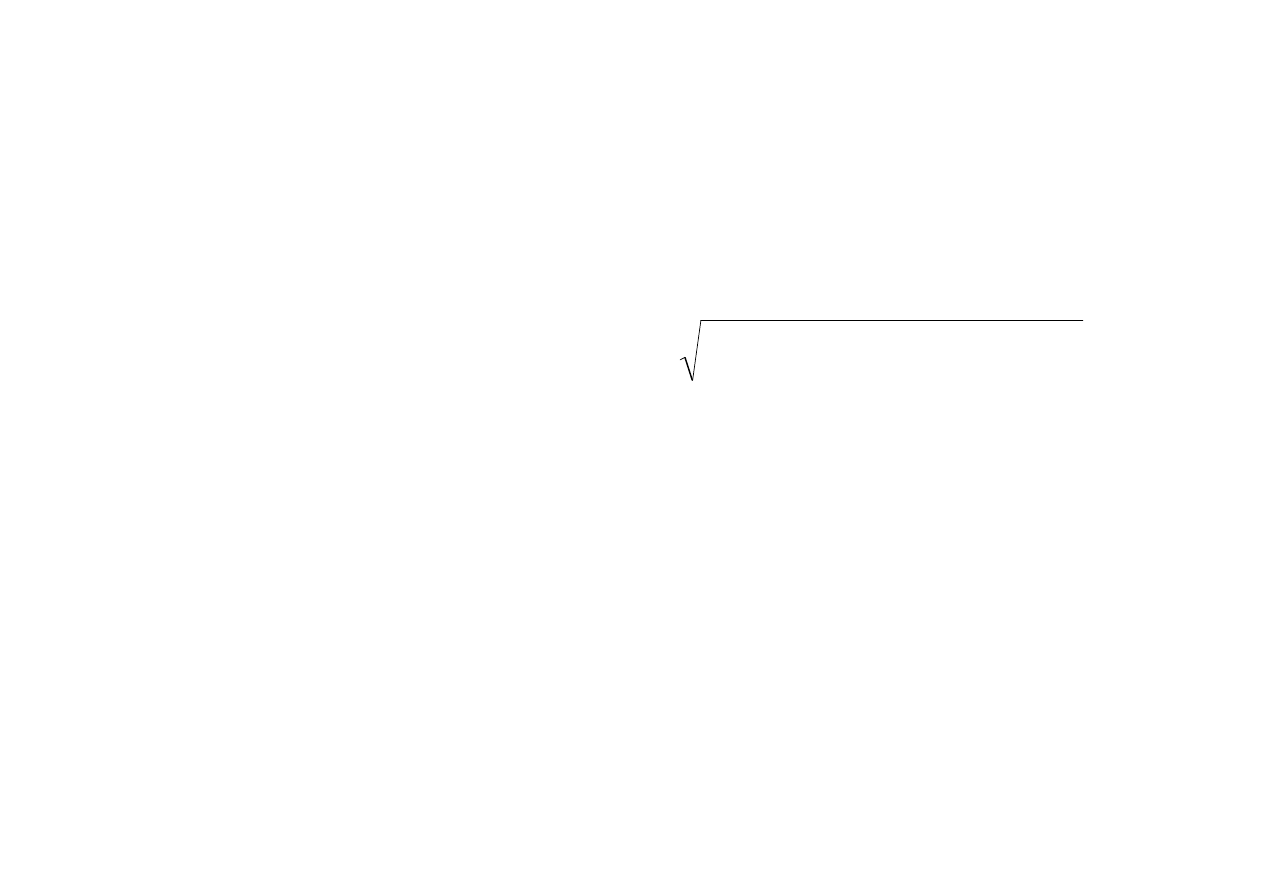
CAŁKI POWIERZCHNIOWE 5 / 25

Twierdzenie 1

(o zamianie całki powierzchniowej niezorientowanej

na całkę podwójną)

Jeżeli funkcja

)

,

,

(

z

y

x

f

jest ciągła na płacie powierzchniowym

regularnym S o równaniu

)

,

(

y

x

g

z

=

, gdzie

D

y

x

∈

)

,

(

, to całka

powierzchniowa niezorientowana istnieje i wyraża się wzorem

[

] [

]

∫∫

∫∫

+

+

=

D

y

x

S

dxdy

y

x

g

y

x

g

y

x

g

y

x

f

dS

z

y

x

f

2

'

2

'

)

,

(

)

,

(

1

))

,

(

,

,

(

)

,

,

(

gdzie D jest obszarem płaskim regularnym będącym rzutem płata S
na płaszczyznę xOy.

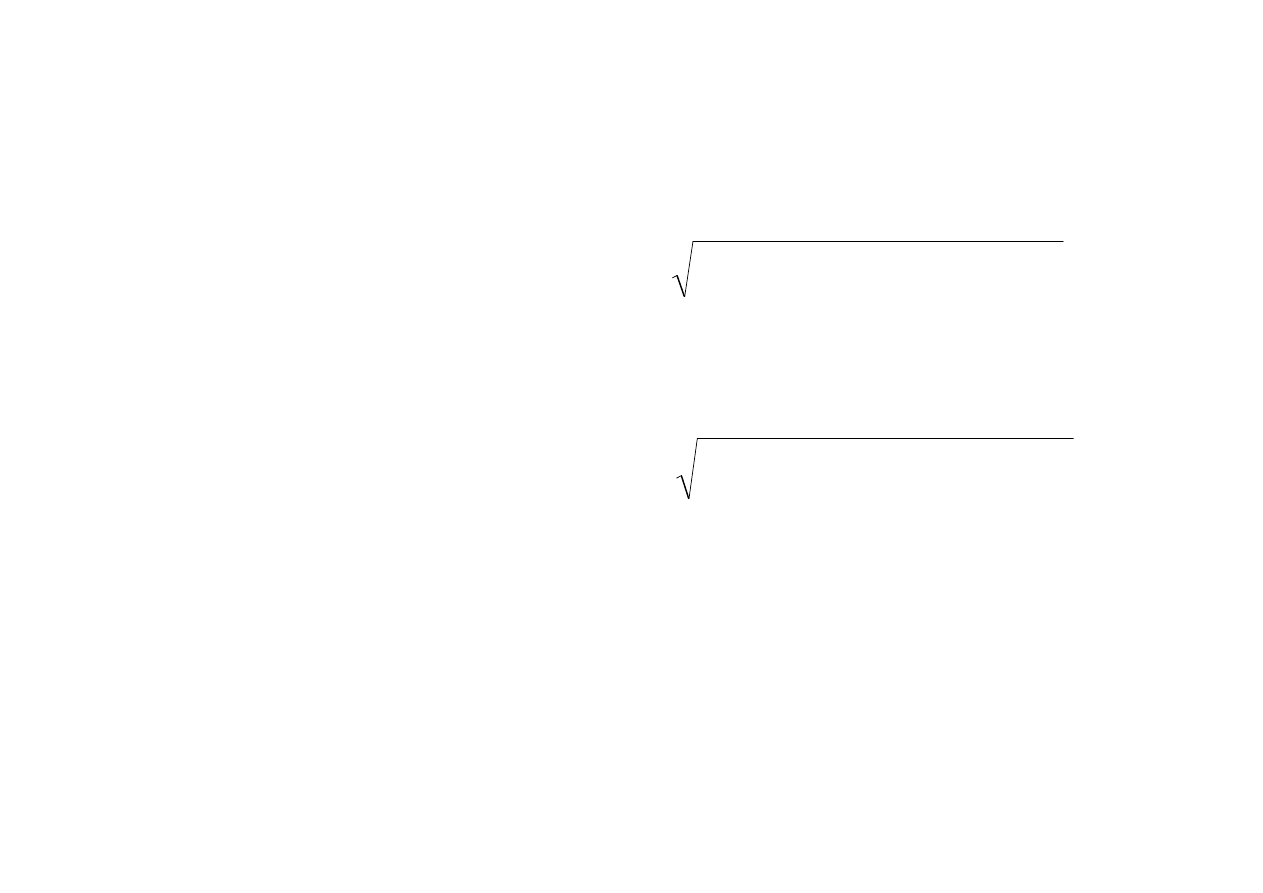
CAŁKI POWIERZCHNIOWE 6 / 25

Analogicznie jeśli:

•

S :

)

,

(

z

x

g

y

=

, gdzie

1

)

,

(

D

z

x

∈

[

] [

]

∫∫

∫∫

+

+

=

D

z

x

S

dydz

z

x

g

z

x

g

z

z

x

g

x

f

dS

z

y

x

f

2

'

2

'

)

,

(

)

,

(

1

)

),

,

(

,

(

)

,

,

(

•

S :

)

,

(

z

y

g

x

=

, gdzie

2

)

,

(

D

z

y

∈

[

] [

]

∫∫

∫∫

+

+

=

D

z

y

S

dydz

z

y

g

z

y

g

z

y

z

y

g

f

dS

z

y

x

f

2

'

2

'

)

,

(

)

,

(

1

)

,

),

,

(

(

)

,

,

(

CAŁKI POWIERZCHNIOWE 7 / 25

Definicja 4

Powierzchnię S o równaniach parametrycznych

)

,

( v

u

x

x

=

,

)

,

( v

u

y

y

=

,

)

,

( v

u

z

z

=

,

∆

∈

)

,

( v

u

,

(1)

nazywamy płatem powierzchniowym regularnym jeśli spełnione
są następujące warunki:
1. różnym punktom

)

,

( v

u

obszaru jednospójnego

∆

odpowiadają

przy przekształceniu (1) różne punkty

)

,

,

(

z

y

x

powierzchni S ,

2. funkcje (1) są ciągłe w obszarze

∆

i na jego brzegu,

3. pierwsze pochodne cząstkowe funkcji (1) są ciągłe

i ograniczone w tym obszarze,

4. nie wszystkie podwyznaczniki stopnia drugiego macierzy





















∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

v

z

v

y

v

x

u

z

u

y

u

x

(2)

znikają jednocześnie w całym obszarze

∆

.

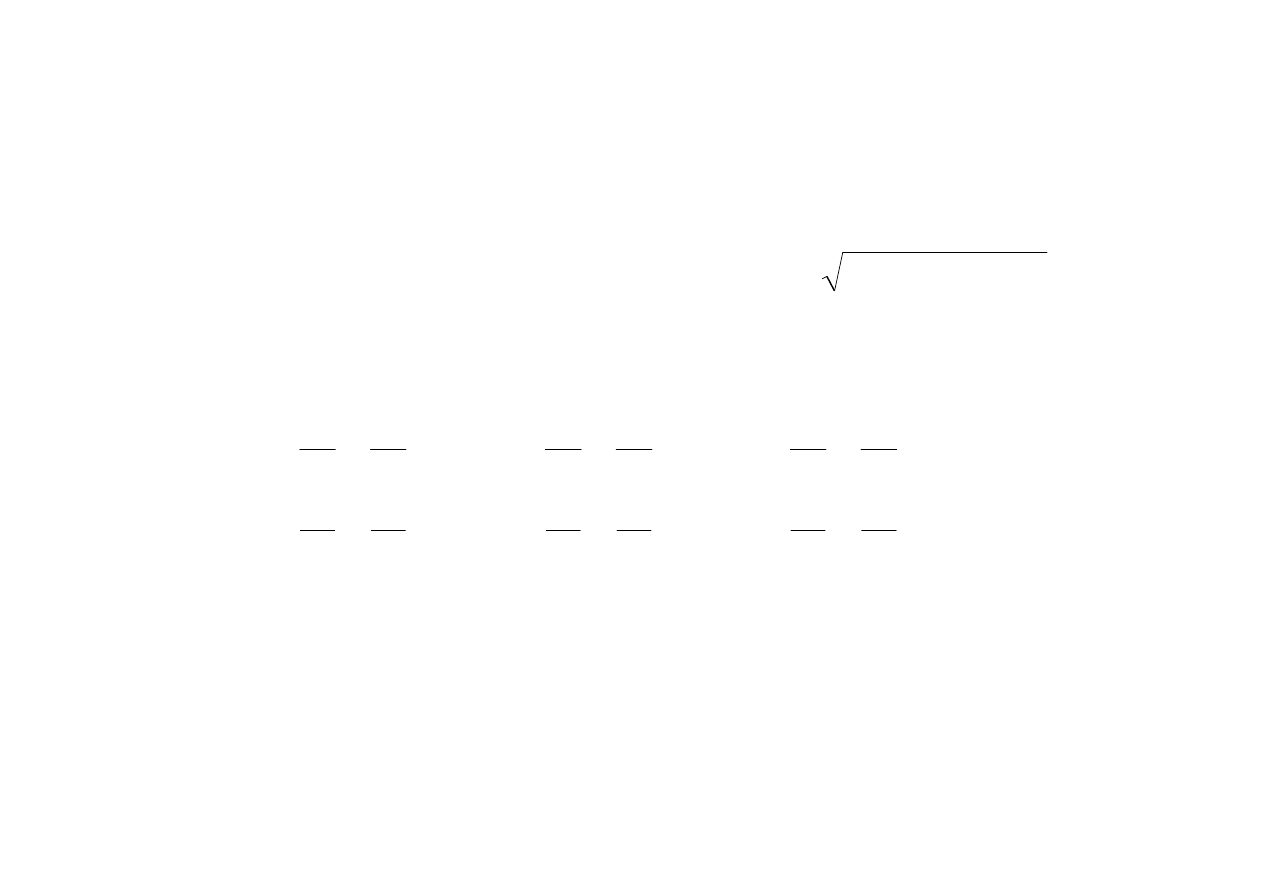
CAŁKI POWIERZCHNIOWE 8 / 25

Twierdzenie 2

Jeżeli funkcja

)

,

,

(

z

y

x

f

jest ciągła na płacie powierzchniowym

regularnym S o równaniach (1), to całka powierzchniowa
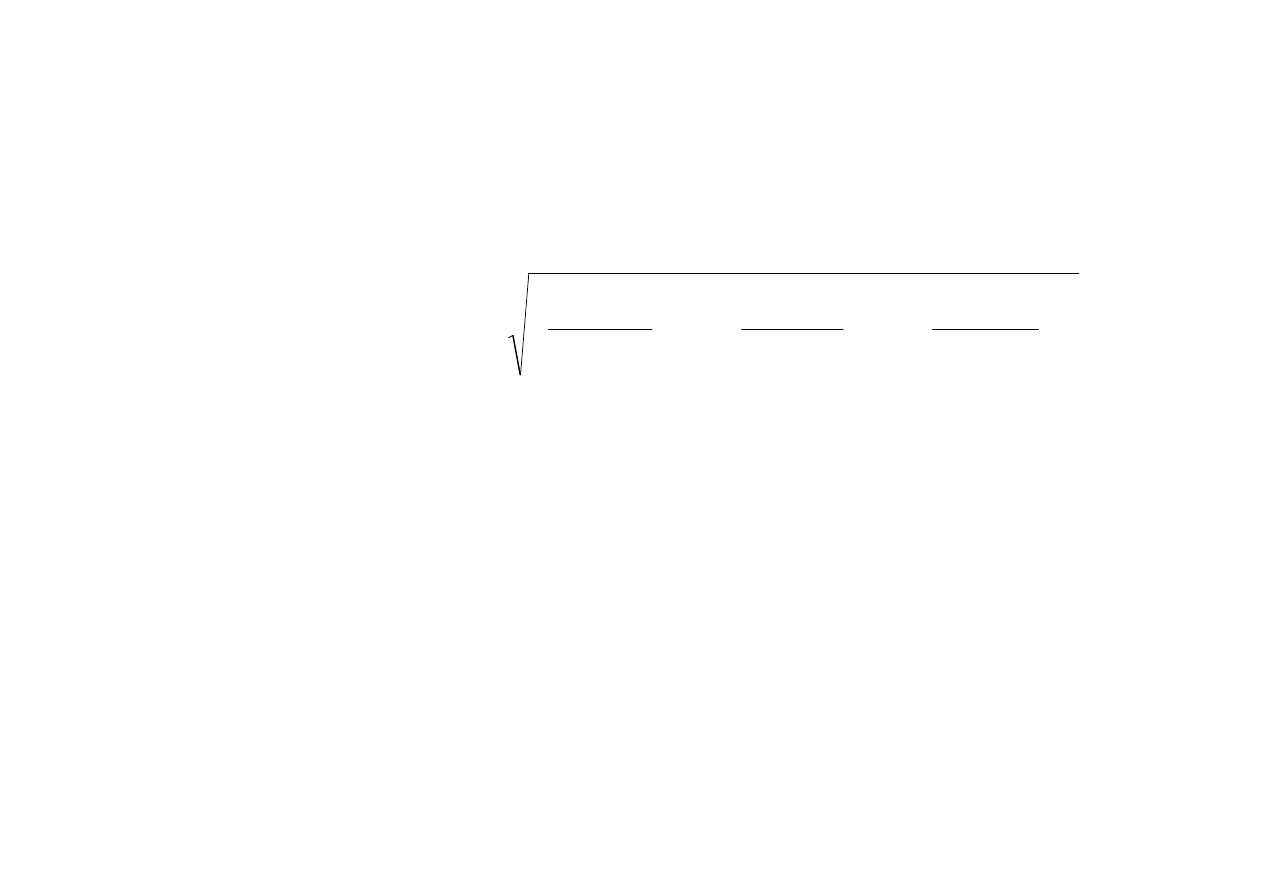
niezorientowana istnieje i wyraża się wzorem

(

)

∫∫

∫∫

+

+

=

D

S

dudv

C

B

A

v

u

z

v

u

y

v

u

x

f

dS

z

y

x

f

2

2

2

)

,

(

),

,

(

),

,

(

)

,

,

(

,

gdzie





















∂

∂

∂

∂

∂

∂

∂

∂

=

v

z

v

y

u

z

u

y

A

,





















∂

∂

∂

∂

∂

∂

∂

∂

=

v

x

v

z

u

x

u

z

B

,





















∂

∂

∂

∂

∂

∂

∂

∂

=

v

y

v

x

u

y

u

x

A

są odpowiednimi wyznacznikami macierzy (2).

CAŁKI POWIERZCHNIOWE 9 / 25

W skrócie

(

)

∫∫

∫∫

∆













+













+













=

=

dudv

v

u

D

y

x

D

v

u

D

x

z

D

v

u

D

z

y

D

v

u

z

v

u

y

v

u

x

f

dS

z

y

x

f

S

2

2

2

)

,

(

)

,

(

)

,

(

)

,

(

)

,

(

)

,

(

)

,

(

),

,

(

),

,

(

)

,

,

(

CAŁKI POWIERZCHNIOWE 10 / 25

Fakt 1 (zastosowania geometryczne)

Pole płata powierzchniowego gładkiego S wyraża się wzorem

∫∫

=

S

dS

S

.

CAŁKI POWIERZCHNIOWE 11 / 25

C

AŁKA POWIERZCHNIOWA ZORIENTOWANA

Rozważmy gładki płat powierzchniowy S o równaniu

)

,

(

y

x

g

z

=

, gdzie

D

y

x

∈

)

,

(

.

Płatu temu można nadać orientację, rozróżniając dwie jego strony:
ujemną, i dodatnią,. Mówimy wówczas, że płat S został zorientowany
od strony nazwanej ujemną, do strony nazwanej dodatnią,.
Zorientowanie płata S powoduje ustalenie pewnego kierunku
normalnej (od strony ujemnej do strony dodatniej płata) w każdym
jego punkcie.

Jeżeli S oznacza płat powierzchniowy, to symbol

S

−

oznacza płat

różniący się od S tylko zorientowaniem (orientacją).
Mówimy, że płaty S i S

−

są przeciwnie zorientowane.

CAŁKI POWIERZCHNIOWE 12 / 25

Uwaga 1

Jeśli powierzchnia S jest zamknięta, to za powierzchnię dodatnią
przyjmuje się jej zewnętrzną stronę.

Uwaga 2

Nie dla każdej powierzchni można ustalić orientację, tj. nie każda
powierzchnia jest powierzchnią dwustronną.

CAŁKI POWIERZCHNIOWE 13 / 25

Definicja 5 (całki powierzchniowej zorientowanej)

Niech

)

,

,

(

z

y

x

P

P

=

,

)

,

,

(

z

y

x

Q

Q

=

,

)

,

,

(

z

y

x

R

R

=

,

Oznaczają trzy funkcje określone i ciągłe na płacie regularnym
zorientowanym S postaci

)

,

(

y

x

f

z

=

, gdzie

D

y

x

∈

)

,

(

,

zaś

α

cos ,

β

cos

i

γ

cos

oznaczają

kosinusy kierunkowe wektora

normalnego do powierzchni

S

, zorientowanego od strony ujemnej

do dodatniej.
Przy tych zało

ż

eniach całk

ę

postaci

(

)

∫∫

+

+

S

dS

R

Q

P

γ

β

α

cos

cos

cos

(*)

nazywamy całk

ą

powierzchniow

ą

zorientowan

ą

po płacie

regularnym zorientowanym

S

.

CAŁKI POWIERZCHNIOWE 14 / 25

Uwzgl

ę

dniaj

ą

c,

ż

e mi

ę

dzy polem

dS

dowolnie małego elementu płata

powierzchniowego

S

i polami

dxdy

,

dydz

i

dxdz

rzutu tego elementu

odpowiednio na płaszczyzny

xOy

,

yOz

i

xOz

zachodz

ą

zwi

ą

zki:

α

cos

dS

dydz

=

,

β

cos

dS

dzdx

=

,

γ

cos

dS

dxdy

=

,

całk

ę

powierzchniow

ą

zorientowan

ą

mo

ż

na zapisa

ć

w postaci

∫∫

+

+

S

Rdxdy

Qdzdx

Pdydz

.

(**)

Przedstawienia (*) i (**) s

ą

równowa

ż

ne.

CAŁKI POWIERZCHNIOWE 15 / 25

Uwaga 3

Je

ż

eli zamienimy stron

ę

dodatni

ą

płata na ujemn

ą

, to funkcje

α

cos ,

β

cos

i

γ

cos zmieniaj

ą

znak. Je

ś

li oznaczymy przez

S

−

płat powierzchniowy zorientowany przeciwnie do

S

, to

(

)

(

)

∫∫

∫∫

+

+

−

=

+

+

−

S

S

dS

R

Q

P

dS

R

Q

P

γ

β

α

γ

β

α

cos

cos

cos

cos

cos

cos

.

CAŁKI POWIERZCHNIOWE 16 / 25

Twierdzenie 3

Je

ż

eli płat powierzchniowy gładki

S

okre

ś

lony jest równaniami

parametrycznymi

)

,

(

v

u

x

x

=

,

)

,

(

v

u

y

y

=

,

)

,

(

v

u

z

z

=

,

∆

∈

)

,

(

v

u

,

to całka powierzchniowa zorientowana

∫∫

+

+

S

Rdxdy

Qdzdx

Pdydz

sprowadza si

ę

do całki podwójnej po obszarze płaskim

∆

, czyli

(

)

+

=

+

+

∫∫

∫∫

∆

)

,

(

)

,

(

)

,

(

),

,

(

),

,

(

[

v

u

D

z

y

D

v

u

z

v

u

y

v

u

x

P

Rdxdy

Qdzdx

Pdydz

S

(

)

+

+

)

,

(

)

,

(

)

,

(

),

,

(

),

,

(

v

u

D

x

z

D

v

u

z

v

u

y

v

u

x

Q

(

)

dudv

v

u

D

y

x

D

v

u

z

v

u

y

v

u

x

R

]

)

,

(

)

,

(

)

,

(

),

,

(

),

,

(

+

.

CAŁKI POWIERZCHNIOWE 17 / 25

Twierdzenie 4

Jeżeli funkcja

)

,

,

(

z

y

x

R

jest ciągła na płacie regularnym S

o równaniu postaci

)

,

(

y

x

f

z

=

, gdzie

D

y

x

∈

)

,

(

, zorientowanym

dodatnio, to całka powierzchniowa zorientowana

∫∫

S

dxdy

z

y

x

R

)

,

,

(

istnieje i daje się wyrazić za pomocą całki podwójnej wzorem

∫∫

∫∫

=

D

S

dxdy

y

x

f

y

x

R

dxdy

z

y

x

R

))

,

(

,

,

(

)

,

,

(

gdzie D jest rzutem płata regularnego S na płaszczyznę xOy.

CAŁKI POWIERZCHNIOWE 18 / 25

Twierdzenie 4

(cd.)

Jeżeli funkcja

)

,

,

(

z

y

x

P

jest ciągła na płacie regularnym S

o równaniu postaci

)

,

(

z

y

g

x

=

, gdzie

1

)

,

(

D

z

y

∈

, zorientowanym

dodatnio (tzn. wektor normalny do S tworzy z dodatnim
kierunkiem osi Ox kąt ostry), to całka powierzchniowa
zorientowana

∫∫

S

dydz

z

y

x

P

)

,

,

(

istnieje i daje się wyrazić za pomocą całki podwójnej wzorem

∫∫

∫∫

=

1

)

,

),

,

(

(

)

,

,

(

D

S

dydz

z

y

z

y

g

R

dydz

z

y

x

P

gdzie

1

D jest rzutem płata regularnego S na płaszczyznę yOz.

CAŁKI POWIERZCHNIOWE 19 / 25

Twierdzenie 4

(cd.)

Jeżeli funkcja

)

,

,

(

z

y

x

Q

jest ciągła na płacie regularnym S

o równaniu postaci

)

,

(

z

x

h

y

=

, gdzie

2

)

,

(

D

z

x

∈

, zorientowanym

dodatnio (tzn. wektor normalny do S tworzy z dodatnim
kierunkiem osi Oy kąt ostry), to całka powierzchniowa
zorientowana

∫∫

S

dxdz

z

y

x

Q

)

,

,

(

istnieje i daje się wyrazić za pomocą całki podwójnej wzorem

∫∫

∫∫

=

2

)

),

,

(

,

(

)

,

,

(

D

S

dxdz

z

z

x

h

x

Q

dxdz

z

y

x

Q

gdzie

2

D jest rzutem płata regularnego S na płaszczyznę xOz.

CAŁKI POWIERZCHNIOWE 20 / 25

Twierdzenie 5

Jeżeli funkcje

)

,

,

(

z

y

x

P

,

)

,

,

(

z

y

x

Q

,

)

,

,

(

z

y

x

R

są ciągłe na płacie

powierzchniowym regularnym opisanym równaniem

)

,

(

y

x

f

z

=

,

gdzie

D

y

x

∈

)

,

(

, to

∫∫

∫∫

+

−

−

=

=

+

+

d

y

x

S

y

x

f

y

x

f

y

x

Q

y

x

f

y

x

f

y

x

P

dxdy

z

y

x

R

dxdz

z

y

x

Q

dydz

z

y

x

P

)

,

(

))

,

(

,

,

(

)

,

(

))

,

(

,

,

(

[

)

,

,

(

)

,

,

(

)

,

,

(

'

'

ε

dxdy

y

x

f

y

x

R

))]

,

(

,

,

(

+

,

przy czym

1

=

ε

, jeżeli płat S zorientowany jest tak, że

0

cos

>

γ

,

natomiast

1

−

=

ε

jeśli orientacja jest przeciwna.

CAŁKI POWIERZCHNIOWE 21 / 25

Fakt 2 (zastosowania geometryczne)

Jeżeli powierzchnia zamknięta i gładka S jest zorientowana
dodatnio, to objętość

V

bryły ograniczonej tą powierzchnią może

być obliczona jako całka powierzchniowa zorientowana

∫∫

+

+

=

S

zdxdy

ydxdz

xdydz

V

3

1

.

CAŁKI POWIERZCHNIOWE 22 / 25

Twierdzenie 6 (

Gaussa-Ostrogradzkiego

)

Jeżeli funkcje

)

,

,

(

z

y

x

P

,

)

,

,

(

z

y

x

Q

,

)

,

,

(

z

y

x

R

są ciągłe wraz

z pochodnymi cząstkowymi

x

P

∂

∂

,

y

Q

∂

∂

,

z

R

∂

∂

wewnątrz i na brzegu

obszaru przestrzennego V , który jest normalny względem
wszystkich płaszczyzn układu współrzędnych i jeżeli brzeg S
obszaru V jest powierzchnią regularną zamkniętą zorientowaną
skierowaniem wektora normalnego do powierzchni S na zewnątrz
obszaru V , to

∫∫∫

∫∫













∂

∂

+

∂

∂

+

∂

∂

=

+

+

V

S

dxdydz

z

R

y

Q

x

P

Rdxdy

Qdzdx

Pdydz

.

CAŁKI POWIERZCHNIOWE 23 / 25

Uwaga 4

Wzór Gaussa-Ostrogradzkiego jest prawdziwy również dla
obszarów, które dają się podzielić na skończoną ilość obszarów
normalnych względem płaszczyzn układu współrzędnych.

CAŁKI POWIERZCHNIOWE 24 / 25

Twierdzenie 7 (

Stokesa)

Jeżeli funkcje

)

,

,

(

z

y

x

P

,

)

,

,

(

z

y

x

Q

,

)

,

,

(

z

y

x

R

są ciągłe wraz

z pochodnymi cząstkowymi pierwszego rzędu w pewnym
obszarze zawierającym powierzchnię dwustronną S ograniczoną
krzywą K przy czym orientacja tej krzywej jest zgodna
z orientacją powierzchni S , to

∫∫

∫













∂

∂

−

∂

∂

+













∂

∂

−

∂

∂

+













∂

∂

−

∂

∂

=

+

+

S

K

dxdy

y

P

x

Q

dzdx

x

R

z

P

dydz

z

Q

y

R

Rdz

Qdy

Pdx

CAŁKI POWIERZCHNIOWE 25 / 25

Uwaga 5

Zgodność orientacji krzywej K będącej brzegiem płata
powierzchniowego S z orientacją tego płata należy rozumieć
w ten sposób, że obieg dodatni na krzywej K wokół wektora
normalnego n

r

do powierzchni S jest zgodny z obiegiem wokół osi

Oz krzywej C , która jest rzutem krzywej K na płaszczyznę xOy.