1
Liczby zespolone
Definicja
Liczbą zespoloną nazywamy uporządowaną parę liczb
rzeczywistych, tj.
z = (x, y)
. Zbiór wszystkich liczb zespolonych
oznaczamy:
C
, zatem
C = { z = (x, y) : x, y ∈ R }
Działania na liczbach zespolonych
Niech
z
1
= (x
1
, y
1
)
i
z
2
= (x
2
, y
2
)
.
• Równość liczb zespolonych
z
1
= z
2
⇐⇒
x
1
= x
2
∧
y
1
= y
2
2
• Dodawanie liczb zespolonych
z
1
+ z
2
= ( x
1
+ x
2
, y
1
+ y
2
)
• Mnożenie liczb zespolonych
z
1
· z
2
= ( x
1
· x
2
− y
1
· y
2
, x
1
· y
2
+ x
2
· y
1
)
Zbiór liczb rzeczywistych
Liczby zespolone postaci
(x, 0)
mają własności:
(x
1
, 0) + (x
2
, 0) = ( x
1
+ x
2
, 0 )
(x
1
, 0) · (x
2
, 0) = ( x
1
· x
2
, 0 )
Przyjmiemy więc, że
(x, 0) = x
a zbiór wszytkich liczb zespolonych
postaci
(x, 0)
utożsamimy ze zbiorem liczb rzeczywistych
R
.
3
Mamy zatem
R ⊂ C
Zbiór liczb urojonych
Liczby zespolone postaci
(0, y)
nazywamy liczbami urojonymi.
Liczbę
(0, 1)
nazywamy jednostką urojoną i oznaczamy symbolem
i
. Mamy wówczas
(0, y) = (0, 1) · (y, 0) = iy
.
Fakt
i
2
= −1
Postać algebraiczna liczby zespolonej
4
z = (x, y) = (x, 0) + (0, y) = x + iy,
x, y ∈ R
Ten sposób przedstawiania liczb zespolonych nazywamy ich postacią
algebraiczną.
• Liczbę
x
nazywamy częścią rzeczywistą (realis) liczby zespolonej
z
, co zapisujemy:
x = Re z
• Liczbę
y
nazywamy częścią urojoną (imaginalis) liczby zespolonej
z
, co zapisujemy:
y = Im z
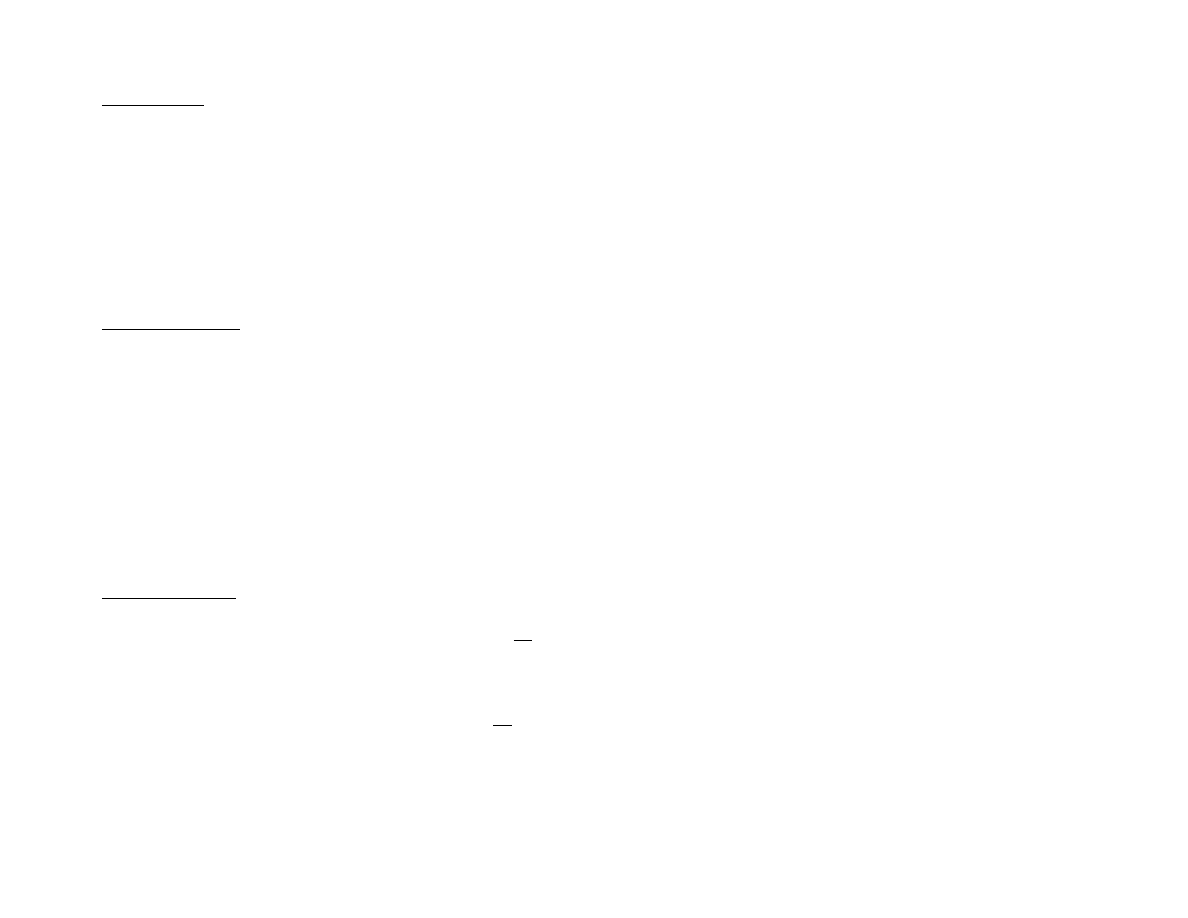
5
Uwaga
Dodawanie, odejmowanie i mnożenie liczb zespolonych w
postaci algebraicznej wykonujemy tak jak dodawanie, odejmowanie
i mnożenie wielomianów zmiennej
i
, z uwzględnieniem faktu
i
2
=
−1
.
Przykład
Oblicz:
a)
(2 − 3i) + 5(1 + 2i)
b)
(1 − i)(4 + 2i) − (1 + i)i
19
Sprzężenie liczby zespolonej
Definicja
Sprzężeniem liczby zespolonej
z = x + iy
, gdzie
x, y ∈ R
, nazywamy liczbę
z
określoną wzorem:
z = x − iy.
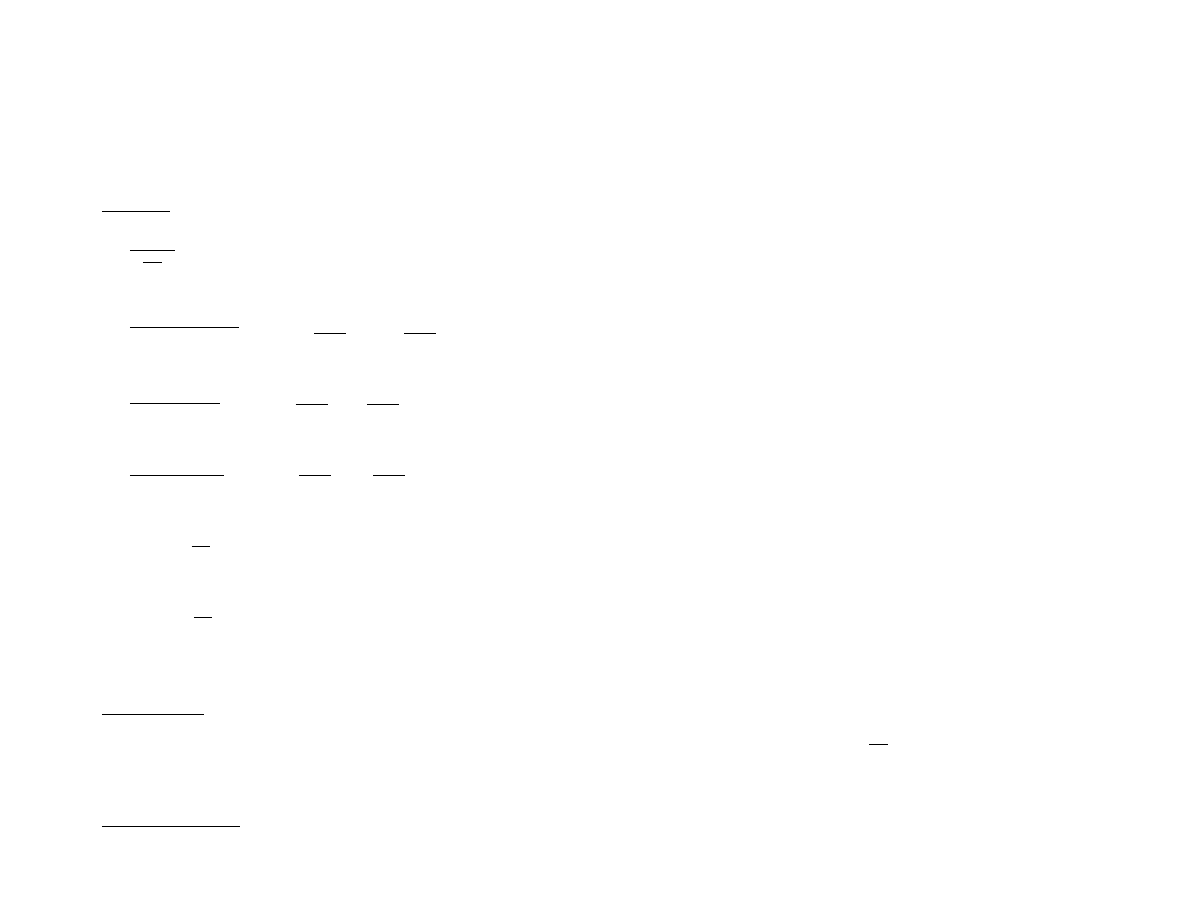
6
Liczba sprzężona do liczby zespolonej jest jej obrazem w symetrii
względem osi
Re z
.
Fakt
(Własności sprzężenia liczb zespolonych)
•
(z) = z
•
z
1
± z
2
= z
1
± z
2
•
z
1
· z
2
= z
1
· z
2
•
z
1
: z
2
= z
1
: z
2
,
z
2
6= 0
•
z + z = 2 Re z
•
z − z = 2i Im z
Uwaga
Przy dzieleniu przez liczbę zespoloną
z = x + iy
należy
dzielną i dzielnik pomnożyć przez liczbę sprzężoną
z = x − iy
.
Przykład
Oblicz:
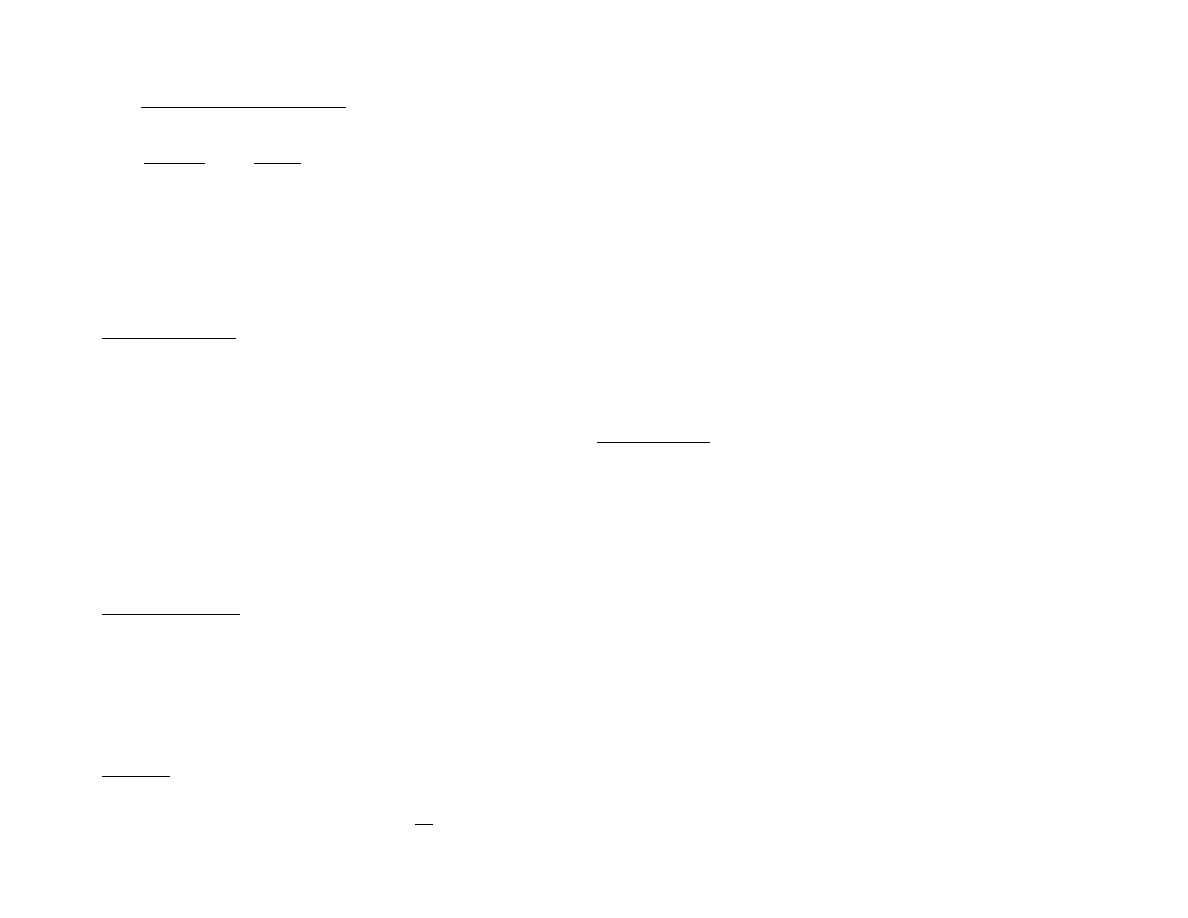
7
a)
(2−3i)+5(1+2i)
1−i
b)
2+i
4+2i
−
1+i
i
Postać trygonometryczna liczby zespolonej
Definicja Modułem liczby zespolonej
z = x+iy
, gdzie
x, y ∈ R
,
nazywamy liczbę rzeczywistą
|z|
określoną wzorem:
|z| =
s
x
2
+ y
2
.
Przykład
Oblicz moduły liczb zespolonych:
a)
z = −i
b)
z = −1 + 3i
Fakt
(Własności modułu liczb zespolonych)
•
|z| = | − z| = |z|
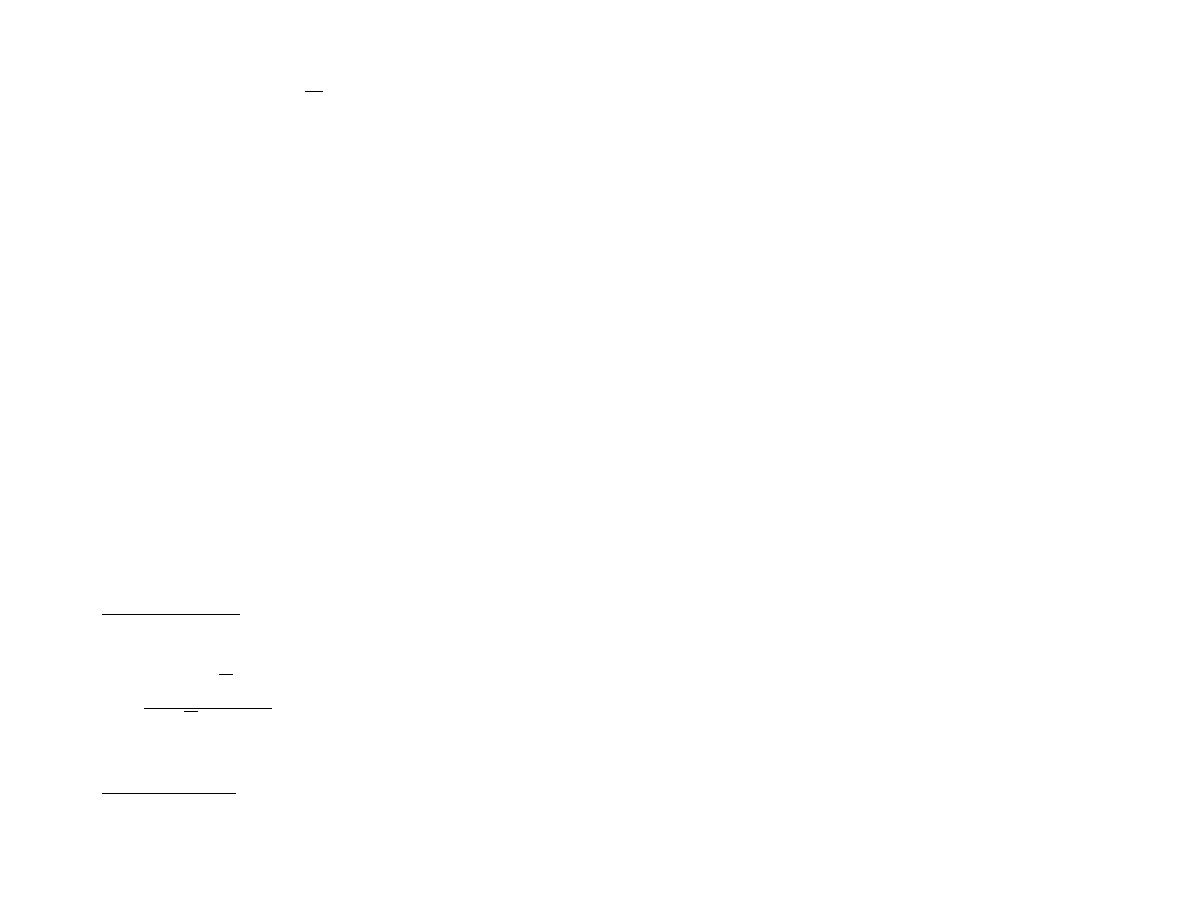
8
•
|z|
2
= z · z
•
|z
1
· z
2
| = |z
1
| · |z
2
|
•
|z
1
: z
2
| = z
1
| : |z
2
|,
z
2
6= 0
•
|z
1
+ z
2
| 6 |z
1
| + |z
2
|
•
| |z
1
| − |z
2
| | 6 |z
1
− z
2
|
•
|Re z| 6 |z|
•
|Im z| 6 |z|
Przykład
Oblicz moduły liczb zespolonych:
a)
(1 + 2i)(3 − 4i)
b)
(3−
√
3 i)
2
(
√
2+2i)
3
Definicja
Argumentem liczby zespolonej
z = x + iy
, gdzie
9
x, y ∈ R
, nazywamy liczbę rzeczywistą
ϕ
, spełniającą warunki:
cos ϕ =
x
|z|
,
sin ϕ =
y
|z|
.
Uwaga
Każda liczba zespolona
z 6= 0
ma nieskończenie wiele
argumentów postaci:
arg z = ϕ + 2kπ.
Definicja
Argumentem głównym liczby zespolonej
z
nazywamy
ten spośród jej argumentów, który należy do przedziału
(−π, π]
.
Argument ten oznaczamy symbolem
Arg z
.
Przykład
Oblicz argumenty główne liczb zespolonych:
a)
z = −i
10
b)
z =
√
3 − i
Fakt
(Własności argumentu liczb zespolonych)
•
arg( z
1
· z
2
) = arg z
1
+ arg z
2
•
arg( z
n
) = n arg z
•
arg( z
1
: z
2
) = arg z
1
− arg z
2
,
z
2
6= 0
Przykład
Oblicz argumenty główne liczb zespolonych:
a)
(1 + i)i
4
b)
(1−
√
3 i)
2
(2+2i)
3
z = x + iy = |z| cos ϕ + i |z| sin ϕ = |z| ( cos ϕ + i sin ϕ )
ϕ = Arg z
11
Ten sposób przedstawiania liczb zespolonych nazywamy ich postacią
trygonometryczną.
Przykład
Zapisz w postaci trygonometrycznej liczby zespolone:
a)
z = −i
b)
z = 3
c)
z = −2 + 2i
d)
z =
√
3 − i
Działania na liczbach zespolonych
w postaci trygonometrycznej
Niech
z
1
= |z
1
| ( cos ϕ
1
+ i sin ϕ
1
)
i
z
2
= |z
2
| ( cos ϕ
2
+ i sin ϕ
2
)
.
•
z
1
· z
2
= |z
1
| · |z
2
| ( cos(ϕ
1
+ ϕ
2
) + i sin(ϕ
1
+ ϕ
2
) )
•
z
1
z
2
=
|z
1
|
|z
2
|
( cos(ϕ
1
− ϕ
2
) + i sin(ϕ
1
− ϕ
2
) ) ,
z
2
6= 0
12
Fakt
(Wzór Moivre’a) Niech
z = |z| ( cos ϕ + i sin ϕ )
. Wówczas
z
n
= |z|
n
( cos(n ϕ) + i sin(n ϕ) ).
Przykład
Zapisz w postaci algebraicznej liczby zespolone:
a)
z = (1 − i)
2007
b)
z =
Pierwiastkowanie liczb zespolonych
Definicja Pierwiastkiem stopnia n z liczby zespolonej
z
nazywamy
każdą liczbę zespoloną
w
, która spełnia warunek
w
n
= z.
13
Przykład
Zauważmy, że:
a)
√
4 = ±2
, bo
2
2
= 4
i
(−2)
2
= 4
b)
√
−4 = ±2i
, bo
(2i)
2
= −4
i
(−2i)
2
= −4
Fakt
Niech
z = |z| ( cos ϕ + i sin ϕ ) 6= 0
. Wówczas
n
√
z =
n
s
|z| ( cos
ϕ + 2kπ
n
+ i sin
ϕ + 2kπ
n
),
gdzie
k = 0, 1, . . . , n − 1
.
Przykład
Oblicz:
a)
4
√
1
b)
3
√
−i
c)
4
s
8
√
3 − 8i
Przykład
(Inne sposoby obliczania pierwiastków)
a)
√
−9
14
b)
√
−3 + 4i
Wielomiany zespolone
Rozwiązywanie równań w zbiorze liczb zespolonych
Wielomianem zespolonym stopnia n nazywamy funkcję postaci:
W (z) = a
n
z
n
+ a
n−1
z
n−1
+ . . . + a
1
z + a
0
,
gdzie
z ∈ C
i
a
k
∈ C
dla
k = 0, 1, . . . , n
.
Twierdzenie
Każdy wielomian zespolony stopnia n ma dokładnie
n pierwiastków zespolonych (uwzględniając pierwiastki wielokrotne).
Przykład
W zbiorze liczb zespolonych rozwiąż równania:
a)
z
4
− (1 + i)
4
= 0
b)
z
2
− (2 + i)z − 1 + 7i = 0
c)
z
4
− 30z
2
+ 289 = 0
15
d)
z
3
= (iz + 1)
3
Twierdzenie
Niech
W (z) = a
n
z
n
+ a
n−1
z
n−1
+ . . . + a
1
z + a
0
,
będzie wielomianem zespolonym o współczynnikach rzeczywistych,
tj.
a
k
∈ R
dla
k = 0, 1, . . . , n
.
Wówczas liczba zespolona
z
0 jest pierwiastkiem wielomianu
W (z)
wtedy i tylko wtedy, gdy liczba zespolona
z
0
jest pierwiastkiem
wielomianu
W (z)
.
Przykład
Wiedząc, że
z
1
= −1 + i
jest pierwiastiem wielomianu
W (z) = z
4
+ 2z
3
+ 5z
2
+ 6z + 6,
znajdź pozostałe pierwiastki tego wielomianu.