VI. Efekty relatywistyczne

Wprowadzenie

Transformacje Lorent-

za to uk∏ad równaƒ pozwa-
lajàcy wyznaczyç punkt
czasoprzestrzeni w drugim
uk∏adzie inercjalnym, jeÊli
znany jest punkt czaso-
przestrzeni w pierwszym
uk∏adzie inercjalnym.

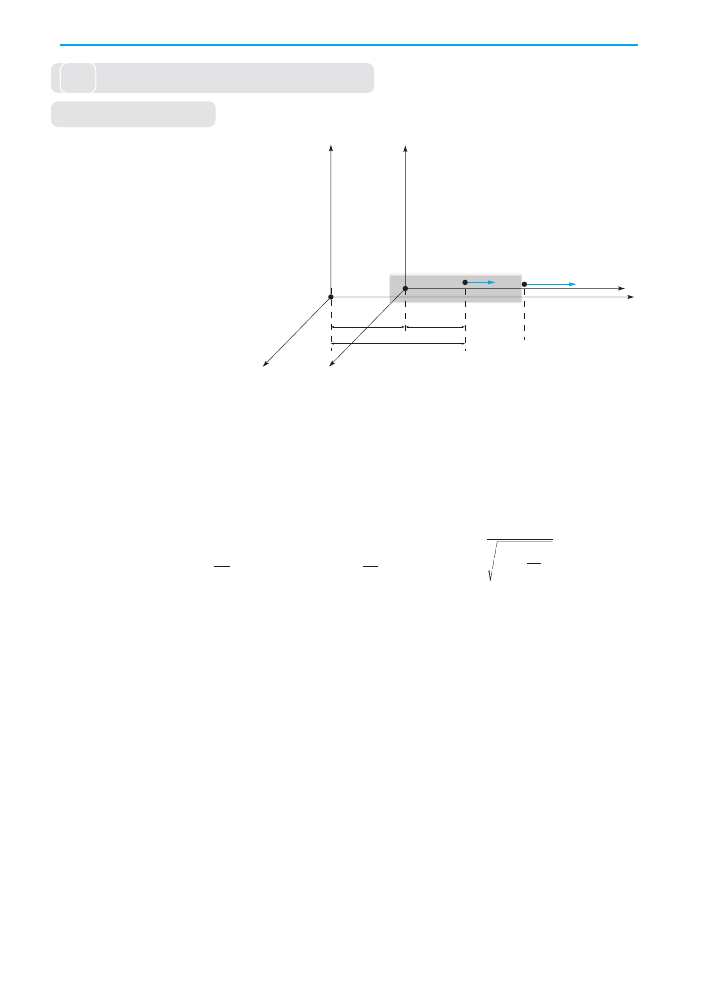
Pierwszy uk∏ad tworzà

osie wspó∏rz´dnych x, y i z,
a drugi – osie '

x , '

y i '

z (ryc.

6.1). Uk∏ad drugi porusza
si´ wzgl´dem pierwszego
wzd∏u˝ osi x ze sta∏à pr´dko-
Êcià '

v

"

. Osie uk∏adów sà wzajemnie równoleg∏e. Transformacje Lorentza stosuje si´ przy

szybkoÊciach porównywalnych z szybkoÊcià Êwiat∏a. Je˝eli '

<<

c

v

, to transformacje Lo-

rentza mo˝na zastàpiç transformacjami Galileusza. Przedstawione poni˝ej transformacje
dotyczà sytuacji, gdy ruch odbywa si´ wzd∏u˝ osi x.

'

'

'

'

'

'

x

x

t

y

y

z

z

t

t

c

x

v

v

2

=

-

=

=

=

-

c

c

^

b

h

l

Z

[

\

]

]

]

]

]

]

lub

'

'

'

'

'

'

' ,

x

x

t

y y

z z

t

t

c

x

v

v

2

=

+

=

=

=

+

c

c

^

b

h

l

Z

[

\

]

]

]

]

]

]

gdzie

'

c

v

1

1

2

=

-

c

b l

O – nieruchomy, inercjalny uk∏ad odniesienia

'

O – ruchomy, inercjalny uk∏ad odniesienia

'

v

"

– pr´dkoÊç uk∏adu '

O wzgl´dem uk∏adu O

u

"

– pr´dkoÊç czàstki w uk∏adzie '

O

'

x – wspó∏rz´dna czàstki zmierzona przez obserwatora '

O

x – wspó∏rz´dna czàstki zmierzona przez obserwatora O
t – czas ruchu uk∏adu '

O zmierzony przez obserwatora O

'

t – czas ruchu uk∏adu '

O zmierzony przez obserwatora '

O

Korzystajàc z transformacji Lorentza, mo˝na wykazaç, ˝e '

s

s

=

. Mówimy, ˝e interwa∏

czasoprzestrzenny jest niezmiennikiem transformacji Lorentza. Odleg∏oÊç mi´dzy dwoma
zdarzeniami czasoprzestrzennymi jest wi´c jednakowa w ka˝dym z inercjalnych uk∏adów
odniesienia. Zarówno obserwator '

O , jak i O, korzystajàc ze swoich pomiarów i obliczeƒ,

podadzà takà samà odleg∏oÊç (interwa∏) pomi´dzy dwoma zdarzeniami czasoprzestrzen-
nymi. Czasoprzestrzeƒ jest wi´c czymÊ absolutnym w szczególnej teorii wzgl´dnoÊci.

Je˝eli w ruchomym uk∏adzie '

O obserwator mierzy d∏ugoÊç pr´ta ustawionego wzd∏u˝

osi '

x , to otrzymuje wynik równy l

0

. Obserwator nieruchomy O, mierzàc d∏ugoÊç tego pr´ta,

otrzymuje wynik równy l, przy czym

<

l

l

0

.

VI. Efekty relatywistyczne

74

v

'

v

'

. t

x

'

x

O '

O

x

'

x

y

z

z'

y

'

"

u

"

Ryc. 6.1.

l

0

tak zwana d∏ugoÊç spoczynkowa (w∏asna) pr´ta:

'

l

l

c

l

v

1

0

2

=

=

-

c

b l

,

'

l l

c

v

1

0

2

=

-

b l

.

Je˝eli w uk∏adzie ruchomym '

O porusza si´ czàstka w kierunku '

x z szybkoÊcià u, to ob-

serwator nieruchomy O stwierdza, ˝e wzgl´dem niego szybkoÊç tej czàstki:

'

'

c

u

u

v

v

v

1

2

=

+

+

(zawsze

c

v

G

).

Je˝eli czàstka spoczywa w uk∏adzie '

O , to obserwator '

O stwierdza, ˝e ma ona mas´ m

0

.

Obserwator nieruchomy O stwierdza, ˝e czàstka ta ma mas´ m. Przy czym:

>

m

m

0

.

'

m

c

m

v

1

2

0

=

-

b l

,

m

0

– masa spoczynkowa czàstki.
Dylatacja czasu to wyd∏u˝enie odst´pu czasu, jeÊli pomiar przeniesiony zostanie do in-

nego ni˝ w∏asny uk∏adu odniesienia:

'

t

c

t

v

∆

∆

1

2

0

=

-

b l

>

t

t

∆

∆

0

^

h

,

t

∆

0

– odst´p czasu mi´dzy dwoma zdarzeniami, które zasz∏y w inercjalnym ruchomym

uk∏adzie '

O i zmierzone zosta∏y przez obserwatora '

O ;

t

∆

– odst´p czasu mi´dzy tymi samymi zdarzeniami zmierzony przez nieruchomego obser-

watora O.

Wed∏ug obserwatora O, czas w uk∏adzie ruchomym p∏ynie wolniej. Gdyby poczàtkowo

uk∏ady O i

'

O by∏y wzgl´dem siebie nieruchome, to zegary w obu uk∏adach mo˝na ustawiç

tak, by odmierza∏y jednakowo odst´py sekundowe t

∆

0

. Póêniej uk∏ad

'

O porusza∏by si´

z szybkoÊcià '

v , a jego zegar odmierza∏by odst´py sekundowe t

∆

(z punktu widzenia ob-

serwatora O). Obserwator

'

O majàcy przy sobie ten zegar stwierdza, ˝e odst´py sekundo-

we sà równe t

∆

0

. Kiedy obserwator O stwierdzi∏by, ˝e up∏yn´∏o na przyk∏ad 60 s

t

∆

60

0

^

h

na

zegarze O, to równie˝ stwierdzi∏by, ˝e w uk∏adzie

'

O up∏yn´∏o na przyk∏ad

t

∆

58

0

.

>

t

t

∆

∆

0

^

h

. Zatem czas w ruchomym uk∏adzie

'

O wed∏ug obserwatora O p∏ynie wolniej.

Równowa˝noÊç mi´dzy masà a energià:

m

c

E

2

=

.

Cia∏u o masie m odpowiada ca∏kowita relatywistyczna energia E proporcjonalna do

masy tego cia∏a.

c

s

m

3 10

8

$

=

– szybkoÊç Êwiat∏a w pró˝ni.

Je˝eli cia∏o spoczywa, to ma mas´ spoczynkowà m

0

, której odpowiada energia:

E

m c

0

0

2

=

.

Gdy cia∏o jest w ruchu:

E

mc

2

=

.

Wprowadzenie

75

Energia kinetyczna cia∏a równa jest ró˝nicy pomi´dzy energià ca∏kowità cia∏a podczas

ruchu a energià, gdy cia∏o by∏o w spoczynku: E

E

E

k

0

=

-

;

'

'

E

mc

m c

c

m c

m c

m c

c

v

v

1

1

1

1

k

2

0

2

2

0

2

0

2

0

2

2

=

-

=

-

-

=

-

-

J

L

K

K

K

KK

b

b

N

P

O

O

O

O

O

l

l

.

Zadania

Dane do zadaƒ rachunkowych:
pr´dkoÊç Êwiat∏a: c

s

m

3 10

8

$

=

.

1.1.

Przy jakiej szybkoÊci wzgl´dnej skrócenie d∏ugoÊci pr´ta wynosi 25%?

1.2.

Z jakà szybkoÊcià powinien poruszaç si´ pr´t w kierunku swojej d∏ugoÊci, by nieru-

chomy obserwator okreÊli∏ jego d∏ugoÊç jako dwukrotnie mniejszà od d∏ugoÊci spo-

czynkowej?

1.3.

Dwie rakiety poruszajà si´ w przeciwne strony z tymi samymi szybkoÊciami równy-
mi , c

0 9

. Oblicz szybkoÊç jednej z rakiet zmierzonà przez obserwatora b´dàcego

w drugiej rakiecie. Wynik porównaj z wynikiem uzyskanym wed∏ug rozwiàzania
zgodnego z zasadami mechaniki klasycznej.

1.4.

W przeciwne strony równoczeÊnie wys∏ano dwa promienie Êwiat∏a. Oblicz szybkoÊç
jednego promienia wzgl´dem drugiego.

1.5.

Do jakiej szybkoÊci powinien byç rozp´dzony elektron, aby jego masa by∏a dwukrot-

nie wi´ksza od masy spoczynkowej?

1.6.

Cia∏o o kszta∏cie walca o d∏ugoÊci spoczynkowej l

0

porusza si´ z du˝à szybkoÊcià

'

c

v

2

3

=

w kierunku x wzd∏u˝ swojej osi. Ile razy g´stoÊç cia∏a poruszajàcego si´ jest

wi´ksza od g´stoÊci cia∏a spoczywajàcego?

1.7.

Rakieta o masie spoczynkowej

t

10

ma lecieç do najbli˝szej gwiazdy Proximy Cen-

tauri z szybkoÊcià '

,

c

v

0 9998

=

. Jakà prac´ powinny wykonaç silniki rakiety, by roz-

p´dziç jà do takiej szybkoÊci?

1.8.

Przy jakiej szybkoÊci energia kinetyczna czàstki równa jest jej energii spoczynkowej?

1.9.

Foton jest kwantem energii elektromagnetycznej. Jakiej masie odpowiada energia
fotonu o d∏ugoÊci fali

m? Dana jest sta∏a Plancka i szybkoÊç Êwiat∏a.

1.10. W 1997 roku Êwiatowe zu˝ycie energii elektrycznej wynosi∏o ,

13 95 10

15

$

Wh. Oblicz,

jakiej masie odpowiada ta energia.

VI. Efekty relatywistyczne

76

Rozwiàzania

77

Rozwiàzania

VI. Efekty relatywistyczne

1.1.

Dane:

Szukane:

,

l

l

∆

0 25

0

=

'

?

v =

c

s

m

3 10

8

$

=

,

,

l l

l

l l

l l

l

l

∆

∆

0 25

0 75

0

0

0

0

0

"

=

-

=

-

=

-

=

,

'

:

l

l

c

l

v

0 75

1

0

0

2

0

=

-

b l

,

'

c

v

0 75

1

2

2

=

-

^

b

h

l

'

c

v

1

4

3

1

16

9

16

7

2

2

2

=

-

=

-

=

^

b

h

l

'

'

,

,

c

c

c

s

m

v

v

16

7

4

7

0 66

1 98 10

2

2

8

"

$

=

=

=

=

^ h

1.2.

Dane:

Szukane:

l

l

2

1

0

=

'

?

v =

c

s

m

3 10

8

$

=

'

l

l

c

v

2

1

1

0

0

2

=

-

b l

'

c

v

4

1

1

2

2

=

-

^ h

'

'

c

c

v

v

4

3

2

3

2

"

=

=

b l

'

,

,

c

c

s

m

v

2

3

0 87

2 6 10

8

$

=

=

=

1.3.

Dane:

Szukane:

'

,

c

v

0 9

=

?

v =

,

u

c

0 9

=

c

Wed∏ug mechaniki klasycznej:

'

,

u

c

v

v

1 8

=

+

=

,

>

c

v

^

h

.

Z rozwiàzania klasycznego wynika, ˝e szybkoÊç wypadkowa jest wi´ksza od szyb-

koÊci Êwiat∏a. Jest to sprzeczne z postulatem szczególnej teorii wzgl´dnoÊci.
Wed∏ug mechaniki relatywistycznej:

'

'

,

,

,

,

,

c

u

u

c

c

c

c

c

c

v

v

v

1

1

0 81

1 8

1 81

1 80

0 995

2

2

2

=

+

+

=

+

=

=

'

<

c

v

^

h

.

1.4.

Dane:

Szukane:

u c

=

?

v =

'

c

v =

Wed∏ug mechaniki klasycznej:

'

u

c

v

v

2

=

+

=

!

>

c

v

^

h

.

Wed∏ug mechaniki relatywistycznej:

'

'

c

u

u

c

c

c

c

c

v

v

v

1

1

2

2

2

2

2

2

=

+

+

=

+

=

=

c

v =

^

h

.

Wynik jest zgodny z postulatem szczególnej teorii wzgl´dnoÊci.

1.5.

Dane:

Szukane:

c

s

m

3 10

8

$

=

'

?

v =

m

m

2

0

=

'

m

c

m

v

1

2

0

=

-

b l

'

:

m

c

m

m

v

2

1

0

2

0

0

=

-

b l

'

'

'

c

c

c

v

v

v

4

1

1

1

4

1

4

3

2

2

2

"

"

=

-

-

=

=

b

b

b

l

l

l

'

'

,

,

c

c

c

s

m

v

v

2

3

2

3

0 86

2 6 10

8

"

$

=

=

=

=

1.6.

Dane:

Szukane:

'

c

v

2

3

=

?

0

=

t

t

G´stoÊç cia∏a podczas spoczynku:

m

l S

m

V

0

0

0

0

0

=

=

t

V – obj´toÊç cia∏a

G´stoÊç cia∏a podczas ruchu:

m

l S

m

V

=

=

t

'

'

'

c

l

c

S

m

c

v

v

v

1

1

1

2

0

2

0

2

0

=

-

-

=

-

t

t

b

b

b

l

l

l

VI. Efekty relatywistyczne

78

x

m

l

S

v

'

"

Ryc. 6.2.

Wymiary cia∏a poprzeczne wzgl´dem kierunku ruchu nie zmieniajà si´, dlatego

przekrój S pozostaje ten sam.

'

c

v

1

1

1

4

3

1

4

1

1

4

0

2

=

-

=

-

=

=

t

t

b l

,

4

0

=

t

t

G´stoÊç cia∏a przy tak olbrzymiej szybkoÊci wzros∏a 4-krotnie.

1.7.

Dane:

Szukane:

m

kg

10

10

t

0

4

=

=

?

W =

'

,

c

v

0 9998

=

c

s

m

3 10

8

$

=

Praca ta jest równa zyskanej energii kinetycznej.

W E

k

=

W mc

m c

2

0

2

=

-

'

,

W m c

c

kg

s

m

v

1

1

1

10

9 10

1

0 9996

1

1

0

2

2

4

16

2

2

$ $

=

-

-

=

-

-

J

L

K

K

K

KK

b

f

N

P

O

O

O

O

O

l

p

,

W

J

4 41 10

22

$

=

Energia ta przewy˝sza oko∏o 880 razy energi´ elektrycznà wyprodukowanà w cià-

gu roku przez wszystkie elektrownie na Ziemi.

1.8.

Dane:

Szukane:

E

E

k

0

=

'

?

v =

E

E

k

0

=

E

E

E

0

0

-

=

E

E

2

0

=

mc

m c

m

m

2

2

2

0

2

0

"

=

=

'

'

m

c

m

c

v

v

2

1

2

1

1

0

2

0

2

"

=

-

=

-

b

b

l

l

'

'

c

c

v

v

1

4

1

4

3

2

2

"

-

=

=

b

b

l

l

'

,

c

v

2

3

0 86

=

=

'

,

c

v

0 86

=

Rozwiàzania

79

1.9.

Dane:

Szukane:

m, c

?

m =

h – sta∏a Plancka

Foton nie ma masy spoczynkowej. Energia fotonu w teorii elektromagnetycznej

fal wyra˝a si´ wzorem:

E

hc

f

=

m

.

W szczególnej teorii wzgl´dnoÊci energia dowolnego obiektu wyra˝a si´ wzorem:

E

mc

2

=

.

Zatem: E

mc

f

2

=

,

mc

hc

m

c

h

2

"

=

=

m

m

.

Na przyk∏ad fotonowi rentgenowskiemu o d∏ugoÊci fali

m

10

10

=

m

-

odpowiada

masa

,

m

kg

2 2 10

32

$

=

-

.

1.10. Dane: Szukane:

,

E

Wh

13 95 10

15

$

=

?

m =

c

s

m

3 10

8

$

=

,

,

,

,

E

Wh

Ws

J

13 95 10

13 95 3 6 10

10

50 22 10

15

3

15

18

$

$

$

$

$

=

=

=

E

mc

2

=

Energii takiej odpowiada masa:

,

m

c

E

s

m

J

kg

9 10

50 22 10

558

2

16

2

2

18

$

$

=

=

=

.

Gdyby jakàkolwiek form´ materii o masie 558 kg (np. odpady zanieczyszczajàce

Êrodowisko naturalne) ca∏kowicie „zamieniç” na energi´, to zaspokoi∏aby ona rocz-
ne zapotrzebowanie Êwiata na energi´. Niestety, nie znamy jeszcze sposobu, by
z cia∏ makroskopowych wydobywaç energi´ w iloÊci równowa˝nej masie tych cia∏.

VI. Efekty relatywistyczne

80