1

Badania

operacyjne

(#3)

dr inż. Marek Rabiński

Wyższa Szkoła Działalności Gospodarczej

2

Badania operacyjne (część 3)

z

Zagadnienie optymalizacji

z

Programowanie liniowe

z

Programowanie w liczbach całkowitych

z

Programowanie nieliniowe.

3

Zagadnienie optymalizacyjne

z

Funkcja celu (kryterium decyzyjne)
f(x) = f(x

1

, x

2

, … , x

n

)

z

Zmienne decyzyjne (wielkości optymalizowane)
x

j

(j=1, 2, … , n)

z

Ograniczenia, warunki ograniczające (funkcja nakładów)
V

i

(x) = V

i

(x

1

, x

2

, … , x

n

)

(i=1, 2, … , m) (warunki uboczne).

z

Funkcje celu i nakładów są ciągłe i różniczkowalne (posiadają ciągłe

pochodne cząstkowe pierwszego i drugiego rzędu) i są określone na

n–wymiarowym wektorze x o nieujemnych składowych
x ≥ 0

(warunki brzegowe)

czyli
x

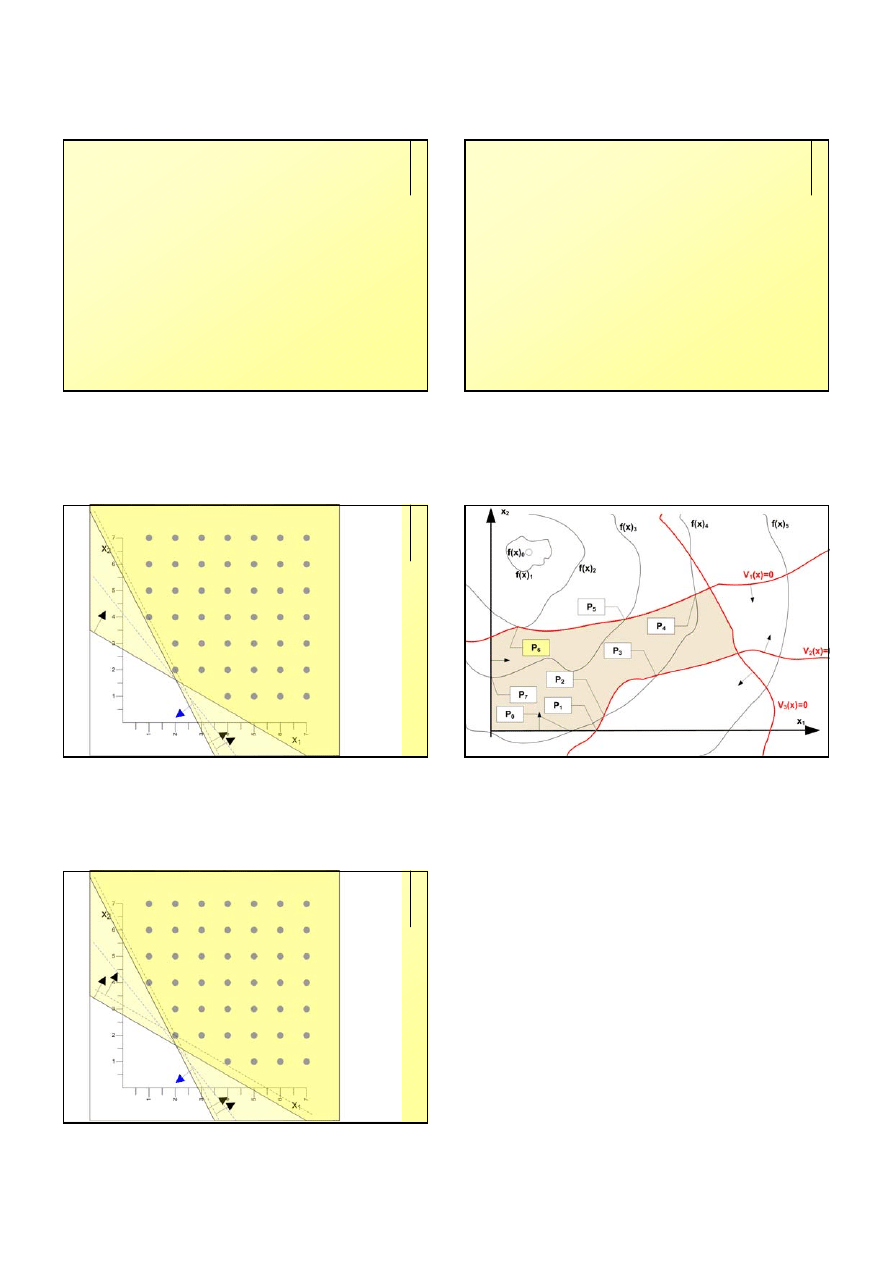
j

≥ 0

(j=1, 2, … , n).

z

Zadanie optymalizacyjne polega na wyznaczeniu ekstremum

(maksimum lub minimum) funkcji celu przy zadanych ograniczeniach.

z

Zadanie optymalizacyjne ma rozwiązanie jeśli nie jest wewnętrznie

sprzeczne (zbiór rozwiązań dopuszczalnych nie jest zbiorem pustym)

oraz gdy m ≤ n.

4

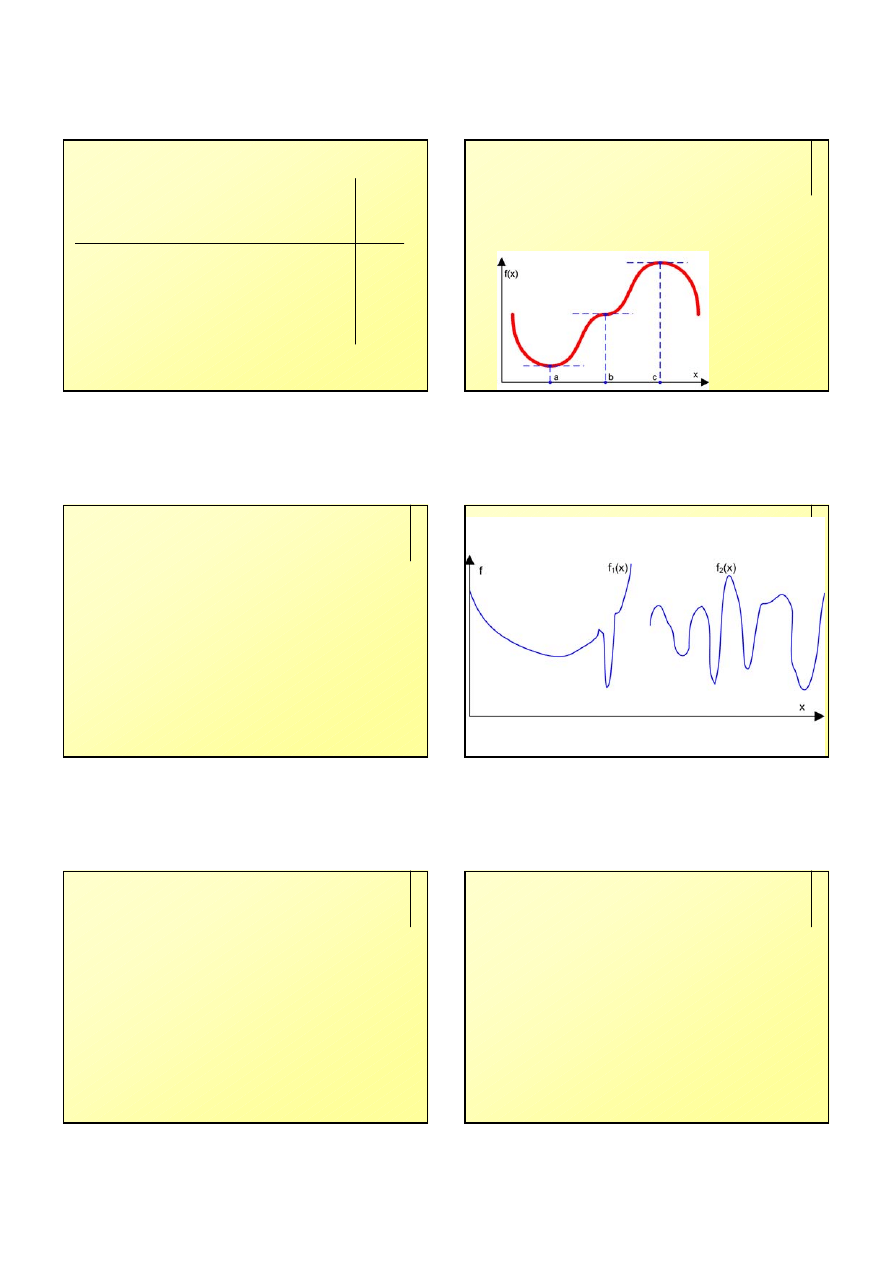
Ekstremum funkcji jednej zmiennej

z

Funkcja celu: f(x)

z

W przedziale istnieje taki punkt x

0

, że f’(x

0

)=0 oraz f’’(x

0

)≠0

z

Druga pochodna f’’(x

0

) jest ciągła – w punkcie x

0

istnieje ekstremum:

z

maksimum jeśli f’’(x

0

)<0

z

minimum jeśli f’’(x

0

)>0.

z

Dla f’’(x

0

)=0 w punkcie x

0

istnieje punkt przegięcia.

5

Funkcje trudne do optymalizacji

6

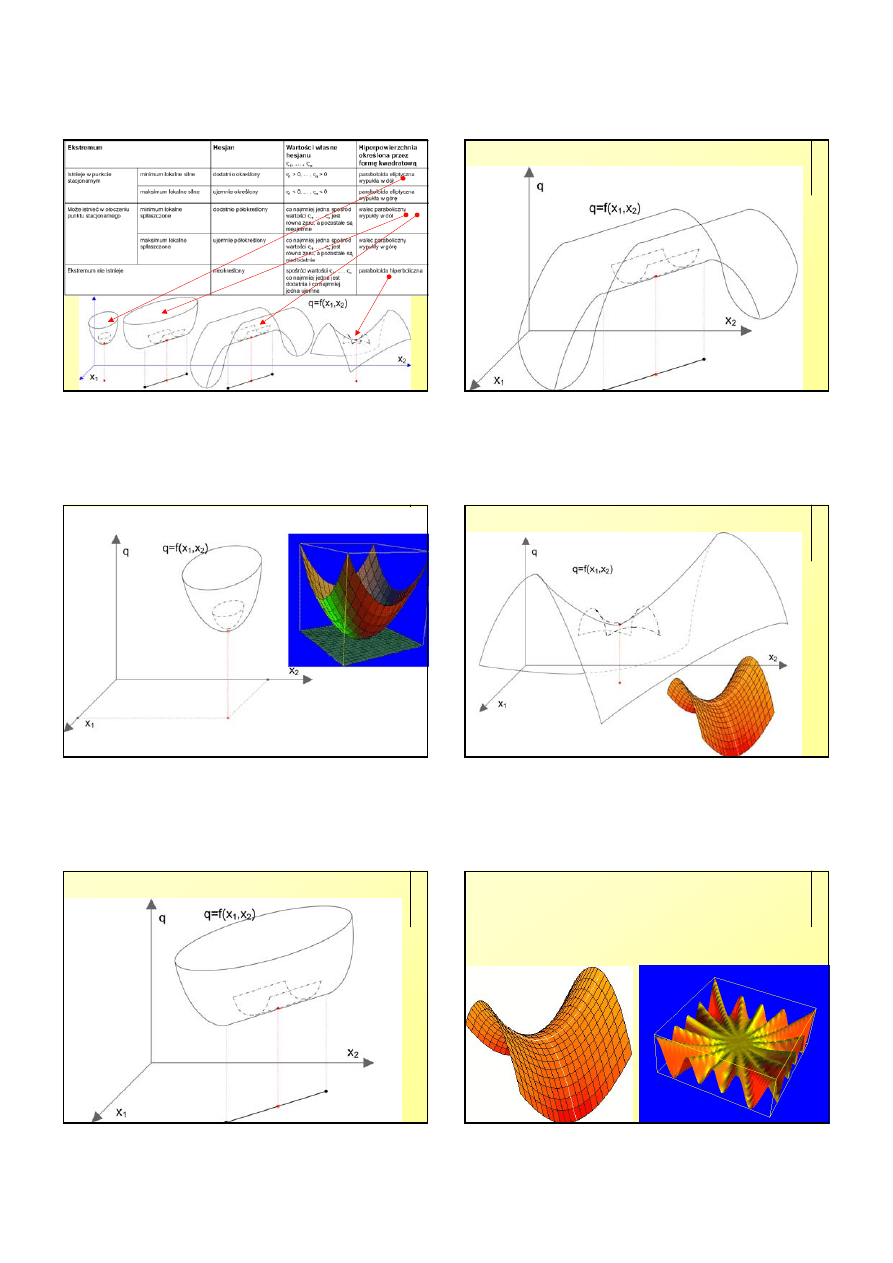
Ekstremum funkcji n zmiennych

z

Funkcja celu – f(x)

z

Hesjan funkcji f(x) w punkcie x=(x

1

, x

2

, … x

n

)

| (∂

2

f / ∂

2

x

1

2

)

x

(∂

2

f / ∂x

1

∂ x

2

)

x

…

(∂

2

f / ∂x

1

∂ x

n

)

x

|

(

Ï

2

f)

x

= |

…

…

…

|

| (∂

2

f / ∂x

n

∂ x

1

)

x

(∂

2

f / ∂x

n

∂ x

2

)

x

… (∂

2

f / ∂

2

x

n

2

)

x

|

2

7

8

Paraboloida eliptyczna wypukła w dół

9

Walec paraboliczny wypukły w dół

z

Minimum spłaszczone

10

Walec paraboliczny wypukły w dół

z

Minimum spłaszczone nie istnieje

11

Paraboloida hiperboliczna

12

Paraboloida hiperboliczna

z

Punkt siodłowy

3

13

Programowanie liniowe

z

Programowanie liniowe (ang: linear programming) – liniowe
zagadnienie optymalizacji.

z

Zagadnienia optymalizacji były rozwijane niezależnie w różnych
dziedzinach nauki, stąd terminologia poszczególnych zagadnień jest
zróżnicowana i niespójna. Spowodowało to powstanie i
upowszechnienie wielu specyficznych określeń, takich jak –
‘programowanie liniowe’, ‘programowanie nieliniowe’.
Określenia te posiadają długą tradycję, stąd w niektórych dziedzinach
(np. ekonomii) są powszechnie używane. Jednak w naukach
technicznych są uznawane za wybitnie mylące, ze względu na
skojarzenia z programowaniem komputerów. Dlatego w teorii
optymalizacji używa się określenia ‘poszukiwanie ekstremum funkcji
liniowych przy liniowych warunkach ograniczających’.

14

Programowanie liniowe

z

Funkcja celu jest:

z

funkcją liniową – zawiera zmienne decyzyjne wyłącznie stopnia pierwszego

(np. f(x

1

) = a*x

1

+ b)

z

lub jest formą liniową – funkcją liniową bez wyrazu wolnego od zmiennej x

1

(np. f(x

1

) = a*x

1

)

z

Warunki uboczne V

i

(x) = V

i

(x

1

, x

2

, … , x

n

) (i=1, 2, … , m) mają postać

układu równań liniowych

z

a

i1

x

1

+ a

i2

x

2

+ … + a

in

x

n

= b

i

(i=1, 2, … , m)

lub nierówności liniowych

z

a

i1

x

1

+ a

i2

x

2

+ … + a

in

x

n

≤ b

i

(i=1, 2, … , m)

z

Warunki uboczne oraz brzegowe wyznaczają dopuszczalny obszar

rozwiązań.

15

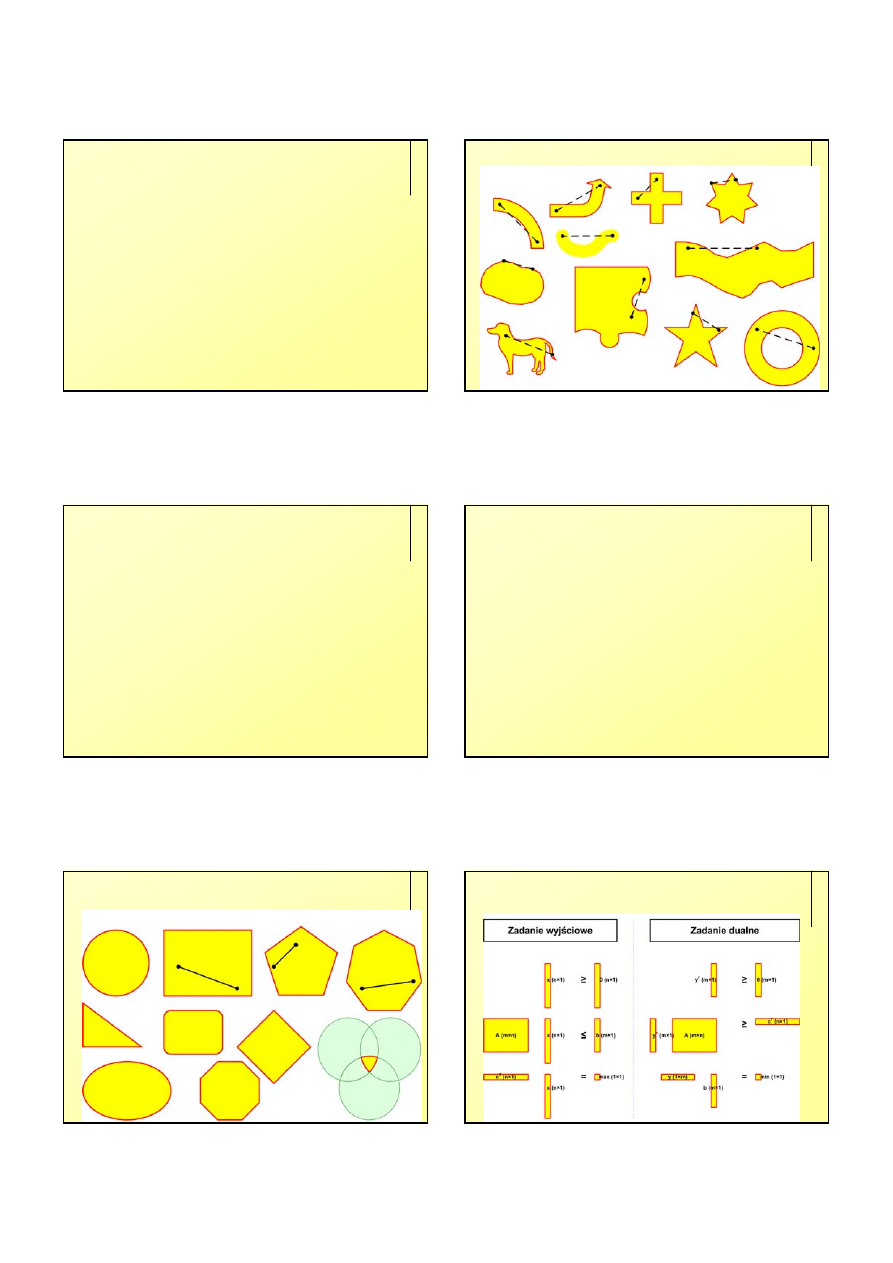
Zbiór wypukły

z

Zbiór punktów, dla którego wszystkie punkty na odcinku łączącym dwa
punkty p i q należące do zbioru – należą również do tego zbioru.

16

Zbiory niewypukłe

17

Zagadnienie dualne
programowania liniowego

z

Pierwotne zadanie wyjściowe
c

T

x → max,

A x ≤ b,
x ≥ 0.

z

Dla każdego zagadnienia programowania liniowego można stworzyć

dualne zagadnienie, które również jest zagadnieniem programowania

liniowego. Między zagadnieniami występują wzajemne zależności – np.

zadanie dualne zagadnienia dualnego jest wyjściowym zadaniem

pierwotnym.

z

Zadanie dualne
y b → min,
y

T

A ≥ c

T

,

y

T

≥ 0.

18

Zagadnienie dualne
programowania liniowego

4

19

Przykład: planowanie produkcji

z

Przedsiębiorstwo może produkować dwa wyroby:

z

X

1

– urządzenie o opanowanej technologicznie produkcji, choć niezbyt

nowoczesne,

z

X

2

– urządzenie nowoczesne, jednak o wyższych kosztach komponentów i

mniejszej zyskowności produkcji.

z

Rozpatrywane zagadnienie polega na określeniu optymalnej wielkości

produkcji obu wyrobów, przynoszącej przedsiębiorstwu maksymalny

zysk.

z

Zmienne decyzyjne:

z

x

1

– wielkość produkcji wyrobu X

1

,

z

x

2

– wielkość produkcji wyrobu X

2

.

z

Swobodę decyzyjną ograniczają zasoby przedsiębiorstwa:

z

99 jednostek surowca,

z

96 jednostek czasu pracy urządzeń produkcyjnych,

z

125 jednostek powierzchni produkcyjnej,

z

utrzymanie się na rynku branży wymaga wyprodukowania co najmniej 1

jednostki (partii) wyrobu X

2

.

20

Przykład: planowanie produkcji

z

Jednostkowe zużycie zasobów (spowodowane stosowanymi

technologiami) wymaga:

z

zużycia surowców –

z

9 jednostek surowca na jednostkę wyrobu X

1

,

z

11 jednostek surowca na jednostkę X

2

.

z

czasu pracy urządzeń –

z

12 jednostek czasu pracy na jednostkę wyrobu X

1

,

z

8 jednostek czasu na jednostkę X

2

.

z

wykorzystania powierzchni produkcyjnej –

z

10 jednostek powierzchni na jednostkę wyrobu X

1

,

z

10 jednostek powierzchni na jednostkę X

2

.

z

Jednostkowe zyski z produkcji wynoszą odpowiednio:

z

6 jednostek monetarnych na jednostkę wyrobu X

1

,

z

2.5 jednostek monetarnych na jednostkę X

2

.

21

z

Model matematyczny zagadnienia:

max f(x) = 6*x

1

+ 2.5*x

2

(zysk z produkcji)

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

(zużycie surowców)

12*x

1

+ 8*x

2

≤ 96

(wykorzystanie urządzeń)

x

2

≥ 1

(warunek utrzymania się na rynku)

10*x

1

+ 10*x

2

≤ 125

(powierzchnia produkcyjna)

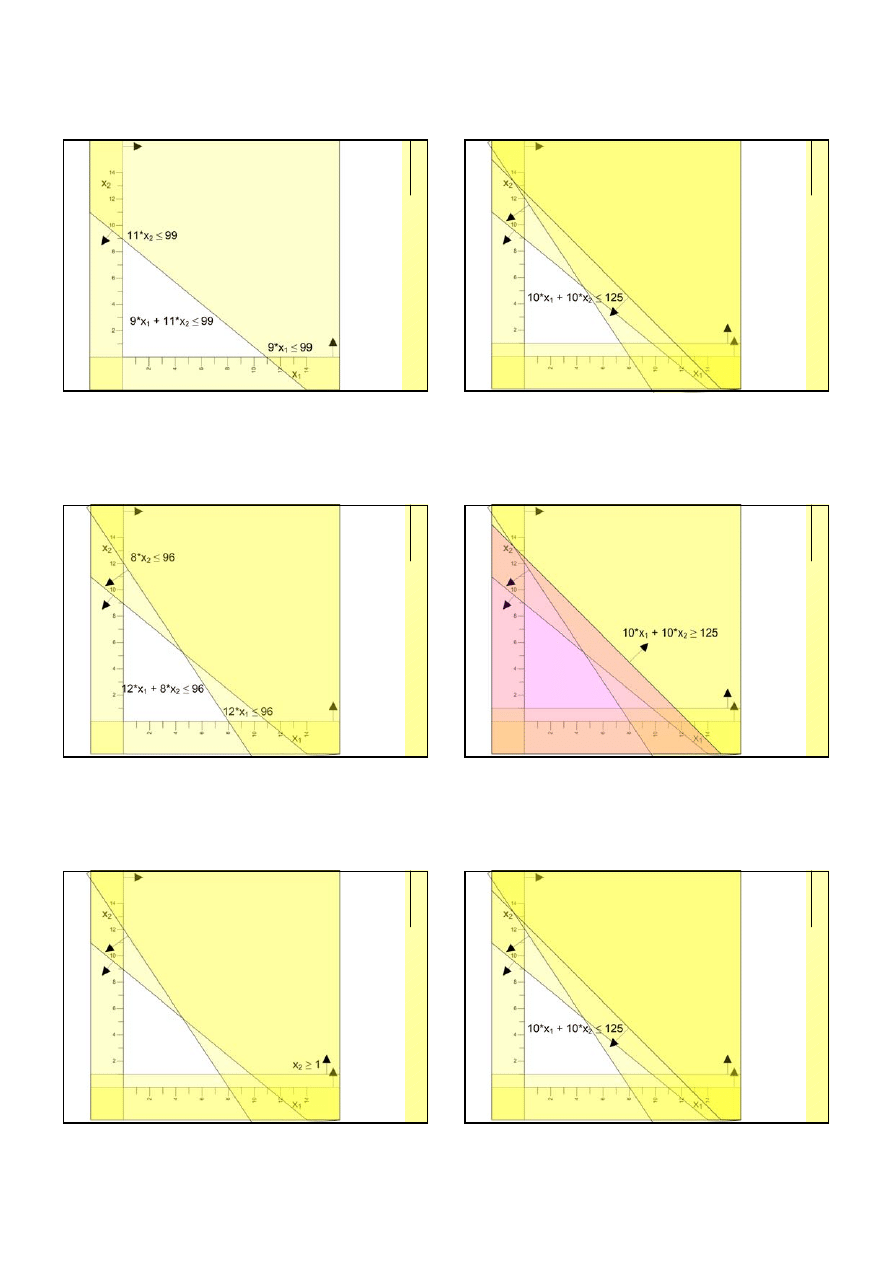
22

max f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

23

max f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

24

max f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

5

25

max f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

26

max f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

27

max f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

28

max f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

29

max f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≥ 125

30

max f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

6

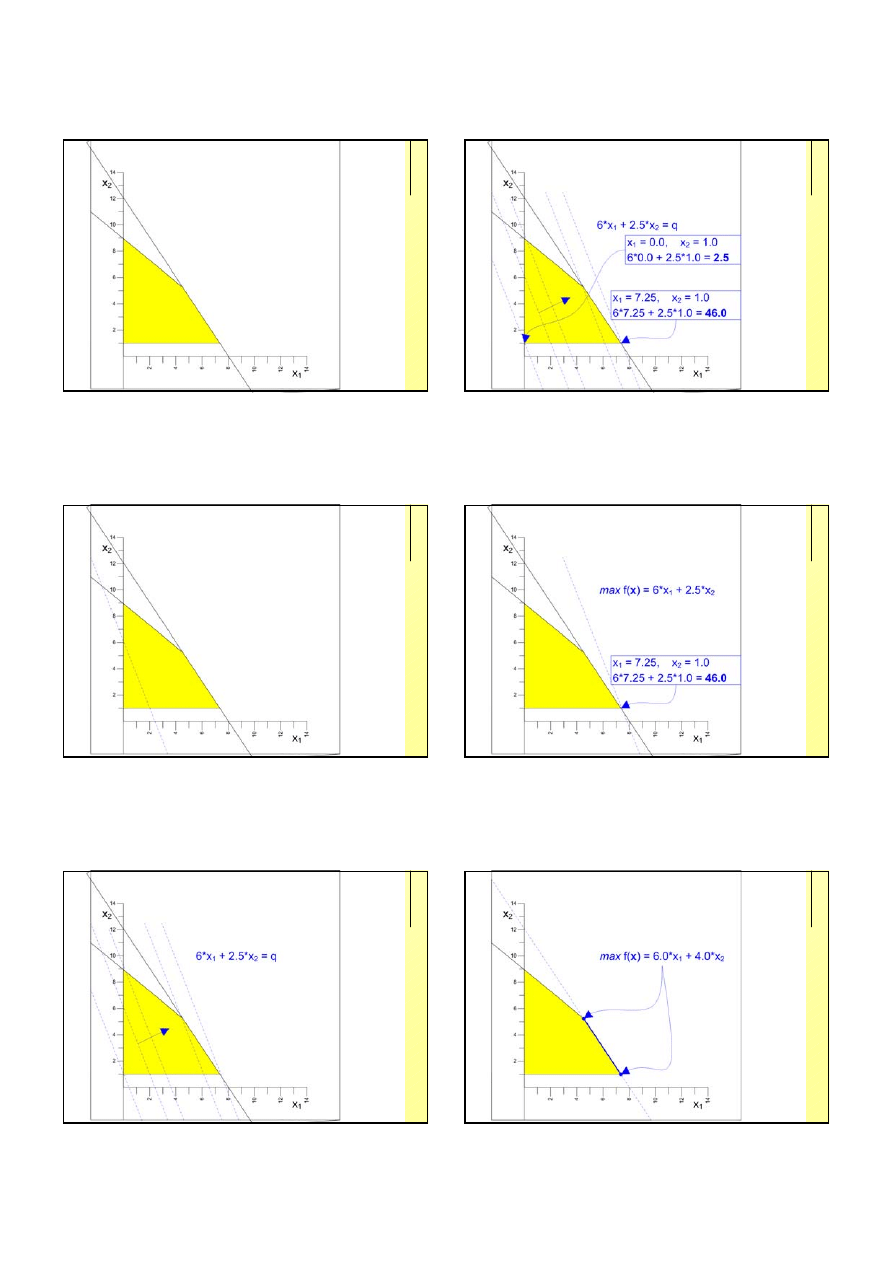
31

max f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

32

max

f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

33

max

f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

34

max

f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

35

max

f(x) = 6*x

1

+ 2.5*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

36

max

f(x) = 6*x

1

+ 4.0*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

7

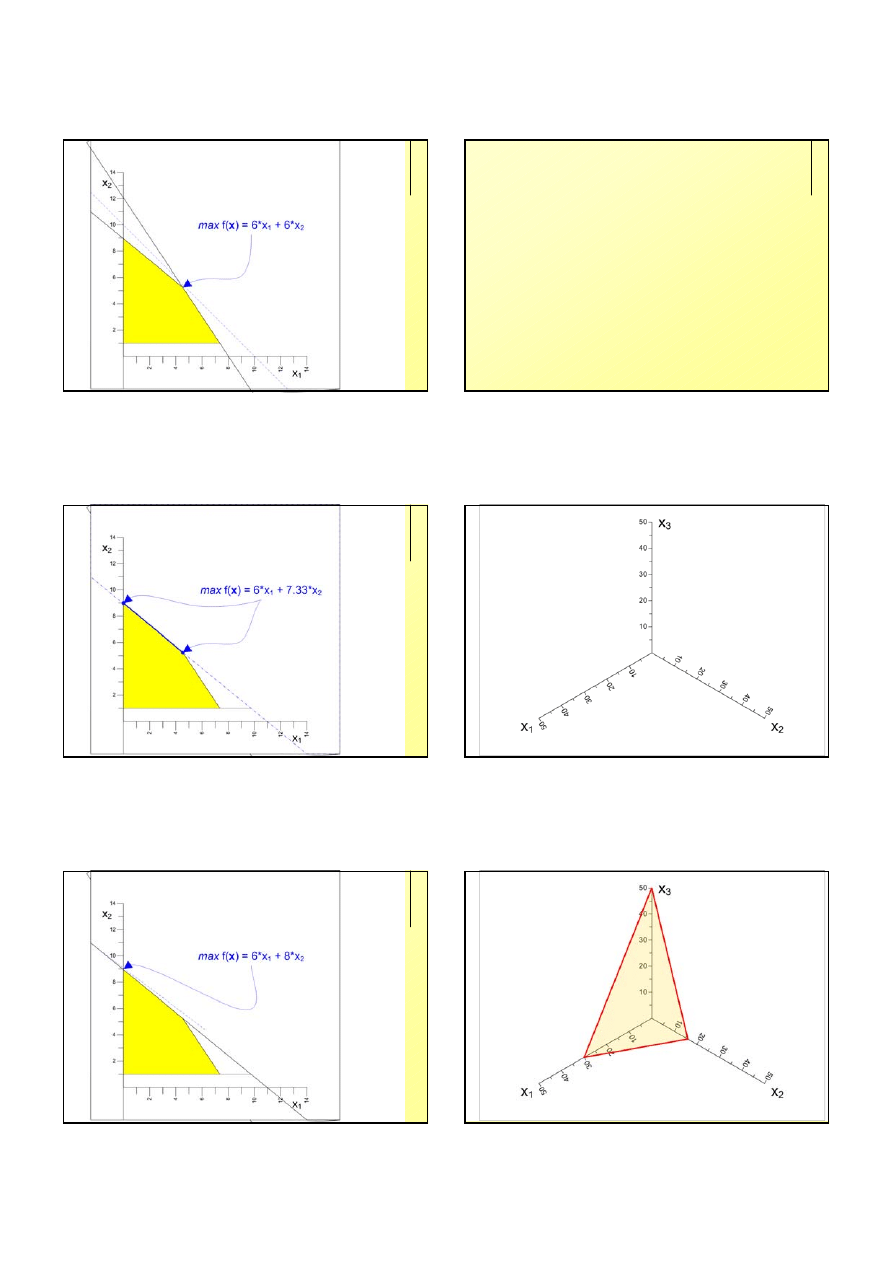
37

max

f(x) = 6*x

1

+ 6.0*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

38

max

f(x) = 6*x

1

+7.33*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

39

max

f(x) = 6*x

1

+ 8.0*x

2

x

1

≥ 0

x

2

≥ 0

9*x

1

+ 11*x

2

≤ 99

12*x

1

+ 8*x

2

≤ 96

x

2

≥ 1

10*x

1

+ 10*x

2

≤ 125

40

Zagadnienie trójwymiarowe

z

Model matematyczny zagadnienia:

max f(x) = 4*x

1

+ 3*x

2

+ 3*x

3

75*x

1

+ 150*x

2

+ 45*x

3

≤ 2250

120*x

1

+ 60*x

2

+ 80*x

3

≤ 2400

100*x

1

+ 40*x

2

+ 25*x

3

≤ 1000

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0

41

z

Aksonometria ‘kawaleryjska’ – identyczna skala na wszystkich osiach

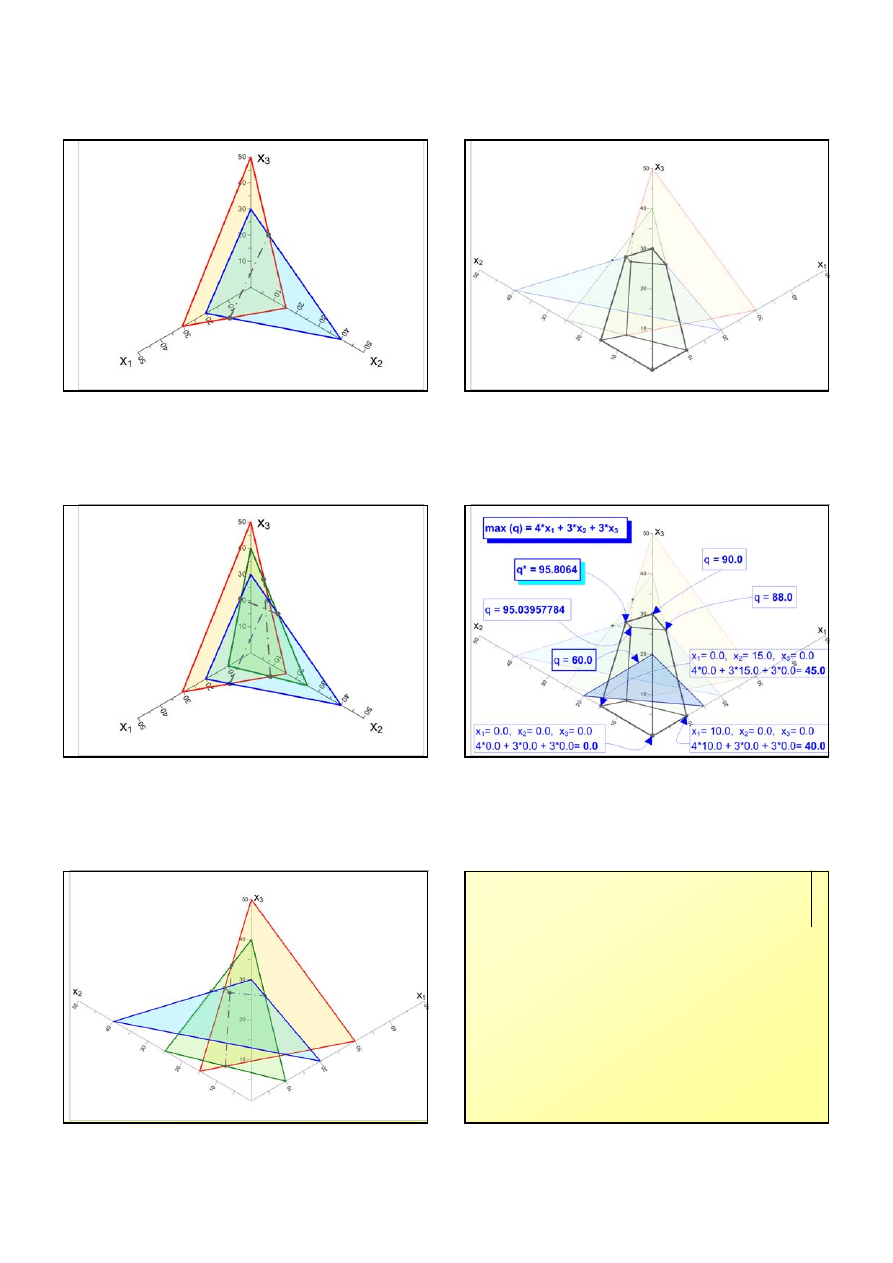
42

75*x

1

+ 150*x

2

+ 45*x

3

≤ 2250

120*x

1

+ 60*x

2

+ 80*x

3

≤ 2400

100*x

1

+ 40*x

2

+ 25*x

3

≤ 1000

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0

8

43

75*x

1

+ 150*x

2

+ 45*x

3

≤ 2250

120*x

1

+ 60*x

2

+ 80*x

3

≤ 2400

100*x

1

+ 40*x

2

+ 25*x

3

≤ 1000

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0

44

75*x

1

+ 150*x

2

+ 45*x

3

≤ 2250

120*x

1

+ 60*x

2

+ 80*x

3

≤ 2400

100*x

1

+ 40*x

2

+ 25*x

3

≤ 1000

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0

45

Wygląd obszaru dopuszczalnych rozwiązań od strony początku układu

współrzędnych

46

75*x

1

+ 150*x

2

+ 45*x

3

≤ 2250

120*x

1

+ 60*x

2

+ 80*x

3

≤ 2400

100*x

1

+ 40*x

2

+ 25*x

3

≤ 1000

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0

47

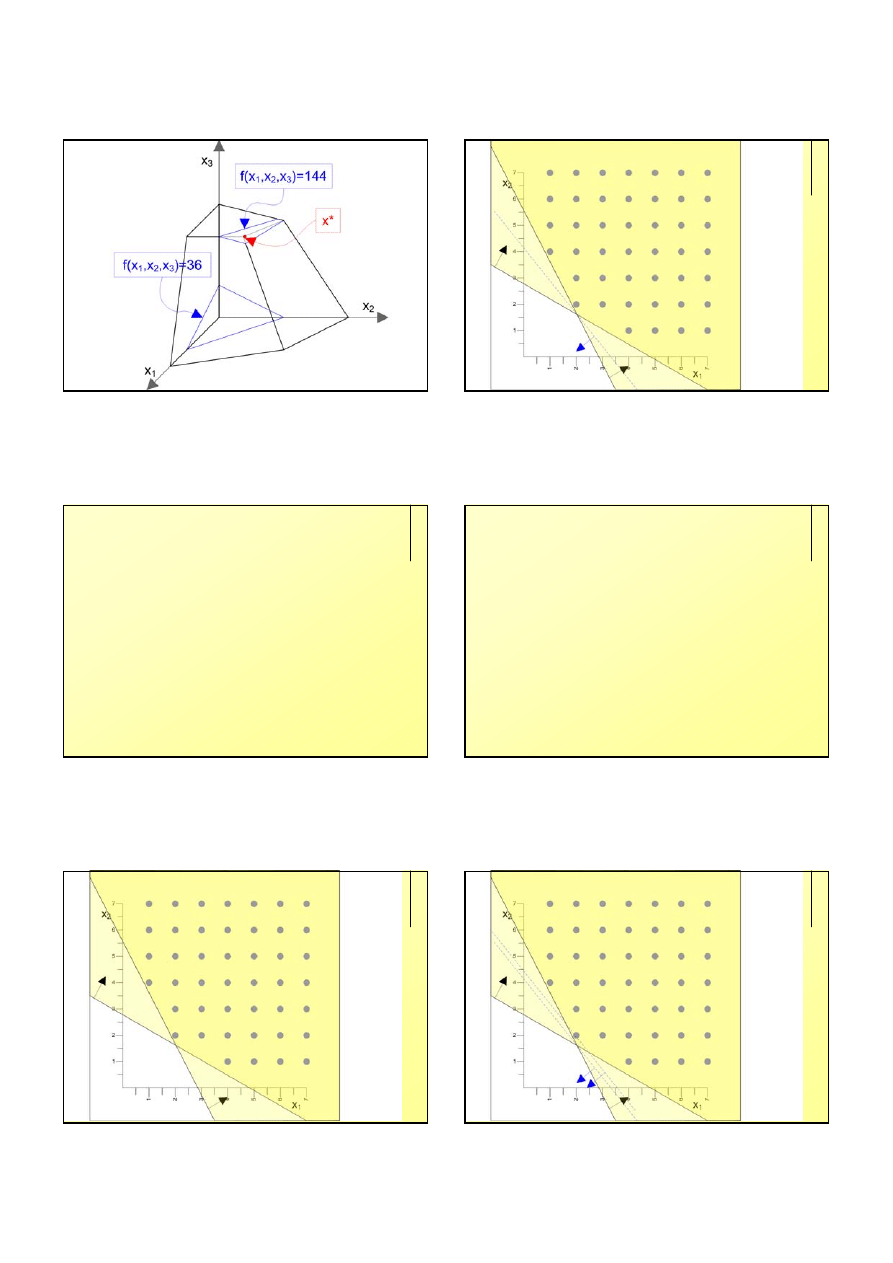
48

Zagadnienie trójwymiarowe

z

Model matematyczny zagadnienia:

max f(x) = 8*x

1

+ 9*x

2

+ 18*x

3

15*x

1

+ 5*x

2

+ 6*x

3

≤ 90

3*x

1

+ 6*x

2

+ 4*x

3

≤ 48

x

1

+ x

2

+ 4*x

3

≤ 28

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0

9

49

max f(x) = 8*x

1

+ 9*x

2

+ 18*x

3

15*x

1

+ 5*x

2

+ 6*x

3

≤ 90

3*x

1

+ 6*x

2

+ 4*x

3

≤ 48

x

1

+ x

2

+ 4*x

3

≤ 28

x

1

≥ 0, x

2

≥ 0, x

3

≥ 0

50

Optymalizacja w liczbach całkowitych

z

Zagadnienie wyznaczenia wartości optymalnej w liczbach całkowitych.
Z przypadkiem takim można się spotkać w odniesieniu do dużych
niepodzielnych obiektów typu samolotów, statków, turbin, zakładów
produkcyjnych, w zagadnieniach transportu towarów.

z

Najprostszą metodą rozwiązania zagadnienia (dającą się zastosować
wyjątkowo rzadko) może być zaokrąglenie do całkowitej wartości
wyniku optymalizacji prowadzonej bez wymogu uzyskania wielkości
całkowitych.

z

Większość pozostałych metod wymaga dwuetapowego procesu
rozwiązania zagadnienia

z

etap pierwszy – wyznaczenie rozwiązania w liczbach ułamkowych,

z

etap drugi – sprowadzenie rozwiązania ułamkowego do rozwiązania w
liczbach całkowitych.

51

52

53

Optymalizacja w liczbach całkowitych

z

Metoda A.H.Landa–A.G.Doiga

z

etap pierwszy – wyznaczenie rozwiązania optymalnego w liczbach
ułamkowych,

z

etap drugi – przejście do rozwiązania w liczbach całkowitych przez
przesunięcie warstwicy optymalnej w głąb obszaru rozwiązań
dopuszczalnych, aż do uzyskania pierwszego rozwiązania całkowitego.
Przesunięcie wiąże się z uzyskaniem gorszej wartości funkcji kryterium.

54

10

55

Optymalizacja w liczbach całkowitych

z

Metoda R.E.Gomory’ego

z

etap pierwszy – wyznaczenie rozwiązania optymalnego w liczbach
ułamkowych,

z

etap drugi – dodanie do warunków ograniczających nowego warunku
(nowych warunków) oraz nowej zmiennej (nowych zmiennych) do zbioru
zmiennych decyzyjnych.

56

57

58

Programowanie nieliniowe

59

Programowanie nieliniowe