MATEMATYKA DYSKRETNA

Skrypt pisany na podstawie wykładu prowadzonego przez

Dr. T. Traczyka

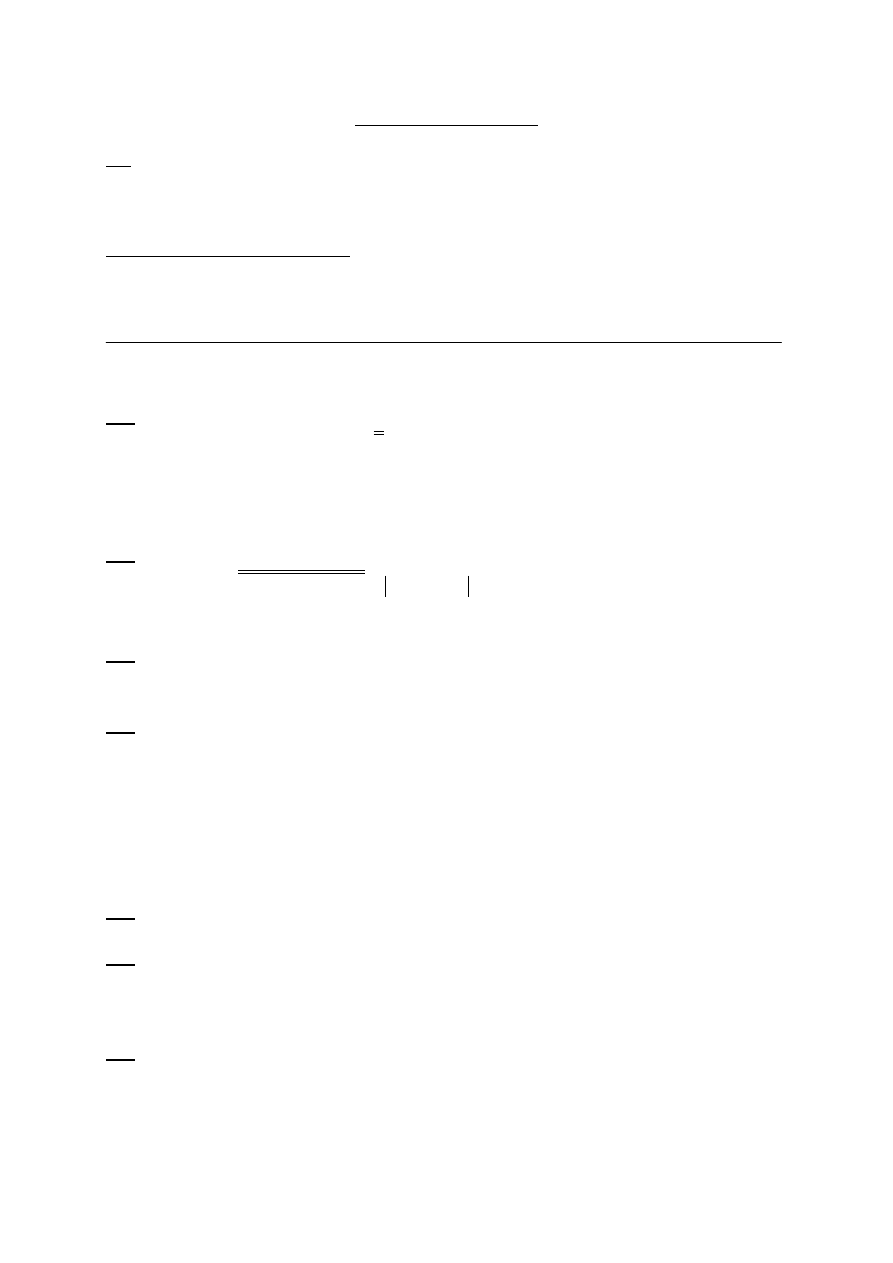
Wiadomości wstępne

Tw. O indukcji matematycznej



   

  















  









n

n

n

k

k

n

k

n

N

n









0

0

0

0

1





















Zasada szufladkowa Dirichleta

Jeżeli do n szuflad włożymy n+1 przedmiotów, to w co najmniej jednej szufladzie
będzie 2 lub więcej przedmiotów.

Definicje

Def.

Grafem nazywamy parę





E

V ,

gdzie

V

– zbiór (skończony) niepusty,

 

 





2

:

2

2













A

V

A

A

V

V

P

E

V

-

zbiór wierzchołków

E - zbiór krawędzi

Def.

Stopniem wierzchołka v w grafie





E

V

G

,



jest liczba

 

 



 



E

uv

u

E

v

u

V

u

v

G











:

,

:

deg

Def.

0

deg



v

wtedy v

– izolowany

1

deg



v

wtedy v

– liść

Def.





E

V

G

,



,

V

v

u



,

u-v

drogą w G nazywamy ciąg





k

v

v

v

,...,

,

1

0

gdzie

1)

v

v

u

v

k





,

0

2)







E

v

v

k

i

i

i











1

,

1

,...,

1

,

0

3)





 







1

1

,

,

1

,

0



















j

j

i

i

v

v

v

v

j

i

k

j

i

Liczbę k nazywamy długością drogi. Jeżeli ponadto









j

i

v

v

j

i

j

i









,

to





k

v

v ,...,

0

jest drogą prostą.

Def. G

jest grafem spójnym













V

v

u,

u-v droga w



G

Def.

Jeżeli w drodze





k

v

v

v

,...,

,

1

0

k

v

v



0

to drogę nazywamy cyklem. Jeżeli w

drodze prostej





k

v

v

v

,...,

,

1

0

0

v sąsiaduje z

k

v , to drogę nazywamy cyklem

prostym.

Def.

Dopełnieniem grafu





E

V

G

,



nazywamy graf

 





E

V

P

V

G

/

,

'

2



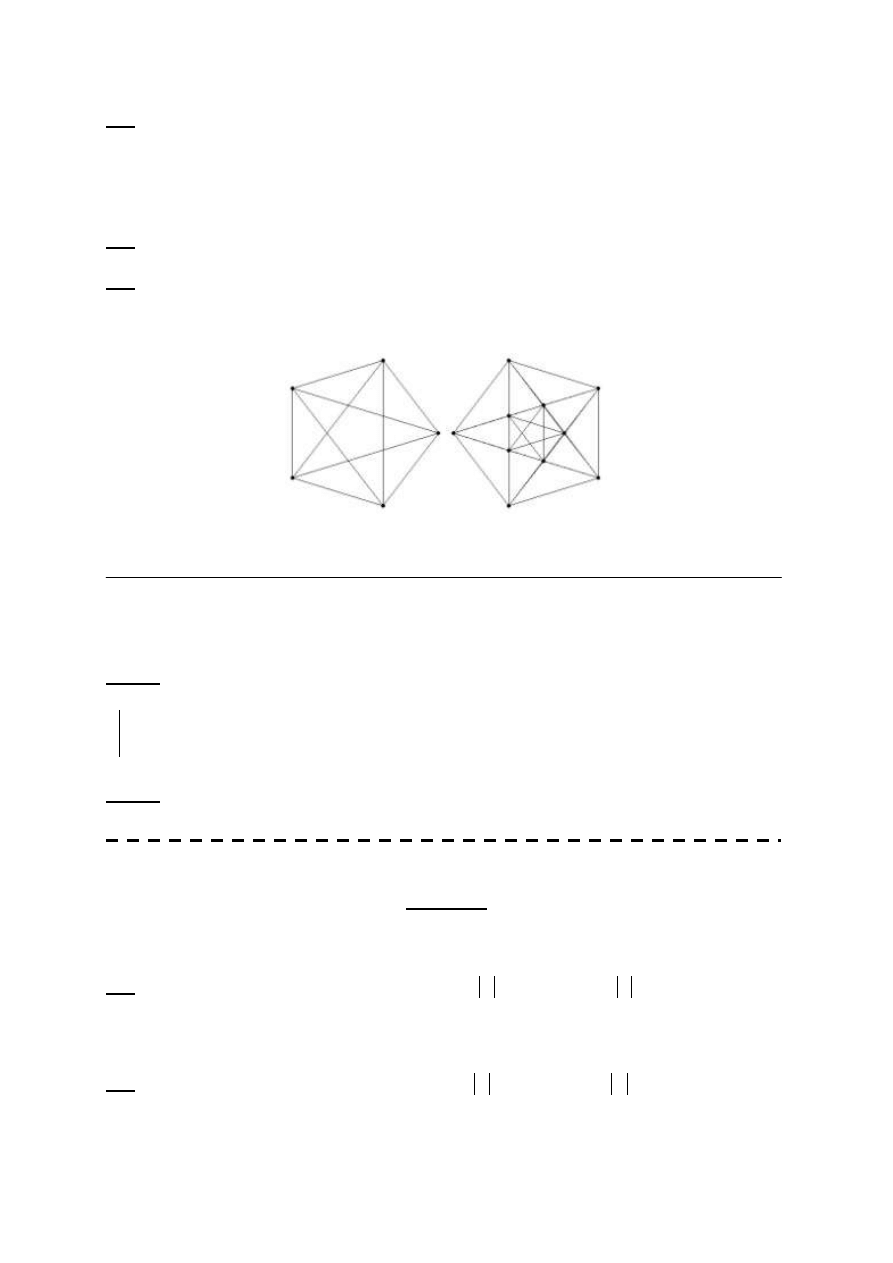
. W dopełnieniu

grafu G s

ąsiadują te, i tylko te wierzchołki, które nie sąsiadowały w G.

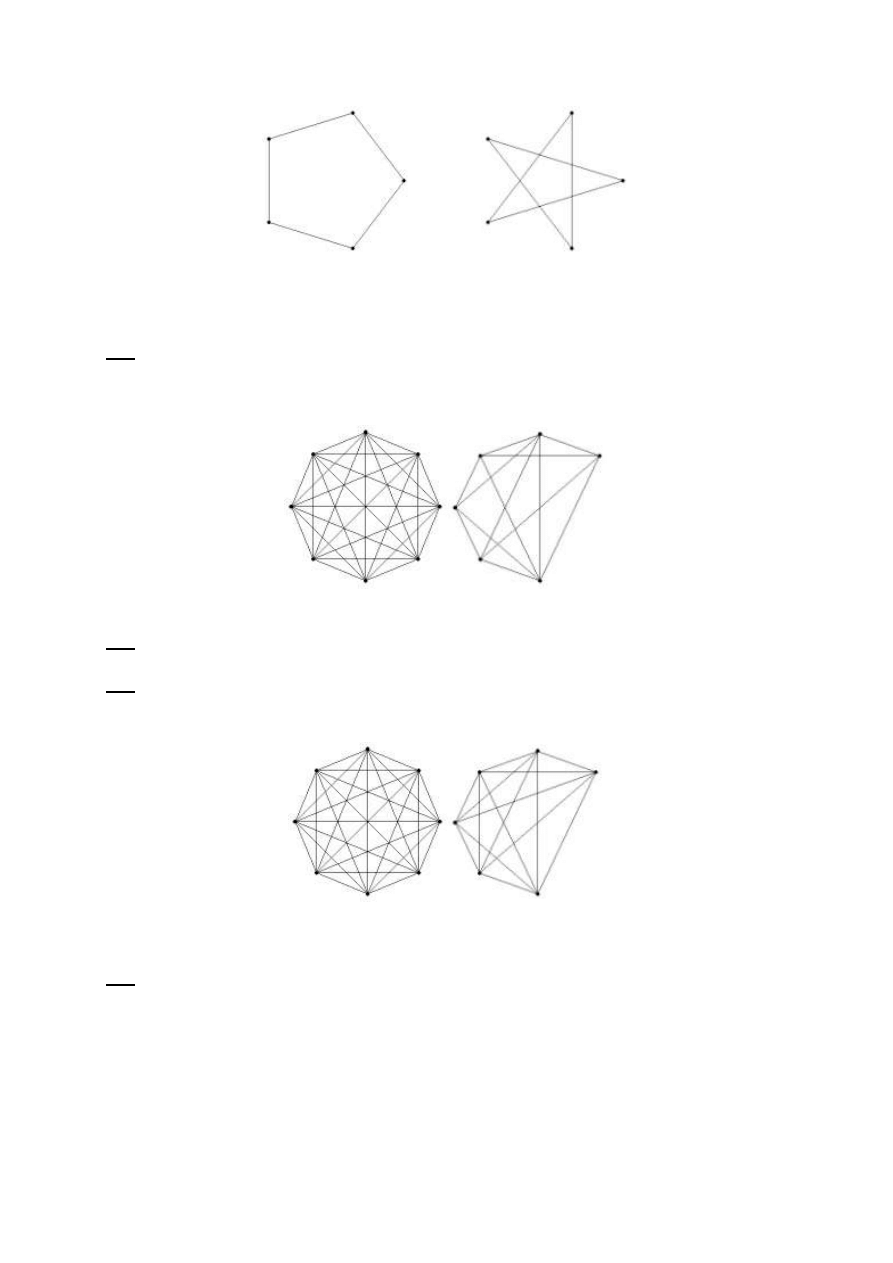
Graf i jego dopełnienie.

Def.





F

W

H

,



jest pograłem







 



 





E

W

P

F

V

W

F

W

H

E

V

G

















2

,

,

Graf i jego podgraf.

Def. H jest nadgrafem G



G jest podgrafem H.

Def.





F

W

H

,



jest pograłem indukowanym



 



 









E

W

P

W

H

V

W

E

V

G













2

,

,

Graf i jego podgraf indukowany.

Def. H

jest podgrafem rozpinającym w

   

G

V

H

V

G





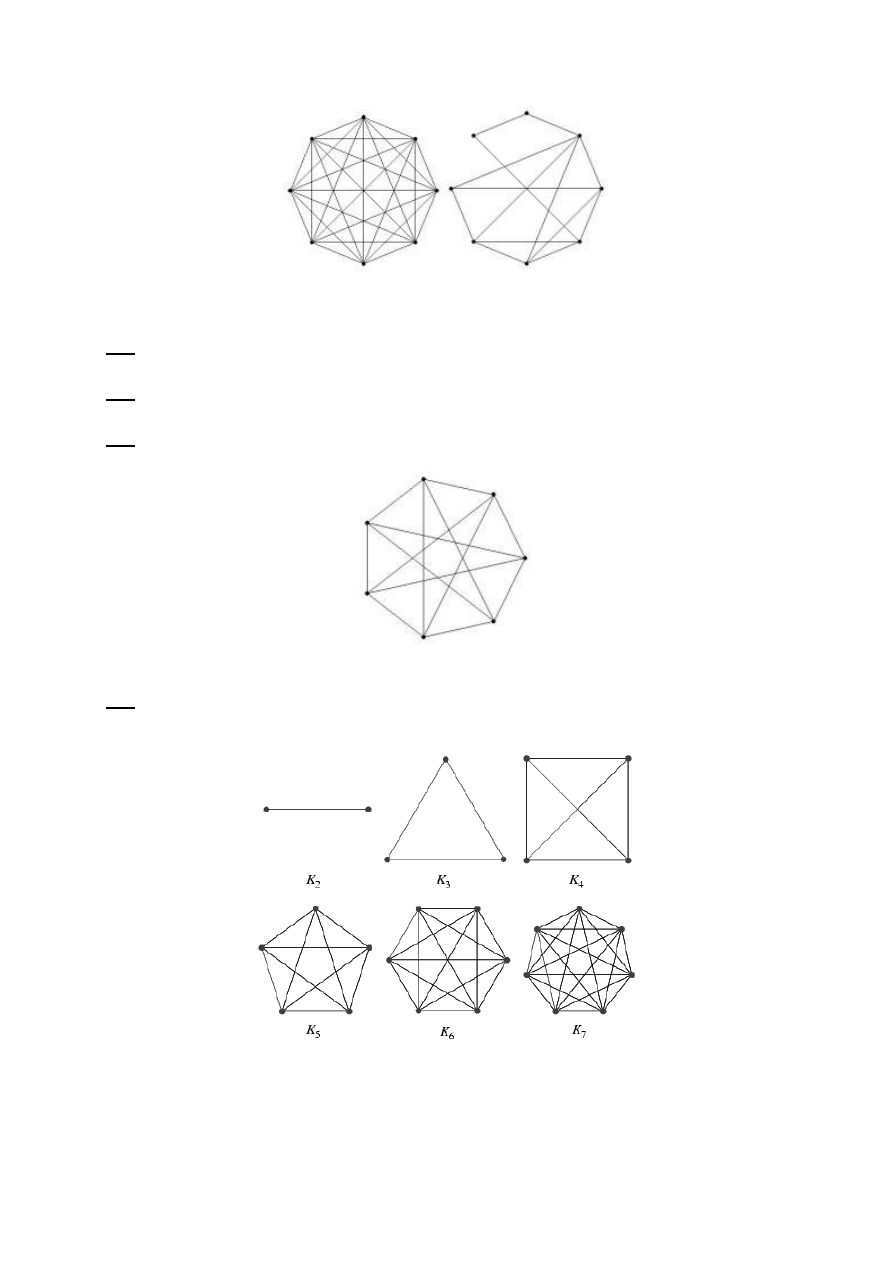
Graf i jego podgraf rozpinający.

Def. Najmniejszy

stopień wierzchołka w grafie G -

 

 

 





G

V

v

v

G





:

deg

min



Def.

Największy stopień wierzchołka w grafie G -

 

 

 





G

V

v

v

G







:

deg

max

Def. G jest r-regularny



  

r

v

V

v









deg

Graf 4-

regularny o 7 wierzchołkach.

Def.

n

K - graf pełny o n wierzchołkach -



 











n

P

n

K

n

,...,

1

,

,...,

1

2



Grafy

pełne.

Def.





1

1

1

, E

V

G



i





2

2

2

, E

V

G



są izomorficzne





   





2

1

1

2

1

1

"

"

1

,

:

E

v

f

u

f

E

uv

V

v

u

V

V

f

na































.

Izomorfizm grafów oznacza się

2

1

G

G



Def. Graf jest acykliczny wtedy i tylko wtedy, kiedy nie zawiera cykli.

Def.

Grafem krawędziowym grafu G nazywamy graf L(G) taki, że istnieje bijekcja z
V(G) do E(L(G))

taka, że wierzchołki odpowiadające krawędziom e i f w grafie

G

są połączone krawędzią w L(G)



e i f

mają wspólny wierzchołek w G.

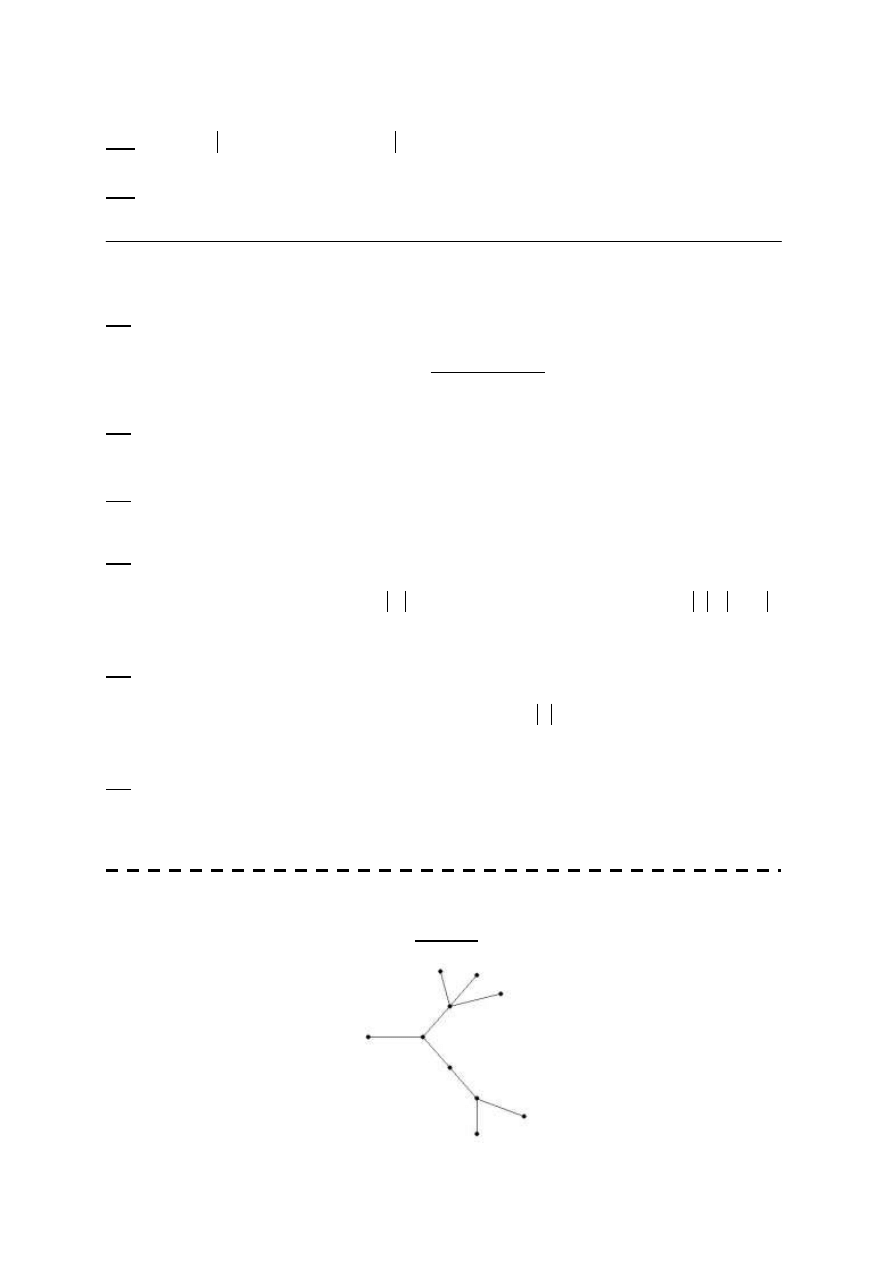
Grafy

5

K i

 

5

K

L

.

Twierdzenia

Lemat

O uściskach dłoni.

 





V

v

G

v

deg

2

Lemat

















2

deg v

V

v

w G istnieje pewien cykl (prosty).

Spójność

Definicje

Def. Graf G jest k-

spójny (wierzchołkowo)











S

G

k

S

V

S

k

V

















spójny). Spójnością grafu G nazywamy największe k takie, ze G jest k-spójny i
oznaczamy

 

G



.

Def. Graf G jest l-

spójny krawędziowo











F

G

l

F

E

F

l

E

















spójny).

Spójnością krawędziową grafu G nazywamy największe l takie, ze G jest l-
spójny krawędziowo i oznaczamy

 

G



Def.

 











E

xy

S

y

V

x

S

N











:

-

ilość sąsiadów podzbioru S

Def.





E

V

G

,



i



 



E

xy

V

y

x







,

. Zbiór

V

S



jest x-y

oddzielający



każda x-y

droga przechodzi przez S



w G-S x i y

są w różnych składowych.

Twierdzenia

Tw.

W grafie prostym mającym n wierzchołków, k składowych i m krawędzi
zachodzi nierówność:







2

1













k

n

k

n

m

k

n

Tw

. Whitney’a

     

G

G

G











Tw.

Graf jest dwuspójny



każde dwa wierzchołki z G leża na pewnym cyklu

prostym

Tw

. Halla (o zawieraniu małżeństw)

G

– graf dwudzielny X na Y. G ma X niezależnych krawędzi





 





S

N

S

V

S









.

Powyższy warunek nosi nazwę warunku Halla.

Tw. Mengera (1927)

Jeśli dla każdego u-v zbioru rozdzielającego S mamy

k

S



, to w G istnieje k

rozłącznych u-v dróg.

Tw

. Këniga – Halla

W każdym grafie dwudzielnym

 

 

G

G

0

1







.

Drzewa

Definicje

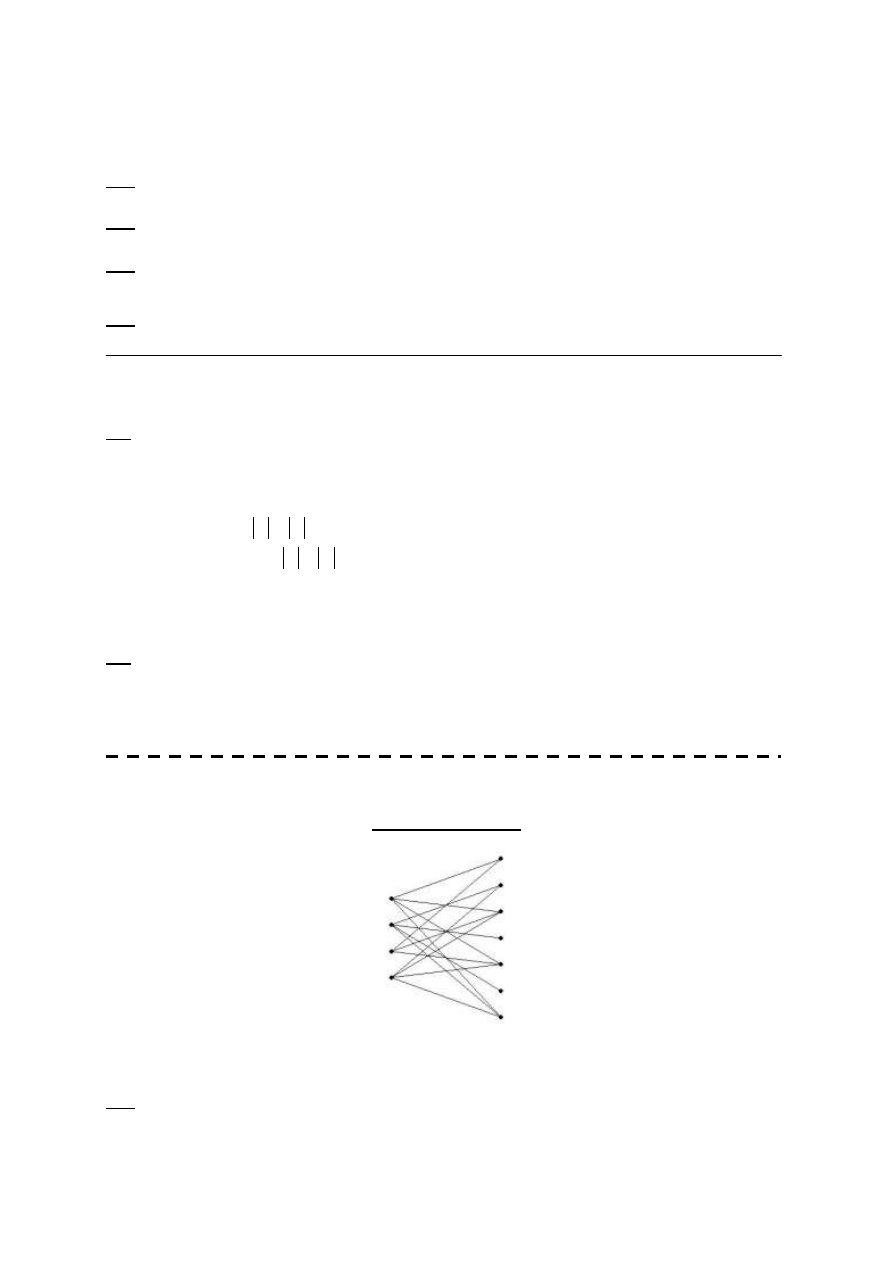
Def.

Drzewem nazywamy spójny graf acykliczny.

Def. Lasem nazywamy graf acykliczny.

Def.

Promieniem grafu nazywamy liczbę

 

 





v

u

dist

G

r

V

v

V

u

,

max

min







Def.

V

v



jest wierzchołkiem centralnym w

 

 

v

u

dist

G

r

G

V

u

,

max







Twierdzenia

Tw.

Następujące warunki są równoważne:

1)





E

V

G

,



jest drzewem.

2)





v

u

V

v

u









!

,

droga) i jest to droga prosta (





!

”istnieje dokładnie jeden”).

3) G

jest spójny i

1





E

V

.

4) G jest acykliczny i

1





E

V

.

5) G

jest spójny i





e

G

E

e







jest niespójny.

6) G jest acykliczny i





uv

G

E

uv







posiada cykl i to dokładnie jeden.

Tw. Jordana

Dla każdego drzewa T centrum T składa się z jednego wierzchołka, lub z dwóch
wierzchołków sąsiadujących ze sobą.

Grafy dwudzielne

Definicje

Def. Graf dwudzielny





 



V

V

V

V

V

V

V

V



















2

1

2

1

2

1

,





 























2

1

V

e

V

e

E

e

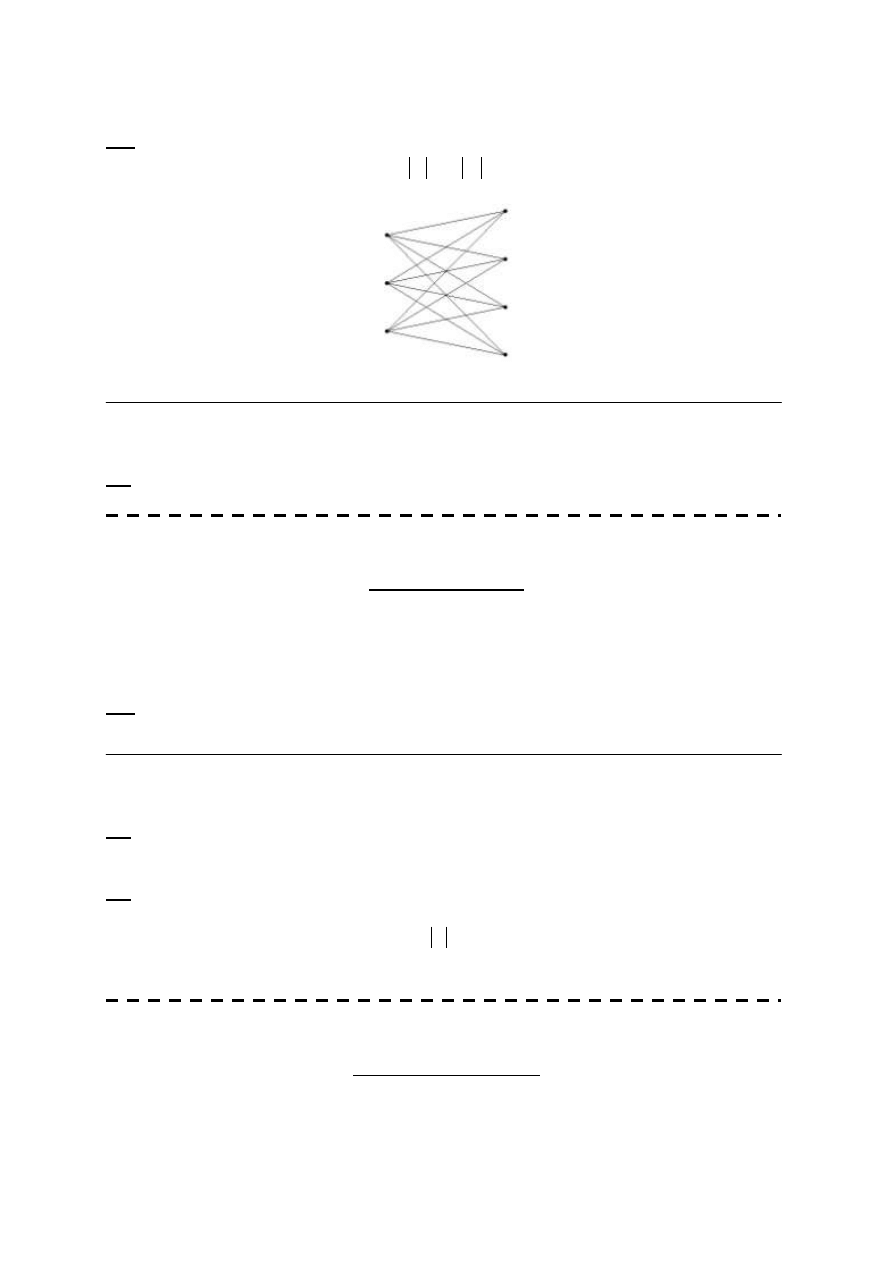
Def.

Graf pełny dwudzielny

G



- dwudzielny i







E

v

v

V

v

V

v









2

1

2

2

1

1

,

.

Oznaczamy go przez

n

m

K

.

, gdzie

2

1

,

V

n

V

m





Graf pełny dwudzielny.

Twierdzenia

Tw. W

grafie dwudzielnym każdy cykl ma parzystą długość.

Grafy eulerowskie

Definicje

Def. Cykl Eulera w grafie G

jest to cykl przechodzący przez wszystkie wierzchołki i

krawędzie grafu G. G jest grafem Eulera



G ma cykl Eulera.

Twierdzenia

Tw.

Jeśli w grafie G stopień każdego wierzchołka jest większy lub równy 2, to graf
ten ma cykl.

Tw. Eulera (1736)

Graf G ma cykl Eulera



G

jest spójny,

1



V

i stopień każdego wierzchołka jest

liczbą parzystą.

Grafy hamiltonowskie

Definicje

Def. Cyklem Hamiltona w grafie G

nazywamy każdy cykl rozpinający. G jest grafem

Hamiltona



G ma cykl Hamiltona.

Def.



-grafy.

Def.

 





n

v

V

v

D

n







deg

:

Def. k-

domknięciem grafu G nazywamy minimalny (ze względu na zbiór krawędzi)

nadgraf H

rozpięty nad G, taki, że

 





 





 

 









k

v

u

H

E

uv

H

V

v

u

H

H













deg

deg

,

. Oznaczamy je

 

G

C

k

.

Def.

n

G to graf, w którym wierzchołki

 

G

V

v

u



,

są połączone krawędzią wtedy i

tylko wtedy, kiedy długość u-v drogi w G nie przekracza n.

Twierdzenia

Tw. G

– graf Hamiltona





V

S







(liczba składowych w G-S nie przekracza

S

.

Tw.

Jeśli graf G jest dwuspójny i nie zawiera



podgrafu, to G ma cykl Hamiltona.

Tw. Diraca (1952)

Jeżeli graf G ma

3



n

wierzchołków oraz





 



















2

deg

n

v

V

v

, to G ma cykl

Hamiltona.

Tw. Ore (1960)

Jeżeli graf G ma

3



n

wierzchołków oraz





 

 





n

v

u

V

v

u









deg

deg

,

, to G ma cykl

Hamiltona.

Tw.

Pòsa (1962)

Jeżeli w grafie G o p wierzchołkach

 



















2

1

p

n

n

zachodzi

n

D

n



, a gdy p

nieparzyste

2

1

2

1







p

D

p

, to G ma cykl Hamiltona.

Tw. Bondy, Chvatal (1976)

Jeśli w grafie G o

3



p

wierzchołkach

 

p

p

K

G

C



, to G ma cykl Hamiltona.

Tw. Sekanina (1968)

Jeżeli graf G o

3



p

wierzchołkach jest spójny, to

3

G ma cykl Hamiltona.

Tw

. Erdös, Chvatal

Jeżeli w grafie G o

3



p

wierzchołkach

 

 

G

G

0







, to G ma cykl Hamiltona.

Faktory

Definicje

Def. k-faktorem w grafie G

nazywamy każdy k-regularny podgraf rozpinający.

Def. k-faktoryzacja grafu G

to zbiór krawędziowo rozłącznych k-faktorów







s

i

E

V

G

i

i

,...,

1

,





,

takich, że



s

i

i

E

E

1





.

Twierdzenia

Tw. Tutte (1947)

G ma jeden faktor





V

S







liczba składowych o nieparzystych ilościach

wierzchołków w grafie G-S nie przekracza

S

Tw.

n

K ma 1-faktoryzację



n jest parzyste.

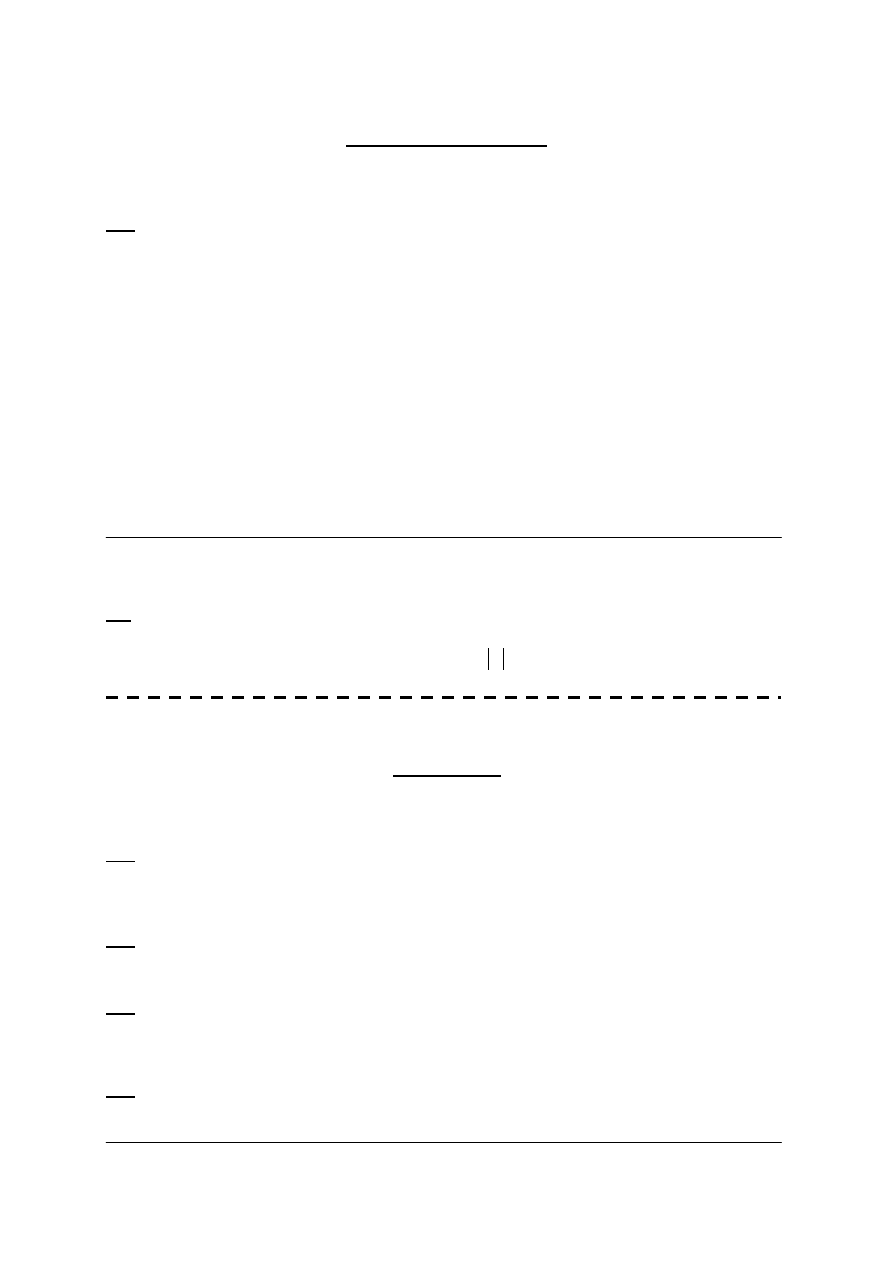
Tw.

1

2



n

K

ma 2-

faktoryzację taką, że każdy 2-faktor jest cyklem Hamiltona.

Pokrycia i niezależność

Definicje

Def.





E

F

V

S

E

V

G







,

,

,

1) S jest zbiorem ni

ezależnych wierzchołków

 









E

S

P

2

2) F

jest zbiorem niezależnych krawędzi



 

 























d

e

d

e

E

d

e,

3) S

jest zbiorem pokrywających wierzchołków



















S

e

E

e

4) F

jest zbiorem pokrywających krawędzi

V

e

F

e









 

G

0



-

najmniejsza liczność pokrywającego zbioru wierzchołków w G

 

G

1



-

najmniejsza liczność pokrywającego zbioru krawędzi w G

 

G

0



-

największa liczność niezależnego zbioru wierzchołków w G

 

G

1



-

największa liczność niezależnego zbioru krawędzi w G

Twierdzenia

Tw. Gallai

 





 

 

 

 





G

G

V

G

G

G

1

1

0

0

0























Kolorowanie

Definicje

Def. Graf jest k-kolorowalny







 

 

























E

i

f

P

i

k

V

f

1

2

,...,

2

,

1

:

-

zbiór

wierzchołków można podzielić na k podzbiorów w ten sposób, aby żadne dwa
wierzchołki należące do jednego podzbioru nie były połączone krawędzią.

Def.

Najmniejsze k takie, że G jest k-kolorowalny nazywamy liczbą chromatyczną
grafu G i oznaczamy

 

G



.

Def. Graf jest k-kolorowal

ny krawędziowo jeżeli jego krawędzie można

pokolorować k kolorami tak, żeby żadna para krawędzi sąsiednich nie miala
tego samego koloru.

Def.

Najmniejsze k takie, że G jest k-kolorowalny krawędziowo nazywamy
indeksem chromatycznym grafu G i oznaczamy

 

G

'



.

Twierdzenia

Tw.

Grafy dwudzielne są dwukolorowalne.

Tw. W grafie G o p

wierzchołkach zachodzi nierówność:

 

1

0

0















p

G

p

Tw

. Szekerés, Wilf (1968)

Jeżeli H są indukowanymi podgrafami G, to zachodzi nierówność:

 

 

1

max





H

G





Tw. Brooks (1941)

Jeżeli G jest spójnym grafem prostym, nie będącym grafem pełnym, i jeśli największy
stopień wierzchołka grafu G wynosi



(gdzie

3





), to graf G jest



-kolorowalny.

Tw. Appel, Haken (1976)

Każdy graf planarny jest 4-kolorowalny.

Tw

. Визинг (1968)

   

   

1

'













G

G

G

G



.

Grafy planarne

Definicje

Def. G jest grafem planarnym



istnieje taka reprezentacja graficzna grafu G na

płaszczyźnie, że łuki reprezentujące krawędzie nie mają punktów wspólnych poza
wierzchołkami w których się łączą.

Twierdzenia

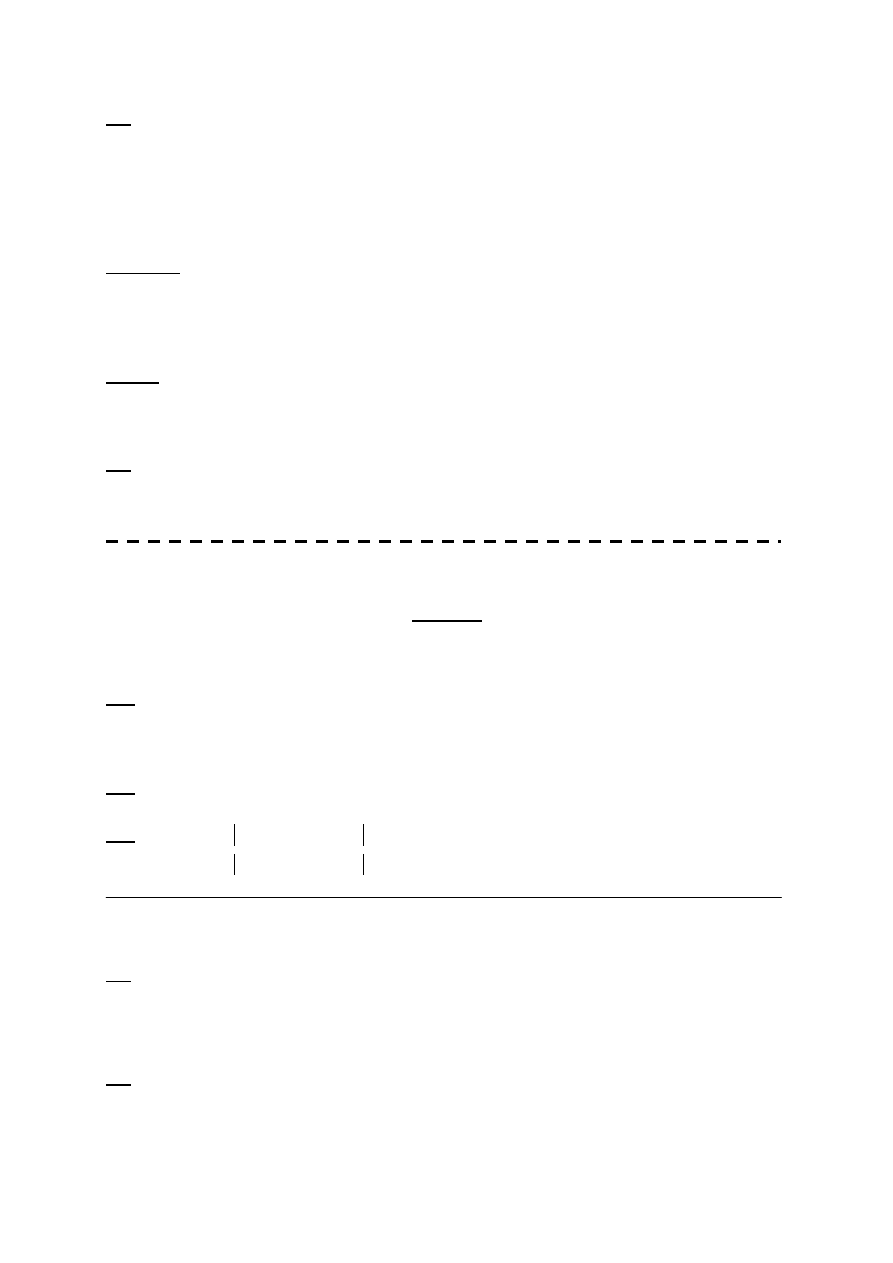
Tw. Kuratowski (1930)

G jest grafem planarnym



G nie zawiera podgrafu homeomorficznego z

5

K , ani

3

,

3

K

.

Tw. Euler (1750)

Niech G

będzie rysunkiem płaskim spójnego grafu płaskiego i niech n, m i f

oznaczają odpowiednio liczbę wierzchołków, krawędzi i ścian grafu G. Wtedy:

2







f

m

n

Wniosek

Jeśli G jest spójnym planarnym grafem prostym, mającym n wierzchołków (gdzie

3



n

) i m

krawędzi, to

6

3





n

m

. Jeśli ponadto graf G nie zawiera

3

K , to

4

2





n

m

Lemat

G

– planarny



 

5



G



Tw. Tutte (1956)

G

– planarny i

 





4

G



G ma cykl Hamiltona.

Turnieje

Definicje

Def.

Turniejem nazywamy graf zorientowany otrzymany z grafu pełnego

n

K przez

nadanie każdej krawędzi jednej z dwóch możliwych orientacji w dowolny
sposób.

Def. T

jest mocno spójnym turniejem

 













T

V

v

u,

w T u-v droga).

Def.

  



E

v

u

V

u

v









)

,

(

:

deg

-

półstopień wejściowy.

  



E

u

v

V

u

v









)

,

(

:

deg

-

półstopień wyjściowy.

Twierdzenia

Tw. Landau (1955)

W każdym turnieju odległość od wierzchołka o maksymalnym wyniku do każdego
innego wierzchołka wynosi 1 albo 2.

Tw

. Rédei (1934)

Każdy turniej ma drogę Hamiltona.

Tw. Moser (1966)

Jeżeli T jest mocno spójnym turniejem i

 

3





p

T

V

, to









p

i

,...,

4

,

3





istnieje w T

cykl długości i.

Twierdzenie Ramsey’a

Def.

Liczba Ramsey’a R(s,t) jest to najmniejsze n takie, że dla każdego podziału
zbioru krawędzi grafu

n

K na czerwone i zielone istnieje czerwony podgraf

s

K

lub zielony

t

K .

Tw. Ramsey (1929)

Dla każdych

2

,

2





t

s

:

1)

  

 



1

,

,

1

,









t

s

R

t

s

R

t

s

R

2)

 





















1

2

,

s

t

s

t

s

R

Matroidy

Def.

Matroidem nazywamy parę M=(E,J) (E – zbiór skończony,

E

J

2



, J

– rodzina

zbiorów niezaleznych) o własnościach:

1)













J

J

2)







 







J

Y

X

Y

J

X

Y

X

E















2

,

3)









 





J

e

Y

Y

e

X

e

Y

X

J

Y

X























1

,

DODATKI

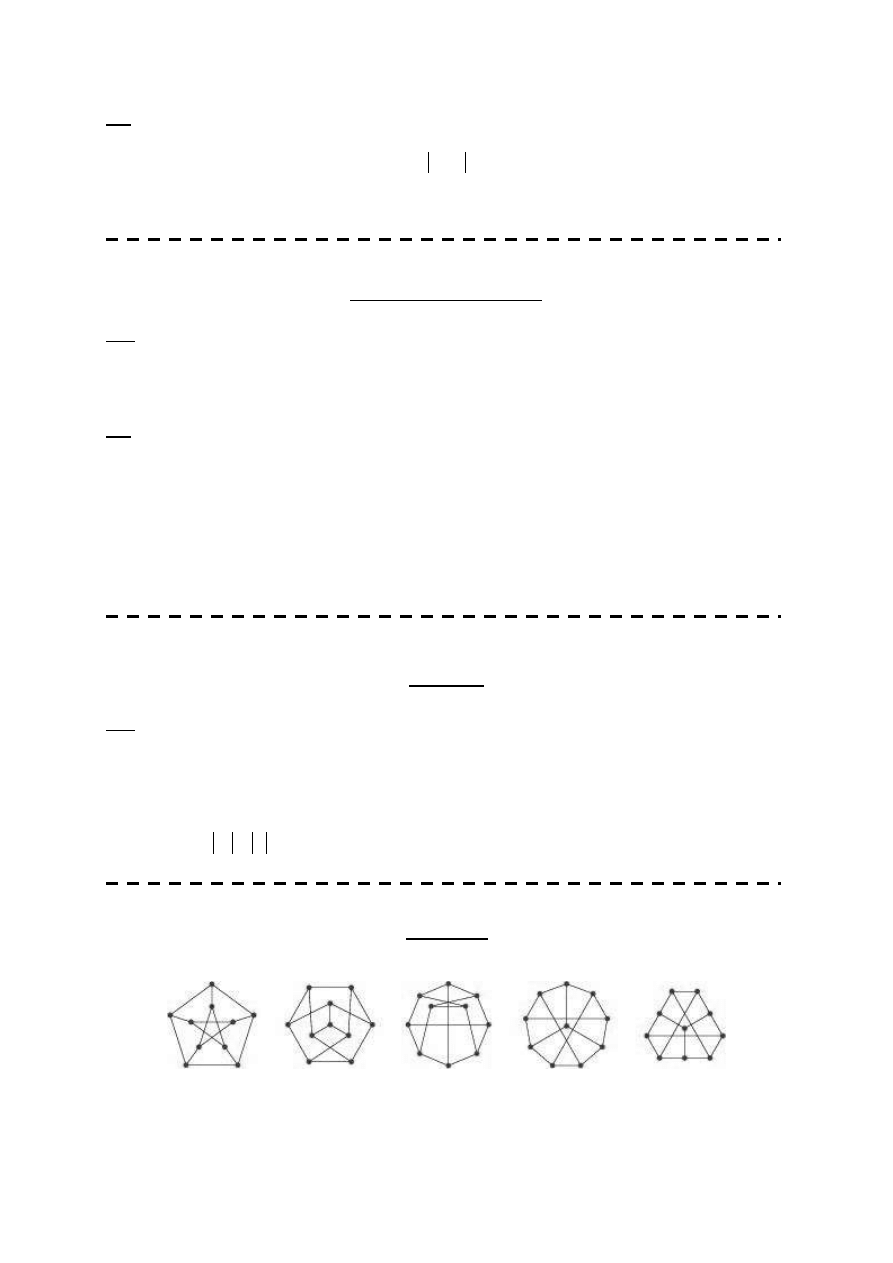
Izomorficzne postacie grafu Petersena.