J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
1
Stany obrotowo – symetryczne w PSN i w PSO
Ćwiczenie 7
Obrotowa symetria
w Teorii Sprężystości i Plastyczności oznacza,
że symetryczne są jednocześnie
F
: geometria, warunki brzegowe
oraz
obciążenia.
Funkcja naprężeń , wyrażona w układzie biegunowym, nie
może wówczas zależeć od kąta
ϕ
, zatem:
( )
F
F r
=
tak więc:
( )
( )
4
2
2
0
F r
F r
∇
= ∇ ∇
=
( )
( )
( )
( )
2
2
2
2
1
1
0
F r
F r
r
r
r
r
r
r
∂
∂
∂
∂
+ ⋅
+ ⋅
=
∂
∂
∂
∂
1
( )
rr
F
r
r
r
σ
∂
= ⋅
∂
Składowe stanu naprężenia:
;
2
2
( )
F
r
r
ϕϕ
σ
∂
=
∂
;
( )
( )
0
r
r
r
r
ϕ
ϕ
σ
σ
=
=
(do porównania ze wzorami ogólnymi)
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
2
Równanie
( )
4
0
F r
∇
= można rozwiązać w postaci ogólnej
(bez
odgadywania funkcji naprężeń)!
Różniczkując wskazane równanie:
( )
( )
2
2
2
2
1
1
0
F
F
r
r
r
r
r
r
∂
∂
∂
∂
+ ⋅
+ ⋅
=
∂
∂
∂
∂
z wykorzystaniem wzoru na
pochodną iloczynu, otrzymamy
(po
przekształceniach):
4
2
2
3
3
2
4
3
2
2
2
2
3
3
3
2
2
2
1
1
1
1
1
1
0
F
F
F
F
F
F
F
F
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
∂
∂
∂
∂
∂
∂
∂
∂
+ ⋅
− ⋅
− ⋅
+ ⋅
+ ⋅
− ⋅
+ ⋅
=
∂
∂
∂
∂
∂
∂
∂
∂
Po redukcji wyrazów podobnych
4
3
2
4
3
2
2
3
2
1
1
0
d F
d F
d F
dF
dr
r
dr
r
dr
r
dr
+ ⋅
−
⋅
+
⋅
=
i wprowadzeniu symbolu
pochodnej zwyczajnej, otrzymujemy:
jest to równanie różniczkowe liniowe o zmiennych współczynnikach!
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
3
Można jednak powyższe równanie sprowadzić do równania
liniowego o
stałych współczynnikach
t
r
e
=
przez podstawienie:
t
dr
e dt
→
= ⋅
Zatem:
4
3
2
4
3
2
2
3
2
1
1
0
d F
d F
d F
dF
dr
r
dr
r
dr
r
dr
+ ⋅
−
⋅
+
⋅
=
4
3
2
4
4
3
3
2
2
2
3
1
2
1
1
1
1
1
0
( )
( )
( )
( )
( )
t
t
t
t
t
t
t
d F
d F
d F
dF
dt
e
e
dt
e
e
dt
e
e
dt
e
⋅
+
⋅
⋅
−
⋅
⋅
+
⋅
⋅
=
4
3
2
4
4
4
4
4
3
2
2
0
t
t
t
t
d F
d F
d F
dF
e
e
e
e
dt
dt
dt
dt
−
−
−
−
⋅
+ ⋅
⋅
−
⋅
+
⋅
=
Czyli:
4
3
2
4
3
2
2
0
d F
d F
d F
dF
dt
dt
dt
dt
+ ⋅
−
+
=

J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
4
Po rozwiązaniu ostatniego równania i powrocie do zmiennych
wyjściowych otrzymamy całkę ogólną równania:
4
3
2
4
3
2
2
3
2
1
1
0
d F
d F
d F
dF
dr
r
dr
r
dr
r
dr
+ ⋅
−
⋅
+
⋅
=
w postaci:
2
2
( )
ln
ln
F r
A
r
B r
r
C r
D
= ⋅
+ ⋅ ⋅
+ ⋅ +
(ćwiczenie: sprawdzić przed postawienie, stałe całkowania dowolne)
(
)
2
( )
1 2ln
2
rr
A
r
B
r
C
r
σ
=
+ ⋅ +
+
Naprężenia wyrażają się wzorami:
(
)
2
( )
3 2ln
2
A
r
B
r
C
r
ϕϕ
σ
= −
+ ⋅ +
+
( )
( )
0
r
r
r
r
ϕ
ϕ
σ
σ
=
=
Z powyższego zapisu można wyprowadzić rozwiązania wszelkich
zagadnień o obrotowo – symetrycznym rozkładzie naprężeń, po
uwzględnieniu odpowiednich warunków brzegowych!
są to naprężenia główne!
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
5
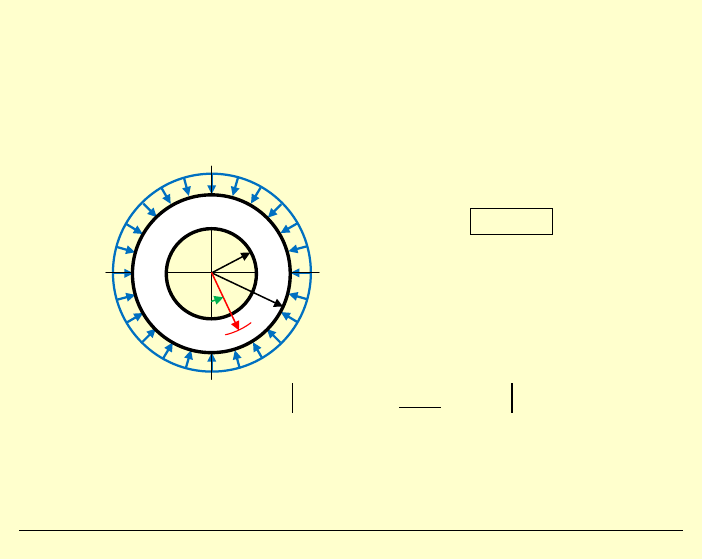
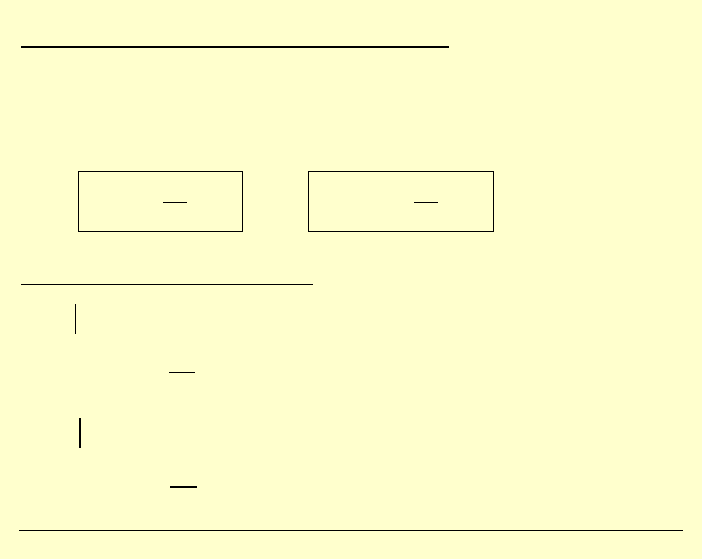
Przykład:
Wyznaczyć naprężenia w zagadnieniu dwuwymiarowym,
panujące w obszarze kolistym z otworem kolistym na środku.
Interpretacja:
→ tarcza z kolistym otworem (PSN)
→ rura grubościenna (PSO)
Warunki brzegowe:
(
)
1)
rr
r b
p
σ
=
= −
oraz
(
)
2)
0
rr
r a
σ
=
=
Uwaga:
Jako trzeci warunek można przyjąć brak przemieszczeń
obwodowych (nieskończenie wiele płaszczyzn symetrii), ale
wówczas obliczenia stają się złożone!
a
r
b
≤ ≤
p
const
=
–
ściskanie
jest równomierne
ϕ
b
r
a
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
6
r
b
= → ∞
Rozumowanie alternatywne (M. T. Huber)
Jeżeli promień
, to obciążenie
0
p
const
=
→
!
Tak więc
( )
0
rr
r
σ
→ oraz
( )
0
r
ϕϕ
σ
→
(wartości te nie mogą wzrastać w sposób logarytmiczny!)
Zatem:
0
B
=
,
stąd:
2
( )
2
rr
A
r
C
r
σ
=
+
oraz
2
( )
2
A
r
C
r
ϕϕ
σ
= −
+
(
)
1)
rr
r b
p
σ
=
= −
Realizując warunki brzegowe:
2
(
)
2
rr
A
r
b
C
p
b
σ
→
=
=
+
= −
(
)
2)
0
rr
r a
σ
=
=
2
(
)
2
0
rr
A
r
a
C
a
σ
→
=
=
+
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
7
Przekształcając równania pochodzące z warunków brzegowych:
2
2
A
C
p
b
+
= − oraz
2
2
0
A
C
a
+
=
otrzymujemy:
2
2
2
2
p a
b
A
b
a
⋅ ⋅
=
−
oraz
2
2
2
2 (
)
p b
C
b
a
⋅
= −
⋅
−
i ostatecznie:
2
( )
2
rr
A
r
C
r
σ
=
+
2
2
2
2
2
2
2
2
1
2
2 (
)
p a
b
p b
b
a
r
b
a
⋅
⋅
⋅
=
⋅
+ ⋅ −
−
⋅
−
2
2
2
2
2
( )
1
rr
p b
a
r
b
a
r
σ
⋅
=
⋅
−
−
oraz:
2
( )
2
A
r
C
r
ϕϕ
σ
= −
+
2
2
2
2
2
2
2
2
1
2
2 (
)
p a
b
p b
b
a
r
b
a
⋅
⋅
⋅
= −
⋅
+ ⋅ −
−
⋅
−
2
2
2
2
2
( )
1
p b
a
r
b
a
r
ϕϕ
σ
⋅
= −
⋅
+
−
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
8
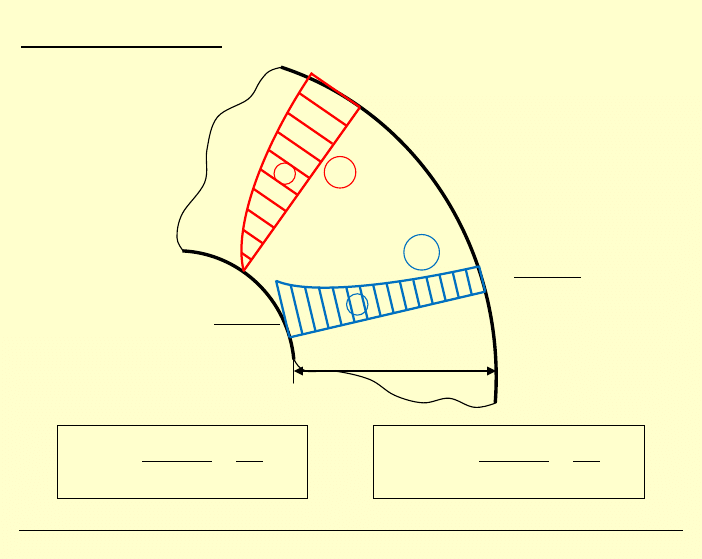
Wykresy naprężeń:
2
2
2
2
2
( )
1
rr
p b
a
r
b
a
r
σ
⋅
=
⋅
−
−
oraz
2
2
2
2
2
( )
1
p b
a
r
b
a
r
ϕϕ
σ
⋅
= −
⋅
+
−
b
a
−
p
2
2
2
2 b
p
a
b
⋅
⋅
−
2
2
2
2
a
b
p
a
b
+
⋅
−
0
ϕϕ
σ
−
rr
σ
−

J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
9
0
a
=
Dyskusja!
1) Przypadek pełnej tarczy:
→ zatem:
Ze wzorów na naprężenia wynika, iż:
( )
2
2
2
2
2
2
2
0
( )
1
1
0
rr
p b
p b
r
p
b
r
b
σ
⋅
⋅
=
⋅
− =
⋅ − = −
−
( )
2
2
2
2
2
2
2
0
( )
1
1
0
p b
p b
r
p
b
r
b
ϕϕ
σ
⋅
⋅
= −
⋅
+
= −
⋅ + = −
−
w każdym punkcie obszaru!
2)
Przypadek płaskiego stanu odkształceń (PSO):
→ pamiętamy, że w kierunku prostopadłym do przekroju zachodzi:
(
)
2
33
2
2
2
rr
b
p
b
a
ϕϕ
σ
ν σ
σ
ν
= ⋅
+
= − ⋅ ⋅ ⋅
−
const
=
→ naprężenia te nie zależą od wielkości promienia
r
, wynika stąd
brak deplanacji przekroju!
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
10
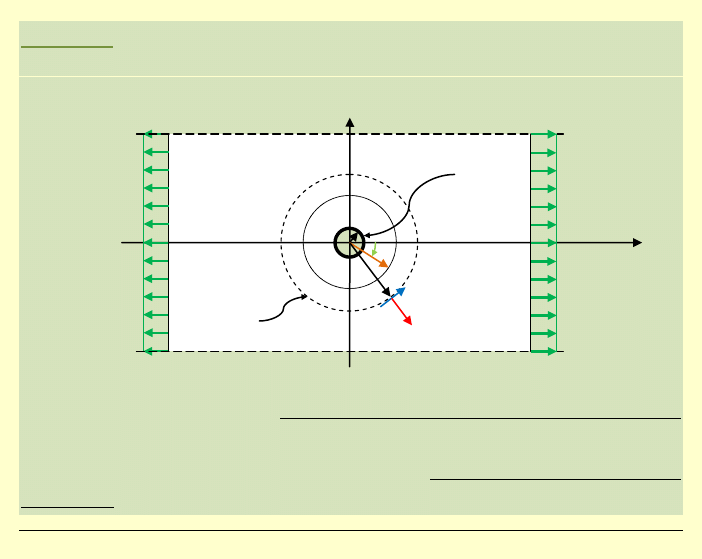
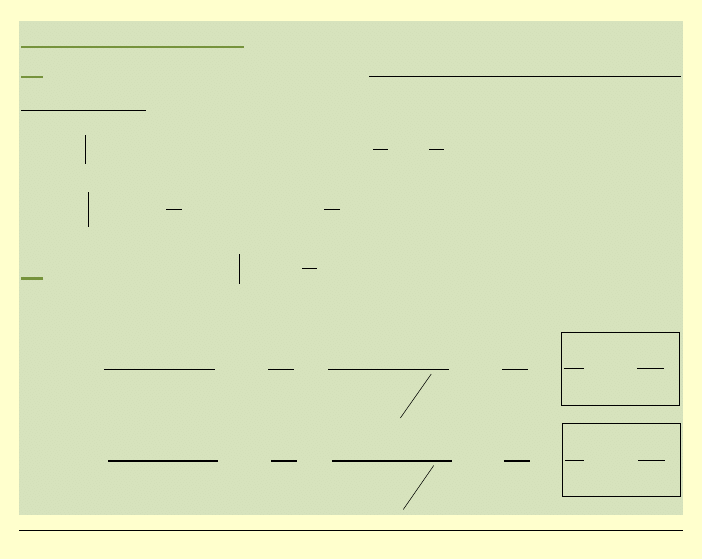
Zadanie:
(jest to podstawowe zadanie z dziedziny analizy koncentracji naprężeń)
Wyznaczyć naprężenia w jednokierunkowo rozciąganej
tarczy z otworem kołowym pośrodku.
Założenia:
1) otwór jest stosunkowo
mały w porównaniu z wymiarami tarczy
1
x
w
płaszczyźnie
2) otwór wpływa na rozkład naprężeń tylko w pewnym swoim
otoczeniu
11
p
σ
=
; poza tym otoczeniem mamy:
,
22
0
σ
= i
12
0
σ
=
1
x
2
x
1
g
=
a
b
r
ϕ
r
ϕ
σ
rr
σ
wyobrażony
okrąg
o promieniu
r
b
=
kolisty
otwór
p
const
=
p
const
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
11
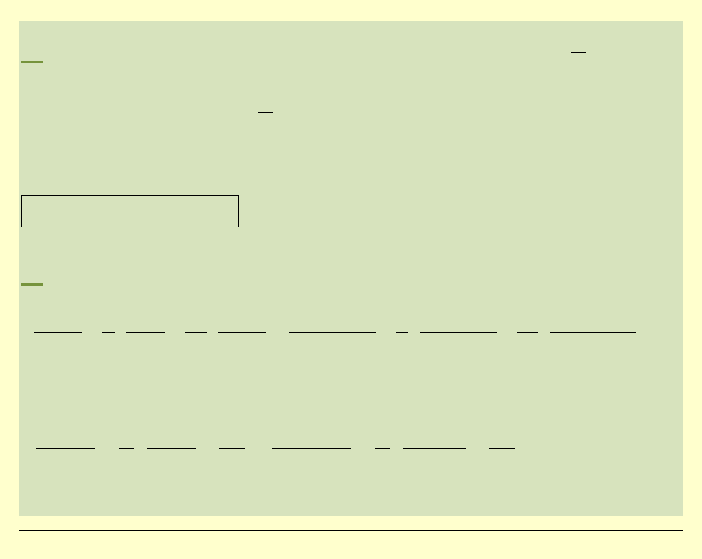
Rozwiązanie zadania:
1°
r
b
=
Dla
(
)
b
a
otrzymamy
skł. stanu naprężeń w układzie
biegunowym
22
0
σ
=
(ze wzorów transformacyjnych;
i
12
0
σ
= ):
→
2
11
(
)
cos
rr
r b
σ
σ
ϕ
=
=
2
cos
p
ϕ
= ⋅
1
1
cos 2
2
2
p
p
ϕ
=
+
⋅
→
11
(
)
1
sin 2
2
r
r b
ϕ
σ
σ
ϕ
=
= − ⋅
1
sin 2
2
p
ϕ
= −
⋅
2°
(
)
1
2
rr
r b
p
σ
=
=
Od obciążenia
, na podstawie wzorów dla tarczy
kolistej z otworem (po zmianie znaku
p
), otrzymamy dla
2
2
b
a
:
(
)
2
2
2
2
2
( )
1
2
I
rr
p b
a
r
r
b
a
σ
⋅
=
⋅ −
⋅
−
(
)
2
2
2
2
1
2 1
p
a
r
a
b
=
⋅ −
≅
⋅ −
2
2
1
2
p
a
r
⋅ −
(
)
2
2
2
2
2
( )
1
2
I
p b
a
r
r
b
a
ϕϕ
σ
⋅
=
⋅ +
⋅
−
(
)
2
2
2
2
1
2 1
p
a
r
a
b
=
⋅ +
≅
⋅ −
2
2
1
2
p
a
r
⋅ +
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
12
3°
1
cos 2
2
p
ϕ
⋅
Pozostała część obciążenia (siły normalne równe
i
siły styczne równe
1
sin 2
2
p
ϕ
⋅
) wywołuje naprężenia, które
wyznaczamy za pomocą funkcji naprężeń, przyjętej w postaci
ze zmiennymi rozdzielonymi:
( , )
( ) cos 2
F r
f r
ϕ
ϕ
=
⋅
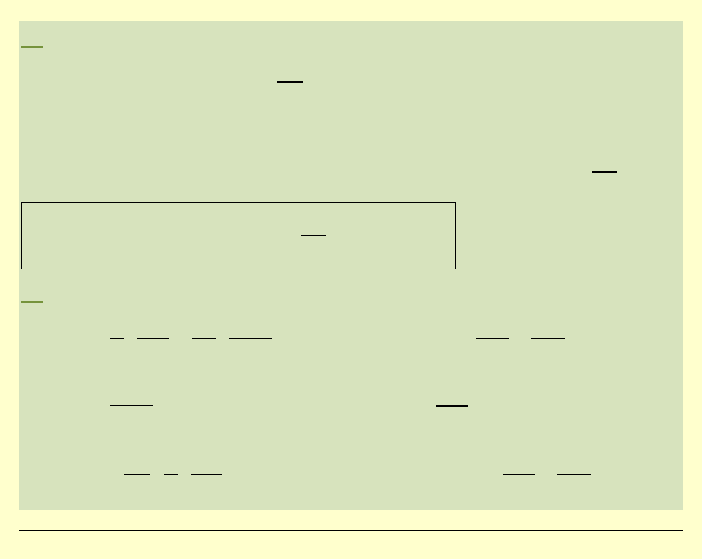
4°
( )
4
,
0
F r
ϕ
∇
=
Po podstawieniu
powyższej funkcji do równania
( )
( )
( )
( )
( )
( )
2
2
2
2
2
2
2
2
2
2
,
,
,
1
1
1
1
0
F r
F r
F r
r
r
r
r
r
r
r
r
ϕ
ϕ
ϕ
ϕ
ϕ
∂
∂
∂
∂
∂
∂
+ ⋅
+ ⋅
+ ⋅
+ ⋅
=
∂
∂
∂
∂
∂
∂
dochodzimy do równania różniczkowego zwyczajnego:
( )
( )
( )
( )
2
2
2
2
2
2
1
4
1
4
( )
0
d
d
d f r
df r
f r
dr
r
dr
r
dr
r
dr
r
+ ⋅
−
+ ⋅
−
⋅
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
13
5°
Całką ogólną powyższego równania jest:
2
4
2
1
( )
f r
A r
B r
C
D
r
= ⋅ + ⋅ + ⋅
+
(ćwiczenie: sprawdzić przed postawienie, stałe całkowania dowolne)
Zatem:
( , )
( ) cos 2
F r
f r
ϕ
ϕ
=
⋅
;
2
4
2
1
( )
f r
A r
B r
C
D
r
= ⋅ + ⋅ + ⋅
+
2
4
2
1
( , )
cos 2
F r
A r
B r
C
D
r
ϕ
ϕ
=
⋅ + ⋅ + ⋅
+
⋅
6°
Naprężenia od pozostałej części obciążenia (w stanie II):
2
2
2
1
1
( )
II
rr
F
F
r
r
r
r
σ
ϕ
∂
∂
= ⋅
+
⋅
→
∂
∂
4
2
6
4
( )
2
cos 2
II
rr
C
D
r
A
r
r
σ
ϕ
= −
+
+
⋅
2
2
( )
II
F
r
r
ϕϕ
σ
∂
=
→
∂
2
4
6
( )
2
12
cos 2
II
C
r
A
B r
r
ϕϕ
σ
ϕ
=
+
⋅ +
⋅
1
( )
II
r
F
r
r r
ϕ
σ
ϕ
∂
∂
= −
⋅
→
∂
∂
2
4
2
6
2
( )
2
6
sin 2
II
r
C
D
r
A
B r
r
r
ϕ
σ
ϕ
=
+
⋅ −
−
⋅

J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
14
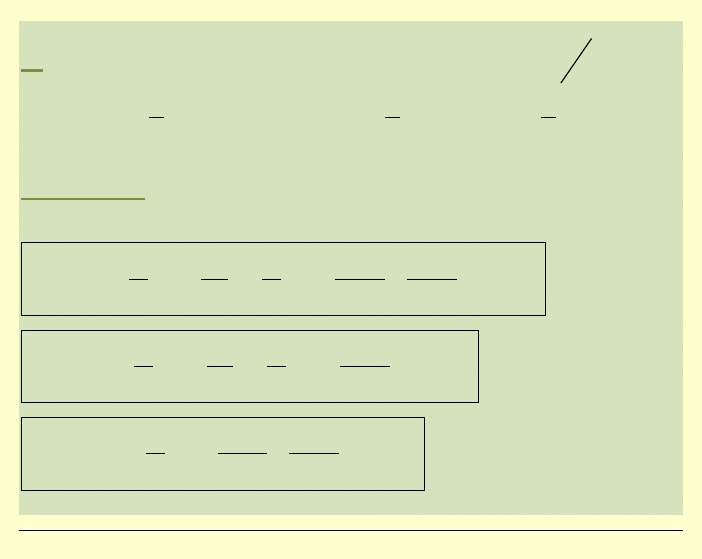
7°
warunek brzegowy 1)
Warunki brzegowe:
1
( )
cos 2
2
II
rr
r
p
σ
ϕ
=
⋅
dla
r
b
=
4
2
6
4
1
2
2
C
D
A
p
b
b
→
+
+
= −
warunek brzegowy 2)
1
( )
sin 2
2
II
r
r
p
ϕ
σ
ϕ
= −
⋅
dla
r
b
=
2
4
2
6
2
1
2
6
2
C
D
A
B b
p
b
b
→
+
⋅ −
−
= −
warunek brzegowy 3)
( )
0
II
rr
r
σ
=
dla
r
a
=
4
2
6
4
2
0
C
D
A
a
a
→
+
+
=
warunek brzegowy 4)
( )
0
II
r
r
ϕ
σ
= dla
r
a
=
2
4
2
6
2
2
6
0
C
D
A
B a
a
a
→
+
⋅
−
−
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
15
8°
, , ,
A B C D
Rozwiązanie stałych
(przy założeniu, że
2
2
0
a
b
≅
):
1
4
A
p
= −
;
0
B
=
;
4
1
4
C
p a
= −
⋅ ;
2
1
2
D
p a
=
⋅
Odpowiedź:
Po podstawieniu
stałych i dodaniu składowych ze
stanu I otrzymamy:
2
4
2
2
4
2
3
4
( , )
1
1
cos 2
2
2
rr
p
a
p
a
a
r
r
r
r
σ
ϕ
ϕ
⋅
⋅
= ⋅ −
+ ⋅ +
−
⋅
2
4
2
4
3
( , )
1
1
cos 2
2
2
p
a
p
a
r
r
r
ϕϕ
σ
ϕ
ϕ
⋅
= ⋅ +
− ⋅ +
⋅
4
2
4
2
3
2
( , )
1
sin 2
2
r
p
a
a
r
r
r
ϕ
σ
ϕ
ϕ
⋅
⋅
= − ⋅ −
+
⋅
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 7 • KMBiM WILiŚ PG
16
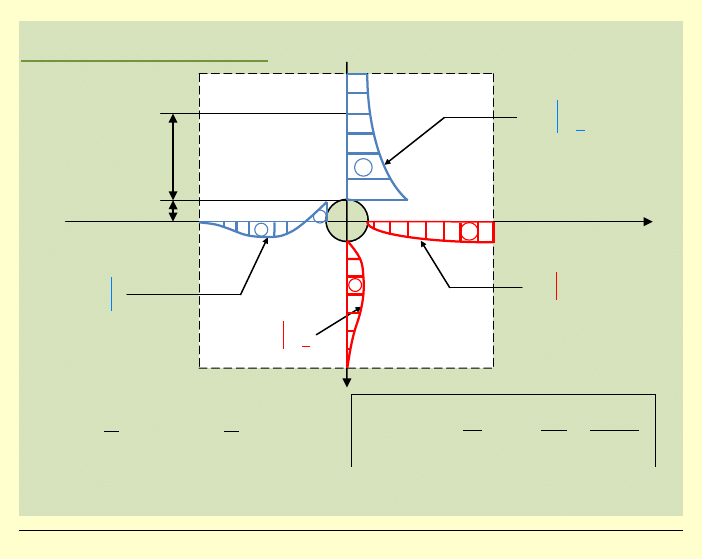
Interpretacja graficzna:
dla:
1
2
ϕ
π
=
lub
3
2
ϕ
π
=
mamy:
2
4
2
4
3
( , )
2
2
p
a
a
r
r
r
ϕϕ
σ
ϕ
⋅
= ⋅
+
+
→ ściśle lokalny charakter (koncentracja) naprężeń!
+
uzasadniony
rozstaw
otworów
a
~ 4a
1
x
2
x
3
2
ϕϕ ϕ π
σ
=
0
rr
ϕ
σ
=
ϕϕ ϕ π
σ
=
1
2
rr
ϕ
π
σ
=
+
−
+
+
p
p
p
3 p
Document Outline
Wyszukiwarka
Podobne podstrony:
34) TSiP 2010 11 ćw13
30) TSiP 2010 11 ćw09
35) TSiP 2010 11 ćw11
36) TSiP 2010 11 ćw12
24) TSiP 2010 11 ćw06
31) TSiP 2010 11 ćw10
29) TSiP 2010 11 ćw08
37) TSiP 2010 11 ćw14
34) TSiP 2010 11 ćw13
30) TSiP 2010 11 ćw09
więcej podobnych podstron