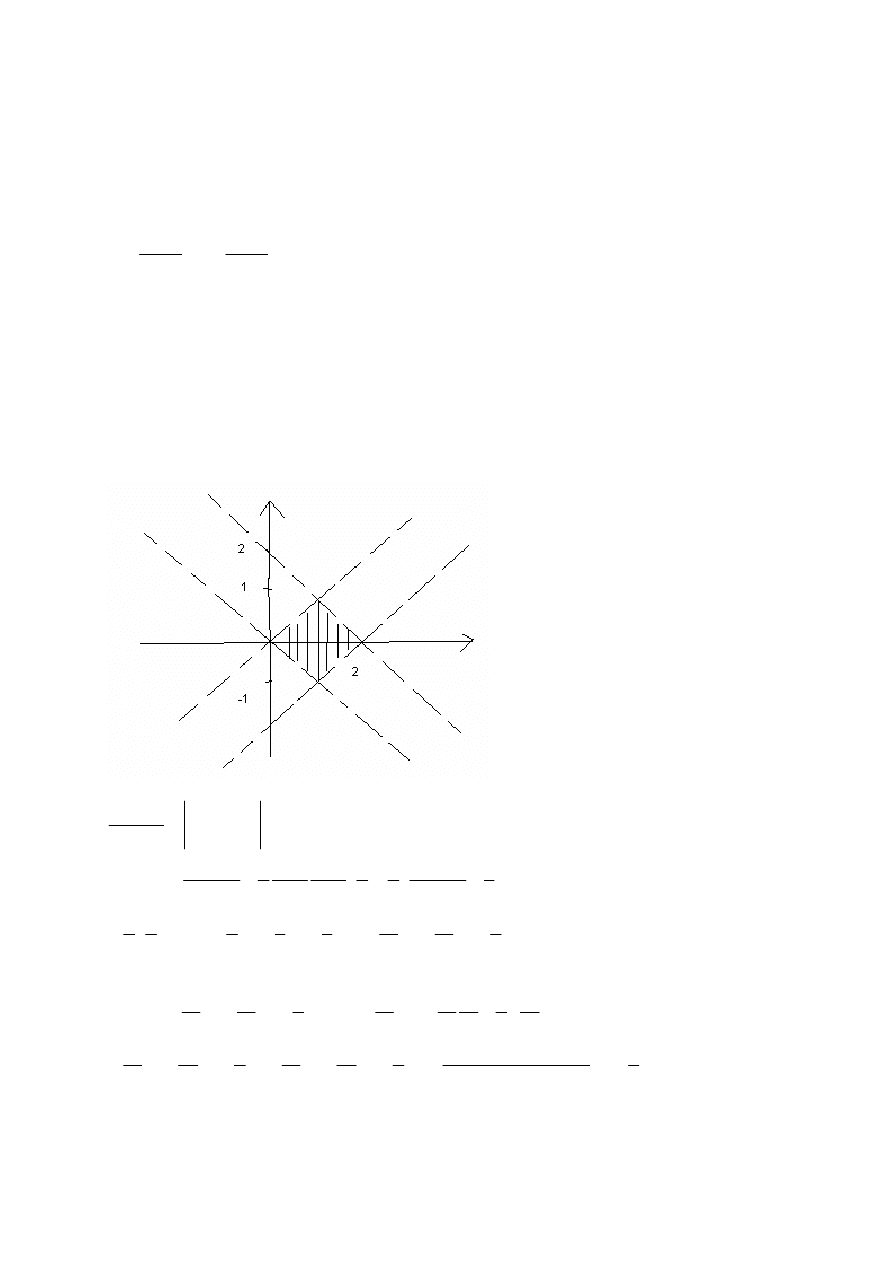
Egzamin dla Aktuariuszy z 30 listopada 2009 r.
Matematyka Ubezpieczeń Majątkowych
Zadanie 1
2
;
2
V
S
X
S
V
Y
−
=
+
=
2
2
2
0
2
0
)
1
;
1
(
)
2
,
0
(
−
>
<
−
<
<
−
<
−
<
<
+
<
−
∈
∈
S
V
S
V
S
V
S
V
S
S
V
V
S
GĘSTOŚĆ BĘDZIE NA TYM OBSZARZE D
0
5
,
0
5
,
0
5
,
0
5
,
0
5
,
0
)
,
(
)
,
(
≠
=
−
=
v
s
D
y
x
D
=
−
+
+
−
=
−
+
+
−
=
)
)(
(
3
1
2
)
(
2
1
2
1
2
2
3
4
2
)
(
)
,
(
2
2
v
s
s
v
v
s
v
s
s
v
v
s
v
s
f
sv
v
s
v
s
v
sv
s
2
1
12
1
12
5
3
1
3
1
2
1
2
1
2
1
2
2
2
2
2
2
−
+
=
−
+
+
−
=
na obszarze D
dla
1
≤
s
∫
−
−
=
−
+
=
−
+
=
s
s
s
s
v
s
v
v
s
dv
sv
v
s
s
f
2
2
1
3
12
1
12
5
2
1
12
1
12
5
)
(
2
3
2
2
2
3
3
3
3
3
3
3
3
9
8
36
9
1
15
9
1
15
4
1
36
1
12
5
4
1
36
1
12
5
s
s
s
s
s
s
s
s
=
+
+
+
−
+
=
+
+
+
−
+
=

(
)
v
v
v
v
f
v
f
s
v
f
s
16
9
32
3
32
15
9
8
2
1
12
1
12
5
)
1
(
)
,
1
(
1
2
2
−
+
=
−
+
=
=
=
(
)
∫
−
−
=
−
+
=
−
+
=
=
1
1
1
1
3
4
2
2
3
3
16
9
4
32
3
2
32
15
16
9
32
3
32
15
1
x
x
x
x
x
x
S
V
E
8
3
24
9
48
18
48
9
128
3
64
15
48
9
128
3
64
15
−
=
−
=
−
=
−
−
−
−
+
=
Zadanie 2
n
n
X
X
X
X
X
X
+
+
≤
→
+
+
≤
...
...
2
2
1
1
1
(
)
=
≤
∧
≤
∧
≤
=
h
pozostalyc
suma
X
h.....
pozostalyc
suma
X
h
pozostalyc
suma
n
2
1
X
P
ODP
(
)
h
pozostalyc
suma
X
ze
n,
istnieje
1
n
>
−
=
P
to są zdarzenia rozłączne tzn nie może być dwóch
i
X większych od sumy pozostałych;
przykład na podstawie dwóch
np.:
(
)
0
...
...
2
...
...
3
3
2
1
2
1
3
1
2
2
1
<
+
+
→
+
+
+
+
>
+
→
+
+
+
>
+
+
>
n
n
dodajac
n
n
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
sprzeczność
czyli:
∑
∑
=
−
≠
−
Γ
≅
≅
>
−
=
>
−
=
n
j
x
j
i
i
j
n
S
S
X
nP
X
X
P
ODP
1
)
;
1
(
,
e
X
oraz
nzl
X
i
S
gdzie
)
(
1
1
λ
λ
λ
∫ ∫
∫
∫
∞ ∞
∞
∞
−
−
−
−
−
−
−
=
−
Γ
=
−
Γ
=
>
0
0
2
2
1
)
1
(
)
1
(
)
(
s
s
x
s
n
n
x
s
n
n
dxds
e
e
s
n
dxds
e
e
s
n
S
X
P
λ
λ
λ
λ
λ
λ
λ
∫
∫
∞
∞
−
−
−
∞
−
−
−
=
−
Γ
=
−
−
Γ
=
0
0
2
2
1
)
1
(
1
)
1
(
ds
e
e
s
n
ds
e
e
s
n
s
s
n
n
s
x
s
n
n
λ
λ
λ
λ
λ
λ
λ
λ
∫
∞
−
−
−
−
−
−
=
−
Γ
−
Γ
=
=
−
=
=
−
Γ
=
0
1
1
1
2
2
1
2
1
)
2
(
)
1
(
)
1
(
2
1
)
1
(
n
n
n
s
n
n
n
n
n
e
s
n
λ
λ
λ
β
α
λ
λ
1
2
1
−
−
=
n
n
ODP
Zadanie 3
−
−
=
−
Π
+
−
Π
=
8
1
4
1
8
3
exp
2
1
2
exp
2
1
8
)
1
(
exp
2
2
1
2
2
2
0
1
x
x
x
x
f
f
)
;
2
(
by
chcemy
i
0
)
2
ln(
8
1
4
1
8
3
8
1
4
1
8
3
exp
2
1
2
2
b
x
t
x
x
t
x
x
K
−
∉
>
−
−
−
=
>
−
−
=
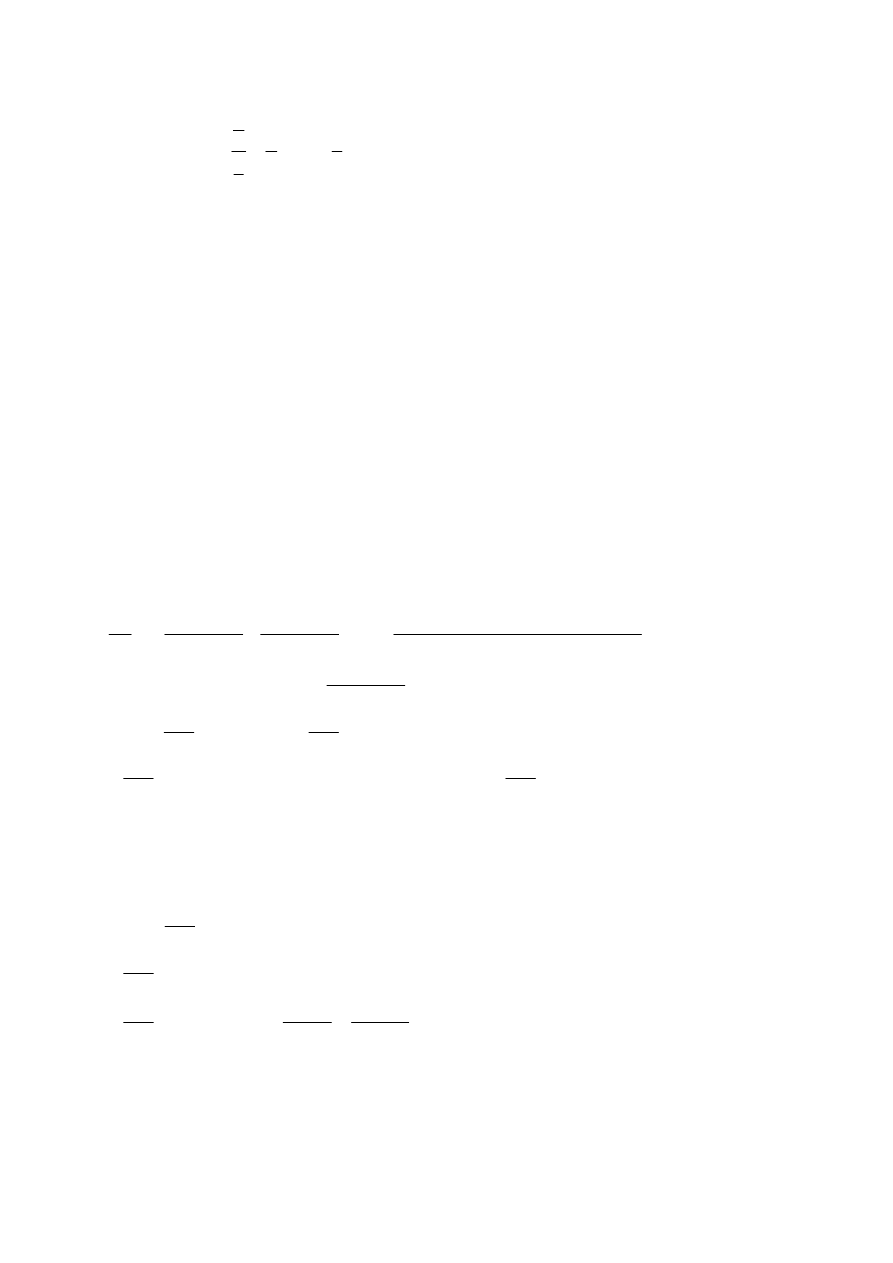
3
8
3
2
8
3
4
1
2
2
1
=
→
=
=
−
=
+
b
b
x
x
(
)
≈
−
−
+
−
=
>
+
−
<
=
5
,
0
)
66
,
2
(
5
,
0
)
2
(
1
)
66
,
2
(
)
2
(
tablic
0
0
F
F
X
P
X
P
z
H
H
α
027
,
0
)
5
,
0
996093
,
0
(
5
,
0
97725
,
0
1
=
−
−
+
−
≈
Zadanie 4
Patrz zadanie 8 z dnia 11.10.2009
ODP=1-P(w tamtym zadaniu)=0,3333
Zadanie 5
Określamy ilość pojawień się poszczególnych kombinacji:
3
2
1
3
2
1
)
2
,
2
(
)
1
,
2
(
)
2
,
1
(
)
1
,
1
(
n
n
n
n
n
n
n
−
−
−
=
−
−
−
[
] [
]
2
1
1
2
3
2
1
3
2
1
)
1
(
)
1
(
)
1
(
)
1
(
2
2
n
n
n
n
n
n
n
n
n
n
n
n
n
L
+
−
+
−
−
−
−
−
=
−
−
−
=
θ
θ
θ
θ
θ
θ
θ
θ
(
)
(
)
)
1
ln(
ln
ln
2
1
1
2
θ
θ
−
+
−
+
+
−
=
n
n
n
n
n
n
L
(
) (
)
0
)
1
(
)
1
(
0
1
2
1
1
2
2
1
1
2
=
−
+
−
−
+
−
−
→
=
−
+
−
−
+
−
=
∂
∂
θ
θ
θ
θ
θ
θ
θ
n
n
n
n
n
n
n
n
n
n
n
n
L
n
n
n
n
n
n
n
n
2
ˆ
0
)
2
(
1
2
1
2
+
−
=
→
=
−
+
−
θ
θ
(
)
[
]
(
)
[
]
=
−
+
=
−
=
2
1
2
1
2
2
1
2
,
cov
2
var
var
4
1
var
4
1
ˆ
var
n
n
n
n
n
n
n
n
θ
(
)
[
]
(
)
[
]
2
1
2
1
2
2
1
2
1
2
1
2
var
var
2
var
2
4
1
var
var
var
var
var
4
1
n
n
n
n
n
n
n
n
n
n
n
n
+
−
+
=
+
+
+
−
+
=
to są rozkłady Bernoulliego, czyli:
(
)
2
2
1
1
var
θ
θ
−
=
n
n
(
)
2
2
2
)
1
(
1
)
1
(
var
θ
θ
−
−
−
=
n
n
(
)
(
)(
)
2
2
2
2
2
1
)
1
(
1
)
1
(
var
θ
θ
θ
θ
−
−
−
−
+
=
+
n
n
n
(
)
(
) (
)(
)
[
]
=
−
−
+
−
−
−
+
−
=
2
2
2
2
2
2
2
2
2
2
1
2
2
)
1
(
2
1
2
4
1
θ
θ
θ
θ
θ
θ
θ
θ
θ
n
n
n
n
ODP
[
]
3
2
2
4
3
4
3
2
2
4
2
2
4
4
2
2
4
4
2
8
8
2
4
2
2
4
1
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
n
n
n
n
n
n
n
n
n
n
n
n
n
n
−
+
+
−
+
−
−
+
−
−
+
−
=
[
]
n
n
n
n
n
2
)
1
(
2
2
2
4
1
2
2
2
θ
θ
θ
θ
θ
θ
−
=
−
=
+
−
=
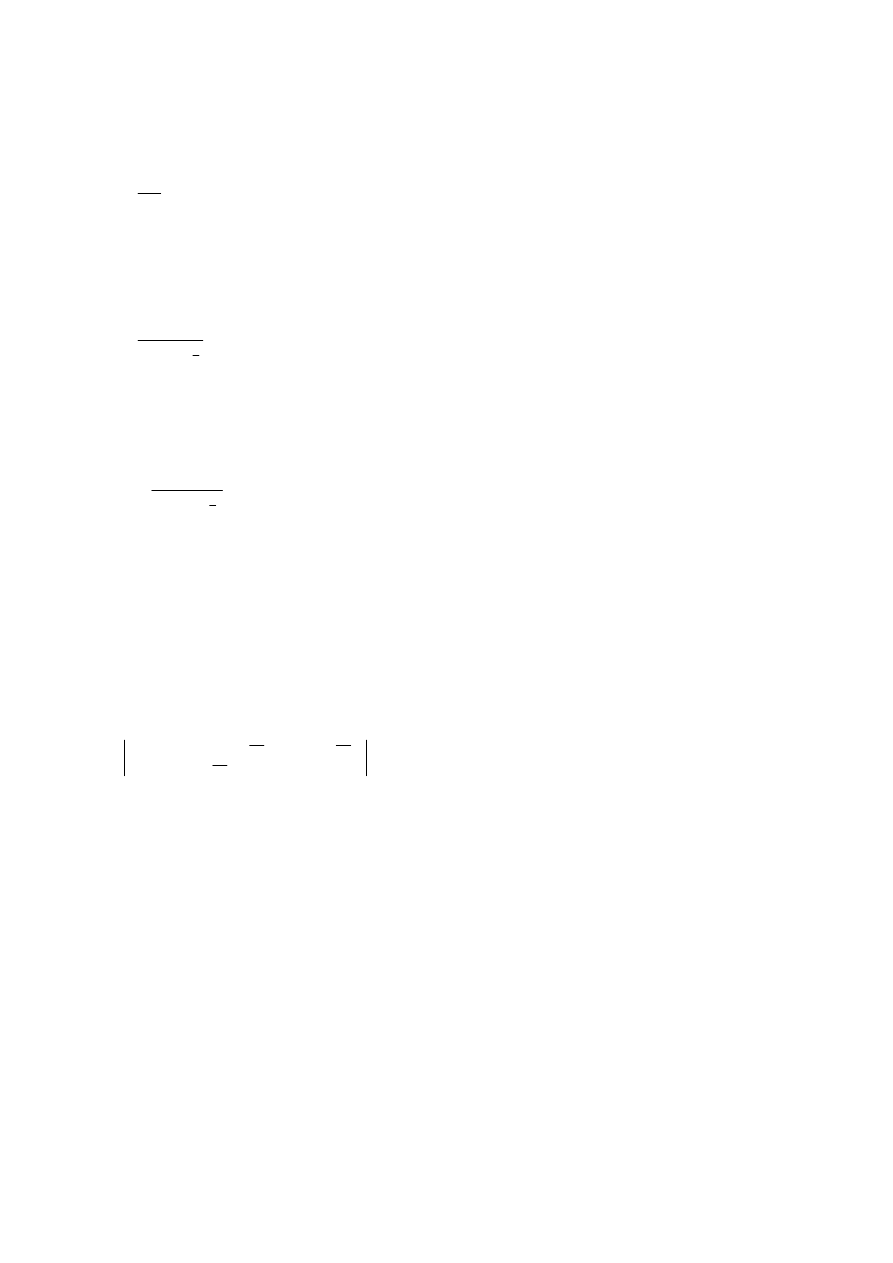
Zadanie 6
Dla sumy niezależnych zmiennych zachodzi:
(
)
2
3
2
3
2
2
3
2
3
3
3
3
2
3
∑
∑
∑
∑
=
=
=
+
−
=
=
j
i
i
i
i
m
m
σ
σ
γ
γ
σ
σ
µ
µ
µ
µ
µ
σ
µ
γ
( )
=
−
+
=
−
+
=
3
,
2
3
3
,
2
,
3
3
2
3
2
3
n
n
n
n
n
n
n
n
n
S
S
S
S
S
S
S
S
S
n
m
m
S
E
µ
µ
σ
γ
µ
µ
µ
(
)
2
3
3
3
2
2
3
3
2
3
n
n
n
n
n
n
n
n
n
n
n
S
S
S
S
S
S
S
S
S
S
S
σ
µ
µ
σ
γ
µ
µ
σ
µ
σ
γ
+
+
=
−
+
+
=
(
)
0
bo
0
,
2
3
2
3
,
=
=
=
∑
∑
X
i
X
i
S
n
γ
σ
σ
γ
γ
bo rozkład symetryczny
µ
µ
n
n
S
=
2
2
σ
σ
n
n
S
=
( )
(
)
2
2
2
2
2
3
3
3
3
3
σ
µ
µ
µσ
µ
+
=
+
=
n
n
n
n
S
E
n
Zadanie 7
(
)
(
)
(
)
( ) ( )
(
)
)
(
)
(
)
(
)
(
)
(
)
(
,
cov
,
cov
,
cov
Z
N
Y
N
Z
N
Y
N
Z
Y
S
E
S
E
S
S
E
S
S
+
=
(
)
(
)
[
]
EYEZ
YZ
E
n
Z
Y
n
Z
Z
Y
Y
S
S
N
N
Z
N
Y
N
−
=
=
+
+
+
+
=
)
(
)
,
cov(
...
,
...
cov
,
cov
1
1
)
(
)
(
=
(
) ( )
=
=
⋅
=
n
d
m
n
d
m
d
X
E
d
X
X
E
wiemy
ze
[
]
+
+
−
−
−
=
)
2
(
)
2
,
min(
)
2
(
2
X
E
X
E
X
E
n
[
]
∫
∞
−
−
−
∞
−
−
−
−
+
=
−
=
+
−
−
=
−
=
−
2
2
2
2
2
2
2
)
2
(
)
2
(
e
e
e
e
e
xe
e
x
X
E
x
x
x
x
2
1
)
2
(
)
2
,
min(
−
+
−
=
−
−
=
e
X
E
EX
X
E
(
)
(
)
[
]
(
)
4
2
2
2
2
)
(
)
(
1
2
,
cov
−
−
−
−
−
+
=
−
−
=
e
e
n
e
e
e
n
S
S
Z
N
Y
N
( )
(
)
(
)
2
1
)
(
1
)
2
,
min(
...
−
−
=
=
+
+
=
e
N
X
NE
Y
Y
E
S
E
N
Y
N
( )
(
)
2
1
)
(
)
2
(
...
−
+
=
−
=
+
+
=
Ne
X
NE
Z
Z
E
S
E
N
Z
N
(
)
(
)
(
)
(
) (
) (
)
=
−
+
+
=
−
+
+
=
−
−
−
−
−
−
−
−
N
e
e
e
e
Ne
e
N
e
e
N
E
ODP
var
1
,
1
cov
2
2
4
2
2
2
4
2
λ
(
) (
)
(
)
2
4
2
4
2
2
2
4
2
2
1
−
−
−
−
−
−
−
−
−
=
−
+
+
=
−
+
+
=
e
e
e
e
e
e
e
e
e
λ
λ
λ
λ
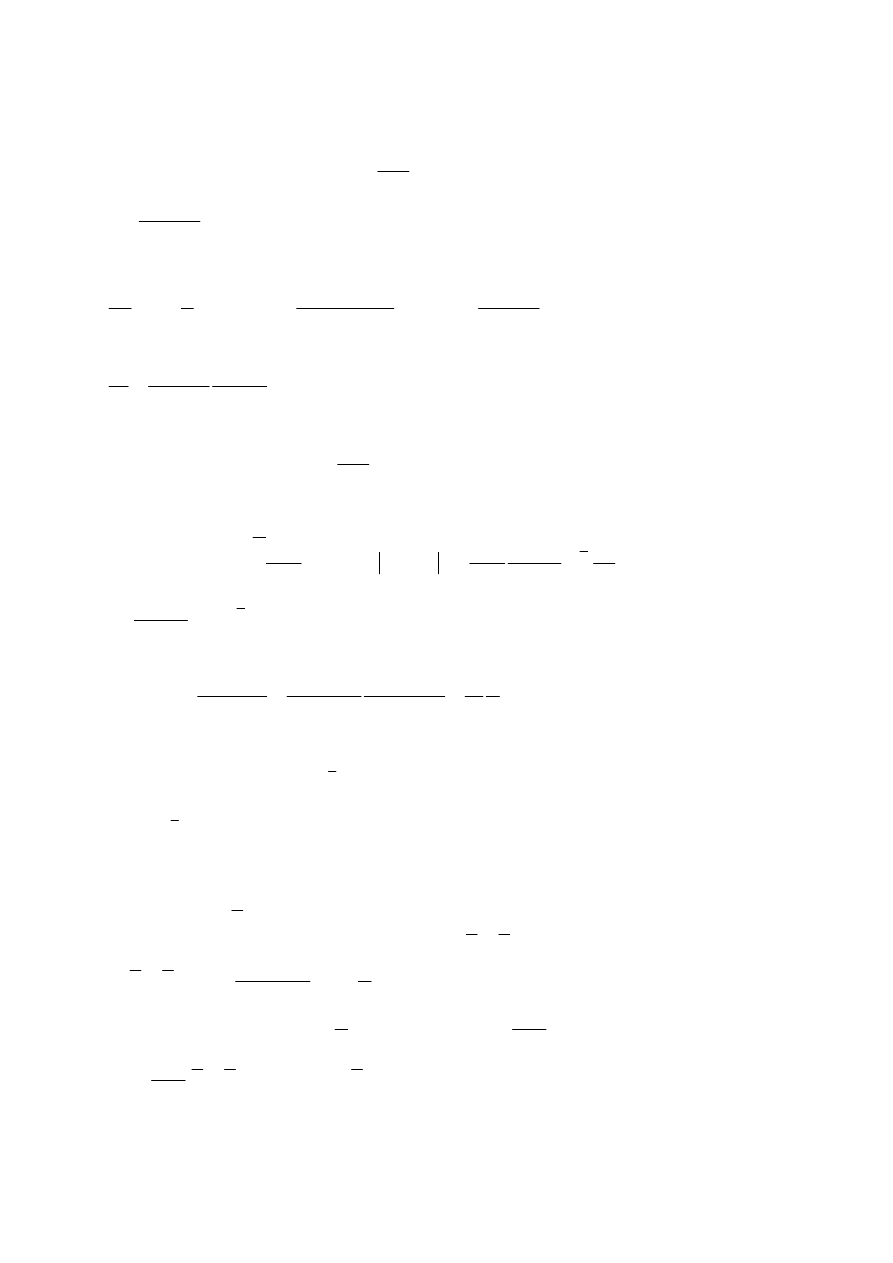
Zadanie 8
Szukamy estymatora dla Pareto:
1
+
=
θ
θ
x
f
( )
1
+
Π
=
θ
θ
i
n
x
L
∑
=
+
−
=
0
ln
)
1
(
ln
ln
i
X
n
L
θ
θ
∑
∑
∑
=
→
=
−
→
−
=
∂
∂
i
i
i
X
n
X
n
X
n
L
ln
ˆ
0
ln
ln
ln
θ
θ
θ
θ
θ
5
ln
ln
4
ˆ
ˆ
5
1
4
1
2
1
∑
∑
=
=
=
i
i
i
i
Y
X
θ
θ
(
)
(
)
∫
≅
→
−
=
=
<
=
<
−
+
)
exp(
1
1
)
(
ln
1
ln
t
i
t
t
i
i
wykl
X
e
x
e
X
P
t
X
P
θ
θ
θ
θ
∑
Γ
≅
)
,
(
ln
θ
n
X
i
(
)
∫
∫
∑
=
Γ
=
=
=
Γ
=
<
−
−
−
−
−
θ
θ
θ
θ
θ
θ
θ
θ
2
0
0
2
1
1
1
2
1
)
2
(
)
(
2
)
(
ln
2
t
t
w
n
n
n
x
n
n
i
dw
e
w
n
w
x
e
x
n
t
X
P
∫
≅
Γ
=
−
−
)
2
(
2
)
(
1
2
2
1
n
e
w
n
w
n
n
χ
przy założeniu, że
)
8
(
),
10
(
gdzie
8
10
ln
2
4
5
ln
2
ln
5
ln
4
2
2
2
1
χ
χ
θ
θ
θ
θ
θ
≅
≅
=
=
=
=
∑
∑
∑
∑
Y
X
Y
X
X
Y
X
Y
i
i
i
i
Z TEGO WYNIKA, ŻE:
(
)
)
10
,
8
(
),
8
,
10
(
gdzie
1
2
1
2
1
Sned
F
Sned
F
t
F
P
t
F
P
rozmiar
≅
≅
>
=
<
=
z tablic:
0,95
dla
F(8,10)
rozkladu
kwantyl
326
,
0
07
,
3
1
≈
→
=
t
t
Zadanie 9
Przyjmijmy
X
=
λ
ˆ
Przyjmijmy na początek, że estymator równa się
2
X
X
+
(
)
2
2
2
2
2
2
by
chcemy
i
λ
λ
λ
λ
λ
λ
λ
λ
+
=
+
+
=
+
+
=
+
n
n
n
n
X
X
E
czyli szukamy a i b by:
→
=
−
=
→
+
=
+
+
1
i
1
2
2
b
n
n
a
n
b
a
λ
λ
λ
λ
λ
X
X
X
n
n
E
i
1
2
2
λ
λ
+
=
+
−
→
jest statystyką dostateczną i zupełną
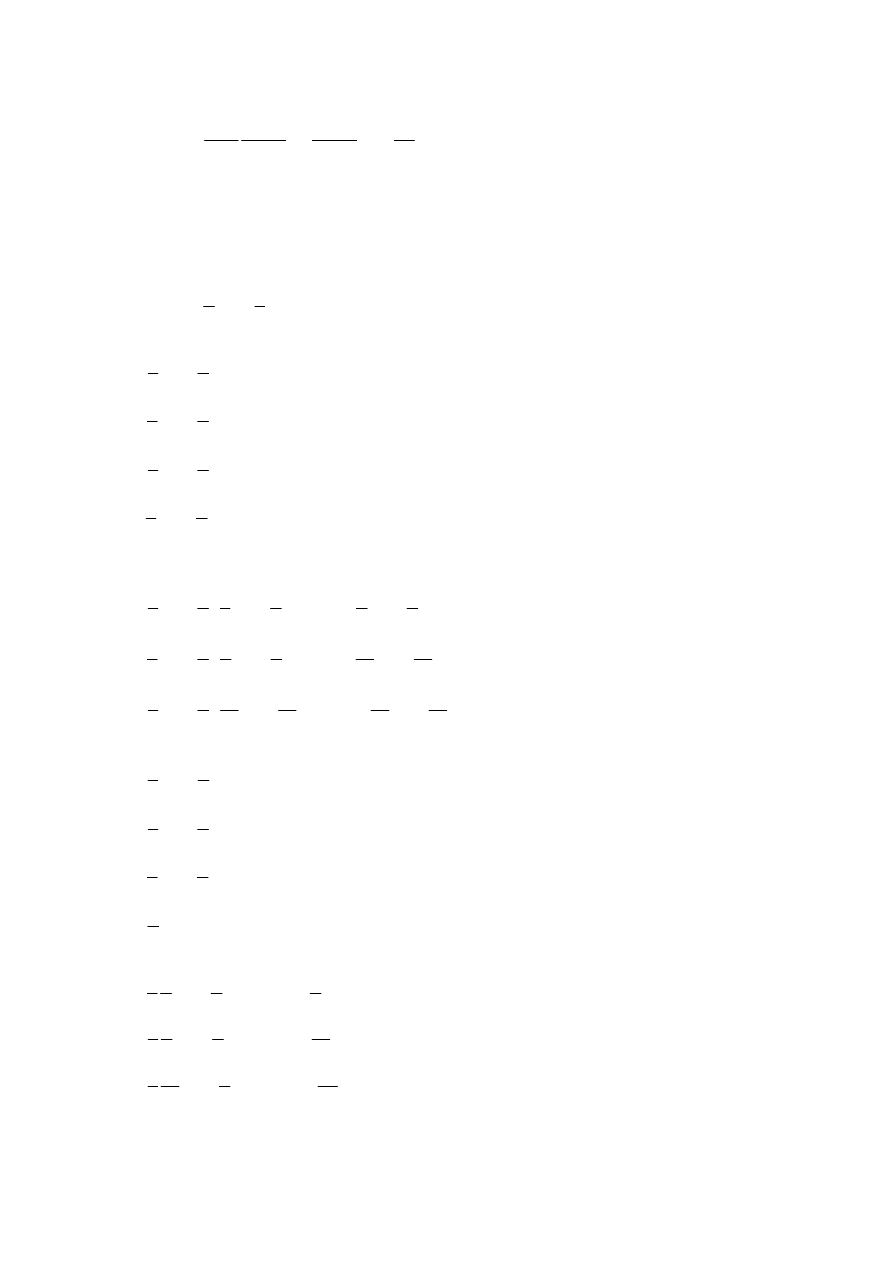
czyli
−
+
=
+
−
=
∑
∑
∑
∑
=
=
n
i
i
n
i
i
i
i
X
n
X
n
n
X
n
X
n
n
ODP
1
2
1
2
2
)
1
(
1
1
Zadanie 10
i
p - prawdopodobieństwo, że startując ze stanu i (i zł) dojdzie do 0 (czyli wszystko przegra)
6
4
5
3
1
3
2
P
p
p
ODP
+
=
=
3
2
3
1
3
2
3
1
3
2
3
1
3
2
3
1
2
1
1
3
2
2
4
3
3
5
4
+
=
+
=
+
=
+
=
p
p
p
p
p
p
p
p
p
p
p
Z tego:
7
4
7
3
3
2
3
1
3
2
3
1
3
2
2
3
2
+
=
→
+
+
=
p
p
p
p
p
15
8
15
7
7
4
7
3
3
2
3
1
4
3
3
4
3
+
=
→
+
+
=
p
p
p
p
p
31
16
31
15
15
8
15
7
3
2
3
1
5
4
4
5
4
+
=
→
+
+
=
p
p
p
p
p
8
9
7
9
8
6
8
7
5
7
6
3
2
3
2
3
1
3
2
3
1
3
2
3
1
p
p
p
p
p
p
p
p
p
p
p
=
+
=
+
=
+
=
czyli
7
8
7
8
8
7
6
3
2
3
2
3
1
p
p
p
p
p
=
→
+
=
6
7
6
7
7
15
14
3
2
7
6
3
1
p
p
p
p
p
=
→
+
=
5
6
5
6
6
31
30
3
2
15
14
3
1
p
p
p
p
p
=
→
+
=

czyli:
97
,
0
33
32
31
30
3
1
31
16
31
15
3
2
5
5
5
5
≈
=
→
+
+
=
p
p
p
p
Wyszukiwarka
Podobne podstrony:
2009 11 30 matematyka finansowaid 26676
2009.11.30 matematyka finansowa
2009 05 30 14;58;11
F II wyklad 11 30 04 12
2004 10 11 prawdopodobie stwo i statystykaid 25166
2009-11-05, pedagogium, wykłady, Teoria edukacji obronnej i bezpieczeństwa publicznego
06 11 12 rachunek kosztów
2009 11 17 arduino basics
2009 11 Informatyka śledcza
2009 05 30 14;58;17id 26810 Nieznany (2)
2009 05 30 14;58;14id 26809 Nieznany
Wyklad 3 makro 12.11, Finanse i Rachunkowość, Semestr I, Makroekonomia, inne
DGP 2014 06 30 rachunkowosc i audyt
2009 05 30 14;57;36id 26802 Nieznany
21ZiIPN12010-11, Finanse i rachunkowość
2009 05 30 14;57;50
więcej podobnych podstron