1. Ze zbioru liczb

wybieramy losowo jedną liczbę. Liczba p jest

prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
A)

B)

C)

D)

2. Ze zbioru liczb

wybieramy losowo jedną liczbę. Liczba p oznacza

prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
A)

B)

C)

D)

3. Ze zbioru liczb

wybieramy losowo jedną liczbę. Niech p oznacza

prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A)

B)

C)

D)

4. Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo

wylosowania co najmniej jednej kuli białej jest równe

, a prawdopodobieństwo wybrania co najwyżej

jednej kuli białej jest równe

. Wobec tego prawdopodobieństwo wybrania dokładnie jednej kuli białej

jest równe
A)

B)

C)

D)

5. Z szuflady zawierającej piłki w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo

wylosowania co najmniej jednej piłki czerwonej jest równe

, a prawdopodobieństwo wybrania co

najwyżej jednej piłki zielonej jest równe

. Wobec tego prawdopodobieństwo wybrania dokładnie jednej

piłki czerwonej jest równe
A)

B)

C)

D)

6. Na loterii jest 10 losów, z których 4 są wygrywające. Kupujemy jeden los. Prawdopodobieństwo

zdarzenia, że nie wygramy nagrody jest równe
A)

B)

C)

D)

7. Na loterii jest 12 losów, z których 8 jest przegrywających. Kupujemy jeden los. Prawdopodobieństwo

zdarzenia, że wygramy nagrodę jest równe
A)

B)

C)

D)

8. Na loterii jest 14 losów, z których 6 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo

zdarzenia, że nie wygramy nagrody jest równe
A)

B)

C)

D)

9. Pewne przedsiębiorstwo postanowiło przyznać każdemu pracownikowi losowy 5-cyfrowy identyfikator,

przy czym ustalono, że w identyfikatorze nie może występować cyfra 0. Prawdopodobieństwo p
otrzymania identyfikatora, w którym każde dwie cyfry są różne spełnia warunek
A)

B)

C)

D)

10. Ze zbioru

losujemy jedną liczbę. Prawdopodobieństwo wylosowania

liczby pierwszej jest równe

A)

B)

C)

D)

11. Ze zbioru

losujemy jedną liczbę. Prawdopodobieństwo

wylosowania liczby pierwszej jest równe

A)

B)

C)

D)

12. Prawdopodobieństwo zdarzenia A jest równe , a prawdopodobieństwo sumy zdarzeń A i B jest równe

. Wobec tego prawdopodobieństwo zdarzenia

jest równe

A)

B)

C)

D)

13. Prawdopodobieństwo zdarzenia B jest równe , a prawdopodobieństwo sumy zdarzeń A i B jest równe

. Wobec tego prawdopodobieństwo zdarzenia

jest równe

A)

B)

C)

D)

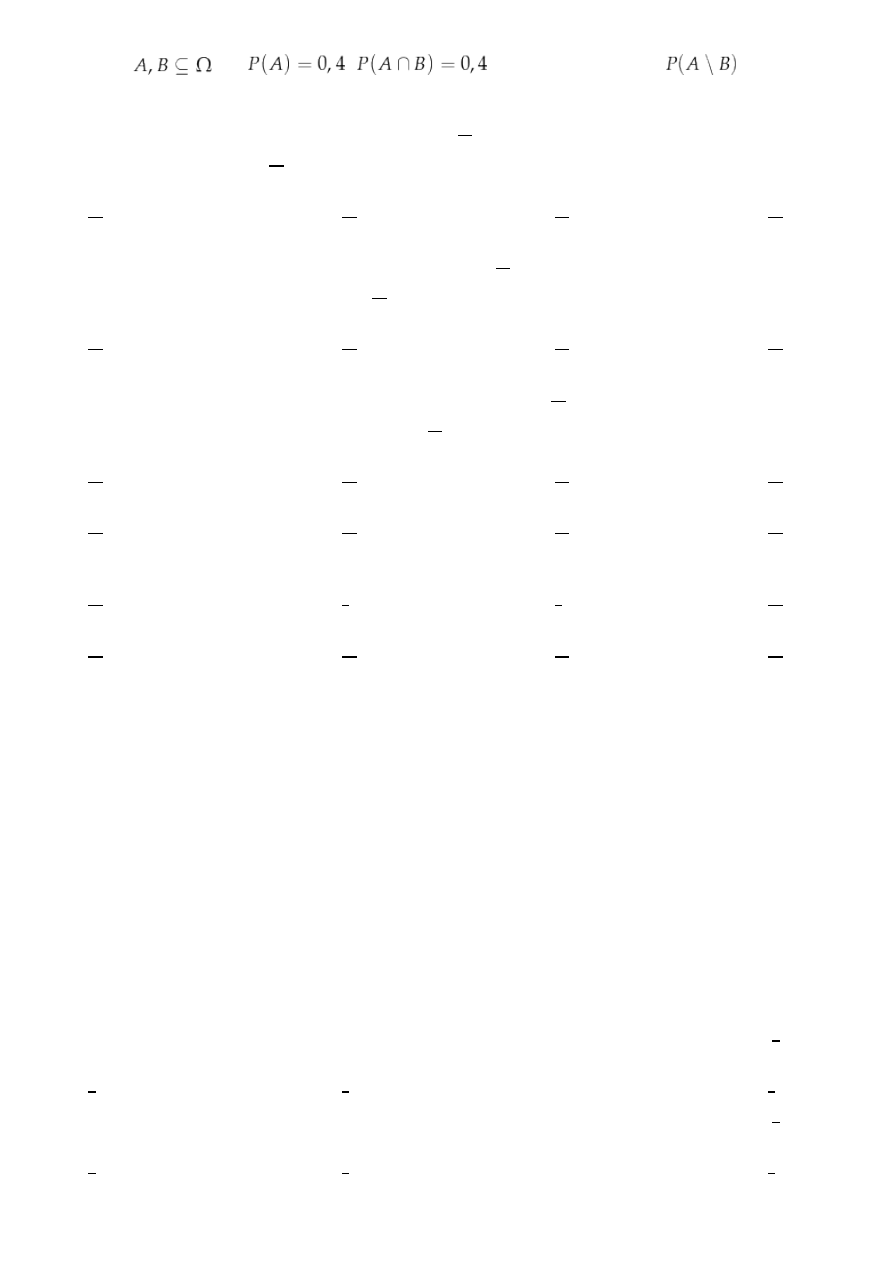
14. Jeżeli

oraz

i

to prawdopodobieństwo

jest równe

A) 0,6

B) 0,4

C) 1

D) 0

15. Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo

wylosowania co najmniej jednej kuli białej jest równe

, a prawdopodobieństwo wybrania co najwyżej

jednej kuli białej jest równe

. Wobec tego prawdopodobieństwo wybrania dokładnie dwóch kul białych

jest równe
A)

B)

C)

D)

16. Z urny zawierającej kule w dwóch kolorach wybieramy losowo dwie. Prawdopodobieństwo

wylosowania co najmniej jednej kuli niebieskiej jest równe

, a prawdopodobieństwo wybrania co

najwyżej jednej kuli czerwonej jest równe

. Wobec tego prawdopodobieństwo wybrania dokładnie

dwóch kul niebieskich jest równe
A)

B)

C)

D)

17. Z pudełka zwierającego losy wygrywające i przegrywające wybieramy dwa losy. Prawdopodobieństwo

wylosowania co najmniej jednego losu wygrywającego jest równe ,

a prawdopodobieństwo wybrania co

najwyżej jednego losu wygrywającego jest równe

. Wobec tego prawdopodobieństwo wybrania

dokładnie dwóch losów wygrywających jest równe
A)

B)

C)

D)

18. . Prawdopodobieństwo, że wylosujemy króla lub kiera, jest równe

A)

B)

C)

D)

19. Z talii 24 kart (od dziewiątek) losujemy jedną. Prawdopodobieństwo, że wylosujemy waleta lub trefla,

jest równe
A)

B)

C)

D)

20. Z talii 52 kart losujemy jedną. Prawdopodobieństwo, że wylosujemy damę lub pika, jest równe

A)

B)

C)

D)

21. Kod, który zapisany jest na karcie dostępu, składa się z czterech cyfr. Chcemy, aby

prawdopodobieństwo odkrycia tego kodu zmniejszyło się stukrotnie. Ile jeszcze cyfr należy dopisać do
kodu?
A) 1

B) 2

C) 100

D) 6

22. Kod dostępu do sejfu składa się z pięciu cyfr. Chcemy, aby prawdopodobieństwo odkrycia tego kodu

zmniejszyło się stukrotnie. Ile cyfr powinien mieć nowy kod?
A) 7

B) 2

C) 100

D) 6

23. Kod, który zapisany jest na karcie dostępu, składa się z czterech cyfr. Chcemy, aby

prawdopodobieństwo odkrycia tego kodu zmniejszyło się tysiąckrotnie. Ile jeszcze cyfr należy dopisać do
kodu?
A) 3

B) 2

C) 1000

D) 7

24. O zdarzeniach losowych A, B wiadomo, że:

i .

Prawdopodobieństwo iloczynu zdarzeń A i B spełnia warunek
A)

B)

C)

D)

25. O zdarzeniach losowych A,B wiadomo, że:

i .

Prawdopodobieństwo iloczynu zdarzeń A i B spełnia warunek
A)

B)

C)

D)

26. Zdarzenie

jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia jest równe

.

Wobec tego suma prawdopodobieństw zdarzeń A i B jest równa
A)

B)

C) 1

D)

27. Zdarzenie

jest zdarzeniem pewnym, a prawdopodobieństwo zdarzenia jest równe

.

Wobec tego suma prawdopodobieństw zdarzeń A i B jest równa
A)

B)

C) 1

D)

28. W pudełku znajdują się tylko kule białe i czarne. Stosunek liczby kul białych do liczby kul czarnych jest

równy 3:4. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania białej kuli jest równe
A)

B)

C)

D)

29. W pudełku znajdują się tylko kule białe i czarne. Stosunek liczby kul czarnych do liczby kul białych jest

równy 4:5. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania białej kuli jest równe
A)

B)

C)

D)

30. Zdarzenia losowe A i B są rozłączne oraz

. Zatem prawdopodobieństwo zdarzenia B może

być równe
A) 0,63

B) 0,53

C) 0,43

D) 1

31. O zdarzeniach losowych A i B zawartych w



wiadomo, że

i . Wtedy

A)

B)

C)

D)

32. O zdarzeniach losowych A i B zawartych w



wiadomo, że

i . Wtedy

A)

B)

C)

D)

33. Rzucamy dwiema kostkami do gry. Jeśli A oznacza zdarzenie „suma wyrzuconych oczek jest równa

11”, a B oznacza zdarzenie „suma wyrzuconych oczek jest równa 9” to
A)

B)

C)

D)

34. Rzucamy dwiema kostkami do gry. Jeśli A oznacza zdarzenie „suma wyrzuconych oczek jest równa

10”, a B oznacza zdarzenie „suma wyrzuconych oczek jest równa 11” to
A)

B)

C)

D)

35. Rzucamy dwiema kostkami do gry. Jeśli A oznacza zdarzenie „suma wyrzuconych oczek jest równa 6”,

a B oznacza zdarzenie „suma wyrzuconych oczek jest równa 10” to
A)

B)

C)

D)

36. Zdarzenia A i B zawarte w zbiorze zdarzeń elementarnych



spełniają warunek

. Zatem
A)

B)

C)

D)

37. Zdarzenia A i B zawarte w zbiorze zdarzeń elementarnych



spełniają warunek

. Zatem
A)

B)

C)

D)

38. Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych

oczek wyniesie co najwyżej 9, jest równe

A)

B)

C)

D)

39. Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych

oczek wyniesie co najwyżej 10, jest równe

A)

B)

C)

D)

40. Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych

oczek wyniesie co najmniej 5, jest równe

A)

B)

C)

D)

41. Prawdopodobieństwa zdarzeń

oraz zdarzeń przeciwnych

spełniają równości

. Wtedy

jest równe

A) 0,5

B) 0,1

C) 0,3

D) 1

42. Prawdopodobieństwa zdarzeń

oraz zdarzeń przeciwnych

spełniają równości

. Wtedy

jest równe

A) 0,4

B) 0,1

C) 0,3

D) 0,2

43. Prawdopodobieństwa zdarzeń

oraz zdarzeń przeciwnych

spełniają równości

. Wtedy

jest równe

A) 0,6

B) 0,8

C) 0,3

D) 1

44. Rzucamy dwukrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że na każdej kostce

wypadną co najmniej 4 oczka, jest równe

A)

B)

C)

D)

45. Rzucamy dwukrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że na każdej kostce

wypadną co najwyżej 3 oczka, jest równe

A)

B)

C)

D)

46. Rzucamy dwukrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że na każdej kostce

wypadnie co najmniej 5 oczek, jest równe

A)

B)

C)

D)

47. Ze zbioru cyfr

losujemy dwa razy po jednej cyfrze bez zwracania.

Prawdopodobieństwo, że wybrane w kolejności losowania cyfry utworzą liczbę parzystą, jest równe

A)

B)

C)

D)

48. Ze zbioru cyfr

losujemy dwa razy po jednej cyfrze bez zwracania.

Prawdopodobieństwo, że wylosowane cyfry (w kolejności losowania) utworzą liczbę podzielną przez 5 jest
równe

A)

B)

C)

D)

49. Ze zbioru cyfr

losujemy dwa razy po jednej cyfrze bez zwracania.

Prawdopodobieństwo, że wyjęte w kolejności losowania cyfry utworzą liczbę nieparzystą, jest równe

A)

B)

C)

D)

50. Losujemy jeden wierzchołek i jedną ścianę sześcianu. Prawdopodobieństwo zdarzenia polegającego na

tym, że wylosowany wierzchołek jest wierzchołkiem wylosowanej ściany jest równe

A)

B)

C)

D)

51. Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia co najmniej raz liczby

oczek podzielnej przez 3 jest równe

A)

B)

C)

D)

52. Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia co najmniej raz liczby

oczek większej od 4 jest równe

A)

B)

C)

D)

53. Ze zbioru

wybieramy dwie liczby (mogą się powtarzać), a ze zbioru

jedną liczbę. Na ile

sposobów można to zrobić tak, aby otrzymane 3 liczby były długościami boków pewnego trójkąta?
A) 2

B) 3

C) 4

D) 6

54. W pewnej szkole 20% uczniów klas trzecich pisało maturę próbną z matematyki, przy czym 90%

spośród piszących otrzymało z próbnej matury więcej niż 35 punktów. Spośród wszystkich uczniów klas
trzecich wybrano losowo jednego ucznia. Prawdopodobieństwo, że wybrano ucznia, który pisał maturę
próbną z matematyki i otrzymał więcej niż 35 punktów jest równe
A) 0,18

B) 0,45

C) 0,9

D) 0,72

55. W pewnej szkole 30% uczniów klas trzecich pisało maturę próbną z matematyki, przy czym 80%

spośród piszących otrzymało z próbnej matury więcej niż 35 punktów. Spośród wszystkich uczniów klas
trzecich wybrano losowo jednego ucznia. Prawdopodobieństwo, że wybrano ucznia, który pisał maturę
próbną z matematyki i otrzymał więcej niż 35 punktów jest równe
A) 0,8

B) 0,24

C) 0,27

D) 0,375

56. W pewnej szkole 40% uczniów klas trzecich pisało maturę próbną z matematyki, przy czym 80%

spośród piszących otrzymało z próbnej matury więcej niż 35 punktów. Spośród wszystkich uczniów klas
trzecich wybrano losowo jednego ucznia. Prawdopodobieństwo, że wybrano ucznia, który pisał maturę
próbną z matematyki i otrzymał więcej niż 35 punktów jest równe
A) 0,68

B) 0,5

C) 0,32

D) 0,72

57. Prawdopodobieństwo, że przy rzucie pięcioma monetami otrzymamy co najmniej trzy orły, jest równe

A)

B)

C)

D)

58. Prawdopodobieństwo, że przy rzucie pięcioma monetami otrzymamy co najmniej trzy reszki, jest równe

A)

B)

C)

D)

59. Prawdopodobieństwo, że przy rzucie pięcioma monetami otrzymamy co najwyżej 2 reszki, jest równe

A)

B)

C)

D)

60. Z talii 52 kart losujemy jedną. Prawdopodobieństwo tego, że wylosujemy kartę trefl lub waleta lub

króla, jest równe

A)

B)

C)

D)

61. Z talii 52 kart losujemy jedną. Prawdopodobieństwo tego, że wylosujemy kartę pik lub damę lub króla,

jest równe

A)

B)

C)

D)

62. Z talii 52 kart losujemy jedną. Prawdopodobieństwo tego, że wylosujemy kartę trefl lub pik lub waleta,

jest równe

A)

B)

C)

D)

63. W konkursie matematycznym, w którym przewidziano tylko jedną nagrodę I stopnia, bierze udział 15

uczniów. Prawdopodobieństwo, że zwycięży Agnieszka jest równe 0,20. Prawdopodobieństwo, że
zwycięży Piotrek jest równe . Prawdopodobieństwo, że zwycięży Agnieszka lub Piotrek jest równe

A) 0,02

B) 0,3

C)

D)

64. W zawodach pływackich, w których przewidziano tylko jedną nagrodę I stopnia, bierze udział 35

uczniów. Prawdopodobieństwo, że zwycięży Jola jest równe 0,10. Prawdopodobieństwo, że zwycięży

Antek jest równe

. Prawdopodobieństwo, że zwycięży Jola lub Antek jest równe

A) 0,3

B)

C) 0,02

D)

65. W konkursie biologicznym, w którym przewidziano tylko jedną nagrodę I stopnia, bierze udział 20

uczniów. Prawdopodobieństwo, że zwycięży Wojtek jest równe 0,30. Prawdopodobieństwo, że zwycięży
Gosia jest równe . Prawdopodobieństwo, że zwycięży Wojtek lub Gosia jest równe

A) 0,25

B)

C) 0,35

D)

66. W kapeluszu znajdują się króliki białe i szare. Królików szarych jest trzy razy więcej niż białych.

Prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe . Zatem prawdopodobieństwo
wyciągnięcia z kapelusza królika szarego jest równe

A)

B)

C)

D)

67. W woreczku znajdują się piłki białe i szare. Piłek szarych jest trzy razy więcej niż białych.

Prawdopodobieństwo wyciągnięcia z woreczka piłki białej jest równe 0,25. Zatem prawdopodobieństwo
wyciągnięcia z woreczka piłki szarej jest równe

A) 0,75

B)

C) 0,25

D) 0,8

68. W kapeluszu znajdują się króliki białe i szare. Królików szarych jest cztery razy więcej niż białych.

Prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe . Zatem prawdopodobieństwo
wyciągnięcia z kapelusza królika białego jest równe

A)

B) 0,75

C)

D)

69. Prawdopodobieństwo zdarzenia

jest 6 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego

do

. Wobec tego prawdopodobieństwo zdarzenia jest równe

A)

B)

C)

D)

70. Prawdopodobieństwo zdarzenia

jest 7 razy większe niż prawdopodobieństwo zdarzenia przeciwnego

do

. Wobec tego prawdopodobieństwo zdarzenia jest równe

A)

B)

C)

D)

71. Prawdopodobieństwo zdarzenia

jest 6 razy większe niż prawdopodobieństwo zdarzenia przeciwnego

do

. Wobec tego prawdopodobieństwo zdarzenia jest równe

A)

B)

C)

D)

72. Jacek bierze udział w olimpiadzie chemicznej i olimpiadzie matematycznej. Prawdopodobieństwo, że

zostanie laureatem olimpiady chemicznej jest równe 0,3, a prawdopodobieństwo, że zostanie laureatem
przynajmniej jednej z tych dwóch olimpiad wynosi 0,72. Prawdopodobieństwo, że będzie laureatem obu
olimpiad jest równe 0,18. Zatem prawdopodobieństwo, że będzie laureatem olimpiady matematycznej jest
równe
A) 0,1

B) 0,6

C) 0,7

D) 0,4

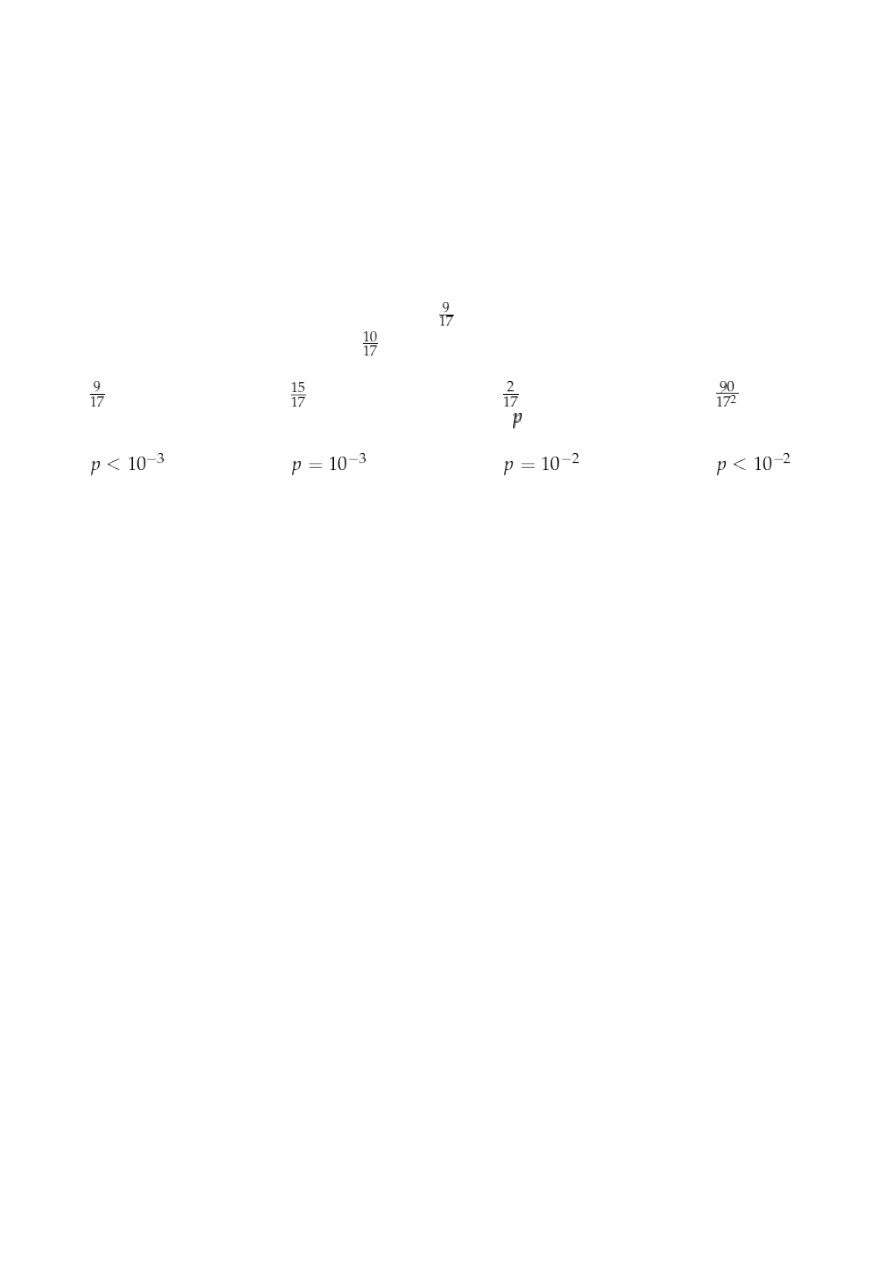
73. Ania bierze udział w olimpiadzie biologicznej i olimpiadzie fizycznej. Prawdopodobieństwo, że

zostanie laureatką olimpiady biologicznej jest równe 0,4, a prawdopodobieństwo, że zostanie laureatką
przynajmniej jednej z tych dwóch olimpiad wynosi 0,62. Prawdopodobieństwo, że będzie laureatką obu
olimpiad jest równe 0,18. Zatem prawdopodobieństwo, że będzie laureatką olimpiady fizycznej jest równe
A) 0,4

B) 0,3

C) 0,5

D) 0,2

74. Tomek bierze udział w olimpiadzie fizycznej i olimpiadzie matematycznej. Prawdopodobieństwo, że

zostanie laureatem olimpiady fizycznej jest równe 0,5, a prawdopodobieństwo, że zostanie laureatem
przynajmniej jednej z tych dwóch olimpiad wynosi 0,74. Prawdopodobieństwo, że będzie laureatem obu
olimpiad jest równe 0,26. Zatem prawdopodobieństwo, że będzie laureatem olimpiady matematycznej jest
równe
A) 0,5

B) 0,6

C) 0,7

D) 0,4

75. Z pudełka zawierającego dwa rodzaje monet wybieramy losowo dwie. Prawdopodobieństwo wybrania

co najmniej jednej monety dwuzłotowej jest równe , a prawdopodobieństwo wybrania co najmniej

jednej monety pięciozłotowej jest równe

. Zatem prawdopodobieństwo wybrania dokładnie jednej

monety dwuzłotowej jest równe

A)

B)

C)

D)

76. Losujemy jedną liczbę trzycyfrową. Prawdopodobieństwo otrzymania liczby, której cyfry to 1,2,3 (w

dowolnej kolejności) spełnia warunek

A)

B)

C)

D)

77.