Arkusz 10: Zginanie proste i ukośne. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych
studiów Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku IMIM w roku akademickim 2014/2015.

Notatki do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn”

Notatki do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn”

Arkusz

Arkusz

10: Zginanie proste i ukośne

10: Zginanie proste i ukośne

1. Zginanie – definicje, pojęcia

Teoria dotycząca zginania – z wykładów, ćwiczeń oraz książek: [1] i [2].

Istnieje kilka różnych typów zginania, które mogą być określone w zależności od:

•

zewnętrznych warunków obciążenia,

•

geometrii konstrukcji i przekroju,

•

rodzaju podparcia.

Poniżej typowa klasyfikacja, z krótkim opisem każdego przypadku:

•

czyste zginanie – przypadek definiowany w celu znalezienia tensora naprężenia i odkształcenia w zginaniu;

•

proste zginanie – jeśli moment zginający M

y

lub M

z

jest jedyną „siłą” przekrojową różną od 0 (F

x

=F

y

=F

z

=0; M

x

=0);

•

zginanie ukośne – jeżeli oba momenty zginające M

y

i M

z

są obecne (nachylony moment M) i są jedynymi „siłami”

przekrojowymi różnymi od 0 (F

x

=F

y

=F

z

=0; M

x

=0);

•

zginanie z siłami ścinającymi – jest to złożony stan mechaniczny; moment zginający (M

y

lub M

z

lub oba) działa

razem z siłami ścinającymi (odpowiednio: F

y

, F

z

);

•

zginania z rozciąganiem/ściskaniem – jest to złożony stan mechaniczny, moment zginający (M

y

lub M

z

lub oba)

jest wynikiem obciążenia zewnętrznego normalnego do powierzchni przekroju poprzecznego (czyli równoległego
do osi pręta), ale które działa poza osią pręta (czyli na mimośrodzie względem niej).

Podczas obecnych zajęć będzie rozważane tylko zginanie proste i zginanie ukośne.

Tensor naprężenia w zginaniu prostym i ukośnym ma postać, która została przedstawiona poniżej. W tych przypadkach,
zgodnie z prawem Hooke'a, mamy do czynienia z przestrzennym stanem odkształcenia:

T

σ

=

[

σ

x

0

0

0

0

0

0

0

0

]

⇔

związki konstytutywne

T

ε

=

[

σ

x

1
E

0

0

0

σ

x

ν
E

0

0

0

σ

x

ν

E

]

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

1

Arkusz 10: Zginanie proste i ukośne. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych
studiów Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku IMIM w roku akademickim 2014/2015.

2. Zginanie proste (M

y

lub M

z

)

2.a) M

y

Związek między funkcją naprężenia oraz siłą przekrojową
ma następującą postać:

gdzie: ▪ M

y

(x) jest momentem zginającym w przekroju o współrzędnej x;

▪ I

y

(x) jest głównym centralnym momentem bezwładności przekroju poprzecznego względem odpowiedniej osi;

▪ z jest bieżącą wysokością w przekroju.

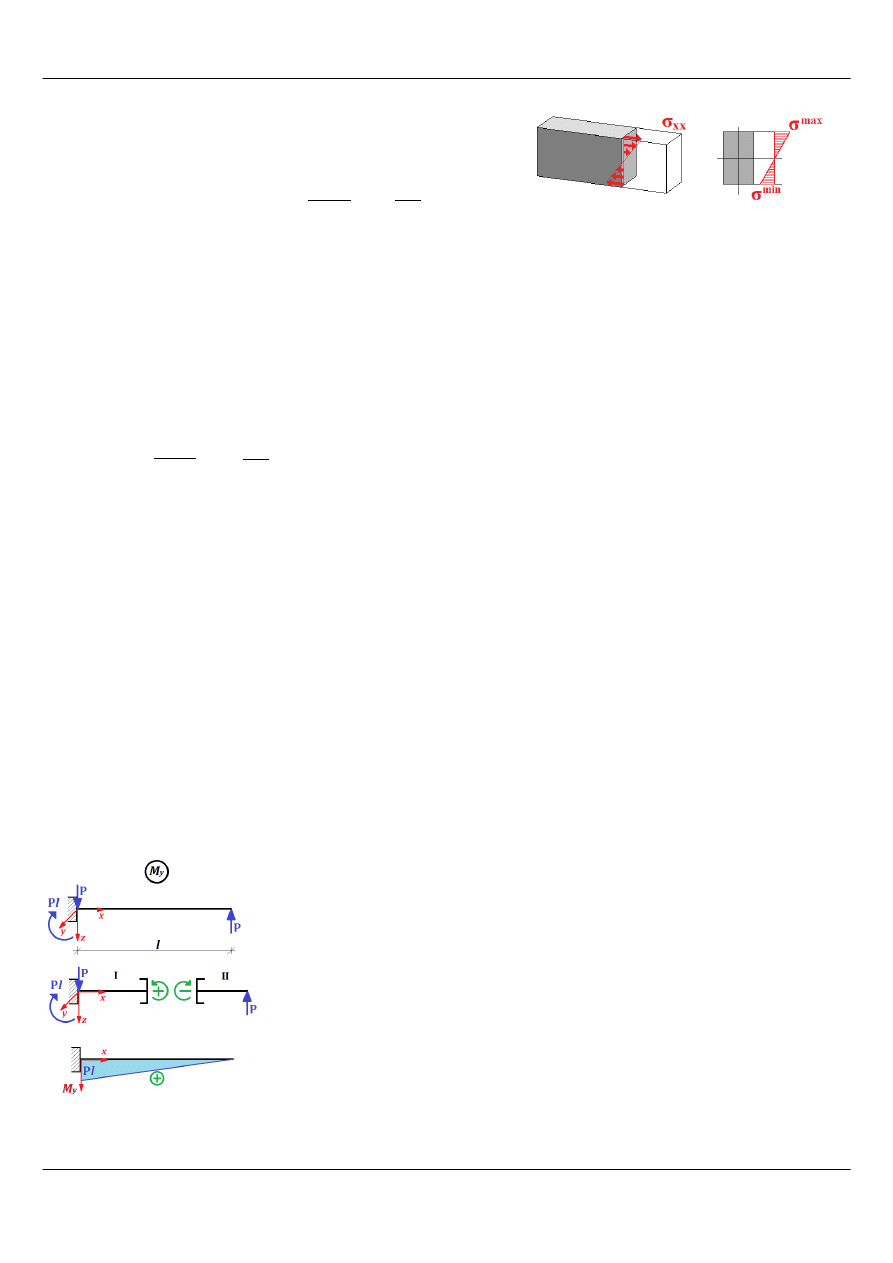
Oś neutralna – jest zdefiniowana jako oś, dla której naprężenia normalne

σ

xx

= 0

. W punkcie przekroju poprzecznego

najodleglejszym od osi obojętnej wystąpią maksymalne naprężenia normalne.
W tym przypadku będzie to miało miejsce dla z=0, a więc będzie leżała w tym samym miejscu geometrycznym co oś y.

2.b) M

z

Związek między funkcją naprężenia oraz siłą przekrojową ma następującą postać:

gdzie: ▪ M

z

(x) jest momentem zginającym w przekroju o współrzędnej x;

▪ I

z

(x) jest głównym centralnym momentem bezwładności przekroju

poprzecznego względem odpowiedniej osi;
▪ y jest bieżącą szerokością w przekroju.

W tym przypadku oś neutralna będzie dla y=0, a więc będzie leżała w tym samym miejscu geometrycznym co oś z.

2.c) Warunek projektowy
Z powyższych wzorów widać, że naprężenia mogą przyjmować wartości ujemne (ściskanie) i dodatnie (rozciąganie),
zależnie od znaku momentu zginającego oraz położenia rozważanego punktu względem kierunku wysokości przekroju.
Stąd, warunek maksymalnych naprężeń musi być rozważany zarówno dla ściskannej, jak i rozciąganej części przekroju:

•

ściskanie:

∣ σ

x , c

max

∣ ⩽ k

g , c

or

∣ σ

x , c

max

∣ ⩽ k

c

or

∣ σ

x , c

max

∣⩽ k

g

(gdzie c oznacza ściskanie, zaś g oznacza zginanie, np.

k

g,c

– dopuszczalne naprężenia ściskające przy zginaniu);

•

rozciaganie:

σ

x , t

max

⩽ k

g , t

or

σ

x , t

max

⩽ k

t

or

σ

x ,t

max

⩽ k

g

(gdzie t oznacza rozciąganie, zaś g oznacza zginanie, np.

k

g,t

– dopuszczalne naprężenia rozciągające przy zginaniu).

Jest także warunek projektowania związany z użytkowaniem, czyli deformacją zginanej konstrukcji, jednak w czasie
obecnego kursu będzie on rozważany później. Dla pełnej informacji ogólnej podamy tutaj, że warunek ten ma formalną
postać:

f

⩽ f

dop

, gdzie f jest strzałką ugięcia.

2.d) Uwaga odnośnie znakowania momentu M

y

i M

z

Zacznijmy od analizy M

y

(Rysunek 2). Mamy wspornik długości l, obciążony na końcu

tylko siłą skupioną –P (ponieważ siła ta jest przeciwnego zwrotu niż oś z). Siła ta
powoduje powstanie na utwierdzeniu reakcji w postaci momentu M

y

rea

=–Pl oraz siły

F

z

rea

=P. Zgodnie ze znanymi zasadami obliczania sił przekrojowych, rozetnijmy

konstrukcję myślowo na dwie części i dla porządku w każdej z nich sprawdźmy, jak
będzie wyglądała funkcja momentu zginającego M

y

(x):

M

y

( x) = [ Pl+ P⋅x]

I

= [P⋅(l x)]

II

= Px+ Pl

Należy zwrócić uwagę, że wewnątrz nawiasów kwadratowych mamy zachowaną
konwencję znakowania: jeżeli zwrot momentu M

y

jest zgodny ze zwrotem osi y, to

uznajemy, że moment jest dodatni. Symbolicznie zostało to zaznaczone na rysunku
strzałkami w kolorze zielonym obrazującymi działanie momentu M

y

, który jest

prostopadły do płaszczyzny kartki i równoległy do zaznaczonej na czerwono osi y.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

2

σ

x

(x , z ) =

M

y

(x)

I

y

(x)

⋅ z

[

Nm

m

4

⋅m = Pa

]

σ

x

( x , y) =

M

z

( x)

I

z

( x)

⋅ y

[

Nm

m

4

⋅m = Pa

]

Rysunek 1: Naprężenia w zginaniu prostym ([4])

Rysunek 2

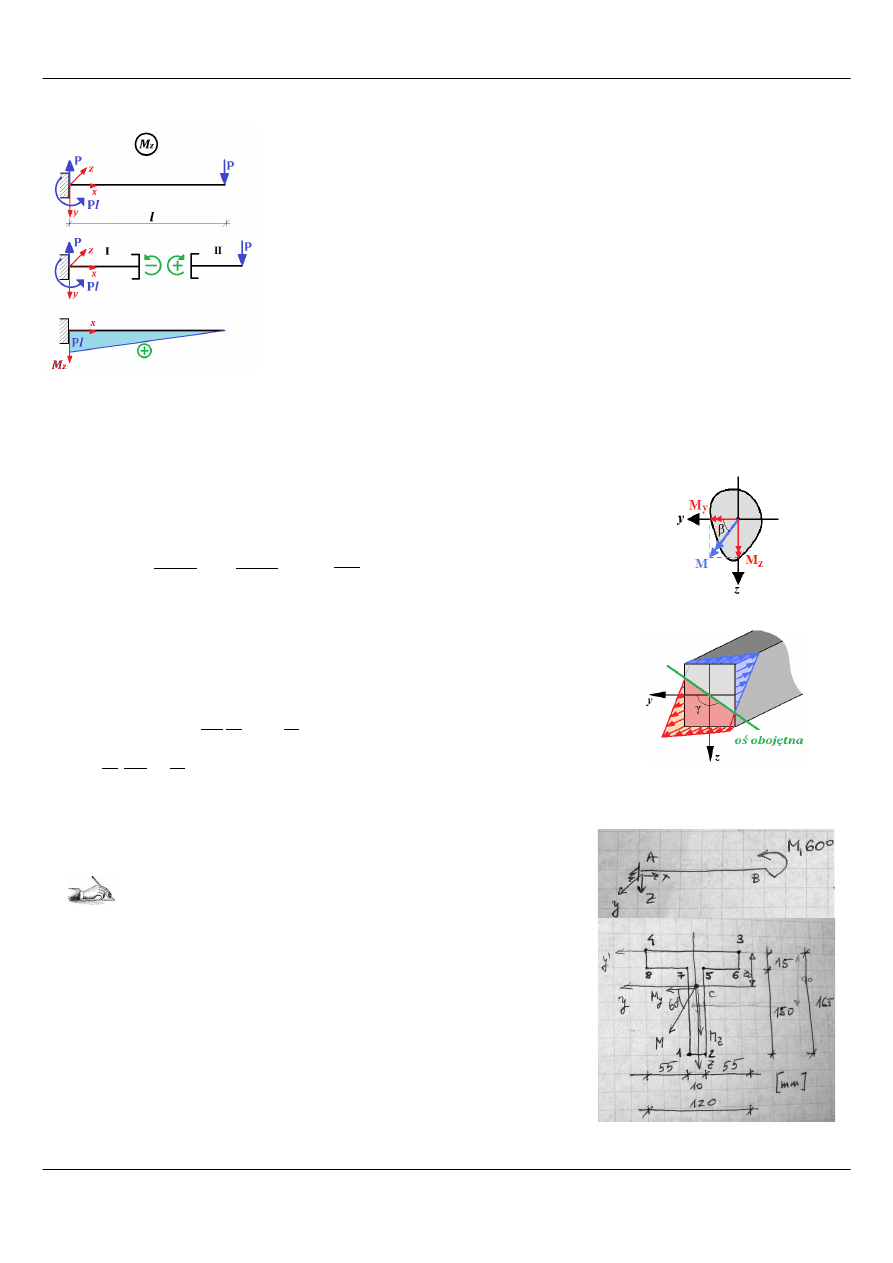
Rysunek 4: Momenty w zginaniu ukośnym ([4])

Arkusz 10: Zginanie proste i ukośne. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych
studiów Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku IMIM w roku akademickim 2014/2015.

Przejdźmy do analizy M

z

(Rysunek 3). Ten sam wspornik długości l, obciążony jest znów

na końcu tylko siłą skupioną P, ale tym razem na kierunku równoległym do y, a nie z.
Dokładnie siłę możemy przyjąć jako +P, ponieważ siła ta jest zgodnego zwrotu z osią y.
Siła ta powoduje powstanie na utwierdzeniu reakcji w postaci momentu M

z

rea

= –Pl oraz

siły F

y

rea

= –P. Zgodnie ze znanymi zasadami obliczania sił przekrojowych, rozetnijmy

konstrukcję myślowo na dwie części i dla porządku w każdej z nich sprawdźmy, jak
będzie wyglądała funkcja momentu zginającego M

z

(x):

M

z

(x) = [ Pl+ P⋅x ]

I

= [P⋅(l x)]

II

= Px+ Pl

W stosunku do obliczania M

y

nic się nie zmieniło! Dalej, rozważając część I dajemy „-”

przed nawiasem kwadratowym i nie ma go przed rozważaniem części II, jak również
dalej wewnątrz nawiasów kwadratowych mamy zachowaną konwencję znakowania:
jeżeli zwrot momentu M

z

jest zgodny ze zwrotem osi z, to uznajemy, że moment jest

dodatni. To co się zmieniło, to zwrot osi w stosunku do której liczymy względem
płaszczyzny kartki. Dla M

y

oś ta „wychodziła” z płaszczyzny kartki, natomiast dla M

z

„wbija” się ona w nią. Tę sytuację odzwierciedlają na rysunku strzałki w kolorze
zielonym obrazujące działanie momentu M

z

.

3. Zginanie ukośne (M

y

+ M

z

)

Związek między funkcją naprężenia oraz siłą przekrojową ma następującą postać:

gdzie: ▪ M

y

(x), M

z

(x) są momentami zginającymi w przekroju o współrzędnej x;

▪ I

y

(x), I

z

(x) są głównymi centralnymi momentami bezwładności przekroju

poprzecznego względem odpowiedniej osi;
▪ z jest bieżącą wysokością, a y jest bieżącą szerokością w przekroju.

Oś obojętna ma następujący wzór:

σ( y , z )=0 ⇒

z

=

M

z

M

y

I

y

I

z

⋅ y =

I

y

I

z

⋅tg β⋅ y

tg

γ =

I

y

I

z

⋅

M

z

M

y

=

I

y

I

z

⋅tg β

Warunki projektowe są analogiczne jak dla zginania prostego.

Zadanie 1

Dla zadanego wspornika (Rysunek 6) wykonanego z teownika
określić bryłę naprężeń w przekroju poprzecznym. Wspornik
poddany jest działaniu momentu zginającego M=5kNm działającego
pod kątem α=60

o

do osi poziomej głównej centralnej teownika.

Należy zacząć od określenia, że konstrukcja jest statycznie wyznaczalna,
następnie przyjąć układ współrzędnych oraz punkty charakterystyczne. W tym
przypadku wyliczenie reakcji nie będzie konieczne, ponieważ wykresy sił
przekrojowych będzie można narysować bez znajomości reakcji. Siły przekrojowe
w tym przypadku ograniczą się do dwóch momentów zginających M

y

i M

z

,

będących rzutami momentu M na odpowiednie kierunki głównych centralnych
osi bezwładności.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

3

σ

x

( x , y , z ) =

M

y

( x)

I

y

( x)

⋅ z

M

z

(x)

I

z

(x)

⋅ y

[

Nm

m

4

⋅m = Pa

]

Rysunek 5: Naprężenia w

zginaniu ukośnym ([4])

Rysunek 3

Rysunek 6: Ilustracja do zadania 1

Arkusz 10: Zginanie proste i ukośne. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych
studiów Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku IMIM w roku akademickim 2014/2015.

M

y

= M sinα = 5⋅10

3

⋅

1
2

= 2,5 [kNm]

Kolejnym krokiem rozwiązania jest obliczenie charakterystyk geometrycznych przekroju poprzecznego:

•

wysokość położenia środka ciężkości przekroju:

z

c

=

S

y'

A

= 45 mm

,

•

moment bezwładności względem osi poziomej głównej centralnej:

I

y

= 8,4⋅10

6

m

4

,

•

moment bezwładności względem osi pionowe głównej centralnej:

I

z

= 2,2⋅10

6

m

4

.

Znając siły przekrojowe (M

y

i M

z

) oraz geometrię przekroju możemy obliczyć naprężenia we wszystkich punktach

charakterystycznych, czyli narożach teownika (punkty 1-8), aby narysować rozkład naprężeń dla niego:

σ

x

1

= σ

x

( x ; y=0,005 m ; z=0,120 m ) = 2,5⋅10

3

8,4

⋅10

6

⋅0,120

4,3

⋅10

3

2,2

⋅10

6

⋅0,005 = 25,9 MPa

σ

x

2

= σ

x

( x ; y= 0,005m ; z=0,120 m) = 2,5⋅10

3

8,4

⋅10

6

⋅0,120

4,3

⋅10

3

2,2

⋅10

6

⋅( 0,005) = 45,5 MPa

σ

x

3

= σ

x

( x ; y= 0,060 m ; z= 0,045 m) = 2,5⋅10

3

8,4

⋅10

6

⋅( 0,045)

4,3

⋅10

3

2,2

⋅10

6

⋅( 0,060) = 103,8 MPa

σ

x

4

= σ

x

( x ; y=0,060 m ; z = 0,045 m ) = 2,5⋅10

3

8,4

⋅10

6

⋅( 0,045)

4,3

⋅10

3

2,2

⋅10

6

⋅0,060 = 130,6 MPa

σ

x

5

= σ

x

( x ; y= 0,005 m ; z= 0,030 m) = 2,5⋅10

3

8,4

⋅10

6

⋅( 0,030)

4,3

⋅10

3

2,2

⋅10

6

⋅( 0,005) = 0,8 MPa

σ

x

6

= σ

x

( x ; y= 0,060 m ; z= 0,030 m) = 2,5⋅10

3

8,4

⋅10

6

⋅( 0,030)

4,3

⋅10

3

2,2

⋅10

6

⋅( 0,060) = 108,3 MPa

σ

x

7

= σ

x

( x ; y=0,005 m ; z= 0,030 m ) = 2,5⋅10

3

8,4

⋅10

6

⋅( 0,030)

4,3

⋅10

3

2,2

⋅10

6

⋅0,005 = 18,7 MPa

σ

x

8

= σ

x

( x ; y=0,060 m ; z = 0,030 m ) = 2,5⋅10

3

8,4

⋅10

6

⋅( 0,030)

4,3

⋅10

3

2,2

⋅10

6

⋅0,060 = 126,2 MPa

Pozostało obliczenie położenia osi obojętnej:

β = artctg

(

I

y

I

z

tg

α

)

= 81,4 deg

, a także samego jej równania:

z

= tgβ y = 6,6 y

. Dzięki temu możemy obliczyć położenie

przecięcia się osi obojętnej z przegami przekroju poprzecznego:

A

= ( y=0,007 ; z= 0,045) oraz B = ( y=0,005 ; z =0,033)

.

Znając przystkie punkty charakterystyczne na wykresie rozkładu
naprężeń w przekroju poprzecznym, można dokonać konstrukcji
tego wykresu (Rysunek 7). Ponieważ bryła naprężeń
zaciemniałaby w tym przypadku informacje, rozłożono ją na
wykres w czterech kierunkach równoległych do poszczególnych
boków teownika.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

4

M

z

= M cos α = 5⋅10

3

⋅

√

3

2

= 4,3[kNm]

Rysunek 7: Wykresy rozkładu naprężeń dla teownika z zad. 1.

Arkusz 10: Zginanie proste i ukośne. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych
studiów Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku IMIM w roku akademickim 2014/2015.

• Zginanie proste: rozwiązać przykłady nr: 10.6.1, 10.6.2, 10.6.3, 10.6.4, 11.6.1, 11.6.4 z książki [2].

• Zginanie ukośne: rozwiązać przykłady nr: 13.4.1, 13.4.3 z książki [2] oraz zadanie 8.17 /str. 98 z książki [3].
Uwaga! We wskazanych tu zadaniach pomijane są naprężenia styczne powstające od sił poprzecznych.

• Znajomość tensora naprężenia i odkształcenia w zginaniu prostym i ukośnym. Wzory na naprężenia
normalne w obu przypadkach.
• Umiejętność rozwiązywania zadań dla przypadków zginania prostego – wyznaczanie naprężeń, wykresy
rozkładu naprężeń w przekrojach poprzecznych, znalezienie osi obojętnej, wyznaczanie wymiarów
konstrukcji z warunku projektowego.
• Umiejętność rozwiązywania zadań dla przypadków zginania ukośnego – wyznaczanie naprężeń, wykresy
brył naprężeń w przekrojach poprzecznych, znalezienie wzoru i położenia osi obojętnej, wyznaczanie
wymiarów konstrukcji z warunku projektowego.
• Oś obojętna, definicja, wzory, znaczenie.

4. Literatura

[1] Piechnik S. "Mechanika techniczna ciała stałego", Wydawnictwo PK, Kraków 2007
[2] Bodnar A. „Wytrzymałość materiałów. Podręcznik dla studentów wyższych szkół technicznych”, wydanie drugie

poszerzone i poprawione, Kraków 2004, rozdziały 10, 11 i 13

[3] Niezgodziński M., Niezgodziński T. "Zadania z wytrzymałości materiałów", Wydawnictwo WNT, Warszawa 2012
[4] dr inż. Paweł Szeptyński, ilustracje

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

5