
1
Rok I semestr 1
STUDIA EKSTERNISTYCZNE
MATEMATYKA
A. Literatura obowiązkowa:
1. J. Piszczała, M. Piszczała, B. Wojsieszyn, Matematyka z zadaniami, Wyd. PWN, Warszawa
(dowolne wydanie).
Literatura pomocnicza:
2. J. Laszuk, Repetytorium z matematyki, Wyd. SGH, Warszawa 1995.
B. PROGRAM NAUCZANIA
I. MACIERZE I DZIAŁANIA NA NICH W TYM:
Dodawanie, odejmowanie macierzy, mnożenie przez liczbę, mnożenie macierzy przez macierz.
Rodzaje macierzy w tym: kwadratowe, prostokątne, trójkątne (górna i dolna) jednostkowa,
macierz zerowa, transponowana, macierze Grama.
Przykładowe zadania
1. Dane są macierze
=
5
2
1
0
1
2
3
4
A
=
3
4
3
2
B
=
2
8
3
4
2
0
5
0
1
2
3
6
C
=
5
1
2
0
D
Zbadać które z niżej podanych działań jest wykonalne?
a) ABD
b) B
T
C+D
c) CA
T
2. Ustalić wymiar macierzy A B i C tak, aby było możliwe wykonanie działań CAB-4BA
3. Dobrać tak parametry a, b aby macierz postaci:
−
−
−
−
−
−
−
+
−
+
=
1
1
1
1
1
1
1
2
2
2
2
2
a
b
b
a
a
a
a
b
b
b
a
b
b
b
a
a
b
b
a
A
była macierzą a) diagonalną b) trójkątną górną, c) trójkątną dolną, d) jednostkową, e) zerową

2
4. Znaleźć iloczyny:
xx
T
;
x
T
x
jeżeli
=
5
4
3
2
x
5. Dobrać, o ile to możliwe, parametry a, b, c, d aby macierze A i B były równe:
=
−
−
=
d
B
c
b
a
A
7
5
0
4
1
2
0
1
3
1
1
1
1
1
3
1
0
6. Wykonać mnożenie AX
a)
=
=
4
3
2
1
2
4
8
2
3
6
5
4
6
3
2
1
x
x
x
x
X
A
b)
=
=
2
1
6
4
3
2
x
x
X
A
II. WYZNACZNIK I JEGO WŁASNOŚCI
Z każdą macierzą kwadratową A, ale tylko taką, związane jest pojęcie liczby zwanej –
wyznacznikiem macierzy. Oznaczamy go symbolem A i czytamy wyznacznik macierzy A.
Np. jak:
A = [5], to det A = det [5] = 5
=
6
4
2
3
A
to det A = det
6
4
2
3
ale zapisy:
2
3
1
det
oraz
5
4
0
1
2
3
det
nie mają sensu! Macierz A nazywamy osobliwą jeżeli det A = 0 i
nieosobliwą jeżeli det A ≠ 0. Jeżeli macierz A jest macierzą postaci:
=
22
21
12
11
a
a
a
a
A
to det A = a
11
a
22
– a
12
a
21
np. jeżeli
39
15
24
5
)
3
(
4
6
4
5
3
6
det
det
4
5
3
6
=
+
=
−
−
×
=
−
=
−
=
A
to
A
Do macierzy A postaci
=
33
32
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
A
stosujemy schemat Sarrusa.
+
+
+
−
−
−
32
31
33
32
31
22
21
23
22
21
12
11
13
12
11
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
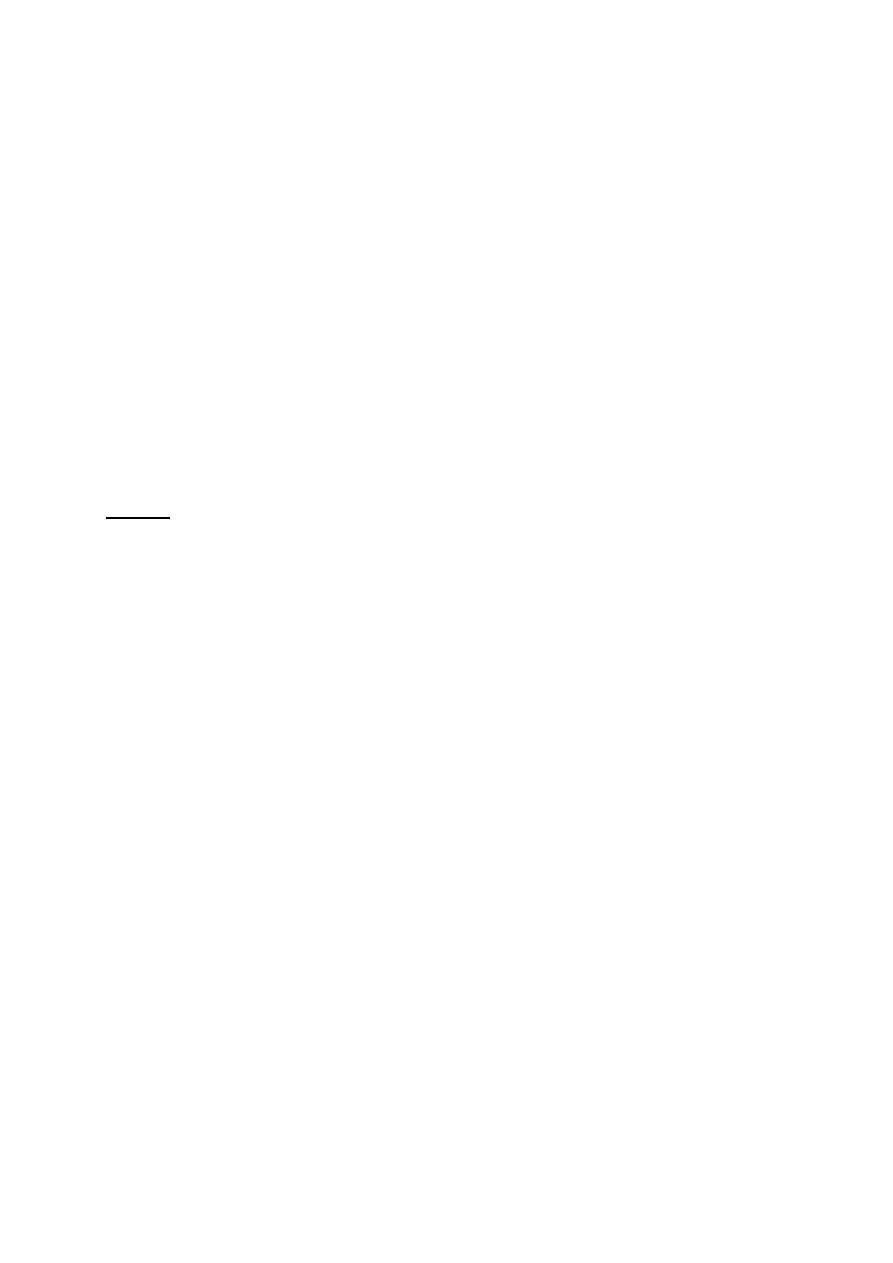
3
W
I
= a
11
a
22
a
33
+ a
12
a
23
a
31
+ a
13
a
21
a
32
W
II
= – (a
31
a
22
a
13
+ a
32
a
23
a
11
+ a
33
a
21
a
12
)
Ostatecznie det A = W
I
– W
II
Dla macierzy stopnia n gdzie n > 3 stosujemy wzory Laplace’a.
Dla i-tego wiersza.
det A = a
i1
A
i1
+ a
i2
A
i2
+ ... + a
in
A
in
dla j-tej kolumny:
det A = a
1j
A
1j
+ a
2j
A
2j
+ ... + a
nj
A
nj
gdzie dopełnienie A
ij
(elementu a
ij
macierzy A) obliczono według wzoru:
A
ij
= (-1)
i+j
det M
ij
zaś macierz M
ij
powstała z macierzy A przez skreślenie i-tego wiersza oraz j-tej kolumny.
Przekształcenia elementarne. Własności wyznacznika. Wyznacznik macierzy transponowanej,
trójkątnej, jednostkowej. Wzory Cramera. Rząd macierzy. Rząd iloczynu macierzy.
Zadania
1. Obliczyć wyznacznik macierzy A jeżeli:
a)
=
0
5
0
1
A
b)
=
9
6
3
7
5
2
5
4
1
A
c)
−
=
6
1
0
0
4
5
1
4
0
3
4
0
2
4
2
3
2
1
2
0
2
1
3
1
0
A
2. Dla jakich α macierz A jest nieosobliwa:
a)
−
−
−
=
1
1
0
1
1
1
0
α
α
A
b)
+
=
5
0
3
2
7
1
6
0
9
4
5
7
2
4
1
α
α
A
3. Rozwiązać równanie i nierówność:
a)
0
1
1
1
1
1
2
1
1
1
1
1
1
1
1
1
1
det
=
−
−
x
x
b)
−
−
−
+
x
x
3
5
2
1
1
1
2
2
det
>0
4. Liczby 168,567 i 336 dzielą się przez 21. Nie obliczając wartości wyznacznika macierzy A,
a korzystając z własności pokazać, że

4
=
6
3
3
7
6
5
8
6
1
det
det A
dzieli się przez 21.
5. Korzystając z własności wyznacznika pokazać, że:
a)
=
+
+
+
+
+
+
3
3
3
2
2
2
1
1
1
3
3
3
3
3
2
2
2
2
2
1
1
1
1
det
det
c
b
a
c
b
a
c
b
a
c
y
b
x
a
b
a
c
y
b
x
a
b
a
c
by
x
a
b
a
b)
0
3
3
3
2
det
=
+
+
b
c
b
b
a
c
b
a
6. Wiedząc że:
10
det
=
w
v
u
r
q
p
c
b
a
obliczyć:
−
−
−
c
r
w
b
q
v
a
p
u
2
2
2
det
7. Znaleźć rząd macierzy
a)
=
4
1
3
5
2
1
4
2
3
A
b)
=
4
2
3
4
2
1
B
c)
=
1
2
4
3
2
1
C
8. Rozwiązać układ równań stosując wzory Cramera:
a)
0
6
2
5
1
3
3
2
1
3
2
1
3
2
1
=
+
−
=
−
+
=
−
+
x
x
x
x
x
x
x
x
x
b)
0
4
6
0
5
3
2
1
2
1
=
+
=
+
x
x
x
x
III. MACIERZ ODWROTNA
Z każdą macierzą nieosobliwą A związana jest jedna i tylko jedna macierz oznaczona symbolem
A
-1
i nazywana macierzą odwrotną.
Jest przy tym:
AA
-1
= A
-1
A
= I
Metody wyznaczania macierzy odwrotnej:
a)
metoda „wyznacznikowa”
b)
wyznaczanie macierzy odwrotnej do macierzy trójkątnej.
c)
Metoda Jordana-Gaussa

5
Zadania
1. Wyznaczyć A
-1
jeżeli:
a)
=
5
2
3
6
A
b)
=
8
0
0
4
2
0
3
6
4
A
c)
=
3
4
2
0
3
4
0
0
1
A
d)
=
10
0
0
0
8
0
0
0
6
A
e)
=
2
0
0
0
2
0
0
0
2
A
f)
=
∑
∑
∑
−
−
−
n
i
i
n
i
i
n
i
i
x
x
x
n
A
1
2
1
1
2. Rozwiązać układ równań AX = b wyznaczając macierz A
-1
a)
8
2
6
5
4
2
1
1
=
−
=
+
x
x
x
x
b)
2
5
1
2
6
5
2
3
3
2
1
3
1
3
2
1
=
+
+
−
=
+
=
−
+
x
x
x
x
x
x
x
x
3. Wyznaczyć macierz X jeżeli:
a)
=
3
1
2
4
5
2
6
3
X
b)
=
2
0
1
3
5
4
2
8
X
4. Wiadomo, że det A ≠ 0. Wyznaczyć A
-1
jeżeli:
a)
1
5
4
1
2
)
2
(
−
=
T
A
b)
=
+
−
5
0
0
2
)
3
(
1
A
I
5. Sprawdzić czy macierz A postaci:
−
−
−
=
2
2
8
0
1
0
1
1
1
A
spełnia równanie macierzowe
0
6
5
3
=
+
+
I
A
A
Jeżeli tak, to zaproponować wyznaczenie macierzy A
-1
.
6. Czy macierz A jest macierzą odwrotną do macierzy B jeżeli:
a)
=
=
6
5
4
3
2
0
0
1
3
2
1
0
5
4
1
2
3
6
B
A
b)
−
−
=
=
2
3
2
3
1
2
6
4
8
6
B
A

6
7. Macierze A i B mają odpowiednio postać:
−
−
−
=
−
=
2
1
2
1
2
1
1
1
0
0
2
2
B
A
Ich iloczyn AB = I . Czy stąd wynika, że macierz A jest macierzą odwrotną macierzy B?
IV. UKŁADY RÓWNAŃ LINIOWYCH
Dany jest układ równań postaci:
AX
= b
(1)
Gdzie A = [a
ij
] jest macierzą o wymiarach mxn natomiast X
T
= [x
1
...x
n
] zaś b
T
= [b
1
b
2
... b
m
]
Układ (1) nazywamy jednorodnym jeżeli b ≡ 0, zaś niejednorodnym jeżeli przynajmniej jedna
składowa b
i
jest różna od zera. Układ (1) ma rozwiązanie wtedy i tylko wtedy, gdy:
R
(A) = R(B) (Twierdzenie Kroneckera-Capelliego)
gdzie:
B
= [A, b]
Jeżeli
R
(A) ≠ R(B)
to układ (1) jest sprzeczny
jeżeli R(A) = R(B) = n (liczba niewiadomych) ten układ (1) ma jedno rozwiązanie
jeżeli R(A) = R(B) = q < n (wspólna wartość rzędów macierzy podstawowej i rozszerzonej jest
mniejsza od liczby niewiadomych) to układ (1) ma nieskończenie wiele rozwiązań.
Ilustracje na przykładach:
6
2
4
1
2
8
5
3
2
1
2
1
2
1
=
+
=
−
=
+
x
x
x
x
x
x
−
=
2
4
1
2
5
3
A
A : 3 × 2
przeto
R(A) ≤ min(3,2) = 2
i jest równy 2 bo np.
0
13
10
3
1
2
5
3
det
≠
−
=
−
−
=
−
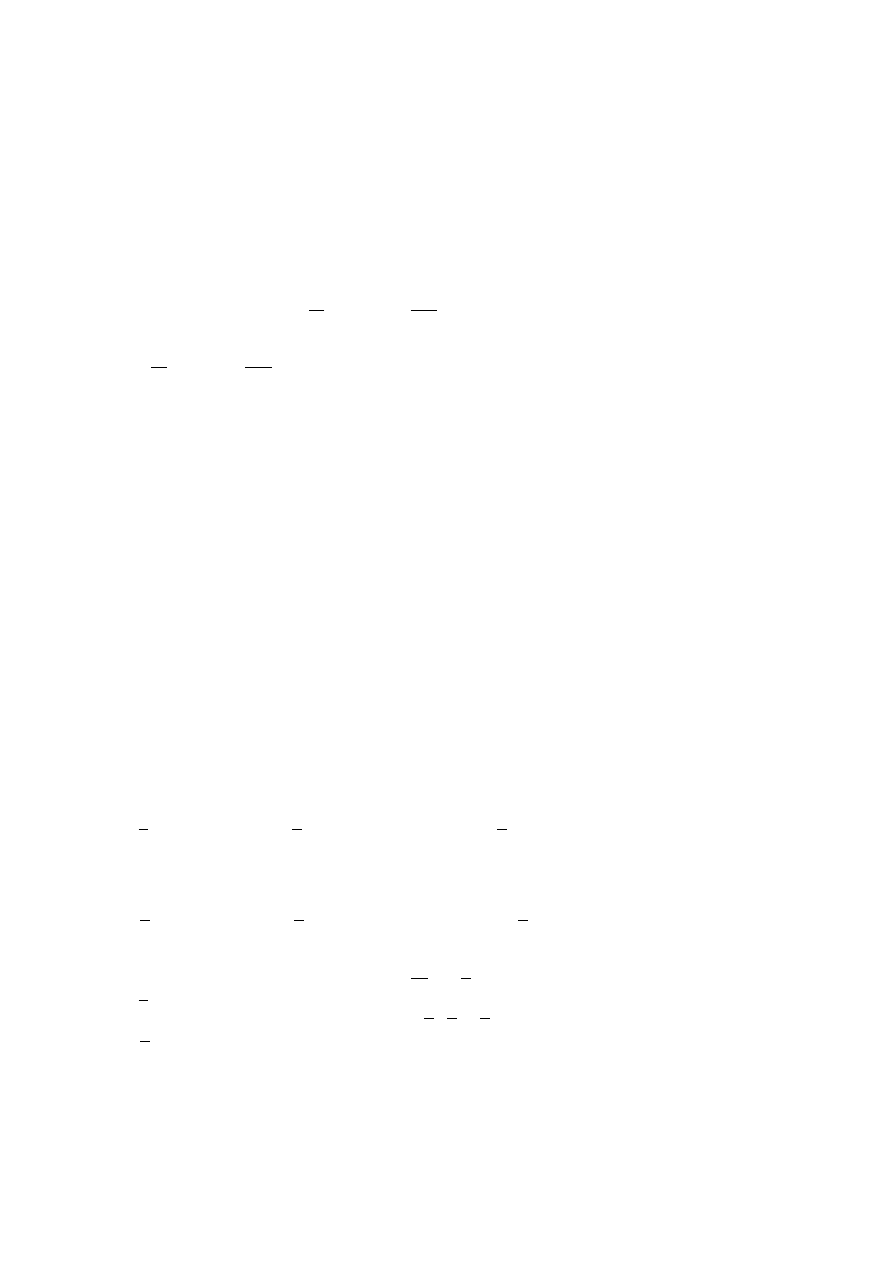
7
3
3
:
6
2
4
1
1
2
8
5
3
×
−
=
B
B
przeto
3
)
3
,
3
min(
)
(
=
≤
B
R
ale
0
6
2
4
1
1
2
8
5
3
det
=
−
czyli
R
(B) = 2, bo np.
0
13
1
2
5
3
det
≠
−
=
−
R
(A) = R(B) =2 (liczba niewiadomych)
1
2
8
5
3
2
1
2
1
=
−
=
+
x
x
x
x
1
13
13
1
1
5
8
det
13
1
1
=
−
−
=
−
−
=
x
1
13
13
1
2
8
3
det
13
1
2
=
−
−
=
−
=
x
jest spełnione równanie trzecie, bo 4 × 1 + 2 × 1 = 6
6
4
3
5
2
2
4
3
2
1
4
3
2
1
=
−
+
+
=
+
−
+
x
x
x
x
x
x
x
x
4
2
:
1
1
4
3
2
1
1
2
×
−
−
=
A
A
R
(A) ≤ min(2,4) = 2
R
(A) = 2, bo np.
0
5
3
8
4
3
1
2
det
≠
=
−
=
−
−
=
6
1
1
4
3
5
2
1
1
2
B
R(B) ≤ min. (2,5) = 2
ale
5
4
3
1
2
det
=
R
(A) = R(B) = 2 (ale 2 jest mniejsze od 4) zaś 4 jest liczbą niewiadomych
4
3
2
1
4
3
2
1
6
4
3
2
5
2
x
x
x
x
x
x
x
x
+
−
=
+
−
+
=
+
)
9
5
14
(
5
1
)
6
8
4
20
(
5
1
4
6
1
2
5
det
5
1
4
3
4
3
4
3
4
3
4
3
1
x
x
x
x
x
x
x
x
x
x
x
−
+
=
−
+
−
−
+
=
+
−
−
+
=
)
8
3
(
5
1
)
6
3
15
2
2
12
(
5
1
6
3
2
5
2
det
5
1
4
3
4
3
4
3
3
3
4
3
2
x
x
x
x
x
x
x
x
x
x
x
+
−
−
=
+
−
−
+
−
=
+
−
−
+
=
)
8
3
(
5
1
)
9
5
14
(
5
1
4
3
2
4
3
1
x
x
x
x
x
x
+
−
−
=
−
−
=
=
=
+
−
−
=
−
−
=
d
x
c
x
d
c
x
d
c
x
4
3
2
1
5
8
5
1
5
3
5
9
5
14
=
=
d
x
c
x
4
3
dowolne stałe.

8
Rozwiązanie szczegółowe np. c = d = 0
0
0
5
3
5
14
4
3
2
1
=
=
−
=
=
x
x
x
x
Układ jednorodny
AX
= 0
1° układ jednorodny ma zawsze rozwiązanie
2° układ jednorodny ma rozwiązani niezerowe
jeżeli R(A) < n (n liczba niewiadomych)
Zadania
1.
Rozwiązać układy równań:
a)
1
2
2
2
3
2
1
3
2
1
=
+
+
−
=
−
+
x
x
x
x
x
x
b)
3
2
1
2
2
2
3
2
1
3
2
1
3
2
2
=
+
−
=
−
+
−
=
+
−
x
x
x
x
x
x
x
x
x
c)
0
5
0
8
0
5
4
3
2
1
3
2
1
3
2
1
=
+
+
−
=
−
+
=
+
+
x
x
x
x
x
x
x
x
x
d)
1
2
5
2
2
2
1
3
4
3
2
4
3
2
1
4
3
2
1
=
−
+
=
−
+
+
=
+
−
+
x
x
x
x
x
x
x
x
x
x
x
d)
10
3
1
2
2
2
2
3
2
1
3
2
1
3
2
1
=
+
−
=
+
+
=
+
−
x
x
x
x
x
x
x
x
x
2. Przedyskutować w zależności od parametru a liczbą rozwiązań układu.
12
2
3
2
1
2
1
=
+
=
−
ax
ax
a
x
ax
V. ROZWIĄZANIA BAZOWE
Liniowa zależność i niezależność układów n wektorów m wymiarowych. Baza w tym baza
jednostkowa zbudowana z wektorów e
i
i = 1,2 ...m
m
i
R
e
∈
Układ równań:
AX = b
(1)
gdzie:
]
,
,
,
[
]
,
,
,
[
]
,
,
,
[
2
1
2
1
2
1
2
1
2
1
2
1
n
m
m
m
T
n
m
m
m
T
n
m
m
m
b
b
b
b
b
b
b
x
x
x
x
x
x
X
a
a
a
a
a
a
A
K
K
K
K
K
K
+
+
+
+
+
+
=
=
=
Zakładamy, że pierwsze m kolumn macierzy A czyli pierwsze m wektorów a
i
i =
1, 2 – m tworzy
bazę. Macierz A oraz wektor X zapisujemy przeto w postaci:
]
,
[
]
,
[
N
m
T
N
m
X
X
X
A
A
=
(2)

9
gdzie
]
,
[
2
1
m
m
a
a
a
A
K
=
(3)
]
,
[
2
1
n
m
m
N
a
a
a
A
K
+
+
=
(4)
]
[
]
[
1
1
n
m
T
N
m
T
m
x
x
X
x
x
X
K
K
+
=
=
Wówczas układ AX = b zapisujemy w równoważnej postaci:
b
X
A
X
A
N
N
m
m
=
+
(5)
Macierz A
m
jest nieosobliwa, bo z założenia wektory a
1
, a
2
... a
m
tworza bazę. Istnieje przeto
1
−
m
A
. Zmiennym niebazowym nadajemy wartość 0. Przyjmując, że X
N
= 0 układ (1) redukuje się
do układu:
b
X
A
m
m
=
(6)
przeto
b
A
X
m
m
1
−
=
(7)
Rozwiązanie bazowe (względem bazy utworzonej z wektorów a
1
, a
2
... a
m
) ma postać:
=
=
−
0
0
1
b
A
X
X
m
m
(8)
Ilustracja na przykładzie
3
5
4
2
8
6
4
3
2
4
3
1
=
+
+
=
+
+
x
x
x
x
x
x
(9)
czyli
=
+
−
+
+
3
2
5
8
4
6
1
0
0
1
4
3
2
1
x
x
x
x
(10)
albo
b
a
x
a
x
e
x
e
x
=
+
+
+
4
4
3
3
2
2
1
1
(11)
gdzie
=
=
=
=
=
3
2
5
8
4
6
1
0
0
1
4
3
2
1
b
a
a
e
e
Bazę tworzą wektory e
1
i e
2
. Tym samym zmienne x
1
i x
2
są zmiennymi bazowymi. Nie
bazowymi są wektory a
3
oraz a
4
a to oznacza, że niebazowymi są zmienne x
3
i x
4
.
Zmienne bazowe tworzą wektor
=
2
1
x
x
X
m
, mamy
=
=
1
0
0
1
]
[
2
1
e
e
A
m
; Zmienne niebazowe
tworzą wektor
=
4
3
x
x
X
N
, zaś macierz
=
=
5
4
8
6
]
[
4
3
a
a
A
N
.

10
Aby znaleźć rozwiązanie bazowe układu (9) względem bazy e
1
i e
2
zmiennym niebazowym
nadajemy wartość zero x
3
=
x
4
= 0 co oznacza, że X
N
=
0. Wówczas układ (9) przechodzi w
układ:
=
3
2
1
0
0
1
2
1
x
x
(11)
skąd x
1
=
2 x
2
=
3
zaś rozwiązanie względem bazy utworzonej z wektorów e
1
i e
2
ma postać:
=
=
=
−
0
0
3
2
0
1
b
A
X
X
X
m
N
m
(12)
Pokażemy w jaki sposób od danego rozwiązania bazowego przejść do nowego rozwiązania
bazowego. Oznacza to, że od bazy (e
1
e
2
) przejdziemy do innej bazy.
Innymi słowy, że starej bazy (e
1
e
2
) usuniemy pewien wektor a na jego miejsce wprowadzimy
nowy wektor (jeden spośród wektorów niebazowych czyli albo wektor a
3
albo wektor a
4
).
Zauważmy, że w bazie zbudowanej z wektorów e
1
i e
2
poszczególne wektory a
1
a
2
a
3
a
4
oraz b
mają rozkład.
2e
1
+ 3e
2
= b
(13)
1e
1
+ 0e
2
= e
1
(14)
0e
1
+ 1e
2
= e
2
(15)
6e
1
+ 4e
2
= a
3
(16)
8e
1
+ 5e
2
= a
4
(17)
Do nowej bazy wprowadzimy wektor a
4
. Wówczas zależność (17) mnożymy obustronnie przez
)
0
(
≠
Θ
Θ
Dostajemy
4
2
1
5
8
a
e
e
Θ
=
Θ
+
Θ
(18)
Odejmujemy stronami od (13) zależności (18).
Dostosujemy
b
a
e
e
=
Θ
+
Θ
−
+
Θ
−
4
2
1
)
5
3
(
)
8
2
(
(19)
Usuwamy z bazy (
e
1
e
2
) jeden z wektorów np.
e
1
przyjmując, że
0
8
2
=
Θ
−
czyli
4
1
=
Θ
.
Podstawiamy tą wartość do (19). Mamy wówczas:
b
a
e
=
+
×
−
4
4
1
2
4
1
)
5
3
(
(20)
b
a
e
=
+
4
4
1
2
4
7
(21)
Otrzymamy nowe rozwiązanie bazowe
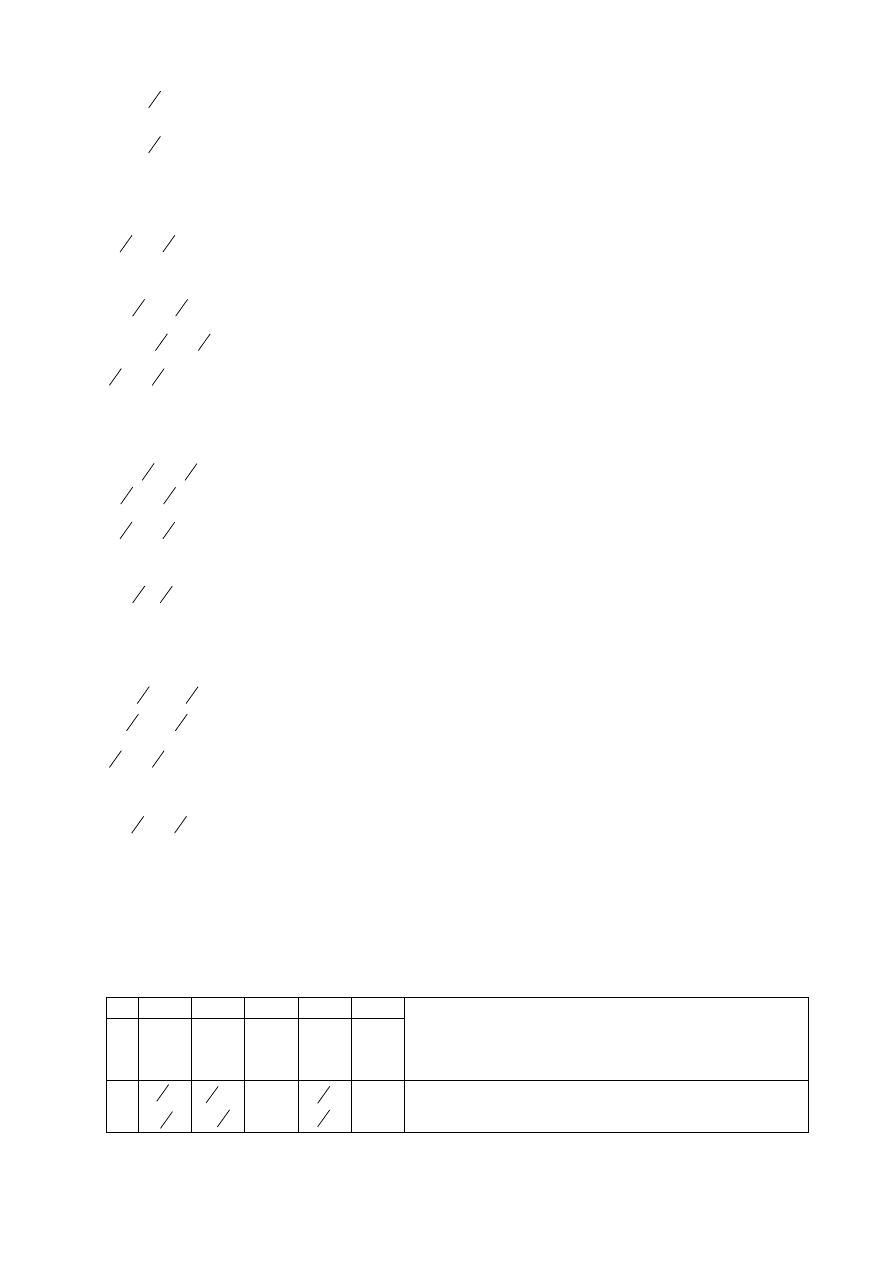
11
=
4
1
4
7
1
0
0
X
(22)
A jak wyglądają rozkłady pozostałych wektorów
e
1
e
2
a
3
i
a
4
w nowej bazie (
e
2
a
4
).
Rozwiązujemy względem
e
1
zależność
.
(17) (do nowej bazy wprowadzamy wektor
a
4
)
1
4
8
1
2
8
5
e
a
e
=
+
−
(23)
e
1
dane wzorem (23) podstawiamy kolejno do (13), (14), (15) i (16). Mamy wtedy kolejno:
(
)
b
e
a
e
=
+
+
−
2
4
8
1
2
8
5
3
2
albo
b
e
a
e
=
+
+
−
2
4
4
1
2
4
5
3
b
a
e
=
+
4
4
1
2
4
7
(24)
[patrz (21)]
Podstawiamy (23) do (14). Wówczas:
(
)
1
2
4
8
1
2
8
5
1
2
4
8
1
2
8
5
0
0
1
e
e
a
e
e
e
a
e
=
=
+
−
=
+
+
−
×
1
4
8
1
2
8
5
e
a
e
=
+
−
(25)
Podstawiamy (23) do (15). Wówczas
2
2
4
8
1
8
5
1
)
(
0
e
e
a
=
+
+
−
2
2
4
1
0
e
e
a
=
+
⋅
(26)
Podstawiamy (23) do (16). Wówczas:
(
)
3
2
4
4
3
2
4
15
3
2
4
8
1
2
8
5
4
4
6
a
e
a
e
a
e
a
e
=
+
+
−
=
+
+
−
3
4
4
3
2
4
1
a
a
e
=
+
(27)
Podstawiamy (23) do (17) dostajemy:
(
)
4
2
4
8
1
2
8
5
5
8
a
e
a
e
=
+
+
−
czyli
4
2
4
2
5
5
a
e
a
e
=
+
+
−
4
2
4
0
1
a
e
a
=
+
(28)
To samo postępowanie wykonamy teraz posługując się tabelarycznym ujęciem.
Zapisujemy w tablicy układ (9)
Komentarz
Nr
b
e
1
e
2
a
3
a
4
1
2
3
1
0
0
1
6
4
8
5
Dane stworzą
e
1
i
e
2
. Do bazy wprowadzamy
a
4
.
Usuwamy z niej
e
1
.
Wektor wprowadzony
a
4
ma mieć
ten sam rozkład co i wektor usuwany z bazy.
Pierwszy wiersz dzielimy przez 8
2
8
14
8
2
8
5
8
1
−
0
1
4
1
8
6
1
0
Przekształcony wiersz mnożymy przez -5 i dodajemy
do drugiego wiersza
czyli:
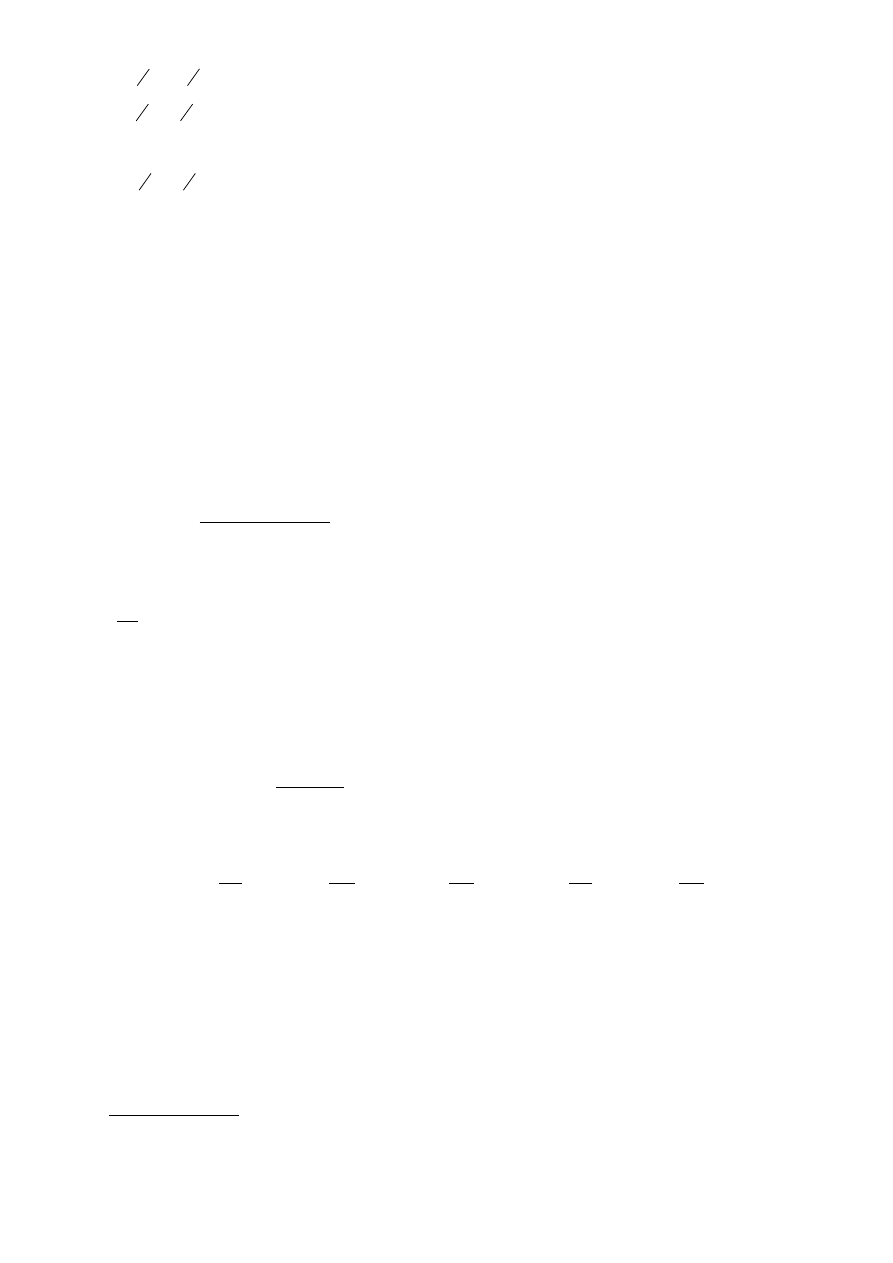
12
2
4
7
4
4
1
e
a
b
+
=
[patrz (24)]
2
8
5
4
8
1
1
e
a
e
+
=
[patrz (25)]
2
4
2
1
0
e
a
e
×
+
×
=
[patrz (26)]
2
4
1
4
4
3
3
e
a
a
+
=
[patrz (27)]
2
4
4
0
1
e
a
a
+
=
[patrz (28)]
VI. REPETYTORIUM Z RACHUNKU RÓśNICZKOWEGO FUNKCJI
JEDNEJ ZMIENNEJ.
Rozpatrujemy funkcję
f(x) określoną w przedziale (a, b). Jest ona różniczkowalna w punkcie
x = x
0
jeżeli istnieje granica:
h
x
f
h
x
f
h
)
(
)
(
0
0
0
lim
−
+
→
granicę tę nazywamy pochodną funkcji
f(x) w punkcie x = x
0
i oznaczany albo
)
(
0
'
x
f
x
albo
0
x
x
dx
df
=
. Z definicji obliczymy pochodną funkcji
f(x) = x
5
.
5
0
0
)
(
x
x
f
=
, zaś
5
0
0
4
1
0
3
2
0
2
3
0
1
4
0
0
5
0
5
0
0
5
5
2
5
3
5
2
5
1
5
0
5
)
(
)
(
h
x
h
x
h
x
h
x
h
x
h
x
h
x
h
x
f
+
+
+
+
+
=
+
=
+
ale jak wiadomo
!
)!
(
!
k
k
n
n
k
n
−
=
dla
n
≥
k
przeto
1
0
5
=
1
!
0
!
5
!
5
5
5
5
!
1
!
4
!
5
4
5
10
!
2
!
3
!
5
3
5
10
!
2
!
3
!
5
2
5
5
!
1
!
4
!
5
1
5
=
=
=
=
=
=
=
=
=
=
, bo 0! = 1
czyli
5
1
0
3
2
0
2
3
0
1
4
0
5
0
0
5
10
10
5
)
(
h
h
x
h
x
h
x
h
x
x
h
x
f
+
+
+
+
+
=
+
wobec tego
5
4
0
3
2
0
2
3
0
1
4
0
0
0
0
5
10
10
5
)
(
)
(
h
h
x
h
x
h
x
h
x
x
f
h
x
f
+
+
+
+
=
−
+
czyli
4
3
0
2
2
0
3
0
4
0
0
0
5
10
10
5
)
(
)
(
h
h
x
h
x
h
x
x
h
x
f
h
x
f
+
+
+
+
=
−
+
13
ostatecznie
4
0
4
3
0
2
2
0
2
0
4
0
0
0
0
0
5
)
5
10
10
5
(
)
(
)
(
lim
lim
x
h
h
x
h
x
h
x
x
h
x
f
h
x
f
h
h
=
+
+
+
+
=
−
+
→
→
Znane są różne interpretacje pochodnych. Podamy jedynie dwie z nich to znaczy interpretację
geometryczną oraz ekonomiczną. Pierwsza z nich oznacza, że jeśli funkcja f(x) ma pochodną w
punkcie x
0
to wykres tej funkcji ma w punkcie
(
)
)
(
,
0
0
x
f
x
styczną, której współczynnik
kierunkowy jest równy f
′
(x
0
).
Równanie styczne do wykresu funkcji f(x), w punkcie
(
)
)
(
,
0
0
x
f
x
ma postać:
)
)(
(
'
)
(
0
0
0
x
x
x
f
fx
y
−
=
−
Jeżeli x oznacza wielkość produkcji, zaś K(x) jest kosztem całkowitym wytworzenia x jednostek
produktu to wyprodukowanie
∆
x dodatkowych jednostek pociąga za sobą to, że całkowity koszt
produkcji wynosi:
)
(
)
(
0
0
x
K
x
x
K
K
−
∆
+
=
∆
albo
x
x
K
x
x
K
X
K
∆
−
∆
+
=
∆
∆
)
(
)
(
0
0
a to oznacza, że:
)
(
'
0
0
lim
x
K
x
K
x
=
∆
∆
→
∆
Wielkość ta nosi nazwę kosztu końcowego. Analogicznie definiujemy utarg krańcowy u
′
(x
0
)
jako pochodną funkcji utargu u(x) = x p(x), gdzie p(x) oznacza cenę.
Rozpatrujemy elastyczność funkcji f(x) którą oznaczamy symbolem E
f
i definiujemy wzorem:
)
(
'
)
(
x
f
x
f
x
E
f
=
(1)
PODSTAWOWE WZORY:
y = c (stałe) y’ = 0
2
'
'
)'
(
'
'
)'
(
'
'
)'
(
g
fg
g
f
fg
g
f
fg
g
f
g
f
g
f
−
=
+
=
+
=
+
Pochodne funkcji elementarnych:
y = x
α
α
≠
–1
y
′
=
α
x
α
–1
y = a
x
y
′
= a
x
ln a
y = c
x
y
′
= cx

14
y =
sin x
y
′
= cos x
y =
cos x
y
′
= –sin x
y =
tg x
x
y
2
cos
1
'
=
y =
ctg x
x
y
2
sin
1
'
−
=
y =
ln x
x
y
1
'
=
y =
log
p
x
x
p
y
1
ln
1
'
⋅
=
Przykłady obliczania pochodnych:
x
x
y
x
y
1
)
(ln
3
'
;
)
(ln
2
3
⋅
=
=
x
x
x
y
x
y
2
cos
)
(sin
5
'
;
)
(sin
2
4
2
5
2
⋅
⋅
=
=
)
3
(
)
1
(
2
1
'
1
2
3
3
2
1
x
x
y
x
y
−
⋅
−
=
−
=
−
x
x
y
3
2
tg
sin
=
2
3
3
2
3
2
)
(tg
)'
(tg
sin
tg
)'
(sin
'
x
x
x
x
x
y
−
=
ale
x
x
x
x
x
3
3
2
tg
cos
sin
2
tg
)'
(sin
⋅
=
zaś
x
x
x
x
x
2
2
2
2
3
cos
1
tg
3
sin
sin
)'
(tg
⋅
⋅
=
3
)
2
5
(
2
+
⋅
=
x
e
y
x
[
]
5
)
2
5
(
)
2
5
(
2
)
2
5
(
)
2
5
(
)'
(
'
2
3
3
3
2
2
2
2
⋅
+
⋅
+
+
⋅
=
+
+
+
=
x
e
x
x
e
x
e
x
e
y
x
x
x
x
Zadania
1. Pokazać, że wzór (1) można zapiać w równoważnej postaci:
'
'
]
[ln
:
)]
(
[ln
x
x
f
x
x
f
E
=
2.
Pokazać, że:
)
,
(
)
(
B
P
AP
E
f
ρ
ρ
=
A(o, y)
B(x
1
,o)
P(x
0
, y
0
)
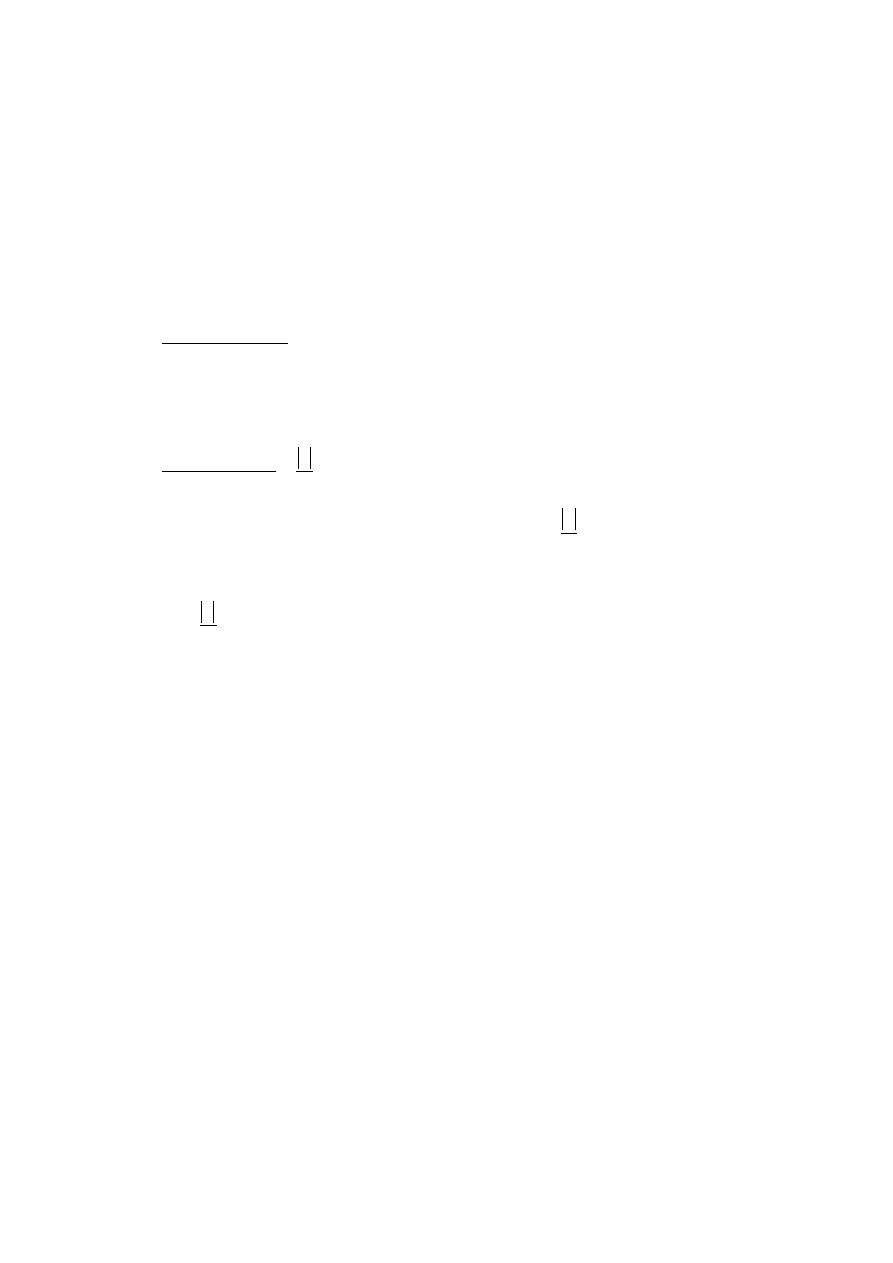
15
gdzie:
ρ
(A P) oznacza odległość punktu A do punktu P, zaś
ρ
(P,B) jest odległością punktu B od
punktu P.
3. Jeżeli elastyczność funkcji f(x) oraz g(x) w punkcie o odciętej x wynosi odpowiednio E
f
oraz
E
g
to elastyczność:
a) iloczynu f(x)
⋅
g(x) jest równa E
f
+ E
q
ilorazu f(x) : g(x) jest równa E
f
–
E
q
elastyczność sumy f(x) + g(x) jest równa średniej wyrażonej postaci:
)
(
)
(
)
(
)
(
x
q
x
f
x
q
E
x
f
E
q
f
+
+
Różniczkowalność a ciągłość – funkcja różniczkowalna w punkcie x
0
jest ciągła w tym punkcie,
ale nie odwrotnie bo np. jeśli: f(x) = x zaś x
0
= 0 to:
h
h
h
o
f
h
o
f
=
−
+
)
(
)
(
zaś jeśli h > o, to wyrażenie to jest równe 1 zaś jeżeli h < o, to
1
−
=
h
h
. Nie istnieje przeto
granica:
h
h
h
lim
0
→
a to oznacza, że funkcja ta nie jest różniczkowalna w funkcje x = x
0
. Innymi słowy ciągłość
funkcji f(x) w punkcie x = x
0
nie wystarzcza na to, aby była ona różniczkowalna w tym punkcie.
MONOTONICZNOŚĆ I EKSTREMA
1. Jeżeli funkcja f(x) jest różniczkowalna w przedziale (a, b) i jej pochodna w tym przedziale
jest dodatnia (ujemna) to funkcja jest w tym przedziale rosnąca (malejąca).
Np. jeżeli w przedziale (a, b) funkcji f(x) jest rosnąca to E
x
> 0 zaś jeżeli jest malejąca to E
x
< 0
[patrz (1)].
2. Jeżeli funkcja f(x) jest różniczkowalna i ma w punkcie c ekstremum to f
′
(c) = 0.
Dodajmy jeszcze, że funkcja f(x) może mieć ekstremum w punkcie i być w tym punkcie
nieróżniczkowalna. Przykładem takiej funkcji jest poprzednio rozpatrywana funkcja f(x) = x.
Ma ona minimum dla x = 0 ale też nie jest w tym punkcie różniczkowalna.
3. Jeżeli różniczkowalna funkcja f(x) jest określona w przedziale [a, b] to przyjmuje wartość
największą (najmniejszą) w punkcie w którym pochodna się zeruje albo na końcu przedziału.

16
Zadania
1. Obliczyć pochodne następujących funkcji.
a)
2
2
cos
1
)
(
x
x
x
f
−
=
b)
4
2
)
sin
1
(
)
(
x
x
f
+
=
c)
x
x
x
x
x
f
tg
sin
)
(
+
=
d)
1
2
1
)
(
2
+
+
=
x
x
x
f
Znana jest tożsamość:
R
b
a
e
a
a
b
b
∈
>
=
0
ln
Na tej podstawie obliczamy pochodną funkcji np.
x
x
x
f
=
)
(
.
W myśl podanej tożsamości mamy:
0
ln
>
=
x
e
x
x
x
x
a stąd
[
]
)
1
(ln
)
1
(ln
)'
(ln
ln
)'
(
)'
ln
(
)'
(
)'
(
ln
ln
ln
ln
+
=
+
=
+
⋅
=
⋅
=
=
x
x
x
e
x
x
x
x
e
x
x
e
e
x
x
x
x
x
x
x
x
x
x
x
Postępując analogicznie obliczyć pochodną funkcji: e) f(x) = (sin x)
tg x
;
g)
)
1
(
2
2
)
3
2
(
)
(
+
+
=
x
x
x
f
2. Wyznaczyć przedziały monotoniczności funkcji:
x
xe
x
f
−
=
)
(
obliczamy f
′
(x). Mamy zatem:
)
1
(
)'
(
)'
(
)
(
'
x
e
xe
e
e
x
e
x
x
f
x
x
x
x
x
−
=
−
=
+
=
−
−
−
−
−
skąd dostajemy
0
)
(
'
>
x
f
dla
0
1
>
−
x
czyli
1
<
x
0
)
(
'
<
x
f
dla
0
1
<
−
x
czyli
1
>
x
a)
x
x
x
f
ln
)
(
2
=
b)
x
e
x
f
x
−
=
)
(
c)
1
)
(
2
+
=
x
x
x
f
d)
1
2
3
)
(
2
3
+
+
−
=
x
x
x
x
f
3. Wyznaczyć ekstremum lokalne funkcji:
x
e
x
f
x
5
)
(
−
=
obliczamy
5
)
(
'
−
=
x
e
x
f
i otrzymaną pochodną przyrównujemy do zera, czyli rozwiązujemy równanie
0
5
=
−
x
e
stąd
5
ln
=
x
Obliczamy drugą pochodną funkcji f(x)
x
x
e
e
x
f
=
−
=
)'
5
(
)
(
'
'
i wyznaczymy jej wartość w miejscu zerowym pierwszej pochodnej czyli:

17
5
ln
)
5
(ln
'
'
e
f
=
Ponieważ
0
5
ln
>
e
przeto w punkcie
5
ln
=
x
istnieje minimum lokalne. Jest ono równe:
5
ln
5
)
5
(ln
5
ln
⋅
−
=
e
f
ZADANIA
Wyznaczyć ekstrema funkcji
a)
x
x
x
f
+
=
2
)
(
b)
4
3
)
(
3
+
−
=
x
x
f
c)
5
ln
15
)
(
x
x
x
f
−
=
4. Wyznaczanie wartości największej (najmniejszej) funkcji f(x) w przedziale [a, b].
Postępowanie realizujące zadanie wymienione w tytule tego punktu dokonuje się według
następującej procedury:
1. obliczamy f
′
(x) i rozwiązujemy równanie:
0
)
(
'
=
x
f
(znajdujemy punkty stacjonarne)
2. obliczamy wartości funkcji w tych punktach oraz na końcach przedziału.
3. Spośród wielkości wyznaczonych w p. 2 wybieramy największą (najmniejszą).
Np. wyznaczyć wartość największą i najmniejszą funkcji
x
e
x
x
f
)
1
(
)
(
−
=
w przedziale [–1, 1]
Zgodnie z p. 1 mamy:
x
e
e
x
e
e
x
e
x
x
f
x
x
x
x
x
=
−
+
=
−
+
−
=
)
1
(
)'
)(
1
(
)'
1
(
)
(
'
a następnie:
0
)
(
'
=
=
x
e
x
f
x
czyli x = 0
zaś zgodnie z punktem 2
0
)
1
(
;
2
2
)
1
(
1
)
0
(
1
=
−
=
−
=
−
−
=
−
f
e
e
f
f
,
Wówczas spośród wartości
e
2
−
, 0, –1 wybieramy najmniejszą (jest nią wartość –1) oraz
największą (jest nią 0). A jak zachować się jak przedział jest nieskończony lub otwarty.
Odwołamy się do przykładu.
Wyznaczyć największą wartość funkcji
x
x
x
f
5
ln
)
(
−
=
w przedziale (0,
∞
) (przedział otwarty)
Obliczamy:
5
1
)'
5
(ln
)
(
'
−
=
−
=
x
x
x
x
f
stąd
5
1
0
)
(
'
−
=
=
x
x
f
czyli
5
1
=
x
.
Obliczamy:
−∞
=
+
→
)
(
lim
0
x
f
x

18
−∞
=
∞
→
)
(
lim
x
f
x
Wartość
5
1
=
x
jest największą wśród wyznaczonych trzech wartości
∞
−
∞
−
,
,
5
1
.
Zadania
a)
1
)
(
3
+
−
=
x
x
x
f
[0, 2]
b)
x
ex
x
f
=
)
(
(1,
∞
)
Dla zastosowań ważne jest twierdzenie Rolle’a które mówi, że jeżeli funkcja f(x) jest określona
w przedziale [a, b], zaś różniczkowalna w przedziale (a, b) przy czym f(a) = f(b) to w tym
przedziale istnieje taki punkt c
)
,
( b
a
c
∈
, że
0
)
(
'
=
c
f
Na podstawie tego twierdzenia można wywnioskować, że pomiędzy dwoma miejscami
zerowymi wielomianu
n
n
n
a
x
a
x
a
x
f
+
+
+
=
−
K
1
1
0
)
(
leży conajmniej jedno miejsce zerowe jego
pochodnej. (Uzasadnić ten wniosek)
Podamy teraz twierdzenie Lagrange’a które przy tak samych założeniach co twierdzenie
Rolle’a nie zakładamy, że
)
(
)
(
b
f
a
f
=
orzeka że:
)
(
)
(
'
)
(
)
(
a
b
c
f
a
f
b
f
−
⋅
+
=
Z tej zależności wynika, że:
)
(
'
)
(
)
(
c
f
a
b
a
f
b
f
=
−
−
ale lewa strona ostatniej równości oznacza współczynnik kierunkowy siecznej przechodzącej
przez punkty
(
) (
)
)
(
,
)
(
,
b
f
b
a
f
a
zaś jej prawa strona jest równa współczynnikowi
kierunkowemu stycznej do wykresu funkcji f(x). Równość ta oznacza zatem, że styczna jest
równoległa do siecznej.
Jakie inne wnioski można wyprowadzić z tej równości?
Wyszukiwarka
Podobne podstrony:
edusat matema rok 1 sem 1 Kolupa
Sciaga koloIII, Budownictwo, Budownictwo - 1 rok, Budownictwo - 1 rok, 2 sem, Matematyka
sciaga kolo 1, Budownictwo, Budownictwo - 2 rok, Budownictwo - 2 rok, 3 sem, Matematyka, 3 semestr,
Zasady zaliczania przedmiotu Matematyka2, STUDIA PŁ, TECHNOLOGIA ŻYWNOŚCI I ŻYWIENIA CZŁOWIEKA, ROK
sciaga z matmy-sem3, Budownictwo, Budownictwo - 2 rok, Budownictwo - 2 rok, 3 sem, Matematyka
PEDOFILIA word, Bezpieczeństwo 2, Bezp II rok, sem I, Przestępczość kryminalna M.Kotowska, do wydruk
+++, STUDIA PŁ, TECHNOLOGIA ŻYWNOŚCI I ŻYWIENIA CZŁOWIEKA, ROK I, SEM 2, FIZYKA 2
WYKlAD 13, Sesja, Rok 2 sem 1, WYKŁAD Psychologia osobowości
zag.13, rok V, sem.zimowy, I spec kliniczna
1416220502. Wprowadzenie do Mechatroniki dzienne new new, SIMR Mechatronika, 2 rok, 2 rok 3 sem, Wpr
Wyklad 10, Sesja, Rok 2 sem 1, WYKŁAD Psychologia osobowości
GiK Gleboznawstwo 15 16 I rok sem 2 dzienne
GiK Gleboznawstwo 15 16 II rok sem 4 zaoczni
prawo halla, STUDIA PŁ, TECHNOLOGIA ŻYWNOŚCI I ŻYWIENIA CZŁOWIEKA, ROK I, SEM 2, FIZYKA 2
Zasady nazewnictwa wybranych klas zwi-zk-w organicznych, STUDIA PŁ, TECHNOLOGIA ŻYWNOŚCI I ŻYWIENIA
Gelogia III, AGH Kier. GiG rok I Sem. I, Geologia
więcej podobnych podstron