Rozdział 7

Sieci samoorganizujące się

7.1

Metody redukcji wymiarowości

Niech X ⊂ R

n

będzie zbiorem n-wymiarowych punktów. Interesuje nas znalezienie takiego

przekształcenia zbioru X w zbiór X

′

⊂ R

n

′

, n

′

<< n, które nie tylko redukuje liczbę wy-

miarów niezbędnych do scharakteryzowania badanych obiektów, ale także zachowuje istotne
(przestrzenne) relacje między oryginalnymi punktami. Taka transformacja wykorzystywana
jest m.in. w zadaniach wizualizacji wysokowymiarowych danych [58]. Jest ona stosowana w
wielu praktycznych zagadnieniach związanych z analizą i kompresją danych w takich dzie-
dzinach jak meteorologia, przetwarzanie obrazów, genomika czy wyszukiwanie informacji.

The principal component analysis aims at dimensionality reduction of input data. One

method was already mentioned, namely the Fisher’s discriminant analysis described in
appendix I. This method has a drawback, namely that it reduces dimensionality from d
(number of dimensions of the input data) to exactly (C-1) (C being the number of classes).
Methods of principal component analysis allow dimensionality reduction to an arbitrary
number of features. They do not take into account target data information and rely solely
upon input data. Therefore, these methods can produce suboptimal results and there is no
guarantee, that the dimensionality reduction will not ”reduce the important information
away”.

Wśród klasycznych metod redukcji wymiarowości ważną rolę odgrywa tzw. (liniowa)

analiza składowych głównych określana często akronimem PCA (Principal Component Ana-
lysis

) [48]. Poświęcamy jej dalsze punkty tego podrozdziału.

Wymogiem stosowania analizy składowych głównych jest konieczność operowania macie-

rzą kowariancji. Skalowanie wielowymiarowe, określane też skrótem MDS (MultiDimensio-
nal Scaling

) oferuje podejście bardziej ogólne polegające na reprezentacji zależności między

obiektami ze zbioru Z w oparciu o relacje podobieństwa/odmienności zachodzące między
parami obiektów.

Niech δ : Z ×Z → {0}∪R

+

mierzy siłę związku między parami obiektów. Jeżeli δ rośnie

monotonicznie ze wzrostem podobieństwa między porównywanymi obiektami – nazywamy
ją miarą podobieństwa; jeżeli natomiast δ rośnie monotonicznie ze wzrostem różnic między
porównywanymi obiektami – nazywamy ją miarą odmienności. Przykładem tej ostatniej
jest odległość euklidesowa. W ogólności δ nie musi być metryką.

Zadanie skalowania metrycznego formułuje się następująco. Zakładamy, że dana jest

pewna miara odmienności δ i dla każdej pary elementów {x

i

, x

j

} ∈ X znana jest war-

tość ich odmienności δ

ij

. Niech dalej d

ij

oznacza odległość euklidesową między elementami

y

i

, y

j

∈ Y. Należy tak dobrać współrzędne punktów ze zbioru Y, aby zminimalizować błąd

(określany też terminem stres)

99

100

ROZDZIAŁ 7. SIECI SAMOORGANIZUJĄCE SIĘ

e =

k



i

=1

k



j

=1

(d

ij

− δ

ij

)

2

(7.1)

Ideę algorytmu skalowania wielowymiarowego można przedstawić następująco: łączy-

my sprężynami k punktów ulokowanych losowo w n-wymiarowej przestrzeni i staramy się
tak modyfikować ich położenia, aby zredukować naprężenia w aktualnej konfiguracji (oczy-
wiście sprężystość połączenia dwóch punktów jest proporcjonalna do ich odmienności w
oryginalnej n-wymiarowej przestrzeni). Do rozwiązania tak postawionego problemu stosuje
się najczęściej różne wersje algorytmu gradientowego (najszybszego spadku).

W celu ujednolicenia wpływu różnych wartości odmienności δ

ij

na wartość błędu, kry-

terium modyfikowane jest często do postaci

E =

k



i

=1



j>i

w

ij

(d

ij

− δ

ij

)

2

(7.2)

W zależności od założonego celu aproksymacji, można stosować albo tzw. wagi globalne,

w

(g)

ij

, przypisujące wszystkim rozbieżnościom identyczną wartość, albo wagi lokalne, w

(l)

ij

,

umożliwiające uwypuklenie lokalnej struktury poprzez redukcję wpływu większych wartości
odmienności

w

(g)

ij

=

1

k
i

=1

j>i

δ

2

ij

, w

(l)

ij

=

2

k(k − 1)δ

2

ij

(7.3)

Odnotujmy, że waga lokalna staje się nieoznaczona, jeśli dana para (i, j) charakteryzuje

się zerową odmiennością.

, to jedna z wcześniejszych metod redukcji wymiarowości, a zarazem jedna z ważnych

technik umożliwiających graficzną prezentację danych wielowymiarowych. Jej dodatkową
zaletą jest to, że oferuje ona rozwiązanie zadania ekstrakcji cech, czyli znalezienia nowych
cech (atrybutów) będących kombinacjami liniowymi znanych cech. Mówiąc nieformalnie,
PCA wspomaga eksplorację statystycznej struktury zbioru danych. Wielowymiarowe dane,
potraktujmy je jak zbiór punktów w przestrzeni R

n

, na ogół nie są równomiernie rozmiesz-

czone wzdłuż wszystkich kierunków układu współrzędnych, lecz koncentrują się w pewnych
podprzestrzeniach przestrzeni R

n

, tzn., większa część wariancji zbioru obserwacji jest zloka-

lizowana w pewnej podprzestrzeni oryginalnej przestrzeni P

n

. PCA pozwala identyfikować

taką podprzestrzeń wprowadzając nowy układ współrzędnych, który jest rotacją oryginal-
nego układu, a ponadto posiada dwie ważne cechy.

–

Po pierwsze, nowe dane uzyskane drogą projekcji na nowy układ współrzędnych są
”zdekorelowane”, tzn. odpowiadająca im macierz kowariancji jest macierzą diagonal-
ną.

–

Po drugie, nowe współrzędne można uporządkować w taki sposób, że pierwsza z
nich (tzn. pierwsza „składowa główna”) wyznacza taki kierunek w R

n

, że rzutując

obserwacje na ten kierunek otrzymujemy zmienne losowe o maksymalnej wariancji.
Kolejna składowa wyznacza kierunek zawierający maksymalną część pozostałej
wariancji, itd.

Składowe główne reprezentowane są przez wektory własne macierzy kowariancji Σ wy-

znaczonej dla „scentrowanych” danych, a wartości własne tej macierzy reprezentują warian-
cję danych zrzutowanych na odpowiedni kierunek. Innymi słowy, wyodrębnianie składowych
głównych reprezentowanych przez wektory własne jest równoznaczne z rotacją maksymali-
zującą wariancję (varimax ) przestrzeni zmiennych. Wyznaczony w ten sposób nowy układ

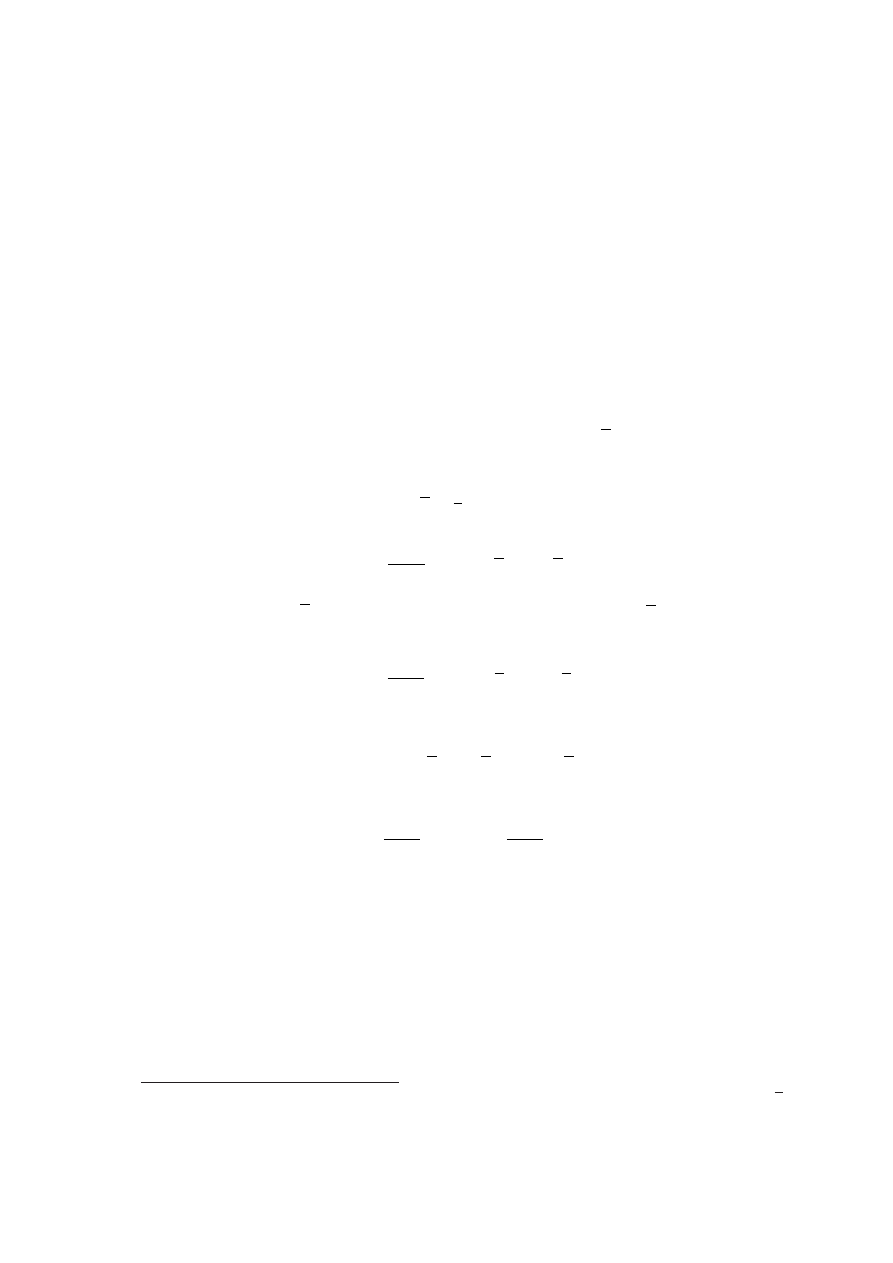
7.1. METODY REDUKCJI WYMIAROWOŚCI

101

współrzędnych charakteryzuje się dodatkowo minimalnym błędem rekonstrukcji, definiowa-
nym jako średniokwadratowa odległość między oryginalnymi obserwacjami a ich projekcja-
mi.

7.1.1

Analiza składowych głównych

Niech X = [x

ij

] będzie macierzą o n wierszach i p kolumnach, tzn. każda kolumna repre-

zentuje pojedynczy obiekt. Innymi słowy macierz X można przedstawić w postaci (wier-
szowego) wektora

X

= (x

1

, x

2

, . . . , x

p

)

(7.4)

gdzie x

i

jest n-wymiarowym (kolumnowym) wektorem reprezentującym współrzędne i-tego

obiektu.

Zakładamy, że próba losowa (7.4) pochodzi z populacji o ciągłym rozkładzie w prze-

strzeni R

n

. Parametry tego rozkładu, czyli wartość oczekiwaną x i macierz kowariancji Σ

wyznaczamy w oparciu o równania

1

x

=

1
p

p



j

=1

x

j

(7.5)

Σ

=

1

p − 1

p



j

=1

(x

j

− x)(x

j

− x)

T

(7.6)

Składowymi wektora x są wartości przeciętne poszczególnych cech, x

i

= (

p
j

=1

x

ij

)/p,

i = 1, . . . , n natomiast elementy macierzy Σ mają postać

σ

ij

=

1

p − 1

p



l

=1

(x

il

− x

i

)(x

jl

− x

j

)

(7.7)

Często wprowadza się tzw. centrowaną macierz obserwacji

Y

= (x

1

− x, x

2

− x, . . . , x

p

− x)

(7.8)

dzięki czemu równanie (7.6) można zapisać w prostszej postaci

Σ

=

1

p − 1

p



j

=1

y

j

y

T

j

=

1

p − 1

YY

T

(7.9)

Celem analizy jest określenie tzw. składowych głównych losowego wektora x. W zbiorze

losowych wektorów a ∈ R

n

o jednostkowej długości poszukuje się takiego wektora γ

1

, że

[48, pkt. 8.2]

Var(γ

T

1

x

) =

max

a

∈R

n

,

!a!=1

Var(a

T

x

)

(7.10)

Wektor ten określa taki kierunek w przestrzeni R

n

, że rzut ortogonalny wektora x na ten

kierunek skutkuje zmienną losową o maksymalnej wariancji. Zmienną losową γ

T

1

x

nazywa-

my pierwszą składową główną wektora x. Podobnie drugą składową główną otrzymujemy
znajdując taki wektor jednostkowy γ

2

∈ R

n

, że zmienna losowa Var(γ

T

2

x

) ma największą

1

Wielkości wyznaczane w oparciu o te równania to estymaty. Formalnie należałoby stosować oznaczenia

!

x,

!

Σ dla odróżnienia ich od wartości teoretycznych. Aby nie komplikować oznaczeń stosujemy jednak identyczny
symbol na oznaczenia wartości teoretycznej i jej estymaty.

102

ROZDZIAŁ 7. SIECI SAMOORGANIZUJĄCE SIĘ

możliwą wariancję i jest nieskorelowana z pierwszą składowa główną. Wektory γ

1

, γ

2

, . . .

nazywamy wektorami ładunków, albo współczynnikami odpowiedniej składowej głównej.
Okazuje się, że jeżeli wektory własne v

1

, v

2

, . . . , v

n

macierzy kowariancji ponumerujemy

w taki sposób, że odpowiadające im wartości własne uszeregowane sa malejąco, to i-temu
ładunkowi odpowiada i-ty (jednostkowy) wektor własny macierzy Σ – por. [48, Tw. 8.1].

Przypomnijmy, że wartości własne to pierwiastki tzw. równania charakterystycznego

det(Σ − λI) = 0

(7.11)

gdzie I oznacza macierz jednostkową. Jest to równanie n-tego stopnia, a więc macierz Σ ma
n (niekoniecznie różnych) wartości własnych. Z kursu algebry liniowej wiadomo ponadto, że:

(w1)

Jeżeli M jest kwadratową macierzą symetryczną o rzeczywistych elementach, to jej

wartości własne są liczbami rzeczywistymi.

(w2)

Jeżeli ponadto M jest macierzą dodatnio półokreśloną, tzn. jest macierzą symetrycz-

ną i dla każdego niezerowego wektora x ∈ R

n

zachodzi x

T

Mx

% 0, to jej wartości

własne są nieujemnymi liczbami rzeczywistymi, przy czym przynajmniej jedna jest
równa zeru. Liczba dodatnich wartości własnych odpowiada rzędowi macierzy M.

jest macierzą dodatnio półokreśloną o rzeczywistych elementach, ma więc rank(Σ) dodat-
nich wartości własnych.

Z kolei wektor własny to wektor v stanowiący rozwiązanie równania

Σv

= λv

(7.12)

Wektory własne odpowiadające różnym wartościom własnym są do siebie prostopadłe, moż-
na więc traktować je jako nowe współrzędne. Jeżeli przez V oznaczymy macierz, której
kolumnami są wektory własne, to konsekwencją ich ortogolnalności jest V

T

V

= VV

T

= I,

tzn. V jest macierzą ortogonalną.

Sposób wyznaczania projekcji n-wymiarowego zbioru danych w l-wymiarowy zbiór Z

przedstawiono w postaci pseudokodu 7.1. Zbiór Z o elementach z

j

∈ R

l

otrzymujemy

stosując liniowe przekształcenie

Z

= F

T

Y

(7.13)

Wynika stąd, że: (a) elementy oryginalnego zbioru X są wstępnie „centrowane”, tzn. przesu-
wane o wartość x, a następnie (b) rzutowane na obrócony o pewien kąt układ współrzędnych
o zredukowanej liczbie wzajemnie prostopadłych osi. Owe osie wyznaczone są przez wektory
ładunków γ

i

(czyli odpowiednie wektory własne macierzy Σ) i tak dobrane by maksymali-

zować wariancje rzutów ortogonalnych obserwacji x na te osie, pod warunkiem, że kolejne
rzuty są nieskorelowane z wcześniejszymi. Przy wyborze wartości l kierujemy się albo po-
trzebami praktycznymi (tzn. należy sporządzić l = 2 wymiarowy wykres), albo własnością
mówiącą, że l pierwszych kierunków własnych objaśnia

λ

1

+ · · · + λ

l

λ

1

+ · · · + λ

n

· 100%

(7.14)

zmienności (wariancji) obserwacji.
Z równania (7.15) wynika, że zredukowana charakterystyka i-tego obiektu ma postać

z

j

= F

T

y

j

(7.15)

7.1. METODY REDUKCJI WYMIAROWOŚCI

103

Algorytm 7.1

Algorytm PCA

Require:

Zbiór danych X = (x

1

, . . . , x

p

), gdzie x

i

∈ R

n

, i = 1, . . . , p. Wymiar l < n nowej

przestrzeni.

Ensure:

Transformowany zbiór danych Z = (z

1

, . . . , z

p

) o elementach z

i

∈ R

l

.

1:

Wyznaczanie średnich: dla każdej cechy (wiersza) wyznacz jej wartość średnią

x

i

=

1
p

p



j

=1

x

ij

2:

Centrowanie danych: utwórz macierz Y o elementach y

ij

= x

ij

− x

i

3:

Wyznacz macierz kowariancji Σ = YY

T

/(p − 1)

4:

Wyznacz wektory i wartości własne macierzy Σ

5:

Wybierz l < n wektorów własnych odpowiadających l największym wartościom wła-
snym. Utwórz wektor cech F = (v

1

, . . . , v

l

), przy czym v

i

to (kolumnowy) wektor

własny.

6:

Przekształć dane zgodnie z równaniem Z = F

T

Y

Składowe tego wektora są równe

z

ij

=

n



t

=1

v

ti

y

tj

(7.16)

Przykład 7.1.1.

Aby zilustrować opisany tu sposób postępowania sięgnijmy do zbioru

irysów [22]. Zawiera on pomiary czterech parametrów dokonane na 150 irysach pochodzą-
cych z trzech gatunków: Iris Setosa, Iris Versicolour oraz Iris Virginica. Z każdego gatunku
pobrano 50 reprezentantów. Ważne jest to, że w 4-wymiarowej przestrzeni cech jedna klasa
jest liniowo separowalna od pozostałych. Dwóch pozostałych klas nie można rozdzielić w
ten sposób.

Postępując zgodnie z opisanym schematem stwierdzamy, że wektor wartości średnich i

macierz kowariancji mają postać

x

=











5.8433
3.0573
3.7580
1.1993











, Σ =











0.6857 −0.0424

1.2743

0.5163

−0.0424

0.1900 −0.3297 −0.1216

1.2743 −0.3297

3.1163

1.2956

0.5163 −0.1216

1.2956

0.5810











Wartości i wektory własne macierzy Σ to

λ

=











0.2427
0.0782
0.0238
4.2282











, V =











0.6566 −0.5820 −0.3155

0.3614

0.7302

0.5979

0.3197 −0.0845

−0.1734

0.0762

0.4798

0.8567

−0.0755

0.5458 −0.7537

0.3583











Wynika stąd, że jeżeli l = 2, to macierz F = (v

4

, v

1

), a więc jej pierwszą kolumną

jest wektor własny z czwartej kolumny macierzy V (odpowiada mu maksymalna wartość
własna λ = 4.2282), a drugą – wektor z pierwszej kolumny macierzy V. Projekcję zbioru X
na 2-wymiarową przestrzeń euklidesową przedstawiono na lewym rysunku 7.1. Zauważmy,
że tak zdefiniowana projekcja objaśnia

0.2427 + 4.2282

0.2427 + 0.0782 + 0.0238 + 4.2282

· 100% = 97.77%

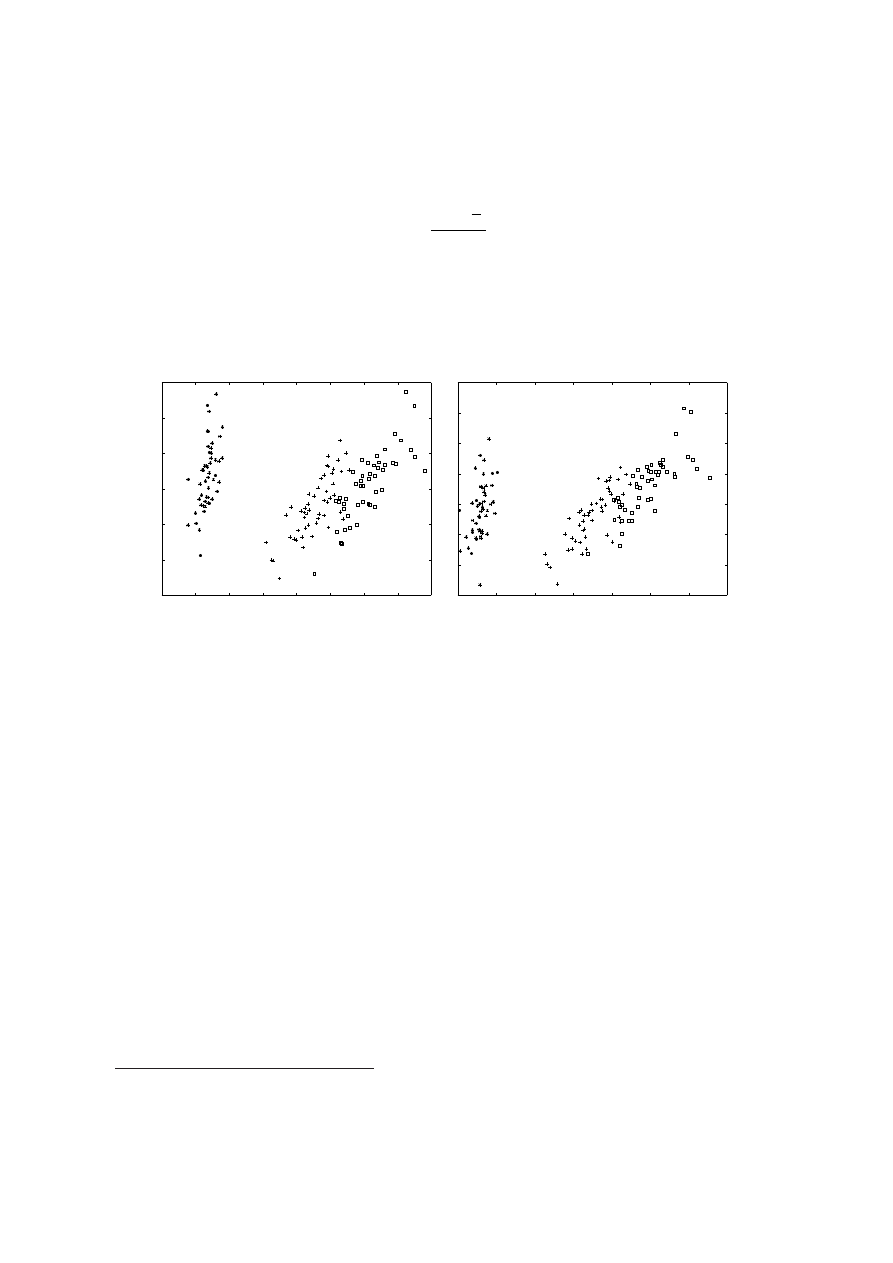
104

ROZDZIAŁ 7. SIECI SAMOORGANIZUJĄCE SIĘ

obserwowanej zmienności.

W pewnych sytuacjach, np. aby pozbyć się zakłóceń, centrowanie zastępuje się standa-

ryzowaniem, tzn. składowe macierzy Y mają postać

y

ij

=

x

ij

− x

i

σ

i

(7.17)

gdzie σ

i

oznacza odchylenie standardowe i-tej cechy. W prawej części rysunku 7.1 przed-

stawiono rezultat analizy otrzymanej z tak określonej macierzy Y.

Jeżeli analizie poddawane są dane zmieniające sie w czasie (np. zdjęcia satelitarne pew-

nego obszaru wykonywane w określonych odstępach czasu), to dodatkowo zamiast macierzy
kowariancji wyznacza się macierz korelacji standaryzowanej macierzy Y.

¤

−4

−3

−2

−1

0

1

2

3

4

−1.5

−1

−0.5

0

0.5

1

1.5

−3

−2

−1

0

1

2

3

4

−1.5

−1

−0.5

0

0.5

1

1.5

2

Rysunek 7.1: Wynik zastosowania algorytmu PCA do zbioru iris. Tutaj p = 150, n = 4.
Zbiór zawiera charakterystyki trzech gatunków irysów. Jeden z gatunków jest wyraźnie róż-
ny od dwóch pozostałych. Należące do niego obiekty zaznaczono symbolem ∗. Lewy rysunek
przedstawia wyniki standardowej analizy PCA, prawy – standaryzowanej analizy PCA.

7.1.2

Zastosowanie w analizie twarzy

Ciekawym zastosowaniem analizy składowych głównych jest rozpoznawanie twarzy. Istotą
pomysłu – zaproponowali go Sirovich i Kirby w 1987 roku, [81], a rozwinęli Turk i
Pentland [84] – jest wydobycie specyficznych cech twarzy z użyciem PCA zastosowanej
do zbioru trenującego złożonego z reprezentatywnej kolekcji zdjęć. Pozyskane w ten
sposób wektory własne traktuje się jako „standaryzowane składniki twarzy” określane
terminem eigenfaces. Każdą twarz reprezentuje się teraz jako kombinację liniową owych
składników. Co ciekawe, nie trzeba wielu składników, aby wiernie opisać dowolną twarz.
Przygotowanie owych eigenfaces odbywa się zgodnie ze schematem 7.1. Poniżej opisujemy
krótko podstawowe kroki prowadzące do uzyskania interesujących nas charakterystyk, a
następnie przedstawiamy sposób, w jaki wykorzystujemy je do klasyfikacji nowych zdjęć.

(a)

Cyfrowe zdjęcie twarzy utożsamia się z dwuwymiarową tablicą T, której elementy
T (x, y) ∈ {0, . . . , 255} opisują stopnie szarości

2

piksela o współrzędnych (x, y). Dla

uproszczenia przyjmujemy, że T jest tablicą kwadratową o n wierszach i n kolumnach

3

.

2

Dla prostoty koncentrujemy się na zdjęciach czarno-białych, ale metoda może być stosowana z powo-

dzeniem do zdjęć kolorowych.

3

Oczywiście liczba wierszy może być różna od liczby kolumn. Ważne jednak, aby wszystkie zdjęcia miały

identyczny rozmiar.

7.1. METODY REDUKCJI WYMIAROWOŚCI

105

W analizie obrazów cyfrowych tablicę tę przedstawia się w postaci kolumnowego wek-
tora x o n

2

składowych. W ten sposób zbiór trenujący złożony z p takich zdjęć jest

reprezentowany w postaci prostokątnej macierzy X = (x

1

, . . . , x

m

) o n

2

wierszach i p

kolumnach.

(b)

Następnie wyznacza się uśrednione zdjęcie x zgodnie z równaniem (7.5) i sprowadza
macierz X do „scentrowanej” macierzy Y zgodnie z (7.8).

(c)

W kolejnym kroku należałoby wyznaczyć macierz kowariancji Σ = YY

T

i wyznaczyć

jej wektory własne. Jednak Σ jest macierzą wymiaru n

2

×n

2

. Oznacza to, że jeżeli np.

analizujemy zdjęcia o wymiarze 256 × 256 pikseli, to każdy wektor x zawiera 65, 536
elementów, a macierz Σ posiada 65, 536 (niekoniecznie różnych) wektorów własnych.
Ich wyznaczenie może być poważnym problemem. Co więcej, jeżeli liczba zdjęć p jest
znacząco mniejsza od n

2

, to macierz Σ ma co najwyżej p − 1 dominujących wektorów

własnych (pozostałym wektorom odpowiadają zerowe wartości własne, co wynika z
własności (w2) ze strony 102).

(d)

W celu redukcji obliczeń stosujemy następujący chwyt [84]. Wyznacza się macierz

S

=

1

p − 1

Y

T

Y

(7.18)

Jej rozmiar to p × p, a zatem ma ona co najwyżej p różnych wektorów własnych w

i

spełniających równanie

Y

T

Yw

i

= λ

i

w

i

(7.19)

Mnożąc je lewostronnie przez Y otrzymujemy równanie

(YY

T

)(Yw

i

) = λ

i

(Yw

i

)

(7.20)

skąd wynika, że wektor v

i

= Yw

i

jest wektorem własnym macierzy Σ = YY

T

.

Zauważmy, że obie macierze Σ oraz S mają identyczne wartości własne. Obliczone w
ten sposób wektory v

i

o długości n

2

są nienormalizowanymi dominującymi wektorami

własnymi macierzy Σ. Stanowią one kombinację liniową „scentrowanych” zdjęć, tzn.

v

i

=

p



j

=1

w

ij

y

j

(7.21)

Normalizowane wektory własne to poszukiwane eigenfaces, czyli „standaryzowane
składniki twarzy”.

Zgodnie z ogólną procedurą wyznaczone za pomocą równania (7.21) wektory własne

rozpinają p

′

-wymiarową „przestrzeń twarzy” T, w której lokują się kolejne zdjęcia. Każde

z nich można przedstawić jako sumę ważoną

!

x

j

=

p

′



i

=1

ω

ij

y

j

+ x

(7.22)

przy czym

ω

ij

= v

T

i

y

j

, i = 1, . . . , p

′

(7.23)

natomiast p

′

to liczba wektorów własnych, którym odpowiadają niezerowe wartości własne.

Waga ω

ij

wskazuje na udział i-tej cechy w j-tym zdjęciu. W ten sposób z każdym zdję-

ciem kojarzy się odpowiadający mu wektor wagowy ω

j

= V

T

y

j

; są to jego współrzędne w

przestrzeni twarzy T.

106

ROZDZIAŁ 7. SIECI SAMOORGANIZUJĄCE SIĘ

Jeżeli x oznacza nowe (nie należące do zbioru trenującego) zdjęcie, to jego współrzędne

w przestrzeni T wyznaczamy stosując powyższe równanie, czyli

ω

i

= v

T

i

(x − x),

i = 1, . . . , p

′

(7.24)

Sirovich i Kirby [81] zauważyli, że w istocie dostatecznie dobre wyniki reprezentacji w prze-
strzeni T zapewnia dalsza redukcja jej wymiaru polegająca na wyborze p

′′

< p

′

wektorów,

którym odpowiadają najwyższe wartości własne. Do wyboru wartości p

′′

można np. sto-

sować kryterium (7.14). W pracy [81] do opisu p = 115 zdjęć wystarczyło p

′

= 40 cech

zapewniających błąd średniokwadratowy rzędu 2%.

Niech ω = (ω

1

, . . . , ω

p

′

)

T

będzie zbiorem wag wskazujących udział poszczególnych cech

w analizowanej twarzy. Można go wykorzystać w zadaniu klasyfikacji polegającym na zna-
lezieniu klasy, do której badane zdjęcie należy. Niech mianowicie ω

j

będzie charakterystyką

j-tej klasy. W najprostszym przypadku przyjmujemy, że klasę stanowi pojedyncze zdjęcie
ze zbioru trenującego. Mamy więc p klas, a każda z nich opisana jest wektorem ω

j

o skła-

dowych ω

kj

określonych równaniem (7.23). Zdjęcie x zaliczamy do klasy minimalizującej

błąd

ǫ

k

= 'ω − ω

k

'

(7.25)

Jeżeli do klasy k zaliczamy kilka obiektów, to opisujący ją wektor ω

k

jest uśrednioną war-

tością wektorów charakteryzujących zdjęcia przypisane do tej klasy.

Przykład 7.1.2.

Do eksperymentów wybrano 20 zdjęć z bazy danych Faces94, którą

przygotował dr Libor Spacek [80]. Oryginalna baza zawiera kolorowe zdjęcia 153 osób (20
kobiet i 133 mężczyzn) o rozmiarze 180 × 200 pikseli. Dla celów ilustracyjnych wybrano
losowo 20 zdjęć i przekształcono je na zdjęcia czarno-białe – por. rysunek 7.2. Na rysunku
7.3 przedstawiono uśrednioną twarz , a na rysunku 7.4 zestaw p − 1 wektorów własnych
macierzy kowariancji Σ. Oryginalne zdjęcie twarzy i jego projekcję na „przestrzeń twarzy”
wykonaną zgodnie z równaniem (7.22) przedstawiono na rysunku 7.5.

¤

Należy podkreślić, zaprezentowana tu metoda należy do najprostszych metod rozpozna-

wania twarzy. Jej podstawową wadą jest to, że wszystkie osoby powinny być fotografowane
w identyczny sposób, tzn. en face (z profilu) i w jednakowych warunkach oświetleniowych.
Nieco mniej wrażliwą okazuje się metoda odwołująca się do liniowej analizy dyskrymina-
cyjnej Fishera (por. [48, pkt. 1.2]) co skutkuje pojęciem Fisherfaces wprowadzonym w [4].

7.2

Projekcje zbioru dokumentów do euklidesowej przestrze-
ni dwu-i-półwymiarowej

Samoorganizujące się sieci neuronowe, zwane też samoorganizującymi się mapami cech (ang.
SOM - Self-Organizing Maps) lub – od nazwiska ich pomysłodawcy – sieciami Kohonena,
nawiązują luźno do wprowadzonej przez Doyle’a koncepcji map semantycznych przezna-
czonych do graficznej reprezentacji pojęć i relacji miedzy tymi pojęciami [?]. Z drugiej
strony stanowią one odległy odpowiednik ”map topograficznych” tworzonych przez neu-
rony w mózgu. Charakterystyczne cechy sieci Kohonena to: (a) reprezentacja częstości i
rozkładu danych wejściowych, (b) oraz konstruktywna metoda projekcji elementów wy-
sokowymiarowej przestrzeni na 2-wymiarową strukturę sieciową. Połączeniem wynikowej
wizualizacji zbioru danych z informacją o gęstości rozkładu jego elementów jest tzw. mapa
dwu-i-półwymiarowa.

7.2. PROJEKCJE ZBIORU DOKUMENTÓW DO EUKLIDESOWEJ PRZESTRZENI DWU-I-PÓŁWYMIAROWEJ

Rysunek 7.2: Zestaw zdjęć stanowiących zbiór trenujący. Wybrano je z bazy danych [80].

Rysunek 7.3: Uśrednione zdjęcie x.

Z formalnego punktu widzenia sieć Kohonena jest sztuczną siecią neuronową. Różni się

jednak ona od innych sieci neuronowych tym, że

•

Składa się z jednej, dwuwymiarowej warstwy neuronów, przy czym każdy neuron jest
połączony ze wszystkimi neuronami tej warstwy.

•

Przeznaczona jest do uczenia się bez nadzoru

4

(w odróżnieniu od innych typów sieci

neuronowych, np. wielowarstwowego perceptronu).

Aby dać pojęcie o istocie SOM, zacytujmy fragment książki [?] (s. 381-382)

4

Istnieją wersje algorytmu przeznaczone do uczenia pod nadzorem, tzw. LVQ (Learning Vector quanti-

zation), zob. [?, ?]

108

ROZDZIAŁ 7. SIECI SAMOORGANIZUJĄCE SIĘ

Rysunek 7.4: Wektory własne (eigenfaces) macierzy kowariancji Σ.

50

100

150

20

40

60

80

100

120

140

160

180

200

Rysunek 7.5: Oryginalne zdjęcie twarzy i jego projekcja (prawe zdjęcie) na „przestrzeń
twarzy” zdefiniowaną przez wektory własne z rysunku 7.4.

50

100

150

20

40

60

80

100

120

140

160

180

200

Rysunek 7.6: Oryginalne zdjęcie twarzy i jego projekcja (prawe zdjęcie) na „przestrzeń
twarzy” zdefiniowaną przez wektory własne z rysunku 7.4 xx.

Kohonen, czerpiąc inspirację z biologii, wprowadził reguły działania sieci zdol-
nej do uczenia się bez nadzoru. (...) kluczowym elementem, pozwalającym na
powstanie samoorganizujących się struktur neuronowych, jest kombinacja od-
działywań pobudzających i hamujących – w tym przypadku połączeń między
neuronami. Neurony położone blisko aktywnej (pobudzonej) komórki – są za-
chęcane do wysłania sygnału, a leżące dalej – hamowane.

Efektem tych procesów jest powstanie nieliniowego odwzorowania przekształcającego

wielowymiarowe wektory w węzły (zazwyczaj dwuwymiarowej) struktury. Odwzorowanie
to zachowuje dużą część informacji topologicznej zawartej w danych wejściowych. Przede

7.2. PROJEKCJE ZBIORU DOKUMENTÓW DO EUKLIDESOWEJ PRZESTRZENI DWU-I-PÓŁWYMIAROWEJ

wszystkim odzwierciedla wewnętrzną strukturę danych: logicznym związkom podobieństwa
między wielowymiarowymi obiektami odpowiada fizyczne sąsiedztwo pobudzanych węzłów
kraty. Można powiedzieć, że algorytm SOM łączy ze sobą konkurencyjne uczenie nienadzo-
rowane z redukcją wymiarowości.

Poniżej omawiamy krótko algorytm SOM, porównujemy własności uzyskiwanej mapy

z metodami omówionymi w poprzednim punkcie, a wreszcie dokonujemy krótkiego prze-
glądu metod wizualizacji map i wskazujemy ich zastosowania w systemach wyszukiwania
informacji. Czytelnika zainteresowanego bardziej szczegółowym opisem odsyłamy do [?].

7.2.1

Algorytm uczenia sieci Kohonena

Problemy związane z uczeniem sieci omawiane są dokładnie w dalszych partiach książki.
Tu chcemy jedynie wprowadzić w tę tematykę niezorientowanego Czytelnika.

Rysunek 7.7: (a) Prostokątna i (b) heksagonala struktura mapy Kohonena.

Jak już wspomniano, sieci Kohonena – podobnie jak większość sieci neuronowych pod-

dawanych uczeniu konkurencyjnemu (por. np. [?]) – składają się z jednej warstwy neuronów
ulokowanych w węzłach (zazwyczaj dwuwymiarowej) kraty. Najczęściej jest to krata pro-
stokątna lub heksagonalna – por. rysunek ??. Każdemu elementowi i ulokowanemu w węźle
kraty przypisany jest wektor tzw. referencyjny (wektor wag neuronów) w

i

o losowo inicjo-

wanych składowych.

5

Proces uczenia polega na sekwencyjnej prezentacji elementów zbioru trenującego, X.

5

W zastosowaniach przetwarzania tekstu istotny jest kierunek tego wektora, ponieważ często jako miarę

podobieństwa obiektu (dokumentu) do wektora referencyjnego stosuje się tzw. miarę kosinusową. Ogólnie
jednak wskazane jest normalizowanie wektora referencyjnego - podczas inicjalizacji jak i po modyfikacji

110

ROZDZIAŁ 7. SIECI SAMOORGANIZUJĄCE SIĘ

Dla każdego elementu x ∈ X wyznaczamy jednostkę (zwycięzcę) i∗, której wektor referen-
cyjny jest najbardziej podobny do prezentowanego wektora x. Następnie składowe wektora
referencyjnego zwycięzcy, jak i wektorów referencyjnych należących do pewnego (zmienne-
go w czasie) otoczenia zwycięzcy modyfikowane są zgodnie wariantem reguły Grossberga
∆w

i

(t) = η(x − w

i

(t)), która przyjmuje teraz postać

∆w

i

(t + 1) = α(t) · f(i, i∗, t) · (x − w

i

(t))

(7.26)

Tutaj α(t) jest współczynnikiem wpływającym na szybkość uczenia, natomiast f(i, i∗, t)

to pewna funkcja sąsiedztwa. Najczęściej stosowaną funkcją sąsiedztwa jest funkcja gaus-
sowska określona wzorem

f (i, i∗, t) = a · exp[−

d(i, i∗)

2 · (σ

2

(t))

]

(7.27)

gdzie a jest stałą, d(i, i∗) oznacza odległość

6

między jednostką i a zwycięzcą i∗, a sigma

2

(t)

oznacza promień sąsiedztwa. Zarówno α(t) jak i promień sąsiedztwa maleją z upływem
czasu. Praktyczną wersję algorytmu przedstawił Lippman w [?].

O ile w przypadku klasycznej reguły Grossberga modyfikowane są tylko składowe wek-

tora zwycięzcy, to w przypadku reguły Kohonena uczeniu poddaje się wszystkie neurony,
przy czym siła modyfikacji ich wektorów referencyjnych maleje wraz z odległością od zwy-
cięzcy. Taki sposób modyfikacji zapewnia, że wektor referencyjny zwycięzcy jest jeszcze
bardziej czuły na podawany sygnał wejściowy i przy ponownej prezentacji tego sygnału
wygenerowany zostanie jeszcze silniejszy sygnał wyjściowy. W przypadku pozostałych neu-
ronów, wzmocnienie lub osłabienie wag połączeń jest czynnikiem separującym różniące się
od siebie wektory wejściowe, oraz powodującym aktywację zbliżonych topograficznie ele-
mentów wyjściowych w przypadku podobych sygnałów wejściowych. Podsumowując można
powiedzieć, że uczenie sieci Kohonena oparte jest na dwóch zasadach:

•

Konkurencja: wektor referencyjny zwycięskiej jednostki upodabnia się do wektora
cech opisującego prezentowany obiekt. W ten sposób mapa ”uczy się” prawidłowej
lokalizacji chmury danych o podobnych cechach.

•

Kooperacja: Modyfikacji podlegają nie tylko współrzędne wektora referencyjnego zwy-
cięskiej jednostki, ale także współrzędne wektorów przypisanych do sąsiadów zwycięz-
cy. W ten sposób następuje proces samoorganizacji.

Sieć Kohonena wymaga wstępnego określenia jej topologii oraz liczby węzłów (neu-

ronów), co w praktycznych sytuacjach może okazać się kłopotliwe. Konieczne jest także
odgórne ustalenie scenariusza α(t). Z tego powodu w pracy [?] przedstawiono zbiór innych
metod uczenia konkurencyjnego, które w wielu sytuacjach znacznie lepiej odzwierciedlają
strukturę zbioru trenującego, a liczba neuronów zaangażowanych w proces uczenia dobie-
rana jest w jego trakcie.

7.2.2

Własności sieci Kohonena

Wynikiem procesu uczenia jest uporządkowany względem podobieństwa zbiór wektorów
referencyjnych. Ich rozkład odzwierciedla nie tylko relacje przestrzenne

7

ale także gęstość

6

jest to odległość Minkowskiego L

p

gdzie zazwyczaj p = 1 (odległość miejska) lub p = 2 (odległość

euklidesowa)

7

tzn. fizycznemu sąsiedztwu jednostek odpowiada podobieństwo wielowymiarowych obiektów

7.2. PROJEKCJE ZBIORU DOKUMENTÓW DO EUKLIDESOWEJ PRZESTRZENI DWU-I-PÓŁWYMIAROWEJ

obiektów w wejściowej przestrzeni X. Dwa skupienia ulokowane blisko siebie na kracie repre-
zentują zbiory oryginalnych obiektów o podobnych własnościach. Należy jednak pamiętać,
że stwierdzenie odwrotne nie jest prawdziwe: środki skupień sąsiadujące w wejściowej prze-
strzeni nie muszą leżeć blisko siebie na kracie. Innymi słowy, odwzorowanie SOM polega
na zanurzeniu kraty w wejściowej przestrzeni bez nadmiernego rozciągania i wykrzywiania
tej kraty [?]. W tym sensie SOM odwzorowuje relacje podobieństwa między obiektami wej-
ściowej przestrzeni na relacje sąsiedztwa na kracie. W zależności od liczby jednostek, ich
wektory referencyjne reprezentują albo wartości przeciętne poszczególnych skupień

8

, albo

pojedyncze elementy z przestrzeni wejściowej wraz z ich generalizacjami.

Rysunek 7.8: Reprezentacja zbioru trenującego (szary pierścień) za pomocą (a) sieci SOM
i (b) sieci GNG [źródło: [?]].

Istnieje pewna relacja między skalowaniem wielowymiarowym a siecią Kohonena. W

pierwszym przypadku mamy nieliniowe odwzorowanie wysokowymiarowej przestrzeni w
przestrzeń metryczną o niskiej liczbie wymiarów. W odróżnieniu od zachowującego topolo-
gię odwzorowania SOM, mamy tu odwzorowanie zachowujące odległość

9

. W konsekwencji

sieć Kohonena nie zapewnia satysfakcjonujących rezultatów odwzorowywania wysokowy-
miarowych obiektów geometrycznych. Służy ona raczej wydobywaniu wiedzy o strukturze
analizowanego zbioru i wizualizacji tejże struktury. Przedstawiony w pracy [?] algorytm
wzrastającego gazu neuronowego (GNG - Growing Neural Gas) znacznie lepiej nadaje się
do reprezentacji relacji strukturalnych między analizowanymi obiektami. Ilustruje to ry-
sunek ??, obrazujący strukturę sieci Kohonena jak i sieci GNG dla zbioru trenującego
zaznaczonego jako szary pierścień. Jak widać z tego rysunku, sieć GNG precyzyjnie dopa-
sowuje się do prezentowanego jej kształtu zbioru, wykorzystując zarazem mniejszą liczbę
neuronów. Jej niedostatkiem jest jednak konieczność stosowania algorytmów wizualizacji
wielowymiarowych danych.

Zasadnicza różnica między SOM i GNG, powodująca lepsze oddanie struktury zbioru

przez GNG, wynika z innego podejścia do relacji między obiektami i ich skupieniami. SOM
zakłada istnienie pewnej regularnej struktury powiązań między obiektami / ich skupie-
niami. GNG natomiast takiej struktury nie zakłada, ale stara się wykryć taką strukturę,
która faktycznie istnieje, nie nakładając ograniczeń przestrzennych (jak np. planarność w
wypadku niektórych wersji SOM).

8

mniejsza liczba jednostek powoduje redukcję danych

9

w ogólnym przypadku: zachowujące relacje odmienności wyrażone przez funkcję δ

112

ROZDZIAŁ 7. SIECI SAMOORGANIZUJĄCE SIĘ

7.2.3

Wizualizacja danych z wykorzystaniem sieci Kohonena

Techniki wizualizacji danych korzystające z sieci Kohonena można podzielić na trzy kate-
gorie (por. [?]): (a) wizualizacja skupień danych i ich kształtu z wykorzystaniem projekcji,
i różnych macierzy odległości, (b) analiza korelacji między składowymi wejściowych wekto-
rów, oraz (c) klasyfikacja nowych obiektów.

Skoncentrujemy się na pierwszej kategorii

10

, którą można podzielić dodatkowo na tech-

niki projekcji przeznaczone do wizualizacji kształtu skupień w niskowymiarowych przestrze-
niach oraz techniki korzystające z macierzy odległości przeznaczone do prezentacji skupień
na kracie SOM. Omówione w podrozdziale ?? metody projekcji mogą być stosowane do
wizualizacji kształtów skupień poprzez rzutowanie wektorów referencyjnych na niskowy-
miarową podprzestrzeń.

Rysunek 7.9: Wizualizacja sieci Kohonena wykorzystująca (a) U-macierz, (b) macierz od-
ległości, (c) kolorowanie podobnych komórek [źródło: [?]].

Jeżeli natomiast interesują nas, odwzorowywane na kracie SOM, relacje sąsiedztwa mię-

dzy obiektami z wejściowej przestrzeni, zaleca się korzystanie z macierzy odległości. Naj-

10

Czytelnika zainteresowanego pozostałymi aspektami zachęcamy do zapoznania się ze znakomitym pakie-

tem demonstracyjnym, który jest dostępny pod adresem http://www.cis.hut.fi/projects/somtoolbox/

7.2. PROJEKCJE ZBIORU DOKUMENTÓW DO EUKLIDESOWEJ PRZESTRZENI DWU-I-PÓŁWYMIAROWEJ

częściej stosowaną jest przedstawiona w [?] metoda tzw. U-macierzy, w której wyznacza się
odległości wektora referencyjnego każdej jednostki od wektorów przypisanych jej sąsiadom.
Poszczególnym elementom uzyskanej w ten sposób macierzy przypisuje się różne odcienie
szarości: im większa odległość, tym ciemniejszy odcień przyjmuje odpowiednie pole – por.
rysunek ??a. Uzyskuje się w ten sposób reprezentację przypominającą nieco odwzorowa-
nie terenu za pomocą mapy kartograficznej - stąd określenie 2.5 wymiarowa reprezentacja
pejzażu

. Tutaj białe kropki reprezentują komórki sieci, a szare sześciokąty ulokowane mię-

dzy nimi wskazują podobieństwo każdej pary wektorów. Jasne obszary na pokolorowanej w
ten sposób mapie wskazują skupienia w wejściowej przestrzeni separowane ciemnymi obsza-
rami. Podobny efekt można uzyskać obliczając dla każdej jednostki średnią, maksymalną
lub minimalną odległość od jej sąsiadów i przeskalować rozmiar każdego oczka kraty pro-
porcjonalnie do wyznaczonej statystyki. Środkowa część rysunku ?? prezentuje uśrednioną
U-macierz. Wreszcie w prawej części rysunku ?? pokazano tę samą mapę, której komórki
oznaczono różnymi kolorami odzwierciedlającymi ich podobieństwo.

Ograniczenie analizy podobieństwa wyłącznie do sąsiednich komórek implikuje szereg

wad opisanej wyżej metody – por. [?]. Przede wszystkim jakość wizualizacji zależy od roz-
kładu wektorów referencyjnych w wejściowej przestrzeni. Aby macierz odległości dostatecz-
nie wiernie reprezentowała zależności między obiektami, wektory referencyjne powinny być
dostatecznie bliskie wektorom charakteryzującym elementy wejściowego zbioru X. Pociąga
to za sobą konieczność długiego uczenia, co może skutkować przeuczeniem sieci. Po drugie,
nie istnieje bezpośrednia relacja między wektorami referencyjnymi a elementami zbioru X.
Efektem tego jest ”abstrakcyjne” przedstawienie przestrzeni wejściowej.

Alternatywne podejście, tzw. P-macierz, zaproponował Sklorz, [?]. Zamiast ograniczać

się do sąsiednich komórek, dla każdej jednostki wyznacza się największe podobieństwo mię-
dzy jej wektorem referencyjnym a wszystkimi wektorami x ∈ X. W efekcie P-macierz
reprezentuje gęstość wejściowej przestrzeni X. Mianowicie, wektory referencyjne jednostek,
które różnią się znacznie od elementów przestrzeni X są rzadko modyfikowane przez algo-
rytm uczący i w konsekwencji reprezentują ”puste obszary” między skupiskami obiektów.
Dla odmiany, skupienia podobnych obiektów powodują intensywne uczenie, a w konsekwen-
cji modyfikację współrzędnych wektorów referencyjnych, jednostek zajmujących pewien ob-
szar mapy. Tym samym wysokie wartości elementów P-macierzy separują rejony podobnych
obiektów. Informacja zawarta w tej macierzy wizualizowana jest za pomocą różnych odcieni
szarości: jasne obszary obiektów podobnych oddzielone są ciemnymi obszarami ”pustki”.
Ideę tej metody przedstawiono na rysunku ??.

7.2.4

Samoorganizujące się mapy dokumentów

Potrzebę tworzenia map semantycznych dla celów wyszukiwania informacji znakomicie wy-
artykułował w 1961 r. Doyle formułując postulat zacieśnienia mentalnego kontaktu między
użytkownikiem (czytelnikiem) a zmagazynowaną informacją, por. [?]. Postulowane przez
niego mapy semantyczne miały służyć jako przewodnik po literaturze i wspomagać użyt-
kownika przy zawężaniu zakresu poszukiwań poprzez rozpoznanie. Uchwycenie naturalnej
charakterystyki i organizacji kolekcji dokumentów winno – zadniem Doyla – odbywać się
poprzez analizę częstości i rozkładu słów w dokumentach. Rolą komputera jest więc ana-
liza i odkrywanie związków semantycznych zarówno w ramach pojedynczych dokumentów
jak i między dokumentami. Proces odnajdywania wysoko skorelowanych par słów w tek-
ście jest odpowiednikiem rozpoznawania takich par przez zawodowego bibliotekarza. Doyle
przykładał dużą wagę do podobieństwa map semantycznych do ”psychologicznych map”
powstających w ludzkim mózgu. Uważał jednak, że 2-wymiarowa reprezentacja takiej ma-

114

ROZDZIAŁ 7. SIECI SAMOORGANIZUJĄCE SIĘ

Rysunek 7.10: (a) Rozkład 12 obiektów w 2-wymiarowej przestrzeni, (b) odpowiadająca mu
mapa SOM, oraz (c) jej wizualizacja przy użyciu P -macierzy [źródło: [?]].

py jest niezmiernie trudna. Mapy Kohonena znakomicie korespondują z ideami Doyla a
jednocześnie przedstawiają niezwykle proste rozwiązanie problemu odwzorowania. Poniżej
omawiamy za [?] przykładowe zastosowanie sieci Kohonena w problemach wyszukiwania
informacji.

7.2.4.1

Mapy kategorii

Jedno z pierwszych zastosowań odwzorowania Kohonena do generowania tzw. map kategorii
zaproponował Lin, [?], [?]. Istotą jego pomysłu jest graficzna reprezentacja zawartości zbioru
dokumentów wraz ze strukturą danej kolekcji uwzględniającą sąsiedztwo kategorii.

Rysunek ?? przedstawia przykładową mapę kategorii dla 140 dokumentów poświęconych

tematowi ”Artificial Intelligence”. Mapa podzielona jest na tzw. obszary pojęć określone
przez dominujące słowa kluczowe. Wynikowa klasyfikacja reprezentuje pewien podział doku-
mentów, tzn. każdy dokument przypisany jest dokładnie do jednego obszaru. Obszary ma-
py, ich pozycja względem sąsiadów i rozmiar zostały wyznaczone automatycznie. Rozmiar
każdego obszaru jest proporcjonalny do częstości występowania danego słowa kluczowego

7.2. PROJEKCJE ZBIORU DOKUMENTÓW DO EUKLIDESOWEJ PRZESTRZENI DWU-I-PÓŁWYMIAROWEJ

Rysunek 7.11: Mapa kategorii dla 140 dokumentów. [źródło: [?]].

w zbiorze dokumentów. Własność zachowywania topologii zbioru wejściowego w odwzo-
rowaniu Kohonena zapewnia, że obszary reprezentujące współwystępujące słowa kluczowe
zajmą sąsiednie położenie na mapie. Liczby występujące na mapie wskazują ilość dokumen-
tów przypisanych do każdego węzła. Powyższe własności pozwalają użytkownikowi uzyskać
szybki wgląd w zawartość tematyczną odwzorowanego zbioru dokumentów, co uzasadnia
– stosowane przez Lina – traktowanie mapy jako swoistego spisu treści. Mapa pozwala na
łatwą identyfikację dominujących tematów (odpowiadają im duże obszary pojęć - por. ob-
szar zajmowany przez termin ”expert systems” na rys. ??). Konstrukcja mapy odbywa się
w trzech zasadniczych krokach:

1.

Przekodowanie dokumentów do postaci wektorowej. Indeksowaniu podlegały jedynie
tytuły dokumentów, a rozmiar wektora ograniczono do 25. Zastosowano binarne wa-
żenie termów.

2.

Trenowanie sieci Kohonena na zadanym zbiorze wektorów. Efektem tego procesu jest
przypisanie węzłom sieci podobnych dokumentów. Wektory referencyjne poszczegól-
nych węzłów kodują informację o strukturze kolekcji dokumentów.

3.

Identyfikacja obszarów pojęciowych i ich graficzna reprezentacja. W celu wyznaczenia
takich obszarów znajduje się wektory jednostkowe (mają one jedynkę tylko na jednej
pozycji, a pozostałe wypełnione są zerami) najbardziej podobne do wektorów refe-
rencyjnych. Węzeł etykietowany jest wyłonionym w ten sposób dominującym słowem.
Jeżeli sąsiednie węzły mają identyczne etykiety – tworzą one spójny obszar.

Podobne podejście zastosowano w pracy [?] poświęconej problemowi kategoryzowania

stron WWW w oparciu o odwzorowanie SOM. O ile w cytowanej wcześniej pracy autorzy
ograniczyli się do niewielkiego zbioru dokumentów, o tyle ambicją autorów tej pracy jest