MATEMATYKA DYSKRETNA

(Semestr zimowy 2002/2003)

Wymiar: 2 2 0 0 0 E
Wymagania: matematyka na poziomie szkoly sredniej
Zaliczenie przedmiotu: Ocena z cwiczen audytoryjnych wystawiona na podstawie zadan domowych
i aktywnosci na cwiczeniach
Zalozenia programowe: Zapoznanie z podstawowymi obiektami i strukturami matematyki
dyskretnej, przydatnymi niemal we wszystkich zajeciach informatycznych; przygotowanie tym
samym do wysluchania dalszych zajec poswieconych projektowaniu i analizie algorytmów i
programów komputerowych.

Wyklad:
1.Elementy teorii zbiorów – rachunek zdan, reguly wnioskowania (modus ponens, zasada
rezolucji),zastosowania w strukturach systemów ekspertowych, zbiory i dzialania na zbiorach,
alfabet, (zastosowania – maszyna Turinga), problemy latwe i trudne, asymptotyka funkcji
liczbowych – zastosowania w zlozonosc obliczeniowej algorytmów, zasada dziel i zwyciezaj

2. Elementy teorii liczb – funkcje calkowitoliczbowe: powala i podloga, podzielnosc liczb –
algorytm Euklidesa, liczby pierwsze i rozklad liczb na czynniki., liczby doskonale, równanie
diofantyczne, NWP, NWW, operator modulo

3.Elementy kombinatoryki – zasada golebnika, zasada wlaczania i wylaczania, permutacje,
kombinacje, podzialy liczb, algorytmy generowania obiektów kombinatorycznych,

4. Elementy kombinatoryki – algorytmy i zaleznosci rekurencyjne, rozwiazywanie zaleznosci
rekurencyjnych – przez podstawianie i za pomoca równania charakterystycznego, symbol Newtona,
trójkat Newtona, kongruencje, schemat Hornera

4.Elementy teorii grafów – relacje, grafy symetryczne i skierowane, drogi, cykle, rodzaje grafów:
drzewa, dwudzielne, pelne

5. Elementy teorii grafów – macierzowe reprezentacje grafów, grafy Eulera i Hamiltona, grafy
plaskie

6. Elementy teorii grafów – przeszukiwanie grafów: metoda w glab i w szerz, zastosowania
grafów: grafy AND/OR, metoda podzialów i ograniczen, algorytmy na grafach – zadania
najkrótszych dróg

Cwiczenia
Cwiczenia polegaja na rozwiazywaniu w klasie zadan opracowanych do poszczególnych
partii materialu z wykladu. Sa to glównie cwiczenia rachunkowe, ale w wielu przypadkach
polegaja na uzyciu algorytmu przedstawionego na wykladzie. Niektóre zadania dotycza
analizy dzialania i zlozonosci algorytmów. Studenci otrzymuja po kazdym wykladzie liste
zadan do wykonania – czesc z nich maja rozwiazac w domu i przeniesc rozwiazania na
zajecia.

Literatura
Ross K.A., Wright C.R.B., Matematyka dyskretna, PWN, Warszawa 1996.
Syslo M.M., Algorytmy, WsiP, Warszawa, 1997
Lipski W., Kombinatoryka dla programistów, WNT, Warszawa, 1982
Wilson R.J., Wprowadzenie do teorii grafów, PWN, Warszawa, 1998.
Ziembinski Z., Logika praktyczna, PWN, Warszawa 2000.

Matematyka dyskretna

Zestaw zadan #1

1. Poslugujac sie diagramami Venny, udowodnij nastepujace zawieranie sie zbiorów:

A

⊕ B ⊆ (A ⊕ C) ∪ (B ⊕ C)

2. Zalózmy, ze alfabet sklada sie z dwóch znaków

Σ = (a,b). Wyobraz sobie slownik

zawierajacy wszystkie niepuste slowa z

Σ*, ulozone w porzadku alfabetycznym. Jak

daleko w tym slowniku musimy szukac slowa ba?

3. Potrafisz bez wiekszego problemu porzadkowac trzy dowolne liczny, wykonujac trzy

porównania. Podaj algorytm porzadkowania dowolnych czterech liczb, w którym jest
wykonywanych nie wiecej niz piec porównan. Przedstaw oba te algorytmy na drzewie
obliczen (porównan).

4. W jaki sposób bedziesz jednoczesnie znajdowal najmniejsza i najwieksza liczbe w

ciagu n liczb?

5. Wyznacz zlozonosc obliczeniowa problemu trójpodzialu?

6. Uporzadkuj nastepujace funkcje tak aby kazda poprzednia funkcja byla funkcja wolniej

rosnac niz funkcja po niej nastepujaca (wszystkie logarytmy sa przy takiej samej
podstawie 2):

log n , (log n)

n

,

n

log n

, log(n

n

) , 2

log n

, n , n

3

, (1 + 1/n)

n

7. Liczba 2

n

– 1 jest rozwiazaniem zagadki znanej jako wieze Hanoi i oznacza liczbe

kamiennych kregów jakie musza przeniesc mnisi z pala na pal. Wedlug legendy n = 64.
Przyjmij, ze rozpoczeli oni przenosic te kregi na poczatku naszej ery i pracuja z
predkoscia ... komputera sredniej mocy, przenoszac 100 milionów pojedynczych
kregów na sekund! Wedlug legendy., po rozwiazaniu przez nich tej lamiglówki ma
nastapic koniec swiata. Oblicz, kiedy to nastapi.

8. Sprawdz prawdziwosc:

∀x∈R ∃!z∈R ∀y∈R [x + y = z] , ∃!x∈R ∀y∈R [x*y = 0] ,

∀y∈R∃!x∈R [x*y = 0]

¬∀x P(x) ⇒ ∃ x P(x) , ∃ x P(x) ⇒ ¬∀x P(x) , ¬∃ x P(x) ⇒ ∀x P(x)

∀x∈{1,2,3} [P(x) ∧ Q(x)] ⇔ (∀x∈{1,2,3} P(x) ∧ ∀x∈{1,2,3} Q(x))

∃x∈{1,2,3} [P(x) ∧ Q(x)] ⇔ (∃x∈{1,2,3} P(x) ∧ ∃x∈{1,2,3} Q(x))

9. Zapisz z pomoca kwantyfikatorów: n*n = 25 , X + 0 = X , x = 3

1. Sprawdz równowaznosci: (p

⇒ ¬p) ∧ (¬p ⇒ p) ⇔ 0 ,

(q

⇒ p) ∧ (¬p ⇒ q) ∧ (q ⇒ q) ⇔ p ∨ ¬q

11 Podaj przyklad ilustrujacy równowaznosc:

¬(∃y Q(y)) ⇔ ∀y [¬Q(y)]

¬(∃x ∀y [y > x]) ⇔ ∀x∃y [y ≤ x]

12. Przedstaw program dla maszyny Turinga umozliwiajacy wykrywanie liczb

nieparzystych.

13. Dana jest baza faktów: a, b, c oraz baza regul:

R1:

If f and e, then g

R2: If a and c, then e
R3: If a and b, then d
R4: If d and e, then f
Czy g nalezy do bazy faktów (daje sie wyprowadzic z ww. baz)?

1.Elementy teorii zbiorów

rachunek zdan,

reguly wnioskowani, prawa (równowaznosci) tautologie (regula modus ponens),

rachunek predykatów (zasada rezolucji),

zastosowania w strukturach systemów ekspertowych,

zbiory i dzialania na zbiorach, alfabet, (zastosowania – maszyna Turinga),

problemy latwe i trudne,

asymptotyka funkcji liczbowych – zastosowania w zlozonosc obliczeniowej

algorytmów, zasada dziel i zwyciezaj

Predykaty

P(x) P(x) = [ x = 3] , P(x) = [Q(x)

∧U(x)] , [pije mleko] , [jest zielone],

P(x

1

,x

2

,...,x

n

)

P(x,y,z) = [x + y = z] , P(x,y) = [x > y] , [jest dzieckiem],

Przyklady

P(Janek,Zosia) = [Janek jest bratem Zosi] ,P(V,x,y,z) = [V = x*y*z]

∀x∈R [x + 0 = x] , ∃x∈N [x = x*x] , ¬∃x∈N [x < 0] , ∃x∈R [x < 0] ,

∀x∈zbiór kotów [x pije mleko] , ∀x∈zbiór szpaków [x jest ptakiem]

∀x∈zbiór dzieci ∃y ∈zbiór rodziców [x jest dzieckiem y]

Rachunek predykatów

∃jeden talerz ∀ student

,

∀ student ∃ jeden talerz

Niech P(x) = [x = x*x] która z tez jest prawdziwa:

∃

x

∈

R P(x) ,

∀

x

∈

R P(x)

∀x ∈{0,1} [x ∧ ¬x ≡ 0]

,

∀x ∈{0,1} [x ∨ ¬x ≡ 0]

sprawdzanie prawdziwosci

∀x P(x) - „jeden zaprzecza wszystkiemu“

∃x P(x) - „jeden wystarcza“

¬(∀x P(x)) ⇔ ∃x [¬P(x)]

przyklad

¬(∀x∈R [x < x + 1] ⇔ ∃ x∈R [x ≥ x + 1]

¬(∃y Q(y)) ⇔ ∀y [¬Q(y)]

¬(∃x ∀y [y > x]) ⇔ ∀x[¬∀y [y > x]) ⇔ ∀x∃y [¬ [y > x]] ⇔ ∀x∃y [y ≤ x]]


Niech U’ = {1,2,3} , U” = {4,5,6,7}sprawdz prawdziwosc:

∃x∈U’ ∃y∈U” [y > x]

∀x∈U’ ∀y∈U” [y > x]

∀x∈U’ ∃y∈U” [y > x]

∃x∈U’ ∀y∈U” [y > x]

∃!x∈R [x*6 = 0]

∀x∈R ∀y∈R ∃!z∈R [x + y = z]

∀x∈{1,2,3} P(x) ⇔ P(1) ∧ P(2) ∧ P(3) ,



(

∀x P(x) ⇒ ∀x P(x)) ⇔ (∃x P(x) ⇒ ∃x Q(x))

∀x P(x) ∃x P(x) ∃x Q(x) ∀x P(x) ⇒ ∀x P(x) ∃x P(x) ⇒ ∃x Q(x)

0

0

0

1

1

0

0

1

1

1

0

1

0

1

0

0

1

1

1

1

1

0

0

1

1

1

0

1

1

1

1

1

0

1

0

1

1

1

1

1

(

∀x P(x) ⇒ ∀x P(x)) ⇔ (∃x P(x) ⇒ ∃x Q(x))

( A

⇒ A )

⇔ ( B ⇒ C )

(

¬

A

∨ A )

⇔ (

¬

B

∨ C )

1

⇔ .....?????....

(

∃x P(x) ⇒ ∃x P(x)) ⇒ (∀x P(x) ⇒ ∃x Q(x))

∃x P(x) ∀x P(x) ∃x Q(x) ∃x P(x) ⇒ ∃x P(x) ∀x P(x) ⇒ ∃x Q(x)

0

0

0

1

1

0

0

1

1

1

0

1

0

1

0

0

1

1

1

1

1

0

0

1

0

1

1

1

0

1

1

1

ZBIORY

Zbiór liczb naturalnych:1, 2, 3 , 4 , 5 , ...

N = {1, 2, 3 , 4 , 5 , ...}

Zbiór liczb wmiernych:1/2, 2/3 , 4/4 , 5/6 , ...

W = {1/2, 2/3 , 4/4, 5/6 , ...}

Zbiór liczb niewmiernych:

√

2,

π

, e ,...

¬ W

Zbiór liczb rzeczywistych -

R

Zbiór liczb calkowitych

-

C

N

⊂

C

⊂

W

⊂

R

;

¬

W

⊄

C ;

¬

W

⊂

R

Suma

A

∪ B = C ;

C = {c

∈ A ∨ c ∈ B}

Iloczyn A

∩ B = C ;

C = {c

∈ A ∧ c ∈ B}

Róznica

A \ B = C ;

C = {c

∈ A ∧ c ∉ B}

Róznica symetryczna
A

⊗ B = C ;C = { c ∈ A ∪ B ∧ c ∈ A ∩ B } = { c ∈ A \ B ∨ c ∈ B \ A }

Zbiór pusty

A =

∅ ⇔ ¬∃ a [a ∈ A ]

Inkluzja dwóch zbiorów( A

⊂ B ) ⇔ ∀a [ a ∈ A ⇒ b ∈ B ]

Przestrzen ( zbiór pelny)

-

1

Dopelnienie A’ zbioru A przestrzeni

1

a

∈ A ⇔ a∈ 1 ∧ a ∉ A

A’ = 1 \ A

N

⊂ W ;

¬(W ⊂ N ) ;

W

∩¬W = ∅

;

N \ W =

∅

Zbiór potegowy P(S) zbioru S – zbiór wszystkich podzbiorów zbioru S.
S={a,b} ; P(S) = {

∅ , {a}, {b} , {a,b}}

|S| = 2 ,

|P(S)| = 2

n

A

A’

1

OBIEKT, MODEL, PROBLEM, METODA

OBIEKT

-

SYSTEM

-

ZADANIE

OBIEKT

Specyfikacja zadania w jezyku naturalnym

Przyklad
Dane sa naczynia o pojemnosci odpowiednio 9 i 4 litra. Czy mozna z ich
pomoca odmierzyc pojemnosc 6 litrów? Wszystko to przy zalozeniu, ze
naczynia te nie sa cechowane, a mozliwe dzialania obejmuja nalewanie
do pelna (badz opróznianie) lub przelewanie z jednego naczynia do
drugiego.


MODEL

Specyfikacja zadania w jezyku symboli (abstrakcji)

Stan = stan wypelnienia naczyn
Stan = (stan wypelnienia naczynia wiekszego, stan wypelnienia naczynia

mniejszego)

Stan = (X, Y), X,Y

∈

N

0

,

Przestrzen stanów:

X < 10

,

Y <5

Stan poczatkowy : S

0

= (0,0)

Stany koncowe : S*

∈

{(6,m), (4,2), . . .}

PROBLEM

Specyfikacja zadania w jezyku symboli (abstrakcji)

Dany jest graf przestrzeni stanów. (Wierzcholkami grafu sa stany dopuszczalne, tzn.
osiagalne ze stanu poczatkowego zgodnie z zadanymi regulami przelewania. Luki grafu
oznaczaja dozwolone przejscia miedzy kolejnymi stanami.)

Czy w danym grafie istnieje sciezka laczaca S

0

z

S*

?

Która ze sciezek laczacych S

0

z

S*

jest najkrótsza?

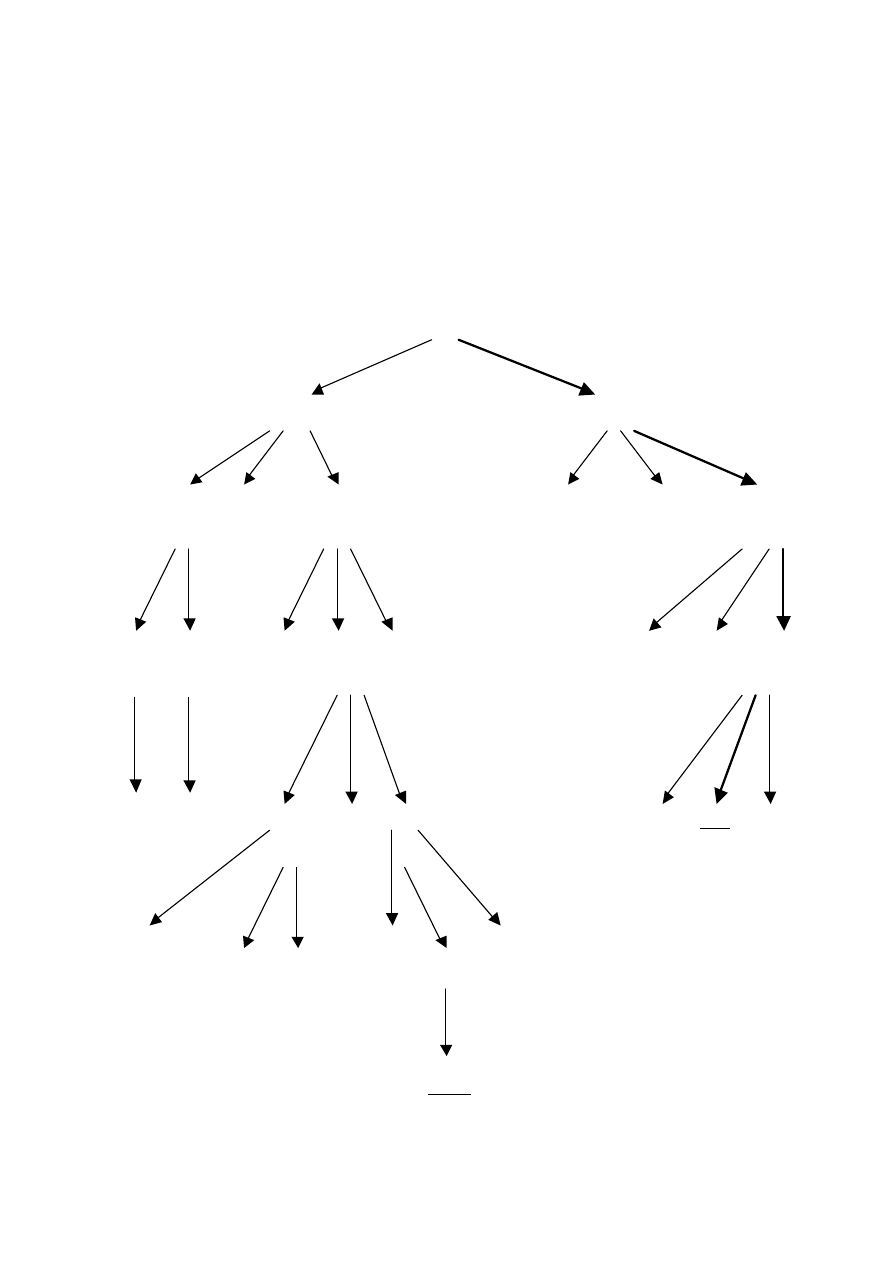
Dane sa naczynia o pojemnosci odpowiednio 4 i 3 litra. Czy mozna z ich
pomoca odmierzyc pojemnosc 2 litrów? Wszystko to przy zalozeniu, ze
naczynia te nie sa cechowane, a mozliwe dzialania obejmuja nalewanie
do pelna (badz opróznianie) lub przelewanie z jednego naczynia do
drugiego.

(4 , 3)
(0 , 0)

(4 , 0)

(0 , 3)

(4,3) (0,0)

(1,3)

(4,3)

(0,0)

(3,0)

(4,0) (0,3)

(4,0) (1,0) (0,3)

(0,0) (0,3)

(3,3)

(1,3) (3,0)

(1,3) (0,0) (0,1)

(0,3) (4,2)

(3,0)

(0,3)

(1,0) (4,0)

(0,0) (4,1) (1,0)

(2,3)

PROBLEM

≡

DANE

+

OGRANICZENIA

+

PYTANIE

PROBLEMY

DECYZYJNE

OPTYMALIZACYJNE

PROBLEMY

TRUDNE

LATWE

PRZYKLADY

PROBLEM SORTOWANIA

{2, 6, 1, 7, 3, 5, 4}

{1, 2, 3, 4, 5, 6 , 7}

PROBLEM PLECAKOWY

•

{D} , wd ,cd

; {R} , wr ,cr

; {P} , wp , cp

; x

1

, x

2

, x

3

∈

N

o

•

x

1

wd +x

2

wr + x

3

wp < W;

•

x

1

cd +x

2

cr + x

3

cp

max

PROBLEM KOMIWOJAZERA

•

N – miast, d

i,j

– odleglosci pomiedzy miastami

•

Startujac z wybranego miasta, nalezy powrócic do niego
przejezdzajac przez kazde z pozostalych miast tylko jeden raz.

•

Która z tras jest najkrótsza?

METODY




PRZYBLIZONE

DOKLADNE

HEURYSTYCZNE

„0” DODATKOWEJ INFOMACJI

DANA DODATKOWA INFORMACJA

przeszukiwanie wszerz

górska wspinaczka

przeszukiwanie w glab

algorytm gradientowy

generuj i testuj

najpierw najlepszy

A*

Y

xxxxxxx

5

5 xxxxxxx

15

20

S

k

xxxxxxx

xxxxxxx

4

4 xxxxxxx

12

3 6

9

12

15

3
XXXXXXXXXXXXX 6

8

xxxxxxx

2

XXXXXXXXXXXXX

xxxxxxx

S

0

2

3

4

5

1

1

2

3

4

5

X

Problem trójpodzialu

Zbiór A sklada sie z 3q elementów o znanych wagach w

i

. Nalezy

dokonac podzialu zbioru A na „q” rozlacznych, trójelementowych
podzbiorów takich, ze suma wag w kazdym z nich równa sie B.

A = {a

i

| i = 1,n & n = 3q & q

∈ N

1

} , w

i

∈ N , i = 1,n

k-ty podzial:

S(k) =

∪{s

j

| j = 1,q & s

j

= {a

k

, a

i

, a

n

} = A

S

j

∩ s

i

=

∅ , ∀i,j = 1,q

w

k

+ w

i

+ w

n

= B,

∀j = 1,q

Problem plecakowy

Dany jest zbiór A = {a

i

| i = 1,n} róznych typów towarów. Kazda

jednostka danego typu towaru ma te sama objetosc g

i

(wage w

i

)

oraz cene c

i

. Dysponujemy plecakiem o pojemnosci G (mozemy

udzwignac W).
Ile, jakich towarów mozna zaladowac do plecaka aby wyjsc z
maksymalnym zyskiem?

Przestrzen stanów N = N x N x ...x N tworzona jest przez wektory
X = (x

1

,x

2

,...,x

n

) , gdzie x

i

∈N

0

– zmienna decyzyjna

X = (0,0,...0)

-

stan poczatkowy

X*= (x

1

,x

2

,...,x

n

) -

stan koncowy

n

Funkcja celu max(

Σ

x

i

c

i

)

i=1

n

Ograniczenia

Σ

x

i

g

i

≤ G

i=1

n

(

Σ

x

i

w

i

≤ W )

i=1

Problem decyzyjny:

pytania sa formulowane w taki sposób aby

udzielana na nie odpowiedz byla postaci TAK lub NIE.

n

Funkcja celu

Σ

x

i

c

i

≤ F

i=1

Problem optymalizacyjny:

pytania sa formulowane w taki

sposób aby udzielana na nie odpowiedz dotyczyla ekstremum
pewnej funkcji celu.

n

Funkcja celu max(

Σ

x

i

c

i

)

i=1

Z kazdym problemem optymalizacyjnym mozna zwiazac problem
decyzyjny.


Funkcja g(n) asymptotycznie dominujaca nad funkcja f(n) wtedy i
tylko wtedy gdy

∃k ≥ 0 ∀n ≥ k : |f(n)| ≤ |g(n)|


Przyklad

Funkcje O(n), O(n

c

) , O(c

n

) , O(n!) sa funkcjami asymptotycznie

zdominowanymi przez funkcje:
F(n) = n

, F(n) = n

c

, F(n) = c

n

, F(n) = n!

Zasada dziel i zwyciezaj

Zbiór danych jest dzielony na dwa rozlaczne zbiory, prawie
równoliczne, dla których w dwóch nastepnych krokach sa
rozwiazywane podobne problemy. Postepowanie takie pozwala
zmniejszyc zlozonosc obliczeniowa algorytmu.

Przyklad

Problem sortowania

Dany jest zbiór: {7, 5, 6, 1, 3, 4 , 2, 9, 8, 10}. Zbiór ten nalezy uporzadkowac
(posortowac) od najmniejszego do najwiekszego elementu, tzn. {1, 2, 3 , 4 ,
5 , 6 , 7 , 8 , 9 , 10}.
Przyjmujac zasade porzadkowania wg. algorytmu „babelkowego” zlozonosc
obliczeniowa dana jest funkcja n

2

/2 + n/2,

czyli: 100/2 + 10/2 = 55 porównan.

W przypadku gdy zbiór ten wstepnie podzielimy na dwa, tzn. {7, 5, 6, 1, 3} ,
{4 , 2, 9, 8, 10} to na wynikowa zlozonosc obliczeniowa skladaja sie trzy
skladniki:
(n/2)

2

/2 + (n/2)/2 + (n/2)

2

/2 + (n/2)/2

+

n

a zatem

5

2

/2 + 5/2 +

5

2

/2 + 5/2

+

10

5

2

+ 5 + 10 = 25 + 5 + 10 = 40 porównan.

Czy dalszy podzial zbioru wyjsciowego na 4 lub 6 podzbiorów zmniejszylby
zlozonosc obliczeniowa?

Jaka jest zlozonosc obliczeniowa algorytmu realizowanego na komputerze
dwuprocesorowym?