2008-03-05
Szczecin
1
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
Zadanie minimalizacji funkcji jednej zmiennej f(x) na zbiorze X,
który jest dowolnym podzbiorem jednowymiarowej przestrzeni
euklidesowej E
1
:
min
x
∈ X ⊂ E
1
f
x
2008-03-05
Szczecin
2
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
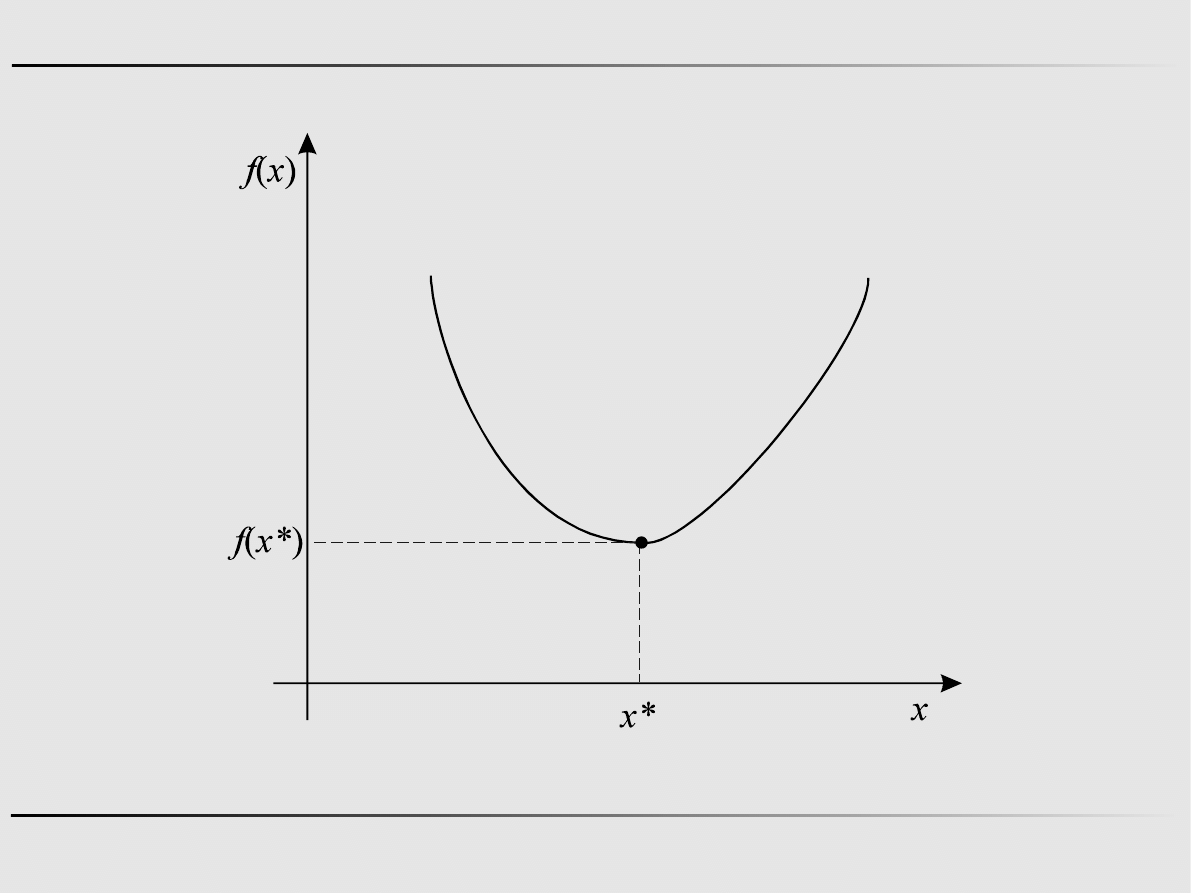
Definicja
Punkt x* jest punktem, w którym funkcja f(x) osiąga minimum
globalne na zbiorze X, jeśli:
dla wszystkich
x
∗
∈ X i
f
x
∗
f x
x
∈ X
2008-03-05
Szczecin
3
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
2008-03-05
Szczecin
4
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
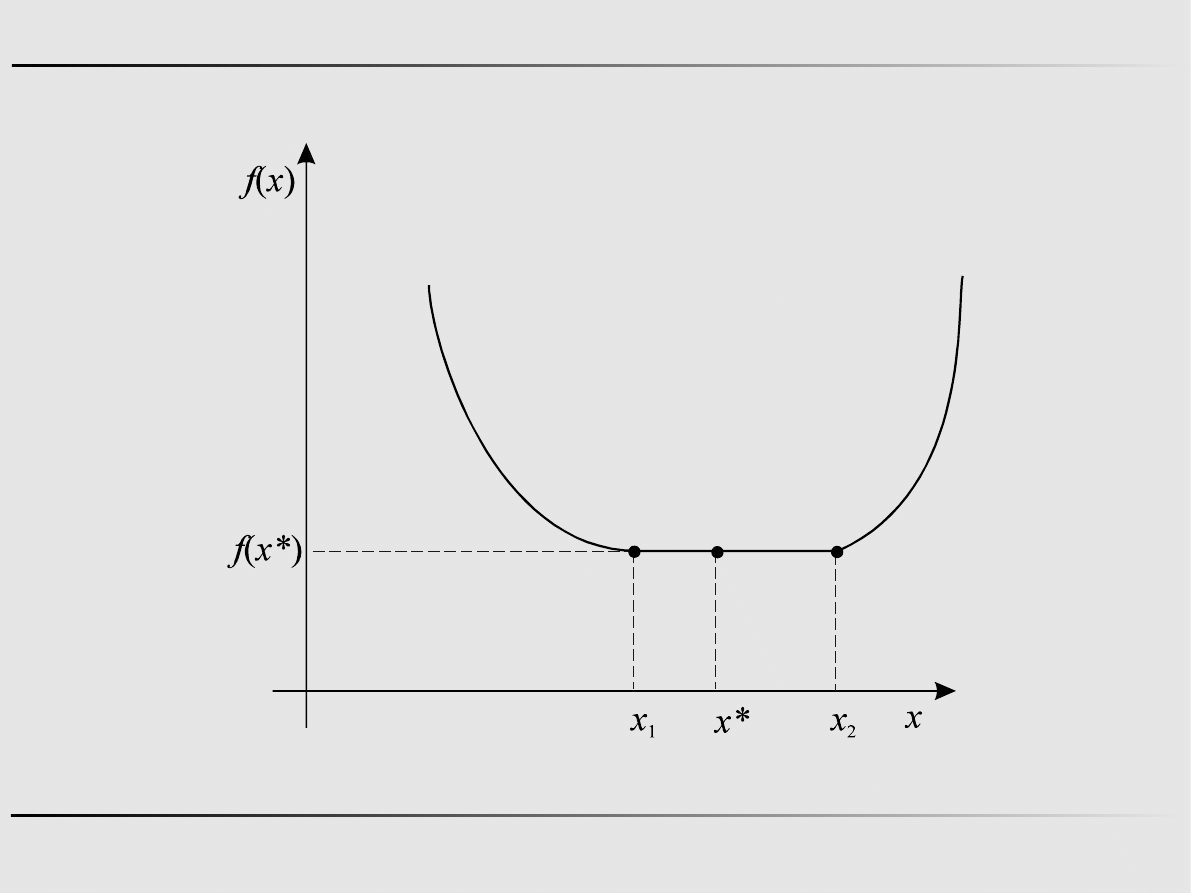
Definicja
Punkt x* jest punktem właściwego minimum globalnego
funkcji f(x) na zbiorze X, jeśli:
dla wszystkich
x
∗
∈ X i
f
x
∗
f x
x
∈ X , x≠x
∗
2008-03-05
Szczecin
5
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
2008-03-05
Szczecin
6
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
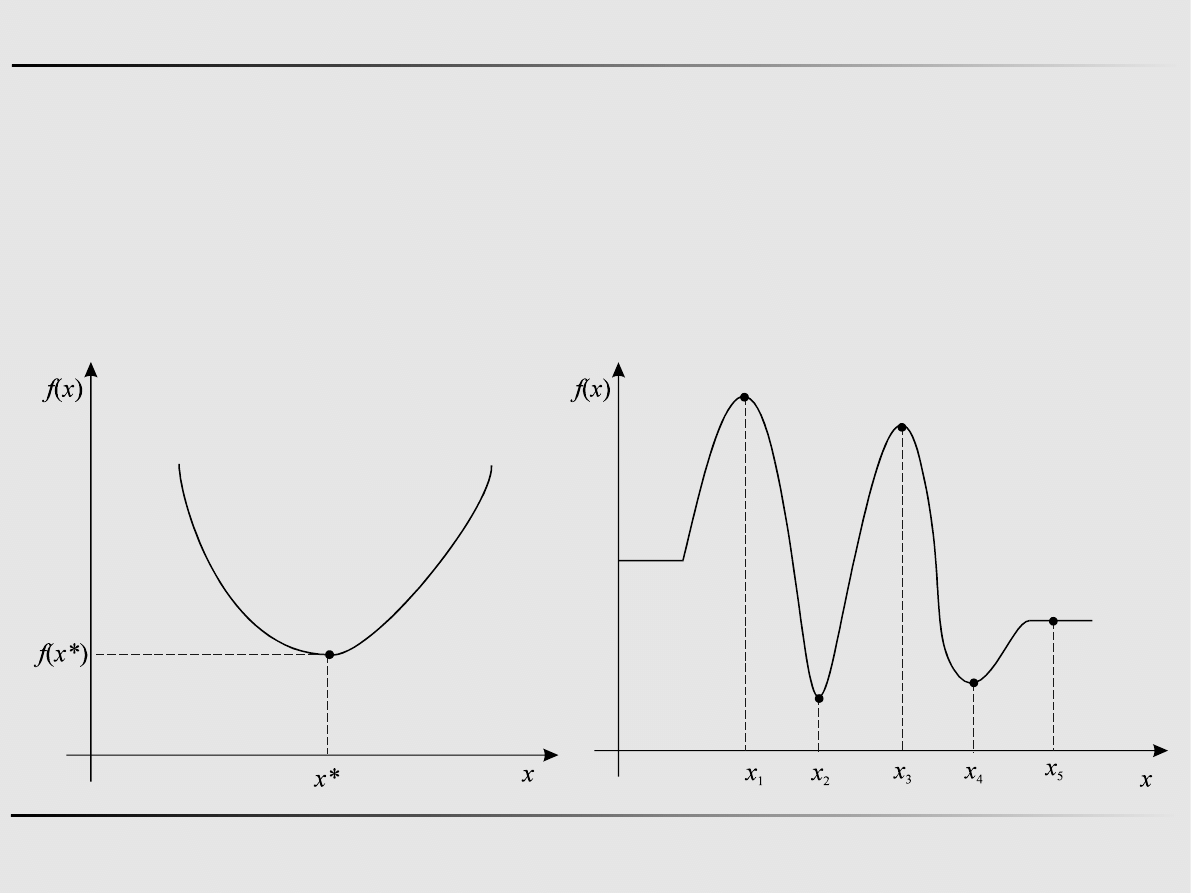
Definicja
Punkt jest punktem, w którym funkcja f(x) osiąga
minimum lokalne na zbiorze X, jeśli przy dowolnym
wystarczająco małym
ε
> 0 dla wszystkich
spełniających warunek
spełniona jest nierówność
x
∗
∈ X
x
≠x
∗
, x
∈ X
∣x−x
∗
∣
f
x
∗
f x
2008-03-05
Szczecin
7
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
Definicja
Funkcję f(x) nazywa się unimodalną na odcinku [a,b], jeśli jest
ona monotoniczna z obydwu stron od jedynego, na
rozpatrywanym
przedziale,
punktu
ekstremum
x*.
2008-03-05
Szczecin
8
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
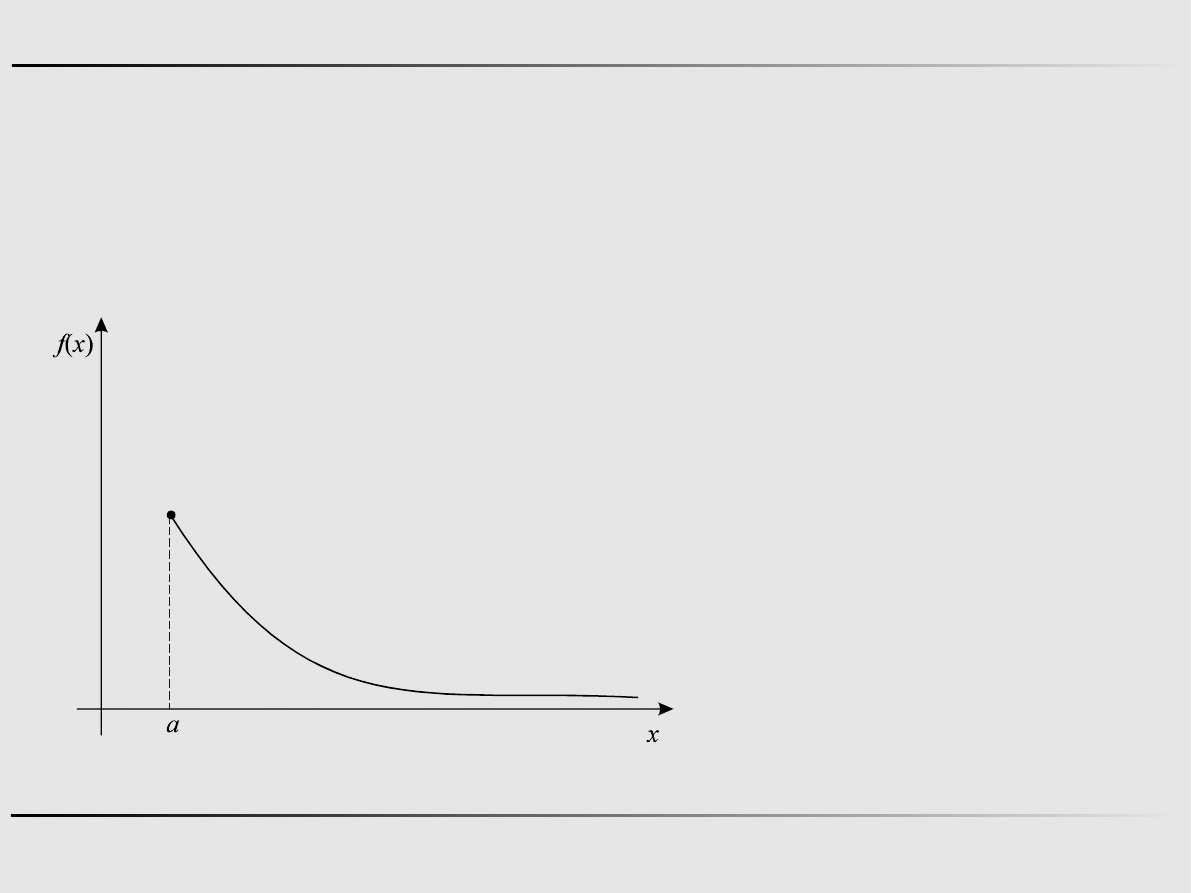
Problem istnienia rozwiązania zadania minimalizacji -
przykład
f
x=e
−x
, X
=
{
x : x
a
}
2008-03-05
Szczecin
9
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
Twierdzenie Weierstrassa
Funkcja ciągła określona na niepustym, domkniętym i
ograniczonym zbiorze osiąga minimum (maksimum) w co
najmniej jednym punkcie tego zbioru.
2008-03-05
Szczecin
10
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
Aby punkt x* był punktem lokalnego minimum dwukrotnie
różniczkowalnej funkcji f(x) na otwartym przedziale (a,b),
konieczne jest spełnienie następujących warunków:
{
df
dx
∣
x
=x
∗
=0
d
2
f
dx
2
∣
x
=x
∗
0
warunek konieczny I rzędu
warunek konieczny II rzędu
2008-03-05
Szczecin
11
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
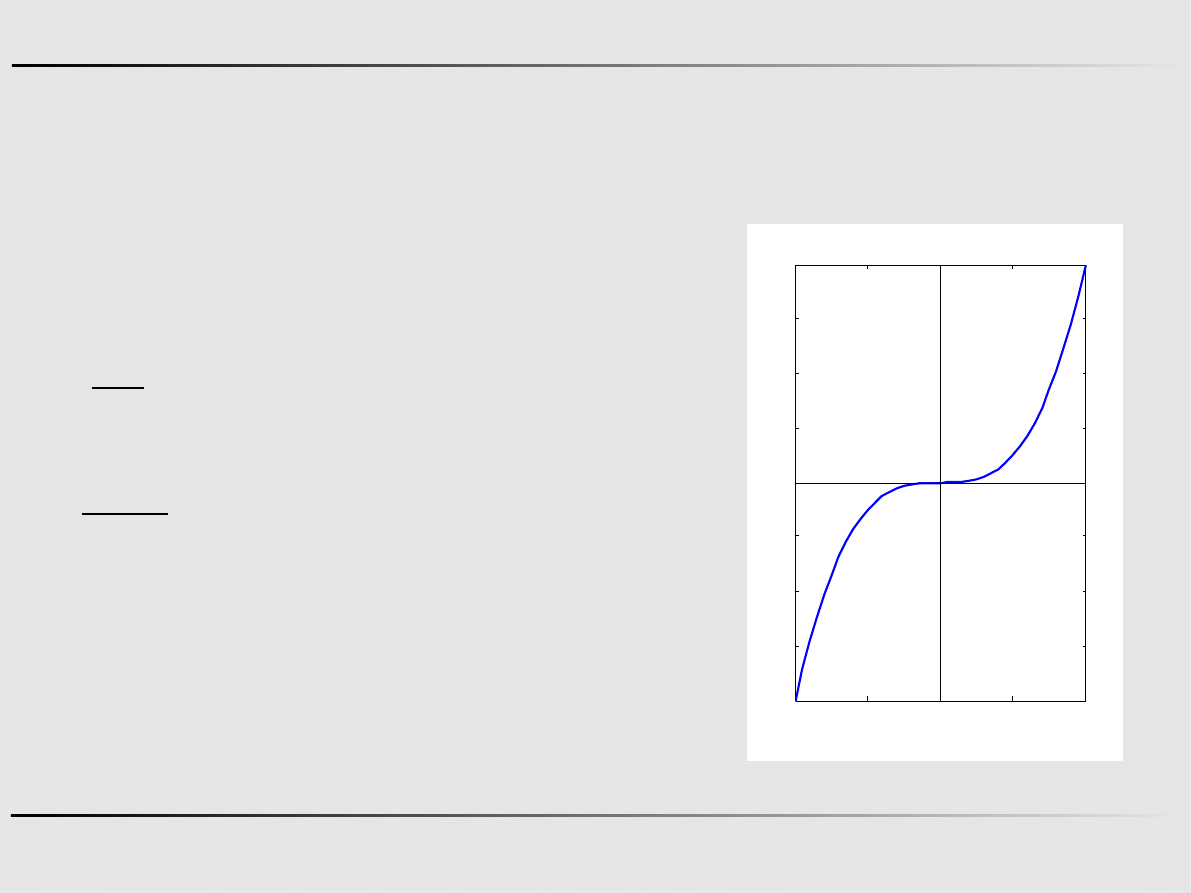
Przykład
Niech f(x)=x
3
. Wówczas punkt x*=0 spełnia konieczne warunki
minimum.
{
df
dx
∣
x
=0
=3 x
2
∣
x
=0
=0
d
2
f
dx
2
∣
x
=0
=6 x
∣
x
=0
=0
Punkt x=0 jest punktem przegięcia,
nie zaś punktem minimum funkcji.
- 2
- 1
0
1
2
- 8
- 6
- 4
- 2
0
2
4
6
8
2008-03-05
Szczecin
12
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
Definicja
Punkt x*, w którym spełniony jest warunek
nazywa się punktem stacjonarnym funkcji f(x).
df
dx
∣
x
=x
∗
=0
2008-03-05
Szczecin
13
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
Niech w punkcie x=x* pochodne funkcji f(x) do rzędu(n-1)
włącznie przyjmują wartość zero, natomiast pochodna rzędu
(n) jest różna od zera. Wówczas następujące warunki są
wystarczającymi warunkami istnienia ekstremum:
1. jeśli n jest liczbą nieparzystą to x* jest punktem przegięcia,
2. jeśli n jest liczbą parzystą to x* jest punktem ekstremum
lokalnego
d
n
f
dx
n
∣
x
=x
∗
0 minimum
d
n
f
dx
n
∣
x
=x
∗
0 maximum
2008-03-05
Szczecin
14
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
df
dx
∣
x
=0
=
d
2
f
dx
2
∣
x
=0
=0
Ponieważ rząd pierwszej różnej się od zera pochodnej
wynosi 3 (liczba nieparzysta), to zgodnie z warunkiem
wystarczającym punkt x*=0 jest punktem przegięcia.
Przykład
f(x)=x
3
d
3
f
dx
3
∣
x
=0
=6
2008-03-05
Szczecin
15
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej
Algorytmy zerowego rzędu:
metoda połowienia,
metoda oparta na liczbach Fibonacciego,
metoda złotego podziału,
aproksymacja kwadratowa.
Algorytmy pierwszego rzędu:
aproksymacja sześcienna,
algorytm stycznych,
algorytm siecznych.
Algorytm drugiego rzędu:
algorytm Newtona.
2008-03-05
Szczecin
16
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
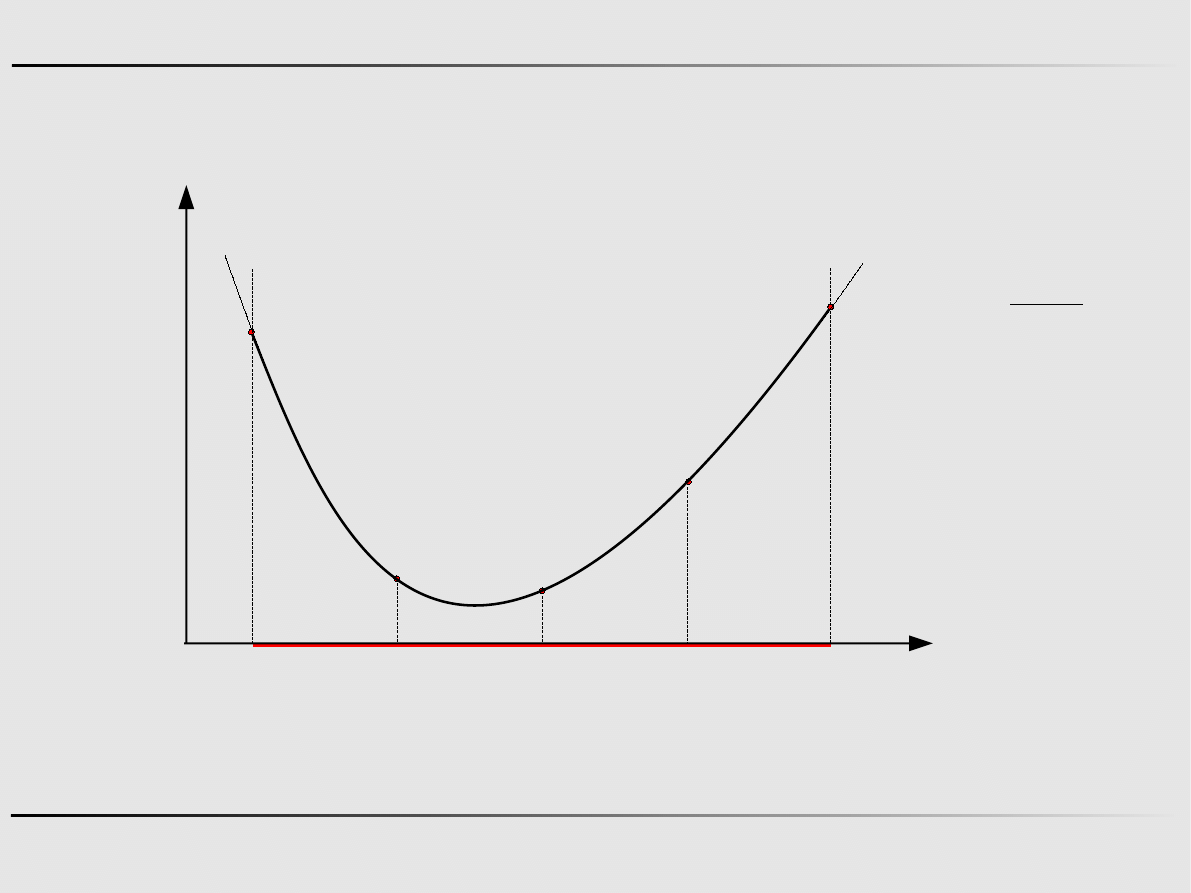
Metoda połowienia
x
m
f(x
m
)
x
1
x
2
f(x
1
)
f(x
2
)
x
m
=
ab
2
x
1
=a0.25⋅L
x
2
=b−0.25⋅L
L
=b−a
L
a
b
f(a)
f(b)
X
f(x)
Krok 0
2008-03-05
Szczecin
17
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
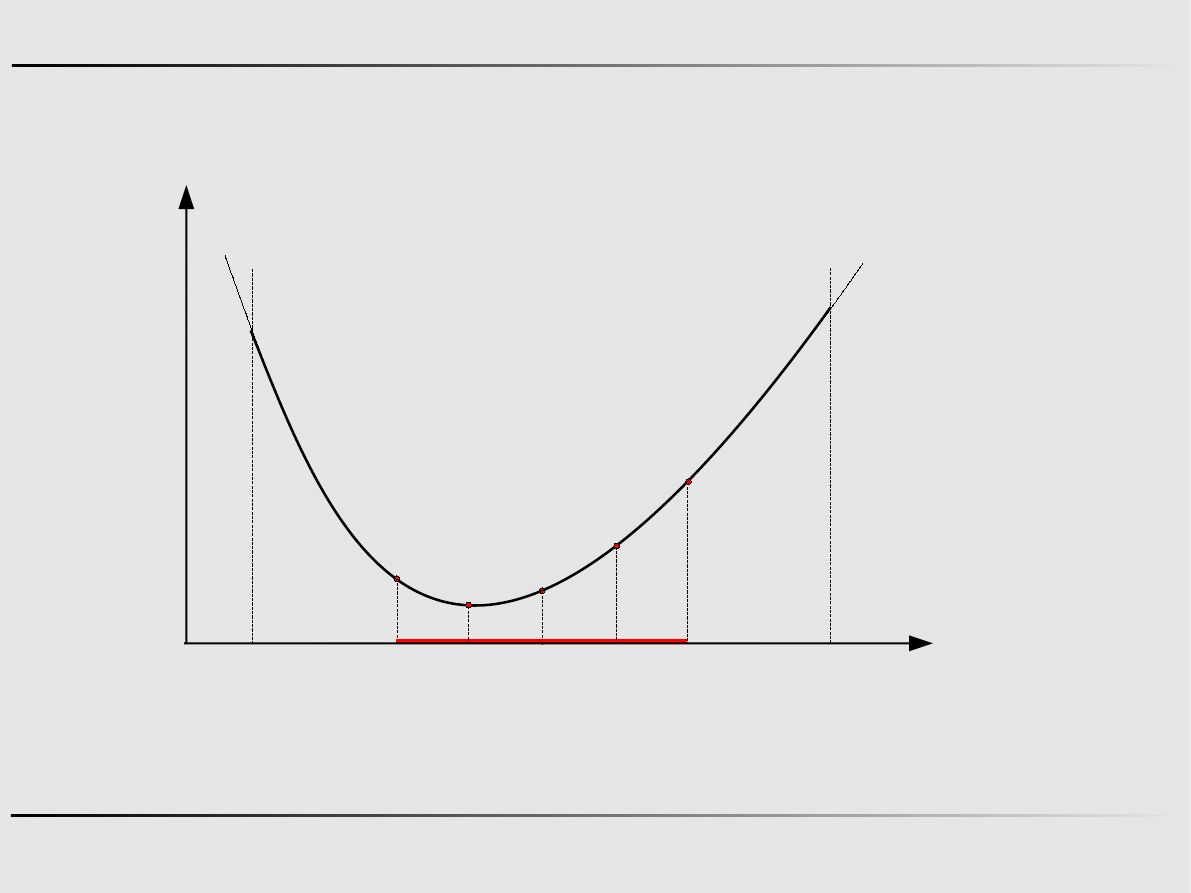
Metoda połowienia
x
m
f(x
m
)
a
b
f(a)
f(b)
L
X
f(x)
Krok 1
x
1
f(x
1
)
x
2
f(x
2
)
x
1
=a0.25⋅L
x
2
=b−0.25⋅L
L
=b−a
2008-03-05
Szczecin
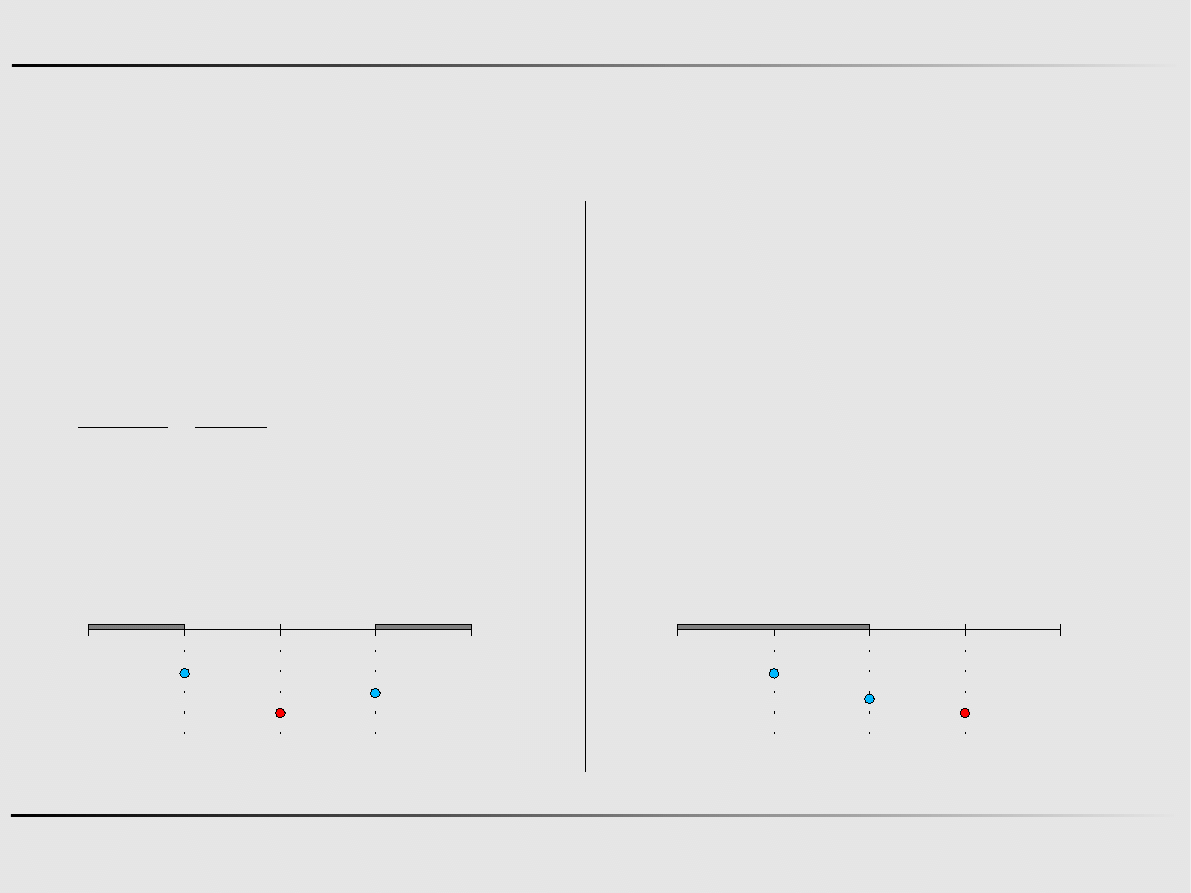
18
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda połowienia - przykład
Znajdz minimum funkcji f
x=5 x
2
−12 x−3, w przedziale 0,2 .
Krok 0
x
m0
=
a
0
b
0
2
=
0
2
2
=1,
f
1=−10
x
10
=a
0
0.25⋅L
0
=00.25⋅2=0.5 , f 0.5=−7.75
x
20
=b
0
−0.25⋅L
0
=2−0.25⋅2=1.5 , f 1.5=−9.75
L
0
=b
0
−a
0
=2−0=2
a
x
10
x
m0
x
20
b
0
a
0
a
0
=0,
f
0=−3
b
0
=2,
f
2=−7
Krok 1
x
11
=a
1
0.25⋅L
1
=0.75 , f 0.75=−9.1875
L
1
=b
1
−a
1
=1.5−0.5=1
a
1
=x
10
=0.5
b
1
=x
20
=1.5
x
21
=b
1
−0.25⋅L
1
=1.25 , f 1.25=−10.1875
x
m1
=x
m0
=1
a
x
11
x
m1
x
21
b
1
a
1
2008-03-05
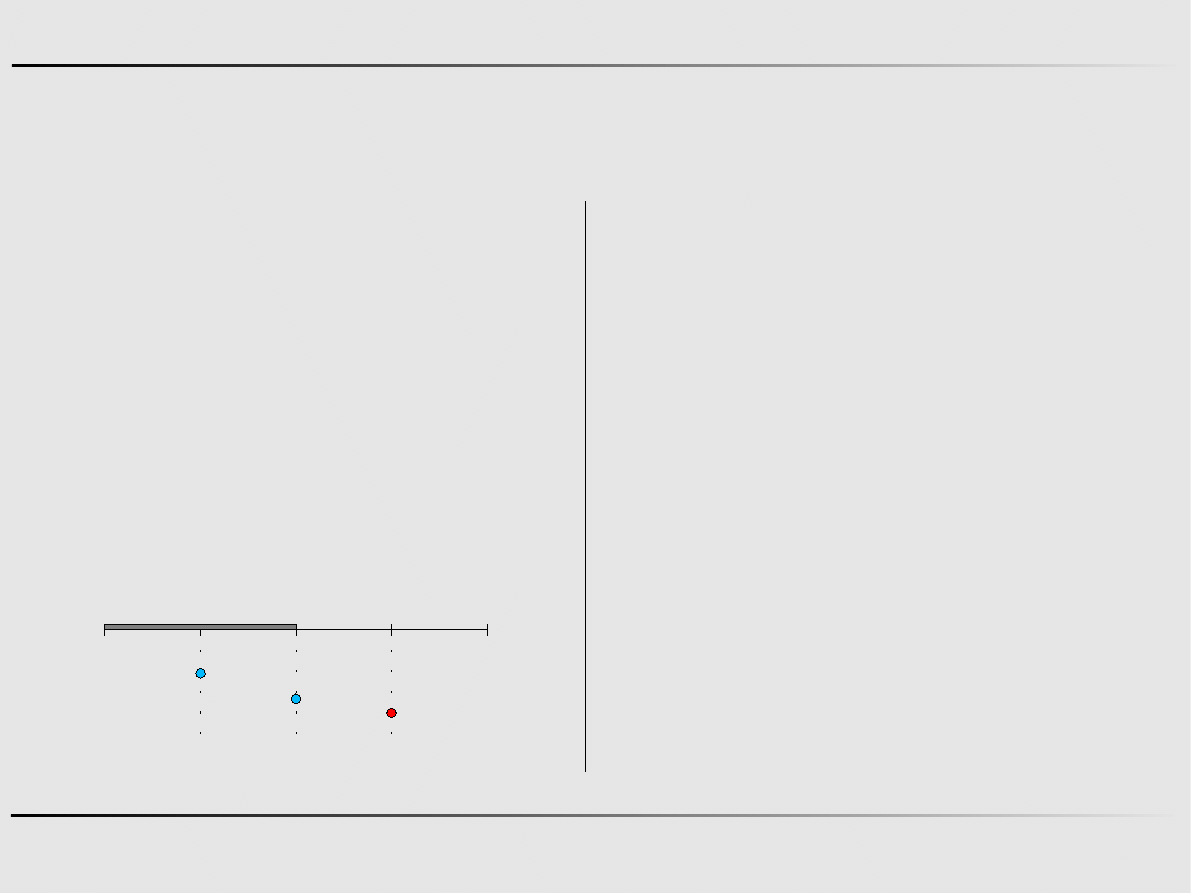
Szczecin
19
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda połowienia - przykład
Znajdz minimum funkcji f
x=5 x
2
−12 x−3, w przedziale 0,2 .
Krok 1
x
11
=a
1
0.25⋅L
1
=0.75 , f 0.75=−9.1875
L
1
=b
1
−a
1
=1.5−0.5=1
a
1
=x
10
=0.5
b
1
=x
20
=1.5
x
21
=b
1
−0.25⋅L
1
=1.25 , f 1.25=−10.1875
x
m1
=x
m0
=1
a
x
11
x
m1
x
21
b
1
a
1
Krok 2
x
12
=
L
2
=b
2
−a
2
=0.5
a
2
=x
m1
=1
b
2
=b
1
=1.5
x
22
=
x
m2
=x
21
=1.25
2008-03-05
Szczecin
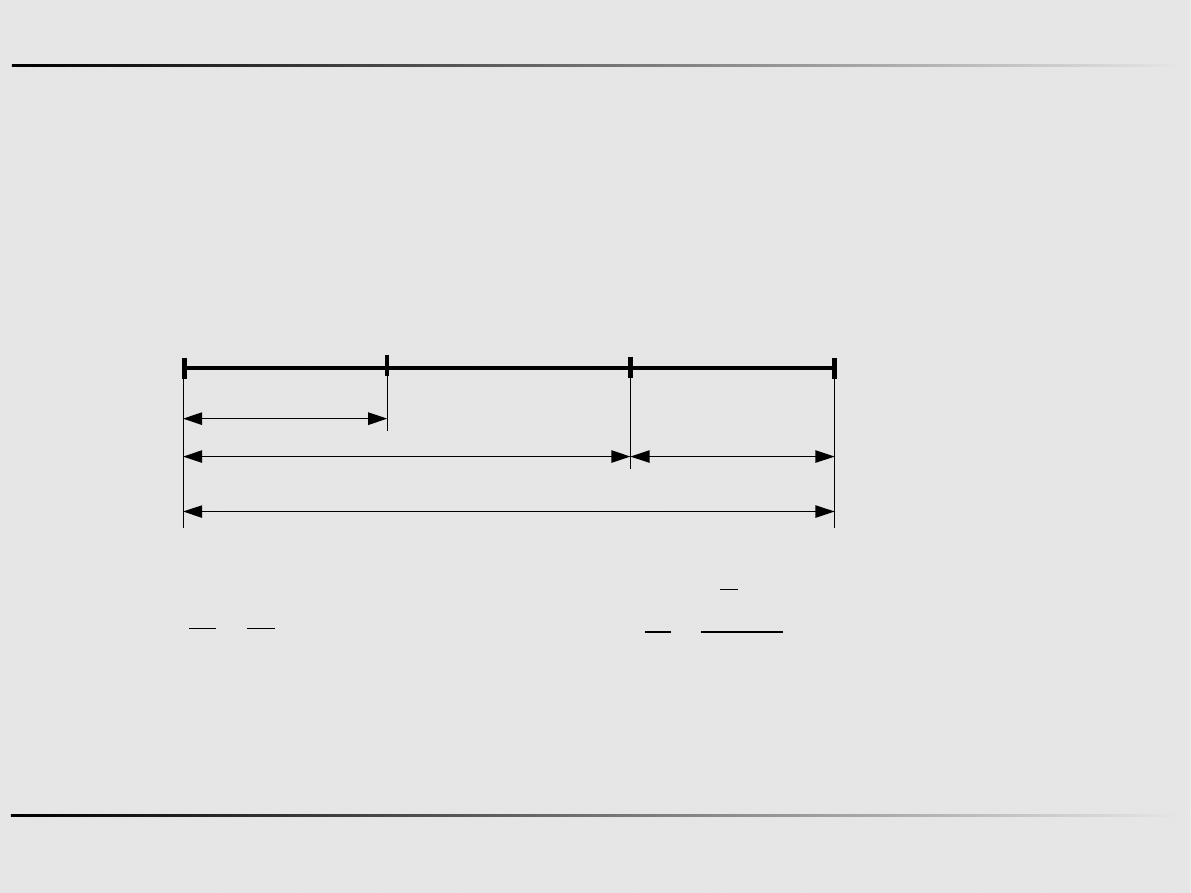
20
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda złotego podziału
Idea złotego podziału odcinka
A
C
B
a
β
b
C
α
B
A
=
C
B
gdzie:
C
=A−B
B
A
=
5
−1
2
≈0.618
2008-03-05
Szczecin
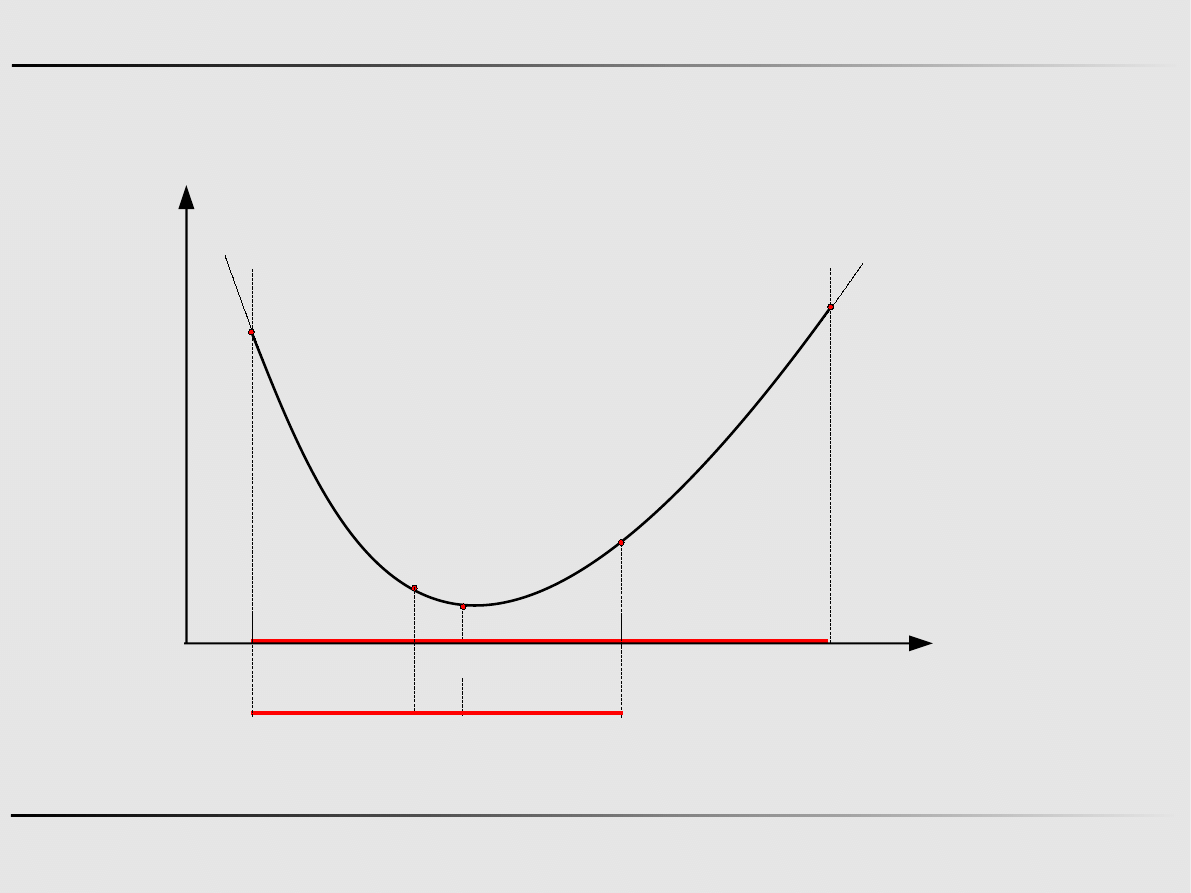
21
Metody optymalizacji, Informatyka
α
β
=b−0.618⋅L
=a0.618⋅L
L
=b−a
L
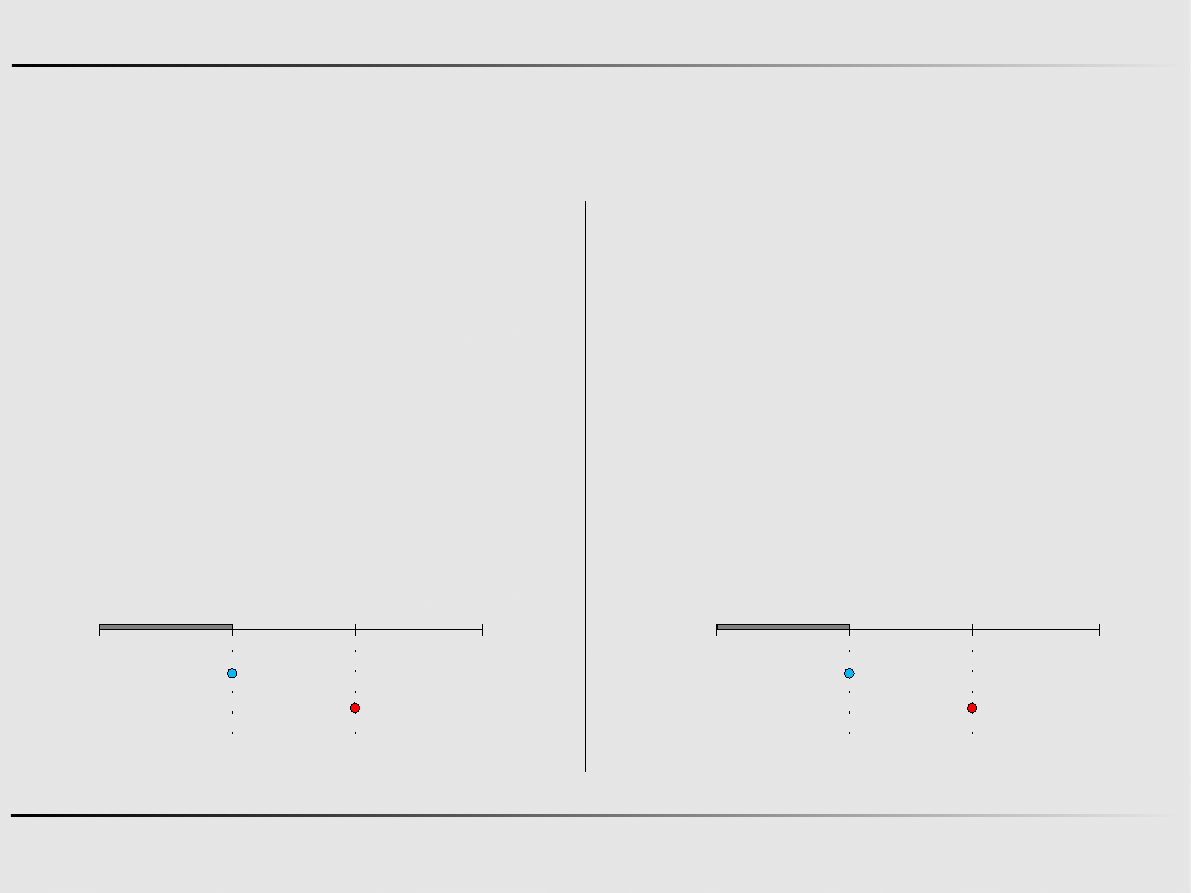
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda złotego podziału
a
b
X
f(x)
f(b)
f(a)
f(
α
)
f(
β
)
f(
α1
)
α1 β1
b1
L1
a1
Krok 0
1=
1=b1−0.618⋅L1
a 1
=a
Krok 1
b 1
=
L1
=b1−a1
2008-03-05
Szczecin
22
Metody optymalizacji, Informatyka
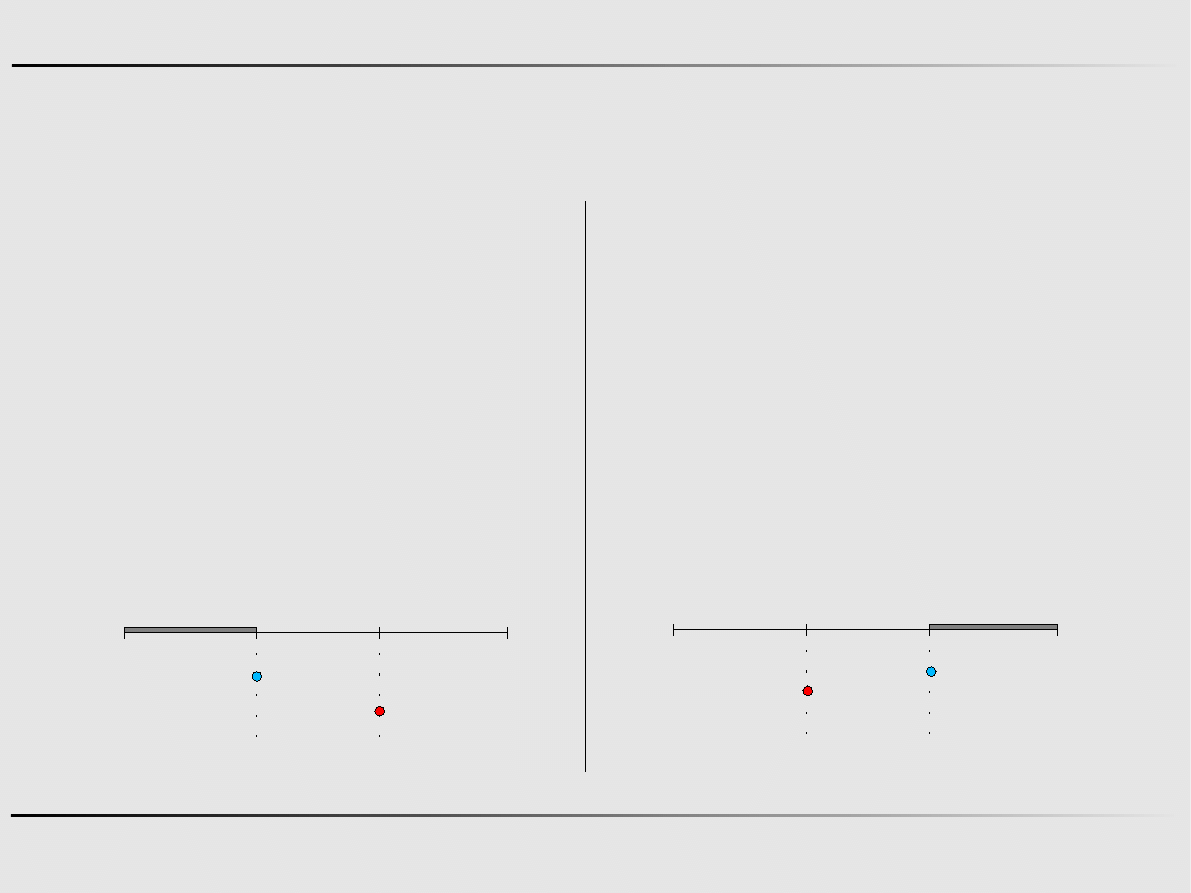
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda złotego podziału - przykład
Znajdz minimum funkcji f
x=5 x
2
−12 x−3, w przedziale 0,2 .
Krok 0
L
0
=b
0
−a
0
=2−0=2
a
α
0
β
0
b
0
a
0
a
0
=0,
f
0=−3
b
0
=2,
f
2=−7
Krok 1
0
=b
0
−0.618⋅L
0
=0.764 , f 0.764=−9.2495
0
=a
0
0.618⋅L
0
=1.236 , f 1.236=−10.1935
L
1
=b
1
−a
1
=1.236
a
1
=
0
=0.764 ,
b
1
=b
0
=2
1
=
0
=1.236
1
=a
1
0.618⋅L
1
=1.5278 , f 1.5278=−9.6626
a
α
1
β
1
b
1
a
1
2008-03-05
Szczecin
23
Metody optymalizacji, Informatyka
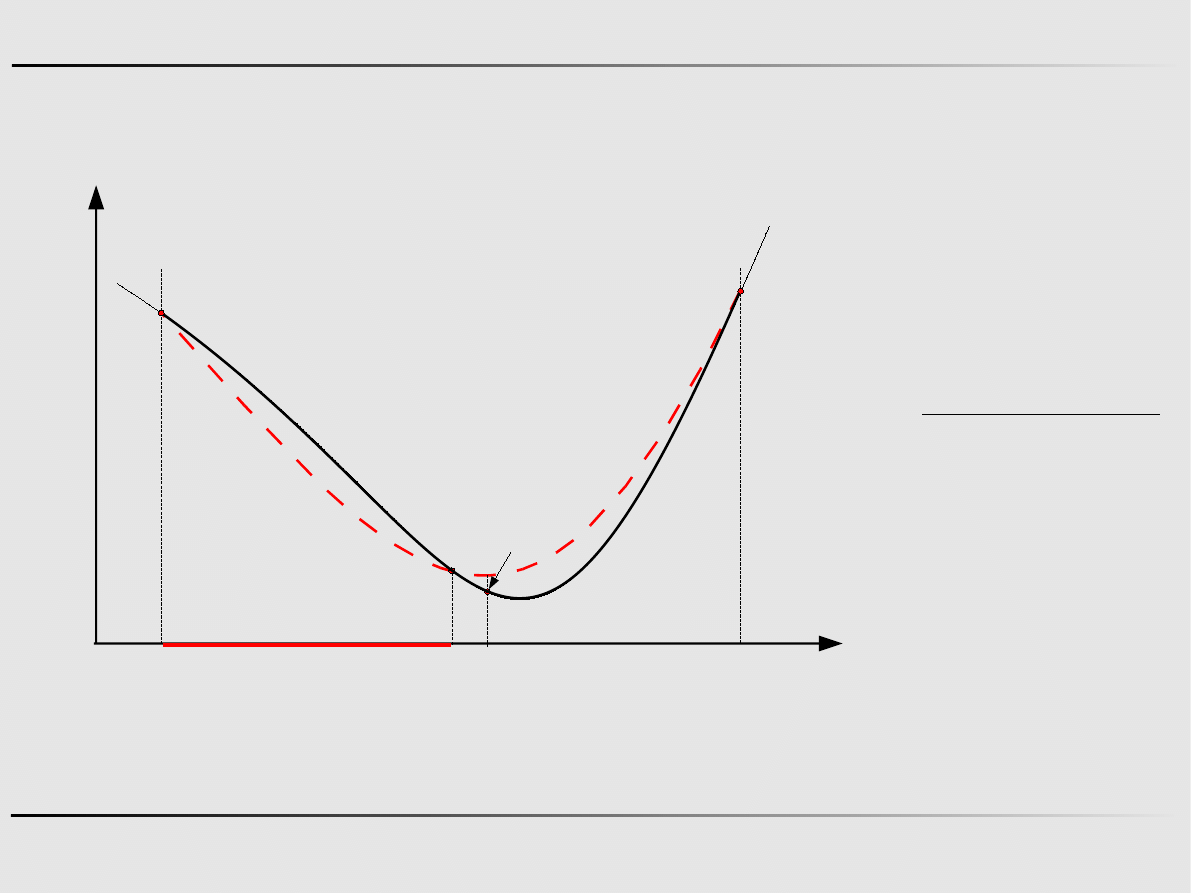
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda połowienia - przykład
Znajdz minimum funkcji f
x=5 x
2
−12 x−3, w przedziale 0,2 .
Krok 1
Krok 2
L
1
=b
1
−a
1
=1.236
a
1
=
0
=0.764 ,
b
1
=b
0
=2
1
=
0
=1.236
1
=a
1
0.618⋅L
1
=1.5278 , f 1.5278=−9.6626
a
α
1
β
1
b
1
a
1
L
2
=b
2
−a
2
=0.764
a
2
=
1
=1.236 ,
b
2
=b
1
=2
2
=
1
=1.5278
2
=a
2
0.618⋅L
2
=1.7082 , f 1.7082=−8.909
a
α
2
β
2
b
2
a
2
2008-03-05
Szczecin
24
Metody optymalizacji, Informatyka
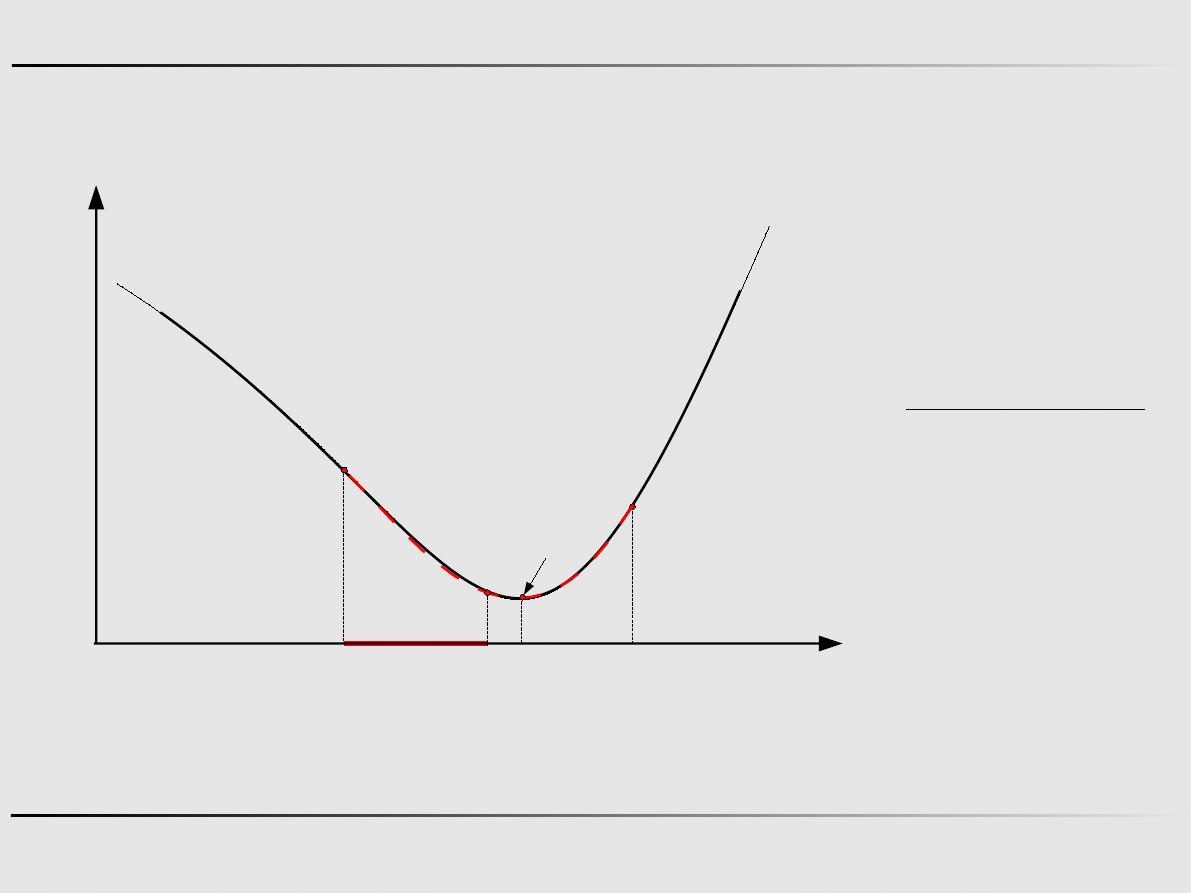
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Aproksymacja kwadratowa funkcji – algorytm Powella
x
1
x
2
x
3
Krok 0
x
2
=x
2
−x
1
=x
3
−x
2
x
m
f(x
m
)
f(x
2
)
x
1
x
3
X
f(x)
f(x
3
)
f(x
1
)
x
m
=x
2
−0.5⋅
f
x
3
− f x
1
f
x
1
−2 f x
2
f x
3
∆
2008-03-05
Szczecin
25
Metody optymalizacji, Informatyka
x
1
x
3
∆
X
f(x)
Krok 1
f(x
3
)
x
2
x
m
f(x
m
)
f(x
2
)
f(x
1
)
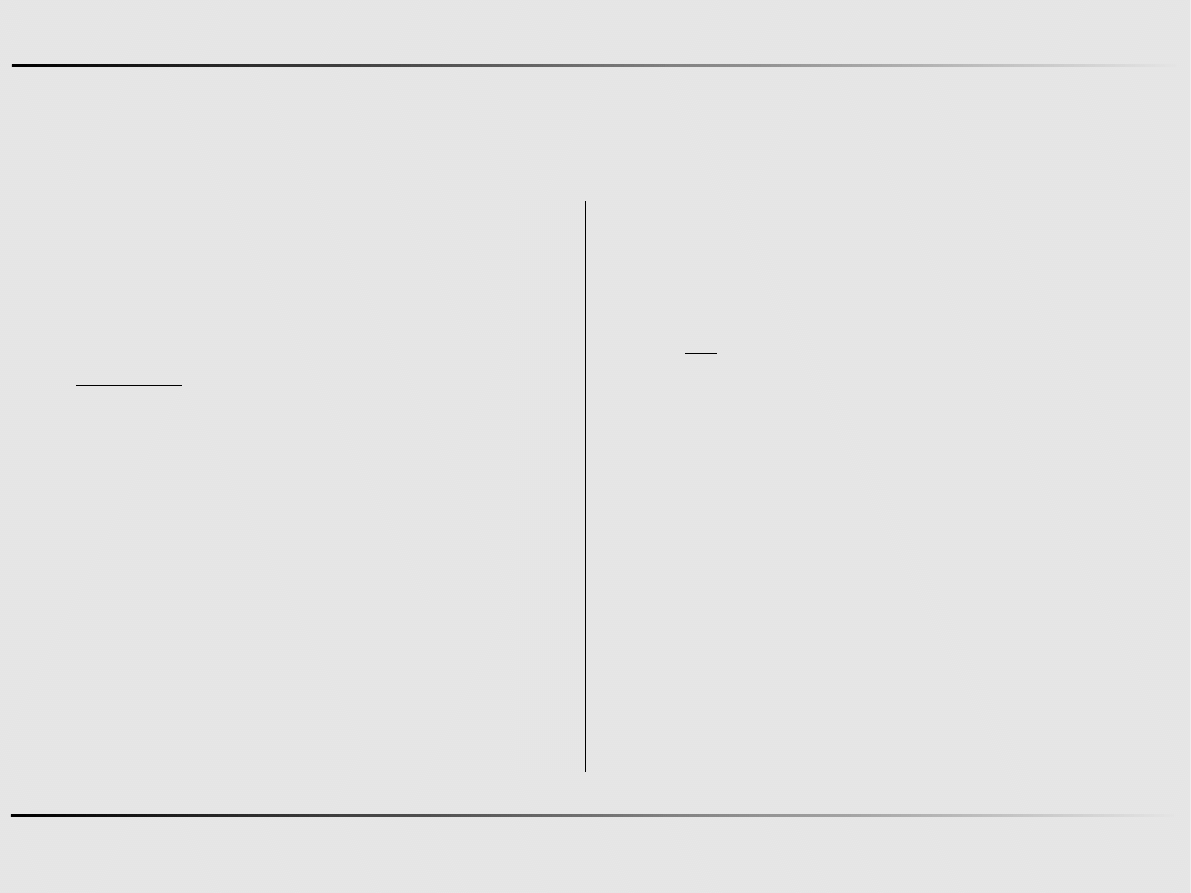
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Aproksymacja kwadratowa funkcji – algorytm Powella
x
1
x
2
x
3
=x
2
−x
1
=x
3
−x
2
x
m
=x
2
−0.5⋅
f
x
3
− f x
1
f
x
1
−2 f x
2
f x
3
2008-03-05
Szczecin
26
Metody optymalizacji, Informatyka
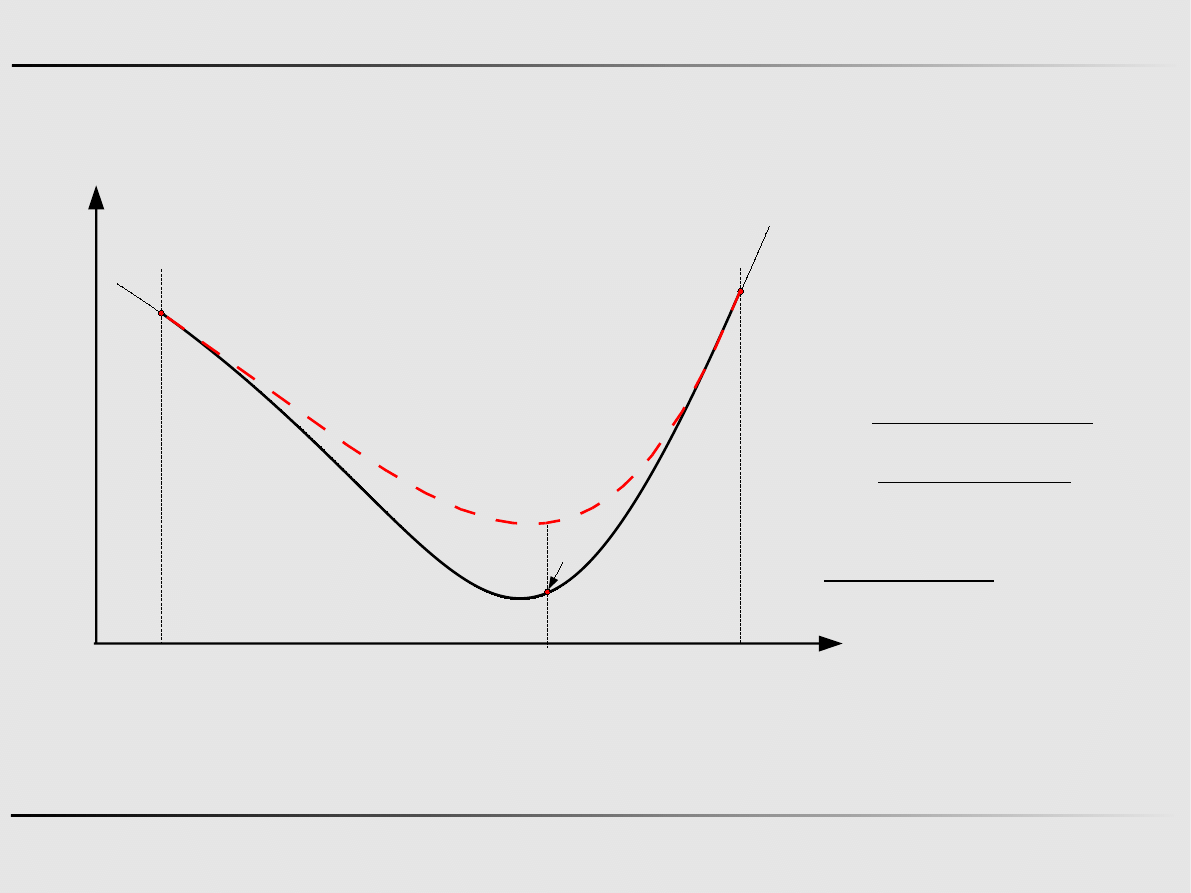
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Aproksymacja kwadratowa - przykład
Znajdz minimum funkcji f
x=5 x
2
−12 x−3, w przedziale 0,2 .
Krok 0
x
20
=
x
10
x
30
2
=1,
f
1=−10
x
10
=0,
f
0=−3
x
30
=2,
f
2=−7
Krok 1
x
m0
=1.2 ,
f
1.2=−10.2
x
21
=x
m0
=1.2 ,
f
1.2=−10.2
x
11
=x
21
−
1
=0.7 ,
f
0.7=−8.95
x
31
=x
22
1
=1.7 ,
f
1.7=−8.95
x
m1
=1.2 ,
f
1.2=−10.2
0
=x
20
−x
10
=1
1
=
0
2
=0.5
2008-03-05
Szczecin
27
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej - algorytmy pierwszego rzędu
Aproksymacja sześcienna funkcji – algorytm Davidona
a
b
f '
a 0, f ' b0
X
f(x)
Krok 0
f(b)
x
m
f(x
m
)
f(a)
x
m
=b−
f '
bQ−Z
f '
b− f ' a2 Q
b−a
Q
=
Z
2
− f ' a⋅f ' b
Z
=
3
[ f a− f b]
b
−a
f ' a f ' b
2008-03-05
Szczecin
28
Metody optymalizacji, Informatyka
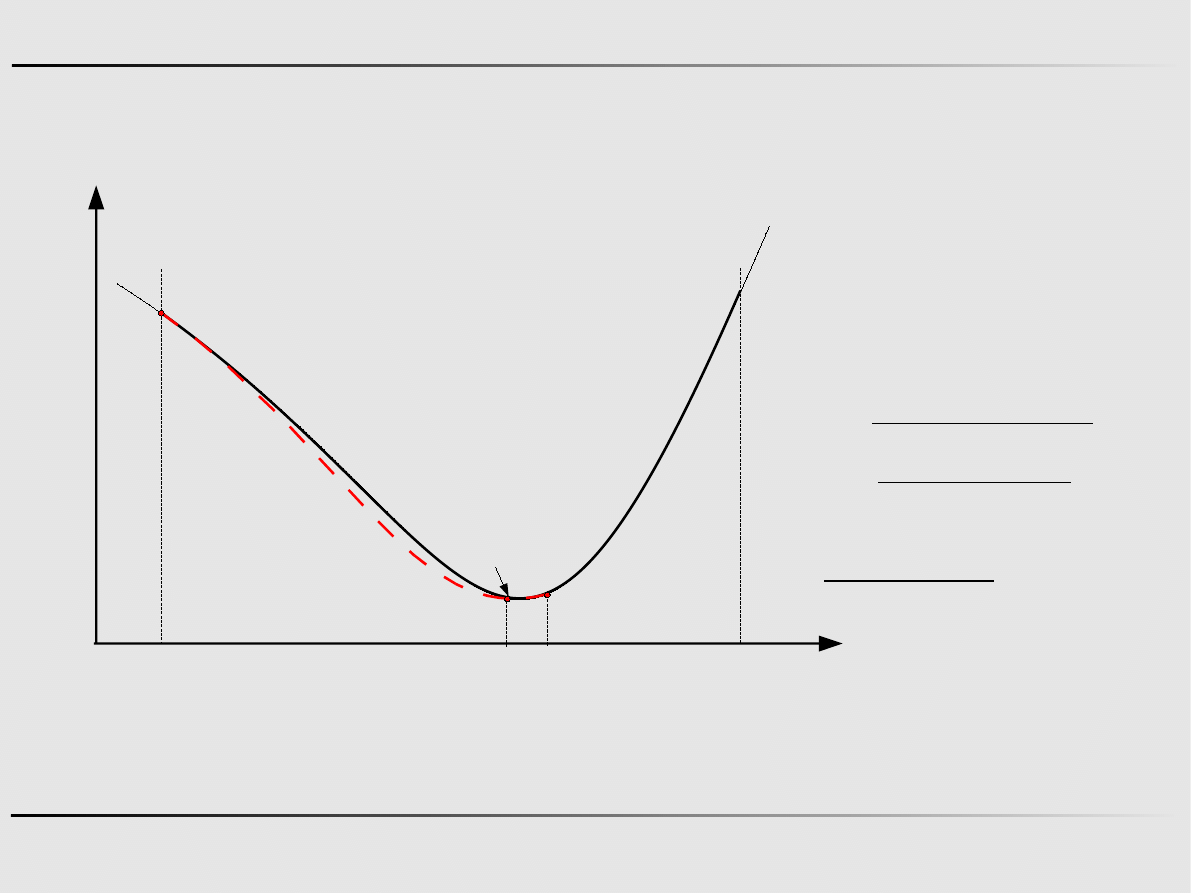
Ekstremum funkcji jednej zmiennej - algorytmy pierwszego rzędu
Aproksymacja sześcienna funkcji – algorytm Davidona
a
X
f(x)
Krok 1
b
f(x
m
)
f(a)
x
m
f(b)
f '
a 0, f ' b0
x
m
=b−
f '
bQ−Z
f '
b− f ' a2 Q
b−a
Q
=
Z
2
− f ' a⋅f ' b
Z
=
3
[ f a− f b]
b
−a
f ' a f ' b
2008-03-05
Szczecin
29
Metody optymalizacji, Informatyka
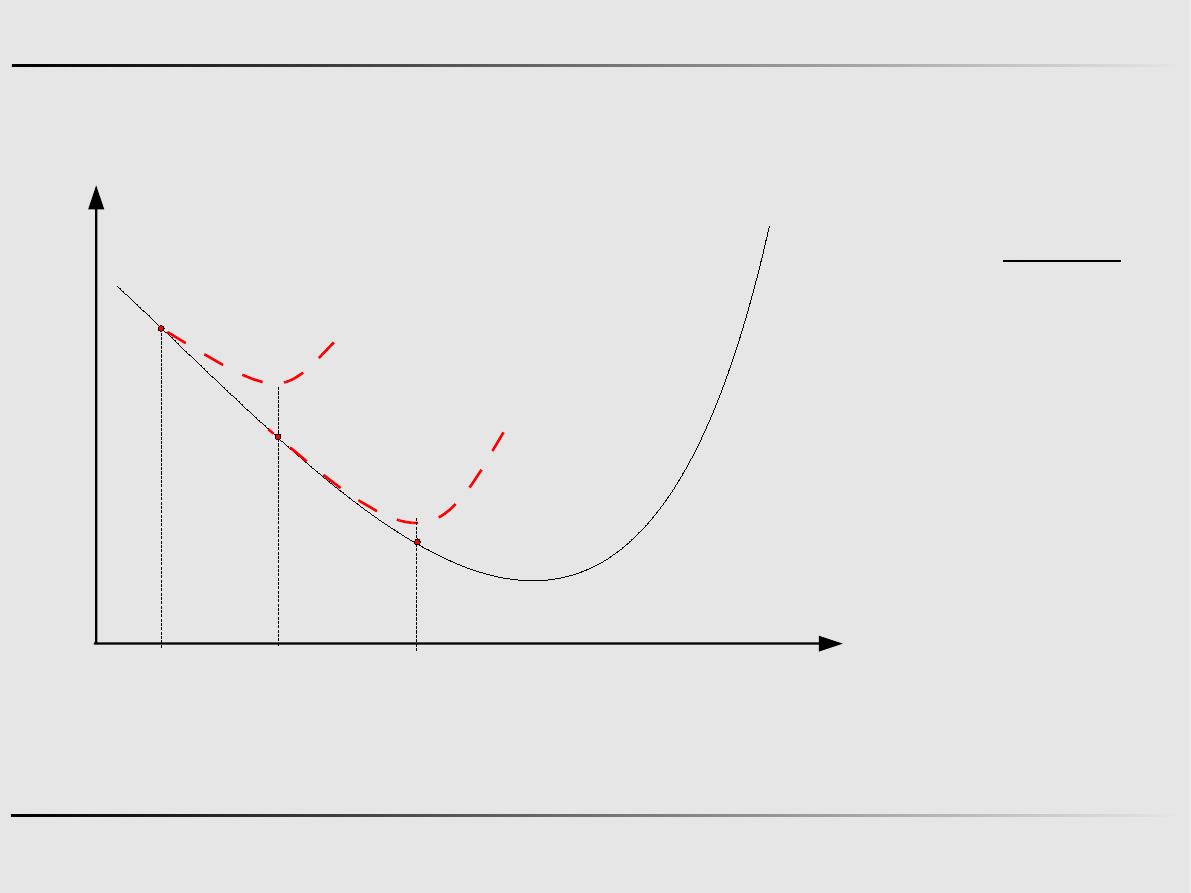
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Aproksymacja sześcienna - przykład
Znajdz minimum funkcji f
x=5 x
2
−12 x−3, w przedziale 0,2 .
Krok 0
f '
x=10 x−12
x
m
=b−
f '
bQ−Z
f '
b− f ' a2 Q
b−a=1.2 , f 1.2=−10.2
Q
=
Z
2
− f ' a⋅f ' b=10
Z
=
3
[ f a− f b]
b
−a
f ' a f ' b=2
a
0
=0,
f
0=−3,
f '
0=−12
b
0
=2,
f
2=−7,
f '
2=8
f '
a 0, f ' b0
f '
1.2=0
2008-03-05
Szczecin
30
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej - algorytmy drugiego rzędu
algorytm Newtona
x
0
X
f(x)
f(x
0
)
x
1
f(x
1
)
x
2
f(x
2
)
x
n
1
=x
n
−
f '
x
n
f ' '
x
n
2008-03-05
Szczecin
31
Metody optymalizacji, Informatyka
Ekstremum funkcji jednej zmiennej - algorytmy zerowego rzędu
Metoda Newtona - przykład
Znajdz minimum funkcji f
x=5 x
2
−12 x−3, w przedziale 0,2 .
Krok 0
f '
x=10 x−12,
f ' '
x=10
a
=0,
f
0=−3,
f '
0=−12,
f ' '
0=10
b
=2,
f
2=−7,
f '
2=8,
f ' '
2=10
x
1
=x
0
−
f '
x
0
f ' '
x
0
=0−−
12
10
=1.2 ,
f
1.2=−10.2
x
0
=a
x
0
=b
x
1
=x
0
−
f '
x
0
f ' '
x
0
=2−
8
10
=1.2 ,
f
1.2=−10.2