
Materiały pomocnicze do wykładu:
Podstawy
Automatyki
Opracował:
doc. dr in . Marek elazny

- 2 -
Wprowadzenie
Niniejsze materiały pomocnicze nie stanowi samodzielnego tekstu
zast puj cego wykład.
Opracowano je, by ułatwi studentom słuchanie wykładów, by
uwolni ich od przenoszenia do własnych notatek wi kszo ci
rysunków i tablic prezentowanych podczas wykładu.
Materiały te stanowi b d istotn pomoc w przygotowaniu
słuchaczy do wicze , laboratoriów i egzaminu, je eli uzupełnione
zostan własnymi notatkami i komentarzami podczas wykładów.
Nale y bowiem pami ta , e wykład zawiera wiele dodatkowych
elementów i tylko jego wysłuchanie, poł czone z mo liwo ci
dyskusji i wyja nienia w tpliwo ci, daje gwarancj dobrego
opanowania przedmiotu PODSTAWY AUTOMATYKI.

- 3 -
Spis Tre ci:
0 POJ CIA PODSTAWOWE…………………………….………………………..….. - 5 -
1 OPIS MATEMATYCZNY UKŁADÓW LINIOWYCH ............................................. - 9 -
2 PODSTAWOWE ELEMENTY LINIOWE ..................................................................15
2.1
Zało enia upraszczaj ce.................................................................................................... 15
2.2
Elementy bezinercyjne (proporcjonalne)......................................................................... 17
2.3
Elementy inercyjne pierwszego rz du.............................................................................. 19
2.4
Elementy całkuj ce ............................................................................................................ 22
2.5
Elementy ró niczkuj ce..................................................................................................... 24
2.6
Elementy oscylacyjne......................................................................................................... 26
2.7
Elementy opó niaj ce ........................................................................................................ 30
3 UKŁADANIE SCHEMATÓW BLOKOWYCH............................................................32
3.1
Zasady budowy schematów blokowych ........................................................................... 32
3.2
W zły informacyjne i sumacyjne...................................................................................... 32
3.3
Przekształcanie schematów blokowych............................................................................ 36
3.4
Przykłady układania (tworzenia) schematów blokowych .............................................. 41
4 CHARAKTERYSTYKI CZ STOTLIWO CIOWE .....................................................43
4.1
Transmitancja widmowa. Rodzaje charakterystyk cz stotliwo ciowych. .................... 43
4.2
Logarytmiczne charakterystyki amplitudowa i fazowa elementu inercyjnego
pierwszego rz du............................................................................................................................. 45
4.3
Charakterystyka amplitudowo-fazowa oraz logarytmiczne charakterystyki elementu
ró niczkuj cego rzeczywistego ...................................................................................................... 48
4.4
Charakterystyka amplitudowo-fazowa oraz logarytmiczne charakterystyki
amplitudowa i fazowa elementu drugiego rz du.......................................................................... 49
4.5
Logarytmiczne charakterystyki cz stotliwo ciowe szeregowego poł czenia
elementów ........................................................................................................................................ 54
5 UKŁADY LINIOWE DYSKRETNE (IMPULSOWE) .................................................55
5.1
Poj cia podstawowe ........................................................................................................... 55
6 REGULATORY PRZEMYSŁOWE..............................................................................60
6.1
Regulator PID..................................................................................................................... 60
6.2
Regulatory mikroprocesorowe.......................................................................................... 62
6.3
Wykorzystanie sterowników PLC do regulacji............................................................... 64
6.4
Regulacja lub sterowanie w trybie „soft-control”........................................................... 64
7 WYMAGANIA STAWIANE UKŁADOM AUTOMATYKI..........................................65
7.1
Stabilno ............................................................................................................................ 65
7.2
Dokładno statyczna......................................................................................................... 79
7.3
Jako dynamiczna ............................................................................................................ 81

- 4 -
8 DOBÓR RODZAJU I NASTAW REGULATORÓW ...................................................85
8.1
Wybór rodzaju (typu) regulatora..................................................................................... 85
8.2
Dobór nastaw regulatora................................................................................................... 86
9 STRUKTURY UKŁADÓW REGULACJI....................................................................88
9.1
Uogólniona struktura jednoobwodowa............................................................................ 88
9.2
Regulacja kaskadowa ........................................................................................................ 88
9.3
Regulacja stosunku ............................................................................................................ 90
9.4
Kaskadowa regulacja stosunku ........................................................................................ 91
9.5
Układy z pomocnicz korekcj dynamiczn : .................................................................. 91
9.6
Układy zamkni to-otwarte................................................................................................ 92
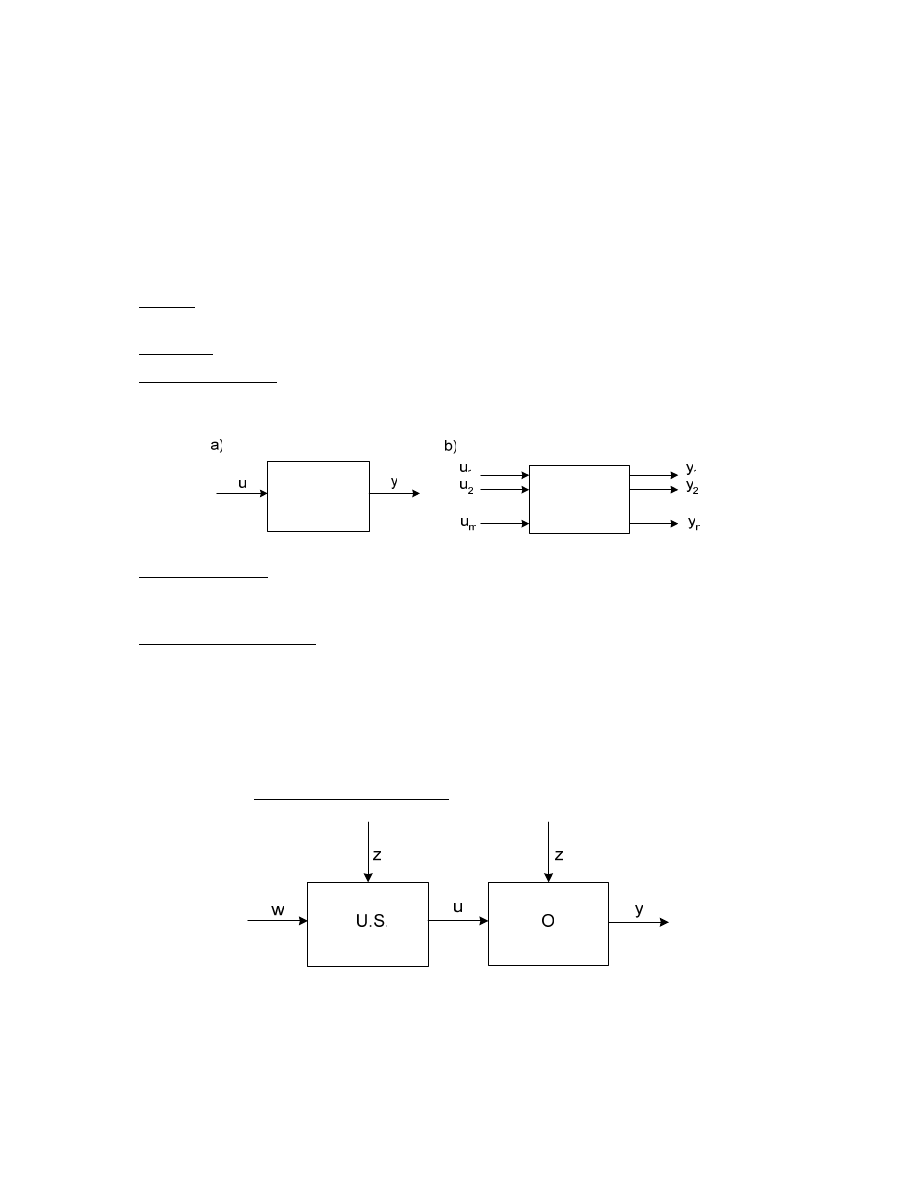
- 5 -
0.
POJ CIA PODSTAWOWE
Szeroki zakres zastosowa automatyki zmusza do u ywania bardzo ogólnych poj
podstawowych i reprezentacji graficznej w postaci schematów blokowych, które to poj cia i
schematy mog by stosowane zarówno przy omawianiu zagadnie teoretycznych jak i
aplikacji przemysłowych, medycznych, wojskowych lub w dowolnej innej - automatyzowanej
- dziedzinie działalno ci człowieka.
Kilka zasadniczych poj :
Sygnał - wielko fizyczna wyst puj ca w procesie sterowania b d ca no nikiem
informacji.
Informacja - warto lub kształt przebiegu sygnału.
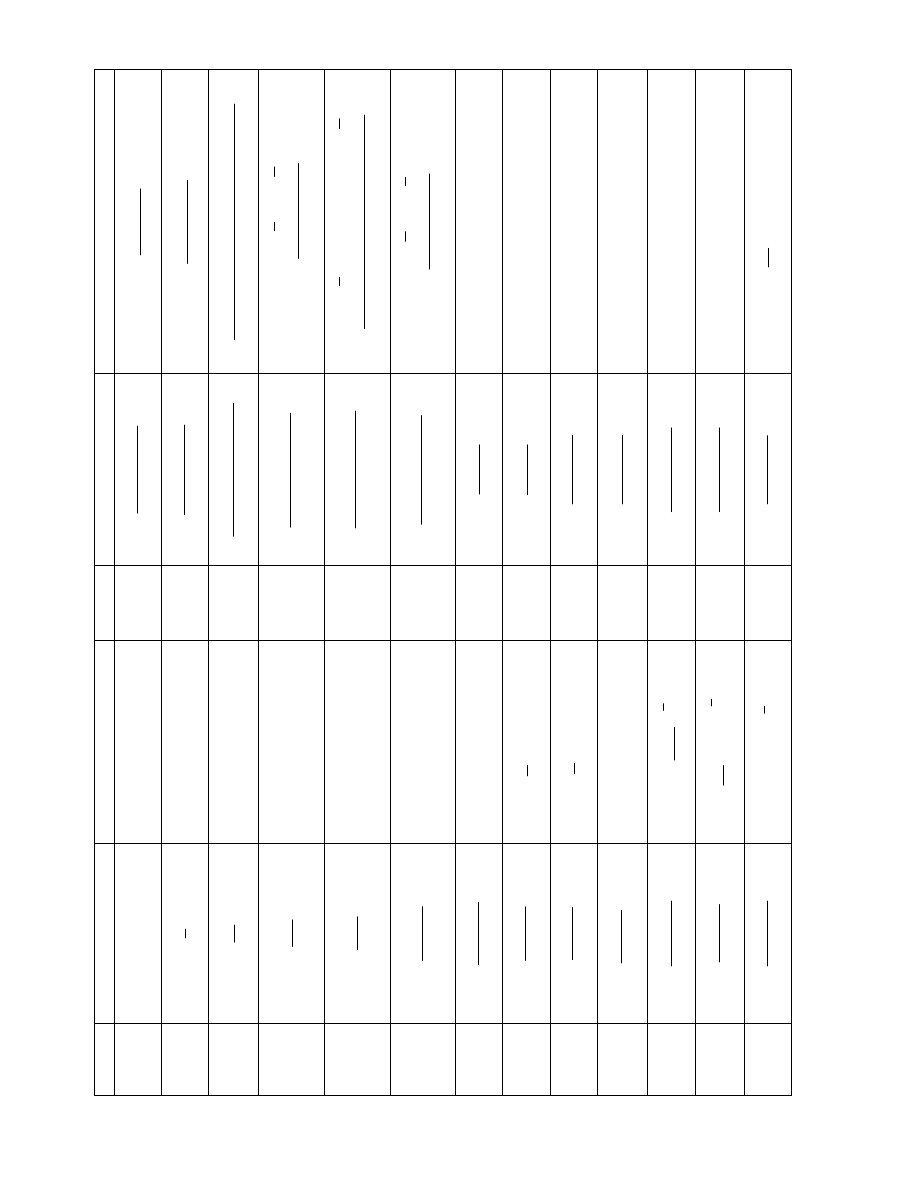
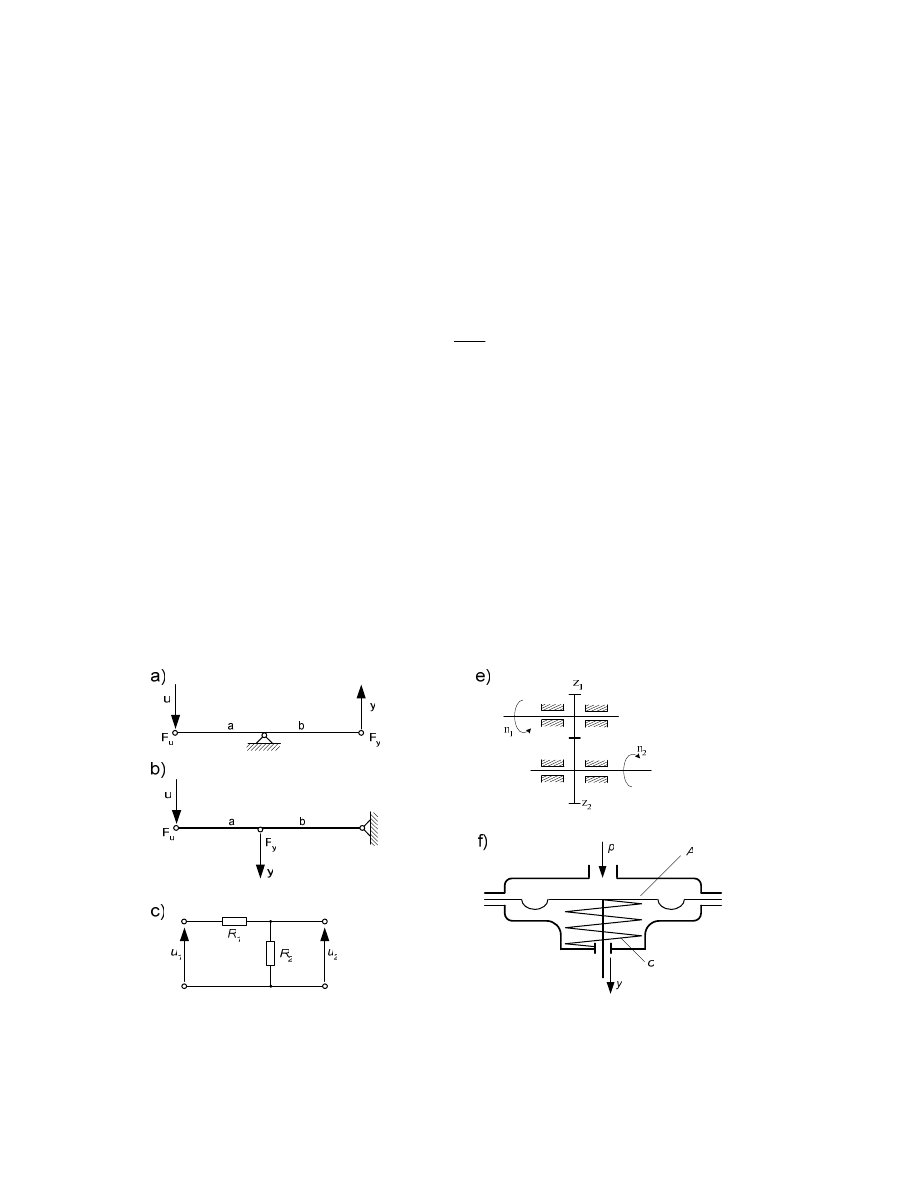
Element automatyki (człon) - podzespół, zespół, przyrz d lub urz dzenie. w którym mo na
wyró ni sygnał wej ciowy i sygnał wyj ciowy - rys. a, lub sygnały wej ciowe i wyj ciowe -
rys. b.
Układ automatyki - zespół wzajemnie powi zanych elementów bior cych udział w
sterowaniu automatycznym danego procesu (uporz dkowany zgodnie z kierunkiem
przekazywania sygnałów)
Sterowanie automatyczne - oddziaływanie na proces, którego zamierzony przebieg chcemy
uzyska bez udziału człowieka, za pomoc urz dze nazywanych ogólnie aparatur
automatyki.
Wyró nia si :
−
sterowanie w układzie otwartym
−
sterowanie w układzie zamkni tym
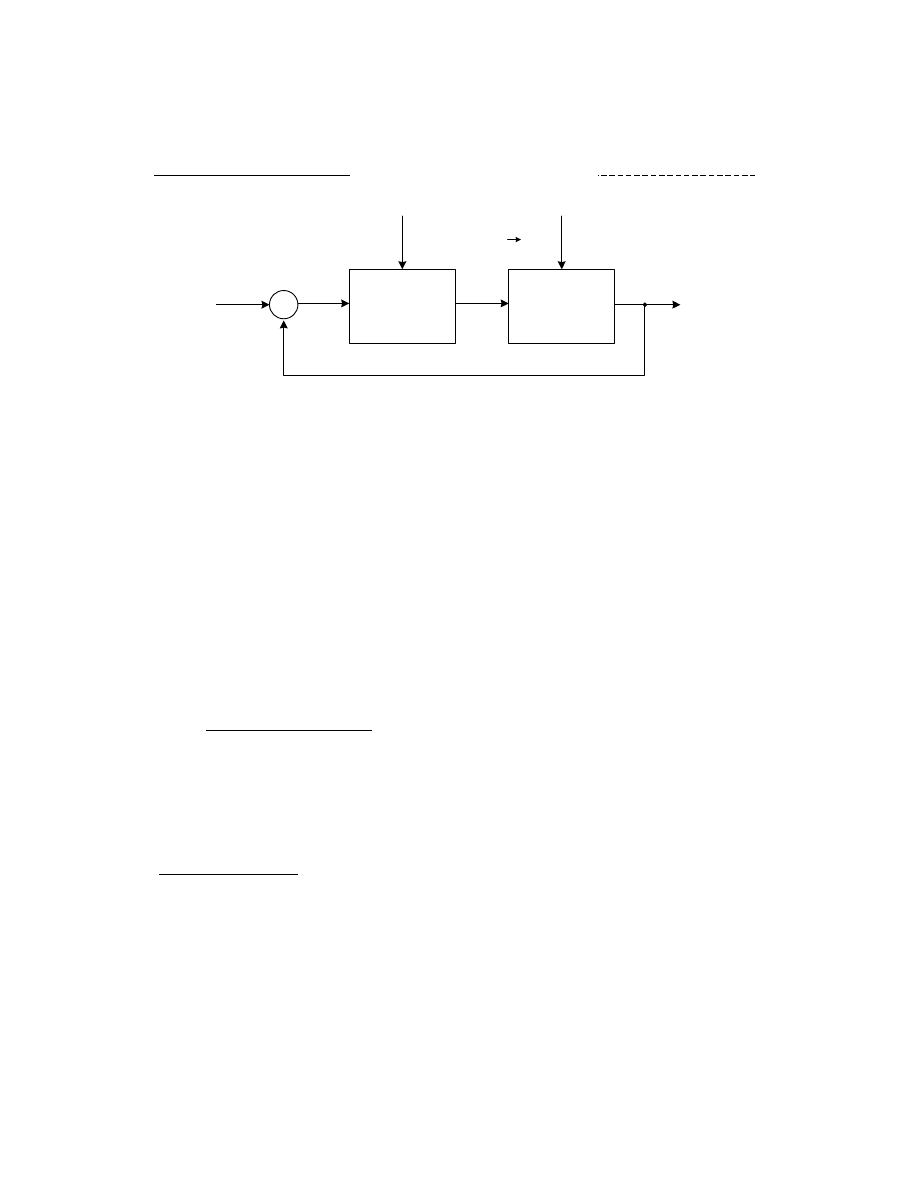
Ogólny schemat otwartego układu sterowania przedstawiono ni ej:
Nomenklatura:
w - warto zadana wielko ci sterowanej
u - sygnał steruj cy
y - wielko sterowana
z - sygnały zakłócaj ce (zakłócenia)
- 6 -
U.S. - urz dzenie steruj ce
O - obiekt (proces) podlegaj cy sterowaniu
Zamkni ty układ sterowania, nazywany cz sto układem ze sprz eniem zwrotnym,
ma nast puj cy schemat blokowy:
gdzie: e - odchyłka (uchyb) sterowania
Tor główny wskazuje zawsze zasadnicz wielko wej ciow układu (w tym przypadku w)
i wielko wyj ciow y. Tor ten ilustruje zwykle przepływ głównego strumienia materiału lub
energii w układzie.
Tor sprz enia zwrotnego słu y do przekazywania informacji. Zapotrzebowanie
energetyczne tego toru jest zwykle pomijanie małe.
Ze wzgl du na zadanie realizowane przez układ wyró nia si :
a)
układy stabilizuj ce
b)
układy programowe
c)
układy nad ne
d)
inne
Te grupy zamkni tych układów sterowania, zwłaszcza dwie pierwsze, nazywa si cz sto
układami regulacji automatycznej. Poci ga to za sob zmian nazewnictwa:
y - wielko regulowana
w - warto zadana wielko ci regulowanej
e - odchyłka regulacji
R - regulator (zamiast urz dzenia steruj cego)
O - obiekt regulacji (proces regulowany)
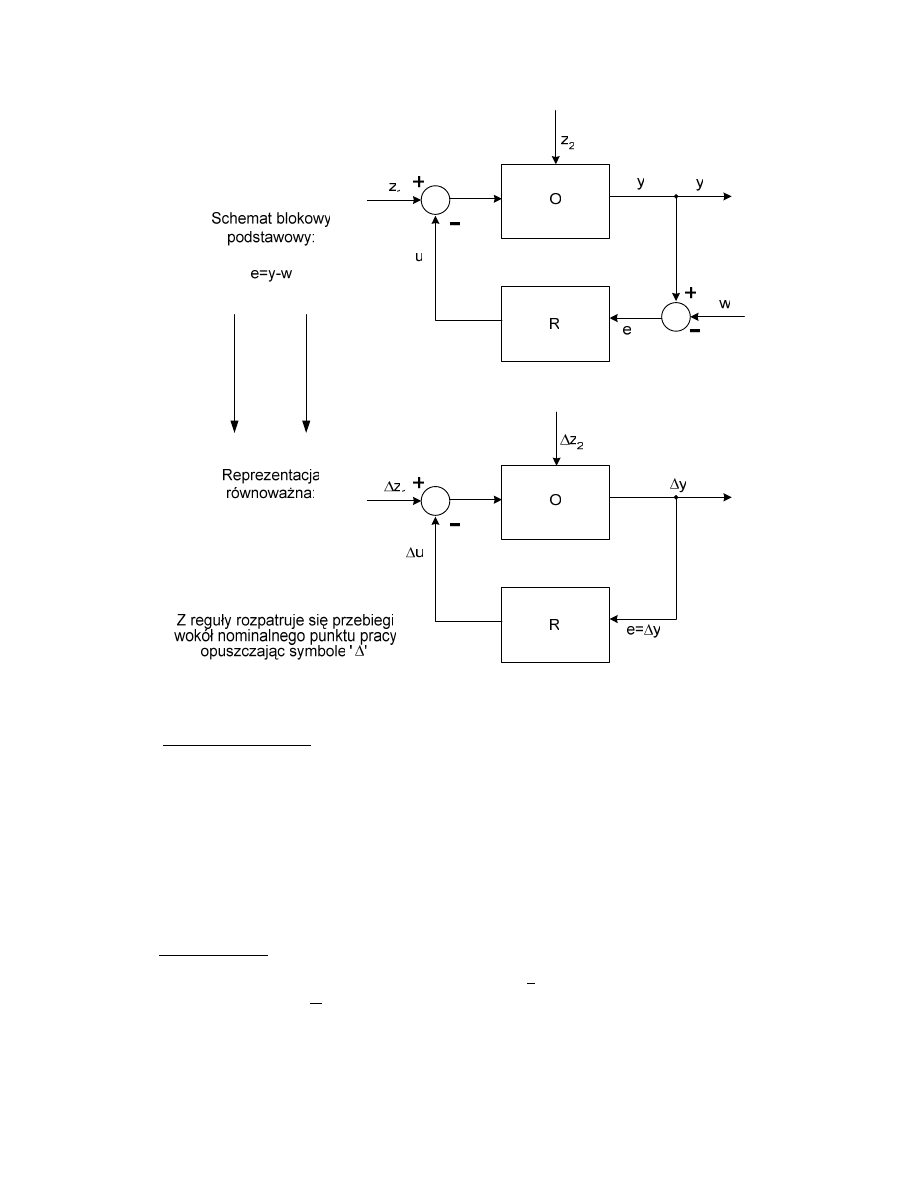
A. Układy stabilizuj ce (układy regulacji stałowarto ciowej), w=const.
Zadaniem układu jest utrzymanie mo liwie stałej, po danej warto ci wielko ci wyj ciowej
oraz minimalizacja wpływu zakłóce na t wielko .
Cz sto główne zakłócenia wchodz wraz ze strumieniem materiału lub energii na obiekt,
tworz c tor główny od z
1
do y.
- 7 -
Przykłady: regulacja ci nienia, poziomu cieczy, nat enia przepływu, pH itd.
B. Układy programowe (regulacji programowej, sterowania programowego), w=w(t).
Zadaniem układu jest uzyskanie przewidzianych okre lonym programem czasowym zmian
wielko ci regulowanej (sterowanej).
Dla powolnych zmian w(t), np. regulacja temperatury w budynku, schemat blokowy ma
posta jak dla p. „A”
,
dla szybkich zmian w(t) - jak dla p. ,.C’”.
Inne przykłady: programowa regulacja temperatury w piecu hartowniczym, w autoklawie,
programowa regulacja jednej lub kilku wielko ci w procesie rozruchu (stopniowe
dochodzenie do nominalnego stanu pracy).
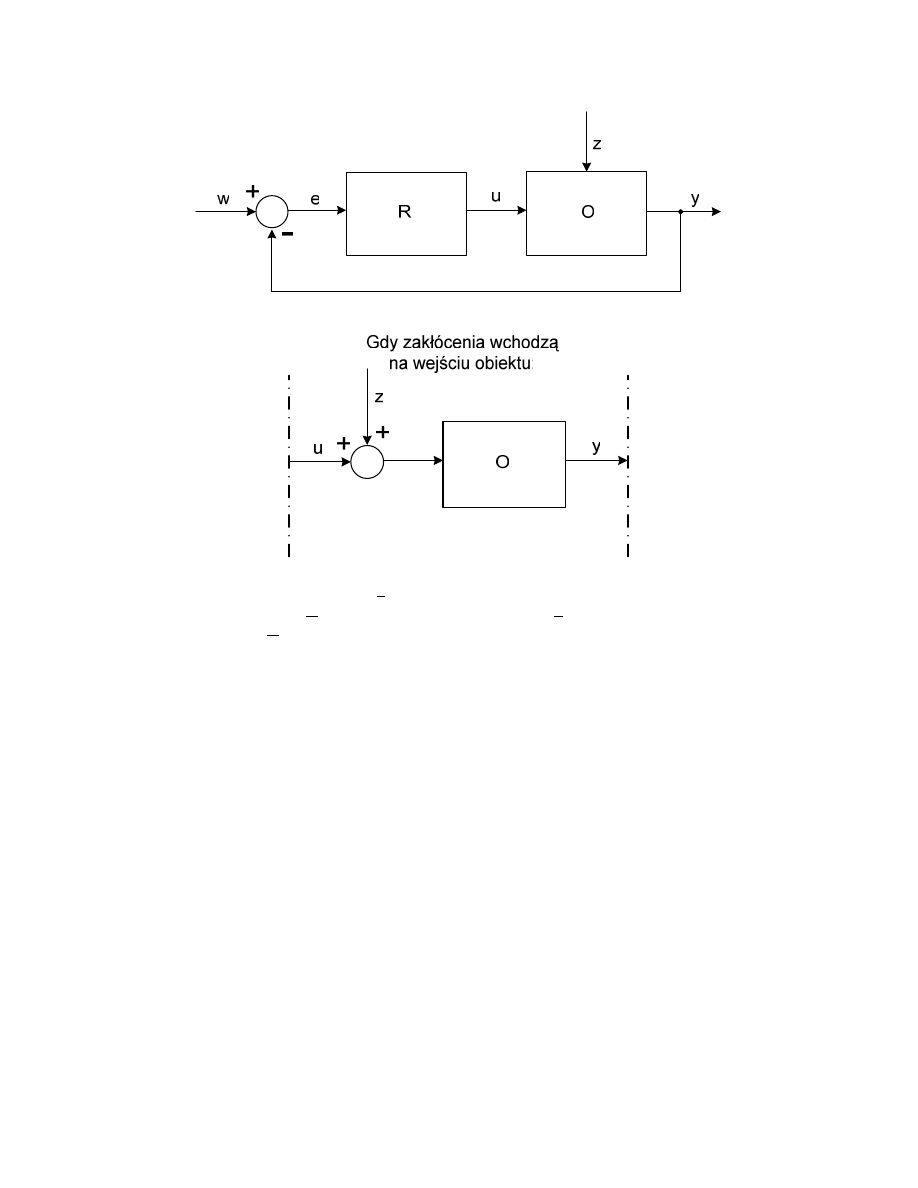
C. Układy nad ne (serwomechanizmy), w=w[
ϕ(t)].
Zadaniem układu jest nad anie wielko ci wyj ciowej y za zmieniaj c si w nieznany nam
sposób warto ci zadan w.
Schemat blokowy podstawowy:
- 8 -
Przykłady: sterowanie poło eniem y dział przeciwlotniczych wg wskaza radaru
okre laj cego poło enie w samolotu; sterowanie poło eniem y pisaka rejestratora wg
aktualnej warto ci w mierzonej i rejestrowanej wielko ci fizycznej.
D.
Inne
W punktach a,b,c wymieniono najcz ciej realizowane zadania układów automatyki o
działaniu ci głym, omawianych w przedmiocie PODSTAWY AUTOMATYKI.
Pełna lista zada jest bardzo szeroka, stale uzupełniana i obejmuje m.in. optymalizacj
przebiegu procesów (np. minimalizacj zu ycia energii, minimalizacj kosztów lub
maksymalizacj zysku przy zało onych ograniczeniach), realizacj procesów dyskretnych
(sekwencyjnych, np. monta u) oraz wiele innych.
- 9 -
1 OPIS MATEMATYCZNY UKŁADÓW LINIOWYCH
Układy rzeczywiste zwykle s nieliniowe, ale dla uproszczenia opisu matematycznego
przeprowadza si ich linearyzacj , co pozwala na sformułowanie przybli onego opisu
liniowego, wa nego w otoczeniu wybranego punktu pracy na charakterystyce statycznej
(punkt ten odpowiada najcz ciej nominalnym lub u rednionym warunkom pracy układu).
Po linearyzacji układy opisywane s za pomoc liniowych równa ró niczkowych o stałych
współczynnikach a
i
i b
i
.
Ogólna posta równania ró niczkowego układu liniowego:
u
b
dt
u
d
b
dt
u
d
b
y
a
dt
y
d
a
dt
y
d
a
m
m
m
m
m
m
n
n
n
n
n
n
0
1
1
1
0
1
1
1
+
+
+
=
+
+
+
−
−
−
−
−
−
( 1.1)
Pocz tek układu współrz dnych oznacza nominalny punkt pracy a u i y s odchyłkami
sygnałów od tego punktu.
Opis własno ci układów:
Charakterystyka statyczna układu liniowego lub zlinearyzowanego w otoczeniu nominalnego
punktu pracy (u,y s odchyłkami od tego punktu) ma posta :
u
a
b
y
0
0
=
Pocz tek układu współrz dnych oznacza nominalny punkt pracy, a u i
y s odchyłkami sygnałów od tego punktu.
Wła ciwo ci dynamiczne ilustruje si zwykle wyznaczaj c przebieg wielko ci wyj ciowej
y(t) po wprowadzeniu na wej cie jednego z typowych wymusze u(t).
Wykresy u(t) i y(t) mo na rysowa ł cznie w nast puj cym układzie współrz dnych:
Typowe wymuszenia:
)
(
1
)
(
t
t
u
=
u
y
- 10 -
)
(
1
)
(
t
u
t
u
st
⋅
=
)
(
)
(
t
t
u
δ
=
at
t
u
=
)
(
Wyznaczanie y(t)
a.
metoda klasyczna
b.
metoda operatorowa
)
(
)
(
s
f
t
f
⇔
,
ω
j
c
s
+
=
∞
−
=
0
)
(
)
(
dt
e
t
f
s
f
st
)]
(
[
)
(
)]
(
[
)
(
1
s
f
L
t
f
t
f
L
s
f
−
=
=
Metoda operatorowa pozwala zast pi równanie ró niczkowe tzw. transmitancj operatorow .
Transmitancja operatorowa:
)
(
)
(
)
(
s
u
s
y
s
G
=
( 1.2)
Wyznaczenie G(s) z równania ró niczkowego (1.1):
)
(
)
(
)
(
)
(
0
1
1
0
1
1
b
s
b
s
b
s
u
a
s
a
s
a
s
y
m
m
m
m
n
n
n
n
+
+
+
⋅
=
+
+
+
⋅
−
−
−
−
( 1.3)
m
n
a
s
a
s
a
b
s
b
s
b
s
G
n
n
n
n
m
m
m
m
≥
+
+
+
+
+
+
=
−
−
−
−
,
)
(
0
1
1
0
1
1
( 1.4)
)
(
)
(
)
(
s
N
s
M
s
G
=
Opis elementów na schematach blokowych:

- 11 -
=
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
2
1
2
22
21
1
12
11
s
G
s
G
s
G
s
G
s
G
s
G
s
G
s
G
s
G
s
MG
nm
n
n
m
m
m
k
n
i
s
u
s
y
s
G
k
i
ik
1
,
1
,
)
(
)
(
)
(
=
=
=
(pozostałe wej cia i warunki pocz tkowe s równe zeru)
Wyznaczenie charakterystyki statycznej z transmitancji operatorowej
Dla
0
1
)
(
u
s
s
u
=
otrzymujemy:
)
(
)
(
lim
)
(
lim
)
(
lim
0
0
0
s
u
s
G
s
s
y
s
t
y
y
s
s
t
⋅
=
⋅
=
=
→
→
∞
→
)
(
lim
0
0
0
s
G
u
y
s
→
=
)
(
lim
0
0
0
s
G
x
y
s
→
=
( 1.5)
Ko cowe równanie charakterystyki statycznej dla układów o jednym wej ciu i jednym
wyj ciu:
0
0
0
0
u
a
b
y
=
12
TA
B
LI
C
A
T
R
A
N
S
FO
R
M
A
T
L
.p
.
T
ra
ns
fo
rm
at
a
F(
s)
O
ry
gi
na
ł f
(t
)
L
.p
.
T
ra
ns
fo
rm
at
a
F(
s)
O
ry
gi
na
ł f
(t
)
1.
1
)
(t
δ
14
.
)
)(
(
1
b
s
a
s
+
+
a
b
e
e
bt
at
−
−
−
−
2.
s
1
1(
t)
15
.
)
)(
(
b
s
a
s
s
+
+
a
b
be
ae
bt
at
−
−
−
−
3.
2
1
s
t
16
.
)
)(
)(
(
1
c
s
b
s
a
s
+
+
+
)
)(
)(
(
)
(
)
(
)
(
a
c
c
b
b
a
e
a
b
e
c
a
e
b
c
ct
bt
at
−
−
−
−
+
−
+
−
−
−
−
4.
1
!
+n
s
n
n
t
17
.
)1
)(1
(
1
2
1
+
+
s
T
s
T
s
1
2
2
1
2
1
1
T
T
e
T
e
T
T
t
T
t
−
−
+
−
−
5.
a
s±
1
at
e
18
.
2
2
1
)1
)(1
(
1
+
+
s
T
s
T
2
2
1
2
2
1
2
1
2
1
)
(
]
)
(
[
2
1
T
T
T
e
t
T
T
T
T
e
T
T
T
t
T
t
−
−
+
−
−
−
6.
2
)
(
1
a
s
±
at
te
19
.
)1
)(1
(
2
1
+
+
s
T
s
T
s
)
(
1
2
2
1
2
1
1
2
T
T
T
T
e
T
e
T
T
t
T
t
−
−
−
−
7.
1
)
(
!
+
+
n
a
s
n
at
n
e
t
−
20
.
2
2
a
s
a
+
at
si
n
8.
)
(
1
a
s
s
+
)
1(
1
at
e
a
−
−
21
.
2
2
a
s
s
+
at
co
s
9.
)
(
1
a
s
s
−
)1
(
1
−
at
e
a
22
.
2
2
2
)
(
2
a
s
as
+
at
ts
in
10
.
2
)
(
a
s
s
+
s
at
e
at
−
−
)
1(
23
.
2
2
2
2
2
)
(
a
s
a
s
+
−
at
tc
os
11
.
2
)1
(
1
+
Ts
s
T
t
e
T
t
T
−
+
−
1
24
.
2
2
)
(
a
b
s
a
+
+
at
e
bt
si
n
−
12
.
2
)1
(
+
Ts
s
T
t
e
t
T
T
−
−
)
(
1
3
25
.
2
2
)
(
a
b
s
b
s
+
+
+
at
e
bt
co
s
−
13
.
)1
(
1
2
+
Ts
s
)
1(
T
t
e
T
t
−
−
−
26
.
)
(
1
2
2
a
s
s
+
)
co
s
1(
1
2
at
a
−
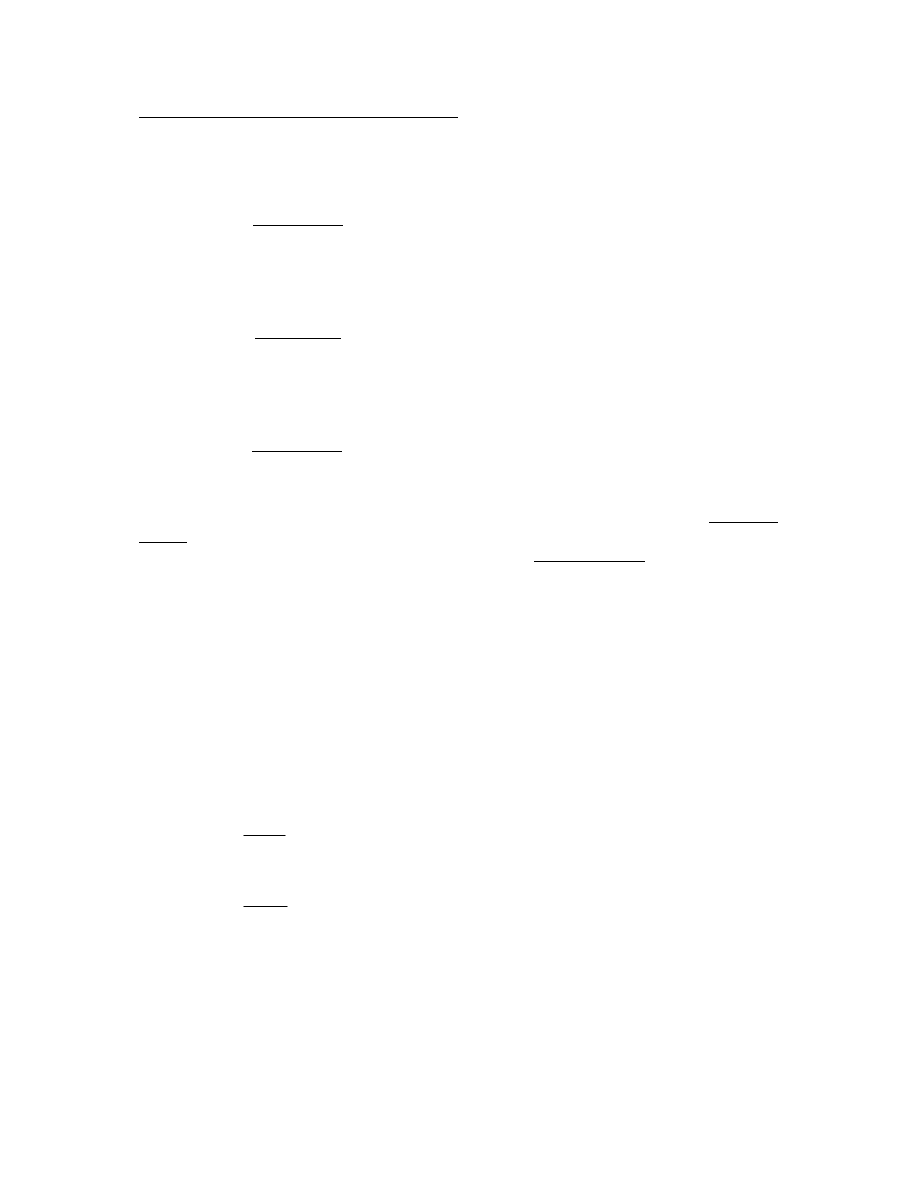
13
Opis układów z u yciem współrz dnych stanu:
W ogólnym opisie układów wielowymiarowych poszczególne wielko ci okre lone s w
postaci wektorów i oznaczaj :
=
)
(
)
(
)
(
)
(
2
1
t
u
t
u
t
u
t
U
n
- wektor wej , którego składowymi s wielko ci wej ciowe u
1
(t), … , u
n
(t)
=
)
(
)
(
)
(
)
(
2
1
t
x
t
x
t
x
t
X
k
- wektor stanu, którego składowymi s współrz dne stanu x
1
(t), … , x
k
(t)
=
)
(
)
(
)
(
)
(
2
1
t
y
t
y
t
y
t
Y
l
- wektor wyj , którego składowymi s wielko ci wyj ciowe y
1
(t), … , y
l
(t)
Zbiór wszystkich mo liwych warto ci wektora stanu X(t) w chwilach t tworzy przestrze
stanów układu (przestrze fazow ). Zbiór warto ci wektora stanu układu w kolejnych
chwilach czasu tworzy w tej przestrzeni krzyw , zwan trajektori stanu układu (trajektori
fazow ).
Równanie stanu układu opisuje si zwykle w postaci:
)]
(
),
(
[
)
(
t
U
t
X
F
t
X
=
( 1.6)
z n warunkami pocz tkowymi
0
0
)
(
X
t
X
=
( 1.7)
Równanie (1.6) jest zawsze równaniem ró niczkowym pierwszego rz du, w ogólnym
przypadku nieliniowym i zale nym jawnie od czasu, a F jest n-elementow funkcj
wektorow . Równania (1.6) i (1.7) mo na wi c rozpisa szczegółowo:
=
=
=
=
0
0
2
1
2
1
10
0
1
2
1
2
1
1
1
)
(
);
;
,
,
,
;
,
,
,
(
)
(
)
(
);
;
,
,
,
;
,
,
,
(
)
(
n
n
k
n
n
n
k
n
x
t
x
t
u
u
u
x
x
x
f
dt
t
dx
x
t
x
t
u
u
u
x
x
x
f
dt
t
dx
( 1.8)
Równanie wyj cia układu ma posta :
)]
(
),
(
[
)
(
t
U
t
X
G
t
Y
=
( 1.9)
przy czym G jest l-elemetow funkcj wektorow . Nie jest to równanie ró niczkowe gdy
cała dynamika układu opisana jest równaniem stanu, jest natomiast zale ne od czasu.
Rozpisuj c szczegółowo równanie (1.9) otrzymamy:

14
=
=
)
;
,
,
,
;
,
,
,
(
)
(
)
;
,
,
,
;
,
,
,
(
)
(
2
1
2
1
2
1
2
1
1
1
t
u
u
u
x
x
x
g
t
y
t
u
u
u
x
x
x
g
t
y
k
n
l
l
k
n
( 1.10)
Równania (1.8) i (1.10) mog by linearyzowane w otoczeniu wybranego stanu ustalonego
(nominalnego punktu pracy), przyjmuj wówczas posta :
t
t
f
u
u
f
u
u
f
u
u
f
x
x
f
x
x
f
x
x
f
dt
t
dx
k
k
n
n
∂
∂
+
∂
∂
+
+
∂
∂
+
∂
∂
+
∂
∂
+
+
∂
∂
+
∂
∂
=
1
1
2
2
1
1
1
1
1
2
2
1
1
1
1
1
)
(
( 1.11)
i tak dalej, natomiast
t
t
g
u
u
g
u
u
g
u
u
g
x
x
g
x
x
g
x
x
g
y
k
k
n
n
∂
∂
+
∂
∂
+
+
∂
∂
+
∂
∂
+
∂
∂
+
+
∂
∂
+
∂
∂
=
1
1
2
2
1
1
1
1
1
2
2
1
1
1
1
1
( 1.12)
i tak dalej.
Równania (1.11) i (1.12) zapisuje si zwykle skrótowo w postaci macierzowej:
)
(
)
(
)
(
)
(
)
(
t
U
t
B
t
X
t
A
t
X
+
=
( 1.13)
)
(
)
(
)
(
)
(
)
(
t
U
t
D
t
X
t
C
t
Y
+
=
( 1.14)
przy czym: A(t) – macierz układu stopnia n×n
B(t) – macierz wej stopnia n×k
C(t) – macierz wyj stopnia l×n
D(t) – macierz transmisyjna układu stopnia l×k
Poszczególne elementy macierzy A,B,C,D odpowiadaj pochodnym cz stkowym
wyst puj cym w równaniach (1.11) i (1.12).
W przypadku szczególnym, gdy układ jest liniowy stacjonarny (o parametrach niezale nych
od czasu), pochodne cz stkowe wzgl dem zmiennych x
1
,…,x
n,
…,u
1
,…,u
k
nie zawieraj czasu
i pochodne cz stkowe wzgl dem czasu s równe zeru. Elementy macierzy s wówczas stałe i
równania (1.13) i (1.14) mo na zapisa w postaci:
)
(
)
(
)
(
)
(
)
(
)
(
t
DU
t
CX
t
Y
t
BU
t
AX
t
X
+
=
+
=
( 1.15)

15
2 PODSTAWOWE ELEMENTY LINIOWE
2.1
Zało enia upraszczaj ce
Wiele elementów automatyki mo na traktowa jako liniowe, je eli ograniczy si zakres ich
pracy i przyjmie nast puj ce zało enia upraszczaj ce:
a)
w odniesieniu do elementów mechanicznych
-
wyst puje jedynie tarcie lepkie (wiskotyczne), a nie tarcie suche (Coulomba);
siła tarcia jest proporcjonalna do pr dko ci;
-
sztywno ci elementów spr ystych s stale, a pozostałych elementów oraz ich
poł cze i zamocowa niesko czenie wielkie;
w odniesieniu do elementów płynowych (hydraulicznych i pneumatycznych)
-
opór przepływu jest stały, tzn. nat enie przepływu płynu jest proporcjonalne
do ró nicy ci nie ;
-
moduł spr ysto ci obj to ciowej płynu (odwrotno ” współczynnika
ci liwo ci) jest stały;
b)
w odniesieniu do elementów elektrycznych
-
rezystancje, indukcyjno ci i pojemno ci s stałe, niezale ne od pr du i
napi cia.
Prócz tych zało e natury ogólnej, w poszczególnych przypadkach robi b dziemy jeszcze
zało enia szczególne, np. idealna szczelno elementów hydraulicznych lub pomijalna masa
niektórych cz ci ruchomych. Nale y wi c pami ta , e równania i charakterystyki
elementów liniowych s uproszczone i cz sto mo na je stosowa tylko do oblicze
wst pnych.
Elementy liniowe klasyfikuje si najcz ciej ze wzgl du na ich własno ci dynamiczne.
Wyró nimy sze grup elementów podstawowych:
1)
bezinercyjne (proporcjonalne),
2)
inercyjne,
3)
całkuj ce,
4)
ró niczkuj ce,
5)
oscylacyjne,
6)
opó niaj ce.
Własno ci statyczne wszystkich elementów okre la b dziemy podaj c równanie i wykres
charakterystyki statycznej y = f (u), a własno ci dynamiczne podaj c równanie ró niczkowe i
odpowiadaj c mu transmitancj operatorowa oraz wykres odpowiedzi y(t) na wymuszenie
skokowe.
Ka d grup elementów ilustruje kilka przykładów, przy czyni w ramach danej grupy s to
przykłady urz dze konstrukcyjnie odmiennych, aby podkre li , e podział ze wzgl du na
własno ci dynamiczne nie jest zale ny od natury fizycznej elementów i e np. elementem
inercyjnym mo e by zarówno urz dzenie mechaniczno, jak i hydrauliczne, pneumatyczne
lub elektryczne.
Przyj to nast puj cy system oznacze :
a.
Warto ci absolutne sygnałów wej ciowych i wyj ciowych oznacza b dziemy
indeksem „O”, np. u
0
, y
0
. Potrzeba wyró niania warto ci absolutnych zachodzi przy
analizie stanów ustalonych, gdy cz sto nie wystarcza znajomo równania

16
charakterystyki statycznej y=f(u) w otoczeniu wybranego punktu pracy, lecz trzeba
zna równie równanie (lub wykres) charakterystyki statycznej y
0
=f(u
0
) w całym
zakresie zmienno ci sygnałów.
b.
Odchyłki sygnałów wej ciowych i wyj ciowych od pocz tkowego stanu ustalonego
oznacza b dziemy nie dodaj c adnych indeksów, np. u, y. Odchyłkami operujemy
zawsze przy zapisie stanów nieustalonych oraz przy zapisie ogólnym.
17
2.2
Elementy bezinercyjne (proporcjonalne)
Ogólna posta równania elementu bezinercyjnego jest nast puj ca;
y=ku
gdzie: y — wielko wyj ciowa, u — wielko wej ciowa, k — współczynnik pro-
porcjonalno ci (współczynnik wzmocnienia).
Transmitancja elementu bezinercyjnego jest równa współczynnikowi proporcjonalno ci:
k
s
u
s
y
s
G
=
=
)
(
)
(
)
(
Równanie charakterystyki statycznej b dzie:
y=ku
lub
y
0
=ku
0
+C
gdzie: C jest stał , okre laj c przesuni cie charakterystyki w stosunku do pocz tku układu
współrz dnych.
Odpowied na wymuszenie skokowe: u(t)=
1(t)u
st
b dzie:
y(t)=
1(t)ku
st
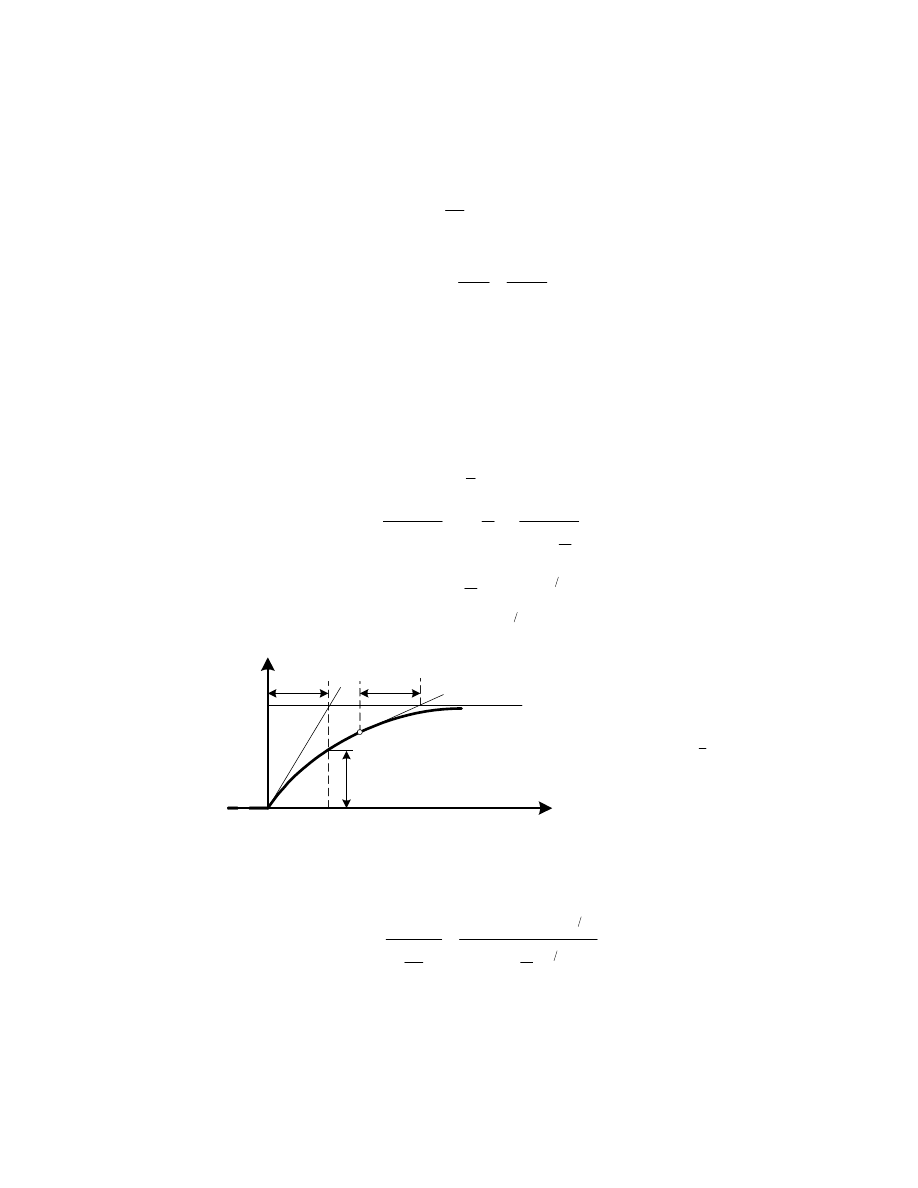
Przykłady kilku elementów traktowanych cz sto jako bezinercyjne przedstawiono na rys. 2.1
18
Rysunek 2.1 Przykłady elementów bezinercyjnych (proporcjonalnych): a, b) d wignia, c) dzielnik
napi cia, d) przekładnia cierna, e) przekładnia z bata, f) siłownik pneumatyczny, g) mechanizm
krzywkowy
19
2.3
Elementy inercyjne pierwszego rz du
Ogólna posta równania ró niczkowego elementu inercyjnego pierwszego rz du jest
nast puj ca:
ku
y
dt
dy
T
=
+
sk d wynika transmitancja
1
)
(
)
(
)
(
+
=
=
Ts
k
s
u
s
y
s
G
gdzie: k – współczynnik proporcjonalno ci
T – stała czasowa (ma wymiar czasu)
Równanie charakterystyki statycznej b dzie
ku
y
=
Odpowied na wymuszenie skokowe u(t)=
1(t)u
st
wynosi:
st
u
s
s
u
1
)
(
=
)
1
(
1
)
1
(
)
(
T
s
s
u
T
k
u
Ts
s
k
s
y
st
st
+
=
+
=
)
1
(
)]
(
[
)
(
1
T
t
st
e
T
u
T
k
s
y
L
t
y
−
−
−
=
=
)
1
(
)
(
T
t
st
e
ku
t
y
−
−
=
)
1
(
)
(
T
t
st
e
ku
t
y
−
−
=
Rysunek 2.2 Odpowied elementu inercyjnego pierwszego rz du na wymuszenie skokowe.
Wykres y(t) przedstawiono na rys.2.2. Stał czasow T mo na okre li wystawiaj c styczn w
dowolnym punkcie krzywej wykładniczej y(t) i wyznaczaj c odcinek podstycznej na
asymptocie:
T
e
T
ku
e
ku
ku
dt
dy
y
ku
podstyczna
T
t
st
T
t
st
st
st
=
−
−
=
−
=
−
−
1
)
1
(
Stał czasow T mo na równie okre li jako czas od chwili t=0 do chwili, kiedy y(t)
osi ga 63,2% swej ko cowej warto ci ustalonej ku
st
. Podstawiaj c t=T otrzymujemy bowiem:
y
t
ku
st
T
T
0,632ku
st

20
st
st
ku
e
ku
t
y
632
,
0
)
1
(
)
(
1
=
−
=
−
Przykład procesu, który po linearyzacji opisywany jest równaniem elementu
inercyjnego I rz du przedstawiony jest na rys. 2.3. Sygnałami wej ciowymi s Q
1
– nat enie
przepływu cieczy oraz f – przekrój przepływowy zaworu. Sygnałem wyj ciowym jest h –
poziom cieczy w zbiorniku.
Warunkiem stanu ustalonego jest:
20
10
Q
Q
=
Rysunek 2.3 Zbiornik z wypływem swobodnym cieczy
Układamy równanie Bernoulliego dla przekrojów 1-1 i 2-2
0
2
2
2
2
2
1
2
1
+
+
=
+
+
γ
γ
p
g
v
h
p
g
v
Przyjmuj c pr dko v
1
=0 oraz p
1
=p
2
(ci nienie atmosferyczne) otrzymamy
gh
v
2
2
=
Na podstawie równania ci gło ci
2
2
fv
Q
=
otrzymujemy
gh
f
Q
2
2
=
Otrzymujemy zatem równanie charakterystyki statycznej:
2
0
2
10
0
2
gf
Q
h
=
Wykres charakterystyki statycznej dla
f
0
=const
przedstawiono na rys. 2.4a, a dla
Q
10
=const
na rys. 2.4b
Rysunek 2.4 Charakterystyki statyczne procesu gromadzenia cieczy w zbiorniku z wypływem swobodnym

21
W stanach nieustalonych zmiany poziomu cieczy w zbiorniku mo na opisa za pomoc
równania:
2
1
Q
Q
dt
dh
A
−
=
gdzie A jest powierzchni przekroju poprzecznego zbiornika (w m
2
).
Poniewa charakterystyki statyczne s krzywoliniowe, aby opisa element za pomoc
liniowego równania ró niczkowego, nale y przeprowadzi linearyzacj . Współrz dne
nominalnego punktu pracy oznaczamy
h
n
, Q
1n
, f
n
. W otoczeniu tego punktu rzeczywiste
przyrosty zmiennych
h
oraz
Q
2
zast pimy przyrostami przybli onymi, które wyst piłyby w
przypadku liniowej charakterystyki statycznej o nachyleniu pokazanym na rys.2.4. Dla
odró nienia zapisu wszystkie przyrosty oznaczymy teraz dodaj c symbol „ ”. Otrzymamy
wi c:
2
1
Q
Q
dt
h
d
A
∆
−
∆
=
∆
Przyrost
∆
Q
2
zast pujemy ró niczk zupełn
h
h
g
f
f
gh
h
h
Q
f
f
Q
Q
n
n
n
n
n
∆
+
∆
=
∆
∂
∂
+
∆
∂
∂
=
∆
2
2
2
2
2
Zatem otrzymamy:
f
k
Q
k
h
dt
h
d
T
∆
−
∆
=
∆
+
∆
2
1
1
gdzie:
n
n
h
g
f
A
T
2
=
,
n
n
h
g
f
k
2
1
1
=
,
n
n
f
h
k
2
2
=
W dalszym ci gu cz sto opuszcza b dziemy znaki „ ”, pami taj c jednak zawsze, e
w równaniu wyst puj przyrosty poszczególnych wielko ci. Napiszemy wówczas
f
k
Q
k
h
dt
dh
T
2
1
1
−
=
+
W przypadkach szczególnych, kiedy
f
0
=const (f=0),
1
1
Q
k
h
dt
dh
T
=
+
,
a kiedy
Q
10
=const (Q
1
=0),
f
k
h
dt
dh
T
∆
−
=
+
2
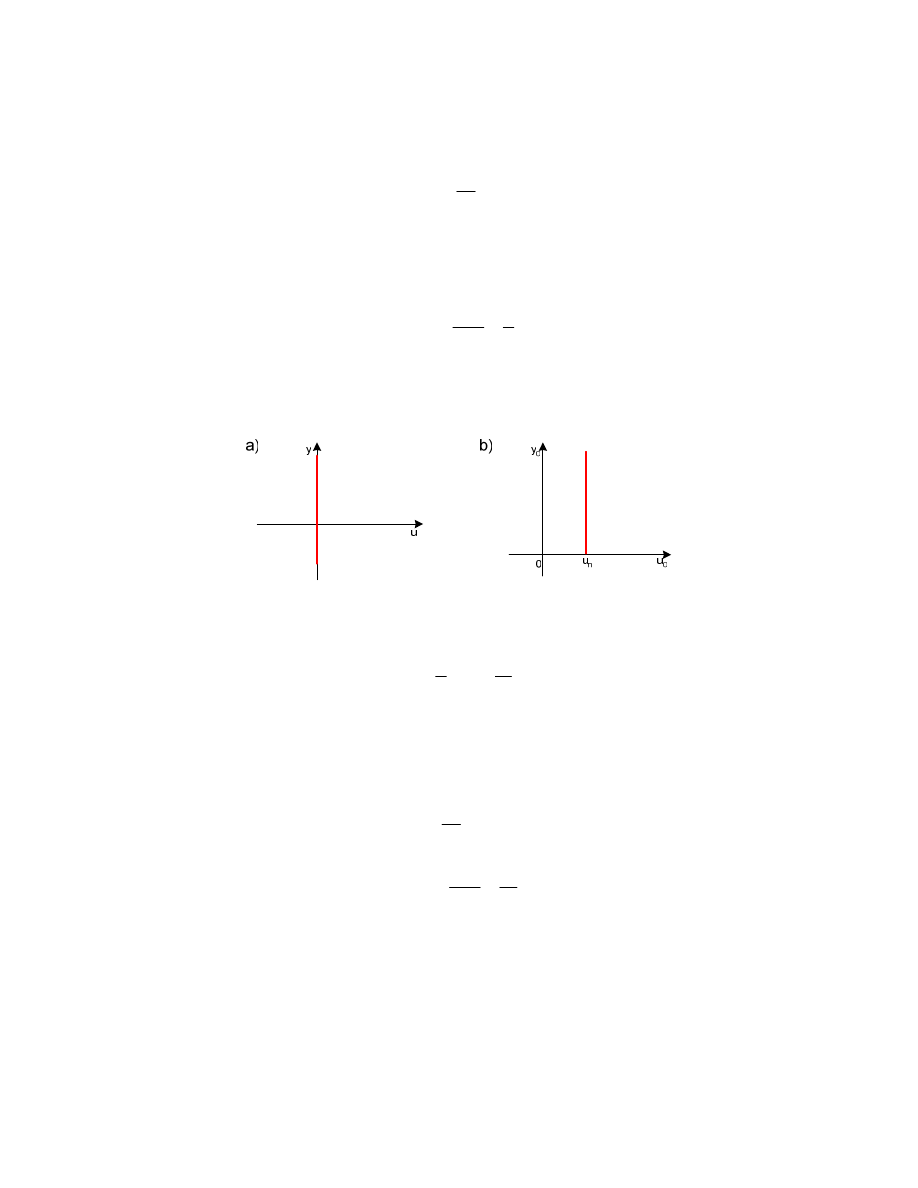
22
2.4
Elementy całkuj ce
Ogólna posta równania ró niczkuj cego elementu całkuj cego jest nast puj ca:
ku
dt
dy =
lub po scałkowaniu, przy zerowych warunkach pocz tkowych,
=
t
udt
k
y
0
st d wynika transmitancja
s
k
s
u
s
y
s
G
=
=
)
(
)
(
)
(
Równanie charakterystyki statycznej ma posta
0
=
u
a jej wykres podano na rys. 2.5
Rysunek 2.5 Charakterystyka statyczna elementu całkuj cego: a) współrz dne odchyłek, b) wspoł®z dne
warto ci absolutnych
Odpowied na wymuszenie skokowe
u(t)=
1
(t)u
st
wyznaczamy:
st
u
s
k
s
u
s
k
s
y
2
)
(
)
(
=
=
t
ku
s
y
L
t
y
st
=
=
−
)]
(
[
)
(
1
Wykres
y(t)
podano na rys. 2.6a.
W przypadku szczególnym, kiedy wej cie i wyj cie s sygnałami jednoimiennymi,
współczynnik
k
ma wymiar odwrotno ci czasu. Wówczas ogólna posta równania
ró niczkowego elementu całkuj cego ma posta :
u
dt
dy
T
=
której odpowiada transmitancja
Ts
s
u
s
y
s
G
1
)
(
)
(
)
(
=
=
gdzie
T
jest stał czasow akcji całkuj cej lub krócej – stał całkowania.
Stał t mo na odszuka na wykresie odpowiedzi skokowej zgodnie z rys. 2.6b.
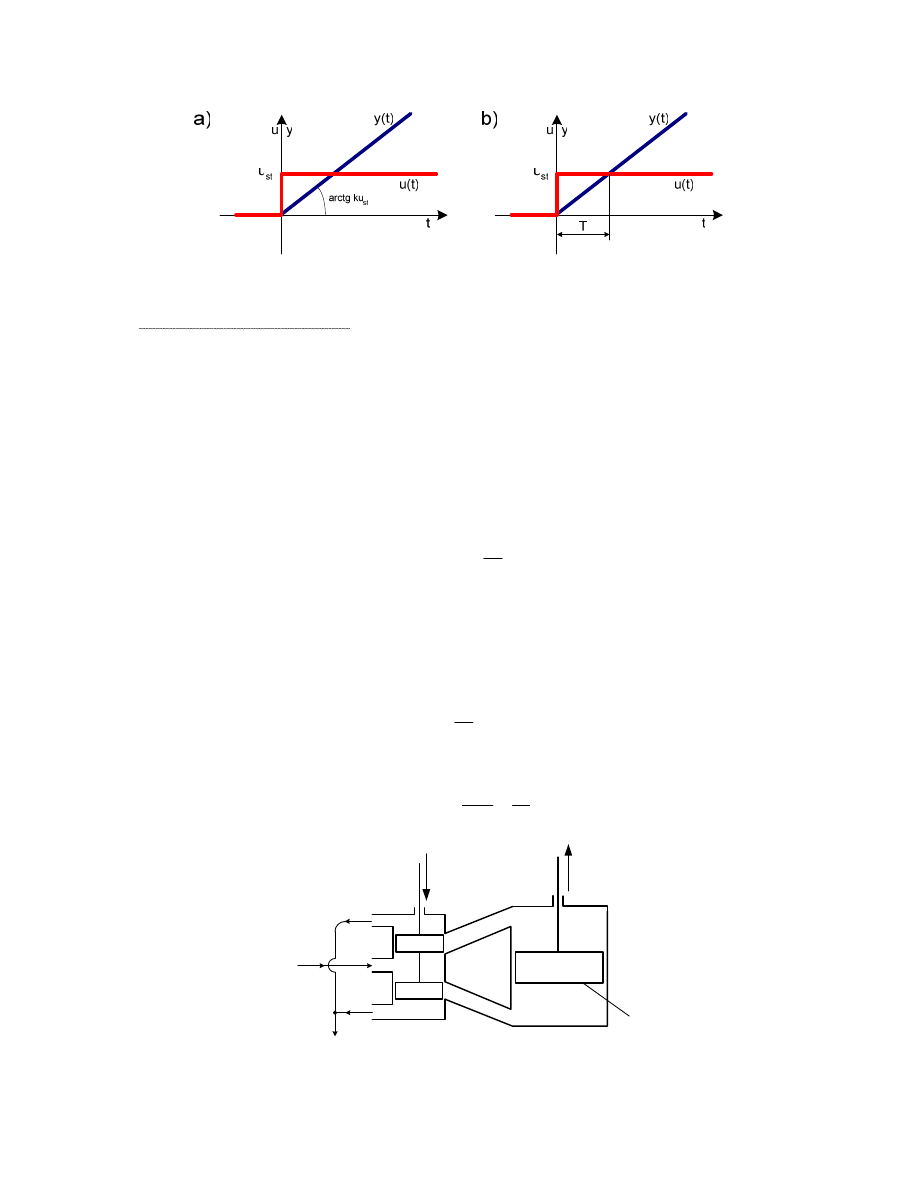
23
Rysunek 2.6 Odpowiedzi skokowe elementu całkuj cego: a) G(s)=k/s, b) G(s)=1/Ts
Przykład elementu całkuj cego:
zespół rozdzielacz – siłownik hydrauliczny
Schemat zespołu przedstawiono na rys. 2.7. Wielko ci wej ciow jest przesuni cie
u
tłoczków rozdzielacza, wielko ci wyj ciow jest przesuni cie
y
tłoczyska siłownika.
Zało enia:
a)
const
p
z
=
,
const
p
s
=
b)
obci enie siłownika ma warto zerow
c)
pr dko przepływu oleju przez szczeliny rozdzielacza
const
v
=
(wynika to z zało e
a i b).
Stan ustalony
const
y
=
zachodzi dla
0
=
u
. Charakterystyka statyczna ma kształt
podany na rys. 2.6a.
Stan dynamiczny:
dt
dy
A
Q
=
gdzie:
Q
– nat enie przepływu oleju przez szczeliny rozdzielacza
A
– powierzchnia efektywna tłoka siłownika
Uwzgl dniaj c równanie ci gło ci
ubv
Q
=
(
ub
jest przekrojem szczeliny przepływowej) otrzymamy
u
dt
dy
T
=
gdzie
bv
A
T
/
=
Transmitancja elementu
Ts
s
u
s
y
s
G
1
)
(
)
(
)
(
=
=
Rysunek 2.7 Zespół rozdzielacz-siłownik hydrauliczny

24
2.5
Elementy ró niczkuj ce
2.5.1
Idealny element ró niczkuj cy
Równanie idealnego elementu ró niczkuj cego jest nast puj ce:
dt
du
k
y
=
sk d wynika transmitancja
ks
s
u
s
y
s
G
=
=
)
(
)
(
)
(
Współczynnik
k
definiuje si jako
dt
du
y
k
=
W stanie ustalonym y=0 (y
0
=const
) dla wszystkich u. Wykresy charakterystyki statycznej
podano na rys.2.8.
Rysunek 2.8 Charakterystyka statyczna elementu ró niczkuj cego: a) współrz dne odchyłek, b)
współrz dne warto ci absolutnych
Odpowied na wymuszenie skokowe jest funkcj Diraca pomno on przez k oraz
przez amplitud skoku u
st
. Mamy bowiem
st
ku
s
ksu
s
y
=
=
)
(
)
(
)
(
)]
(
[
)
(
1
t
ku
s
y
L
t
y
st
δ
=
=
−
>
=
∞
<
=
0
dla
0
0
dla
0
dla
0
)
(
t
t
t
t
y
W przypadku szczególnym, kiedy wej cie i wyj cie s sygnałami jednoimiennymi,
równanie idealnego elementu ró niczkuj cego zapisuje si w postaci
dt
du
T
y
=
której odpowiada transmitancja
Ts
s
u
s
y
s
G
=
=
)
(
)
(
)
(
gdzie T jest stał czasow akcji ró niczkuj cej lub krócej – stał ró niczkowania.
Odpowied na wymuszenie skokowe jest w tym przypadku funkcj Diraca pomno on
przez Tu
st
.
Idealnego elementu ró niczkuj cego nie mo na zrealizowa praktycznie, ale poznanie
jego własno ci jest celowe z tego wzgl du, e cz sto w elementach zło onych wyodr bnia
jako jeden ze składników idealne działanie ró niczkuj ce. Ponadto, idealny element
25
ró niczkuj cy traktuje si niekiedy jako pierwsze przybli enie rzeczywistego elementu
ró niczkuj cego.
2.5.2
Rzeczywiste elementy ró niczkuj ce
Ogólna posta równania rzeczywistego elementu ró niczkuj cego jest nast puj ca:
dt
du
k
y
dt
dy
T
=
+
sk d wynika transmitancja
1
)
(
)
(
)
(
+
=
=
Ts
ks
s
u
s
y
s
G
gdzie k współczynnikiem proporcjonalno ci, a T stał czasow elementu.
Je eli wej cie i wyj cie s sygnałami jednoimiennymi, równanie ró niczkowe zapisuje
si w postaci:
dt
du
T
y
dt
dy
T
=
+
której odpowiada transmitancja
1
)
(
)
(
)
(
+
=
=
Ts
Ts
s
u
s
y
s
G
Charakterystyka statyczna b dzie oczywi cie identyczna z podan na rys. 2.8, natomiast
odpowied na wymuszenie skokowe wyznaczamy (z ogólnej postaci transmitancji)
T
s
u
T
k
Ts
ku
s
u
Ts
ks
s
y
st
st
1
1
1
)
(
1
)
(
+
=
+
=
+
=
T
t
st
e
u
T
k
s
y
L
t
y
−
−
=
=
)]
(
[
)
(
1
Wyznaczaj c t odpowied z transmitancji gdzie wej cie i wyj cie s sygnałami
jednoimiennymi otrzymamy:
T
t
st
e
u
t
y
−
=
)
(
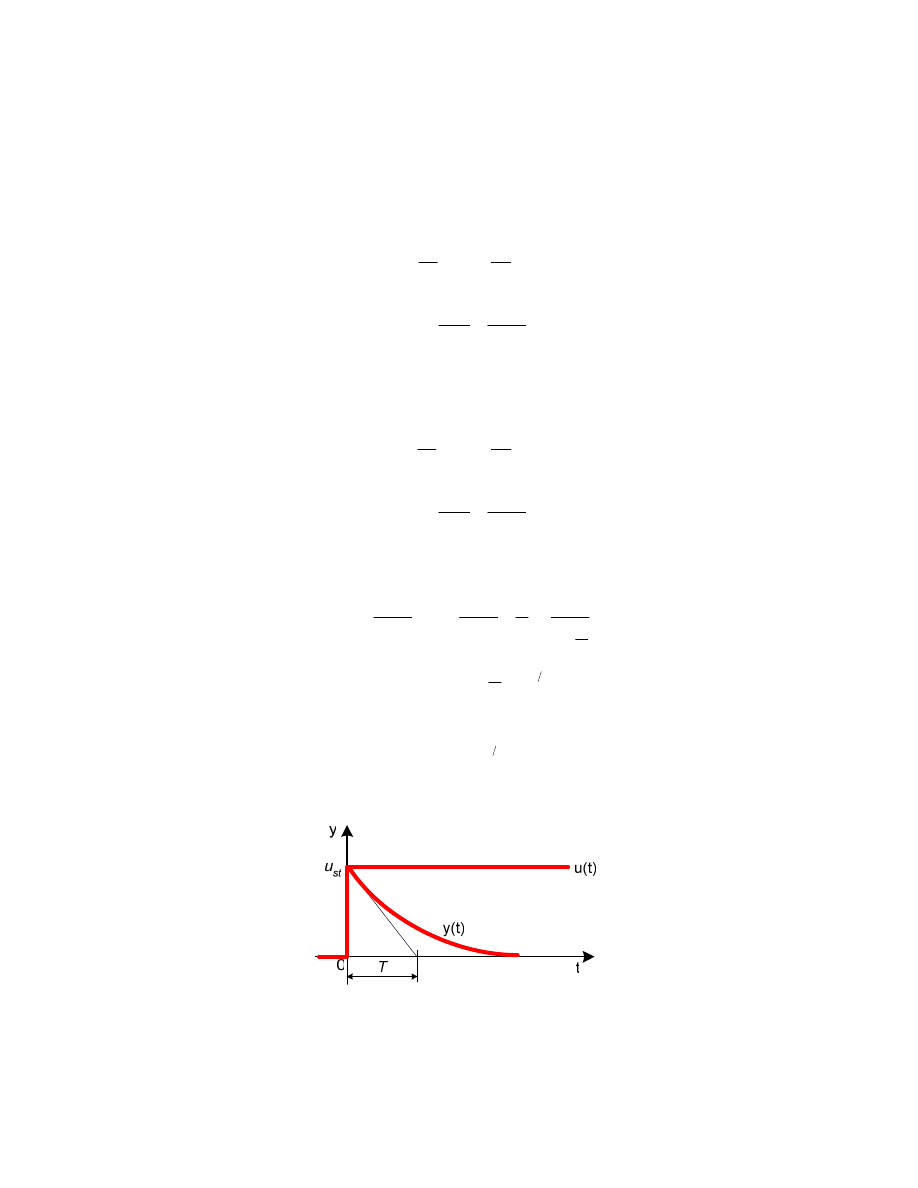
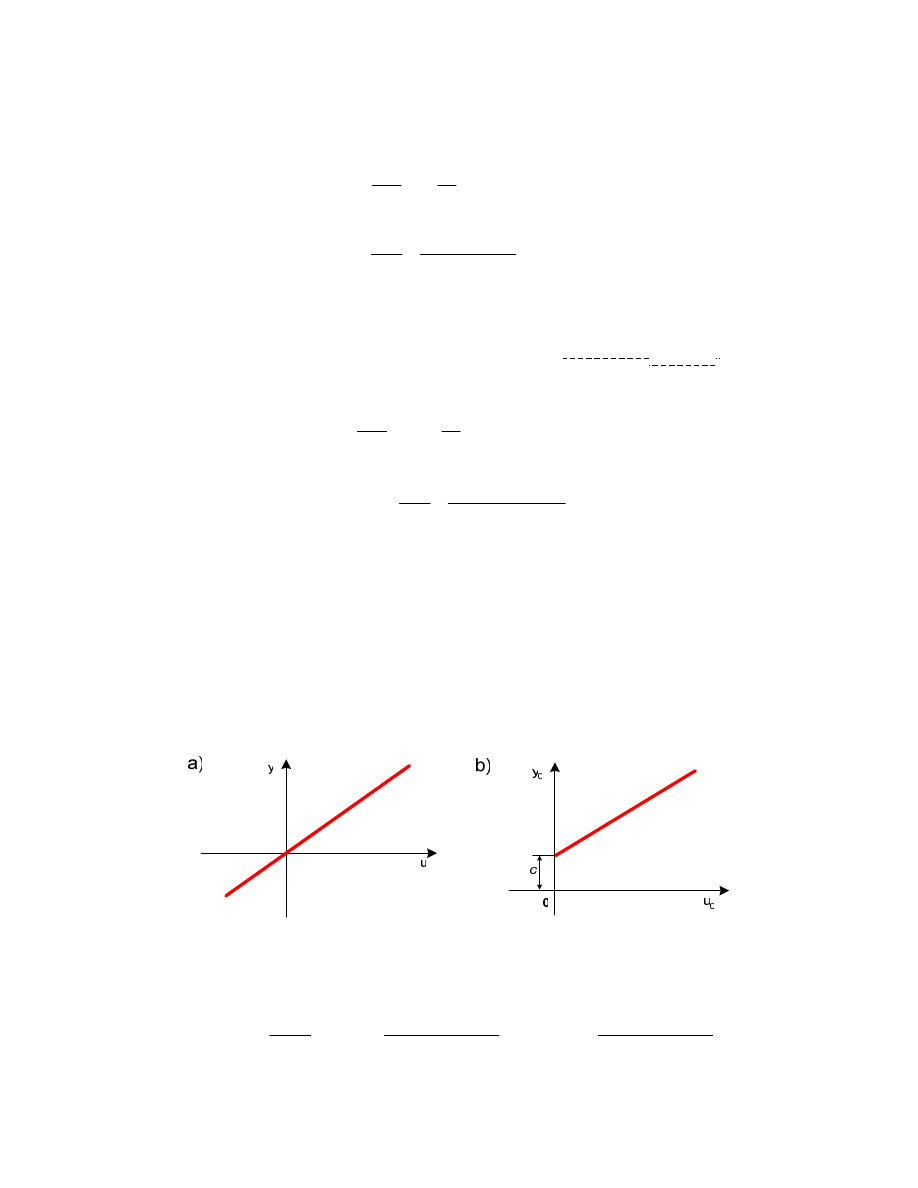
Wykres y(t) przedstawiono na rys. 2.9.
Rysunek 2.9 Odpowied rzeczywistego elementu ró niczkuj cego na wymuszenie skokowe
26
2.6
Elementy oscylacyjne
Ogólna posta równania ró niczkowego elementu oscylacyjnego jest nast puj ca:
ku
y
dt
dy
T
dt
y
d
T
=
+
+
2
2
2
2
1
(*)
przy czym
2
1
2
2
4T
T
<
. Równaniu (*) odpowiada transmitancja:
1
)
(
)
(
)
(
2
2
2
1
+
+
=
=
s
T
s
T
k
s
u
s
y
s
G
(**)
gdzie k jest współczynnikiem proporcjonalno ci, T
1
i T
2
s stałymi czasowymi elementu.
Nale y podkre li , e to nie posta równania (*) lub (**) decyduje o tym, e element jest
oscylacyjny (taka sama mo e by posta równa elementu inercyjnego drugiego rz du, w
którym adne oscylacje odpowiedzi skokowej nie wyst puj ), ale warunek
2
1
2
2
4T
T
<
.
Cz sto spotyka si równie nast puj c posta równania ró niczkowego, która ułatwia
interpretacj przebiegów przej ciowych elementu oscylacyjnego:
u
k
y
dt
dy
dt
y
d
2
0
2
0
0
2
2
2
ω
ω
ζω
=
+
+
przy czym
1
2
<
ζ
. Wówczas transmitancja
2
0
0
2
2
0
2
)
(
)
(
)
(
ω
ζω
ω
+
+
=
=
s
s
k
s
u
s
y
s
G
gdzie: k – współczynnik proporcjonalno ci
1
0
/
1 T
=
ω
– pulsacja oscylacji własnych elementu
1
2
2
/ T
T
=
ζ
– zredukowany (wzgl dny) współczynnik tłumienia
Równanie charakterystyki statycznej we współrz dnych odchyłek b dzie
ku
y
=
a we współrz dnych warto ci absolutnych
C
ku
y
+
=
0
0
gdzie C jest stał wynikaj c z warunków pocz tkowych.
Wykresy charakterystyki statycznej podano na rys. 2.10.
Rysunek 2.10 Charakterystyka statyczna elementu oscylacyjnego: a) współrz dne odchyłek b)
współrz dne warto ci absolutnych
Odpowied na wymuszenie skokowe u(t)=
1(t)u
st
obliczamy według wzoru:
+
+
=
+
+
=
=
−
−
−
)
1
(
1
)
1
(
)
(
)
(
)
(
2
2
2
1
1
2
2
2
1
1
1
s
T
s
T
s
L
ku
u
s
T
s
T
s
k
L
u
s
sN
s
M
L
t
y
st
st
st

27
Pierwiastkami wielomianu N(s) s :
−
−
=
−
±
−
=
1
2
2
1
2
4
2
1
2
1
2
1
2
1
2
1
2
2
2
2
,
1
T
T
T
T
T
T
T
T
T
s
lub dla oznacze :
1
0
1
T
=
ω
oraz
1
2
2T
T
=
ζ
)
1
(
2
0
2
,
1
−
−
=
ζ
ζ
ω
s
Odpowied na wymuszenie skokowe b dzie mie charakter oscylacyjny, je eli spełniony
jest podany na wst pie warunek:
2
1
2
2
4T
T
<
lub, co jest jednoznaczne:
1
2
<
ζ
Pierwiastki s
1
i s
2
zapiszemy wówczas w postaci:
−
−
=
2
1
2
1
2
1
2
,
1
2
1
2
1
T
T
j
T
T
T
s
lub
)
1
(
2
0
2
,
1
ζ
ζ
ω
−
−
=
j
s
otrzymujemy
−
+
−
+
=
t
s
t
s
st
e
s
s
s
T
e
s
s
s
T
ku
t
y
2
1
)
(
1
)
(
1
1
)
(
1
2
2
2
1
2
1
1
2
1
Stosuj c wzory Eulera
*)
oraz wcze niej przyj te oznaczenia, mo na przedstawi y(t) w
postaci:
+
−
−
−
=
−
)
1
sin(
1
1
)
(
2
0
2
1
0
ϕ
ζ
ω
ζ
ζω
t
e
e
ku
t
y
t
s
t
st
gdzie:
ζ
ζ
ϕ
2
1
−
= arctg
Rysunek 2.11 Odpowied elementu oscylacyjnego na wymuszenie skokowe 1(t)u
st
*)
)
sin
(cos
v
j
v
e
e
u
jv
u
+
=
+
,
)
sin
(cos
v
j
v
e
e
u
jv
u
−
=
−
28
Wykres y(t) przedstawiono na rys. 2.11. Składowa ustalona przebiegu wynosi ku
st
, a
składowa przej ciowa jest gasn c sinusoid , której okres jest stały i wynosi:
2
0
1
2
ζ
ω
π
−
=
T
W przypadku szczególnym, kiedy =0 (tzn. T
2
=0), wyst puj drgania zachowawcze (nie
tłumione) o pulsacji
0
. Wówczas:
]
cos
1
[
)
(
)]
90
sin(
1
[
)
(
0
0
t
ku
t
y
t
ku
t
y
st
st
ω
ω
−
=
+
−
=
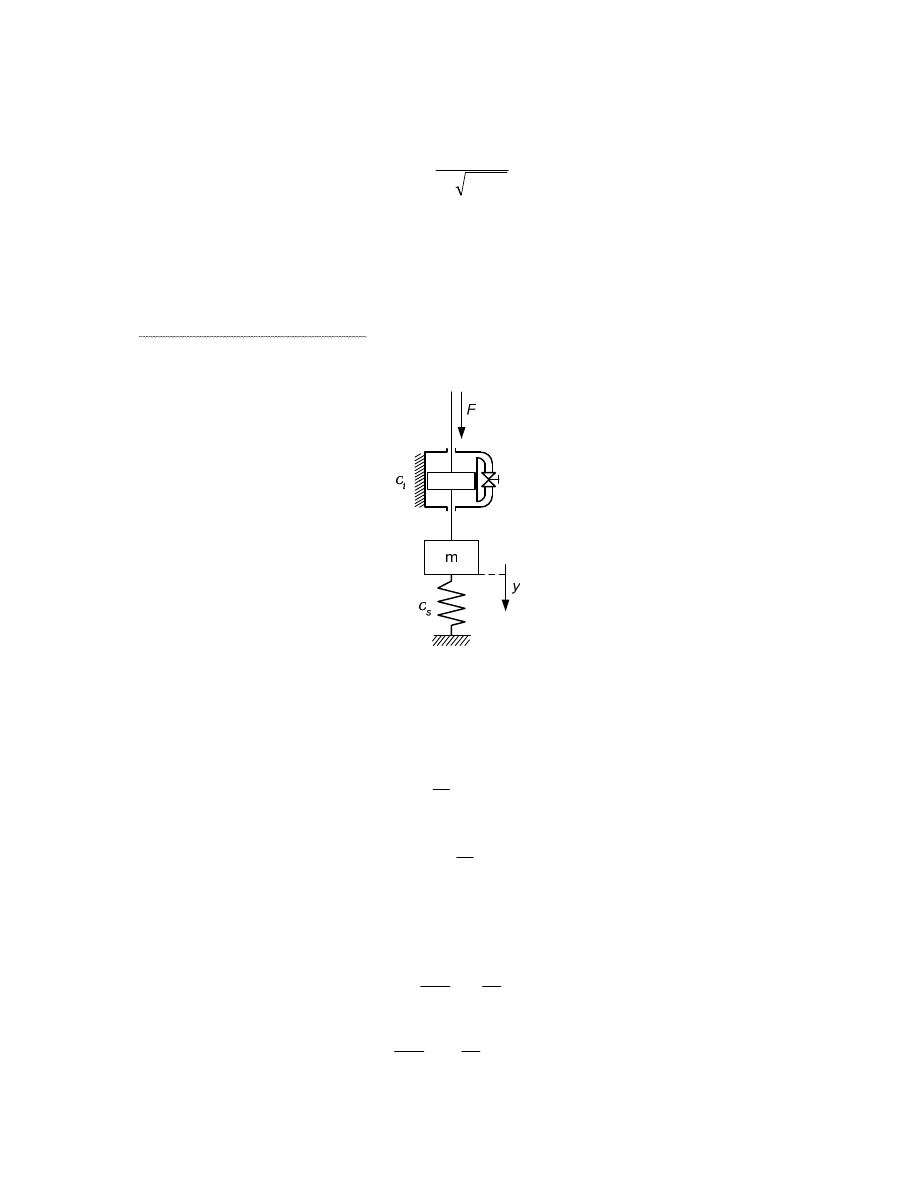
Przykład elementu oscylacyjnego
Schemat elementu podano na rys. 2.12. Sygnałem wej ciowym jest siła F, sygnałem
wyj ciowym jest przesuni cie y.
Rysunek 2.12 Zespół masa-tłumik-spr yna
W stanie ustalonym siła F oraz ci ar mg s równowa one sił wywieran przez ugi t
spr yn . We współrz dnych warto ci absolutnych warunek ten zapiszemy
0
0
y
c
mg
F
s
=
+
sk d
)
(
1
0
0
mg
F
c
y
s
+
=
natomiast we współrz dnych odchyłek (przyrostów)
F
c
y
s
1
=
Wykresy charakterystyki statycznej s przedstawione na rys. 2.13.
W stanach nieustalonych, uwzgl dniaj c zało enia upraszczaj ce, podane w p. 2.1,
otrzymamy nast puj ce równanie równowagi:
y
c
dt
dy
c
dt
y
d
m
F
s
t
+
+
=
2
2
sk d
kF
y
dt
dy
T
dt
y
d
T
=
+
+
2
2
2
2
1

29
gdzie
s
c
m
T
=
1
,
s
t
c
c
T
=
2
,
s
c
k
1
=
Przedstawionemu równaniu odpowiada transmitancja:
1
)
(
)
(
)
(
2
2
2
1
+
+
=
=
s
T
s
T
k
s
F
s
y
s
G
Rysunek 2.13 Charakterystyka statyczna elementu przedstawionego na rys. 2.12: a) współrz dne
odchyłek, b) współrz dne warto ci absolutnych
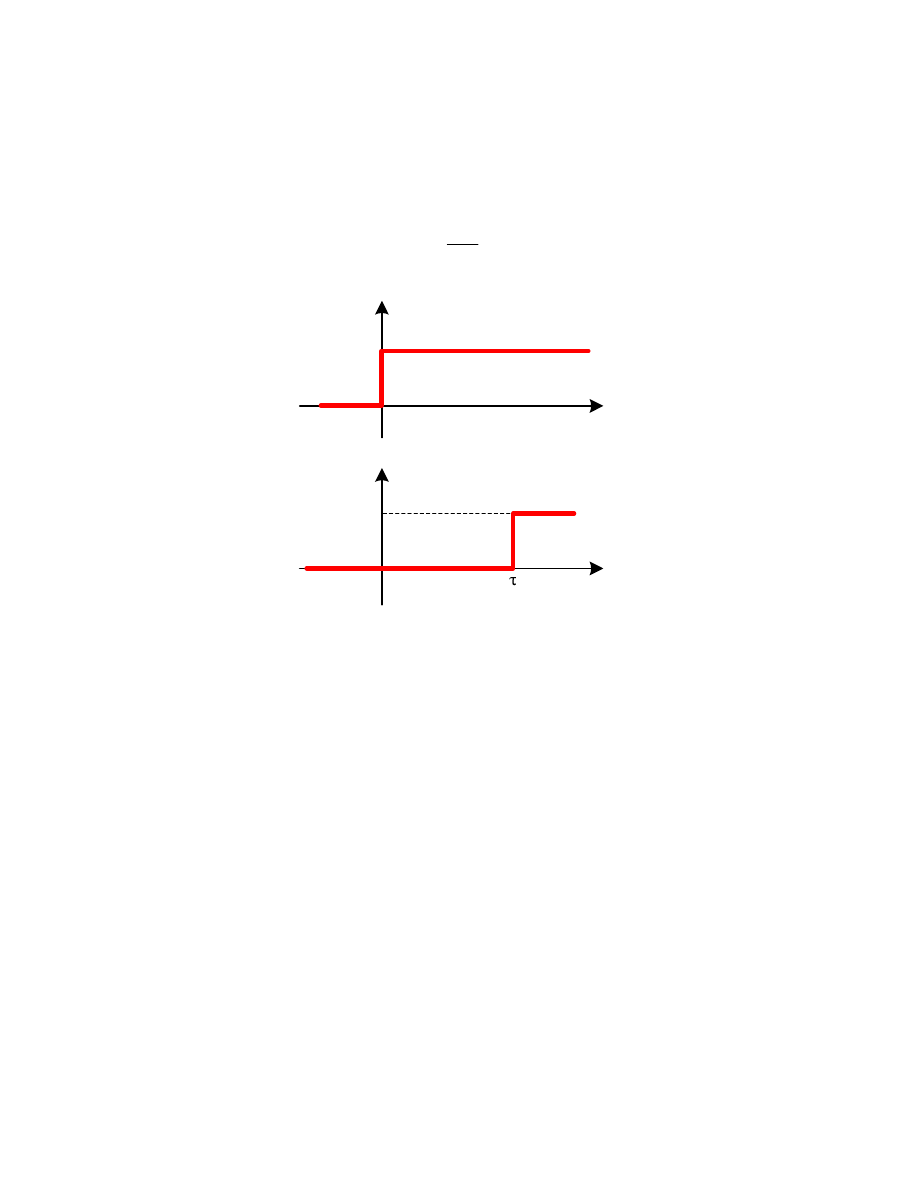
30
2.7
Elementy opó niaj ce
Równanie elementu opó niaj cego ma posta
)
(
)
(
τ
−
= t
u
t
y
sk d wynika transmitancja
s
e
s
u
s
y
s
G
τ
−
=
=
)
(
)
(
)
(
Rysunek 2.14 Wymuszenie u(t)=1(t)u
st
i odpowied y(t)=1(t- )u
st
elementu opó niaj cego
Z podanych równa wynika, e element opó niaj cy nie zniekształca sygnału wej ciowego,
lecz jedynie przesuwa go w czasie. Charakterystyka statyczna b dzie zatem
u
y
= lub
0
0
u
y
=
a odpowied na wymuszenie skokowe b dzie takim samym sygnałem skokowym
przesuni tym w czasie o wielko opó nienia . Wykresy wymuszenia i odpowiedzi skokowej
pokazano na rys. 2.14.
Elementami opó niaj cymi s w szczególno ci urz dzenia słu ce do przemieszczania
(transportu) substancji, je eli miejsce wprowadzania sygnału wej ciowego u i miejsce
odbioru sygnału wyj ciowego y znajduj si w pewnej odległo ci od siebie.
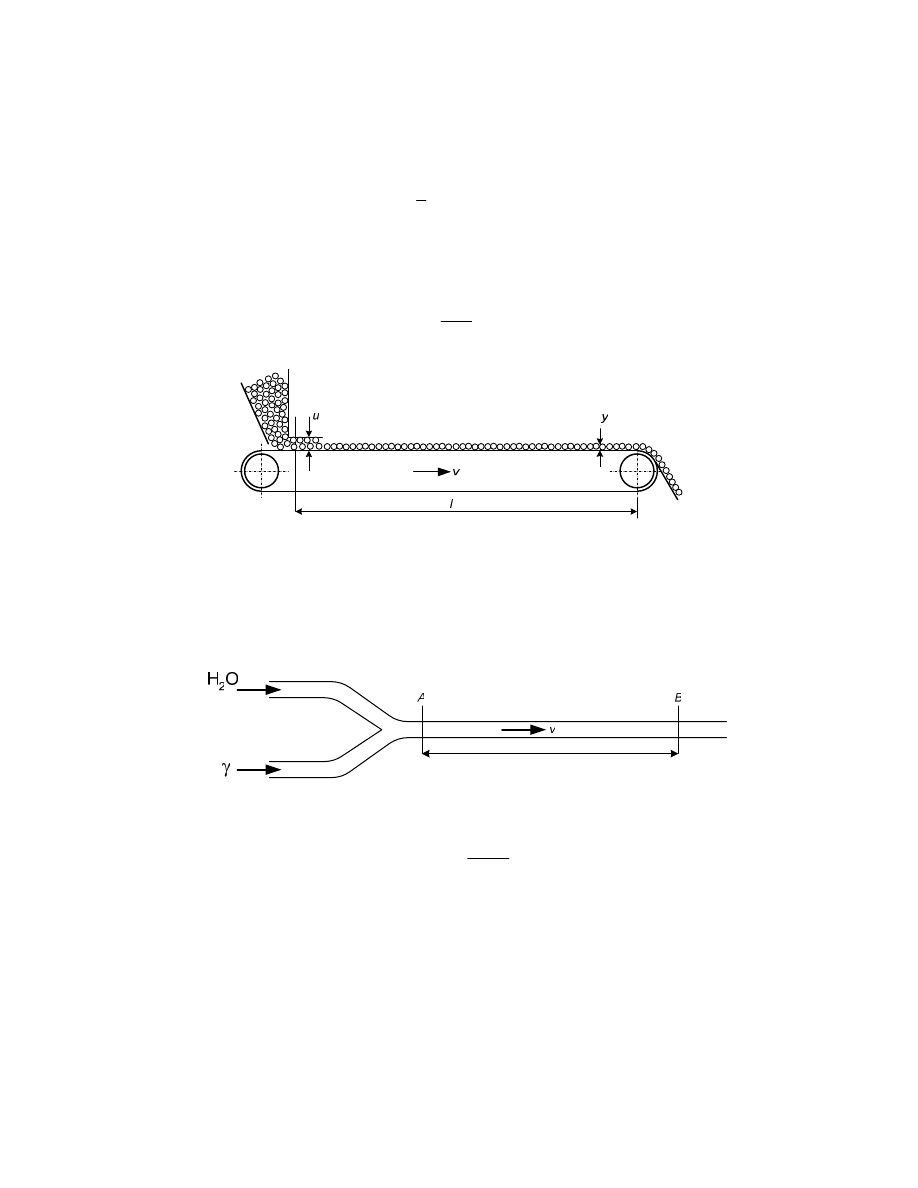
31
Przykład 1. Podajnik ta mowy.
Schemat elementu przedstawiono na rys. 2.15. Sygnałem wej ciowym jest grubo u
warstwy na pocz tku podajnika, a sygnałem wyj ciowym grubo y warstwy na ko cu
podajnika.
Opó nienie wynosi:
v
l
=
τ
gdzie: l – odległo [m]
v – pr dko ta my [m/s]
Transmitancja podajnika
s
e
s
u
s
y
s
G
τ
−
=
=
)
(
)
(
)
(
,
Rysunek 2.15 Schemat podajnika ta mowego
Przykład 2. Odcinek ruroci gu.
Schemat elementu podano na rysunku poni ej. Sygnałem wej ciowym jest st enie
substancji
γ w przekroju A, sygnałem wyj ciowym – st enie tej substancji w przekroju B
ruroci gu.
Przy zało eniu, e nast puje dokładne wymieszanie substancji i w danym przekroju jej
st enie jest jednakowe, otrzymamy
s
A
B
e
s
C
s
C
s
G
τ
−
=
=
)
(
)
(
)
(
gdzie: C
A
– st enie substancji
γ w przekroju A,
C
B
– st enie substancji
γ w przekroju B,
=l/v – opó nienie

32
3 UKŁADANIE SCHEMATÓW BLOKOWYCH
3.1
Zasady budowy schematów blokowych
Schematy blokowe, nazywane równie strukturalnymi, przedstawiaj wzajemne powi zania
pomi dzy poszczególnymi zespołami analizowanego elementu lub układu, tzn. podaj
kierunki przepływu sygnałów oraz zwi zki mi dzy sygnałami wej ciowymi i wyj ciowymi
wszystkich zespołów. Znajomo schematu blokowego ułatwia wyznaczenie opisu
matematycznego (najcz ciej transmitancji) układu i analiz jego własno ci.
Sporz dzanie schematów blokowych elementów lub układów automatyki na podstawie ich
schematów konstrukcyjnych sprawia zwykle pocz tkowo wiele trudno ci. Przyczyn tego jest
konieczno dokładnego zrozumienia działania rozpatrywanego urz dzenia, rozró nienia
wej i wyj , a zatem „kolejno ci” oddziaływania jednych zespołów na drugie, wzi cia pod
uwag natury fizycznej wyst puj cych sygnałów itd.
Proste elementy reprezentowane s na schematach blokowych przez jeden „blok” –
prostok t, wewn trz którego wpisuje si transmitancj (rzadziej równanie ró niczkowe) lub
wrysowuje si charakterystyk danego elementu, najcz ciej odpowied skokow dla
elementów liniowych lub charakterystyk statyczn dla elementów nieliniowych.
Zło one elementy maj własne schematy blokowe, w których poszczególne bloki
reprezentuj z reguły kolejne zespoły (elementy podstawowe) wchodz ce w skład elementu
zło onego.
Schematy blokowe układów, zwłaszcza zawieraj cych elementy zło one mog by dosy
rozbudowane. Dla zwi kszenia ich czytelno ci przekształcamy cz sto schemat elementów
zło onych do postaci pojedynczego bloku i dopiero wówczas wstawiamy je do schematu
całego układu.
Kierunek przepływu sygnałów jest jednoznaczny , poniewa w ka dym układzie wyst puje
co najmniej jeden element skierowany, tzn. element o działaniu jednokierunkowym.
3.2
W zły informacyjne i sumacyjne
W zły informacyjne (zaczepowe) reprezentuj na schematach blokowych urz dzenia, które
pozwalaj pobiera t sam informacj do kilku gał zi układu. Symbol graficzny
podstawowego w zła informacyjnego, w którym pobiera si informacj do dwóch gał zi
układu, jest nast puj cy:
Przykłady urz dze spełniaj cych rol w złów informacyjnych podano na rys. 3.1
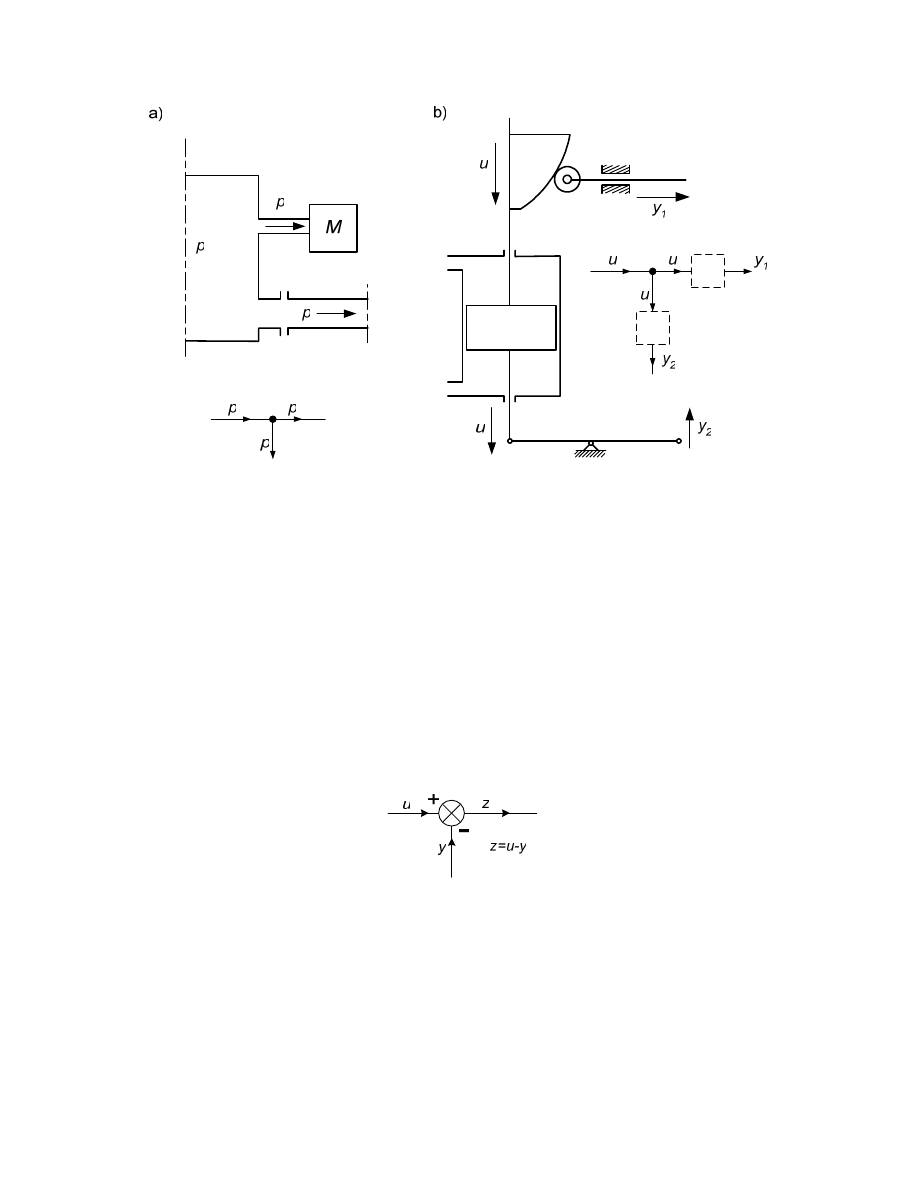
33
Rysunek 3.1
Pierwszy przykład pokazuje zbiornik ci nieniowy, w którym znajduje si medium o
ci nieniu p, odprowadzane ruroci giem do dalszych cz ci instalacji oraz działaj ce na
czujnik przetwornika pomiarowego lub miernika
M tego ci nienia. Je eli zało ymy, e w
całym zbiorniku i wychodz cych z niego przewodach panuje to samo ci nienie p, to
otrzymany typowy przypadek w zła informacyjnego, z którego wychodzi tyle gał zi o
sygnałach p, ile jest wyprowadze tego ci nienia ze zbiornika.
Drugi przykład pokazuj tłoczysko siłownika hydraulicznego, na którym zainstalowana
jest krzywka. Przesuni cie u jest zatem zarówno przesuni ciem tłoczyska i zwi zanego z nim
ko ca d wigni, jak i przesuni ciem krzywki.
W zły sumacyjne reprezentuj na schematach blokowych urz dzenia, w których
zachodzi algebraiczne (z uwzgl dnieniem znaków) sumowanie sygnałów. Symbol graficzny
podstawowego w zła sumacyjnego, w którym zachodzi sumowanie dwóch sygnałów, jest
nast puj cy:
W urz dzeniu reprezentowanym przez ten w zeł realizowana jest zale no z=u–y.
Kilka przykładów urz dze spełniaj cych rol w złów sumacyjnych przedstawiono na
rys. 3.2.
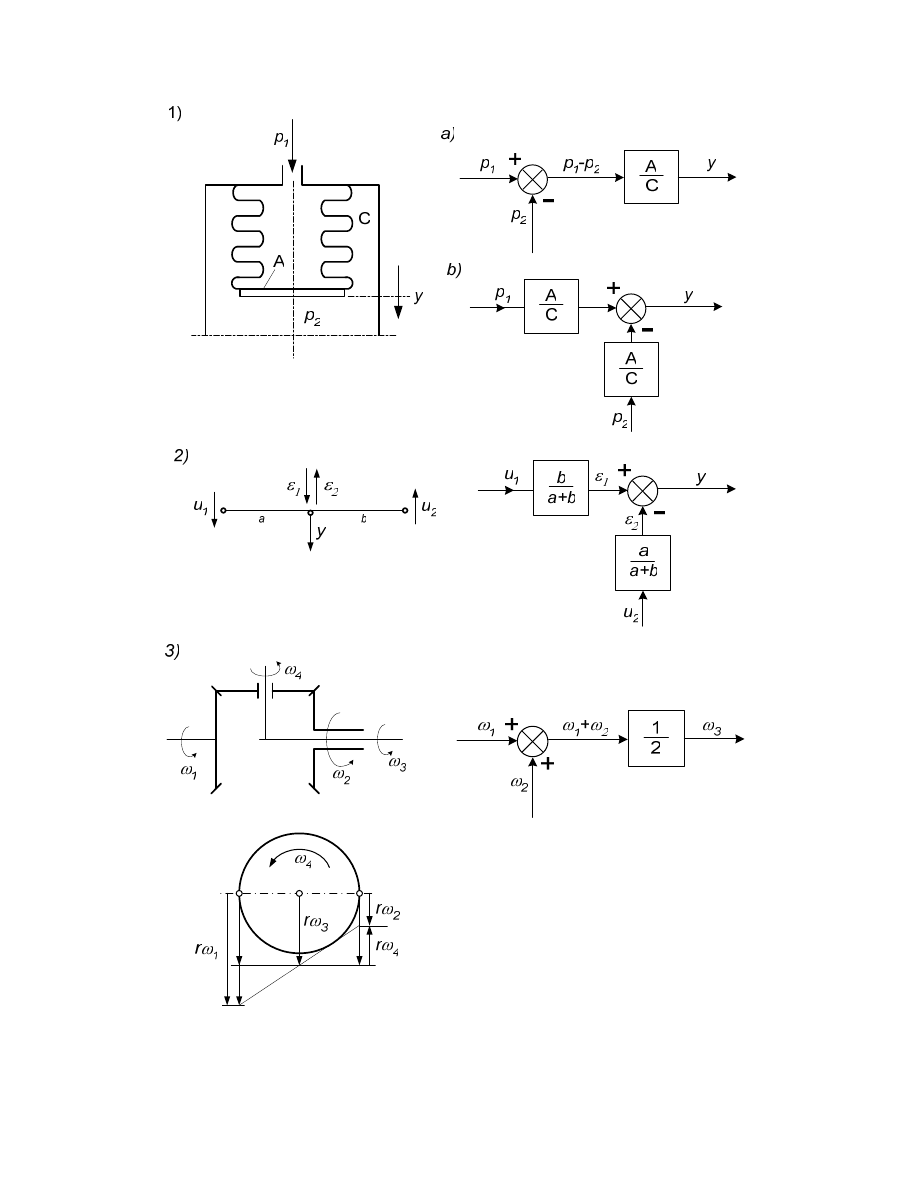
34
Rysunek 3.2 1) czujnik mieszkowy ró nicy ci nie , 2) d wignia, 3) mechanizm ró nicowy

35
Przedstawione na rys. 3.2 schematy blokowe stanowi graficzne odzwierciedlenie
równa opisuj cych własno ci tych urz dze .
1.
Równanie sił działaj cych na mieszek spr ysty
cy
A
p
p
=
−
)
(
2
1
sk d
)
(
2
1
p
p
c
A
y
−
=
( 3.1)
Gdzie:
p
1
,p
2
– sygnały wej ciowe (ci nienia)
y
– sygnał wyj ciowy (przesuni cie)
A – powierzchnia efektywna mieszka spr ystego
C - sztywno mieszka
Schematy blokowe a) oraz b) odpowiadaj równaniu (3.1) i ka dy z nich jest
poprawny
2.
Przy niewielkich przemieszczeniach ko ców d wigni mo na napisa , zgodnie
z zasad superpozycji:
2
1
2
1
u
b
a
a
u
b
a
b
y
+
−
+
=
−
=
ε
ε
( 3.2)
Gdzie:
u
1
, u
2
– sygnały wej ciowe (przesuni cia)
y
– sygnał wyj ciowy (przesuni cia)
ε
1
,
ε
2
– składowe przesuni cia y
a, b
– ramiona d wigni
3.
Mechanizm ró nicowy opiszemy za pomoc równa pr dko ci
poszczególnych punktów koła ró nicowego:
4
3
2
4
3
1
ω
ω
ω
ω
ω
ω
r
r
r
r
r
r
−
=
+
=
Dodaj c stronami otrzymamy
)
(
2
1
2
1
3
ω
ω
ω
+
=
( 3.3)
Gdzie:
ω
1,
ω
2
– sygnały wej ciowe (pr dko ci k towe)
ω
3
– sygnał wyj ciowy
r
– promienie podziałowe wszystkich kół z batych.
Je eli sygnałami wej ciowymi i wyj ciowymi b d k ty obrotu kół z batych,
otrzymamy
)
(
2
1
2
1
3
α
α
α
+
=
( 3.4)
Budowa schematu blokowego pozostanie wi c identyczna, jedynie zamiast „
ω” nale y
wsz dzie wpisa „
α”.
Zmianie kierunku pr dko ci k towej (lub k ta) odpowiada zmiana znaku na wej ciu w zła
sumacyjnego.

36
3.3
Przekształcanie schematów blokowych
Pierwotna posta schematu blokowego jest niekiedy dosy uwikłana i nie mo na
bezpo rednio zastosowa do niej adnego ze wzorów okre laj cych transmitancje poł cze
podstawowych. W pierwszej kolejno ci nale y wi c przekształci schemat blokowy do takiej
postaci, aby wyst powały w niej tylko poł czenia szeregowe, równoległe i ze sprz eniem
zwrotnym. Postacie ogólne transmitancji tych poł cze dla elementów o jednym wej ciu i
wyj ciu (jednowymiarowych) s nast puj ce:
a)
poł czenie szeregowe
∏
=
=
n
i
i
s
G
s
G
1
)
(
)
(
( 3.5)
b)
poł czenie równoległe
=
=
n
i
i
s
G
s
G
1
)
(
)
(
( 3.6)
c)
poł czenie ze sprz eniem zwrotnym
)
(
)
(
1
)
(
)
(
2
1
1
s
G
s
G
s
G
s
G
±
=
( 3.7)
Gdzie:
∏
– symbol iloczynu
– symbol sumy
)
(
s
G
i
– transmitancje elementów składowych
)
(
1
s
G
– transmitancja toru głównego
)
(
2
s
G
– transmitancja toru sprz enia zwrotnego
„+” – obowi zuje dla ujemnego sprz enia zwrotnego
„
−
” – obowi zuje dla dodatniego sprz enia zwrotnego
Dla elementów o wielu wej ciach i wyj ciach (wielowymiarowych) odpowiednie
zale no ci maj identyczn posta , jedynie zamiast transmitancji G(s) wyst puj wsz dzie
macierze transmitancji G(s). W iloczynie (3.5) nie wolno zmienia kolejno ci macierzy.
Przekształcenia sprowadzaj ce schemat blokowy do postaci pozwalaj cej na
zastosowanie wzorów (3.5) i (3.7) polegaj na przesuni ciach w złów informacyjnych i (lub)
sumacyjnych. W ka dym przypadku przekształcania schematu blokowego musi by spełniony
warunek, e w cz ci układu nie podlegaj cej przekształceniu adna wielko nie ulega
zmianie (oznacza to, e wej cia i wyj cia przekształconej cz ci schematu musz pozosta nie
zmienione)
Kilka najcz ciej stosowanych przekształce schematów blokowych (lub ich cz ci)
zawieraj cych wył cznie elementy liniowe zestawiono w tab. 3.1.
Przekształcenia nr 1
÷
4 polegaj na przesuni ciach w złów informacyjnych lub
sumacyjnych w przód lub w tył, tzn. z wej cia bloku o transmitancji
G(s)
na jego wyj cie lub
odwrotnie. Przekształcenia te pozostaj wa ne równie dla elementów o wielu wej ciach i
wyj ciach, z tym zastrze eniem, e przekształcenia nr 2 i 4 s wykonalne tylko dla macierzy
kwadratowych nieosobliwych (o wyznaczniku ró nym od zera), gdy tylko wówczas istnieje
macierz odwrotna
[G(s)]
-1
.
Przekształcenia nr 5 i 6 pokazuj , e mo na zmienia kolejno w złów jednego
rodzaju (informacyjnych lub sumacyjnych), a nr 7 i 8 podaj zasady zmiany kolejno ci
w złów ró nego rodzaju, tzn. przesuwania w zła informacyjnego przed sumacyjny lub
odwrotnie.

37
Ni ej podane zostan dwa przykłady wyznaczania transmitancji zło onych układów
na podstawie ich schematów blokowych. Wybrano takie przypadki, w których konieczne s
obydwa etapy post powania, tzn. najpierw doprowadzenie schematu za pomoc przekształce
podanych w tabl. 3.1 do postaci poł cze podstawowych, a nast pnie zwijanie tych poł cze
za pomoc zale no ci (3.5) do (3.7) ,a do postaci pozwalaj cej na wyznaczenie transmitancji
całego układu.
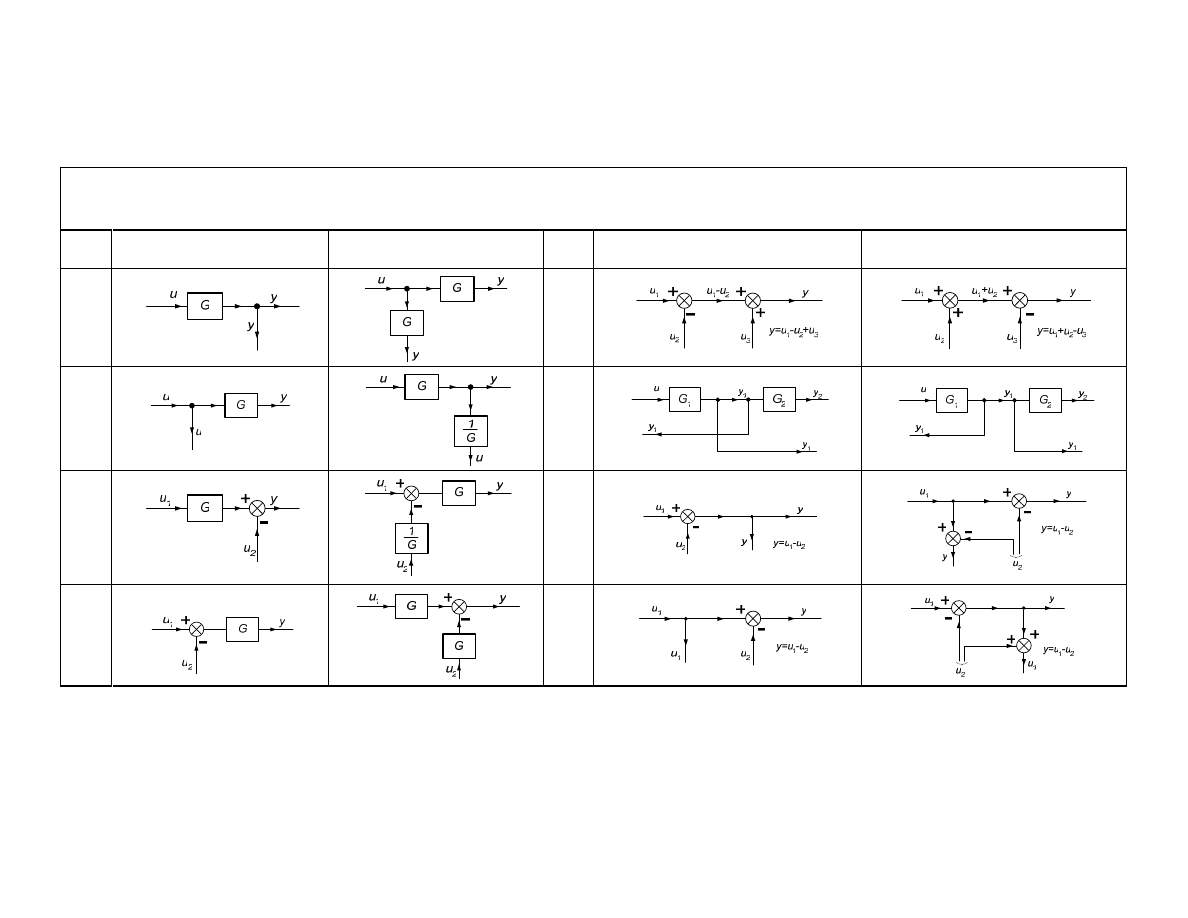
38
tablica 3.1
Przesuni cia w złów informacyjnych i sumacyjnych
L.p.
Schemat pierwotny
Schemat równowa ny
L.p.
Schemat pierwotny
Schemat równowa ny
1
5
2
6
3
7
4
8
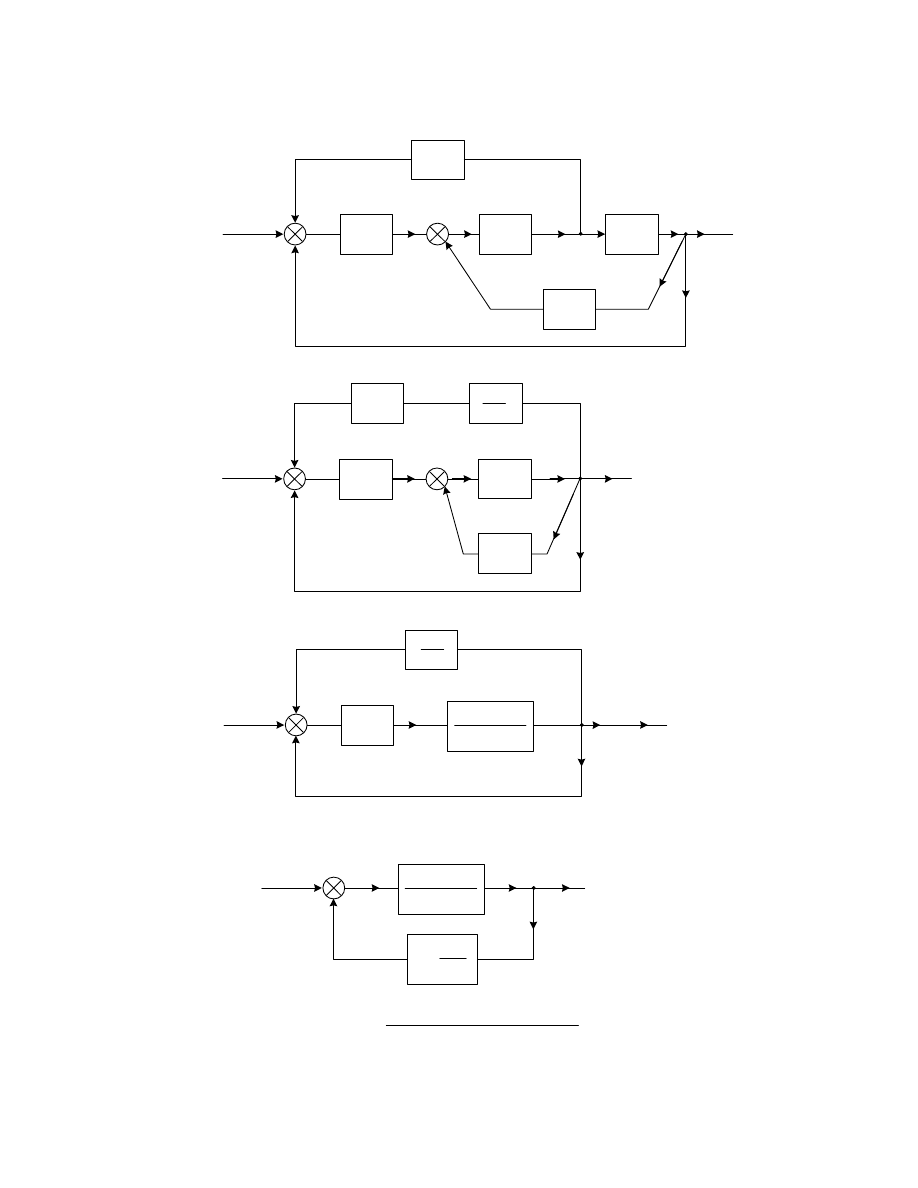
39
Przykład 1.
)
(
1
)
(
4
3
2
1
5
3
2
3
2
1
G
G
G
G
G
G
G
G
G
G
s
G
−
+
+
=
Rysunek 3.3
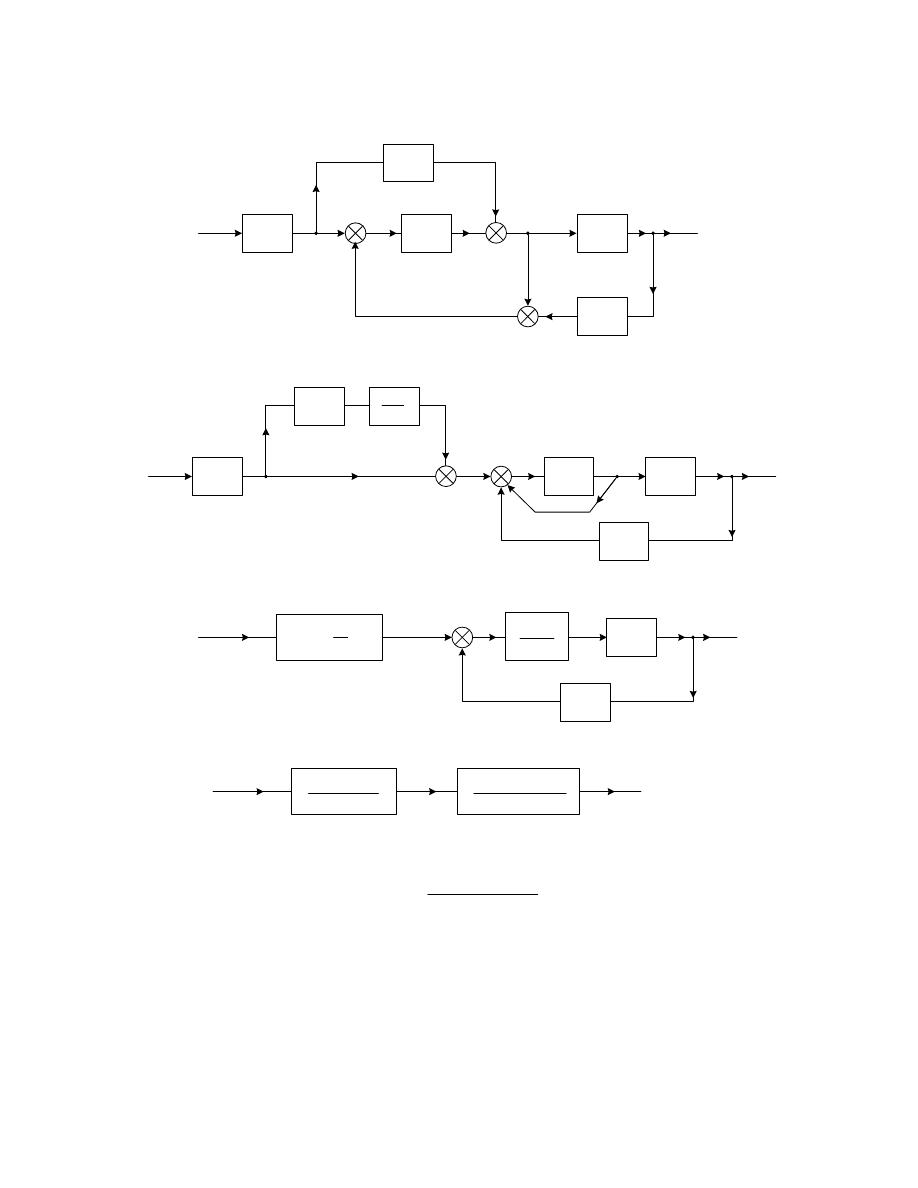
40
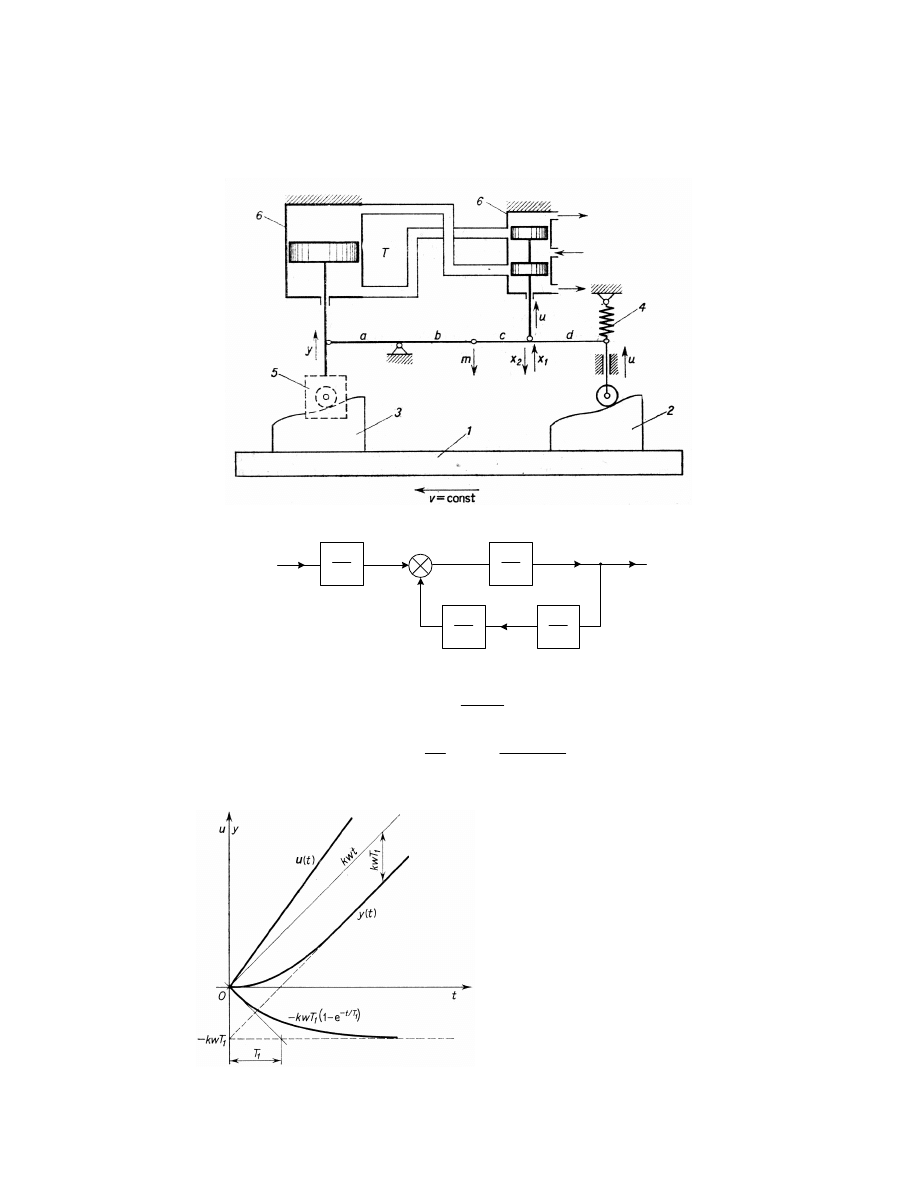
Przykład 2.
)
1
(
1
)
(
)
(
5
3
2
4
2
3
1
−
+
−
=
G
G
G
G
G
G
G
s
G
Rysunek 3.4
41
3.4
Przykłady układania (tworzenia) schematów blokowych
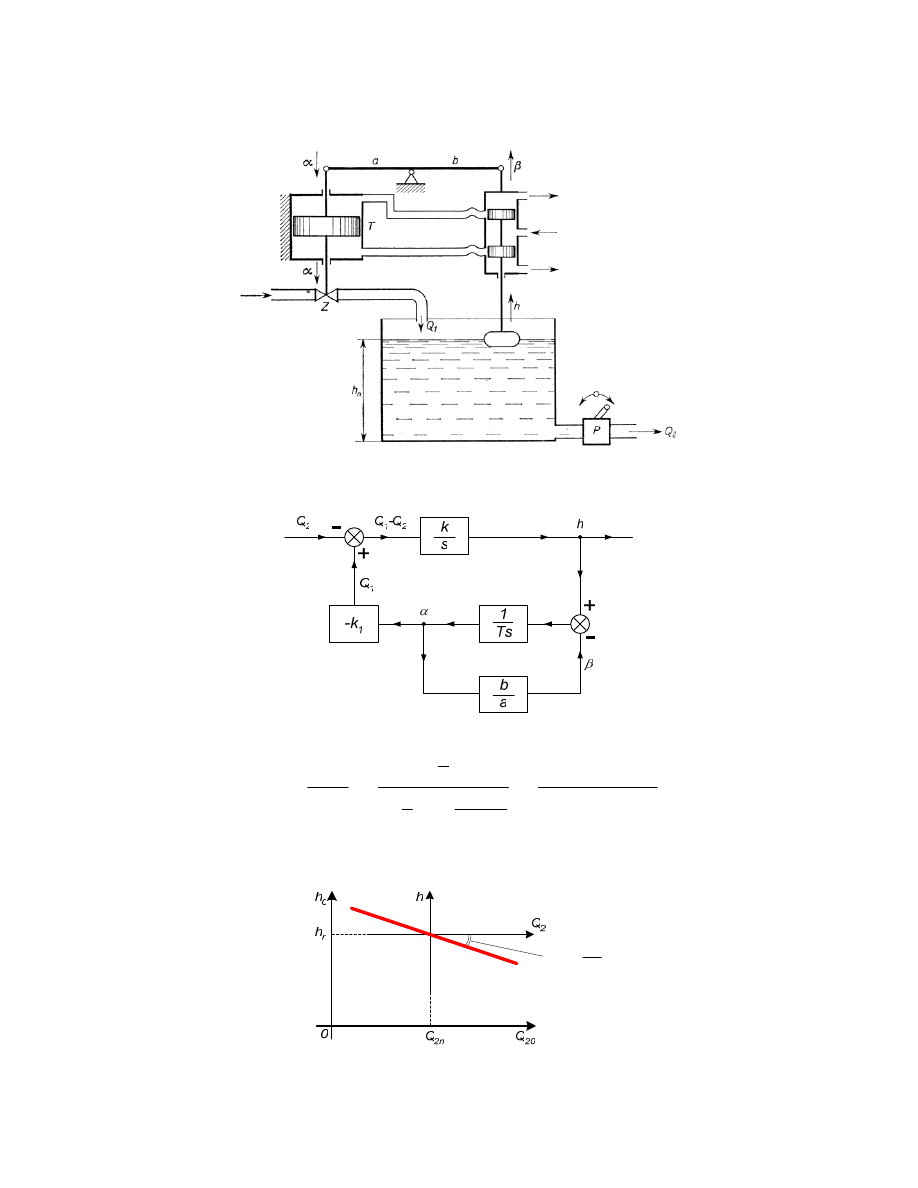
3.4.1
Schemat kopiału hydraulicznego
Uło enie schematu blokowego:
1
)
(
1
+
=
s
T
k
s
G
gdzie:
bd
ac
k
=
,
bd
d
c
Ta
T
)
(
1
+
=
Wyznaczenie odpowiedzi na wymuszenie u(t)=wt:
)]
1
(
[
)
(
1
/
1
T
t
e
T
t
kw
t
y
−
−
−
=
42
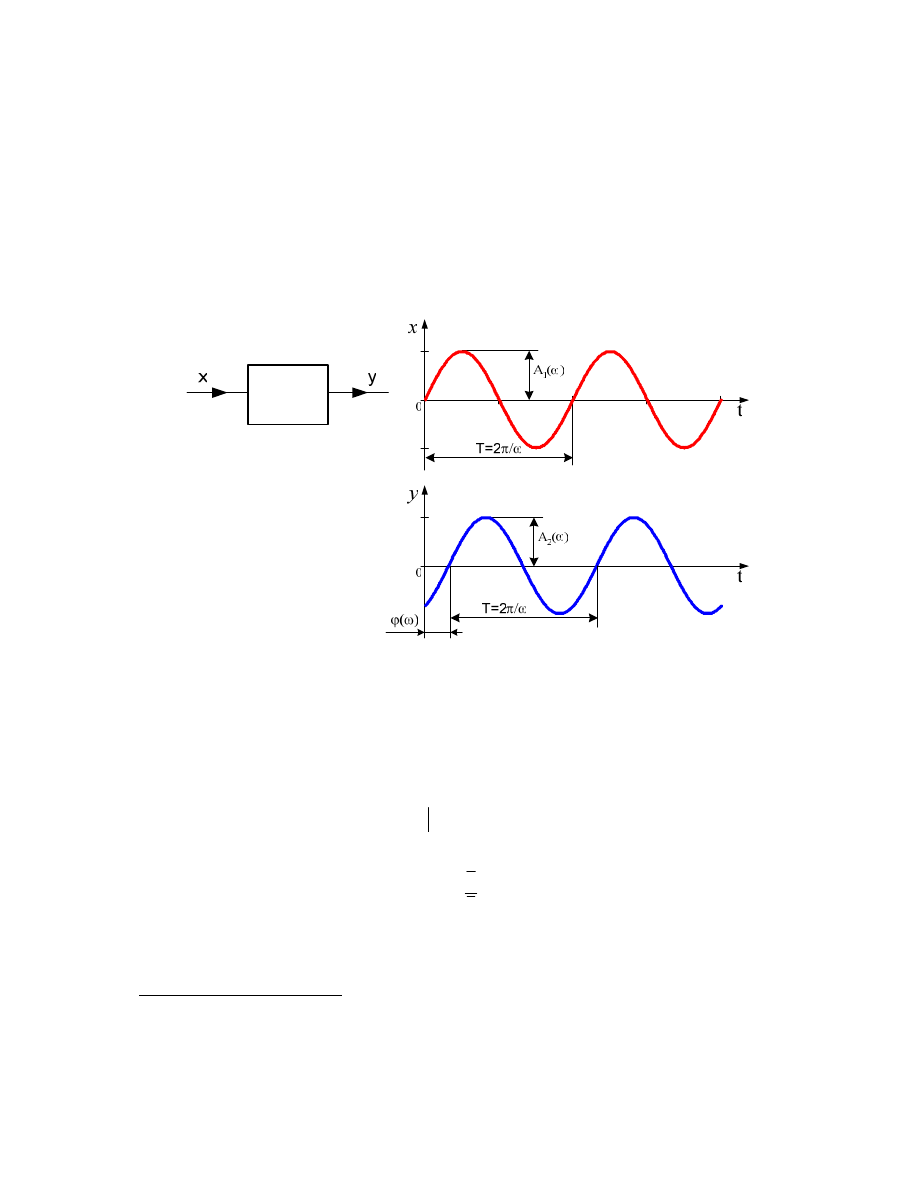
3.4.2
Przykład układu regulacji poziomu cieczy w zbiorniku
Schemat blokowy:
Transmitancja układu:
a
kk
b
aTs
s
b
aTs
k
b
aTs
a
k
s
k
s
k
s
Q
s
h
s
G
1
1
2
)
(
)
(
)
(
1
)
(
)
(
)
(
+
+
+
−
=
+
−
−
−
=
=
Wyznaczenie charakterystyki statycznej:
−
1
ak
b
arctg
43
4 CHARAKTERYSTYKI CZ STOTLIWO CIOWE
4.1
Transmitancja widmowa. Rodzaje charakterystyk cz stotliwo ciowych.
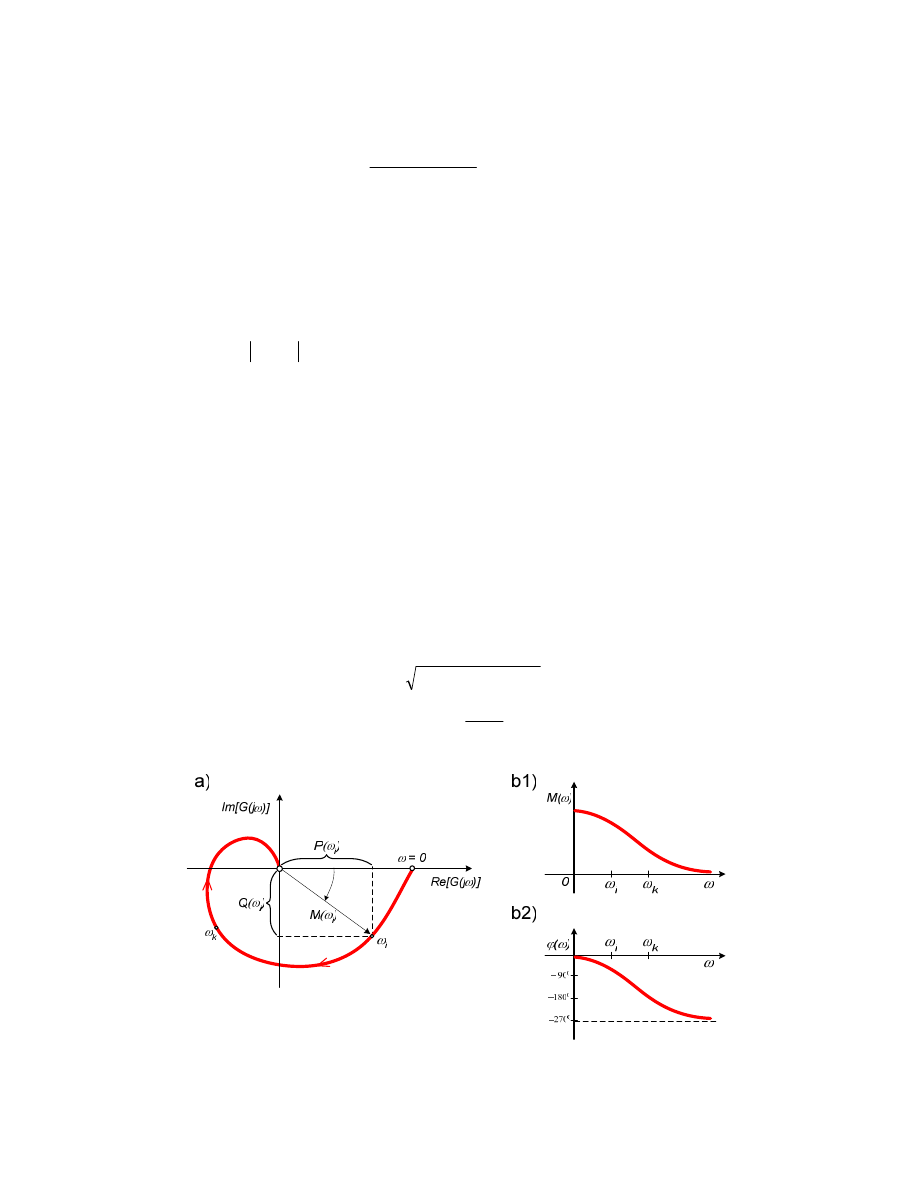
Je eli na wej cie elementu lub układu liniowego stabilnego wprowadzone zostanie
wymuszenie sinusoidalne o stałej cz stotliwo ci, to na wyj ciu, po zanikni ciu przebiegu
przej ciowego, ustali si odpowied sinusoidalna o tej samej cz stotliwo ci, ale w ogólnym
przypadku, o innej amplitudzie i fazie ni wymuszenie. Na rysunku przedstawiono przypadek,
gdy odpowied jest przesuni ta w kierunku ujemnym wzgl dem wymuszenia, tzn.
0
)
(
<
ω
ϕ
.
)]
(
sin[
)
(
sin
)
(
2
1
ω
ϕ
ω
ω
ω
ω
+
=
=
t
A
y
t
A
x
Rysunek 4.1 Przechodzenie sygnału sinusoidalnego przez element liniowy
Charakterystyki cz stotliwo ciowe okre laj zachowanie si elementu lub układu przy
wszystkich cz stotliwo ciach wymuszenia, podaj c stosunek amplitud odpowiedzi do
wymuszenia oraz przesuni cie fazowe mi dzy odpowiedzi a wymuszeniem jako funkcje
cz stotliwo ci.
Teoretyczn podstaw charakterystyk cz stotliwo ciowych stanowi transmitancja
widmowa, któr mo na uwa a za szczególny przypadek transmitancji operatorowej:
)
(
)
(
)
(
)
(
ω
ϕ
ω
ω
ω
j
j
s
e
A
s
G
j
G
=
=
=
( 4.1)
i któr definiuje si cz sto:
x
y
j
G
=
)
(
ω
( 4.2)
gdzie y jest warto ci zespolon składowej ustalonej odpowiedzi układu wywołanej
wymuszeniem sinusoidalnym, a x warto ci zespolon tego wymuszenia. Podstawiaj c za x i
y par odpowiadaj cych sobie funkcji harmonicznych zapisanych w postaci wykładniczej
*)
:
*)
Je eli na wej cie elementu lub układu liniowego wprowadzimy wymuszenie harmoniczne
]
sin
)[cos
(
)
(
1
1
t
j
t
A
e
A
t
j
ω
ω
ω
ω
ω
+
=
, to na wyj ciu ustali si odpowied harmoniczna
)]}
(
sin[
)]
(
){cos[
(
)
(
2
)]
(
[
2
ω
ϕ
ω
ω
ϕ
ω
ω
ω
ω
ϕ
ω
+
+
+
=
+
t
j
t
A
e
A
t
j
.
44
t
j
e
A
x
ω
ω)
(
1
=
,
)]
(
[
2
)
(
ω
ϕ
ω
ω
+
=
t
j
e
A
y
,
otrzymamy:
)
(
1
)
(
2
)
(
)
(
)
(
)
(
ω
ϕ
ω
ω
ϕ
ω
ω
ω
ω
ω
j
t
j
j
t
j
e
M
e
A
e
e
A
j
G
=
=
( 4.3)
gdzie:
)
(
/
)
(
)
(
1
2
ω
ω
ω
A
A
M
=
jest modułem charakterystyki cz stotliwo ciowej (stosunkiem
amplitud odpowiedzi do wymuszenia).
Wykres
)
(
ω
j
G
nazywa si charakterystyk amplitudowo-fazow lub zespolon charakterystyk
cz stotliwo ciow , lub wykresem transmitancji widmowej. Wykres ten jest miejscem geometrycznym
ko ców wektorów, których długo reprezentuje stosunek amplitud odpowiedzi do wymuszenia, a k t
- przesuni cie fazowe mi dzy odpowiedzi a wymuszeniem. Zamiast wykresu
)
(
ω
j
G
mo na poda
oddzielne wykresy jego współrz dnych biegunowych
)
(
ω
j
M
i
)
(
ω
ϕ
j
.
Nazywaj si one:
)
(
)
(
ω
ω
j
G
M
=
-
amplitudowa charakterystyka cz stotliwo ciowa (wykres
modułu charakterystyki cz stotliwo ciowej),
)
(
arg
)
(
ω
ω
ϕ
j
G
=
-
fazowa charakterystyka cz stotliwo ciowa (wykres argumentu
charakterystyki cz stotliwo ciowej).
Poniewa
)
(
ω
j
G
jest funkcj zespolon , mo na rozło y j na cz
rzeczywist i cz
urojon [współrz dne prostok tne
)
(
ω
j
G
]:
)
(
)
(
)
(
ω
ω
ω
jQ
P
j
G
+
=
( 4.4)
gdzie
)]
(
Re[
)
(
ω
ω
j
G
P
=
- cz
rzeczywista
)
(
ω
j
G
)]
(
Im[
)
(
ω
ω
j
G
Q
=
- cz
urojona
)
(
ω
j
G
Z rysunku 4.2 wynikaj nast puj ce zwi zki, bardzo istotne przy analitycznym
wyznaczaniu charakterystyk cz stotliwo ciowych:
2
2
)]
(
[
)]
(
[
)
(
ω
ω
ω
Q
P
j
M
+
=
( 4.5)
)
(
)
(
)
(
ω
ω
ω
ϕ
P
Q
arctg
=
( 4.6)
∞
=
ω
Rysunek 4.2 Charakterystyki cz stotliwo ciowe: a) charakterystyka amplitudowo-fazowa (zespolona
charakterystyka cz stotliwo ciowa), bl) charakterystyka amplitudowa, b2) charakterystyka fazowa

45
Charakterystyki amplitudowa i fazowa s przedstawiane zwykle we współrz dnych
logarytmicznych i nazywaj si wówczas:
)
(
log
20
)
(
ω
ω
M
L
=
— logarytmiczna charakterystyka amplitudowa
)
(
ω
ϕ
— logarytmiczna charakterystyka fazowa.
Rysunek 4.3 Współrz dne logarytmicznych charakterystyk amplitudowej L(ω
ωω
ω) i fazowej ϕϕϕϕ(ω
ωω
ω)
Współrz dne tych charakterystyk przedstawiono na rys. 4.3. Podziałka osi
ω jest
logarytmiczna, dekadowa, tzn. ka dej dekadzie
ω przyporz dkowany jest odcinek o
jednakowej długo ci na osi co. Podziałk osi L(
ω) jest liniowa, skalowana w decybelach (dB).
Cz sto na tej osi odkłada si bezpo rednio stosunek amplitud M(
ω). Podziałka osi M(ω) jest
wówczas logarytmiczna.
Warto ci
)
(
ω
L
obliczamy według wzoru:
)
(
log
20
)
(
ω
ω
M
L
=
( 4.7)
4.2
Logarytmiczne charakterystyki amplitudowa i fazowa elementu
inercyjnego pierwszego rz du
Transmitancja widmowa elementu inercyjnego pierwszego rz du jest nast puj ca:
1
)
(
+
=
ω
ω
Tj
k
j
G
( 4.8)
Cz ci rzeczywist i urojon G(j
ω
) wyznaczamy mno c licznik i mianownik transmitancji
przez liczb zespolon sprz on z mianownikiem:
1
1
1
1
2
2
−
−
+
−
=
−
−
+
ω
ω
ω
ω
ω
T
kTj
k
Tj
Tj
Tj
k
St d:
1
)
(
2
2
+
=
ω
ω
T
k
P
,
1
)
(
2
2
+
−
=
ω
ω
ω
T
kT
Q
( 4.9)
Logarytmiczna charakterystyka amplitudowa:
[
] [
]
1
log
20
)
(
)
(
log
20
)
(
log
20
)
(
2
2
2
2
+
=
+
=
=
ω
ω
ω
ω
ω
T
k
Q
P
M
L
46
1
log
20
log
20
)
(
2
2
+
−
=
ω
ω
T
k
L
( 4.10)
∞
=
ω
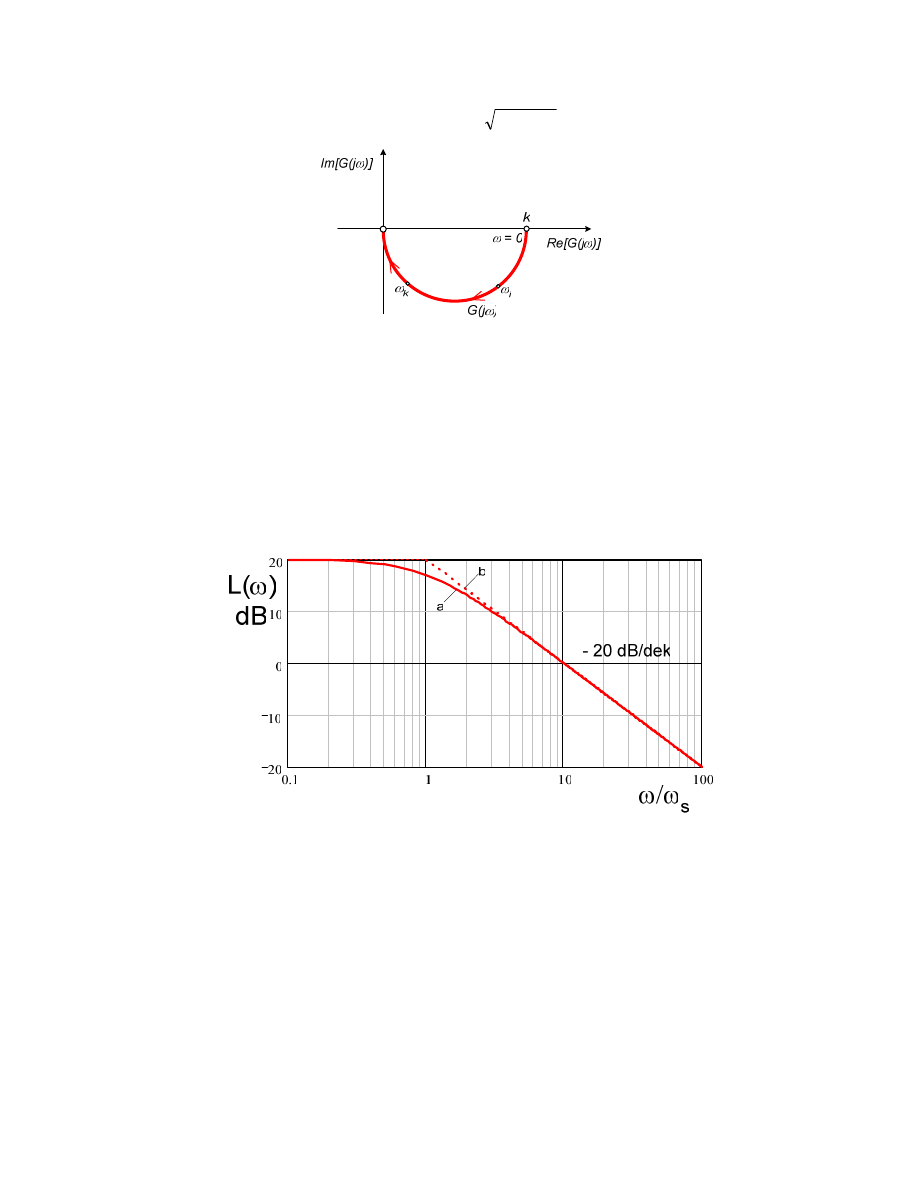
Rysunek 4.4
Charakterystyka amplitudowo-fazowa G(j
ω
ωω
ω
) elementu inercyjnego pierwszego rz du
Wykres L(
ω) mo na upro ci , pomijaj c we wzorze (4.10) dla
T
/
1
<
ω
składnik
2
2
ω
T
, a dla
T
/
1
>
ω
składnik
1
pod pierwiastkiem. Otrzymamy wówczas tzw.
asymptotyczn logarytmiczn charakterystyk amplitudow :
dla
T
/
1
<
ω
k
L
log
20
)
(
=
ω
dla
T
/
1
>
ω
ω
ω
T
k
L
log
20
log
20
)
(
−
=
Pulsacja (cz stotliwo k towa)
T
/
1
=
ω
nazywana jest pulsacj sprz gaj c i oznacza si j
symbolem
s
ω
lub
0
ω
.
Rysunek 4.5
Logarytmiczna charakterystyka amplitudowa elementu inercyjnego pierwszego rz du dla k = 10:
a — rzeczywista, b — asymptotyczna
Wykresy rzeczywistej i asymptotycznej charakterystyki amplitudowej podano na rys.
4.5. Nachylenie opadaj cego odcinka charakterystyki asymptotycznej (dla
T
/
1
<
ω
)
okre limy obliczaj c przyrost
)
(
ω
L
na dekad :
dB
T
k
T
k
L
L
20
)
10
log(
20
)
log(
20
log
20
)
10
log(
20
log
20
)
(
)
10
(
−
=
−
=
+
−
−
=
−
ω
ω
ω
ω
( 4.11)
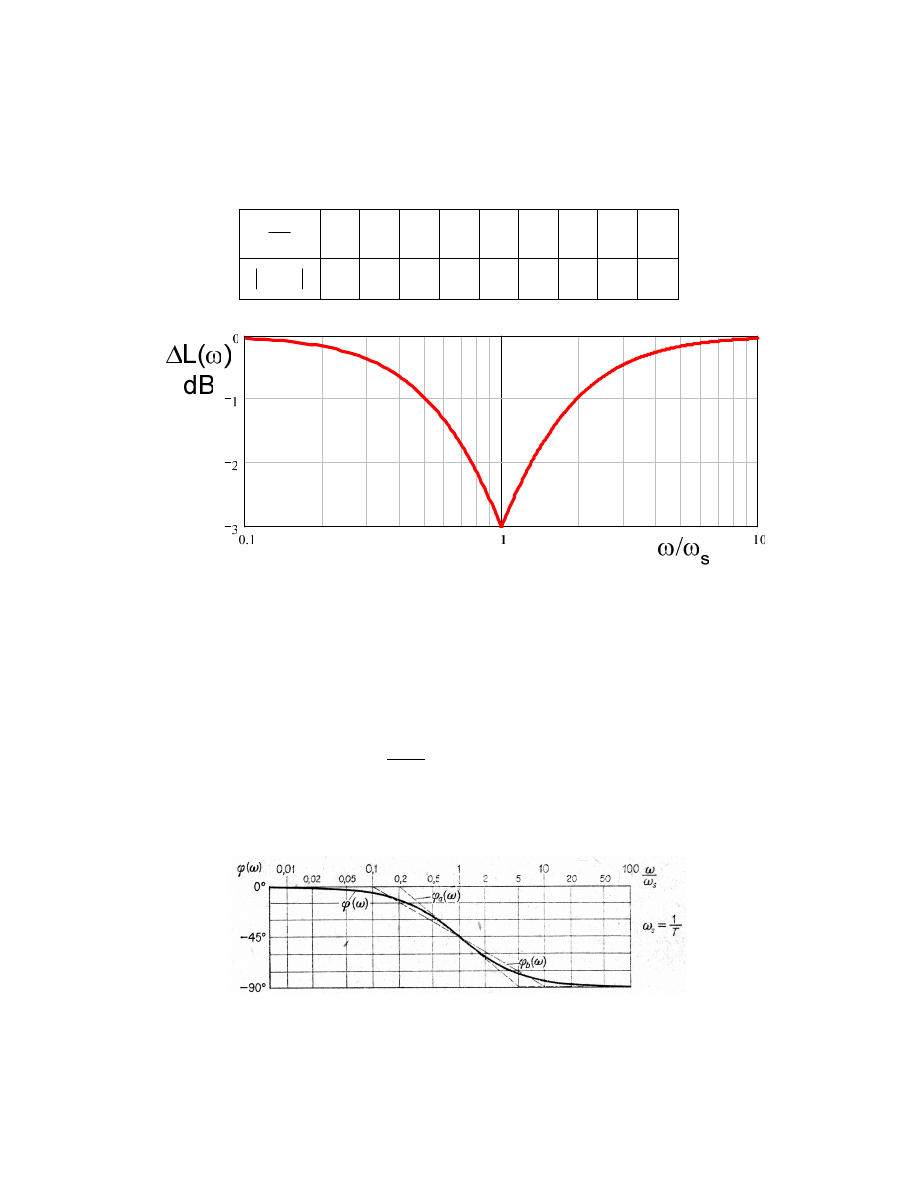
47
W tablicy 4.1 zestawiono kilka warto ci bł du popełnianego przy operowaniu charakterystyk
asymptotyczn , a na rys. 4.6 przedstawiono wykres tego bł du jako funkcj
S
ω
ω /
.
Tablica 4.1
S
ω
ω
0,1 0,25 0,4 0,5 1,0 10 2,5 4,0 10,0
)
(
ω
L
∆
0,04 0,32 0,65 1,0 3,01 1,0 0,65 0,32 0,04
Rysunek 4.6 Wykres bł du
)
(
ω
L
∆
W praktyce, przy obliczeniach wst pnych posługujemy si charakterystykami
asymptotycznymi, a przy obliczeniach dokładnych charakterystykami rzeczywistymi, które
otrzymujemy przez dodanie wykresu przedstawionego na rys. 4.8 (lub poprawek według
tablicy 4.1) do charakterystyk asymptotycznych.
Logarytmiczna charakterystyka fazowa:
)
(
)
(
)
(
)
(
)
(
ω
ω
ω
ω
ω
ϕ
T
arctg
T
arctg
P
Q
arctg
−
=
−
=
=
Wykres
)
(
ω
ϕ
podano na Rysunek 4.7. Na tym samym rysunku liniami kreskowanymi
zaznaczono stosowane niekiedy aproksymacje trójodcinkowe krzywej
)
(
ω
ϕ
.
Rysunek 4.7 Logarytmiczna charakterystyka fazowa elementu inercyjnego pierwszego rz du
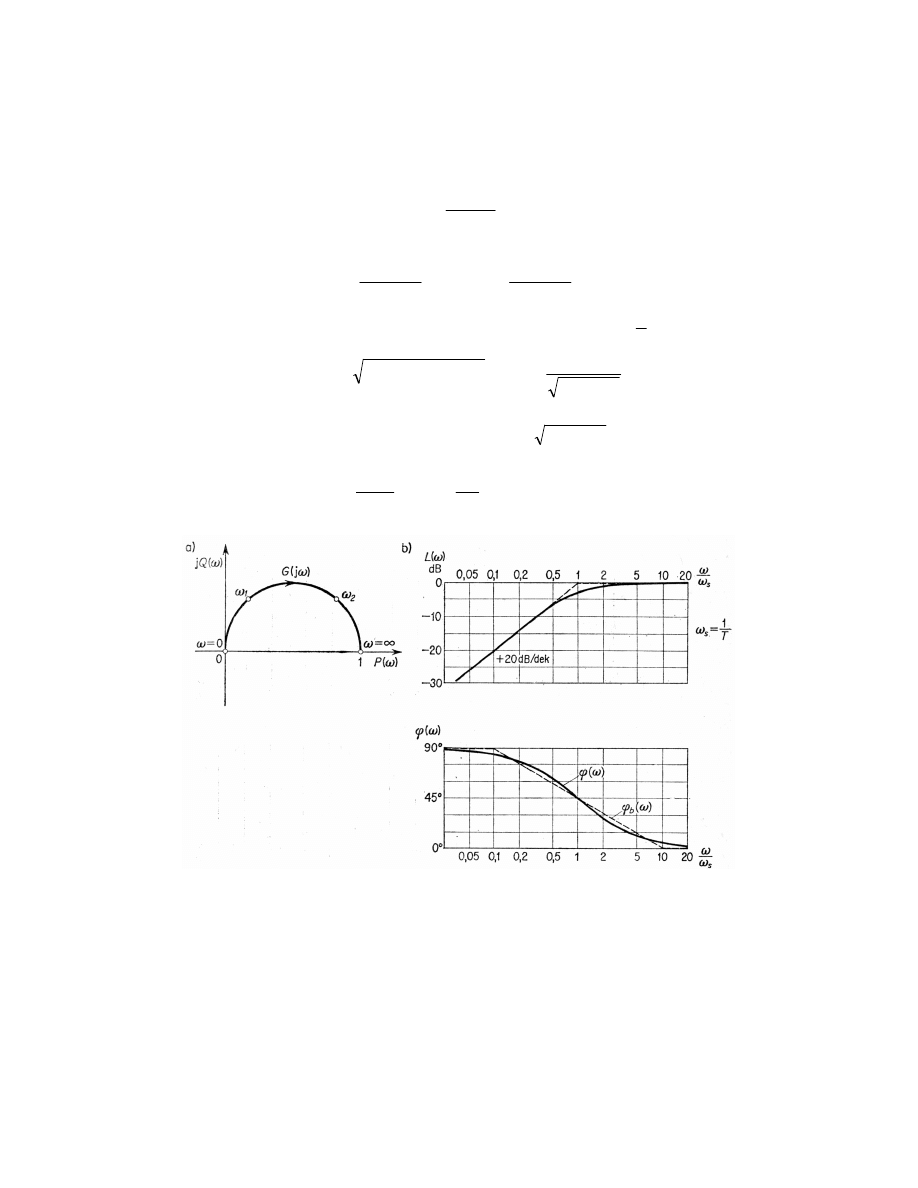
48
4.3
Charakterystyka amplitudowo-fazowa oraz logarytmiczne charakterystyki
amplitudowa i fazowa elementu ró niczkuj cego rzeczywistego
Transmitancja widmowa rzeczywistego elementu ró niczkuj cego ma posta :
1
)
(
+
=
ω
ω
ω
Tj
Tj
j
G
( 4.12)
Cz ci rzeczywista i urojona
)
(
ω
j
G
:
1
)
(
2
2
2
2
+
=
ω
ω
ω
T
T
P
,
1
)
(
2
2
+
=
ω
ω
ω
T
T
P
( 4.13)
Wykres
)
(
ω
j
G
ma posta półokr gu o rednicy l, ze rodkiem w punkcie
0
,
2
1
j
(rys. 4.8).
[
] [
]
1
log
20
)
(
)
(
log
20
)
(
2
2
2
2
+
=
+
=
ω
ω
ω
ω
ω
T
T
Q
P
L
( 4.14)
1
log
20
log
20
)
(
2
2
+
−
=
ω
ω
ω
T
T
L
)
(
90
)
1
(
)
(
)
(
)
(
0
ω
ω
ω
ω
ω
ϕ
T
arctg
T
arctg
P
Q
arctg
−
=
=
=
( 4.15)
Rysunek 4.8 Charakterystyki rzeczywistego elementu ró niczkuj cego: a) charakterystyka
amplitudowo-fazowa, b) logarytmiczne charakterystyki amplitudowa i fazowa
Wykresy
)
(
ω
L
i
)
(
ω
ϕ
przedstawiono powy ej. Liniami ci głymi zaznaczono
charakterystyki rzeczywiste, a liniami kreskowanymi charakterystyki asymptotyczne, przy
czym asymptotyczn charakterystyk fazow narysowano zgodnie z aproksymacj
)
(
ω
ϕ
b
.
Wszystkie uwagi dotycz ce dokładno ci charakterystyk asymptotycznych, a w szczególno ci
wykresy bł du podane na rys. 4.6, pozostaj wa ne.
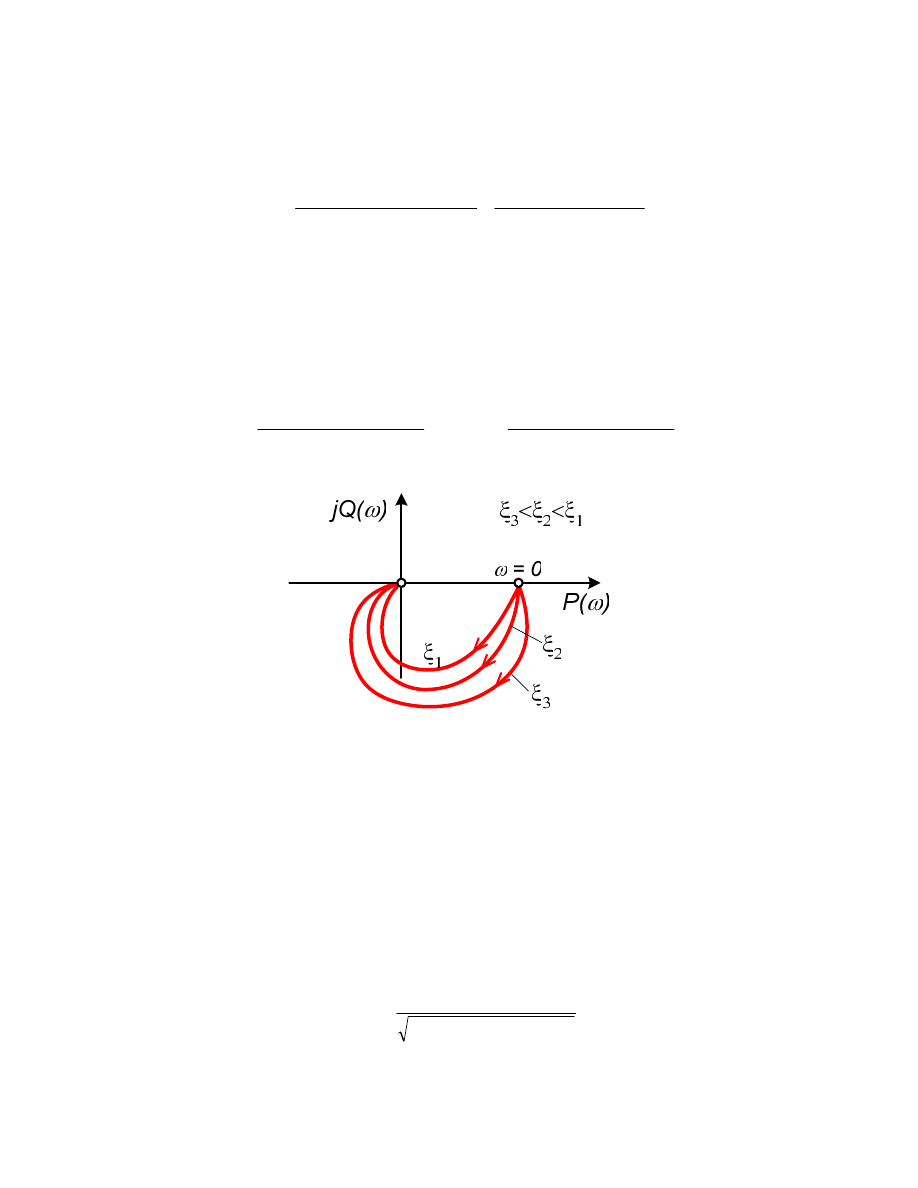
49
4.4
Charakterystyka amplitudowo-fazowa oraz logarytmiczne charakterystyki
amplitudowa i fazowa elementu drugiego rz du
Zbadamy charakterystyki elementu o transmitancji widmowej:
( )
( ) ( )
0
2
2
0
2
0
2
0
0
2
2
0
2
2
)
(
ζωω
ω
ω
ω
ω
ω
ζω
ω
ω
ω
⋅
+
−
=
+
+
=
j
k
j
j
k
j
G
( 4.16)
Gdzie: k — współczynnik proporcjonalno ci
0
ω
— pulsacja oscylacji własnych elementu
ζ — zredukowany (wzgl dny) współczynnik tłumienia
Element ten omówiono w p. 2.6, zale nie od warto ci jego odpowiedzi skokowe mog by
oscylacyjne lub aperiodyczne.
Cz ci rzeczywista i urojona:
2
0
2
2
2
0
2
2
0
2
0
)
2
(
)
(
)
(
)
(
ω
ζω
ω
ω
ω
ω
ω
ω
+
−
−
=
k
P
,
2
0
2
2
2
0
3
0
)
2
(
)
(
2
)
(
ω
ζω
ω
ω
ω
ζω
ω
+
−
=
k
Q
( 4.17)
∞
=
ω
Rysunek 4.9 Charakterystyka amplitudowo-fazowa
)
(
ω
j
G
elementu drugiego rz du dla ró nych
warto ci ζζζζ
Wykres
)
(
ω
j
G
przedstawiono na rys. 4.9. Wykres ten rozpoczyna si zawsze w punkcie
(
)
0
, j
k
, poniewa :
k
P
=
)
0
(
,
0
)
0
(
=
Q
a ko czy si w punkcie
(
)
0
,
0 j
, poniewa :
0
)
(
=
∞
P
,
0
)
(
=
∞
Q
Kształt krzywej zale y od warto ci edukowanego współczynnika tłumienia
ζ.
Logarytmiczna charakterystyka amplitudowa:
2
0
2
2
2
0
2
0
)
2
(
)
(
log
20
)
(
ω
ζω
ω
ω
ω
ω
+
−
=
k
L
( 4.18)
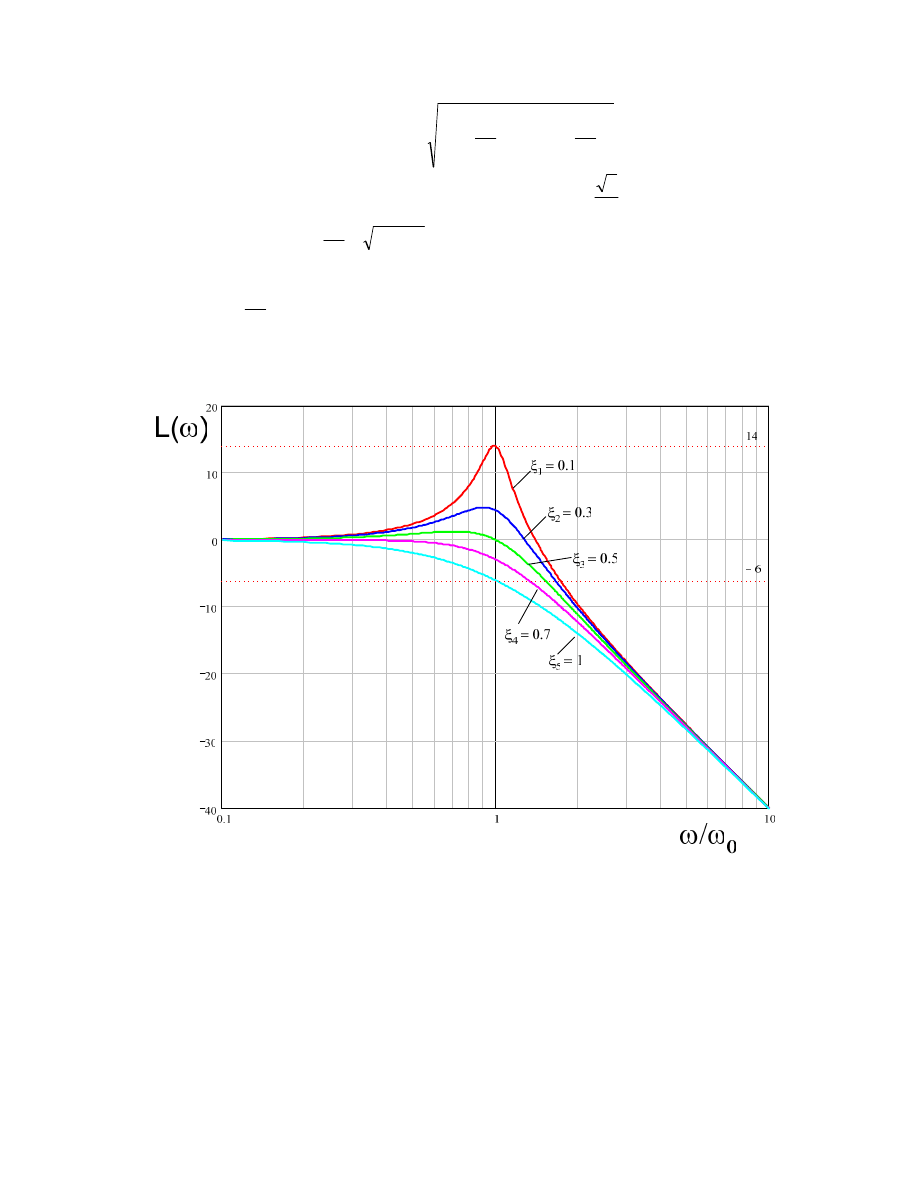
50
2
0
2
2
0
2
1
log
20
log
20
)
(
+
−
−
=
ω
ω
ζ
ω
ω
ω
k
L
( 4.19)
Wykresy
)
(
ω
L
dla kilku warto ci
ζ podano na rys. 4.10. Dla
2
2
<
ζ
charakterystyka
)
(
ω
L
osi ga maksimum przy
2
0
2
1
ζ
ω
ω
−
=
, przy czym warto tego-maksimum jest tym
wi ksza, im mniejsz warto ma zredukowany współ
czynnik tłumienia
ζ. Dla ζ=0 maksimum
wyst puje przy
1
0
=
ω
ω
i ma warto niesko czenie wielk . Wykresy na rys. 4.10 i 4.11 obejmuj
obszar warto ci charakterystyczny dla elementów oscylacyjnych ( <1). Warto ci graniczn jest
=1, kiedy element przestaje by oscylacyjny (odpowied skokowa jest wtedy aperiodyczna, jest
to przypadek szczególny – przebieg aperiodyczny najkrócej trwaj cy).
Rysunek 4.10
Logarytmiczna charakterystyka amplitudowa elementu oscylacyjnego, dla
1
=
k
)
0
log
20
(
=
k
Ze wzgl du na nieregularny kształt charakterystyk
)
(
ω
L
aproksymacja za pomoc
charakterystyk asymptotycznych jest stosowana tylko przy obliczeniach wst pnych, dla
1
3
,
0
≤
≤
ξ
(wówczas bł d
)
(
ω
L
∆
jest mniejszy od 6 dB. Asymptotyczn charakterystyk
amplitudow oraz wykres bł du
)
(
ω
L
∆
przedstawiono na rys. 4.11.
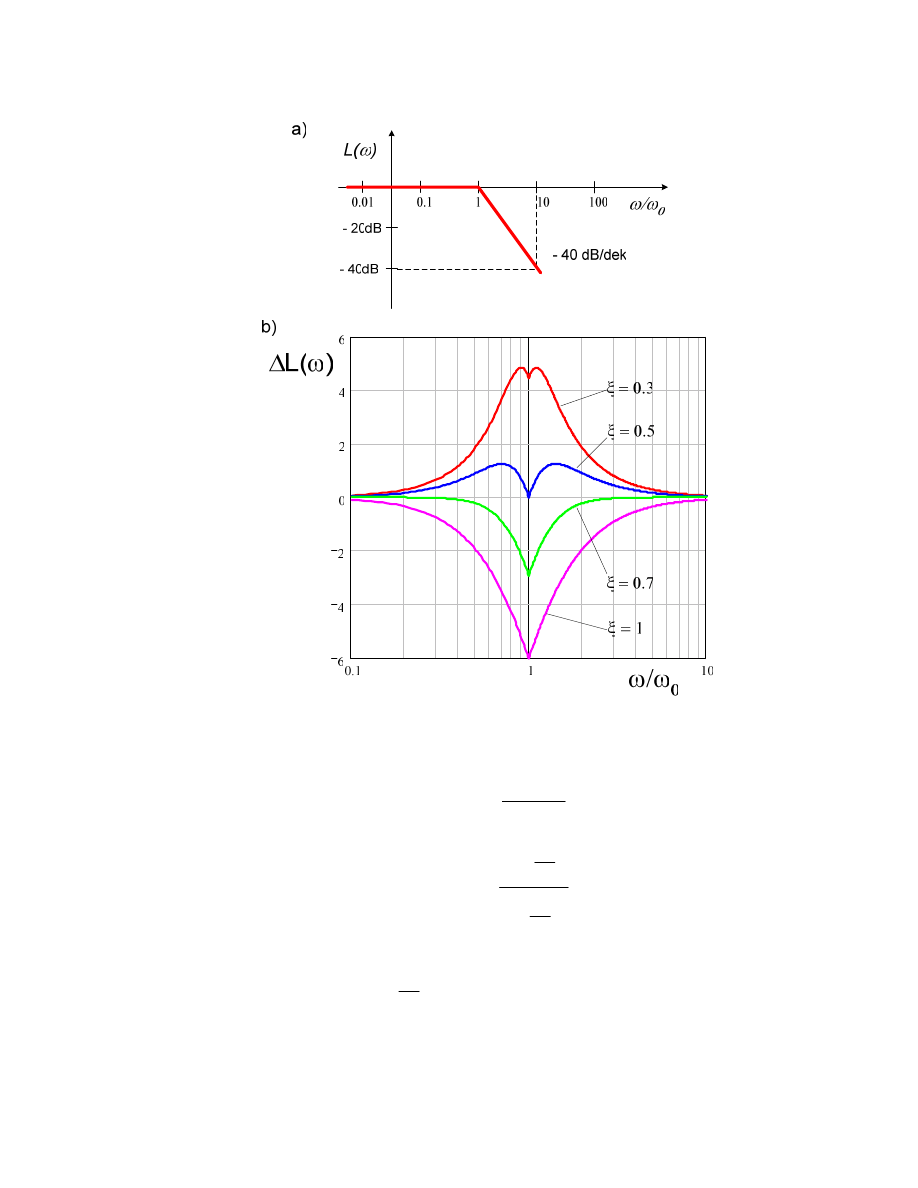
51
Rysunek 4.11 a) asymptotyczna charakterystyka amplitudowa elementu oscylacyjnego (dla
1
=
k
)
b) wykres bł du
)
(
ω
L
∆
Logarytmiczna charakterystyka fazowa:
( 4.20)
−
−
=
2
2
0
0
2
)
(
ω
ω
ω
ζω
ω
ϕ
arctg
( 4.21)
−
−
=
2
0
0
1
2
)
(
ω
ω
ω
ω
ζ
ω
ϕ
arctg
Wykresy
)
(
ω
ϕ
podano na rys. poni ej. Przy zmianie
ω od 0 ∞ przesuni cie fazowe zmienia
warto od 0 do -180
0
, przy czym dla
1
0
=
ω
ω
wynosi zawsze -90
0
.
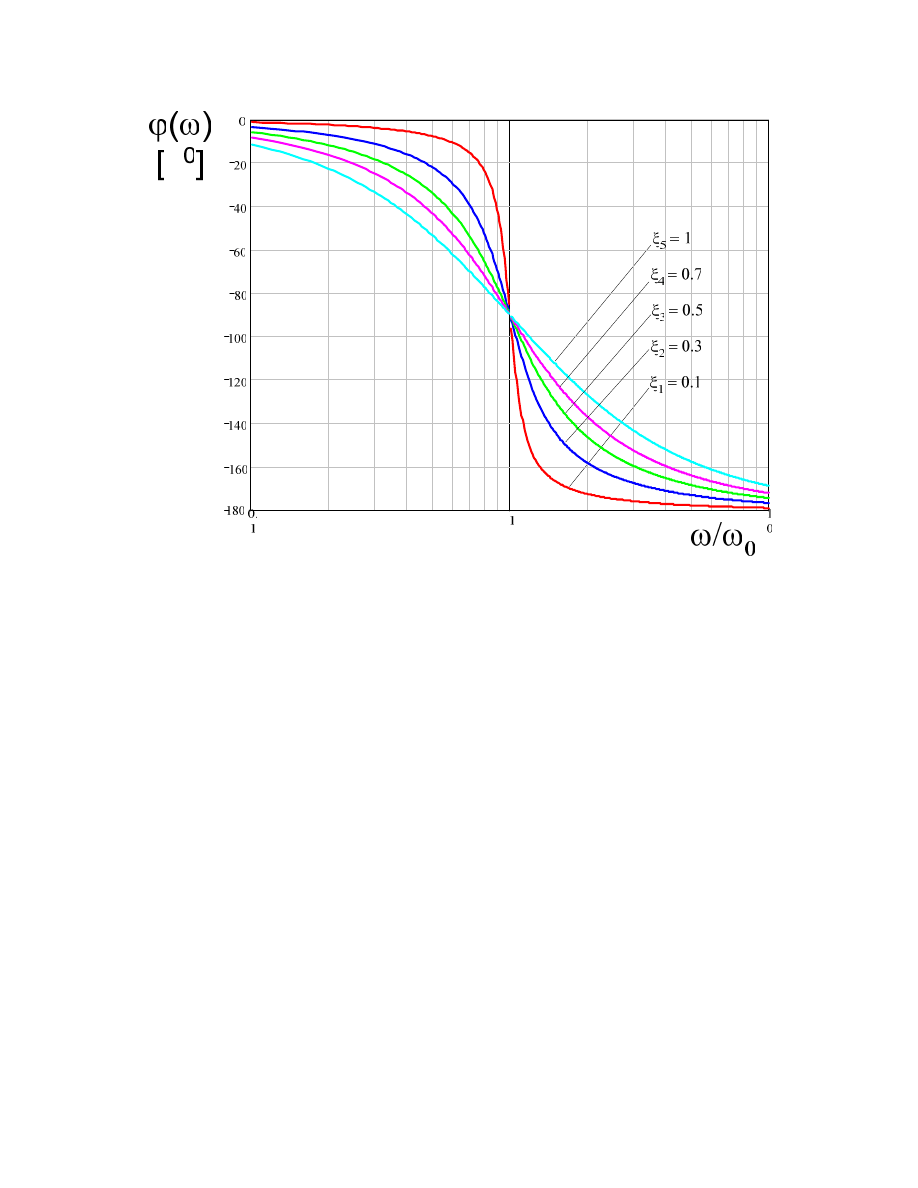
52
Rysunek 4.12 Logarytmiczna charakterystyka fazowa elementu oscylacyjnego
Tablica charakterystyk cz stotliwo ciowych wszystkich elementów podstawowych
przedstawiona została na str. 53.
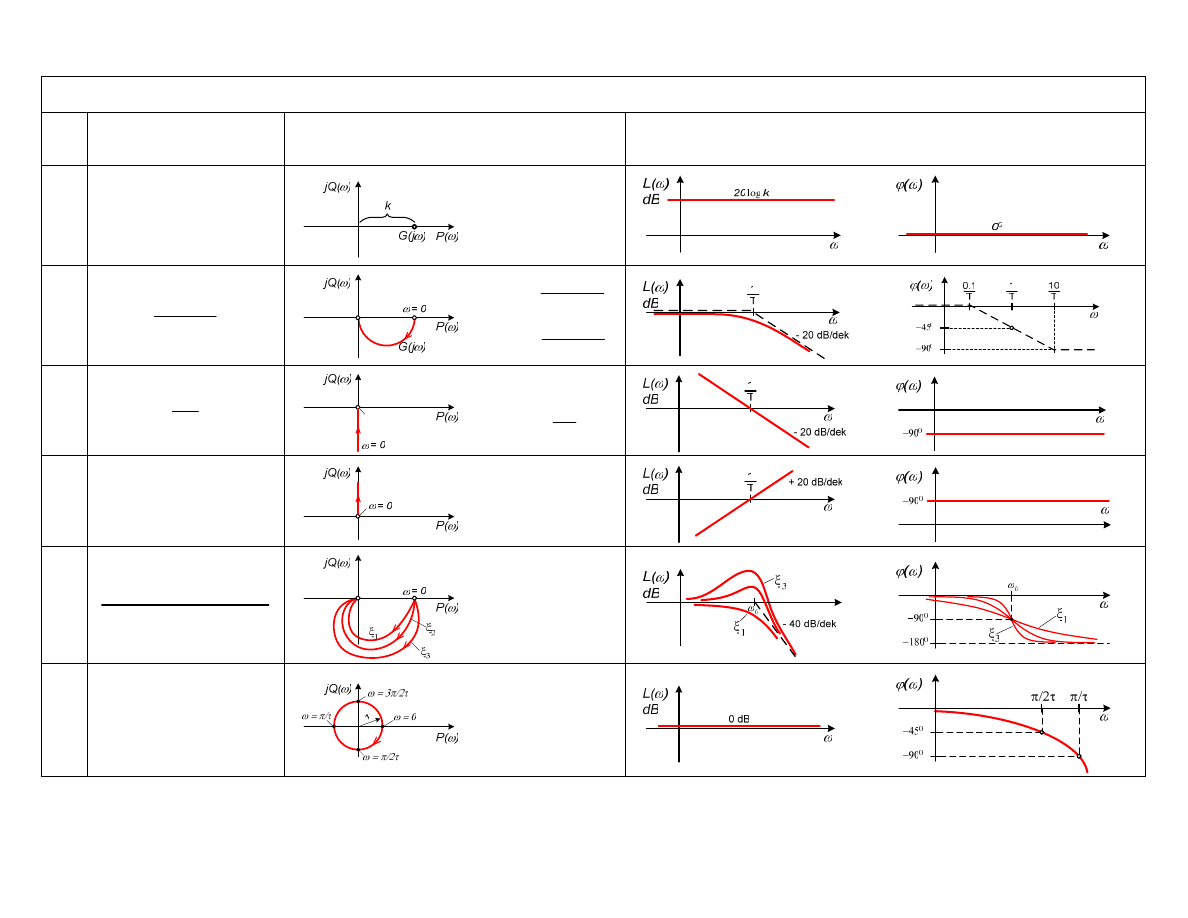
53
CHARAKTERYSTYKI CZ STOTLIWO CIOWE ELEMENTÓW PODSTAWOWYCH
L.p.
Transmitancja
operatorowa
)
(s
G
Wykres charakterystyki amplitudowo-fazowej
)
(
ω
j
G
(transmitancji widmowej)
Wykresy logarytmicznych charakterystyk amplitudowej
)
(
ω
L
i fazowej
)
(
ω
ϕ
1
k
0
)
(
)
(
=
=
ω
ω
Q
k
P
2
1
1
+
Ts
∞
=
ω
1
)
(
1
1
)
(
2
2
2
2
+
−
=
+
=
ω
ω
ω
ω
ω
T
T
Q
T
P
3
Ts
1
∞
=
ω
ω
ω
ω
T
Q
P
1
)
(
0
)
(
−
=
=
4
Ts
∞
=
ω
ω
ω
ω
T
Q
P
=
=
)
(
0
)
(
5
2
0
0
2
2
0
2
ω
ξω
ω
+
+
s
s
k
∞
=
ω
1
2
3
ξ
ξ
ξ
<
<
6
s
e
τ
−
ωτ
ω
ωτ
ω
sin
)
(
cos
)
(
−
=
=
Q
P

54
4.5
Logarytmiczne charakterystyki cz stotliwo ciowe szeregowego
poł czenia elementów
Rozwa my szeregowe poł czenie n elementów, których transmitancje widmowe
oznaczymy
)
(
,
),
(
),
(
2
1
ω
ω
ω
j
G
j
G
j
G
n
.
Na podstawie wzoru (4.3) poszczególne transmitancje wyrazimy w postaci:
)
(
)
(
2
2
)
(
1
1
)
(
)
(
)
(
)
(
)
(
)
(
2
1
ω
ϕ
ω
ϕ
ω
ϕ
ω
ω
ω
ω
ω
ω
n
j
n
n
j
j
e
M
j
G
e
M
j
G
e
M
j
G
=
=
=
Transmitancja widmowa szeregowego poł czenia elementów równa si iloczynowi
transmitancji tych elementów:
)
(
)]
(
)
(
)
(
[
2
1
)
(
)
(
)
(
)
(
)
(
2
1
ω
ϕ
ω
ϕ
ω
ϕ
ω
ϕ
ω
ω
ω
ω
ω
j
j
n
e
M
e
M
M
M
j
G
n
=
=
+
+
+
gdzie:
)
(
)
(
)
(
)
(
2
1
ω
ω
ω
ω
n
M
M
M
M
=
=
=
n
i
i
1
)
(
)
(
ω
ϕ
ω
ϕ
Logarytmiczna charakterystyka amplitudowa, na podstawie (4.7)
)
(
log
20
)
(
log
20
)
(
log
20
)
(
log
20
)
(
2
1
ω
ω
ω
ω
ω
n
M
M
M
M
L
+
+
+
=
=
=
=
n
i
i
L
L
1
)
(
)
(
ω
ω
gdzie
)
(
,
),
(
),
(
2
1
ω
ω
ω
n
L
L
L
s logarytmicznymi charakterystykami amplitudowymi
kolejnych elementów.
Logarytmiczne charakterystyki amplitudow
)
(
ω
L
i fazow
)
(
ω
ϕ
szeregowego poł czenia
elementów b dziemy wi c wyznacza zgodnie ze wzorami, sumuj c odpowiednie
charakterystyki kolejnych elementów.
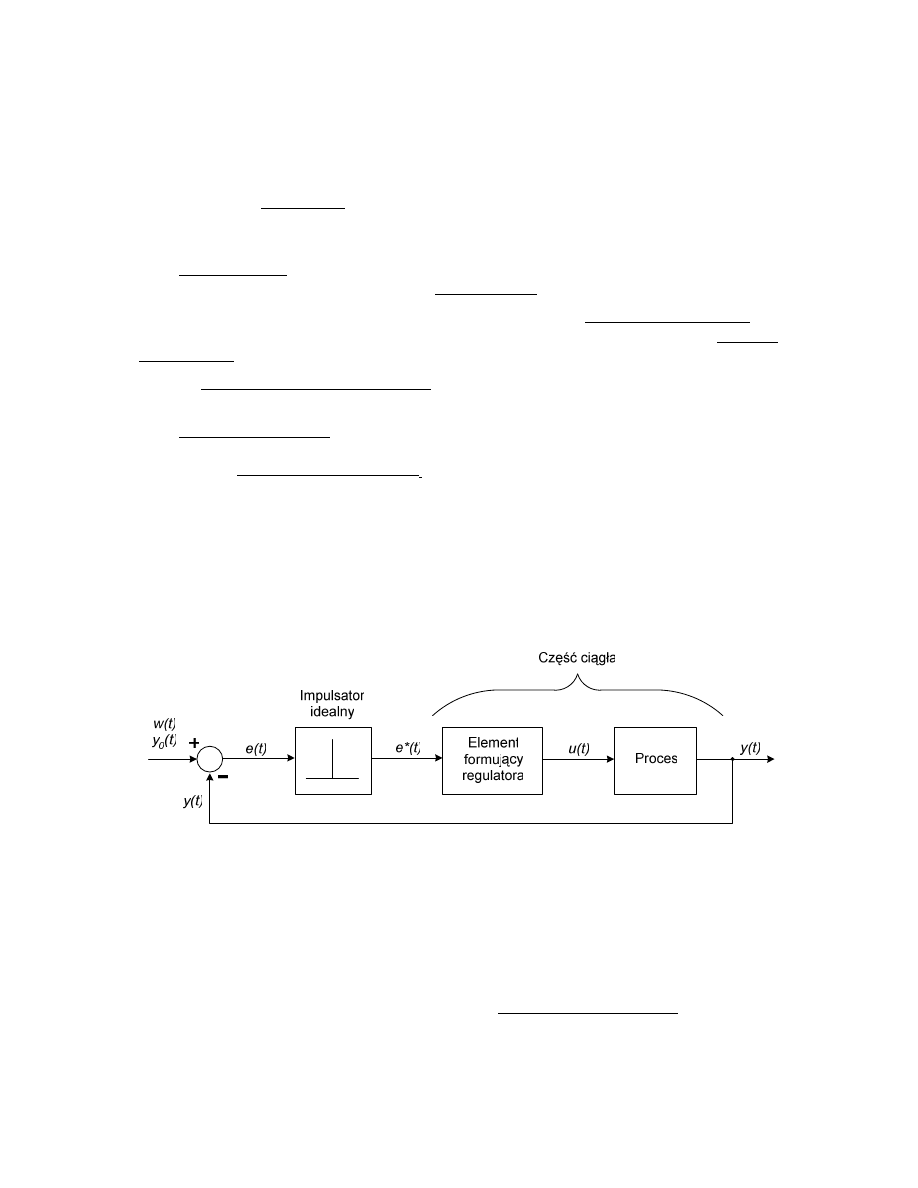
55
5 UKŁADY LINIOWE DYSKRETNE (IMPULSOWE)
5.1
Poj cia podstawowe
Układami dyskretnymi regulacji automatycznej nazywamy układy, w których
informacja jest przekazywana za pomoc sygnałów dyskretnych (nieci głych) w poziomie lub
w czasie.
Kwantowaniem sygnału nazywa si przekształcanie sygnału ci głego w dyskretny.
Kwantowanie sygnału w czasie nazywa si próbkowaniem.
Układy z kwantowaniem sygnału w czasie nazywa si układami impulsowymi. W
układach tych informacja przekazywana jest tylko w dyskretnych chwilach, tzw. chwilach
impulsowania.
W układach impulsowych liniowych warto ci sygnałów w dyskretnych chwilach czasu
s zwi zane zale no ciami liniowymi.
Modulacj impulsów nazywa si przedstawienie funkcji ci głej w postaci ci gu
impulsów, których amplituda, szeroko lub poło enie wewn trz okresu próbkowania -
zwanego te okresem impulsowania T
i
- zale od warto ci tej funkcji w dyskretnych
chwilach czasu t = nT
i
(n=0,1,2,...).
Układ z modulacj amplitudy impulsów o liniowej cz ci ci głej jest układem
liniowym, a układ z modulacj szeroko ci impulsów - nieliniowym. Je eli jednak najwi ksza
szeroko impulsu jest o wiele mniejsza od okresu impulsowania, to układ taki (o liniowej
cz ci ci głej) mo na w przybli eniu traktowa jak układ liniowy.
Schemat blokowy jednowymiarowego układu impulsowego regulacji automatycznej
mo na przedstawi nast puj co:
Impulsator idealny jest elementem (nierealizowalnym ci le fizycznie) przekształcaj cym
funkcj ci gł czasu e(t) w ci g impulsów Diraca
e(0)
δ(t), e(T
i
)
δ(t-T
i
), e(2 T
i
)
δ(t-2 T
i
), …
przesuni tych wzgl dem siebie o okres impulsowania T
i
, o polach impulsów równych
warto ciom funkcji e(t) w chwilach impulsowania t=nT
i
(n=0, l, 2, ...).
Proces modulacji realizowany przez impulsator idealny jest równowa ny
(matematycznie) pomno eniu funkcji e(t) przez tzw. funkcj impulsowania S(t)
+∞
−∞
=
−
=
n
i
nT
t
t
S
)
(
)
(
δ
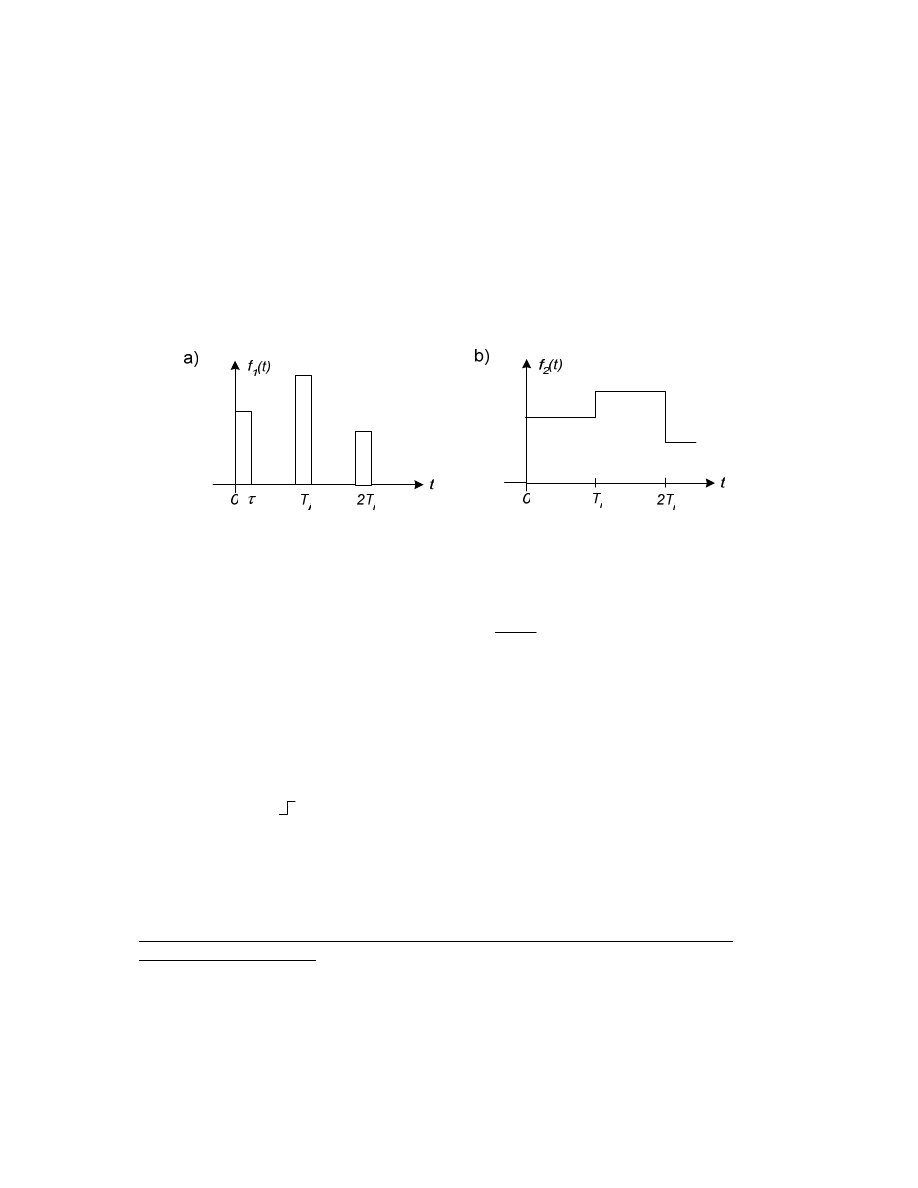
56
Bior c pod uwag , e e(t)=0 dla t<0, mo na napisa
∞
=
−
=
=
0
)
(
)
(
)
(
)
(
)
(
*
n
i
i
nT
t
nT
e
t
S
t
e
t
e
δ
s
nT
n
i
i
e
nT
e
t
e
L
s
E
−
∞
=
=
=
0
)
(
)]
(
*
[
)
(
*
Ci g impulsów prostok tnych (a) lub funkcj schodkow (b) mo na traktowa jako
przykładowe odpowiedzi układów zwanych elementami formuj cymi, na wymuszenia w
postaci ci gu impulsów Diraca.
Impuls prostok tny g(t) o amplitudzie jednostkowej i szeroko ci t mo na zapisa :
)
(
)
(
)
(
τ
−
−
=
t
t
t
g
1
1
s
e
t
g
L
s
G
s
τ
−
=
=
1
)]
(
[
)
(
Odpowied układu o transmitancji G(s) na wymuszenie w postaci impulsu
δ(t) ma posta
impulsu prostok tnego g(t), a na wymuszenie w postaci ci gu impulsów Diraca
f
1
(0)
δ(t),
f
1
(T
i
)
δ(t-T
i
),
f
1
(2T
i
)
δ(t-2T
i
)
posta ci gu impulsów prostok tnych f
1
(t) – rys. a)
W przypadku szczególnym gdy =T
i
z ci gu impulsów prostok tnych otrzymujemy
funkcj schodkow f
2
(t), a gdy
→0 - funkcj dyskretn .
Dla zapisu przebiegów wyst puj cych w układach impulsowych stosuje si funkcje
dyskretne lub funkcje schodkowe. W punktach nieci gło ci warto funkcji schodkowej jest
równa jej prawostronnej granicy w tym punkcie.
Dalej rozpatrywa b dziemy funkcje dyskretne dla T
i
=1
Ró nica pierwszego rz du
∆f(m) funkcji dyskretnej f(n) w punkcie n=m jest analogiem
pochodnej funkcji ci głej:
)
(
)
1
(
)
(
m
f
m
f
m
f
def
−
+
=
∆
)
,
2
,
1
,
0
(
=
m
( 5.1)
Ró nica k-tego rz du:
)
(
)
1
(
)
(
1
1
m
f
m
f
m
f
k
k
def
k
−
−
∆
−
+
∆
=
∆
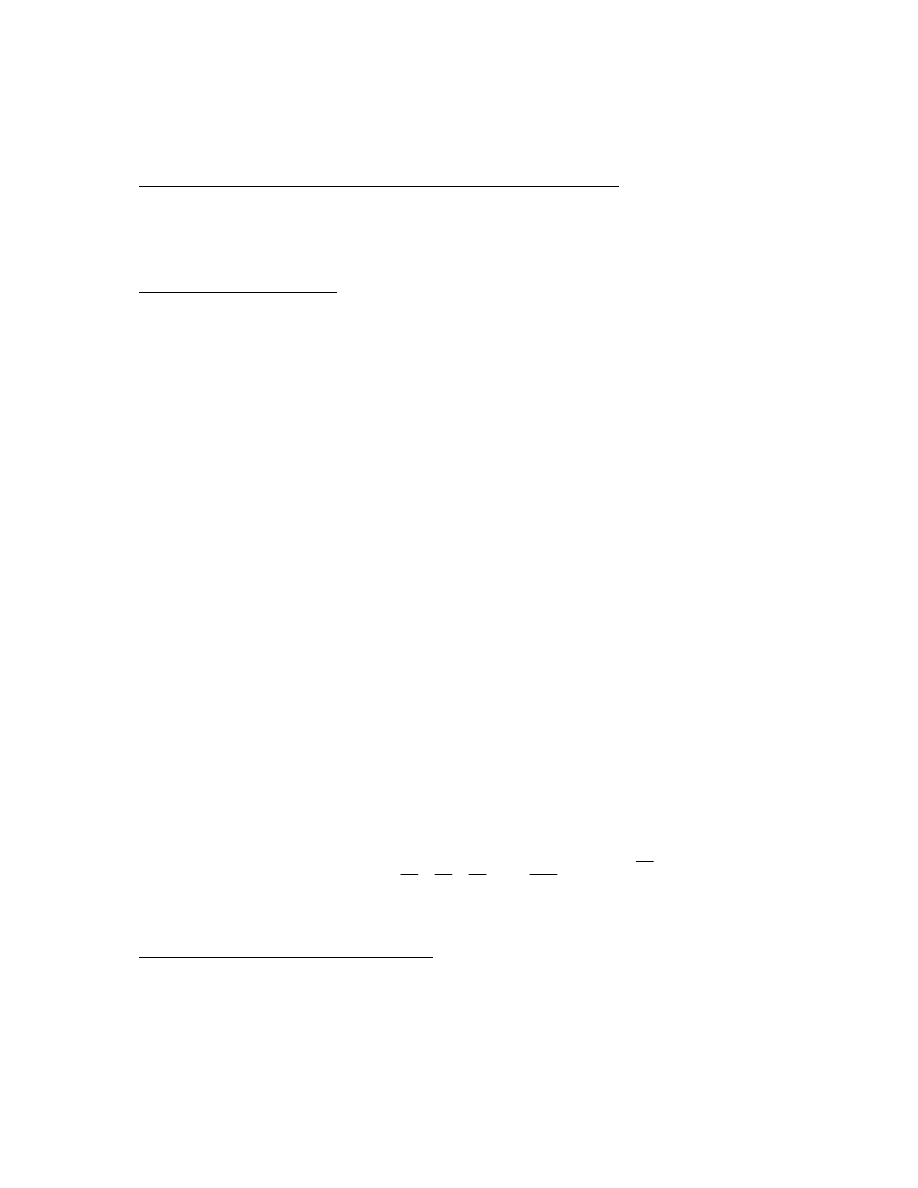
57
Dla k=2:
)
(
)
1
(
2
)
2
(
)
(
2
m
f
m
f
m
f
m
f
+
+
−
+
=
∆
Suma
ϕ(m) funkcji dyskretnej f(n) jest analogiem całki funkcji ci głej:
−
=
=
1
0
)
(
)
(
m
i
def
i
f
m
ϕ
( 5.2)
Liniowe równania ró nicowe
Liniowym równaniem ró nicowym k-tego rz du o stałych współczynnikach a
k
, a
k-1
, … , a
0
nazywamy równanie o postaci:
)
(
)
(
)
(
0
1
1
n
f
x
a
n
x
a
n
x
a
n
k
k
k
k
=
+
+
∆
+
∆
−
−
Gdy f(n)=0 - równanie jednorodne, gdy f(n)
≠0 – niejednorodne.
Warunki pocz tkowe:
)
0
(
)
0
(
)
0
(
1
1
1
0
x
x
x
x
x
x
k
k
−
−
∆
=
∆
=
=
Wprowadzaj c nowe zmienne:
),
(
)
(
1
n
x
n
x
=
)
(
)
(
),
(
)
(
1
2
n
x
n
x
n
x
n
x
k
k
−
∆
=
∆
=
mo emy podane równanie ró nicowe zapisa w postaci układu równa ró nicowych
pierwszego rz du:
x
(n+1)=
Ax
(n)+
B
f(n)
przy czym:
=
(n)
x
(n)
x
(n)
x
(n)
k
2
1
x
+
=
−
1
...
1
...
0
0
0
...
...
...
...
...
...
1
1
0
0
...
0
1
1
1
2
1
0
k
k
k
k
k
a
a
a
a
a
a
a
a
A
=
k
a
1
0
0
B
Przekształcenie Z i transmitancja dyskretna
Przekształceniem (transformacj ) Z nazywamy przekształcenie okre lone wzorem:
∞
=
−
=
0
)
(
)
(
n
n
def
z
n
f
z
F
( 5.3)

58
przyporz dkowuj ce funkcji dyskretnej f(n) powstałej z dyskretyzacji danej funkcji ci głej f(t)
(f(n)=0 dla n<0) funkcj F(z) zmiennej zespolonej z. Nazwy:
f(t) - oryginał ci gły
f(n) - oryginał dyskretny
F(z) - transformata Z funkcji f(n)
F(z) istnieje je eli szereg (5.3) jest zbie ny. Transformaty Z istniej dla funkcji dyskretnych,
które rosn nie szybciej od funkcji wykładniczych.
Np. dla funkcji dyskretnych f(n)=n! oraz
2
)
(
an
e
n
f
=
(a
≠0) transformaty Z nie istniej .
Tablic transformat F(z) kilkunastu cz ciej wyst puj cych funkcji przedstawiono na
nast pnej stronie.
Twierdzenie o warto ci pocz tkowej f(0) funkcji dyskretnej f(n):
)
(
lim
)
(
lim
)
0
(
0
z
F
n
f
f
z
n
∞
→
→
=
=
( 5.4)
Twierdzenie o warto ci ko cowej f(co) funkcji dyskretnej f(n):
)
(
)
1
(
lim
)
(
lim
)
(
1
z
F
z
n
f
f
z
n
−
=
=
∞
→
∞
→
( 5.5)
Wzory (5.4) i (5.5) mo na równie zapisa w postaci:
)
(
1
lim
)
0
(
z
F
z
z
f
z
−
=
∞
→
( 5.6)
)
(
1
lim
)
(
1
z
F
z
z
f
z
−
=
∞
→
( 5.7)
Transmitancj dyskretn G(z) układu nazywamy stosunek transformaty Z odpowiedzi Y(z) do
transformaty Z wymuszenia U(z) przy zało eniu, e warunki pocz tkowe s zerowe.
)
(
)
(
)
(
z
U
z
Y
z
G
def
=
( 5.8)
Dyskretn charakterystyk (odpowiedzi ) impulsow g(n) nazywamy dyskretn odpowied
układu impulsowego na wymuszenie w postaci funkcji Diraca przy zerowych warunkach
pocz tkowych. Pomi dzy dyskretn charakterystyk impulsow g(n) i ci gł charakterystyk
impulsow g(t) układu impulsowego zachodzi zale no :
i
nT
t
t
g
n
g
=
=
)
(
)
(
( 5.9)
Transmitancja dyskretna G(z) jest transformat Z dyskretnej charakterystyki impulsowej g(n)
tego układu
)]
(
[
)
(
n
g
Z
z
G
=
( 5.10)
Dyskretn charakterystyk (odpowiedzi ) skokow h(n) nazywamy dyskretn odpowied
układu impulsowego na wymuszenie l(t) przy zerowych warunkach pocz tkowych
i
nT
t
t
h
n
h
=
=
)
(
)
(
( 5.11)
gdzie h(t) - ci gła charakterystyka skokowa układu impulsowego.

59
TABLICA TRANSFORMAT
Funkcja ci gła f(t) Funkcja dyskretna f(n)
Transformata F(z)
Promie
zbie no ci
szeregu
1
(t)
)
(
i
nT
1
1
−
z
z
1
>
z
A
1
(t)
)
(
i
nT
A
1
⋅
1
−
z
z
A
1
>
z
t
1
(t)
)
(
)
(
i
i
nT
nT
1
⋅
2
)
1
(
−
z
z
T
i
1
>
z
)
(
2
t
t
1
)
(
)
(
2
i
i
nT
nT
1
⋅
3
2
)
1
(
)
1
(
−
+
z
z
z
T
i
1
>
z
)
(
3
t
t
1
)
(
)
(
3
i
i
nT
nT
1
⋅
4
2
3
)
1
(
)
1
4
(
−
+
+
z
z
z
z
T
i
1
>
z
)
(
4
t
t
1
)
(
)
(
4
i
i
nT
nT
1
⋅
5
2
3
4
)
1
(
)
1
11
11
(
−
+
+
+
z
z
z
z
z
T
i
1
>
z
)
(
5
t
t
1
)
(
)
(
5
i
i
nT
nT
1
⋅
6
2
3
4
5
)
1
(
)
1
26
66
26
(
−
+
+
+
+
z
z
z
z
z
z
T
i
1
>
z
)
(t
e
at
1
)
(
i
anT
nT
e
i
1
i
aT
e
z
z
−
i
aT
e
z
>
)
(t
e
at
1
−
)
(
i
anT
nT
e
i
1
−
i
aT
e
z
z
−
−
i
aT
e
z
>
)
(
1
(
t
)
e
i
aT
1
−
−
)
(
1
(
i
anT
nT
)
e
i
1
−
−
)
)(
1
(
)
1
(
i
i
aT
aT
e
z
z
e
z
−
−
−
−
−
i
aT
e
z
−
>
)
(t
te
at
1
−
)
(
i
anT
i
nT
e
nT
i
1
−
2
)
(
)
i
i
aT
aT
i
e
z
ze
T
−
−
−
i
aT
e
z
−
>
t
t
β
sin
)
(
1
i
i
nT
nT
β
sin
)
(
1
1
cos
2
sin
2
+
−
i
i
T
z
z
T
z
β
β
1
>
z
t
t
β
cos
)
(
1
i
i
nT
nT
β
cos
)
(
1
1
cos
2
cos
2
2
+
−
−
i
i
T
z
z
T
z
z
β
β
1
>
z
t
e
t
at
β
sin
)
(
−
1
i
anT
i
nT
e
nT
i
β
sin
)
(
−
1
aTi
i
aT
i
aT
e
T
ze
z
T
ze
i
i
2
2
cos
2
sin
−
−
−
+
−
β
β
i
aT
e
z
−
>
t
e
t
at
β
cos
)
(
−
1
i
anT
i
nT
e
nT
i
β
cos
)
(
−
1
aTi
i
aT
i
aT
e
T
ze
z
T
ze
z
i
i
2
2
2
cos
2
cos
−
−
−
+
−
−
β
β
i
aT
e
z
−
>
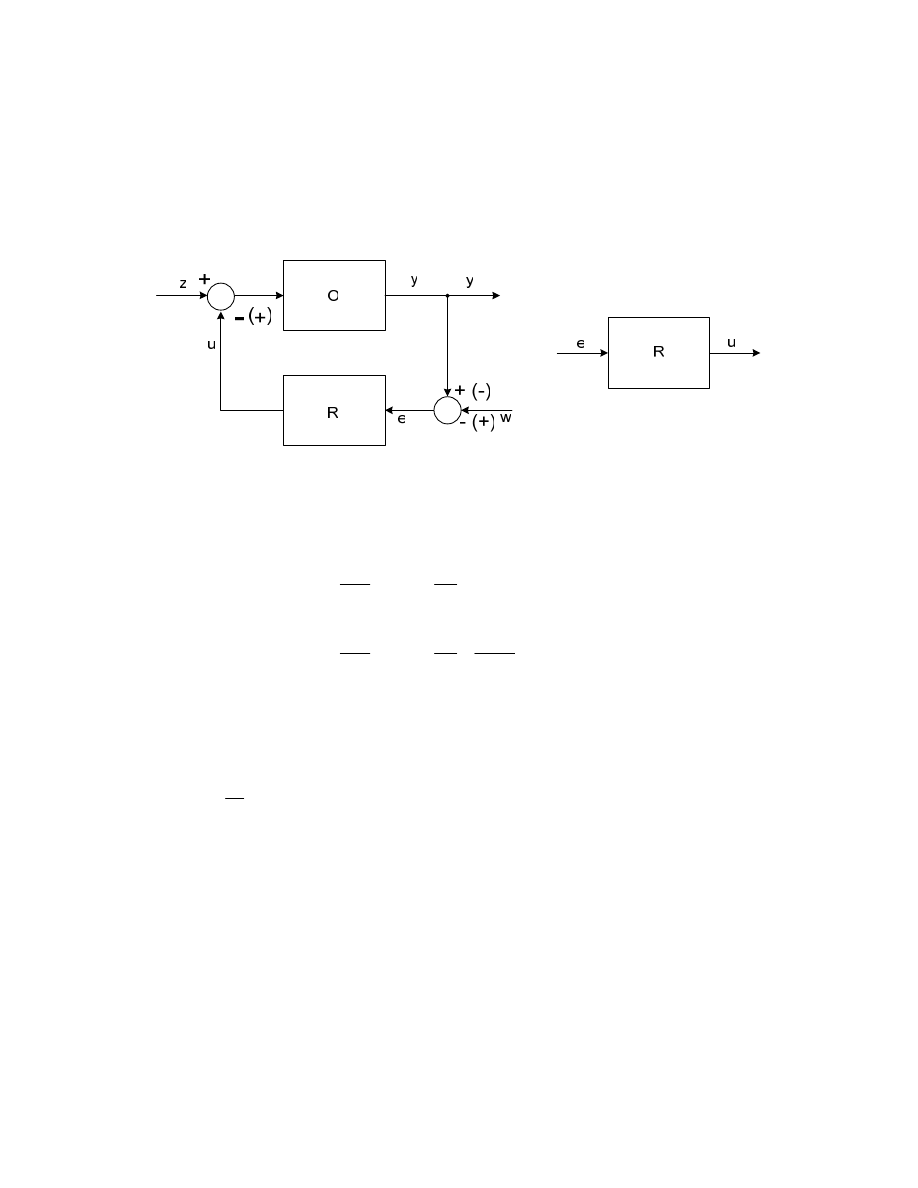
60
6 REGULATORY PRZEMYSŁOWE
6.1
Regulator PID
Usytuowanie regulatora w układzie regulacji automatycznej pokazano na poni szym
rysunku. Sygnałem wej ciowym jest odchylenie regulacji e=y-w, a wyj ciowym – sygnał
steruj cy u.
Podstawowe rodzaje regulatorów o działaniu ci głym lub quasi-ci głym realizuj funkcje PID
(działania: P – proporcjonalne, I – całkuj ce, D – ró niczkuj ce).
Dla liniowych regulatorów o działaniu ci głym algorytm PID ma posta :
a)
idealny
)
1
1
(
)
(
)
(
)
(
s
T
s
T
k
s
e
s
u
s
G
d
i
p
+
+
=
=
b)
rzeczywisty
)
1
1
1
(
)
(
)
(
)
(
+
+
+
=
=
Ts
s
T
s
T
k
s
e
s
u
s
G
d
i
p
gdzie:
p
k
– wzmocnienie proporcjonalne
i
T – czas zdwojenia (stała czasowa akcji całkuj cej)
d
T – czas wyprzedzenia (stała czasowa akcji ró niczkuj cej)
T
T
k
d
d
=
– wzmocnienie dynamiczne (najcz ciej 4
÷10)
Je eli działanie PID realizowane jest na drodze cyfrowej (w regulatorze
mikroprocesorowym lub komputerze), to uzyskuje si je za pomoc algorytmu pozycyjnego
lub przyrostowego, ale dla operatora efekt ko cowy jest taki sam.
Tablica odpowiedzi skokowych regulatorów PID przedstawiona jest na nast pnej stronie.
W konkretnych rozwi zaniach konstrukcyjnych regulatorów przyrz dy te realizuj –
oprócz algorytmów PID – wiele dodatkowych funkcji. W szczególno ci w regulatorach
wyznaczane s zawsze odchyłki regulacji e=y-w lub e=w-y (działanie proste lub odwrotne)
oraz generowany jest wewn trzny sygnał warto ci zadanej w.
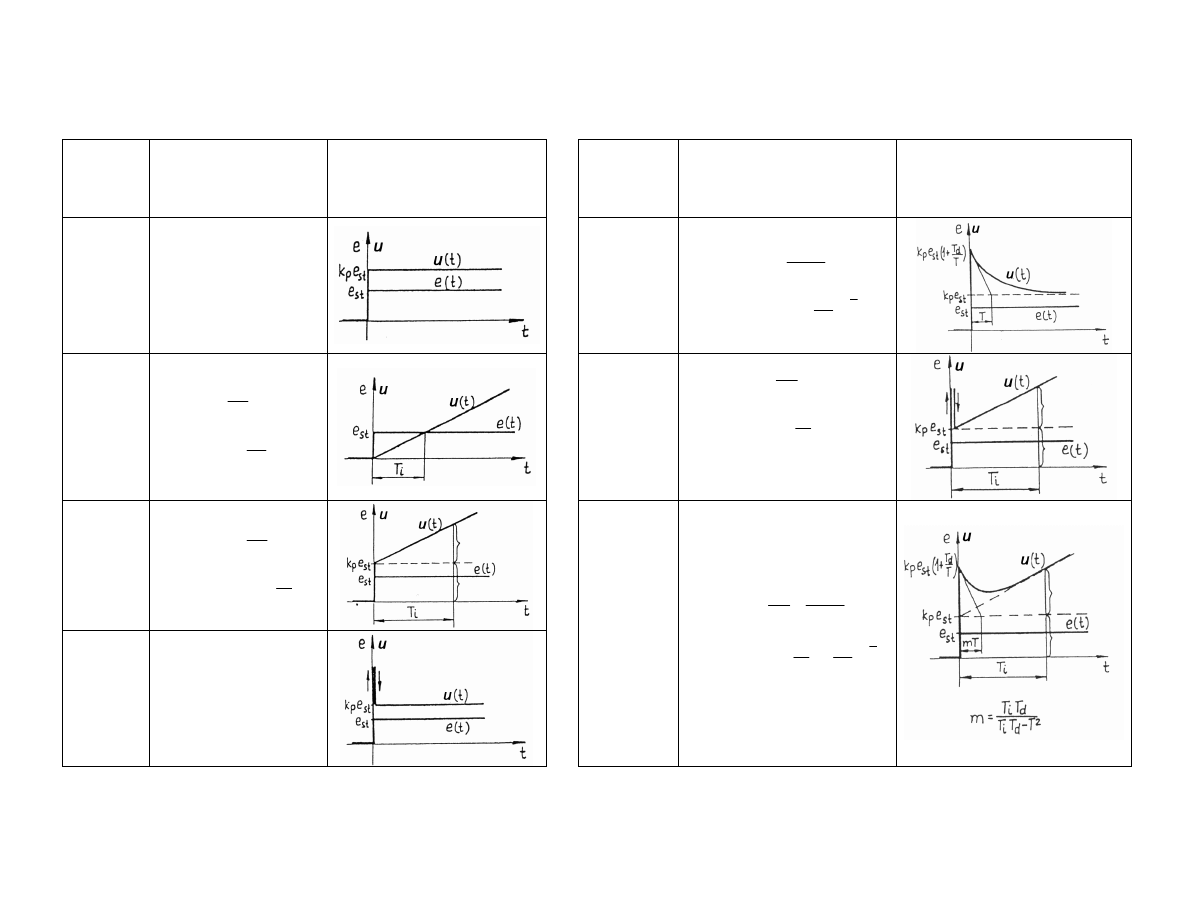
61
Rodzaj
regulatora
Transmitancja i
równanie
charakterystyki
skokowej
Charakterystyka skokowa
Rodzaj
regulatora
Transmitancja i równanie
charakterystyki skokowej
Charakterystyka skokowa
P
p
k
)
(
1
)
(
t
e
k
t
u
st
p
=
PD
rzeczywisty
)
1
1
(
+
+
Ts
s
T
k
d
p
)
1
(
)
(
T
t
d
st
p
e
T
T
e
k
t
u
−
+
=
I
s
T
i
1
t
T
e
t
u
i
st
=
)
(
PID
)
1
1
(
s
T
s
T
k
d
i
p
+
+
)]
(
1
1
[
)
(
t
T
t
T
e
k
t
u
d
i
st
p
δ
+
+
=
gdzie:
)
(t
δ jest funkcj
Diraca
PI
)
1
1
(
s
T
k
i
p
+
)
1
1
(
)
(
t
T
e
k
t
u
i
st
p
+
=
PD
)
1
(
s
T
k
d
p
+
)]
(
1
[
)
(
t
T
e
k
t
u
d
st
p
δ
+
=
gdzie:
)
(t
δ jest funkcj
Diraca
PID
rzeczywisty
)
1
1
1
(
+
+
+
Ts
s
T
s
T
k
d
i
p
)
1
1
(
)
(
T
t
d
i
st
p
e
T
T
t
T
e
k
t
u
−
+
+
=
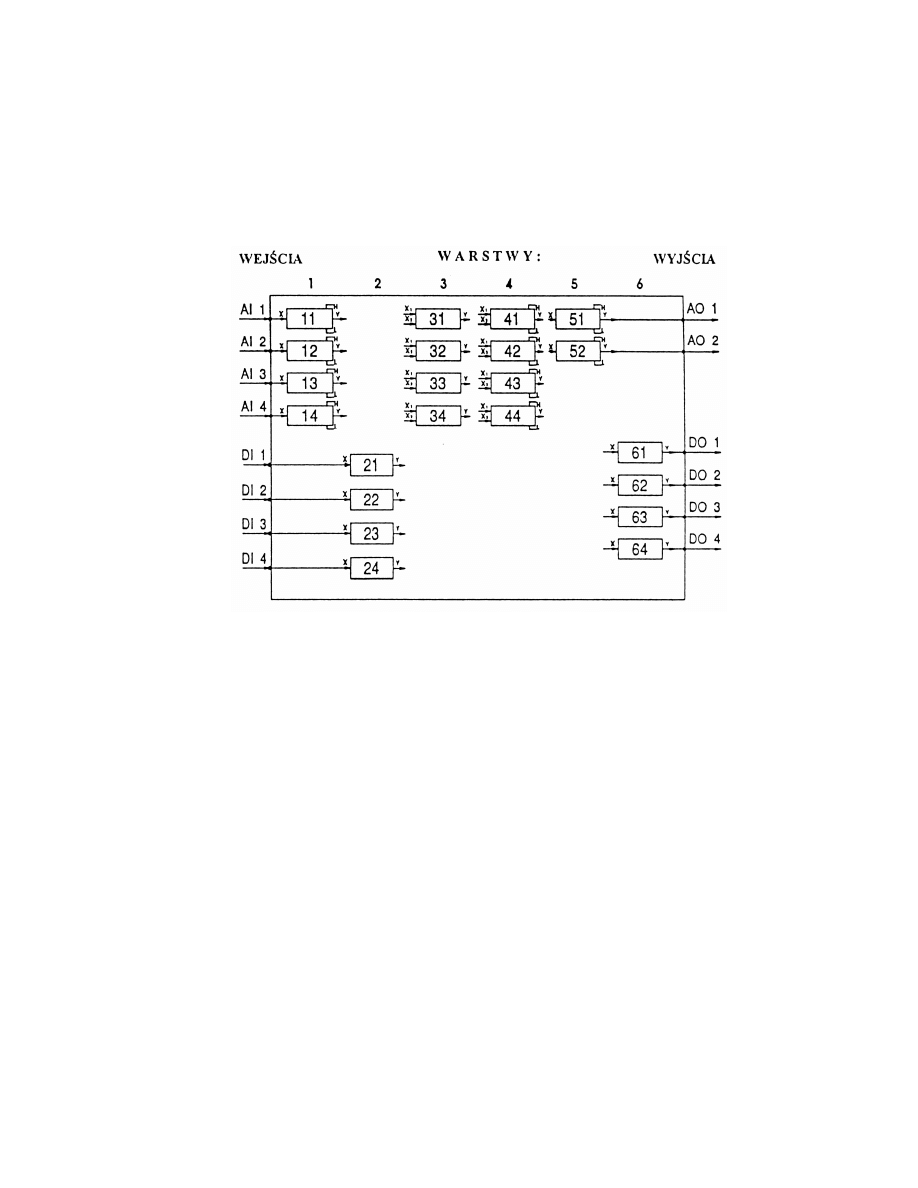
62
6.2
Regulatory mikroprocesorowe
S urz dzeniami programowalnymi o bardzo szerokich mo liwo ciach funkcjonalnych,
o wielu wej ciach i wyj ciach, z kilkoma blokami PID, z mo liwo ci kształtowania
wyj ciowych sygnałów steruj cych quasi-ci głych, dwustawnych (2P) lub trójstawnych (3P).
Przykładowa struktura funkcjonalna regulatora mikroprocesorowego EFTRONIK X
pokazana została ni ej.
W strukturze tej mo na wyró ni 6 warstw, w których znajduj si 22 programowalne bloki
funkcjonalne (w wersji 4-wej ciowej) nazywane tak e blokami programowalnymi lub krótko
blokami.
Oznaczenia: AI – wej cia analogowe (Analog Input)
DI – wej cie dyskretne (Digital Input)
AO – wyj cie analogowe (Analog Output)
DO – wyj cie dyskretne (Digital Output)
H – warto górna (High)
L – warto dolna (Low)
Wej cia bloków w warstwie 1 s bezpo rednio poł czone z wyj ciami przetworników
a/c, a wyj cia bloków w warstwie 5 z wej ciami przetworników c/a, w zwi zku z czym ka dy
wej ciowy sygnał analogowy musi przechodzi przez warstw 1, a uzyskanie analogowego
sygnału wyj ciowego musi odbywa si przez warstw 5.
Oznaczenia poszczególnych bloków s dwucyfrowe: pierwsza cyfra oznacza numer
warstwy, a druga kolejny numer bloku w danej warstwie.
Ka dy blok mo e realizowa jeden z algorytmów, wybrany w trakcie programowania,
z biblioteki algorytmów dla danej warstwy.
Wewn trz danej struktury funkcjonalnej wszystkie operacje realizowane s na sygnałach
cyfrowych, których znormalizowany zakres zmienno ci wynosi 0
…1.
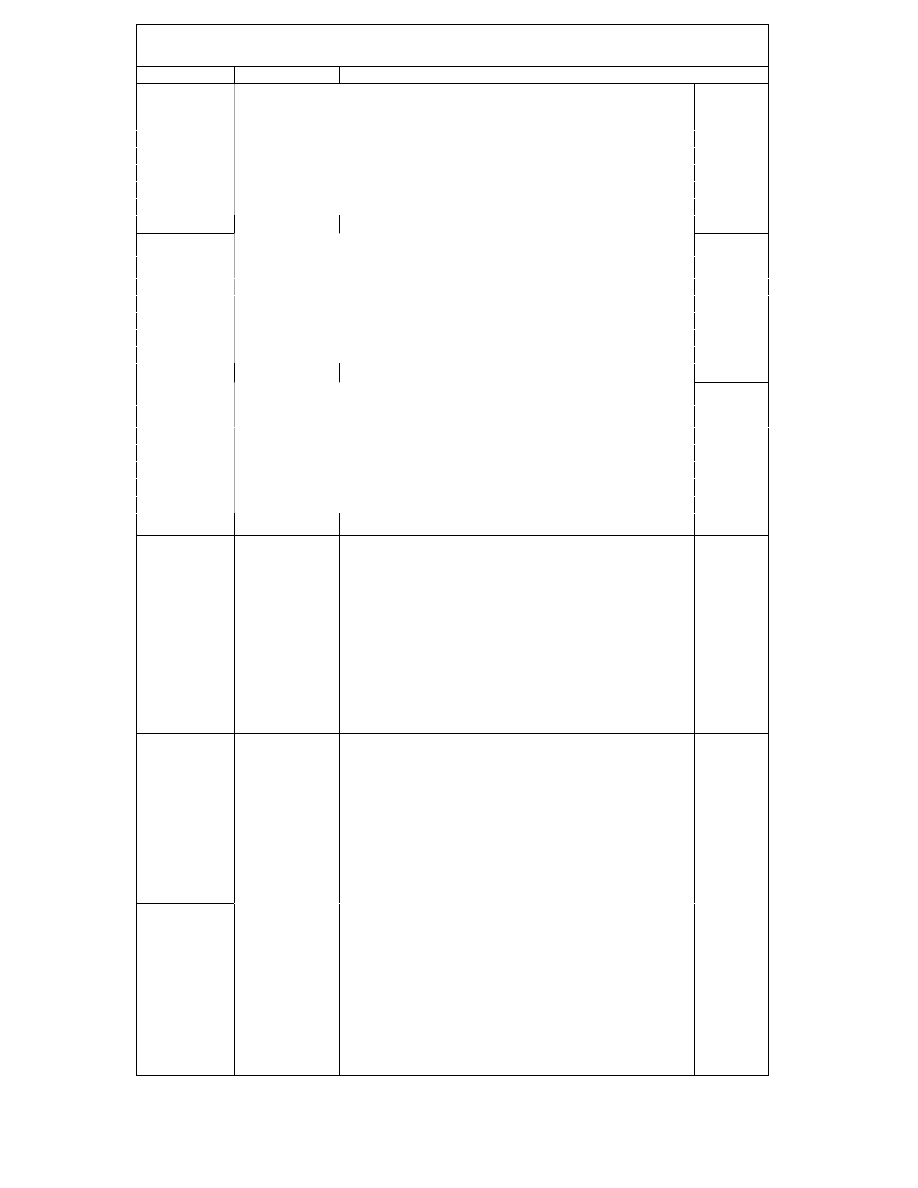
63
PRZYKŁADY Z BIBLIOTEKI ALGORYTMÓW EF-X
1
2
3
4
1-1-01
2
3*
4*
5**
6**
7**
8**
0000 ...0127
[s]
T
f
– stała filtracji (stal czasowa członu inercyjnego 1-
go
rz du nastawiana od 0 do 127 s).
1-1-02
2
3*
4*
5**
6**
7**
8**
-999 ... 9999
PV min.
– Warto minimalna wielko ci mierzonej
w
jednostkach fizycznych
1-1-03
2
3*
4*
5**
6**
7**
8**
-999 ... 9999
PV max.
– Warto maksymalna wielko ci
mierzonej w
jednostkach fizycznych
1-1-08
Algorytmy funkcji przetwarzania sygnału:
2
0000
-Y=X;
3*
0001
-Y = K1*X+K2;
4*
0002
-Y=K1*(1-X)+K2;
5**
0003
-Y=K1*SQRT(X)+K2;
6**
0004
-Y=Kl*X
2
-fK2;
7**
0005
-Y=K1*SQRT(X
3
)+K2;
8**
0006
- REZERWA;
0007
-Y = SQRT(K1*X+K2);
0008
-Y = K1*100%;
0009
- linearyzacja charakterystyki termorezystora PT100
3-1-05
Kod algorytmu:
2
0000
-.Y- Xl;
3
0002
- Y = K2+(K1*X1+X2)/(K1+1);
4
0003
- Y = K2+(Kl*Xl-X2+2)/(Kl+l);
5
0004
-Y = K1*X1*X2+K2;
6
0005
-Y = K1*X1/X2+K2 X2>X1;
7
0006
- Y = max (X1,X2) wybierak max ;
0007
- Y = min (Xl,X2) wybierak min ;
0008
- Y=K1*Xl+X2+K2;
- Y = K1*X1-X2+K2;
4-1-08
Algorytmy regulacji:
2
0001
-PID-
3*
0002
- PID RATIO;
4*
0003
-PID AUTO RATIO;
5**
0004
-PID AUTO BLAS;
6**
0005
- P z nastawnym punktem pracy (4 - x - 09);
7**
0006
-PID DDCCM;
0007
-PID DDC CMA;
0008
-PID DDCSPC;
0009...0010
- REZERWA;

64
6.3
Wykorzystanie sterowników PLC do regulacji
Wi kszo sterowników, oprócz mo liwo ci realizacji sterowania sekwencyjnego, ma
tak e algorytmy PID w swej bibliotece, co pozwala tworzy układy automatyki o
zró nicowanych zadaniach sterowania, zawieraj cych m.in. klasyczne obwody regulacji.
6.4
Regulacja lub sterowanie w trybie „soft-control”
Niektóre firmy proponuj ju technik sterowania polegaj c na realizacji wszystkich
funkcji regulatora lub sterownika przez komputer.
Technika ta ma jeszcze ograniczony zasi g, gdy w rozwi zaniach przemysłowych
najistotniejsza jest niezawodno działania i trzeba dysponowa urz dzeniami mog cymi
przej sterowanie w przypadku awarii komputera.
65
7 WYMAGANIA STAWIANE UKŁADOM AUTOMATYKI
7.1
Stabilno
A.
Definicja i warunki stabilno ci układów liniowych (ci głych, stacjonarnych)
Stabilno jest cech układu, polegaj c na powracaniu do stanu równowagi stałej po
ustaniu działania zakłócenia, które wytr ciło układ z tego stanu.
Rysunek 7.1 Schemat zamkni tego układu regulacji automatycznej: O – obiekt regulacji, R - regulator
Zamkni ty układ liniowy (rys 7.1) b dziemy wi c uwa a za stabilny, je eli przy
ka dej sko czonej warto ci zakłócenia z(t) i warto ci zadanej w(t) oraz dla dowolnych
warunków pocz tkowych sygnał wyj ciowy y(t) d y b dzie do sko czonej warto ci
ustalonej dla czasu t d
cego do niesko czono ci. Niekiedy precyzuje si dodatkowo, e
gdy po zanikni cie zakłócenia układ powraca do tego samego stanu równowagi co
zajmowany poprzednio, wówczas jest stabilny asymptotycznie. Przykłady przebiegów y(t)
wyst puj cych w układach stabilnych i niestabilnych pokazano na rys 7.2.
Je eli układ zamkni ty opisany jest za pomoc liniowego równania ró niczkowego
z
b
dt
z
d
b
dt
z
d
b
y
a
dt
y
d
a
dt
y
d
a
m
m
m
m
m
m
n
n
n
n
n
n
0
1
1
1
0
1
1
1
+
+
+
=
+
+
+
−
−
−
−
−
−
( 7.1)
lub odpowiadaj cej mu transmitancji operatorowej:
)
(
)
(
)
(
)
(
)
(
0
1
1
0
1
1
s
N
s
M
a
s
a
s
a
b
s
b
s
b
s
z
s
y
s
G
n
n
n
n
m
m
m
m
=
+
+
+
+
+
+
=
=
−
−
−
−
( 7.2)
to czasowy przebieg sygnału wyj ciowego t(y) po dowolnym zakłóceniu o warto ci
sko czonej opisany jest wzorem o nast puj cej postaci ogólnej
*)
:
st
n
k
t
s
k
z
e
A
A
t
y
k
+
=
=1
0
)
(
( 7.3)
gdzie s
k
s pierwiastkami równania charakterystycznego układu zamkni tego (mianownika
transmitancji operatorowej równego zeru)
*)
Przy zało eniu, e równanie charakterystyczne nie ma pierwiastków wielokrotnych ani równych zeru.
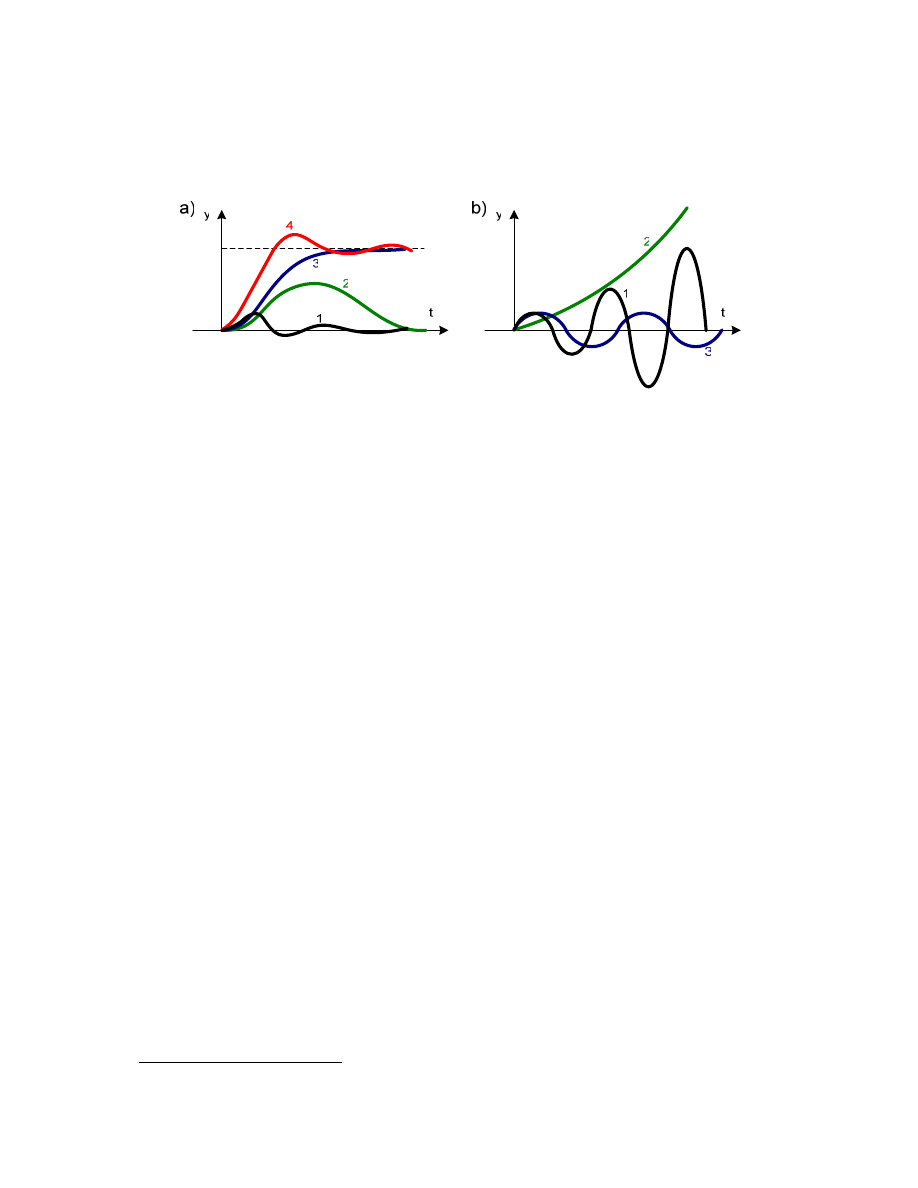
66
0
)
(
=
s
N
( 7.4)
a z
st
jest warto ci zakłócenia. Zakłócenie z(t) mo e by wprowadzone w dowolnym miejscu
układu, w szczególno ci zakłóceniem mo e by równie zmiana warto ci zadanej w(t).
Rysunek 7.2 Przebiegi przej ciowe: a) w układach stabilnych, b) w układach niestabilnych
Koniecznym i dostatecznym warunkiem stabilno ci asymptotycznej układu jest, aby
pierwiastki równania charakterystycznego układu zamkni tego miały ujemne cz ci
rzeczywiste.
0
)
Re(
<
k
s
( 7.5)
Wówczas
st
t
z
A
t
y
0
)
(
lim
=
∞
→
( 7.6)
gdzie A
0
jest współczynnikiem o warto ci sko czonej i układ jest stabilny w podanym
uprzednio sensie. Składowe przej ciowe wielko ci wyj ciowej zanikaj wówczas do zera przy
t
→∞, a pozostaje jedynie składowa ustalona, okre lona statycznymi własno ciami układu.
Przypadki pierwiastków zespolonych oraz wielokrotnych omówione s w [1].
B.
Kryterium Hurwitza
Aby wszystkie pierwiastki równania charakterystycznego
*)
0
0
1
1
1
=
+
+
+
+
−
−
a
s
a
s
a
s
a
n
n
n
n
( 7.7)
miały cz ci rzeczywiste ujemne, musz by spełnione nast puj ce warunki:
a)
wszystkie współczynniki równania (7.7) istniej i s wi ksze od zera (jest to warunek
konieczny, ale nie dostateczny)
0
,
,
0
,
0
0
1
>
>
>
−
a
a
a
n
n
*)
Równanie to odpowiada równaniu (7.4)

67
b)
podwyznaczniki
∆
i
, od i=2 do i=n-1, wyznacznika głównego
∆
n
s wi ksze od zera.
Wyznacznik
∆
n
, utworzony ze współczynników równania (7.7) ,ma n wierszy i n
kolumn:
3
4
5
6
7
1
2
3
4
5
1
2
3
1
0
0
0
0
−
−
−
−
−
−
−
−
−
−
−
−
−
−
=
∆
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
Podwyznaczniki
∆
i
maj posta :
,
0
,
3
4
5
1
2
3
1
3
2
3
1
2
−
−
−
−
−
−
−
−
−
−
=
∆
=
∆
n
n
n
n
n
n
n
n
n
n
n
n
a
a
a
a
a
a
a
a
a
a
a
a
Przedstawiono praktyczne sformułowanie kryterium. W oryginalnym sformułowaniu
Hurtwitza wymaga si , aby wszystkie podwyznaczniki
∆
i
, tzn. Od i=1 do i=n, były wi ksze
od zera. Poniewa jednak zachodzi:
1
0
1
1
,
−
−
∆
=
∆
=
∆
n
n
n
a
a
zatem w przypadku spełnienia warunku a.) sprawdzenie dodatnio ci podwyznacznika
∆
1
i
wyznacznika głównego
∆
n
jest niecelowe.
C.
Kryterium Michajłowa
Kryterium Michajłowa pozwala na wykre lne sprawdzenie stabilno ci układu regulacji
automatycznej. Podane zostanie wyprowadzenie tego kryterium.
Równanie charakterystyczne układu zamkni tego mo na przedstawi w postaci:
0
)
)...(
)(
(
)
(
2
1
=
−
−
−
=
n
n
s
s
s
s
s
s
a
s
N
( 7.8)
gdzie s
1
, s
2
,… s
n
s pierwiastkami tego równania.
Jako zmienn niezale n s mo emy wybra m.in. zbiór punktów poło onych na osi liczb
urojonych, wówczas s = j i lewa strona równania charakterystycznego przyjmuje
nast puj c posta :
)
)...(
)(
(
)
(
2
1
n
n
s
j
s
j
s
j
a
j
N
−
−
−
=
ω
ω
ω
ω
( 7.9)
Ka dy z czynników (j – s
k
) mo na przedstawi graficznie jako ró nic dwóch wektorów,
wektora j oraz wektora s
k
przedstawiaj cego k-ty pierwiastek równania charakterystycznego.
Funkcj N(j ), jako funkcj zmiennej zespolonej, mo na przedstawi w postaci
wykładniczej:
φ
ω
ω
j
e
j
N
j
N
)
(
)
(
=
gdzie:
n
n
s
j
s
j
s
j
a
j
N
−
−
−
=
ω
ω
ω
ω
...
)
(
2
1
oznacza moduł funkcji N(j ), natomiast

68
)
arg(
...
)
arg(
)
arg(
)
(
arg
2
1
n
s
j
s
j
s
j
j
N
−
+
+
−
+
−
=
=
ω
ω
ω
ω
φ
( 7.10)
oznacza argument funkcji N(j ).
Je eli przyjmujemy, e spo ród n pierwiastków równania charakterystycznego (n-m)
pierwiastków znajduje si w lewej półpłaszczy nie, a m pierwiastków w prawej, to zmiana
argumentu N(j ) przy zmianie od - do + wyniesie:
π
ω
ω
)
(
)
(
arg
m
n
j
N
−
=
∆
∞
<
<
∞
−
( 7.11)
Poniewa warunkiem stabilno ci jest, aby wszystkie pierwiastki równania
charakterystycznego miały ujemne cz ci rzeczywiste, układ b dzie wi c stabilny, je eli
0
=
m
, tzn. je eli
π
ω
ω
n
j
N
=
∆
∞
<
<
∞
−
)
(
arg
( 7.12)
Warunek ten mo na upro ci , je eli wyka emy, e N(j ) jest krzyw symetryczn
wzgl dem osi liczb rzeczywistych. Podstawiaj c w równaniu (7.7) s = j zapiszemy lew
stron w postaci:
0
)
(
)
(
)
(
)
(
0
1
1
1
=
+
+
+
+
=
−
−
a
j
a
j
a
j
a
j
N
n
n
n
n
ω
ω
ω
ω
( 7.13)
Cze rzeczywista i urojona N(j ) wynosz :
+
−
+
−
=
+
−
+
−
=
7
7
5
5
3
3
1
6
6
4
4
2
2
0
)
(
)
(
ω
ω
ω
ω
ω
ω
ω
ω
ω
a
a
a
a
Q
a
a
a
a
P
( 7.14)
Oraz
)
(
)
(
)
(
ω
ω
ω
jQ
P
j
N
+
=
,
)
(
)
(
)
(
ω
ω
ω
jQ
P
j
N
−
=
−
( 7.15)
Wystarczy wi c zbada przebieg jednej z gał zi krzywej N(j ), dla pulsacji zmieniaj cej si
od 0 do + .
Kryterium Michajłowa mo na sformułowa ostatecznie jak nast puje: układ regulacji
automatycznej jest stabilny wtedy i tylko wtedy, gdy zmiana argumentu krzywej N(j ) przy
zmianie pulsacji od 0 do + wynosi n /2, gdzie n oznacza stopie równania
charakterystycznego.
2
)
(
arg
π
ω
ω
n
j
N
=
∆
∞
<
<
∞
−
( 7.16)
Krzyw N(j ) nazywa si niekiedy krzyw charakterystyczn lub hodografem Michałowa.
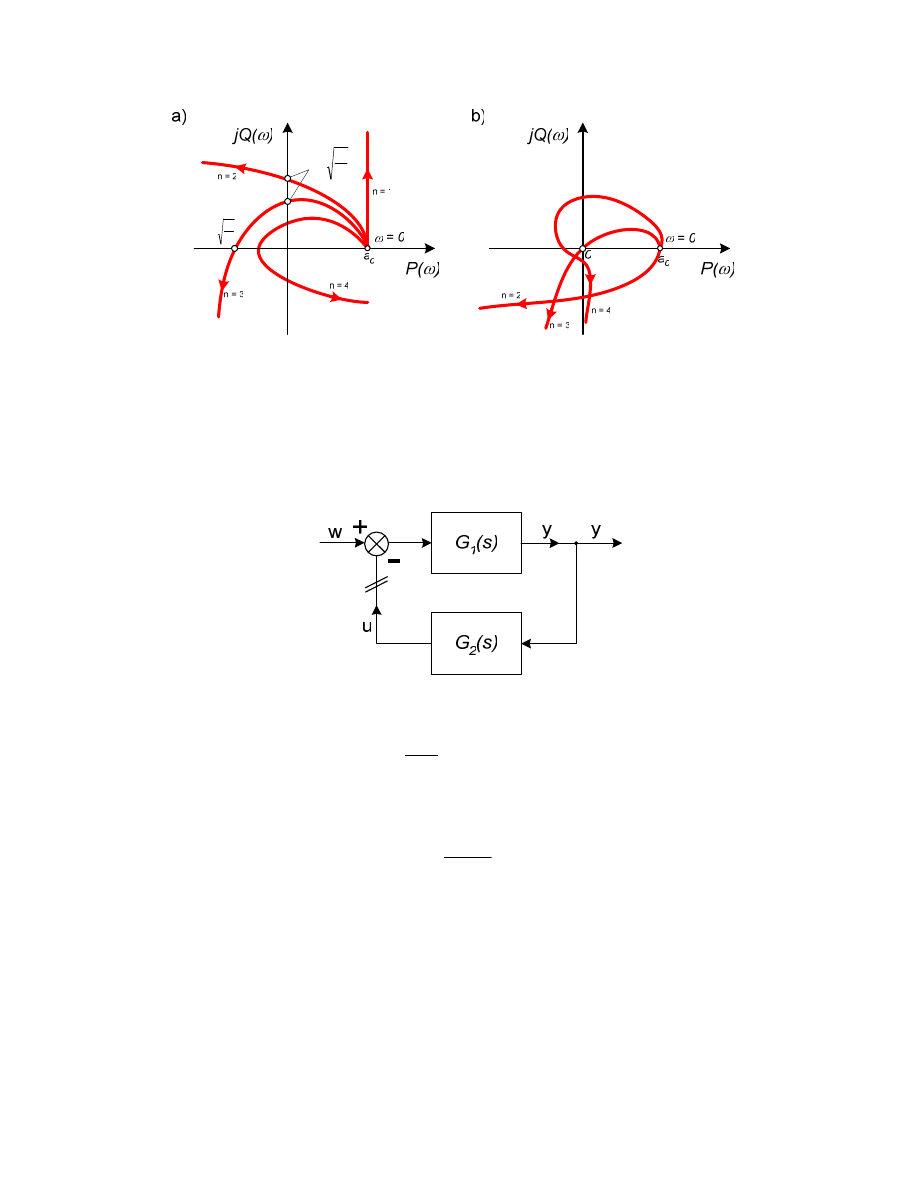
69
∞
→
ω
∞
→
ω
2
0
1
a
a
=
ω
3
1
2
a
a
=
ω
Rysunek 7.3 Krzywe charakterystyczne układów: a) stabilnych, b) niestabilnych
D.
Kryterium Nyquista
Kryterium Nyquista ma du e znaczenie praktyczne, poniewa pozwala bada stabilno
układu zamkni tego na podstawie przebiegu charakterystyki cz stotliwo ciowej układu
otwartego, któr mo na wyznaczy zarówno analitycznie, jak i do wiadczalnie.
Rozpatrzmy układ liniowy o schemacie blokowym przedstawionym poni ej:
Rysunek 7.4 Schemat blokowy układu
Transmitancja układu otwartego wynosi
)
(
)
(
)
(
)
(
)
(
2
1
s
G
s
G
s
w
s
u
s
G
O
=
=
( 7.17)
Przedstawiaj c t transmitancj w postaci ilorazu wielomianów zmiennej s otrzymamy:
)
(
)
(
)
(
s
N
s
M
s
G
O
O
O
=
( 7.18)
przy czym
0
)
(
=
s
N
O
( 7.19)
jest równaniem charakterystycznym układu otwartego; zakładamy, e stopie tego równania
równa si n.
Transmitancja układu zamkni tego wynosi

70
)
(
)
(
1
)
(
)
(
)
(
)
(
2
1
1
s
G
s
G
s
G
s
w
s
y
s
G
Z
+
=
=
( 7.20)
Równanie charakterystyczne układu zamkni tego
0
)
(
)
(
)
(
=
+
=
s
N
s
M
s
N
O
O
Z
( 7.21)
jest równie stopnia n, poniewa stopie M
O
(s) nie jest nigdy wi kszy od stopnia N
O
(s).
Zbadamy zmian argumentu funkcji
)
(
)
(
)
(
1
ω
ω
ω
j
N
j
N
j
G
O
Z
O
=
+
( 7.22)
)
(
arg
)
(
arg
)]
(
1
[
arg
0
0
0
ω
ω
ω
ω
ω
ω
j
N
j
N
j
G
O
Z
O
∞
<
<
∞
<
<
∞
<
<
∆
−
∆
=
+
∆
( 7.23)
Przypadek 1. Układ otwarty jest stabilny. Równanie charakterystyczne układu otwartego
ma wszystkie pierwiastki w lewej półpłaszczy nie zmiennej s. Zgodnie z kryterium
Michajłowa:
2
)
(
arg
0
π
ω
ω
n
j
N
O
=
∆
∞
<
<
Układ zamkni ty b dzie stabilny, je eli
2
)
(
arg
0
π
ω
ω
n
j
N
Z
=
∆
∞
<
<
Warunek stabilno ci układu zamkni tego mo na wi c zapisa
0
)]
(
1
[
arg
0
=
+
∆
∞
<
<
ω
ω
j
G
O
( 7.24)
Oznacza to, e wykres krzywej
)]
(
1
[
ω
j
G
O
+
nie mo e obejmowa pocz tku układu
współrz dnych (musi si zaczyna i ko czy na jednej prostej wychodz cej z pocz tku
układu). Ten sam warunek odniesiony do charakterystyki cz stotliwo ciowej (amplitudowo-
fazowej) układu otwartego G
O
(j ) b dzie sformułowany jak nast puje:
Je eli otwarty układ regulacji automatycznej jest stabilny i jego charakterystyka
amplitudowo-fazowa G
O
(j ) dla pulsacji od 0 do + nie obejmuje punktu (-1,j0), to wtedy
i tylko wtedy po zamkni ciu b dzie on równie stabilny.
Przykładowe wykresy krzywych
)]
(
1
[
ω
j
G
O
+
oraz G
O
(j ) układów stabilnego i
niestabilnego (po zamkni ciu) zestawiono na rysunku 7.5:
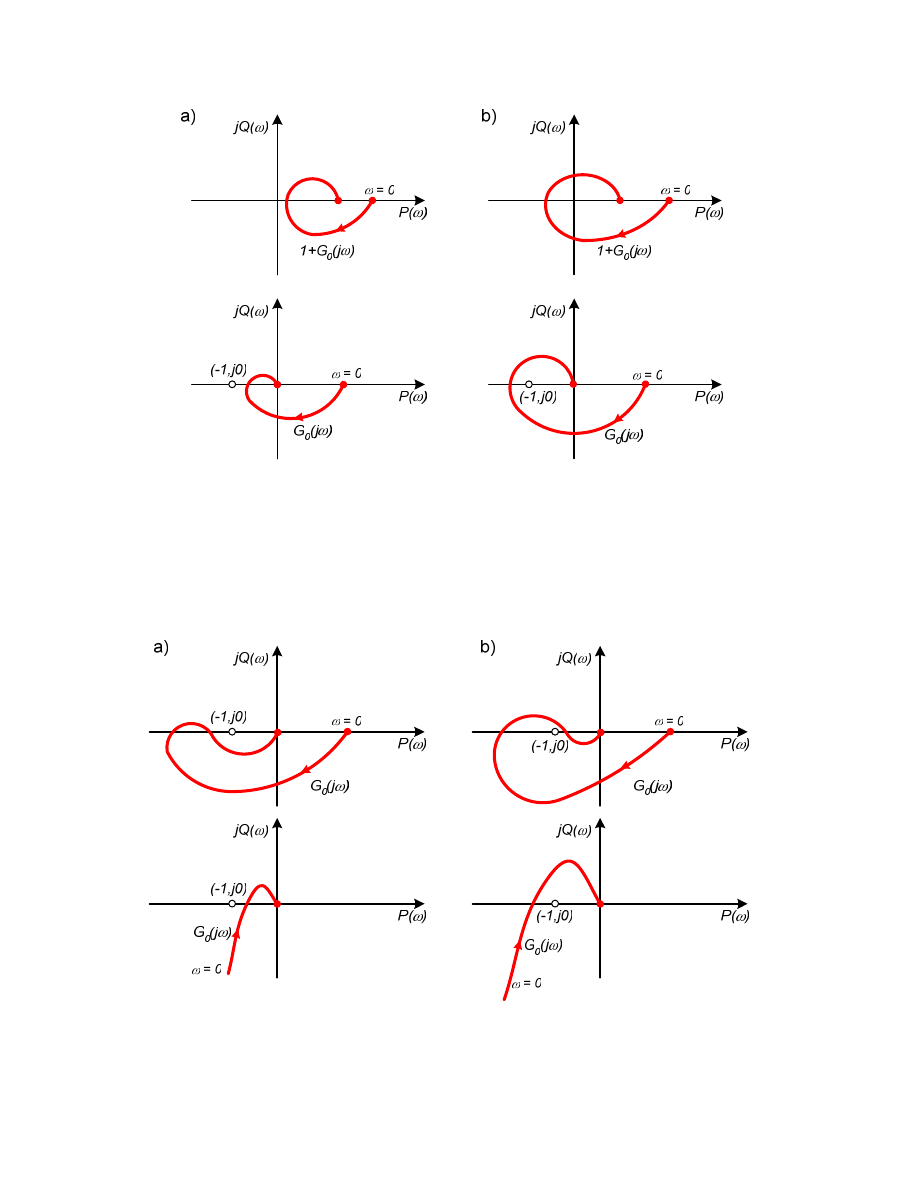
71
∞
=
ω
∞
=
ω
∞
=
ω
∞
=
ω
Rysunek 7.5 Charakterystyki układów, które po zamkni ciu b d : a) stabilne, b) niestabilne
W przypadku zło onego kształtu krzywych G
O
(j ) wygodnie jest posługiwa si
wynikaj c bezpo rednio z podanego kryterium tzw. „reguł lewej strony”, która mówi, e
układ zamkni ty jest stabilny wtedy, kiedy punkt (-1,j0) znajduje si w obszarze le cym po
lewej stronie charakterystyki G
O
(j ), id c w stron rosn cych . Zastosowanie tej reguły
mo na sprawdzi na przykładzie charakterystyk podanych na rys. 7.6.
∞
=
ω
∞
=
ω
∞
=
ω
∞
=
ω
Rysunek 7.6 Charakterystyki G
O
(j ) układów, które po zamkni ciu b d : a) stabilne, b) niestabilne
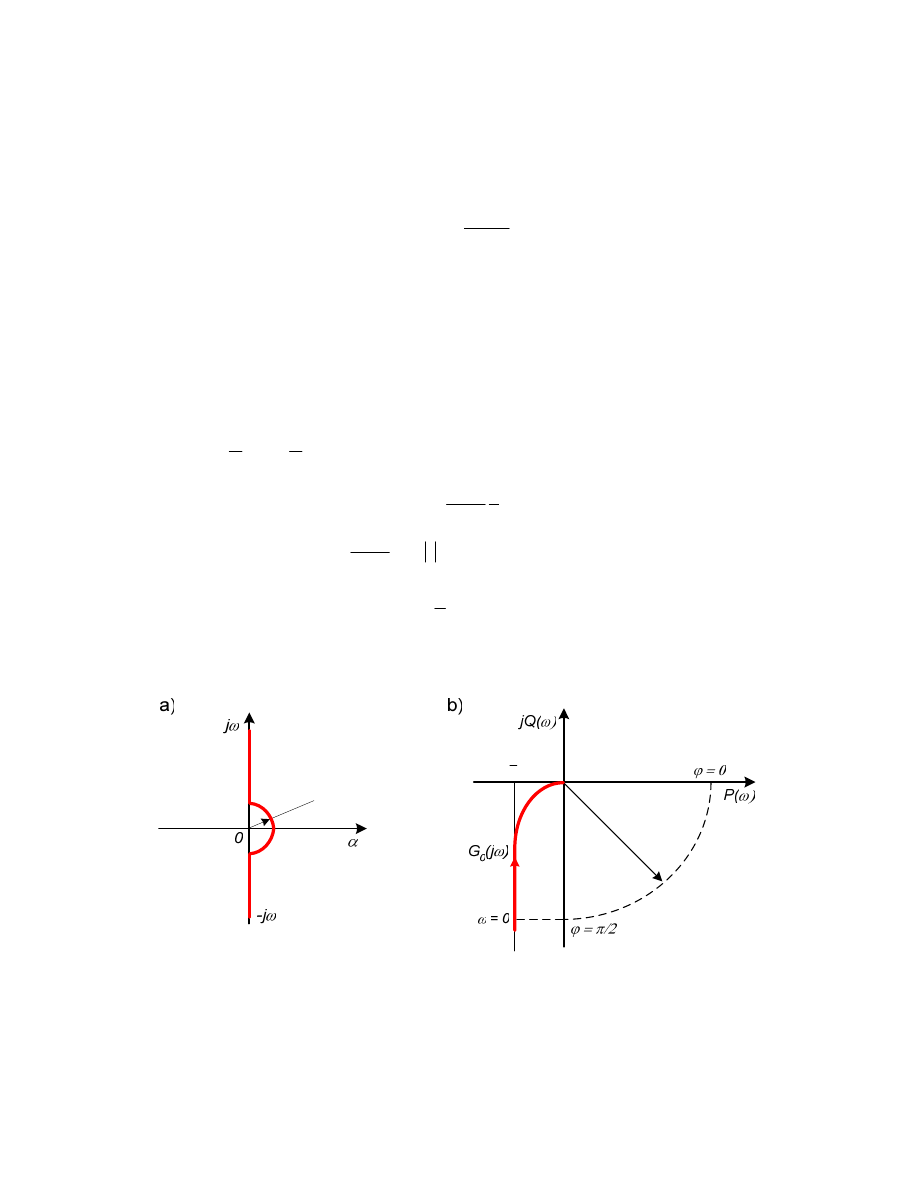
72
Przypadek układów astatycznych, których charakterystyki pokazano w dolnej cz ci
rys. 7.6, wymaga bli szego wyja nienia. Je eli układ otwarty zawiera np. jeden element
całkuj cy, to charakterystyka G
O
(j ) dla = 0 zaczyna si w punkcie o współrz dnej
urojonej –j i mog powsta w tpliwo ci, czy charakterystyka ta obejmuje punkt (-1,j0), czy
nie. Transmitancja operatorowa układu otwartego ma wówczas posta
)
(
)
(
)
(
1
s
sN
s
M
s
G
O
=
Transmitancja widmowa G
O
(j ) jest odwzorowaniem osi liczb urojonych płaszczyzny
zespolonej s za pomoc funkcji G
O
(s). W danym przypadku charakterystyka G
O
(j ) ma dla
pulsacji = 0 punkt nieci gło ci; amplituda przyjmuje warto niesko czenie wielk , a faza
zmienia si skokowo o 180
o
.
Je eli zaliczymy biegun zerowy transmitancji G(s) do lewej półpłaszczyzny, to
mo emy obej go półokr giem o niesko czenie małym promieniu r, zgodnie z rys. 7.7a. Dla
warto ci s bliskich zera mamy wtedy:
ϕ
j
re
s
=
przy czym
2
2
π
ϕ
π
<
<
−
, a transmitancja G
O
(s) przyjmuje posta :
ϕ
j
O
e
r
s
N
s
M
s
G
−
=
1
)
(
)
(
)
(
1
Poniewa iloraz wielomianów
)
(
)
(
1
s
N
s
M
dla
0
→
s
ma stał warto k, zatem:
ϕ
ϕ
j
j
O
e
R
e
r
k
s
G
−
−
⋅
=
=
)
(
przy czym R
. Je eli teraz wektor
ϕ
j
re
s
=
zmienia swój argument od 0 do /2 (interesuj
nas dodatnie warto ci ), to G
O
(s) zmienia argument od 0 do – /2 po okr gu o promieniu R.
ϕ
j
re
∞
=
ω
∞
→
R
a
1
−
Rysunek 7.7 Odwzorowanie osi j z wył czeniem bieguna zerowego dla układu astatycznego o
transmitancji
)
(
/
1
)
(
0
α
ω
ω
ω
+
=
j
j
j
G
Przypadek 2. Układ otwarty jest niestabilny. Równanie charakterystyczne układu
otwartego ma (n-m) pierwiastków w lewej półpłaszczy nie zmiennej s oraz m
pierwiastków w prawej półpłaszczy nie. Zgodnie z wzorem (7.11):
73
π
ω
ω
)
2
(
)
(
arg
0
m
n
j
N
−
=
∆
∞
<
<
∞
−
lub, poniewa N
0
(j ) jest krzyw symetryczn wzgl dem osi liczb rzeczywistych,
2
)
2
(
)
(
arg
0
0
π
ω
ω
m
n
j
N
−
=
∆
∞
<
<
Układ zamkni ty b dzie stabilny, je eli
2
)
(
arg
0
π
ω
ω
n
j
z
N
=
∆
∞
<
<
Warunek stabilno ci układu zamkni tego mo na wi c zapisa
π
ω
ω
2
2
)]
(
1
[
arg
0
0
m
j
G
=
+
∆
∞
<
<
( 7.25)
Warunek ten, odniesiony do charakterystyki amplitudowo-fazowej układu otwartego
G0(j ), b dzie sformułowany jak nast puje:
Je eli otwarty układ regulacji automatycznej jest niestabilny i ma m pierwiastków
swego równania charakterystycznego w prawej półpłaszczy nie zmiennej s, to po zamkni ciu
b dzie on stabilny wtedy i tylko wtedy, gdy charakterystyka amplitudowo-fazowa układu
otwartego dla pulsacji od 0 do + okr a m/2 razy punkt (-1,j0) w kierunku dodatnim
*
.
Zastosowanie kryterium Nyquista w podanym ostatnio sformułowaniu wymaga wi c
znajomo ci liczby pierwiastków równania charakterystycznego układu otwartego z dodatni
cz ci rzeczywist , co bardzo ogranicza jego znaczenie.
Omawiany przypadek jest bardzo rzadki, gdy układy automatyki spotykane w
praktyce s zwykle w stanie otwartym stabilne (m=0).
*
Jako kierunek dodatni przyjmuje si kierunek przeciwny do ruchu wskazówek zegara.
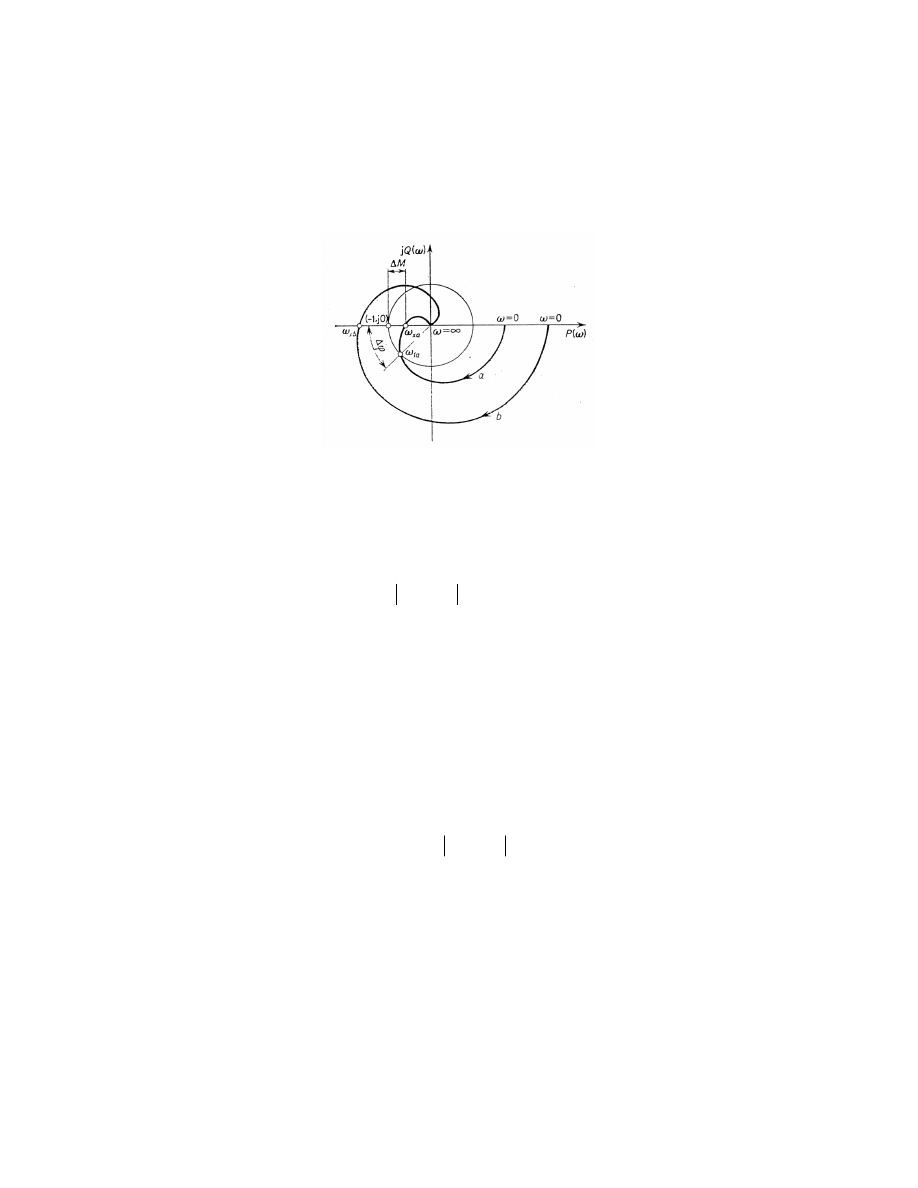
74
E.
Logarytmiczne kryterium Nyquista
Rozwa my dwa układy otwarte, których charakterystyki amplitudowo-fazowe
przedstawiono na rys. 7.8.
Rysunek 7.8 Charakterystyki amplitudowo-fazowe
)
(
ω
j
G
O
układów otwartych: a – układ zamkni ty
stabilny, M – zapas modułu, – zapas fazy, b- układ zamkni ty niestabilny
Układ b dzie po zamkni ciu stabilny, natomiast układ b niestabilny. Z kryterium Nyquista
wynika bezpo rednio nast puj cy warunek stabilno ci:
1
)
(
<
x
O
j
G
ω
( 7.26)
Gdzie
x
jest pulsacj , dla której
O
x
O
j
G
180
)
(
arg
−
=
ω
( 7.27)
Równocze nie na wykresie okre li mo na tzw. zapas stabilno ci układu a, w postaci zapasu
modułu M i zapasu fazy .
Je eli charakterystyka cz stotliwo ciowa układu otwartego podana jest w postaci
logarytmicznych charakterystyk amplitudowej L( ) i fazowej ( ), to warunek (7.26) mo na
zast pi równowa nym warunkiem:
0
)
(
log
20
)
(
<
=
x
O
x
j
G
L
ω
ω
( 7.28)
Dla prostych układów automatyki o charakterystykach cz stotliwo ciowych typu
przedstawionego na rys. 7.8
kryterium stabilno ci mo na sformułowa nast puj co:
Zamkni ty układ regulacji automatyczne jest stabilny wtedy, gdy logarytmiczna
charakterystyka amplitudowa stabilnego układu otwartego ma warto ujemn przy pulsacji
odpowiadaj cej przesuni ciu fazowemu -180
o
.
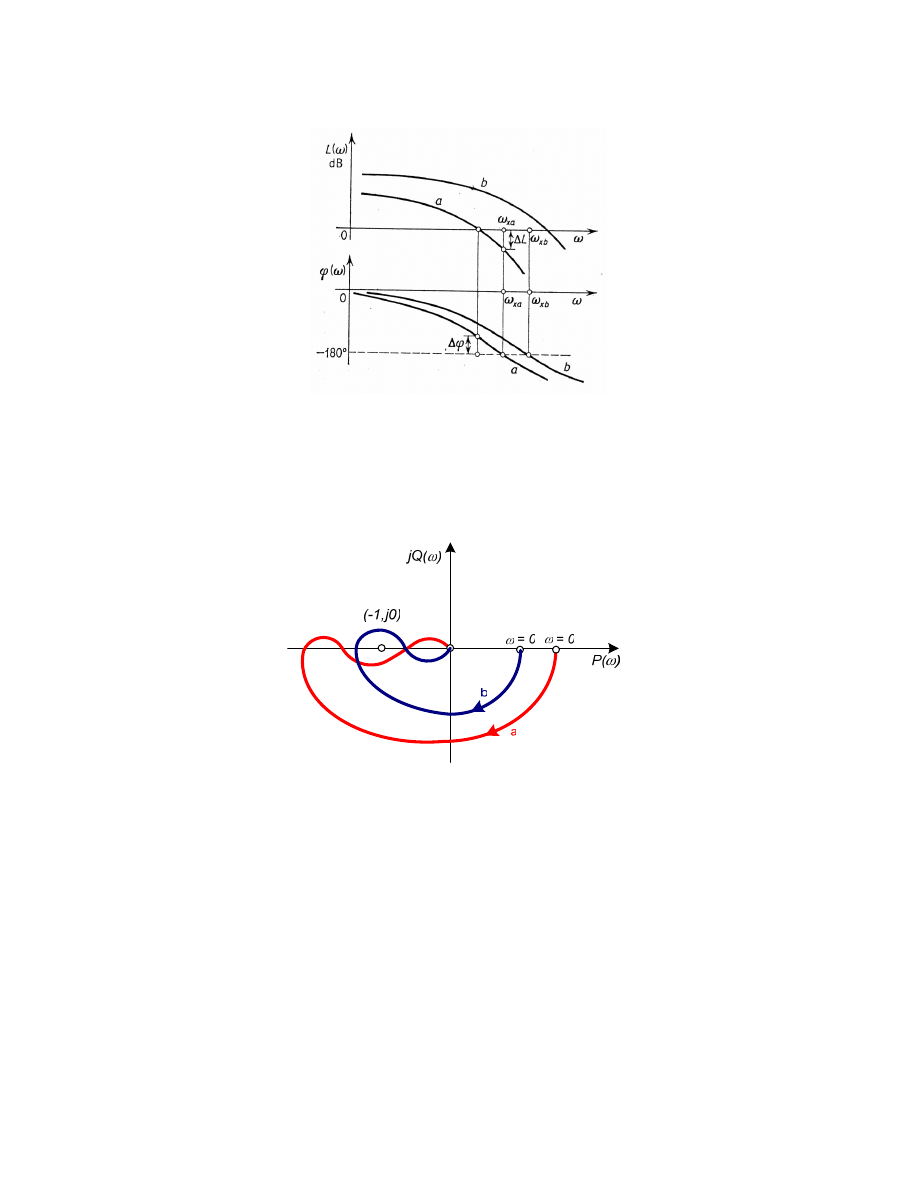
75
Rysunek 7.9 Wyznaczanie zapasu modułu M i zapasu fazy na wykresach charakterystyk
logarytmicznych
W przypadkach układów o charakterystykach bardziej zło onych, typu przedstawionego na
rysunku poni ej, istnieje kilka pulsacji
z
, dla których charakterystyka fazowa przyjmuje
warto -180
o
.
∞
=
ω
Rysunek 7.10 Przykłady charakterystyk zło onych układów: a) stabilnych, b) niestabilnych
Ka dej z tych pulsacji odpowiada jedna warto logarytmicznej charakterystyki amplitudowej
L( ). Je eli układ otwarty jest stabilny, to układ zamkni ty stabilny jest wtedy, gdy liczba
warto ci dodatnich L(
x
) jest parzysta, a niestabilny – gdy liczba warto ci dodatnich L(
x
)
jest nieparzysta. Warunek ten zilustrowano na rys. 7.11, gdzie przedstawiono charakterystyki
L( ) i ( ) odpowiadaj ce charakterystykom G
O
(j ) z rys. 7.10.
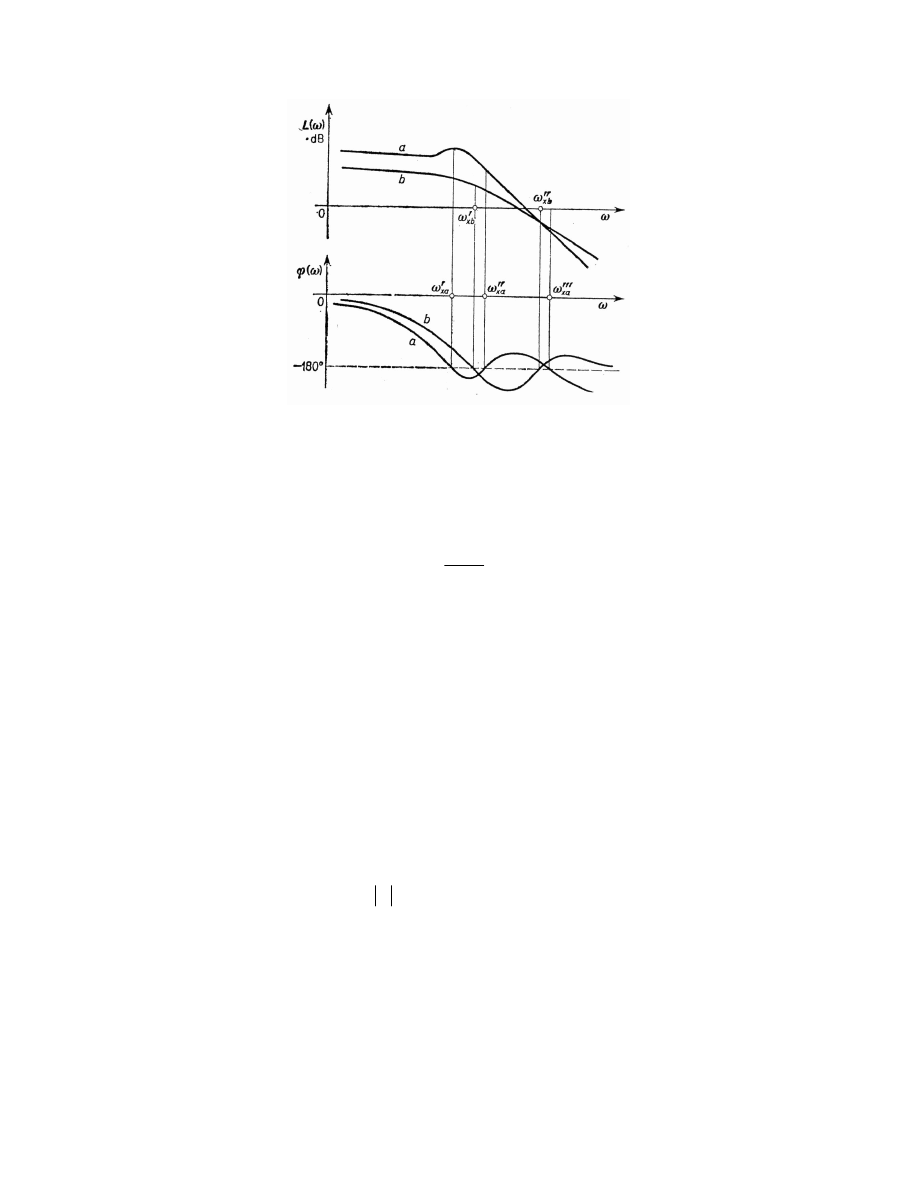
76
Rysunek 7.11 Logarytmiczne charakterystyki amplitudowa i fazowa układu otwartego: a – układ
zamkni ty stabilny; b – układ zamkni ty niestabilny
F.
Stabilno układów dyskretnych
Transmitancj dyskretn układu impulsowego przestawimy w postaci:
)
(
)
(
)
(
z
M
z
L
z
G
=
( 7.29)
Gdzie:
0
1
0
1
)
(
)
(
a
z
a
z
a
z
M
b
z
b
z
b
z
L
k
k
l
l
+
+
+
=
+
+
+
=
Równaniem charakterystycznym układu impulsowego (zamkni tego) jest:
0
)
(
=
z
M
( 7.30)
Układ impulsowy nazywamy stabilnym asymptotycznie, je eli dyskretne warto ci składowej
przej ciowej odchyłki (uchybu) regulacji w chwilach impulsowania malej do zera n
.
Liniowy stacjonarny układ impulsowy jest stabilny wtedy i tylko wtedy, gdy pierwiastki z
i
równania charakterystycznego M(z)=0 tego układu spełniaj warunek:
1
<
i
z
dla
k
i
,
,
2
,
1
=
tzn. le na płaszczy nie zmiennej zespolonej z wewn trz okr gu o promieniu równym
jedno ci i o rodku w pocz tku układu współrz dnych.
Je eli dany układ dyskretny opisany jest równaniem stanu:
x(n+1)=Ax(n)+Bu(n)
( 7.31)
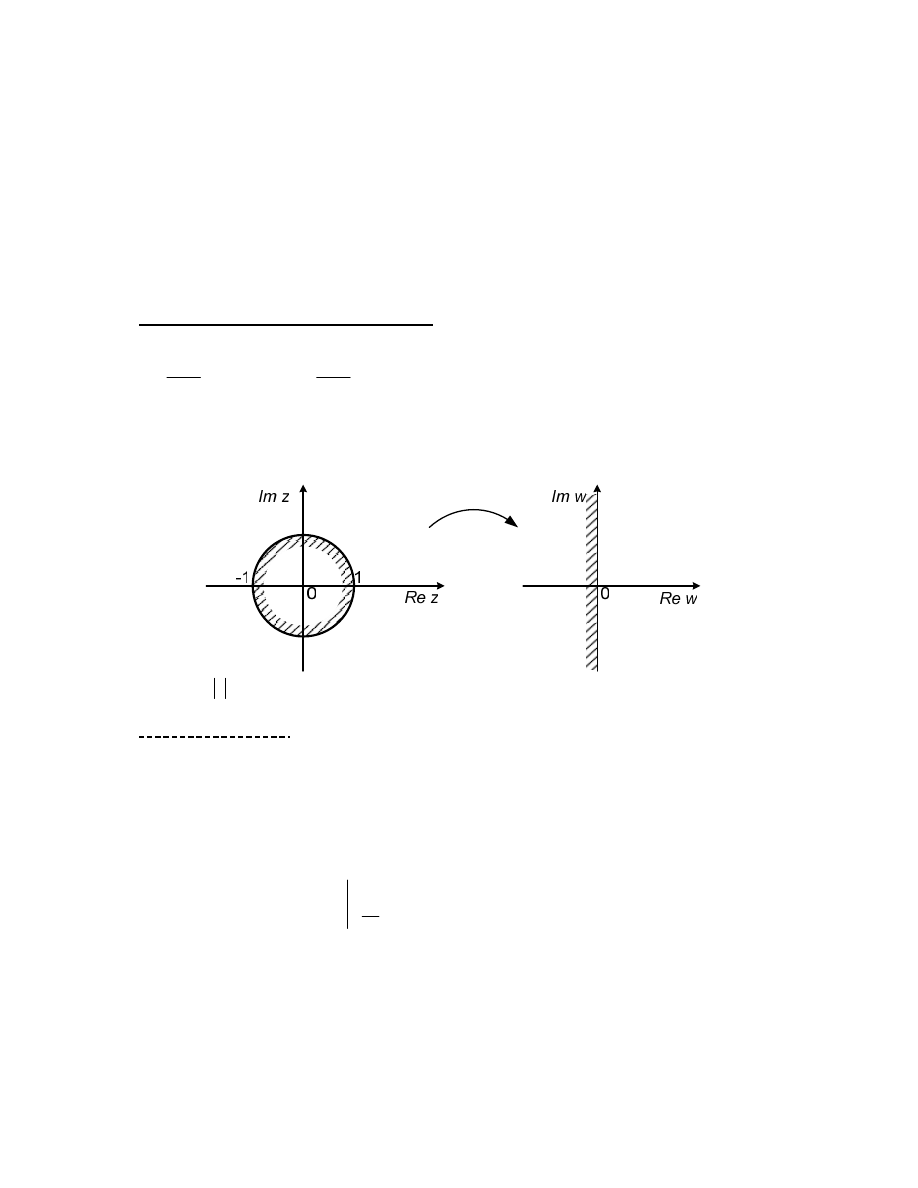
77
przy czym
x(n) i u(n) s odpowiednio wektorami stanu i sterowania, a A i B macierzami o
stałych, niezale nych od n elementach, to jest on stabilny wtedy i tylko wtedy, gdy warto ci
własne z
i
macierzy
A czyli pierwiastki równania
M(z)=det[z
I-A]=0
( 7.32)
le na płaszczy nie zmiennej zespolonej z wewn trz okr gu o promieniu jedno ci i rodku w
pocz tku układu współrz dnych.
Kryteria stabilno ci Hurwitza i Nyquista liniowych stacjonarnych układów impulsowych.
Mo na wykaza [Kaczorek], e funkcja
1
1
−
+
=
w
w
z
lub
w
w
z
−
+
=
1
1
odwzorowuje obszar koła o promieniu r = 1 i rodku 0 w lew półpłaszczyzn płaszczyzny
zmiennej zespolonej w.
Zatem dla
1
<
z
zachodzi
0
)
Re(
<
w
Kryterium Hurwitza
Równanie charakterystyczne o postaci
0
)
(
0
1
1
1
=
+
+
+
+
=
−
−
a
z
a
z
a
z
a
z
M
k
k
k
k
,
0
>
k
a
( 7.33)
lub po przekształceniu
0
)
(
)
(
0
1
1
1
1
1
=
+
+
+
+
=
=
−
−
−
+
=
b
w
b
w
b
w
b
z
M
w
N
k
k
k
k
w
w
z
( 7.34)
ma wszystkie pierwiastki na płaszczy nie zmiennej zespolonej z wewn trz okr gu o
promieniu r = 1 ( w lewej półpłaszczy nie w) wtedy i tylko wtedy, gdy wszystkie wyrazy
ci gu
1
,
2
,…,
k
s dodatnie
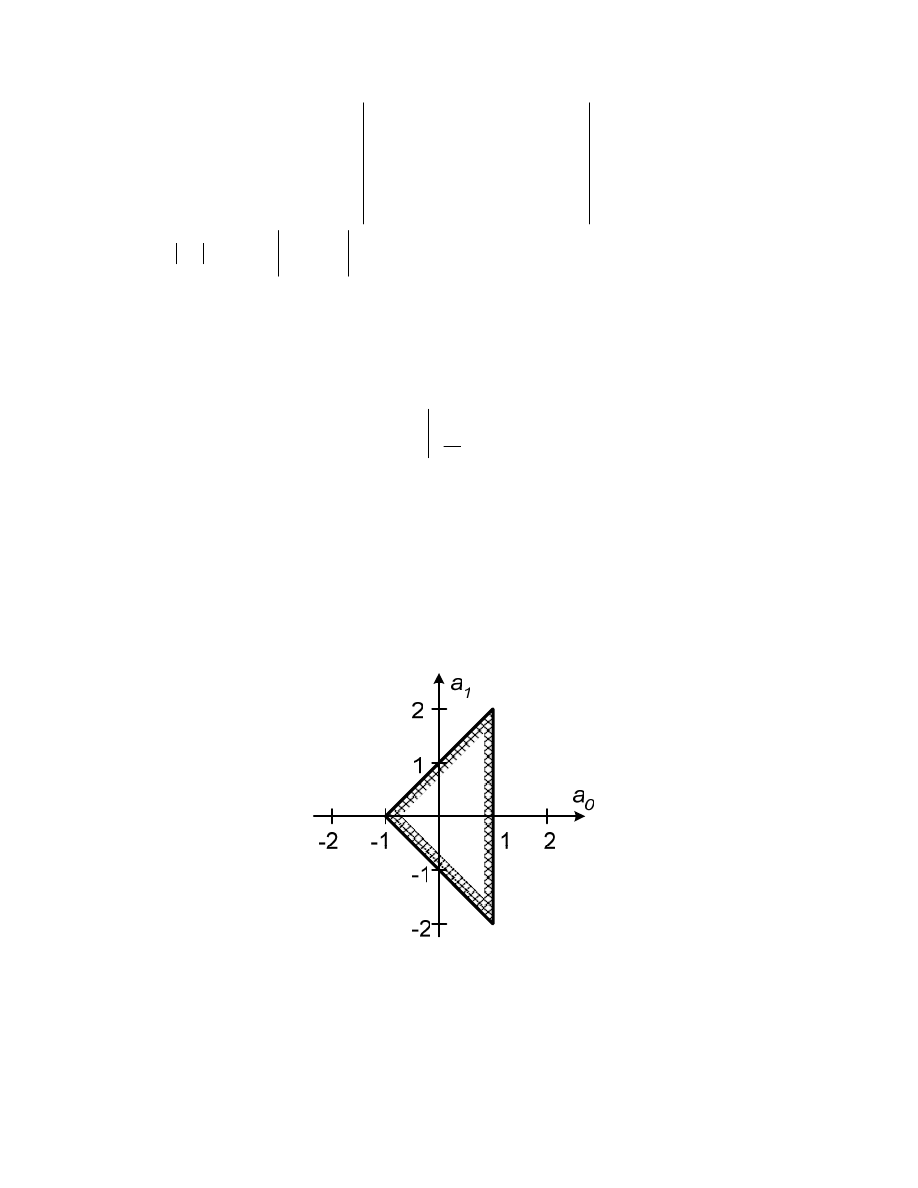
78
3
4
5
6
7
1
2
3
4
5
1
2
3
1
0
0
0
0
−
−
−
−
−
−
−
−
−
−
−
−
−
−
=
∆
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
b
1
1
−
=
∆
k
b
,
2
3
1
2
−
−
−
=
∆
k
k
k
k
b
b
b
b
,
itd.
Warunek konieczny:
0
>
i
a
dla
1
,
,
2
,
1
,
0
−
=
k
i
Przykład
0
)
(
0
1
2
=
+
+
=
a
z
a
z
z
M
0
1
2
2
1
1
)
(
)
(
b
w
b
w
b
z
M
w
N
w
w
z
+
+
=
=
−
+
=
przy czym:
0
1
2
1
a
a
b
+
+
=
,
)
1
(
2
0
1
a
b
−
=
,
0
1
0
1
a
a
b
+
−
=
warunki Hurwitza:
,
0
0
>
b
,
0
1
>
b
,
0
2
>
b
czyli:
0
1
0
1
>
+
+
a
a
0
1
0
>
− a
0
1
0
1
>
+
−
a
a
Na płaszczy nie parametrów
a
1
,
a
0
:
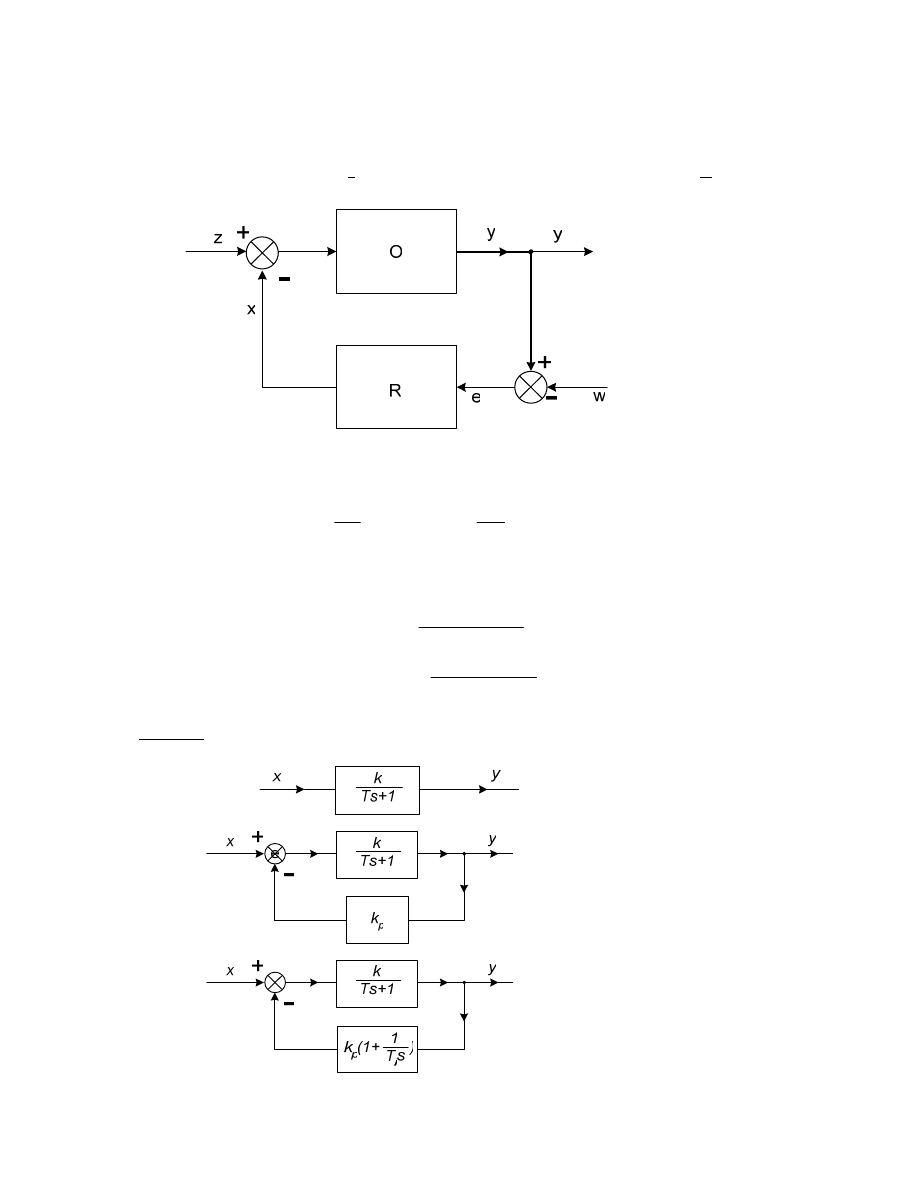
79
7.2
Dokładno statyczna
Dokładno t ocenia si na podstawie warto ci odchyłki statycznej e
st
. Na warto e
st
wpływaj zarówno zakłócenia z na wej ciu obiektu, jak i zmiany warto ci zadanej w na
wej ciu regulatora.
st
w
st
z
st
t
st
e
e
e
t
e
e
)
(
lim
+
=
=
∞
→
Wymagan dokładno statyczn okre la si podaj c liczbowe warto ci dopuszczalnych
odchyłek e
st
, lub oddzielenie e
z st
i e
w st
albo procentowe warto ci wska ników odchyłek e
1
i
e
2
:
1
%
100
e
y
e
n
st
z
≤
⋅
,
2
%
100
e
w
e
n
st
w
≤
⋅
gdzie:
y
n
, w
n
– warto ci nominalne (punkt pracy), niekiedy maksymalne
Wyliczenie warto ci odchyłek statycznych:
)
(
)
(
1
)
(
)
(
lim
)
(
lim
)
(
lim
0
0
s
G
s
G
s
G
s
z
s
s
e
s
t
e
e
r
ob
ob
s
z
s
z
t
st
z
+
⋅
=
⋅
=
=
→
→
∞
→
)
(
)
(
1
)
(
)
(
lim
)
(
lim
)
(
lim
0
0
s
G
s
G
s
G
s
w
s
s
e
s
t
e
e
r
ob
ob
s
w
s
w
t
st
w
+
⋅
=
⋅
=
=
→
→
∞
→
Przykład:
a.)
obiekt bez regulatora
b.)
układ z regulatorem P
c.)
układ z regulatorem PI
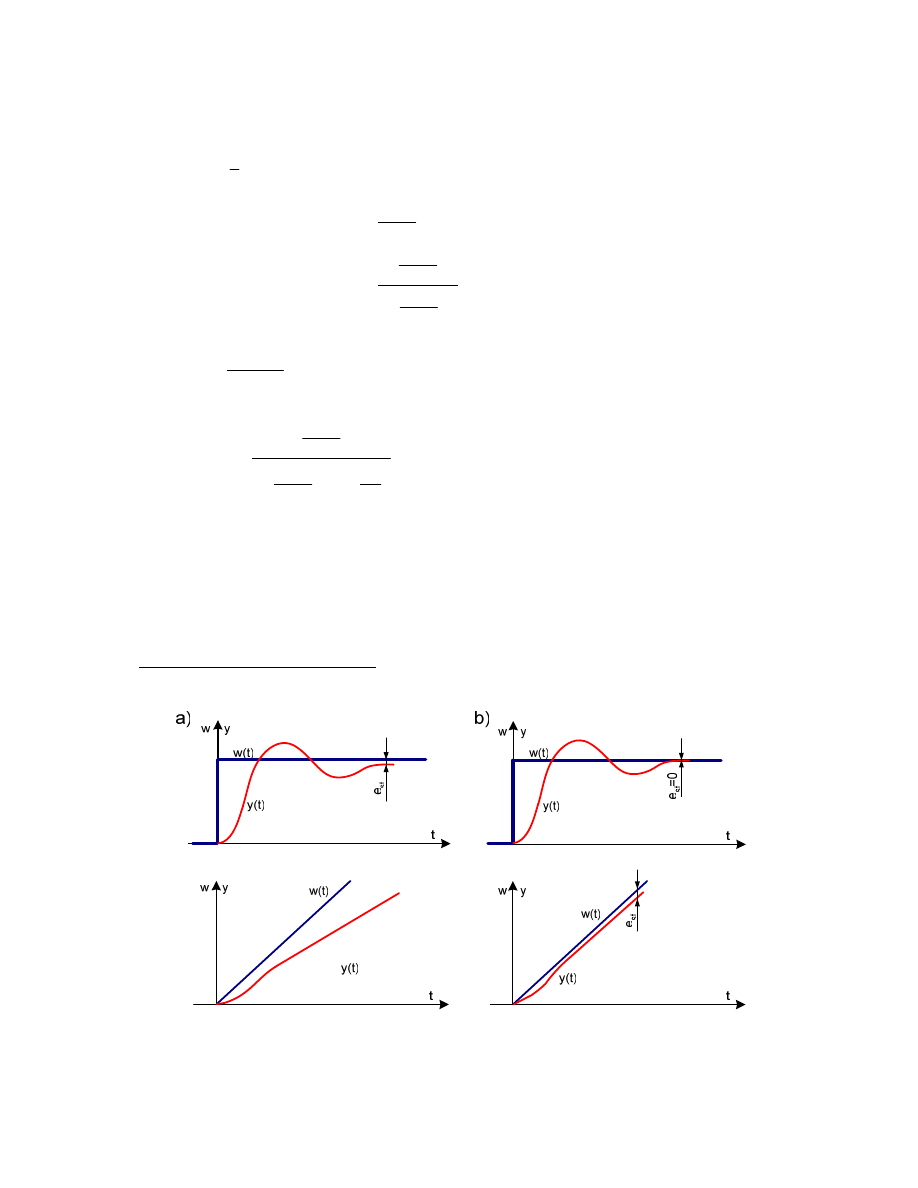
80
zało enie:
w
0
=const
,
w=
0
zatem:
e = y, e
st
= e
z st
= y
st
Je eli
st
z
s
s
z
1
)
(
=
, to:
a.)
st
st
s
s
st
st
z
z
k
Ts
z
k
s
y
s
y
e
⋅
=
+
⋅
=
⋅
=
=
→
→
1
lim
)
(
lim
0
0
b.)
st
p
s
s
st
st
z
z
k
Ts
k
Ts
k
s
y
s
y
e
⋅
+
+
+
=
⋅
=
=
→
→
1
1
1
lim
)
(
lim
0
0
p
st
st
k
k
z
k
y
⋅
+
⋅
=
1
c.)
0
1
1
1
1
1
lim
0
=
⋅
+
+
+
+
=
→
st
i
p
s
st
z
s
T
k
Ts
k
Ts
k
y
!!!
Wpływ akcji P I D regulatora na dokładno statyczn :
•
gdy
k
p
ro nie to
e
st
maleje (uwaga na stabilno !)
•
obecno akcji całkuj cej likwiduje odchyłk statyczn (
e
st
= 0
dla ka dej
sko czonej, ustalonej warto ci wymuszenia)
•
obecno akcji ró niczkuj cej nie ma wpływu na warto
e
st
Przykłady odpowiedzi skokowych:
układ z regulatorem P
układ z regulatorem PI
∞
→
st
e
*Dyskusja: wymuszenia liniowo narastaj ce i inne.

81
7.3
Jako dynamiczna
Mo na j oceni za pomoc szeregu wska ników.
7.3.1
Wska niki dotycz ce cech odpowiedzi skokowej
A.
Czas regulacji
t
r
Jest to czas liczony od chwili wyst pienia zakłócenia do chwili, po której odchyłka
regulacji
e
jest stale mniejsza od |
e
|. Cz sto przyjmuje si
e=
5%
e
m
.
Podana
definicja jest umowna, oparta na wynikach eksperymentów i obserwacji zachowania
układów rzeczywistych.
B.
Odchyłka maksymalna
e
m
Jest to najwi ksza warto odchyłki
e(t),
czyli ró nicy mi dzy
y(t)
i
w(t)
, wyst puj ca
podczas przebiegu przej ciowego (dla 0 t )
C.
Przeregulowanie
%
100
1
2
⋅
=
e
e
κ
( 7.35)
gdzie:
e
1
,
e
2
– amplitudy pierwszego i drugiego odchylenia od ko cowej warto ci
ustalonej
Do cz sto
e
1
= e
m
, ale zapis
%
100
2
⋅
=
m
e
e
κ
, jest poprawny tylko dla przebiegów w
układach z regulatorem astatycznym (z akcj I), a dla pozostałych przypadków
przedstawionych w tabl. 7.1, oznaczonych
(b) i (c), nale ałoby napisa :
b)
%
100
2
⋅
−
=
st
m
e
e
e
κ
c)
%
100
2
2
⋅
−
=
e
e
e
m
κ
poniewa dla b) e
m
-e
st
=e
1
oraz dla c) e
m
-e
2
=e
1
,
wi c tylko definicja (7.35)
ma charakter ogólny
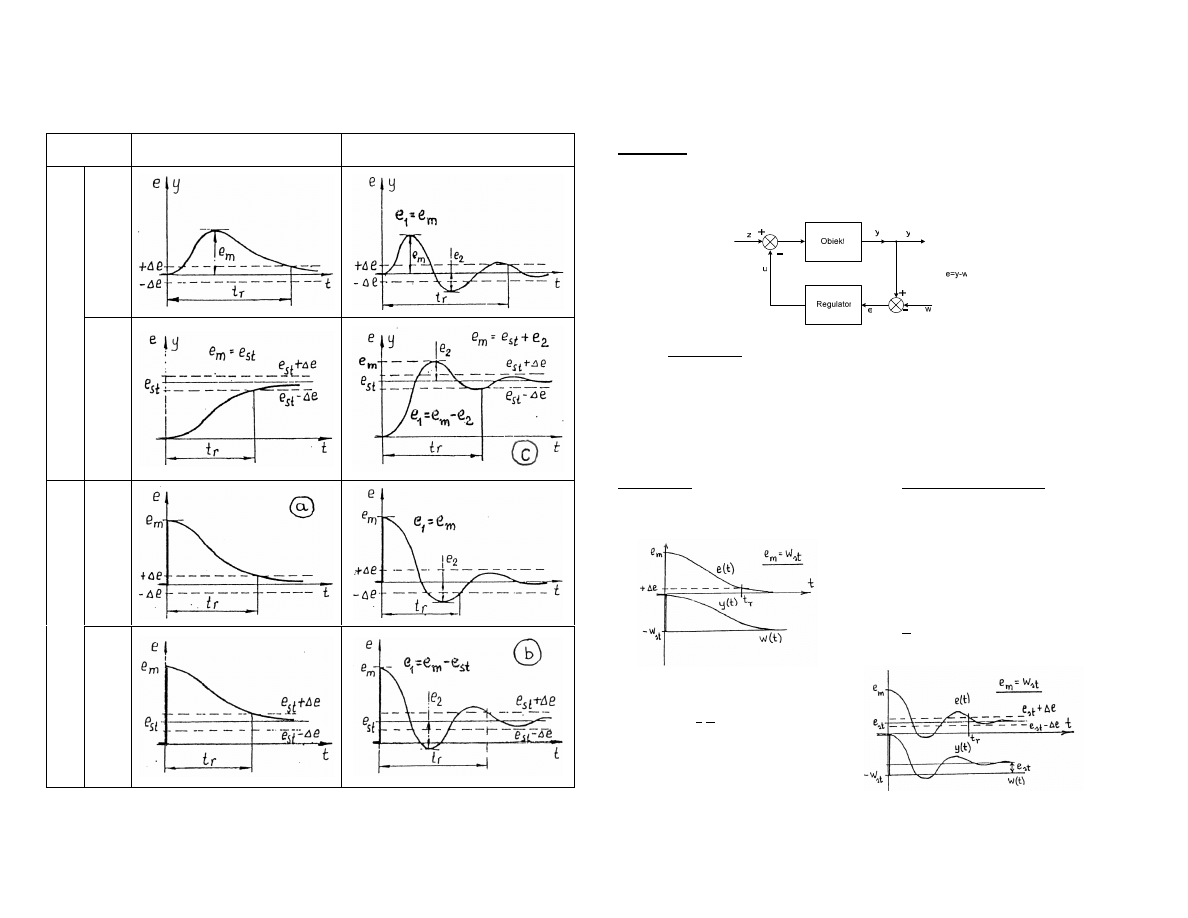
82
Komentarz
do tablicy odpowiedzi skokowych typowych układów regulacji
Rozwa any jest układ regulacji o nast puj cej strukturze:
Przypadek 1: zakłócenie skokowe z (w kierunku dodatnim) na wej ciu
obiektu,
const
w
=
Przebieg odchyłki regulacji e jest wówczas identyczny jak przebieg odchyłki y
wielko ci regulowanej y od jej warto ci zadanej w. Odchyłk y=y-w oznacza si
cz sto dla uproszczenia zapisu przez y, co jest zgodne z ogóln konwencj
operowania tylko odchyłkami od nominalnego punktu pracy. Poziom e=0 oznacza
w tym przypadku warto zadan w.
Przypadek 2: zakłócenie w na wej ciu regulatora (zmiana warto ci zadanej!)
Pełny obraz przebiegu sygnałów y,w oraz e, odpowiadaj cy rysunkowi
(a)
tablicy, przedstawiono poni ej:
Przyj to, podobnie jak w pozostałych
przypadkach tej cz ci tablicy, e
warto zadana zmieniła si skokowo
w kierunku ujemnym, z amplitud
skoku w
st
Dla rysunku
(b) tablicy przebiegi
sygnałów y,w,e przedstawiono obok
m
e
e
⋅
=
∆
%
5
ODPOWIEDZI SKOKOWE TYPOWYCH UKŁADÓW REGULACJI
Rodzaj
przebiegu
Aperiodyczny
Oscylacyjny
R
eg
ul
at
or
a
st
at
yc
zn
y
W
ym
us
ze
ni
e
na
w
ej
!
ci
u
ob
ie
kt
u
R
eg
ul
at
or
s
ta
ty
cz
ny
R
eg
ul
at
or
as
ta
ty
cz
ny
W
ym
us
ze
ni
e
na
w
ej
!
ci
u
re
gu
la
to
ra
R
eg
ul
at
or
s
ta
ty
cz
ny
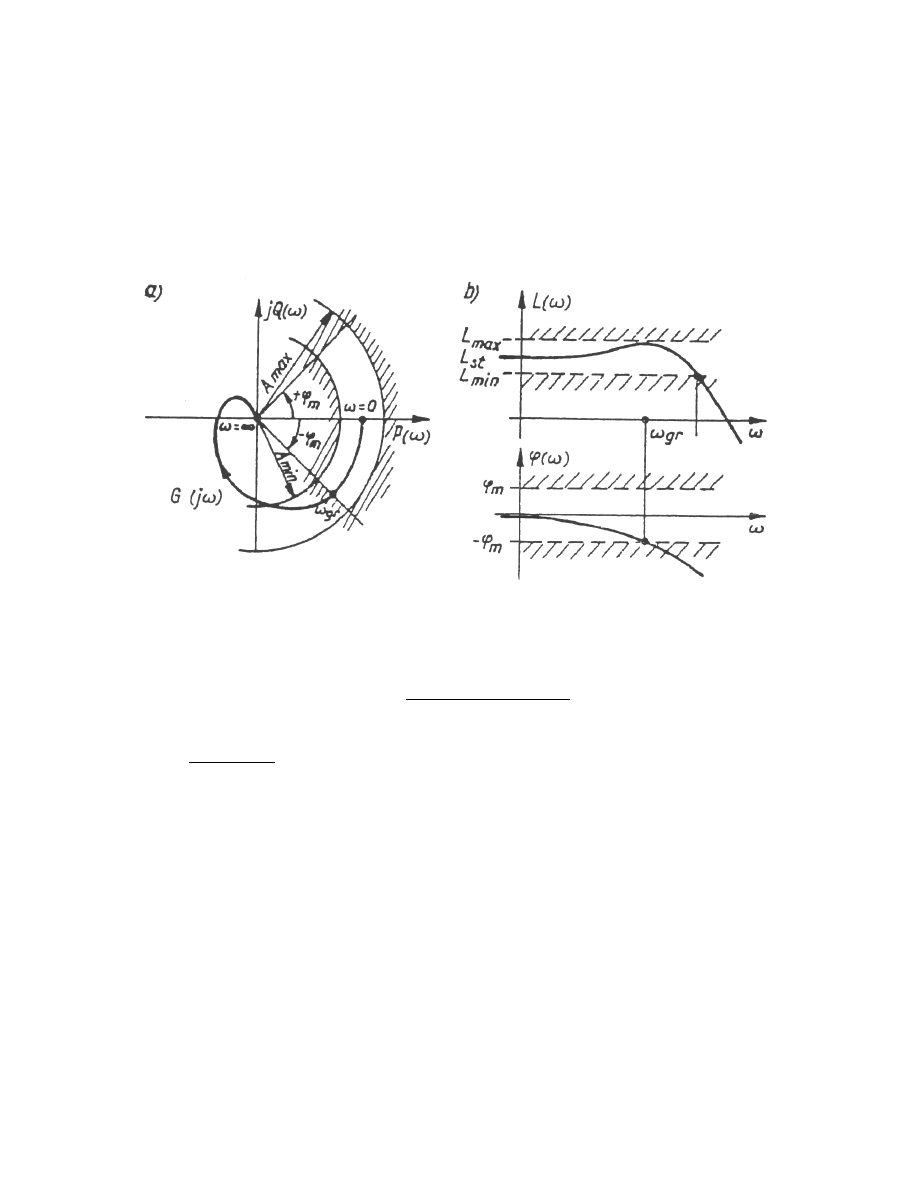
83
7.3.2
Wska niki cz stotliwo ciowe
a)
Pasmo przenoszenia
•
definicja:
jest to zakres cz stotliwo ci, w którym spełnione s wymagania
dotycz ce stosunku amplitud wyj cia do wej cia (modułu) oraz przesuni cia
fazowego pomi dzy wyj ciem a wej ciem
•
interpretacja na wykresach charakterystyk cz stotliwo ciowych
pasmo przenoszenia:
0
gr
b)
Wska nik regulacji (wska nik skuteczno ci regulacji)
)
regulatora
(bez
)
('
m)
regulatore
(z
)
(
)
(
ω
ω
ω
j
e
j
e
j
q
=
Wymagania:
1
)
(
<
ω
j
q
dla zakresu cz stotliwo ci pracy układu, im mniejsza jest
warto
)
(
ω
j
q
tym skuteczniejsze oddziaływanie regulatora
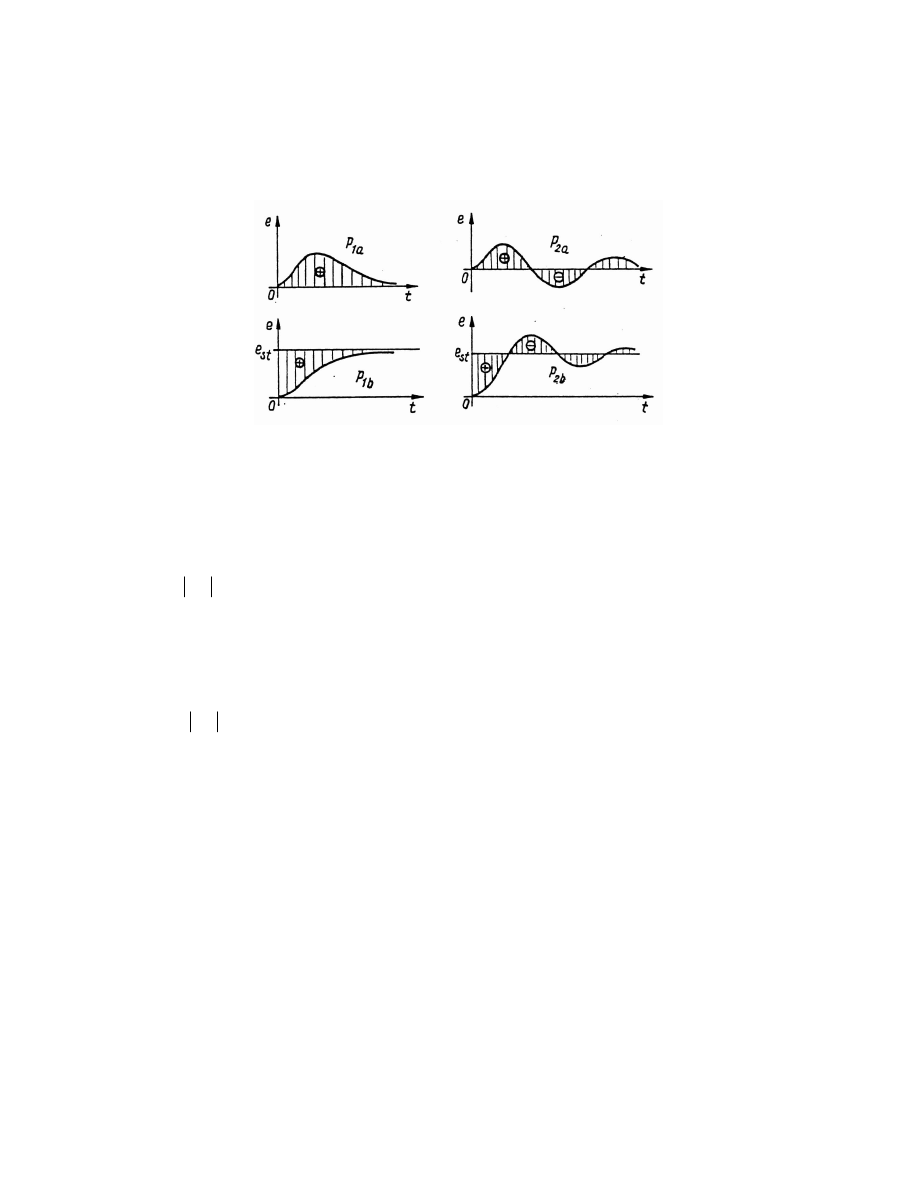
84
7.3.3
Całkowe wska niki jako ci regulacji
Miar jako ci regulacji mo e by wielko pola pod krzyw odchyłki regulacji. D y si do
minimalizacji tego pola.
∞
=
0
1
)
(
dt
t
e
I
a
∞
−
=
0
1
)]
(
[
dt
t
e
e
I
st
b
∞
=
0
2
2
)
(
dt
t
e
I
a
∞
−
=
0
2
2
)]
(
[
dt
t
e
e
I
st
b
lub
∞
=
0
3
)
(
dt
t
e
I
dla układów czasooptymalnych:
∞
=
0
4
)
(
dt
t
te
I
∞
=
0
5
)
(
dt
t
e
t
I

85
8 DOBÓR RODZAJU I NASTAW REGULATORÓW
8.1
Wybór rodzaju (typu) regulatora
Regulatory dwustawne (2P) - obiekty statyczne,
2
,
0
<
T
τ
, dopuszczalne oscylacje w
normalnym trybie pracy (np. proste procesy termiczne, zał czanie-wył czanie).
Regulatory trójstawne (3P) - zespoły wykonawcze z trójstawnym elementem
nap dowym, np. silnikiem nawrotnym („-1”- w lewo, „0”- stop, „+1”- w prawo) lub z
dwoma torami działania, np. w układach klimatyzacyjnych („-1”- chłodzenie, „0”- stop,
„+1”- grzanie).
Regulatory ci głe (P, I, PI, PD, PID) - najszerszy obszar zastosowa , obiekty statyczne i
astatyczne,
1
≤
T
τ
Regulatory impulsowe - obiekty z du ymi opó nieniami transportowymi lub
zast pczymi,
1
>
T
τ
Regulatory cyfrowe o algorytmach specjalnych, np.:
minimalnowariancyjne
predykcyjne
Smith’a
Najbardziej rozpowszechnione s regulatory ci głe lub quasi-ci głe (cyfrowe) o
algorytmach P, PI, PID. Przy wyborze jednego z tych algorytmów nale y pami ta o kilku
ogólnych zaleceniach:
akcja całkuj ca (np. w algorytmach PI, PID) jest niezb dna dla
uzyskania odchyłek statycznych bliskich zeru (teoretycznie równych
zeru)
akcja ró niczkuj ca jest zalecana w przypadku obiektów wy szych
rz dów (np. procesy termiczne), gdy pozwala na wytworzenie
silnego oddziaływania korekcyjnego regulatora ju przy małych
odchyłkach regulacji
regulator PI zapewnia dobr jako regulacji tylko przy zakłóceniach
o małych cz stotliwo ciach
regulator PD zapewnia szersze pasmo regulacji ni regulator PI,
jednak przy zakłóceniach wolnozmiennych warto ci wska ników
jako ci regulacji s gorsze
regulator PID ł czy zalety obu poprzednich regulatorów
Wg zalece E. Kollmana (Regelungstechnik, 1992), dla procesów o własno ciach
bliskich bezinercyjnym (np. przepływ), inercyjnych I rz du lub całkuj cych wła ciwe s
zwykle regulatory P, PI, niekiedy I, natomiast dla procesów inercyjnych wy szego rz du
lub całkuj cych z inercj (astatycznych) nale y wybiera regulatory PD lub PID.

86
8.2
Dobór nastaw regulatora
Wyró nia si metody analityczne i do wiadczalne doboru nastaw, dla regulatorów SISO i
MIMO. W niniejszym punkcie omówione b d tylko dwie metody do wiadczalne dla
regulatorów o jednym wej ciu i jednym wyj ciu (SISO)
8.2.1
Metoda Zieglera-Nicholsa
Stosowana jest wówczas, gdy regulator i inne elementy układu s ju zainstalowane, ich
funkcjonowanie jest sprawdzone, nale y tylko dobra nastawy regulatora.
Procedura:
a)
pozostawi tylko działanie P regulatora (wył czy I, D)
b)
zwi ksza stopniowo
k
p
a do osi gni cia granicy stabilno ci (oscylacje o stałej
amplitudzie)
c)
zmierzy okres oscylacji T
osc
(na rejestratorze lub ekranie monitora) i zanotowa
warto
k
pkr
,
przy której wyst piły niegasn ce oscylacje
d)
zale nie od typu regulatora, nale y przyj nastawy:
dla regulatora P
:
k
p
=0,5
k
pkr
dla regulatora PI
:
k
p
=0,45
k
pkr
,
T
i
=0,85
T
osc
dla regulatora PID :
kp
=0,6
k
pkr
,
T
i
=0,5
T
osc
,
T
d
=0,12
T
osc
W układzie z tak dobranymi nastawami regulatora wyst powa b d przebiegi przej ciowe
oscylacyjne z przeregulowaniem =20-30%.
8.2.2
Metoda tabelarycznego doboru nastaw po do wiadczalnej
identyfikacji obiektu
Przyjmuje si , e obiekt identyfikowany był metod odpowiedzi skokowych, na podstawie
których wyznaczono nast puj ce parametry:
- dla obiektów statycznych
k
ob
, , T
(model:
1
)
(
+
=
−
Ts
k
e
s
G
ob
s
τ
)
- dla obiektów astatycznych
, T
(model:
Ts
e
s
G
s
1
)
(
τ
−
=
, niekiedy
Ts
k
e
s
G
ob
s
τ
−
=
)
(
(*)
)
Znaj c te parametry okre la si nastawy regulatora zapewniaj ce okre lony charakter
przebiegów przej ciowych na podstawie zał czonych tablic. Tablice te pozwalaj równie
wyznaczy warto ci podstawowych wska ników jako ci regulacji: czasu regulacji
t
r
i
odchyłki maksymalnej
e
m
.
(*)
przypadek omawiany na wykładzie
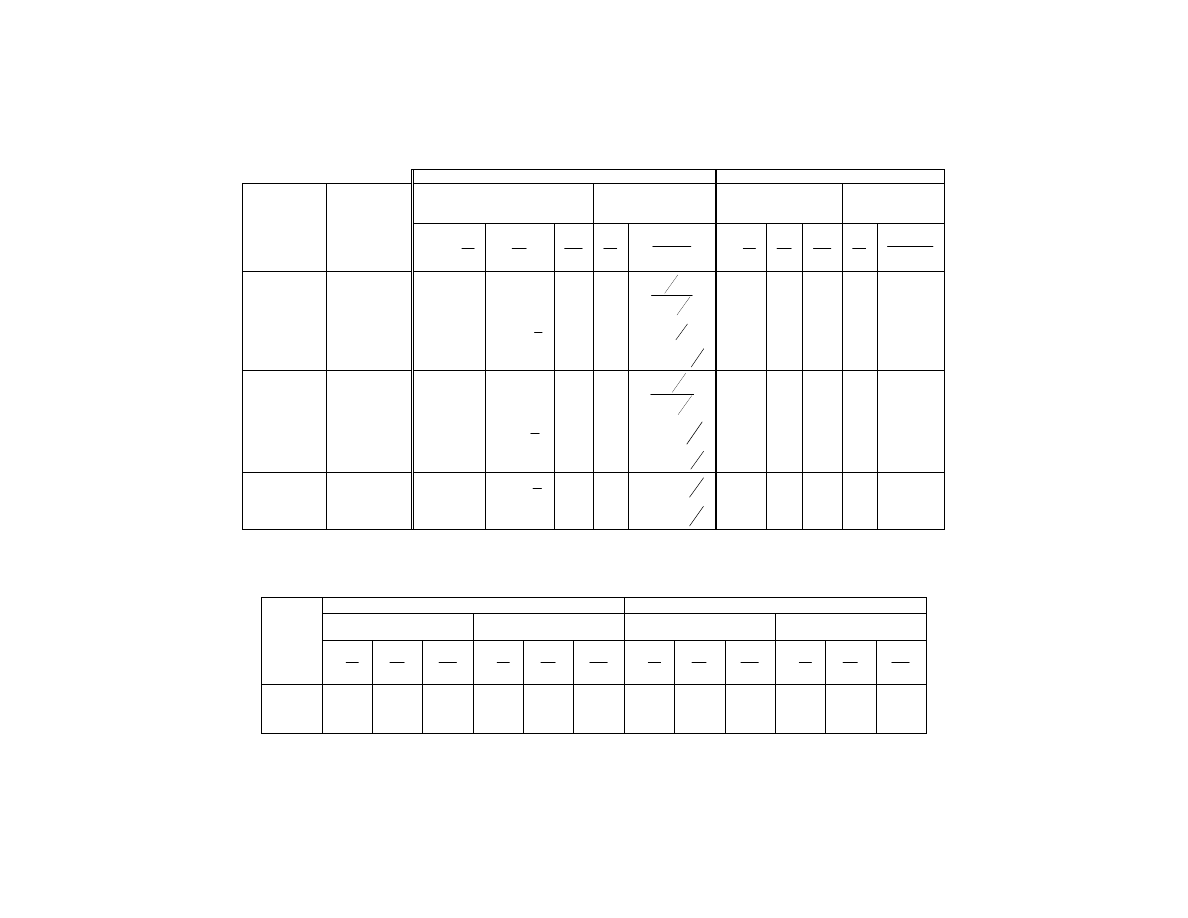
87
TABLICE DOBORU NASTAW REGULATORÓW
Obiekty statyczne
Obiekty astatyczne
Optymalne nastawy regulatora
Wska niki przebiegu
przej ciowego
Optymalne nastawy
regulatora
Wska niki
przebiegu
przej ciowego
Rodzaj
przebiegu
przej ciowego
Rodzaj
regulatora
T
k
k
ob
r
τ
τ
i
T
τ
d
T
τ
r
t
st
ob
m
z
k
e
T
k
r
τ
τ
i
T
τ
d
T
τ
r
t
τ
st
ob
m
z
k
e
P
0,3
−
−
4,5
T
T
τ
τ
+
3
,
0
0,37
−
−
5,5
2,7
PI
0,6
τ
T
0,5
0,8
+
−
8
T
τ
+
1
,
0
0,46
5,75
−
13,2
1,9
0%
min t
r
PID
0,95
2,4
0,4
5,5
T
τ
0,84
0,06
+
0,65
5,0
0,23
9,8
1,38
P
0,7
−
−
6,5
T
T
τ
τ
+
7
,
0
2
,
1
0,7
−
−
7,5
1,43
PI
0,7
τ
T
0,3
1
+
−
12
0,05+0,95
T
τ
0,7
3,0
−
15
1,62
20%
min t
r
PID
1,2
2,0
0,4
7
T
τ
0,78
0,05
+
1,1
2,0
0,37
12
1,12
PI
1,0
τ
T
0,35
1
+
−
16
T
τ
9
,
0
03
,
0
+
1,05
4,3
−
18
1,44
∞
0
2
)
(
min
dt
t
e
PID
1,4
1,3
0,5
10
T
τ
0,7
0,05
+
1,37
1,6
0,51
15
1,03
Optymalne nastawy regulatorów PID według Chiena, Hronesa i Reswicka, z wyró nieniem miejsca wprowadzenia zakłóce (dla
układów z obiektami statycznymi)
= 0%, minimum t
r
= 20%, minimum t
r
)
(
1
)
(
t
z
t
z
st
=
)
(
1
)
(
t
w
t
w
st
=
)
(
1
)
(
t
z
t
z
st
=
)
(
1
)
(
t
w
t
w
st
=
Rodzaj
regulatora
T
k τ
τ
i
T
τ
d
T
T
k τ
τ
i
T
τ
d
T
T
k τ
τ
i
T
τ
d
T
T
k τ
τ
i
T
τ
d
T
P
0,3
−
−
0,3
−
−
0,7
−
−
0,7
−
−
PI
0,6
4,0
−
0,35
1,2
−
0,7
2,3
−
0,6
1,0
−
PID
0,95
2,4
0,42
0,6
1,0
0,5
1,2
2,0
0,42
0,95
1,35
0,47
r
ob
k
k
k
⋅
=
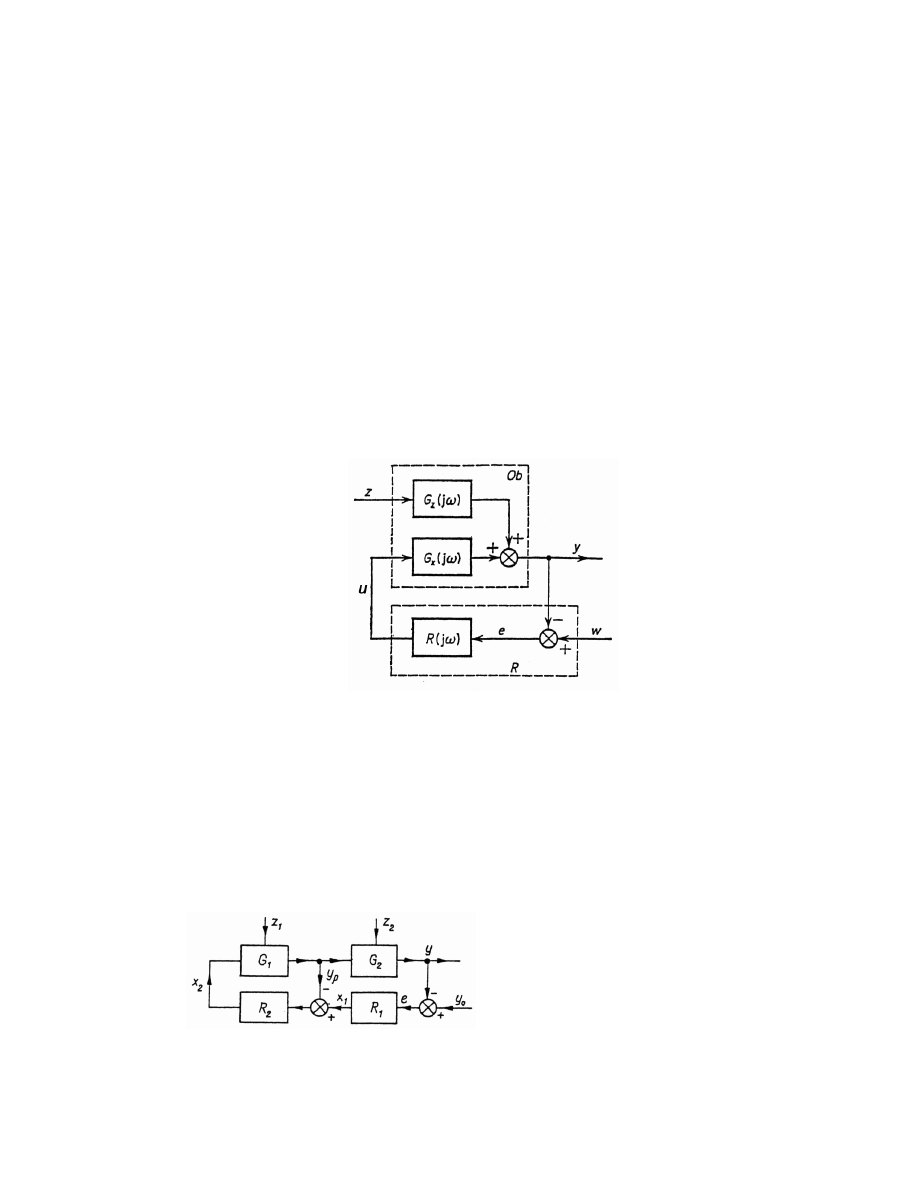
88
9 STRUKTURY UKŁADÓW REGULACJI
Wszystkie struktury przedstawiane s przy zało eniu, e własno ci zespołów
wykonawczych i przetworników pomiarowych wł czone s do obiektu. Transmitancja
obiektu opisuje wi c wypadkowe własno ci poł czenia: zespół wykonawczy + obiekt +
przetwornik pomiarowy.
Omówiono tylko podstawowe rodzaje struktur zło onych, w projektach przemysłowych
układów automatyki spotyka si równie rozwi zania bardziej rozbudowane, stanowi ce
ró ne poł czenia omawianych struktur.
9.1
Uogólniona struktura jednoobwodowa
W strukturze tej, przedstawionej ni ej, uwzgl dnia si fakt, e transmitancja
G
x
(s)
,
opisuj ca zwi zek pomi dzy sterowaniem
u
i wyj ciem
y
, mo e by inna ni transmitancja
G
z
(s),
opisuj ca zwi zek pomi dzy zakłóceniem
z
i wyj ciem
y
(ró ne tory oddziaływania
u
i
z
).
Uogólniona struktura jednoobwodowa
9.2
Regulacja kaskadowa
Regulacja ta jest celowa dla obiektów wieloinercyjnych, obiektów o stałych rozło onych
lub obiektów z opó nieniem transportowym w cz ci
G
2
, gdzie reakcja wielko ci wyj ciowej
y
na zakłócenie wprowadzane na wej cie obiektu nast puje ze znacznym opó nieniem ( ci le:
nie jest zauwa ana przez znaczny czas).
Warunkiem utworzenia kaskadowego układu regulacji jest istnienie w obiekcie mierzalnej
pomocniczej wielko ci regulowanej
y
p
, która szybciej reaguje na to zakłócenie ni główna
wielko regulowana
y
.
Struktura ogólna kaskadowego układu regulacji:
G
1
,
G
2
- obiekt regulacji
R
1
- regulator główny
R
2
- regulator pomocniczy
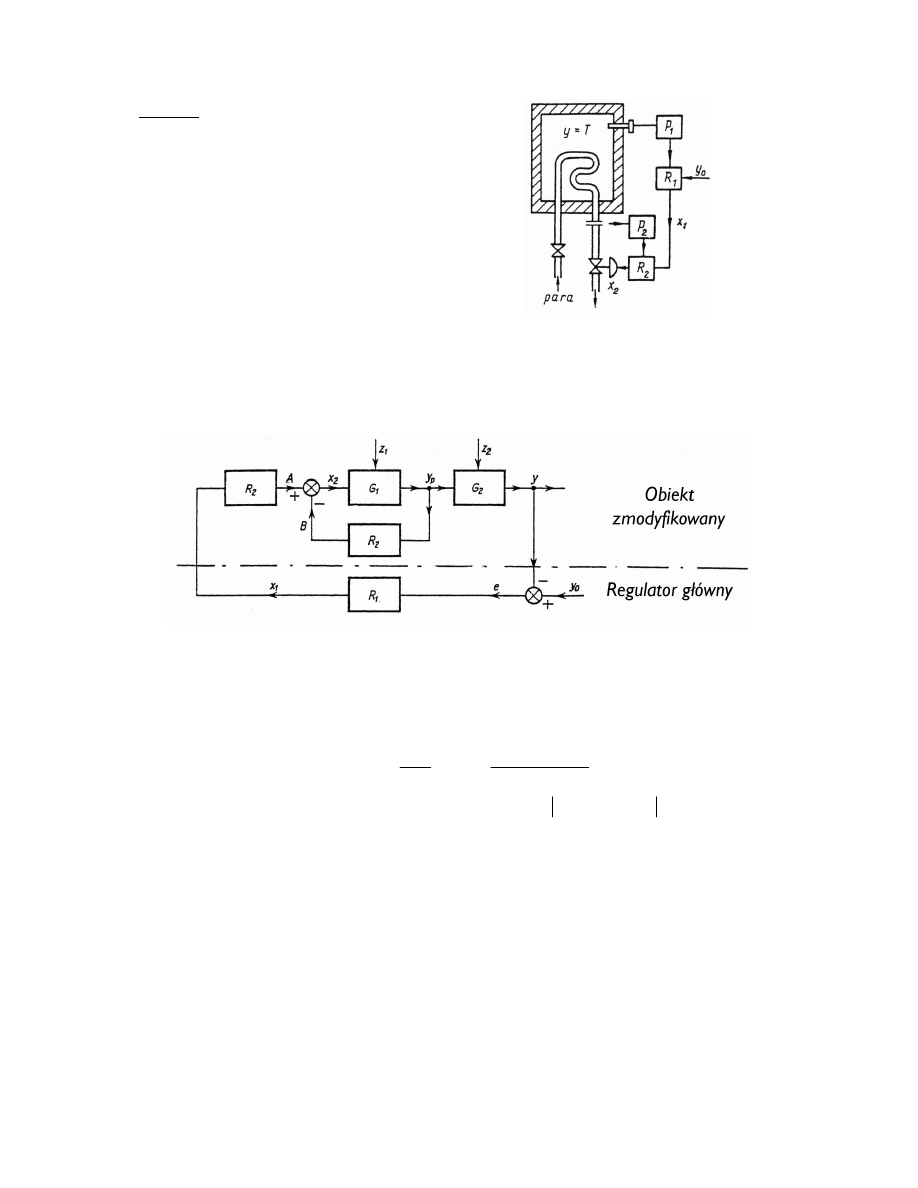
89
Przykład: regulacja temperatury
y
na wyj ciu
wymiennika ciepła, z nat eniem
przepływu pary jako wielko ci
pomocnicz
y
p
Zalety regulacji kaskadowej w stosunku do jednoobwodowej łatwo wykaza po przek-
ształceniu układu kaskadowego do równowa nego układu jednoobwodowego z obiektem
zmodyfikowanym o transmitancji
G
ob.m
(s)
i regulatorem głównym
R
1
.
Struktura równowa na:
Zalety:
a)
neutralizacja wła ciwo ci dynamicznych cz ci G
1
obiektu
•
transmitancja pierwotna obiektu: G
ob
(s) = G
1
(s) G
2
(s)
•
transmitancja obiektu zmodyfikowanego:
)
(
)
(
1
)
(
)
(
)
(
)
(
)
(
)
(
2
1
2
1
2
.
s
R
s
G
s
R
s
G
s
G
s
x
s
y
s
G
m
ob
+
=
=
z czego wynika, e w pa mie cz stotliwo ci, w którym
1
)
(
)
(
2
1
>>
ω
ω
j
R
j
G
zachodzi
)
(
)
(
2
.
ω
ω
j
G
j
G
m
ob
≈
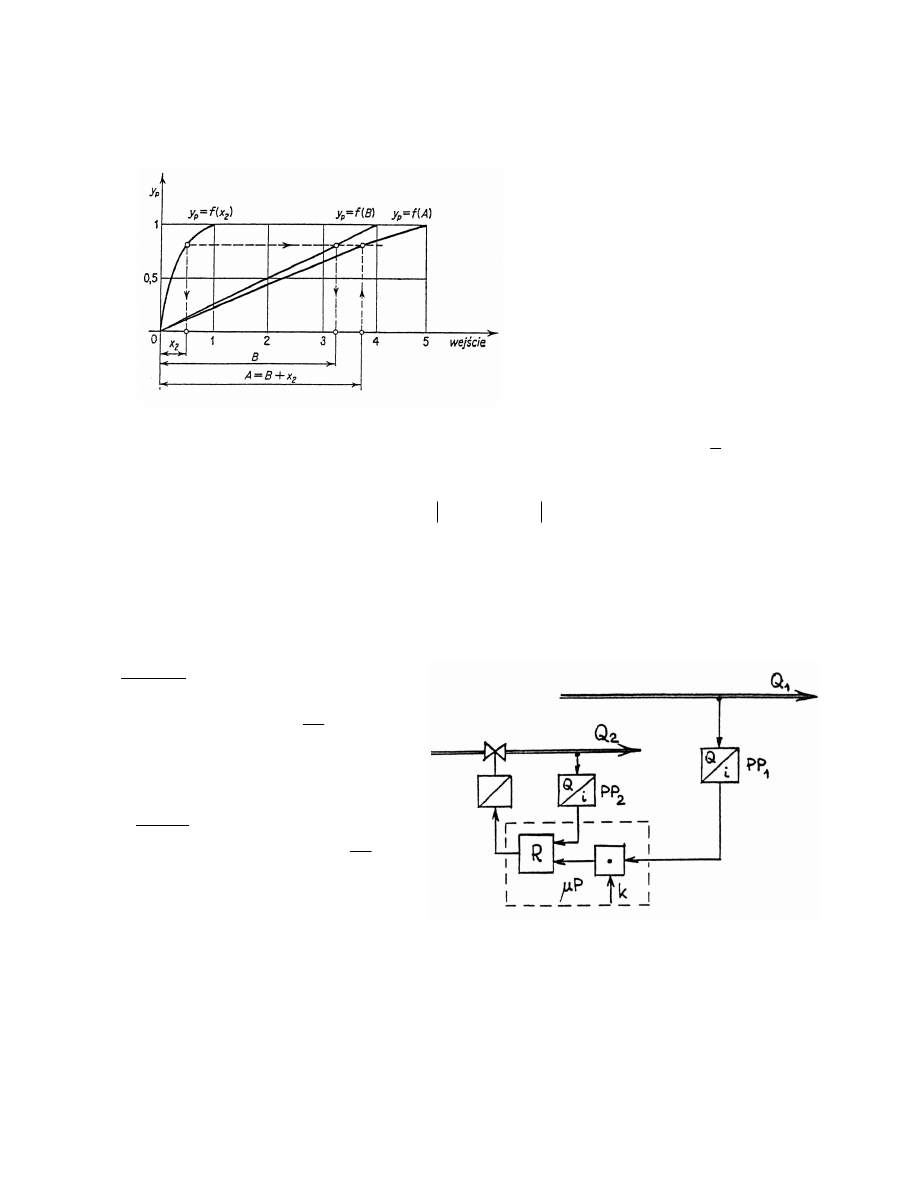
90
b)
linearyzacja charakterystyki statycznej cz ci
G
1
obiektu
)
(
2
x
f
y
p
=
- pierwotna charakterystyka
statyczna
)
(A
f
y
p
=
- zmodyfikowana
charakterystyka statyczna
B
A
x
−
=
2
, st d:
B
x
A
+
=
2
(na rysunku przyj to, e
R
2
jest regulatorem P o wzmocnieniu
k
p
=
4, st d
B
y
p
4
1
=
)
c)
skuteczniejsza kompensacja zakłóce
z
1
Zakłócenia
z
1
kompensowane s
[
]
)
(
)
(
1
2
1
ω
ω
j
R
j
G
+
- krotnie silniej ni w układzie
jednoobwodowym z regulatorem
R
1
.
9.3
Regulacja stosunku
Struktura układu zale y od warunków pracy instalacji i mo liwo ci oddziaływanie na
wielko ci, których stosunek chcemy utrzyma stały
Przykład:
Regulacja stosunku
k
Q
Q =
1
2
, z
mo liwo ci oddziaływania jedynie na Q
2
.
(Uwaga: wpływ zakresów pomiarowych
przetworników PP
1
i PP
2
na
1
2
Q
Q
!)
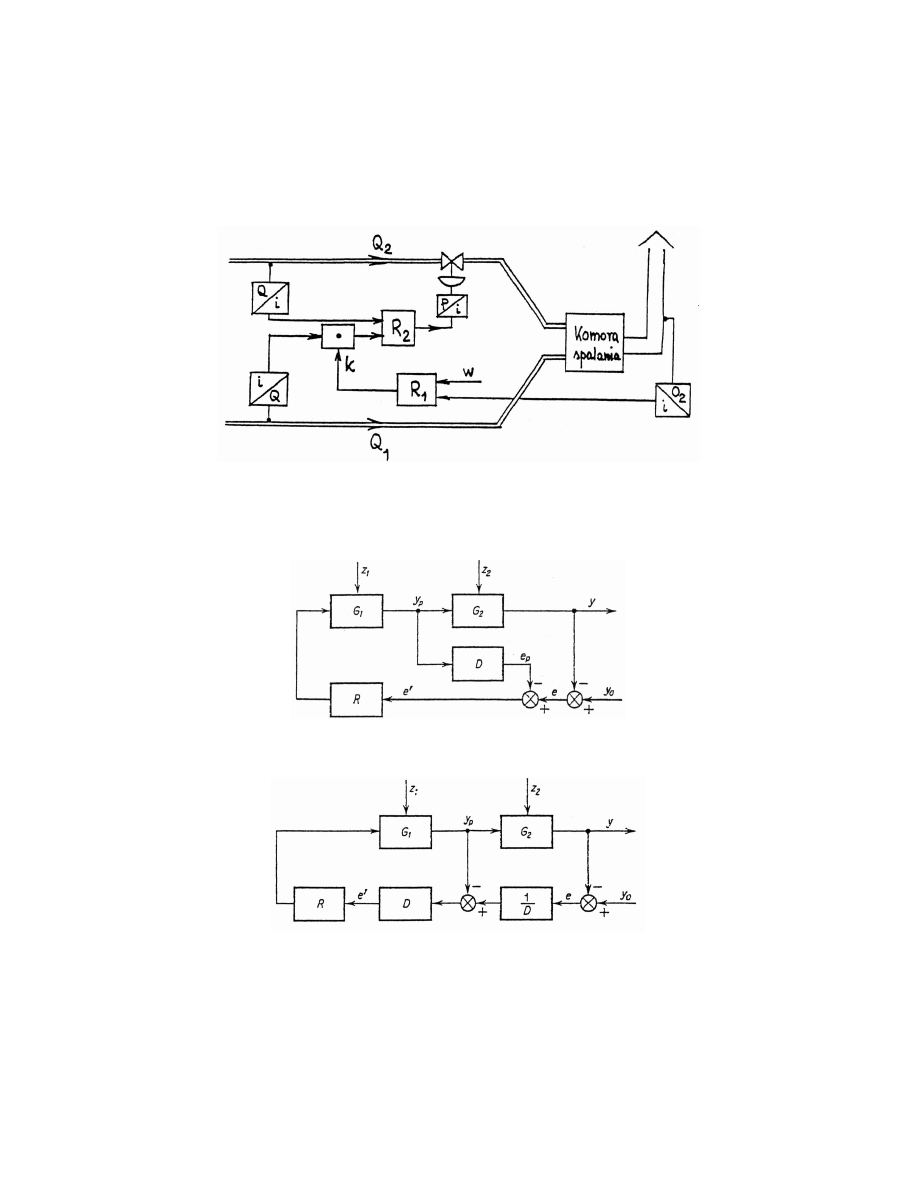
91
9.4
Kaskadowa regulacja stosunku
Przykład optymalizacji procesu spalania przez utrzymywanie stałej zawarto ci
O
2
w
spalinach:
9.5
Układy z pomocnicz korekcj dynamiczn :
a)
Struktura pierwotna
b)
Struktura przekształcona do równowa nego układu kaskadowego
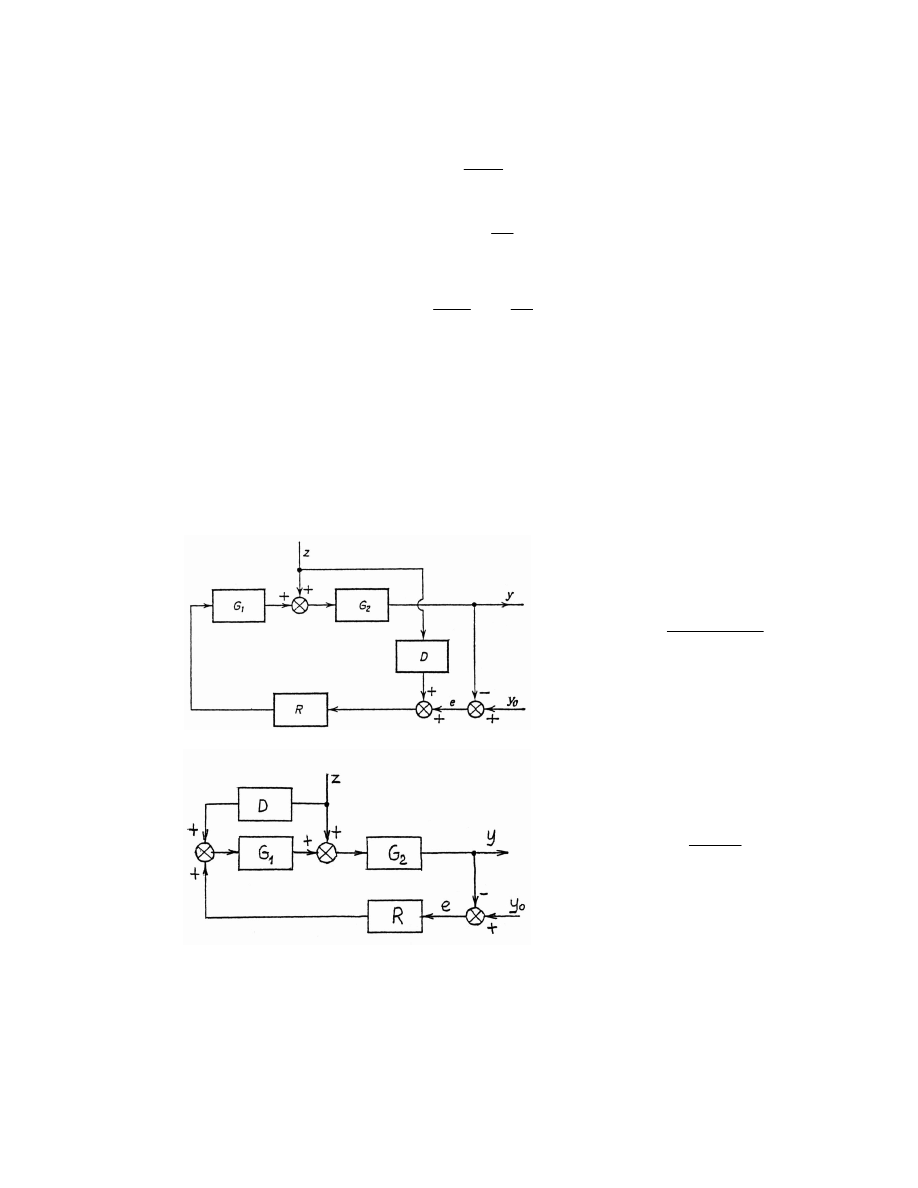
92
Najcz ciej:
1
)
(
+
=
Ts
Ts
s
D
)
1
1
(
)
(
s
T
k
s
R
i
p
+
=
Co odpowiada, dla T=T
i
, u yciu w układzie kaskadowym regulatora głównego typu PI:
s
T
S
D
i
1
1
)
(
1
+
=
oraz regulatora pomocniczego typu P:
p
k
s
D
s
R
=
)
(
)
(
9.6
Układy zamkni to-otwarte
W układach tych wykorzystuje si bezpo redni pomiar zakłócenia do wytworzenia
oddziaływania kompensuj cego wpływ tego zakłócenia na wyj cie obiektu
Typowe struktury
Warunki całkowitej
eliminacji wpływu
z
na
y
:
a)
)
(
)
(
1
)
(
1
ω
ω
ω
j
G
j
R
j
D
−
=
b)
)
(
1
)
(
1
ω
ω
j
G
j
D
−
=
Ograniczenia:
a)
zwykle zakłóce jest wiele, cz
z nich mo e by trudna lub
niemo liwa do zmierzenia
b)
wła ciwo ci obiektu
G
1
nie s stałe w czasie
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron