zad.1

Na początek kilka definicji:

W informatyce grafem nazywamy strukturę G=(V, E) składającą się z węzłów (wierzchołków,
oznaczanych przez V) wzajemnie połączonych za pomocą krawędzi (oznaczonych przez E).

Grafy dzielimy na grafy skierowane i nieskierowane:

Rys.1. Graf nieskierowany

Rys.2. Graf skierowany

Jeśli krawędź łączy dwa wierzchołki to jest z nimi incydentna.

Pętla własna to krawędź łączące wierzchołek z samym sobą.

Stopień wierzchołka w grafie nieskierowanym to liczba incydentnych z nim krawędzi.

Istnieje kilka algorytmów do przechowania grafu w pamięci.

a)

Omówmy najpierw macierz sąsiedztwa.

Budujemy tablicę o rozmiarach V*V, gdzie V-liczba wierzchołków. Następnie wypełniamy ją
zerami- jeśli dwa wierzchołki nie są połączone krawędzią i jedynkami- jeśli dwa wierzchołki są
połączone. Oto macierz sąsiedztwa dla grafu z rysunku 1:

1

2

3

4

5

1

0

1

1

0

1

2

1

0

1

1

1

3

1

1

0

1

0

4

0

1

1

0

1

5

1

1

0

1

0

Złożoność pamięciowa: O(V2)

Widać, że macierz jest symetryczna. Stosując tablicę dynamiczną można więc zmniejszyć rozmiar
macierzy do połowy zapisując ją jako macierz dolno-(górno)-trójkątną.

c)

Lista sąsiedztwa.

Należy utworzyć listę dla każdego wierzchołka v, w której przechowujemy zbiór wierzchołków
połączonych krawędzią z v. Lista dla grafu z rysunku 1 wygląda następująco:

1: 2, 3, 5

2: 1, 3, 4

3: 1, 2, 4

4: 2, 3, 5

5: 4, 1

Złożoność pamięciowa: O(V+E)

Lista krawędzi jest to lista, na której przechowujemy wszystkie krawędzie występujące w grafie.

Przykład dla grafu skierowanego z rys.2:

1 - 2

2 - 4

2 - 5

3 - 1

3 - 2

4 - 3

5 - 1

5 - 4

Zapisując przy pomocy tej reprezentacji graf, w którym występują krawędzie skierowane i
nieskierowane należy w przypadku krawędzi nieskierowanej z u do v zapisać krawędź
dwukrotnie: u - v oraz v - u.

Złożoność pamięciowa: O(E)

b)

Macierz incydencji to tablica o rozmiarach V*E. Składa się ona z E kolumn i V wierszy, jeśli
krawędź wychodzi z danego wierzchołka to piszemy w odpowiedniej kolumnie (-1), jeśli do niego
wchodzi piszemy (+1), jeśli wierzchołek nie należy do krawędzi piszemy 0, jeśli jest to pętla
własna piszemy 2.

Oto przykład dla grafu z rys. 2.

1

2

3

4

5

1 - 2

-1

1

0

0

0

1 - 3

1

0

-1

0

0

1 - 5

1

0

0

0

-1

2 - 4

0

-1

0

1

0

2 - 5

0

-1

0

0

1

2 - 3

0

1

-1

0

0

3 - 4

0

0

1

-1

0

5 - 1

1

0

0

0

-1

5 - 4

0

0

0

1

-1

Złożoność pamięciowa: O(E*V)

zad.2.

Procedury przeglądania grafu w głąb (DFS) i wszerz (BFS) są bardzo często wykorzystywane w
innych, bardziej złożonych algorytmach (np. badania spójności).

W strategii DFS wybrany wierzchołek należy umieścić na stosie, zaznaczyć jako odwiedzony a
następnie przejść do jego następnika. Następnik również umieszczamy na stosie, zaznaczamy
jako odwiedzony przechodzimy do jego następnika. Jak widać procedurę można wywoływać
rekurencyjnie. Jeśli dojdziemy do takiego wierzchołka, że nie ma on krawędzi incydentych z
nieodwiedzonymi wierzchołkami, należy usunąć go ze stosu i pobrać ze stosu kolejny
wierzchołek do przeszukania. W praktyce stosuje się zasadę, że jeśli przeszukiwany wierzchołek
jest połączony krawędziami z wieloma wierzchołkami, wybiera się do przeszukania wierzchołek o
najmniejszej liczbie porządkowej. Dlatego szukając kolejny nieodwiedzony następnik należy
rozpoczynać od końca macierzy. Przeszukiwanie DFS wykorzystuje się do badania spójności
grafu. Jeśli procedura wywołana dla pierwszego wierzchołka "dotrze" do wszystkich
wierzchołków grafu to graf jest spójny.

Aby przeszukać graf wszerz (BFS) należy zamiast stosu wykorzystać kolejkę do przechowywania
wierzchołków a kolejnych nieodwiedzonych następników szukać od początku macierzy.

a)

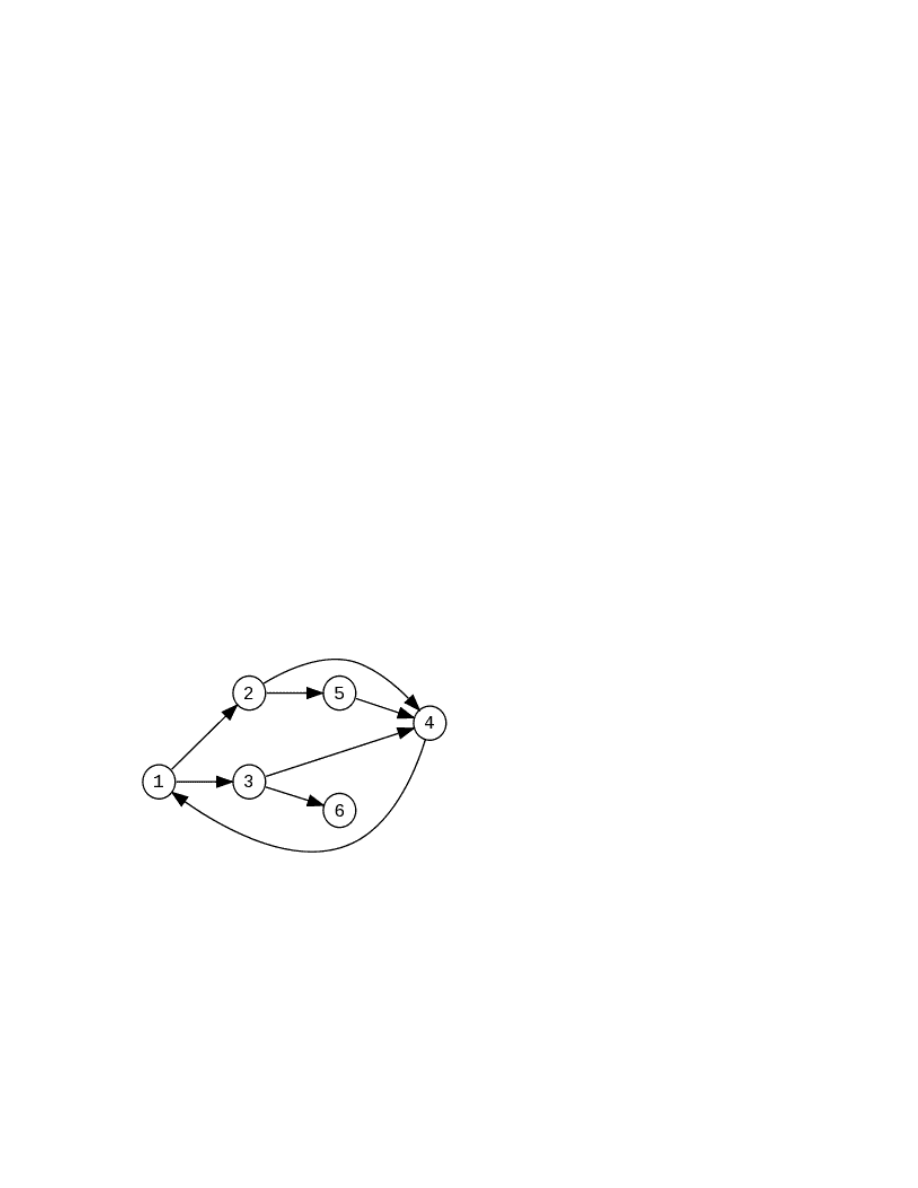
Oto przykładowy graf:

PRZYKŁAD:

Przeszukiwanie w głąb (DFS):

Zaczynamy od wierzchołka 1, odwiedzamy go i wrzucamy na stos wszystkie jego następniki, w
kolejności od tego z największym indeksem:

Odwiedzone: 1; Stos: 3, 2;

Bierzemy wierzchołek ze stosu, odwiedzamy go i znów wrzucamy wszystkie jego nieodwiedzone

jeszcze następniki na stos:

Odwiedzone: 1, 2; Stos: 3, 5, 4;

Bierzemy wierzchołek ze stosu, odwiedzamy go, jedynym następnikiem 4 jest 1, ale ten
wierzchołek już odwiedzaliśmy więc nie wrzucamy nic na stos:

Odwiedzone: 1, 2, 4; Stos: 3, 5;

Bierzemy wierzchołek ze stosu, odwiedzamy go, jedynym następnikiem 5 jest 4, ale ten
wierzchołek już odwiedzaliśmy więc nie wrzucamy nic na stos:

Odwiedzone: 1, 2, 4, 5; Stos: 3;

Bierzemy wierzchołek ze stosu, odwiedzamy go, jedynym następnikiem 3 jest 6, ten wierzchołek
jeszcze nie jest odwiedzony więc wrzucamy go na stos:

Odwiedzone: 1, 2, 4, 5, 3; Stos: 6;

Bierzemy wierzchołek ze stosu, odwiedzamy go, wierzchołek 6 nie ma następników, więc nie ma
czego wrzucić na stos:

Odwiedzone: 1, 2, 4, 5, 3, 6; Stos: ;

Stos jest pusty zatem zakończyliśmy przeszukiwanie grafu w głąb.

b)

Przeszukiwanie w szerz (BFS):

Zaczynamy od wierzchołka 1, odwiedzamy go i wrzucamy do kolejki wszystkie jego następniki, w
kolejności od tego z najmniejszym indeksem:

Odwiedzone: 1; Kolejka: 2, 3;

Bierzemy wierzchołek z kolejki, odwiedzamy go i znów wrzucamy wszystkie jego nieodwiedzone
jeszcze następniki do kolejki:

Odwiedzone: 1, 2; Kolejka: 3, 4, 5;

Bierzemy wierzchołek z kolejki, odwiedzamy go, jedynym następnikiem 3 jest 6 więc wrzucamy
go do kolejki:

Odwiedzone: 1, 2, 3; Kolejka: 4, 5, 6;

Bierzemy wierzchołek z kolejki, odwiedzamy go, jedynym następnikiem 4 jest 1, ale ten
wierzchołek już odwiedzaliśmy więc nie wrzucamy go do kolejki:

Odwiedzone: 1, 2, 3, 4; Kolejka: 5, 6;

Bierzemy wierzchołek z kolejki, odwiedzamy go, jedynym następnikiem 5 jest 4, ale ten
wierzchołek już odwiedzaliśmy więc nie wrzucamy go do kolejki:

Odwiedzone: 1, 2, 3, 4, 5; Kolejka: 6;

Bierzemy wierzchołek z kolejki, odwiedzamy go, wierzchołek 6 nie ma następników, więc nie ma
czego wrzucić do kolejki:

Odwiedzone: 1, 2, 3, 4, 5, 6; Kolejka: ;

Kolejka jest pusta zatem zakończyliśmy przeszukiwanie grafu w szerz.

zad.3.

Jeśli graf jest zadany macierzą incydencji, to każdy wiersz tej macierzy reprezentuje w grafie
jeden wierzchołek o numerze równym numerowi wiersza (wiersz 0 → wierzchołek 0, wiersz 1 →
wierzchołek 1, itd.). Kolejne elementy wiersza związane są z kolejnymi krawędziami w grafie
(kolumna 0 → krawędź 0, kolumna 1 → krawędź 1, itd.). Jeśli graf jest grafem skierowanym, to j-
ty element i-tego wiersza może przyjąć tylko jedną z trzech wartości:

0 : j-ta krawędź nie zawiera 1 - j-ta krawędź wychodzi -1 - j-ta krawędź wchodzi

i-tego wierzchołka

z i-tego wierzchołka do j-tego wierzchołka

Stopień wejściowy to liczba krawędzi wchodzących do wierzchołka. Liczymy go obliczając ilość
elementów wiersza równych -1. Podobnie stopień wyjściowy to liczba krawędzi wychodzących z
wierzchołka, którą znajdziemy obliczając ilość elementów równych 1. W tym celu tworzymy dwa
liczniki:

lkwy - licznik krawędzi wyjściowych

lkwe - licznik krawędzi wejściowych

Przeglądamy kolejne wiersze macierzy incydencji. Najpierw zerujemy oba liczniki, następnie
przeglądamy kolejne elementy wiersza. Jeśli natrafimy na element równy 1, to zwiększamy
licznik lkwy. Jeśli natrafimy na element równy -1, zwiększamy lkwe. Po przeglądnięciu całego
wiersza wypisujemy numer wiersza (czyli numer wierzchołka grafu) oraz kolejno stan liczników
lkwe i lkwy. Tak postępujemy z każdym wierszem macierzy.

zad.4

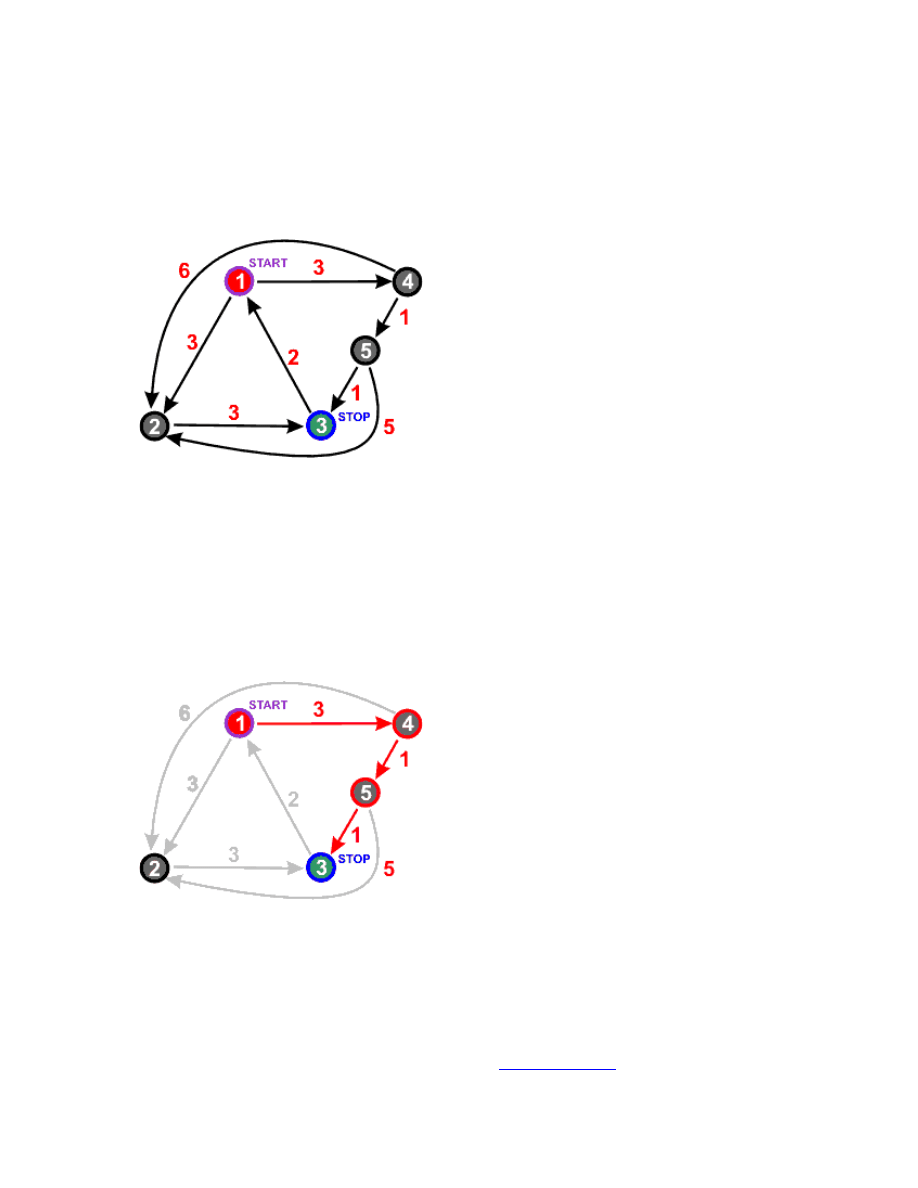
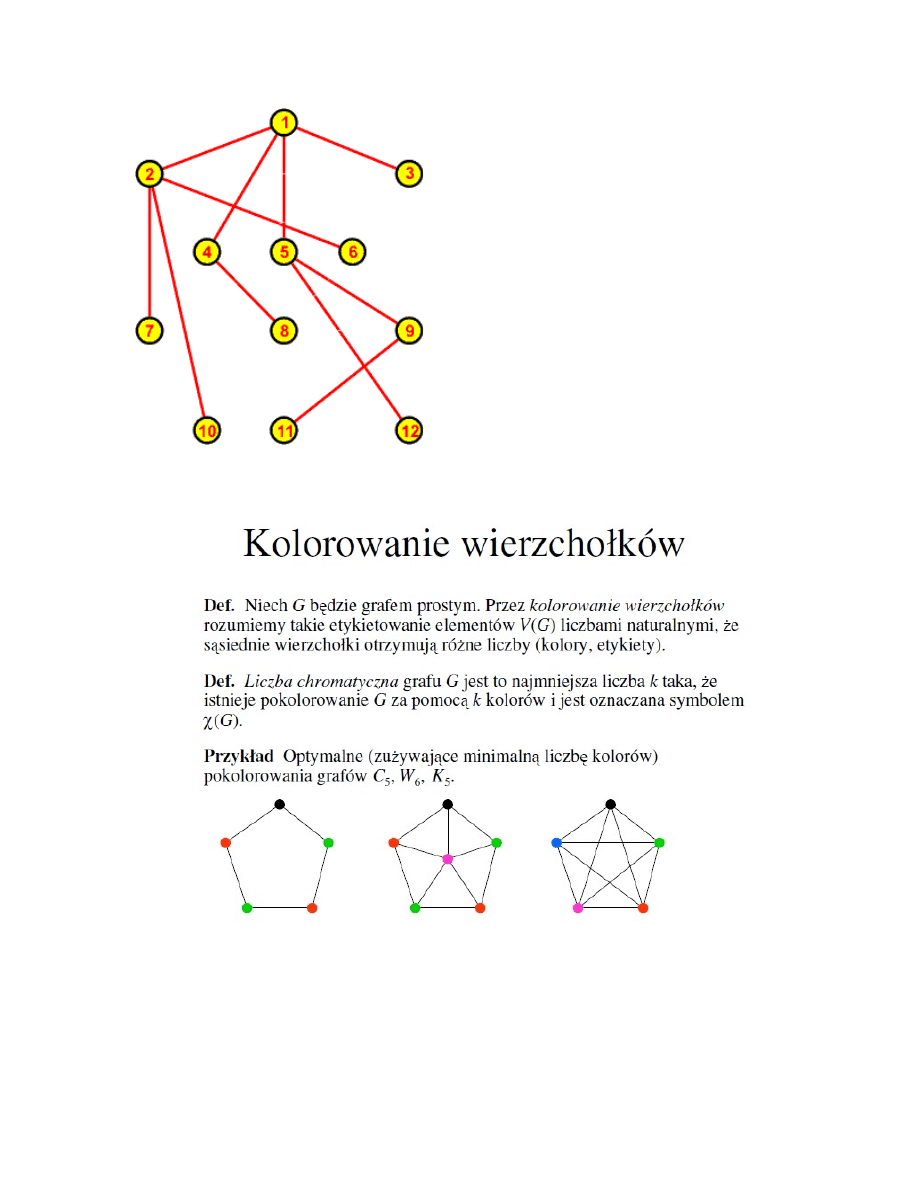
Jednym z podstawowych problemów w teorii grafów jest znajdowanie połączeń
pomiędzy dwoma wybranymi wierzchołkami. Ścieżką (ang. path) nazywamy
uporządkowany zbiór wierzchołków, które musimy kolejno przejść, aby dotrzeć w grafie
od jednego wybranego wierzchołka do innego wybranego wierzchołka. Ścieżek takich
może być kilka (lub może nie istnieć żadna - wtedy wierzchołki nazywamy
izolowanymi).

Od wierzchołka

1

do wierzchołka

3

można dojść wieloma różnymi
ścieżkami:
ścieżka nr 1:

1

- 2 -

3

ścieżka nr 2:

1

- 4 - 5 -

3

ścieżka nr 3:

1

- 4 - 5 - 2 -

3

ścieżka nr 4:

1

- 4 - 2 -

3

Jeśli z krawędziami grafu związane są wagi, to każda ze ścieżek posiada swój koszt
przejścia równy sumie wag krawędzi łączących poszczególne wierzchołki ścieżki. Dla
podanego wyżej grafu ścieżki od wierzchołka 1 do 3 mają następujący koszt:
ścieżka nr 1 - koszt = 3 + 3 = 6
ścieżka nr 2 - koszt = 3 + 1 + 1 = 5
ścieżka nr 3 - koszt = 3 + 1 + 5 + 3 = 12
ścieżka nr 4 - koszt = 3 + 6 + 3 = 12

Przez najkrótszą ścieżkę (ang. the shortest path) łączącą w grafie dwa wybrane
wierzchołki będziemy rozumieli ścieżkę o najmniejszym koszcie przejścia.

Od wierzchołka

1

do wierzchołka

3

najkrótszą ścieżką jest

ścieżka nr 1: 1 - 2 - 3

ścieżka nr 2:

1

- 4 - 5 -

3

ścieżka nr 3: 1 - 4 - 5 - 2 - 3
ścieżka nr 4: 1 - 4 - 2 - 3

o koszcie przejścia równym 5.

Gdyby przykładowy graf był grafem nieskierowanym, to najkrótszą ścieżką byłaby
ścieżka 1 - 3 o koszcie 2.
Algorytm Dijkstry znajduje w grafie wszystkie najkrótsze ścieżki pomiędzy wybranym
wierzchołkiem a wszystkimi pozostałymi. Dodatkowo wylicza również koszt przejścia
każdej z tych ścieżek. Bardzo ważnym założeniem w algorytmie Dijkstry są nieujemne
wagi krawędzi. Jeśli krawędzie mogą przyjmować wagi ujemne, to

NIE WOLNO

stosować algorytmu Dijkstry (zobacz na algorytm

Bellmana-Forda

).

zad.5

Drzewo rozpinające (ang. spanning tree) grafu jest jego podgrafem-drzewem, które zawiera

wszystkie wierzchołki grafu. Dany graf może posiadać wiele różnych drzew rozpinających.

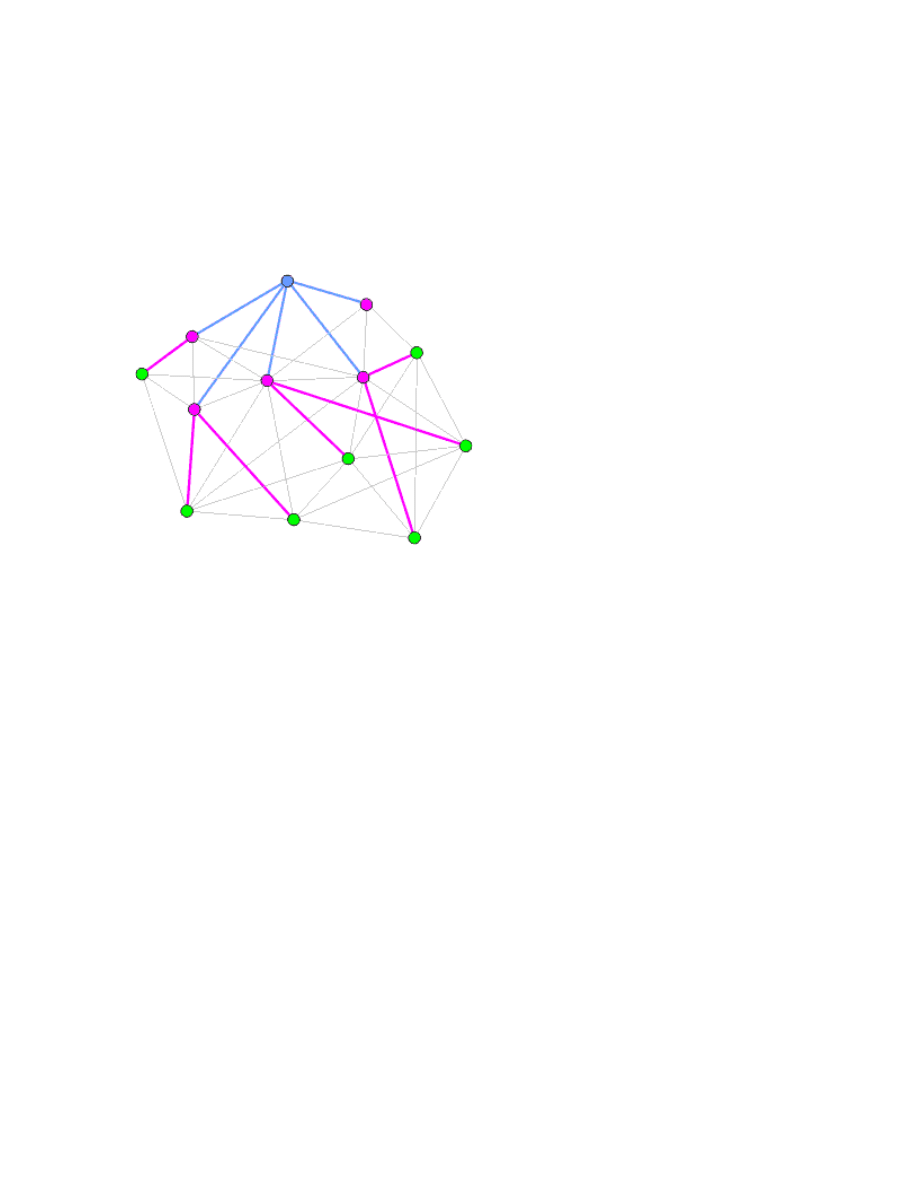
Drzewo rozpinające w szerz (ang. BFST - Breadth First Spanning Tree) powstaje w trakcie

przechodzenia przez graf za pomocą algorytmu BFS. Jeśli wierzchołkiem startowym będzie
najwyższy wierzchołek grafu.

Najpierw tworzymy krawędzie pierwszego poziomu do wszystkich wierzchołków (fioletowych)
połączonych krawędzią z wierzchołkiem startowym (krawędzie niebieskie). Następnie

przechodzimy przez kolejne wierzchołki drugiego poziomu (fioletowe) łącząc je krawędziami
fioletowymi ze wszystkimi sąsiadującymi wierzchołkami (zielonymi), które jeszcze nie zostały

umieszczone w drzewie rozpinającym. Dla tego konkretnego grafu wierzchołki zielone są już
liśćmi drzewa rozpinającego i nie tworzą w nim dalszych krawędzi.

Algorytm tworzenia drzewa rozpinającego w szerz

przykład:

w głąb

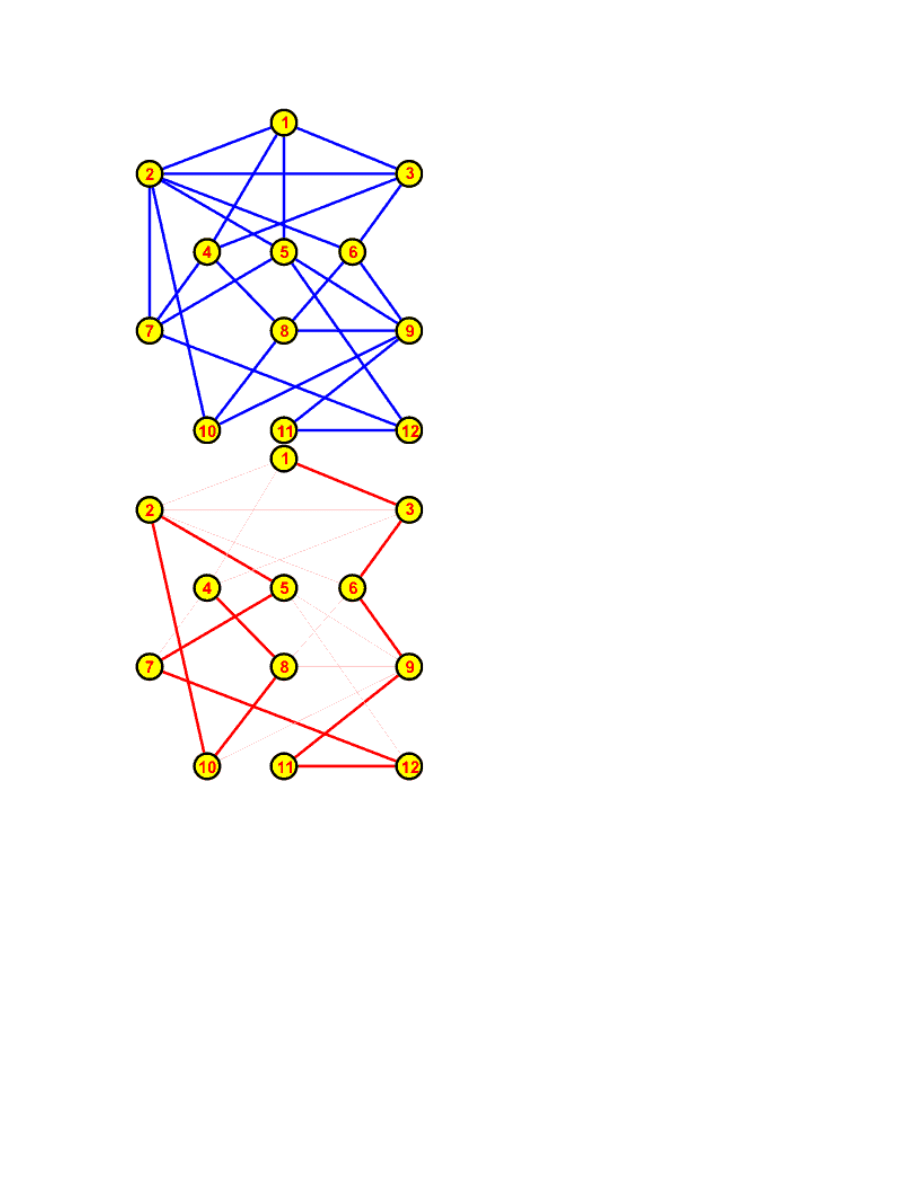
w szerz

zad.6