AKADEMIA

GÓRNICZO-HUTNICZA

Identyfikacja i Analiza Sygnałów

PROJEKT

Kulawik Bartosz

GR. 23, IMiR

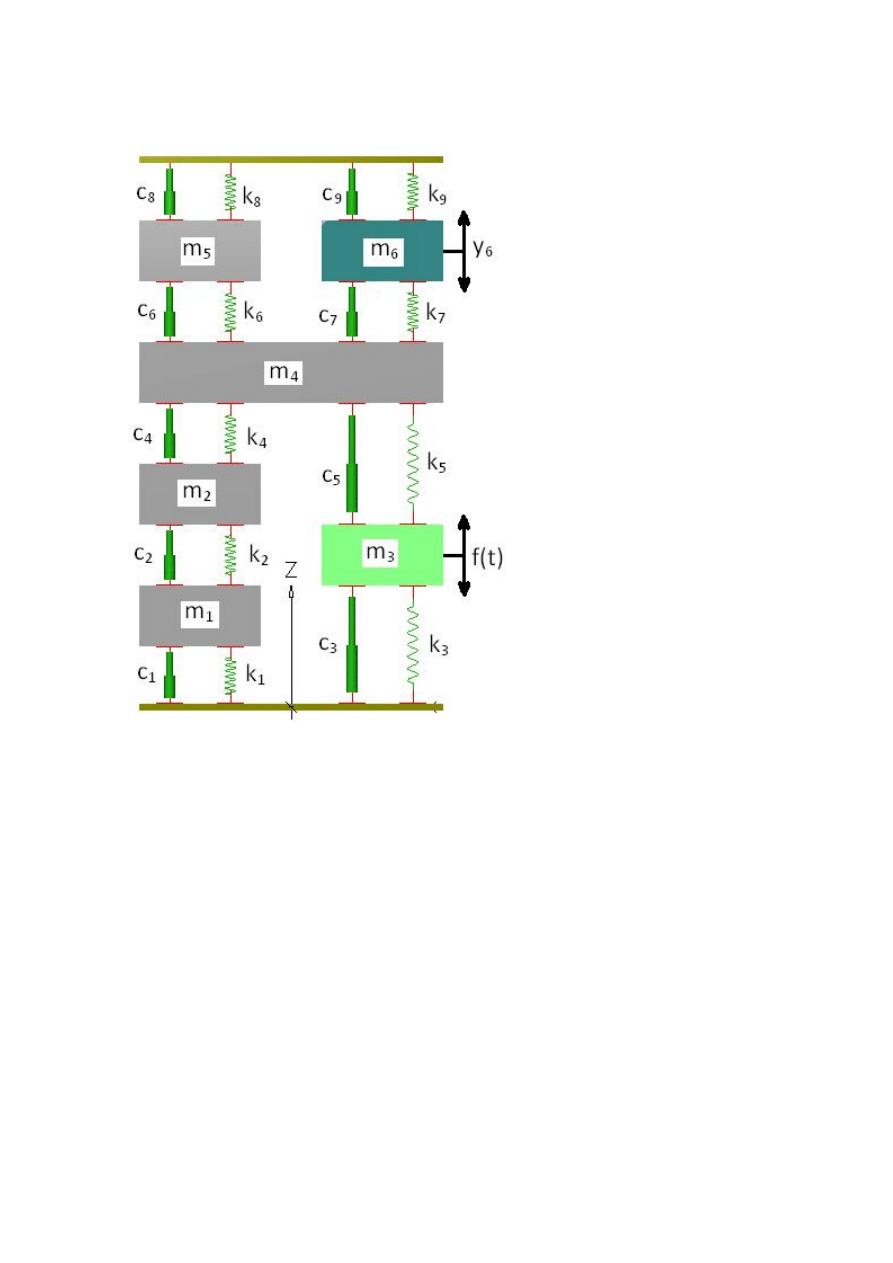
1. Schemat układu:

Parametry układu:
Masy: m

1

=4.5, m

2

=3, m

3

=4.5, m

4

=8, m

5

=4, m

6

=4.5

Współczynniki tłumienia: c

1

=5, c

2

=4, c

3

=1, c

4

=18, c

5

=10, c

6

=12, c

7

=4, c

8

=16,

c

9

=3

Współczynniki sprężystości: k

1

=19000, k

2

=21000, k

3

=18000, k

4

=11000,

k

5

=15000, k

6

=14000, k

7

=15000, k

8

=17000, k

9

=19000

2. Równania dynamiki w postaci równań czasowych

̈

+ ̇

+

+

(

−

̇

̇ ) +

(

−

) = 0

̈

+

(

−

̇

̇ ) +

(

−

) +

(

−

̇

̇ ) +

(

−

) = 0

̈

+ ̇

+

+

(

−

̇

̇ ) +

(

−

) =

̈

+

(

−

̇

̇ ) +

(

−

) +

(

−

̇

̇ ) +

(

−

) +

(

−

̇

̇ )

+

(

−

) +

(

−

̇

̇ ) +

(

−

) = 0

̈

+ ̇

+

+

(

−

̇

̇ ) +

(

−

) = 0

̈

+ ̇

+

+

(

−

̇

̇ ) +

(

−

) = 0

3. Równania w postaci macierzowej:

⎣

⎢

⎢

⎢

⎢

⎡

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

⎦

⎥

⎥

⎥

⎥

⎤

⎣

⎢

⎢

⎢

⎢

⎡

̈
̈
̈
̈
̈
̈ ⎦

⎥

⎥

⎥

⎥

⎤

+

⎣

⎢

⎢

⎢

⎢

⎡

+

−

0

0

0

0

−

+

0

−

0

0

0

0

+

−

0

0

0

−

−

+

+

+

−

−

0

0

0

−

+

0

0

0

0

−

0

+

⎦

⎥

⎥

⎥

⎥

⎤

⎣

⎢

⎢

⎢

⎢

⎡

̇

̇
̇
̇
̇
̇ ⎦

⎥

⎥

⎥

⎥

⎤

+

⎣

⎢

⎢

⎢

⎢

⎡

+

−

0

0

0

0

−

+

0

−

0

0

0

0

+

−

0

0

0

−

−

+

+

+

−

−

0

0

0

−

+

0

0

0

0

−

0

+

⎦

⎥

⎥

⎥

⎥

⎤

⎣

⎢

⎢

⎢

⎢

⎡

⎦

⎥

⎥

⎥

⎥

⎤

=

⎣

⎢

⎢

⎢

⎢

⎡

0
0

0
0
0 ⎦

⎥

⎥

⎥

⎥

⎤

4. Przedstawić analityczne rozwiązanie układu

Parametry układu wyznaczam rozwiązując układ równań macierzowych z
punktu 3.
Program służący do rozwiązania zagadnienia własnego w mat labie:

% Liczba stopni swobody

n=6;

% Masy w układzie

m1=4.5; m2=3; m3=4.5; m4=8;

m5=4; m6=4.5;

% Współczynniki tłumienia

c1=5; c2=4; c3=1; c4=18;

c5=10; c6=12; c7=4; c8=16; c9=3;

% Współczynniki sztywności

k1=19000; k2=21000; k3=18000; k4=11000;

k5=15000; k6=14000; k7=15000; k8=17000; k9=19000;

%macierz mas

M = [m1 0 0 0 0 0

0 m2 0 0 0 0

0 0 m3 0 0 0

0 0 0 m4 0 0

0 0 0 0 m5 0

0 0 0 0 0 m6];

%macierz współczynników tłumienia

C = [c1+c2, -c2, 0, 0, 0, 0

-c2, c2+c4, 0, -c4, 0, 0

0, 0, c3+c5, -c5, 0, 0

0, -c4, -c5, c4+c5+c6+c7, -c6, -c7

0, 0, 0, -c6, c8+c6, 0

0, 0, 0, -c7, 0, c9+c7];

%macierz współczynników sztywności

K = [k1+k2, -k2, 0, 0, 0, 0

-k2, k2+k4, 0, -k4, 0, 0

0, 0, k3+k5, -k5, 0, 0

0, -k4, -k5, k4+k5+k6+k7, -k6, -k7

0, 0, 0, -k6, k8+k6, 0

0, 0, 0, -k7, 0, k9+k7];

%budowanie macierzy

ZER = zeros(size(M));

A = [ZER,M;M,C];

B = [-M,ZER;ZER,K];

%rozwiązanie zgadnienia własnego

[PHI,LAMBDA]=eig(-B,A);

%czestotliwosci drgan wlasnych tlumionych

WD=imag(diag(LAMBDA))/2/pi;

%czestotliwosci drgan wlasnych

WW=sqrt(imag(diag(LAMBDA)).^2+real(diag(LAMBDA)).^2)/2/pi;

%tlumienie modalne

KSI=-real(diag(LAMBDA))./sqrt(imag(diag(LAMBDA)).^2+real(diag(LAMBDA)).^2);

disp(

'Czest. drgań Tłumienia '

)

disp(

'własnych: modalne:'

)

[WW KSI]

Rezultat działania skryptu:

Czest. drgań Tłumienia

własnych: modalne:

ans =

20.1077 0.0305

20.1077 0.0305

16.9611 0.0296

16.9611 0.0296

7.3003 0.0085

7.3003 0.0085

10.7026 0.0278

10.7026 0.0278

13.9259 0.0292

13.9259 0.0292

13.7330 0.0128

13.7330 0.0128

5. Za pomocą dowolnej metody przeprowadzić symulacje układu

Układ symuluje korzystając z równań stanu. Wymuszenie na masie 3,
rejestruje przemieszczenie masy 6. Skrypt:

%współczynniki sprężystości

k1=19000; k2=21000; k3=18000; k4=11000;

k5=15000; k6=14000; k7=15000; k8=17000; k9=19000;

%współczynniki tłumienia

c1=5; c2=4; c3=1; c4=18;

c5=10; c6=12; c7=4; c8=16; c9=3;

%masy

m1=4.5; m2=3; m3=4.5; m4=8;

m5=4; m6=4.5;

%równania stanu

A=[0 1 0 0 0 0 0 0 0 0 0 0;

-(k1+k2)/m1 -(c1+c2)/m1 k2/m1 c2/m1 0 0 0 0 0 0 0 0;

0 0 0 1 0 0 0 0 0 0 0 0;

k2/m2 c2/m2 -(k2+k4)/m2 -(c2+c4)/m2 0 0 k4/m2 c4/m2 0 0 0 0;

0 0 0 0 0 1 0 0 0 0 0 0;

0 0 0 0 -(k3+k5)/m3 -(c3+c5)/m3 k5/m3 c5/m3 0 0 0 0;

0 0 0 0 0 0 0 1 0 0 0 0;

0 0 k4/m4 c4/m4 k5/m4 c5/m4 -(k4+k5+k6+k7)/m4 -(c4+c5+c6+c7)/m4 k6/m4

c6/m4 k7/m4 c7/m4;

0 0 0 0 0 0 0 0 0 1 0 0;

0 0 0 0 0 0 k6/m5 c6/m5 -(k6+k8)/m5 -(c6+c8)/m5 0 0;

0 0 0 0 0 0 0 0 0 0 0 1;

0 0 0 0 0 0 k7/m6 c7/m6 0 0 -(k7+k9)/m6 -(c7+c9)/m6];

B=[0; 0; 0; 0; 0; 1/m3; 0; 0; 0; 0; 0; 0];

C=[1 0 0 0 0 0 0 0 0 0 0 0

0 0 1 0 0 0 0 0 0 0 0 0

0 0 0 0 1 0 0 0 0 0 0 0

0 0 0 0 0 0 1 0 0 0 0 0

0 0 0 0 0 0 0 0 1 0 0 0

0 0 0 0 0 0 0 0 0 0 1 0];

D=[0; 0; 0; 0; 0; 0];

sys=ss(A, B, C, D);

t=0:0.001:10;

u=10*rand(1, length(t));

Y_out=lsim(sys, u, t);

plot(t, Y_out(:,6),

'r'

,

'LineWidth'

,2)

title(

'Wymuszenie szumem'

);

xlabel(

'Czas [s]'

)

grid

on

figure

Y_out=impulse(sys,t);

plot(t, Y_out(:,6),

'r'

,

'LineWidth'

,2)

title(

'Wymuszenie impulsem'

);

xlabel(

'Czas [s]'

)

grid

on

Efekt działania skryptu:
Wymuszenie układu impulsem – odpowiedź masy 6

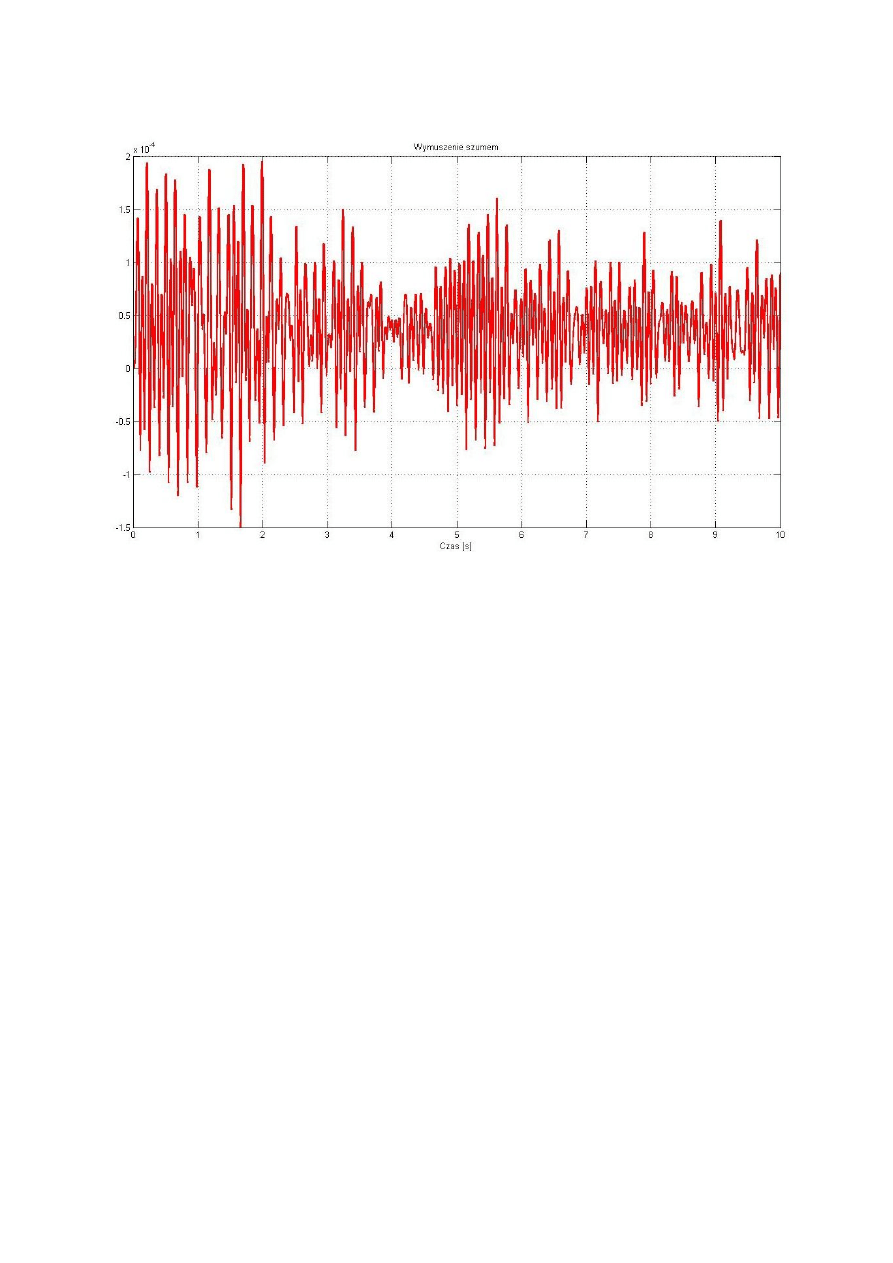
Wymuszenie układu szumem – odpowiedź masy 6

6. Identyfikacja parametryczna układu

Identyfikacje parametryczną przeprowadzam z wykorzystaniem modeli
ARMAX i ARX.
Skrypt w Matlabie:

sys=ss(A, B, C, D);

%wyznaczenie wsp. tlumienia i czest. drgan

[Wn,Z] = damp(sys);

t = 0:0.01:50;

u = 0.5*rand(1,length(t));

Y_out = lsim(sys,u,t);

%zbudowanie modelu ARMAX

model_armax = armax([Y_out(:,6) u'],[24 24 24 0]);

model_z = zpk(model_armax);

%wyznaczenie czest. drgan własnych i wsp. tlum.

%na podstawie modelu

disp(

'Model ARMAX'

)

[Wn_es, Z_es] = damp(model_z);

disp(

'Czestotliwosci drgan wlasnych'

)

disp(

'wyznaczone: wyestymowane:'

)

[Wn(:)/2/pi Wn_es(2:13)/2/pi*100]

disp(

'Wspolczynniki tłumienia'

)

disp(

'wyznaczone: wyestymowane:'

)

[Z(:) Z_es(2:13)]

%zbudowanie modelu ARX

model_arx=arx([Y_out(:,6) u'],[24 24 0]);

model_z=zpk(model_arx);

[Wn_es, Z_es] = damp(model_z);

disp(

'Model ARX'

)

[Wn_es, Z_es] = damp(model_z);

disp(

'Czestotliwosci drgan wlasnych'

)

disp(

'wyznaczone: wyestymowane:'

)

[Wn(:)/2/pi Wn_es(2:13)/2/pi*100]

disp(

'Wspolczynniki tłumienia'

)

disp(

'wyznaczone: wyestymowane:'

)

[Z(:) Z_es(2:13)]

Zestawienie wyników:

Parametry wyznaczone

Parametry estymowane

modelem ARX

Parametry estymowane

modelem ARMAX

Częstotliwość

drgań własnych

Tłumienia

modalne

Częstotliwość

drgań

własnych

Tłumienia

modalne

Częstotliwość

drgań

własnych

Tłumienia

modalne

7.3003

0.0085

7.3003

0.0085

7.3003

0.0085

7.3003

0.0085

7.3003

0.0085

7.3003

0.0085

10.7026

0.0278

10.7027

0.0278

10.7030

0.0278

10.7026

0.0278

10.7027

0.0278

10.7030

0.0278

13.7330

0.0128

13.7334

0.0128

13.7316

0.0130

13.7330

0.0128

13.7334

0.0128

13.7316

0.0130

13.9259

0.0292

13.9250

0.0294

13.9236

0.0281

13.9259

0.0292

13.9250

0.0294

13.9236

0.0281

16.9611

0.0296

16.9611

0.0296

16.9613

0.0296

16.9611

0.0296

16.9611

0.0296

16.9613

0.0296

20.1077

0.0305

20.1171

0.0304

20.1077

0.0309

20.1077

0.0305

20.1171

0.0304

20.1077

0.0309

7. Identyfikacja nieparametryczna

Skrypt:

sys=ss(A, B, C, D);

Fs=1000;

t = 0:1/Fs:10;

u = 1*rand(1,length(t));

Y_out1 = lsim(sys,u,t);

xn1=Y_out1(:,6);

Y_out=impulse(sys,t);

xn=Y_out(:,6);

figure

%periodogram

ilosc=8192;

Pxx=(abs(fft(xn, ilosc)).^2)/ilosc;

plot((0:(ilosc-1))/ilosc*Fs,10*log10(Pxx),

'black'

)

xlabel(

'Czestotliwosc [Hz]'

)

ylabel(

'Widmo mocy [dB]'

)

title(

'Periodogram'

)

xlim([0 30])

grid

on

figure

w1 = flattopwin(length(xn));

y = fft(xn.*w1);

f = (0:length(y)-1)'*Fs/length(y);

ind=find(f<=Fs/2);

f2=f(ind); am2 = 20*log10(abs(y(ind)/norm(w1)));

plot(f2,am2)

xlim([0 30])

grid

on

figure

%funkcja przejścia

nfft=ilosc;

window=hanning(nfft+1);

tfestimate(u,xn1,window,2048,nfft,Fs);

xlim([0 0.025])

figure

%funkcja koherencji

window=hanning(4096);

mscohere(xn1,u,window,3000,4096, Fs);

xlim([0 0.025])

figure

%gętość widmowa mocy

pwelch(xn, window, 2048, 4096, Fs)

xlim([0 0.05])

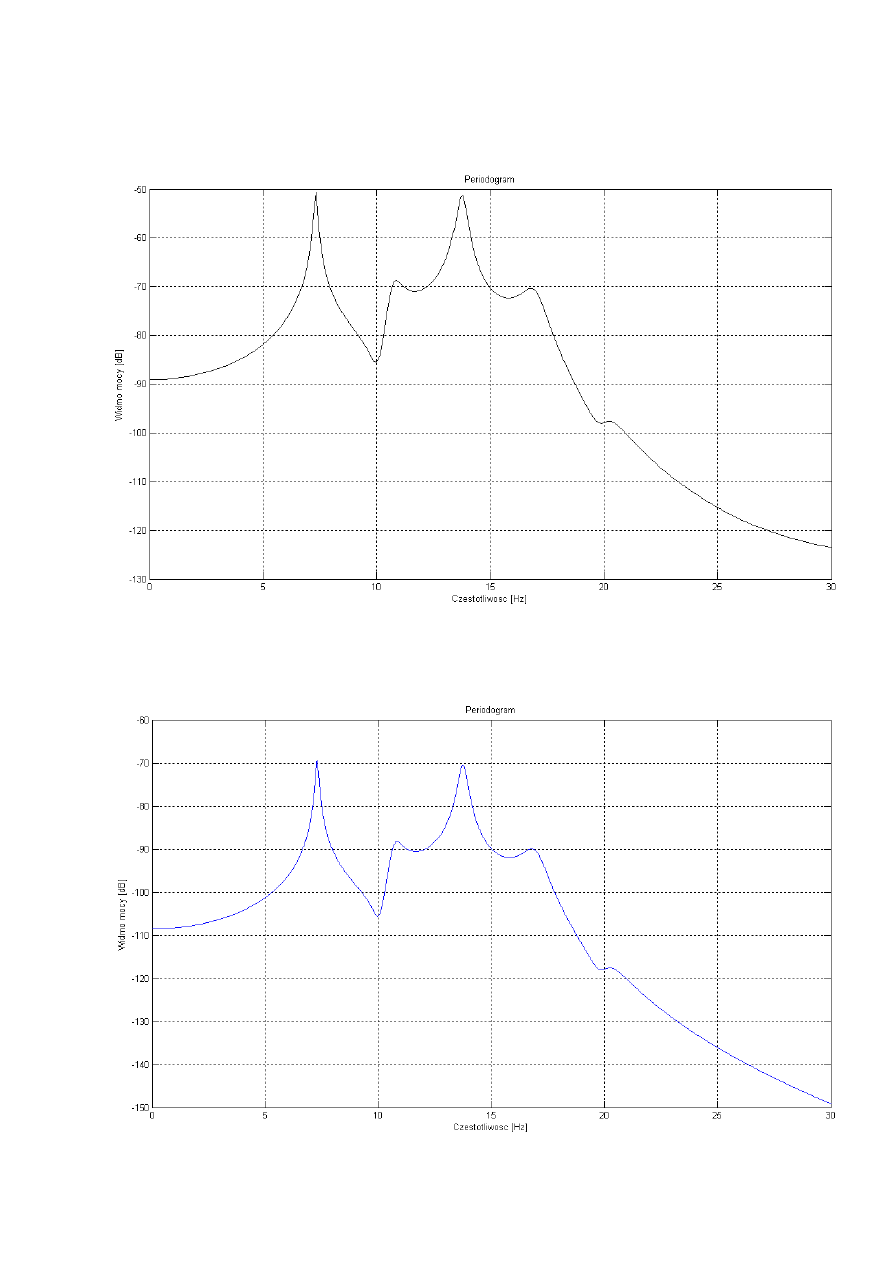
Wykresy:
Periodogram

Periodogram uzyskany przy Fs=100, czasie symulacji t=0:1/Fs:400 i ilości próbek
32768

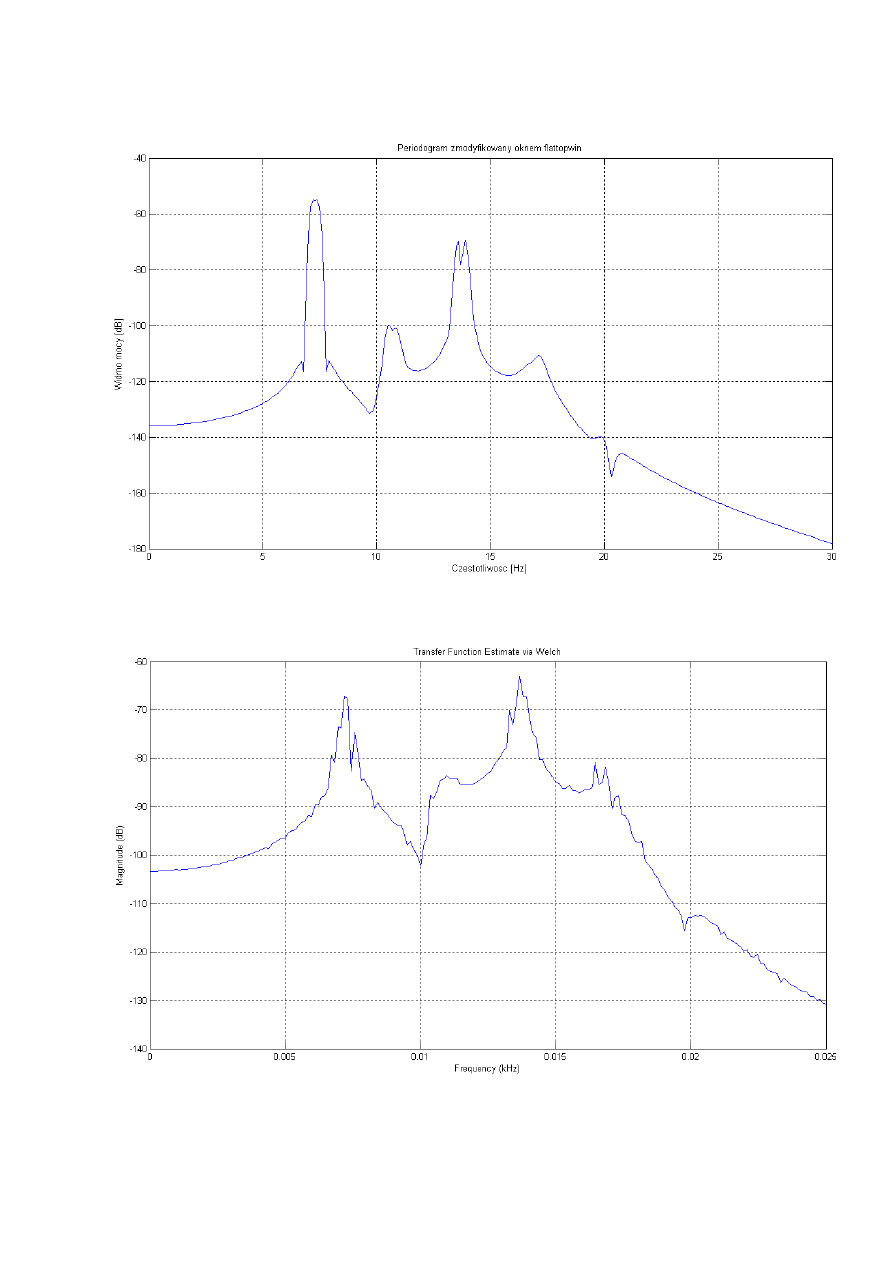
Periodogram zmodyfikowany oknem flattopwin

Funkcja przejścia

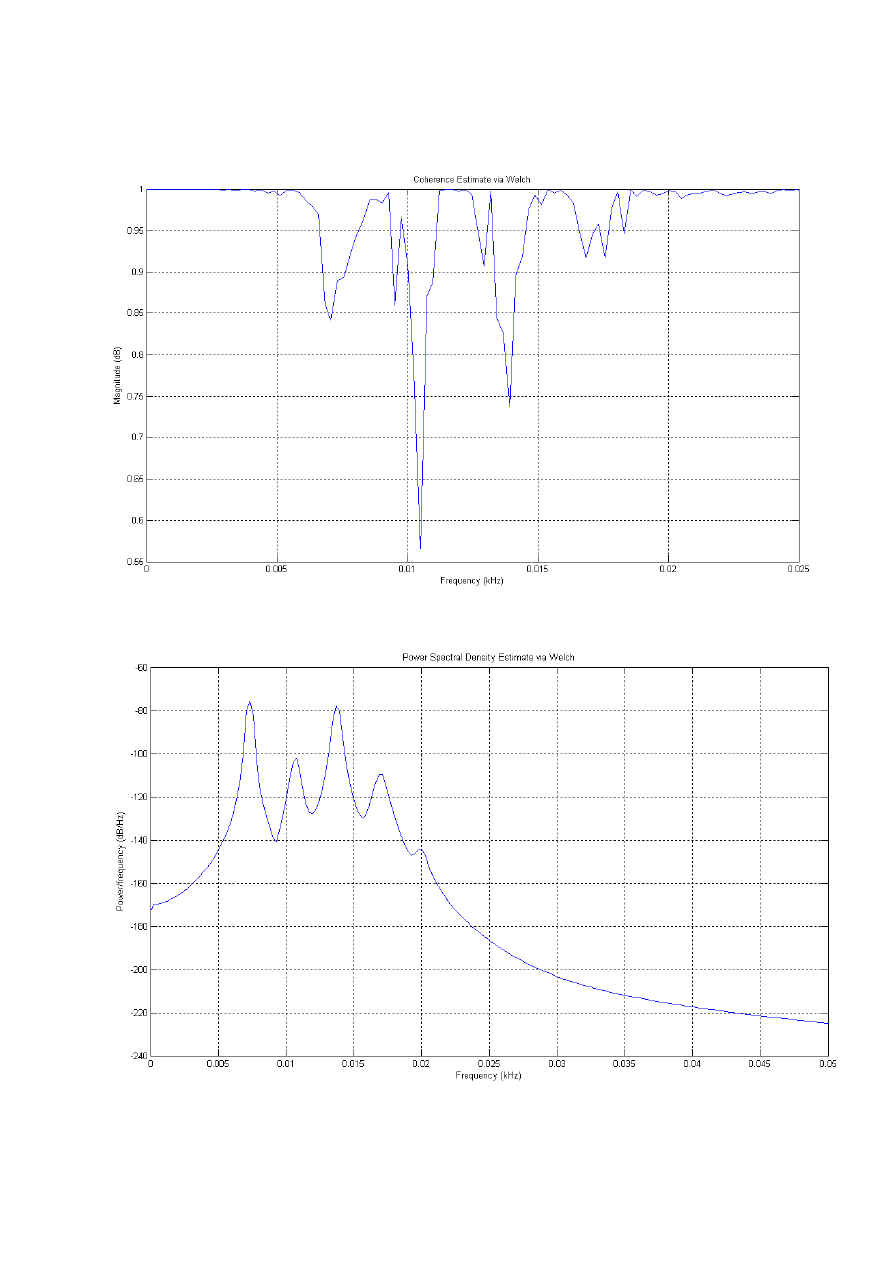
Funkcja koherencji

Funkcja gęstości widmowej mocy

8. Identyfikacja układu przy pomocy transformaty falkowej

sys=ss(A, B, C, D);

Fs=200;

t = 0:1/Fs:20;

u = 10*rand(1,length(t));

%Y_out = lsim(sys,u,t);

Y_out=impulse(sys,t);

xn=Y_out(:,5)';

falka=

'cmor40-4'

;

s1=0;

F_max=Fs/2;

F_max_zadana=30;

F_min_zadana=5;

%tworzenie wektora skali

while

s1<=F_max_zadana

s1=scal2frq(F_max,falka,1/Fs);

F_max=F_max-1;

end

s1=F_min_zadana+1;

F_min=1;

while

s1>=F_min_zadana

s1=scal2frq(F_min,falka,1/Fs);

F_min=F_min+1;

end

wektor_skali=F_max:1:F_min;

figure

funkcja = cwt(xn ,wektor_skali, falka,

'plot'

) ;

figure

surf(abs(funkcja)) ;

shading

interp

view([0 90])

ylabel(

'Parametry skali'

,

'FontSize'

,12)

xlabel(

'Próbki skali'

,

'FontSize'

,12)

title(

'Skalogram zlozonego sygnalu'

)

figure

rozmiar_f=size(funkcja);

time = repmat(t,rozmiar_f(1,1),1) ;

fr = scal2frq(wektor_skali,falka,1/Fs);

freq = repmat(fr,rozmiar_f(1,2),1);

surf(time, freq', abs(funkcja)) ;

shading

interp

;

view([90 0]) ;

grid

on

title(

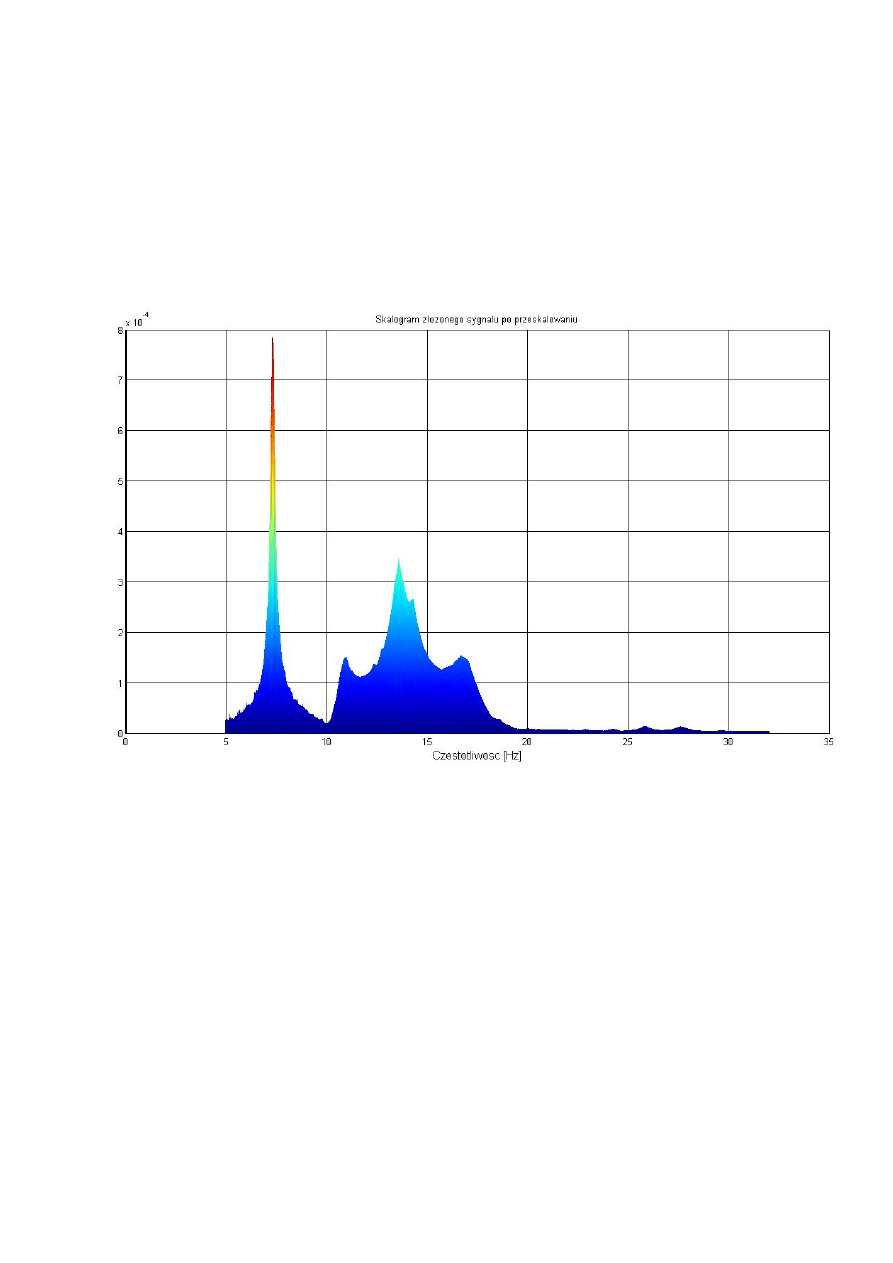
'Skalogram zlozonego sygnalu po przeskalowaniu'

)

ylabel(

'Czestotliwosc [Hz]'

,

'FontSize'

,12)

xlabel(

'Czas'

,

'FontSize'

,12)

figure

l=log(abs(funkcja(86,:)));

plot(t,l)

title(

'wykres logarytmu obwiedni dla 7Hz'

)

p1 = polyfit(t(1,[700:3500]),l(1,[700:3500]),1);

v=p1(1)*t+p1(2);

hold

on

plot(t, v,

'--r'

)

grid

on

p1(1)/(2*pi*7)

Na skalogramie widać częstotliwości drgań własnych układu. Najbardziej widoczne
są częstotliwość 10.7 Hz, 13.73 Hz i 13.92 Hz. Dominują również na wykresie
gęstości widmowej mocy. Grzbiety częstotliwości 10.7 Hz i 16.96 Hz są już mniej
widoczne podobnie jak na wykresie gęstości widmowej mocy. Częstotliwość 20.1
Hz na skalogramie jest niewidoczna.

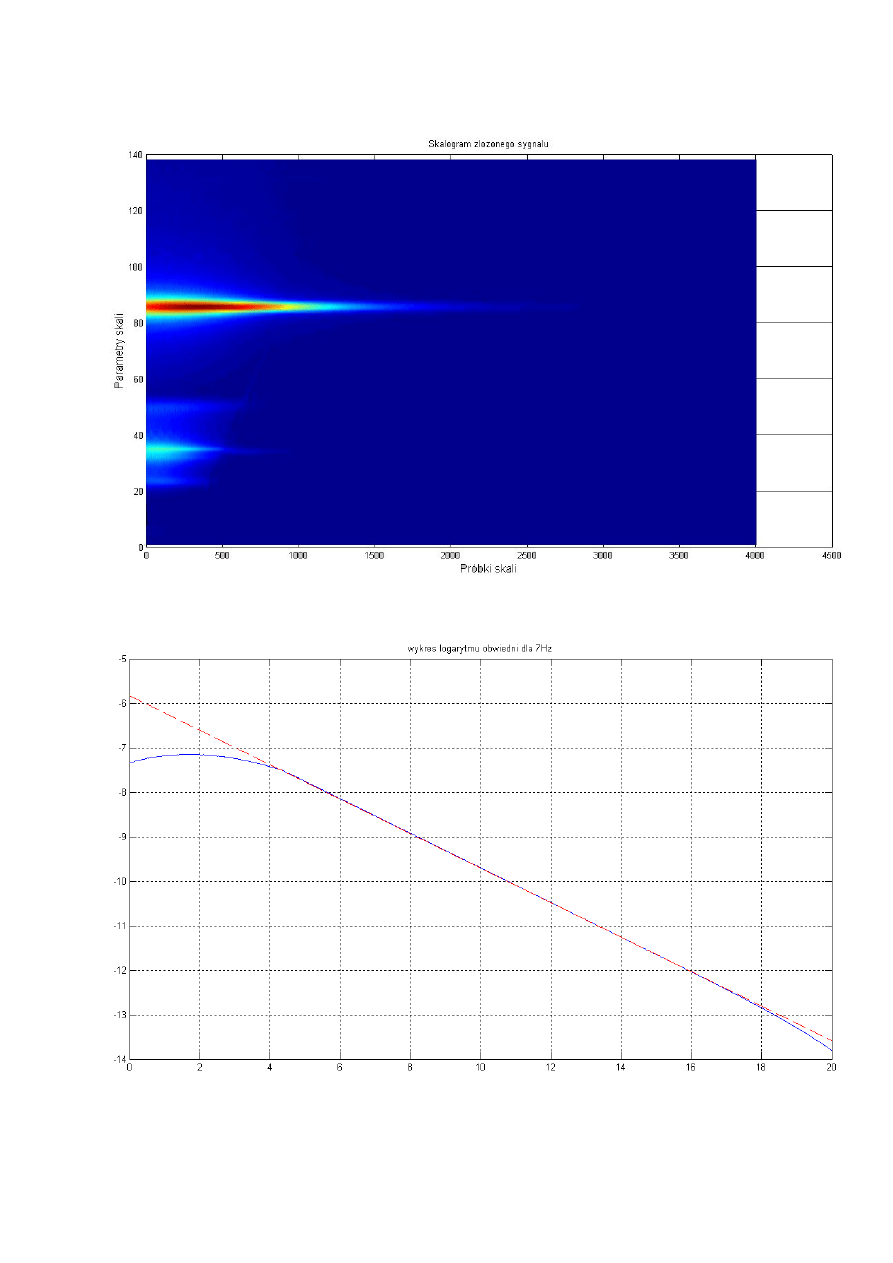
Skalogram nieprzeskalowany

Wykres logarytmu obwiedni dla częstotliwości 7.3 Hz

Na podstawie współczynnika nachylenia prostej można wyznaczyć współczynnik
tłumienia.
ans =

-0.0088

Wyznaczony współczynnik nie różni się od rzeczywistego.

9. Podsumowanie

Najlepsze wyniki dała analiza parametryczna, są one najbardziej zbliżone do
wyznaczonych analitycznie. Analiza parametryczna nie daje jednak informacji na
temat mocy każdej częstotliwości. Taką informacje daje analiza nieparametryczna
– wykres gęstości widmowej mocy. Analiza nieparametryczna nie pozwala na
wyznaczenie tłumień modalnych. Najwięcej informacji na temat układu daje
transformata falkowa. Na skalogramie widać częstotliwości drgań własnych
układu, można także ocenić ich moc na podstawie wysokości grzbietu. Ponadto
można zobaczyć również przebieg częstotliwości w czasie.