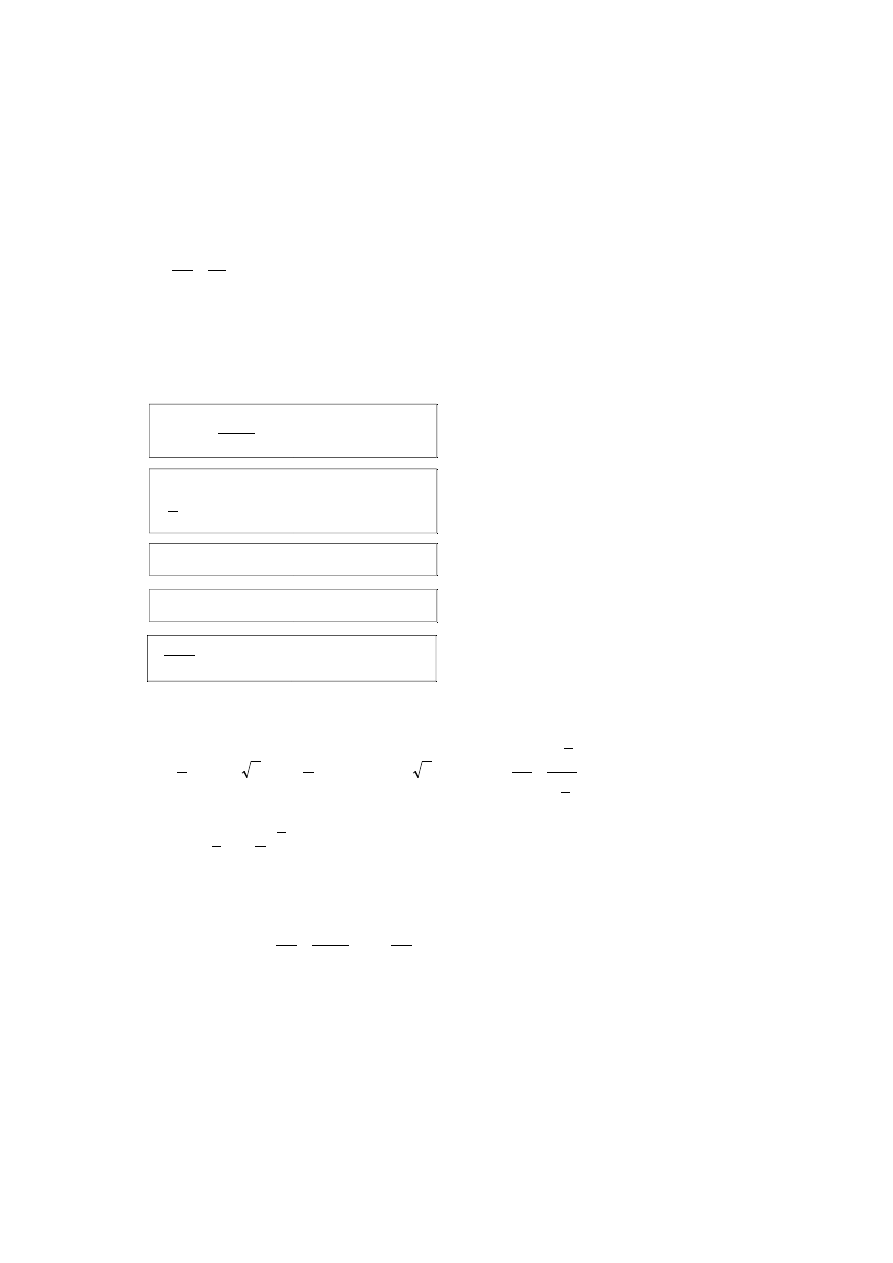
Pojęcia całki - jest to działanie odwrotne do pochodnej.
′
=
+
=
= ⋅
+
+
f
x
x
x
F x
F x
x
x
C
( )
( )
?
( )
5 2
6
5
3
3
6
2
Obliczyć całkę to odpowiedzieć na pytanie jak wyglądała funkcja która ma taką pochodną.
gdzie stała C może byc dowolną liczbą
f x dx
F x
C
F x
f x
( )
( )
( )
( )
∫
=
+
′
=
Wzory:
1.
xndx
xn
n
C
n
=
+
+
+
≠ −
∫
1
1
1
dla
2.
gdy x = -1 to
1
x
dx
x C
=
∫
+
ln| |
3. Cf x dx
C f x dx
( )
( )
=
∫
∫
4.
(
)
f x
g x dx
f x dx
g x dx
( )
( )
( )
( )
±
=
±
∫
∫
∫
5.
1
1
1
x
dx
x
dx
C
−
∫
=
−
+
ln(
)
Przykład:
1
5 2
1
5
2
5
3
3
1
1
2
1
1
2
5
3
3
3
2
3
2
x
x
x dx
x
dx
x dx
xdx
x
x
x
C
x
x
x
C
+
+
=
∫
+
∫
+
∫
=
+ ⋅
+
+ =
∫
=
+
+
+
ln| |
ln| |
Przykład:
(
)
x
dx
xdx
dx
x
x
C
x
x
C
+
=
+
=
+
+
+
+ =
+ +
∫
∫
∫
1
1
2
2
0 1
0
1
2
2
Przykład:

3 5
5
2
1
3
1
5
5
2
1
2
+
+
+
∫
=
∫
+
+
− +
−
∫
∫
∫
=
x
x
x
dx
dx
x dx
x
x
=
+
+
+
+
+
+
− +
− +
+
− +
− +
+ =
+
+ −
− +
+ =
3
0 1
0
1
1
5
1
1
1
5
5
2 1
2
1
1
2
1
1
2
1
3
5
6
6
5
5
1
1
2
1
2
x
x
x
x
C
x
x
x
x
C
(
)
=
+
− − +
+
3
5
6
6
5
5
1
2
1
2
x
x
x
x
C
Przykład:
1
1
1
1
1
x
dx
x
t
x
dx
dx
dt
−
∫
=
− =
− ′ =
=
podstawiamy
liczymy pochodną stronami:
(
)
(
)
1
1
1
x
dx
dt
t C
x
dx
C
−
∫
=
=
+ =
−
+
∫
1
t
ln| |
ln(
)
Przykład:
1
3
2
3
2
3
3
x
dx
x
t
dx
dt
dx
dt
+
∫
=
+
=
=
=
podstawiamy
liczymy pochodną stronami:
(
)
1
3
1
3
1
1
3
1
3
3
2
t
dt
t
dt
t C
x
C
=
=
+ =
∫
∫
=
+ +
ln| |
ln|
|
Przykład:
(
)
3
5
3
5
3
3
x
dx
x
t
dx
dt
dx
dt
+
∫
=
+
=
=
=
podstawiamy
liczymy pochodną stronami:
(
)
(
)
(
)
3
5
1
3
1
3
1
2
1
3
1
2
1
1
2
1
1
3
2
3
3
2
2
9
3
2
2
9
3
5
3
2
x
dx
dx
t dt
t dt
t
C
t
C
t
C
x
C
+
∫
=
∫
=
∫
=
∫
= ⋅
+
+
+ = ⋅ ⋅
+ =
+ =
=
+
+
t
Przykład:

x
x
dx
x
t
x dx
dt
dx
dt
2
3
5
3
5
3
2
3
+
∫
=
+
=
=
=
podstawiamy
liczymy pochodną stronami:
x2
(
)
=
∫
=
∫
= ⋅
+
+
+ = ⋅ ⋅
+ = ⋅
+
+
t
dt
t
t dt
t
C
t
C
x
C
1
3
1
2
1
3
1
2
1
1
2
1
1
3
2
3
2
3
2
9
3
5
3
2
Uproszczenia możliwe w obliczeniach:
Uproszczenie 1.
Wyprowadzenie:
Rozwiążmy poniższy przykład:
1
2
1
2
1
2
2
x
dx
x
t
dx
dt
dx
dt
+
∫
=
+ =
=
=
podstawiamy
liczymy pochodną stronami:
(
)
=
=
∫
+ +
1
2
1
2
2
1
t
dt
x
C
ln|
|
Uproszczenie 1.
Końcowy wzór:
Jeżeli w mianowniku jest funkcja a w liczniku
jest pochodna tej funkcji
to całka jest równa:
ln| ( )|
f x
C
+
Przykład1:
(
)
(
)
1
2
1
1
2
2
2
1
1
2
2
2
1
1
2
2
1
x
dx
x
dx
x
dx
x
C
+
∫
=
⋅
∫
+
=
+
=
∫
+ +
ln|
|
Przykład2:
1
2
5
1
2
2
2
5
1
2
2
2
5
1
2
2
5
x
dx
x
x
dx
x
x
dx
x
C
+
∫
=
⋅
∫
+
=
∫
+
=
+ +
ln|
|
Uproszczenie 2.
Wyprowadzenie:
Rozwiążmy następujący przykład:
dx
x
x
2
5
6
+
+
∫
Nie możemy zastosować poznanych wcześniej wzorów. Stosujemy metodę rozkładu na ułamki proste.
Sprowadzamy mianownik do postaci rozłożonej.
∆ =
−
=
−
=
b
ac
2
4
25
24
1
∆ =
1
x1
5 1
2
3
= − − = −
x1
5 1
2
2
= − + = −

dx
x
x
dx
dx
x
x
x
x
dx
dx
x
x
dx
2
5
6
1
2
3
2
+
+
∫
=
−
−
∫
=
+
+
∫
(
)(
)
(
)(
)
Gdyby wyrażenie:
1
3
2
(
)(
)
x
x
+
+
można było przedstawić jako sumę dwu wyrażeń
A
x
B
x
(
)
(
)
+
+
+
3
2
to można by było zastosować znane już wzory.
Zakładamy, że są takie wartości A i B które spełniają te wyrażenia. Dokonajmy więc przekształcenia takiej sumy
wyrażeń:
1
3
2
3
2
2
3
3
2
2
3
3
2
2
3
3
2
(
)(
)
(
)
(
)
(
)
)
(
)(
)
(
)(
)
(
)
(
)(
)
x
x
A
x
B
x
A x
B( x
x
x
Ax
A
Bx
B
x
x
x A
B
A
B
x
x
+
+
=
+
+
+
=
+
+
+
+
+
=
+
+
+
+
+
=
+
+
+
+
+
czyli:
1
3
2
2
3
3
2
(
)(
)
(
)
(
)(
)
x
x
x A
B
A
B
x
x
+
+
=
+
+
+
+
+
Jeżeli strony równania są równe przy jednakowych mianownikach, więc liczniki są też równe. Możemy więc
napisać:
1
2
3
=
+
+
+
x A
B
A
B
(
)
Obliczamy wartość A i B dla których równanie będzie prawdziwe. Aby „x” nie miał wpływu na wyrażenie musi
być spełniony warunek :
x(A+B) = 0
będzie to zawsze spełnione gdy:
A + B = 0
Przy takim warunku całe wyrażenie 1
2
3
=
+
+
+
x A
B
A
B
(
)
będzie prawdziwe gdy 2A+3B = 1
Możemy napisać układ równań z których wyliczymy wartość A i B :
A
B
A
B
+ =
⋅
+
=
0
2
3
1
| (-2)
−
− =
+
=
+ =
=
2
2
0
2
3
1
0
1
1
A
A
B
B
B
A
B
A
A
+ =
+ =
= −
0
1
0
1
Całe nasze wyrażenie przybierze postać:
dx
x
x
dx
x
dx
x
dx
x
dx
x
dx
x
x
C
(
)(
)
ln|
| ln|
|
+
+
∫
=
−
+
+
∫
+
=
∫
−
+
+
∫
+
=
∫
−
+ +
+ +
3
2
1
3
1
2
1
3
1
2
3
2
Uproszczenie 2.
Końcowy wzór:

dx
x
x
dx
x
x
C
(
)(
)
ln|
| ln|
|
+
+
∫
= −
+ +
+ +
3
2
3
2
Temat:
Pojęcia całki - część dalsza
Wzory:
e
x
dx
e
x
C
∫
=
+
sin
cos
xdx
x
C
= −
+
∫
cos
sin
xdx
x
C
=
+
∫
tgxdx
x
x
dx
=
∫
∫
=
sin
cos
cos
sin
sin
x
t
xdx
dt
xdx
dt
=
−
=
= −
obl. pochodną z obu stron
= −
∫
= −
+
= −
+
∫
dt
t
x C
tgxdx
x C
ln|cos |
ln|cos |
f x g x dx
g x F x
F x g x dx
( ) ( )
( ) ( )
( ) ( )
=
−
′
∫
∫
Przykład:
x e xdx
f x
e x
F x
e x
g x
x
g x
x
x e
x
dx
x e
x
xe
x
dx
2
2
2
2
2
2
∫
=
→
=
=
→
′
=
∫
=
−
∫
- mamy tu całkę z mnożenia
- mamy tu następną całkę z mnożenia, postępujemy podobnie
( )
( )
( )
( )
f x
e x
F x
e x
g x
x
g x
( )
( )
( )
( )
=
→
=
=
→
′
=
1
=
−
∫
=
−
−
∫
=
=
−
−
+
x e x
xe xdx
x e x
xe x
e xdx
x e
x
xe
x
e
x
C
2
2
2
2
2
2

Przykład:
x
x dx
f x
x
F x
x
g x
x
g x
x
3
3
4
4
1
ln
( )
( )
( )
ln
( )
- mamy tu całkę z mnożenia
∫
=
→
=
=
→
′
=
=
−
⋅
∫
−
∫
=
=
− ⋅
+
x
x
x
x
dx
x
x
x dx
x
x
x
C
4
4
4
4
1
4
4
1
4
3
4
4
1
4
4
4
ln
ln
ln
=
Przykład:
ln
ln
ln
x dx
x dx
x dx
- nie mamy wzoru na taką całkę, ale możemy ją zapisać jako:
=
∫
∫
⋅
∫ 1
mamy więc całkę z mnożenia :
Rozwiązujemy ją w znany sposób:
1
1
1
1
⋅
∫
⋅
∫
=
→
=
=
→
′
=
ln
ln
( )
( )
( )
ln
( )
x dx
x dx
f x
F x
x
g x
x
g x
x
= ⋅
−
⋅
∫
−
∫
=
=
− +
x
x
x
x
dx
x
x
dx
x
x
x
C
ln
ln
ln
1
=
= ⋅
−
⋅
∫
−
∫
=
∫
=
− +
x
x
x
x
dx
x
x
dx
x dx
x
x
x
C
ln
ln
ln
ln
1
=
Przykład:
x
x dx
f x
x
F x
x
g x
x
g x
sin
( )
sin
( )
cos
( )
( )
- mamy tu całkę z mnożenia
∫
=
→
= −
=
→
′
=
1
= − ⋅
−
−
∫
− ⋅
+
∫
=
= − ⋅
+
+
x
x
x dx
x
x
xdx
x
x
x
C
cos
( cos )
cos
cos
cos
sin
1
=
1
1
2
+
∫
=
+
x
dx
arctgx
C
Wzór do zapamiętania!
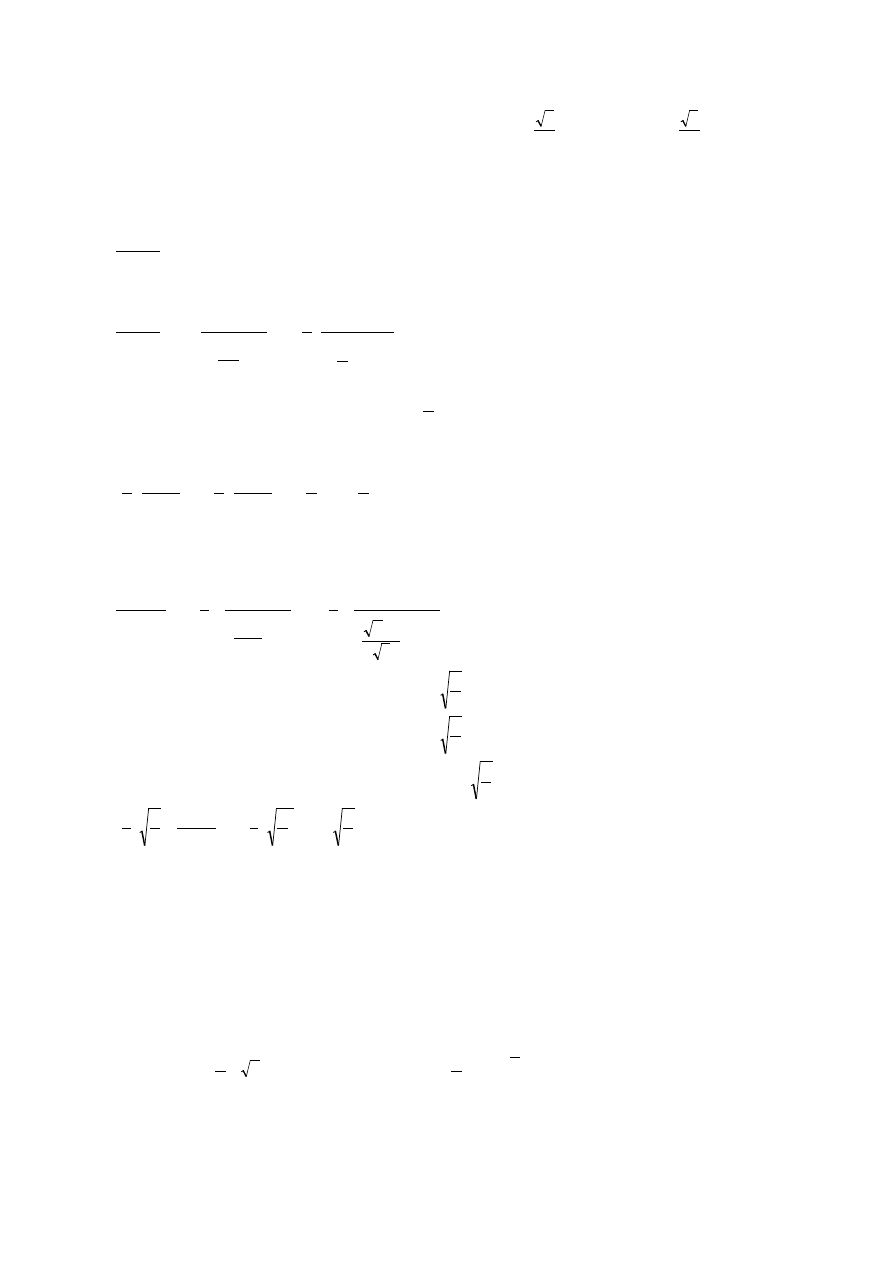
Co to jest arctg? tg
arctg
30
0
3
3
3
3
30
0
=
→
=
tg
arctg
450
1
1
450
=
→
=
Przykład:
dx
x2
4
+
∫
dx - wykorzystamy powyższy wzór:
dx
x
dx
x
dx
x
x
t
x= t
dx= dt
2
4
4
2
4
1
1
4
2
2
1
2
2
2
+
∫
=
+
∫
=
+
∫
=
=
∗
dx
dx
dx
| 2
=
+
∫
=
+
∫
=
+
1
4
2
2
1
1
2
2
1
1
2
2
dt
t
dt
t
arctg
x
C
dx
dx
Przykład:
dx
x
dx
x
dx
x
x
t
dx
dt
dt
dt
t
arctg
x
C
2
2
5
2 2
5
1
2
5
2
1
2
5
2
5
5
2
5
2
2
1
5
2
2
5
+
∫
⋅
+
∫
⋅
⋅
+
∫
=
⋅ =
=
= ⋅
⋅
+
∫
= ⋅
⋅
+
dx =
1
5
dx =
1
5
dx
dx =
1
5
dx
1
5
Matematyka.
Ćwiczenia - Rozwiązywanie całek..
Przykład:
3
2
5
7
1
3
2
5
7
1
1
x
x
x
x dx
x
xdx
dx
x
dx
x x dx
−
+ − +
=
−
−
∫
−
+
∫
∫
∫
∫
=
∫

=
−
−
−
−
+ =
−
−
−
−
+
3
3
3
5
2
2
7
3
2
3
2
3
5
2
2
7
2
3
3
2
x
x
x
x
x
C
x
x
x
x
x
C
ln| |
ln| |
Przykład:
7 3
21
5
1
2
5
7
3
21
1
5
2
5
1
2
7
4
4
21
2
2
x
x
x
x
x
dx
x dx
xdx
x dx
x
x
x
x
C
−
+
−
+
=
∫
−
∫
+
∫
−
−
∫
+
∫
=
−
+
∫
Przykład:
1
2
1
2
1
2
2
1
2
1
2
1
2
1
2
2
1
x
dx
x
t
dx
dt
dx
dt
t
dt
dt
t
t C
x
C
+
=
+ =
=
=
=
⋅
=
=
+ =
=
+ +
∫
∫
∫
.
(
)
ln| |
ln|
|
podstawiamy
liczymy pochodną stronami:
Przykład:
6
5
7
6
6
5
7
5
7
5
6
1
5
6
5
1
6
5
6
5
5
7
x
dx
x
dx
x
t
dx
dt
t
dt
t
dt
t
C
x
C
−
=
−
=
− =
=
=
⋅
=
=
+ =
=
− +
∫
∫
∫
∫
podstawiamy
liczymy pochodną stronami:
5dx = dt
ln
ln|
|
Przykład:
(
)
7
9
7
9
7
7
1
7
1
2
1
7
3
2
3
2
1
7
2
3
3
2
2
21
7
9
3
2
x
x
t
dx
dt
dx
dt
t dx
t
C
t
C
x
C
+ =
+ =
=
=
=
= ⋅
+ = ⋅ ⋅
+ =
=
+
+
∫
∫
podstawiamy
liczymy pochodną stronami
Przykład:

(
)
1
2 3
9
1
2
1
3
9
1
2
3
9
3
3
x
dx
x
dx
x
t
dx
dt
dx
dt
+
=
+
=
+ =
=
=
∫
∫
podstawiamy
liczymy pochodną stronami:
(
)
=
=
−
= ⋅ ⋅
− +
− +
+ = ⋅ ⋅
+ = ⋅ ⋅ ⋅
+ =
= ⋅
+
+
∫
∫
1
2
1
1
2
3
1
2
1
2
1
2
1
3
1
2
1
1
2
1
1
2
1
3
1
2
1
2
1
2
1
3
2
1
1
2
1
3
3
9
1
2
t
dt
t
dt
t
C
t
C
t
C
x
C
Przykład:
1
1
2
(
)(
)
..............................
x
x
dx
−
+
=
∫
??????????????????????????????????
=
−
−
+
=
∫
∫
1
3
1
1
1
3
1
2
(
)
(
)
x
dx
x
dx
=
−
−
+ +
1
3
1
1
3
2
ln|
|
ln|
|
x
x
C
Przykład:
2
1
2
6
5
36
20
16
4
1
6
4
2
1
2
6
4
2
5
2
1
2
6
5
2
1
1
5
2
1
1
5
2
1
5
2
5
1
1
5
x
x
x
dx
x
x
x
x
dx
x
x
x
dx
A
x
x
dx
B
x
Ax
x
dx
B
x
Ax x
B x
x
x
dx
−
−
+
∫
=
=
−
=
=
= − =
= + =
−
−
+
∫
=
−
−
−
∫
=
−
+
⋅
−
∫
= ⋅
−
+
−
∫
∫
=
− +
−
−
−
∫
=
∫
x
∆
∆
(
)(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)(
)
=
−
+
−
−
−
∫
+ =
−
− = −
−
=
= −
=
=
∫
+
−
∫
=
∫
+
−
∫
=
A x
Ax
Bx
B
x
x
B
A
B
A
A
dx
x
dx
dx
x
dx
2
2
10
1
5
2
5
1
4
1
1
4
2
1
4
2
1
4
5
2
1
4
1
5
(
)(
)
??????????????????
............................................
A
dodajemy stronami
_ _ _ _ _ _ _ _ _ _
B
-
1
4
x - 1
-
1
4
1
x - 1
= -
1
4
ln|
|
ln|
|
x
x
C
− +
− +
1 2
1
4
5

Przykład:
dx
x
x
x
x
x
x
A
x
B
x
C
x
A x
x
B( x
x
C x
x
x
x
x
(
)(
)(
)
(
)(
)(
)
(
)(
)
)(
)
(
)(
)
(
)(
)(
)
−
+
+
=
∫
−
+
+
=
−
+
+
+
+
=
+
+
+
−
+
+
−
+
−
+
+
=
1
1
2
1
1
1
2
1
1
2
1
2
1
2
1
1
1
1
2
=
+
+ +
+
+
− −
+
−
−
+
+
=
+
+
+
+
−
+
−
−
+
+
=
=
+
+
+
+
−
+
−
−
+
+
=
+ +
+
+
+
−
−
−
+
+
=
A(x
x
x
B( x
x
x
C x
(x
)(x
)(x
)
(Ax
Ax
A
Bx
Bx
B
Cx
C
(x
)(x
)(x
)
Ax
Ax
A
Bx
Bx
B
Cx
C
(x
)(x
)(x
)
x
A
B
C
x
A
B
A
B
C
(x
)(x
)(x
)
2
2
2
2
2
2
2
1
1
1
2
2
3
2
2
2
2
1
1
2
2
3
2
2
2
2
1
1
2
2
3
2
2
1
1
2
)
)
(
)
)
(
)
(
)
(
)
(
)
Jeżeli ułamki:
1
1
1
2
2
3
2
2
1
1
2
(
)(
)(
)
(
)
(
)
x
x
x
x
A
B
C
x A
B
A
B
C
(x
)(x
)(x
)
−
+
+
=
+ +
+
+
+
−
−
−
+
+
są równe to i liczniki tych ułamków są równe. Możemy więc napisać:
x
A
B
C
x A
B
A
B
C
2
3
2
2
1
(
)
(
)
+ +
+
+
+
−
− =
Obliczamy wartość A, B, C
A + B + C = 0
3A + B + 0 = 0
2A - 2B - C = 1
______________
Z drugiego równania obliczamy B:
B = -3A
A - 3A + C = 0
2A - 2(-3A) - C = 1
__________________
-2A +C = 0
8A - C = 1
_______________
6A = 1
A = 1/6
B = -3A = - 3(1/6) = - 1/2
B = - 1/2
A + B + C = 0
A + B = - C
1
6
1
2
1 3
6
+ − = −
− = −
C
C
− = −
=
1
3
1
3
C
C

A
=
= −
=
1
6
1
2
1
3
B
C
Nasze równanie przybierze więc postać:
dx
x
x
x
x
dx
x
dx
x
dx
x
x
x
C
(
)(
)(
)
(
)
(
)
(
)
ln|
|
ln|
|
ln|
|
−
+
+
∫
=
−
+
∫
−
+
+
∫
+
=
∫
=
−
−
+
+
+ +
1
1
2
1
6
1
1
2
1
1
3
2
1
6
1
1
2
1
1
3
2
Przykład:
(
)(
)
5
7
4
256
5
7
2
16
2
16
5
7
4
4
2
16
x
x
dx
x
x
x
dx
x
x
x
x
dx
−
−
∫
=
−
−
+
∫
=
−
−
+
+
∫
=
(
)
(
)(
)
(
)(
)
=
−
+
+
+
+
+
∫
=
+
+
+
−
+
+
+
−
+
−
+
+
∫
=
A
x
B
x
Cx
D
x
dx
A x
x
B x
x
Cx
D x
x
x
x
x
dx
4
4
2
16
4
2
16
4
2
16
4
4
4
4
2
16
(
)(
)
(
)
(
)(
)
=
+
+
+
−
+
−
+
−
+
−
−
+
+
∫
=
4
2
16
64
3
4
2
16
64
3
16
2
16
4
4
2
16
Ax
A
A
Bx
Bx
Bx
B
Cx
Cx
Cx
D
x
x
x
dx
(
)(
)
=
+ +
+
−
+
+
+
−
+
−
−
−
+
+
∫
=
x
A
B
C
x
A
B
D
x
A
B
C
A
B
D
x
x
x
dx
3
2
4
4
16
16
16
64
64
16
4
4
2
16
(
)
(
)
(
)
Aby obliczyć wartości A, B, C, D, piszemy układy równań:
A
B
C
A
B
D
A
B
C
A
B
D
+ + =
∗
−
+ =
∗
+
−
=
−
−
= −
0
4
4
0
16
16
16
5
64
64
16
7
16
16
Dodajemy pierwsze i trzecie równanie :
16
16
16
0
16
16
16
5
32
32
5
A
B
C
A
B
C
A
B
+
+
=
+
−
=
+
=
Dodajemy drugie i czwarte równanie :
64
64
16
0
64
64
16
7
128
128
7
A
B
D
A
B
D
A
B
−
+
=
−
−
= −
−
= −
W wyniku tych działań otrzymujemy dwa równania:
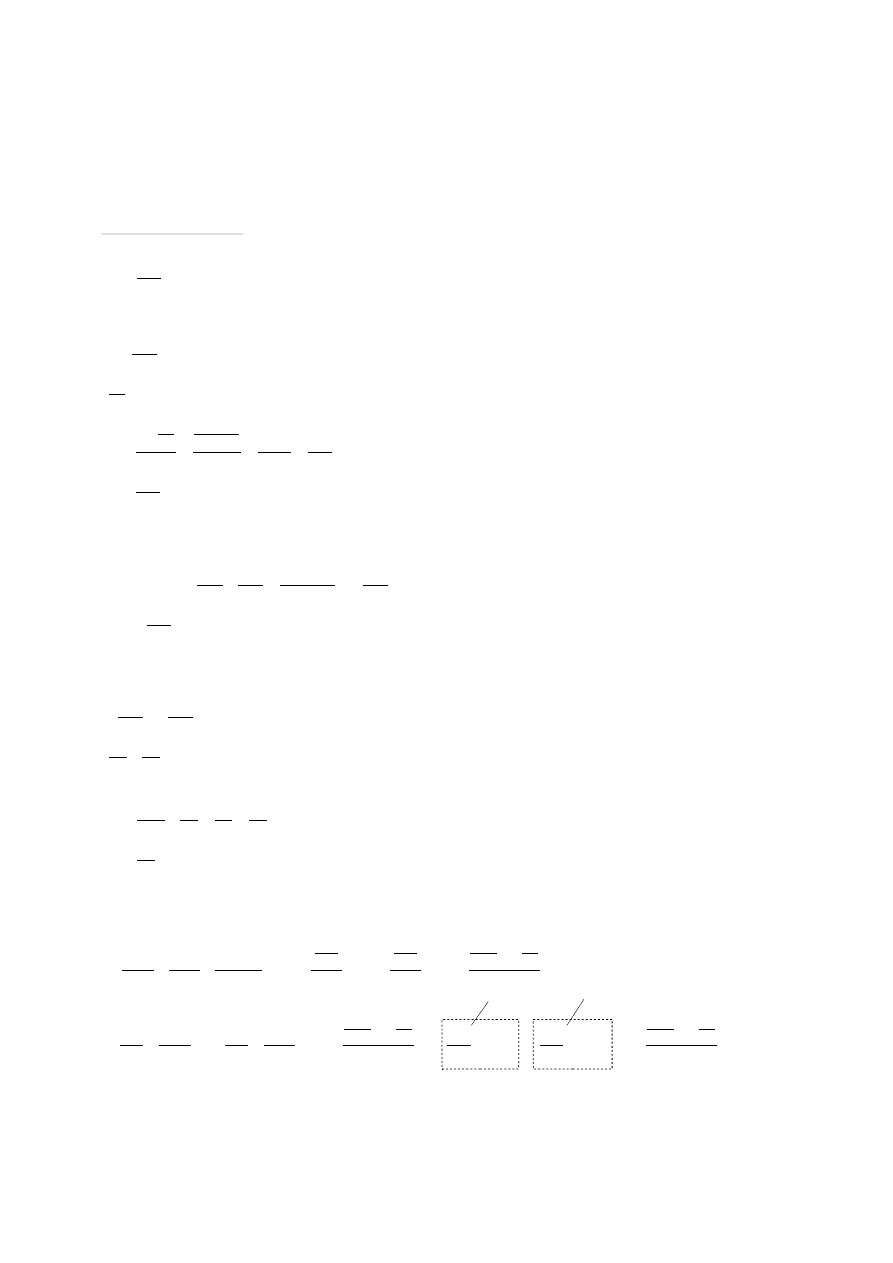
32
32
5
128
128
7
128
128
20
128
128
7
256
13
13
256
A
B
A
B
A
B
A
B
A
A
+
=
∗
−
= −
+
=
−
= −
=
=
4
Z równania 32
32
5
A
B
+
=
obliczamy B
32
13
256
32
5
13
8
32
5
5
13
8
32
40
13
8
32
27
8 32
27
256
27
256
⋅
+
=
+
=
=
−
=
−
=
⋅
=
=
B
B
B
B
Z równania A + B + C = 0 obliczamy C
C
A
B
C
= − − = − −
= − −
= −
= −
13
256
27
256
13
27
276
40
256
40
256
Z równania 4A - 4B + D = 0 obliczamy D
4
13
256
4
27
256
0
13
64
27
64
0
13
64
27
64
14
64
7
32
7
32
−
+ =
−
+ =
= −
+
=
=
=
D
D
D
D
Podstawiamy obliczone wartości A, B, C, D do równania:
A
x
B
x
Cx
D
x
dx
x
dx
x
dx
x
x
dx
x
dx
x
dx
x
x
dx
−
+
+
+
+
+
∫
=
−
∫
+
+
∫
+
−
+
+
∫
=
=
−
∫
+
+
∫
+
−
+
+
∫
=
4
4
2
16
13
256
4
27
256
4
40
256
7
32
2
16
13
256
1
4
27
256
1
4
40
256
7
32
2
16
13
256
4
27
256
4
40
256
7
32
2
16
ln|
|
ln|
|
x
x
x
x
dx
−
+
+
+
−
+
+
∫
a
b

( )
( )
= + +
−
+
+
∫
= + +
−
⋅
+
+
∫
= + +
−
+
+
+
∫
=
= + +
−
+
∫
+
+
a
b
x
x
dx
a
b
x
x
dx
a
b
x
x
x
dx
a
b
x
x
dx
x
40
256
7
32
2
16
40
256
1
2
2
7
32
2
16
40
512
2
2
16
7
32
2
16
40
512
2
2
16
7
32
2
16
∫
= + + −
+
∫
+
+
∫
=
dx
a
b
x
x
dx
x
dx
40
512
2
2
16
7
32
1
2
16
= + + −
+
+
+
∫
= + + +
+
∫
=
= + + +
⋅
+
∫
=
=
=
=
= + + +
⋅
+
a
b
x
x
dx
a
b
c
x
dx
a
b
c
dx
x
x
t x
t dx
dt
a
b
c
dt
t
40
512
2
16
7
32
1
2
16
7
32
1
16
2
16
1
7
32
1
16
4
2
1
4
4
4
7
32
1
16
4
2
1
ln|
|
podstawiamy
∫
= + + +
⋅
+
∫
= + + +
⋅
= + + +
⋅
=
= + + +
a
b
c
dt
t
a
b
c
arctgt
a
b
c
arctg
x
a
b
c
arctg
x
7
32
4
16
2
1
7
32
1
4
7
32
1
4
4
7
128
4
Przykład:
dx
x
dx
x
dx
x
x
t
x
t
dx
dt
dt
t
dt
t
arctgt
C
arctg
x
C
2
7
7
2
7
1
1
7
7
2
1
7
7
7
7
1
7
7
2
1
7
7
2
1
7
7
7
7
7
+
∫
=
+
∫
= ⋅
+
∫
=
=
∗
=
⋅
=
= ⋅
⋅
+
∫
=
⋅
+
∫
=
=
+ =
+
c
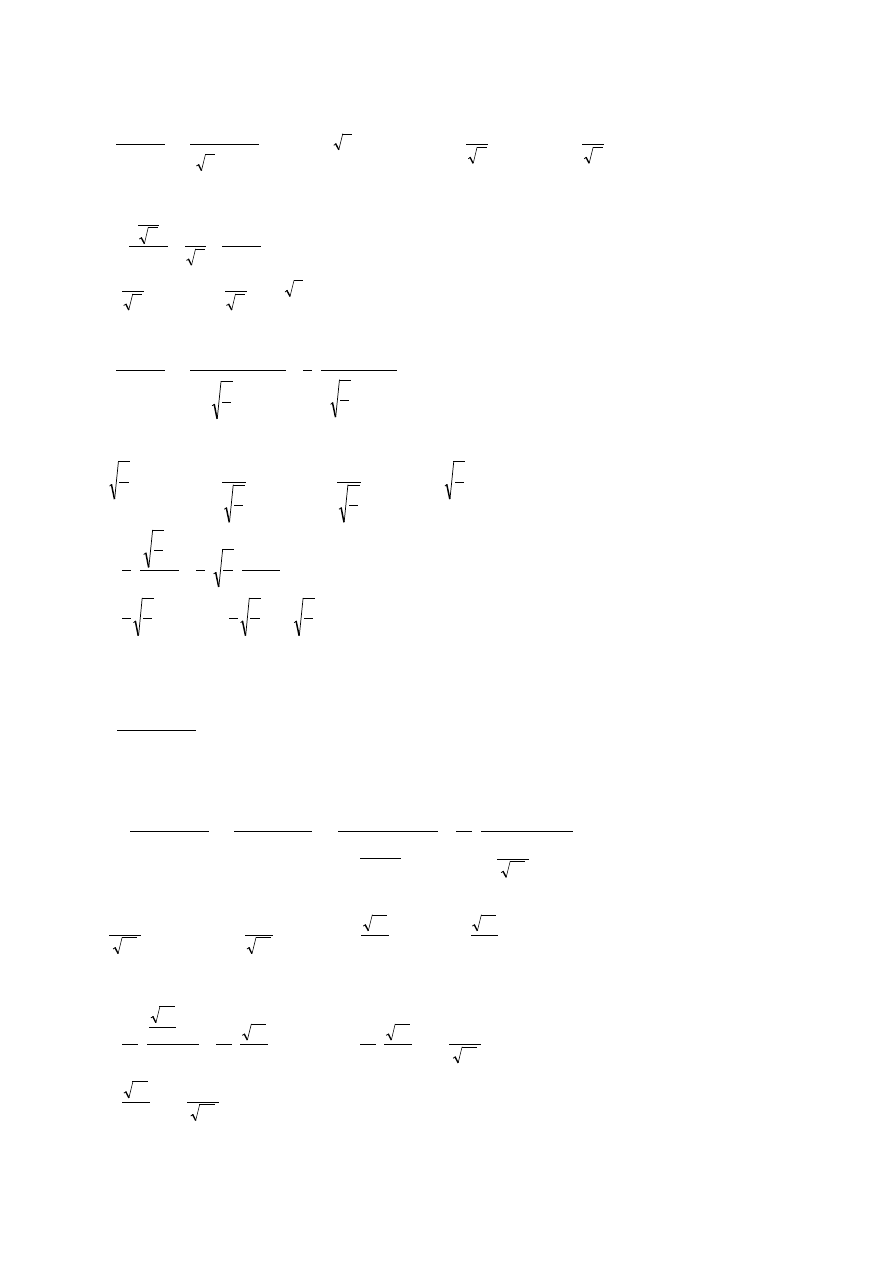
Przykład:
( )
dx
x
dx
x
x
t
x
t
dx
dt
dt
t
dt
t
arctgt
C
arctg
x
C
2
2
1
2
2
1
2
2
2
2
2
1
1
2
2
1
1
2
1
2
2
+
∫
=
+
∫
=
⋅ =
=
=
=
+
∫
=
⋅
+
∫
=
=
+ =
⋅
+
|
|
Przykład:
dx
x
dx
x
dx
x
x
t x
t
dt
dt
dt
t
dt
t
arctgt
C
arctg
x
C
3
2
5
5
3
5
2
1
1
5
3
5
2
1
3
5
3
5
3
5
5
3
1
5
5
3
2
1
1
5
5
3
2
1
1
5
5
3
1
5
5
3
5
3
+
∫
=
+
∫
=
+
∫
⋅ =
=
=
=
=
+
∫
= ⋅
+
∫
=
=
+ =
⋅
+
dx
dx
|
|
Przykład:
(
)
(
)
(
)
(
)
(
)
dx
x
x
a
ab
b
x
x
x
x
x
x
x
dx
x
x
dx
x
dx
x
dx
x
x
t
x
t
x
2
6
24
2
2
2
2
2
6
24
2
6
9
15
2
6
9
15
3 2
15
2
6
24
3 2
15
15
3
15
2
1
1
15
3
15
2
1
3
15
3
15
3
15
15
+
+
=
=
+
+
+
+
=
+
+ +
=
+
+ +
=
+
+
=
+
+
=
+
+
=
+
+
=
+
+
=
+
=
+ =
+ =
⋅
∫
∫
∫
∫
∫
a + b
( )
t
x
dt
dt
t
arctg t
C
arctg
x
C
arctg
x
C
d
+
=
⋅
=
⋅
+
=
⋅
+ =
⋅
+
+
=
+
∫
15
15
1
15
15
15
2
1
1
15
15
15
1
15
15
15
3
15
15
15
3
15
.........................
| |
|
|
|
|
Temat:
cd całki.
Powtórka:
1
1
2
+
∫
=
+
x
dx
arctgx
C
Przykład:
dx
x
x
2
3
7
9
28
19
+
+
∫
= −
= −
∆
delta ujemna, do rozwiązania należy wykorzystać inną metodę.
Wykorzystać można wzór:
(
)
a
b
a
ab
b
+
=
+
+
2
2
2
2
dx
x
x
dx
x
x
dx
x
x
dx
dx
x
dx
x
x
t
x
2
3
7
2
2
3
2
9
4
9
4
7
3
2
2
19
4
4
19
3
2
2
19
4
19
4
4
19
3
2
2
19
4
1
4
19
3
2
19
2
2
1
3
2
19
2
3
2
19
2
+
+
∫
+ ⋅
+ − +
∫
=
+
+
∫
=
+
+
∫
=
+
+
∫
=
=
+
+
∫
+
=
+ =
⋅
=
podstawiamy za
t
dx
dt
=
⋅
19
2
=
+
∫
=
⋅
+
∫
=
+
+
4
19
19
2
2
1
4
19
19
2
2
1
2 19
19
2
3
2
19
2
dt
t
dt
t
arctg
x
C
Przykład:
5
7
2
7
20
x
x
x
dx
+
+
+
=
∫
Przypomnienie wzoru:
′
∫
=
+
f
x
f x
f x
C
( )
( )
ln| ( )|
pochodna z mianownika naszego przykładu była by:
x
x
x
2
7
20
2
7
+
+
′
=
+
licznik z naszego przykładu jest :
5
7
x
+
aby doprowadzić go do postaci:
2
7
x
+
należy dokonać przekształcenia:

(
)
(
)
(
)
(
)
5
7
5
1
2
2
7
7
2
7
5
2
2
7
5 7
2
7
5
2
2
7
35
2
14
2
5
2
2
7
21
2
x
x
x
x
x
x
+ =
+ −
+ =
+ −
⋅
+ =
+ −
+
=
=
+ −
Wracamy do naszej całki:
(
)
5
7
2
7
20
5
2
2
7
21
2
2
7
20
5
2
2
7
2
7
20
21
2
2
7
20
x
x
x
dx
x
x
x
dx
x
x
x
dx
dx
x
x
+
+
+
=
∫
+ −
+
+
=
∫
+
+
+
∫
−
+
+
∫
=
=
+
+
−
+ ⋅
+
−
+
∫
= −
+
+
∫
5
2
2
7
20
21
2
2
2
7
2
49
4
49
4
80
4
21
2
7
2
2
31
4
ln|
|
x
x
K
dx
x
x
B
K
dx
x
B
B
dx
x
x
dx
dx
x
dx
x
=
+
+
∫
=
+
+
∫
=
⋅
+
+
∫
=
⋅
+
+
∫
=
7
2
2
31
4
4
31
7
2
2
31
4
31
4
4
31
7
2
2
31
4
1
4
31
7
2
31
2
2
1
x
t
x
t
dx
dt
+
=
+ =
⋅
=
⋅
7
2
31
2
7
2
31
2
31
2
| całkujemy stronami
B
dx
x
dt
t
arctg
x
C
=
⋅
+
+
∫
=
⋅
+
∫
=
+
+
4
31
7
2
31
2
2
1
4
31
31
2
2
1
2 31
31
7
2
31
2
|
|
Przykład:
(
)
dx
x
x
dx
x
x
t
dx
dt
2
2
1
1
2
1
+
+
∫
=
+
∫
=
+ =
=
=
∫
= −
∫
=
−
−
+ =
+
+
dt
t
t
dt
t
C
x
C
2
2
1
1
1
1
Temat2: Całki oznaczone.
Wszystkie poznane do tej pory całki to całki nieoznaczone.
Całka oznaczona to całka dla której określa się przedział. Musi być różniczkowalna.
f x dx
a
b
F b
F a
( )
( )
( )
∫
=
−
Przykład:
xdx
x
1
3
2
2 1
3
32
2
12
2
9
2
1
2
8
2
4
∫
=
=
−
= − = =
|
Przykład:
1
1
5
10
x
dx
−
∫
=
podstawiamy:
x
t
dx
dt
− =
=
1
dla
x
x
=
=
5
10
t
t
( )
(
)
5
4
10
9
=
=
Przy metodzie podstawiania trzeba zmienić granice całkowania bo zmienia się zmienna.
Wracamy do przykładu:
1
1
5
10
1
4
9
4
9
9
4
9
4
x
dx
t
dt
−
∫
=
∫
=
=
=
−
=
ln
|
ln
ln
ln
| t |
Twierdzenia:
f x dx
f f dx
a
c
f f dx
c
b
a
b
c
a b
( )
(
)
(
)
( , )
=
+
∫
∫
∫
∈
f x dx
a
a
( )
=
∫
0
f x
a b
( )
( , )
>
0
P
a b
| |
( )
P
f x dx
a
b
=
∫
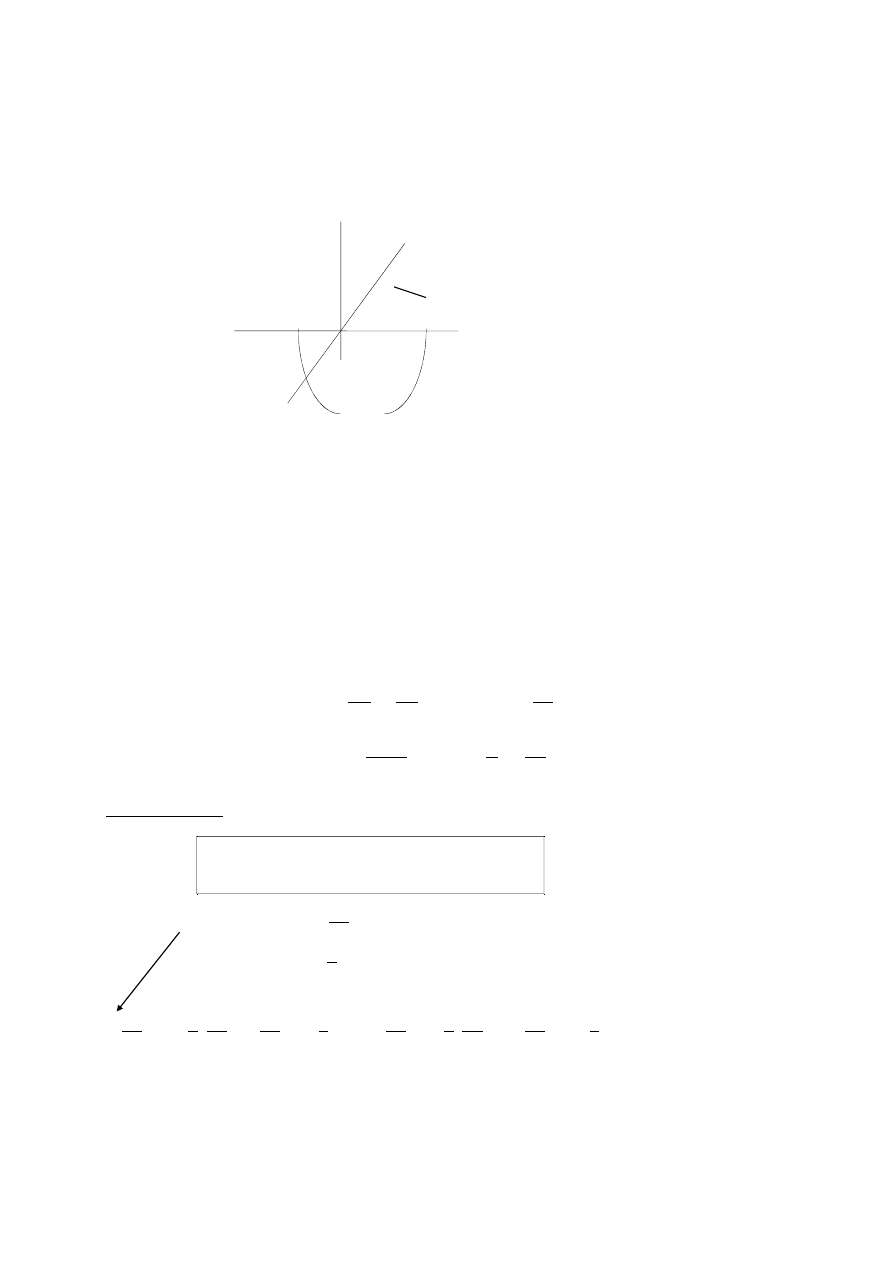
Przykład:
Mamy dwie funkcje:
f x
x
g x
x
( )
( )
=
=
2
4
x
2
4x
Obliczyć pole zawarte między jednym a drugim wykresem w obszarze między przecięciami się tych wykresów.
Wykresy przecinają się dla x który jest równy:
x
x
2
4
=
x
x
x x
x
x
2
4
0
4
0
0
4
−
=
−
=
=
=
(
)
Pole będzie równe różnicy :
Pole
xdx
x dx
x
x
=
−
∫
∫
=
=
−
=
−
−
−
=
−
⋅
=
−
=
4
4
2
3
4 8
0
64
3
0
32
32 2
3
32 1
2
3
32
3
2
0
4
0
4
2
0
4
3
0
4
|
|
(
)
25.04.98 ćwiczenia
Przykład:
f x
g x
g x
F x
F x
g x dx
C
( )
( )
( )
( )
( )
( )
⋅
=
⋅
−
⋅ ′
+
∫
∫
x
xdx
f
x
F
x
g
x
g
x
x
x
x
x
dx
x
x
x dx
x
x
x
C
x
x
C
2
2
3
3
1
3
3
1
3
3
3
3
1
3
2
3
3
1
3
3
3
3
3
1
3
ln
ln
ln
ln
ln
ln
=
=
=
∫
=
′ =
=
−
⋅
∫
=
−
∫
=
− ⋅
+ =
−
+
Miejsce przecięcia się obu wykresów

Przykład:
x
xdx
f
x
F
x
g
x
g
x
x
xdx
x
x
x
C
sin
sin
cos
cos
cos
cos
sin
=
=
= −
∫
=
′ =
= −
+
∫
= −
+
+
1
Przykład:
1
1
1
1
1
x
x
dx
x
t
x
dx
dt
dt
x
x
dx
dx
x
x
dx
x
t
dt
t
dt
t
t
C
x
C
ln
ln
ln
ln
ln
ln(ln )
∫
=
=
=
=
=
∫
=
∫
=
⋅ =
⋅ =
∫
=
∫
+ =
+
∫
dx
x
Przykład:
1
2
2
2
1
1
1
1
x
x
dx
x
t
dx
dx
dt
t
t
dt
t
C
t
C
x
C
ln
ln
ln
∫
=
=
=
=
∫
= −
∫
=
−
−
+ = − + = −
+
1
x
Przykład:
dx
x
x
x
x
A
x
B
x
A x
B( x
x
x
Ax
A
Bx
x
x
x A
B
A
B
x
x
x
t
x
z
x
dt
(
)(
)
(
)(
)
(
)
(
)
(
)
)
(
)(
)
(
)(
)
(
)
(
)(
)
−
+
∫
=
−
+
=
−
+
+
=
+ +
−
−
+
=
=
+ +
−
−
+
=
+
+ −
−
+
=
− =
+ =
=
5
1
1
5
1
5
1
1
5
5
1
5
5
1
5
5
1
5
1
d
dx
dz
=
A
B
A
B
+ =
−
=
0
5
1
(-1)
− − =
−
=
A
B
A
B
0
5
1
−
=
= −
6
1
1
6
B
B
A
A
− =
=
1
6
0
1
6
=
−
∫
−
+
∫
=
∫
−
∫
=
1
6
1
5
1
6
1
1
1
6
1
1
6
1
x
dx
x
dx
t
dt
z
dz
=
−
+ =
− −
+ +
1
6
1
6
1
6
5
1
6
1
ln
ln
ln
ln
t
z
C
x
x
C
Przykład:
(
)
(
)
(
)
1
2
11
1
2
1 10
1
1
10
1
10
1
10
1
1
10
1
10
1
2
2
2
2
2
x
x
dx
x
x
dx
x
dx
dx
x
dx
x
+
+
∫
=
+
+ +
∫
=
+
+
∫
=
∫
⋅
+
+
=
+
+
∫
=
x
t
x
t
dx
dt
+
=
+ =
⋅
=
⋅
1
10
1
10
10
=
+
∫
=
⋅
+
∫
=
⋅
+
+
1
10
10
1
10
10
1
10
10
1
10
2
2
dt
t
dt
t
arctg
x
C
Przykład:
dx
x
x
x
x
x
x
x
x
2
2
7
2 2
7
2
2
2
2
2
7
2
2
2
2
4
1
16
1
16
7
2
+ +
∫
=
+ + =
+
⋅ +
=
+ ⋅ +
−
+
=
wyciągnijmy przed mianownik 2 i przedstawmy go w postaci:
=
+ ⋅ +
−
+
=
+
−
+ ⋅
=
+
+
=
2
2
2
4
1
16
1
16
7
2
2
1
4
2
1
16
8 7
16
2
1
4
2
55
16
x
x
x
x
Podstawiamy do naszego przykładu:
dx
x
x
2 2
7
2
55
16
1
2
2
55
16
1
2
16
55
2
55
16
55
16
55
16
+ +
∫
=
+
∫
=
⋅
+
∫
=
⋅
+
∫
=
dx
2
x +
1
4
dx
x +
1
4
dx
x +
1
4
= ⋅
+
∫
=
+
∫
=
=
=
⋅
=
⋅
1
2
16
55
2
55
16
2
1
8
55
55
4
2
1
55
4
55
4
55
4
dx
x +
1
4
x +
1
4
podstawiamy:
x +
1
4
x +
1
4
różniczkujemy:
dx
t
t
dx
dt
=
+
∫
=
⋅
+
∫
=
⋅
+ =
⋅
+
+
8
55
55
4
2
1
8
55
55
4
2
1
2 55
55
2 55
55
1
4
55
4
dt
t
dt
t
arctg t
C
arctg
x
C
Przykład:
3
7
6 2
4
x
x
x
+
+ +
∫
=
zastosujemy wzór
′
∫
=
+
f
x
f x
f x
C
( )
( )
ln| ( )|
Obliczamy pochodną mianownika:
(
)
(
)
(
)
6
2
4
12
1
3
7
3
1
12
12
1
1
12
7
1
4
12
1
1
4
7
1
4
12
1
27
4
x
x
x
x
x
x
x
+ +
′
=
+
+ =
+ −
+ =
+ − + =
+ +
aby licznik doprowadzić do takiej wartości,
należy dokonać w nim następujących przekształceń:
Podstawiamy obliczoną wartość w miejsce licznika:
(
)
(
)
(
)
=
+ +
+ +
=
+
+ +
+
+ +
=
+
+ +
+
+ +
=
∫
∫
∫
∫
∫
1
4
12
1
27
4
6 2
4
1
4
12
1
6 2
4
27
4
6 2
4
1
4
12
1
6 2
4
27
4
6 2
4
x
x
x
dx
x
x
x
dx
x
x
dx
x
x
x
dx
dx
x
x
dx
=
+ + +
+ +
=
+ +
∫
1
4
6
2
4
27
4
6 2
4
1
4
6
2
4
ln
ln
x
x
dx
x
x
dx
x
x
oznaczmy A =
= +
+ +
∫
A
dx
x
x
dx
27
4
6 2
4
Rozpisujemy mianownik aby można było zastosować wzór:
1
1
2
+
∫
=
+
x
dx
arctgx
C
6
2
4
6
2
2
2 6
4
6
6
2
2
12
1
144
1
144
2
3
6
1
12
2
1
144
2
3
6
1
12
2
95
144
x
x
x
x
x
x
x
x
+ + =
+
⋅
+
=
+
+
−
+
=
+
−
+
=
+
+
Wracamy do obliczeń całki:
= +
+ +
= +
+
+
= +
⋅
⋅
+
+
=
= +
⋅
+
+
=
∫
∫
∫
∫
A
dx
x
x
dx
A
dx
x
A
dx
x
A
dx
x
27
4
6
2
4
27
4
6
1
12
2
95
144
27
4
1
6
144
95
1
12
2
95
144
1
162
95
1
12
2
95
12
2
1
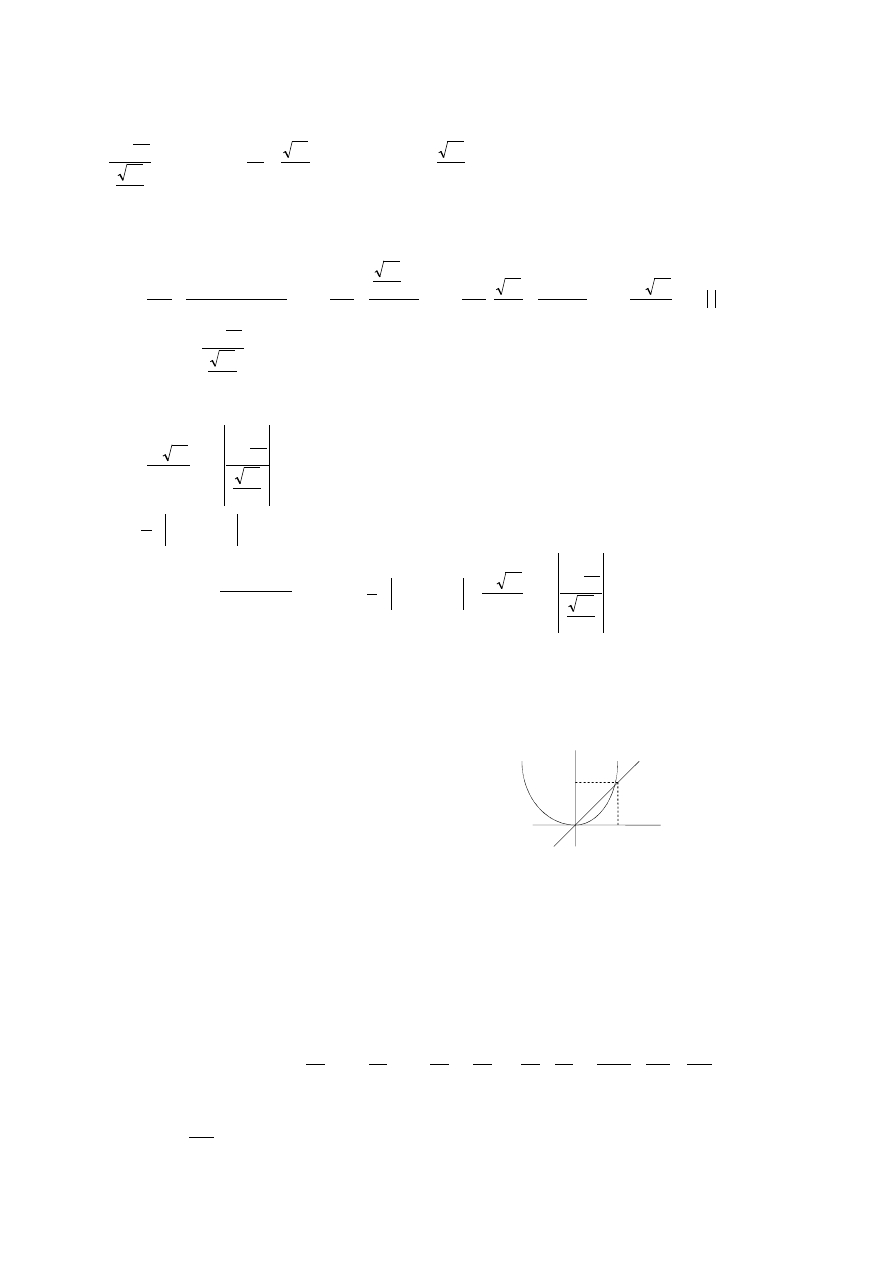
Podstawiamy:
x
t
x
t
dx
dt
+
=
+
=
⋅
=
1
12
95
12
1
12
95
12
95
12
Wstawiamy to do przykładu:
= +
⋅
+
+
= +
⋅
+
= +
⋅
⋅
+
= +
⋅
+ =
= +
⋅
+
+
∫
∫
∫
A
dx
x
A
dt
t
A
dt
t
A
arctg t
C
A
arctg
x
C
162
95
1
12
95
12
2
1
162
95
95
12
2
1
162
95
95
12
2
1
81 95
6 95
81 95
6 95
1
12
95
12
A =
1
4
6
2
4
ln x
x
+ +
Rozwiązaniem
3
7
6 2
4
x
x
x
+
+ +
∫
jest: =
1
4
6
2
4
ln x
x
+ + +
⋅
+
+
81 95
6 95
1
12
95
12
arctg
x
C
Przykład:
Obliczyć pole między wykresami funkcji:
y
x
=
2
y
x
=
7
7
Obliczamy miejsca przecięcia się tych wykresów (wspólne wartości X dla obu wykresów):
x
x
x
x
x x
2
7
2
7
0
7
0
=
−
=
−
=
(
)
Dla
x1 0
=
oraz x2
7
=
wykresy tych funkcji przecinają się.
Pole między wykresami tych funkcji będzie równe różnicy całek oznaczonych tych funkcji dla przedziału 0,7
P
xdx
x dx
x
x
P
=
−
=
−
=
−
−
−
= ⋅
−
=
=
∫
∫
7
0
7
2
0
7
7
2
2 0
7
3
3 0
7
7
7
2
2
7
0
2
2
7
3
3
0
3
3
7 49
2
343
3
343
6
343
6
|
|

Przykład:
Obliczyć pole między wykresami funkcji:
y
x
=
y
x
=
2
1/4
Obliczamy miejsca przecięcia się tych wykresów (wspólne wartości X dla obu wykresów):
x
x
x
x
x
x
x
x
=
=
− =
− =
2
4 2
4
2
0
4
1
0
(
)
Dla wartości:
wykresy przecinają się.
x
x
1
0
2
1
4
=
=
Pole między wykresami tych funkcji będzie równe różnicy całek oznaczonych tych funkcji dla przedziału 0
1
4
,
P
xdx
xdx
x dx
xdx
x
=
−
=
−
=
−
=
∫
∫
∫
∫
0
1
4
2
0
1
4
1
2
0
1
4
2
0
1
4
2
3
2
3
0
1
4
0
1
4
|
|
2
x
2
2
= ⋅
−
= ⋅ −
=
−
= − =
=
2
3
1
64
1
16
2
3
1
8
1
16
1
12
1
16
4
3
48
1
48
1
48
P

Wzory na obliczanie całek:
1.
xndx
xn
n
C
n
=
+
+
+
≠ −
∫
1
1
1
dla
gdy x = -1 to
1
x
dx
x C
=
∫
+
ln| |
2.
Cf x dx
C f x dx
( )
( )
=
∫
∫
3.
(
)
f x
g x dx
f x dx
g x dx
( )
( )
( )
( )
±
=
±
∫
∫
∫
4.
1
1
1
x
dx
x
dx
C
−
∫
=
−
+
ln(
)
5.
Jeżeli w mianowniku jest funkcja a w liczniku
jest pochodna tej funkcji
to całka jest równa:
′
∫
=
+
f
x
f x
f x
C
( )
( )
ln| ( )|
6.
1
3
2
3
2
(
)(
)
ln|
| ln|
|
x
x
dx
x
x
C
+
+
= −
+ +
+ +
∫
7.
e
x
dx
e
x
C
∫
=
+
8.
sin
cos
xdx
x
C
= −
+
∫
9.
cos
sin
xdx
x
C
=
+
∫
10.
tgxdx
x C
= −
+
∫
ln|cos |
11.
f x g x dx
g x F x
F x g x dx
( ) ( )
( ) ( )
( ) ( )
=
−
′
∫
∫
12.
ln
ln
x dx
x
x
x
C
∫
=
− +
13.
1
2
1
x
dx
arctgx
C
+
=
+
∫
14.
f x dx
a
b
F b
F a
( )
( )
( )
∫
=
−
15.
Twierdzenia:
1.
f x dx
f f dx
a
c
f f dx
c
b
a
b
c
a b
( )
(
)
(
)
( , )
=
+
∫
∫
∫
∈
2.
f x dx
a
a
( )
=
∫
0
Wyszukiwarka
Podobne podstrony:
24 11 id 30514 Nieznany (2)
Matematyka (24 strony)
Matematyka (24 strony)
piel cz 24 szczepienia id 3571 Nieznany
Cw 24 cw070 id 648300 Nieznany
Matematyka teoria 1 sem id 2838 Nieznany
Matematyka czerwiec 2012 id 283 Nieznany
matematyka 24 strony
matma Matematyka (24 strony)
matematyka 2007 maj id 284061 Nieznany
24 KONST id 30635 Nieznany
24 Klimat id 30634 Nieznany
Matematyka (24 strony) calki, pojecia calki
24 13 id 30516 Nieznany (2)
Kwantowa strony 2,3,7,8 id 7484 Nieznany
matematyka zbiur zadan id 2830 Nieznany
24 11 id 30514 Nieznany (2)
więcej podobnych podstron