Całkowanie numeryczne
Całkowanie numeryczne to przybliżone obliczanie
całek oznaczonych
. Proste
metody całkowania numerycznego polegają na przybliżeniu całki za pomocą
odpowiedniej sumy ważonej całkowanej funkcji w kilku punktach.
Całkowanie numeryczne zalicza się do
metod numerycznych
.
Prawdopodobnie najprostszym wzorem jest metoda punktu środkowego (
midpoint
rule
):
Jeśli funkcja
f
(
x
) zmienia się w niewielkim stopniu na przedziale całkowania, reguła
taka da dobre przybliżenie całki.
Żeby uzyskać dokładniejsze przybliżenie można podzielić przedział całkowania na
niewielkie fragmenty i w każdym z nich osobno oszacować całkę.
Przykład
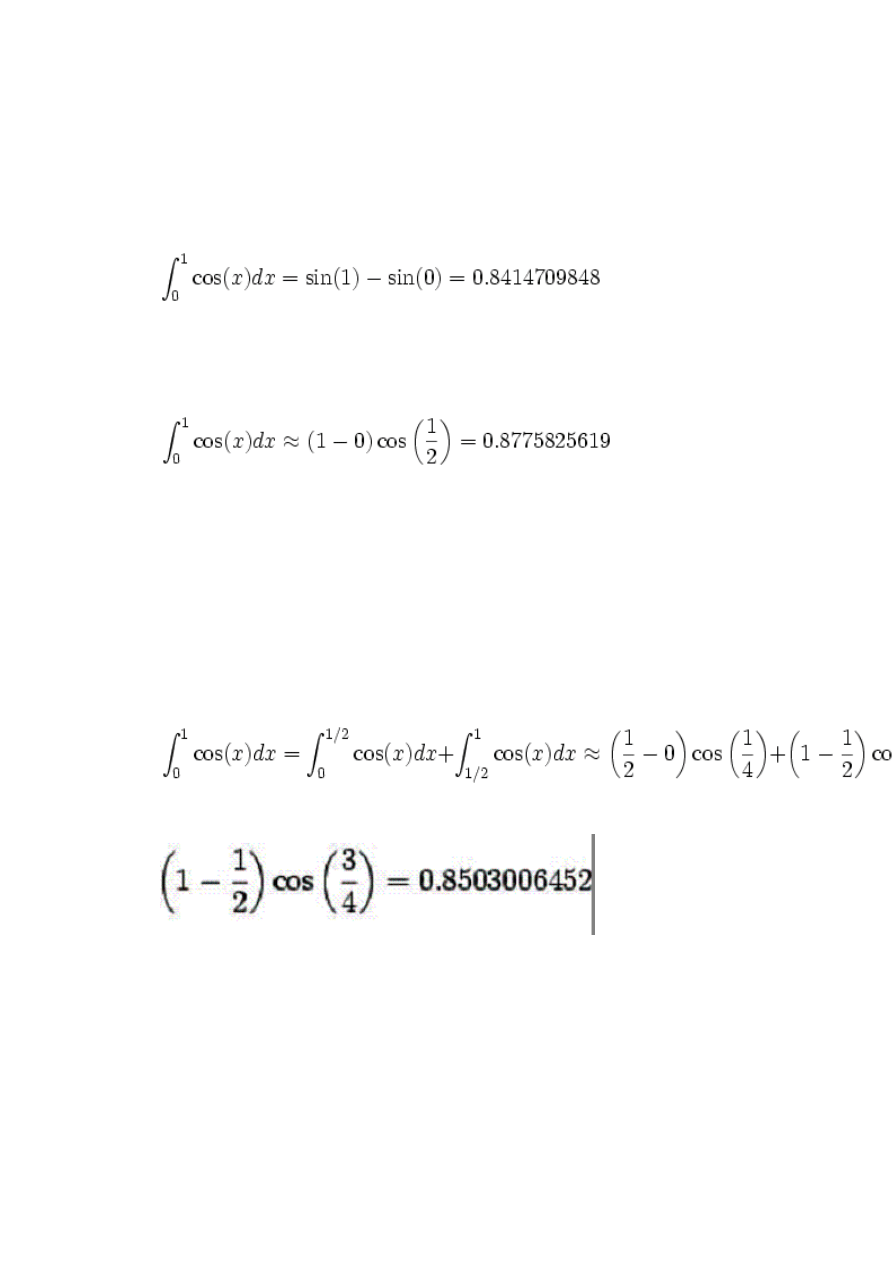
Spróbujmy scałkować funkcję cos(
x
) na przedziale od 0 do 1. Ponieważ da się ją
scałkować analitycznie, znamy dokładny wynik i możemy łatwo obliczać błąd
przybliżenia różnych metod całkowania. Z dokładnością do 10 miejsc dziesiętnych
prawidłowy wynik wynosi:
Całkowanie numeryczne za pomocą zasady punktu środkowego da nam wynik:
co daje błąd 0.0361115771 (błąd względny 4.3%) – niewielki jak na tak prostą
metodę, jednak oczywiście niezadowalający do wielu zastosowań.
Żeby uzyskać lepsze przybliżenia możemy podzielić przedział całkowania:
Z błędem bezwzględnym 0.0088296604 lub względnym 1%.
Dzieląc przedział całkowania na więcej fragmentów możemy uzyskać lepsze
przybliżenie:
Ilość części
Wynik
Błąd
1
0.8775825619
0.0361115771
2
0.8503006452
0.0088296604
4
0.8436663168
0.0021953320
8
0.8420190672
0.0005480824
Przykład 2
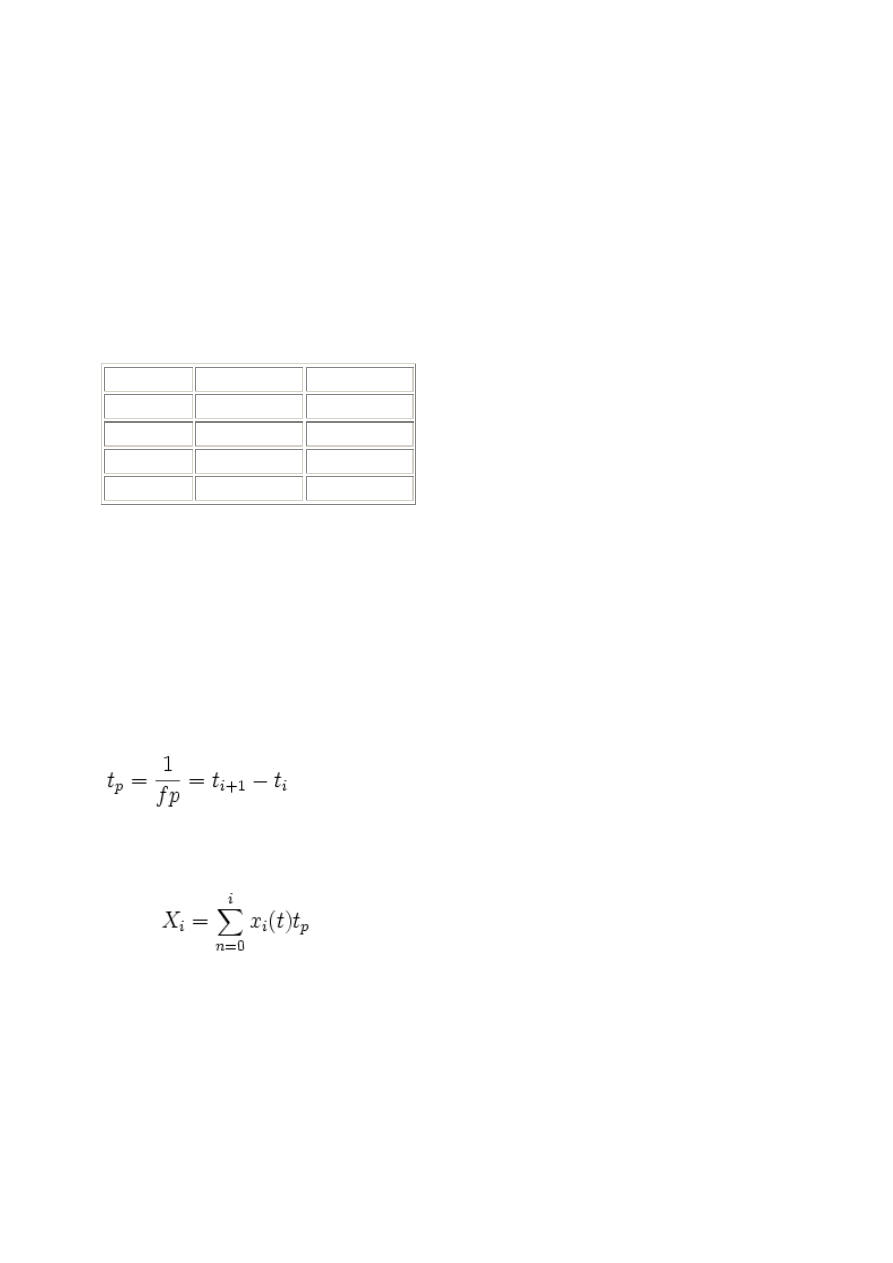
Całkowanie numeryczne przebiegów czasowych. Spróbujmy scałkować
spróbkowany przebieg sin(
t
) na przedziale od 0 do 4 * π [s]. Załóżmy, że
częstotliwość próbkowania
f
p
przebiegu wynosi
f
p
[Hz].
Do obliczeń wykorzystamy metodę prostokątów. Średnica podziału
wynosi 1. Niech
X
(
t
)
i
oznacza próbkę po całkowaniu. Każdy wyraz
X
i
można obliczyć
jako sumę częściową:
Im mniejsza średnica podziału (wyższa częstotliwość próbkowania), tym wynik
dokładniejszy. Uwaga: po scałkowaniu amplituda przebiegu wzrasta, tym bardziej, im
mniejsza średnica podziału.
Ogólnie mamy metodę:
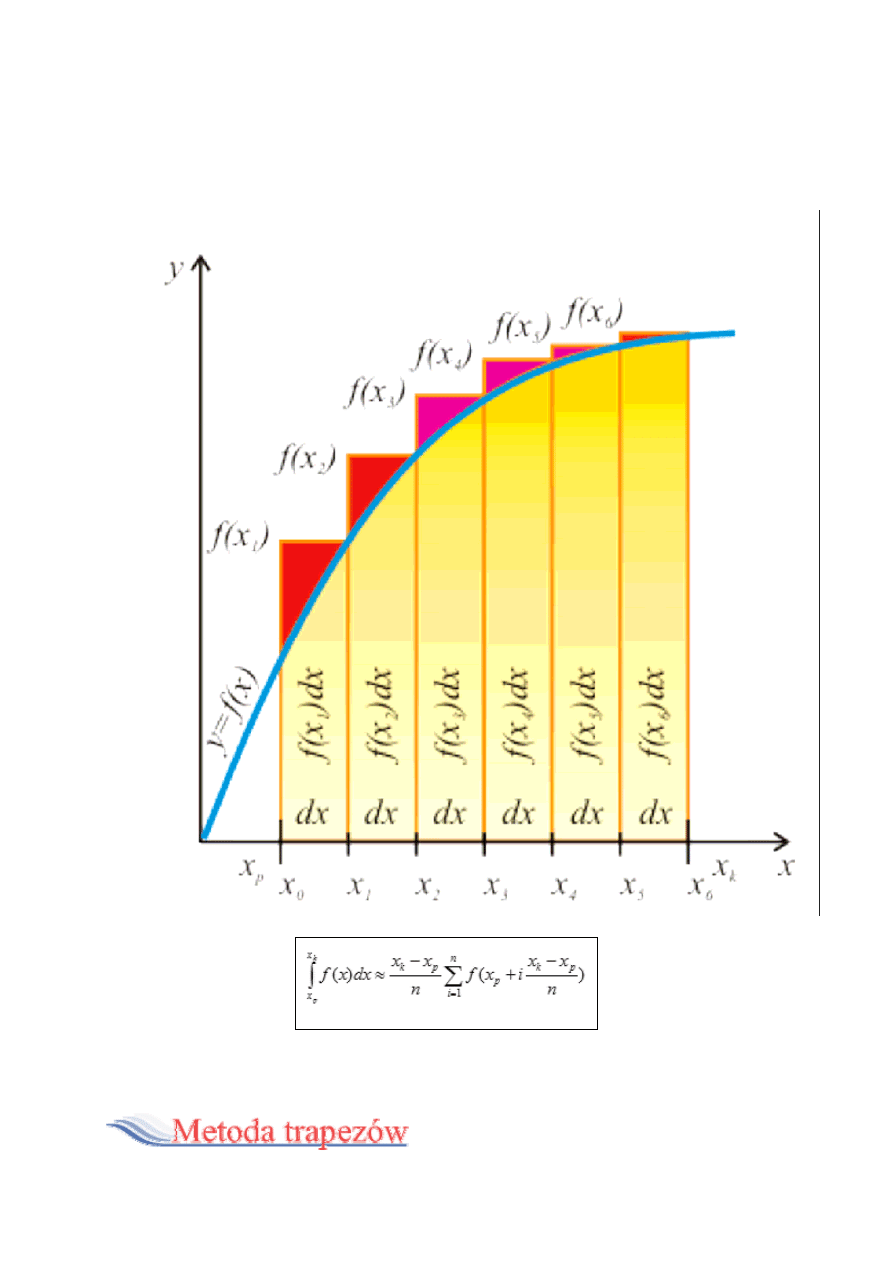
W metodzie prostokątów korzystamy z definicji całki oznaczonej
Riemanna , w której wartość całki interpretowana jest jako suma pól
obszarów pod wykresem krzywej w zadanym przedziale całkowania
<x ,x >
p k
. Sumę tę przybliżamy przy pomocy sumy pól odpowiednio
dobranych prostokątów. Sposób postępowania jest następujący:
Przedział całkowania <x ,x >
p k
dzielimy na n równo odległych punktów
x ,x ,...,x
1 2
n
. Punkty te wyznaczamy w prosty sposób wg wzoru:
dla i = 1,2,...,n
i
x = x +
i
p
n
(x - x )
k
p
Obliczamy odległość między dwoma sąsiednimi punktami - będzie to
podstawa każdego prostokąta:
x - x
k
p
dx =
n
Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość
funkcji f(x) w tym punkcie:
f = f(x )
i
i
, dla i = 1,2,...,n
Obliczamy sumę iloczynów wyznaczonych wartości funkcji przez
odległość dx między dwoma sąsiednimi punktami - da to sumę pól
poszczególnych prostokątów ograniczonych wykresem funkcji:
S = f dx + f dx + ... + f dx
1
2
n
a po wyprowadzeniu wspólnego czynnika przed nawias:
S = dx (f + f + ... + f )
1
2
n
Otrzymana suma jest przybliżoną wartością całki oznaczonej funkcji f(x)
w przedziale <x ,x
p k
>.
Obliczymy ręcznie przybliżoną wartość całki oznaczonej z funkcji f(x) =
sin(x)
w przedziale <0,π>.
Przedział podzielimy na n = 4 punkty:
Odległość między dwoma sąsiednimi punktami wynosi:
Dla każdego z wyznaczonych punktów obliczamy wartość funkcji f(x) =
sin(x):
Obliczamy sumę pól prostokątów:
S = dx (f
+ f
+ f
+ f )
1
2
3
4
S = 0,7854 (0,7071 + 1,000 + 0,7071 + 0,0000)
S = 0,7854
2,4142
S = 1,8961
Dokładna wartość takiej całki oznaczonej wynosi wg tablic:
Zatem popełniliśmy błąd równy: 2 - 1,8961 = 0,1039, co stanowi nieco
ponad 5% wartości dokładnej. W sumie nie jest to zły wynik zważywszy
na ilość wykonanych przez nas rachunków. Jeśli chcemy zwiększyć
dokładność, to musimy zsumować więcej prostokątów, ale to
zostawimy już komputerom.
Dane wejściowe
x
p
- początek przedziału całkowania, x
p
R
x
k
- koniec przedziału całkowania, x
k
R
n
- liczba punktów podziałowych, n N
f(x) - funkcja rzeczywista, której całkę liczymy
Dane wyjściowe
Wartość całki oznaczonej funkcji f(x) w przedziale <x ,x >
p k
. Wynik jest
liczbą rzeczywistą.
Zmienne pomocnicze
s -
suma wysokości prostokątów, którą później zamieniamy w wartość całki, s
R
dx - odległość między dwoma sąsiednimi punktami podziałowymi, dx R
i - licznik punktów podziałowych, i N
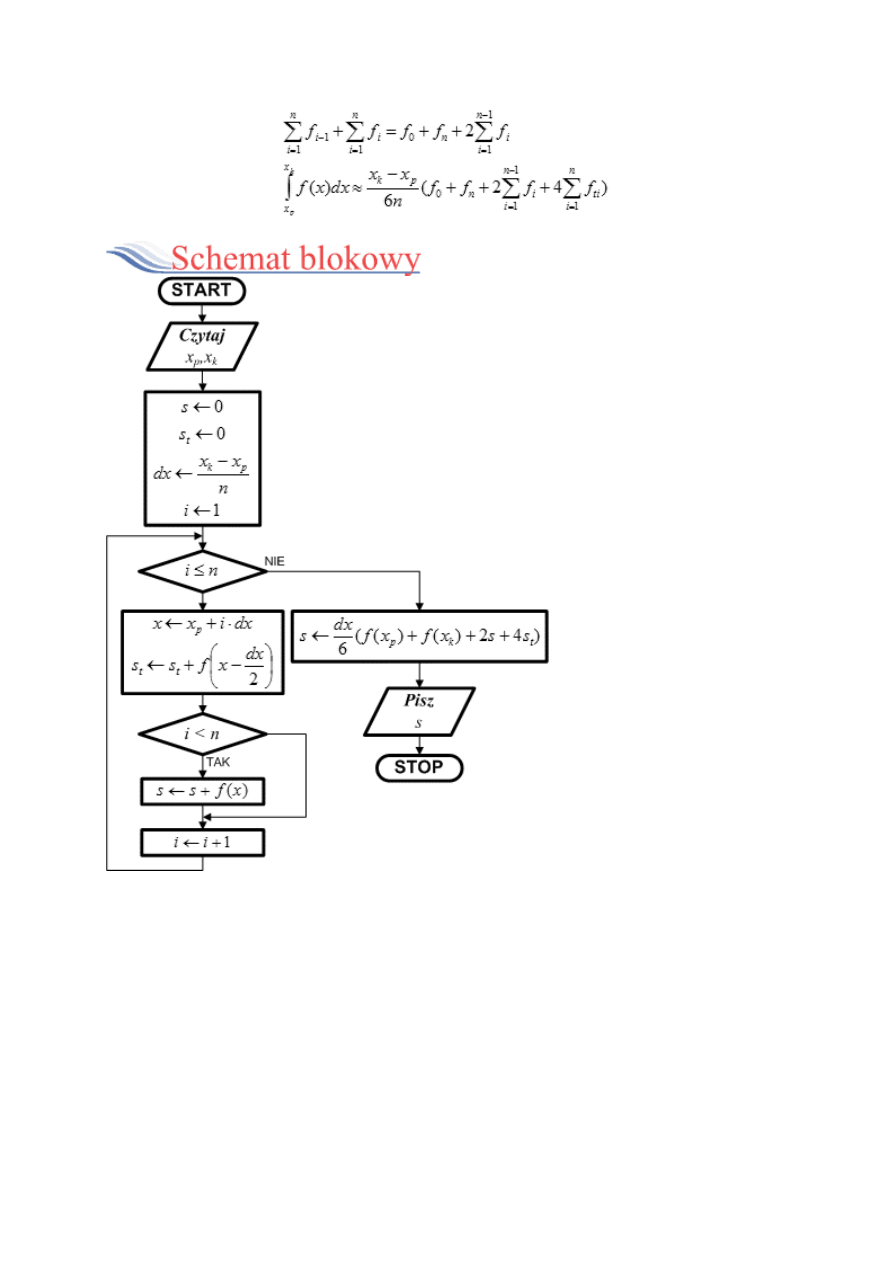
krok 1: Czytaj x x
p
k
krok 2: s
0
krok 3:
x
k
- x
p
dx
n
krok 4: Dla i = 1,2,...,n, s
s + f(x + i
p
dx)
krok 5: s
s dx
krok 6: Pisz s i zakończ algorytm
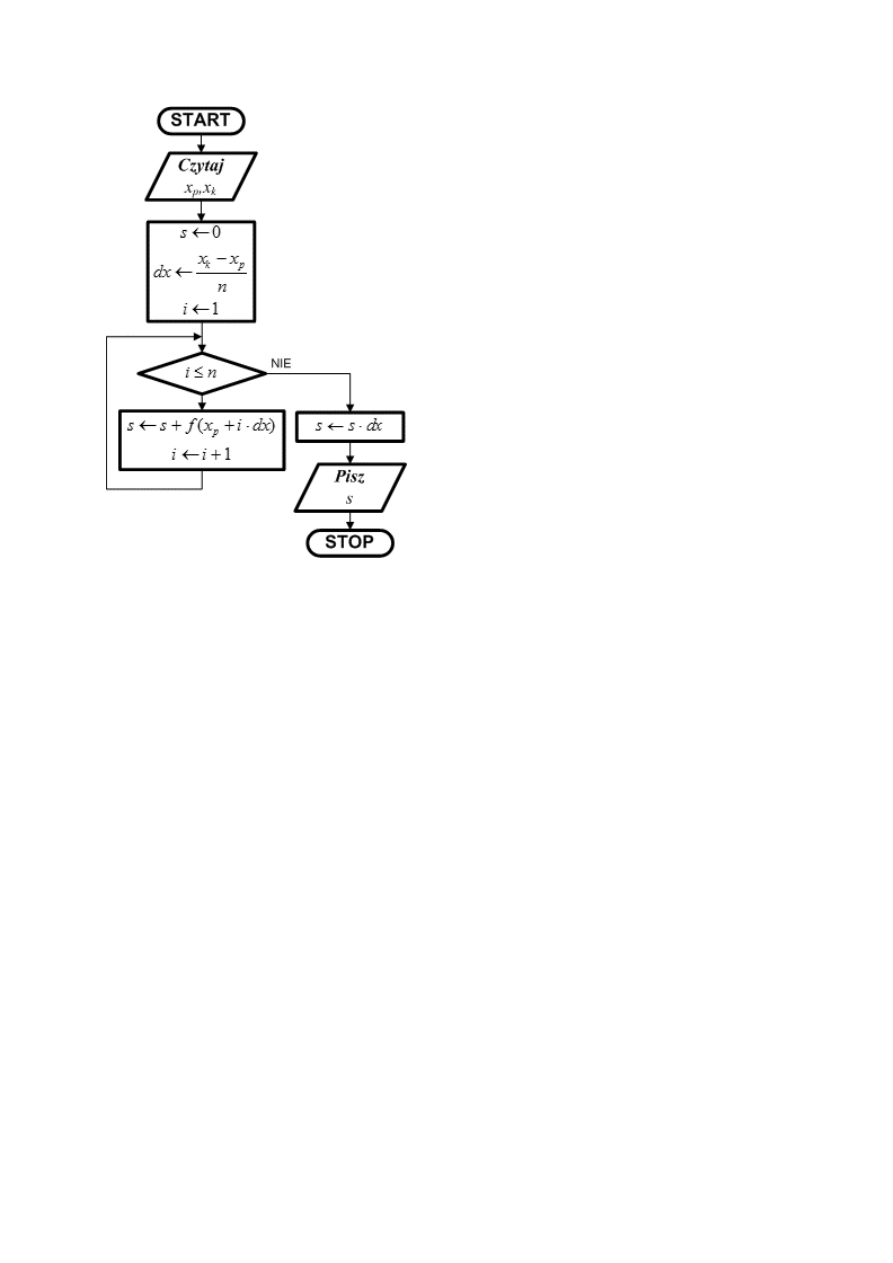
Po odczytaniu informacji o krańcach x
p
i x
k
przedziału całkowania
ustawiamy sumę s na 0, obliczamy odległość dx pomiędzy sąsiednimi
punktami podziałowymi i ustawiamy ich licznik na 1.
Rozpoczynamy pętlę iteracyjną, która wykona się n-razy. Wewnątrz
pętli obliczamy i-ty punkt podziałowy oraz wartość funkcji w tym
punkcie, którą dodajemy do sumy s.
Po zakończeniu pętli sumę s musimy jeszcze pomnożyć przez
szerokość podstawy prostokątów, czyli odległość dx Po tej operacji s
zawiera wartość przybliżoną całki. Zwracamy ją użytkownikowi i
kończymy algorytm.
Prezentowane poniżej programy wyliczają całkę oznaczoną funkcji f(x)
= x + 2x
2
. Przedział całkowania jest dzielony na n=1000 punktów. W
przedziale <0,1> całka oznaczona ma wartość dokładną równą
4
/ =
1.3333...
3
_Podsumowanie:
Całka przybliżana jest sumą pól prostokątów:
Metoda ta obarczona jest dosyć dużym błędem, ponieważ prostokąty
niezbyt dobrze przybliżają pole pod wykresem funkcji. Błąd maleje wraz
ze wzrostem n. Zaletą jest prosty wzór wyliczania całki.
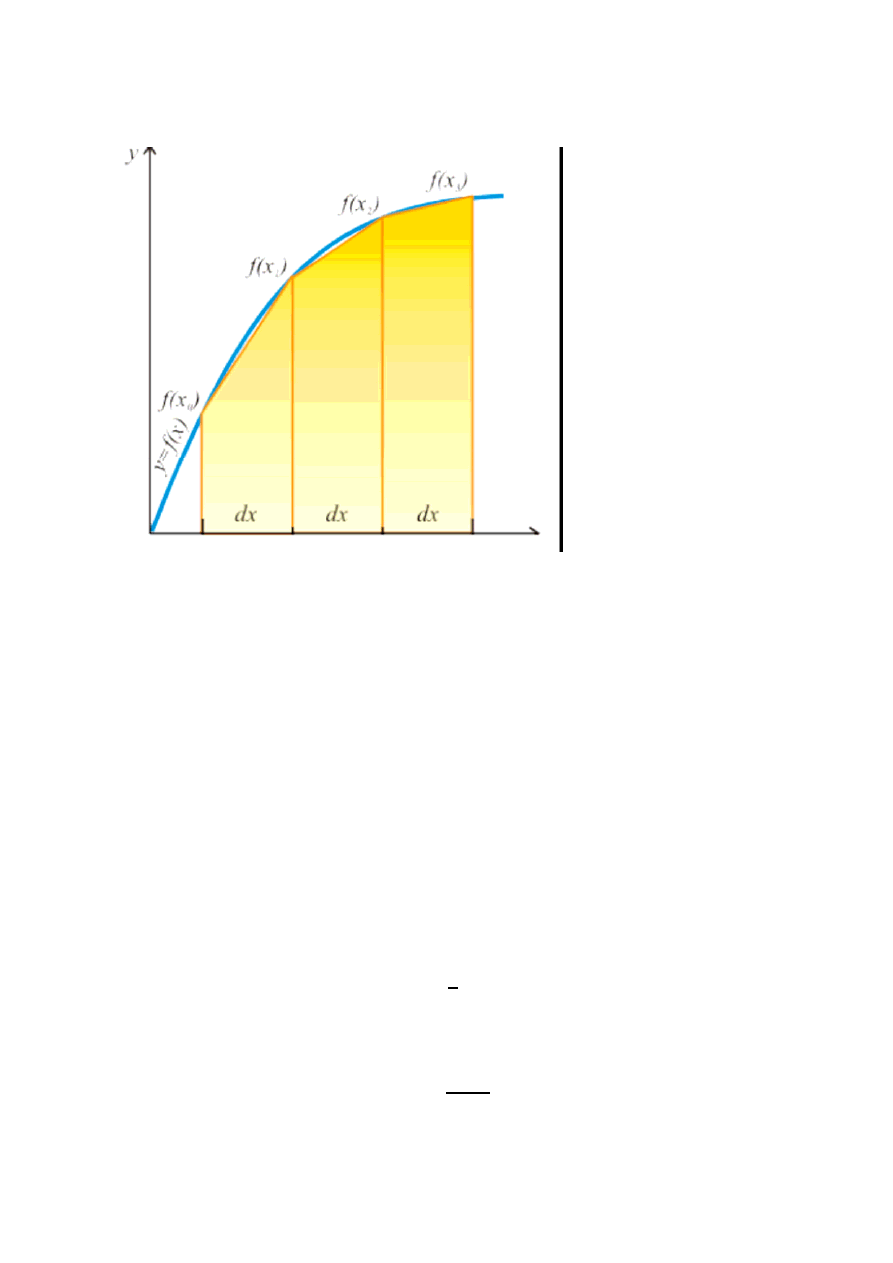
Opisana w poprzednim rozdziale metoda prostokątów nie jest zbyt
dokładna, ponieważ pola użytych w niej prostokątów źle odwzorowują
pole pod krzywą. Dużo lepszym rozwiązaniem jest zastosowanie
zamiast nich trapezów o podstawie dx i bokach równych odpowiednio
wartości funkcji w punktach krańcowych.. Sama zasada nie zmienia się.
Przedział całkowania <x ,x >
p k
dzielimy na n+1 równo odległych punktów
x ,x ,x ,...,x
0 1 2
n
. Punkty te wyznaczamy w prosty sposób wg wzoru:
dla i = 0,1,2,...,n
i
x = x +
i
p
n
(x - x )
k
p
Obliczamy odległość między dwoma sąsiednimi punktami - będzie to
podstawa każdego trapezu:
x - x
k
p
dx =
n
Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość
funkcji f(x) w tym punkcie:
dla i = 0,1,2,...,n
f = f(x )
i
i
Pole pod wykresem funkcji przybliżane jest polami n trapezów. Pole i-
tego trapezu obliczamy wg wzoru:
dla i=1,2,...,n
f
i-1
+ f
i
P
i
=
2
dx
Przybliżona wartość całki jest sumą pól wszystkich otrzymanych w ten
sposób trapezów:
s = P + P + ... + P
1
2
n
czyli
Wyprowadzony na końcu wzór jest podstawą przybliżonego wyliczania
całki w metodzie trapezów.
pola
kolejnych trapezów wynoszą:
gdzie dla jednolitości oznaczono
a
=
x
0
i
b
=
x
n
.
Suma pól trapezów jest w przybliżeniu równa polu całego obszaru, czyli:
.
Ten właśnie wzór nazywany jest wzorem trapezów.
W przypadku
funkcji ciągłej
na
przedziale
[
a
,
b
], wzór trapezów pozwala obliczać jej
całkę oznaczoną na tym przedziale z dowolną dokładnością, wystarczy w tym celu
wziąć za
n
odpowiednio dużą liczbę. Błąd przybliżenia daje się oszacować w
przypadku funkcji, która ma na przedziale [
a
,
b
] ciągłą
drugą pochodną
:
gdzie
K
oznacza największą wartość funkcji |
f
′′(
x
)| w przedziale [
a
,
b
].
Obecnie wzór trapezów ma znaczenie wyłącznie historyczne – dostępne programy
do całkowania numerycznego stosują o wiele dokładniejsze metody i pozwalają
uniknąć czasochłonnych rachunków.
Przykład:
Obliczymy ręcznie przybliżoną wartość całki oznaczonej z funkcji f(x) =
sin(x)
w przedziale <0,π>.
Przedział podzielimy na n+1 = 5 punktów:
Odległość między dwoma sąsiednimi punktami wynosi:
Dla każdego z wyznaczonych punktów obliczamy wartość funkcji f(x) =
sin(x):
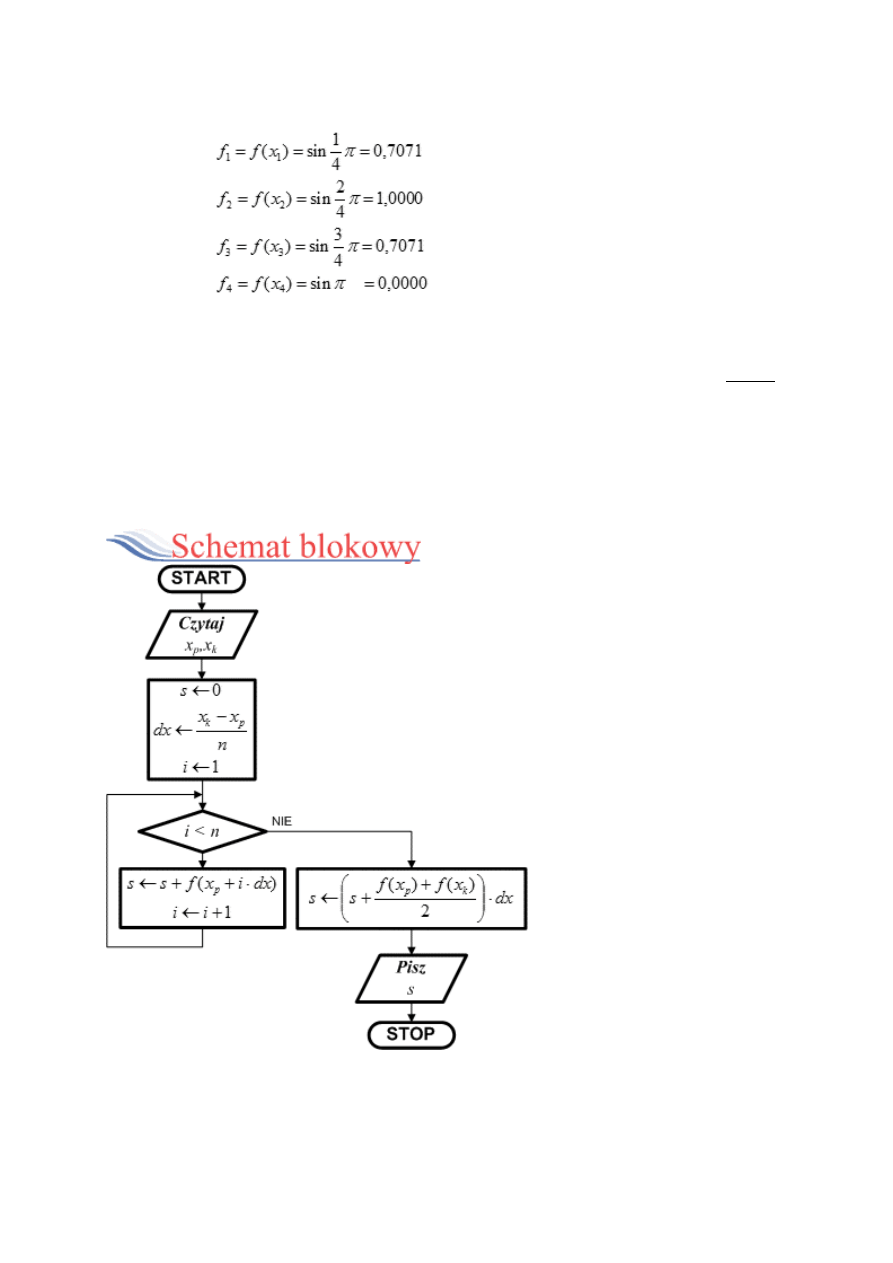
f = f
o
(x )
= sin 0
= 0,0000
o
Obliczamy sumę pól trapezów:
f + f
o
4
s = dx( f + f + f +
1
2
3
2
)
s = 0,7854(0.7071+1+0.7071) = 1,8961
Otrzymaliśmy wynik identyczny jak w przypadku metody prostokątów -
dlaczego?
Całka przybliżana jest sumą pól trapezów:
Trapezy dużo lepiej przybliżają pole pod wykresem funkcji. Dlatego
metoda ta jest dokładniejsza od metody prostokątów. W praktyce
oznacza to mniejszą wartość n, czyli mniej obliczeń w celu uzyskania
porównywalnej dokładności wyniku.
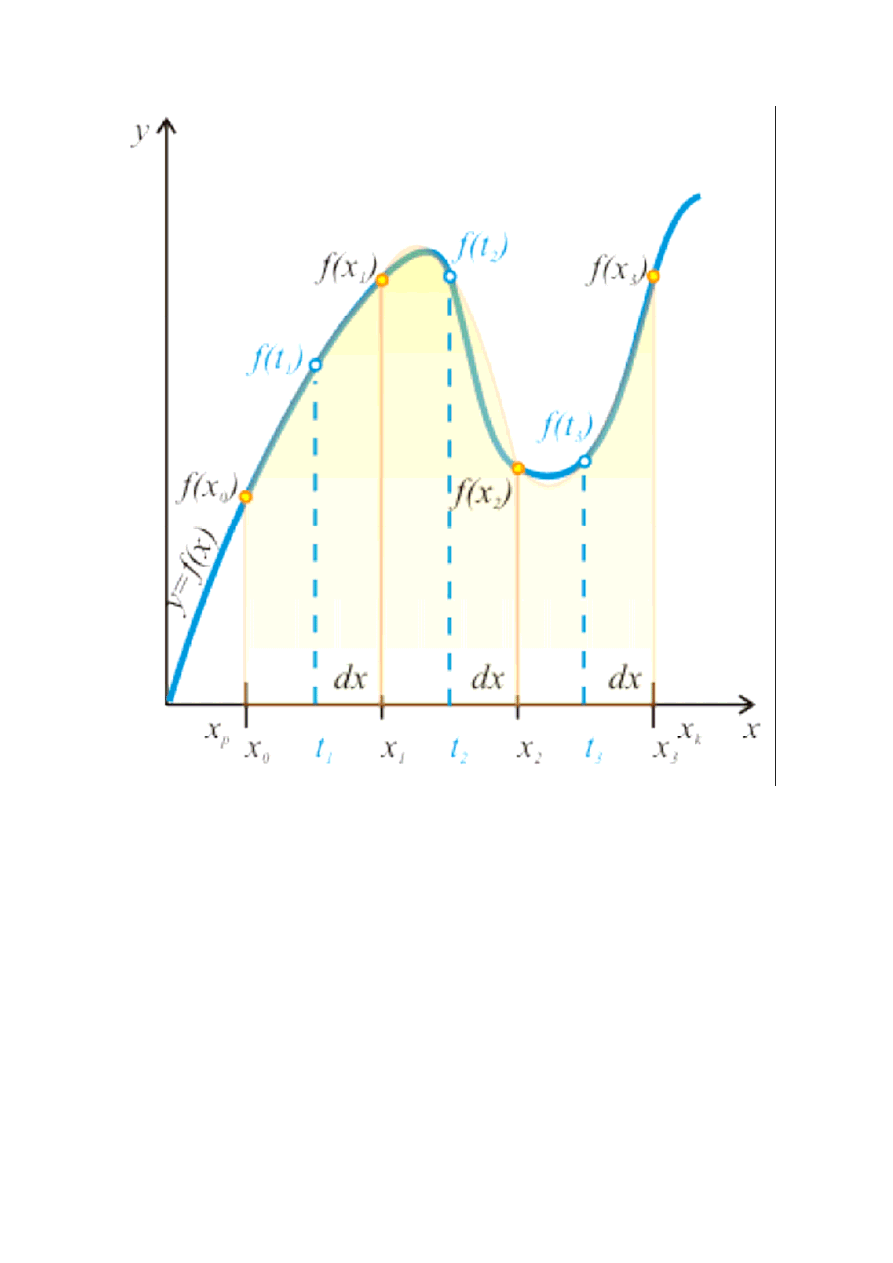
Metoda Simpsona jest szczególnym przypadkiem
metody Newtona-Cotesa
, która
polega na interpolacji funkcji (zadanej tabelką lub spróbkowanej) za pomocą funkcji
kwadratowej (stąd
metoda parabol
).
Metoda Simpsona dla trzech punktów
Żeby zastosować metodę Simpsona potrzebujemy przynajmniej trzech punktów.
Niech dane będą wartości funkcji f(x) w trzech punktach
a
=
x
,
x
,
b
=
x
0 1
2
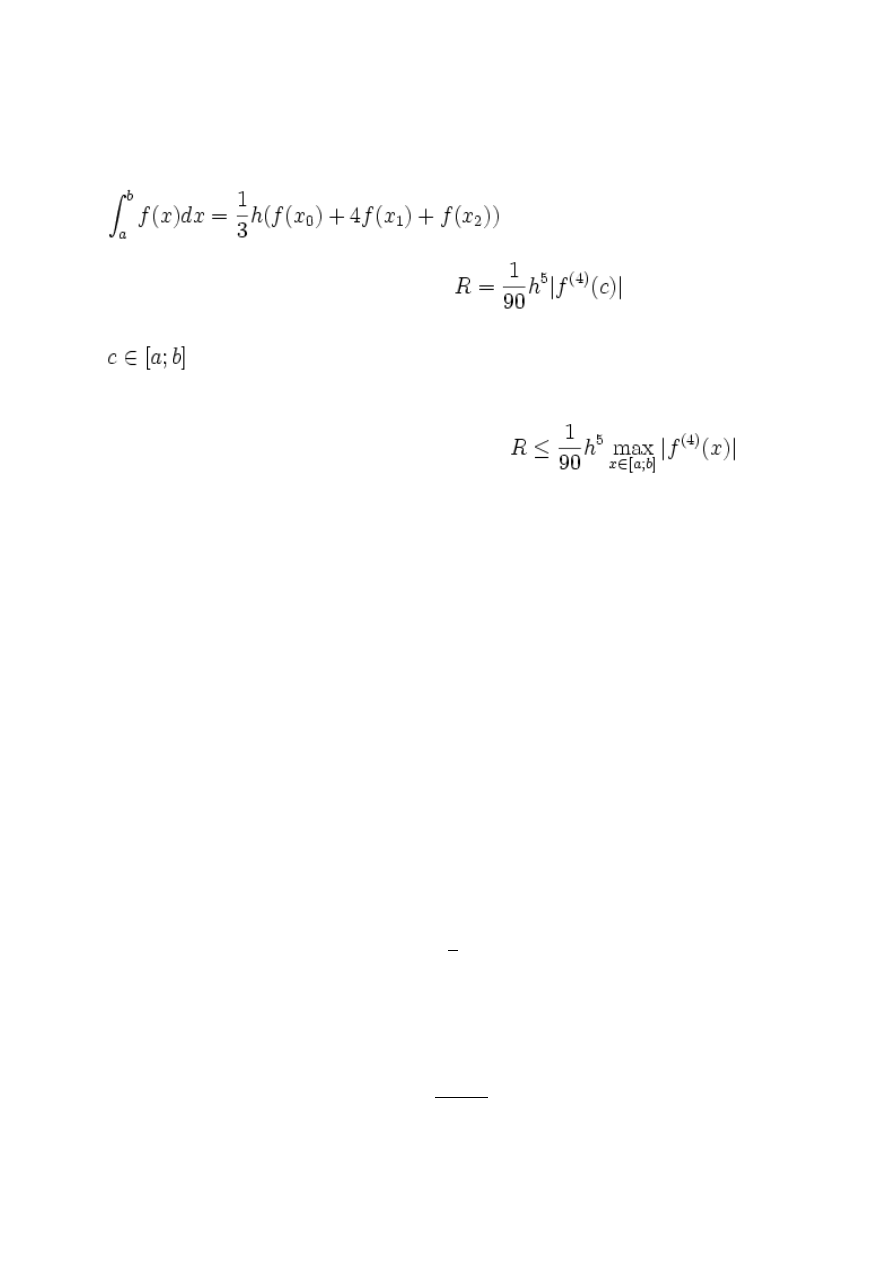
Niech odległość punktu
x
1
od pozostałych wynosi h.
Całkę
możemy
(z
pewną
dokładnościa
wyrazić
wzorem)
Błąd który przy tym popełniamy jest równy:
gdzie:
Oczywiście nie znamy położenia punktu c więc zamiast błędu R używamy
oszacowania błędu spełniającego nierówność:
Lewa
strona nierówności służy do szacowania błędu w obliczeniach numerycznych
Metoda Simpsona jest najdokładniejszą z dotąd poznanych przez nas
metod przybliżonego całkowania. W metodzie prostokątów całka
oznaczona przybliżana była funkcjami stałymi - liczyliśmy sumę pól
prostokątów. W metodzie trapezów całkę przybliżaliśmy za pomocą
funkcji liniowych - obliczaliśmy sumy pól trapezów. W metodzie
Simpsona stosujemy jako przybliżenie parabolę - będziemy obliczali
sumy wycinków obszarów pod parabolą. Zasada jest następująca:
Przedział całkowania <x ,x >
p k
dzielimy na n + 1 równo odległych
punktów x , x , x ,..., x
o
1
2
n
:
dla i = 0,1,2,...,n
i
x = x +
i
p
n
(x - x )
k
p
Dla każdych dwóch sąsiednich punktów wyznaczamy punkt środkowy t
i
wg wzoru:
dla i = 1,2,...,n
x + x
i-1
i
t =
i
2
Obliczamy odległość między dwoma sąsiednimi punktami.
x - x
k
p
dx =
n
Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość
funkcji f(x) w tym punkcie:
punkty podziałowe punkty środkowe
dla i = 0,1,2,...,n
f = f(x )
i
i
dla i = 1,2,...,n
f = f(t )
ti
i
W każdym podprzedziale <x ,x >
i-1 i
przybliżamy funkcję za pomocą
paraboli g(x) o następującej postaci:
dla i = 1,2,...,n
g (x) = a x + b x + c , x
i
i
2
i
i
<x , x >
i-1
i
Parabola g (x)
i
musi przechodzić przez punkty: (x ,f ), (t ,f ), (x ,f )
i-1 i-1
i ti
i i
.
Współczynniki a , b i c
i
i
i
wyznaczymy zatem z układu trzech równań:
dla i = 1,2,...,n
Pole pod parabolą w przedziale <x ,x >
i-1 i
będzie równe całce
oznaczonej:
dla i = 1,2,...,n
Funkcja pierwotna jest bardzo prosta w tym przypadku i ma wzór
następujący:
dla i = 1,2,...,n
Wartość całki obliczymy zgodnie z definicją
Newtona-Leibniza
:
dla i = 1,2,...,n
Teraz postaramy się uprościć maksymalnie otrzymane wyrażenie. W
tym celu wyciągamy przed nawias wspólny czynnik i całość dzielimy
przez 6:
dla i = 1,2,...,n
Zwróćcie uwagę, iż wyrażenia w nawiasach są odpowiednio
wartościami funkcji f
i-1
, f
i
oraz f
ti
. Natomiast różnica
x - x
i
i-1
jest odległością dx pomiędzy dwoma sąsiednimi punktami
podziałowymi. Zatem po uproszczeniu otrzymujemy ostateczny wzór:
dla i = 1,2,...,n
Wzór ten pozwala wyliczyć pole obszaru pod parabolą aproksymującą
funkcję f(x) w przedziale <x ,x >.
i-1 i
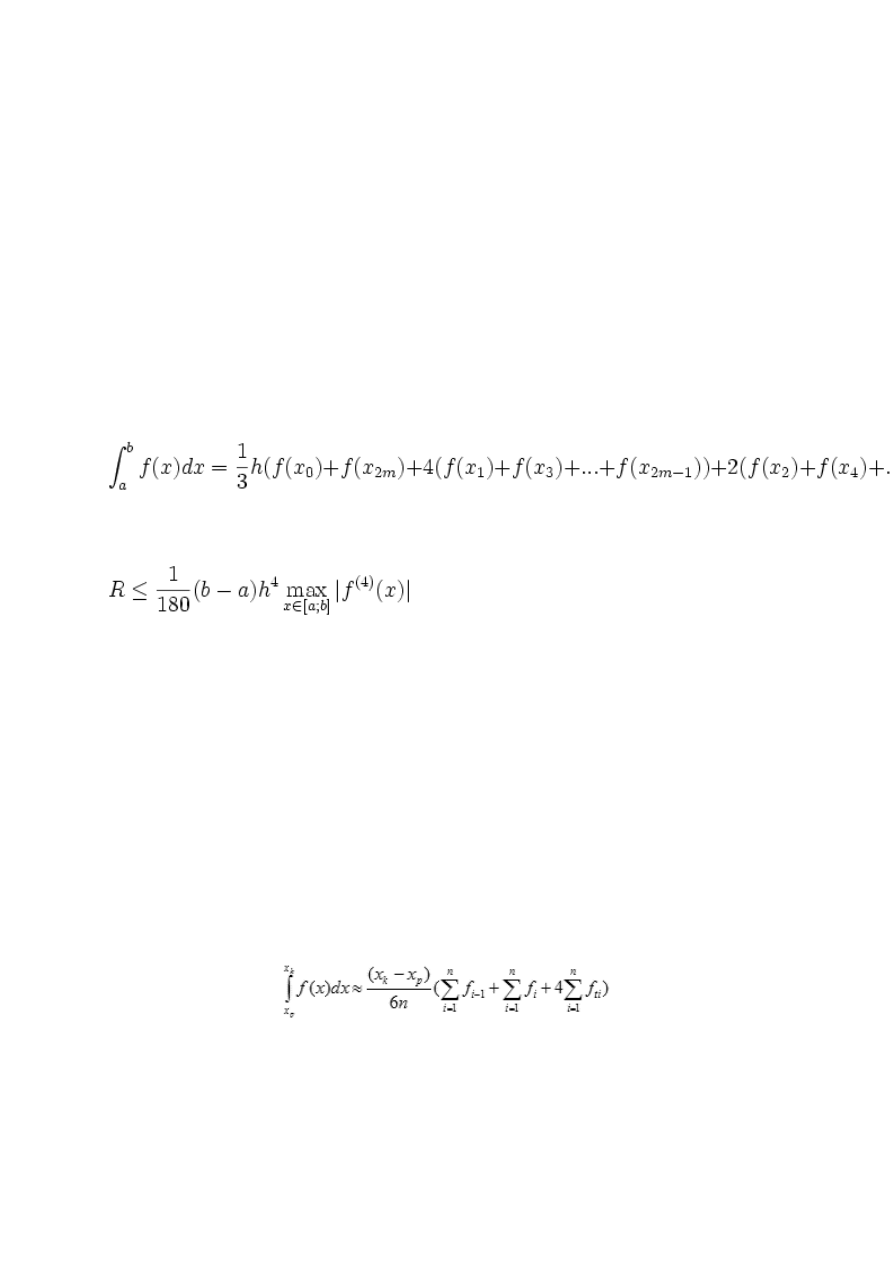
Uogólniony wzór Simpsona Wzór Simpsona dla trzech punktów (dyskutowany
powyżej) daje słabe przybliżenie całki oznaczonej. Dlatego zwykle stosuje się podział
przedziału [a;b], w którym liczymy całkę na większą ilość podprzedziałów.
Załóżmy, że dysponjemy nieparzystą ilością punktów rozmieszczonych równomiernie
o kroku dyskretyzacji h :
a
=
x
,
x
,
x
,...,
x
=
b
0 1 2
2
m
Stosując wzór Simpsona dla trzech punktów do każdego z rozłącznych przedziałów
[
x
;
x
]
i
− 1
i
+ 1
otrzymujemy uogólniony wzór Simpsona:
Błąd szacujemy z następującej nierówności:
x
i
, dla
i
= 0, ...,
n
. (Dla punktów oddalonych od siebie o inne odległości ma
zastowanie inna klasa wzorów, kwadratura Gaussowska.)
Inaczej mówiąc
Wartość całej całki otrzymamy sumując te pola, czyli:
Jest to wzór wyliczania przybliżonej wartości całki oznaczonej za
pomocą metody Simpsona. Ponieważ w obliczanych sumach wartości
funkcji się powtarzają dwukrotnie
(z wyjątkiem pierwszej i ostatniej)
, do
obliczeń komputerowych stosujemy efektywniejszy wzór otrzymywania
powyższej sumy:
Całka przybliżana jest sumą pól ograniczonych parabolami:
Parabole przybliżają wykres funkcji z małym błędem. Stąd metoda
paraboliczna jest najdokładniejszą metodą wyznaczania wartości całek
oznaczonych z tutaj opisanych. W praktyce n może być małe (np. w
granicach 100...1000). Dokładność okupiona jest nieco
skomplikowanym wzorem obliczeniowym.
Aby zrozumieć zasadę
metody Monte Carlo
wyobraźcie sobie, iż
chcecie wyznaczyć pole koła wpisanego w kwadrat o boku równym 2
(pole to co do wartości jest równe liczbie pi, ale na razie udajmy, że o
tym nie wiemy).
W tym celu wyznaczamy wewnątrz kwadratu dużo
losowych punktów. Następnie zliczamy te punkty, które wpadają do
wnętrza koła. Pole koła jest w przybliżeniu równe:
P
koło
- pole koła
P
kwadrat
- pole kwadratu
n
koło
- liczba punktów w kole
n
koło
P
koło
=
n
P
kwadrat
n
- liczba wszystkich punktów
Oczywiście wynik jest bliski liczbie π = 3,1415926535... dopiero dla
dużych wartości n. Zaczynają wtedy obowiązywać prawa
dużych liczb
i pomimo przypadkowości wyboru punktów, pojawia się prawidłowość.
Ponieważ punkty rozkładają się równomiernie w obrębie pola kwadratu,
to stosunek liczby punktów wewnątrz koła do liczby wszystkich punktów
w kwadracie jest równy stosunkowi pola koła do pola kwadratu. Stąd
właśnie pochodzi nasz wzór:
n
koło
P
=
koło
n
P
kwadrat
Wzór ten jest podstawą wyznaczania wartości całki oznaczonej za
pomocą metody Monte Carlo, czyli losowania punktów. Zasada jest
następująca:
Dla danej funkcji f(x), której całkę oznaczoną chcemy obliczyć w
przedziale całkowania <x ,x >
p k
, wyznaczamy prostokąt obejmujący pole
pod wykresem tej funkcji o wysokości h i długości podstawy (x - x
k
p
). W
dalszej kolejności losujemy n punktów i zliczamy te punkty n
w
, które
wpadają w pole pod wykresem funkcji. Wartość całki wyraża się
wzorem przybliżonym:
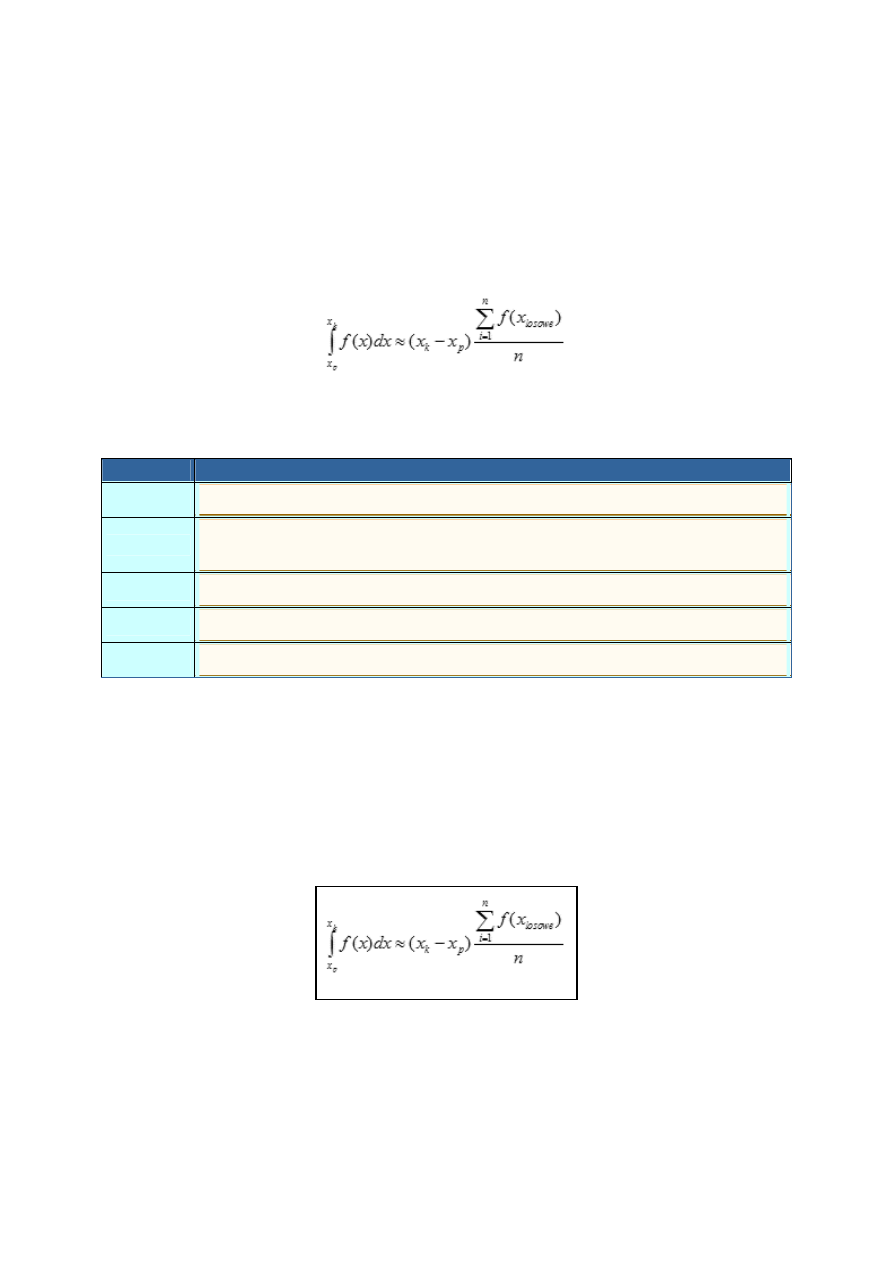
Otrzymany wzór ma kilka wad. Na przykład w ogólnym przypadku
trudno wyznaczyć wysokość h. Również kłopoty pojawiają się, gdy
funkcja zmienia znak w przedziale całkowania. Dlatego częściej jako
metodę Monte Carlo przyjmuje się metodę, która wyznacza średnią z
wartości funkcji w przedziale całkowania na podstawie serii losowo
wybranych współrzędnych x. Następnie średnia ta jest mnożona przez
długość przedziału całkowania i otrzymujemy przybliżoną wartość całki
oznaczonej. Wzór ma następującą postać:
x
losowe
jest wartością pseudolosową zmiennoprzecinkową z przedziału
<x , x
p
k
> Wartość tę otrzymujemy wg wzorów:
Język
Instrukcja
Pascal
xlosowe
:=
xp
+ random * (
xk
-
xp
);
C++
xlosowe
=
xp
+ (
double
)rand()/(
double
)(RAND_MAX+
1
) *
(
xk
-
xp
);
Basic
xlosowe
=
xp
+
rnd
* (
xk
-
xp
)
Python
xlosowe
=
xp
+
random
.
uniform
(
0
,
dx
)
JavaScript
xlosowe
=
xp
+
Math
.random() * (
xk
-
xp
)
Całka przybliżana jest średnią wartością funkcji w przedziale
pomnożoną przez szerokość przedziału. Średnia wyznaczana jest w
sposób pseudolosowy jako suma n wartości funkcji w przypadkowo
wybranych punktach przedziału całkowania.
Jest to najmniej dokładna z opisanych metod. Jej jakość porównywalna
jest z metodą prostokątów. Zaletą natomiast będzie prosty wzór
obliczeniowy.
Kwadratury Gaussa
Definiuje się dwa typy wzorów Newtona-Cotesa:
- zamknięte, które nie wykorzystują wartości funkcji w
skrajnych punktach, oraz
- otwarte, wykorzystujące wszystkie wartości funkcji.
Zamknięty wzór Newtona-Cotesa rzędu
n
:
gdzie
x
i
=
h
i
+
x
0
, z
h
(nazywanym rozmiarem kroku) równym (
x
n
-
x
0
)/
n
oraz
w
i
są wagami.
Wagi można wyporwadzić z wielomianów bazowych Lagrange'a. To
oznacza, że zależą tylko od
x
i
a nie od funkcji
f
.
L
(
x
)
wielomianem interpolacji w postaci Lagrange'a dla punktów (
x
0
,
f
(
x
0
) ),..,(
x
n
,
f
(
x
n
) )
Zamknięty wzór Newtona-Cotesa rzędu
n
:
wagi znajdujemy w sposób analogiczny do powyższego.
Możemy skonstruować wzór Newtona-Cotesa dowolnego rzędu. Niektóre wzory
niskich rzędów mają swoje tradycyjne nazwy. W poniższej tabeli znajdują się wzory
Newtona-Cotesa typu zamkniętego. Notacja
f
i
oznacza
f
(
x
)
i
.
Rząd
Tradycyjna
nazwa
Wzór
Błąd
1
wzór trapezów
2
wzór Simpsona
3
reguła 3/8
4
wzór Boole'a
Wykładnik o kroku
h
w wyrazie błędu pokazuje szybkość zmniejszania się błędu
przybliżenia. Pochodna
f
w wyrazie błędu pokazuje który wielomian może być
scałkowany dokładnie
(tzn. z błędem równym 0). Zauważ, że pochodna
f
w wyrazie błędu wzrasta o 2 dla
każdego innego wzoru. Liczba ξ zwiera się pomiędzy
a
i
b
.
W poniższej tabeli znajdują się wzory Newtona-Cotesa typu zamkniętego.
Rząd
Tradycyjna nazwa
Wzór
Błąd
0
wzór prostokątów
1
2
3
Zwróć uwagę, że aby wzór dawał dobre przybliżenie, krok
h
musi być mały, co
oznacza,
że przedział całkowania [
a
,
b
] również musi być mały, co zazwyczaj nie jest
spełnione. Z tego powodu dzielimy przedział na mniejsze podprzedziały i stosujemy
metodę
Newtona-Cotesa na każdym z tych podprzedziałów a następnie dodając wyniki. Jest
to
metoda złożona
.
Document Outline