1

Egzamin maturalny z matematyki

poziom rozszerzony

Czas pracy: 180 minut

Zadanie 1. (4 pkt)

Rozwiąż równanie

3

1

18

x

x

x

    

.

Zadanie 2. (5 pkt)

Wyznacz wszystkie wartości parametru

m

, dla których równanie

2

1 0

x

mx m



  

ma dwa różne pierwiastki rzeczywiste

1

2

,

x x

spełniające warunek

1

2

1

2

2

x

x

x x







.

Zadanie 3. (4 pkt)

Wykaż, że jeżeli

4

x y

 

, to

3

3

16

x

y





.

Zadanie 4. (4 pkt)

Ciąg





, , 4

a b

jest arytmetyczny, a ciąg





4, ,

a b

jest geometryczny. Oblicz

a

oraz

b

.

Zadanie 5. (4 pkt)

Wykaż, że jeżeli

2

2

x

k





 

, gdzie

k

jest liczbą całkowitą, to

cos

tg

4

2

1 sin

x

x

x





















.

Zadanie 6. (4 pkt)
Prosta przechodząca przez środek jednego z boków trójkąta równobocznego i tworząca
z tym bokiem kąt ostry



dzieli ten trójkąt na czworokąt i trójkąt. Stosunek pola

czworokąta do pola trójkąta jest równy

5 : 3

. Oblicz tangens kąta



.

Zadanie 7. (6 pkt)
W trapezie równoramiennym podstawy mają długości 9 i 12, a kąt miedzy ramieniem

trapezu i dłuższą podstawą ma miarę

60



. Oblicz promień okręgu opisanego na tym

trapezie.

Zadanie 8. (5 pkt)

Bok kwadratu opisanego na okręgu o równaniu

2

2

5

x

y





zawiera się w prostej

o równaniu

2

5

0

x

y



 

. Oblicz współrzędne wierzchołków tego kwadratu.

2

Zadanie 9. (4 pkt)

W prostopadłościanie długości krawędzi o wspólnym wierzchołku są równe

a

,

b

,

c

,

długość przekątnej prostopadłościanu jest równa

d

. Wykaż, że

3

a b c d

  

.

Zadanie 10. (5 pkt)

Podstawą ostrosłupa jest trójkąt prostokątny

ABC

, w którym

AB

a



,

90

ACB

 



,

CAB







. Wszystkie krawędzie boczne ostrosłupa są nachylone do płaszczyzny

podstawy pod kątem o mierze



. Wyznacz objętość tego ostrosłupa.

Zadanie 11. (5 pkt)
Oblicz prawdopodobieństwo, że w pięciu rzutach symetryczną sześcienną kostką do gry
suma uzyskanych liczb oczek będzie równa 8.

Odpowiedzi

Zadanie 1.

Zapisujemy równanie w przedziałach:









; 3 ,

3;1 , 1;

.

 





1.





; 3

x

  

3

1

18

x

x

x

     

20

3

x

 

2.



3;1

x

 

3

1

18

x

x

x

    



14

3;1

x

 

 

, brak rozwiązań

3.



1;

x

 

3

1

18

x

x

x

    

16

x



Odpowiedź:

20

3

x

 

lub

16

x



.

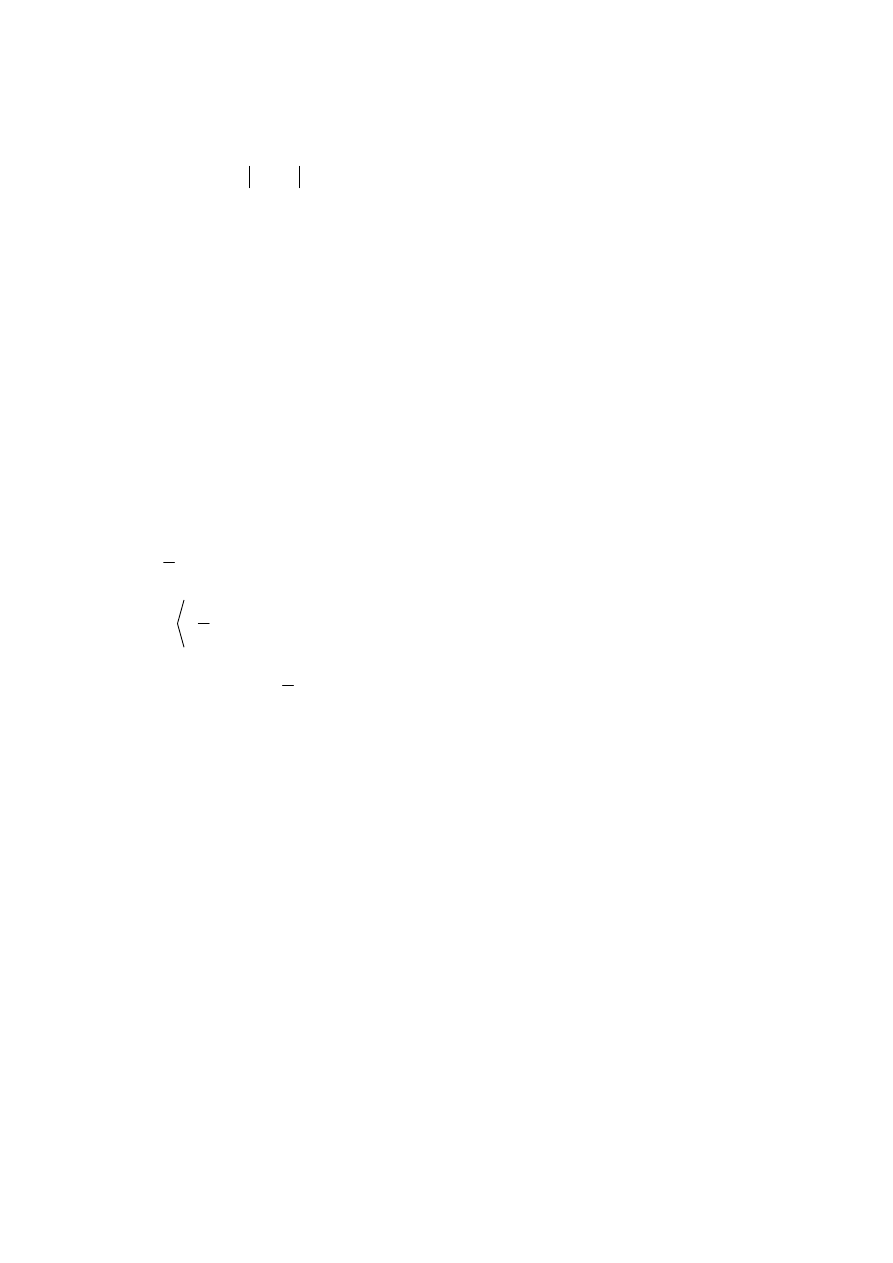
3

Zadanie 2.

Warunki zadania

1

2

1

2

0

2

x

x

x x

 



   



są równoważne alternatywie warunków

1.

1

2

0

0

x x

 



  



lub

2.









1

2

2

2

1

2

1

2

0

0

4

x x

x

x

x x

 



 

















2

2

m

 



,

0

2

m

  



1

2

1

x x

m



 

1

2

0

1

x x

m

 





1

2

0

1

x x

m

 









2

1

2

x

x



 

Ad. 1.

1

m



Ad. 2.













2

2

2

4

1

0

3

4

0

m

m

m m









 





4

0;

3

m 











,

stąd

4

1;

3

m









.

Odpowiedź:

4

;

3

m 



 









.

Zadanie 3.







 



3

3

2

2

2

2

4

x

y

x y x

xy y

x

xy y

















Z warunków zadania wyznaczamy

4

y

x

 

i określamy funkcję

f

:

 



 







2

2

2

4

4

4

12

48

64

f x

x

x

x

x

x

x







 







Funkcja

f

jest funkcją kwadratową i przyjmuje najmniejszą wartość dla

2

x



.

Odpowiedź:

 

2

16

f



.

Zadanie 4.
Zapisujemy układ równań zgodnie z warunkami zadania:

2

2

4

4

b a
a

b

 









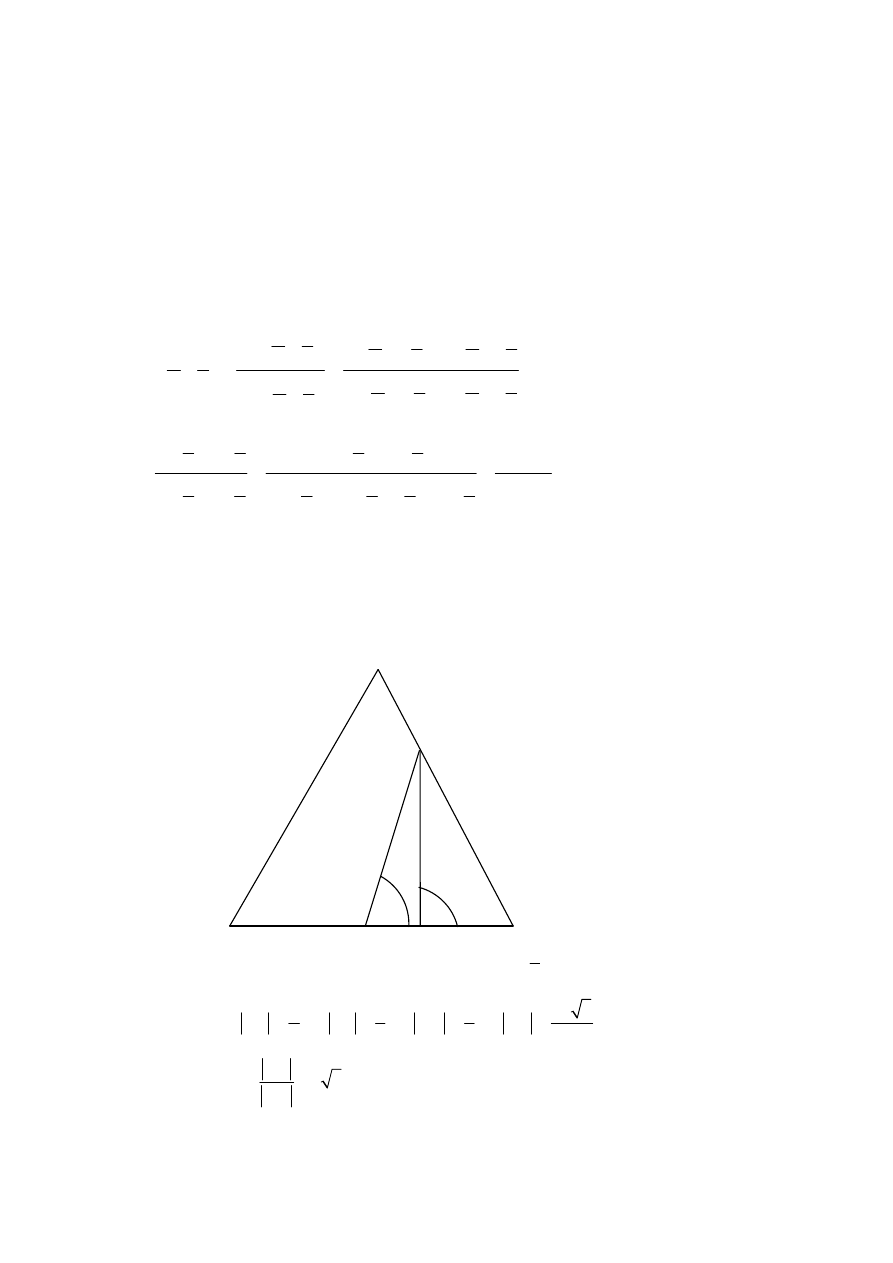
4

Wyznaczamy

b

z pierwszego równania, podstawiamy do drugiego i zapisujemy równanie

kwadratowe:

2

2

8

0

a

a



 

,

stąd

1

2

2,

4

a

a

 



Odpowiedź:

2 i

1

a

b

 



albo

4 i

4

a

b





.

Zadanie 5.

sin

sin

cos

cos

sin

4

2

4

2

4

2

tg

4

2

cos

cos

sin

sin

cos

4

2

4

2

4

2

x

x

x

x

x

x

x



































































2

2

2

2

cos

sin

cos

sin

cos

2

2

2

2

1 sin

cos

sin

cos

2 cos

sin

sin

2

2

2

2

2

2

x

x

x

x

x

x

x

x

x

x

x

x



















Zadanie 6.
Rysujemy rysunek pomocniczy i wprowadzamy oznaczenia. Długość boku trójkąta
równobocznego oznaczamy

a

.

Z warunków zadania wynika, że pole trójkąta

DBE

, to

3

8

pola trójkąta

ABC

.

Stąd wynika, że:

3

4

BE

a



,

3

8

FB

a



,

1

8

DF

a



,

3

3

8

a

EF



.

Odpowiedź:

tg

3 3

EF

DF







.

A

C

B

D

E

F

α

.

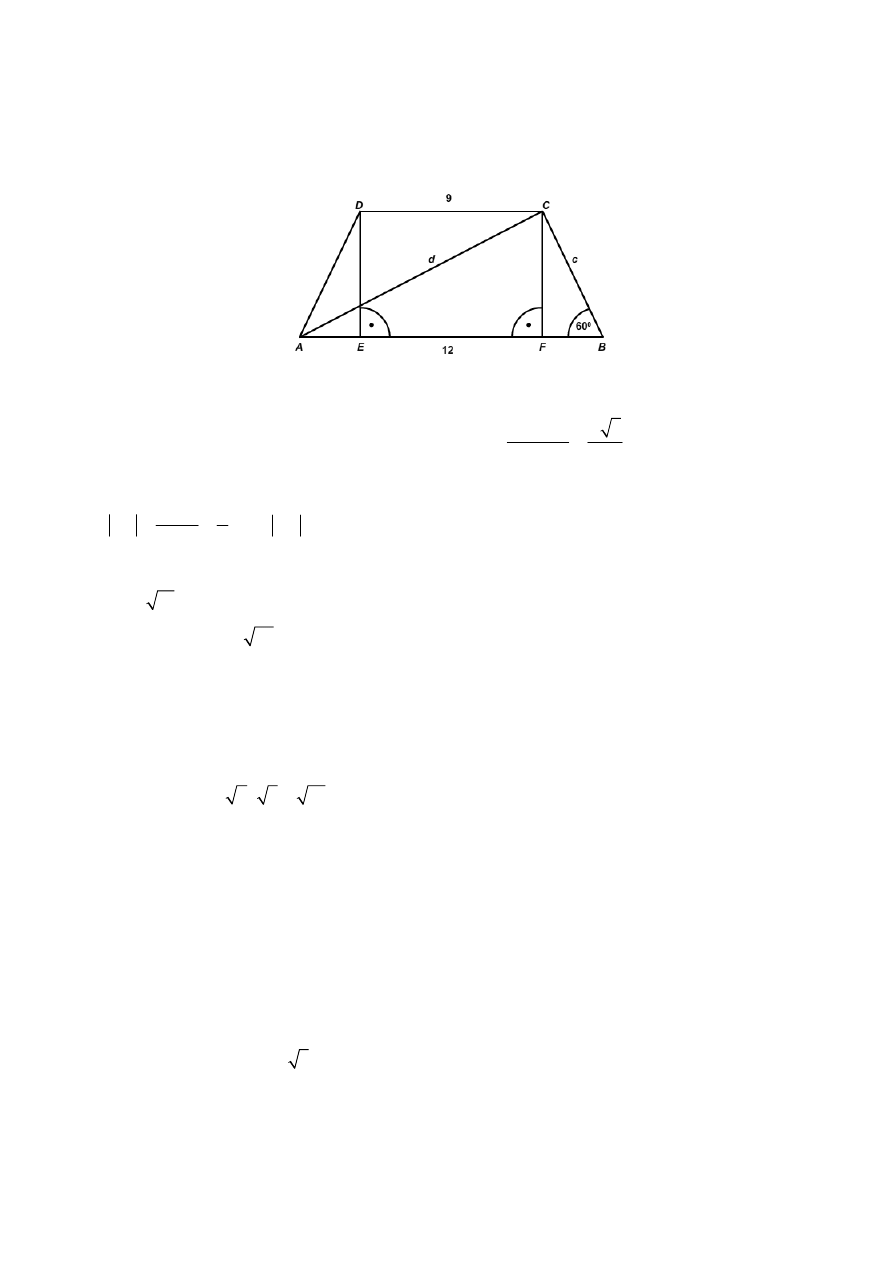
5

Zadanie 7.
Rysujemy rysunek pomocniczy i wprowadzamy oznaczenia.

Okrąg opisany na trapezie

ABCD

to okrąg opisany na trójkącie

ABC

. Promień tego

okręgu możemy obliczyć z twierdzenia sinusów:

3

2 sin 60

3

d

d

R







.

Kolejno obliczamy:

12 9

3

2

2

FB







,

3

c

BC





.

Z twierdzenia kosinusów zastosowanego w trójkącie

ABC

obliczamy

d

:

3 13

d



.

Odpowiedź:

39

R



.

Zadanie 8.

Z warunków zadania wynika, że dwa wierzchołki kwadratu, oznaczmy je przez

A

i

B

,

leżą na prostej o równaniu

2

5

0

x

y



 

oraz na okręgu o środku w punkcie

 

0, 0

i promieniu

2

5

10

r







.

Zapisujemy układ równań.

2

2

10

2

5

0

x

y

x

y











 



Rozwiązując ten układ równań, otrzymujemy

 

3,1

A



,





1, 3

B

 

. Punkt

 

0, 0

jest

środkiem symetrii kwadratu, stąd wynika, że





3, 1

C

  

,





1, 3

D





.

Zadanie 9.

Nierówność

3

a b c d

  

jest równoważna z nierównością





2

2

3

a b c

d

 



.

Korzystając z tego, że

2

2

2

2

a

b

c

d







, otrzymujemy nierówność równoważną

2

2

2

2

2

2

2

2

2

ab

ac

bc

a

b

c











, którą możemy zapisać w postaci:

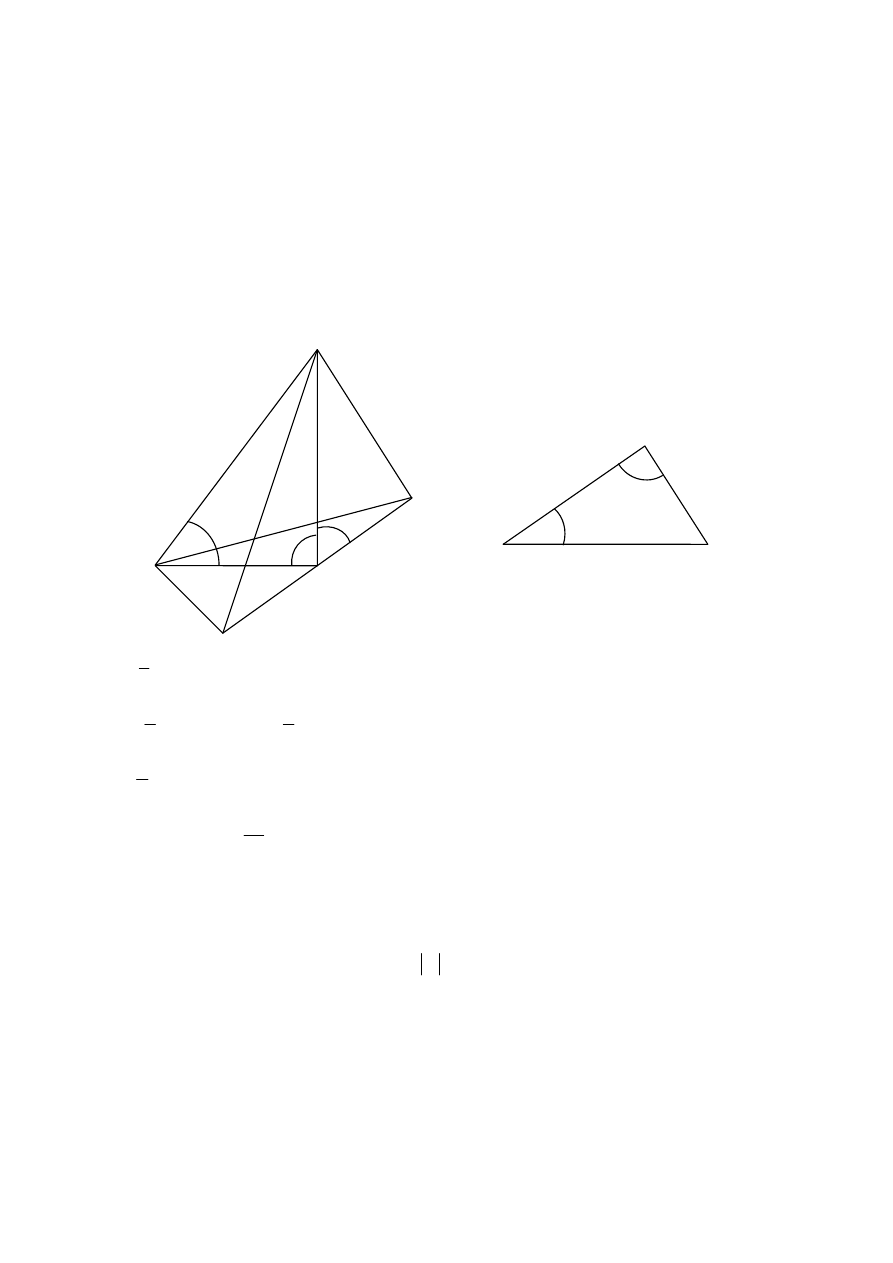
6



 

 



2

2

2

0

a b

a c

b c







 



.

Ostatnia nierówność jest prawdziwa dla wszystkich

a

,

b

,

c

.

Zadanie 10.
Z warunków zadania wynika, że spodek wysokości ostrosłupa jest środkiem okręgu

opisanego na podstawie. Jest to środek przeciwprostokątnej

AB

. Rysujemy rysunek

pomocniczy i wprowadzamy oznaczenia.

1

3

p

V

P h





2

1

1

sin

cos

sin 2

2

4

p

P

a

a

a













tg

2

a

h





Odpowiedź:

3

1

sin 2

tg

24

V

a









Zadanie 11.
Zdarzeniami elementarnymi są pięcioelementowe wariacje z powtórzeniami zbioru





1, 2, 3, 4, 5, 6

. Jest to model klasyczny

5

6

 

.

Możliwe przedstawienia liczby

8

w postaci sumy pięciu składników ze zbioru





1, 2, 3, 4, 5, 6

są następujące:

8 1 1 1 1 4

    

8 1 1 1 2 3

    

8 1 1 2 2 2

    

A

B

C

S

h

. .



A

B

C

.

α

a

7

Oznaczając przez

A

zdarzenie opisane w treści zadania, otrzymujemy:

5

5

4

5

35

1

1

1

2

A

       











       

       

Odpowiedź:

 

5

35

6

P A



.