
opracował: Radek Kołkowski
Funkcja Blocha
W sieci krystalicznej w każdej komórce elementarnej prawdopodobieństwo przebywania elektronu jest takie
samo – co wynika z periodyczności sieci:
)
(
*
)
(
)
(
*
)
(
r
r
R
r
R
r
ψ
ψ
ψ
ψ
⋅
=
+
⋅
+
Jednak nie możemy na tej podstawie powiedzieć, że:
)
(
)
(
r
R
r
ψ
ψ
=
+
Jak porównać ze sobą
)
(r
ψ
i
)
(
R
r
+
ψ
?
Zadziałajmy na
)
(r
ψ
operatorem translacji
)
(
1
R
T
)
, tzn. przesuwamy się w sieci do innej komórki
elementarnej, zmieniając położenie o wektor
3
3
2
2
1
1
1
a
n
a
n
a
n
R
+
+
=
, gdzie
3
2
1
,
,
a
a
a
to stałe sieciowe,
a
C
n
n
n
∈
3
2
1
,
,
.
Jeśli dwie funkcje mają równe kwadraty, mogą się różnić co najwyżej o czynnik fazowy:
)
(
1
1
)
(
)
(
)
(
)
(
R
f
i
e
r
R
r
r
R
T
ψ
ψ
ψ
=
+
=
)
Wykonując ponownie translację o jakiś inny wektor
2
R
otrzymujemy:
)
(
)
(
)
(
2
)
(
2
1
2
2
1
1
1
)
(
)
(
)
(
)
(
)
(
)
(
)
(
R
f
i
R
f
i
R
f
i
R
f
i
e
e
r
e
R
r
e
r
R
T
r
R
T
R
T
ψ
ψ
ψ
ψ
=
+
=
=
)
)
)
Operacja ta jest równoważna przesunięciu o sumę wektorów
1
R
i
2
R
:
)
(
)
(
)
(
1
2
2
1
R
T
R
T
R
R
T
)
)
)
=
+
)
(
2
1
2
1
2
1
)
(
)
(
)
(
)
(
R
R
f
i
e
r
R
R
r
r
R
R
T
+
=
+
+
=
+
ψ
ψ
ψ
)
Wynika stąd, że
)
(
)
(
)
(
2
1
2
1
)
(
)
(
R
R
f
i
R
f
i
R
f
i
e
r
e
e
r
+
=
ψ
ψ
,
a więc
)
(
)
(
)
(
1
2
2
1
R
R
f
R
f
R
f
+
=
+
Jedyną funkcją spełniającą powyższy warunek jest funkcja liniowa:
R
k
R
f
⋅
=
)
(
Tym sposobem dochodzimy do funkcji Blocha, która ma następującą postać:
)
(
)
(
r
u
e
r
k
r
k
i
⋅
=
ψ
, gdzie funkcja
)
(r
u
k
jest periodyczna:
)
(
)
(
r
u
R
r
u
k
k
=
+
| |
funkcja funkcja
wolnozmienna szybkozmnienna
Funkcja Blocha spełnia narzucone warunki:
)
(
)
(
)
(
)
(
)
(
)
(
)
(
R
f
i
R
k
i
k
R
k
i
r
k
i
k
R
r
k
i
e
r
e
r
r
u
e
e
R
r
u
e
R
r
⋅
=
⋅
=
⋅
=
+
⋅
=
+
+
ψ
ψ
ψ
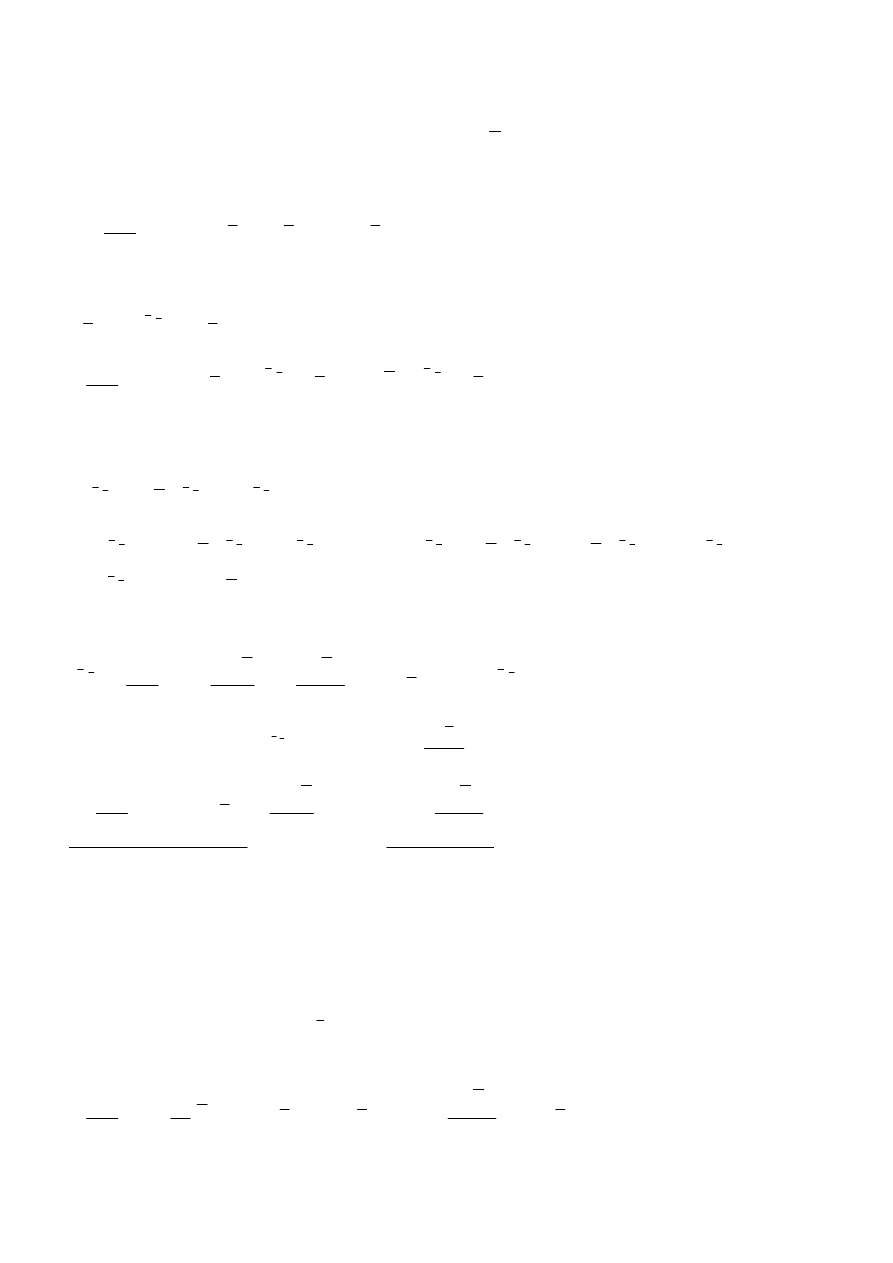
Równanie kp
Obliczając energię elektronu w krysztale, stosujemy następujące przybliżenia:
1. przybliżenie adiabatyczne (zakładamy, że atomy nie drgają – rdzenie
atomowe są sztywno utwierdzone w swoich miejscach:
0
=
∆
i
R
)
2. przybliżenie jednolektronowe (zakładamy, że w krysztale o periodycznym
potencjale znajduje się tylko jeden elektron:
)
(
)
(
)
(
V
ˆ
2
kr
2
2
r
E
r
r
m
ψ
ψ
=
+
∇
−
h
Wygodnym wyjściem do obliczenia energii elektronu w krysztale stanowi funkcja Blocha:
)
(
)
(
r
u
e
r
k
r
k
i
⋅
=
ψ
)
(
)
(
)
(
)
(
V
ˆ
2
kr
2
2
r
u
e
k
E
r
u
e
r
m
k
r
k
i
k
r
k
i
=
+
∇
−
h
Ż
eby rozwiązać powyższe równanie, musimy obliczyć pochodne:
u
e
u
e
k
i
u
e
r
k
i
r
k
i
r
k
i
∇
+
=
∇
( ) (
)
=
∇
+
∇
+
∇
+
−
=
∇
+
∇
=
∇
u
e
u
e
k
i
u
e
k
i
u
e
k
u
e
u
e
k
i
u
e
r
k
i
r
k
i
r
k
i
r
k
i
r
k
i
r
k
i
r
k
i
2
2
2
(
)
u
u
k
i
u
k
e
r
k
i
2
2
2
∇
+
∇
+
−
−
=
Wstawiamy to, co uzyskaliśmy:
Eu
e
u
r
m
k
m
k
i
m
e
r
k
i
r
k
i
=
+
+
∇
−
∇
−
)
(
V
ˆ
2
2
kr
2
2
2
2
2
h
h
h
dzielimy obustronnie przez
r
k
i
e
oraz odejmujemy
u
m
k
2
2
2
h
:
u
m
k
E
u
m
k
i
r
m
−
=
∇
−
+
∇
−
2
)
(
V
ˆ
2
2
2
2
kr
2
2
h
h
h
← równanie kp
|
||
||
0
ˆ
H
- ten wyraz jest taki sam, zaburzenie
zb
Hˆ
'
E - łatwa do policzenia różnica
jak w równaniu wyjściowym
Wyrażenie
∇
−
h
i
jest równoważne działaniu operatora pędu pˆ :
∇
−
=
h
i
pˆ
Trzeba też zauważyć, że funkcji
)
(r
u
k
o tym samym k może być wiele, dlatego trzeba je ponumerować.
Ostatecznie dostajemy równanie kp w postaci, od której wzięło swoją nazwę:
)
(
2
)
(
)
(
V
ˆ
ˆ
2
,
2
2
,
kr
2
2
r
u
m
k
E
r
u
r
p
k
m
m
k
n
k
n
−
=
+
+
∇
−
h
h
h
n
odróżnia niezdegenerowane stany energetyczne dla danego wektora falowego k

*Rachunek zaburzeń i masa efektywna
Wychodzimy od równania kp:
u
E
u
m
k
E
u
m
k
i
r
m
'
2
)
(
V
ˆ
2
2
2
2
kr
2
2
=
−
=
∇
−
+
∇
−
h
h
h
m
k
E
E
2
'
2
2
h
+
=
Zamiast rozwiązywać równanie dla całej sieci rozwiązujemy je wyłącznie dla czynnika Blochowskiego.
Stosujemy rachunek zaburzeń: rozpisujemy hamiltonian na sumę hamiltonianu zerowego i hamiltonianu
zaburzenia:
zb
H
H
H
ˆ
ˆ
ˆ
0
+
=
Przy czym znane jest działanie hamiltonianu zerowego na funkcję falową, która jest jego funkcją własną:
0
0
0
0
ˆ
m
m
m
E
H
ψ
ψ
=
Problem polega na znalezieniu nieznanej funkcji własnej hamiltonianu będącego sumą
zb
H
H
ˆ
ˆ
0
+
.
W tym celu rozpisujemy tą nieznaną funkcję w szereg funkcji znanych:
∑
∞
=
=
1
0
m
m
nm
n
c
ψ
ψ
Działamy na to hamiltonianem:
(
)
∑
∑
∞
=
∞
=
=
+
1
0
1
0
0
ˆ
ˆ
m
m
nm
n
m
m
nm
zb
c
E
c
H
H
ψ
ψ
Ponieważ hamiltonian jest operatorem liniowym:
(
)
∑
∑
∞
=
∞
=
=
+
1
0
1
0
0
ˆ
ˆ
m
m
n
nm
m
m
zb
nm
E
c
H
H
c
ψ
ψ
Możemy działanie hamiltonianu zerowego zastąpić przez jego wynik:
(
)
∑
∑
∞
=
∞
=
=
+
1
0
1
0
0
ˆ
m
m
n
nm
m
m
zb
m
nm
E
c
H
E
c
ψ
ψ
Mnożymy obustronnie przez funkcję
*
0
l
ψ
ortonormalną do
0
m
ψ
i całkujemy po objętości kryształu:
∑
∫
∑
∫
∫
∞
=
∞
=
=
+
1
0
*
0
1
0
*
0
0
*
0
0
ˆ
m
m
V
l
n
nm
m
m
V
zb
l
m
V
l
m
nm
dV
E
c
dV
H
dV
E
c
ψ
ψ
ψ
ψ
ψ
ψ
Ponieważ
*
0
l
ψ
i
0
m
ψ
są ortonormalne,
lm
m
l
δ
ψ
ψ
=
0
*
0
(delta Kronneckera), stąd:
n
nl
m
m
V
zb
l
nm
l
nl
E
c
dV
H
c
E
c
=
+
∑ ∫
∞
=
1
0
*
0
0
ˆ
ψ
ψ
Możemy przyjąć, że
n
l
=
:
n
nn
m
m
V
zb
n
nm
n
nn
E
c
dV
H
c
E
c
=
+
∑ ∫
∞
=
1
0
*
0
0
ˆ
ψ
ψ
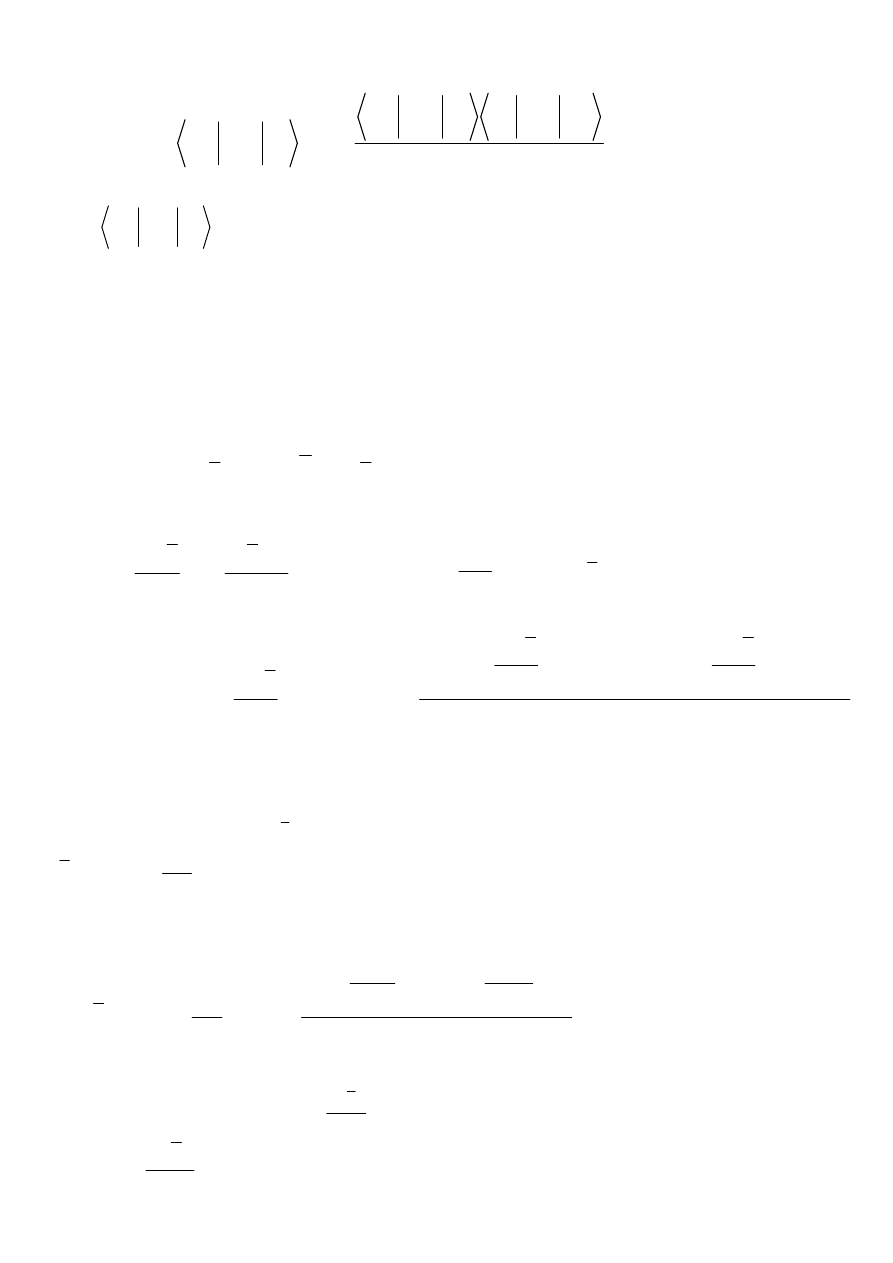
A więc
...
0
+
=
E
E
n
(energia jest sumą energii z hamiltonianu zerowego i nieskończonej sumy całek z
zaburzeń). Po przekształceniach uzyskamy wzór, na którym opiera się rachunek zaburzeń:
∑
∞
≠
=
−
+
+
=
n
l
l
l
n
zb
zb
zb
n
n
E
E
n
H
l
l
H
n
l
H
n
E
E
1
0
0
0
0
ˆ
0
0
ˆ
0
0
ˆ
0
gdzie
0
ˆ
0
l
H
n
zb
oznacza skrócony zapis całki
dV
H
l
V
zb
n
0
*
0
ˆ
ψ
ψ
∫
Wszystko to działa przy założeniu, że
zb
H
H
ˆ
ˆ
0
>>
(hamiltonian zaburzenia daje niewielki wkład
energetyczny w porównaniu z hamiltonianem zerowym) – wówczas wystarczą pierwsze 3 lub 4 wyrazy
szregu, aby uzyskać poprawny wynik.
0
0
l
n
E
E
−
jest różnicą pomiędzy poziomami zerowymi
Łączymy rachunek zaburzeń z funkcją Blocha:
(
)
)
(
)
(
)
(
ˆ
ˆ
0
r
u
k
E
r
u
H
H
k
n
k
zb
=
+
gdzie, jak wynika z poprzednich przekształceń:
m
p
k
m
k
i
H
zb
ˆ
ˆ
2
⋅
=
∇
−
=
h
h
+
∇
−
=
)
(
V
ˆ
2
ˆ
kr
2
2
0
r
m
H
h
Wstawiamy to do wzoru na energię w rachunku zaburzeń:
∑
∫
∫
∫
∞
≠
=
−
∇
−
⋅
∇
−
+
∇
−
+
=
n
l
l
l
n
n
V
l
l
V
n
n
V
n
n
n
E
E
dV
u
m
k
i
u
dV
u
m
k
i
u
dV
u
m
k
i
u
E
E
1
0
0
0
2
*
0
0
2
*
0
0
2
*
0
0
h
h
h
Dla
0
=
k
pochodna energii po wektorze falowym się zeruje:
0
=
∇
E
k
, co oznacza, że funkcja
)
(k
E
ma w
tym punkcie ekstremum. W powyższym wzorze znika drugi człon, zależny liniowo od k .
Jednocześnie iloczyn skalarny
∇
⋅
k
możemy zapisać jako:
∑
=
∂
∂
=
∇
⋅
3
1
i
i
i
x
k
k
Zauważamy dodatkowo, że w liczniku mamy iloczyn dwóch całek wzajemnie sprzężonych, a więc kwadrat
całki, który jest zawsze dodatni – możemy zlikwidować minusy. Uzyskujemy:
j
i
j
i
n
l
l
l
n
V
i
n
l
V
i
l
n
n
n
k
k
E
E
dV
x
u
u
dV
x
u
u
m
E
k
E
∑ ∑
∫
∫
=
∞
≠
=
−
∂
∂
⋅
∂
∂
+
=
3
1
,
1
0
0
0
*
0
0
*
0
2
4
0
)
(
h
Do tej energii musimy jeszcze dodać
m
k
2
2
2
h
:
m
k
E
E
2
'
2
2
h
+
=
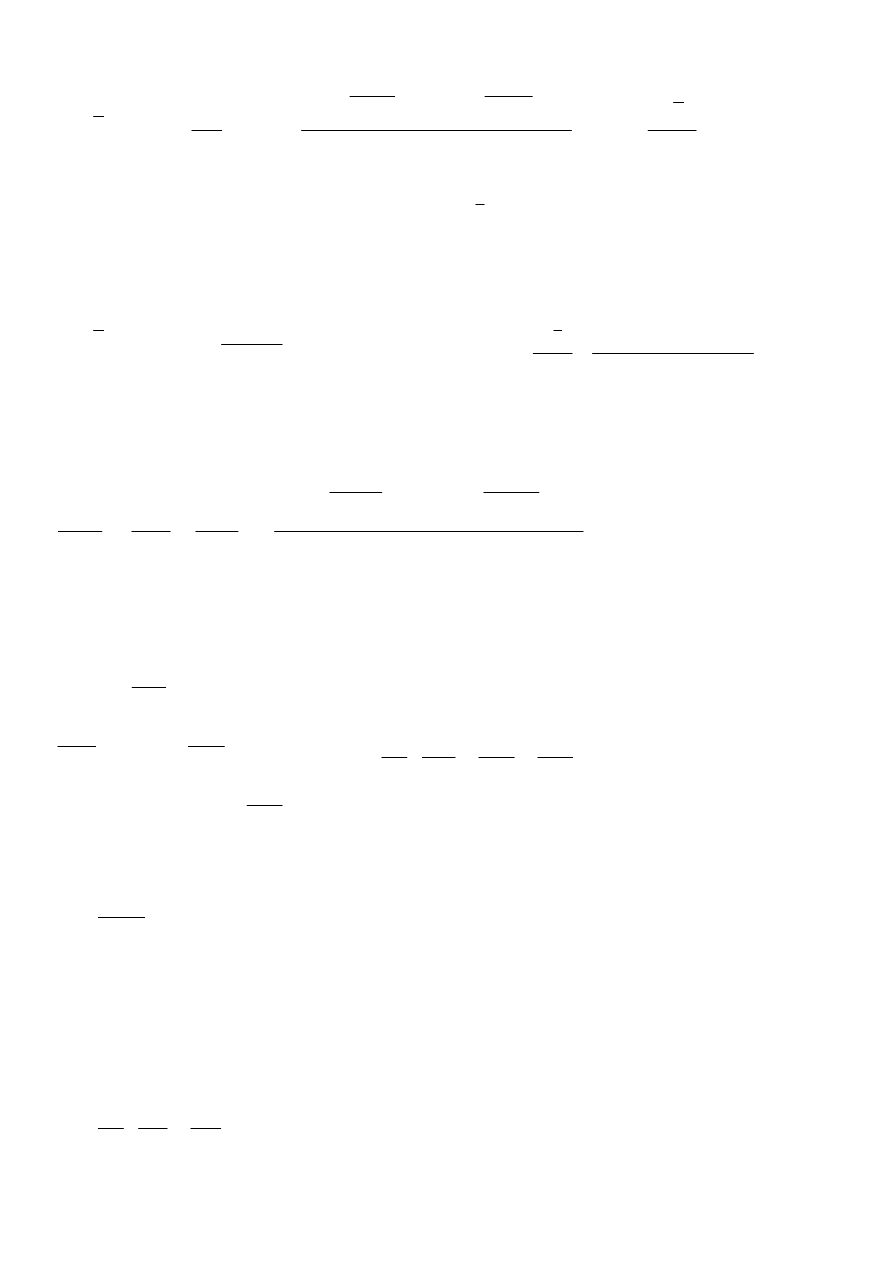
Ostatecznie:
m
k
k
k
E
E
dV
x
u
u
dV
x
u
u
m
E
k
E
j
i
j
i
n
l
l
l
n
V
i
n
l
V
i
l
n
n
n
2
)
(
2
2
3
1
,
1
0
0
0
*
0
0
*
0
2
4
0
h
h
+
−
∂
∂
⋅
∂
∂
+
=
∑ ∑
∫
∫
=
∞
≠
=
Jak widać, w krysztale dla elektronu o wektorze falowym
k
, w przeciwieństwie do elektronu swobodnego,
pojawiają się pasma energetyczne.
Energię elektronu w krysztale możemy wyrazić skrótowo, przez analogię do elektonu swobodnego:
∑
=
+
=
3
1
,
*
2
0
2
)
(
j
i
j
i
j
i
n
n
m
k
k
E
k
E
h
(w elektronie swobodnym:
m
k
k
k
k
k
k
m
k
2
)
(
2
3
3
2
2
1
1
2
2
2
+
+
=
h
h
)
*
j
i
m
jest tzw. masą efektywną elektronu na danym kierunku, wynikającą z anizotropii rozkładu energii w sieci
krystalicznej:
∑
∫
∫
∞
≠
=
−
∂
∂
⋅
∂
∂
+
=
n
l
l
l
n
V
i
n
l
V
i
l
n
j
i
j
i
E
E
dV
x
u
u
dV
x
u
u
m
m
m
1
0
0
0
*
0
0
*
0
2
2
*
2
1
h
δ
Elektron w krysztale zachowuje się jak elektron swobodny, tyle że zachowuje się tak, jakby miał w każdym
kierunku inną masę. Masa efektywna jest tensorem, który, jeśli weźmiemy osie główne kryształu, będzie
wyglądał następująco:
=
*
33
*
22
*
11
*
1
0
0
0
1
0
0
0
1
1
m
m
m
m
j
i
+
+
=
*
33
2
3
*
22
2
2
*
11
2
1
2
2
m
k
m
k
m
k
E
h
Z kolei w kryształach izotropowych, np. kubicznych (Si, Ge, GaAs) wszystkie trzy osie są równoważne:
*
2
2
2
m
k
E
h
=
Możemy też mieć do czynienia z kryształem, w którym wyróżniona jest jedna oś:
2
2
2
2
2
||
y
x
z
k
k
k
k
k
+
=
=
+
Wówczas:
+
=
+
+
*
2
*
||
2
||
2
2
m
k
m
k
E
h
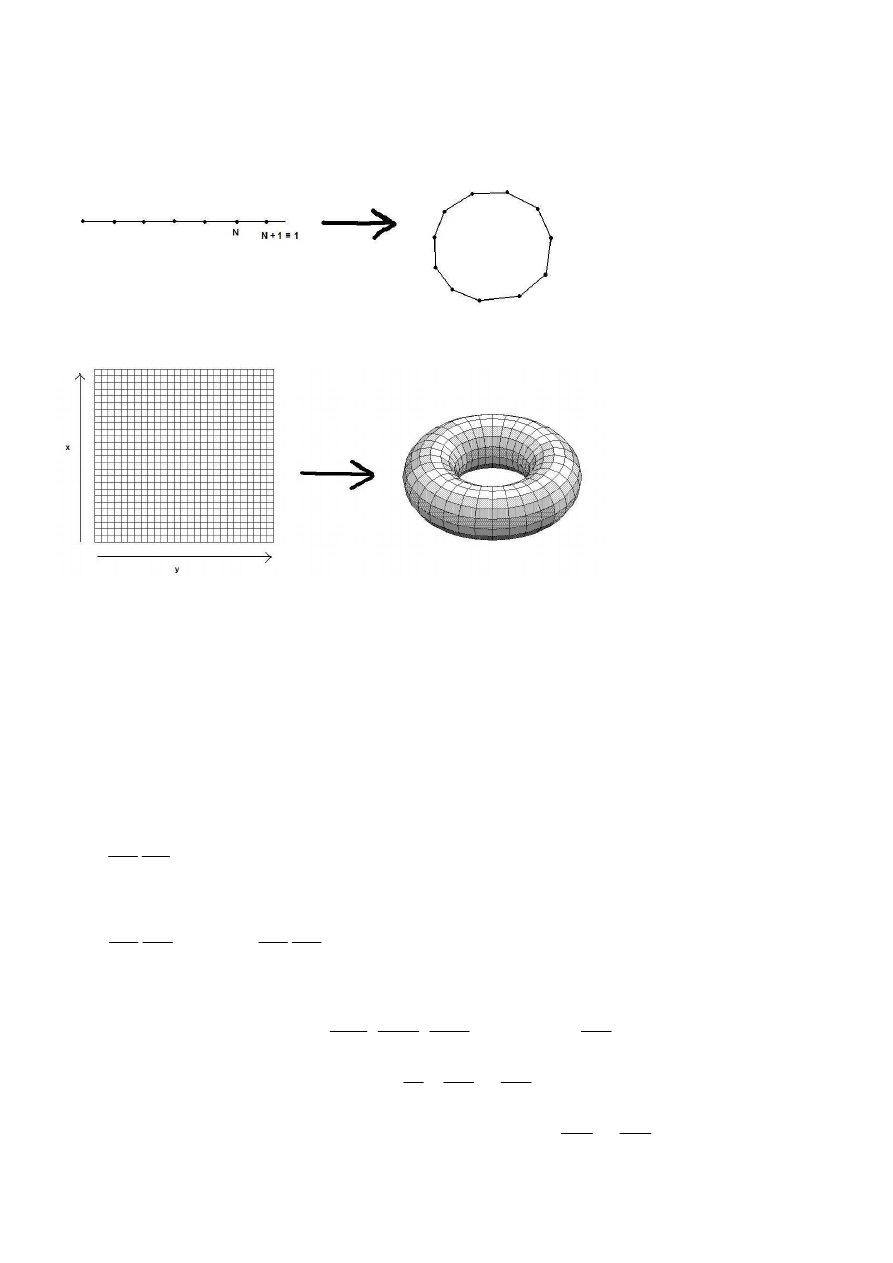
Warunki periodyczności Borna-Karmana:
Aby opisać kryształ o skończonej liczbie N atomów, musimy atomowi o indeksie
1
+
N
przypisać numer 1.
Można sobie wyobrazić, że gdy mamy jednowymiarowy kryształ, zamykamy go w „kryształ cykliczny”:
Z kolei kryształ 2-wymiarowy: w torus
(nie sposób sobie wyobrazić analogicznej operacji na krysztale 3-wymiarowym, ale dokonujemy tego w
rachunkach)
Funkcja Blocha musi zatem spełniać warunek:
)
(
)
(
1
1
)
(
1
1
x
u
e
a
N
x
u
e
k
x
k
i
k
a
N
x
k
i
x
x
=
+
+
, (gdy rozpatrujemy jeden kierunek, np.
x
)
1
1
1
=
a
N
k
i
x
e
, gdy
1
1
1
2 n
a
N
k
x
π
=
,
1
1
...,
,
3
,
2
,
1
N
n
=
Wynika stąd, że wektor falowy musi być równy:
1
1
1
2
N
n
a
k
x
n
π
=
Analogicznie dla pozostałych kierunków:
2
2
2
2
N
n
a
k
y
n
π
=
3
3
3
2
N
n
a
k
z
n
π
=
Wszystkich atomów mamy
3
2
1
N
N
N
N
⋅
⋅
=
Objętość komórki elementarnej:
V
L
L
L
N
a
N
a
N
a
V
k
3
3
2
1
3
3
2
2
1
1
8
2
2
2
π
π
π
π
=
⋅
⋅
=
⋅
⋅
=
, gdzie
V - objętość kryształu
Gęstość stanów w przestrzeni kryształu:
3
3
8
1
8
1
)
(
π
π
ρ
→
=
=
V
V
k
k
, jeśli przyjmiemy jednostkową objętość
Gdy uwzględnimy spin, gęstość stanów wzrośnie dwukrotnie:
3
3
4
1
4
)
(
π
π
ρ
→
=
V
k

Model ciasnego wiązania
Zakładamy, że dla konkretnego atomu znamy:
0
0
0
0
ˆ
ψ
ψ
E
H
=
Rozważmy jeden kierunek w sieci kryształu, w której atomy powtarzają się periodycznie o
a
i ponumerujmy kolejne atomy:
i
i
E
H
ψ
ψ
0
0
ˆ
=
Funkcje
i
ψ
będą miały ten sam kształt, ale będą przesunięte w fazie:
2
0
2
ψ
ψ
=
i
Weźmy się za równanie:
ψ
ψ
E
H
=
ˆ
, gdzie
Hˆ
jest hamiltonianem dla całego kryształu
Dla atomu poza kryształem:
)
(
V
ˆ
2
ˆ
at
2
2
2
0
x
dx
d
m
H
+
−
=
h
W krysztale:
)
(
V
ˆ
ˆ
)
(
V
ˆ
2
ˆ
p
0
kr
2
2
2
x
H
x
dx
d
m
H
+
=
+
−
=
h
gdzie
p
V
ˆ to tzw. potencjał perturbacji, wynikający z umieszczenia atomu w sieci krystalicznej:
)
(
V
ˆ
)
(
V
ˆ
)
(
V
ˆ
at
kr
p
x
x
x
−
=
Ponieważ funkcja
ψ
zostaje zmieniona przez potencjał perturbacji, nie jest już funkcją własną hamiltonianu.
Musimy ją rozpisać w szereg funkcji, które znamy:
∑
=
=
N
i
i
i
c
1
ψ
ψ
, gdzie N jest liczbą atomów w sieci kryształu
Jeśli uwzględnimy tylko oddziaływanie najbliższych sąsiadów:
W
dx
dx
i
i
i
i
−
=
=
+
∞
∞
−
∞
∞
−
−
∫
∫
1
p
*
p
*
1
V
ˆ
V
ˆ
ψ
ψ
ψ
ψ
gdzie
0
>
W
- potencjał perturbacji obniża energię całkowitą (inaczej kryształ byłby niestabilny).
Wstawiamy
∑
=
=
N
i
i
i
c
1
ψ
ψ
do
ψ
ψ
E
H
=
ˆ
:
∑
∑
=
=
=
N
i
i
i
N
i
i
i
c
E
c
H
1
1
ˆ
ψ
ψ
- całkujemy obustronnie: /
dx
m
∫
∞
∞
−
*
ψ
(
)
dx
c
E
dx
c
H
N
i
i
i
m
N
i
i
i
m
∑
∫
∑
∫
=
∞
∞
−
=
∞
∞
−
=
+
1
*
1
p
0
*
V
ˆ
ˆ
ψ
ψ
ψ
ψ

Lewa strona jest równa:
(
)
=
+
=
+
∑
∫
∫
∑
∫
=
∞
∞
−
∞
∞
−
=
∞
∞
−
N
i
i
m
i
m
i
N
i
i
i
m
dx
dx
H
c
dx
c
H
1
p
*
0
*
1
p
0
*
V
ˆ
ˆ
V
ˆ
ˆ
ψ
ψ
ψ
ψ
ψ
ψ
||
i
E
ψ
0
)
(
V
ˆ
1
1
0
p
*
1
*
1
0
+
−
∞
∞
−
=
∞
∞
−
=
+
−
=
+
=
∫
∑
∫
∑
m
m
m
i
m
N
i
i
i
m
N
i
i
c
c
W
E
c
dx
c
dx
E
c
ψ
ψ
ψ
ψ
||
||
↑
mi
δ
W
−
uwzględniamy tylko najbliższych sąsiadów
Zgadujemy rozwiązanie w postaci fali:
ma
k
i
m
s
Ae
c
=
, gdzie
x
ma
=
(
a
to stała sieciowa)
E
Ae
Ae
Ae
W
E
Ae
ma
k
i
a
m
k
i
a
m
k
i
ma
k
i
s
s
s
s
=
+
−
+
−
)
(
)
1
(
)
1
(
0
dzielimy obustronnie przez
ma
k
i
s
Ae
:
E
e
e
W
E
a
k
i
a
k
i
s
s
=
+
−
−
)
(
0
I tym sposobem otrzymujemy zależność energii od wektora falowego:
a
k
W
E
E
s
cos
2
0
−
=
Wynik jest bardzo prosty, ale to tylko dzięki temu, że rozpatrywaliśmy wyłącznie jeden kierunek.
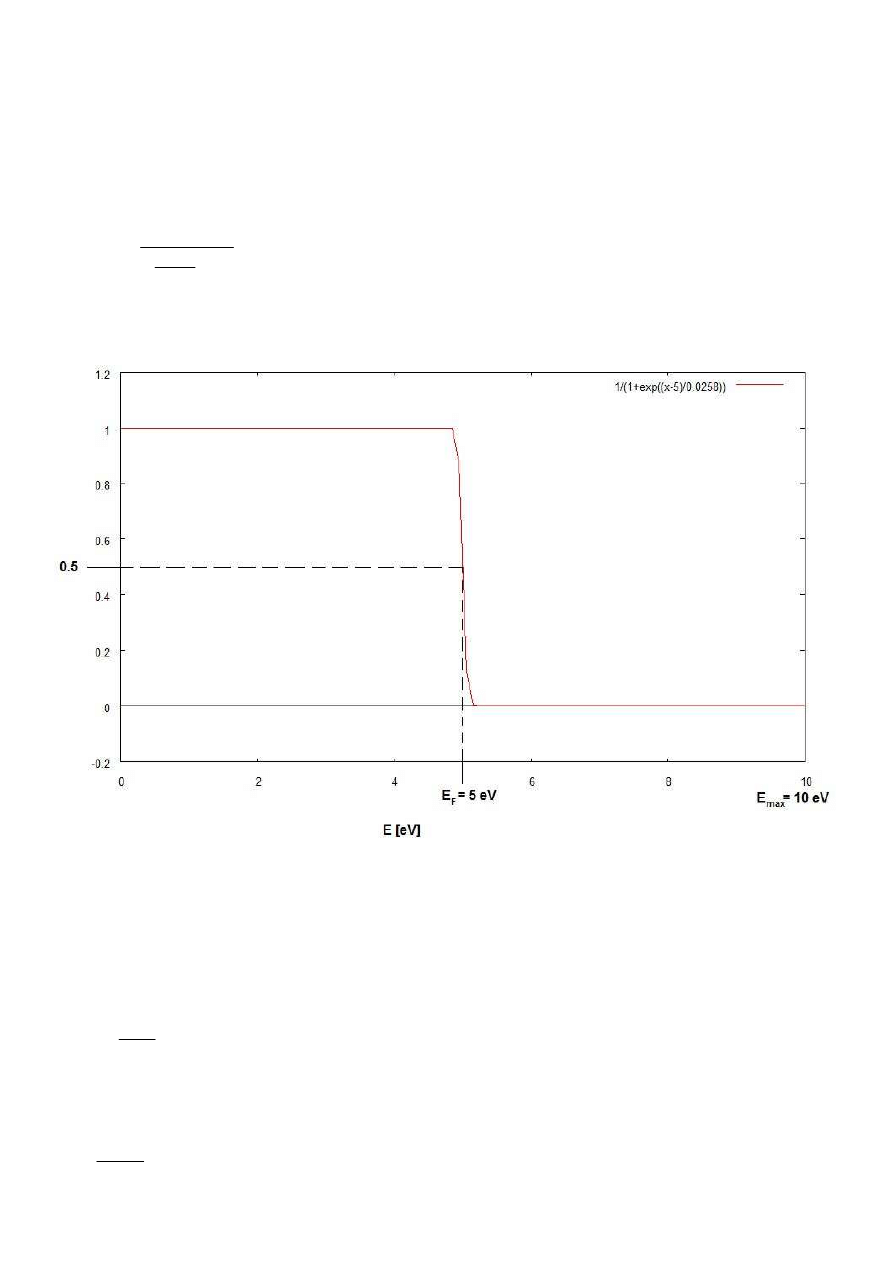
Koncentracja nośników w półprzewodnikach
Prawdopodobieństwem zajmowania danego stanu energetycznego przez fermiony rządzi
statystyka Fermiego-Diraca:
1
1
)
(
+
=
−
kT
E
E
F
e
E
f
, gdzie k jest stałą Boltzmanna, zaś
F
E
to energia Fermiego
Przykładowo, dla metali, w temperaturze ok. 300 K:
W przestrzeni odwrotnej poziom Fermiego tworzy kulę, znajdującą się w środku strefy Brillouina.
Stany poniżej poziomu Fermiego (wewnątrz kuli) są obsadzone, z kolei poza kulą – praktycznie puste. Prąd
jest przewodzony przez elektrony rozmyte na powierzchni kuli – jest ich o dwa rzędy wielkości mniej, niż
wewnątrz, ale i tak nie wszystkie biorą udział w przewodzeniu.
Na sferze o promieniu wyznaczanym przez wektor falowy k gęstość stanów jest jednorodna:
3
4
1
)
(
π
ρ
=
k
Gęstość zależy od energii, a ta jest proporcjonalna do kwadratu wektora falowego:
*
2
2
2
m
k
E
h
=
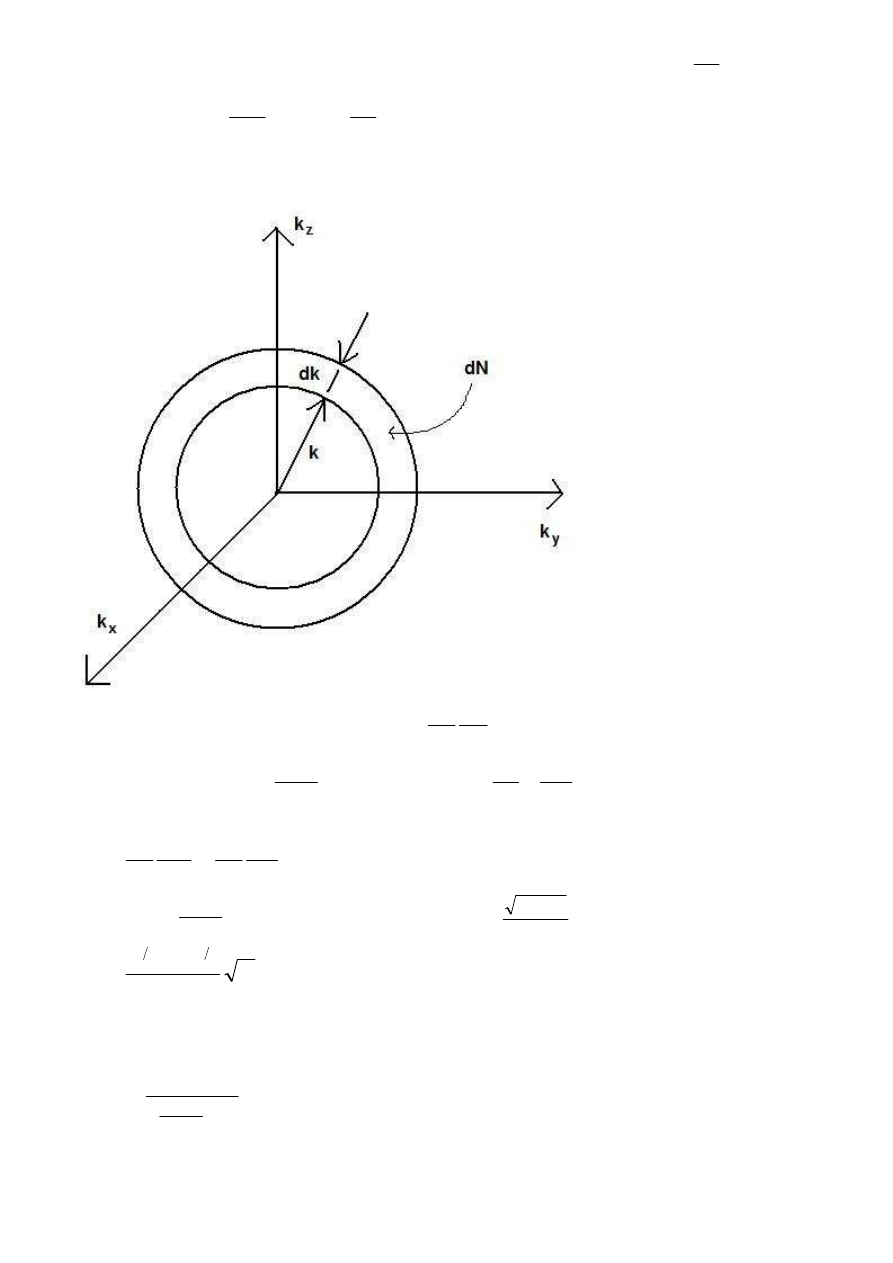
Gęstość nośników możemy wyrazić jako stosunek ich koncentracji do objętości:
dV
dN
k
=
)
(
ρ
stąd:
dk
k
dk
k
dV
k
dN
2
2
2
3
4
4
1
)
(
π
π
π
ρ
=
=
=
Jednocześnie możemy napisać:
dE
E
dN
)
(
ρ
=
Łącząc powyższe równości uzyskujemy:
dE
dk
k
E
2
2
)
(
π
ρ
=
Korzystając z zależności
*
2
2
2
m
k
E
h
=
obliczamy pochodną:
*
2
m
k
dk
dE
h
=
2
2
2
2
2
*
*
)
(
h
h
m
k
k
m
k
E
π
π
ρ
=
=
Z równania
*
2
2
2
m
k
E
h
=
mamy również wyrażenie na k :
h
E
m
k
*
2
=
, które wstawiamy tego powyżej:
E
m
E
3
2
2
3
2
1
*)
(
2
)
(
h
π
ρ
=
- jest to zależność prawdziwa na dnie pasma przewodnictwa, tam, gdzie nośniki przewodzą prąd
Nośnikami ładunku mogą być zrówno elektrony, o rozkładzie:
1
1
)
(
+
=
−
kT
E
E
e
F
e
e
E
f
,
jak i dziury, oznaczające brak elektronu:
e
d
e
d
E
E
E
f
E
f
−
=
→
−
=
)
(
1
)
(
, stąd:
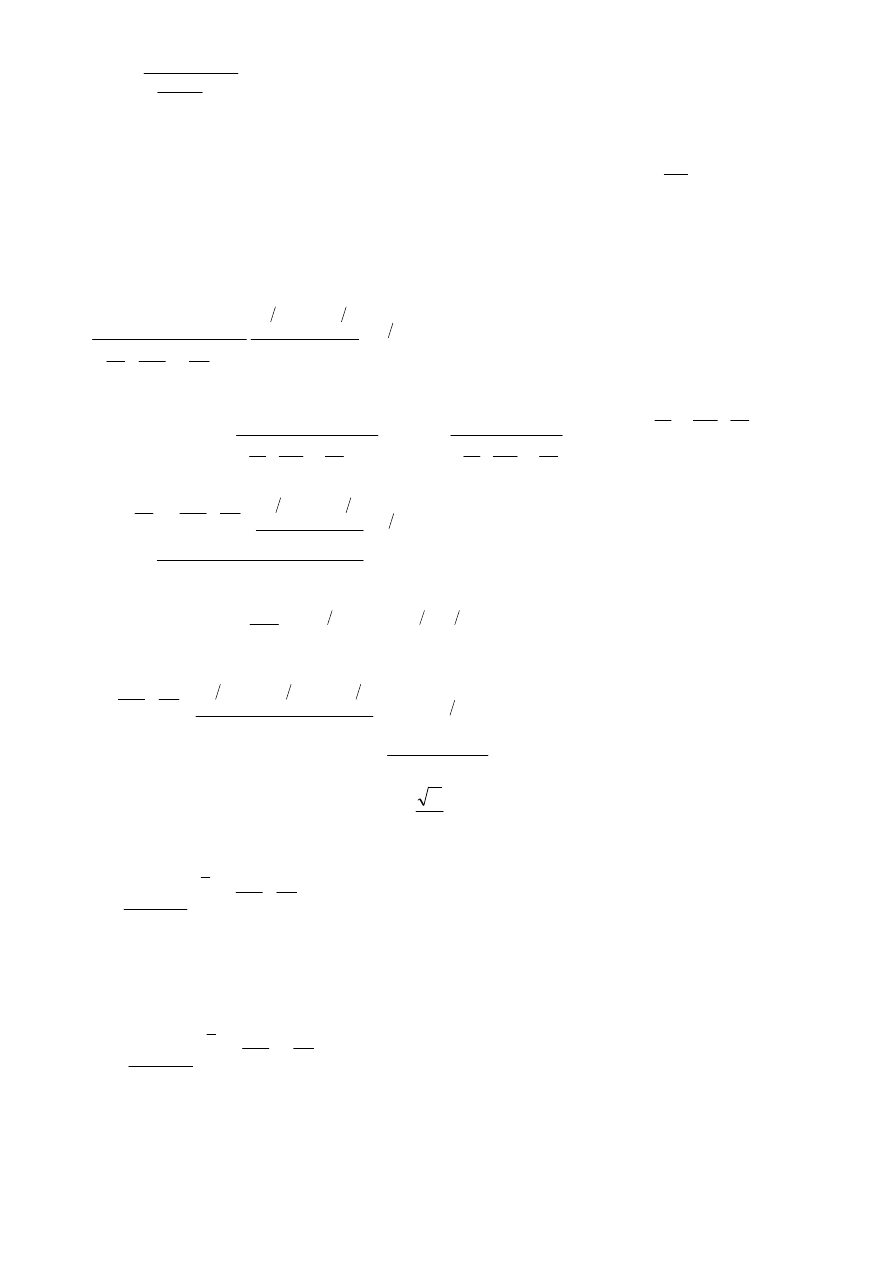
1
1
)
(
+
=
+
kT
E
E
d
F
d
e
E
f
- poziom Fermiego jest taki sam dla elektronów i dziur, znajduje się mniej więcej w połowie przerwy
energetycznej, tam też wybieramy poziom zerowy: przeskalowujemy energię
e
g
e
E
E
E
+
→
2
Koncentracja elektronów w paśmie przewodnictwa – całka po strefie Brillouina:
=
=
=
∫
∫
∞
0
)
(
)
(
)
(
)
(
e
e
e
SB
dE
E
E
f
dE
E
E
f
n
ρ
ρ
∫
∞
−
+
=
0
2
1
3
2
2
3
2
1
2
*)
(
2
1
1
e
e
kT
E
kT
E
kT
E
dE
E
m
e
e
e
F
g
e
h
π
Stosujemy przybliżenie:
kT
E
kT
E
kT
E
kT
E
kT
E
kT
E
kT
E
kT
E
kT
E
F
g
e
F
g
e
F
g
e
e
e
e
e
e
e
e
e
e
2
2
2
1
1
1
−
−
−
−
=
≈
+
∫
∞
−
−
⋅
=
0
2
1
3
2
2
3
2
1
2
*)
(
2
e
e
kT
E
kT
E
kT
E
dE
E
m
e
e
e
n
F
g
e
h
π
= const
Zamiana zmiennych:
kT
E
x
e
=
,
2
1
2
1
2
1
)
(
x
kT
E
e
=
,
dx
kT
dE
e
=
dx
x
e
kT
m
e
e
n
x
kT
E
kT
E
F
g
∫
∞
−
−
⋅
⋅
=
0
2
1
3
2
2
3
2
3
2
1
2
)
(
*)
(
2
h
π
||
2
π
Ostatecznie:
kT
E
kT
E
e
F
g
e
e
kT
m
n
2
2
3
2
*
2
2
−
=
h
π
- koncentracja elektronów w paśmie przewodnictwa
Wykonując analogiczne obliczenia w przypadku dziur otrzymalibyśmy:
kT
E
kT
E
d
F
g
e
e
kT
m
p
−
−
=
2
2
3
2
*
2
2
h
π
- koncentracja dziur w paśmie walencyjnym
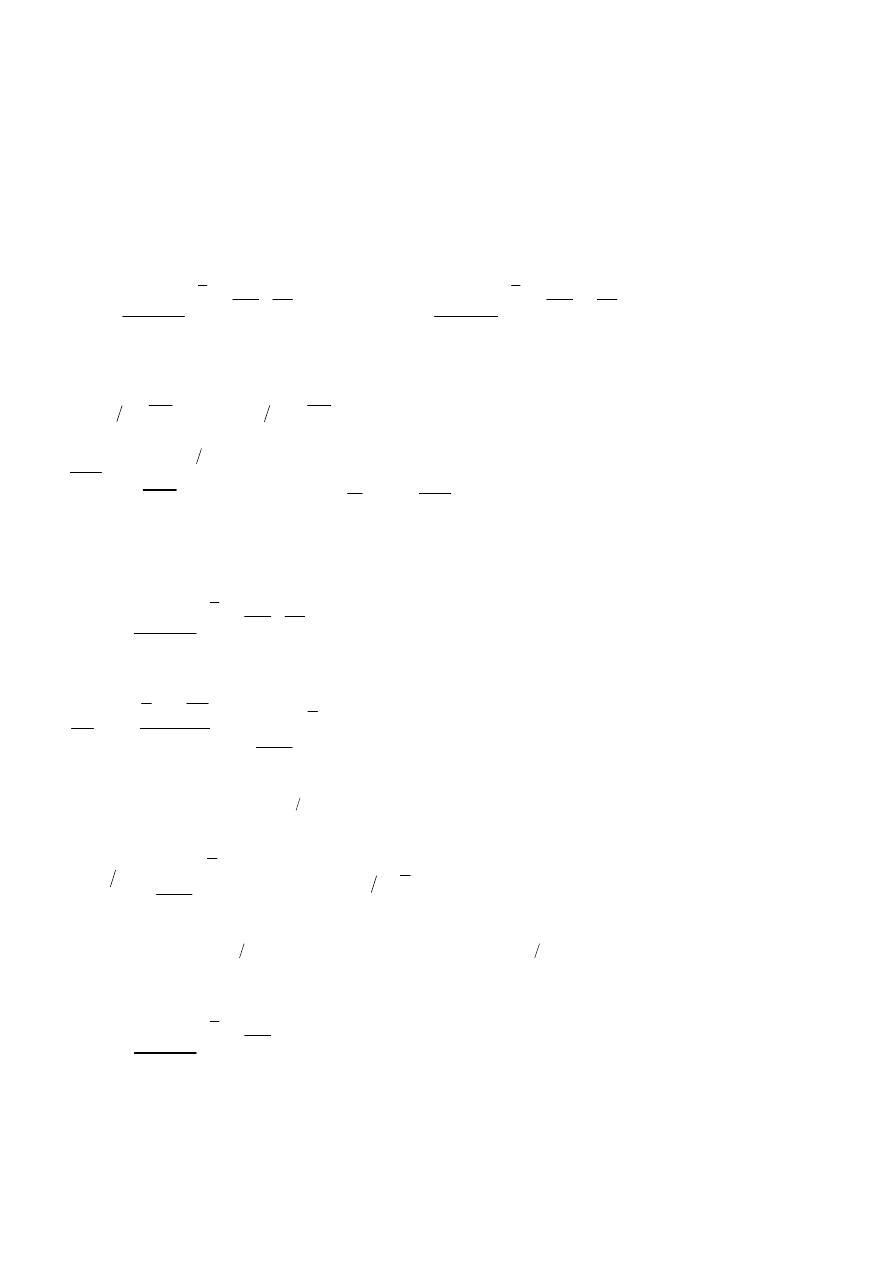
Półprzewodniki samoistne
Poziom Fermiego dla półprzewodnika niedomieszkowanego (samoistnego) oznaczamy symbolem
S
F
E
.
W półprzewodniku takim liczba elektronów jest równa liczbie dziur:
S
n
p
n
=
=
Korzystając ze wzorów:
kT
E
kT
E
e
F
g
e
e
kT
m
n
2
2
3
2
*
2
2
−
=
h
π
i
kT
E
kT
E
d
F
g
e
e
kT
m
p
−
−
=
2
2
3
2
*
2
2
h
π
Otrzymujemy zależność:
kT
E
d
kT
E
e
S
F
S
F
e
m
e
m
−
=
2
3
*
2
3
*
)
(
)
(
2
3
*
*
2
=
e
d
kT
E
m
m
e
S
F
*
*
ln
4
3
e
d
S
F
m
m
kT
E
=
→
Mając poziom Fermiego, możemy policzyć koncentrację nośników
S
n :
kT
E
kT
E
e
S
S
F
g
e
e
kT
m
n
2
2
3
2
*
2
2
−
=
h
π
4
3
*
*
ln
4
3
*
*
=
=
e
d
kT
m
m
kT
kT
E
m
m
e
e
e
d
S
F
Mnożymy ten wyraz przez
( )
2
3
*
e
m
:
( )
(
)
[
]
2
3
2
1
*
*
4
3
*
*
2
3
*
d
e
e
d
e
m
m
m
m
m
⋅
=
⋅
Wyrażenie
(
)
2
1
*
*
d
e
m
m
⋅
to masa zredukowana:
(
)
*
2
1
*
*
r
d
e
m
m
m
=
⋅
A więc:
kT
E
r
S
g
e
kT
m
n
2
2
3
2
*
2
2
−
=
h
π
- koncentracja samoistna zależy tylko od masy zredukowanej, przerwy energetycznej i temperatury
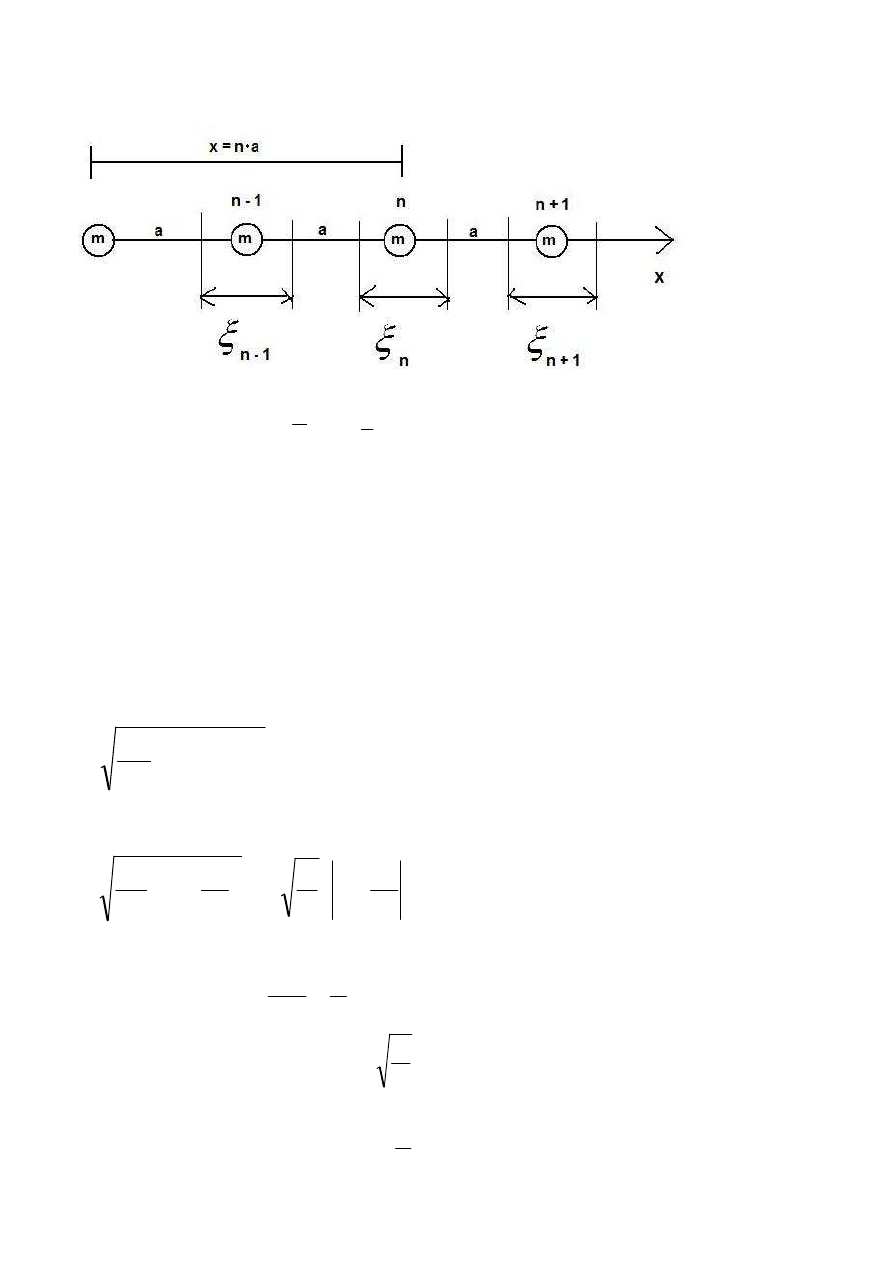
Fonony akustyczne
Fonony to drgania atomów w sieci kryształu. Najłatwiej jest je wyprowadzić z sieci liniowej:
Siła działająca na atom wychylony z położenia równowagi:
x
F
α
−
=
, gdzie
α
- stała siłowa
Z II prawa dynamiki Newtona:
a
m
F
w
=
← przyspieszenie = druga pochodna wychylenia po czasie:
n
n
n
n
n
m
ξ
α
ξ
α
ξ
α
ξ
α
ξ
−
+
−
=
+
−
1
1
&
&
(
)
1
1
2
+
−
+
−
=
n
n
n
n
m
ξ
α
ξ
α
ξ
α
ξ
&
&
-
n
- te równanie, dotyczące wychylenia
n
-tego atomu
Równanie to jest skojarzone z równaniem
1
−
n
i
1
+
n
.
Szukamy rozwiązania w postaci fali płaskiej:
(
)
qna
t
i
n
Ae
−
=
ω
ξ
, gdzie
x
na
=
to położenie atomu w sieci
(
)
2
2
−
+
=
−
−
iqa
iqa
e
e
m
α
ω
(
)
2
cos
2
2
−
=
−
qa
m
α
ω
(
)
qa
m
cos
1
2
−
=
α
ω
Korzystamy z własności funkcji trygonometrycznych:
x
x
x
x
x
x
2
cos
1
sin
2
sin
2
1
sin
cos
2
cos
2
2
2
2
−
=
→
−
=
−
=
2
sin
2
2
sin
4
2
qa
m
qa
m
⋅
=
=
α
α
ω
- jest to wyrażenie na dyspersję sieci
Najkrótsza możliwa fala akustyczna, jaka może się rozchodzić w ciele stałym:
a
2
min
=
λ
, stąd
a
q
π
λ
π
=
=
min
max
2
Dla małych
α
:
α
α
≈
sin
→
uq
qa
m
=
⋅
=
α
ω
, gdzie
u
- prędkość dźwięku w krysztale
Po skwantowaniu tego pola harmonicznego uzyskamy fonony – elementarne drgania atomów:
Energia całkowita drgań:
+
=
2
1
n
E
ω
h
- okazuje się, że dla
0
=
n
występują drgania zerowe (atomy w sieci nie mogą być nieruchome)
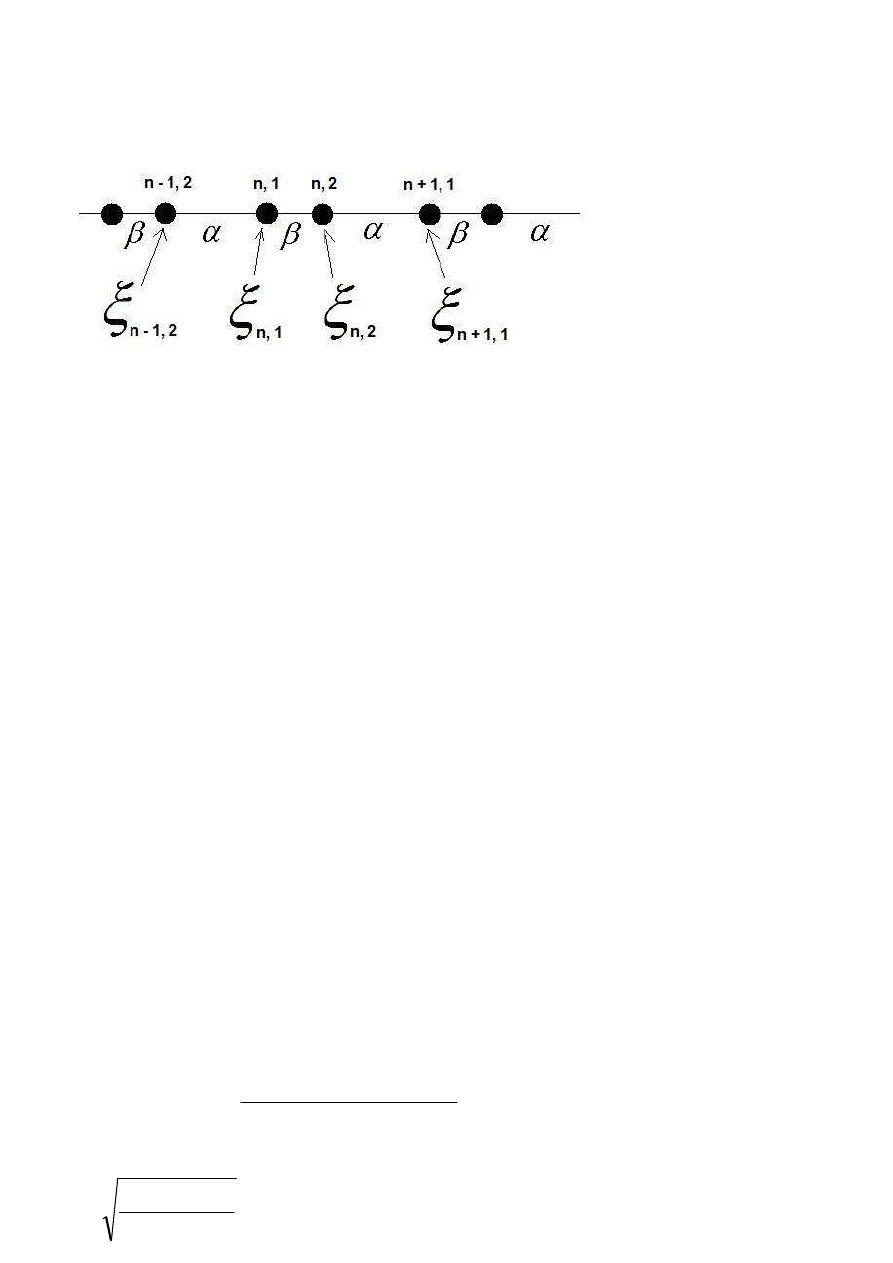
Fonony optyczne
Rozpatrujemy sieć, w której mamy po dwa atomy na węzeł:
1
,
2
,
1
,
2
,
1
1
,
1
n
n
n
n
n
m
ξ
β
ξ
β
ξ
α
ξ
α
ξ
−
+
−
=
−
&
&
2
,
1
,
1
2
,
1
,
1
,
2
n
n
n
n
n
m
ξ
α
ξ
α
ξ
β
ξ
β
ξ
−
+
−
=
+
&
&
(
)
qna
t
i
n
Ae
−
=
ω
ξ
1
,
(
)
qna
t
i
n
Ae
−
=
ω
ξ
2
,
Dla obu atomów częstość i wektor falowy są takie same, różne są natomiast amplituda i faza.
Otrzymujemy układ równań:
−
+
−
=
−
−
+
−
=
−
−
B
Ae
B
A
B
m
A
B
A
Be
A
m
iqa
iqa
α
α
β
β
ω
β
β
α
α
ω
2
2
2
1
=
−
+
+
−
−
=
+
−
−
+
−
0
]
)
[(
)
(
0
)
(
]
)
[(
2
2
2
1
ω
β
α
α
β
β
α
ω
β
α
m
B
e
A
e
B
m
A
iqa
iqa
W zapisie macierzowym:
=
−
+
+
−
+
−
−
+
−
0
0
)
(
)
(
)
(
)
(
2
2
2
1
B
A
m
e
e
m
iqa
iqa
ω
β
α
β
α
β
α
ω
β
α
Rozwiązanie nietrywialne istnieje wtedy, gdy wyznacznik macierzy
0
≠
.
0
)
)(
(
]
)
][(
)
[(
2
2
2
1
=
+
+
−
−
+
−
+
−
β
α
β
α
ω
β
α
ω
β
α
iqa
iqa
e
e
m
m
gdy przyjmiemy, że
m
m
m
=
=
2
1
, ilość rozwiązań się nie zmieni, a za to równanie się uprości:
0
)
cos
2
(
]
)
[(
2
2
2
2
=
+
+
−
−
+
qa
m
αβ
β
α
ω
β
α
2
δ
=
δ
ω
β
α
±
=
−
+
2
)
(
m
m
δ
β
α
ω
±
+
=
)
(
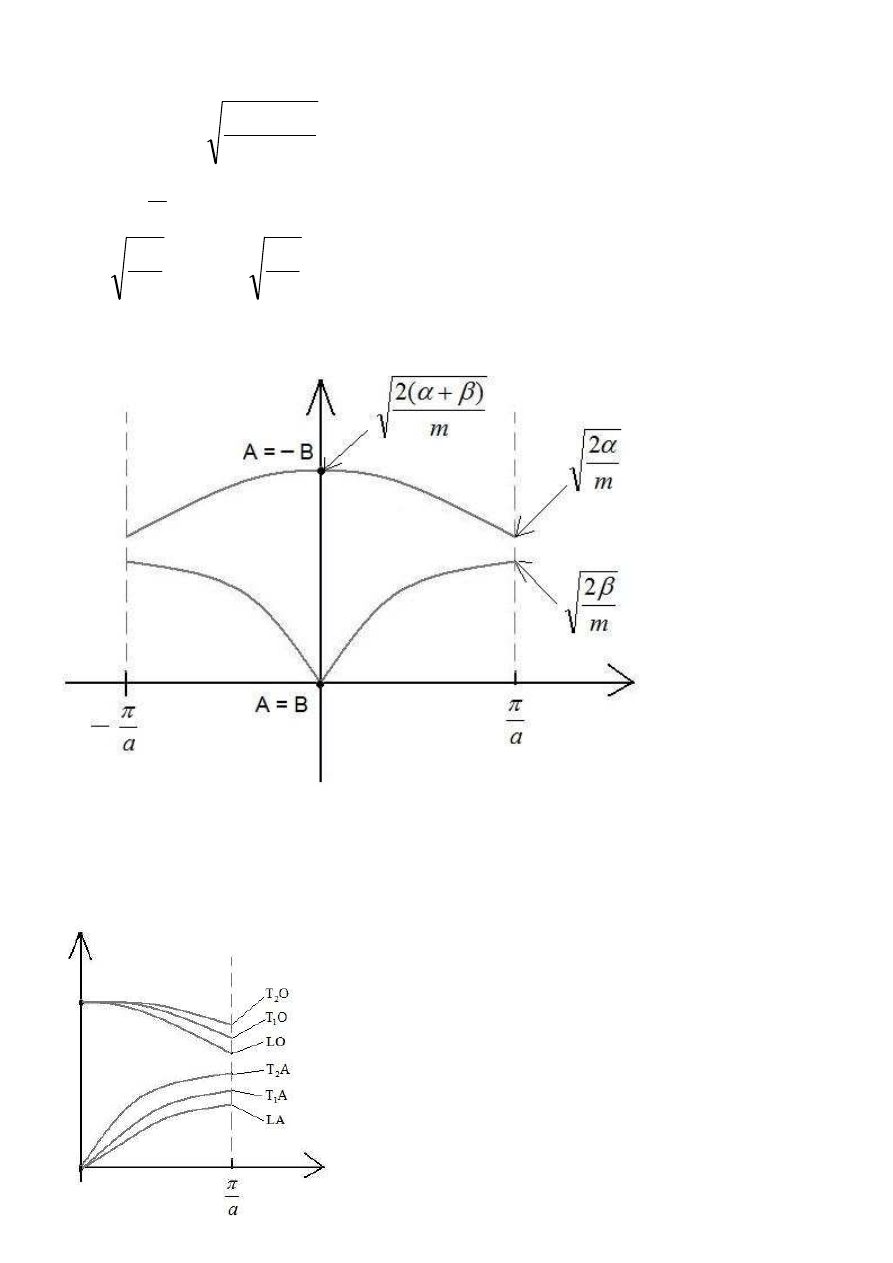
Gdy
0
=
q
,
2
2
2
2
)
(
2
β
α
αβ
β
α
δ
+
=
+
+
=
m
)
(
2
,
0
β
α
ω
ω
+
=
=
+
−
Gdy
a
q
π
=
,
2
2
2
2
)
(
2
β
α
αβ
β
α
δ
−
=
−
+
=
m
m
α
ω
β
ω
2
,
2
=
=
+
−
Jak zinterpretować to rozwiązanie?
Górna linia to drgania optyczne – atomy z jednego węzła wychylają się w przeciwne strony.
Dolna linia – drgania akustyczne, w których atomy z jednego węzła wychylają się w tę samą stronę.
Wśród tych drgań wyróżniamy jeszcze fale poprzeczne:
1
T
i
2
T
, oraz fale podłużne L.
Tworzą one tzw. gałęzie: 3 gałęzie akustyczne, oraz 3(n-1) gałęzi optycznych.
Wyszukiwarka
Podobne podstrony:
FCS Wszystko, co trzeba
METODY NUMERYCZNE wszystko co trzeba do zadan z wykładu
BTS Wszystko, co trzeba wiedzieć o królach K POPU Zupełnie nieoficjalny przewodnik Mackenzie Malcol
Biedny milioner Jak miec wszystko co trzeba i cieszyc sie zyciem
inne biedny milioner jak miec wszystko co trzeba i cieszyc sie zyciem tadeusz niwinski ebook
Biedny milioner Jak miec wszystko co trzeba i cieszyc sie zyciem biemil
Biedny milioner Jak miec wszystko co trzeba i cieszyc sie zyciem
Mikrofony z Tu 154 Nie wszystko co ważne stało się w kabinie
Wszystko co potrzebne do nauki na egzamin, Politechnika Gdańska, Zarządzanie WZiE, semestr 3, Zarząd
Co trzeba umieć
1326 wszystko, co mam r gawliński Y44BR22ZEACGMRBZHQNHIDFECE7JDHAI65JYMEY
CO zadania id 118396 Nieznany
więcej podobnych podstron