
PODSTAWY INFORMATYKI
KWANTOWEJ
EDWARD KWA´SNIEWICZ
GLIWICE, 2011

ii

Contents
Wst ¾
ep
v
ELEMENTY ALGEBRY LINIOWEJ
vii
0.1
LINIOWE PRZESTRZENIE WEKTOROWE . . . . . . . . . .
vii
0.1.1
Notacja i dodawanie wektorów . . . . . . . . . . . . . . .
vii
0.1.2
Liniowa kombinacja wektorów . . . . . . . . . . . . . . . . viii
0.1.3
Norma wektora . . . . . . . . . . . . . . . . . . . . . . . .
ix
0.1.4
Przestrze´n Hilberta . . . . . . . . . . . . . . . . . . . . . .
ix
0.2
OPERATORY LINIOWE . . . . . . . . . . . . . . . . . . . . . .
xi
0.2.1
Okre´slenie operatorów . . . . . . . . . . . . . . . . . . . .
xi
0.2.2
Relacja zupe÷
no´sci . . . . . . . . . . . . . . . . . . . . . .
xii
0.2.3
Macierzowa reprezentacja operatorów . . . . . . . . . . . xiii
0.2.4
Iloczyn zewn ¾
etrzny i reprezentacja macierzowa . . . . . . xiv
0.2.5
Macierze Pauliego . . . . . . . . . . . . . . . . . . . . . . xiv
0.2.6
Operatory rzutowe . . . . . . . . . . . . . . . . . . . . . .
xv
0.2.7
Warto´sci w÷
asne i wektory w÷
asne . . . . . . . . . . . . . . xvi
0.2.8
Operatory hermitowskie . . . . . . . . . . . . . . . . . . . xvii
0.2.9
Operator odwrotny . . . . . . . . . . . . . . . . . . . . . . xix
0.2.10 Operatory unitarne . . . . . . . . . . . . . . . . . . . . . . xix
0.2.11 Zmiana bazy . . . . . . . . . . . . . . . . . . . . . . . . . xix
0.2.12 Twierdzenie o diagonalizacji operatorów komutuj ¾
acych . .
xx
0.2.13
Rozk÷
ad spektralny operatora i twierdzenie spektralne . . xxi
0.2.14 ´Slad macierzy . . . . . . . . . . . . . . . . . . . . . . . . . xxii
0.2.15 Iloczyn tensorowy
. . . . . . . . . . . . . . . . . . . . . . xxiii
ELEMENTY MECHANIKI KWANTOWEJ
xxvii
0.2.16
Do´swiadczenie Sterna-Gerlacha
. . . . . . . . . . . . . . xxvii
0.2.17 Do´swiadczenie Younga . . . . . . . . . . . . . . . . . . . . xxix
0.2.18 Postulaty mechaniki kwantowej . . . . . . . . . . . . . . . xxx
0.2.19 Do´swiadczenie Sterna-Gerlacha w ´swietle postulatów mechanik
kwantowej
. . . . . . . . . . . . . . . . . . . . . . . . . . xxxvii
0.2.20 Stany spl ¾
atane. Paradoks EPR . . . . . . . . . . . . . . . xxxix
0.2.21 Nierówno´s´c Bella . . . . . . . . . . . . . . . . . . . . . . . xlii
iii

iv
CONTENTS
OPERATOR G ¾
ESTO´SCI
xlv
0.2.22 Operator g ¾
esto´sci dla stanu czystego . . . . . . . . . . . . xlvi
0.2.23 Ewolucja w czasie operatora g ¾
esto´sci . . . . . . . . . . . . xlvi
0.2.24 Operator g ¾
esto´sci dla stanów mieszanych
. . . . . . . . . xlvii
OBWODY KWANTOWE
li
0.2.25
Kubit . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
li
0.2.26 Sfera Blocha
. . . . . . . . . . . . . . . . . . . . . . . . .
lii
0.2.27 Pomiar stanu kubitu . . . . . . . . . . . . . . . . . . . . .
liii
0.2.28 Obwodowy model oblicze´n kwantowych . . . . . . . . . .
liv
0.2.29 Bramki dzia÷
aj ¾
ace na pojedy´nczy kubit
. . . . . . . . . .
lvi
0.2.30 Obroty sfery Blocha . . . . . . . . . . . . . . . . . . . . . lvii
0.2.31 Bramki kontrolne i generowanie stanów spl ¾
atanych . . . . lviii
0.2.32 Baza Bella
. . . . . . . . . . . . . . . . . . . . . . . . . . lxii
0.2.33 Uniwersalne bramki kwantowe
. . . . . . . . . . . . . . . lxii

Wst ¾
ep
Wyniki bada´n naukowych w ostatnich kilkudziesi ¾
eciu latach pokazuj ¾
a, ·
ze na-
jbardziej spektakularne osi ¾
agni ¾
ecia w nauce i technice pojawiaj ¾
a si ¾
e w obszarze
bada´n interdyscyplinarnych. Wybitnym tego przyk÷
adem s ¾
a obliczenia kwan-
towe i kwantowe przetwarzanie informacji, procesy oparte na prawach …zyki
kwantowej , które leg÷
y u podstaw nowej dyscypliny naukowej - informatyki
kwantowej.Drugim …larem informatyki kwantowej jest matematyka, której takie
dzia÷
y jak algebra, teoria liczb, rachunek prawdopodobie´nstwa dostarczaj ¾
a narz ¾
edzido
opisu algorytmów kwantowych. Wreszcie do skostruwania samego narz ¾
edzia
informatyki kwantowej - komputera kwanntowego - konieczny jest trzeci …lar
zaawansowanych technologii in·
zynierskich.
Obliczenia kwantowe wykonywane s ¾
a na komputerze kwantowym, w kórym
no´snikami informacji s ¾
a obiekty o dwóch bazowych stanach kwantowych, takie
jak na przyk÷
ad pojedy´ncze elektrony, atomy, nukleony, j ¾
adra atomowe, itp .
Uk÷
ady takich skorelowanych obiektów mikroskopowych mog ¾
a znajdowa´c si ¾
e
w stanach kwantowych, które zgodnie z podstawow ¾
a zasad ¾
a mechaniki kwan-
towej -zasad ¾
a superpozycji- s ¾
a superpozycj ¾
a stanów kwantowych poszczegónych
obiektów. Zgodnie z zasad ¾
a superpozycji takie uk÷
ady kwantowe, najogólniej
mówi ¾
ac komputery kwantowe, mog ¾
a przyjmowa´c ró·
zne stany równocze´snie. Za-
tem stan wej´sciowy komputera kwantowego mo·
ze by´c superpozycj ¾
a wielu mo·
zli-
wych danych wej´sciowych (reprezentowanych przez superpozycj ¾
e odpowiednich
stanów wej´sciowych), a stan wyj´sciowy superpozycj ¾
a wyników ró·
znych danych
wej´sciowych. Mo·
zna wi ¾
ec na komputerze kwantowym wykonywa´c równocze´snie
obliczenia zadane okre´slonym algorytmem dla wielu ró·
znych danych wej´sciowych.
Ten fakt wskazuje na ogromne, potencjalne mo·
zliwo´sci obliczeniowe komputerów
kwantowych, nieosi ¾
agalne na komputerach klasycznych.
Inn ¾
a cech ¾
a stanów kwantowych uk÷
adów z÷
o·
zonych z obiektów o dwóch
stanach jest ich spl ¾
atanie, które przejawia w tym, ·
ze indywidualne cechy poszczegónych
sk÷
adników uk÷
adu nie s ¾
a dok÷
adnie okre´slone. Stany spl ¾
atane wykazuj ¾
a nie spo-
tykane w …zyce klasycznej w÷
asno´sci, które podobnie jak superpozycja stanów,
s ¾
a podstaw ¾
a oblicze´n kwantowych i kwantowego przetwarzania informacji (za-
gadnienia teleportacji, kryptogra…i kwantowej, superg ¾
estego kodowania).
Obliczenia na komputerze kwantowym polegaj ¾
a na odpowiednim sterowa-
niu uk÷
adów z÷
o·
zonych z mikroskopowych obiektów o dwóch bazowych stanach
kwantowych. Najogólniej mowi ¾
ac sterowanie uk÷
adami kwantowyymi polega na
odpowienim przygotowaniu stanu wej´sciowego takiego ukladu (wprowadzeniu
v

vi
WST ¾
EP
danych wej´sciowych) oraz przekszta÷
ceniu go przy pomocy zadanego algorytmu
do stanu wyj´sciowego i w konsekwencji do otrzymania wyników oblicze´n. Jednak
od razu wida´c, ·
ze sterowanie uk÷
adami z÷
o·
zonymi z obiektów mikroskopowych
jest bardzo trudne bowiem mechanika kwantowa uczy, ·
ze ka·
zda ingerencja w
uk÷
ad mikroskopowy powodujeniepowtarzaln ¾
a zmian ¾
e jego stanu. Dlatego kom-
putery kwantowe nie wysz÷
y jeszcze poza stadium konstrukcji laboratoryjnych,
ale jak pokazuje historia bada´n naukowych powszechne u·
zytkowanie komput-
erów kwantowych jest tylko kwesti ¾
a czasu.
Dotychczasowe badania teoretyczne dowodz ¾
a, ·
ze obliczenia kwantowe s ¾
a
nieporównywalnie szybsze od oblicze´n na komputerze klasycznym. Wybitnym
tego przyk÷
adem jest kwantowy algorytm Shora faktoryzacji du·
zych liczb na
czynniki pierwsze. Jego implementacja na komputerze kwantowym, je´sli taki
powstanie, pozwoli÷
aby szybko z÷
ama´c powszechnie stosowane kody zabezpiecza-
j ¾
ace ró·
zne sekretne dane.
Równie·
z kwantowe systemy przetwarania danych
oparte na zjawisku teleportacji stanu kwantowego obiektu mikroskopowego umo·
zli-
wiaj ¾
a. tworzenie systemów kryptogra…cznych, które nie mo·
zna z÷
ama´c.

ELEMENTY ALGEBRY
LINIOWEJ
0.1
LINIOWE PRZESTRZENIE WEKTOROWE
0.1.1
Notacja i dodawanie wektorów
Podstawowym narz ¾
edziem opisu zagadnie´n z informatyki kwantowej s ¾
a sko´nc-
zone, zespolone liniowe przestrzenie wektorowe C
n
.
Wed÷
ug notacji zapro-
ponowanejj przez Diraca dowolny wektor nale·
zacy do przestrzeni C
n
zapisujemy
j i =
2
6
6
6
6
6
6
4
1
2
:
:
:
n
3
7
7
7
7
7
7
5
(1)
gdzie liczby
1
;
2
; :::;
n
2 C (C-zbiór liczb zespolonych) s ¾
a wspo÷
rz ¾
ednymi
wektora j i. Wektor j i nazywamy wektorem/stanem "ket". Dwa wektory
"ket" mo·
zna dodawa´c, tzn.wektor j i 2 C
n
jest sum ¾
a wektorów j i i j i 2 C
n
gdy
i
=
i
+
i
, i = 1; 2; :::; n
(2)
Dla dowolnych wektorów
j i ; j i ; j i 2 C
n
i dowolnych c; d 2 C dzia÷anie
dodawania wektorów posiada nast ¾
epuj ¾
ace w÷
asno´sci
j i + j i = j i + j i
(3)
j i + (j i + j i) = (j i + j i) + j i
(4)
c j i 2 C
n
(5)
c(j i + j i) = c j i + c j i
(6)
(c + d) j i = c j i + d j i
(7)
(cd) j i = c(d j i)
(8)
vii

viii
ELEMENTY ALGEBRY LINIOWEJ
Wektor zerowy 0 2 C
n
de…niujemy: dla dowolnego j i 2 C
n
j i + 0 = j i :
W tym miejscu zwracamy uwag ¾
e, ·
ze do oznaczenia wektora zerowego nie stosu-
jemy oznaczenia j0i gdy·
z jest ono zarezerwowane do oznaczania jednego z wek-
torów bazowych dwówymiarowej przestrzeni Hilberta C
2
(de…nicja przestrzeni
Hilberta podana jest w rozdziale....).
0.1.2
Liniowa kombinacja wektorów
Niech zbiór liczb c
1
; c
2
; :::; c
n
2 C; a zbiór wektorów j
1
i ; j
2
i ; :::; j
n
i 2 C
n
.
Wyra·
zenie
c
1
j
1
i + c
2
j
2
i + :::c
n
j
n
i =
n
X
i=1
c
i
j
i
i
(9)
nazywamy liniow ¾
a kombinacj ¾
a tych wektorów, która w ogólno´sci te·
z jest wek-
torem, elementem przestrzeni C
n
Gdy równanie
c
1
j
1
i + c
2
j
2
i + :::c
n
j
n
i = 0
(10)
zachodzi wtedy i tylko wtedy gdy c
1
= c
2
= ::: = c
n
= 0 to wektory j
1
i ; j
2
i ; :::; j
n
i
2 C
n
s ¾
a liniowo niezale·
zne. W przeciwnym razie, gdy chocia·
z jede ze wspó÷
czyn-
ników c
i
6= 0 to wektory j
i
i s ¾
a liniowo zale·
zne. Wektory liniowo niezale·
zne
rozpinaj ¾
a przestrze´n C
n
poniewa·
z dowolny wektor z tej przestrzeni mo·
zna
wyrazi´c w postaci (9).
Iloczyn skalarny wektorów
Iloczyn skalarny dwóch wektorów j i, j i 2 C
n
jest liczb ¾
a zespolon ¾
a, któr ¾
a
zapisujemy h j i, spe÷niaj ¾
ac ¾
a nast ¾
epuj ¾
ace warunki:
h j i = h j i
gdzie znak ( ) oznacza zespolone sprz ¾
e·
zenie,
(11)
h j c + d i = c h j i + d h j i gdzie j i ; j i ; j i 2 C
n
; c; d 2 C
(12)
h j i
0 dla dowolnego j i 2 C
n
; równo´s´c zachodzi tylko wtedy gdy j i = 0
(13)
Na podstawie w÷
asno´sci (??) mo·
zna sprawdzi´c, ·
ze
hc j i = c h j i
(14)
Aby policzy´c iloczyn skalarny dwóch wektorów musimy zde…niowa´c co rozu-
miemy przez symbol h j :Otó·
z oznacza on hermitowskie sprz ¾
e·
zenie wektora j i,
tzn
h j = (j i)
y
=
2
6
6
6
6
6
6
4
1
2
:
:
:
n
3
7
7
7
7
7
7
5
y
=
1
2
:
:
:
n
(15)
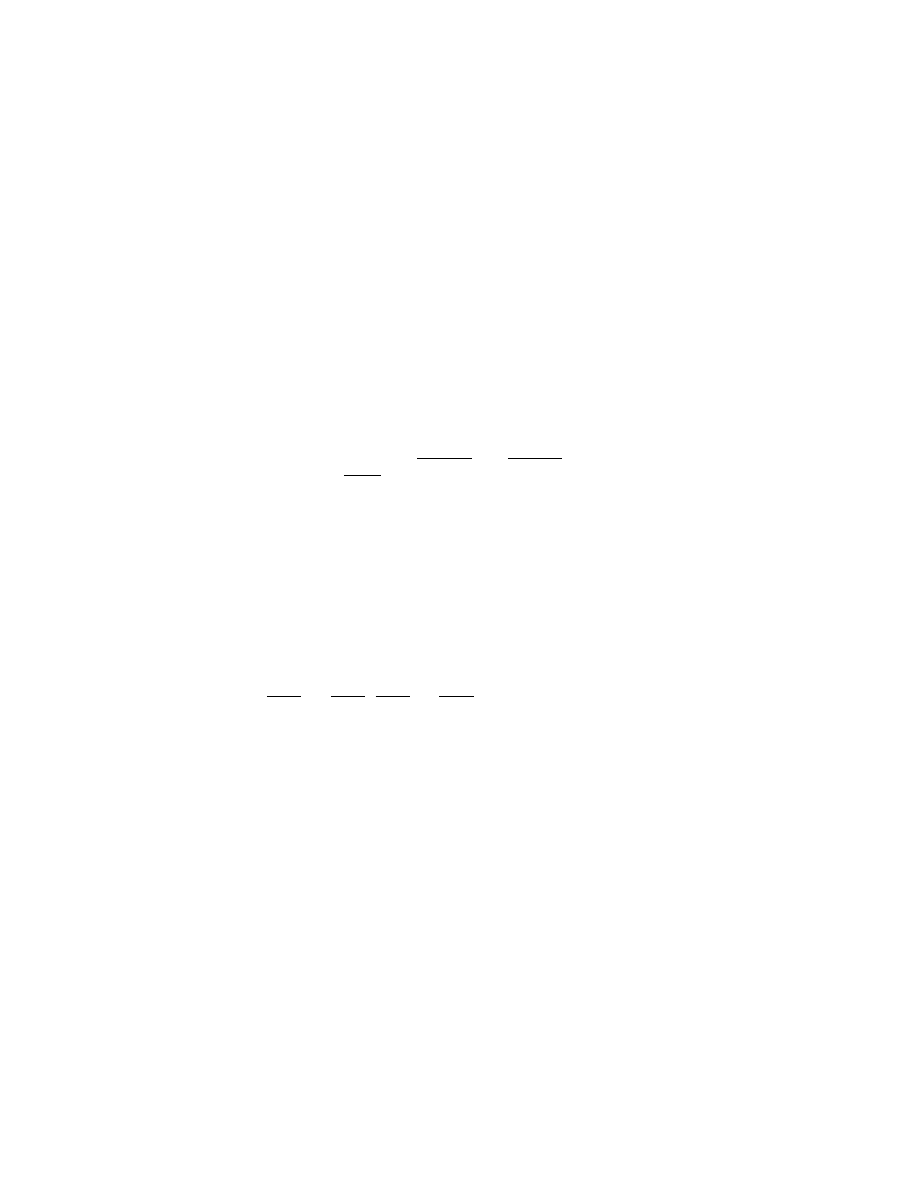
0.1.
LINIOWE PRZESTRZENIE WEKTOROWE
ix
Wektor h j nazywamy dualnym wektorem do wektora j i albo cz ¾
e´sciej wektorem
"bra". Zgodnie z powy·
zsz ¾
a notacj ¾
a loczyn skalarny dwóch wektorów j i i j i
2 C
n
h j i =
1
2
:
:
:
n
2
6
6
6
6
6
6
4
1
2
:
:
:
n
3
7
7
7
7
7
7
5
=
n
X
i=1
i
i
(16)
0.1.3
Norma wektora
Norm ¾
e wektora
j i 2 C
n
de…niujemy
kj ik =
p
h j i =
v
u
u
t
n
X
i=1
i
i
=
v
u
u
t
n
X
i=1
j
i
j
2
(17)
Wektor j i jest unormowany gdy iloczyn skalarny h j i = 1
h j i = 1
(18)
Je´sli nie jest spe÷
niony warunek (18) to mówimy, ·
ze wektor j i = (
1
;
2
; :::;
n
)
T
jest wektorem nieunormowanym (górny indeks T
oznacza transponowanie).
Mo·
zna go zawsze unormowa´c dziel ¾
ac jego wspó÷
rz ¾
edne przez norm ¾
e (17) . Un-
ormowany wektor
j
0
i =
j i
kj ik
= (
1
kj ik
;
2
kj ik
; :::;
n
kj ik
)
T
= (
0
1
;
0
2
; :::;
0
n
)
T
(19)
0.1.4
Przestrze´
n Hilberta
Przed podaniem de…nicji przestrzeni Hilberta, zde…niujemy poj ¾
ecie przestrzeni
unitarnej i przestrzeni zupe÷
nej.
Liniow ¾
a , zespolon ¾
a przestrze´n wektorow ¾
a,
w której jest zde…niowany iloczyn skalarny nazywamy przestrzeni ¾
a unitarn ¾
a.
Natomiast przestrze´n jest zupe÷
na wtedy gdy dowolny ci ¾
ag o wyrazach nale·
z ¾
a-
cych do danej przestrzeni posiada granic ¾
e, która te·
z jest elementem tej przestrzeni
Pos÷
uguj ¾
ac si ¾
e poj ¾
eciami przestrzeni unitarnej i przestrzeni zupe÷
nej de…nicja
przestrzeni Hilberta jest nast ¾
epuj ¾
aca.
Przestrzeni ¾
a Hilberta nazywamy unitarn ¾
a przestrze´
n zupe÷
n ¾
a.
Przestrze´n Hilberta mo·
ze by´c sko´nczona, gdy wymiar przestrzeni jest sko´nc-
zony, lub nieskonczona gdy jej wymiar jest niesko´nczony. W drugim przypadku
musi by´c jednak przstrzeni ¾
a przeliczaln ¾
a tzn. zbiór wektorów bazowych rozpina-
j ¾
acych przestrze´n musi by´c przeliczalny.

x
ELEMENTY ALGEBRY LINIOWEJ
Nierowno´s´c Couchy’ego -Schwartza i nierówno´s´c trójk ¾
ata
Dla dowolnych dwóch wektorów j i, j i 2 C
n
spe÷
niona jest tzw. nierówno´s´c
Couchy’ego-Schwartza
jh j ij
2
h j i h j i
(20)
W szczególnym przypadku gdy iloczyn skalarny jest rzeczywisty nieróno´s´c Couchy’ego-
Schwartza ma prost ¾
a interpretacj ¾
e geometryczn ¾
a. Nierówno´s´c (20) upraszcza
si ¾
e do wyra·
zenia
1
h j i
kj ik kj ik
1
(21)
a sam iloczyn skalarny
h j i = kj ik kj ik cos #
(22)
gdzie # jest k ¾
atem mi ¾
edzy wektorami j i i j i.
Nierówno´s´c
p
h + j + i
p
h j i +
p
h j i
(23)
nazywamy nierówno´sci ¾
a trójk ¾
ata. Pos÷
uguj ¾
ac si ¾
e de…nicj ¾
a normy wektora (rów-
nanie (17)) mo·
zna j ¾
a zapisa´c nast ¾
epuj ¾
aco
kh + j + ik
kh j ik + kh j ik
(24)
co oznacza, ·
ze d÷
ugo´s´c sumy wektorów nie mo·
ze by´c wi ¾
eksza od sumy d÷
ugo´sci
tych wektorów podobnie jak w trójk ¾
acie suma d÷
ugo´sci boków przyleg÷
ych do
danego k ¾
ata nie mo·
ze by´c mniejsza od d÷
ugo´sci boku przeciwleg÷
ego do tego
k ¾
ata.
Ortonormalno´s´c stanów
Dwa wektory j i i j i s ¾
a ortogonalne gdy iloczyn skalarny
h j i = 0
(25)
Gdy dodatkowo s ¾
a one unormowane do jedno´s´ci tzn. gdy kj ik = 1 i kj ik = 1
to mówimy, ·
ze s ¾
a ortonormalne. Zbiór wektorów fj
1
i ; j
2
i ; :::; j
n
ig tworzy
zbiór wektorów ortonormalnych gdy
h
i
j
j
i =
ij
(i; j = 1; 2; :::; n)
(26)
Zgodnie z de…nicj ¾
a liniowej niezale·
zno´sci wektorów (wzór 10) wektory orto-
normalne s ¾
a liniowo niezale·
zne.
Wymiar n przestrzeni wektorowej V
n
jest
równy maksymalnej liczbie liniowo niezale·
znych wektorów fj
1
i ; j
2
i ; :::; j
n
ig
2 V
n
. Wektory te tworz ¾
a baz ¾
e przestrzeni V
n
:Dodatkowo, je´sli s ¾
a one ortonor-
malne to tworz ¾
a baz ¾
e ortonormaln ¾
a przestrzeni V
n
.
W ortonormalnej bazie
fj
1
i ; j
2
i ; :::; j
n
ig dowolny wektor j i 2 V
n
mo·
zna zapisa´c
j i =
n
X
i=1
a
i
j
i
i
(27)

0.2. OPERATORY LINIOWE
xi
Korzystaj ¾
ac z warunku (26) wspó÷
czynniki a
i
wyliczamy z wzoru
a
i
= h
i
j i
(28)
Je´sli przestrze´n V
n
jest przestrzeni ¾
a zepolon ¾
a tzn. gdy V
n
= C
n
to wspó÷
czyn-
niki a
i
( 28) s ¾
a zespolone. Mówimy te·
z, ·
ze ortonormlna baza fj
1
i ; j
2
i ; :::; j
n
ig
przestrzeni V
n
(C
n
) tworzy zupe÷
ny zbiór wektorów, a zbiór wspó÷
czynników
fa
1
; a
2
; :::; a
n
) stanowi reprezentacj ¾
e wektora j i w bazie fj
1
i ; j
2
i ; :::; j
n
ig.
Ortonormalizacja Grama-Schmidta
Ortonormalizacja Grama-Schmidta jest procedur ¾
a, która pozwala otrzyma´c baz ¾
e
ortonormaln ¾
a przestrzeni V
n
z bazy nieortogonalnej (czyli z dowolnego zbioru o
maksymalnej liczbie n wektorów liniowo niezale·
znych w przestrzeni V
n
). Niech
zbiór wektorów fj
1
i ; j
2
i ; :::; j
n
ig tworzy baz ¾
e n-wymiarowej przestrzeni
V
n
, niekoniecznie ortogonaln ¾
a
i unormowan ¾
a.
Utwórzmy z
tych wektorów now ¾
a baz ¾
e wektorów, które s ¾
a ortogonalne stosuj ¾
ac nast ¾
epuj ¾
ac ¾
a
procedur ¾
e Grama-Schmidta
j
1
i = j
1
i
(29)
j
2
i = j
2
i
h
1
j
2
i
h
1
j
1
i
j
1
i
(30)
:
(31)
:
(32)
:
(33)
j
n
i = j
2
i = j
n
i
h
1
j
n
i
h
1
j
1
i
j
1
i
h
2
j
n
i
h
2
j
2
i
j
2
i
:::
h
n 1
j
n
i
h
n 1
j
n 1
i
j
n 1
i
(34)
Normuj ¾
ac otrzymane wektory (34) otrzymujemy ortonormaln ¾
a baz ¾
e
fj
i
i =
j
i
i
kj
i
ik
g; i =; 2; :::; n
(35)
przestrzeni V
n
(lub C
n
). Dowolny wektor nale·
z ¾
acy do tej przestrzeni mo·
zna
rozwin ¾
a´c w bazie (35) wed÷
ug wzoru (27).
0.2
OPERATORY LINIOWE
0.2.1
Okre´slenie operatorów
Operator okre´sla matematyczne odwzorowanie, które przekszta÷
ca dan ¾
a funkcj ¾
e
w inn ¾
a funkcj ¾
e. Operatory cz ¾
esto oznaczane s ¾
a literami, nad którymi umieszcza
si ¾
e daszek. Na przyk÷
ad mo·
zemy zde…niowa´c operator ró·
zniczkowania
b
D =
d
dx
(36)

xii
ELEMENTY ALGEBRY LINIOWEJ
który owzorowuje funkcj ¾
e f (x) w jej pochodn ¾
a. Uogólniaj ¾
ac, mo·
zemy okre´sli´c
operatory w przestrzeniach wektorowych. Wówczas operator b
A okre´sla matem-
atyczn ¾
a regu÷¾
e, wed÷
ug której wektor ket j i jest przekszta÷cany w wektor ket
j i
b
A j i = j i
(37)
Operatory mog ¾
a równie·
z dzia÷
a´c na wektory bra
h j b
A = h j
(38)
Za÷
ó·
zmy, ze dany jest operator
b
A , który odwzorowuje dowolny wektor
j i 2 V
n
na inny wektor j i 2 V
n
tj. j i = b
A j i .
b
A
jest operatorem
liniowym je´sli dla dowolnych wektorów
j i ; j i i dowolnych liczb a; b 2 C
posiada w÷
asno´s´c
b
A(a j i + b j i) = a b
A j i + b b
A j i
(39)
W szczególno´sci operatorem liniowym jest operator identyczno´sci (b
I j i = j i).
Podobnie operatorem linowym jest operator b
N , który dowolny wektor odw-
zorowuje w wektor zerowy ( b
N j i = 0). Dwa operatory b
A; b
B s ¾
a równe, tzn
b
A = b
B gdy dla dowolnego wektora j i zachodzi równo´s´c
b
A j i = b
B j i
(40)
Sum ¾
e dwóch operatorów liniowych
b
C = b
A + b
B de…niujemy
b
C j i = ( b
A + b
B) j i = b
A j i + b
B j i
(41)
Produkt (z÷
o·
zenie) dwóch operatorów liniowych
b
D = b
A b
B de…niujemy przy
pomocy zwi ¾
azku
b
D j i = b
A b
B j i = b
A( b
B j i)
(42)
Zawsze b
A + b
B = b
B + b
A , ale nie zawsze b
A b
B = b
B b
A.
Je´sli b
A b
B = b
B b
A to
mówimy, ·
ze operatory b
A i b
B komutuj ¾
a.
0.2.2
Relacja zupe÷
no´sci
W iemy, ·
ze w ortonormalnej bazie fj
1
i ; j
2
i ; :::; j
n
ig dowolny wektor j i 2
V
n
mo·
zna zapisa´c j i =
P
n
i=1
a
i
j
i
i, gdzie a
i
= h
i
j i. Znaczy to, ·
ze
j i =
n
X
i=1
a
i
j
i
i =
n
X
i=1
j
i
i h
i
j i
(43)
Z wzoru (43) ÷
atwo wywnioskowa´c, ·
ze
P
n
i=1
j
i
i h
i
j jest operatorem poniewa·
z
zgodnie z (??) przekszta÷
ca on wektor w wektor. Ponaddto, relacja (43) jest
s÷
uszna dla dowolnego wektora j i 2 V
n
i przekszta÷
ca go w siebie, co oznacza
·
ze operator
P
n
i=1
j
i
i ha
i
j
jest operatorem identyczno´sci. Relacj ¾
e
b
I =
n
X
i=1
j
i
i h
i
j
(44)

0.2. OPERATORY LINIOWE
xiii
nazywamy relacj ¾
a zupe÷
no´sci dla przestrzeni V
n
.
0.2.3
Macierzowa reprezentacja operatorów
Niech operator b
A dzia÷
a na dowolny wektor j i 2 V
n
daj ¾
ac w wyniku wektor
j i 2 V
n
tj.
b
A j i = j i
(45)
Wektory j i i j i mo·
zna przedstawi´c jako kombinacja liniowa wektorów zu-
pe÷
nej, ortonormalnej bazy fj
1
i ; j
2
i ; :::; j
n
ig rozpinaj ¾
acej przestrze´n V
n
. Mamy
j i = b
I j i =
n
X
i=1
j
i
i h
i
j i =
n
X
i=1
a
i
j
i
i
(46)
oraz
j i = b
I j i =
n
X
i=1
j
i
i h
i
j i =
n
X
i=1
b
i
j
i
i
(47)
Z wzorów (45), (46) i (47) otrzymujemy b
i
= h
i
j i = h
i
j b
A j i =
P
n
j=1
h
i
j b
A
j
a
j
czyli
b
i
=
n
X
j=1
A
ij
a
j
gdzie A
ij
= h
i
j b
A
j
; i = 1; 2; :::; n
(48)
Uk÷
ad równa´n (48) mo·
zna zapisa´c w postaci macierzowej
2
6
6
6
6
6
6
4
b
1
b
2
:
:
:
b
n
3
7
7
7
7
7
7
5
=
2
6
6
6
6
6
6
4
A
11
A12
:
:
:
A
1n
A
21
A
22
:
:
:
A
2n
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
A
n1
A
n2
:
:
:
A
nn
3
7
7
7
7
7
7
5
2
6
6
6
6
6
6
4
a
1
a
2
:
.
:
a
n
3
7
7
7
7
7
7
5
(49)
gdzie zgodnie z notacj ¾
a wprowadzon ¾
a w rozdziale (0.1.2) wektor j i zapiszemy
jako wektor kolumnowy
j i =
2
6
6
6
6
6
6
4
a
1
a
2
:
:
.
a
n
3
7
7
7
7
7
7
5
(50)
a wektor h j = (j i)
y
zapiszemy w formie macierzy jednowierszowej, tj.
h j =
b
1
b
2
:
:
:
b
n
(51)

xiv
ELEMENTY ALGEBRY LINIOWEJ
Macierz
[A
ij
] nazywamy reprezentacj ¾
a macierzow ¾
a operatora b
A
w bazie
fj
1
i ; j
2
i ; :::; j
n
ig.
Korzystaj ¾
ac z operatora identyczno´sci (??) operator b
A
mo·
zna wyrazi´c nast ¾
epuj ¾
aco
b
A = b
I b
A b
I = (
n
X
i=1
j
i
i h
i
j) b
A(
n
X
i=1
j
i
i h
i
j) =
n
X
i=1
h
i
j b
A
j
j
i
i
j
(52)
Oczywi´scie, ten sam operator mo·
zna w identyczny sposób wyrazi´c w innej orto-
normalnej bazie, czyli reprezentacja macierzowa operatora zale·
zy od wyboru
bazy (patrz rozdzia÷(??)).
0.2.4
Iloczyn zewn ¾
etrzny i reprezentacja macierzowa
Iloczyn stanu ket j i ze stanem bra h j ; który zapisujemy jako j i h j nazy-
wamy iloczynem zewn ¾
etrznym. Wielko´s´c ta jest operatorem, bo je´sli zadzia÷
amy
na niego dowolnym stanem j i, tj.
(j i h j) j i = h j i j i
(53)
to otrzymamy stan ket j i pomno·
zony przez liczb ¾
e zespolon ¾
a h j i.
Je´sli
rozwiniemy stany j i i h j w ortonormalnej bazie fj
1
i ; j
2
i ; :::; j
n
ig wedlug
wzoru (43), a nast ¾
epnie skorzystamy z notacji macierzowej tych stanów, tj.
j i = [ a
1
a
2
:
:
:
a
n
]
T
(54)
oraz
h j = [ b
1
b
2
:
:
:
b
n
]
(55)
to w reprezentacji macierzowej
j i h j =
2
6
6
6
6
6
6
4
a
1
a
2
:
:
:
a
n
3
7
7
7
7
7
7
5
[ b
1
b
2
:
:
:
b
n
]
2
6
6
6
6
6
6
4
a
1
b
^
1
a
1
b
2
:
:
:
a
1
b
n
a
2
b
1
a
2
b
2
:
:
:
a
2
b
n
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
:
a
n
b
1
a
n
b
2
:
:
:
a
n
b
n
3
7
7
7
7
7
7
5
(56)
Znowu widzimy, ·
ze macierzowa reprezentacja iloczynu zewn ¾
etrznego j i h j za-
le·
zy o wyboru bazy, w ktorej rozwijamy stany h j i j i.
0.2.5
Macierze Pauliego
Macierze Pauliego w mechanice kwantowej maj ¾
a podstawowe znaczenie dla opisu
cz ¾
astek, których spin w jednostkach
h
jest równy
1
2
: Maj ¾
a one równie·
z funda-
mentalne znaczenie w kwantowych obliczeniach. S ¾
a one nast ¾
epuj ¾
ace
x
=
0
1
1
0
,
y
=
0
i
i
0
,
z
=
1
0
0
1
(57)

0.2. OPERATORY LINIOWE
xv
Jak ÷
atwo si ¾
e przekona´c stanom w÷
asnym macierzy
z
j0i =
1
0
i j1i =
0
1
(58)
odpowiadaj ¾
a warto´sci w÷
asne 1 i
1 (patrz rozdzia÷(0.2.7)) co mo·
zemy zapisa´c
tak
z
j0i = j0i ;
z
j1i =
j1i
(59)
Bezpo´srednio otrzymujemy, ·
ze dzia÷
anie operatorów
x
i
y
na stany (58) jest
nast ¾
epuj ¾
ace
x
j0i = j1i ;
x
j1i = j0i
(60)
y
j0i = i j1i ;
y j1i = i j0i
(61)
Operator
x
nazywany jest te·
z operatorem negacji NOT.
Macierze Pauliego spe÷
niaj ¾
a nast ¾
epuj ¾
ace zwi ¾
azki
2
x
=
2
y
=
2
z
= I gdzie I =
1
0
0
1
(62)
x
y
= i
z
,
y
z
= i
x
oraz
z
x
= i
y
(63)
0.2.6
Operatory rzutowe
Operatory rzutowe to klasa operatorów liniowych. Je´sli np. j i 2 V
n
jest
wektorem jednostkowym to rzut dowolnego wektora j i na kierunek wektora
j i jest wektorem, który mo·
zna zapisa´c
j i = b
P j i = j i h j i
(64)
Operator b
P = j i h j nazywamy operatorem rzutowym. Od razu otrzymujemy
b
P j i = j i oraz b
P j i = 0 gdy h j i = 0:Ponadto operator rzutowy spe÷nia
zwi ¾
azek
b
P = b
P
2
(65)
Operator (65) mo·
zna uogólni´c na operator rzutuj ¾
acy na podprzestrze´n V
m
przestrzeni V
n
(m < n) rozpinan ¾
a przez ortonormalny zbiór wektorów fj
1
i ; j
2
i ; :::; j
m
ig
b
P =
m
X
i=1
j
i
i h
i
j
(66)
Poniewa·
z h
i
j
j
i =
ij
otrzymujemy
b
P = b
P
2
(67)
Ka·
zdy operator, który spe÷
nia równanie (67) jest operatorem rzutowym.

xvi
ELEMENTY ALGEBRY LINIOWEJ
0.2.7
Warto´sci w÷
asne i wektory w÷
asne
Wektor j i (j i 6= 0) jest wektorem w÷asnym operatora liniowego b
A gdy
b
A j i = j i
(68)
Zespolon ¾
a liczb ¾
e
w równaniu (68) nazywamy waro´sci ¾
a w÷
asn ¾
a odpowiadaj ¾
ac ¾
a
wektorowi w÷
asnemu j i operatora b
A:Zagadnienie w÷
asne okre´slone równaniem
(68) ma zawsze rozwi ¾
azanie. Rzeczywi´scie, korzystaj ¾
ac z relacji zupe÷
no´sci( 44)
wektory j i i b
A j i mo·
zna rozwin ¾
a´c w ortonormalnej bazie fj
1
i ; j
2
i ; :::; j
n
ig
rozpinaj ¾
acej przestrze´n V
n
otrzymuj ¾
ac
j i = b
I j i =
n
X
i=1
j
i
i h
i
j i =
n
X
i=1
a
i
j
i
i gdzie a
i
= h
i
j i
(69)
oraz
b
A j i = b
I b
A j i =
n
X
i=1
j
i
i h
i
j b
A j i =
n
X
i=1
c
i
j
i
i gdzie c
i
= h
i
j b
A j i
(70)
Z drugiej strony
c
i
= h
i
j b
A b
I j i =
n
X
j=1
h
i
j b
A
j
h
j
j i =
n
X
j=1
A
ij
a
j
(71)
Wstawiaj ¾
ac (??) do (68) otrzymujemy równanie
n
X
i=1
(
n
X
j=1
A
ij
a
j
a
i
) j
i
i = 0
(72)
które jest spe÷
nione gdy
n
X
j=1
A
ij
a
j
a
i
=
n
X
j=1
(A
ij
ij
)a
j
= 0 dla i = 1; 2; :::; n
(73)
Uk÷
ad n jednorodnych linowych równa´n (73) ma rozwi ¾
azanie niezerowe je´sli
warto´sci w÷
asne
spe÷
niaj ¾
a równanie charakterystyczne
det(A
I) = det
A
11
A
12
:
:
A
1n
A
21
A
22
:
:
A
2n
:
:
:
:
:
:
:
:
:
:
A
n1
A
n2
:
:
A
nn
= 0
(74)
Wiemy, ·
ze det(A
I) jest wielomianem stopnia n ze wzgl ¾
edu na niewiadom ¾
a
. Fundamentalne twierdzenie algebry mówi, ·
ze równanie det(A
I) = 0
ma n zespolonych pierwiastków
1
;
2
; :::;
n
co oznacza, ·
ze równanie w÷
asne
(68) ma zawsze rozwi ¾
azanie. Mo·
zna pokaza´c, ·
ze równanie charakterystyczne
(74) zale·
zy tylko od operatora b
A, a nie zale·
zy od wyboru bazy (macierzowej
reprezentacji operatora A). Dlatego te·
z warto´sci w÷
asne nie zale·
z ¾
a od macier-
zowej reprezentacji operatora b
A .

0.2. OPERATORY LINIOWE
xvii
0.2.8
Operatory hermitowskie
Dla dowolnego operatora b
A dzia÷
aj ¾
acego w przestrzeni Hilberta H istnieje tylko
jeden operator A
y
(te·
z dzia÷
aj ¾
acy w przestrzeni H ) zwany operatorem sprz ¾
e·
zonym
po hermitowsku do operatora b
A , taki ·
ze dla wszystkich wektorów j i ; j i 2 H
h j b
A i = h b
A
y
j i
(75)
Z de…nicji (75) wynika, ·
ze
h b
A j i = h
b
A
y
E
(76)
Rzeczywi´scie, korzystaj ¾
ac z w÷
asno´sci iloczynu skalarnego (11) h b
A j i = h
b
A
E
=
h b
A
y
j i = h
b
A
y
E
.Równie·
z otrzymujemy, ·
ze ( b
A
y
)
y
= b
A .
Przy obliczaniu wyra·
ze´n sprz ¾
e·
zonych po hermitowsku post ¾
epujemy nast ¾
epu-
j ¾
aco; wszystkie sta÷
e wyst ¾
epuj ¾
ace w danym wyra·
zeniu zast ¾
epujemy ich zespolonym
sprz ¾
e·
zeniem, wszystkie stany ket zast ¾
epujemy ich stanami bra, a stany bra za-
st ¾
epujemy ich stanami ket, natomiast operatory zast ¾
epujemy ich sprz ¾
e·
zeniami
po hermitowsku. Gdy w wyra·
zeniu wyst ¾
epuje iloczyn operatorów to porz ¾
adek
ich sprz ¾
e·
ze´n po hermitowsku musi by´c odwrócony. Typowe przypadki sprz ¾
ega-
nia po hermitowsku wyra·
ze´n wyja´sniaj ¾
a nast ¾
epuj ¾
ace wzory
( b
A)
y
=
b
A
(77)
(j i)
y
= h j
(78)
(h j)
y
= j i
(79)
( b
Ac
B)
y
= b
B
y
b
A
y
(80)
( b
A j i)
y
= h j b
A
y
(81)
( b
A b
B j i)
y
= h j b
B
y
b
A
y
(82)
Szczególne znaczenie w mechanice kwantowej i informatyce kwantowej maj ¾
a
operatory hermitowskie (nazywane te·
z samosprz ¾
e·
zonymi) tj. takie , ·
ze
b
A
y
= b
A
(83)
Gdy spe÷
niony jest warunek (83) iloczyn skalarny h
b
A
E
jest liczb ¾
a rzeczy-
wist ¾
a.
Dowód jest nast ¾
epuj ¾
acy: h
b
A
E
= h b
A j i = h b
A
y
j i = h
b
A
E
.
Ta w÷
asno´s´c iloczynu skalarnego implikuje , ·
ze warto´sci w÷
asne operatora her-
mitowskiego s ¾
a rzeczywiste. Wynika to z nast ¾
epuj ¾
acego rozumowania. Je´sli
b
A j i = j i to h
b
A
E
= h j i, a poniewa·
z h
b
A
E
oraz h j i s ¾
a liczbami
rzeczywistymi to
musi by´c liczb ¾
a rzeczywist ¾
a.
Wektory w÷
asne nale·
z ¾
ace do

xviii
ELEMENTY ALGEBRY LINIOWEJ
ró·
znych warto´sci w÷
asnych s ¾
a ortogonalne.
Niech
i
6=
j
b ¾
ed ¾
a waro´sciami
w÷
asnymi wektorów w÷
asnych j
i
i i j
j
i operatora b
A. Mamy
h
j
j b
A
i
i =
i
h
j
j
i
i
(84)
oraz
h b
A
j
j
i
i =
j
h
j
j
i
i
(85)
Poniewa·
z operator b
A jest hermitowski(h
j
j b
A
i
i = h b
A
j
j
i
i) odejmuj ¾
ac stron-
ami od równania 84 równanie 85 otrzymujemy
h
j
j b
A
i
i
h
j
j b
A
i
i = 0 = (
i
j
)h
j
j
i
i
(86)
a poniewa·
z
i
6=
j
wnioskujemy, ·
ze wektory j
i
i i j
j
i s ¾
a ortogonalne. Z
za÷
o·
zenia przyjmujemy, ·
ze wektory w÷
asne operatora hermitowskiego s ¾
a unor-
mowane, je´sli nie to je normujemy. W przypadku degeneracji tzn. gdy tej
samej warto´sci w÷
asnej
odpowiada wi ¾
ecej ni·
z jeden liniowo niezale·
znych wek-
torów w÷
anych mo·
zna stosuj ¾
ac np. ortonormalizacj ¾
e Grama-Schmidta (patrz
rozdzia÷(0.1.4)) otrzyma´c zbiór ortonormalnych wektorów w÷
asnych odpowiada-
j ¾
acych tej samej warto´sci w÷
asnej. Reasumuj ¾
ac, dla dowolnego operatora hermi-
towskiego b
A mo·
zna zawsze skonstruowa´c ortonormaln ¾
a baz ¾
e wektorów w÷
asnych
rozpinaj ¾
acych przestrzen H tak ¾
a, ·
ze dowolny wektor nale·
z ¾
acy do przestrzeni
H mo·
zna wyrazi´c jako superpozycj ¾
e (kombinacj ¾
e liniow ¾
a) wektorów bazy (wek-
torów w÷
asnych operatora hermitowskiego). Zatem ortonormalne wektory w÷
asne
operatora hermitowskiego tworz ¾
a baze zupe÷
n ¾
a
Niech b ¾
edzie dany oprerator b
A sprz ¾
e·
zony po hermitowsku oraz zupe÷
na baza
fj
1
i ; j
2
i ; :::; j
n
ig rozpinaj ¾
aca przestrze´n H , Reprezentacj ¾
e operatora b
A w
bazie H tworzy macierz o elementach
A
ij
= h
i
A
j
(87)
Chcemy zna´c reprezentacj ¾
e macierzow ¾
a operatora A
y
. Z wzoru (76) wynika,
·
ze
hA
i
j
= h
i
A
y
j
(88)
Korzystaj ¾
ac z w÷
asno´sci (11) iloczynu skalarnego
h
j
jA
i
i = h
i
A
y
j
czyli A
ji
= A
y
ij
(89)
Oznacza to, ·
ze elementy macierzowe operatora b
A
y
sprz ¾
e·
zonego po hermitowsku
z operatorem b
A s ¾
a równe sprz ¾
e·
zonym, zespolonym elementom macierzy A
T
transponowanej do macierzy A:Inaczej mo·
zemy to zapisa´c nast ¾
epuj ¾
aco
A
ji
= A
y
ij
() A
y
= (A
T
)
(90)
Je´sli operator b
A jest operatorem hermitowskim (samosprz ¾
e·
zonym) tzn. gdy
b
A = b
A
y
=) A = (A
T
)
(91)
czyli elementy macierzowe operatora hermitowskiego b
A spe÷
niaj ¾
a zwi ¾
azek A
ji
=
A
ij
, a w szczególno´sci elementy diagonalne macierzy A s ¾
a rzeczywiste (A
ii
=
A
ii
).

0.2. OPERATORY LINIOWE
xix
0.2.9
Operator odwrotny
Niech b
A b ¾
edzie operatorem liniowym. Je´sli istnieje taki operator b
B, ·
ze
b
A b
B = b
B b
A = b
I
(92)
to b
B jest operatorem odwrotnym do operatora b
A i piszemy b
B = b
A
1
.
Je´sli
zatem j i = b
A j i to j i = b
A
1
j i . Mo·
zna pokaza´c, ·
ze operator b
B odwrotny do
operatora b
A istnieje wtedy i tylko wtedy gdy równanie b
A j i = 0 implikuje to,
·
ze j i jest wektorem zerowym. Mo·
zna te·
z pokaza´c, ·
ze macierzowa reprezentacja
operatora b
B odwrotnego do operatora b
A istnieje wtedy tylko gdy wyznacznik
macierzy A reprezentuj ¾
acej operator b
A jest ró·
zna od zera (det A 6= 0).
0.2.10
Operatory unitarne
Mówimy, ·
ze operator b
U jest unitarny gdy
b
U b
U
y
= b
U
y
b
U = b
I
(93)
Z de…nicji (92) wynika, ·
ze b
U
y
= b
U
1
oraz b
U
y
jest te·
z operatorem unitarnym.
Iloczyn dwóch operatorów unitarnych b
U i b
V jest operatorem unitarnym poniewa·
z
zgodnie (93)
b
U b
V ( b
U b
V )
y
= b
U b
V b
V
y
b
U
y
= b
I
(94)
W równaniu (94) skorzystali´smy z to·
zsamo´sci ( b
U b
V )
y
= b
V
y
b
U
y
, która wynika
z de…nicji operatora hermtowskiego. (w÷
asno´sci (??) operatora sprz ¾
e·
zonego po
hermitowsku). Operatory unitarne posiadaj ¾
a bardzo wa·
zn ¾
a z punktu widzenia
teorii kwantowej cech ¾
e - zachowuj ¾
a warto´s´c iloczynu skalarnego wektorów pod-
danych linowym operacjom unitarnym, a tym samym zachowuj ¾
a norm ¾
e wek-
tora. ×atwo mo·
zemy si ¾
e o tym przekona´c wykonuj ¾
ac nast ¾
epuj ¾
ace kroki. Niech
b ¾
ed ¾
a dane dwa wektory j i i j i. W wyniku dzia÷ania operatora unitarnego
b
U na te wektory otrzymujemy j i = b
U j i, j i = b
U j i. Iloczyn skalarny
h j i = h b
U
b
U
E
= h j b
U
y
b
U j i = h j i. Je´sli j i = j i.to od razu wida´c, ·
ze
h j b
U
y
b
U j i = h j i.
0.2.11
Zmiana bazy
Za÷
ó·
zmy, ·
ze chcemy przej´s´c z ortonormalnej bazy fj
1
i ; j
2
i ; :::; j
n
ig do orto-
normalnej bazy fj
;
1
i ; j
;
2
i ; :::; j
;
n
ig przy pomocy unitarnej transformacji
j
;
i
i =
n
X
j=1
S
ji
j
(i = 1; 1; :::; n)
(95)

xx
ELEMENTY ALGEBRY LINIOWEJ
Dowolny wektor
j i =
n
X
i=1
a
i
j
i
i
gdzie a
i
= h
i
j i
(96)
w nowej bazie mo·
zna zapisa´c nast ¾
epuj ¾
aco
j i =
n
X
j=1
a
;
j
;
j
=
n
X
i;j=1
a
;
j
S
ij
j
i
i
(97)
Z równa´n (??) otrzymujemy
a
i
=
n
X
j=1
S
ij
a
;
j
(98)
Mo·
zna pokaza´c, ·
ze macierzowe reprezentacja operatora b
A w bazach fj
1
i ; j
2
i ; :::; j
n
ig
i fj
;
1
i ; j
;
2
i ; :::; j
;
n
ig powi ¾
azane s ¾
a nast ¾
epuj ¾
acym zwi ¾
azkiem
A
0
= S
1
A S = S
y
AS
(99)
gdzie unitarn ¾
a macierz S nazywamy macierz ¾
a przej´scia z bazy nieprimowanej
do bazy primowanej.
0.2.12
Twierdzenie o diagonalizacji operatorów komutu-
j ¾
acych
Komutatorem operatorów b
A i b
B nazywamy wyra·
zenie
h
b
A; b
B
i
= b
A b
B
b
B b
A
(100)
Mówimy, ·
ze operatory komutuj ¾
a gdy ich komutator jest równy 0 .
Korzystaj ¾
ac
z de…nicji komutatora (100) bezpo´srednio otrzymujemy
h
b
A; b
B
i
=
h
b
B; b
A
i
(101)
oraz
h
b
A b
B; b
C
i
= b
A
h
b
B; b
C
i
+
h
b
A; b
C
i
b
B
(102)
Mo·
zna te·
z pokaza´c, ·
ze je´sli b
A i b
B s ¾
a operatorami hermitowskimi to równie·
z
i
h
c
A; b
B
i
jest operatorem hermitowskim. Zajmiemy si ¾
e teraz twierdzeniem o
równoczesnej diagonalizacji operatorów normalnych tj. takich, które spe÷
niaj ¾
a
nast ¾
epuj ¾
acy zwi ¾
azek
h
b
A; b
A
y
i
= 0
(103)
Twierdze-
nie
: Dwa normalne operatory b
A i b
B komutuj ¾
a wtedy i tylko wtedy gdy ist-
nieje ortonormalna baza, w której obydwa operatory mo·
zna wyrazi´c w formie

0.2. OPERATORY LINIOWE
xxi
macierzy diagonalnych. Dowód:
Niech fjiig b ¾
edzie ortonormaln ¾
a baz ¾
a dla
operatorów b
A i b
B, tzn.
b
A jii =
i
jii
(104)
b
B jii =
i
jii
(105)
Zatem
b
A b
B jii = b
A
i
jii =
i i
jii =
i i
jii = b
B b
A jii =)
h
b
A; b
B
i
= 0
(106)
Za÷
ó·
zmy teraz odwrotnie, ·
ze operatory b
A i b
B komutuj ¾
a oraz wektory w÷
asne
operatora b
A (104) tworz ¾
a ortonormaln ¾
a baz ¾
e fjiig i nie s ¾
a wektorami w÷
asnymi
operatora b
B . Przedstawmy operator b
B w bazie fjiig
b
B jii =
n
X
j=1
jji hjj b
B jii
(107)
Zgodnie z przyj ¾
etym za÷
o·
zeniem,·
ze operatory b
A i b
B komutuj ¾
a, posi÷
kuj ¾
ac si ¾
e
wzorem (107) oraz korzystaj ¾
ac z relacji zupe÷
no´sci (44) otrzymujemy
h
c
A; b
B
i
jii = b
A b
I b
B jii
b
I b
B b
A jii =
n
X
j=1
jji hjj b
B jii (
j
i
) = 0
(108)
Je´sli
i
6=
j
gdy i 6= j to hjj b
B jii = 0:Gdy natomiast przyjmiemy , ·
ze hjj b
B jji =
j
to
hjj b
B jii =
j ij
(109)
Podstawiaj ¾
ac 109 do107 otrzymujemy
b
B jii =
i
jii
(110)
co oznacza, ·
ze stan jii jest równie·
z wektorem w÷
asnym operatora b
B.
Dowód
mo·
zna rozszerzy´c na przypadek degeneracji warto´sci w÷
asnych
i
operatora
b
A.
0.2.13
Rozk÷
ad spektralny operatora i twierdzenie spek-
tralne
Operator normalny b
A (de…nicja (103)) mo·
zna przedstawi´c w formie
b
A =
n
X
i=1
j
i
i
i
h
i
j
(111)
gdzie
i
, j
i
i, i = 1; 2; :::; n s ¾
a warto´sciami i unormowanymi do jedno´sci wek-
torami w÷
asnymi operatora b
A.
×atwo si ¾
e przekona´c, ·
ze tak zapisany operator
spe÷
nia równanie w÷
asne
b
A j
i
i =
i
j
i
i.
Przedstawienie (111) nazywamy
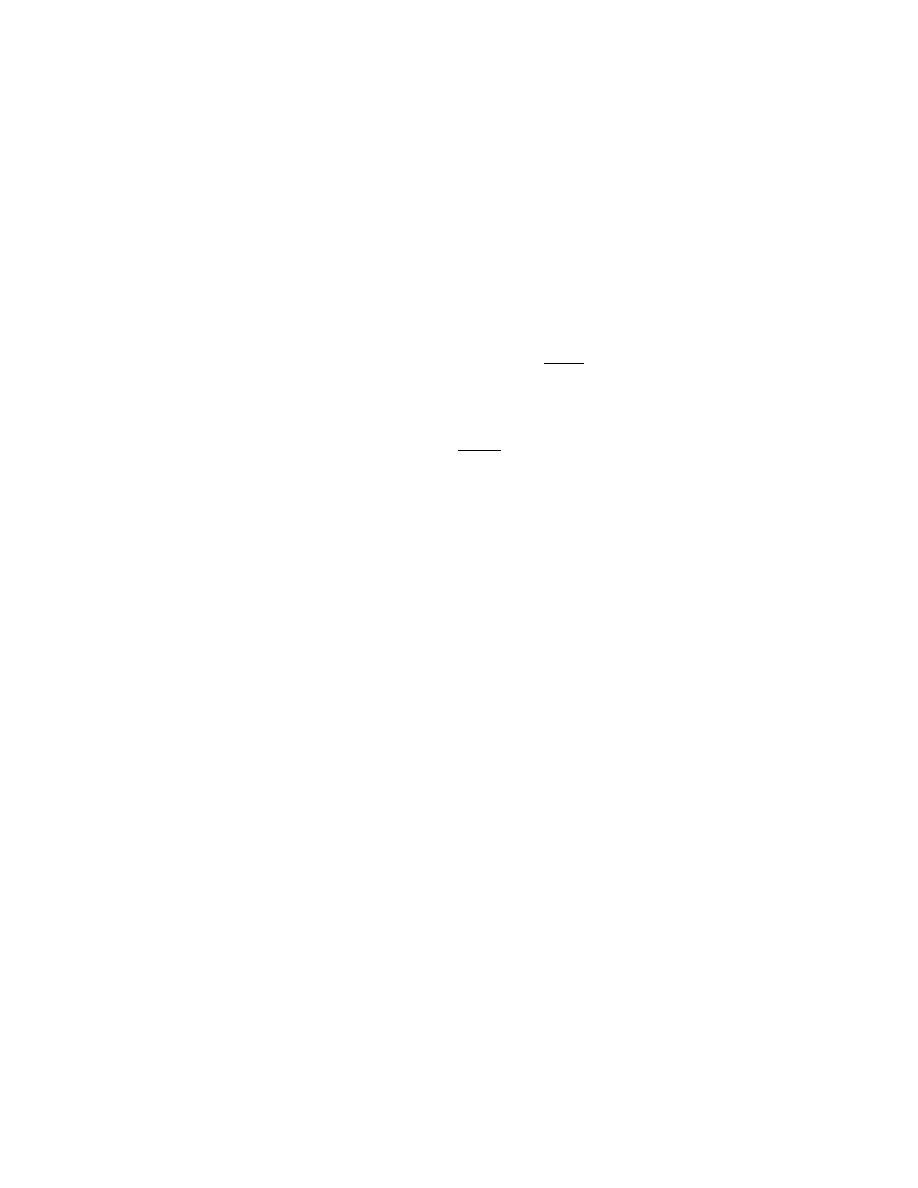
xxii
ELEMENTY ALGEBRY LINIOWEJ
spektralnym rozk÷
adem operatora normalnego b
A: Korzystaj ¾
ac z warunku orto-
normalno´sci stanów w÷
asnych j
i
i otrzymujemy, ·
ze np.
( b
A)
N
= (
n
X
i=1
j
i
i
i
h
i
j)
N
=
n
X
i=1
j
i
i
N
i
h
i
j
(112)
Rozwa·
zmy dla przyk÷
adu funkcj ¾
e operatorow ¾
a f (a b
A) = exp( b
A),
2 C, któr ¾
a
mo·
zna formalnie rozwin ¾
a´c na szereg Maclaurina
exp( b
A) = b
I +
1
X
k=1
( b
A)
k
k!
(113)
Korzystaj ¾
ac z wzoru (112) otrzymujemy, ·
ze
exp( b
A) = b
I +
n
X
i=1
1
X
k=1
j
i
i
(
i
)
k
k!
h
i
j =
n
X
i=1
j
i
i exp(
i
) h
i
j
(114)
Uogólnieniem tego wyniku na funkcje operatorowe, które mo·
zna przedstawi´c
(lub przybli·
zy´c) w postaci wielomianu formalnej zmiennej
b
A jest nast ¾
epuj ¾
ace
twierdzenie.
Twierdzenie spektralne.
Funkcj ¾
e operatorow ¾
a f ( b
A) operatora normal-
nego b
A, którego rozk÷
ad spektralny okre´sla wzór (111) mo·
zna wyrazi´c nast ¾
epu-
j ¾
aco
f ( b
A) =
n
X
i=1
j
i
i f(
i
) h
i
j
(115)
gdzie funkcja f musi by´c dobrze okre´slona na zbiorze warto´s´ci w÷
asnych
i
operatora b
A.
0.2.14
´Slad macierzy
´Sladem macierzy kwadratowej o wymiarze (n
n) nazywamy wyra·
zenie
T r(A) =
n
X
i=1
A
ii
(116)
×atwo sprawdzi´c, ·
ze dla dowolnych dwóch macierzy kwadratowych A i B o tych
samych wymiarach
T r(A + B) = T r(A) + T r(B);
(117)
T r(cA) = cT r(A) gdzie c 2 C;
(118)
T r(AB) = T r(BA)
(119)
Z w÷
asno´sci (119) wynika,·
ze dla n operatorów b
A
1
; b
A
2
; :::; b
A
n
T r(A
1
A
2
; :::; A
n 1
A
n
) = T r(A
1
A
2
; :::; A
n
A
n 1
) = T r(A
n
A
1
A
2
; :::; A
n 2
A
n 1
)
(120)

0.2. OPERATORY LINIOWE
xxiii
´Slad macierzy nie zale·
zy od wyboru bazy, tzn.
´slad macierzy A, ktora jest
reprezentacj ¾
a operatora liniowego b
A w okre´slonej bazie nie zale·
zy od wyboru tej
bazy. Dowód tego faktu jest nast ¾
epuj ¾
acy. Rozwa·
zmy dwie ortonormalne bazy
fjiig i fjjig. Korzystaj ¾
ac z relacji zupe÷
no´sci (44) dla tych baz otrzymujemy
T r(A)
=
n
X
i=1
hij b
A jii =
n
X
i=1
hij b
I b
A b
I jii =
n
X
i;j;k=1
hi jji hjj b
A jki hk jii (121)
=
n
X
i;j;k=1
hk jii hi jji hjj b
A jki =
n
X
j;k=1
jk
hjj b
A jki
(122)
=
n
X
j
hjj b
A jji = T r(A)
(123)
Z w÷
asno´sci (119) bezpo´srednio otrzymujemy, ·
ze transformacje unitarne za-
chowuj ¾
a ´slad macierzy poniewa·
z
T r(U
y
AU ) = T r(U
y
U A) = T r(IA)T r(A)
(124)
´Slad macierzy podobnie jak iloczyn skalarny dwóch wektorów jest niezmien-
nikiem transformacji unitarnych.
0.2.15
Iloczyn tensorowy
W mechanice kwantowej, a tak·
ze w informatyce kwantowej, oprócz izolowanych
ukladów jednocz ¾
astkowych badamy uk÷
ady wielocz ¾
astkowe. Do opisu uk÷
adów
wielocz ¾
astkowych konstruujemy przestrzenie Hilberta H z przestrzeni opisuj ¾
a-
cych oddzielnie ka·
zd ¾
a pojedy´ncz ¾
a cz ¾
astk¾
e. Ta skomplikowana procedura tworzenia
przestrzeni H opiera si ¾
e na iloczynach tensorowych albo inaczej mówi ¾
ac na
iloczynach Kroneckera przetrzeni jednocz ¾
astkowych. Nasze rozwa·
zania ograniczymy
do przestrzeni H, które s ¾
a iloczynem tensorowym dwóch przestrzeni jednocz ¾
astkowych.
Rozwa·
zmy dwie przestrzenie Hilberta H
1
i H
2
o wymiarach m i n. Mówimy,
·
ze przestrze´n Hilberta H
jest iloczynem tensorowym przestrzeni H
1
i H
2
,
co zapisujemy H = H
1
H
2
, je´sli mo·
zemy ka·
zdej parze wektorów j i 2 H
1
i
j i 2 H
2
przypisa´c wektor nale·
z ¾
acy do H , który oznaczamy j i
j i i
nazywamy iloczynem tensorowym wektorów j i i j i : Z de…nicji ka·
zdy wek-
tor nale·
z ¾
acy do przestrzeni H jest liniow ¾
a superpozycj ¾
a (kombinacj ¾
a) wek-
torów j i
j i. Iloczyn tensorowy wektorów posiada nast ¾
epuj ¾
ace w÷
asno´sci;
1) dla dowolnych wektorów j i 2 H
1
, j i 2 H
2
i c 2 C
c(j i
j i) = (c j i)
j i = j i
(c j i)
(125)
2) dla dowolnych wektorów j
1
i i j
2
i 2 H
1
oraz j i 2 H
2
(j i + j
2
i)
j i) = j
1
i
j i + j
2
i
j i
(126)

xxiv
ELEMENTY ALGEBRY LINIOWEJ
( 3) dla dowolnych wektorów j i 2 H
1
i j
1
i ; j
2
i 2 H
2
j i
(j
1
i + j i) = j i
j
1
i + j i
j
2
i
(127)
Zamiast zapisu j i j i cz ¾
estostosuje si ¾
e skrócon ¾
a notacj ¾
e j i j i = j i j i =
j ; i = j
i .
Wymiar przestrzeni H = H
1
H
2
jest równy iloczynowi
wymiarów przestrzeni H
1
i H
2
(dim H = dim H
1
dim H
2
) . Je´sli fjiig i fjjig
s ¾
a ortonolmalnymi bazami przestrzeni H
1
i H
2
to ortonormaln ¾
a baz ¾
e przestrzeni
H = H
1
H
2
tworz ¾
a iloczyny jii jji (i = 1; 2; :::; dim H
1
; j = 1; 2; :::; dim H
2
) .
Np. je´sli ortonormalnymi bazami przestrzeni H
1
i H
2
s ¾
a wektory fj1 = 0i ; j1ig
to ortonormaln ¾
a baz ¾
e przestrzeni H = H
1
H
2
tworz ¾
a wektory
fj0i
j0i ; j0i
j1i ; j1i
j0i ; j1i
j1ig
(128)
Dowolny wektor j i 2 H mo·
zna w bazie (128) zapisa´c nast ¾
epuj ¾
aco
j i = c
00
j00i + c
01
j01i + c
10
j10i + c
11
j11i gdzie c
ij
= hij j i
(129)
Je´sli b
A i b
B s ¾
a liniowymi operatorami dzia÷
aj ¾
acymi odpowiednio w przestrzeniach
H
1
i H
2
to dzia÷
anie operatora b
A
b
B na dowolny wektor j i =
P
i;j
c
ij
jii
jji 2 H de…niuje si ¾
e nast ¾
epuj ¾
aco
( b
A
b
B) j i = ( b
A
b
B)(
X
i;j
c
ij
jii
jji) =
X
i;j
c
ij
b
A jii
b
B jji
(130)
Mo·
zna pokaza´c, ·
ze dowolny operator liniowy b
O dzia÷
aj ¾
acy w przestrzeni H
mo·
zna zapisa´c jako liniow ¾
a superpozycj ¾
e iloczynów tensorowych operatorów
liniowych b
A
i
dzia÷
aj ¾
acych w przestrzeni H
1
i operatorów b
B
j
dzia÷
aj ¾
acych w
przestrzeni H
2
, tj.
b
O =
X
i;j
ij
b
A
i
b
B
j
(131)
Iloczyn skalarny dwóch wektorów
j i =
X
i;j
c
ij
jiji
(132)
oraz
j i =
X
i;j
d
ij
jiji
(133)
nale·
z ¾
acych do przestrzeni H = H
1
H
2
( jii 2 H
1;
jji 2 H
2
) de…niuje si ¾
e
nast ¾
epuj ¾
aco
h j i =
X
i;j
c
ij
d
ij
(134)
Mo·
zna sprawdzi´c, ·
ze de…nicja (134) spe÷
nia wszystkie w÷
asno´sci (11)-(13) iloczynu
skalarnego.
Chc ¾
ac policzy´c iloczyn skalarny dwóch wektorów
h
1
j
2
i = (h
1
j
h
1
j) j(
2
i
j
2
i) = h
1
j
2
i h
1
j 2i
(135)

0.2. OPERATORY LINIOWE
xxv
Wzór ten, jak ÷
atwo si ¾
e przekona´c, jest konsystentny z wzorem (134), gdy ka·
zdy
z wektorów j
i
i oraz j
i
i mo·
zna rozwin ¾
a´c w odpowiednich bazach rozpinaj ¾
a-
cych przesytrzenie H
1
i H
2
. Rozwa·
zmy kolejny przypadek gdy operator b
A dzia÷
a
na wektor j i 2 H
1
, a operator b
B dzia÷
a na wektor j i 2 H
2
. Wynik dzia÷
ania
iloczynu tensorowego b
A
b
B na wektor j i = j i
j i jest nast ¾
epuj ¾
acy
( b
A
b
B) j i = ( b
A
b
B)(j i
j i) = ( b
A j i)
( b
B j i)
(136)
W obliczeniach cz ¾
esto operatory reprezentowabe s ¾
a przez macierze. Wówczas
iloczyn tensorowy operatorów zast ¾
epuje iloczyn tensorowy odpowiadaj ¾
acych im
macierzy.Macierzowa reprezentacja operatora b
A
b
B w bazie jki
jiji nu-
merowanej przez pojedy´nczy wska´znik k = 1; 2; :::; m n , gdzie k = (i
1)n + j;
i = 1; 2; :::; m , j = 1; 2; :::; n wyra·
za si ¾
e nast ¾
epuj ¾
aco
A
B =
2
6
6
6
6
4
A
11
B
A
12
B
:
:
A
1m
B
A
21
B
A
22
B
:
:
A
2m
B
:
:
:
:
:
:
:
:
.
:
A
m1
B
A
m2
B
:
:
A
mm
B
3
7
7
7
7
5
(137)
gdzie cz÷
ony A
ij
B okre´slaj ¾
a podmacierze o wymiarze n
n , a A i B s ¾
a macier-
zowymi reprezentacjami operatorów b
A i b
B o wymiarach odpowiednio m
m i
n
n . Jako przyk÷
ad policzmy iloczyn tensorowy macierzy Pauliego
x
z
.
Otrzymujemy
x
z
=
0
1
1
0
1
0
0
1
=
0
z
1
z
1
z
0
z
=
2
6
6
4
0
0
1
0
0
0
0
1
1
0
0
0
0
1
0
0
3
7
7
5
(138)

xxvi
ELEMENTY ALGEBRY LINIOWEJ

ELEMENTY MECHANIKI
KWANTOWEJ
0.2.16
Do´swiadczenie Sterna-Gerlacha
Do´swiadczenie Sterna-Gerlacha jest jednym z dobitnych przyk÷
adów, które pokazuj ¾
a
bezradno´s´c …zyki klasycznej przy opisie zjawisk zachodzacych w skali mikroskopowej,
a wi ¾
ec zjawisk zachodz ¾
acych w uk÷
adach atomowych, j ¾
adrowych, itp. Zjawiska
mikroskopowe zmuszaj ¾
a nas do porzucenia klasycznego, w duchu mechaniki
klasycznej opisu uk÷
adów o rozmiarach porównywalnych lub mniejszych od d÷
u-
go´sci fali ´swietlne j. Do´swiadczenie Sterna-Gerlacha pokazuje kwantowo-mechaniczne
w÷
a´sno´sci typowe dla uk÷
adów mikroskopowych.Schemat obrazuj ¾
acy do´swiad-
czenie Sterna-Gerlacha jest na rysunku 1
Rysunek1.
Wi ¾
azka atomów o momencie magnetycznym ! biegnie do obszaru, w którym
jest pole magnetyczne o indukcji B skierowane w kierunku osi z. Pole to nie jest
jednorodne, lecz posiada gradient
!
rB w kierunku osi z. Zgodnie z klasyczn ¾
a
elektrodynamik ¾
a na ka·
zdy atom dzia÷
a si÷
a
!
F skierowana wzdu·
z osi z o warto´sci
F
z
=
z
jrBj =
z
dB
dz
(139)
W wyniku dzia÷
ania si÷
y F
z
(139) tor lotu poszczegolnych atomów zanim os-
i ¾
agn ¾
a ekran S zostanie odchylony. Na ekranie S nale·
zy si ¾
e spodziewa´c plamki
obrazuj ¾
acej miejsce uderzenia poszczególnych atomow w ekran. Stopie´n za-
ciemnienia poszczególnych obszarów plamki powinie odzwierciedla´c nat ¾
e·
z ¾
enie
atomów
uderzaj ¾
acych w odpowiednie obszary ekranu. Poniewa·
z momenty
magnetyczne ! atomów w wi ¾
azce przchodz ¾
acej przez obszar dzialalania pola
magnetycznego zorientowane s ¾
a w ro·
znych kierunkach (rozk÷
ad orientacji mo-
mentow magnetycznych atomów wzgl ¾
edem osi z powinien zmienia´c si ¾
e w sposób
ci ¾
ag÷
y od warto´sci
z
= j!j do warto´sci
z
=
j!j) nale·
zy si ¾
e spodziewa´c, ·
ze
xxvii

xxviii
ELEMENTY MECHANIKI KWANTOWEJ
na ekranie S powstanie plamka o najwi ¾
ekszym zaciemnieniu w ´srodku i male-
j ¾
acym zaciemnieniu w sposob ci ¾
ag÷
y w miar ¾
e oddalania si ¾
e od ´srodka plamki.
Jednak·
ze wynik eksperymentu jest w drastycznej sprzeczno´sci z takim obrazem.
Na ekranie obserwujemy kilka równoleg÷
ych, równo odleg÷
ych ciemnych pasków.
Fakt ten oznacza, ·
ze rzut momentu magnetycznego
z
na kierunek osi z przyj-
muje tylko warto´sci dyskretne. W przypadku wi ¾
azki atomów srebra obserwu-
jemy dwa ciemne paski co oznacza, ·
ze
z
= + j!j lub
z
=
j!j.
W
przypadku innych atomów obserwujemy wi ¾
ecej ciemnych pasków na ekranie.
Zjawisko to znalaz÷
o wyt÷
umaczenie na gruncie mechaniki kwantowej i zwi ¾
azane
jest ca÷
kowitym kr ¾
etem atomu. W my´sl mechaniki kwantowej ca÷
kowity kr ¾
et
atomu (który jest sum ¾
a kr ¾
etów elektronów na orbitach i spinów w÷
asnych elek-
tronów) okre´slony jest liczb ¾
a kwantow ¾
a
j, a rzut kr ¾
etu ca÷
kowitego atomu na
wyró·
znion ¾
a o´s z
okre´slony jest liczb ¾
a kwantow ¾
a m, która mo·
ze przyjmowa´c
jedn ¾
a z waro´sci
j;
j + 1;
j + 2; :::; j
2; j
1; j: Zatem , je´sli na przyk÷
ad
kr ¾
et atomu jest okre´slony liczb ¾
a j = 2 to w do´swiadczeniu Sterna -Gerlacha
obserwujemy 5 ciemnych pasków.
Wi ¾
azk¾
e, w której
wszystkie atomy maj ¾
a tak ¾
a sam ¾
a liczb ¾
e kwantow ¾
a m
nazywamy wi ¾
azk ¾
a spolaryzowan ¾
a. Na przyk÷
ad wi ¾
azka atomów, których kr ¾
et
jest okre´slony liczb ¾
a kwatow ¾
a j =
1
2
mo·
ze by´c spolaryzowana na dwa sposoby;
pierwszy gdy m =
1
2
i drugi gdy m =
1
2
. Kolejne eksperymenty z z uk÷
adem
dwóch urz ¾
adze´n Sterna-Gerlacha pokazuj ¾
a efekty nie do wyobra·
zenia z punktu
widzenia …zyki klasycznej . Rozwa·
zmy uk÷
ad jak na rysunku 2
Rysunek 2
Niespolaryzowana wi ¾
azka atomów o spinie j =
1
2
przechodzi przez urz ¾
adzenie
Sterna =Gerlacha, w którym gradient indukcji pola magnetycznego jest zori-
entowany wzd÷
u·
z osi z . Wi ¾
azka ulega rozszczepieniu na dwie spolaryzowane
wi ¾
azki. W jednej wi ¾
azce atomy s ¾
a w stanie m
z
=
1
2
, a w drugiej wi ¾
azce w
stanie m
z
=
1
2
, któr ¾
a to wi ¾
azk¾
e wygaszamy przez ustawienie na jej drodze za
urz ¾
adzeniem Sterna-Gerlacha przes÷
ony. Nat ¾
epnie pierwsz ¾
a wi ¾
azk¾
e (m
z
=
1
2
)
przepuszczamy przez drugie urz ¾
adzenie Sterna-Gerlacha o identycznej orien-
tacji gradientu pola magnetycznego magnetycznego jak w pierwszym urz ¾
adze-
niu. Urz ¾
adzenie to przepuszcza ca÷¾
a wi ¾
azk¾
e w stanie m
z
=
1
2
.
Rozpatrzmy
teraz uk÷
ad jak na rysunku 3.
Rysunek 3.
W drugim urz ¾
adzeniu Sterna-Gerlacha gradient indukcji pola magnetycznego
jest zorientowany w kierunku osi y prostopad÷
ej do osi z.
Pomimo, i·
z do
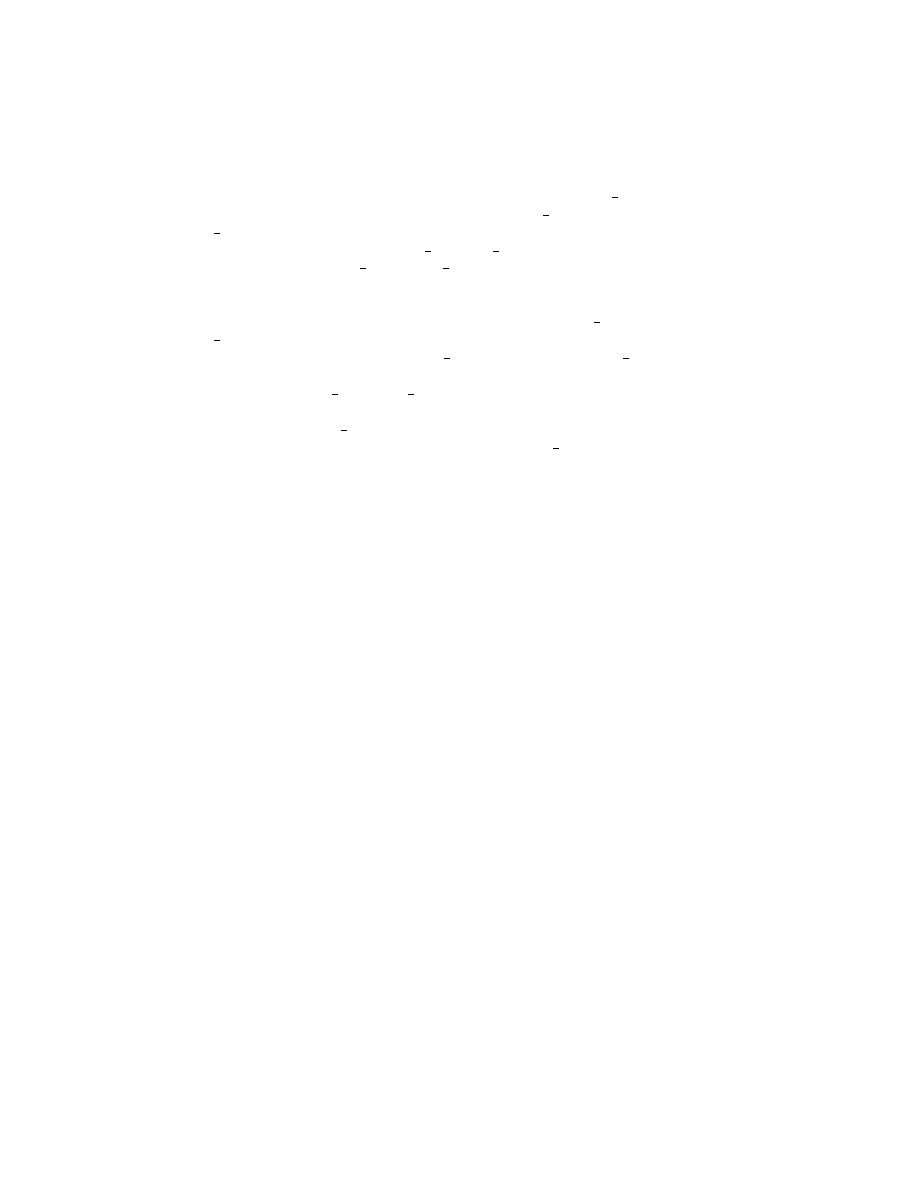
xxix
drugiego urz ¾
adzenia dociera tylko wi ¾
azka atomów w stanie m
z
=
1
2
na jego
wyj´sciu obsrwujemy dwie wi ¾
azki, jedn ¾
a w stanie m
y
=
1
2
i
drug ¾
a w stanie
m
y
=
1
2
: Czy wobec tego mo·
zna uwa·
za´c, ·
ze 50% atomów dobiega do drugiego
urz ¾
adzenia równocze´snie w stanie m
z
=
1
2
i m
y
=
1
2
, a pozosta÷
e 50% atomów
rownocze´snie w stanie m
y
=
1
2
i m
y
=
1
2
?
To, ·
ze taka interpretacja jest
nieuzasadniona przekonuje nas do´swiadczenie, którego schemat jest narysunku
4. W tym do´swiadczeniu pierwsze dwa urz ¾
adzenia Sterna-Gerlacha spe÷
niaj ¾
a
rol ¾
e …ltrów, które zatrzymuj ¾
a wi ¾
azki atomów w stanie m
z
=
1
2
i w stanie
m
y
=
1
2
: Pomimo tego na wyj´sciu trzeciego urz ¾
adzenia Sterna-Gerlacha obser-
wujemy dwie wi ¾
azki, jedn ¾
a w stanie m
z
=
1
2
i drug ¾
a w stanie m
z
=
1
2
. Je´sli
tak jest to rozumowanie, ·
ze atomy dobiegaj ¾
a do trzeciego urz ¾
adzenia Sterna-
Gerlacha w stanie m
z
=
1
2
i m
y
=
1
2
jest b÷¾
edne. Co wi ¾
ecej, je´sli usuniemy
przes÷
on ¾
e, która absorbowa÷
a za drugim urz ¾
adzeniem Sterna-Gerlacha wi ¾
azk¾
e
atomów w stanie m
y
=
1
2
; to na wyj´sciu trzeciego urz ¾
adzenia Sterna Ger-
lacha zaobsewujemy tylko wi ¾
azk¾
e atomów w stanie m
z
=
1
2
.
Do´swiadczenie
przedstawione na rysunku 4 obrazuje fundamentaln ¾
a cech ¾
e mechaniki kwan-
towej: ko´ncowy stan uk÷
adu zale·
zy tylko od stanu atomów, które docieraj ¾
a
do ostatniego urz ¾
adzenia Sterna-Gerlacha i dzia÷
ania tego urz ¾
adzenia na atomy
niezale·
znie od ich wcze´sniejszej historii. W ogólno´sci wnioskujemy, ·
ze system
aparatura-cz ¾
astki nie posiada pami ¾
eci do przechowania swej wcze´sniejszej his-
torii.
0.2.17
Do´swiadczenie Younga
Zjawisko interferencji ´swiat÷
a przechodz ¾
acego przez dwie szczeliny o rozmiarach
rz ¾
edu d÷
ugo´sci fali ´swielnej i odleg÷
e od siebie te·
z rz ¾
edu kilka d÷
ugo´sci fali ´swielnej
jet kolenym przyk÷
adem ilustruj ¾
acym charakterystyczne w÷
asno´sci kwantowe
uk÷
adów mikroskopowych. Przez d÷
ugi okres czasu, poczynaj ¾
ac od Newtona,
uczonych nurtowa÷
o pytanie czy wi ¾
azka ´swiat÷
a jest strumieniem cz ¾
astek czy
jest wi ¾
azk ¾
a falow ¾
a? Do´swiaczenie Younga, w którym wi ¾
azka ´swiat÷
a monochro-
matycznego ( tj. wi ¾
azka ´swiat÷
a o jednej d÷
ugo´sci fali) i spójnego (tj, takiego,
·
ze na szczeliny padaj ¾
a fale ´swietne o tej samej fazie) przechodz ¾
ac przez uk÷
ad
dwóch szczelin (rysunek...) daje za szczelinami na ekranie obraz interferen-
cyjny. Charakterystyczn ¾
a cech ¾
a interferencji jest to, ·
ze nat ¾
e·
zenie ´swiat÷
a I(x)
na ekranie ró·
zni si ¾
e od algebraicznej sumy nat ¾
e·
ze´n I
1
(x) i I
2
(x) pochodz ¾
acych
z szczelin oddzielnie (gdy jedna z szczelin jest przes÷
oni ¾
eta) tzn.
I(x) 6= I
1
(x) + I
2
(x)
(140)
Rysunek...
Zjawisko interferencji ´swiat÷
a pokazuje , ·
ze ´swiat÷
o jest fal ¾
a , a równania
Maxwella , ·
ze ´swiat÷
o jest fal ¾
a elektromagnetyczn ¾
a. Z drugiej strony okaza÷
o si ¾
e,
·
ze rozk÷
ad energii (ilo´s´c energii emitowanej w jednostkowym przedziale energii
w ci ¾
agu jednej sekundy w zale·
zno´sci od energii fali) emitowanej przez cia÷
o

xxx
ELEMENTY MECHANIKI KWANTOWEJ
doskonale czarne nie da si ¾
e opisa´c na gruncie falowej teorii ´swiat÷
a. Trudno´s´c t ¾
a
mo·
zna pokona´c je´sli przyjmiemy zgodnie z postulatem Plancka, ·
ze ´swiat÷
o jest
emitowane lub absorbowane porcjami enegii, które s ¾
a ca÷
kowit ¾
a wielokrotno´sci ¾
a
jednostki energii zwanej kwantem energii okre´slonej wzorem
E = ~
(141)
gdzie
jest cz ¾
esto´sci ¾
a ´swiat÷
a a ~ sta÷¾
a …zyczn ¾
a zwan ¾
a sta÷¾
a Plancka.
Równie·
z Einstein by wyja´sni´c efekt fotoelektryczny musia÷odwo÷
a´c si ¾
e do
idei Plancka przyjmuj ¾
ac, ·
ze swiat÷
o jest wi ¾
azk ¾
a cz ¾
astek zwanych fotonami, z
których ka·
zda posiada energi ¾
e ~ i p ¾
ed p = ~ =c:Widzimy zatem, ·
ze istniej ¾
a
zjawiska, które wskazuj ¾
a na falow ¾
a natur ¾
e ´swiat÷
a (np. interferencja ´swiat÷
a)
i zjawiska, które przemawiaj ¾
a za kurpuskularn ¾
a (cz ¾
asteczkow ¾
a) natur ¾
a ´swiat÷
a
(np. wspomniane zjawisko fotoelektryczne).
Wyniki ni·
zej opisanych wariantów do´swiadzenia Younga prowadz ¾
a do wniosku,
·
ze ich pe÷
ny opis jest mo·
zliwy je´sli zakceptujemy podwójn ¾
a (dualn ¾
a) natur ¾
e
´swiat÷
a. Przez powójn ¾
a natur ¾
e ´swiat÷
a b ¾
edziemy rozumie´c sytuacj ¾
e kiedy ´swiat÷
o
w zale·
zno´sci od obsewowanego zjawiska przejawia natur ¾
e falow ¾
a b ¾
ad´z natur ¾
e
kurpuskularn ¾
a.
Wyobra´zmy sobie, ·
ze intensywno´sc wi ¾
azki ´swiat÷
a zosta÷
a tak zredukowana,
·
ze ´zród÷
o emituje pojedy´ncze fotony, jeden za drugim.
Je´sli ekspozycja fo-
tonów b ¾
edzie trwa÷
a bardzo krótko to na ´swiat÷
oczu÷
ej kliszy ekranu zaobser-
wujemy kilka pojedynczych punktów b ¾
ed ¾
acych ´sladami absorbcji fotonów w
kliszy. Nie ma wi ¾
ec efektu interferencyjnego, ´swiat÷
o zachowuje si ¾
e jak cz ¾
astki
Je´sli natomiast ekspozycja ´swiat÷
a b ¾
edzie trwa÷
a d÷
u·
zej to rozk÷
ad liczby fo-
tonów absorbowanych w poszczególnych miejscach kliszy (a wi ¾
ec intensywno´s´c
zaczernienia kliszy) b ¾
edzie typowym obrazem interferencyjnym jak na rysunku
.(....).Ten ostatni fakt mo·
zna wyja´sni´c przyjmuj ¾
ac, ·
ze ´swiat÷
o jest fal ¾
a.
Za-
tem musimy pogodzi´c si ¾
e z tym, ·
ze nie potra…my wyja´sni´c wszystkich zaob-
serwowanych wyników do´swiadcze´n przyjmuj ¾
ac tylko kurpuskularn ¾
a b ¾
ad´z tylko
falow ¾
a natur ¾
e ´swiat÷
a. Musimy porzuci´c rozumowanie, ·
ze teoria falowa i teo-
ria kurpuskularna ´swiatla s ¾
a wzajemnie wykluczaj ¾
acymi si ¾
e teoriami. Musimy
przyj ¾
a´c, ·
ze teoria kurpuskularna i teoria falowa s ¾
a komplementarnymi teoriami
´swiat÷
a. W pewnych warunkach ´swiat÷
o przejawia natur ¾
e kurpuskularn ¾
a, a w
innych natur ¾
e falow ¾
a
Wszystkie dotychcza przeprowadzone do´swiadczenia, nie tylko ze ´swiat÷
em
ale równie·
z z innymi obiektami jak np. elektrony, nukleony, atomy potwierdzaj ¾
a
, ·
ze obiekty te wykazuj ¾
a jednocze´snie podwojn ¾
a natur ¾
e; falow ¾
a i kurpuskularn ¾
a.
Ten fakt krótko nazywamy dualizmem falowo-kurpuskularnym.
0.2.18
Postulaty mechaniki kwantowej
W mechanice klasycznej stan dowolnego du·
zego (mówimy makroskopowego)
obiektu …zycznego mo·
zna w dowolnej chwili t
0
dok÷
adnie okre´sli´c podaj ¾
ac jego
po÷
o·
zenie
!
r (t
0
) oraz pr ¾
edko´s´c
!
V (t
0
) w wybranym uk÷
adzie wspó÷
rz ¾
ednych.
Znaj ¾
ac stan obiektu w chwili t
0
na podstawie zasad Newtona mo·
zna dok÷
adnie

xxxi
przewidzie´c stan uk÷
adu, tj.po÷
o·
zenie !
r (t) i pr ¾
edko´sc
!
V (t) w dowolnej chwili
t: Poniewa·
z zasadom Newtona podlegaj ¾
a wszystkie obiekty …zyczne, na pod-
stawie znajomo´sci stanu obiektów w chwili t
0
mo·
zna przewidzie´c ich przysz÷
o´s´c
w dowolnej chwili t:Mówimy, ·
ze mechanika klasyczna jest teori ¾
a deterministy-
czn ¾
a gdy·
z przysz÷
o´s´c dowolnego obiektu makroskopowego w chwili t jest uza-
le·
zniona od jego stanu w chwili t
0
.
W ´swiecie obiektów ma÷
ych, o rozmiarach rzedu d÷
ugo´sci fali ´swietlnej i
mniejszych, mechanistyczny opis zjawisk …zycznych zupe÷
nie zawodzi. Teoria
która opisuje zjawiska zachodz ¾
ace w mikro´swiecie opiera sie na zupe÷
nie innych
zasadach ni·
z mechanika klasyczna.
W oparciu o systematyk¾
e wyników eksperymentów oraz ich poprawnego
opisu przy pomocy odpowiedniego aparatu matematycznego mo·
zna sformu÷
owa´c
kilka podstawowy postulatów, na których opiera si ¾
e teoria kwantów powszechnie
zwana mechanik ¾
a kwantow ¾
a.
Postulat 1
. Stan …zycznego uk÷
adu S jest ca÷
kowicie opisany przez unor-
mowany do jedno´sci wektor j i, który nazywamy wektorem stanu lub funkcja
falow ¾
a, i który nale·
zy do przestrzeni Hilberta H
S
stowarzyszonej z uk÷
adem S.
Ewolucj ¾
a w czasie wektora stanu j i rz ¾
adzi równanie Schrödingera
i}
d
dt
j i = b
H j i
(142)
gdzie b
H jest operatorem hermitowskim zwanym hamiltonianem uk÷
adu, a sta÷
a
} zwana sta÷¾
a Plancka jest sta÷¾
a wyznaczon ¾
a eksperymentalnie (}
6:626
10
34
J ).
Równanie Schrödingera jest liniowym równaniem rózniczkowym pierwszego
rz ¾
edu wzgl ¾
edem czasu t. Dlatego, je´sli znamy stan pocz ¾
atkowy j (t
0
)i w chwili
t
0
to stan j (t)i w dowolnej chwili t jest jest jednoznacznie okre´slony przez
rozwi ¾
azanie rownania Schrödingera. Poniewa·
z równanie Schrödingera jest rów-
naniem liniowym to superpozycja dwóch
rozwi ¾
aza´n j
1
(t)i i j
2
(t)i, tzn.
j (t)i = j
1
(t)i + j
2
(t)i, gdzie
i
s ¾
a liczbami zespolonymi, jest równie·
z
rozwi ¾
azaniem równania Schrödingera.
Je´sli hamiltonian H nie zale·
zy w sposób jawny od czasu
to formalnym
rozwi ¾
azaniem równania Schrödingera jest funkcja falowa
j (t)i = exp[
i
}
b
H(t
t
0
)] j (t
0
)i
(143)
W przypadku gdy operator c
H jest jawn ¾
a funkcj ¾
a czasu to
j (t)i = b
T exp[
i
}
Z
t
0
b
H(t
t
0
)] j (t
0
)i
(144)
gdzie b
T
jest operatorem chronologicznym porz ¾
adkuj ¾
acym czas.
Ewolucj ¾
e w czasie wektora stanu j i opisuje operator b
U w sposób nast ¾
epu-
j ¾
acy
j (t)i = b
U (t; t
0
) j (t
0
)i
(145)

xxxii
ELEMENTY MECHANIKI KWANTOWEJ
Je´sli hamiltonian H nie zale·
zy jawnie od czasu to z równa´n
(143) i (145)
otrzymujemy, ·
ze w chwili t > t
0
U (t
t
0
) = exp[
i
}
b
H(t
t
0
)]
(146)
gdzie exponent ¾
e operatora
i
}
H(t
t
0
) de…niujemy nast ¾
epuj ¾
aco
exp[
i
}
b
H(t
t
0
)] =
1
X
n=0
1
n!
[
i
}
(t
t
0
)]
n
( b
H)
n
(147)
Pami ¾
etaj ¾
a´c, ·
ze H jest operatorem hermitowskim ÷
atwo jest pokaza´c, ·
ze operator
b
U jest operatorem unitarnym. Unitarno´s´c operatora gwarantuje, ·
ze norma stanu
j (t)i jest zachowana, tzn. h
(t) j (t)i = h (t
0
) b
U
y
(t; t
0
) b
U (t; t
0
) j (t
0
)i =
h (t
0
) j (t
0
)i = 1
Postulat 2
.
Ka·
zdej mierzalnej wielko´sci …zycznej A zwanej obserwabl ¾
a,
która jest odpowiednikiem jednej z dynamicznych wielko´sci w mechanice klasy-
cznej takich jak po÷
o·
zenie, p ¾
ed, moment p ¾
edu, energia, itp. przyporz ¾
adkowany
jest samosprz ¾
e·
zony operator b
A . Jedynymi mo·
zliwymi warto´sciami pomiaru ob-
serwabli A s ¾
a warto´sci w÷
asne operatora b
A tj warto´sci a
i
spe÷
niaj ¾
ace równanie
b
A jii = a
i
jii ; i = 1; 2; :::; N
(148)
Wektory jii zwane wektorami w÷asnymi tworz ¾
a zupe÷
n ¾
a ortonormaln ¾
a baze
przestrzeni Hilberta H
s
:Je´sli dowolny stan j (t)i rozwiniemy w ortonormalnej
bazie fjii ; i = 1; 2; :::; Ng wektorów w÷asnych operatora b
A
j (t)i =
N
X
i=1
c
i
(t) jii
(149)
to prawdopodobie´nswo, ·
ze w wyniku pomiaru obserwabli A w chwili t otrzy-
mamy warto´s´c a
i
wynosi
p
i
(t) = p(a = a
i
j t) =j hi j (t)i j
2
=j c
i
(t) j
2
(150)
Postulat ten dla przejrzysto´sci zosta÷sformu÷
owany dla przypadku gdy warto´sci
w÷
asne a
i
nie s ¾
a zdegenerowane. Interpretacja postulatu 2 w przypadku degen-
eracji tj. gdy tej samej warto´sci w÷
asnej a
i
odpowiada kilka wektorów w÷
asnych
zostanie podana po uwzgl ¾
ednieniu nast ¾
epuj ¾
acych uwag.
(i) Jak ju·
z podkre´slono w postulacie 2 obserwable s ¾
a odpowiednikami (analogami)
tylko dynamicznych wielko´sci w mechanice klasycznej (po÷
o·
zenie, p ¾
ed, moment
p ¾
edu, energia, itp). Natomiast takie wielko´sci charakteryzuj ¾
ace uk÷
ad jak masa,
÷
adunek elektryczny nie zaliczamy do klasy obserwabli lecz s ¾
a parametrami
opisuj ¾
acymi uk÷
ad kwantowy.
(ii) Poniewa·
z jedynymi mo·
zliwymi warto´sciami pomiaru obserwabli A s ¾
a
warto´sci w÷
asne operatora b
A, a mierzone wielko´sci s ¾
a rzeczywiste, to obserwable

xxxiii
musz ¾
a by´c reprezentowane przez operatory samosprz ¾
e·
zone (bo warto´sci w÷
asne
operatora samosprz ¾
e·
zonego s ¾
a rzeczywiste). Ponadto wektory w÷
asne operatora
b
A tworz ¾
a zupe÷
n ¾
a ortonormaln ¾
a baz ¾
e przestrzeni Hilberta H
s
, a stan j (t)i
posiada norm ¾
e równ ¾
a 1, onacza to ·
ze,
N
X
i=1
j c
i
(t) j
2
=
N
X
i=1
p
i
(t) = 1
(151)
czyli ca÷
kowite prawdopodobie´nstwo otrzymania wszystkich mo·
zliwych wyników
pomiaru obserwabli A jest równe 1. St ¾
ad te·
z wynika zawarty w postulacie 1
warunek normalizacji do jedno´sci wektora stanu j (t)i opisuj ¾
acego uk÷
ad S.
(iii) W szczególnym przypadku gdy wektor stanu j (t
0
)i w chwili t
0
pokrywa
si ¾
e z wektorem w÷
asnym jii operatora b
A , tzn. gdy
j (t
0
)i = jii
(152)
to pomiar obserwabli A w chwili t
0
daje w wyniku warto´s´c w÷
asn ¾
a a
i
z praw-
dopodobie´nstwem 1.
(iv) Je´sli j
1
i i j
2
i s ¾
a dwoma unormowanymi stanami w÷
asnymi operatora
b
A z warto´sciami w÷
asnymi a
1
i a
2
to z zasady superpozycji wynika, ·
ze stan
j i =
1
j
1
i +
2
j
2
i
(153)
jest równie·
z dozwolonym stanem uk÷
adu pod warunkiem, ·
ze stan ten jest un-
ormowany do jedno´sci, tzn j
1
j
2
+ j
2
j
2
= 1. Wówczas je´sli dokonamy pomi-
aru obserwabli A to zgodnie z wzorem (150) otrzymamy warto´s´c a
1
z praw-
dopodobie´nstwem j
1
j
2
=j h
1
j i j
2
oraz warto´s´c a
2
z prawdopodobie´nstwem
j
2
j
2
=j h
2
j i j
2
. Wynik ten jest s÷
uszny gdy stan
j i ewoluuje w czasie,
czyli gdy wspó÷
czynniki
1
=
1
(t) i
2
=
2
(t) oraz gdy stan ten nie zale·
zy od
czasu, tj. gdy wspó÷
czynniki
1
i
2
nie zale·
z ¾
a od czasu.
Je´sli hamiltonian b
H uk÷
adu S nie zale·
zy w sposób jawny od czasu to mówimy,
·
ze uk÷
ad S jest uk÷
adem zachowawczym b ¾
ad´z uk÷
adem konserwatywnym. Wów-
czas równanie Schrödingera (142) dla cz ¾
e´sci niezale·
znej od czasu sprowadza si ¾
e
do zagadnienia w÷
asnego operatora Hamiltona b
H
b
H jni = E
n
jni
(154)
Poniewa·
z b
H nie zale·
zy od czasu to równie·
z warto´sci w÷
asne E
n
i wektory w÷
asne
jni nie zale·
z ¾
a odczasu. Przyjmuj ¾
ac dla wygody, ·
ze widmo warto´sci w÷
asnych
E
n
jest niezdegerowane czyli E
m
6= E
n
gdy m 6= n, rozwi ¾
azanie równania
Schrödingera (142) mo·
zna rozwin ¾
a´c w bazie wektorów w÷
asnych fjnig operatora
b
H
j (t)i =
X
n
c
n
(t) jni
(155)
gdzie
c
n
(t) = hn j (t)i
(156)

xxxiv
ELEMENTY MECHANIKI KWANTOWEJ
Wektor stanu j (t)i jest jednoznacznie okre´slony przez warunek pocz ¾
atkowy
j (t
0
)i, mo·
zemy na przyk÷
ad przyj ¾
a´c t
0
= 0:Z kolei warunek pocz ¾
atkowy j (t
0
)i
jest okre´slony gdy wspó÷
czynnniki c
n
(t
0
) = hn j (t
0
)i s ¾
a jednoznacznie zadane.
Podstawiaj ¾
ac (155) do równania ( 142) otrzymamy równanie
i}
d
dt
c
n
= E
n
c
n
(157)
którego rozwi ¾
azaniem jest
c
n
(t) = c
n
(0) exp(
i
}
E
n
t)
(158)
a funkcja falowa j (t)i w chwili t
j (t)i =
X
n
c
n
(0) exp(
i
}
E
n
t) jni
(159)
W szczególnym przypadku kiedy w chwili t
0
= 0 stan j (0)i = jni rozwi ¾
azanie
(159) równania ( 142) redukuje si ¾
e do funkcji
j (t)i = exp(
i
}
E
n
t) jni
(160)
która ró·
zni si ¾
e od j (0)i = jni tylko nie maj ¾
acym praktycznego znaczenia glob-
alnym czynnikiem fazowym exp(
i
}
E
n
t). Dla ´scis÷
o´sci postulat 1 powinien
b´c uzupe÷
niony o stwierdzenie, ·
ze stan …zycznego uk÷
adu
kwantowego jest
ca÷
kowicie opisany przez ka·
zdy unormowany do jedno´sci wektor j i ze zbioru
wektorów ró·
zni ¾
acych sie czynnikem fazowym exp(i ): Stany w÷
asne niezale·
znego
od czasu hamiltonianu nazywamy stanami stacjonarnymi.
Rozwa·
zmy teraz problem; jak proces pomiaru wp÷
ywa na stan uk÷
adu? Za-
÷
ó·
zmy, ·
ze dokonujemy pomiaru oberwabli A. Poniewa·
z zgodnie z postulatem
2 obsrwabli tej odpowiada operator samosprz ¾
e·
zony b
A, a wynikiemi pomiaru
mo·
ze by´c tylko warto´s´c w÷
asna a
n
(na razie zak÷
adamy, ·
ze uk÷
ad nie jest zde-
generowany) tego operatora. z prawdopodobie´nstwem p
i
(t) =j hi j (t)i j
2
=j
c
i
(t) j
2
(równanie (150)). Je´sli pomiar nie zniszczy÷uk÷
adu i dokonamy kole-
jnego pomiaru obserwabli A to znowu otrzymamy warto´s´c a
n
lecz tym razem
z prawdopodobie´nstwem równym jedno´sci. Ten wynik t÷
umaczymy tak; je´sli
uk÷
ad bezpo´srednio przed pomiarem by÷w stanie j i to pomiar na tym stanie
powoduje jego rozpad na na stan w÷
asny jni odpowiadaj ¾
acy warto´sci w÷
asnej
a
n
.
W przypadku gdy widmo warto´sci w÷
asnych operatora b
A jest zdegerowane
to stan j i przed pomiarem mo·
zna zapisa´c nast ¾
epuj ¾
aco
j i =
X
n
r
n
X
j
c
n
j
jn
j
i
(161)
gdzie r
n
okre´sla krotno´s´c degeneracji warto´sci w÷
asnej a
n
; tj. rozmiar pod-
przestrzeni rozpinanej przez wektory w÷
asne odpowiadaj ¾
ace warto´sci w÷
asnej

xxxv
a
n
. Po pomiarze, w wyniku którego otrzymujemy warto´s´c w÷
asn ¾
a a
n
,
stan (
161 ) rozpada si ¾
e na
j
a
n
i =
1
qP
r
n
j=1
c
n
j
2
r
n
X
j
c
n
j
jn
j
i
(162)
Otrzymany stan jest rzutem stanu j i na podprzestrze´n odpowiadaj ¾
ac ¾
a zdegen-
erowanej warto´sci w÷
asnej a
n
:Mo·
zemy zatem sformu÷
owa´c nast ¾
epuj ¾
acy postulat.
Postulat 3.
Je´sli uk÷
ad jest opisany przez funkcj ¾
e falow ¾
a j i i w wyniku
pomiaru obserwabli A otrzymamy warto´s´c a
n
(waro´s´c w÷
asn ¾
a operatora samo-
sprz ¾
e·
zonego b
A odpowiadaj ¾
acego obserwabli A ) to bezpo´srednio po pomiarze
stan uk÷
adu jest dany przez funkcj ¾
e falow ¾
a
j
0
i =
b
P
n
j i
rD
b
P
n
E
(163)
gdzie b
P
n
jest operatorem rzutowym na podprzestrze´n odpowiadaj ¾
ac ¾
a warto´sci
w÷
asnej a
n
.
Zaua·
zmwy, ·
ze je´sli funkcja falowa j i jest dana równaniem (161) to operator
rzutowy
b
P
n
=
r
n
X
j=1
jn
j
i hn
j
j
(164)
Poniewa·
z wektory w÷
asne operatora b
A tworz ¾
a ortonormaln ¾
a baz ¾
e rozpinaj ¾
ac ¾
a
przestrze´n Hilberta H
s
(zwi ¾
azan ¾
a z opisywanym uk÷
adem) ÷
atwo mo·
zna si ¾
e
przekona´c, ·
ze operatory rzutowe b
P
n
spe÷
niaj ¾
a relacj ¾
e zupe÷
no´sci
X
n
b
P
n
= b
I
(165)
oraz warunek ortonormalno´sci
b
P
n
b
P
m
=
nm
b
P
m
(166)
W przypadku braku degeneracji r
n
= 1; zgodnie z równaniem (163) funkcja
falowa uk÷
adu j i (równanie 155) po pomiarze rozpada si ¾
e na stan
j
0
i =
c
n
jc
n
j
jni
(167)
który z dok÷
adno´sci ¾
a do nieistotnego dla pomiaru globalnego czynnika fazowego
jest równy stanowi jni odpowiadaj ¾
acemu warto´sci w÷
asnej a
n
.
W uk÷
adzie

xxxvi
ELEMENTY MECHANIKI KWANTOWEJ
opisanym przez funkcj ¾
e falow ¾
a (161) prawdopodobie´nstwo otrzymania podczas
pomiaru obserwabli A warto´sci a
n
wynosi
p
n
=
D
b
P
n
E
(168)
Znaj ¾
ac prawdopodobie´nstwa p
n
otrzymania w wyniku pomiaru warto´sci a
n
mo·
zemy wyliczy´c ´sredni ¾
a warto´sc obserwabli A
hAi =
X
n
a
n
p
n
=
X
n
a
n
D
b
P
n
E
=
*
X
n
a
n
b
P
n
+
=
D
b
A
E
(169)
gdzie skorzystali´smy ze spektralnego przedstawienia operatora
b
A =
X
n
a
n
b
P
n
(170)
Zasada nieoznaczono´sci Heisenberga
Zasada nieoznaczono´sci, sformu÷
owana przez Heinsenberga, podaje ograniczenia
zwi ¾
azane z jednoczesnym pomiarem kwantowych obserwabli …zycznych. Za-
÷
ó·
zmy, ·
ze obserwablom A i B odpowiadaj ¾
a samosprz ¾
e·
zone operatory b
A i b
B:
W stanie j i warto´s´c ´srednia ka·
zdej z tych obserwabli okre´slona jest wzorem
(169), a wariancja wzorem
V ar (A)
=
D
( b
A
hAi)
2
E
=
D
( b
A
hAi)( b
A
hAi)
E
= (171)
=
( b
A
hAi) j i
2
(172)
Zatem iloczyn wariancji obserwabli A i B w stanie j i
V ar (A)V ar (B) = ( b
A
hAi) j i
2
( b
B
hBi) j i
2
(173)
Poniewa·
z z nierówno´sci Couchy’ego-Schwartza
( b
A
hAi) j i
2
( b
B
hBi) j i
2
h j ( b
A
hAi)( b
B
hBi) j i
2
(174)
wprowadaj ¾
ac dla skrócenia zapisu oznaczenia b
A
1
= b
A
hAi i b
B
1
= b
B
hBi na
podstawie wzorów (173) i (174) mo·
zemy napisa´c, ·
ze
V ar (A)V ar (B)
h j b
A
1
b
B
1
j i
2
(175)
=
h j
1
2
( b
A
1
b
B
1
+ b
B
1
b
A
1
) +
1
2
( b
A
1
b
B
1
b
B
1
b
A
1
) j i
2
(176)
=
1
4
h j ( b
A
1
b
B
1
+ b
B
1
b
A
1
) + [ b
A; b
B] j i
2
(177)
=
1
4
h j ( b
A
1
b
B
1
+ b
B
1
b
A
1
) j i + i h j b
C j i
2
(178)

xxxvii
W ostatnim wzorze b
C =
i[ b
A; b
B] =
i( b
A b
B
b
B c
A) jest operatorem samo-
sprz ¾
e·
zonym poniewa·
z operatory b
A i b
B s ¾
a samosprz ¾
e·
zone. Ostatecznie otrzymu-
jemy, ·
ze
V ar (A)V ar (B)
1
4
h j ( b
A
1
b
B
1
+ b
B
1
b
A
1
) j i
2
+ h j b
C j i
2
1
4
h j b
C j i
2
(179)
Równanie (179) mo·
zna tak·
ze zapisa´c nast ¾
epuj ¾
aco
V ar (A)V ar (B)
1
4
jh [A; B] ij
2
(180)
Je´sli w komutatorze [ b
A; b
B] za operatory b
A i b
B podstawimy kartezja´nskie sk÷
ad-
owe operatorów po÷
o·
zenia b
X i p ¾
edu b
P to zgodnie z mechanik ¾
a kwantow ¾
a
[
b
x;
b
p
x
] =
i};
[
b
y;
b
p
y
] =
i}; [b
z;
b
p
z
] =
i}
(181)
Wstawiaj ¾
ac do wzoru (180) ka·
zdy z tych komutatorow za komutator [A; B],
otrzymamy s÷
ynne relacje nieoznaczono´sci Heisenberga dla po÷
o·
zenia i p ¾
edu
kwantowej cz ¾
astki
( x)
2
( p
x
)
2
1
4
}
2
, ( y)
2
( p
y
)
2
1
4
}
2
; ( z)
2
( p
z
)
2
1
4
}
2
(182)
0.2.19
Do´swiadczenie Sterna-Gerlacha w ´swietle postu-
latów mechanik kwantowej
Eksperyment Sterna-Gerlacha jest przyk÷
adem pokazuj ¾
acym przygotowanie stanu
kwantowego lub pomiaru warto´sci obserwabli w tym stanie.
Je´sli urz ¾
adze-
nie Sterna-Gerlacha (S-G) jest zorientowane wzd÷
u·
z osi z (to znaczy gradient
pola magnetycznego jest zorientowany wzd÷
u·
z osi z ) to mo·
zliwe s ¾
a na wyj´s-
ciu urz ¾
adzenia S-G dwa rozdzielone stany spinu j0i i j1i, ktore s ¾
a stanami
w÷
asnymi operatora (czyli obserwabli)
z
z warto´sciami w÷
asnymi
1, tj.
z
j0i = 1 j0i ;
z
j1i = 1 j1i
(183)
Je´sli przes÷
onimy na wyj´sciu urz ¾
adzenia S-G stan j0i to pozostanie stan j1i o
warto´sci w÷
asnej
1 i odwrotnie, je´sli przes÷
onimy stan j1i to pozostanie stan
j0i o warto´sci w÷asnej +1. Natomiast, je´sli urz ¾
adzenie S-G jest zorientowane
wzd÷
u·
z osi x to otrzymamy na wyj´sciu dwa rozdzielone stany
j+i
x
=
1
p
2
(j0i + j1i)
(184)
oraz
j i
x
=
1
p
2
(j0i
j1i)
(185)

xxxviii
ELEMENTY MECHANIKI KWANTOWEJ
b ¾
ed ¾
ace wektorami w÷
asnymi operatora
x
o warto´sciach w÷
asnych
1. Ogólnie,
dowolny stan spinu mo·
zna zapisa´c
j i = j0i + j1i gdzie j j
2
+ j j
2
= 1
(186)
Je´sli urz ¾
adzenie S-G jest zorientowane wzd÷
u·
z kierunku wektora jednostkowego
!
u = (u
x
; u
y
; u
z
) to jego sk÷
adowe w uk÷
adzie sferycznym wynosz ¾
a
u
x
= sin # cos ', u
y
= sin # sin ', u
z
= cos #
(187)
a operator spinu w kierunku wektora !
u
!
u
=
x
u
x
+
y
u
y
+
z
u
z
(188)
Macierzowa reprezentacja tego operatora w bazie wektorów w÷
asnych operatora
z
jest nast ¾
epuj ¾
aca
u
=
cos #
sin #e
i'
sin #e
i'
cos #
(189)
Wektory w÷
asne operatora (189) s ¾
a nast ¾
epuj ¾
ace
j+i
u
= cos
#
2
e
i
'
2
j0i + sin
#
2
e
i
2
j1i
(190)
j i
u
=
sin
#
2
e
i
'
2
j0i + sin
#
2
e
i
2
j1i
(191)
a warto´sci w÷
asne wynosz ¾
a odpowiednio +1 i
1.
Urz ¾
adzenie S-G mo·
ze by´c u·
zyte do przygotowania jakiego´s stanu lub jego
analizy.
W pierwszym przypadku urz ¾
adzenie S-G jest polaryzatorem, a w
drugim analizatorem. Za÷
ó·
zmy, ·
ze wi ¾
azka cz ¾
astek o spinie
1
2
biegn ¾
aca wzd÷
u·
z
osi y pada na urz ¾
adzenie S-G zorientowane wzd÷
u·
z osi x. Na wyj´sciu otrzy-
mujemy dwie wi ¾
azki j+i
x
i j i
x
. Je´sli przes÷
onimy wi ¾
azk¾
e j i
x
to pozostanie
tylko wi ¾
azka j+i
x
.
W tym przypadku urz ¾
adzenie S-G przygotowuje stan
j+i
x
, czyli dzia÷
a jako polaryzator. Je´sli tak przygowana wi ¾
azka przechodzi
przez urz ¾
adzenie S-G zorientowane wzd÷
u·
z osi z to pracuje ono jako analizator.
Na przyk÷
ad, je´sli przez tak zorientowane urz ¾
adzenie S-G przechodzi cz ¾
astka w
stanie j+i
x
=
1
p
2
(j0i + j1i) to jest on superpozycj ¾
a stanów w÷
asnych j0i i j1i
operatora
z
: Z drugiego postulatu wynika, ·
ze pomiar
z
daje w wyniku dwie
warto´sci: +1 i
1 z równymi prawdopodobie´nstwami p
+
= p
=
1
2
poniewa·
z
p
+
=
jh0j +i
x
j
2
= (h+j P
0
j+i)
x
=
1
2
(192)
p
=
jh1j +i
x
j
2
= (h j P
1
j i)
x
=
1
2
(193)
gdzie
P
0
= j0i h0j ; P
1
= j1i h1j ; P
0
+ P
1
= I,
P
0
P
1
= 0
(194)
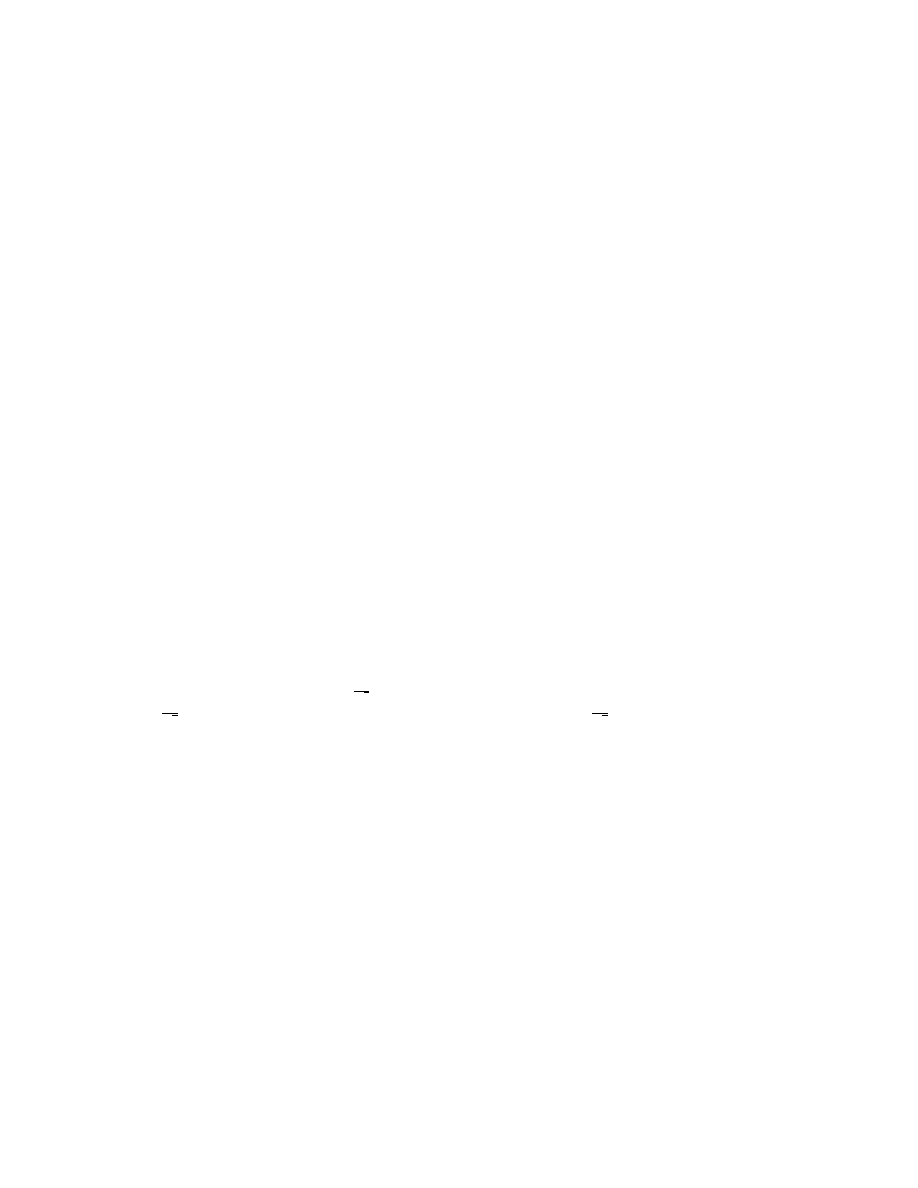
xxxix
0.2.20
Stany spl ¾
atane. Paradoks EPR
Niech ortonormaln ¾
a baz ¾
e przestrzeni Hilberta H
1
tworz ¾
a wektory
fjii ; i =
1; 2; :::; N g, a ortonormaln ¾
a baz ¾
e przestrzeni H
2
wektory fj ji ; j = 1; 2; :::; Mg.
Przestrze´n H
rozpinan ¾
a przez
wektory f jii
jji
jiji , i = 1; 2; :::; n;
j = 1; 2; :::; mg nazywamy iloczynem tensorowym przestrzeni H
1
i H
2
i zapisu-
jemy H = H
1
H
2
.
Wymiar przestrzeni H jest równy iloczynowi wymiarów
przestrzeni H
1
i H
2
. Jako przyk÷
ad rozwa·
zmy dwie dwuwymiarowe przestrze-
nie H
1
i H
2
; których ortonormalne bazy s ¾
a odpowiednio B
1
: f j0i
1
; j1i
1
g oraz
B
2
: f j0i
2
, j1i
2
g. Baz ¾
e przestrzeni H = H
1
H
2
tworz ¾
a wektory f j0i
1
j0i
2
;
j0i
1
j1i
2
; j1i
1
j0i
2
; j1i
1
j1i
2
}.
Z zasady superpozycji wynika, ·
ze w przestrzeni H = H
1
H
2
najbardziej
ogólnym stanem jest stan
j i =
X
i;j
c
ij
jii
jji
X
i;j
c
ij
jiji
(195)
który jest superpozycj ¾
a stanów bazy B : f jiji, i = 1; 2; :::; N ; j = 1; 2; :::; M).
Mówimy, ·
ze stan j i 2 H = H
1
H
2
jest stanem spl ¾
atanym je´sli nie mo·
zna
zapisa´c go jako tensorowy produkt stanów
j
1
i =
N
X
i=1
c
1
i
jii 2 H
1
i j
2
i =
M
X
j=1
c
2
j
jji 2 H
2
(196)
to znaczy.
j i 6= j
1
i
j
2
i =
N
X
i=1
M
X
j=1
c
1
i
c
2
j
jii
jji
(197)
Na przyk÷
ad stan
j
1
i =
1
p
2
(j00i + j11i)
jest spl ¾
atany, a stan
j
2
i =
1
p
2
(j01i + j11i) nie jest spl ¾
atany, bo mo·
zna go zapisa´c j
2
i =
1
p
2
(j0i + j1i)
j1i.
Jednym z niezwyk÷
ych i intryguj ¾
acych aspektów mechaniki kwantowej jest
spl ¾
atanie cz ¾
astek lub uk÷
adów cz ¾
astek. Najprostszy spl ¾
atany uk÷
ad kwantowy
sk÷
ada si ¾
e z dwóch obiektów (np. atomów, elektronów, fotonów, itp.) nazwi-
jmy te obiekty literami A i B. W stanie spl ¾
atanym warto´sci pewnych wielko´sci
obiektu A s ¾
a skorelowane z warto´sciami tych samych wielko´sci obiektu B. Wielko´sci
te pozostaj ¾
a skorelowane nawet gdy te dwa obiekty s ¾
a przestrzennie rozdzielone.
Nieklasyczne w÷
asno´sci stanów spl ¾
atanych by÷
y rozwa·
zane przez Einsteina, Podol-
skiego i Rosena (EPR). Autorzy ci wykazali, ·
ze teoria kwantów prowadzi do
sprzeczno´sci ( paradoks EPR) je´sli przyjmiemy jako naturalne (s÷
uszne) nast ¾
epu-
j ¾
ace postulaty:
1.
Postulat raalno´sci
: Je´sli mo·
zemy przewidzie´c z pewno´sci ¾
a
(tj. z
prawdopodobiestwem równym 1) warto´s´c wielko´sci …zycznej to warto´sc ta jest
realno´sci ¾
a …zycznn ¾
a niezale·
znie od naszej obserwacji.Warto´s´c ta jest okre´slona
niezale·
znie od tego czy dokonujemy jej pomiaru czy te·
z nie. Na przyk÷
ad, je´sli
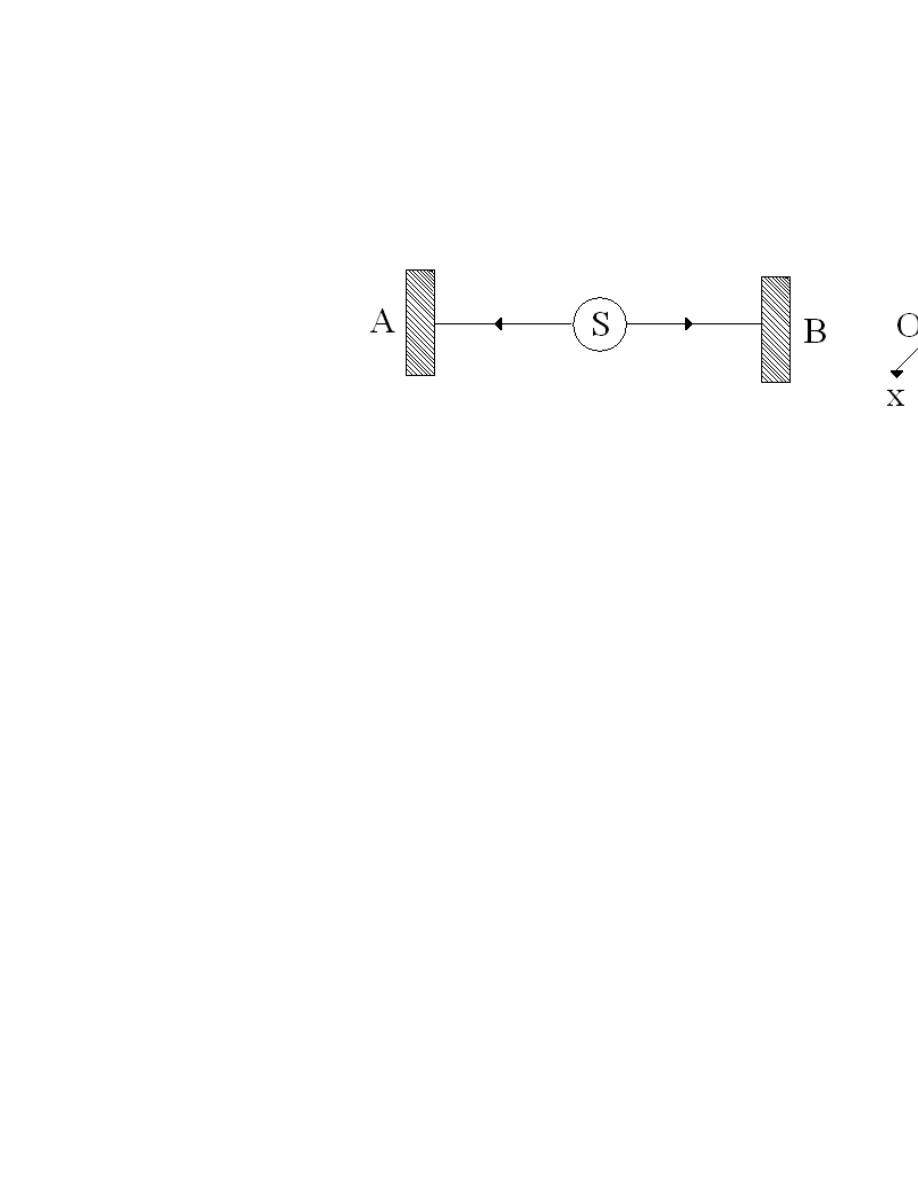
xl
ELEMENTY MECHANIKI KWANTOWEJ
funkcja falowa j i jest stanem w÷asnym operatora b
A reprezentuj ¾
acego wielko´s´c
…zyczn ¾
a A zwan ¾
a dalej obserwabl ¾
a , czyli b
A j i = a j i to warto´s´c a obserwabli
A jest elementem realno´sci …zycznej niezale·
znie od tego czy j ¾
a mierzymy czy
nie.
2.Postulat lokalno´sci: Je·
zeli dwa uk÷
ady …zyczne s ¾
a uk÷
adami nie b ¾
ed ¾
a-
cymi w zwi ¾
azku przyczynowym, albo inaczej uk÷
adami przyczynowo roz÷¾
acznymi,
to wynik dowolnego pomiaru przeprowadzonego na jednym uk÷
adzie nie ma
wp÷
ywu na wynik pomiaru wykonanego na drugim uk÷
adzie.
W my´sl szczególnej teorii wzgl ¾
edno´sci dwa zdarzenia pomiaru s ¾
a przyczynowo
roz÷¾
aczne (nie ma mi ¾
edzy nimi kontaktu ´swietlnego) gdy odleg÷
o´s´c przestrzenna
mi ¾
edzy nimi w inercjalnym uk÷
adzie odniesienia jest wi ¾
eksza od od÷
eg÷
o´sci ´swi-
etlnej, tj. gdy
(x
2
x
1
)
2
> c
2
(t
2
t
1
)
2
(198)
gdzie (x
1
; t
1
) i (x
2
; t
2
) s ¾
a wspó÷
rz ¾
enymi przestrzenno-czasowymi obu zdarze´n.
Z postulatu realno´sci od razu wynika,
·
ze w mechanice kwantowej dwie
wielko´sci …zyczne A i B, którym odpowiadaj ¾
a operatory b
A i b
B nie mog ¾
a równocze´snie
posiada´c realno´s´c …zyczn ¾
a gdy komutator
h
b
A; b
B
i
6= 0 poniewa·
z zgodnie z zasad ¾
a
nieoznaczono´sci Heisenberga ( 180) nie mo·
zemy równocze´snie zmierzy´c warto´s´c
obserwabli A i warto´s´c obserwabli B z prawdopodobie´nstwem 1. Dok÷
adny po-
miar warto´sci jednej wielko´sci niszczy informacj ¾
e o warto´sci drugiej wielko´sci.
.Paradoks EPR przeanalizujemy w wersji podanej przez Bohma (19....r.).
Schemat eksperymentu podany jest na rysunku ........

xli
Rysunek. Schemat do my´slowego eksperymentu EPR.
´Zród÷o S emituje par ¾
e cz ¾
astek, ka·
zda o spinie
1
2
, w stanie spl ¾
atanym
j i =
1
p
2
(j01i
j10i)
(199)
Stan ten jest spinowym stanem singletowym, to znaczy ·
ze wypadkowy spin
cz ¾
astek S = 0. Je´sli zatem rzut spinu jednej cz ¾
astki na o´s z wynosi
z
= +1
to rzut spinu drugiej cz ¾
astki na o´s z musi by´c równy
z
=
1:o Jedna cza-
stka jest wysy÷
ana do obserwatora A, a druga do obserwatora B. Odleg÷
o´s´c
mi ¾
edzy obserwatorami jest tak du·
za, ·
ze pomiar wykonywany przez obserwa-
tora A nie ma wp÷
ywu na wynik pomiaru obserwatora B i odwrotnie, pomiar
wykonywany przez obserwatora B nie wp÷
ywa na wynik pomiaru obsewatora
A. Innymi s÷
owy
eksperymenty wykonywane przez ka·
zdego z obserwatorów
s ¾
a przyczynowo roz÷¾
aczne, spe÷
niony jest postulat lokalno´sci. Je´sli obserwator
A rejestruje cz ¾
astk¾
e, której rzut na o´s z wynosi
A
z
= +1 (czyli cz ¾
astk¾
e w
stanie j0i) to zgodnie z trzecim postulatem mechaniki kwantowej stan (199)
rozpada si ¾
e na stan j01i i obserwator B zarejestruje cz ¾
astk¾
e w stanie
B
z
=
1
(czyli cz ¾
astk¾
e w stanie j1i) z prawdopodobie´nstwem równym 1. Podobnie, je´sli
obserwator A zmierzy cz ¾
astk¾
e w stanie
A
z
=
1 to wynik pomiaru obserwa-
tora B b ¾
edzie równy
B
z
= +1. Zatem wyniki pomiarów obu obserwatorów
s ¾
a
antyskorelowane. Jest on zgodny z nasz ¾
a intuicj ¾
a, poniewa·
z mo·
zna po-
da´c klasyczny opowiednik opisanego eksperymentu. Jako przyk÷
ad wyobra´zmy
sobie dwie kulki, jedn ¾
a czarn ¾
a i drug ¾
a bia÷¾
a. Ka·
zda z kulek jest zamkni ¾
eta
w pude÷
ku. Jedno pude÷
ko przesy÷
amy do obserwatora A, drugie do obserwa-
tora B. Je´sli obserwator A otworzy otrzymane pude÷
ko i znajdzie w nim kulk¾
e,
powiedzmy
bia÷¾
a, to obserwator B z pewno´sci ¾
a (z pradopodobie´nstwem 1)
znajdzie w pude÷
ku czarn ¾
a kulk¾
e.
Wracaj ¾
ac do naszego eksperymentu z obiektami kwantowymi, dochodzimy
do zaskakuj ¾
acych wniosków je´sli stan spl ¾
atany (199 ) zapiszemy w formie
j i =
1
p
2
(j+ i
j +i)
(200)
gdzie j+i =
1
p
2
(j0i + j1i) i j i =
1
p
2
(j0i
j1i) s ¾
a stanami w÷
asnymi operatora
x
z warto´sciami w÷
asnym odpowiednio +1 i
1:Je´sli obserwator A zmierzy
warto´s´c w÷
asn ¾
a operatora
A
x
i otrzyma warto´s´c
A
x
= +1 to zgodnie z postu-
latem 3
mechaniki kwantowej stan (200) rozpada si ¾
e na stan j+ i i obserwator
B z pomiaru warto´sci operatora
B
x
otrzyma ze 100% pewno´sci ¾
a , ·
ze
B
x
=
1.
Widzimy zatem, ·
ze stan jednej cz ¾
astki zale·
zy od rodzaju obserwabli mierzonej
na drugiej cz ¾
astce. Je´sli obserwator A mierzy warto´s´c obserwabli
A
z
to stan
cz ¾
astki obserwatora B rozpada si ¾
e na stan w÷
asny operatora
B
z
.
Je´sli nato-
miast obserwator A mierzy warto´s´c obserwabli
A
x
to stan cz ¾
astki obserwatora
B rozpada si ¾
e na stan w÷
asny operatora
B
x
. W pierwszym przypadku wi ¾
a·
zemy
element realno´sci …zycznej z obserwabl ¾
a
B
z
, w drugim z obserwabl ¾
a
B
x
. Nie
mo·
zemy jednak przypisa´c jednoczesn ¾
a realno´s´c …zyczn ¾
a obydwu obserwablom
poniewa·
z one nie komutuj ¾
a,
B
z
;
B
x
6= 0.

xlii
ELEMENTY MECHANIKI KWANTOWEJ
Nale·
zy jeszcze raz podkre´sli´c, istotn ¾
a cech ¾
a tego eksperymentu jest fakt, ·
ze
ka·
zdy z obserwatorów dokonuje pomiaru gdy cz ¾
astki s ¾
a daleko od siebie. Dlat-
ego, zgodnie z postulatem lokalno´sci dowolny pomiar wykonany przez obserwa-
tora A nie mo·
ze zmody…kowa´c stanu cz ¾
astki rejestrowanej przez obserwatora
B. Je´sli zatem uznamy
za s÷
uszne postulaty realno´sci i lokalno´sci to teoria
kwantowa prowadzi do sprzeczno´sci. Paradoksem jest znajomo´sc wyniku po-
miaru obserwatora B na podstawie wyniku pomiaru obserwatora A pomimo
braku jakiegokolwiek kontaktu mi ¾
edzy obserwatorami.
Zatem wniosek Ein-
steina, Rosena i Podolskiego by÷nast ¾
epuj ¾
acy: teoria kwantowa jest teori ¾
a
niekompletn ¾
a
.
0.2.21
Nierówno´s´c Bella
Mo·
zliwo´s´c odpowiedzi na pytanie czy teoria kwantowa jest teori ¾
a kompletn ¾
a po-
jawi÷
a si ¾
e w momencie sformu÷
owania przez Bella nierówno´sci (1964) (zwanych
od nazwiska ich autora nierówno´sciami Bella), które umo·
zliwiaj ¾
a eksperymen-
taln ¾
a wery…kacj ¾
e dylematu czy teoria kwantów jest teori ¾
a niekomletn ¾
a. Nierówno´sci
Bell wyprowadzi÷zak÷
adaj ¾
ac s÷
uszno´s´c postulatow realno´sci i lokalno´sci.
Z
drugiej strony je´sli wyprowadzimy takie nierówno´sci w oparciu o prawa mechaniki
kwantowej to nierówno´sci Bella zostan ¾
a z÷
amane. Zatem eksperymentalna wery-
…kacja nierówno´sci Bella z ich odpowiednikami wyprowadzonymi na podstawie
praw mechaniki kwantowej pozwala rozstrzygn ¾
a´c dylemat czy teoria kwantów
jest teori ¾
a kompletn ¾
a.
Wyobra´zmy sobie, ·
ze ´zród÷
o emituje parami du·
z ¾
a liczb ¾
e c·
z ¾
astek o spinie
ro·
znym od zera w singletowym stanie spl ¾
atanym(stan (199)). C·
z ¾
astki nale·
z ¾
ace
do danej pary biegn ¾
a w przeciwnych kierunkach, jedna do obserwatora A, a
druga do obserwatora B. Odleg÷
o´s´c mi ¾
edzy obserwatorami mo·
ze by´c dowolnie
du·
za. Pami ¾
etamy, ·
ze niezale·
znie od ich wzajemnej odleg÷
o´sci cz ¾
astki s ¾
a ca÷
y
czas w stanie spl ¾
atanym. Obserwatorzy rejestruj ¾
a cz ¾
astk¾
e-cz÷
onka ka·
zdej pary
i mierz ¾
a jej polaryzacj ¾
e ( orientacj ¾
e spinu) wzgl ¾
edem trzech wybranych osi a ,
b
, c . Rejestrowane cz ¾
astki dzielimy na grupy nast ¾
epuj ¾
aco. Je´sli na przyk÷
ad,
obserwator A zmierzy, ·
ze warto´sci w÷
asne obserwabli
A
a
,
A
b
i
A
c
wynosz ¾
a
odpowiednio +1; +1;
1 to zaznaczamy, ·
ze cz ¾
astka nale·
zy do grupy (a+,b+,c-
),
podobnie gdy warto´sci w÷
asne obserwabli
A
a
,
A
b
i
A
c
wynosz ¾
a odpowiednio
+1,
1;
1 to cz ¾
astk¾
e zaliczamy do grupy (a+,b-,c-), itd. W eksperymencie
nie zak÷
adamy, ·
ze
A
a
,
A
b
i
A
c
s ¾
a mierzone równocze´snie, je´sli obserwator
mierzy
A
a
to oznacza to, ·
ze nie mierzy
A
b
i
A
c
Jednak·
ze, zgodnie z postu-
latem realno´s´ci ka·
zda z warto´sci w÷
anych obserwabli
A
a
,
A
b
i
A
c
posiada
okre´slon ¾
a warto´s´c, czyli jest realno´sci ¾
a …zyczn ¾
a niezale·
znie od naszej obserwacji.
Ale wci ¾
a·
z pami ¾
etamy, ·
ze wyniki pomiarów obu obserwatorów s ¾
a silnie antysko-
relowane, je´sli na przyk÷
ad c·
z ¾
astka zmierzona przez obserwatora A nale·
zy do
grupy (a+,b+,c-) to cz ¾
astka zmierzona przez obserwatora B nale·
zy do grupy
(a-,b-,c+) . Wszystkie wzajemnie wykluczaj ¾
ace si ¾
e grupy cz ¾
astek zebrane s ¾
a
w Tabeli....

xliii
Tabela.... Podzia÷cz ¾
astek stanu singletowego na wzajemnie wykluczaj ¾
ace
si ¾
e grupy.
Populacja
cz ¾
astki obserwatora A
cz ¾
astki obserwatora B
N
1
N
2
N
3
N
4
N
5
N
6
N
7
N
8
(a+; b+; c+)
(a+; b+; c )
(a+; b ; c+)
(a+; b ; c )
(a ; b+; c+)
(a ; b+; c )
(a ; b ; c+)
(a ; b ; c )
(a ; b ; c )
(a ; b ; c+)
(a ; b+; c )
(a ; b+; c+)
(a+; b ; c )
(a+; b ; c+)
(a+; b+; c )
(a+; b+; c+)
Niech p(a+; b+) oznacza prawdopodobie´nstwo, ·
ze obserwator A otrzyma w
wyniku pomiaru
A
a
= +1, a obserwator B otrzyma
B
b
= +1.
Z Tabeli ...
wynika, ·
ze
p(a+; b+) =
N
3
+ N
4
N
t
gdzie N
t
=
8
X
i=1
N
i
(201)
Podobnie otrzymujemy
p(a+; c+) =
N
2
+ N
4
N
t
oraz p(c+; b+) =
N
3
+ N
7
N
t
(202)
Poniewa·
z N
i
0, mamy
N
3
+ N
4
(N
2
+ N
4
) + (N
3
+ N
7
)
(203)
sk ¾
ad bezpo´srednio dostajemy nierówno´s´c Bella
p(a+; b+)
p(a+; c+)+ p(c+; b+)
(204)
Zwró´cmy uwag ¾
e, ·
ze nierówno´s´c (204) zosta÷
a wyprowadzona
zak÷
adaj ¾
ac, ·
ze
spe÷
niony jest postulat lokalno´sci. Je´sli na przyk÷
ad para nale·
zy do grupy 1 (pa-
trz tabela....) i obserwator A wybierze do pomiaru obserwabl ¾
e
A
a
to otrzyma ze
100% prawdpodobie´nstwem warto´s´c równ ¾
a 1 niezale·
znie od tego czy obserwator
B wybierze do pomiaru polaryzacji swojej cz ¾
astki o´s a , b czy c:
Policzmy prawdopodobie´nstwa wyst ¾
epuj ¾
ace we wzorze (204) wed÷
ug teorii
kwantowej. Zacznijmy od p(a+; b+). Je´sli obserwator A zmierzy
A
a
= 1 (co
oznacza, ·
ze cz ¾
astka obsewatora A jest w stanie w÷
asnym j+i
a
operatora
A
a
)
to stan cz ¾
astki obserwatora B rozpadnie si ¾
e na stan w÷
asny j i
a
operatora
B
a
o warto´sci w÷
asnej
1. Zatem, je´sli
A
a
= +1 to ÷
atwo mo·
zna sprawdzi´c,·
ze
obserwator B otrzyma
B
b
= +1 z
prawdopodobie´nstwem
j
b
h+j i
a
j
2
=
sin
2
(
ab
=2) gdzie
ab
jest k ¾
atem mi ¾
edzy osiami a i b. (patrz wzory (190) i (191)).
Poniewa·
z obserwator A otrzymuje wynik
A
a
= +1 z prawdopodobie´nstwem
1
2
(bo cz ¾
astki s ¾
a w stanie (199)) otrzymujemy, ·
ze
p(a+; b+) =
1
2
sin
2
(
ab
=2)
(205)

xliv
ELEMENTY MECHANIKI KWANTOWEJ
W taki sam sposób mo·
zna wyliczy´c
p(a+; c+)
i
p(c+; b+): Ostatecznie,
nierówno´s´c Bella (204) w wersji kwantowej jest nast ¾
epuj ¾
aca
sin
2
(
ab
=2)
sin
2
(
ac
=2) + sin
2
(
cb
=2)
(206)
Je´sli zorientujemy osie a , b i c w taki sposób; ·
ze
ab
= 2 ,
ac
=
cb
=
to nierówno´s´c ( 206) b ¾
edzie ÷
amana dla
0 <
<
2
. Czy tak jest naprawd ¾
e
rozstrzyga eksperyment. Z po´sród wielu eksperymentów , których celem by÷
o
zwery…kowanie nierówno´sci Bella, najbardziej spektakularne by÷
o do´swiadczenie
Aspekta i wspó÷
pracowników (1982r.) . Wynik tego eksperymentu oraz wyniki
eksperymentów wykonanych pó´zniej przez innych autorów (....) potwierdzaj ¾
a
niezbicie ÷
amanie nierówno´sci (204). Ten fakt utwierdza nas w przekonaniu,
·
ze mechanika kwantowa jest teori ¾
a nielokaln ¾
a, a w mikro´swiecie postulaty Ein-
steina, Rosena i Podolskiego nie obowi ¾
azuj ¾
a. Ko´ncz ¾
ac ten rozdzia÷nale·
zy pod-
kre´sli´c, ·
ze nierówno´sci Bella by÷
y podstaw ¾
a do´swiadczalnych dowodów potwierdza-
j ¾
acych, ·
ze mechanika kwantowa jest teori ¾
a kompletn ¾
a.

OPERATOR G ¾
ESTO´SCI
W wielu przypadkach badamy nie pojedy´ncze uk÷
ady kwantowe lecz
raczej
zespo÷
y uk÷
adów kwantowych. Zespó÷kwantowy mo·
ze znajdowa´c si ¾
e w wielu
ro·
znych stanach kwantowych, wyst ¾
epowanie ka·
zdego z tych stanów okre´slone
jest pewnym prawdopodobie´nstwem. Jako przyk÷
ad rozwa·
zmy przestrze´n Hilberta
rozpinan ¾
a przez dwa wektory bazowe fj i ; j ig. Za÷ó·
zmy, ·
ze przygotowali´smy
uk÷
ad gdzie ka·
zdy cz÷
onek uk÷
adu jest w jednym z unormowanych do jedno´sci
(ja
i
j
2
+ jb
i
j
2
= 1; i = 1; 2) stanów
j i = a
1
j i + b
1
j i ;
j i = a
2
j i + b
2
j i
(207)
Prawdopodobie´nstwo zaobserwowania, ·
ze stan j i jest stanem j i jest równe
ja
1
j
2
, a prawdopodobie´nstwo stanu j i wynosi jb
1
j
2
(regu÷
a Borna). Podobne
wyniki otrzymamy w przypadku stanu j i Rozwa·
zmy teraz sytuacj ¾
e gdy przy-
gowali´smy n uk÷
adów (207) w stanie j i i n uk÷adów w stanie j i . Ca÷kowita
liczna uk÷
adów w zespole N = n + n , sk ¾
ad
n
N
+
n
N
= 1
(208)
co oznacza, ·
ze je´sli przypadkowo wybierzemy cz÷
onka zespo÷
u to z prawdopodobie´nst-
wem p = n =N b ¾
edzie to stan j i ; a z prawdopodobie´nstwem 1
p = n =N
stan j i.
W przytoczonym przyk÷
adzie poj ¾
ecie prawdopodobie´nstwa
wyst ¾
epuje w dwóch znaczeniach; 1) prawopodobie´nstwo zaobserwowania okre´slonego
stanu bazowego w jednym z cz÷
onków uk÷
adu (207) obliczane wed÷
ug obow-
i ¾
azuj ¾
acej w mechanice kwantowej regu÷
y Borna 2) prawdopodobie´nstwo wys-
t ¾
epowania jednego ze stanów (207) w zespole kwantowym, które ma charakter
klasyczny.
Charakter prawdopodobie´nstwa 2) oznacza ·
ze zespó÷kwantowy jest statysty-
czn ¾
a mieszanin ¾
a stanów kwantowych. Pojawia si ¾
e zatem pytanie jak opisy-
wa´c systemy, które s ¾
a miesznin ¾
a
stanów kwantowych z okre´slonymi praw-
dopodobie´nstwami. W takich przypadkach powinni´smy obliczy´c wed÷
ug regu÷
kwantowych warto´sci oczekiwane operatorora reprezentuj ¾
acego interesuj ¾
ac ¾
a nas
obserwabl ¾
e w ka·
zdym ze stanów kwantowych mieszaniny, a nast ¾
epnie obliczy´c
ich warto´s´c wa·
zon ¾
a przez prawdopodobie´nstwa stanów kwantowych w mieszaninie.
Do opisu warto´sci oczekiwanych obserwabli …zycznych systemów, które s ¾
a mieszan-
in ¾
a stanów kwantowych s÷
u·
zy operator g ¾
esto´sci
xlv

xlvi
OPERATOR G ¾
ESTO´SCI
0.2.22
Operator g ¾
esto´sci dla stanu czystego
Rozwa·
zmy uk÷
ad, który jest
w unormowanym stanie j i : Stan ten mo·
zna
rozwin ¾
a´c w pewnej ortonormalnej bazie fju
i
ig
j i =
n
X
i=1
c
i
ju
i
i
(209)
gdzie prawdopodobie´nstwo, ·
ze uk÷
ad jest w stanie ju
i
i wynosi jc
i
j
2
. Je´sli uk÷
ad
jest w stanie (209) to mówimy, ·
ze jest on w stanie czystym. Warto´s´c oczekiwana
operatora b
A w stanie (209) zgodnie z wzorem (47) wynosi
hAi = h j b
A j i =
X
i;j
c
i
c
j
hu
i
j b
A ju
j
i
(210)
Poniewa·
z
c
i
c
j
= hu
j
j ih ju
i
i
(211)
zatem
hAi = h j b
A j i =
X
i;j
hu
j
j ih ju
i
i hu
i
j b
A ju
j
i
(212)
Je´sli zde…niujemy operator
= j i h j
(213)
który odt ¾
ad nazywa´c b ¾
edziemy operatorem g ¾
esto´sci dla stanu czystego j i to
korzystaj ¾
ac z relacji zupe÷
no´sci I =
P
n
i=1
ju
i
i hu
i
j warto´s´c oczekiwan ¾
a operatora
b
A mo·
zna wyrazi´c wzorem
hAi =
X
i;j
hu
j
j ju
i
i hu
i
j b
A ju
j
i =
X
;j
hu
j
j b
A ju
j
i = T r( b
A)
(214)
×atwo si ¾
e przekona´c, ·
ze w szczególno´sci
T r( ) =
X
;j
hu
j
j ju
j
i =
X
;j
hu
j
j ih ju
j
i =
X
j
c
j
c
j
=
X
j
jc
j
j
2
= 1
(215)
czyli tak jak powinno by´c, bo suma prawdopodobie´nstw zaobserwowania stanu
j i w stanach bazowych ju
i
i musi by´c zawsze równa jedno´sci.
0.2.23
Ewolucja w czasie operatora g ¾
esto´sci
Równanie opisuj ¾
ace ewolucj ¾
e w czasie operatora g ¾
esto´sci mo·
zna wyprowadzi´c
bezpo´srednio po÷
uguj ¾
ac si ¾
e równaniem Schrödingera
i~
d
dt
j i = H j i
(216)
Poniewa·
z H = H
y
, s÷
uszne jest równie·
z równanie
i}
d
dt
h j = h j H
(217)

xlvii
Korzystaj ¾
ac z de…nicji (??) operatora g ¾
esto´sci otrzymujemy, ·
ze
d
dt
=
d
dt
(j i h j) = (
d
dt
j i) h j + j i (
d
dt
h j)
(218)
Posi÷
kuj ¾
ac si ¾
e teraz wzorami (216) oraz (217) z powy·
zszego wzoru dostajemy
d
dt
=
(
H
i}
j i) h j + j i (h j
H
i}
) =
(219)
=
H
i}
H
i}
=
1
i}
[H; ]
(220)
lub
i}
d
dt
= [H; ]
(221)
Dla uk÷
adu zamkni ¾
etego ewolucj ¾
e w czasie operatora g ¾
esto´sci mo·
zna równie·
z
opisa´c przy pomocy unitarnego operatora U . Je´sli (t) jest operatorem g ¾
esto´sci
w chwili t, a (t
0
) reprezentuje ten sam operator w chwili t
0
< t to
(t) = U (t
0
)U
y
(222)
gdzie
U = exp( iHt=})
(223)
Latwo wywnioskowa´c, ·
ze operator g ¾
esto´sci jest jest operatorem hermitowskim
bowiem z de…nicji (??)
y
= (j i h j)
y
= j i h j =
(224)
W przypadku stanów czystych
2
= (j i h j)(j i h j) = j i ( j i) h j =
(225)
Zatem je´sli stan j i jest stanem czystym to
T r(
2
) = 1
(226)
Wzór ten w wielu przypadkach stanowi dogodny test na sprawdzenie czy dany
stan jest stanem czystym.
0.2.24
Operator g ¾
esto´sci dla stanów mieszanych
W ogólno´sci uk÷
ad mo·
ze znajdowa´c si ¾
e w jednym z unormowanych do jedno´sci
stanów j
i
i (i = 1; 2; :::; n). Dla stanu j
i
i operator g ¾
esto´sci zgodnie z wzorem
(209)
i
= j
i
i h ij. Je´sli prawdopodobie´nstwo, ·
ze uk÷
ad znajduje si ¾
e w stanie
j
i
i wynosi p
i
to operator g ¾
esto´sci dla ca÷
ego uk÷
adu
=
n
X
i=1
p
i i
=
n
X
i=1
p
i
j
i
i h
i
j
(227)

xlviii
OPERATOR G ¾
ESTO´SCI
Maj ¾
ac na uwadze w÷
asno´sci ´sladu operatorów (wzory (116) - (120)) otrzymu-
jemy, ·
ze
T r( ) = T r(
n
X
i=1
p
i
j
i
i h
i
j) =
n
X
i=1
p
i
T r(j
i
i h
i
j) =
n
X
i=1
p
i
h
i
j
i
i =
n
X
i=1
p
i
= 1
(228)
Wyka·
zemy teraz, ·
ze operator g ¾
esto´sci jest operatorem dodotnio okre´slonym.
Mówimy, ·
ze operator A jest operatorem dodatnio okre´slonym gdy hu jAj ui
0
dla dowolnego stanu jui. We´zmy zatem dowolny stan j i i rozwa·
zmy wyra·
zenie
h j j i. Stosuj ¾
ac równanie (227) dostajemy
h j j i =
n
X
i=1
p
i
h j
i
i h
i
j i =
n
X
i=1
p
i
jh j
i
ij
2
(229)
Poniewa·
z
0
p
i
1 (i = 1; 2; :::; n) oraz dla iloczynu skalarnego dwóch
dowolnych wektorow
jh j
i
ij
2
0,
przeto h j j i
0.
Wykazali´smy
wi ¾
ec, ·
ze operator g ¾
esto´sci jest operatorem dodatnio okre´slonym. Z tej w÷
asno´sci
automatycznie wynika, ·
ze operator g ¾
esto´sci jest operatorem hermitowskim, a
wobec tego jego warto´sci w÷
asne
i
0: Mo·
zna zatem u·
zyc rozk÷
adu spektral-
nego do wyra·
zenia operatora g ¾
esto´sci w reprezentacji diagonalnej
=
X
i
i
ju
i
i hu
i
j
(230)
gdzie ju
i
i, i = 1:2::::; n s ¾
a wektorami w÷
asnymi operatora :
Zatem podsumowuj ¾
ac, podstawowe w÷
asno´sci, które musi spe÷
nia´c operator
g ¾
esto´sci s ¾
a nast ¾
epuj ¾
ace
1. operator g ¾
esto´sci jest operatorem hermitowskim, to znaczy
=
y
,
2. T r( ) = 1,
3.
jest operatorem dodatnio okre´slonym, co oznacza ·
ze hu j j ui
0 dla
dowolnego stanu jui.
W rozdziale ........ pokazali´smy, ·
ze w okre´slonej bazie dany operator mo·
zna
przedstawi´c w formie macierzy (tj. poda´c jego reprezentacj ¾
e macierzow ¾
a). Mo·
zna
si ¾
e przekona´c, ·
z ¾
e wa·
znym wska´znikiem ´swiadcz ¾
acym o tym czy dany stan jest
stanem czystym czy te·
z mieszanin ¾
a stanów jest obecno´s´c elementów pozadiag-
onalnych w macierzy g ¾
esto´sci.
Ich obecno´s´c wskazuje na to, ·
ze stan mo·
ze
by´c stanem czystym, a ich brak wyklucza tak ¾
a sytuacj ¾
e - stan jest statysty-
czn ¾
a mieszanin ¾
a stanów.
Wynika to z faktu, ·
ze ró·
zne cz÷
ony funkcji falowej
mog ¾
a ze sob ¾
a interferowa´c. Tak ¾
a interferencj ¾
e obserwuje si ¾
e w przypadku stanów
czystych (mówimy wtedy o koherencji stanów). Natomiast w przypadku statysty-
cznej mieszaniny stanów nie ma koherencji, a wi ¾
ec elementy pozadiagonalne
macierzy g ¾
esto´sci s ¾
a równe zero.Jednak·
ze reprezentacja macierzowa operatora
w jednej bazie ró·
zni si ¾
e od jego reprezentacji w innej bazie . W szczególno´sci
mo·
zna wybra´c tak ¾
a baz ¾
e, w której operator g ¾
esto´sci przyjmuje form ¾
e macierzy
diagonalnej. Dlatego konieczne jest mocniejsze kryterium, które by przes ¾
adza÷
o
czy operator g ¾
esto´sci reprezentuje stan czysty czy raczej stan mieszany.

xlix
Wiemy, ·
ze operator g ¾
esto´sci stanu czystego jest operatorem rzutowym, tj. =
2
. Dlatego w tym przypadku T r( ) = T r(
2
) = 1.
Taka sytuacja nie ma
miejsca w przypadku macierzy g ¾
e´sto´sci dla stanów mieszanych (operator g ¾
esto´sci
nie jest operatorem rzutowym). Dla stanów mieszanych T r(
2
) < 1:Zatem
warto´s´c ´sladu macierzy rozstrzyga czy dany stan jest stanem czystym, czy te·
z
stanem mieszanym.

l
OPERATOR G ¾
ESTO´SCI

OBWODY KWANTOWE
0.2.25
Kubit
Klasyczny "bit" to uk÷
ad, który mo·
ze znajdowa´c si ¾
e w dwóch stanach s÷
u·
z ¾
acych
do reprezentowania 0 i 1 - pojedynczych cyfr uk÷
adu dwójkowego (binarnego).
Jedynymi operacjami na takim uk÷
adzie to operacja identyczno´sci ( 0 =) 0;
1 =) 1) i operacja NOT ( 0 =) 1, 1 =) 0).
Kwantowy bit czyli "kubit" (od angielskiej nazwy quantum bit) jest uk÷
adem
kwantowym o dwóch stanach opisanych w dwuwymiarowej przestrzeni Hilberta.
W tej przestrzeni mo·
zna wybra´c dwa unormowane i wzajemnie ortogonalne
stany kwantowe
,
j0i =
1
0
, j1i =
0
1
,
(231)
które reprezentuj ¾
a warto´sci 0 i 1 klasycznego bitu. Stany (231) tworz ¾
a tak
zwan ¾
a obliczeniow ¾
a baz ¾
e. Zgodnie z zasad ¾
a superpozycji dowolny stan kubitu
mo·
zna zapisa´c
j i = j0i + j1i
(232)
gdzie
;
2 C i spe÷niaj ¾
a warunek normalizacji
j j
2
+ j j
2
= 1
(233)
Poniewa·
z ka·
zdy wektor stanu (?? ) spe÷
nia warunek normalizacji (??) oraz
wystarczy go okre´sli´c z dok÷
adno´sci ¾
a do czynnika fazowego (fazy globalnej).
Zatem mo·
zna przyj ¾
a´c, ·
ze czynnik
we wzorze (232) jest liczb ¾
a rzeczywist ¾
a, a
czynnik
liczb ¾
a zespolon ¾
a. Ogólnie stan kubitu mo·
zna zapisa´c nast ¾
epuj ¾
aco
j i = cos
#
2
j0i + e
i'
sin
#
2
j1i =
cos
#
2
e
i'
sin
#
2
gdzie 0
#
a 0
'
2
(234)
Dlatego w odró·
znieniu od klasycznego bitu, który mo·
ze przyjmowa´c warto´sci
0 lub 1; kwantowy bit czyli kubit jest wektorem o wspó÷
rz ¾
ednych sparametry-
zowanych przez przez ci ¾
ag÷
e zmienne
,
(232) lub #, ' ( 234), czyli stany
li

lii
OBWODY KWANTOWE
kubitowe tworz ¾
a zbiór kontinuum. W odró·
znieniu w od klasycznego bitu kwan-
towy bit mo·
ze znajdowa´c si ¾
e w nieprzeliczlnej ilo´sci stanów.Na tym poziomie
wiedzy mo·
zemy powiedzie´c, ·
ze w odró·
znieniu od klasycznego bitu, kubit mo·
ze
by´c u·
zyty do gromadzenia informacji na niesko´nczon ¾
a ilo´s´c sposobów
( w
rozumieniu, ·
ze dowolna para wspó÷
czynników
;
(lub #; ) jest no´snikiem
okre´slonej informacji).
Uk÷
ad o dwóch stanach kwantowych mo·
ze w praktyce by´c wykorzystany jako
kubit je´sli potra…my wykonywa´c na nim nat ¾
epuj ¾
ace operacje:
1. przygotowa´c qubit w dobrze okre´slonym stanie, np. w stanie [0i,
2. dowolny stan kubitu przetransformowa´c na inny stan kubitowy (takie
transformacje, jak si ¾
e przekonamy s ¾
a transformacjami unitarnymi),
3. zmierzy´c stan kubitu w bazie obliczeniowej fj0i i j1i g.
Uwaga!.
W dos÷
ownym znaczeniu, stanu uk÷
adu kwantowego nie potra…my
zmierzy´c. Natomiast potra…my zmierzy´c prawdopodobie´nstwo, ·
ze dany obiekt
znajduje si ¾
e w okre´slonym stanie. Zatem odt ¾
ad pod has÷
em "pomiar stanu ku-
bitu" b ¾
edziemy rozumie´c pomiar prawdopodobie´nstwa, ·
ze kubit jest w okre´slonym
stanie.
Zmierzy´c
stan kubitu w bazie obliczeniowej fj0i i j1i goznacza , ·
ze mo·
zemy zmierzy´c po-
laryzacj ¾
e qubitu wzd÷
u·
z osi z.( prawdopodobie´nstwo, ·
ze jest w stanie j0i lub w
stanie j1i) Hermitowskim operatorem zwi ¾
azanym z tym pomiarem jest operator
Pauliego
z
, którego wektorami
w÷
asnymi
s ¾
a stany [0i i j1i. Je´sli stan ku-
bitu jest opisany równaniem (234) to zgodnie z drugim postulatem mechaniki
kwantowej w wyniku pomiaru otrzymujemy warto´sci w÷
asne +1 lub
1 z praw-
dopodobie´nstwem
p
0
= jh0j ij
2
= cos
2
#
2
lub p
1
= jh1j ij
2
= sin
2
#
2
(235)
0.2.26
Sfera Blocha
Geometrycznym obrazem kubitu jest jego przedstawienie na sferze Blocha. Poniewa·
z
stan kubitu jest unormowany do jedynki to mo·
ze on by´c przedstawiony jako
punkt na sferze o promieniu r = 1; zwanej sfer ¾
a Blocha, którego wspó÷
rz ¾
edne
w uk÷
adzie kartezja´nskim wynosz ¾
a
x = sin # cos ', y = sin # sin ', z = cos #
(236)
Zatem zgodnie z wzorami (234) i (236)
j i =
2
4
q
1+z
2
x+iy
p
2(1+z)
3
5
(237)
Mo·
zna powiedzie´c, ·
ze wektor Blocha
(237) jest wektorem wyznaczaj ¾
acym
punkt na sferze Blocha o wspó÷
rz ¾
ednych x, y, z (x
2
+ y
2
+ z
2
= 1). Jednym
z zastosowa´n reprezentacji (234) i reprezentacji (237) stanu j i w bazie {j0i ,
j1ig jest macierzowe przedstawienie operatora rzutowego

liii
P = j i h j =
cos
2 #
2
e
i'
sin
#
2
cos
#
2
e
i'
sin
#
2
cos
#
2
sin
2 #
2
=
1
2
1 + z
x
iy
x + iy
1
z
(238)
gdzie P
ij
= hij P jji , (i; j = 0; 1 ).
0.2.27
Pomiar stanu kubitu
Stan kubitu (234) mo·
zna w zasadzie zmierzy´c pod warunkiem, ·
ze dysponu-
jemy du·
z ¾
a liczb ¾
a identycznie przygotowanych takich kubitów. Do zrozumienia
tego zagadnienia po·
zyteczna jest reprezentacja Blocha gdy·
z wspó÷
rz ¾
edne x, y,
z
kubitu na sferze Blocha mog ¾
a by´c mierzone. Je´sli przedstawimy operatory
Pauliego w bazie obliczeniowej f j0i , j1i g to znaczy gdy
x
=
0
1
1
0
,
y
=
0
i
i
0
,
z
=
1
0
0
1
(239)
to dla stanu (234) mamy
x
j i = e
i'
sin
#
2
j0i + cos
#
2
j1i
(240)
y
j i = e
i'
sin
#
2
j0i + i cos
#
2
j1i
(241)
z
j i = cos
#
2
j0i
e
i'
sin
#
2
j1i
(242)
a warto´sci oczekiwane tych operatorów w stanie j i wynosz ¾
a
h j
x
j i = sin # cos ' = x
(243)
h j
y
j i = sin # sin ' = y
(244)
h j
z
j i = cos # = z
(245)
Wspó÷
rz ¾
edne (x; y; z) mo·
zna wyznaczy´c z dowoln ¾
a dok÷
adno´sci ¾
a przy pomocy
rzutowania stanu j i na stany bazy obliczeniowej (lub innymi s÷owy mierz ¾
ac
warto´s´c oczekiwan ¾
a operatora
z
w stanie j i ). Rzeczywi´s´cie, z wzorów (235)
i (245)
p
0
p
1
= jh0j ij
2
jh1j ij
2
= cos
2
#
2
sin
2
#
2
= cos # = z
(246)
Je´sli dysponujemy du·
z ¾
a liczb ¾
a N identycznie przygotowanych qubitów w stanie
j i to z =
N
0
N
N
1
N
, gdzie N
0
to liczba wyników pomiaru qubitu w stanie j0i , a
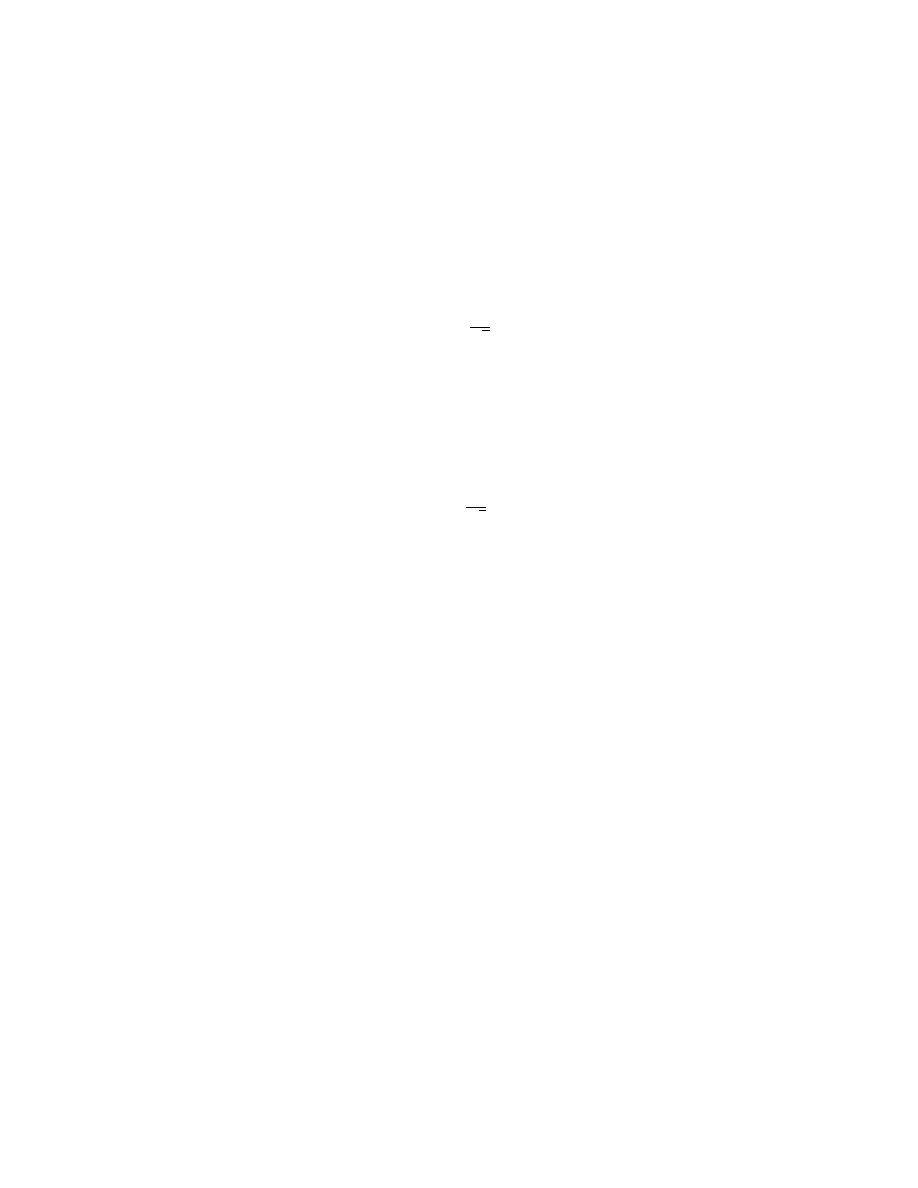
liv
OBWODY KWANTOWE
N
1
to liczna wyników pomiaru qubitu w stanie j1i. Zatem sk÷adow ¾
a z kubitu w
stanie j i mo·
zna wyznaczy´c na podstawie wyników otrzymanych z du·
zej liczby
pomiarów na identycznych stanach j i. Wspó÷rz ¾
edne x, y mo·
zna otrzyma´c w
wyniku odpowiedniej transformacji unitarnej stanu j i , a nast ¾
epnie wyrzu-
towania tak otrzymanego stanu na stan j0i lub stan j1i czyli wyrzutowania na
o´s z. Je´sli transformacj ¾
e unitarn ¾
a opisuje macierz
U
1
=
1
p
2
1
1
1
1
(247)
to U
1
j i = j
1
i , a w wyniku rzutowania stanu j
1
i na o´s z otrzymujemy
p
0
= jh0j
1
ij
2
i
p
1
= jh1j
1
ij
2
(248)
i wobec tego
p
0
p
1
= cos ' sin # = x
(249)
Je´sli zastosujemy transformacj ¾
e
U
2
=
1
p
2
1
i
i
1
(250)
to otrzymamy stan j
2
i = U
2
j i , a nast ¾
epnie
p
0
p
1
= sin ' sin # = y
(251)
gdzie podobnie jak wy·
zej
p
0
= jh0j
2
ij
2
i
p
1
= jh1j
2
ij
2
s ¾
a
praw-
dopodobie´nstwami otrzymania stanu j0i oraz stanu j1i z pomiaru rzutowania
kubitu j
2
i wzd÷u·
z osi z .
0.2.28
Obwodowy model oblicze´
n kwantowych
Dla przypomnienia klasyczny komputer, najogólniej mówi ¾
ac, mo·
zna przedstawi´c
jako sko´nczony rejestr n bitów. Elementarne operacje takie jak NOT, END,....
mo·
zna wykonywa´c na pojedy´nczych bitach lub parach bitów. Operacje te s ¾
a
wykonywane w uporz ¾
adkowany sposób tak by sekwencja operacji dawa÷
a jak ¾
a´s
z÷
o·
zon ¾
a, logiczn ¾
a funkcj ¾
e.
Ten model mo·
zna przenie´s´c na obliczenia kwantowe. Kwantowy komputer
mo·
zna sobie wyobrazi´c jako zbiór n kubitów czyli kwantowy rejestr rozmiaru n.
Stan n-bitowego rejestru w notacji binarnej jest opisany przez liczb ¾
e ca÷
kowit ¾
a
i 2 0; 2
n 1
, tj.
i = i
n 1
2
n 1
+ ::: + i
1
2 + i
0
gdzie i
0
; i
1
; :::; i
n 1
2 [0; 1]
(252)
Stan n-kubitowego komputera
j i =
2
n
1
X
i=0
c
i
jii =
1
X
i
n
1
=0
:::
1
X
i
1
=0
1
X
i
0
=0
c
i
n
1;:::;
i
1
i
0
ji
n 1
i
:::
ji
1
i
ji
0
i (253)

lv
gdzie c
i
to liczby zespolone ograniczone warunkiem normalizacji
h j i = 1; tj.
2
n
1
X
i=0
jc
i
j
2
= 1
(254)
Zatem stanem kwantowego komputera o n kubitowym rejestrze jest funkcja
falowa j i w 2
n
- wymiarowej przestrzeni Hilberta, powsta÷¾
a jako produkt ten-
sorowy n dwuwymiarowych przestrzeni Hilberta. Uwzgl ¾
edniaj ¾
ac warunek nor-
malizacji oraz fakt, ·
ze stan dowolnego uk÷
adu kwantowego mo·
ze by´c okre´slony z
dok÷
adno´sci ¾
a do globalnej fazy, stan kwantowego komputera jest okre´slony przez
2(2
n
1) niezale·
znych parametrów.
Jako przyk÷
ad rozpatrzmy przypadek komputera o n = 2 kubitach. Dowolny
stan dwukubitowego komputera mo·
zna zapisa´c
j i = c
0
j0i + c
1
j1i + c
2
j2i + c
3
j3i =
(255)
=
c
00
j0i
j0i + c
01
j0i
j1i + c
10
j1i
j0i + c
11
j1i
j1i
(256)
=
c
00
j00i + c
01
j01i + c
10
j10i + c
11
j11i gdzie jiji = jii
jji(257)
Uogólniaj ¾
ac powy·
zsz ¾
a notacj ¾
e stan (253) mo·
zna zapisa´c
j i =
1
X
i
n
1
;:::;i
1;
i
0=0
c
i
n
1;:::;
i
1
i
0
j i
n 1
; :::; i
1;
i
0
i
(258)
Konsekwencje wynikaj ¾
ace z zasady superpozycji stanów wyra´znie wida´c na
przyk÷
adzie równania (258). Klasyczny n bitowy rejestr mo·
ze zapisa´c jedn ¾
a
liczb ¾
e ca÷
kowit ¾
a. Kwantowy n kubitowy rejestr jest superpozycj ¾
a 2
n
stanów
bazowych i liczba ta ro´snie wyk÷
adniczo ze wzrostem liczby kubitów.
Daje
to nowe mo·
zliwo´sci oblicze´n. Na klasycznym komputerze dla ka·
zdego zestawu
danych wej´sciowych trzeba wykona´c niezale·
zne obliczenia, tzn. dla ka·
zdego
zestawu danych wymagany jest odr ¾
ebny cykl obliczeniowy. Natomiast na kom-
puterze kwantowym w jednym cyklu obliczeniowym mo·
zna wykona´c obliczenia
dla 2
n
niezale·
znych danych wej´sciowych.
·
Zeby wykona´c obliczenia na kwantowym komputerze nale·
zy:
1) przygotowa´c kwantowy komputer w stanie pocz ¾
atkowym j
i
i np. w stanie
j00:::0i ;
2) dokona´c operacji unitarnej U , która przeprowadza stan pocz ¾
atkowy j
i
i
w stan …nalny j
f
i = U j
i
i,
3)wykona´c algorytm co odpowiada standardowemu pomiarowi (w obliczeniowej
bazie fj0i ; j1ig) stanu polaryzacji
z
ka·
zdego qubitu.
Poniewa·
z kwantowy komputer jest n
kubitowym uk÷
adem, którego ewolucj ¾
e
w czasie opisuje równanie Schrödingera to ewolucj ¾
e w czasie funkcji falowej tego
uk÷
adu opisuje operator unitarny, którego struktur ¾
e okre´sla Hamiltonian uk÷
adu
n kubitów. Nale·
zy zwróci´c uwag ¾
e, ·
ze chocia·
z ewolucja n kubitowej funkcji
falowej jest opisana przez unitarn ¾
a macierz o wymiarze 2
n
2
n
to mo·
ze ona
by´c roz÷
o·
zona na iloczyn tensorowy unitarnych operacji dzia÷
aj ¾
acych na jeden

lvi
OBWODY KWANTOWE
lub dwa kubity.
Operacje te s ¾
a realizowane przez kwantowe bramki. Mo·
zna
wykaza´c, ·
ze dowolny, z÷
o·
zony pomiar stanu wielokubitowego rejestru mo·
zna
zawsze wykona´c w bazie obliczeniowej je´sli jest on poprzedzony odpowiedni ¾
a
transformacj ¾
a unitarn ¾
a wej´sciowego stanu rejestru .
Przyk÷
adem tej proce-
dury jest znany pomiar na jednym kubicie.
Wspó÷
rz ¾
ene x; y pojedy´nczego
kubitu na sferze Blocha mo·
zna wyznaczy´c je´sli dokonamy unitarnej transforma-
cji poprzedzaj ¾
acej rzutowanie kubitu na stany bazy obliczeniowej.
0.2.29
Bramki dzia÷
aj ¾
ace na pojedy´
nczy kubit
Operacje na kubicie musz ¾
a zachowywa´c warunek normalizacji stanu kubitu.
Je´sli stan j i zostanie przekszta÷cony w stan
0
E
to je´sli h j i = 1 równie·
z
h
0
0
E
= 1:Wiemy, ·
ze norm ¾
e wektora zachowuj ¾
a operacje unitarne, zatem
operacje na pojedy´nczym kubicie opisuj ¾
a unitarne macierze o wymiarze 2
2. Dalej poka·
zemy, ·
ze bramki Hadamarda i
przesuni ¾
ecia fazowego
wystarczaj ¾
a do wykonania dowolnej unitarnej operacji na pojedy´
nczym
kubicie.
Bramk¾
e Hadamarda de…niuje nast ¾
epuj ¾
aca macierz
H =
1
p
2
1
1
1
1
(259)
Przy pomocy bramk (259) baza obliczeniowa f j0i ; j1i g zostaje przetrans-
formowana w now ¾
a ortonormaln ¾
a baz ¾
e dwuwymiarow ¾
a f j+i ; j i g czyli
H j0i =
1
p
2
(j0i + j1i); H j1i =
1
p
2
(j0i
j1i)
(260)
Poniewa·
z H
2
= I
to H
1
= H, rownie·
z H = H
y
poniewa·
z (H
T
) = H .
Bramk¾
e przesuni ¾
ecia fazowego okre´sla macierz
R
z
( ) =
1
0
0
e
i
(261)
Od razu wida´c, ·
ze R
z
( ) j0i = j0i oraz R
z
( ) j1i = e
i
j1i. Dzia÷anie bramki
(261) na dowolny stan (234) jest nast ¾
epuj ¾
ace.
R
z
( ) j i =
1
0
0
e
i
cos
#
2
e
i'
sin
#
2
=
cos
#
2
e
i('+ )
sin
#
2
(262)
=
cos
#
2
j0i + e
i('+ )
sin
#
2
j1i
(263)
Z równania (262) wida´c, ·
ze bramka przesuni ¾
ecia fazowego generuje na sferze
Blocha obrót o k ¾
at
wokó÷osi z zgodny z ruchem wskazówek zegara. Natomiast
dowolna unitarna transformacja przeprowadza stan kubitu z jednego punktu
na sferze Blocha do innego punktu na sferze Blocha. W szczególno´sci stan

lvii
j i = cos
#
2
j0i + e
i'
sin
#
2
j1i mo·
zna osi ¾
agn ¾
a´c dzia÷
aj ¾
a´c na stan j0i w sposób
nast ¾
epuj ¾
acy
R
z
(
2
+ ')HR
z
(#)H j0i = e
i
#
2
(cos
#
2
j0i + e
i'
sin
#
2
j1i)
(264)
Otrzymany stan ro·
zni si ¾
e od stanu j i faz ¾
a globaln ¾
a co nie poci ¾
aga ·
zadnych
praktycznych konsekwencji. Przyk÷
ad ten pokazuje, ·
ze dowolna unitarna oper-
acja na pojedy´nczym kubicie jest wynikiem dzia÷
ania odpowiedniej sekwencji
bramek Hadamarda i bramek przesuni ¾
ecia fazowego.
0.2.30
Obroty sfery Blocha
Obroty sfery Blocha wokó÷dowolnie zorientowanej osi nale·
z ¾
a do klasy transfor-
macji unitarnych.
Na pocz ¾
atku rozwa·
zmy operator O taki, ·
ze O
2
= I , wówczas O
k
= I gdy
k parzyste, O
k
= O gdy k nieparzyste. Zatem rozwijaj ¾
a´c na szereg Taylora
wyra·
zenie e
i O
otrzymamy
e
i O
= (1
2
2!
+ :::)I
i(
3
3!
+ :::) = cos( )I
i sin( )O
(265)
Poniewa·
z operatory (macierze) Pauliego spe÷
niaj ¾
a warunek
2
x
=
2
y
=
2
z
= I mo·
zna wi ¾
ec zastosowa´c wzór (265) do tych operatorów, w szczególno´sci
do operatora
z
. Otrzymujemy
e
i
2
z
= cos(
2
)I
i sin(
2
)
z
= e
i
2
1
0
0
e
i
= R
z
( )
(266)
Zauwa·
zmy, ·
ze wyra·
zenie (266) ró·
zni si ¾
e od de…nicji (261) tylko globaln ¾
a faz ¾
a
e
i
2
, ale jak wiemy faza ta nie ·
zadnego …zycznego znaczenia.
Je´sli x; y;
z
s ¾
a kartezja´nskimi wspó÷
rz ¾
ednymi wektora stanu kubitu j i, a x
;
; y
;
; z
;
wspó÷
rz ¾
enymi wektora R
z
( ) j i (tj. wektora obróconego o k ¾
at
dooko÷
a osi z
) to wspó÷
rz ¾
edne transformuj ¾
a si ¾
e nast ¾
epuj ¾
aco
x
;
= x cos
y sin ; y
;
= x sin + y cos ; z
;
= z
(267)
Zatem operator R
z
( ) odpowiada rotacji sfery Bloch a o k ¾
at
dooko÷
a osi z
zgodnie z ruchem wskazówek zegara.
Analogicznie mo·
zna otrzyma´c unitarne
macierze/operatory odpowiadaj ¾
ace obrotowi sfery Blocha (zgodnie z ruchem
wskazówek zegara) wokó÷osi x
e
i
2
x
=
cos(
2
)
i sin(
2
)
i sin(
2
)
cos(
2
)
= R
x
( )
(268)
i wokó÷osi y
e
i
2
y
=
cos(
2
)
sin(
2
)
sin(
2
)
cos(
2
)
= R
y
( )
(269)
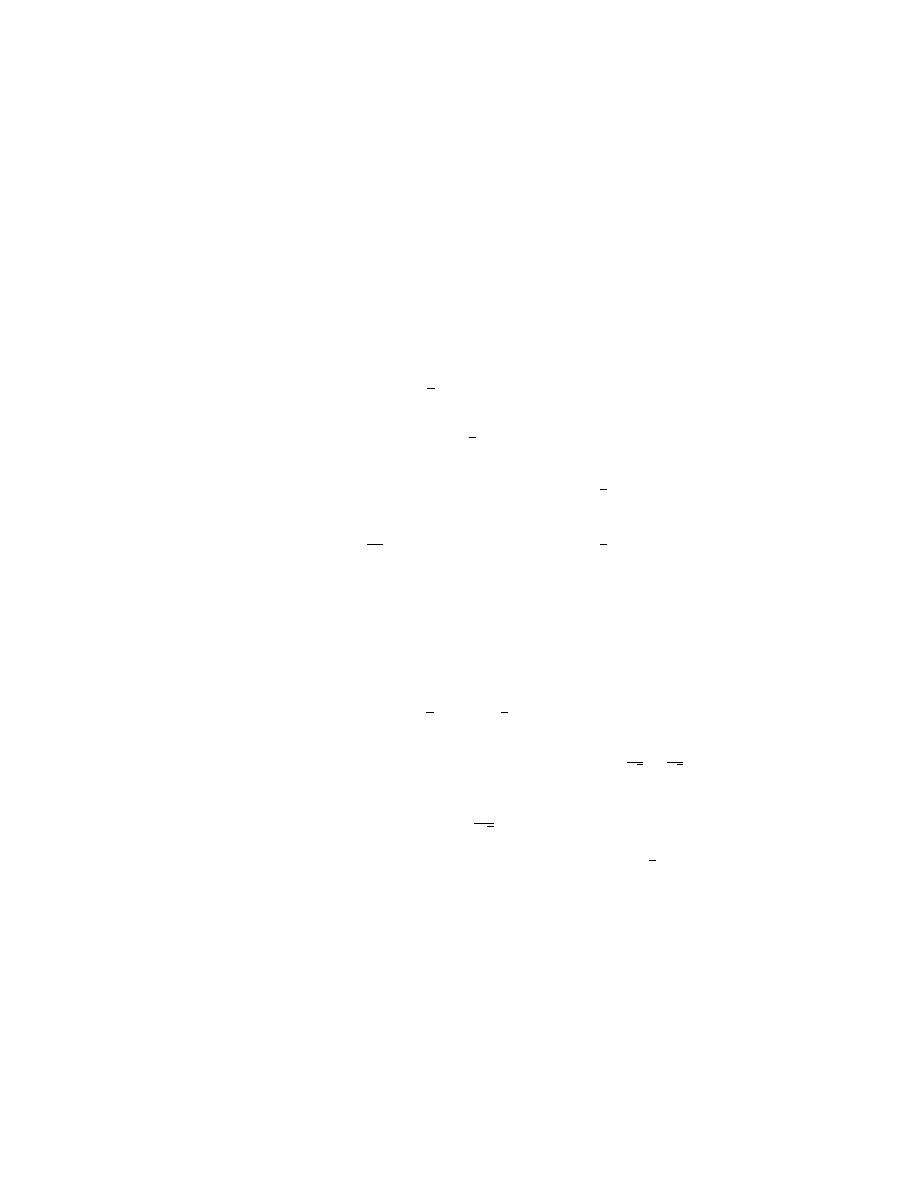
lviii
OBWODY KWANTOWE
Obrót dooko÷
a dowolnie zorientowanej osi mo·
zna otrzyma´c korzystaj ¾
ac z w÷
as-
no´sci sk÷
adania obrotów in…nitezymalnych tj. obrotów o bardzo ma÷
y k ¾
at
(transformacj ¾
e nazywamy in…nitezymalna gdy w rozwini ¾
eciu funkcji zale·
znej od
parametru
na szereg Taylora wystarczy uwgl ¾
edni´c tylko pierwsze dwa cz÷
ony)
. Mianowicie obrót o k ¾
at
wokó÷wektora jednostkowego !
n = (n
x
; n
y
; n
z
) jest
generowany przez operator
R
!
n
( )
R
x
(n
x
)R
x
(n
y
)R
z
(n
z
) gdy
1
(270)
Poniewa·
z rozwini ¾
ecie Taylora (265) dla
1 daje
R
i
(n
i
)
I
i
2
n
i
i
;
i = 1; 2; 3 ( lub i = x; y; z)
(271)
zatem
R
!
n
( )
I
i
2
(n
x
x
+ n
y
y
+ n
z
z
)
(272)
Obrót o sko´nczony k ¾
at
dooko÷
a wektora !
n = (n
x
; n
y
; n
z
) mo·
zna otrzyma´c w
wyniku z÷
o·
zenia k in…nitezymalnych rotacji o k ¾
at
=
k
, tj.
R
!
n
( ) = lim
k
!1
(I
i
2k
(n
x
x
+n
y
y
+n
z
z
))
k
= exp( i
2
(n
x
x
+n
y
y
+n
z
z
))
k
(273)
Poniewa·
z
(n
x
x
+ n
y
y
+ n
z
z
)
2
= n
2
x
2
x
+ n
2
y
2
y
+ n
2
z
2
z
= (n
2
x
+ n
2
y
+ n
2
z
)I = I (274)
stosuj ¾
ac do równania (274) rozwini ¾
ecie (265) otrzymujemy
R
!
n
( ) = cos(
2
)I
i sin(
2
)(n
x
x
+ n
y
y
+ n
z
z
)
(275)
Z równania (275) wynika, ·
ze bramka Hadamarda (259)
jest równowa·
zna
rotacji wektora na sferze Blocha o k ¾
at
dooko÷
a osi !
n = (
1
p
2
; 0;
1
p
2
). Rzeczy-
wi´scie, z równania (275) mamy
H =
1
p
2
(
x
+
z
)
(276)
z dok÷
adno´sci ¾
a do globalnego czynnika fazowego
i = exp( i
2
):W wyniku tej
transformacji o´s x przechodzi w o´s z, a o´s z w o´s x.
0.2.31
Bramki kontrolne i generowanie stanów spl ¾
atanych
Spl ¾
atanie stanów, intryguj ¾
aca w÷
asno´s´c mechaniki kwantowej, pojawia si ¾
e ju·
z w
przypadku dwóch kubitów. Ogólny dwukubitowy stan mo·
zna w bazie obliczeniowej
fj0i ; j1igzapisa´c

lix
j i = j00i + j01i + j10i + j11i
(277)
gdzie
; ; ;
2 C j j
2
+ j j
2
+ j j
2
+ j j
2
= 1: Poniewa·
z faza globalna stanu
(277) mo·
ze by´c dowolna i spe÷
niony jest warunek normalizacyjny j j
2
+ j j
2
+
j j
2
+ j j
2
= 1, stan ten jest okre´slony przez 6 rzeczywistych paramertrów. Nie
mo·
zna go wi ¾
e´c przedstawi´c w formie produktu tensorowego dwóch stanów jed-
nokubitowych j
1
i i j
2
i poniewa·
z stan j i = j
1
i
j
2
i jest okre´slony przez
4 parametry (do okre´slenia ka·
zdego ze stanów j
1
i i j
2
i wystarcz ¾
a dwa para-
metry).. Sytuacja staje si ¾
e coraz bardziej z÷
o·
zona wraz ze wzrostem liczby ku-
bitów tworz ¾
acych dany stan spl ¾
atany, z÷
o·
zono´s´c ro´snie wyk÷
adniczo ze wzrostem
liczby kubitów. Do opisania najbardziej z÷
o·
zonego n-kubitowego stanu spl ¾
a-
tanego potrzeba 2(2
n
1) niezale·
znych parametrów.
Oczywiste jest, ·
ze jednokubitowe bramki nie mog ¾
a generowa´c w uk÷
adach n-
kubitowych stanów spl ¾
atanych. Je´sli np. podzia÷
amy na stan j i = j
n 1
i
j
n 2
i
:::
j
0
i bramkami jednokubitowymi to otrzymamy stan j
0
i =
0
n 1
0
n 2
:::
j
0
o
i gdy·
z dowolny stan j
i
i (i = n
1; n
2; :::; 0)
w wyniku dzia÷
ania bramki zostanie przetransformowany na sferze Blocha w
stan j
0
i
i, który w dalszym ci ¾
agu b ¾
edzie superpozycj ¾
a stanów j0i i j1i, czyli w
dalszym ci ¾
agu b ¾
edzie stanem niespl ¾
atanym.
Aby wygenerowa´c stan spl ¾
atany konieczne jest oddzia÷
ywanie mi ¾
edzy ku-
bitami, co mo·
zna zrealizowa´c przy pomocy bramki dwukubitowej. Prototypem
takiej bramki jest bramka CNOT czyli bramka kontrolowanej negacji. Jej dzi-
a÷
anie na stany bazy obliczeniowej f ji
1
i
0
i = j00i ; j01i ; j10i ; j11i g jest nast ¾
epu-
j ¾
ace
CN OT (jxi jyi) = jxi jx
yi
(278)
gdzie x; y przyjmuj ¾
a warto´sci 0; 1 a znak
oznacza dodawanie modulo 2. Pier-
wszy kubit dzia÷
a jako kubit kontrolny, a drugi jako kubit bazowy lub podsta-
wowy. Bramka CNOT zmienia stan kubitu podstawowego je´sli kubit kontrolny
jest w stanie j1i (tzn. zmienia stan j0i w stan j1i lub stan j1i w stan j0i je´sli
kubit kontrolny jest w stanie j1i), gdy natomiast kubit kontrolny jest w stanie
j0i to nie zmienia on stanu kubitu podstawowego. Je´sli wektory bazy przestrzeni
dwuqubitowej zapiszemy
joi
j0i
j0i
j00i =
2
6
6
4
1
0
0
0
3
7
7
5 , j1i
j0i
j1i
j01i =
2
6
6
4
0
1
0
0
3
7
7
5 (279)
j2i
j1i
j0i
j10i =
2
6
6
4
0
0
1
0
3
7
7
5 ; j3i
j1i
j1i
j11i =
2
6
6
4
0
0
0
1
3
7
7
5 (280)

lx
OBWODY KWANTOWE
to w reprezentacji macierzowej bramk¾
e CNOT jako
CN OT =
2
6
6
4
1
0
0
0
0
1
0
0
0
0
0
1
0
0
1
0
3
7
7
5
(281)
gdzie element
(CN OT )
ij
= hij CNOT jji , i; j = 0; 1; 2; 3.
Na przyk÷
ad
h2j CNOT j3i = h10j CNOT j11i = 1 bo CNOT j11i = j1i j1
1i = j1i j0i =
j10i. Z wzoru (281) od razu wida´c, ·
ze operator CNOT jest samoodwracalny, bo
(CN OT )
2
= I . CNOT mo·
ze generowa´c stany spl ¾
atane co pokazuje poni·
zszy
przyk÷
ad
CN OT ( j0i + j1i) j0i = j00i + j11i
(282)
Stan (282) jest oczywi´scie spl ¾
atany gdy
6= 0 i
6= 0.
De…nicj ¾
e bramki CNOT mo·
zna uogólni´c. Zale·
znie od tego, który z kubitów
jest kubitem kontrolnym, a który kubitem podstawowym mamy cztery mo·
zli-
woci. Pierwsz ¾
a z nich opisuje macierz (281).
Trzy pozosta÷
e mo·
zliwo´sci s ¾
a
reprezentowane przez nast ¾
epuj ¾
ace operatory
B =
2
6
6
4
0
1
0
0
1
0
0
0
0
0
1
0
0
0
0
1
3
7
7
5 ; C =
2
6
6
4
1
0
0
0
0
0
0
1
0
0
1
0
0
1
0
0
3
7
7
5 ; D =
2
6
6
4
0
0
1
0
0
1
0
0
1
0
0
0
0
0
0
1
3
7
7
5
(283)
gdzie: B - bramka, która zmienia stan drugiego kubitu gdy pierwsz jest w stanie
j0i ; C - bramka, która zmienia stan pierwszego kubitu gdy drugi jest w stanie
j1i, D - bramka, która zmienia stan piewszego kubitu gdy drugi jest w stanie
j0i. Schemat uogólnionych bramek CNOT jest na rysunku
Rysunek
(
) oznacz, ·
ze kubit podstawowy ulega zmianie gdy kubit kontrolny
jest w stanie j1i (j0i )
Okazuje si ¾
e, ·
ze wszystkie uogólnione bramki CNOT mo·
zna skonstruowa´c
przy pomocy standardowej bramki CNOT (281) i bramek jednokubitowych.
Na przyk÷
ad uogólnion ¾
a bramk¾
e CNOT, której dzia÷
anie opisuje macierz C (??)
mo·
zna otrzyma´c w wyniku dzia÷
ania na stan dwukubitowy operatorem (H
H)C(H
H) co przedstawione jest na rysunku...
Rysunek

lxi
W szczefó÷
no´sci bramk¾
e SWAP mo·
zna zrealizowa´c przy pomocy obwodu
......... z÷
o·
zonego z bramek CN OT C CN OT
Rysunek
Dwukubitow ¾
a bramk¾
e, która zmienia faz ¾
e podstawowego kubitu gdy kon-
trolny kubit jest w stanie j1i, zwan ¾
a CP HASE( ) w postaci macierzowej de…ni-
ujemy
CP HASE( ) =
2
6
6
4
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
e
i
3
7
7
5
(284)
Na przyk÷
ad:
CP HASE( ) j11i =
2
6
6
4
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
e
i
3
7
7
5
2
6
6
4
0
0
0
1
3
7
7
5 =
2
6
6
4
0
0
0
1e
i
3
7
7
5 = e
i
j11i.
Bramk¾
e CP HASE( ) mo·
zna zast ¾
api´c uk÷
adem ·
z÷
o·
zonym z bramek CN OT
i jednokubitowych bramek przesuni ¾
ecia fazowego wed÷
ug schematu...
Rysunek
De…niuje si ¾
e te·
z bramk¾
e CM IN U S, która jest jest równowa·
zna bramce
CP HASE( ).
Zwi ¾
azki mi ¾
edzy bramkami CM IN U S i CN OT
podane s ¾
a
na schemacie.......
Rysunek
Maj ¾
ac dany kubit w stanie j i =
j0i + j1i b÷¾
ad amplitudy
okre´sla
transformacja
j i =) j
a
i = j0i + j1i
(285)
a b÷¾
ad fazy
okre´sla transformacja
j i =) j
p
i = j0i
j1i
(286)
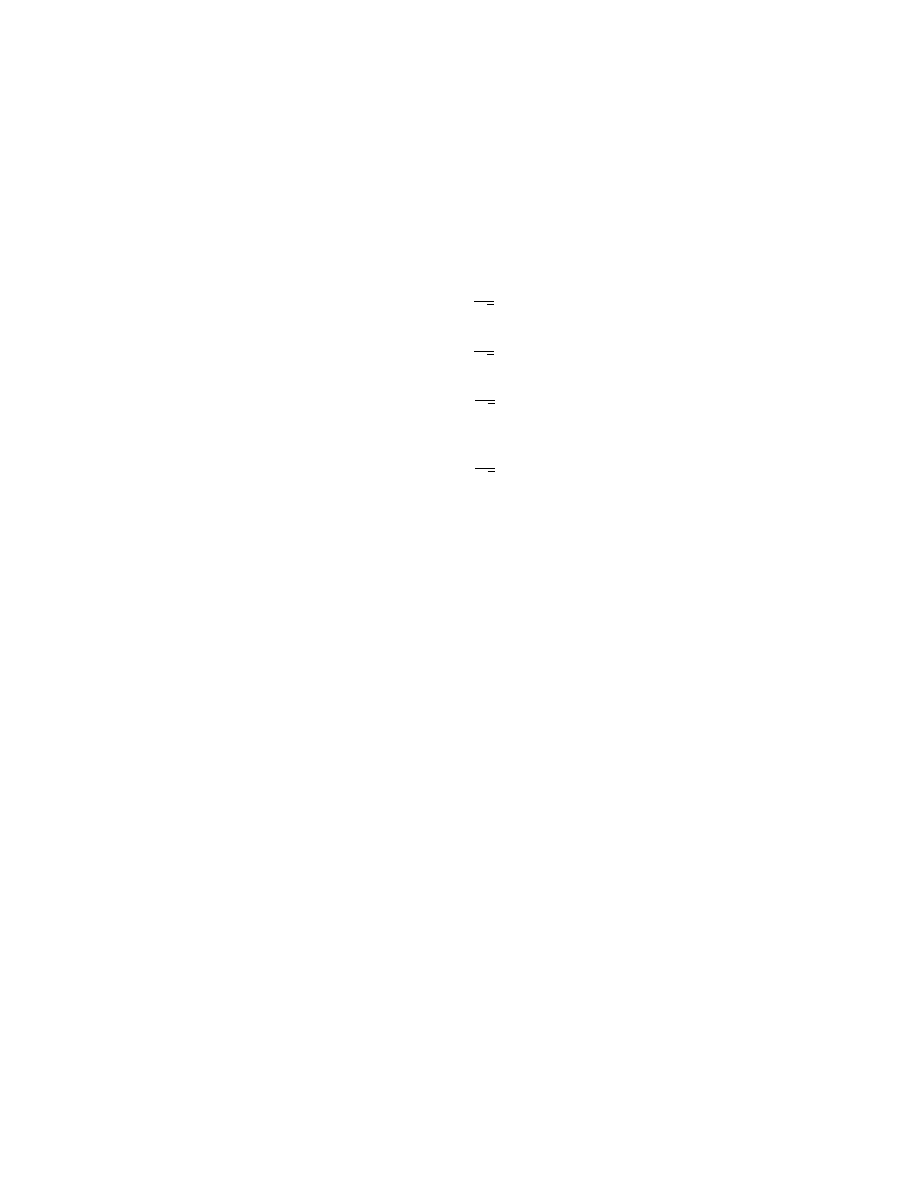
lxii
OBWODY KWANTOWE
0.2.32
Baza Bella
Wiemy ju·
z, ·
ze bramka CN OT
mo·
ze generowa´c stany spl ¾
atane.
Tak zwana
baza Bella de…niuje baz ¾
e stanów spl ¾
atanych przy pomocy stanów bazy obliczeniowej
fj0i ; j1ig w sposob nast ¾
epuj ¾
acy
+
=
1
p
2
(j00i + j11i)
(287)
=
1
p
2
(j00i
j11i)
(288)
+
=
1
p
2
(j01i + j10i)
(289)
=
1
p
2
(j01i
j10i)
(290)
Stany bazy Bella mo·
zna otrzyma´c ze stanów bazy obliczeniowej fj00i ; j01i ; j10i ; j11ig
przy pomocy nat ¾
epuj ¾
acego uk÷
adu
Rysunek
Ob-
wód ....... dokonuje nast ¾
epuj ¾
acej transformacji: j00i =)
+
, j10i =)
;
j01i =)
+
, j11i =)
. Ta transformacja mo·
ze by´c odwrócona powodu-
j ¾
ac dzia÷
anie obwodu........w odwrotnym kierunku gdy·
z bramki CN OT i H s ¾
a
samoodwracalne. W wyniku takiego dzia÷
ania stany bazy Bella s ¾
a transfor-
mowane na stany bazy obliczeniowej.
0.2.33
Uniwersalne bramki kwantowe
W opisie oblicze´n na komputerze klasycznym model obwodowy pozwala przed-
stawi´c dowolnie z÷
o·
zone obliczenia przy pomocy sekwencji elementarnych oper-
acji jak na przyk÷
ad AN D; N AN D; COP Y;.... Dalej poka·
zemy, ·
ze równie·
z w
przypadku oblicze´n kwantowych (na komputerze kwantowym) dowoln ¾
a unitarn ¾
a
operacj ¾
e w przestrzeni Hilberta rozpinanej przez n kubitów mo·
zna roz÷
o·
zy´c na
sekwencj ¾
e bramek jednokubitowych i dwukubitowych bramek CN OT . Dowód
tego wa·
znego faktu rozpoczniemy od de…nicji U -kontrolowanej operacji. Oper-
acja U -kontrolowana oznacza, ·
ze unitarna operacja U dzia÷
a na bazowy (pod-
stawowy) kubit ji
0
i gdy kontrolny kubit ji
1
i jest w stanie j1i, to znaczy
ji
1
i ji
0
i =) ji
1
i U
i
1
ji
0
i
(291)
Poka·
zemy, ·
ze U -kontrolowana bramka mo·
ze by´c zrealizowana przy pomocy tylko
bramek jednokubitowych i bramki CN OT .
Macierz unitarn ¾
a U
o wymiarze (2
2) mo·
zna w ogólnej postaci zapisa´c
nast ¾
epuj ¾
aco
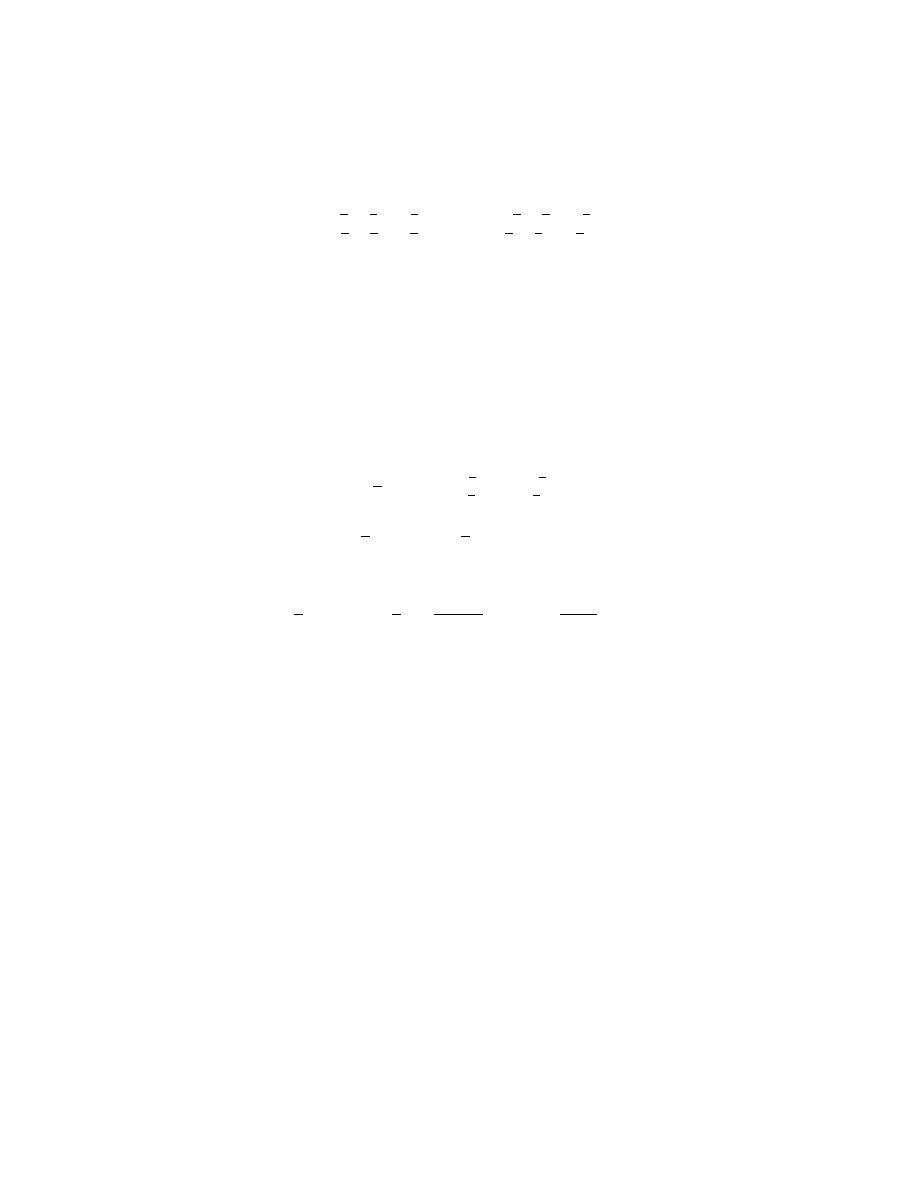
lxiii
U =
exp i(
2
2
) cos
#
2
exp i(
2
+
2
) sin
#
2
exp i( +
2
2
) sin
#
2
exp i( +
2
+
2
) cos
#
2
(292)
gdzie
; ;
i # s ¾
a rzeczywistymi parametrami. Zatem macierz (292) mo·
zna
roz÷
o·
zy´c na iloczyn macierzy
U =
( )R
z
( )R
y
(#)R
z
( )
(293)
gdzie
( ) =
exp(i )
0
0
exp(i )
(294)
a R
y
i R
z
s ¾
a macierzami obrotów wokó÷osi y i osi z, które okre´slone s ¾
a nast ¾
epu-
j ¾
acymi wzorami
R
y
(#) = exp( i
#
2
y
) =
cos(
#
2
)
sin(
#
2
)
sin(
#
2
)
cos(
#
2
)
(295)
R
z
( ) = exp( i
2
z
) = exp( i
2
)
1
0
0
exp(i )
(296)
Rzeczywi´scie, dla dowolnej macierzy (292) istniej ¾
a unitarne macierze A; B i C
A = R
z
( )R
y
(
#
2
); B = R
y
(
#
2
)R
z
(
2
); C = R
z
(
2
)
(297)
takie, ·
ze
ABC = I
(298)
oraz
( )A
x
B
x
C = U
(299)
Równanie (298) jest trywialne, natomiast równanie (299) mo·
zna ÷
atwo sprawdzi´c
pami ¾
etaj ¾
ac, ·
ze
2
x
= I,
x
R
y
( )
x
= R
y
(
) i
x
R
z
( )
x
= R
z
(
) .
Dzia÷
anie bramki U -kontrolowana mo·
zna przedstawi´c na schemacie.....
Rysunek
Je´sli
zatem kontrolny kubit jest w stanie j0i to na kubit bazowy dzia÷a operator
ABC = I : Gdy natomiast kontrolny kubit jest w stanie j1i to na bazowy kubit
dzia÷
a operator A
x
B
x
C =
(
)U , w którym dwukrotne dzia÷
anie macierzy
Pauliego
x
odzwierciedla efekt dzia÷
ania bramek CN OT na kubit bazowy. Op-
erator ten ró·
zni si ¾
e od operatora U tylko czynnikiem fazowym
(
) = e
i
I .
Ostatnia bramka na schemacie......... usuwa nieporz ¾
adany czynnik fazowy. Jej
reprezentacja macierzowa jest nast ¾
epuj ¾
aca

lxiv
OBWODY KWANTOWE
R
z
( )
I =
1
0
0
e
i
I =
2
6
6
4
1
0
0
0
0
1
0
0
0
0
e
i
0
0
0
0
e
i
3
7
7
5
(300)
Na tym ko´nczy si ¾
e dowód, ·
ze obwód....
stanowi implementacj ¾
e bramki U -
kontrolowana.
Rozwa·
zmy teraz bramk¾
e C
k
U , która dokonuje unitarnej transformacji
U na bazowym kubicie gdy wszystkie k kontrolne kubity s ¾
a w staniej1i. Bramka
C
k
U mo·
ze by´c zrealizowana przy pomocy bramek jednokubitowych i bramek
CN OT :Szczególnym przypadkiem jest bramka C
2
N OT , zwana te·
z bramk ¾
a
To¤oli’ego, która powoduje dzia÷
anie operacji N OT na bazowy kubit gdy ka·
zdy
z dwóch kontrolnych kubitów jest w stanie j1i . Schemat bramki C
2
N OT
jest na rysunku........
Rysunek
Operacja
V =
1
0
0
i
(301)
oraz jej hermitowskie sprz ¾
e·
z ¾
enie V
y
s ¾
a operacjami unitarnymi. Przy pomocy
sekwencji bramek V , V
y
i bramki CN OT
mo·
zna zrealizowa´c bramk¾
e Tof-
foli’ego, s ¾
a wi ¾
ec one jakby sk÷
adowymi bramki To¤oli’ego. Jest to wa·
zne z
nast ¾
epuj ¾
acych powodów: 1) bramka To¤oli’ego jest uniwersaln ¾
a bramk ¾
a dla
oblicze´n klasycznych, kwantowe obwody sk÷
adaj ¾
ace si ¾
e jednokubitowych i bramek
CN OT
obejmuj ¾
a tak·
ze klasyczne obliczenia, 2) w przeciwie´nstwie do kwan-
towych oblicze´n, w klasycznych obliczeniach jedno- i dwubitowe bramki odwracalne
nie s ¾
a bramkami uniwersalnymi. Dla dowolnej unitarnej macierzy U bramka
C
2
U mo·
ze by´c zrealizowana przez obwód jak na rysunku... .
gdzie V jest
macierz ¾
a tak ¾
a, ·
ze V
2
= U
Rysunek
Bramka To¤oli’ego jest szczególnie u·
zyteczna przy konstrukcji bramki C
k
U . Przyk÷
ad takiej bramki w przypadku k = 4 jest na rysunku.......
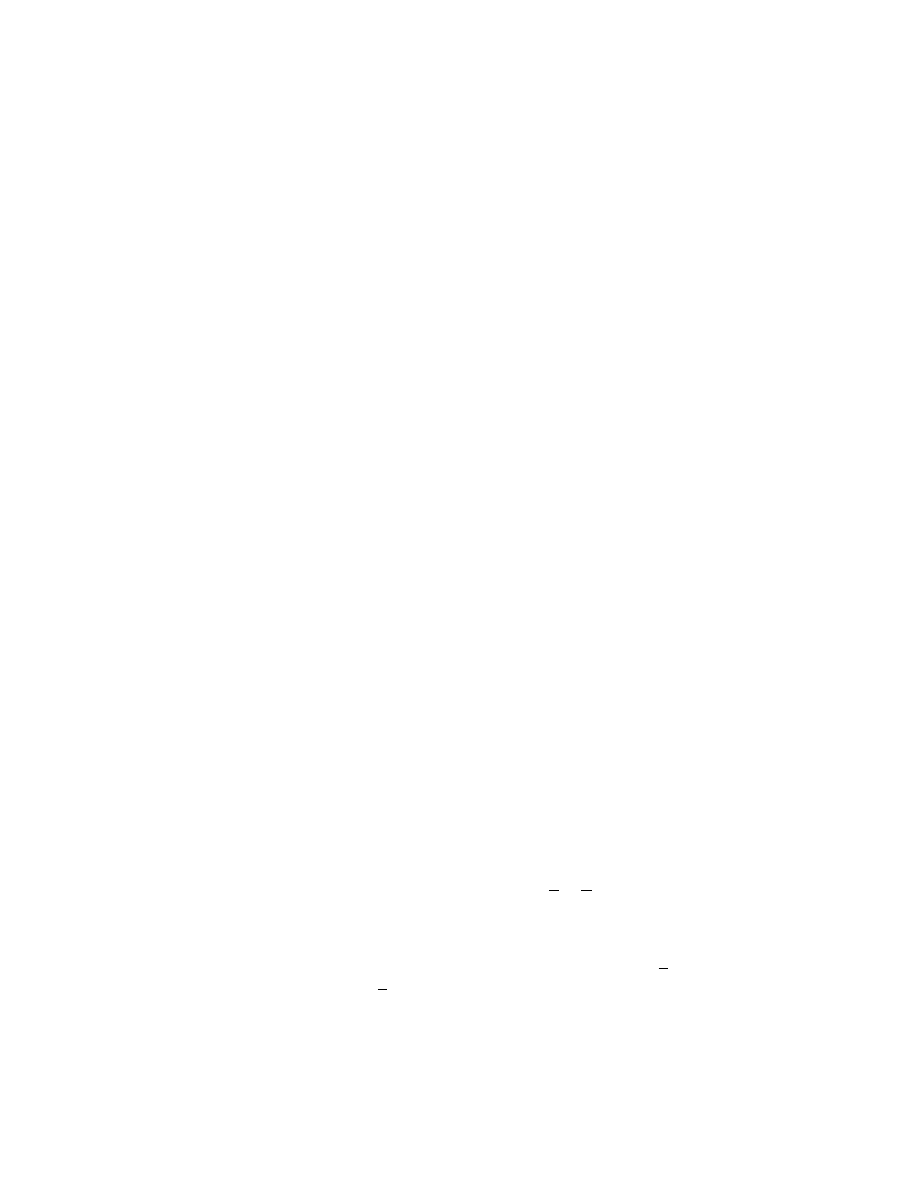
lxv
Rysunek
Bramka C
k
U posiada k
1 pomocniczych kubitów pocz ¾
atkowo ustaw-
ionych w stanie j0i : Pierwsze k 1 bramki To¤oli’ego zmieniaj ¾
a stan ostatniego
pomocniczego kubitu do stanu jji , gdzie j = i
k
1
i
k
2
:::i
1
i
0
, który jest równy
j1i wtedy i tylko wtedy gdy wszystkie kontrolne kubity na pocz ¾
atku s ¾
a w stanie
j1i . Wówczas kontrolowana U-operacja, dla której ostatni pomocniczy kubit
spe÷
nia rol ¾
e kubitu kontrolnego, realizuje C
k
U
bramk¾
e. Po tej operacji
wszystkie k
1 bramki To¤oli’ego przywracaja pomocnicze kubity do ich stanu
pocz ¾
atkowego j0i.
Powy·
zsze rozwa·
zania dowodz ¾
a, ·
ze jednokubitowe bramki i dwukubitowa
bramka CN OT s ¾
a uniwersalnymi bramkami w obliczeniach kwantowych. Dla
podsumowania; g÷
ówne kroki w dowodzie tej tezy s ¾
a nast ¾
epuj ¾
ace: 1) w przy-
padku dowolnej rotacju U pojedy´nczego kubitu U -kontrolowana bramka mo·
ze
by´c zast ¾
apiona sekwencj ¾
a bramek jednokubitowych i bramek CN OT , 2) bramka
To¤oli’ego (C
2
N OT ) mo·
ze by´c zrealizowana przy pomocy sekwencji bramek
CN OT , U
CON T ROL i bramek Hadamarda, 3) dowolna C
k
U bramka
(k > 2) mo·
ze by´c roz÷
o·
zona na bramki To¤oli’ego i bramki U
CON T ROL,
4) dowolny unitarny operator U
(n)
dzia÷
aj ¾
acy na stany n-kubitowej przestrzeni
Hilberta mo·
ze by´c roz÷
o·
zony przy pomocy sekwencji bramek C
k
U:
Przedstawione wy·
zej sposoby rozk÷
adu z÷
o·
zonych operacji na operacje uni-
wersalne s ¾
a z regu÷
y ma÷
o efektywne, tj. wymagaj ¾
a wykonania operacji elemen-
tarnych, których liczba ro´snie eksponencjalnie do liczby kubitów. Na przyk÷
ad,
w przypadku dowolnej unitarnej transformacji U na n kubitach potrzebujemy
elementarnych bramek w liczbie proporcjonalnej do exp(n) gdy·
z macierz U jest
okre´slona przez O(4
n
) rzeczywistych parametrów.
Wci ¾
a·
z otwartym, o fundamentalnym znaczeniu, problemem oblicze´n kwan-
towych jest pytanie - jak znale´z´c klas ¾
e unitarnych transformacji, które na kom-
puterze kwantowym by÷
yby wykonywane przy pomocy elementarnych bramek
w liczbie okre´slonej wielomianem W (n). Interesuj ¾
ac ¾
a metod ¾
e rozk÷
adu dowolnej
unitarnej macierzy o wymiarze 2
n
2
n
na sekwencj ¾
e elementarnych operacji po-
da÷Tucci (1999r). W metodzie tej stosuje si ¾
e rozk÷
ad CS (rozk÷
ad na kosinusy
i sinusy). Dowolna unitarna macierz U o wymiarze N
N (gdzie N liczna
parzysta) mo·
ze by´c przedstawiona w formie
U =
L
0
0
0
L
1
D
R
0
0
0
R
1
(302)
gdzie L
0
; L
1
; R
0
; R
1
s ¾
a unitarnymi macierzami o wymiarze
N
2
N
2
, a
D =
D
c
D
s
D
s
D
c
(303)
gdzie D
c
i D
s
s ¾
a diagonalnymi macierzami; D
c
= diag(cos
1
; cos
2
; :::; cos
N
2
)
, D
s
= diag(sin
1
; sin
2
; :::; sin
N
2
);
i
- odpowiedni k ¾
at. Zgodnie z rownaniem
(302)

lxvi
OBWODY KWANTOWE
U =
L
0
D
c
R
0
L
0
D
s
R
1
L
1
D
s
R
0
L
1
D
c
R
1
(304)
Bior ¾
ac N = 2
n
(n - liczba kubitów), w wyniku iteracji mo·
zna dan ¾
a macierz
roz÷
o·
zy´c na macierze coraz to mniejszych rozmiarów. Zatem mo·
zna operacj ¾
e
(macierz) U zredukowa´c do sekwencji elementarnych operacji. Jednak·
ze rozk÷
ad
ten nie jest w ogólno´sci wydajny poniewa·
z generuje on O(2
n
) kontrolnych macierzy
o wymiarze 2
2. Jako przyk÷
ad rozpatrzmy rozk÷
ad unitarnej macierzy U o
wymiarze 4
4: Obwód, który wykonuje to zadanie (zgodnie z wzorem 302 )
jest na rysunku........
Rysunek
Natomiast uk÷
ad , który dokonuje rozk÷
adu macierzy D o wymiarze 4
4
(wed÷
ug wzoru 303 ) na elementarne bramki jest na rysunku........ Ko´ncz ¾
ac ten
rozdzia÷warto zwróci´c uwag ¾
e, ·
ze w przeciwie´nstwie do klasycznych oblicze´n,
obliczenia kwantowe zale·
z ¾
a od ci ¾
ag÷
ych parametrów poniewa·
z obwody kwan-
towe sk÷
adaj ¾
a si ¾
e z sekwencji bramek kwantowych Hadamarda, bramek CN OT
i bramek przesuni ¾
ecia fazowego, które zale·
z ¾
a od ci ¾
ag÷
ych parametrów (k ¾
atów).
Wyszukiwarka
Podobne podstrony:
Kartografia Wglebna KW GG id 72 Nieznany
zw org 2 kw kar id 593471 Nieznany
Inf kp wyd V id 212921 Nieznany
zrodla kw 2012 id 592968 Nieznany
Kartografia Wglebna KW GG id 72 Nieznany
inf 2 id 212896 Nieznany
el inf 11 part05 fale02 id 1572 Nieznany
Inf Lab02 id 212934 Nieznany
Inf testy1112 id 212971 Nieznany
el inf 11 part06 faleEM id 1572 Nieznany
karta inf brzoska 1350564014 id Nieznany
M INST inf s id 274726 Nieznany
prezentacja KW id 390661 Nieznany
Inf 2 2 id 212904 Nieznany
inf 1 4 id 212899 Nieznany
inf 2 id 212896 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
więcej podobnych podstron