W

W

Y

Y

K

K

Ł

Ł

A

A

D

D

1

1

0

0

R

R

Ó

Ó

W

W

N

N

A

A

N

N

I

I

E

E

N

N

A

A

V

V

I

I

E

E

R

R

A

A

–

–

S

S

T

T

O

O

K

K

E

E

S

S

A

A

“Gallery of Fluid Motion”-M. Samimy, K.S. Breuer

W

W

Y

Y

P

P

R

R

O

O

W

W

A

A

D

D

Z

Z

E

E

N

N

I

I

E

E

R

R

Ó

Ó

W

W

N

N

A

A

N

N

I

I

E

E

R

R

U

U

C

C

H

H

U

U

D

D

L

L

A

A

P

P

Ł

Ł

Y

Y

N

N

U

U

N

N

E

E

W

W

T

T

O

O

N

N

A

A

Wychodzimy

z równania Cauchy’ego. Przypomnijmy to równanie

dla składowych





i tensor

naprężenia dla płynu Newtona

i

k

l

ik

ik

ik

k

i

l

v

v

v

T

p

x

x

x





 















 





























ik

k

k

k

T

dv

F

dt

x













Wstawmy definicję tensora do równania Cauchy’go. Dostaniemy
wtedy :









k

k

k

k

dv

F

v

div v

dt

x







 





  





Dla gazu, którego cząsteczki mają właściwości zderzeniowe kulek
sprężystych, suma lepkości dynamicznej i objętościowej jest
równa:




Dla gazu o niesymetrycznych własnościach zderzeniowych:

3



 

 

'

3



 



  

druga lepkość

R

R

Ó

Ó

W

W

N

N

A

A

N

N

I

I

A

A

N

N

A

A

V

V

I

I

E

E

R

R

A

A

-

-

S

S

T

T

O

O

K

K

E

E

S

S

A

A

Biorąc pod uwagę powyższe informacje dostaniemy

trzy

równania

ruchu

dla płynu Newtona zwane równaniami Naviera – Stokesa.

Postać równań dla składowych k=1,2,3:

Forma wektorowa:

k

i

k

k

k

k

i

dv

v

p

F

v

'

dt

x

3

x

x





























  

























dv

F grad p

v

' grad diw v

dt

3



















  











przyspieszenie

pole sił

zewnętrznych

siły wynikające

z ciśnienia

siły wynikające z lepkości

Równania Naviera - Stokesa są równaniami ruchu. Wiążą one

pole przyspieszeń z polem sił zewnętrznych, polem sił

ciśnieniowych i siłami wynikającymi z lepkości.

Zawiera

ją trzy pola: wektorowe pole prędkości i dwa pola

skalarne

-

ciśnienia i masy właściwej, czyli pięć niewiadomych:

v

1

, v

2

, v

3

, p, ρ

Aby znaleźć rozwiązania równań Naviera – Stokesa trzeba
dołączyć:



Równanie ciągłości



R

ównanie energii wraz z określeniem energii wewnętrznej i

wektora strumienia ciepła oraz pomocnicze związki opisujące
lepkości, itp.,



Warunek

początkowy na pole prędkości



Prędkość brzegową, określoną tak, by dawała zbilansowaną

masę.

T

T

R

R

U

U

D

D

N

N

O

O

Ś

Ś

C

C

I

I

W

W

Y

Y

N

N

I

I

K

K

A

A

J

J

Ą

Ą

C

C

E

E

P

P

R

R

Z

Z

Y

Y

R

R

O

O

Z

Z

W

W

I

I

Ą

Ą

Z

Z

Y

Y

W

W

A

A

N

N

I

I

U

U

R

R

Ó

Ó

W

W

N

N

A

A

Ń

Ń

N

N

A

A

V

V

I

I

E

E

R

R

A

A

-

-

S

S

T

T

O

O

K

K

E

E

S

S

A

A

Równanie N - S jest

równaniem drugiego rzędu –

potrzeba więcej danych

granicznych niż dla

równania Eulera

1

2

Równanie N - S jest równaniem o

niewielkim współczynniku przy

najwyższych pochodnych (lepkość µ

jest dla wielu ważnych przypadków

niewielka). Powoduje to

niestateczność rozwiązania, czyli

istotną zmianę rozwiązania przy

niewielkiej zmianie danych

3

Aby uzyskać dobrą

aproksymację rozwiązania

równania N - S przy użyciu

metod numerycznych trzeba

wprowadzić wiele punktów

dyskretyzacji

U

U

P

P

R

R

O

O

S

S

Z

Z

C

C

Z

Z

E

E

N

N

I

I

E

E

R

R

Ó

Ó

W

W

N

N

A

A

N

N

I

I

A

A

N

N

A

A

V

V

I

I

E

E

R

R

A

A

–

–

S

S

T

T

O

O

K

K

E

E

S

S

A

A

D

D

L

L

A

A

C

C

I

I

E

E

C

C

Z

Z

Y

Y

Gęstość jest stała –

ρ = const

Równanie ciągłości

Równanie N - S

+ warunki początkowe i brzegowe.

Dla szczególnie prostych kształtów obszaru ruchu i przy wielu
założeniach dotyczących kinematyki równania N – S można
rozwiązać analitycznie

diw v

0



dv

F grad p

v

dt











 

P

P

R

R

Z

Z

Y

Y

K

K

Ł

Ł

A

A

D

D

1

1

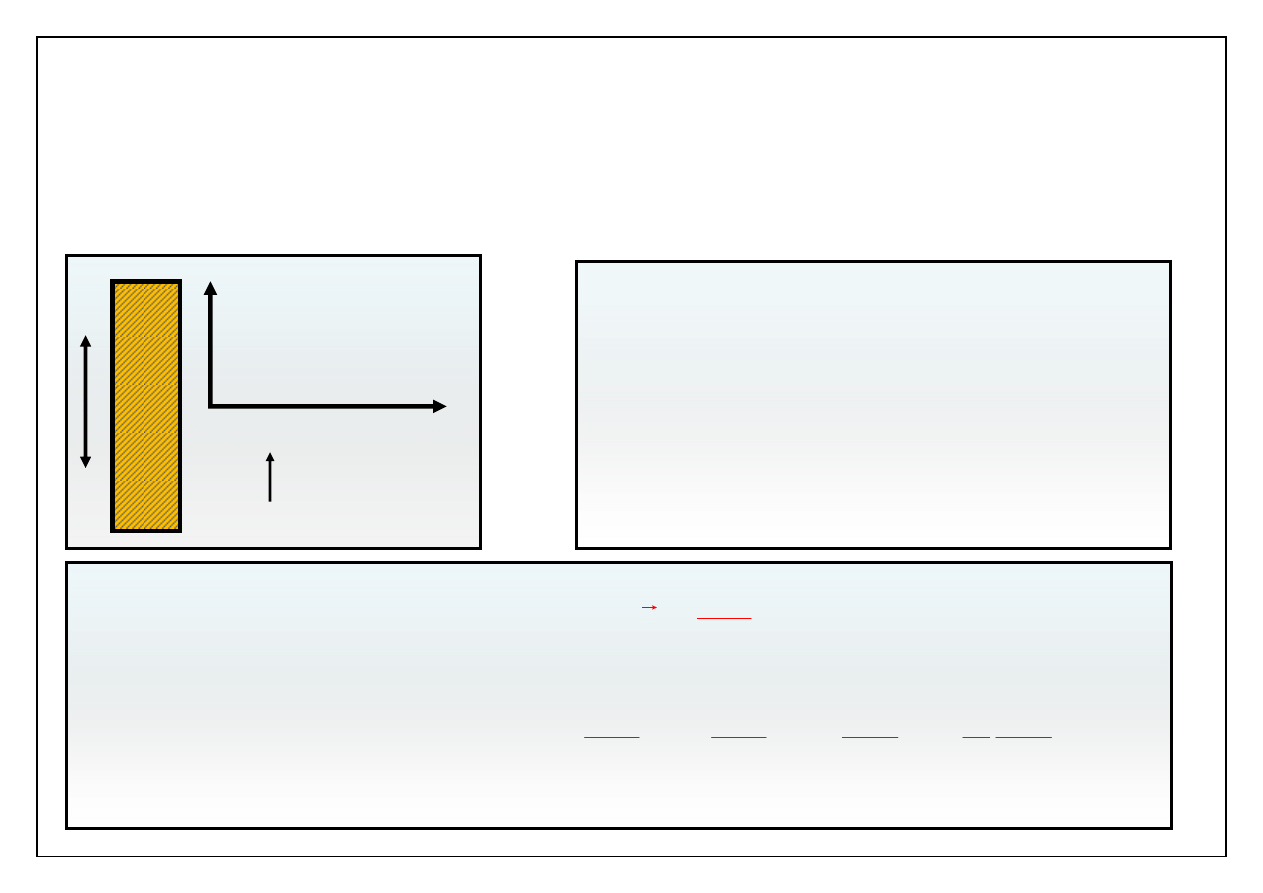
Drgająca wzdłużnie płyta w nieograniczonym zbiorniku

wypełnionym cieczą. Płyta wykonuje ruch w kierunku 0x

2

.

x

1

x

2

v

2

0

Pole prędkości ma jedyną niezerową

składową:

v

2

= v

2

(t, x

1

)

.

Prędkość

v

2

nie zależy od

x

2

, bo wobec

nieograniczoności płyty i zbiornika, dla

każdego

x

2

ruch jest taki sam.

Równanie ciągłości:

Równanie ruchu w kierunku

0x

2

:





2

2

2

1

2

v

diw v

0,

bo

v

v

t, x

x











2

2

2

1

2

2

1

2

0

0

2

v

v

v

1

p

v

v

v

t

x

x

x





















 

 









Po rozpisaniu laplasjanu i uproszczeniu otrzymamy:

2

2

2

2

2

1

v

v

1

p

t

x

x











 









Określmy ciśnienie. Z równania ruchu dla kierunku

0x

1

wobec znikania

v

1

pozostaje

1

1

p

0

x





 



Stąd

p = f(x

2

)

– nie zależy od

x

1

.

Dla wielkich

x

1

ciśnienie jest takie samo jak na powierzchni płyty. Ale

dostatecznie daleko od miejsca wzbudzenia ruchu prędkość znika, a
ciśnienie jest stałe:

2

f (x )

const

p

const



 

Równanie ruchu po uproszczeniu ma postać:

2

2

2

2

1

v

v

t

x













Jeśli płyta drga harmonicznie to wtedy

1

i t

2 x 0

v

A e







a

daleko od płyty ruch zanika i

1

2 x

v

0





Rozwiązaniem zadania jest:

1

x

1

i

t

2

2

2

1

1

v (t, x )

Be

x e





























P

P

R

R

Z

Z

Y

Y

K

K

Ł

Ł

A

A

D

D

2

2

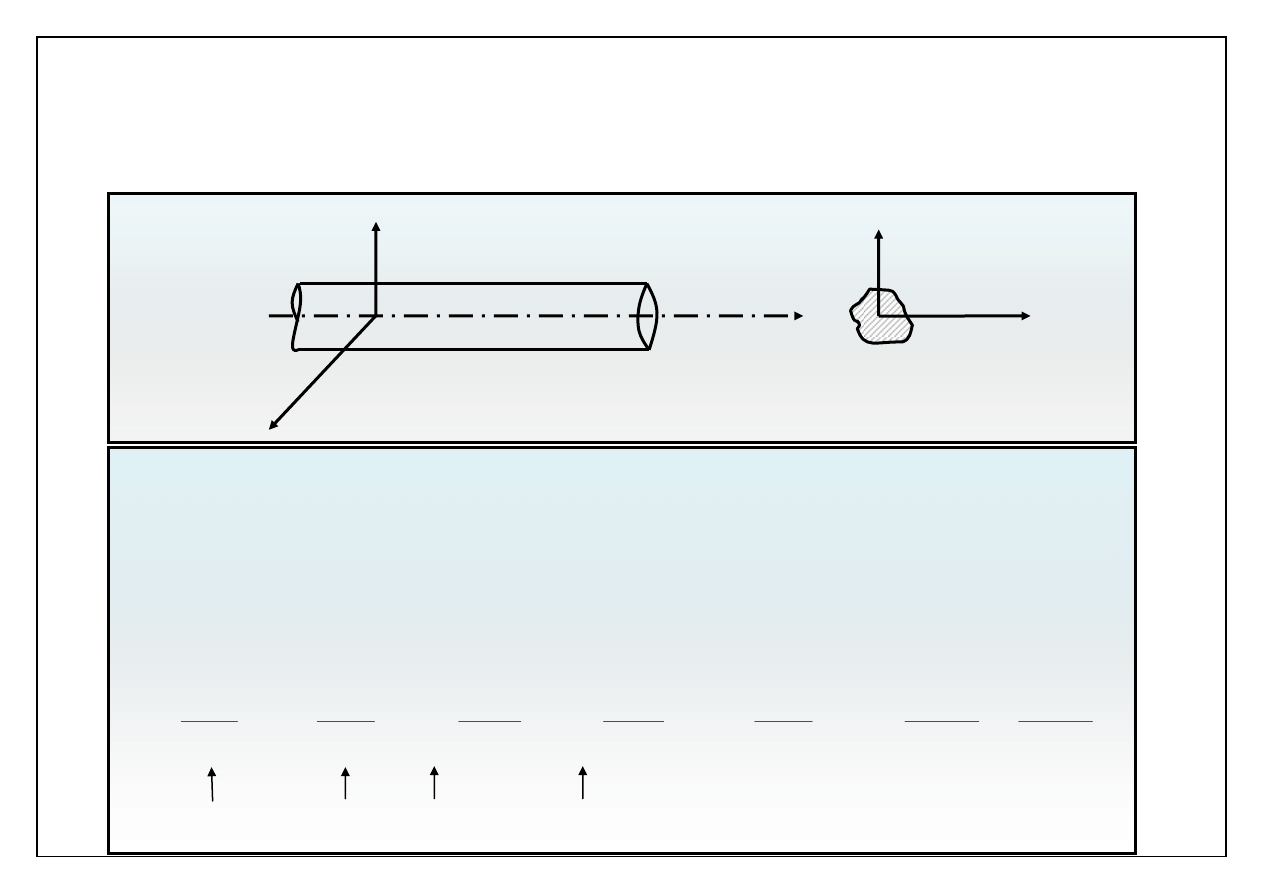
Ruch ustalony w nieskończenie długim przewodzie o

niezmiennym przekroju.

x

3

x

3

x

2

x

2

x

1

Rura ma nie

ograniczoną długość, więc dla każdego

x

1

ruch jest taki

sam a pole prędkości nie zależy od

x

1

.

Załóżmy też, że

2

3

1

1

2

3

v

v

0 i v

v (x , x )







To równanie ruchu dla kierunku

0x

1

ma postać:

2

2

1

1

1

1

1

1

1

2

3

2

2

1

2

3

1

2

3

v

v

v

v

v

v

p

v

v

v

t

x

x

x

x

x

x

































 



































0

0

0

0

Dla pozostałych kierunków wobec znikania

2

3

v i v

mamy:

 

1

2

3

p

p

0 i

0

p

p x

x

x







 







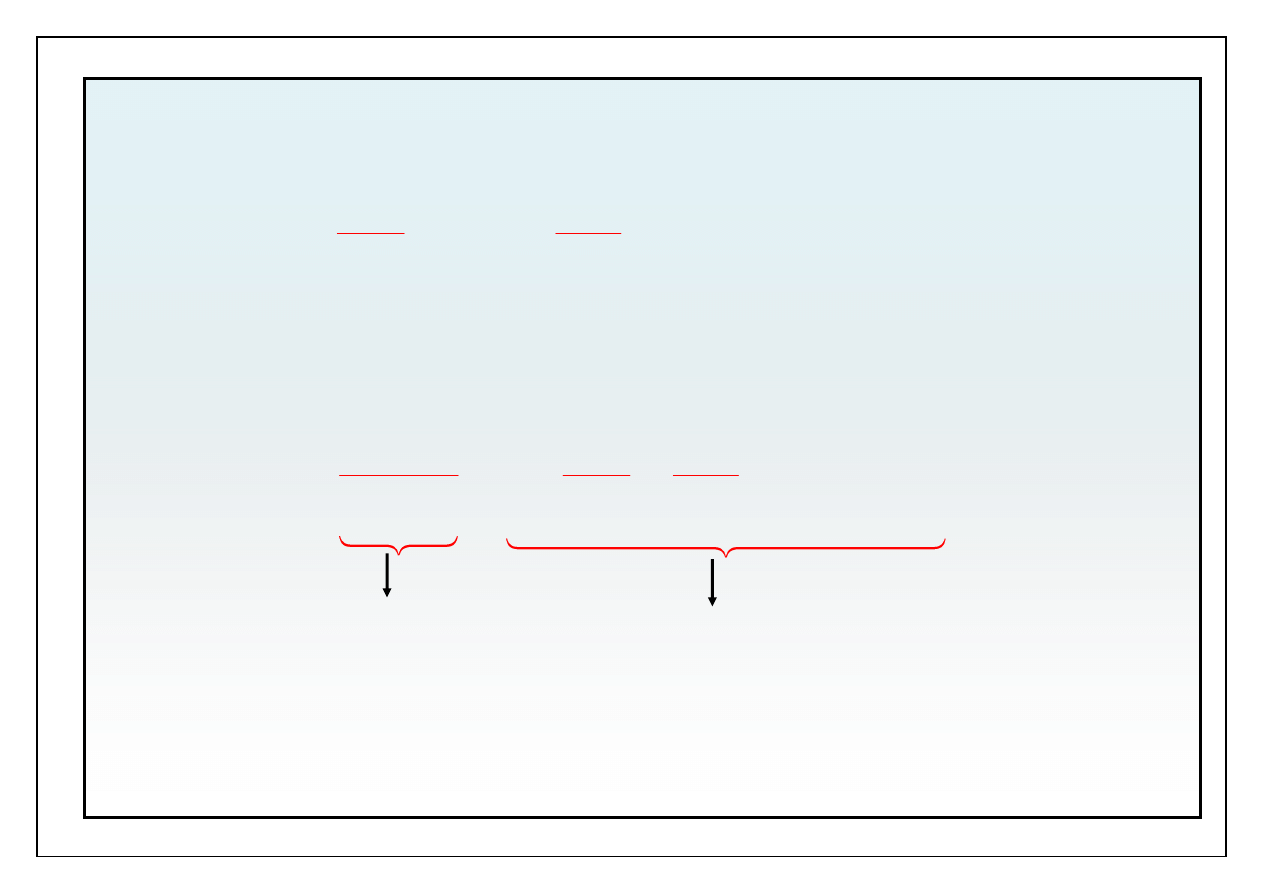
Równanie ruchu upraszcza się do postaci:





2

2

1

1

2

3

1

2

3

dp(x )

v x , x

dx

x

x



























Wniosek:

lewa strona musi mieć wartość niezależną od x

1,

czyli stałą!

zależy od x

1

zależy od x

2

i x

3

Zatem:





2

2

1

1

2

3

1

2

3

dp(x )

v x , x

dx

x

x

 









  















Ciśnienie:





Prędkość:

0

1

p

p

x







Jest liniową funkcją długości
przewodu

x

1

p(x

1

)

p

0

1

1 brzeg

v

v

0




  



Wyraża warunek przylepienia cieczy

do rury.

Zagadnienie Dirichleta

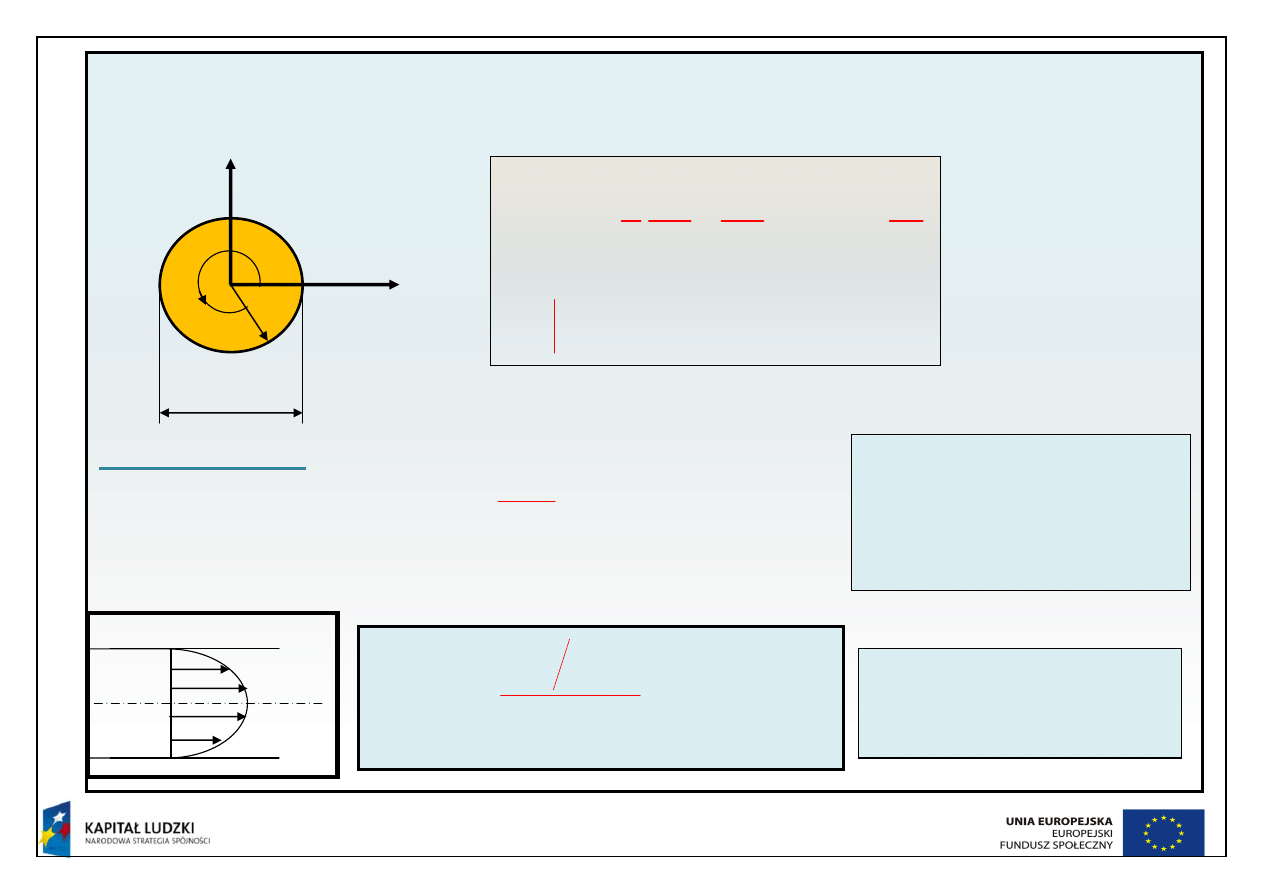
Dla przewodu kołowego:

Rozwiązanie:


Ostatecznie

x

2

x

3

r

θ

2R

1

1

1 r R

1 d

d

v

r

v

r dr dr

v

0






 

 



2

1

v

r

A ln r

B

4





 





A=0

bo

r = 0

należy do

obszaru ruchu,

B

wyznaczamy z

warunku brzegowego





2

2

1

1

dp dx

v

R

r

4



 



Rozkład prędkości jest

paraboliczny