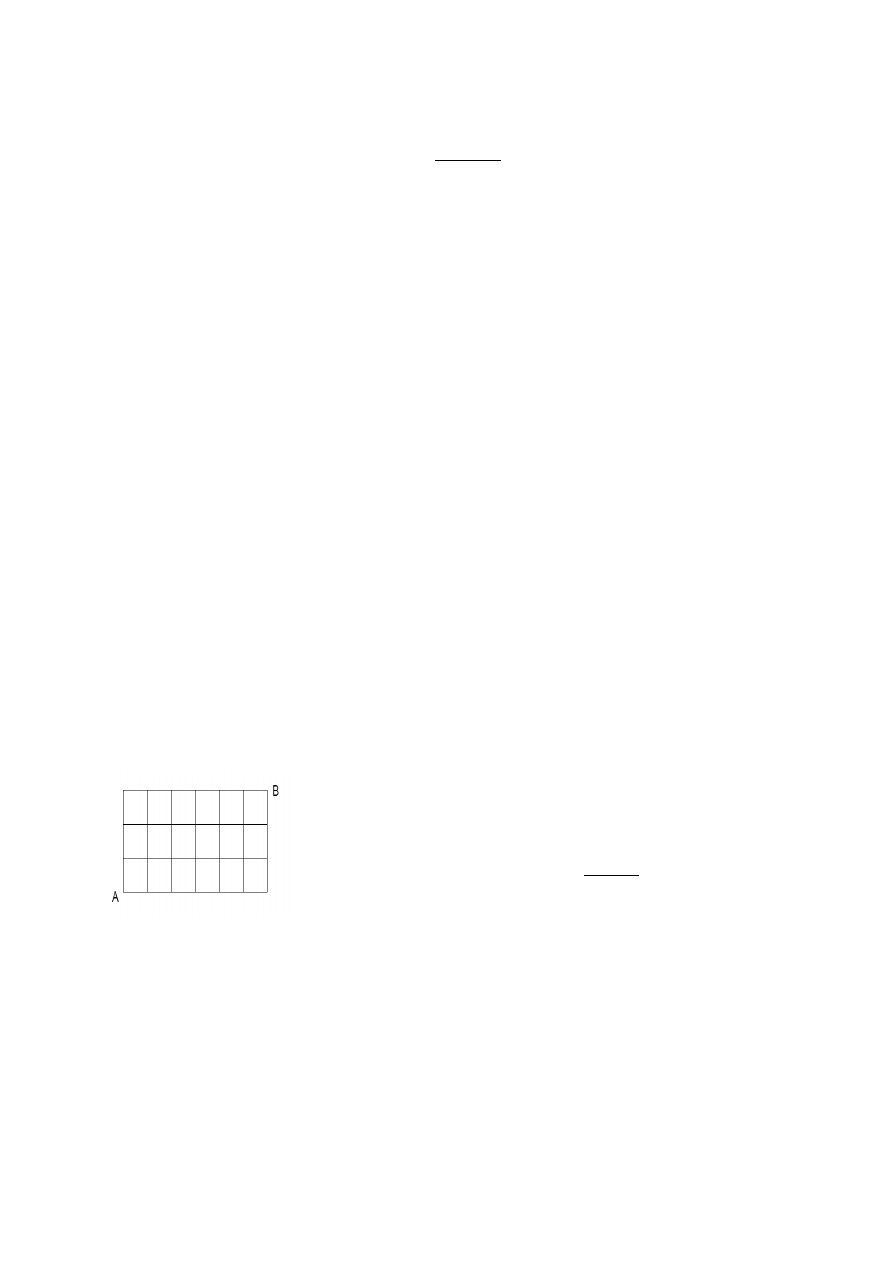
1. Symbol Newtona.

Liczbę podzbiorów k- elementowych zbioru n- elementowego oznacza się przez

Jest to tak zwany symbol Newtona. Inaczej, jest to liczba sposobów na
jakie można wybrać k elementów ze zbioru n elementowego.

2. Ile jest podzbiorów zbioru n- elementowego? Pokazać kilkoma sposobami.

Policzmy teraz, ile podzbiorów ma skończony zbiór n- elementowy.
Jeżeli zbiór składa się z trzech elementów: {a,b,c} to możemy łatwo wypisać wszystkie jego podzbiory :



, {a}

,{b}, {c},{a, b}, {a, c}, {b, c} ,{a,b,c}.
Rozważmy teraz ogólnie podzbiory zbioru {1,2,3,...,n}.
Z każdym podzbiorem związana jest funkcja charakterystyczna określona wzorem:

Dziedziną funkcji jest zbiór {1,2,...,n}, a przeciwdziedziną zbiór {0,1}. Zauważmy, że każdemu podzbiorowi
odpowiada jedna funkcja charakterystyczna, i na odwrót, jeżeli weźmiemy dowolną funkcję:
to wyznacza ona zbiór
Z powyższych rozważań wynika, że liczba podzbiorów zbioru n- elementowego jest równa liczbie funkcji ze
zbioru {1,2,...,n} w zbiór {0,1}. Czyli na podstawie twierdzenia:
Jeżeli zbiór A zawiera k elementów, a zbiór B n elementów to liczba funkcji ze zbioru A w zbiór B wynosi

mamy twierdzenie: Każdy zbiór n elementowy ma

podzbiorów.

3. Zasada szufladkowa Dirichleta, przykłady zastosowań.

Jeżeli n obiektów jest rozmieszczonych w m szufladach i n > m, to istnieje co najmniej jedna szuflada z
przynajmniej dwoma obiektami.
Zastosowanie: Zasada szufladkowa wykorzystywana w dowodach wielu głębokich twierdzeń matematycznych i
często samo zauważenie, że można ją zastosować jest kluczem do rozwiązania problemu.

4. Zasada włączania i wyłączania.

Zasada włączeń i wyłączeń - reguła kombinatoryczna, pozwalająca na określenie liczby elementów skończonej
sumy mnogościowej skończonych zbiorów.

W szczególności o ile tylko A, B są skończone.

5. Rozwiązywanie równań diofantycznych, szukanie najkrótszych dróg.

Ile jest najkrótszych dróg z punktu A do punktu B?

Mamy 9 skrzyżowań, wybieramy 6 na których idziemy na wschód lub 3 na
których idziemy na północ. A więc mamy 9 po 3 lub 9 po 6 rozwiązań (94.)
W ogólności, dla kratki rysujemy m+n odcinków, a więc najkrótszych
dróg jest:

Przykład: Ile rozwiązań ma równanie

, gdzie x

i

są

liczbami naturalnymi?

Użyjemy kratki . Suma poziomych odcinków daje 7 i jest dokładnie 5 takich odcinków, po jednym na
każdym poziomie. Jeśli długość tych odcinków oznaczymy odpowiednio przez x

0

,x

1

,x

2

,x

3

,x

4,

to każda taka

droga(łamana) na kratce ustala pewne rozwiązanie naszego równania, i każde rozwiązanie równania wyznacza
dokładnie jedną drogę. Zatem istnieje

rozwiązań równania.

Ogólnie: Równanie

ma

rozwiązań.

6. Twierdzenie o rozwiązywaniu równania rekurencyjnego drugiego rzędu(równanie liniowe,

jednorodne).

Liniowa, jednorodna relacja rekurencji ze stałymi współczynnikami jest to relacja rekurencji postaci

, gdzie c

1, … ,

c

k

i c

k

Liniowa oznacza, że każde a

i

jest w potędze co najwyżej pierwszej;

Jednorodna oznacza, że każdy człon po prawej stronie jest pomnożony przez
jakieś a

i

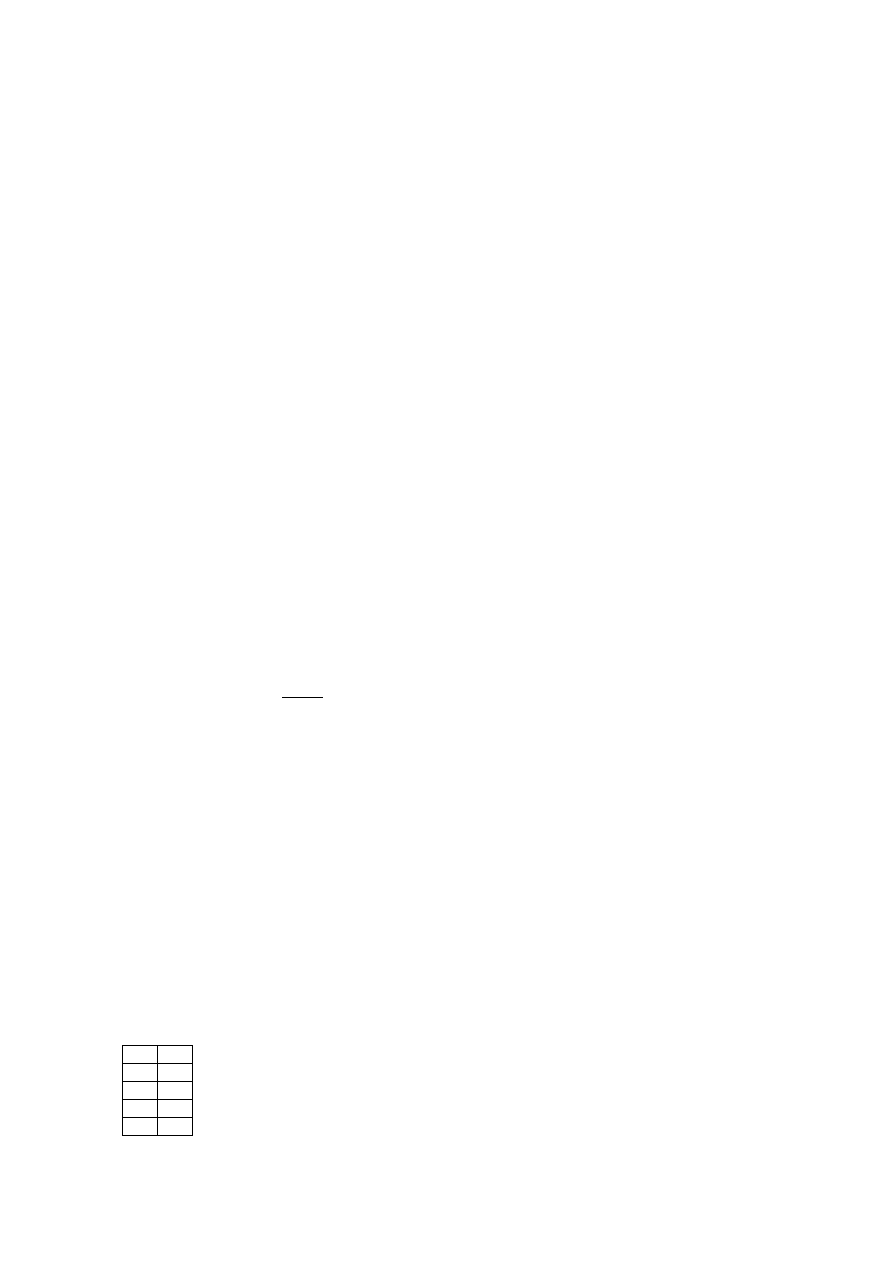
Wszystkie współczynniki c

i

są stałe (czyli niezależne od n);

Ponieważ a

k

zależy od k swoich poprzedników, więc rzędem relacji

jest k.
Aby rozwiązać relację rekurencji, będziemy potrzebowali k warunków
początkowych: a

0

= c

0

, a

1

= c

1

,..., a

k

= c

k

.

Twierdzenie. Niech



i



będą różnymi rozwiązaniami równania

charakterystycznego, gdzie a, b



R i b



0. Wtedy każde rozwiązanie

Równania a

n

= a a

n-1

+ b a

n-2

, gdzie a

0

= c

0

i a

1

= c

2

jest postaci

, dla pewnych stałych A i B.

Zauważmy, że twierdzenie nie może być stosowane, jeśli



=



. Można jednak je stosować, jeśli



i



są

liczbami zespolonymi.
Rozwiązania

są rozwiązaniami podstawowymi, natomiast rozwiązanie relacji rekurencji

jest kombinacją liniową rozwiązań podstawowych.
Przykład. Rozwiązać metodą przewidywań:

Tak więc rozwiązaniem jest

7. Rozwiązywanie równań rekurencyjnych- metoda funkcji tworzących.

Niech a

1

, a

2

,..., a

n

,... będzie ciągiem liczb rzeczywistych.

Funkcją tworzącą dla ciągu (an) nazywamy funkcję postaci:

Najczęściej używana funkcja tworząca:

8. Algorytm Euklidesa, podstawowy i rozszerzony.

Największy wspólny dzielnik NWD:
Dla dwóch liczb całkowitych a i b, ich największy wspólny dzielnik to największa liczba całkowita n, która
dzieli a i b. Największy wspólny dzielnik liczb a i b będziemy oznaczać przez NWD(a, b). Na przykład: NWD(4,
6) = 2,
NWD(4, 0) = 4.
Największy wspólny dzielnik dwóch liczb dodatnich można obliczyć za pomocą algorytmu Euklidesa.
Algorytm Euklidesa: Aby obliczyć największy wspólny dzielnik
dwóch dodatnich liczb naturalnych a, b, powtarzamy aż do skutku:
* dopóki a



b



0, wykonuj:

** jeżeli a



b, to a := a mod b,

** w przeciwnym wypadku b := b mod a.
* NWD(a, b) = a + b,
Powyższy algorytm oblicza resztę z dzielenia większej liczby przez
mniejszą tak długo, aż otrzyma zero. Wtedy wynikiem działania
algorytmu jest ta druga liczba (jeżeli a = 0, to a + b = b, a jeżeli b = 0,
to a + b = a).
W poniższej tabeli pokazano kolejne kroki działania algorytmu Euklidesa na parze liczb 36 i 15:

P

Q

36

15

6

15

6

3

0

3

Poprawność algorytmu Euklidesa wynika z poniższego lematu:
Niech p i g będą dwoma liczbami naturalnymi i niech 0<q<p. Wtedy para p, q ma taki sam zbiór wspólnych
dzielników jak para p mod q, q.
Dowód: Z definicji ilorazu i reszty mamy p=(p/q)* q +p mod q
Jeżeli liczba r jest wspólnym dzielnikiem pary (p mod q), q. Na odwrót, jeżeli liczba r jest wspólnym dzielnikim
pary (p mod q), q to r dzieli także p, czyli r jest wspólnym dzielnikiem pary p, q.
Algorytm Euklidesa można tak zmodyfikować, aby oprócz największego wspólnego dzielnika NWD(a, b),
wyliczał także liczby x i y, takie że: xa + yb = NWD(a, b).
Rozszerzony algorytm Euklidesa

Dane wejściowe: dwie liczby naturalne a,b.

Dane wyjściowe: NWD(a,b) oraz liczby całkowite x,y takie, że
xa + yb = NWD(a, b).
* podstaw: xa := 1, ya := 0, xb := 0, yb := 1.
* dopóki a



b



0, wykonuj:

** jeżeli a



b, to a := a mod b,

xa := xa – xb



(a



b);

ya := ya – yb



(a



b);

** w przeciwnym wypadku: b := b mod a,
xb := xb – xa



(b



a);

yb := yb – ya



(b



a).

* NWD(a,b): = a+b.
* Jeżeli a > 0, to x := xa ; y:= ya.
* Jeżeli b > 0, to x := xb ; y:= yb.
W poniższej tabeli pokazano kolejne kroki działania rozszerzonego algorytmu Euklidesa na parze liczb 36 i 15:
a b xa ya xb yb
36 15 1 0 0 1
6 15 1 -2 0 1
6 3 1 -2 -2 5
0 3 5 -12 -2 5
Tak więc liczbę 3 można przedstawić jako kombinację liczb 15 i 36
w następujący sposób:
3 = (-2)



36 + (5)



15.

9. Elementy odwracalne w pierścieniu Zm.

Element

jest odwracalny, jeżeli istnieje

takie, że b nazywamy elementem

odwrotnym do a i oznaczamy przez

Twierdzenie: Liczba

jest odwracalna wtedy i tylko wtedy, gdy NWD(a,m)=1

Zbiór liczb odwracalnych w

oznaczamy przez

Jeżeli liczba m jest pierwsza, to każdy element jest odwracalny, czyli pierścień

jest ciałem.

10. Równania z kongruencją:

Twierdzenie: Równanie ma rozwiązanie wtedy i tylko wtedy gdy NWD(a,m) dzieli b.
Jeśli mamy równanie to rozwiązaniem jest

.

11. Funkcja Eulera, własności, zastosowania, twierdzenie Eulera.

Definicja: Funkcja Eulera jest to funkcja, która liczbie m przypisuje liczbę elementów odwracalnych w

. Z definicji przyjmujemy

.

Jeżeli p jest liczbą pierwszą, to dla dowolnego

W szczególności

Jeżeli m i n są względnie pierwsze, to
Twierdzenie: Jeśli

są liczbami względnie pierwszymi, to m dzieli liczbę

, gdzie

oznacza wartość funkcji Eulera, czyli liczbę tych liczb całkowitych dodatnich mniejszych od m, które są z m
względnie pierwsze. Czyli zachodzi wzór

12. Twierdzenie chińskie o resztach:

Niech m

1

, m

2

, … ,m

r

będą dodatnimi liczbami względnie pierwszymi, to znaczy dla każdej pary

mamy NWD(m

i

, m

j

)=1 oraz niech a

1

, a

2

, … , a

r

będą dowolnymi resztami. Wtedy istnieje liczba całkowita a,

taka że:

a

1

= a (mod m

1

)

a

2

= a (mod m

2

)

….
a

r

= a (mod m

r

)

13. Kody RSA

Kodowanie:
Niech litery alfabetu to liczby 1-26; pauza 27, a pozostałe znaki- powyżej 27.
Z danego słowa otrzymujemy liczbę L np.: ADAM: 01040113; L=1040113
Niech p, q- liczby względnie pierwsze, r = p



q, L



<0,r) i niech s- liczba naturalna taka, że NWD(s,p-1)=1 i

NWD(s, q-1)=1.
Kod C liczby L obliczamy według wzoru:

Odkodowywanie:
Z tego, że NWD(s,p-1)=1 wynika, że istnieją liczby całkowite a, b takie, że sa+(p-1)b = 1.
W takim razie

Ponieważ z twierdzenia Eulera mamy, że

Podobnie z tego, że NWD(s,q-1)=1 otrzymamy, że

L otrzymamy rozwiązując układ równań:

14. Izomorfizm grafów – Grafy G i F nazywamy izomorficznymi, jeżeli istnieje bijekcja zbioru

wierzchołków grafu G na zbiór wierzchołków grafu F, która zachowuje strukturę grafu (krawędzie). Intuicyjnie
oznacza to, że grafy G i F są tym samym grafem, jedynie poddanym jakiejś permutacji wierzchołków.

15. Podgrafy indukowane wierzchołkowo i krawędziowo- definicje, umieć pokazać różnice.

Podgraf danego grafu G to graf powstały przez usunięcie z grafu G pewnej liczby wierzchołków lub krawędzi (z
tym zastrzeżeniem, że usuwając pewien wierzchołek usuwamy wszystkie do niego przyległe krawędzie).W
szczególności każdy graf jest swoim podgrafem.
Podgrafem indukowanym wierzchołkowo danego grafu G nazywamy graf powstały przez usunięcie z grafu G
pewnej liczby wierzchołków oraz wszystkich wychodzących z nich i wchodzących do nich krawędzi. Inaczej
mówiąc jest to graf, którego zbiór wierzchołków jest zawarty (jest podzbiorem) w zbiorze wierzchołków grafu
G, a zbiór krawędzi składa się ze wszystkich krawędzi grafu G, których końce należą do zbioru wierzchołków
nowo powstałego grafu. Zbiór wierzchołków tego podgrafu nie może być pusty.
Podgrafem indukowanym krawędziowo danego grafu G nazywamy graf powstały z grafu G, którego zbiór
krawędzi jest zawarty (jest podzbiorem) w zbiorze krawędzi grafu G, a zbiór wierzchołków stanowią końce
krawędzi.

16. Lemat o uściskach dłoni.

Twierdzenie 1 (lemat o uściskach dłoni) Dla każdego grafu G=(V,E),



v



V dG(v) = 2|E|.

Twierdzenie 2 (wniosek) W każdym grafie G=(V,E) liczba wierzchołków stopnia nieparzystego jest parzysta.
Twierdzenie 3 Jeśli G jest grafem spójnym o n wierzchołkach, to n-1



|E|



n(n-1)/2.

17. Algorytmy znajdowania cyklu Eulera w grafach eulerowskich.

Szlak Eulera (cykl Eulera)- szlak domknięty, przechodzący przez wszystkie krawędzie grafu.
Graf eulerowski- graf zawierajacy szlak Eulera.
Algorytm- jak przejść po grafie eulerowskim używając każdej
krawędzi dokładnie raz? (korzystając z dowodu twierdzenia E-H)
1. Wybieramy dowolny wierzchołek v0



V(G) i cykl c zawiera v0;

2. Wszystkie krawędzie c oznaczamy cechą 0;
3. Wybieramy cykl c’, „sąsiedni” z cyklem już wybranym i jego krawędziom przypisujemy cechę c+1, gdzie c
jest cechą poprzednio wybraną- tak do wyczerpania grafu G;
4. Startujemy z v0 i idziemy wzdłuż cyklu oznaczonego symbolem 0 aż do spotkania wierzchołka vi
incydentnego z nie odwiedzaną jeszcze krawędzią oznaczoną wyższym symbolem. Wybieramy
krawędź z najwyższą cechą aż do wyczerpania wszystkich krawędzi.

18. Kody Prufera, opis i zastosowanie algorytmów.

a)

Algorytm wyznaczania kodu Prüfera

Dane: drzewo o zbiorze wierzchołków {1,2,..,n} Wynik: kod Prüfera (ciąg (n-2) wyrazowy liczb ze zbioru {1,2,...,n})

1.

Znajdź wierzchołek wiszący (stopnia jeden) z najmniejszym numerem, powiedzmy v. Niech w będzie sąsiadem v.

2.

Zapisać w do ciągu oraz usunąć krawędź {v,w}.

3.

Jeżeli w drzewie pozostała więcej niż jedna krawędź to przejść do 1.,

W przeciwnym razie zakończyć działanie algorytmu.

b)

Algorytm wyznaczania drzewa o zbiorze wierzchołków {1,2,...,n}, którego kodem Prüfera jest zadany ciąg (n-2)
wyrazowy liczb ze zbioru {1,2,...,n}

Dane: ciąg (a

1

,a

2

,...,a

n-2

) o wyrazach ze zbioru {1,2,...,n} Wynik: T=(V,E)-drzewo o zborze V={1,2,...,n} z k. (a

1

,a

2

,...,a

n-2

)

1.

Zapisać dwie listy L

1

=(a

1

,a

2

,...,a

n-2

), L

2

={1,2,...,n}; V={1,2,...,n}; E=Ø

2.

Wyznaczyć z L

2

najmniejsze i które nie występuje w liście L

1

; E:=E



{i,a

1

}; L

1

=(a

2

,...,a

n-2

); L

2

={1,2,...,n}-{i}

3.

Jeżeli L

1

zawiera co najmniej jedną liczbę to przejść do 2., przeciwnie (L

1

= Ø i L

2

={l,k}) E:=E



{l,k} i koniec

T=(V,E)

19. Twierdzenie Eulera-Hierholtza o grafach eulerowskich.

W grafie spójnym G istnieje cykl Eulera wtedy i tylko wtedy, gdy każdy wierzchołek w G ma stopie« parzysty.
Algorytmem służącym do znajdowania w grafie cyklu Eulera jest algorytm Fleury'ego. Przedstawia się on
następująco: Startujemy z dowolnego wierzchołka. Każda kolejna krawędź, po której przechodzimy, wybierana
jest spośród krawędzi wychodzących z wierzchołka, w którym aktualnie się znajdujemy. Wybieramy
oczywiście krawędź, po której jeszcze nie przeszliśmy. O ile jest to możliwe, usunięcie wybranej krawędzi
nie powinno rozspójnić grafu (rozciąć go na dwa 'kawałki'). Jeżeli uda nam się postępując w ten sposób dojść
do wierzchołka, z którego wyruszyliśmy i przejść przez wszystkie krawędzie, to otrzymana droga jest cyklem
Eulera.

20. Twierdzenie Orego o grafach hamiltonowskich.

Def. Spójny graf G jest grafem Hamiltona (hamiltonowskim), jeśli zawiera cykl przechodzący przez wszystkie
wierzchołki grafu G.
Twierdzenie Orego:
Jeżeli dla każdych dwóch nie sąsiednich wierzchołków grafu G suma ich stopni jest nie mniejsza niż ilość
wszystkich wierzchołków w G, to G jest hamiltonowski.

21. Twierdzenie Koniga o kolorowaniu krawędzi w grafach dwudzielnych.

Jeśli G jest grafem dwudzielnym, gdzie wierzchołek o największym stopniu ma stopień



, to



e(G) =



.

22. Podać trzy wersje twierdzenie Halla.

a) W skończonej grupie dziewcząt każda może wybrać męża spośród chłopców, których zna, wtedy i

tylko wtedy, gdy w każdym n- elementowym podzbiorze dziewcząt, dziewczęta te znają co najmniej n
chłopców.

b) (wersja transwelowa) Rodzina R=(A

1

, A

2

, … , A

n

) ma transwersale wtedy i tylko wtedy gdy dla

każdego podzbioru

Ai

1

- zbiór chłopców znanych dziewczynie 1

Ai

r

– zbiór chłopców znanych dziewczynie r

R= |I| - moc podzbioru dziewcząt

c) Jeżeli G=(V1, V2, E) jest dwudzielny, to istnieje skojarzenie zbioru V1 w zbiór V2 wtedy i tylko

wtedy, gdy dla każdego X



V1, |NG(X)|



|X|.

Skojarzenia- zawarte związki małżeńskie;
Ilość sąsiadów- ilość znajomych chłopców;
Graf ma skojarzenie wtedy i tylko wtedy, gdy każda dziewczyna znajdzie męża spośród chłopców, których
zna

23. Znajdowanie wielomianów chromatycznych.