
Podstawy elektroniki cyfrowej
Wstęp
1. Tranzystor MOS
2. Matematyczne podstawy elektroniki cyfrowej
2.1. Podstawy logiki matematycznej
2.2. Podstawowe prawa logiki matematycznej
2.3. Tworzenie formuł zdaniowych oraz ich minimalizacja
2.4. System binarny
3. Podstawy elektroniki cyfrowej
3.1. Idea układów cyfrowych
3.2. Przykłady układów cyfrowych
3.3. Projektowanie układów cyfrowych
4. Bramki logiczne CMOS
4.1. Inwerter
4.2. Bramki logiczne CMOS
4.3. Projekt sumatora jednobitowego — dokończenie
Podsumowanie
Bibliografia
„Komputery w przyszłości nie będą ważyć dużo więcej
niż półtorej tony.”
„Popular Mechanics”, 1949

2
Wstęp
W module tym poznasz najważniejszy z punktu widzenia informatyki dział elek-
troniki, a mianowicie elektronikę cyfrową. To bardzo ciekawy dział i przynajm-
niej dla mnie najprostszy. Myślę, że i tobie — jako informatykowi — elektronika
cyfrowa przypadnie do gustu. Jest to niewątpliwie najważniejszy moduł tego kur-
su i stanowi jego „serce”. Informacje zawarte w tym module będą niezbędne do
wykonania projektu układu scalonego. Zanim jednak przejdziemy do szczegółów,
poznamy najważniejszy z punktu widzenia mikroelektroniki przyrząd, a mianowi-
cie tranzystor MOS. Następnie krótko przypomnimy elementy logiki matematycz-
nej oraz matematyki dyskretnej, ponieważ elektronika cyfrowa ma swoje korzenie
właśnie w matematyce. Po poznaniu tych dwóch elementów przystąpimy do sedna
— budowy układów elektroniki cyfrowej. Bardzo dużo pracy przed nami, ale mam
nadzieje, że będzie ona dla ciebie równie ciekawa i pasjonująca jak i dla mnie!
3
1. Tranzystor MOS
Tranzystor MOS jest najważniejszym elementem z punktu widzenia mikroelektroni-
ki. Należy on do grupy tranzystorów unipolarnych. Posiada cztery elektrody: źródło,
dren, bramkę i podłoże. Rezystancja wyjściowa jest, tak jak w każdy tranzystorze uni-
polarnym, między elektrodami źródła i drenu. Sterowny jest napięciem bramka–pod-
łoże. Działa on w bardzo prosty sposób — po przyłożeniu napięcia bramka–podłoże
między elektrodami źródła i drenu wytwarza się odpowiednia rezystancja.
We współczesnej mikroelektronice najczęściej stosowany jest tranzystor MOS z tzw. ka-
nałem wzbogaconym — to właśnie jego działanie zostanie omówione w tym module.
Wyróżniamy dwa typy tranzystorów MOS:
— z kanałem typu N,
— z kanałem typu P.
Przyjrzyjmy się tranzystorowi MOS z kanałem typu N. Otóż, jeśli napięcie bram-
ka–podłoże jest równe zero, tranzystor jest w stanie wyłączonym, posiada bardzo
dużą rezystancję między źródłem a drenem. Kiedy zwiększamy napięcie, rezystan-
cja zaczyna maleć. Od pewnej wartości napięcia spadek ten jest bardzo gwałtowny
— napięcie, przy którym się to dzieje nazywamy napięciem progowym. Dla napię-
cia wyższego niż progowe wyjściowa rezystancja jest już bardzo mała, tranzystor
jest otwarty i bez przeszkód przewodzi prąd. Oczywiście wzrost napięcia powyżej
napięcia progowego powoduje dalsze zmniejszanie rezystancji wyjściowej i jeszcze
lepsze przewodzenie tranzystora.
Dla tranzystora MOS z kanałem typu N można wykreślić charakterystyki. No wła-
śnie, charakterystyki, a nie charakterystykę jak w przypadku diody. Czemu? Po-
nieważ w diodzie możesz jedynie zmieniać napięcie między anodą i katodą i mie-
rzyć prąd. W tranzystorze MOS możesz zmieniać już dwa napięcia: źródło–dren
oraz bramka–podłoże i mierzyć dwa prądy. My jednak skupimy się na jednej, naj-
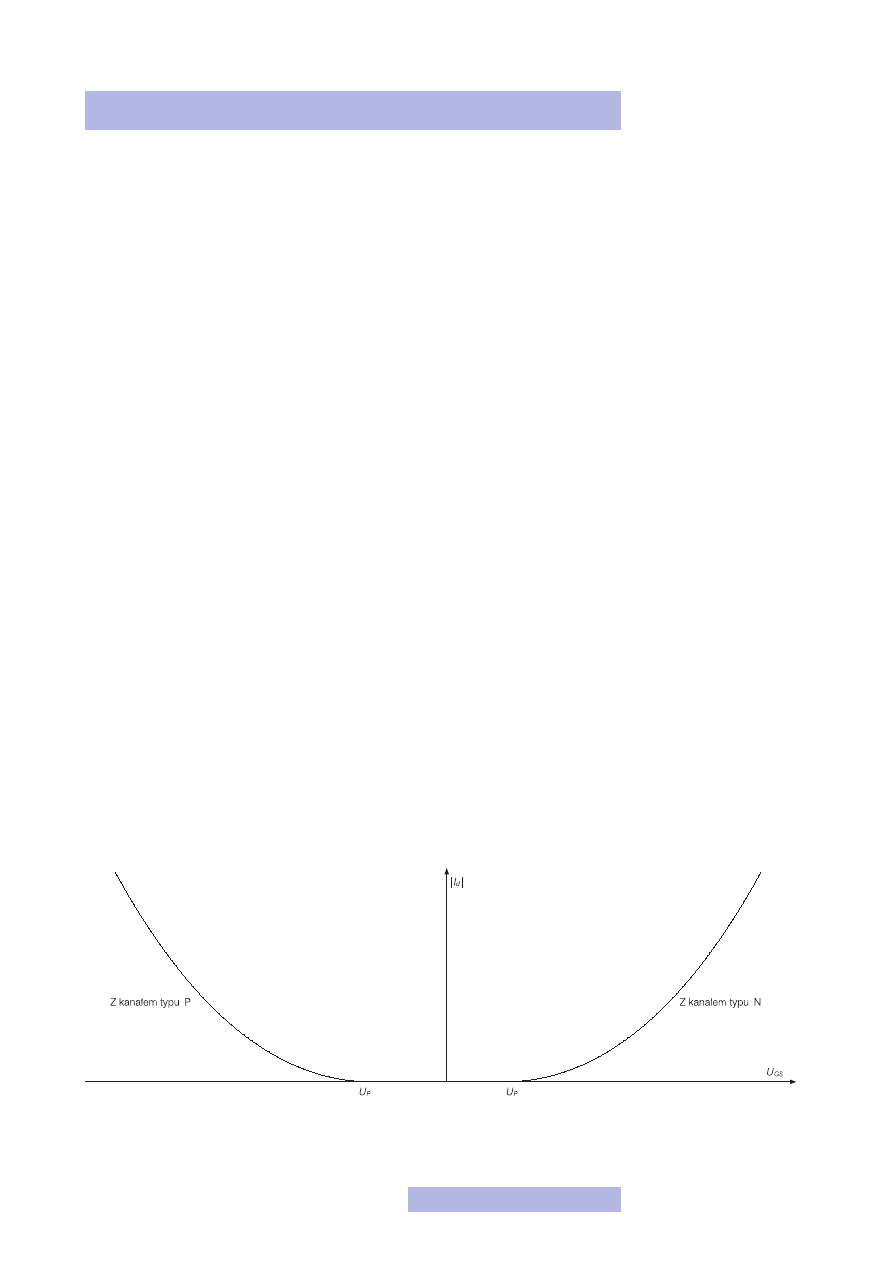
ważniejszej dla nas charakterystyce, nazwanej charakterystyką przejściową (rys.
1). Przedstawia ona zależność prądu drenu od napięcia bramka–podłoże. Jak się ją
wykonuje? Otóż przykłada się jakieś stałe napięcie dren–źródło, a zmienia się na-
pięcie bramka–podłoże, mierząc równocześnie prąd płynący na wyjściu, czyli prąd
płynący przez elektrody drenu i źródła (rys. 2).
Rysunek 1
Charakterystyki przejściowe
tranzystorów MOS
z kanałem wzbogaconym
4
Zastanów się i spróbuj wytłumaczyć, czemu ta charakterystyka tak
właśnie wygląda. Pamiętaj, że dla napięć bramka–podłoże od zera
do napięcia progowego rezystancja jest duża, a potem drastycznie
spada. Ponadto z prawa Ohma wynika, że jeśli napięcie jest stałe,
a zmienia się rezystancja, to musi zmieniać się również prąd.
Tranzystor z kanałem typu P działa identycznie jak z kanałem N. Je-
dyna różnica polega na tym, że tranzystor ten włącza się napięciem
ujemnym, czyli gdy napięcie bramka–podłoże jest równe zero, re-
zystancja wyjściowa jest bardzo duża, a więc prąd drenu jest bliski
zeru. Natomiast gdy napięcie bramka–podłoże zaczyna spadać po-
niżej 0 V, rezystancja również zaczyna spadać, a po przekroczeniu
pewnego napięcia progowego spada drastycznie (rys. 1).
Reasumując, tranzystor MOS z kanałem wzbogaconym działa na-
stępująco: kiedy napięcie bramka–podłoże jest równe 0 V, tranzystor na wyjściu
ma bardzo dużą rezystancję. Zatem gdy przyłożysz napięcie źródło–dren prąd bę-
dzie bliski zeru. W tranzystorze z kanałem typu N włączenie następuje po poda-
niu dodatniego napięcia bramka–podłoże, większego od napięcia progowego. Na-
tomiast w tranzystorze z kanałem typu P włączenie następuje po podaniu ujem-
nego napięcia, mniejszego od napięcia progowego. Włącznie tranzystora oznacza,
że rezystancja wyjściowa jest bardzo mała i po przyłożeniu napięcia dren–źródło
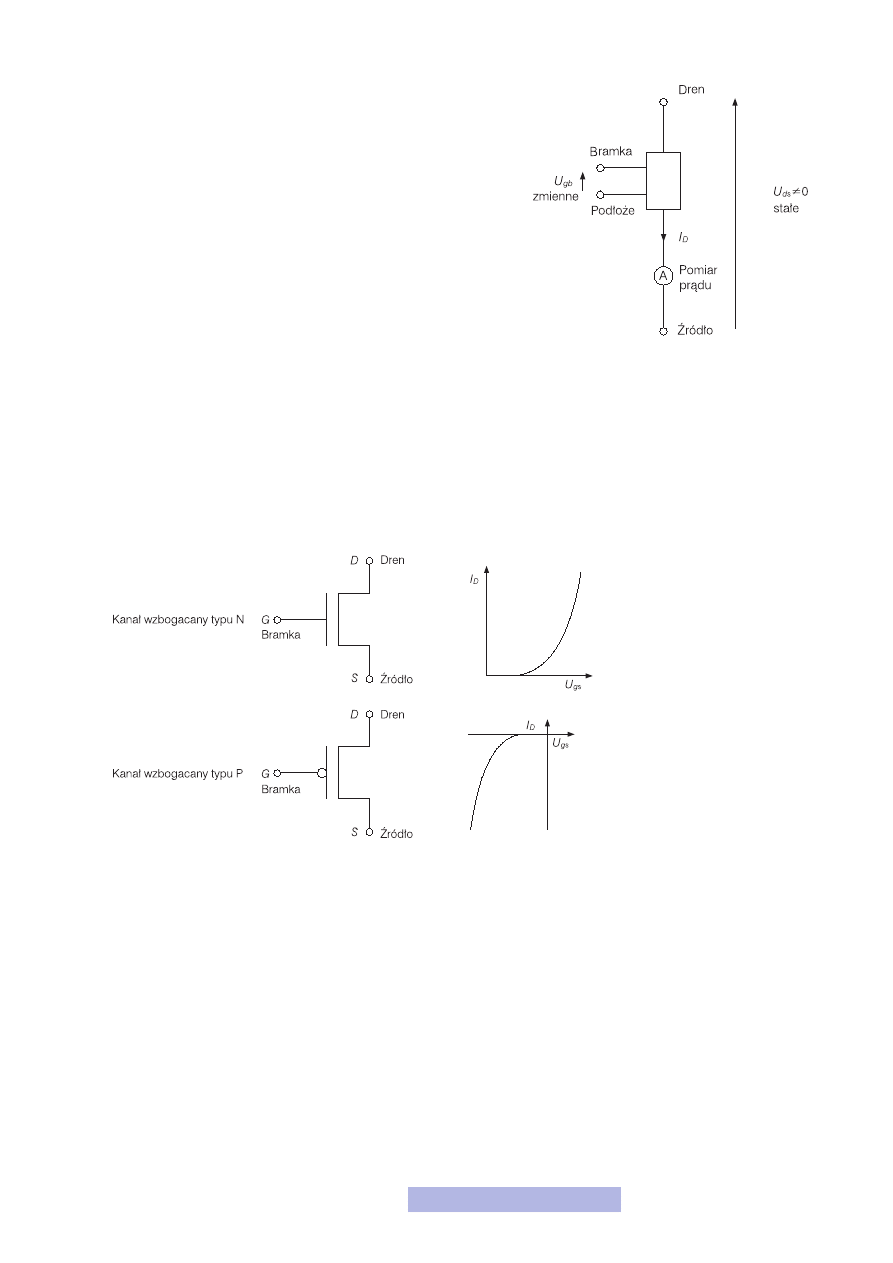
prąd może swobodnie płynąć. Symbole tranzystorów MOS zostały przedstawione
na rysunku 3.
Przyglądając się przedstawionym symbolom na pewno od razu zapytasz, co się sta-
ło z elektrodą podłoża, czemu jej nie ma? W praktyce w tranzystorach z kanałem
typu N jest ona podłączona do masy układu, a więc potencjału zerowego, nato-
miast w tranzystorach z kanałem typu P jest podłączona do zasilania, a więc po-
tencjału dodatniego. W tranzystorze z kanałem typu N sprawa jest oczywista, po-
nieważ gdy na bramkę podamy zerowy potencjał, to napięcie bramka–podłoże jest
również równe 0 V, a więc tranzystor nie przewodzi. Gdy podamy potencjał dodat-
ni, to napięcie bramka–podłoże będzie dodatnie i tranzystor będzie przewodził.
Natomiast w tranzystorze z kanałem typu P musimy jakoś wytworzyć napięcie
ujemne z dodatniego. Układ cyfrowy jest najczęściej zasilany stałym napięciem do-
datnim i napięcie ujemne trzeba wytworzyć sztucznie. Jeśli elektroda podłoża jest
podłączona do napięcia zasilania i na bramkę podamy potencjał zerowy, to oka-
zuje się, że napięcie bramka–podłoże jest ujemne (zero minus dodatni potencjał
daje ujemne napięcie), a więc tranzystor jest włączony. Gdy natomiast potencjał na
Rysunek 2
Sposób otrzymania
charakterystyki przejściowej
tranzystora MOS
Rysunek 3
Symbole tranzystorów MOS
5
bramce będzie równy zasilaniu, to napięcie bramka–podłoże będzie równe zero,
a więc tranzystor będzie wyłączony — czyli odwrotnie jak przy kanale N. Tutaj
przy zerze na bramce tranzystor przewodzi, a przy dodatnim potencjale nie. I, jak
zobaczysz, stanowi to sedno działania wszystkich układów cyfrowych.
W związku z tranzystorami MOS chciałbym poruszyć jeszcze dwie istotne kwestie.
Po pierwsze, rezystancja wejściowa, czyli rezystancja między bramką a podłożem,
jest ogromna, tak więc prąd przez elektrodę bramki nie płynie. Drugim bardzo
ważnym faktem jest to, że wartość napięcia sterującego (bramka–podłoże) jest z ta-
kiego samego zakresu jak napięcia na wyjściu (dren–źródło). Jak przekonasz się już
niedługo, fakty te będą miały ogromne znaczenie w układach cyfrowych.
Na koniec chciałbym krótko powiedzieć o tranzystorach MOS z kanałem zubożo-
nym. Nie będziemy z nich korzystać, ale dobrze, żebyś wiedział czym różnią się one
od pozostałych typów tranzystorów. Podstawowa różnica jest taka, że tranzystory
te przewodzą przy zerowym napięciu sterującym (bramka–podłoże). Jakie są tego
konsekwencje? Weźmy tranzystor z kanałem typu N — żeby go wyłączyć, trzeba
podać napięcie ujemne, natomiast aby go „bardziej otworzyć” dodatnie, analogicz-
nie dla tranzystora z kanałem typu P. Sterowanie tymi tranzystorami nie jest łatwe,
ponieważ trzeba zmieniać napięcia sterujące od ujemnych do dodatnich, a to jest
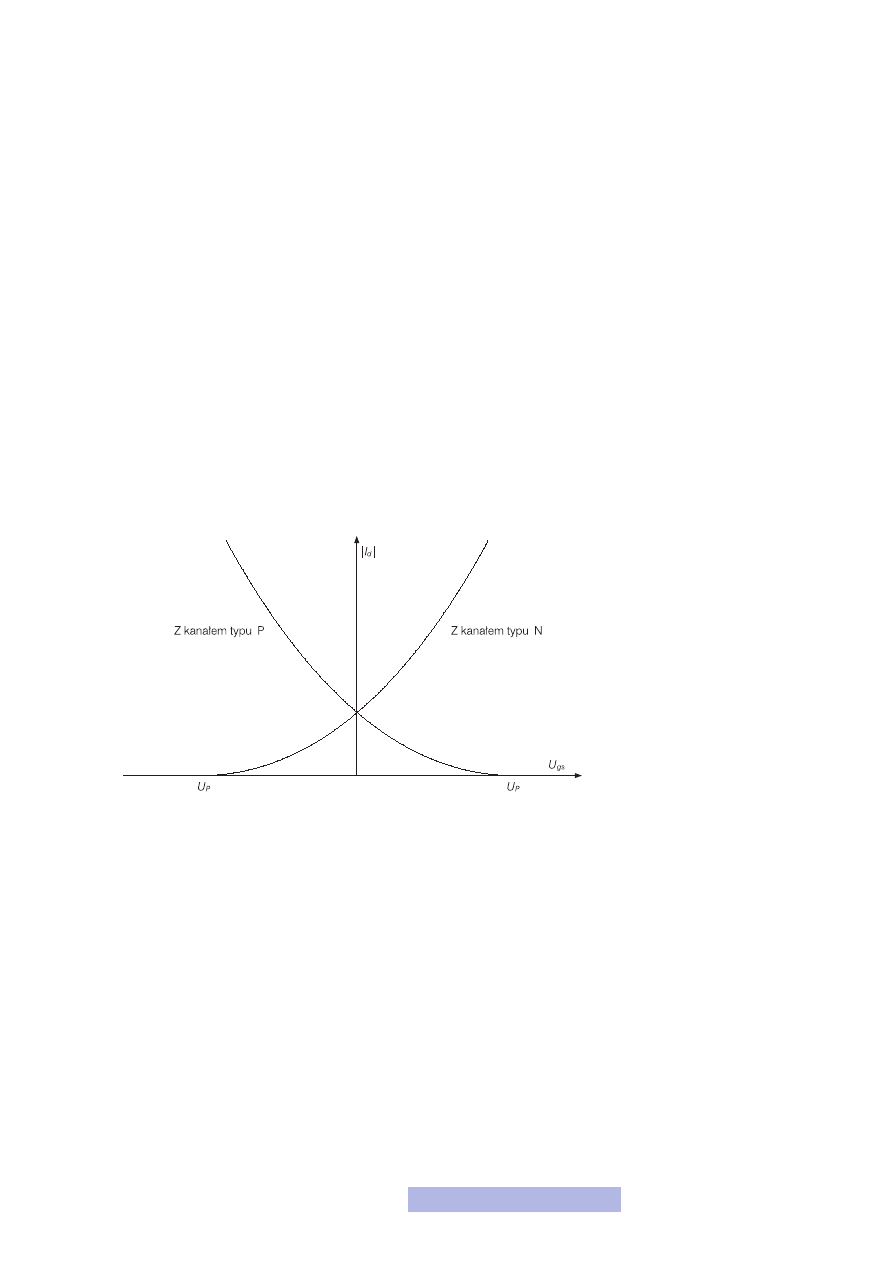
skomplikowane z praktycznego punktu widzenia. Na rysunku 4 przedstawiona zo-
stała charakterystyka przejściowa tranzystora MOS z kanałem zubożonym, którą
porównaj z charakterystyką tranzystora z kanałem wzbogaconym (rys. 1).
Rysunek 4
Charakterystyka przejściowa
tranzystora z kanałem
zubożonym

6
2. Matematyczne podstawy
elektroniki cyfrowej
Do tej pory poznałeś najważniejsze pojęcia związane z elektrycznością i podstawo-
we elementy stosowane w elektronice. Za ich pomocą tworzyłeś nawet proste ukła-
dy elektroniczne. I to jest już wystarczająca wiedza z dziedziny elektroniki, aby
zacząć mówić o tym, co nas najbardziej interesuje, a więc o układach elektroniki
cyfrowej. Jednak do pełni szczęścia brakuje nam jeszcze wiedzy z... matematyki.
Elektronika cyfrowa — jak już sama nazwa wskazuje — opiera się bardzo mocno
na matematyce (oczywiście nie na całej matematyce, tylko na jednym z jej działów,
a mianowicie logice matematycznej). Zanim zaczniemy budować układy cyfrowe,
musimy przypomnieć sobie potrzebne elementy logiki matematycznej, a następnie
wykazać ich związek z elektroniką.
2.1. Podstawy logiki matematycznej
Logika matematyczna opiera się na przypisaniu dowolnemu zdaniu jednego z dwóch
stanów, a mianowicie prawdy lub fałszu. Dla naszej wygody oznaczmy prawdę jako
1, a fałsz jako 0. Logika zajmuje się wyłącznie zadaniami, którym można przypisać
taką wartość, np.:
1. Warszawa leży nad Wisłą.
2. Leonardo da Vinci odkrył Amerykę.
3. Britney Spears jest ładną kobietą.
Zadanie 1 jest oczywiście prawdziwe, a jego wartość logiczna wynosi 1. Zdanie 2
jest fałszywe, a więc ma wartość 0. Natomiast wartości zdania 3 nie można stwier-
dzić, ponieważ niektórym Britney Spears podoba się, a innym nie. Logika nie zaj-
muje się zdaniami, których wartości nie można ocenić.
Na zdaniach można wykonywać operacje logiczne — np. łączyć je ze sobą. Naj-
prostszą operacją jest negacja, która zmienia wartość logiczną zadania na przeciw-
ną, a więc z prawdziwego robi nieprawdziwe, natomiast z nieprawdziwego praw-
dziwe, np.:
1. Warszawa nie leży nad Wisłą.
2. Leonardo da Vinci nie odkrył Ameryki.
Często dla zdań tworzy się tzw. tabele prawdy, mówiąca o tym jaka jest wartość lo-
giczna przed operacją i po niej. Dla negacji tabela prawdy jest bardzo prosta:
p
~p
0
1
1
0
Jak taką tabelkę odczytywać? Jeśli np. weźmiesz zdanie o wartości logicznej rów-
niej 0 i zanegujesz je, to zanegowane zadanie będzie miało wartość logiczną 1, czy-
7
li, mówiąc inaczej, jeśli było nieprawdziwe, to po zanegowaniu będzie prawdzi-
we. Negację oznacza się najczęściej symbolem tyldy (~) i często nazywa operacją
NOT.
Jak już wspomniałem, zdania można ze sobą łączyć i to za pomocą różnych spój-
ników, np.:
1. Warszawa leży nad Wisła i Leonardo da Vinci odkrył Amerykę.
2. Warszawa nie leży nad Wisła lub Leonardo da Vinci nie odkrył Ameryki.
Oczywiście zdania takie nie zawsze są zrozumiałe, lecz my w tej chwili nie będzie-
my zajmować się ich sensem logicznym. Zastanówmy się nad prawdziwością po-
wyższych zdań. Pierwsze zadanie składa się z dwóch części — pierwszej prawdzi-
wej, drugiej fałszywej — połączonych spójnikiem „i”. Intuicyjnie czujesz, że spój-
nik „i” oznacza, że zadanie będzie poprawne, gdy pierwszy i drugi człon będzie
prawdziwy, a w pozostałych przypadkach zadanie będzie fałszywe. I słusznie, po-
nieważ tak właśnie będzie! Operacja połączenia zdań spójnikiem „i” nazywana jest
koniunkcją (iloczynem) zdań i oznaczana jest najczęściej symbolem mnożenia (·).
Często będziemy również nazywali ją operacją AND. Tabela prawdy dla tej opera-
cji jest następująca:
p
q
p · q
0
0
0
0
1
0
1
0
0
1
1
1
Jak tę tabelkę rozumieć? Otóż, jeśli weźmiesz dwa zdania oznaczone jako p i q,
z których np. p prawdziwe, a q nieprawdziwe, to po połączeniu spójnikiem „i”
otrzymasz zdanie p · q, które będzie nieprawdziwe.
W przypadku spójnika „lub” wystarczy, aby choć jeden z członów był prawdziwy
i całe zdanie będzie prawdziwe. Tak więc podane powyżej zdanie 2 jest oczywi-
ście prawdziwe. Operacja połączenia zdań spójnikiem „lub” nazywa się alternatywą
(sumą) zdań i oznacza się ją najczęściej symbolem dodawania (+). Operację tę często
będziemy również nazywali OR. Tabela prawdy dla tej operacji jest następująca:
p
q
p + q
0
0
0
0
1
1
1
0
1
1
1
1
Operacji logicznego łączenia można oczywiście wymyślać wiele, np.:
p
q
p q
p
q
p ⊗ q
0
0
1
0
0
0
0
1
1
0
1
1
1
0
1
1
0
1
1
1
0
1
1
0
Pierwsza z tych operacji to tzw. NAND — jest to dokładnie odwrócony AND. Na-
tomiast druga tabela to tzw. XOR, czyli kontrola parzystości. Operacje te podałem
nieprzypadkowo — proponuje je zapamiętać, ponieważ wrócimy do nich.

8
Póki co wykonywaliśmy operację łączenia dwóch zdań jednym spójnikiem, lecz nic
nie stoi na przeszkodzie, aby połączyć większą liczbę zadań i to różnymi spójnika-
mi, np.: Warszawa leży nad Wisłą lub Leonardo da Vinci odkrył Amerykę i PUW
to nie jest skrót od Polski Uniwersytet Wirtualny.
Czy to zdanie jest poprawne? Gdyby zapisać je w postaci symbolicznej, wygląda-
łoby ono następująco:
p + q · ~r
Najpierw należy ustalić kolejność wykonywania operacji. Naturalnie, tak jak przy
działaniach arytmetycznych, najpierw wykonuje się funkcję negacji, następnie ilo-
czyn, a na koniec sumę logiczną. Zatem zdanie r — PUW to jest skrót od Polski
Uniwersytet Wirtualny — jest prawdziwe, a jego zaprzeczenie ~r nieprawdziwe.
Następnie zadanie q — Leonardo da Vinci odkrył Amerykę — jest nieprawdziwe,
czyli iloczyn dwóch zadań nieprawdziwych jest nieprawdziwy. Na koniec wyko-
nujemy sumę. Zdanie p — Warszawa leży nad Wisła — jest prawdziwe, suma zda-
nia prawdziwego i nieprawdziwego jest prawdziwa. Ostatecznie powyższe zdanie,
choć nie ma większego sensu językowego, to w świetle praw logiki matematycznej
jest prawdziwe.
W ten sposób doszliśmy do najważniejszego dla nas pojęcia, a mianowicie formuły
logicznej, czyli zadania zbudowanego z wielu zdań, których wartość logiczną po-
trafimy określić, połączonych różnymi spójnikami. Z takich formuł będziesz ko-
rzystał już do końca kursu, będziesz je tworzył, a następnie implementował w ukła-
dzie scalonym. Ale zanim do tego dojdziemy, musimy dowiedzieć się, jakie najważ-
niejsze prawa rządzą tymi formułami i jak się je tworzy.
2.2. Podstawowe prawa logiki matematycznej
Istnieje ogromna liczba praw logiki matematycznej. Chciałbym jednak przedstawić
tylko te najważniejsze, z których będziemy korzystać, resztę można znaleźć w lite-
raturze. W poniższych prawach symbol ⇔ oznacza równoważność, tzn. to, co stoi
po lewej stronie symbolu jest równoważnego temu, co po prawej.
Prawo podwójnego przeczenia:
~(~p) ⇔ p
Własności wartości stałych:
p · 1 ⇔ p p · 0 ⇔ 0
p + 1 ⇔ 1 p + 0 ⇔ p
~0 ⇔ 1 ~1 ⇔ 0
Prawa idempotentności:
p + p ⇔ p p · p ⇔ p
Prawo wyłączonego środka:
p + ~p ⇔ 1

9
Prawo sprzeczności:
p · ~p ⇔ 0
Prawa rozdzielności:
p + (q · r) ⇔ (p + q) · (p + r)
p · (q + r) ⇔ (p · q) + (p · r)
Prawa de Morgana:
~(p + q) ⇔ ~p · ~q
~(p · q) ⇔ ~p + ~q
Zapewne zastanawiasz się, skąd biorą się te prawa. Otóż większość z nich jest dość
intuicyjna, np. jeśli dwa razy zaprzeczysz jakiemuś zadaniu, to otrzymasz to zda-
nie
, a przy prawach
z wartościami stałymi wystarczy spojrzeć na tabelkę prawdy i już
wszystko wiadomo. Natomiast nie zawsze od razu widać, skąd się to prawo wzięło
i czy jest poprawne. Wówczas niezawodną, choć żmudną metodą jest sprawdzenie
wszystkich możliwości — czy wartości po lewej i po prawej stronie się zgadzają.
Pokaże tę metodę na przekładzie prawa wyłączonego środka:
p
~p
p + ~p
0
1
1
1
0
1
Jak widać, nieważne, czy weźmiemy zdanie p prawdziwe czy nie — p + ~p jest za-
wsze prawdziwe.
Znamy już najważniejsze prawa logiki matematycznej, przejdźmy więc do tworze-
nia formuł zdaniowych oraz ich minimalizacji.
2.3. Tworzenie formuł zdaniowych oraz ich minimalizacja
Wspomniałem wcześniej tylko o trzech operacjach logicznych: NOT, AND i OR.
Okazuje się, że jest to tzw.
układ zupełny
, tzn. każdą funkcję logiczną czy formułę
zdaniową można zapisać za pomocą właśnie tych trzech operacji. Przykładem może
być np. podana funkcja XOR — można ją zapisać za pomocą NOT, AND, OR na-
stępująco:
p ⊗ q ⇔ p · (~q) + (~p) · q.
W ramach ćwiczeń sprawdź, że tak właśnie jest. Na pewno powiesz, że to prosty
przykład, nietrudno było to wydedukować na podstawie powyższych praw i tabel
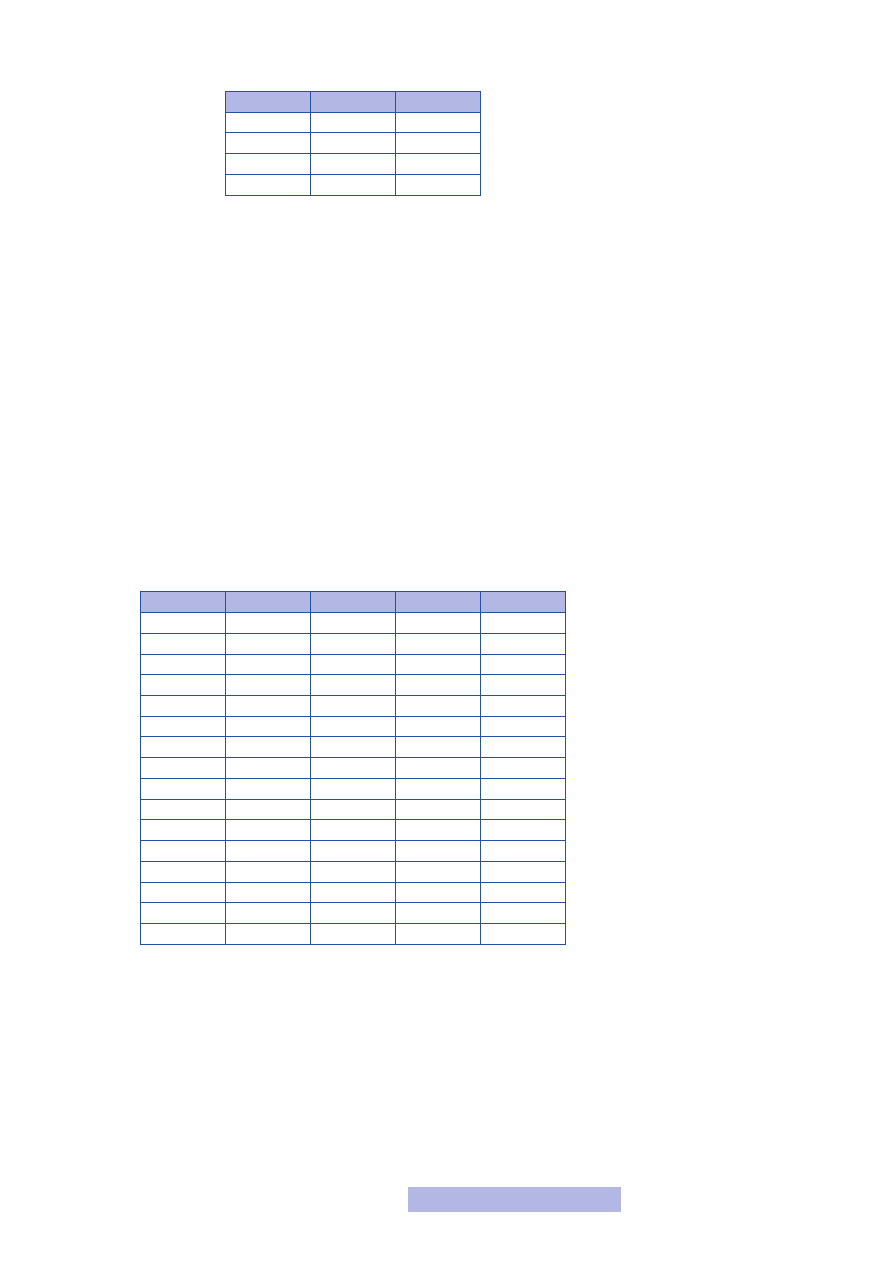
prawdy. ale jeśli wymyślę sobie jakąś operację p ? q o tabeli prawdy:
10
p
q
p ? q
0
0
1
0
1
0
1
0
1
1
1
0
to jak ją zapisać za pomocy tych trzech operacji?
Nic prostszego! Oto sposób:
1. Patrzysz, gdzie wynikiem operacji jest prawda, czyli 1. W naszym przypadku jest
to pierwsza i trzecia linijka.
2. Następnie patrzysz kolejno na te linijki i sprawdzasz, czy p i q było w nich praw-
dą, czy nie. Jeśli było prawdą, to zapisujesz to zdanie bez zmian, jeśli niepraw-
dą — negujesz je. Następnie zapisujesz wszystko w postaci iloczynu. W naszym
przypadku mamy: dla pierwszej linijki: p jest 0, q jest 0, a więc: (~p) · (~q); dla
trzeciej linijki: p jest 1, q jest 0, a więc: p · (~q).
3. Uzyskane w ten sposób iloczyny sumujesz i otrzymujesz poszukiwaną formułę.
W naszym przypadku ostatecznie otrzymujemy: p ? q ⇔ (~p) · (~q) + p · (~q).
Musisz obiektywnie przyznać, że to prosty sposób. Koniecznie sprawdź, czy uzy-
skana formuła jest prawidłowa i czy zgadza się z powyższą tabelą prawdy!
Oczywiście mieliśmy tutaj tylko dwa zdania składowe: p i q, a co zrobić, gdy zdań
jest więcej, np. cztery? To samo! Oto przykład wymyślonej, całkowicie przypadko-
wej tabeli prawdy dla czterech zdań: p, q, r, s:
p
q
r
s
Wynik
0
0
0
0
0
0
0
0
1
1
0
0
1
0
0
0
0
1
1
0
0
1
0
0
1
0
1
0
1
1
0
1
1
0
0
0
1
1
1
0
1
0
0
0
0
1
0
0
1
0
1
0
1
0
1
1
0
1
1
0
1
1
0
0
1
1
1
0
1
1
1
1
1
0
1
1
1
1
1
1
Wygląda groźnie, ale to tylko pozory. Stosując opisany już algorytm, uzyskujemy
następującą formułę:
(~p) · (~q) · (~r) · s + (~p) · q · (~r) · (~s) + (~p) · q · (~r) · s + p · (~q) · r · (~s)
+ p · q · (~r) · (~s) + p · q · (~r) · s + p · q · r · (~s) +p · q · r · s.
Sprawdź, czy jest ona poprawna! Jeśli się nie pomyliłem, to jest. Zapewne zastana-
wiasz się, czy nie dałoby się jej uprościć. I w ten sposób dochodzimy do drugiego
ważnego zagadnienia tego podtematu. Potrafimy już stworzyć dowolną, nawet naj-

11
bardziej wymyślną formułę zdaniową, ale nadal nie wiemy, czy jest ona najprost-
sza. To bardzo ważne zagadnienie! Redukcja choć jednego składnika (a co dopiero
połowy) w tej formule, to nie tylko prostsze wyrażenie, ale i — w momencie im-
plementacji formuły do układu scalonego — ogromna oszczędność elementów, co
się dalej przekłada na szybkość działania układu oraz jego koszt. A każdy przecież
chce mieć jak najtańszy i jak najszybszy procesor.
Weźmy drugi i trzeci składnik sumy:
(~p) · q · (~r) · (~s) + (~p) · q · (~r) · s.
Korzystając z prawa rozdzielności, otrzymujemy:
(~p) · q · (~r) · (s + ~s).
A teraz korzystając z prawa wyłączonego środka, otrzymujemy:
(~p) · q · (~r) · 1.
I na mocy własności stałych:
(~p) · q · (~r),
czyli ostatecznie:
(~p) · q · (~r) · (~s) + (~p) · q · (~r) · s ⇔ (~p) · q · (~r).
A więc nie dość, że udało się zredukować jeden składnik sumy, to jeszcze czynnik
w iloczynie. Ale to nie wszystko! Przyjrzyjmy się teraz ostatnim czterem składni-
kom sumy. Stosując kolejno prawa rozdzielności, wyłączonego środka i własności
stałych, otrzymujemy:
p · q · (~r) · (~s) + p · q · (~r) · s + p · q · r · (~s) +p · q · r · s ⇔ p · q · (~r) · (~s + s)
+ p · q · r · (~s + s) ⇔ p · q · (~r) + p · q · r ⇔ p · q · (~r + r) ⇔ p · q.
Musisz przyznać, że zredukowanie czterech składników do jednego iloczynu to
już ogromna oszczędność! Nasza formuła zadaniowa mieści się już w jednej linijce
i nadal realizuje to, co chcemy:
(~p) · (~q) · (~r) · s + (~p) · q · (~r) + p · (~q) · r · (~s) + p · q.
Ogromne uproszczenie! A może da się ją jeszcze bardziej uprościć? Ja nie widzę
już więcej możliwości, ale mogę się mylić. Trzeba się teraz zastanowić, czy istnie-
je jakaś „algorytmiczna” metoda upraszczania — taka, żeby nawet osoba mało
spostrzegawcza mogła uzyskać jak najprostszą formułę zdaniową. Oczywiście, że
istnieje i to nie jedna. Nikt raczej nie „bawi się” w ręczną minimalizację formuł
— są do tego specjalne programy. Trudno byłoby ręcznie minimalizować formu-
łę składającą się nawet z 8 zdań (a to oznacza kilkadziesiąt składników w sumie!),
a w normalnych projektach mikroelektronicznych tych zdań może być nawet kilka-
dziesiąt (co daje nawet kilkaset tysięcy składników w sumie).
Warto jednak znać również „ręczne” metody minimalizacji prostych formuł. Jedną
z takich metod jest tzw. siatka Karnaugh. Polega ona w wypełnieniu pewnej tabelki
(siatki) i graficznym sklejaniu sąsiadujących ze sobą pól z jedynkami. Dzięki naszej
spostrzegawczości zminimalizowaliśmy powyżej formułę zdaniową. Wykonajmy
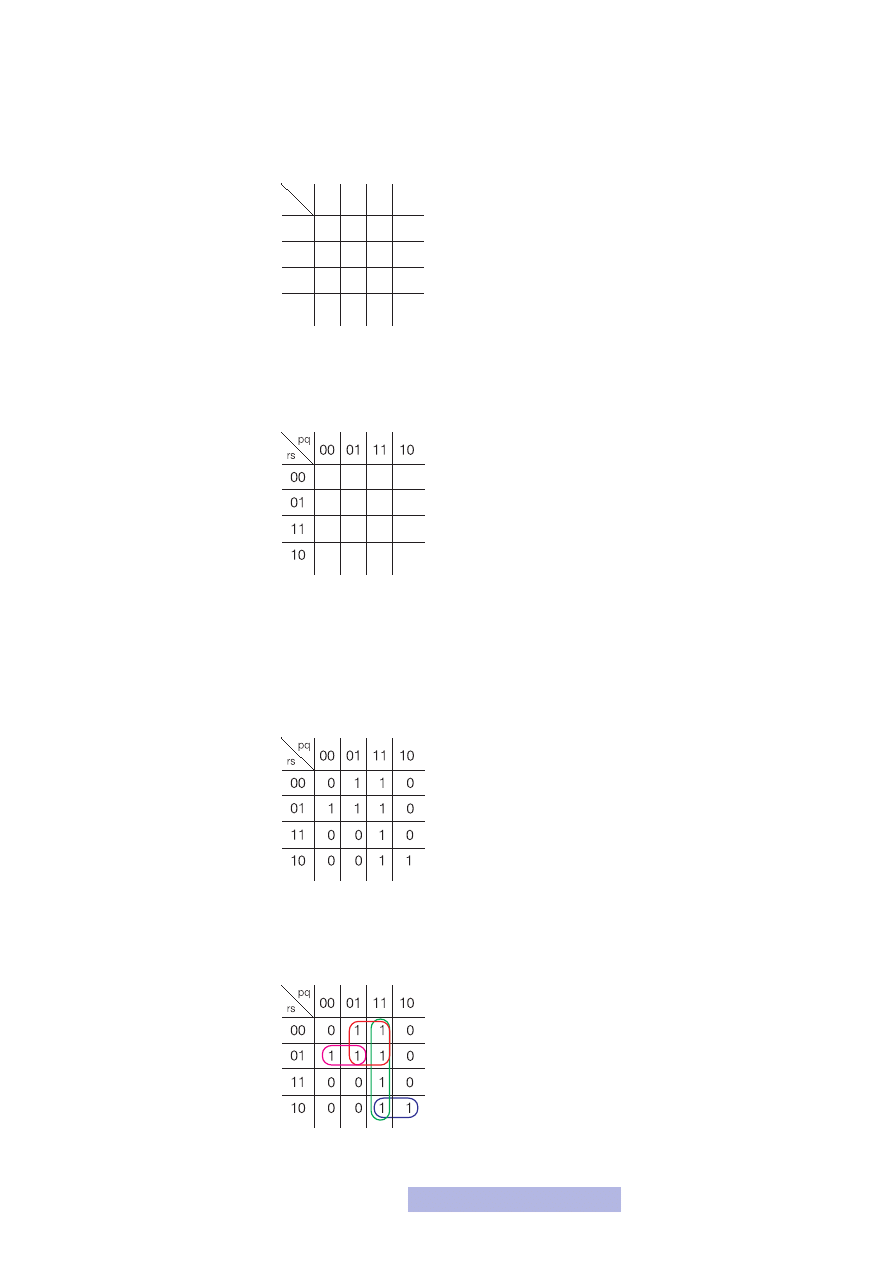
12
teraz jej minimalizację, posługując się algorytmem. W szczegółach dla czterozda-
niowej formuły wygląda to następująco:
1. Tworzysz tabelkę o wymiarach 4 na 4 (gdyby zdań tworzących formułę było 5,
to tabelka miałaby wymiar 8 na 4, dla 6 — 8 na 8 itd.):
2. Wybierasz dwa zdania i umieszczasz je w poziomie, dwa pozostałe w pionie.
Etykiety poszczególnych kolumn wypełniasz w pionie i poziomie tzw. kodem
Graya (00, 01, 11, 10):
3. Wybierasz pole, które chcesz wypełnić. Patrzysz, jakie są wartości zdań p, q, r
oraz s, odszukujesz taką kombinację w tabeli prawdy i wpisujesz ją w to pole.
W naszym przypadku wypełnimy np. pole leżące na przecięciu trzeciego wiersza
i drugiej kolumny. Dla tego pola p = 0, q = 1, r = 1, s = 1. formuła zdaniowa
dla tych wartości jest nieprawdziwa, a więc w to pole wpisujemy 0. I tak wypeł-
niamy całą tabelkę.
4. Minimalizujemy, a więc sklejamy sąsiadujące jedynki. Sklejamy wyłącznie pola,
w których jedynki są sklejone całymi ścianami lub znajdują się po przeciwległych
stronach tabeli. Sklejamy wszystko co się da!
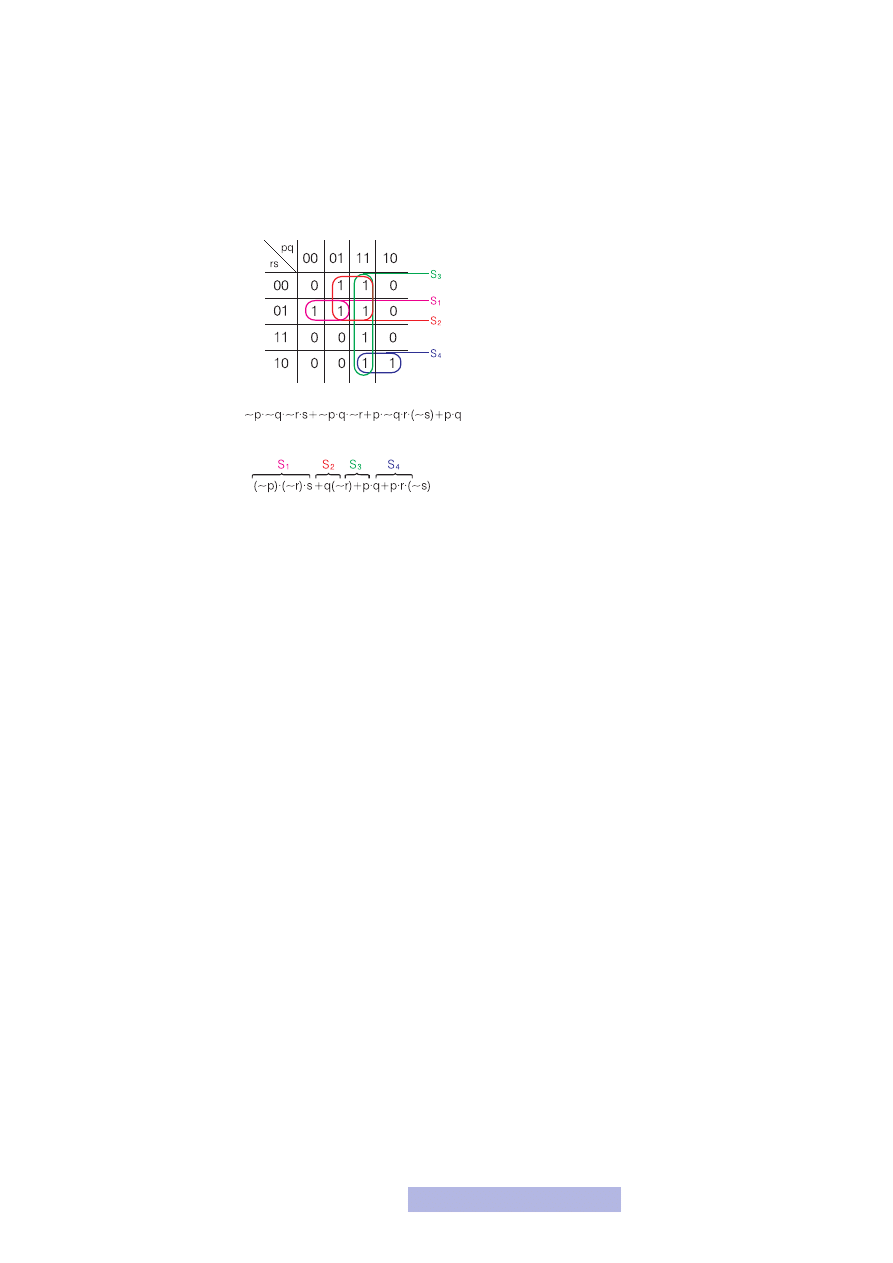
13
5. Na koniec pozostaje zapisanie wyniku. Wynik jest zapisywany w postaci sumy
pewnych iloczynów. Kolejne iloczyny tworzymy według zasady: jeśli jedynka
nie jest sklejona z żadną inną jedynką, to wpisujemy do sumy — podobnie jak
poprzednio — iloczyn, tzn. patrzymy, czy przy zdaniach jest zero, czy jedynka
i wpisujemy z negacją lub nie. Jeśli jedynki są sklejone, patrzymy, które zdanie
(zdania) powtarza się w sklejeniu z różnymi wartościami (!) i eliminujemy je, za-
pisując wyłącznie te, których wartość w takim sklejeniu jest stała.
A więc nasza spostrzegawczość zawiodła! Jak widzisz, formułę można było jeszcze
bardziej zminimalizować.
Na koniec chciałbym powiedzieć o jeszcze jednej bardzo praktycznej rzeczy. Na po-
czątku wspomniałem o tym, iż spójniki zdaniowe NOT, AND i OR tworzą układ
zupełny, czyli, że za ich pomocą można wygenerować dowolną formułę zdaniową.
Okazuje się, że podobny układ tworzy sam NAND. A więc za pomocą tego jednego
spójnika można wygenerować każdą formułę zdaniową. Brzmi nieprawdopodob-
nie, ale tak jest. Spróbuj samodzielnie to uzasadnić. Czemu o tym mówię? Otóż
w praktyce właśnie najczęściej za pomocą spójnika NAND realizuje się formuły
zdaniowe. Jednak z punktu widzenia dydaktycznego łatwiej i przejrzyściej tworzyć
ją w oparciu o NOT, AND i OR i my tak będziemy postępować (choć tam, gdzie
będzie to możliwe, pokażę jak realizować to za pomocą spójnika NAND).
2.4. System binarny
Ostatnią rzeczą, o której należy wspomnieć, aby mówić o elektronice cyfrowej, jest
dwójkowy system liczenia.
Każdą liczbę w systemie dziesiątkowym można zapisać następująco:
,
10
10
10
10
10
0
0
1
1
2
2
1
1
a
a
a
a
a
n
n
n
n
gdzie a
1
, ..., a
n
to kolejne cyfry (z zakresu od 0 do 9) liczby, a 10 to podstawa sys-
temu, na przykład:
.
10
7
10
5
10
3
357
0
1
2

14
Uogólniając, podstawą może być dowolna liczba naturalna większa bądź równa 1,
natomiast cyfry są z zakresu od 0 do (podstawa – 1). Czemu więc nie wziąć naj-
mniejszej możliwej podstawy, a więc 2? Wówczas cyframi w liczbie mogą być 0
lub 1. Zatem liczbę zapisuje się w postaci ciągu 0 i 1, np.: 10011
(2)
(ta mała dwójka
w nawiasie oznacza, że liczba jest zapisana w systemie dwójkowym) i przedstawia
w systemie dziesiątkowym następująco:
.
19
1
2
16
2
1
2
1
2
0
2
0
2
1
10011
0
1
2
3
4
2
Zamiana w drugą stronę jest też bardzo prosta, ponieważ każdą liczbę zapisaną
w systemie dziesiątkowym można zapisać dwójkowo, np.:
.
11011
27
2
.
I oto cała wiedza matematyczna, potrzebna do zrozumienia podstaw elektroniki
cyfrowej. Zalecam, abyś wykonał wszystkie zaproponowane powyżej ćwiczenia
oraz dołączone zadania, gdyż przedstawioną tu wiedzę będziemy w dalszej części
kursu dość mocno eksploatować i musisz się nią biegle posługiwać.
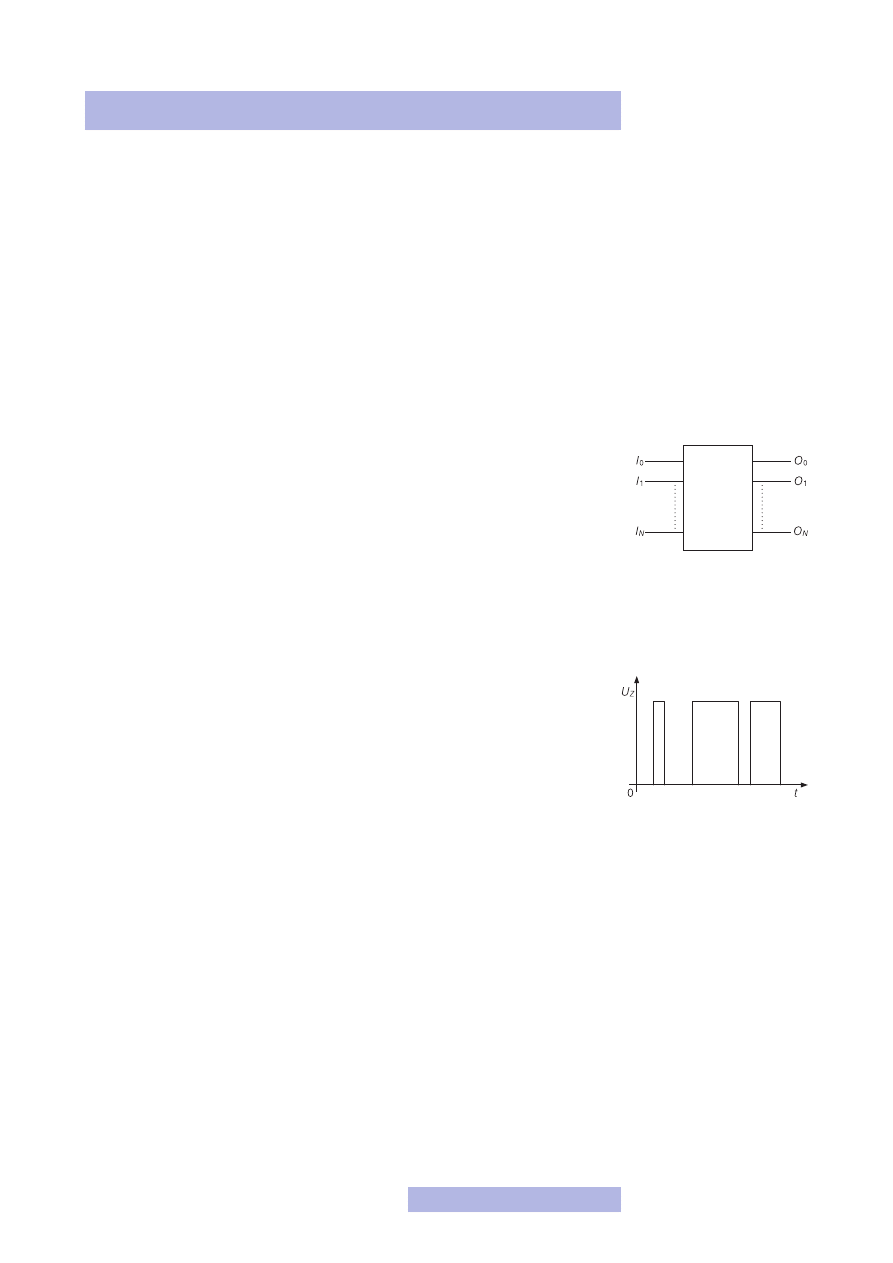
15
3. Podstawy elektroniki cyfrowej
Posiadasz już wystarczającą wiedzę, aby zająć się elementami elektroniki cyfrowej.
I temu właśnie poświęcimy niniejszy temat. Dowiesz się z niego, co to są układy
cyfrowe i do czego służą. Następnie poznasz zasady ich budowy, a na koniec zoba-
czysz, jak budować je za pomocą poznanych elementów elektronicznych. Myślę, że
to najważniejszy temat całego kursu, ale jednocześnie najciekawszy.
3.1. Idea układów cyfrowych
Najpierw odpowiedzmy sobie na pytanie, co to są właściwie układy cyfrowe i cze-
mu są takie ważne. Najprościej mówiąc, są to układy przetwarzające sygnały cyfro-
we (na wejściu i na wyjściu układu mamy sygnały cyfrowe — rys. 5).
Pozostaje wyjaśnić tylko kwestię, co to jest sygnały cyfrowy. Otóż jest to najczę-
ściej napięcie, które przyjmuje tylko dwie wybrane wartości — zero albo napięcie
zasilania (rys. 6). Na każde z wejść układu podawane jest zero albo napięcie zasila-
nia, układ ten przetwarza sygnał i na wyjściu również otrzymujemy sygnał cyfro-
wy, czyli każde z wyjść jest ustawione na zero bądź na napięcie zasilania. W ukła-
dach analogowych, np. w dzielniku napięciowym, podawane napięcie było z jakie-
goś zakresu i każda wartość z tego zakresu była przetworzona, natomiast w ukła-
dach cyfrowych wyróżnione są tylko i wyłącznie dwa stany i żadne inne nie są
przyjmowane.
Chyba dość dobrze widoczna jest w tym momencie analogia do logiki matema-
tycznej. Tam również były dwa stany: prawa i fałsz (oznaczane jako 0 i 1) i każde
ze zdań mogło przyjmować jeden z nich. W układach cyfrowych również mamy
dwa stany: wysokiego i niskiego napięcia (również oznaczane 0 i 1) i każde z wejść
i wyjść układu może jeden z tych dwóch stanów przyjąć.
Ostatnią kwestią wymagającą wyjaśnienia jest interpretacja tych zerojedynkowych
sygnałów. Pod koniec poprzedniego tematu pokazałem, że każdą liczbę można za-
pisać w postaci dwójkowej. Skoro tak, to wejścia i wyjścia układu można potrakto-
wać po prostu jako liczby. Tak więc można powiedzieć, że na wejście podaje się ja-
kąś liczbę i na wyjściu jakąś liczbę otrzymuje się. Oczywiście interpretacja jest do-
wolna, co zresztą za chwilę pokażę na kilku przykładach układów cyfrowych.
3.2. Przykłady układów cyfrowych
Chciałbym teraz przedstawić przykłady układów cyfrowych, które pozwolą ci le-
piej zrozumieć przedstawioną powyżej ideę oraz samemu odpowiedzieć na pytanie,
czemu te układy są tak ważne.
Pierwszym przykładem będzie tzw. dekoder temperaturowy. Działa on następują-
co: na wejście układu podaj się pewną liczbę zapisaną w postaci dwójkowej i w za-
Rysunek 5
Idea układy cyfrowego
Rysunek 6
Sygnał cyfrowy
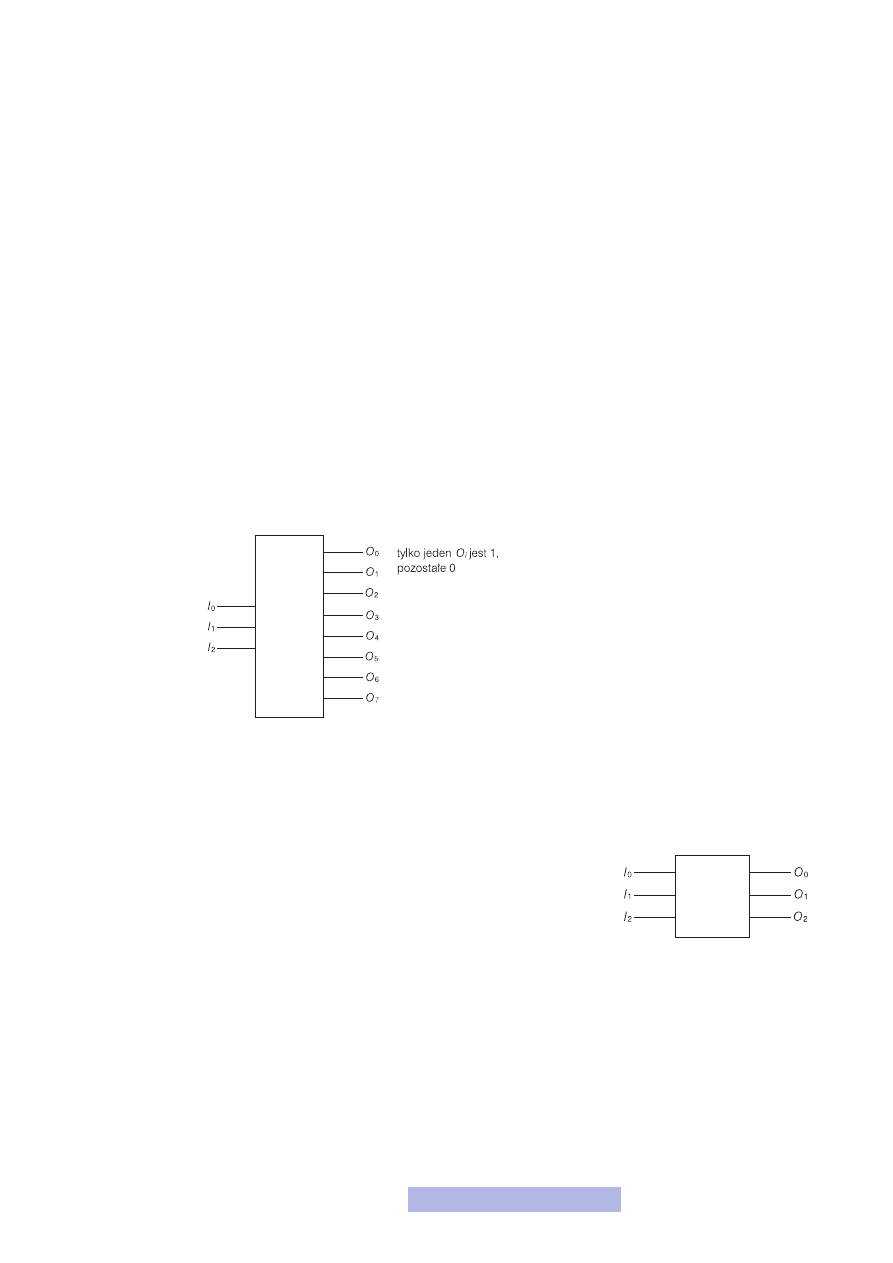
16
leżności od tej liczby ustawiane jest wyjście o odpowiednim numerze, czyli — mó-
wiąc precyzyjniej — na wyjściu o odpowiednim numerze pojawi się stan 1, a na
pozostałych 0. Jeśli zmienisz liczbę na wejściu, to zmieni się również wyjście, na
którym jest stan 1.
Rozważmy konkretny przypadek. Mamy dekoder o trzech wejściach. Za pomo-
cą trzech bitów możemy zapisać każdą liczbę z przedziału 0–7, ponieważ 0 to stan
000, natomiast 7 to stan 111, a np. 6 to 110. Zatem musi być osiem wyjść, ozna-
czonych O
0
, O
1
, ..., O
7
(od ang. Output). Oczywiście wejścia są oznaczone również
I
0
, I
1
, I
2
, gdyż podając np. liczbę 6, tzn. 110, musimy wiedzieć, gdzie podać jedyn-
ki, a gdzie zera. Najczęściej w takich przypadkach mówi się o bicie najmłodszym
i najstarszym — bit najmłodszy jest po prawej stronie liczby (czyli u nas 0), a naj-
starszy po lewej (czyli u nas 1). Bit najstarszy podaje się na najwyższe wejście (czyli
u nas I
2
), najmłodszy na I
0
, a pozostałe w kolejności. Z czasem nabierzesz wprawy
w używaniu tej terminologii. Tak więc podajesz na wejście liczbę 6, czyli I
0
= 0,
I
1
= 1, I
2
= 1 i na wyjściu otrzymujesz: O
0
= 0, O
1
= 0, O
2
= 0, O
3
= 0, O
4
= 0,
O
5
= 0, O
6
= 1, O
7
= 0.
Pewnie zastanawiasz się do czego może być potrzebny taki układ. Zastosowań jest
wiele, jednym z nich może być np. włącznik jednej wybranej żarówki. Wyobraź so-
bie, że masz osiem żarówek i chcesz włączać jedną wybraną. Podajesz więc jej nu-
mer i na wyjściu pojawi się 1, a więc stan wysokiego napięcia tylko przy wybranej
żarówce.
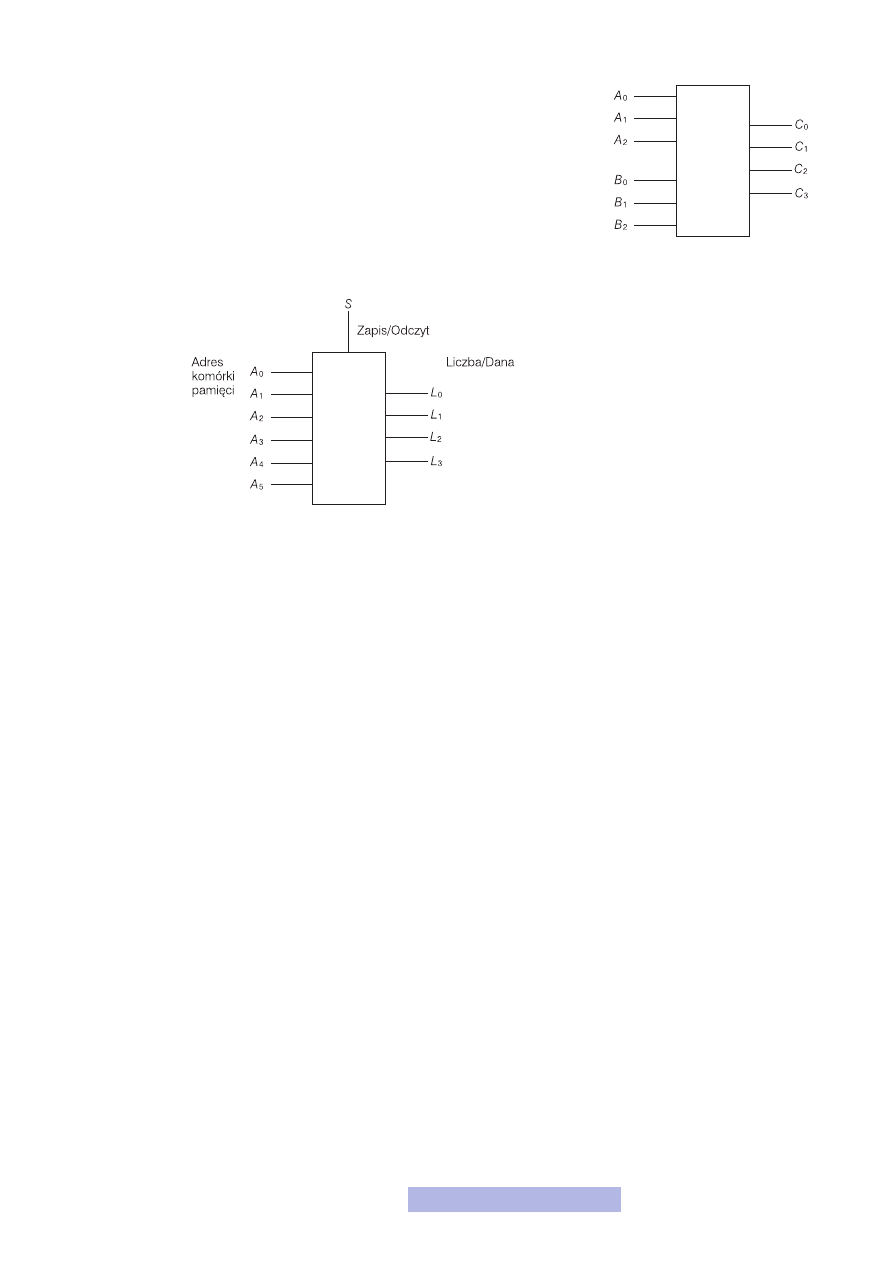
Drugim przykładem układu cyfrowego, może być układ kodujący (rys. 8). Na wej-
ście podajesz jakąś liczbę i na wyjściu otrzymujesz inną. Najprostszy 3-bitowy ko-
der na stałe przypisuje np. 0 — 6, 1 — 2, 2 — 7, 3 — 0, 4 — 1, 5 — 4, 6 — 3,
7 — 5. Podajesz pierwszą liczbę na wejście i otrzymujesz drugą. Zastosowania ta-
kiego kodera są chyba oczywiste.
Kolejnym przykładem może być sumator. Tym razem na wejście podajesz dwie
liczby, a na wyjściu uzyskujesz jedną. Przyjrzyjmy się sumatorowi trzybitowemu
— na wejście podajesz 6 bitów: A
2
A
1
A
0
i B
2
B
1
B
0
, gdzie A i B oznaczają dwie licz-
by, natomiast na wyjściu otrzymuje się wynik 4-bitowy: C
3
C
2
C
1
C
0
. Czemu 4-bito-
wy? Weźmy dwie liczby 3-bitowe, np. 2 (010) i 4 (100). Ich suma wynosi 6 (110),
więc liczba jest 3-bitowa. Jednak gdy weźmiemy np. 3 (011) i 6 (110), to w wyniku
otrzyma się 9 (1001), a więc już liczbę 4-bitową. Ten dodatkowy bit C
3
nazywany
jest często bitem przeniesienia.
Ostatnim przykładem układu cyfrowego będzie pamięć. Służy ona oczywiście do
przechowywania danych. Jako przykład weźmy 4-bitową pamięć o 32 komórkach,
a więc w tej pamięci można przechowywać liczby 4-bitowe (od 0 do 15) i może ich
być 32. Aby zapisać taką liczbę w pamięci należy podać ją na wejście oraz podać
miejsce (adres), gdzie ma się znaleźć. Odczyt z pamięci polega na podaniu miej-
sca (adresu), z którego ma zostać odczytana liczba. Ponieważ nigdy równocześnie
nie odczytujemy i nie zapisujemy danych do pamięci, więc do podawania adresu
Rysunek 7
Dekoder temperaturowy
Rysunek 8
Prosty koder
17
mogą służyć w przypadku odczytu i zapisu te same bity. Podobnie jest z dany-
mi — w trakcie zapisu na te same bity możemy podawać daną liczbę, natomiast
w czasie odczytu pojawi się na nich poszukiwana wartość. Mamy zatem 4 bity
L
3
L
2
L
1
L
0
(są to bity, na które podajemy, lub z których odczytujemy liczbę), 5
bitów adresu (liczba z zakresu od 0 do 31) A
4
A
3
A
2
A
1
A
0
oraz jeden bit sterujący
S, mówiący o tym, czy jest to zapis, czy odczyt. Ustalmy, że gdy na S jest 1, to
jest zapis, gdy 0, to odczyt. Jeśli chcesz zapisać liczbę do pamięci, to podajesz ją
na bity L
3
L
2
L
1
L
0
, a na bity A
4
A
3
A
2
A
1
A
0
jej adres, czyli miejsce, w którym ma się
znaleźć oraz ustawiasz bit S na 1. Kiedy chcesz odczytać liczbę z pamięci, poda-
jesz na A
4
A
3
A
2
A
1
A
0
jej adres, ustawiasz bit S na 0 i wynik pojawia się na L
3
L
2
L
1
L
0
.
Przykłady układów cyfrowych można mnożyć niemal w nieskończoność — jako
informatyk jesteś w stanie podać ich bardzo wiele, szczególnie układów znajdują-
cych się w komputerze.
3.3. Projektowanie układów cyfrowych
Chciałbym jeszcze na chwilę wrócić do podanych przykładów i zwrócić uwagę na
jedną bardzo ważną kwestię. Otóż w trzech pierwszych przykładach układów cy-
frowych to, co działo się na wyjściu było jednoznacznie zdeterminowane przez
wejście. W pierwszym przykładzie podawałeś na wejście liczbę i wiadomo było, co
otrzymasz na wyjściu, który bit będzie 1, a które 0. W drugim przykładzie liczba
na wejściu jednoznacznie określała liczbę na wyjściu, w trzecim natomiast suma
dwóch liczb również była jednoznacznie określona. W przypadku pamięci już tak
nie jest. Podajesz na wejście adres, ustawiasz bit sterujący na odczyt i otrzymasz
dane zapisane w komórce. Tak więc na podstawie samego adresu i bitu sterujące-
go nie możesz powiedzieć, jaki będzie wynik. Żeby podać wynik, musisz znać jesz-
cze historię, a więc to, co działo się z pamięcią wcześniej i to, co zostało zapisane
w komórce. Inaczej mówiąc, wynik zależy nie tylko od wejść, ale i od stanu układu
w danej chwili. Różnica ta stanowi główny podział układów cyfrowych na:
— układy kombinacyjne,
— układy sekwencyjne.
Układy kombinacyjne to układy, w których wyjście jest po prostu kombinacją wej-
ścia. Przykładami są właśnie trzy pierwsze układy poprzedniego podtematu. Nato-
miast układy sekwencyjne to takie, w których wyjście jest zależne od stanu (histo-
rii) układu oraz od wejścia. Przykładami układów sekwencyjnych są pamięci, reje-
stry itp. (czyli — mówiąc nieprecyzyjnie — wszystko to, co ma jakąś pamięć).
Rysunek 9
Sumator 3-bitowy
Rysunek 10
Pamięć
18
Skupimy się teraz wyłącznie na układach kombinacyjnych, ponieważ układy se-
kwencyjne są najczęściej bardziej rozbudowane i skomplikowane. Oba typy ukła-
dów projektuje się bardzo podobnie. Jeśli jesteś zainteresowany układami sekwen-
cyjnymi, to bardzo wiele informacji znajdziesz w literaturze zalecanej do tego mo-
dułu.
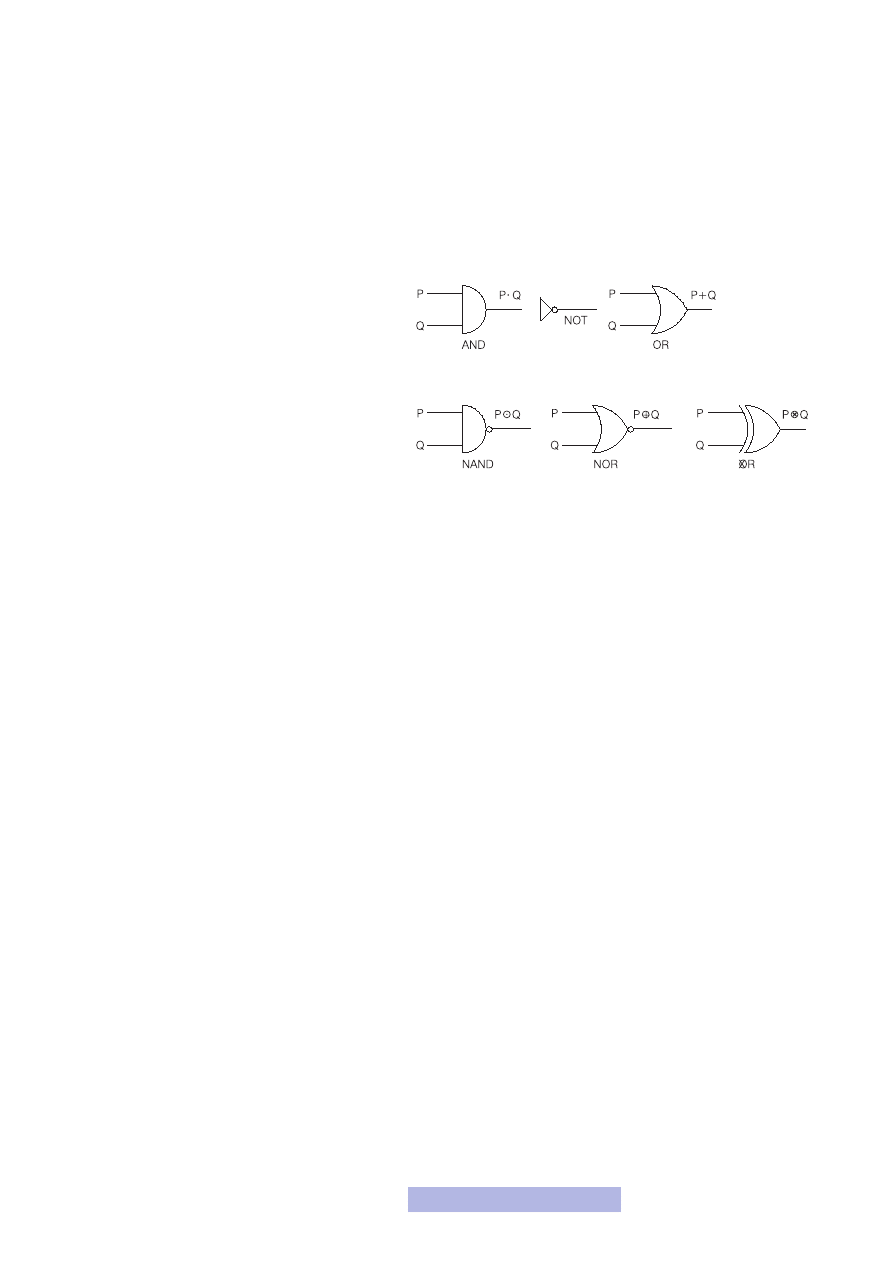
Bramki logiczne
Zanim przystąpimy do samego procesu projektowania, chciałbym jeszcze powie-
dzieć o potrzebnych nam elementach, a mianowicie o bramkach logicznych. Tak
jak wspomniałem na początku tego tematu, stany logiczne prawda (1) i fałsz (0) ist-
nieją w układzie elektronicznym jako stany wy-
sokiego lub niskiego napięcia. Jeśli chcesz spraw-
dzić, czy na wyjściu jest 0, czy 1, mierzysz po pro-
stu napięcie i już wiesz. Skoro tak, to zapewne
przypuszczasz, że istnieją również „elektroniczne
spójniki”. Nie mylisz się. Istnieją układy elektro-
niczne nazywane bramkami logicznymi, które re-
alizują znane ci funkcje logiczne i nawet nazywa-
ją się tak samo, a więc NOT, AND i OR. Ich sym-
bole zostały pokazane na rysunku 11. Oczywiście
istnieją również bramki NOR, XOR i najczęściej
stosowana w praktyce bramka NAND. Wejścia zostały oznaczone literami P i Q
przez analogię do oznaczeń zdań prawdziwych i fałszywych (p i q).
Bramki logiczne realizują dokładnie takie same funkcje jak odpowiednie operatory
logiczne, tyle że operacje wykonywane są nie na prawdzie i fałszu, lecz po prostu
na napięciach. I tak NOT odwraca napięcie, tzn. jeśli na wejście jest podane 0, to
na wyjściu będzie napięcie zasilania, natomiast, gdy na wejściu jest napięcie zasi-
lania, to na wyjściu będzie 0. AND na wyjściu daje napięcie zasilania tylko wtedy,
gdy na obu wejściach jest napięcie zasilania, w pozostałych przypadkach jest 0. OR
daje zero na wyjściu tylko wtedy, gdy na obu wejściach jest 0, w pozostałych przy-
padkach daje napięcie zasilania.
Bramki są oczywiście zbudowane z podstawowych elementów elektronicznych.
Można je budować na różne sposoby, z wykorzystaniem różnych tranzystorów. Jed-
nak obecnie zdecydowana większość bramek budowana jest z tranzystorów MOS
(pod koniec tego modułu pokażę jak z tych tranzystorów można zbudować różne-
go rodzaju bramki).
Sposób projektowanie układów cyfrowych
Układy cyfrowe projektuje się najczęściej według zasady od ogółu do szczegółu.
I tak po kolei:
1. Definiujemy, co dany układ ma robić, jaką ma pełnić funkcję.
2. Ustalamy, co ma być na wejściach, a co na wyjściach.
3. Zapisujemy jak wyjście zależy od wejścia w postaci tabeli prawdy, z której otrzy-
mujemy minimalne (!) formy zdaniowe. Ewentualnie można od razu uzyskać
formuły, jeśli wiadomo, jakie powinny być.
4. Otrzymane formuły przedstawiamy w postaci schematu elektronicznego złożo-
nego z bramek logicznych.
5. Na koniec zamiast bramek wstawiamy układy zbudowane z elementów elektro-
nicznych (w naszym przypadku będą to tranzystory MOS) i w ten sposób mamy
zaprojektowany układ cyfrowy realizujący zadaną funkcję.
Jako że proces projektowania układu cyfrowego jest zajęciem praktycznym, najle-
piej pokazać go na przykładzie.
Rysunek 11
Bramki logiczne

19
Projekt sumatora jednobitowego
Naszym zadaniem jest zaprojektowanie sumatora jednobitowego. Jest to układ,
który znajdziesz w każdym procesorze, oczywiście w wersji rozszerzonej (np. su-
matora 32-bitowego). Najważniejsze jest jednak, abyś zobaczył jak przebiega cały
proces projektowania, jak wyglądają poszczególne etapy opisane powyżej.
A więc zaczynamy od określenia zadania układu:
Zadaniem układu ma być arytmetyczne dodatnie dwóch liczb jednobitowych i po-
danie na wyjściu wyniku tego dodawania.
Liczbą jednobitową jest liczba 0 lub 1. Jako że zapis liczby 0 i 1 jest dokładnie taki
sam w systemie dziesiątkowym i dwójkowym, wejściem mogą być więc te liczby.
Natomiast na wyjściu możemy uzyskać liczby: 0, 1, 2. Liczba 2 w systemie dwój-
kowym zapisana jest jako: 10, czyli na wyjściu musimy mieć dwa bity. Ostatecz-
nie wejściem będą dwa bity: I
0
— pierwsza liczba (składnik sumy), I
1
— druga licz-
ba (składnik sumy). Wyjściem natomiast będą dwa bity tworzące wynik zapisany
w systemie dwójkowym: O
0
— młodszy bit wyniku, O
1
— starszy bit wyniku.
Następnym etapem jest stworzenie tablicy prawdy:
0 + 0 = 0, czyli 00
0 + 1 = 1, czyli 01
1 + 0 = 1, czyli 01
1 + 1 = 2, czyli 10
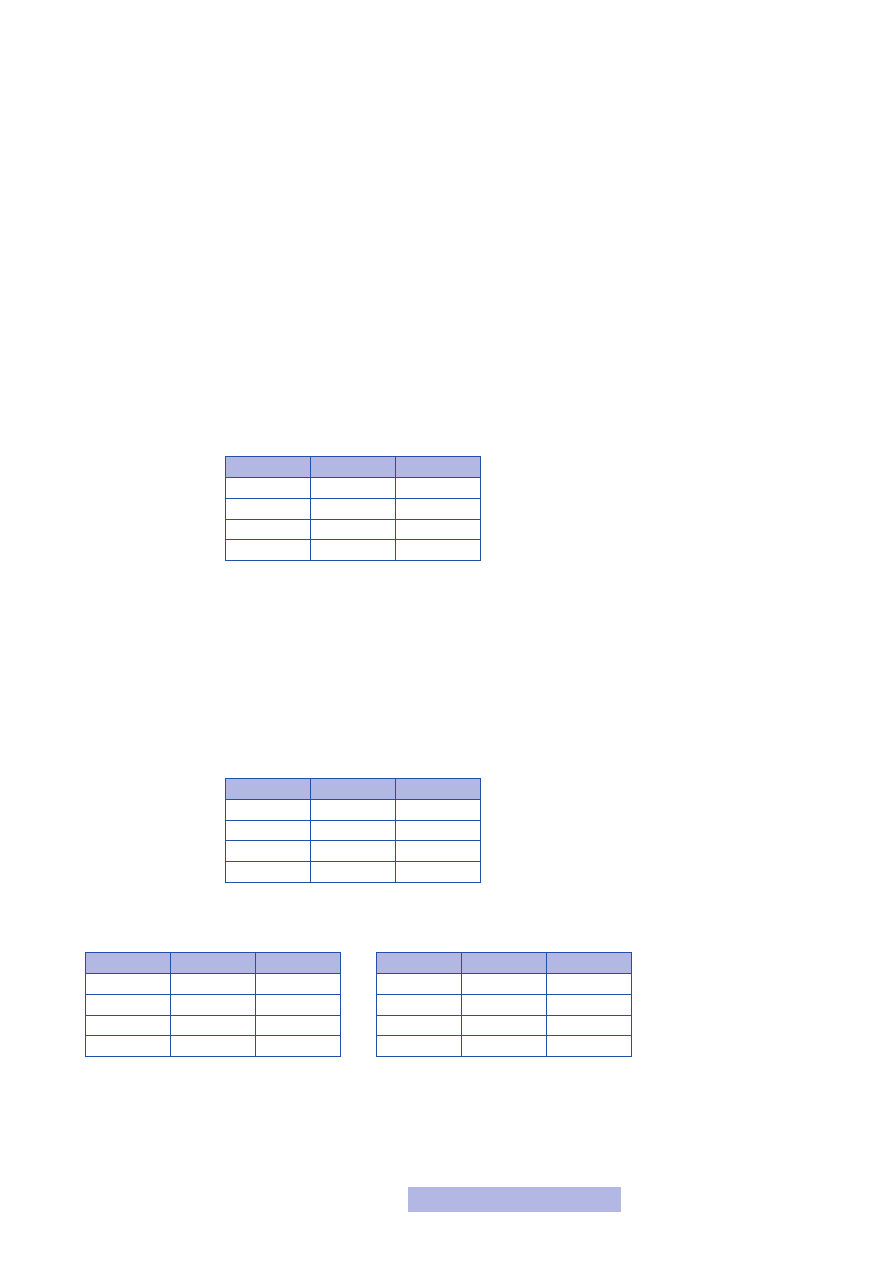
Tak więc tabele prawdy będą wyglądała następująco:
Dla wyjścia O
1
:
I
0
I
1
O
1
0
0
0
0
1
0
1
0
0
1
1
1
Dla wyjścia O
0
:
I
0
I
1
O
0
0
0
0
0
1
1
1
0
1
1
1
0
Jeśli chodzi o pierwszą tabelę, od razu widać, że jest to po prostu AND, natomiast
druga to XOR. Zastanów się zatem, czemu ta funkcja jest nazywana kontrolą pa-
rzystości? Tak więc korzystając z wyników z poprzedniego podtematu, otrzymuje-
my równania:
O
0
= I
0
· (~I
1
) + (~I
0
) · I
1
O
1
= I
0
· I
1
Teraz przedstawimy powyższe równania za pomocą bramek logicznych (rys. 12):

20
Pozostał ostatni punkt, którego — póki co — nie potrafimy wykonać i którym zaj-
miemy się w następnym temacie. Poza tym praca skończona — tak właśnie wyko-
nuje się projekt układu cyfrowego. Spróbuj teraz samodzielnie wykonać projekt
jednego z podanych przykładów, np. dekodera temperaturowego. W przypadku
dekodera będzie już więcej pracy, ponieważ ma on 8 wyjść, opisujące je równania
są jednak niezwykle proste, więc bez problemu powinieneś sobie poradzić.
Rysunek 12
Schemat sumatora
jednobitowego
21
4. Bramki logiczne CMOS
Pozostał ostatni element naszej układanki, a więc problem powiązania bramek lo-
gicznych z tranzystorami MOS, czyli — mówiąc precyzyjniej — problem wyglądu
schematu elektrycznego poszczególnych bramek. Teraz właśnie tę lukę wypełnimy.
Jak już wspomniałem, bramki można budować na różne sposoby. Można wręcz
powiedzieć, że historia konstrukcji bramek logicznych to historia elektroniki. Od
lat 70. zeszłego wieku „króluje” jeden sposób wykonywania bramek, a mianowicie
przy wykorzystaniu pary tranzystorów: MOS z kanałem typu N i MOS z kanałem
typu P, stąd nazwa CMOS (od ang. Complementary MOS, czyli komplementarna
para tranzystorów MOS). I póki co, nie widać, aby jakakolwiek inna technologia
mogła w najbliższym czasie konkurować z CMOS. Dlatego przedstawię budowę
bramek logicznych właśnie w tej technologii.
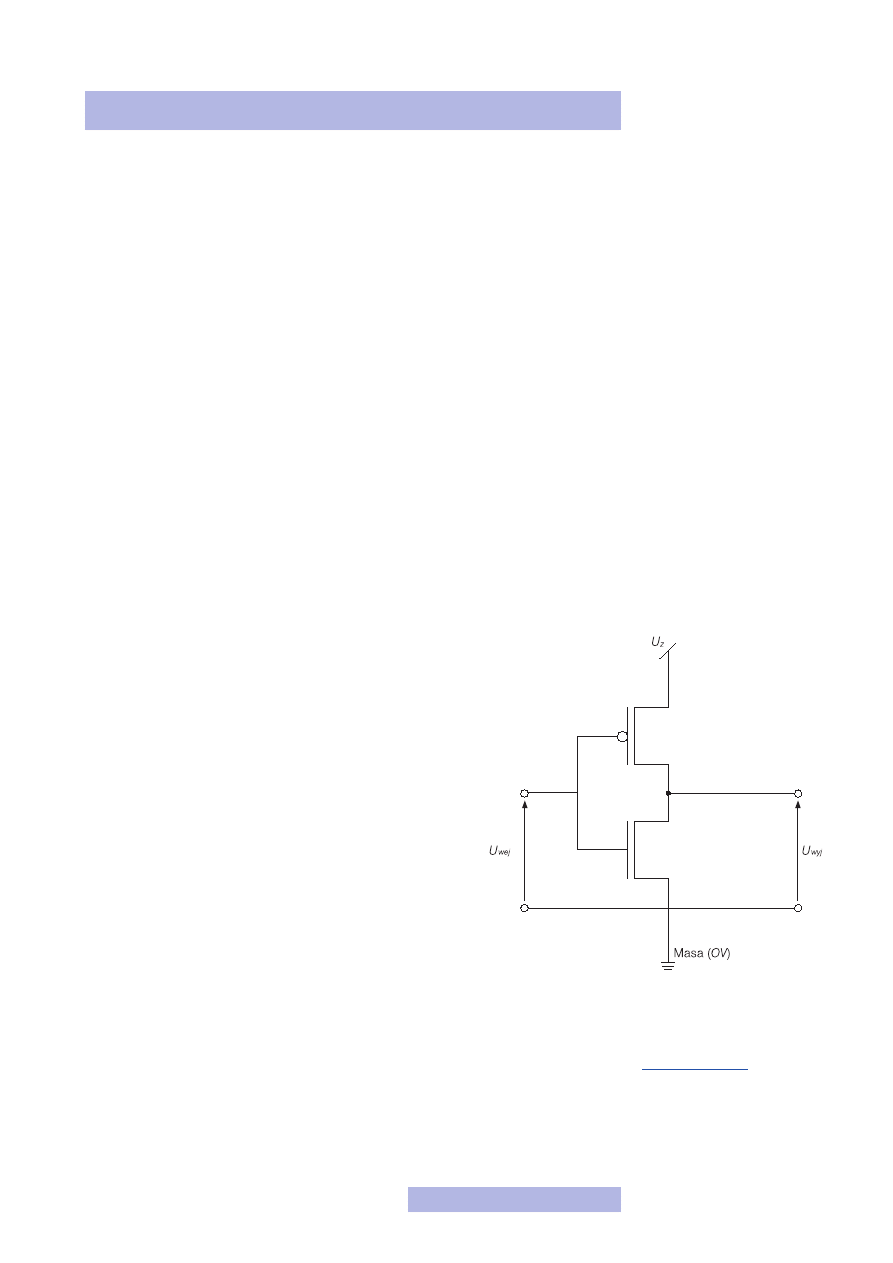
4.1. Inwerter
Pierwszą bramką, jaką chciałbym się zająć i której poświęcę najwięcej uwagi, jest
inwerter, czyli bramka realizująca funkcję NOT. Zadaniem inwertera jest odwró-
cenie napięcia podawanego na wejście bramki, czyli gdy podajemy napięcie zasi-
lania, to na wyjściu chcemy mieć 0 V, a gdy podajemy 0 V,
to chcemy mieć napięcie zasilania. W tym momencie proszę,
abyś przerwał czytanie i spróbował samodzielnie stworzyć
taki układ. Podpowiem, że do jego wykonania będziesz po-
trzebował tylko dwóch tranzystorów MOS, jednego z kana-
łem typu N, drugiego z kanałem typu P.
Mam nadzieje, że udało ci się wymyślić ten schemat. Popraw-
ny schemat pokazany jest na rysunku 13. Tak jak mówiłem,
składa się on z dwóch tranzystorów MOS: z kanałem typu
N i P, połączonych szeregowo i podłączonych do zasilania.
Na bramki tych tranzystorów podane jest wejście, a wyjściem
jest napięcie z dolnego tranzystora.
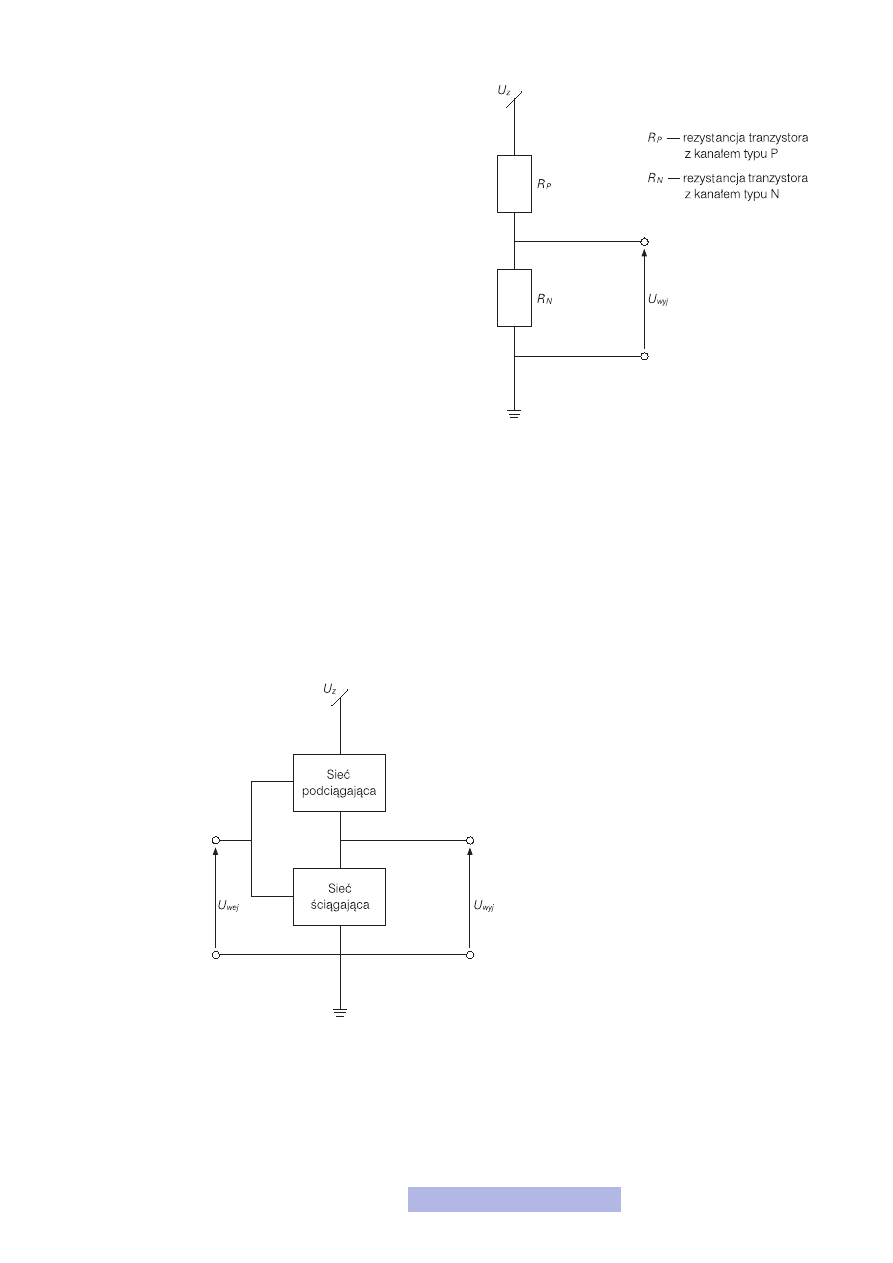
Przyjrzyjmy się bliżej jak działa taki układ. Jak wiesz, tran-
zystor to inaczej sterowana rezystancja. W tranzystorze MOS
ta rezystancja jest między elektrodą źródła i drenu, a stero-
waniem jest napięcie na bramce. Schemat inwertora przedsta-
wiony jest na rysunku 14. Czy ten układ podłączony do zasi-
lania nie przypomina ci czegoś? Oczywiście, jest to doskonale znany dzielnik na-
pięciowy podłączony do napięcia zasilania. Jeśli teraz na wejście inwertera podane
jest napięcie 0 V, to na bramki obu tranzystorów zostanie podane właśnie napięcie
0 V. Jak pamiętasz z początku tego modułu, tranzystor NMOS
1
przy 0 V na bramce
nie przewodzi, czyli ma bardzo wysoką rezystancję, natomiast tranzystor P–MOS
przewodzi, czyli ma bardzo małą rezystancję. W module 2 przy analizie dzielni-
ka napięciowego rozpatrywaliśmy właśnie taki przypadek co się dzieje w dzielni-
ku, gdy jeden z rezystorów jest znacznie większy od drugiego. Wówczas na wyjściu
było napięcie zasilające dzielnik, bądź 0V. W naszym przypadku ponieważ górny
Rysunek 13
Schemat inwertera
1
Jest to skrótowa nazwa
tranzystora MOS z kana-
łem typu N, analogicznie
PMOS to tranzystor
z kanałem typu P.
22
rezystor jest bardzo mały, a dolny bardzo duży, to na wyjściu
będzie po prostu napięcie zasilania. I o to właśnie chodziło!
Na wejściu inwertera mieliśmy 0 V, a na wyjściu mamy na-
pięcie zasilania. Mówiąc inaczej, na wejściu mieliśmy 0, a na
wyjściu mamy 1.
Jeśli teraz na wejście podamy napięcie zasilania, czyli 1, to
przewodzi tranzystor NMOS, czyli dolny, a górny PMOS jest
wyłączony, ma bardzo dużą rezystancję. A więc sytuacja jest
odwrotna — na górze mamy bardzo dużą rezystancję, a na
dole bardzo małą. Wówczas, z własności dzielnika napięcio-
wego, na wyjściu jest 0 V i o to chodziło! Na wejście podali-
śmy napięcie zasilania, a na wyjściu mamy 0 V, mówiąc ina-
czej — na wejściu jest 1, to na wyjściu 0.
Jeśli masz jakiekolwiek wątpliwości dotyczące działania in-
wertera, koniecznie raz jeszcze przeczytaj dokładnie ten frag-
ment, w razie potrzeby wróć jeszcze raz do początku modu-
łu, aby przypomnieć sobie działanie tranzystora MOS oraz
do modułu 2, aby przypomnieć sobie działanie dzielnika napięciowego. To bardzo
ważne zagadnienie.
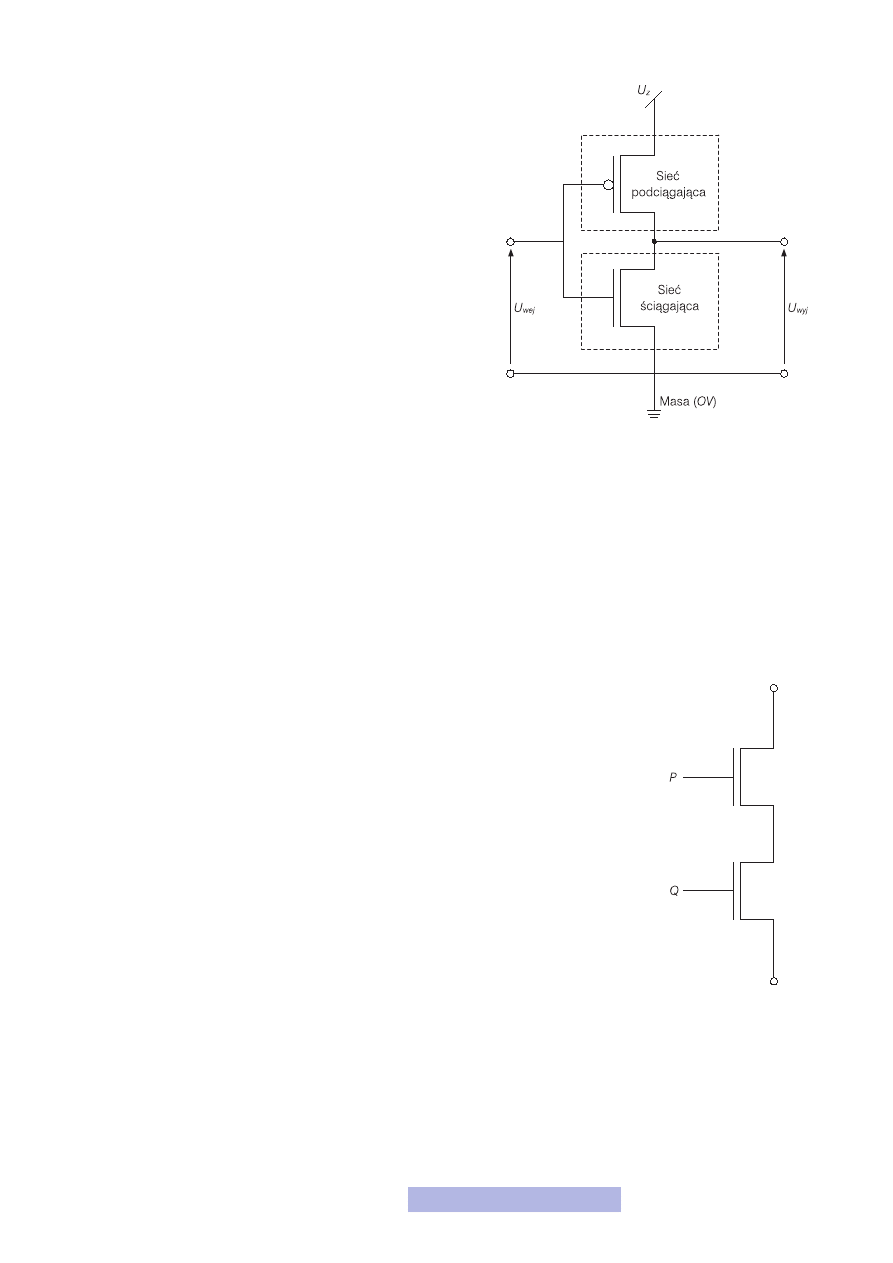
Chciałbym, abyś jeszcze inaczej spojrzał na inwertor jako na urządzenie złożo-
ne z dwóch części (rys. 15), pośrodku których jest wyjście układu. Jedna (górna)
z tych części ma za zadanie pociągnąć wyjście do zasilania, kiedy na wejściu jest
0 V, natomiast zadaniem drugiej (dolnej) części jest ściągnięcie wyjścia do masy,
gdy na wejściu inwertera jest 0 V. Do obu części podłączone jest oczywiście wej-
ście inwertera. Pozostaje jeszcze odpowiedzieć na pytanie, co to znaczy pociągnąć
do zasilania? Oznacza to po prostu połączyć z zasilaniem. Analogicznie ściągnąć
do masy to znaczy połączyć z masą. Połączenie następuje wtedy, gdy rezystancja
jest mała.
Jeśli spojrzysz w ten sposób na inwerter (rys. 16), to podciąganie do zasilania na-
stępuje wtedy, gdy przewodzi górny tranzystor, a więc PMOS, czyli gdy na jego
bramce jest 0 V, natomiast ściąganie do masy wtedy, gdy przewodzi dolny tranzy-
stor, czyli NMOS, a więc gdy na bramce jest 1 V. Oczywiście gdy wyjście podcią-
gnięte jest do zasilania, to na wyjściu jest napięcie zasilania, a gdy jest ściągnięte do
Rysunek 14
Zasada działania inwertera
Rysunek 15
Schemat ideowy bramki CMOS
23
masy, to na wyjściu jest 0 V. Ten sposób patrzenia na inwerter
przyda się nam przy bramkach, których budowę poznamy za
chwilę.
Ostatnią kwestią, którą chciałbym poruszyć jest moc, jaką po-
biera inwerter. Zauważ, że niezależnie od wejścia jeden z rezy-
storów ma bardzo dużą wartość (rys. 14), czyli szeregowe po-
łączenie tych rezystorów ma również bardzo dużą wartość. Za-
tem mimo przyłożonego napięcia płynie przez nie bardzo mały
prąd. A skoro płynie bardzo mały prąd, to i moc pobierana
przez taki inwerter jest bardzo mała. Tak więc największą zale-
tą układów CMOS i jednocześnie przyczyną ich popularności
jest to, że praktycznie nie pobierają mocy, gdy są w stanie sta-
cjonarnym, czyli gdy na wejściu jest ustalone napięcie.
4.2. Bramki logiczne CMOS
Skoro już wiesz jak działa inwerter, myślę, że bez większego problemu byłbyś w sta-
nie zbudować bramki AND i OR. Nie pokażę ci ich od razu — zbudujemy je razem.
Zacznijmy od bramki AND.
Bramka AND
Bramka AND ma mieć na wyjściu 1, gdy na wejściu są jedynki, w pozostałych przy-
padkach 0. Czyli wyjście musi być podciągnięte do zasilania tylko i wyłącznie, gdy
na obu wejściach są napięcia zasilania. Musisz zatem zaprojektować układ, który
będzie miał bardzo małą rezystancję, gdy na obu wejściach będzie napięcie zasila-
nia, a dla pozostałych stanów będzie miał bardzo dużą rezystancję.
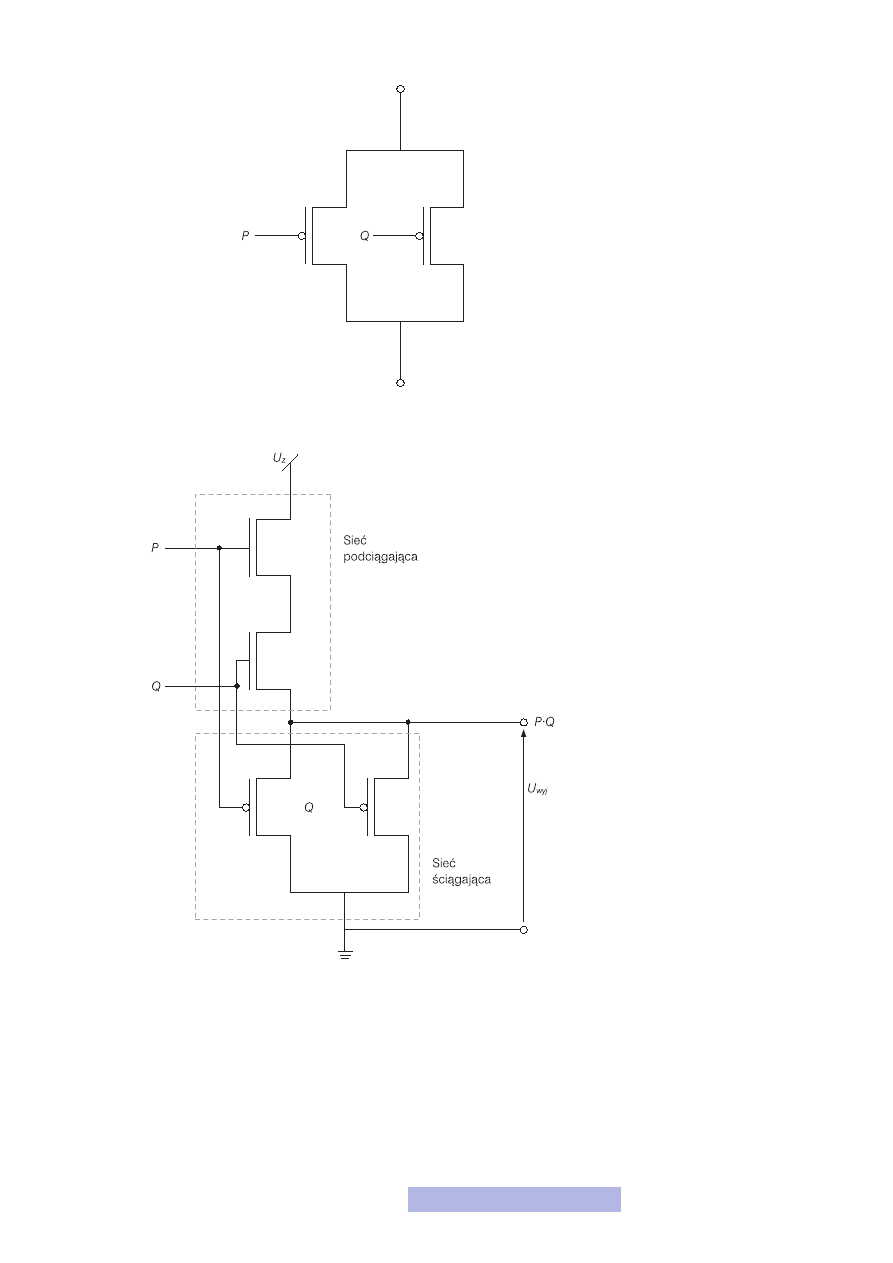
Myślę, że z tym zadaniem nie będziesz miał większego problemu, po prostu trzeba
szeregowo połączyć dwa tranzystory NMOS (rys. 17). Otrzymamy wówczas połą-
czenie szeregowe dwóch rezystancji. W przypadku, gdy obie są małe, ich połącze-
nie szeregowe też jest małe, czyli mogą podciągać do zasilania. Co więcej, taki stan
jest dla napięcia zasilania na bramkach obu tranzystorów, a więc dla dwóch jedy-
nek. Jeśli pojawi się choć jedno zero na obojętnie którym tranzystorze, to jego re-
zystancja będzie bardzo duża; połączona szeregowo z drugą daje oczywiście dużą
rezystancję całego połączenia i o to nam chodziło. No to mamy już pół bramki.
Pozostaje teraz zbudować sieć ściągającą do masy, która będzie miała bardzo małą
rezystancję, jeśli na wejściu będzie choć jedno zero. Myślę, że i z tym zadaniem
poradziłbyś sobie bez problemu — wystarczy połączyć równolegle dwa tranzysto-
ry PMOS (rys. 18). W przypadku, gdy choć na jednym będzie zero, tranzystor ten
przewodzi, czyli ma bardzo małą rezystancję. Równoległe połączenie dwóch re-
zystancji, z których jedna jest mała, jest małe (bez względu na drugą). Zatem ta
sieć przewodzi, gdy na wejściu mamy choć jedno zero. Natomiast, gdy na wejściu
są dwie jedynki, to żaden z tranzystorów nie przewodzi, równoległe połączenie
dwóch bardzo dużych rezystancji jest nadal duże, a więc sieć nie przewodzi.
Rysunek 16
Inwerter CMOS
Rysunek 17
Sieć podciągająca bramki AND
24
Ostatecznie bramka AND wygląda tak jak na rysunku 19.
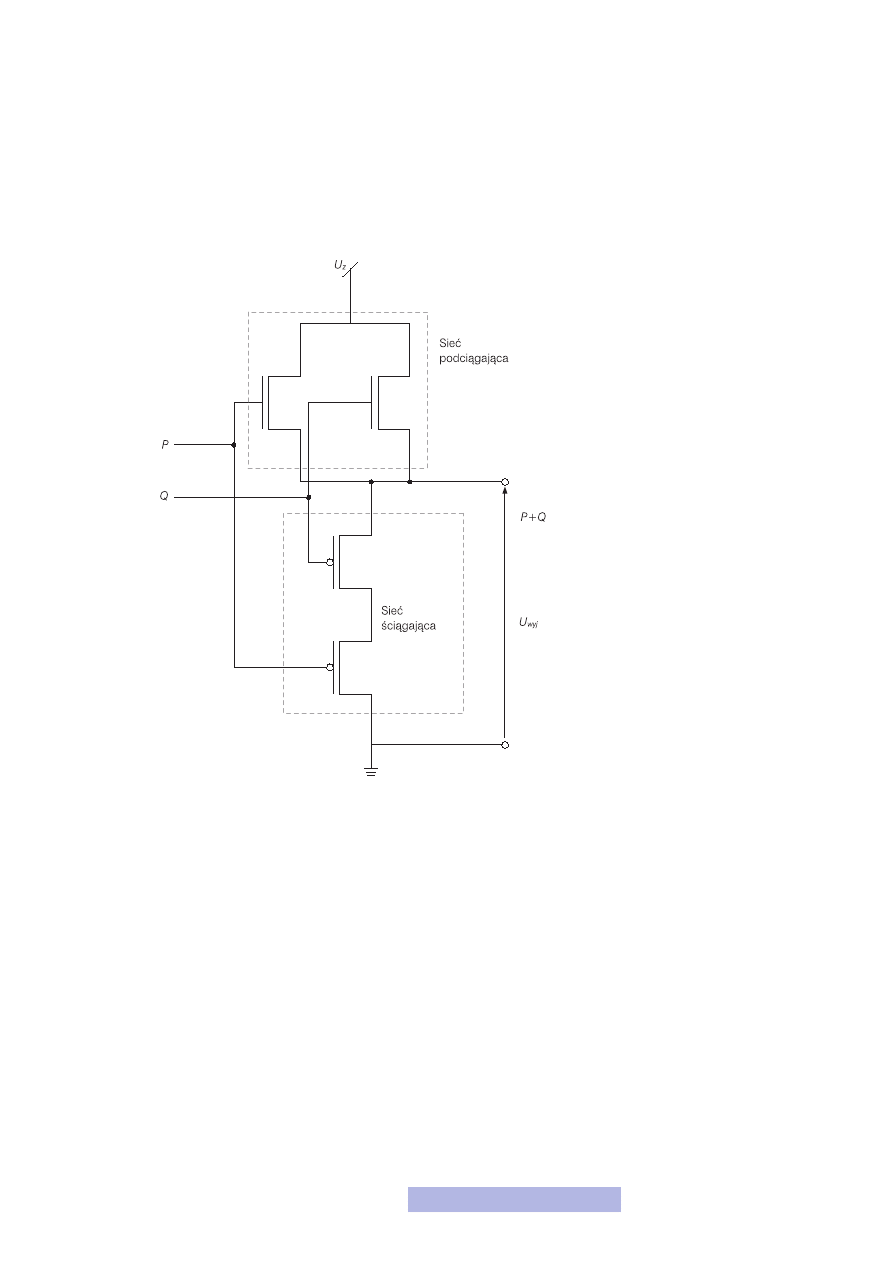
Bramka OR
Po doświadczeniach z bramką AND myślę, że bramka OR nie będzie już stanowiła
dla ciebie żadnej zagadki. Jej budowa została przedstawiona na rysunku 20. Zapro-
ponuję ci jeszcze inny rodzaj analizy bramki (rys. 21). Bramka OR ma na wyjściu
jedynkę, gdy na wejściu jest choć jedna jedynka, a zero, gdy na wejściach są same
zera. Rozważmy najpierw przypadek, gdy na wejściu P jest jedynka, a na Q zero
(rys. 21a). Wówczas otwarte są tranzystory T
1
i T
4
. Tak więc zasilanie ma otwarty
dostęp do wyjścia przez tranzystor T
1
, natomiast masa może przejść przez tranzy-
stor T
4
, ale na drodze do wyjścia staje tranzystor T
3
, który jest zamknięty. Jeśli na
Rysunek 18
Sieć ściągająca
Rysunek 19
Bramka AND
25
A jest zero i na B jedynka, to sytuacja jest analogiczna (rys. 21b), tzn. zasilanie ma
otwarty dostęp przez tranzystor T
2
, natomiast masa jest odcięta przez tranzystor
T
4
. Jeśli są dwie jedynki (rys. 21c), to zasilanie podłączone jest do wyjścia przez
tranzystor T
1
i T
2
(może sobie nawet wybrać, którym iść), natomiast masa jest od-
cięta od wyjścia przez oba tranzystory T
3
i T
4
, które są zamknięte. W przypadku,
gdy na obu wejściach są zera (rys. 21d), oba tranzystory T
1
i T
2
są zamknięte, czy-
li zasilanie nie ma jak dostać się do wyjścia, natomiast oba tranzystory T
3
i T
4
są
otwarte, czyli masa ma dojście do wyjścia. I to wszystko!
Rysunek 20
Bramka OR
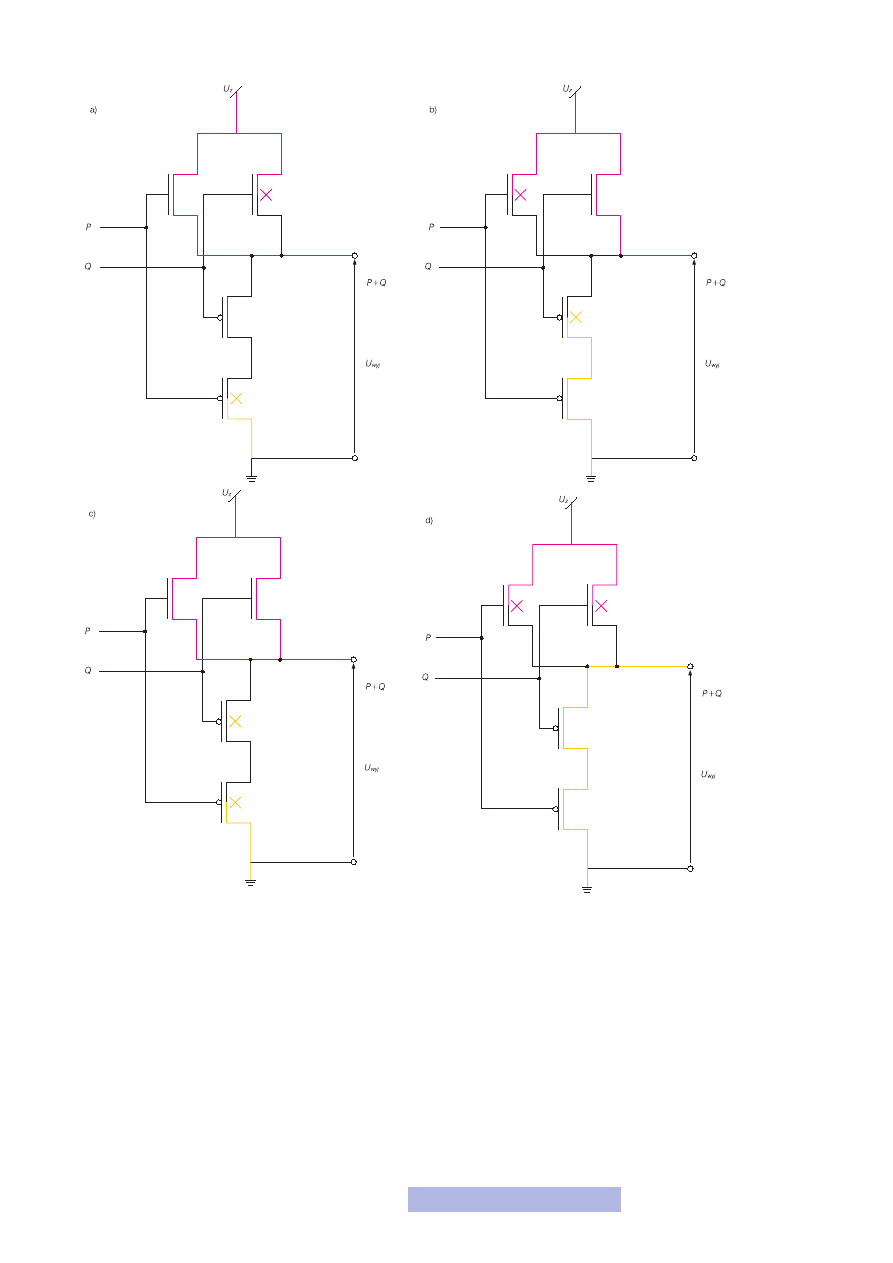
26
Rysunek 21
Analiza bramki OR
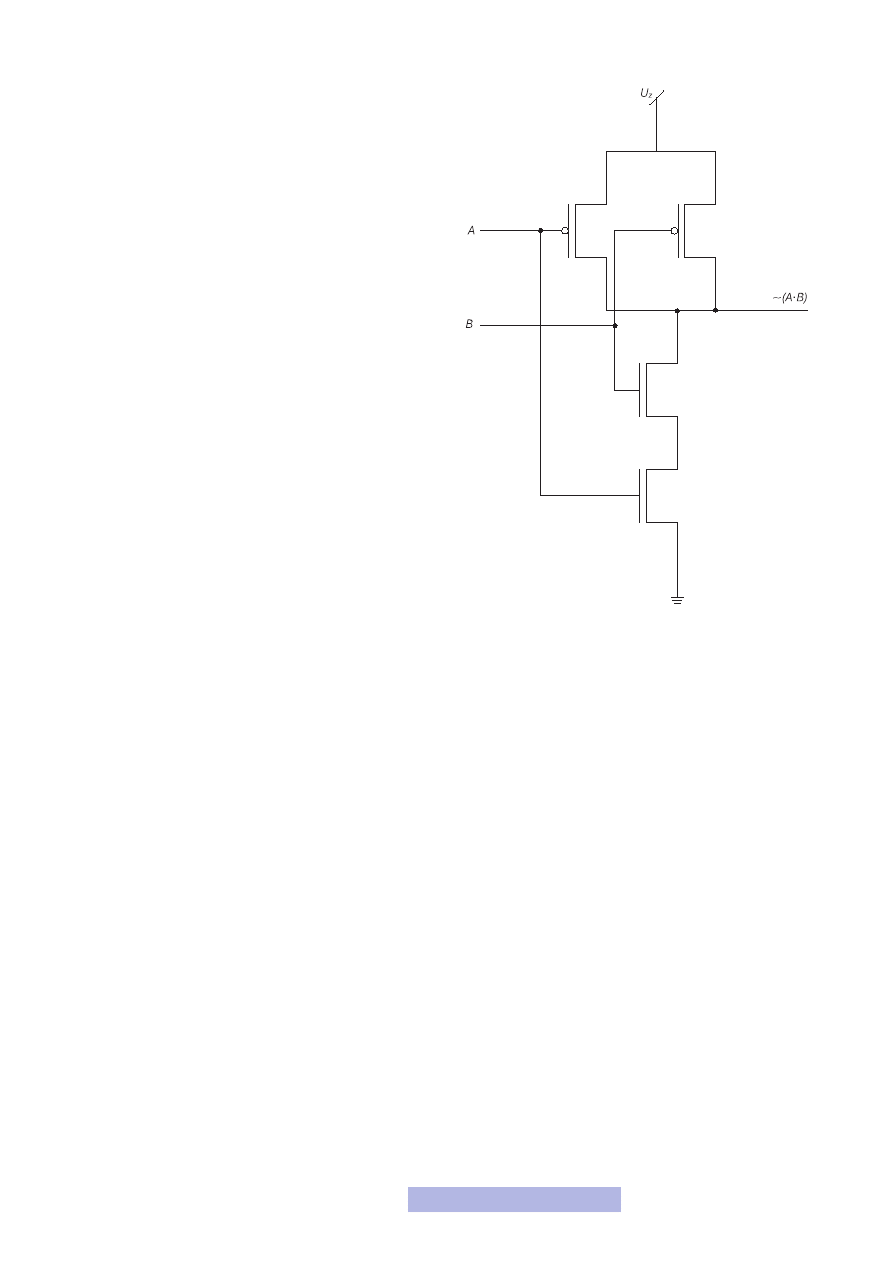
27
Bramka NAND
Który sposób analizy i budowy bramki najbardziej ci od-
powiada, to już twoja decyzja. Każdy jest dobry. Spróbuj
teraz wybranym sposobem samodzielnie przeanalizować
działanie bramki NAND (rys. 22).
Bramki wielowejściowe
Do tej pory wszystkie bramki, które poznałeś miały dwa
wejścia, a więc na wejście mogłeś podać dwa sygnały.
Jednak w równaniach często masz więcej niż dwa skład-
niki w sumie. Podobnie możesz mieć ponad dwa czynni-
ki w iloczynie, np.:
(~I
0
) · (~I
1
) · (~I
2
) · I
3
+ (~I
0
) · I
1
· (~I
2
) + I
0
· (~I
1
) · I
2
· (~I
3
) + I
0
· I
1
.
Zapewne zapytasz w tym momencie, czy istnieją bramki,
które mają więcej wejść niż dwa. Oczywiście, że tak. Ist-
nieją zarówno bramki AND, jak i OR o dowolnej liczbie
wejść. Buduje się je dokładnie na takiej samej zasadzie jak
bramki dwuwejściowe, dodając po prostu kolejny tranzy-
stor w szeregu i kolejny równolegle i podłączając do ich
bramek trzecie wejście. Na rysunku 23 pokazany został
schemat 3-wejściowej bramki AND. Działa ona w nastę-
pujący sposób: jeśli na wszystkie wejściach są jedynki, to
na wyjściu też jest jedynka, w każdym innym przypad-
ku jest zero. Patrząc na schemat bramki, widać, że sieć
podciągająca do zasilania, to trzy szeregowo połączone
tranzystory. Zatem wyjście zostanie podciągnięte do masy wyłącznie wtedy, gdy
wszystkie te tranzystory będą otwarte, czyli gdy na wejściu wszędzie będą jedyn-
ki. Natomiast w sieci ściągającej do masy zawsze przez któryś z tranzystorów bę-
dzie można połączyć masę z wyjściem, z wyjątkiem sytuacji, gdy wszystkie będą
zamknięte, czyli gdy na wejściu będą same jedynki. Podobnie tworzy się wielowej-
ściowe bramki OR (rys. 24), których analizę pozostawiam tobie.
Rysunek 22
Bramka NAND
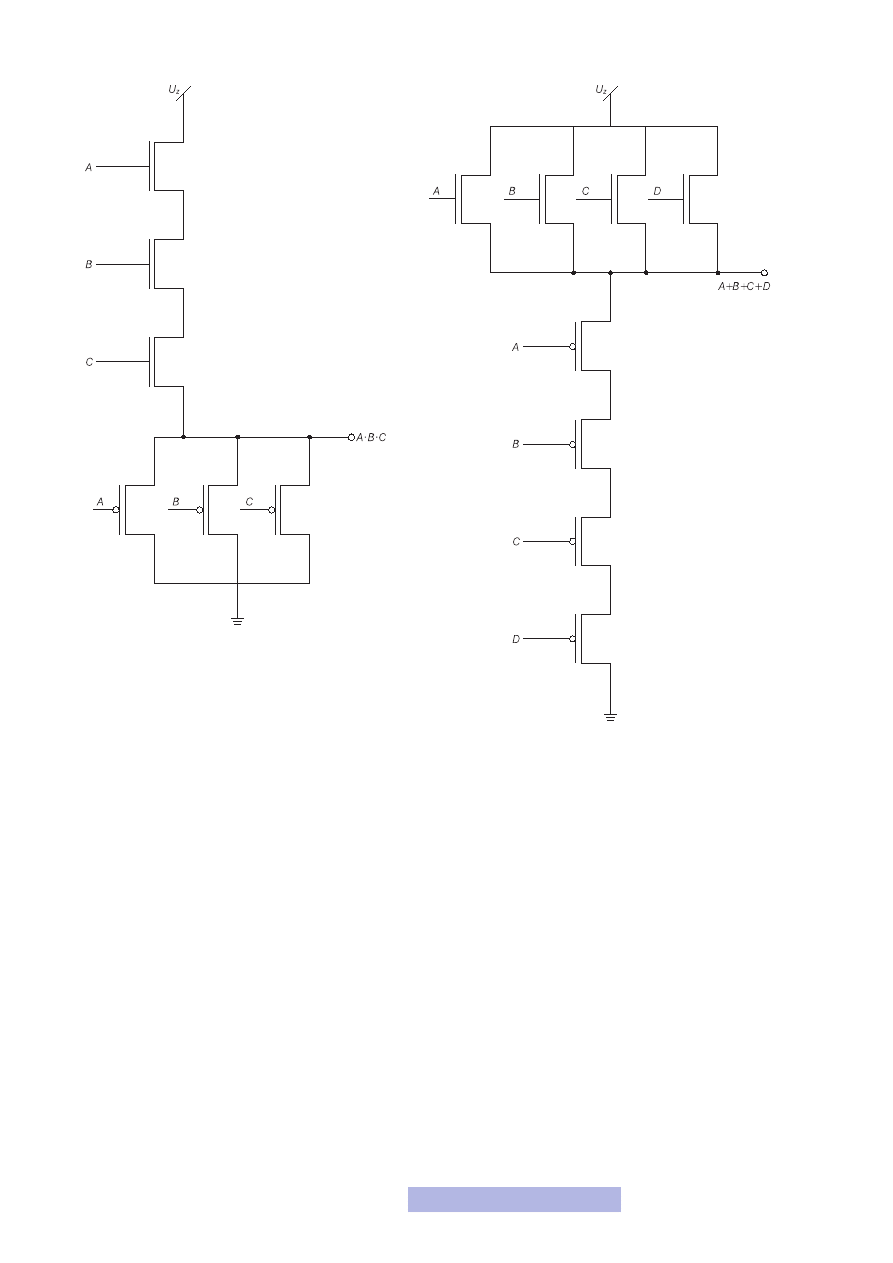
28
Zauważ, że każda bramka składa się co najmniej z 4 rezystorów. Mam nadzieje, że
nie masz już wątpliwości, czemu należy minimalizować formuły zdaniowe, opisują-
ce układ cyfrowy. Każdy składnik w formule mniej to co najmniej dwa tranzystory
mniej! Takie podejście nie dość, że zmniejsza liczbę elementów, a więc i koszt, to
jeszcze poprawia niezawodność układu, ponieważ mniej elementów może się po-
psuć, oraz poprawia szybkość jego działania, ponieważ przez mniejszą liczbę ele-
mentów musi przejść sygnał. Pamiętaj o tym za każdym razem, gdy będziesz pro-
jektował układ!
4.3. Projekt sumatora jednobitowego — dokończenie
Na koniec chciałbym wrócić do zaczętego projektu sumatora jednobitowego. Do-
szliśmy tam do schematu zbudowanego z bramek logicznych (rys. 12). Teraz jed-
nak już wiesz, jak wyglądają schematy poszczególnych bramek (rys. 13, 19, 20).
Zastępując na schemacie układu sumatora symbole bramek logicznych ich schema-
Rysunek 23
3-wejściowa bramka AND
Rysunek 24
4-wejściowa bramka OR
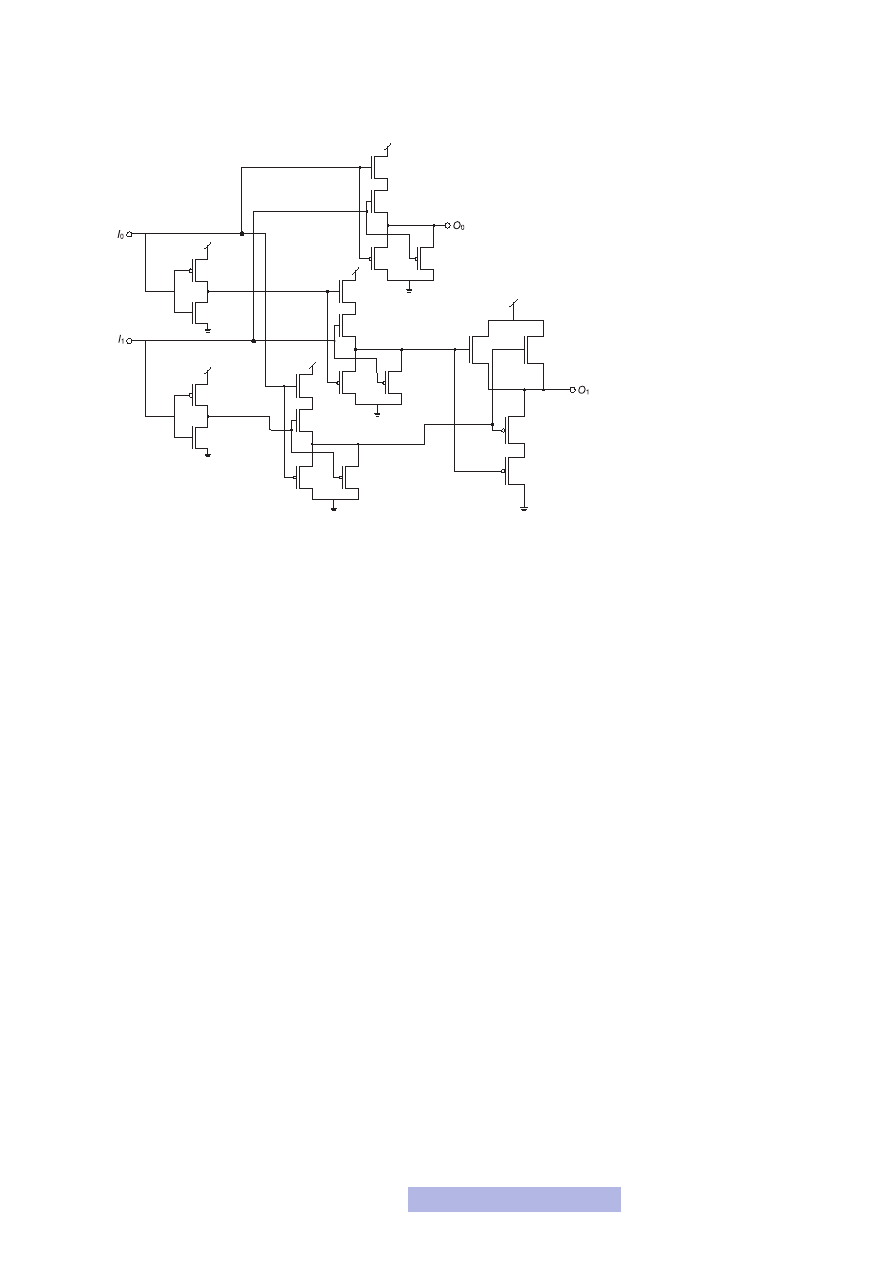
29
tami elektronicznymi, otrzymujemy ostatecznie projekt sumatora jednobitowego
(rys. 25).
Gdybyś teraz poszedł do sklepu, kupił tranzystory, zlutował układ według powyż-
szego schematu i podłączył do zasilania, otrzymałbyś prawdziwy sumator jednobi-
towy. Jeśli masz na to czas, gorąco proponuję ci przeprowadzić takie doświadcze-
nie. Gwarantuję niesamowitą satysfakcję, jeśli zadziała.
Natomiast budowanie sumatora jednobitowego z elementów dyskretnych nie jest
takie łatwe, zajmuje sporo czasu, przy lutowaniu może pojawić się wiele błędów,
a przede wszystkim nie jest najtańsze. W następnym module pokażę, jak taki sche-
mat wykonać w układzie scalonym. Wierz mi, zapowiada się naprawdę ciekawie,
bo wreszcie układ scalony nie będzie dla ciebie czarną kostką z nóżkami, lecz bę-
dziesz dokładnie wiedział co jest w środku!
Rysunek 25
Ostateczny schemat sumatora
jednobitowego

30
Podsumowanie
W module tym zapoznałeś się z najważniejszym z punktu widzenia mikroelektro-
niki działem elektroniki, a mianowicie elektroniką cyfrową. Właściwie można po-
wiedzieć, że od tego modułu zacząłeś się uczyć mikroelektroniki.
Poznałeś najpierw elementy służące do budowy układów elektroniki cyfrowej,
a więc tranzystory MOS, następnie zapoznałeś się z matematycznymi podstawa-
mi budowy układów cyfrowych, przede wszystkim z metodami minimalizacji for-
muł zadaniowych. Później przeszedłeś już do praktyki i zobaczyłeś jak buduje się
taki układ, na czym polega praca projektanta. Przy okazji zaprojektowałeś sumator
jednobitowy. Na koniec zobaczyłeś, jak taki układ buduje się z podstawowych ele-
mentów elektronicznych, czyli tranzystorów. Poskładałeś te wszystkie wiadomości
w całość i uzyskałeś pełny schemat działającego układu cyfrowego.

31
Bibliografia
1. Beck R., 1991: Technologia krzemowa, PWN, Warszawa.
2. Europractice. Witryna internetowa.
, stan z 26 wrze-
śnia 2006 r.
3. IBM. Witryna internetowa.
, stan z 26 września 2006 r.
4. Intel. Witryna internetowa.
, stan z 26 września 2006 r.
5. International Technology Roadmap for Semiconductors. Witryna internetowa.
, stan z 26 września 2006 r.
6. Kalisz J., 1998: Podstawy elektroniki cyfrowej, Wydawnictwa Komunikacji
i Łączności, Warszawa.
7. Marciniak W., 1984: Przyrządy półprzewodnikowe i układy scalone, Wydaw-
nictwa Naukowo-Techniczne, Warszawa.
8. Marciniak W., 1991: Przyrządy półprzewodnikowe MOS, Wydawnictwa Na-
ukowo-Techniczne, Warszawa.
9. Massucci J., 2001: Projekt Milenium, Wydawnictwo Amber sp. z o. o., Warszawa.
10. Napieralska M., Jabłoński G., 2002: Podstawy mikroelektroniki, Wydawnic-
twa PŁ, Łódź.
11. University of California, Berkeley. Witryna internetowa.
, stan z 26 września 2006 r.
Document Outline
- Podstawy elektroniki cyfrowej
Wyszukiwarka
Podobne podstrony:
A-03 Komparator, Elektrotechnika AGH, Semestr V zimowy 2014-2015 - MODUŁ C, semestr V (moduł C), Pod
sumator szeregowy projekt, Elektrotechnika AGH, Semestr V zimowy 2014-2015 - MODUŁ C, semestr V (mod
Licznniki, Elektrotechnika AGH, Semestr V zimowy 2014-2015 - MODUŁ C, semestr V (moduł C), Podstawy
jh, Elektrotechnika AGH, Semestr V zimowy 2014-2015 - MODUŁ C, semestr V (moduł C), Podstawy sterowa
substraktor jakis ale spoko, Elektrotechnika AGH, Semestr V zimowy 2014-2015 - MODUŁ C, semestr V (m
Liczniki1, Elektrotechnika AGH, Semestr V zimowy 2014-2015 - MODUŁ C, semestr V (moduł C), Podstawy
TC-S-04 Rejestry, Elektrotechnika AGH, Semestr V zimowy 2014-2015 - MODUŁ C, semestr V (moduł C), Po
Sprawko PSL, Elektrotechnika AGH, Semestr V zimowy 2014-2015 - MODUŁ C, semestr V (moduł C), Podstaw
15 ćwiczeń laboratoryjnych z Podstaw Elektroniki i Techniki Cyfrowej
15 ćwiczeń laboratoryjnych z Podstaw Elektroniki i Techniki Cyfrowej
Podstawy elektroniki i miernictwa2
Podstawy elektroniki i energoelektroniki prezentacja ppt
podstawy elektrotechniki
Modul 5 Podstawowe zagadnienia wspolczesnej gospodarki pienieznej i rynku dobr
lista 4a, Elektrotechnika, PODSTAWY ELEKTROTECHNIKI, ćwiczenia
zadania na egzaminie czerwcowym 2009, Elektrotechnika, PODSTAWY ELEKTROTECHNIKI, pytania
więcej podobnych podstron