Wydział Podstawowych Problemów Techniki

Ś

rodowisko programowe

do symulacji zjawiska tunelowania

Praca dyplomowa inżynierska

Michał Chometa

Opiekun:

dr hab. inż. Włodzimierz Salejda prof. PWr.

Wrocław 2006

2

Opiekunowi prof. Włodzimierzowi Salejdzie

serdecznie dziękuję za pomoc, cenne rady i dyskusję.

Bez Jego cierpliwości niniejsza praca by nie powstała.

3

Spis Treści

1.

Wprowadzenie .............................................................................................. 4

2.

Równanie Schrödingera............................................................................... 5

3.

Tunelowanie – analiza ilościowa zjawiska ................................................. 7

4.

Macierze przejść ......................................................................................... 10

4.1. Macierz przejścia M

1

................................................................................................. 11

4.2. Macierz przejścia M

2

................................................................................................. 12

4.3. Macierz przejścia M

3

................................................................................................. 14

4.4. Macierz przejścia M

4

................................................................................................. 15

4.5. Macierz przejścia M

5

................................................................................................. 17

4.6. Macierz przejścia M

6

................................................................................................. 19

4.7. Macierz transmisji ..................................................................................................... 20

5.

Opis środowiska programowego............................................................... 22

6.

Wybrane wyniki.......................................................................................... 28

6.1. Bariera prostokątna ................................................................................................... 28

6.2. Podwójna symetryczna bariera.................................................................................. 30

6.3. Podwójna prostokątna bariera niesymetryczna ......................................................... 31

6.4. Wielokrotne studnie potencjału................................................................................. 34

6.5. Tunelowanie cząstek o różnych masach ................................................................... 35

7.

Wnioski ........................................................................................................ 38

8.

Podsumowanie ............................................................................................ 41

9.

Literatura .................................................................................................... 42

4

1. Wprowadzenie

Celem pracy było opracowanie środowiska obliczeniowego pozwalającego

użytkownikowi na projektowanie układu prostokątnych barier potencjalnych (ich wysokości i

szerokości) oraz wyznaczanie, dla zaprojektowanego układu barier, współczynnika

tunelowania i transmisji cząstek kwantowych.

Przenikanie cząstek przez bariery potencjału o skończonej grubości jest efektem

czysto kwantowym, nie dającym się uzasadnić na gruncie fizyki klasycznej. W fizyce

atomowej jednak wykryto zjawiska nie dające się wytłumaczyć inaczej niż jako przenikanie

przez bariery potencjału, co zostało nazwane efektem tunelowym [1], [2]. Jądra atomów

utrzymywane są w całości silnym potencjałem przypominającym zwężający się na szczycie

wał. Energie nukleonów, z których są zbudowane jądra nawet w stanach wzbudzonych mają

energie mniejszą od wysokości tego wału potencjału. Pomimo tego obserwujemy przenikanie

cząstek α na zewnątrz pola oddziaływań jądrowych [3]. W ten sposób można rozumieć

zjawisko promieniotwórczości, samorzutne rozszczepianie się niektórych jąder, tzw. zimną

emisję elektronów z metalu, zjawiska kontaktowe w ciałach stałych i inne.

Fakt, że cząstki o energii wyższej od bariery potencjału również ulegają rozproszeniu

jest tłumaczony znaczną zmianą pędu (zależnego od potencjału ) [4].

W następnym rozdziale przedstawiamy krótkie wprowadzenie do zjawiska

tunelowania w ramach mechaniki kwantowej. Rozdział trzeci zawiera analizę ilościową

zjawiska tunelowania w przypadku jednowymiarowym, oraz przykład tunelowania

obserwowany w mikroelektronice. W rozdziale czwartym przedstawimy niezbędne

przekształcenia

numeryczne

wykorzystywane

w

zaprojektowanym

ś

rodowisku

programowym. Rozdział piąty zawiera opis środowiska programowego. Rozdział szósty jest

poświęcony prezentacji wybranych wyników i ich porównaniu z wynikami analitycznymi.

W rozdziale

siódmym

i

ósmym

przedstawiono

odpowiednio

wnioski

końcowe

i podsumowanie pracy. Ostatni rozdział zawiera spis literatury.

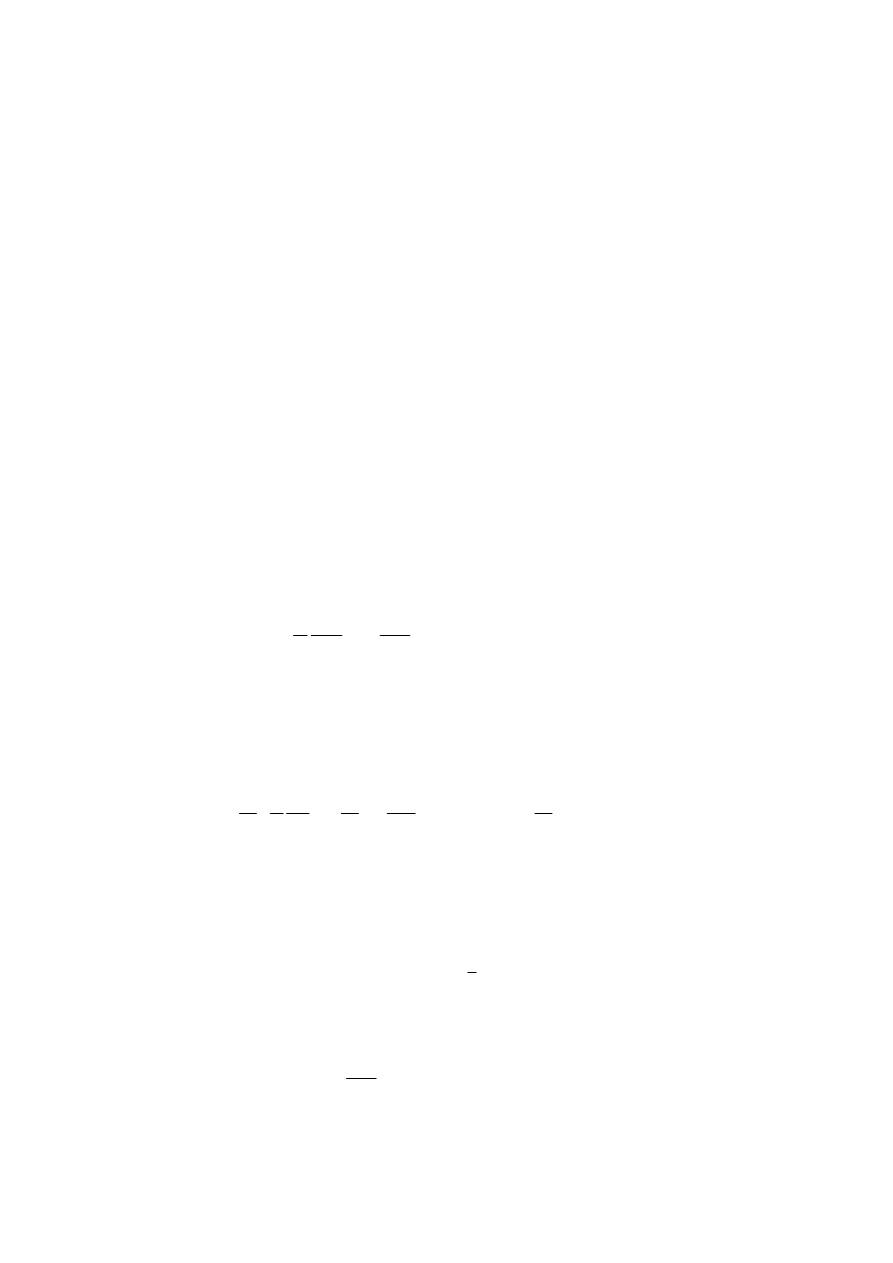
5

2. Równanie Schrödingera

Przełom wieków XIX i XX zaowocował eksperymentami, które ukazywały dualność

natury na poziomie atomowym. Falowe własności cząstek i korpuskularność promieniowania

wynikające z tych doświadczeń stały w jawnej sprzeczności z ówczesną wiedzą. Fizyka

klasyczna precyzyjnie określała położenia cząstek. Ponadto wiadomo było że cząstki

elementarne są niepodzielne – nie można zaobserwować lub uzyskać połówki elektronu.

Natomiast fale można dzielić, ale nie można ich precyzyjnie zlokalizować. Fale posiadają

długość λ i częstotliwość υ i są rozciągnięte w czasoprzestrzeni.

Ta dualność stawia nas przed dylematem: opis cząstki zdaje się być niekompatybilny

z opisem fali, w szczególności, w przypadku zjawiska interferencji. Relacje de Broglie’a,

p = h /

λ

, oraz Bohr’a, E = h υ, określają dynamiczne własności cząstki, właśnie dzięki

zjawisku interferencji .

Równanie Schrödingera dla cząstki poruszającej się pod wpływem niezależnej od

czasu siły potencjalnej [5]:

Ψ

=

Ψ

+

Ψ

∇

−

=

∂

Ψ

∂

−

H

V

m

t

i

2

2

2

h

h

(2.1)

może zostać przekształcone na niezależne od czasu równanie funkcji

(

)

z

y

x

,

,

ψ

zakładając, że

( ) (

)

z

y

x

t

f

,

,

ψ

=

Ψ

,

(2.2)

skąd otrzymujemy

{ }

.

1

2

1

1

2

2

const

H

V

m

t

f

i

f

=

=













+

∇

−

=













∂

∂

−

ψ

ψ

ψ

ψ

ψ

h

h

(2.3)

Ponieważ musi to być prawdziwe dla wszystkich wartości t oraz x, y, z, lewa i prawa

strona równania muszą być równe stałej.

Fizyczne znaczenie stałej może być rozumiane jako energia E

( )

,

Et

i

e

t

f

h

−

=

(2.4)

oraz

ψ

ψ

ψ

E

V

m

=

+

∇

−

2

2

2

h

.

(2.5)

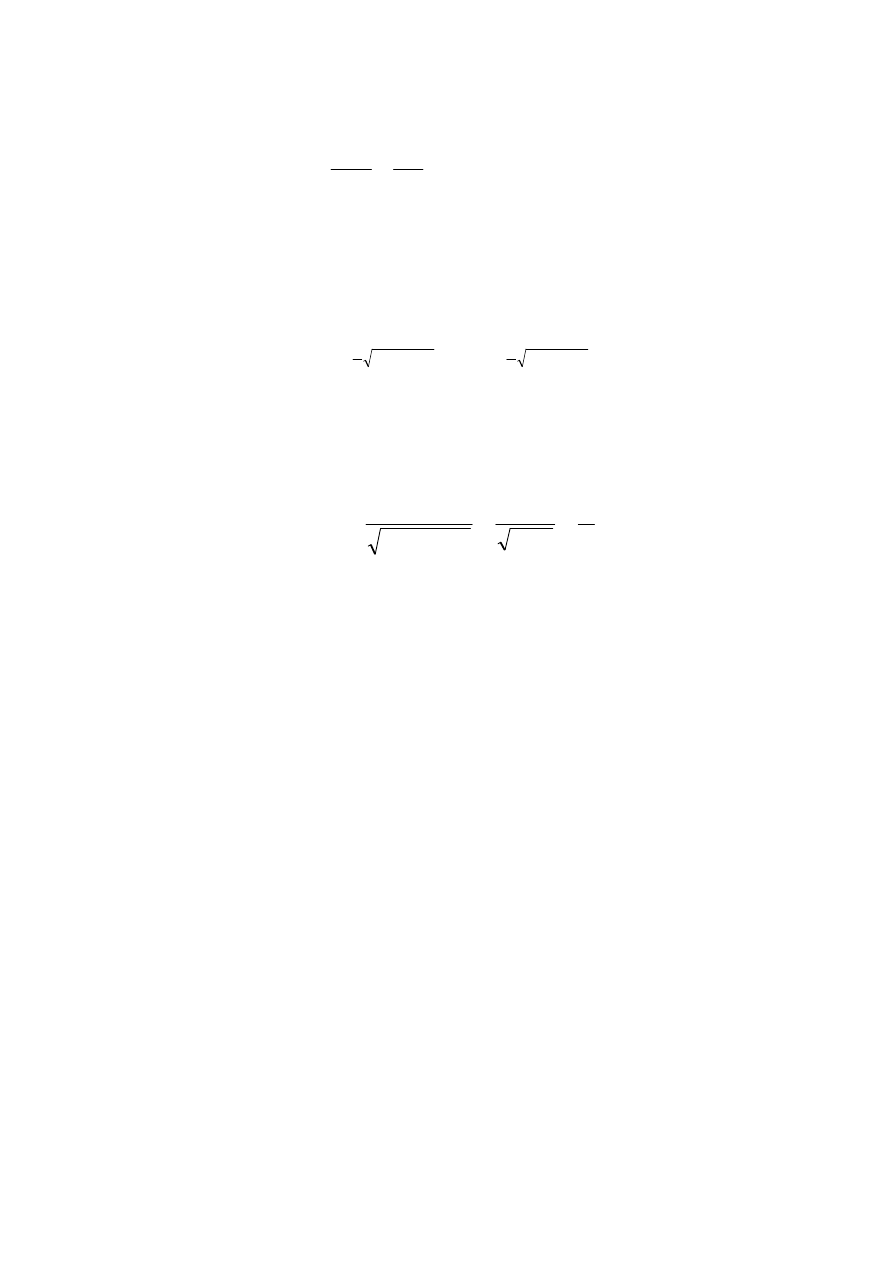
6

W szczególności dla jednego wymiaru

( )

(

)

.

0

2

2

2

2

=

−

+

ψ

ψ

x

V

E

m

dx

d

h

(2.6)

Załóżmy, że potencjał oraz energia całkowita cząstki E są stałe. Wtedy energia

kinetyczna

T = E – V = p

2

/ 2ma

(2.7)

a ogólne rozwiązanie równania (2.6) ma postać

(

)

(

)

x

V

E

m

i

x

V

E

m

i

Be

Ae

−

−

−

+

=

2

2

h

h

ψ

(2.8)

gdzie A i B są stałymi całkowania [6].

Widzimy, że stanowi ono superpozycję dwóch fal biegnących w przeciwnych

kierunkach. Długość tych fal odpowiada długości fali de Broglie’a

(

)

p

h

mT

h

V

E

m

=

=

−

=

2

2

2 h

π

λ

.

(2.9)

7

3. Tunelowanie – analiza ilo

ś

ciowa zjawiska

Wyobraźmy sobie teraz strumień cząstek padających z x = -∞ na barierę potencjału

zadaną wzorem







≤

≤

>

<

=

a

x

V

a

x

x

V

0

,

lub

0

,

0

0

.

(3.1)

Eksperymentalnie możemy zauważyć, że nie wszystkie cząstki o energii większej niż

wysokość bariery potencjału są rejestrowane po drugiej stronie bariery, gdzie wykrywamy

cząstki o energii niższej od bariery.

Tunelowanie można opisać jako zjawisko kwantowe polegające na przejścia cząstki

kwantowej pomiędzy dwoma obszarami dozwolonymi, o jednakowej energii, poprzez

oddzielającą je barierę potencjału o większej energii.

Przykładem omawianego zjawiska może być tunelowanie elektronów poprzez bariery

tlenkowe [4], co bezpośrednio prowadzi do wycieku prądu w tranzystorach polowych

(MOSFET). Jest to podstawowym ograniczeniem w postępującej miniaturyzacji układów

elektronicznych. Dla ścieżek nanoskopowych rozmiarach, tranzystor nie może poprawnie

funkcjonować ponieważ obserwujemy znaczne i niepożądane efekty tunelowania nośników

prądu przez nanoelementy układu elektronicznego.

Analiza ilościowa jednowymiarowego zjawiska tunelowania jest prowadzona w

ramach równania Schrödingera

(

)

,

0

2

0

2

2

=

Ψ

−

+

Ψ

∇

−

E

V

m

h

(3.2)

które rozwiązujemy po obu stronach oraz wewnątrz bariery.

Wyobraźmy sobie cząstkę o energii

0

E opisywaną funkcją falową Ψ(x) padającą na

barierę potencjału opisaną (3.1), o wysokości

0

0

E

V

>

. Wtedy funkcja falowa ma postać:

( )

( )

( )

( )











≥

=

≤

≤

+

=

≤

+

=

=

Ψ

−

−

a

x

Ee

x

a

x

De

Ce

x

x

Be

Ae

x

x

x

ik

x

ik

x

ik

x

ik

x

ik

3

2

2

1

1

3

2

1

0

0

ϕ

ϕ

ϕ

(3.3)

gdzie

(

)

2

0

0

2

2

2

0

2

1

2

2

h

h

E

V

m

k

,

mE

k

−

=

=

.

8

Naszym zadaniem będzie obliczenie prawdopodobieństwa (szansy) na zajście

zjawiska tunelowania przy określonych parametrach modelu (energia i masa cząstki;

szerokość i wysokość bariery). W tym celu obliczamy współczynniki transmisji T i odbicia R

.

2

2

2

2

A

B

R

i

A

E

T

=

=

(3.4)

Funkcja falowa musi być klasy C1, a więc ciągła wraz ze swoją pochodną.

W szczególności ciągłość musi być zachowana w miejscach zszycia funkcji, a więc na

granicy barier

(

)

(

)

(

)















=

−

=

+

−

=

−

+

=

+

−

−

a

ik

a

k

a

k

a

ik

a

k

a

k

Ee

ik

De

Ce

k

Ee

De

Ce

D

C

k

B

A

ik

D

C

B

A

1

2

2

1

2

2

1

2

2

1

.

(3.5)

Dwa ostatnie równania pozwalają wyznaczyć wartości współczynników C i D

(

)

(

)

,

1

2

,

1

2

2

1

2

1

2

1

2

1

a

k

ik

a

k

ik

e

k

k

i

E

D

e

k

k

i

E

C

+

−













−

=













+

=

(3.6)

co po podstawieniu do dwóch pierwszych równań daje

( )

( )

( )

( )

( )

.

sh

ch

2

2

,

sh

ch

2

sh

1

2

2

1

2

1

2

2

2

1

2

2

1

2

1

2

2

2

2

2

1

2

2

2

1

1

−

−

−













−

+

=













−

+

+

−

=

a

k

k

k

k

k

i

a

k

e

A

E

a

k

k

k

k

k

i

a

k

a

k

k

k

k

k

i

A

B

a

ik

(3.7)

Znając zależności (3.7) można przystąpić do wyznaczania współczynników (3.4)

( )

( )

( )

( )

( )

( )

(

)

( )

1

2

2

2

2

1

2

2

2

1

1

2

2

2

2

1

2

2

2

1

1

2

2

2

2

1

2

1

2

2

2

2

2

2

1

2

2

2

2

1

2

1

2

2

2

2

2

2

2

2

1

2

2

2

1

2

2

sh

4

1

1

sh

4

sh

ch

4

4

sh

ch

4

sh

2

2

−

=

−

−

−





























+

+

=













+

=

⇒





























−

+

=

=





























−

+













+

=

=

a

k

k

k

k

k

T

a

k

k

k

k

k

T

R

a

k

k

k

k

k

a

k

A

E

T

a

k

k

k

k

k

a

k

a

k

k

k

k

k

A

B

R

x

sh

x

ch

(3.8)

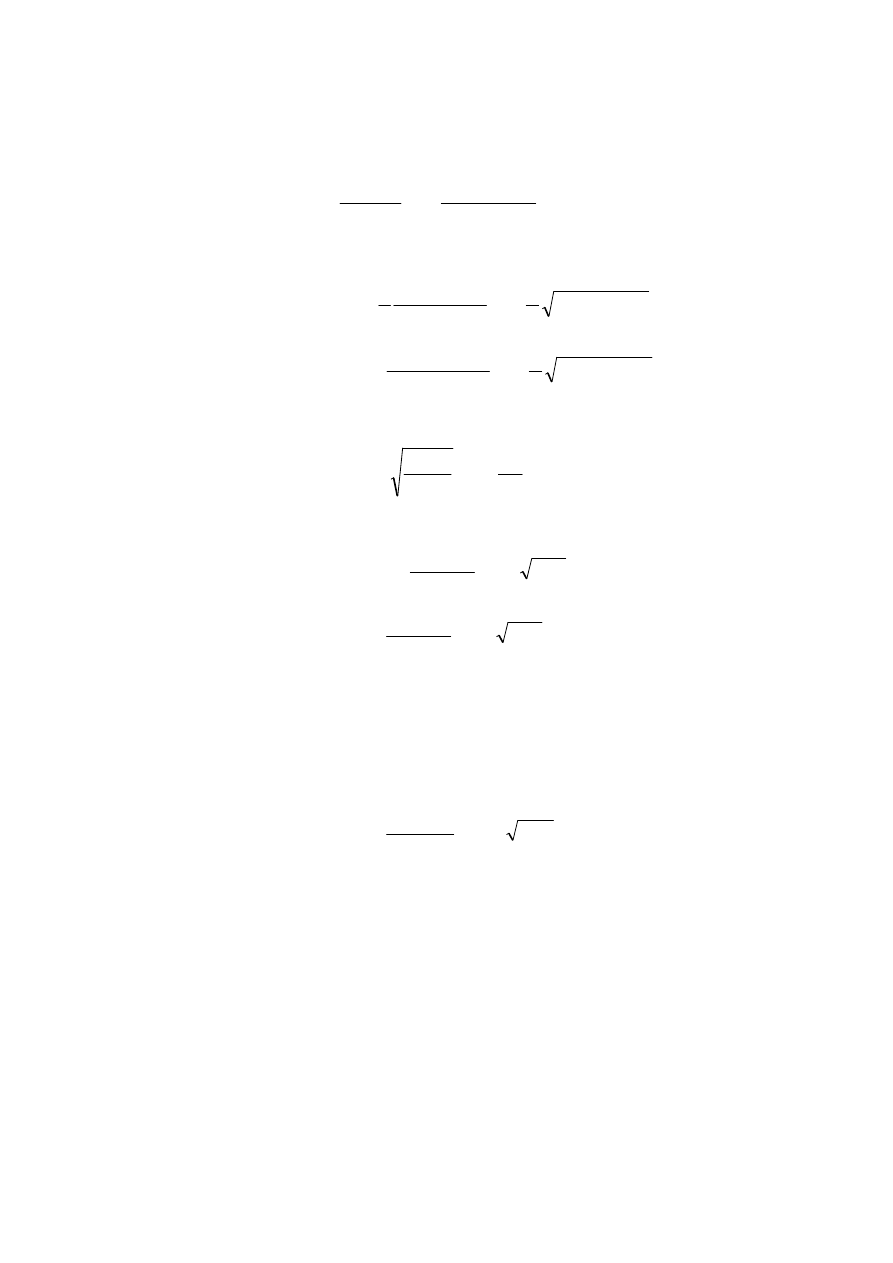
9

Współczynniki odbicia i transmisji można przedstawić na kilka sposobów. Korzystając

z zależności

(

)

0

0

0

2

0

2

2

1

2

2

2

1

E

V

E

V

k

k

k

k

−

=













+

(3.9)

uzyskujemy

(

)

(

)

(

)

(

)

1

0

0

2

0

0

0

2

0

0

0

2

0

0

0

2

0

2

sh

4

1

2

sh

4

1

−

























−

−

+

=













−

−

=

E

V

m

a

E

V

E

V

T

E

V

m

a

E

V

E

T

V

R

h

h

(3.10)

a podstawiając do (3.10)

0

0

2

0

2

V

E

mV

a

=

=

ε

λ

i

h

(3.11)

ostatecznie otrzymujemy

( )

(

)

( )

(

)

R

ε

λ

ε

ε

T

ε

λ

ε

ε

T

R

−

=













−

−

+

=

−

−

=

−

1

1

sh

1

4

1

1

1

sh

1

4

1

2

2

(3.12)

Powyższe wzory (3.8, 3.10, 3.12) są analitycznymi formułami dla pojedynczej

prostokątnej bariery przy założeniu, że energia cząstki jest mniejsza od wysokości bariery.

Jeżeli energia cząstki jest większa od wysokości bariery analityczny wzór na

współczynnik przejścia przyjmuje następującą postać:

(

)

(

)

R

T

−

=













−

−

+

=

=

1

1

sin

1

4

1

1

1

2

ε

λ

ε

ε

(3.13)

Poniżej opisane środowisko obliczeniowe korzysta z metod numerycznych, opisanych

w następnym rozdziale, pozwalających na obliczanie współczynnika transmisji przez kilka

rodzajów barier potencjału, zaprojektowanych przez użytkownika z klawiatury PC lub po

wczytaniu parametrów modelu.

10

4. Macierze przej

ść

Macierze przejścia wyliczam korzystając z warunków ciągłości funkcji falowej i jej

pierwszej pochodnej w punktach charakterystycznych potencjału.

Zaprezentuję macierze dla wszystkich rozpatrywanych rodzajów przejść cząstki

kwantowej przez granice barier potencjalnych.

Najprostszy wariant to bariera prostokątna. Do opisania wszystkich możliwych

przypadków wystarczą cztery macierze przejścia: M

1

, M

2

, M

3

, M

4

(patrz rys.4.1).

Rys.4.1. Prostokątna bariera potencjału z zaznaczonymi 4 różnymi macierzami przejścia.

Jeżeli pójdziemy krok dalej, to uzyskamy barierę schodkową. By rozpatrzyć wszystkie

przypadki potrzeba sześciu macierzy: czterech przedstawionych wyżej, oraz M

5

, M

6

(patrz

rys.4.2)

Rys.4.2. Prostokątna bariera potencjału z zaznaczonymi 6 macierzami przejścia.

M

1

M

2

M

3

M

4

M

1

M

2

M

3

M

4

M

5

M

6

11

We wszystkich rozpatrywanych w pracy przypadkach cząstki kwantowe padają

z lewej strony na bariery potencjalne.

Poniżej przedstawiamy kolejno jawne postacie macierzy przejść odpowiadających

przypadkom: cząstka wchodzi do obszaru o wyższym potencjale (

M

1

); cząstka wchodzi do

obszaru o niższym potencjale (

M

2

).

4.1. Macierz przej

ś

cia M

1

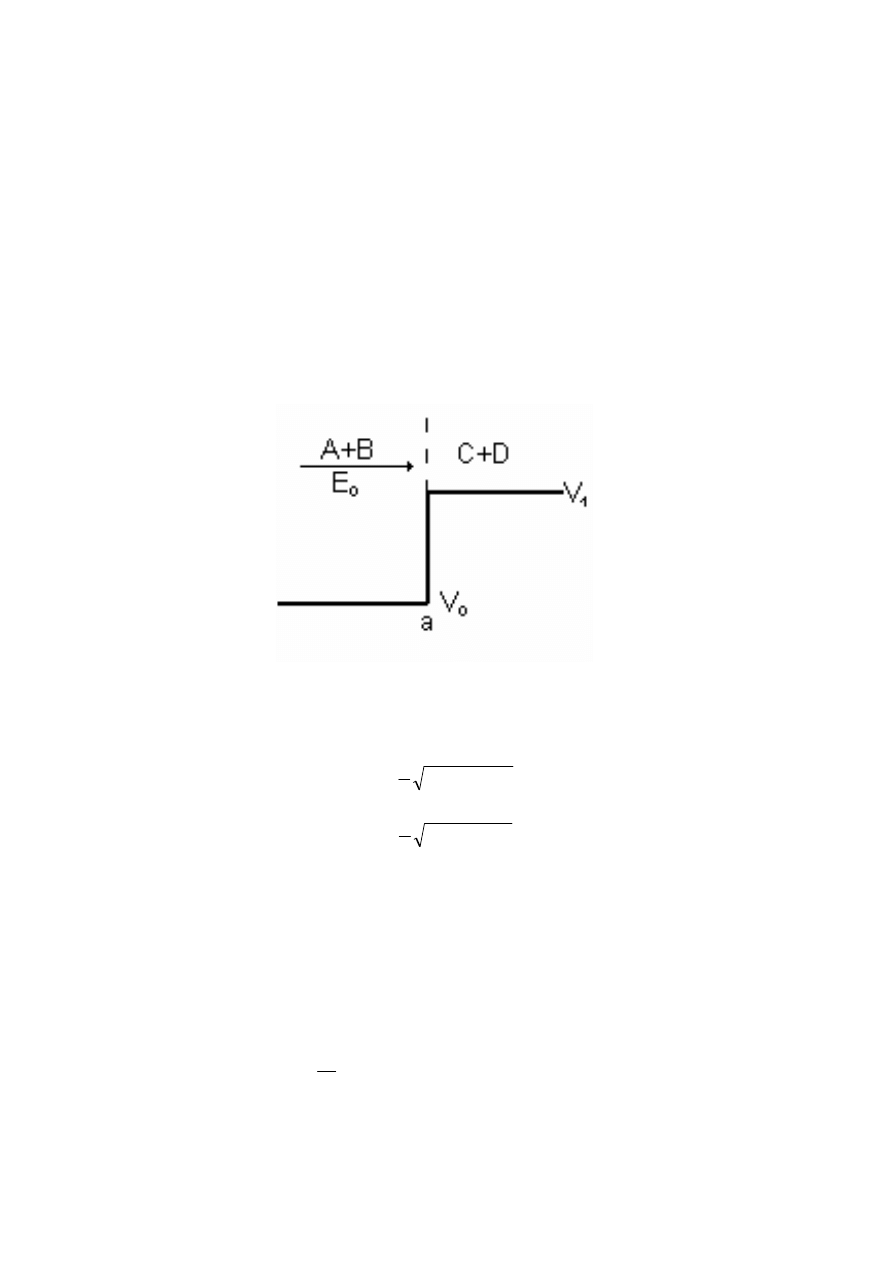
W tym przypadku cząstki mają energię E

0

większą od wysokości bariery (rys.4.3),

a wektor falowy jest rzeczywisty po obu stronach bariery.

Rys.4.3. Skok potencjału; cząstka kwantowa ma energię większą od wysokości bariery.

Dwie pierwsze macierze dotyczą przypadku E

0

> V

1

> V

0

. Stosujemy następujące

oznaczenia:

(

)

0

0

2

1

V

E

m

k

−

=

h

,

(4.1.1)

(

)

1

0

2

1

'

V

E

m

k

−

=

h

.

(4.1.2)

Z warunków ciągłości otrzymujemy







−

=

−

+

=

+

−

−

−

−

'

:

/

'

'

'

'

'

'

ik

De

ik

Ce

ik

ikBe

ikAe

De

Ce

Be

Ae

a

ik

a

ik

ika

ika

a

ik

a

ik

ika

ika

.

(4.1.3)

Poniżej prezentujemy (4.1.4 – 4.1.11) wyprowadzenie elementów macierzy przejścia

M

1

. Przytaczamy jedynie wzory bez zbytecznych komentarzy.

(

)

a

ik

a

ik

ika

ika

De

Ce

Be

Ae

k

k

'

'

'

−

−

−

=

−

,

(4.1.4)

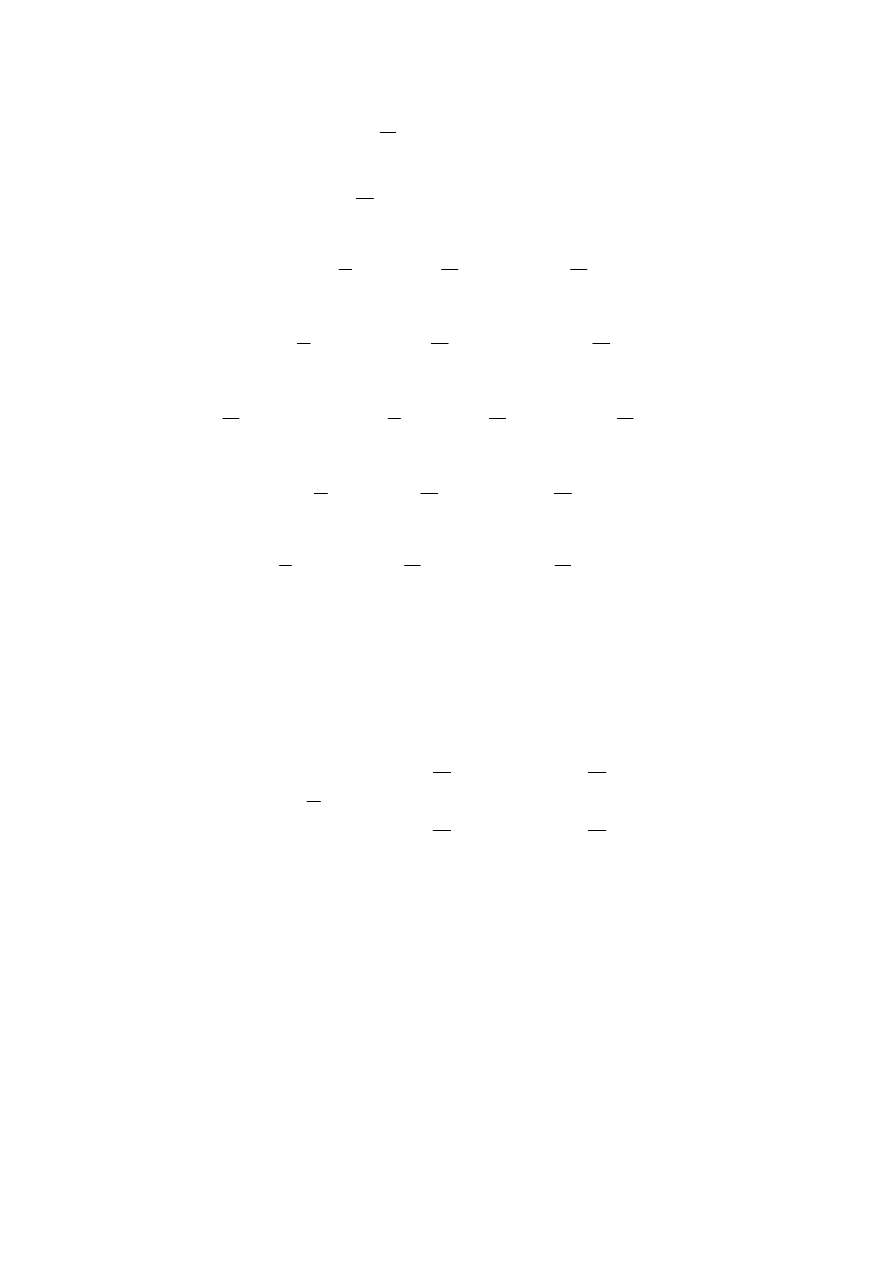
12

(

)

a

ik

ika

ika

a

ik

De

Be

Ae

k

k

Ce

'

'

'

−

−

+

−

=

,

(4.1.5)

(

)

a

ik

a

ik

ika

ika

ika

ika

De

De

Be

Ae

k

k

Be

Ae

'

'

'

−

−

−

−

+













+

−

=

+

,

(4.1.6)

























+

+













−

=

−

−

'

1

'

1

2

1

'

k

k

Be

k

k

Ae

De

ika

ika

a

ik

,

(4.1.7)

(

)

(

)

























+

+













−

=

−

−

+

'

1

'

1

2

1

'

'

k

k

Be

k

k

Ae

D

a

k

k

i

a

k

k

i

,

(4.1.8)

(

)







































+

+













−

+

−

=

−

−

'

1

'

1

2

1

'

'

k

k

Be

k

k

Ae

Be

Ae

k

k

Ce

ika

ika

ika

ika

a

ik

,

(4.1.9)

























−

+













+

=

−

'

1

'

1

2

1

'

k

k

Be

k

k

Ae

Ce

ika

ika

a

ik

,

(4.1.10)

(

)

(

)

























−

+













+

=

+

−

−

'

1

'

1

2

1

'

'

k

k

Be

k

k

Ae

C

a

k

k

i

a

k

k

i

.

(4.1.11)

Składamy (4.1.11) i (4.1.8) w macierz













=













B

A

M

D

C

1

,

(4.1.12)

gdzie

(

)

(

)

(

)

(

)

.

'

1

'

1

'

1

'

1

2

1

'

'

'

'

1





































+













−













−













+

=

−

−

+

+

−

−

k

k

e

k

k

e

k

k

e

k

k

e

M

a

k

k

i

a

k

k

i

a

k

k

i

a

k

k

i

(4.1.13)

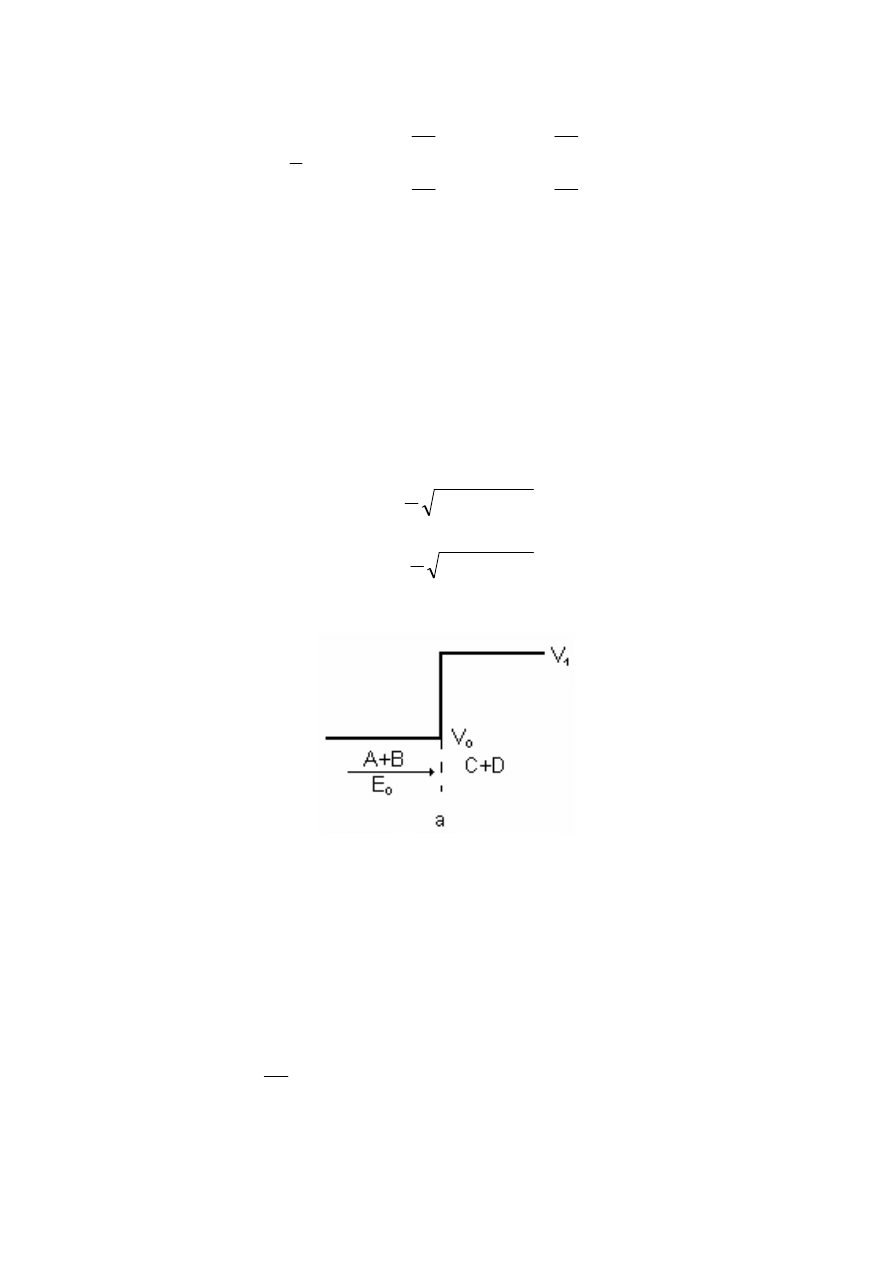
4.2. Macierz przej

ś

cia M

2

Oznaczenia (4.1.1) i (4.1.2) nadal są aktualne, ale tym razem mamy do czynienia

z wychodzeniem cząstki kwantowej z obszaru podwyższonego potencjału (rys.4.4).

13

Rys.4.4 Skok potencjału; cząstka kwantowa ma energię większą od „stopnia” bariery.

Jak w poprzednim przypadku wychodzimy z warunków ciągłości funkcji falowej i jej

pierwszej pochodnej i dalej prowadzimy obliczenia analogicznie do przedstawionych

wcześniej







−

=

−

+

=

+

−

−

−

−

ikb

ikb

b

ik

b

ik

ikb

ikb

b

ik

b

ik

Fe

ik

Ee

ik

De

ik

Ce

ik

Fe

Ee

De

Ce

'

'

'

'

'

'

'

'

,

(4.2.1)

(

)

ikb

ikb

b

ik

b

ik

Fe

Ee

De

Ce

k

k

−

−

−

=

−

'

'

'

,

(4.2.2)

(

)

ikb

b

ik

b

ik

ikb

Fe

De

Ce

k

k

Ee

−

−

+

−

=

'

'

'

,

(4.2.3)

(

)

ikb

ikb

b

ik

b

ik

b

ik

b

ik

Fe

Fe

De

Ce

k

k

De

Ce

−

−

−

−

+













+

−

=

+

'

'

'

'

'

,

(4.2.4)

























+

+













−

=

−

−

k

k

De

k

k

Ce

Fe

b

ik

b

ik

ikb

'

1

'

1

2

1

'

'

,

(4.2.5)

(

)

(

)

























+

+













−

=

−

−

+

k

k

De

k

k

Ce

F

b

k

k

i

b

k

k

i

'

1

'

1

2

1

'

'

,

(4.2.6)

(

)







































+

+













−

+

−

=

−

−

k

k

De

k

k

Ce

De

Ce

k

k

Ee

b

ik

b

ik

b

ik

b

ik

ikb

'

1

'

1

2

1

'

'

'

'

'

, (4.2.7)

























−

+













+

=

−

k

k

De

k

k

Ce

Ee

b

ik

b

ik

ikb

'

1

'

1

2

1

'

'

,

(4.2.8)

14

(

)

(

)

























−

+













+

=

+

−

−

k

k

De

k

k

Ce

E

b

k

k

i

b

k

k

i

'

1

'

1

2

1

'

'

,

(4.2.9)













=













D

C

M

F

E

2

,

(4.2.10)

gdzie

(

)

(

)

(

)

(

)

.

'

1

'

1

'

1

'

1

2

1

'

'

'

'

2





































+













−













−













+

=

−

−

+

+

−

−

k

k

e

k

k

e

k

k

e

k

k

e

M

b

k

k

i

b

k

k

i

b

k

k

i

b

k

k

i

(4.2.11)

4.3. Macierz przej

ś

cia M

3

Teraz rozpatrzymy przypadek, gdy cząstka znajduje się „pod” barierą,

1

0

0

V

E

V

<

<

(patrz rys.4.5). Wprowadzamy nowe oznaczenie

(

)

,

2

1

0

1

1

E

V

m

−

=

ℵ

h

(4.3.1)

dla wektora falowego, gdy x > a; dla x < a dalej obowiązuje (4.1.1). Spełniona jest relacja

1

1

ℵ

=

i

k

.

(4.3.2)

Rys.4.5. Skok potencjału; cząstka kwantowa ma energię mniejszą od wysokości bariery.

Poniżej prezentujemy jawne przekształcenia prowadzące do elementów macierzy M

3







ℵ

ℵ

+

−ℵ

=

−

+

=

+

ℵ

ℵ

−

−

ℵ

−ℵ

−

1

1

:

/

1

1

1

1

a

a

ika

ika

a

a

ika

ika

De

Ce

ikBe

ikAe

De

Ce

Be

Ae

,

(4.3.3)

(

)

a

a

ika

ika

De

Ce

Be

Ae

ik

1

1

1

ℵ

ℵ

−

−

+

−

=

−

ℵ

,

(4.3.4)

15

(

)

a

ika

ika

a

De

Be

Ae

ik

Ce

1

1

1

ℵ

−

ℵ

−

+

+

−

ℵ

=

,

(4.3.5)

(

)

a

a

ika

ika

ika

ika

De

De

Be

Ae

ik

Be

Ae

1

1

1

ℵ

ℵ

−

−

+













+

+

−

ℵ

=

+

,

(4.3.6)



























ℵ

−

+













ℵ

+

=

−

ℵ

1

1

1

1

2

1

1

ik

Be

ik

Ae

De

ika

ika

a

,

(4.3.7)

(

)

(

)



























ℵ

−

+













ℵ

+

=

ℵ

+

−

ℵ

−

1

1

1

1

2

1

1

1

ik

Be

ik

Ae

D

a

ik

a

ik

,

(4.3.8)

(

)









































ℵ

−

+













ℵ

+

+

+

−

ℵ

=

−

−

ℵ

−

1

1

1

1

1

2

1

1

ik

Be

ik

Ae

Be

Ae

ik

Ce

ika

ika

ika

ika

a

, (4.3.9)



























ℵ

+

+













ℵ

−

=

−

ℵ

−

1

1

1

1

2

1

1

ik

Be

ik

Ae

Ce

ika

ika

a

,

(4.3.10)

(

)

(

)



























ℵ

+

+













ℵ

−

=

ℵ

+

ℵ

+

1

1

1

1

2

1

1

1

ik

Be

ik

Ae

C

a

ik

a

ik

,

(4.3.11)













=













B

A

M

D

C

3

,

(4.3.12)

gdzie

(

)

(

)

(

)

(

)

.

1

1

1

1

2

1

1

1

1

1

3

1

1

1

1









































ℵ

−













ℵ

+













ℵ

+













ℵ

−

=

ℵ

+

−

ℵ

−

ℵ

−

−

ℵ

+

ik

e

ik

e

ik

e

ik

e

M

a

ik

a

ik

a

ik

a

ik

(4.3.13)

4.4. Macierz przej

ś

cia M

4

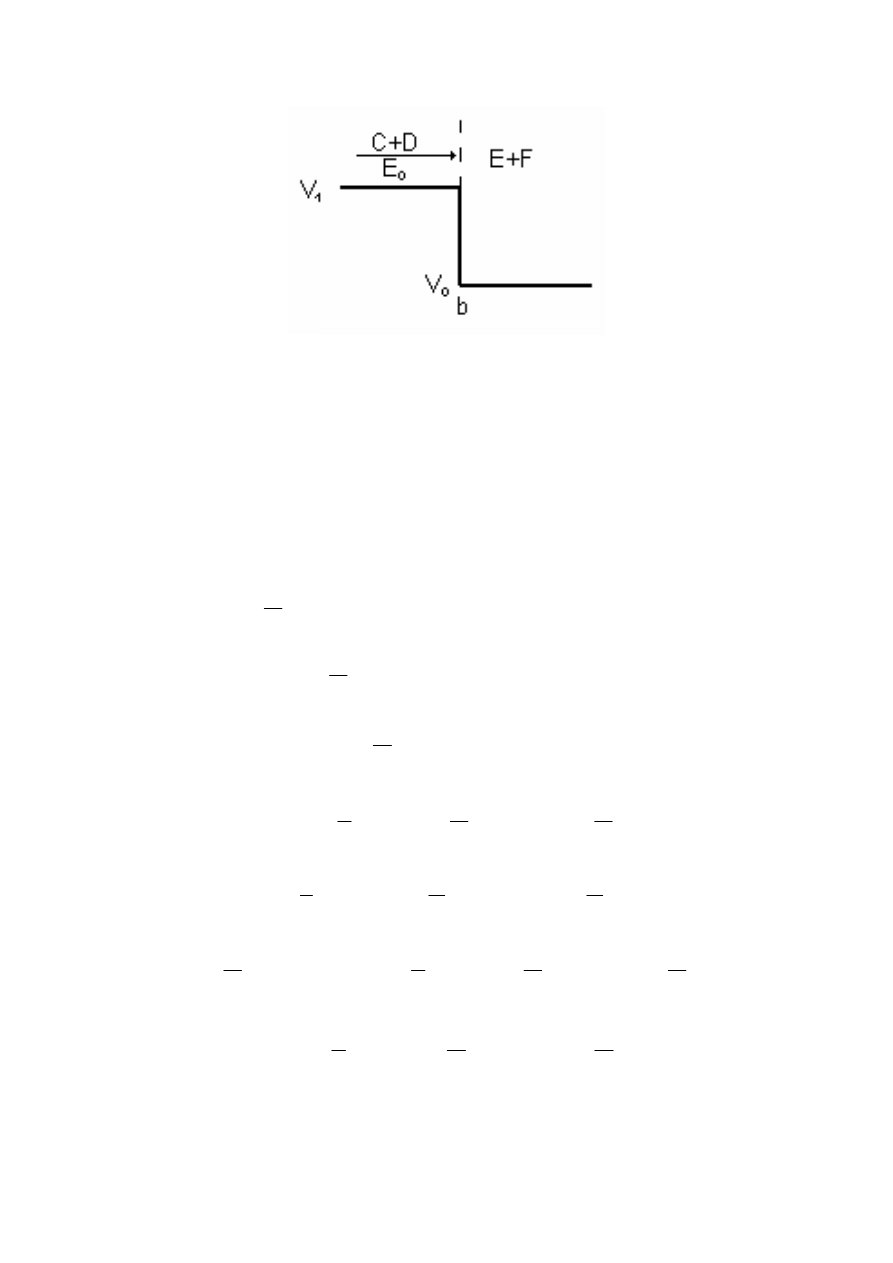
Stosujemy oznaczenia (4.1.1) oraz (4.3.1). Rozpatrujemy przypadek tunelowanie,

który ilustruje rysunek 4.6.

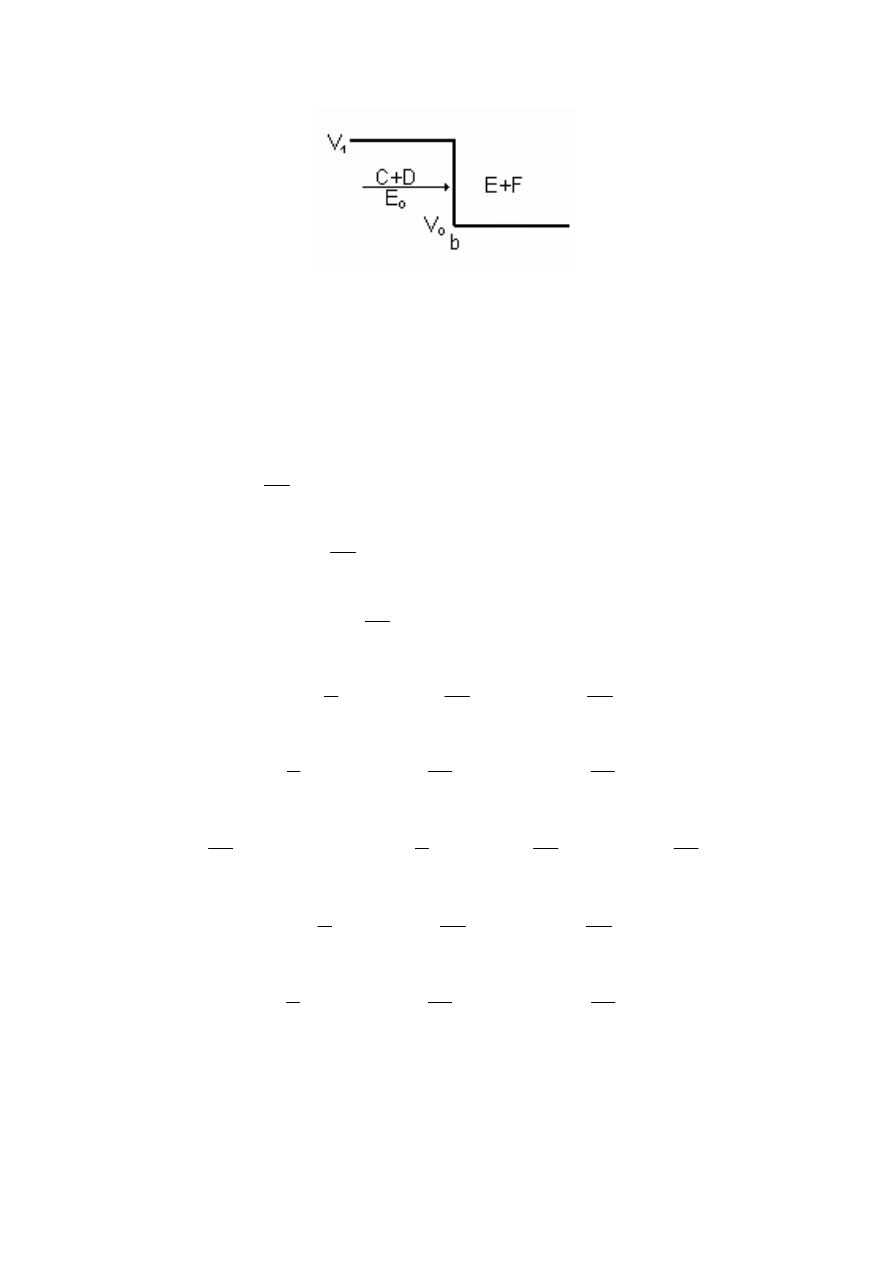
16

Rys.4.6. Skok potencjału; cząstka kwantowa ma energię mniejszą od wysokości bariery.

Wyprowadzenie wyrażeń na elementy macierzy M

4







−

=

ℵ

+

ℵ

−

+

=

+

−

ℵ

ℵ

−

−

ℵ

ℵ

−

ikb

ikb

b

b

ikb

ikb

b

b

ikFe

ikEe

De

Ce

Fe

Ee

De

Ce

1

1

1

1

1

1

,

(4.4.1)

(

)

ikb

ikb

b

b

Fe

Ee

De

Ce

ik

−

ℵ

ℵ

−

−

=

+

−

ℵ

1

1

1

,

(4.4.2)

(

)

ikb

b

b

ikb

Fe

De

Ce

ik

Ee

−

ℵ

ℵ

−

+

+

−

ℵ

=

1

1

1

,

(4.4.3)

(

)

ikb

ikb

b

b

b

b

Fe

Fe

De

Ce

ik

De

Ce

−

−

ℵ

ℵ

−

ℵ

ℵ

−

+













+

+

−

ℵ

=

+

1

1

1

1

1

,

(4.4.4)

























ℵ

−

+













ℵ

+

=

ℵ

ℵ

−

−

ik

De

ik

Ce

Fe

b

b

ikb

1

1

1

1

2

1

1

1

,

(4.4.5)

(

)

(

)

























ℵ

−

+













ℵ

+

=

+

ℵ

−

ℵ

−

ik

De

ik

Ce

F

b

ik

b

ik

1

1

1

1

2

1

1

1

,

(4.4.6)

(

)







































ℵ

−

+













ℵ

+

+

+

−

ℵ

=

ℵ

ℵ

−

ℵ

ℵ

−

ik

De

ik

Ce

De

Ce

ik

Ee

b

b

b

b

ikb

1

1

1

1

1

2

1

1

1

1

1

,(4.4.7)

























ℵ

+

+













ℵ

−

=

ℵ

ℵ

−

ik

De

ik

Ce

Ee

b

b

ikb

1

1

1

1

2

1

1

1

,

(4.4.8)

(

)

(

)

























ℵ

+

+













ℵ

−

=

−

ℵ

+

ℵ

−

ik

De

ik

Ce

E

b

ik

b

ik

1

1

1

1

2

1

1

1

,

(4.4.9)













=













D

C

M

F

E

4

,

(4.4.10)

gdzie

17

(

)

(

)

(

)

(

)

.

1

1

1

1

2

1

1

1

1

1

4

1

1

1

1





































ℵ

−













ℵ

+













ℵ

+













ℵ

−

=

+

ℵ

−

ℵ

−

−

ℵ

+

ℵ

−

ik

e

ik

e

ik

e

ik

e

M

b

ik

b

ik

b

ik

b

ik

(4.4.11)

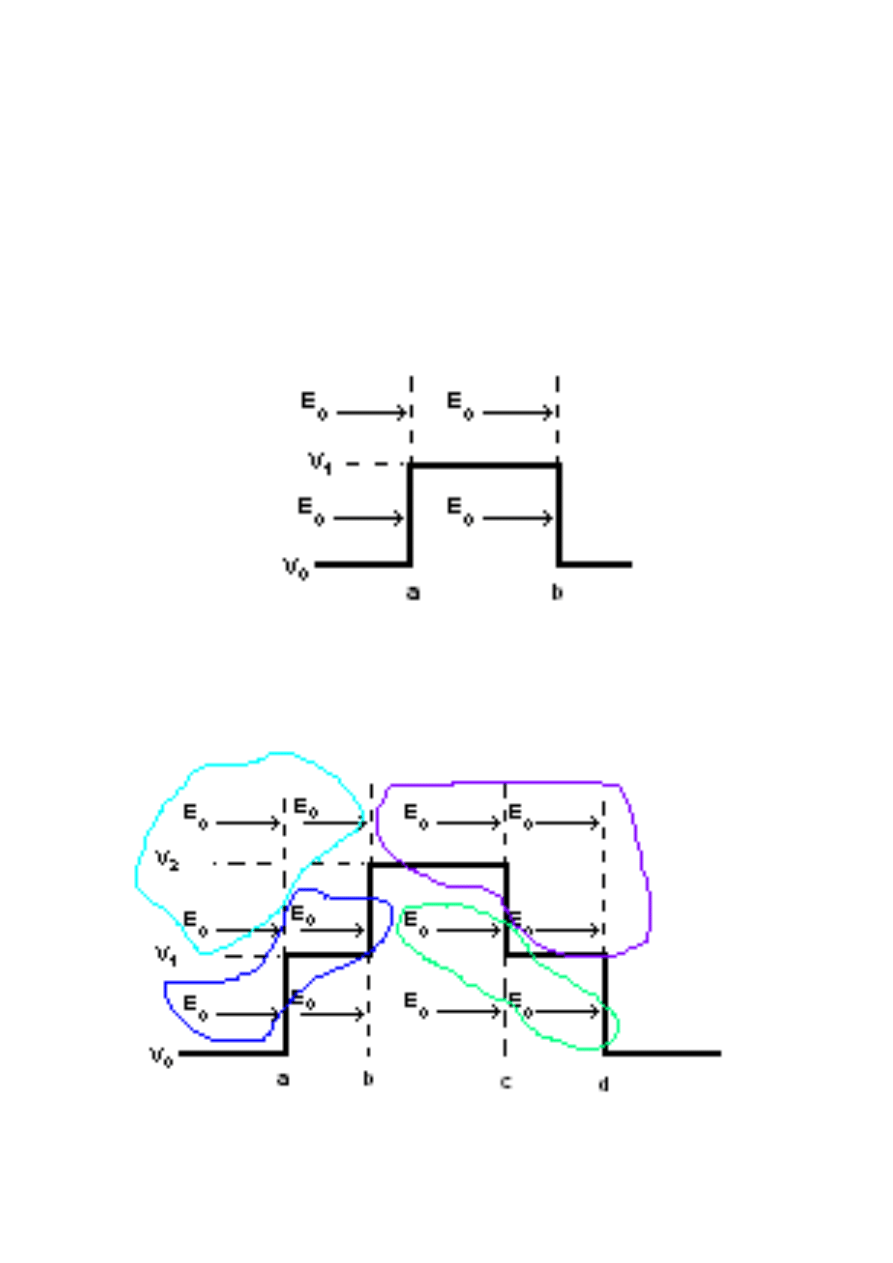
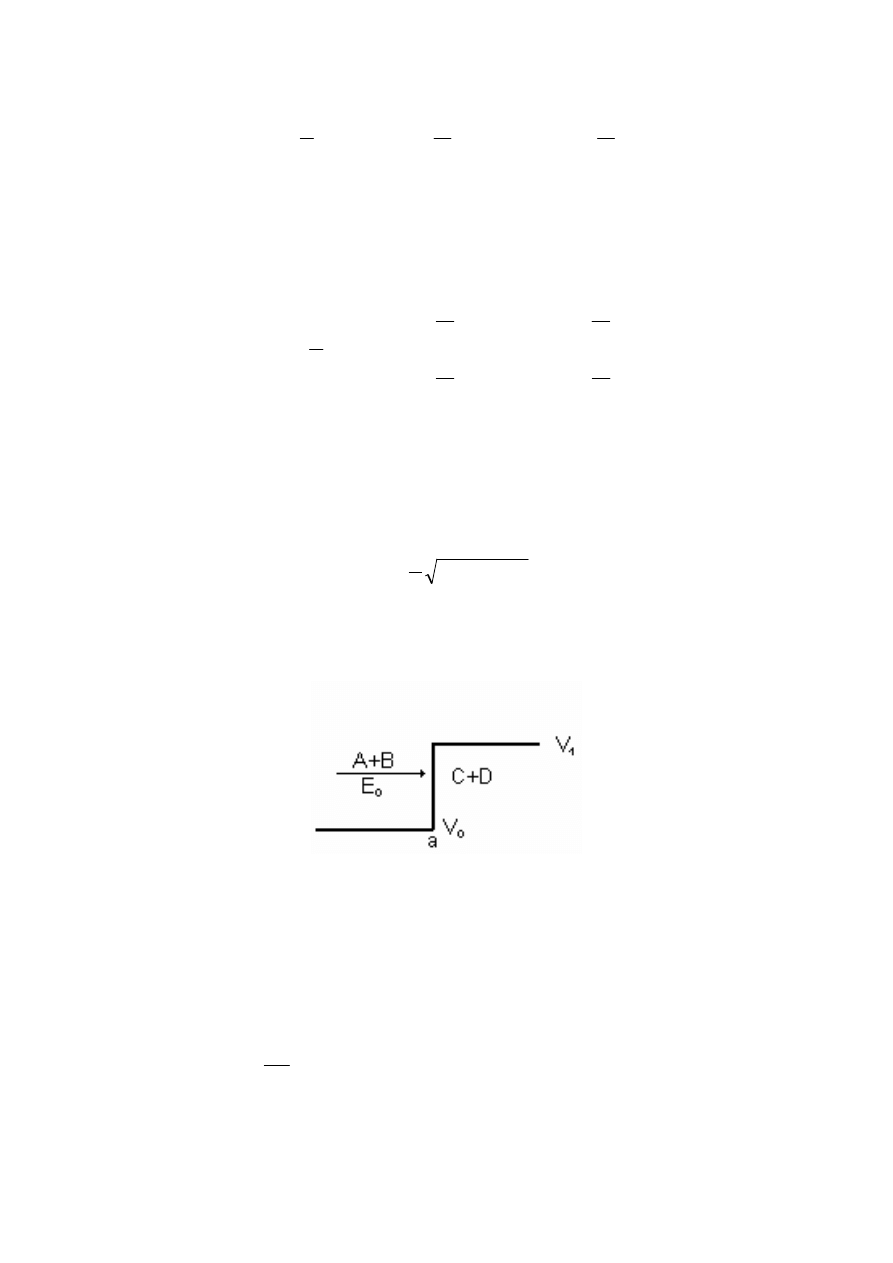
4.5. Macierz przej

ś

cia M

5

Dwie ostatnie macierze opisują przypadek cząstek, przechodzących przez granicę

dwóch potencjałów, o energiach mniejszych od wysokości potencjału: E0 < V0 < V1

(rys.4.7).

Stosujemy oznaczenia

(

)

,

2

1

0

0

E

V

m

−

=

ℵ

h

(4.5.1)

(

)

,

2

1

0

1

1

E

V

m

−

=

ℵ

h

(4.5.2)

które będą obowiązywać w tym i następnym podrozdziale.

Rys.4.7. Skok potencjału; cząstka kwantowa ma energię mniejszą od wartości potencjału na

dnie bariery.

Wyprowadzenie wyrażeń na elementy macierzy M

5







ℵ

ℵ

+

−ℵ

=

ℵ

+

ℵ

−

+

=

+

ℵ

ℵ

−

ℵ

ℵ

ℵ

−ℵ

ℵ

−ℵ

1

1

:

/

1

1

1

1

a

a

a

a

a

a

a

a

De

Ce

Be

Ae

De

Ce

Be

Ae

,

(4.5.3)

(

)

a

a

a

a

De

Ce

Be

Ae

1

1

1

ℵ

ℵ

−

ℵ

ℵ

−

+

−

=

+

−

ℵ

ℵ

,

(4.5.4)

18

(

)

a

a

a

a

De

Be

Ae

Ce

1

1

1

ℵ

ℵ

ℵ

−

ℵ

−

+

−

ℵ

ℵ

=

,

(4.5.5)

(

)

a

a

a

a

a

a

De

De

Be

Ae

Be

Ae

1

1

1

ℵ

ℵ

ℵ

ℵ

−

ℵ

ℵ

−

+













+

−

ℵ

ℵ

=

+

,

(4.5.6)



























ℵ

ℵ

+

+













ℵ

ℵ

−

=

ℵ

ℵ

−

ℵ

1

1

1

1

2

1

1

a

a

a

Be

Ae

De

,

(4.5.7)

(

)

(

)



























ℵ

ℵ

+

+













ℵ

ℵ

−

=

ℵ

−

ℵ

ℵ

+

ℵ

−

1

1

1

1

2

1

1

1

a

a

Be

Ae

D

,

(4.5.8)

(

)









































ℵ

ℵ

+

+













ℵ

ℵ

−

+

−

ℵ

ℵ

=

ℵ

ℵ

−

ℵ

ℵ

−

ℵ

−

1

1

1

1

1

2

1

1

a

a

a

a

a

Be

Ae

Be

Ae

Ce

,(4.5.9)



























ℵ

ℵ

−

+













ℵ

ℵ

+

=

ℵ

ℵ

−

ℵ

−

1

1

1

1

2

1

1

a

a

a

Be

Ae

Ce

,

(4.5.10)

(

)

(

)



























ℵ

ℵ

−

+













ℵ

ℵ

+

=

ℵ

+

ℵ

ℵ

−

ℵ

−

1

1

1

1

2

1

1

1

a

a

Be

Ae

C

,

(4.5.11)













=













B

A

M

D

C

5

,

(4.5.12)

gdzie

(

)

(

)

(

)

(

)

.

1

1

1

1

2

1

1

1

1

1

5

1

1

1

1









































ℵ

ℵ

+













ℵ

ℵ

−













ℵ

ℵ

−













ℵ

ℵ

+

=

ℵ

−

ℵ

ℵ

+

ℵ

−

ℵ

+

ℵ

ℵ

−

ℵ

−

a

a

a

a

e

e

e

e

M

(4.5.13)

19

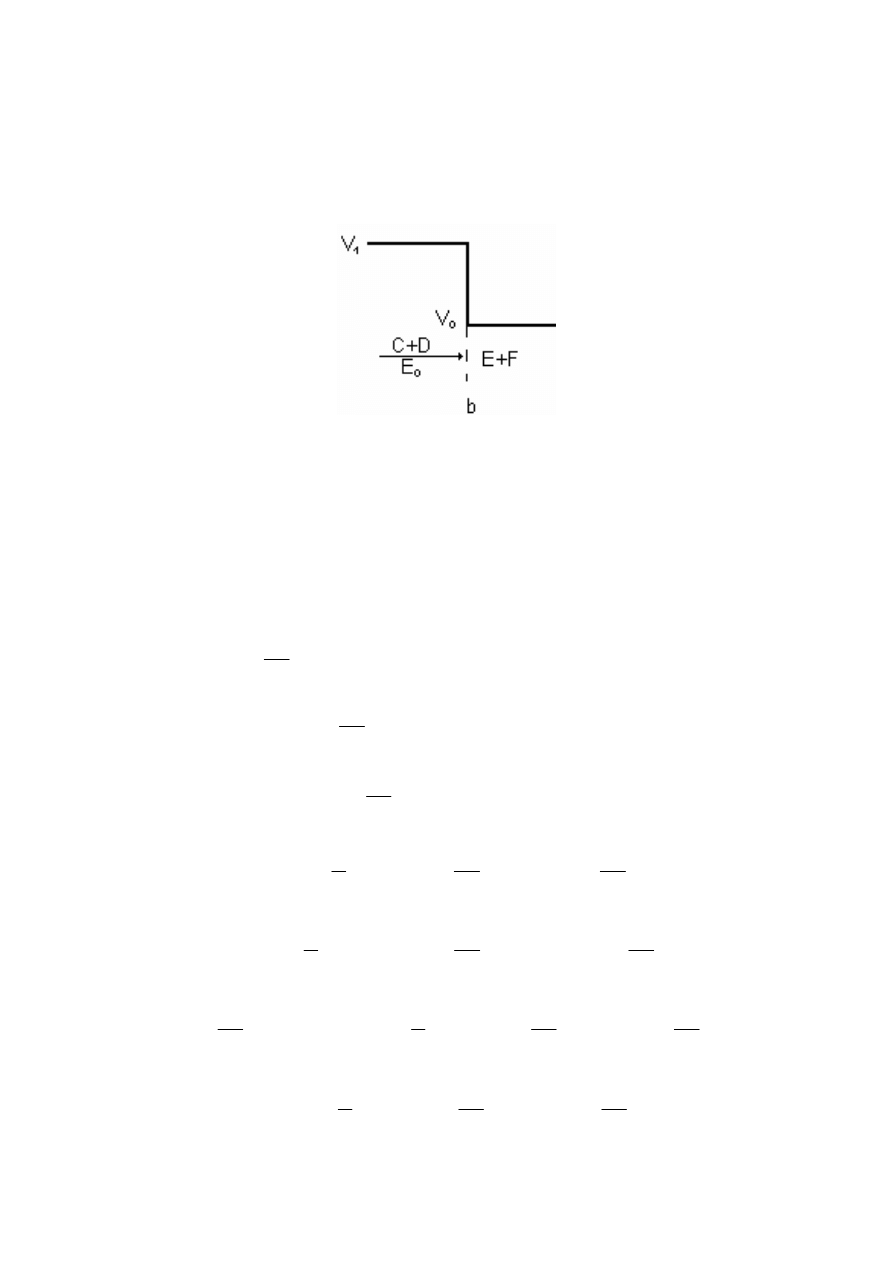
4.6. Macierz przej

ś

cia M

6

Zajmiemy się zjawiskiem przejścia cząstki przez obszar przedstawiony na rys.4.8.

Rys.4.8. Skok potencjału; cząstka kwantowa ma energię mniejszą od wartości potencjału na

dnie bariery.

Wyprowadzenie wyrażeń na elementy macierzy M

6







ℵ

ℵ

+

−ℵ

=

ℵ

+

ℵ

−

+

=

+

ℵ

ℵ

−

ℵ

ℵ

−

ℵ

−ℵ

ℵ

−ℵ

:

/

1

1

1

1

b

b

b

b

b

b

b

b

Fe

Ee

De

Ce

Fe

Ee

De

Ce

,

(4.6.1)

(

)

b

b

b

b

Fe

Ee

De

Ce

ℵ

ℵ

−

ℵ

ℵ

−

+

−

=

+

−

ℵ

ℵ

1

1

1

,

(4.6.2)

(

)

b

b

b

b

Fe

De

Ce

Ee

ℵ

ℵ

ℵ

−

ℵ

−

+

−

ℵ

ℵ

=

1

1

1

,

(4.6.3)

(

)

b

b

b

b

b

b

Fe

Fe

De

Ce

De

Ce

ℵ

ℵ

ℵ

ℵ

−

ℵ

ℵ

−

+













+

−

ℵ

ℵ

=

+

1

1

1

1

1

,

(4.6.4)

























ℵ

ℵ

+

+













ℵ

ℵ

−

=

ℵ

ℵ

−

ℵ

1

1

1

1

2

1

1

1

b

b

b

De

Ce

Fe

,

(4.6.5)

(

)

(

)

























ℵ

ℵ

+

+













ℵ

ℵ

−

=

ℵ

−

ℵ

ℵ

+

ℵ

−

1

1

1

1

2

1

1

1

b

b

De

Ce

F

,

(4.6.6)

(

)







































ℵ

ℵ

+

+













ℵ

ℵ

−

+

−

ℵ

ℵ

=

ℵ

ℵ

−

ℵ

ℵ

−

ℵ

−

1

1

1

1

1

2

1

1

1

1

1

b

b

b

b

b

De

Ce

De

Ce

Ee

,(4.6.7)

























ℵ

ℵ

−

+













ℵ

ℵ

+

=

ℵ

ℵ

−

ℵ

−

1

1

1

1

2

1

1

1

b

b

b

De

Ce

Ee

,

(4.6.8)

20

(

)

(

)

























ℵ

ℵ

−

+













ℵ

ℵ

+

=

ℵ

+

ℵ

ℵ

−

ℵ

−

1

1

1

1

2

1

1

1

b

b

De

Ce

E

,

(4.6.9)













=













D

C

M

F

E

6

,

(4.6.10)

gdzie

(

)

(

)

(

)

(

)

.

1

1

1

1

2

1

1

1

1

1

6

1

1

1

1





































ℵ

ℵ

+













ℵ

ℵ

−













ℵ

ℵ

−













ℵ

ℵ

+

=

ℵ

−

ℵ

ℵ

+

ℵ

−

ℵ

+

ℵ

ℵ

−

ℵ

−

b

b

b

b

e

e

e

e

M

(4.6.11)

4.7. Macierz transmisji

Każda z macierzy przejścia (M

1

÷ M

6

) opisuje także zmiany fazy funkcji falowej

w trakcie propagacji cząstki przez odcinek stałego potencjału.

Dysponując macierzowym opisem współczynników funkcji falowych w każdym

możliwym (dla jednowymiarowych barier) przypadku możemy przystąpić do wyznaczania

współczynnika transmisji. Dla bariery przedstawionej na rysunku 4.1 macierz transmisji

M wygląda następująco:

,

0

1

2

2













=













=













=













B

A

M

B

A

M

M

D

C

M

E

(4.7.1)

gdzie M

2

to macierz dana wzorem (4.2.11) lub (4.4.11), a M

1

definiują formuły (4.1.13) lub

(4.3.13). Macierz transmisji powstaje poprzez wymnożenie wszystkich macierzy przejścia

opisujących dany przypadek. Współczynnik transmisji T przez barierę potencjalną opisaną

macierzą M jest równy

,

1

2

11

M

T

=

(4.7.2)

gdzie

11

M

to element pierwszego wiersza z pierwszej kolumny macierzy M.

Otrzymany współczynnik transmisji opisuje prawdopodobieństwo przejścia przez

układ barier (bezpośrednio za ostatnią barierą).

21

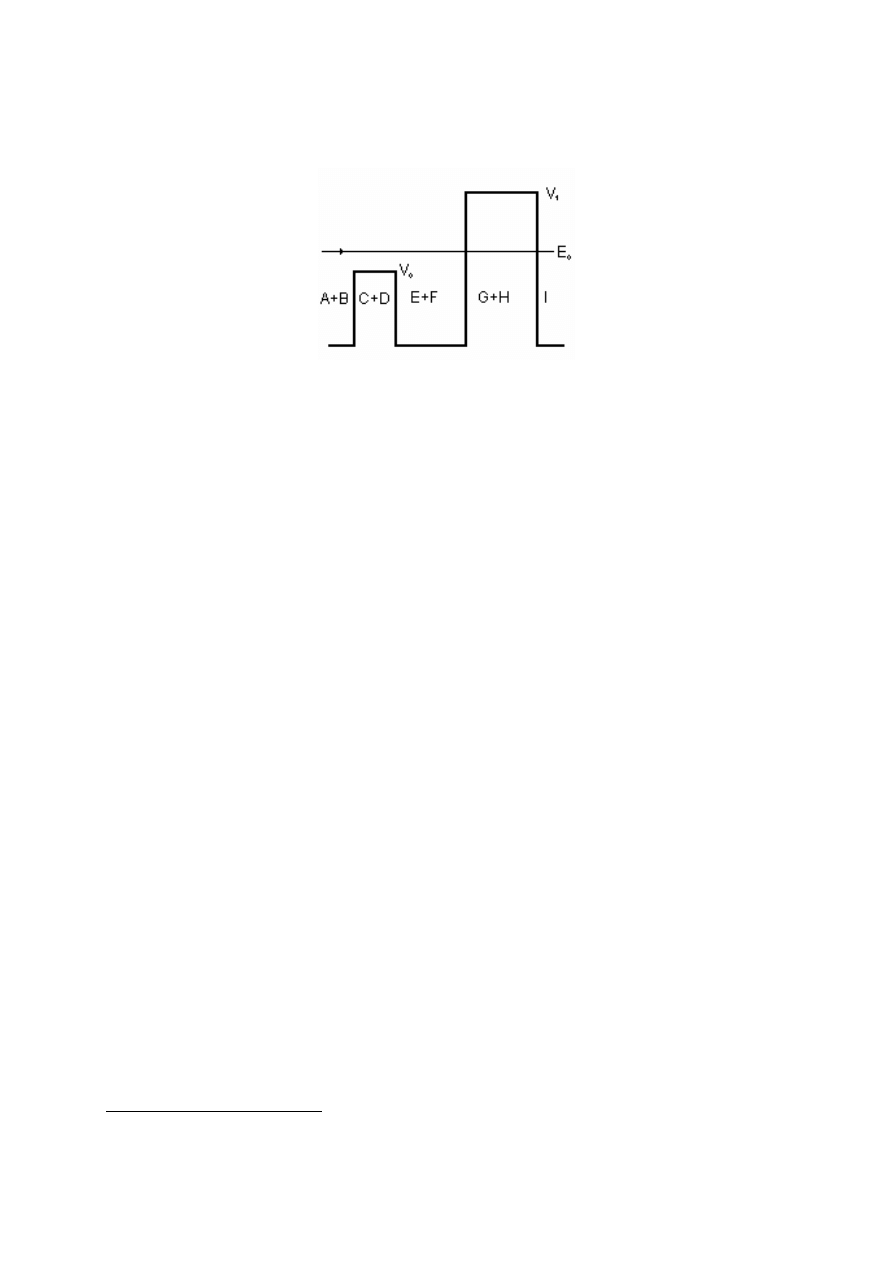
Korzystam z powyższego wzoru przy rysowaniu map transmisji dla rozważanych

w pracy układów barier, np. dla układu z rysunku 4.9

Rys.4.9. Przykładowy układ barier prostokątnych.

macierz transmisji M opisana jest zależnością (4.7.3)













=













=













=













=













=













B

A

M

B

A

M

M

M

M

D

C

M

M

M

F

E

M

M

H

G

M

I

1

2

3

4

2

3

4

3

4

4

0

(4.7.3)

Wyniki obliczeń numerycznych (patrz rozdział 6) zaprezentujemy w postaci

dwuwymiarowych map transmisji, które przedstawiają wyznaczone wartości współczynników

dla danych wartości parametrów modelu (naniesionych na osiach).

Dla każdego piksela, któremu odpowiada określona wartość parametrów modelu

odkładanych na osiach OX i OY, obliczana jest macierz transmisji. Tak więc każdy piksel na

mapie oznacza inne parametry bariery (w kolumnach parametry barier są stałe) lub parametry

cząstki (energia jest stała w wierszach). Z tego też powodu obliczenia dla skomplikowanych

barier (złożonych z wielu klocków

*

) są czasochłonne. Ale dzięki takiemu podejściu

otrzymujemy bardzo dobrą dokładność wyników.

*

słowo klocek oznacza barierę lub studnię potencjalną.

22

5. Opis

ś

rodowiska programowego

Po uruchomieniu programu na ekranie pojawia się ekran powitalny

Rys.5.1 Ekran powitalny.

W lewym górnym rogu widzimy trzy zakładki, z których pierwsza jest aktywna.

Rys.5.2 Zakładki widoczne po uruchomieniu programu.

Aby uruchomić środowisko obliczeniowe należy przejść na zakładkę Ustawienia, co

czynimy poprzez kliknięcie na jej nazwie. Ukaże się nowy ekran zamieszczony na rys.5.3.

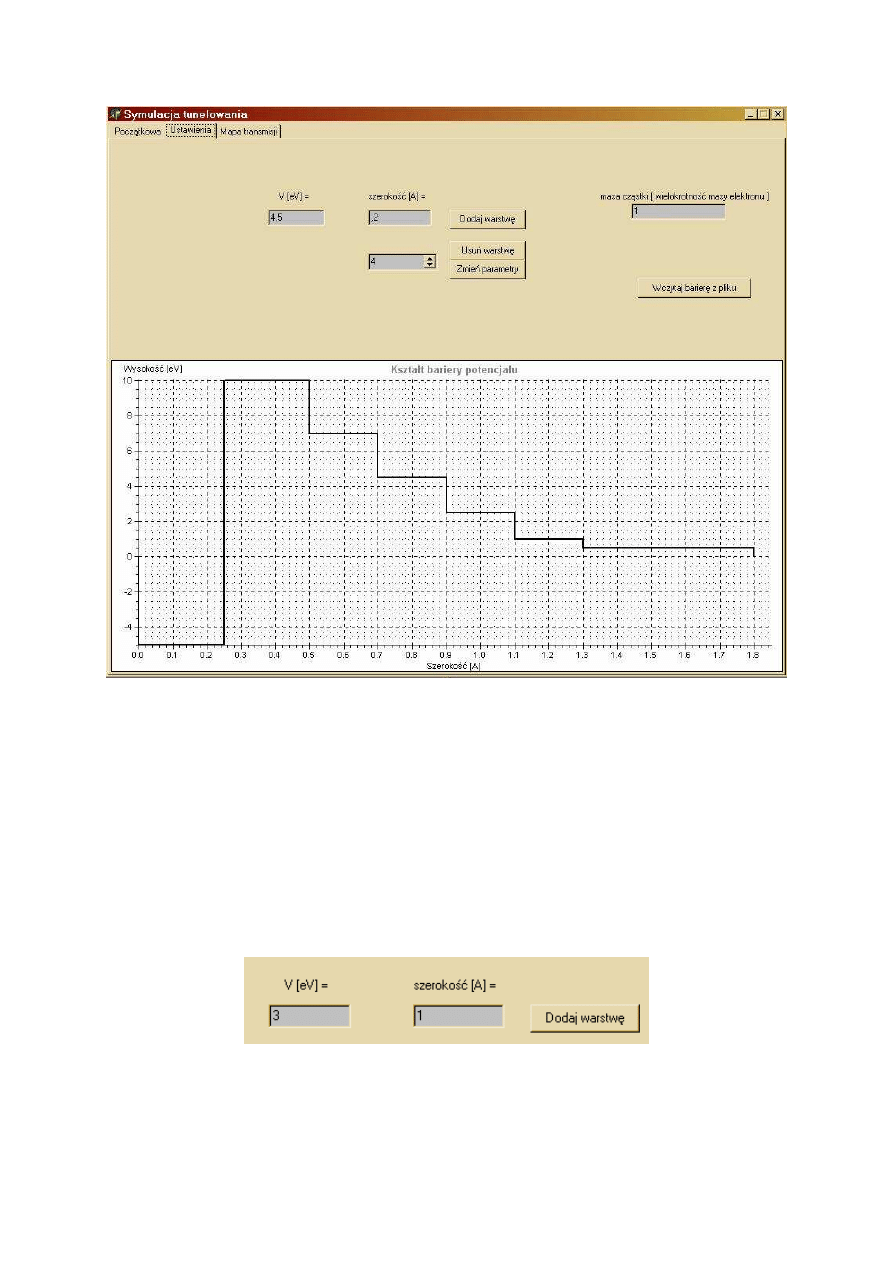
23

Rys.5.3 Ekran, na którym ustalane są parametry barier.

Mamy tutaj możliwość ustalenia masy cząstek – będących wielokrotnością masy elektronu,

oraz skonstruowania układu barier potencjalnych (lub wczytania już gotowego z pliku

tekstowego). Budowa pliku jest bardzo prosta: w każdej linii powinny znajdować się dwa

parametry klocka oddzielone spacjami. Pierwsza kolumna danych to wysokości bariery w eV,

a druga to grubość danej części w Å (1Å = 10

-10

m).

Aby skonstruować barierę w środowisku programowym należy wprowadzić parametry

bariery do odpowiednich pól edycyjnych i zatwierdzić je przez kliknięcie na przycisku Dodaj

warstwę

Rys.5.4 Pola do wprowadzanie parametrów klocka

Wprowadzenie nowych parametrów i ponowne kliknięcie Dodaj warstwę spowoduje

umieszczenie nowego klocka po prawej stronie już utworzonej bariery. Aby badać zjawisko

24

tunelowania cząstek przez dwie prostokątne bariery potencjału należy umieścić między nimi

warstwę, o żądanej szerokości i wysokości V = 0 eV.

Wprowadzoną barierę można modyfikować na dwa sposoby. Można usunąć wybraną

warstwę, co spowoduje przesunięcie następnych warstw (tych po prawej stronie) na jej

miejsce. Można również zmienić parametry warstwy. W obu przypadkach należy wybrać

numer warstwy (są numerowane od jedynki począwszy od lewej strony bariery) i kliknąć na

wybrany przycisk (przy zmianie parametrów należy najpierw wprowadzić nowe wartości do

pól przedstawionych na rysunku 5.4).

Rys.5.5 Pole do wpisania nr zmienianego klocka

Utworzona, lub wczytana z pliku, bariera zostanie nakreślona w polu na dole ekranu.

Rys.5.6 Wykres pokazujący wygląd przykładowej bariery potencjalnej

Po ustaleniu kształtu bariery i masy tunelującej cząstki można przejść do trzeciej, ostatniej

zakładki programu czyli Mapy transmisji. Po kliknięciu na zakładce z jej nazwą ukaże się

niemal pusty ekran, na którym ustalamy zakres energii padającej cząstki od E

min

do E

max

;

wartości te wpisujemy z klawiatury w pola edycyjne oznacznone symbolami Min i Max.

Użytkownik ma możliwość skalowania wymiarów liniowych układu barier poprzez wpisanie

minimalnej i maksymalnej skali do pól edycyjnych umieszczonych na dole ekranu (patrz

rys.5.7).

25

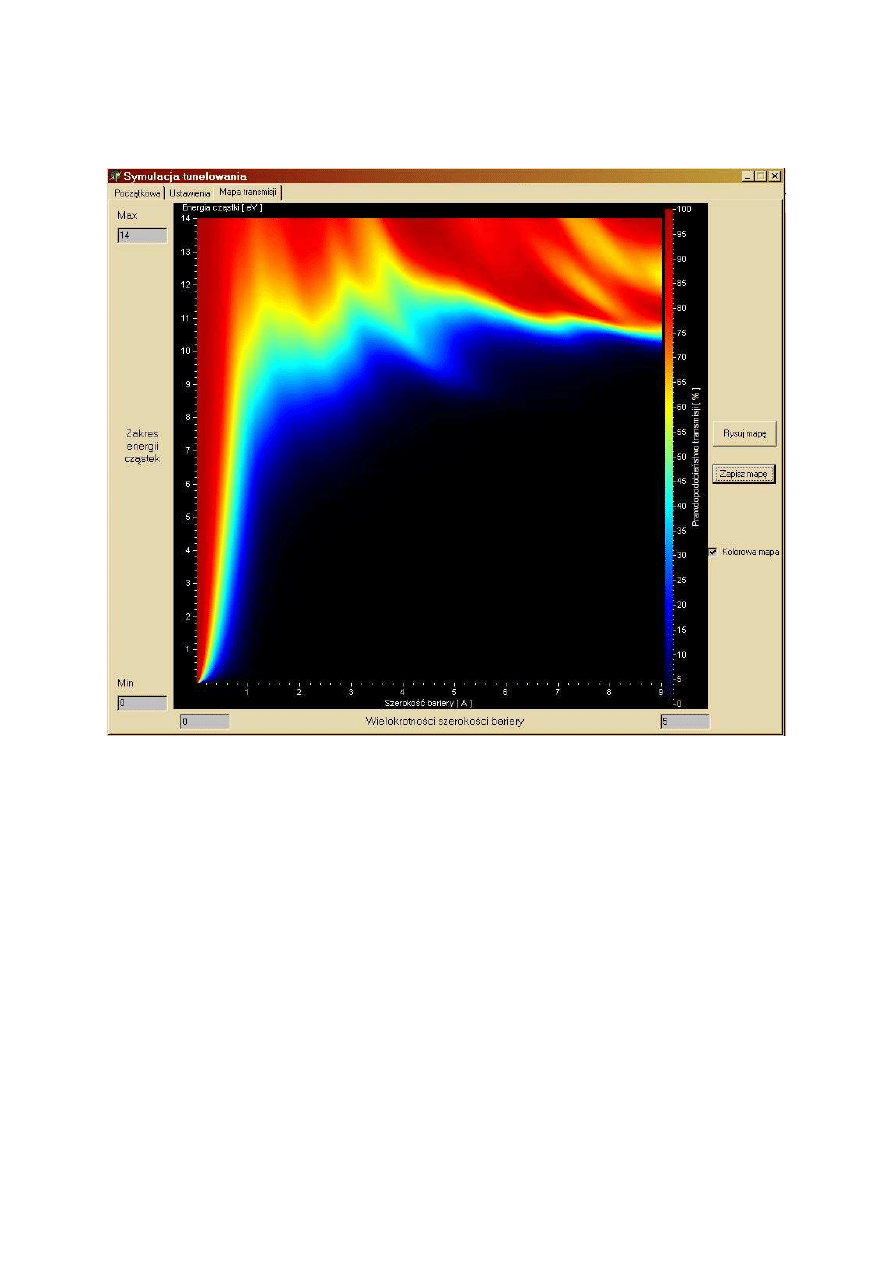
Rys5.7 Ekran, na którym może zostać narysowana mapa transmisji

Ważnym faktem jest to, że ustalamy wielokrotność szerokości stworzonej bariery,

a nie jej szerokość. Jednostką energii jest 1eV, a szerokości 1Å.

Dodatkowo możemy zdecydować tutaj czy mapa transmisji ma być wykreślona

w skali szarości czy przy użyciu pełnej palety barw. Domyślnie jest tworzona mapa kolorowa.

Aby uzyskać wykres w skali szarości należy odznaczyć pole przy napisie Kolorowa mapa.

Rys.5.8 Kontrolka wybierająca typ kolorystyczny rysowanej mapy transmisji

26

Po kliknięciu przycisku Rysuj mapę i odczekaniu chwili niezbędnej na obliczenia

można otrzymać podobny do widocznego na rys.5.9 obraz.

Rys.5.9 Współczynnik transmisji T(E, a) przez barierę widoczną na rysunku 5.3,

gdzie E – energia cząstki, a – szerokość bariery.

Po prawej stronie wykresu widnieje skala, na której barwom są przypisane

odpowiadające im wartości współczynnika transmisji (w procentach). Dodatkowo pojawiają

się opisane osie energii cząstki (rzędna) i szerokości bariery (odcięta).

Jeżeli chcemy poznać dokładne parametry jakiegoś punktu na mapie transmisji

wystarczy, że klikniemy i przytrzymamy lewy przycisk myszy nad wybranym punktem.

Pojawią się prowadnice, które można przesuwać po mapie ruszając myszą, a parametry

wyświetlą się w górnej części wykresu (Rys.5.10).

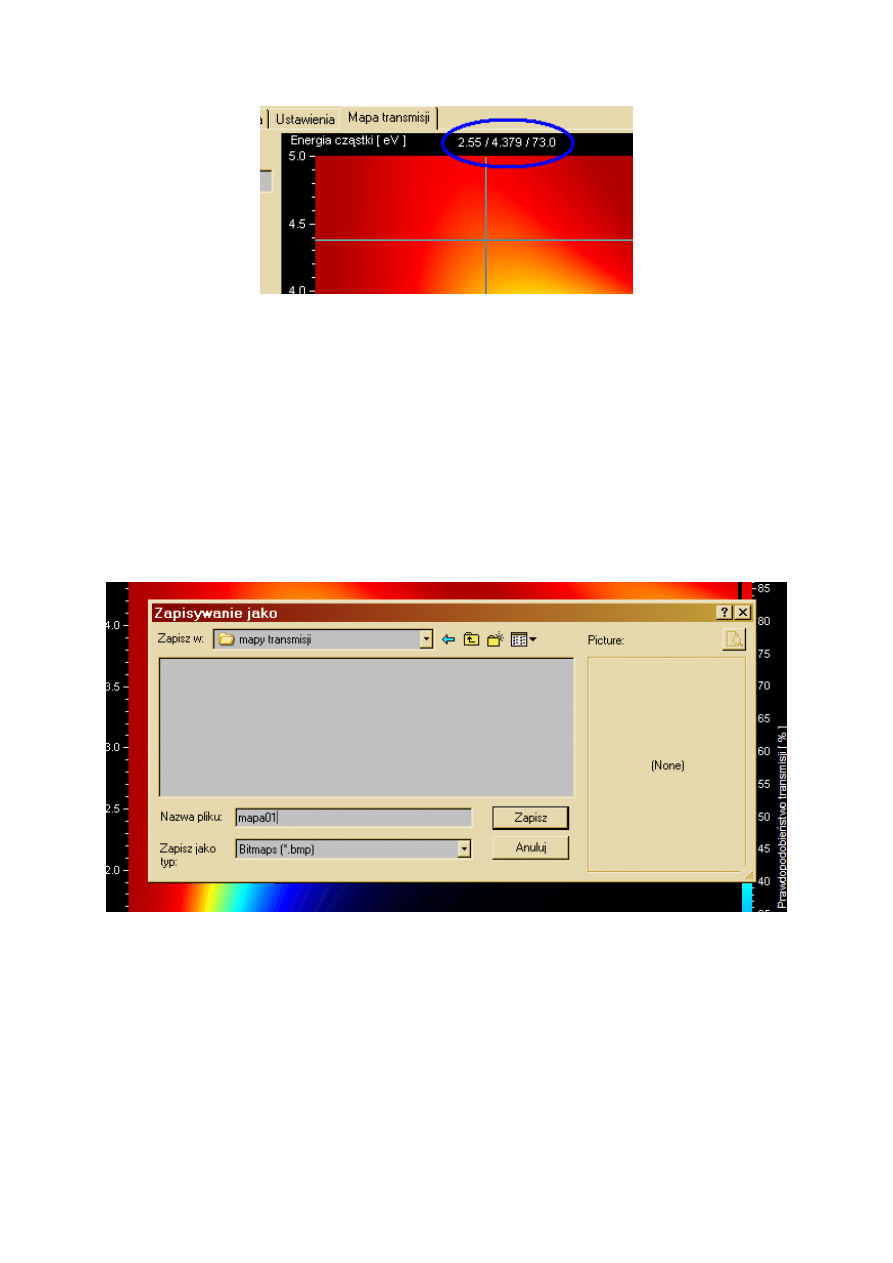
27

Rys.5.10 Prowadnice oraz szerokość bariery, energia cząstki i współczynnik transmisji

Trzy wyświetlane liczby, oddzielone od siebie znakiem ‘ / ’, oznaczają, kolejno,

szerokość bariery, energię cząstki i procentowo wyrażony współczynnik transmisji.

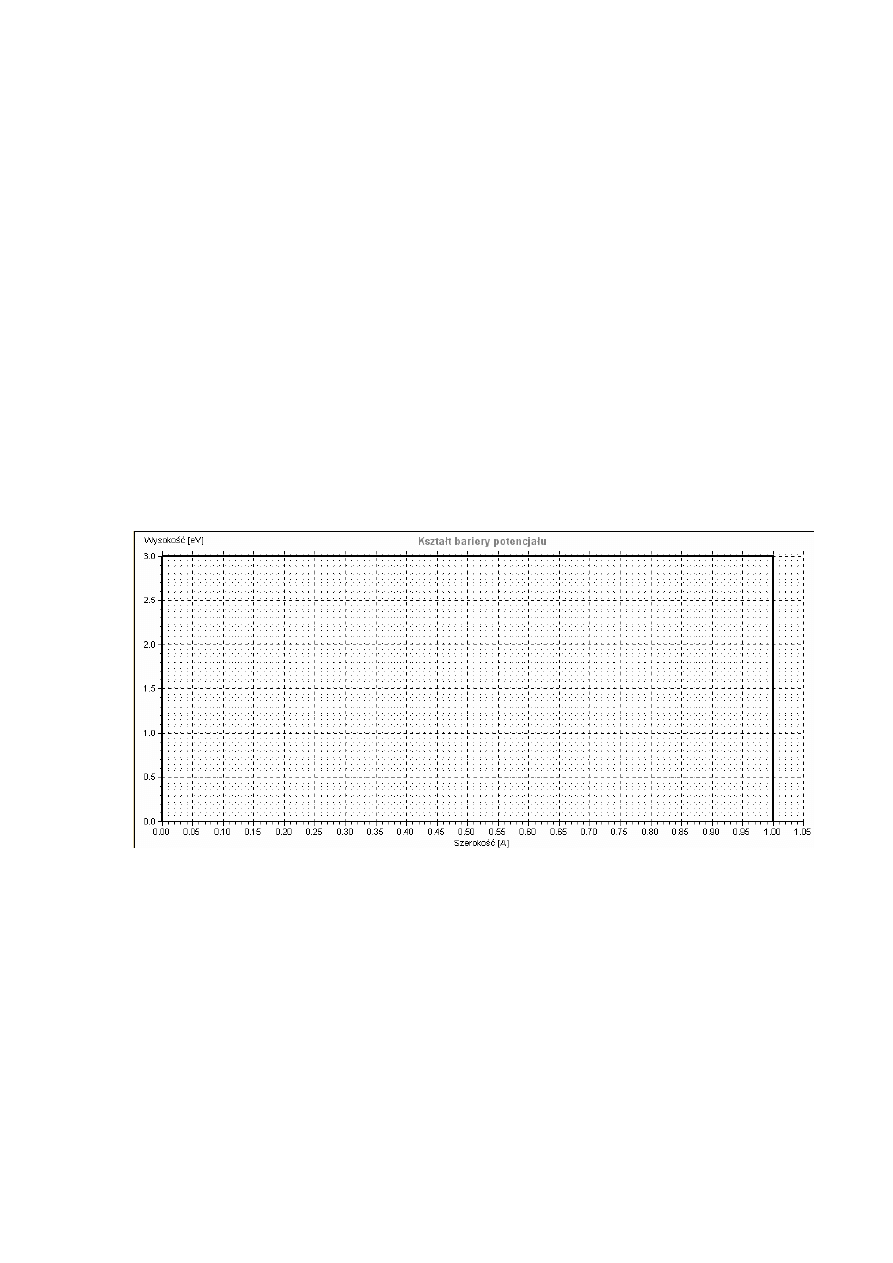
Mając już wykreśloną mapę transmisji można skorzystać z drugiego przycisku

widocznego na rysunku 5.8: Zapisz mapę. Kliknięcie na nim zaowocuje pojawieniem się okna

dialogowego, w którym należy wskazać miejsce docelowe dla pliku, w którym zostanie

zapisana mapa transmisji w formacie .bmp. Bardzo ważne jest by system Windows miał

ustawioną 32 bitową głębię kolorów, w przeciwnym przypadku zapisane mapy będą

nieprawidłowe.

Rys.5.11 Okno zapisu mapy transmisji do pliku

Po wygenerowaniu mapy transmisji i jej ewentualnym zapisaniu, można zmienić

parametry tworzenia mapy (np. zakres energii cząstki) lub przejść do zakładki Ustawienia

i zmienić wygląd bariery (lub masę cząstki).

Opisany powyżej program powstał w środowisku programistycznym Borland Delphi5.

Do rysowania kształtu bariery oraz mapy transmisji wykorzystaliśmy dodatkowo biblioteki

zawarte w pakiecie XYGraph v.2.2.1 autorstwa Wilko C. Emmensa.

28

6. Wybrane wyniki

W tym rozdziale zaprezentujemy wybrane wyniki. Przedstawione poniżej mapy

transmisji zostaną omówione w następnym rozdziale.

6.1. Bariera prostok

ą

tna

Przykładowa bariera prostokątna, zaprojektowana w oknie środowiska programowego,

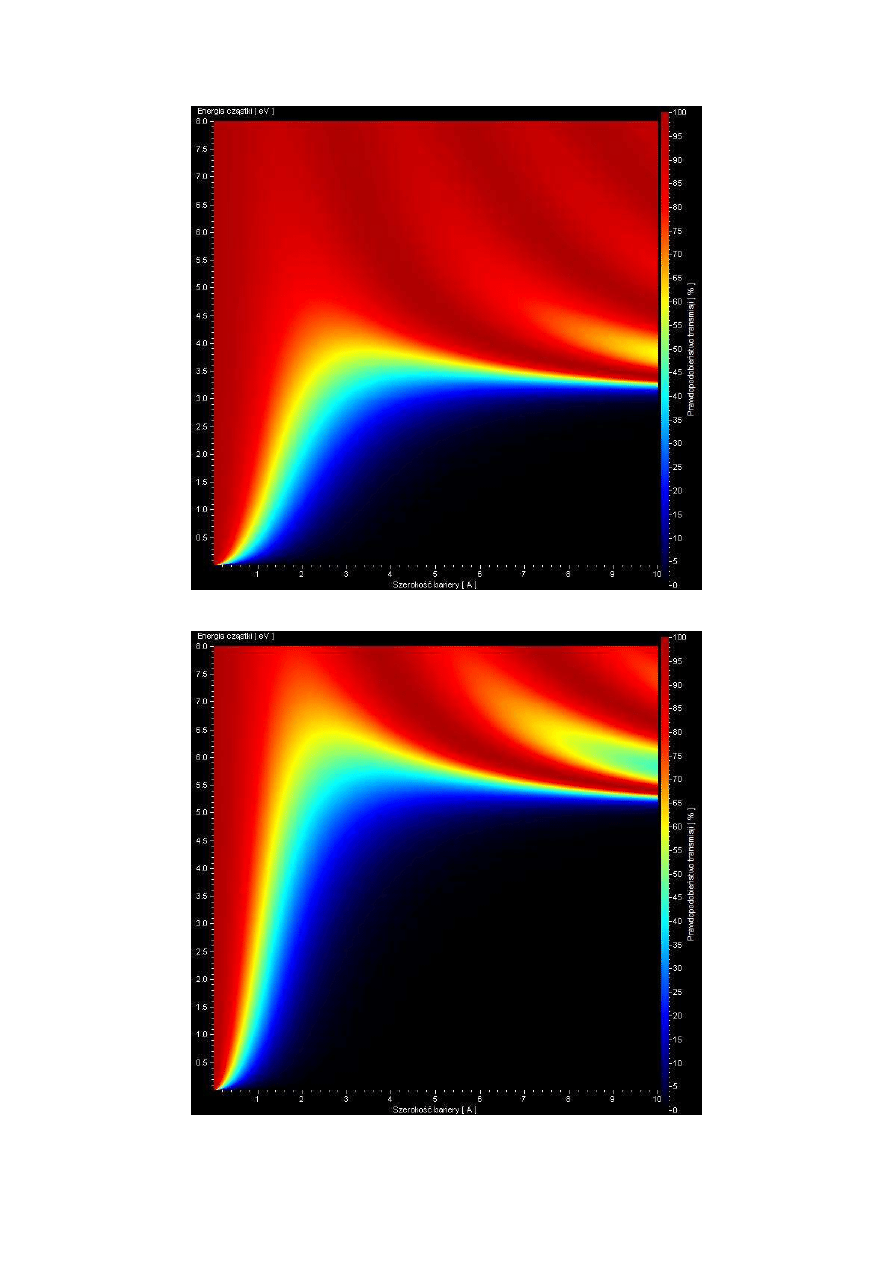
jest pokazana na rysunku 6.1. Dla takiej bariery o wysokości 3eV, zmieniając jej szerokość od

0 do 10Å, utworzyliśmy mapę pokazaną na rysunku 6.2, natomiast rysunek 6.3 prezentuje

mapę transmisji przez analogiczną barierę o wysokości 5eV.

Rys. 6.1 Pojedyncza bariera o wysokości 3eV i szerokości 1Å

29

Rys. 6.2 Pojedyncza bariera 3eV, masa cząstki równa masie elektronu

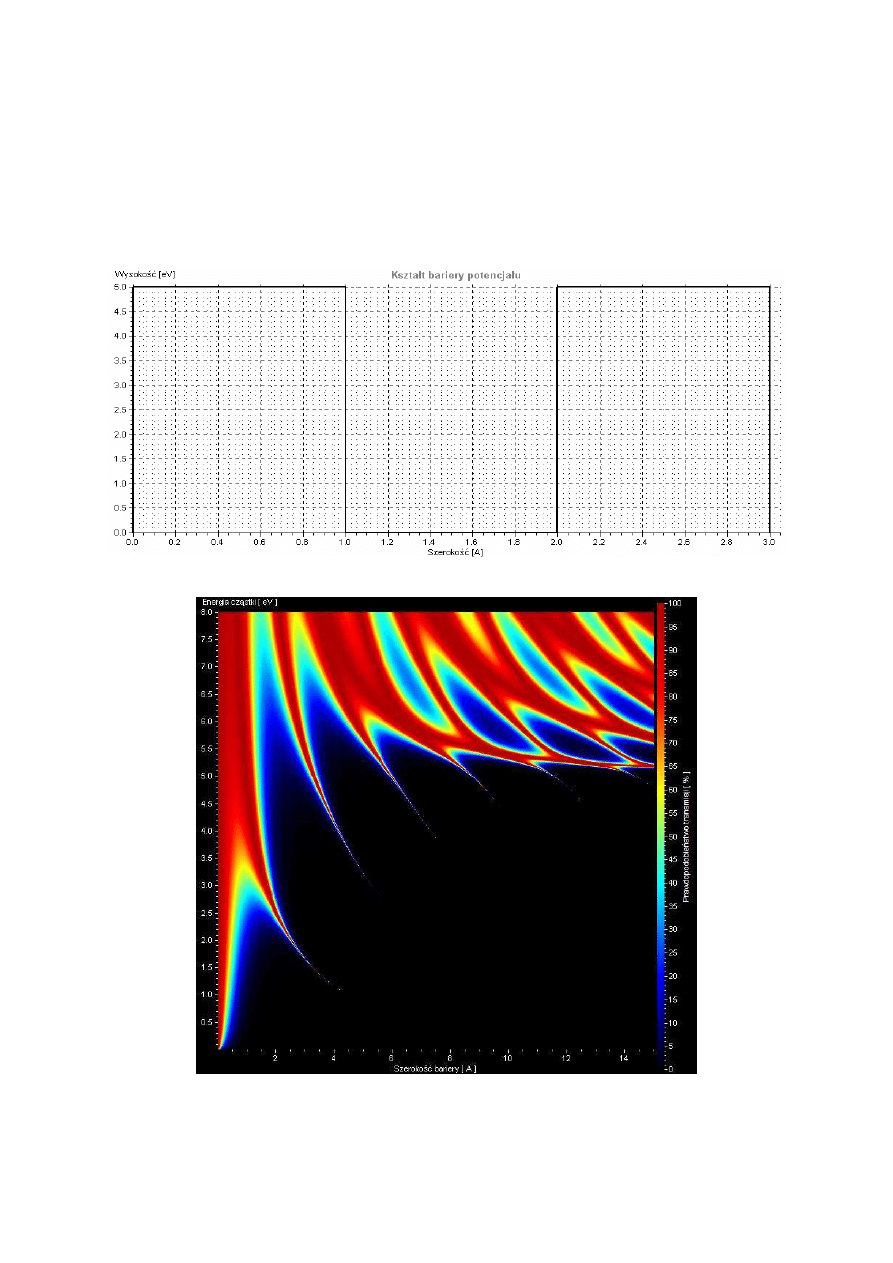
Rys. 6.3 Pojedyncza bariera 5eV, masa cząstki równa masie elektronu

30

6.2. Podwójna symetryczna bariera

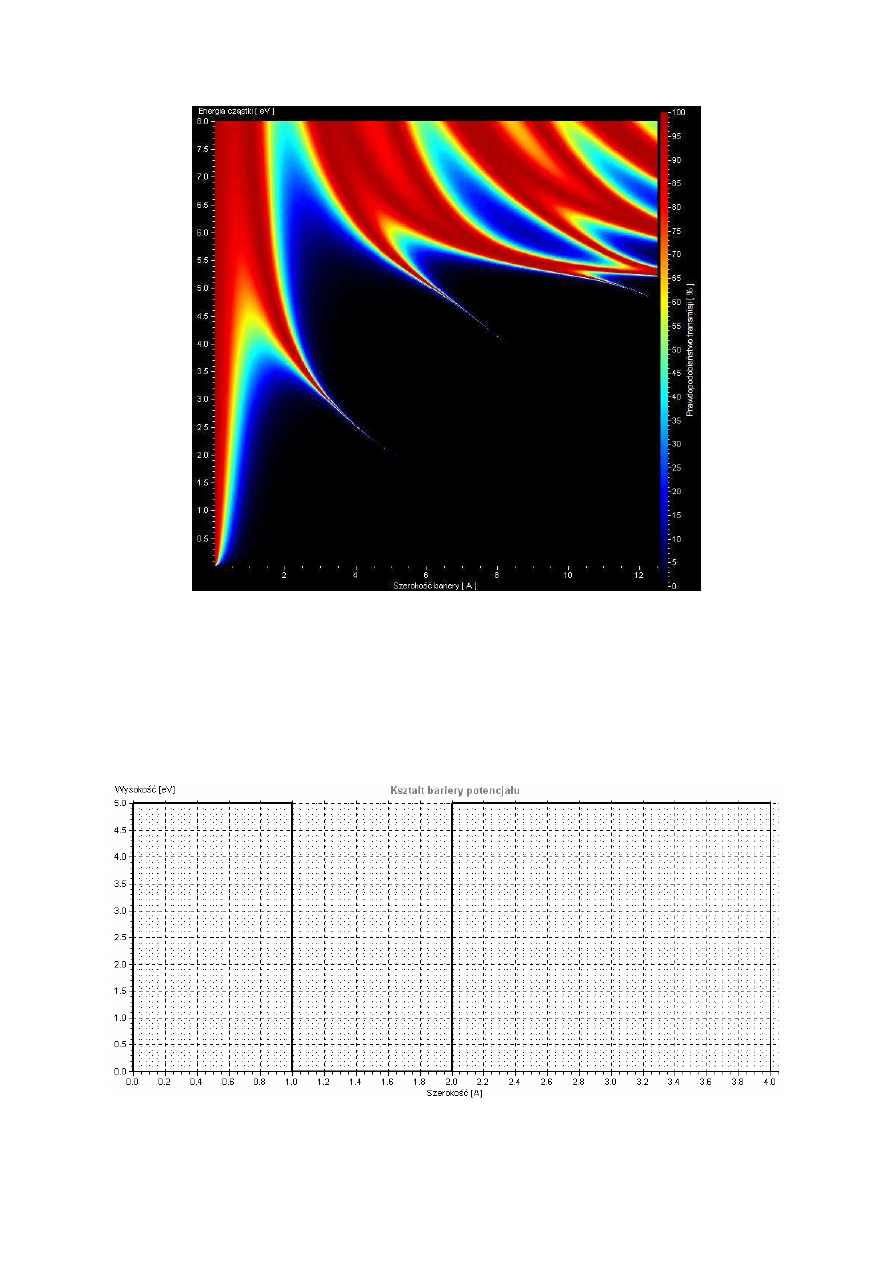
Poniżej przedstawiamy mapy transmisji przez barierę złożoną z trzech klocków, jej

kształt jest widoczny na rysunku 6.4 (wysokość barier 5 eV). Mapa z rysunku 6.6 prezentuje

mapę transmisji przez układ, w którym przerwa między barierami (środkowy klocek) została

zmniejszona o połowę.

Rys. 6.4 Podwójna bariera symetryczna – dwie bariery oddzielone studnią

Rys. 6.5 Podwójna bariera z rysunku 6.4, masa cząstki równa masie elektronu

31

Rys. 6.6 Podwójna bariera o zwężonej o połowę studni, masa cząstki równa masie elektronu

6.3. Podwójna prostok

ą

tna bariera niesymetryczna

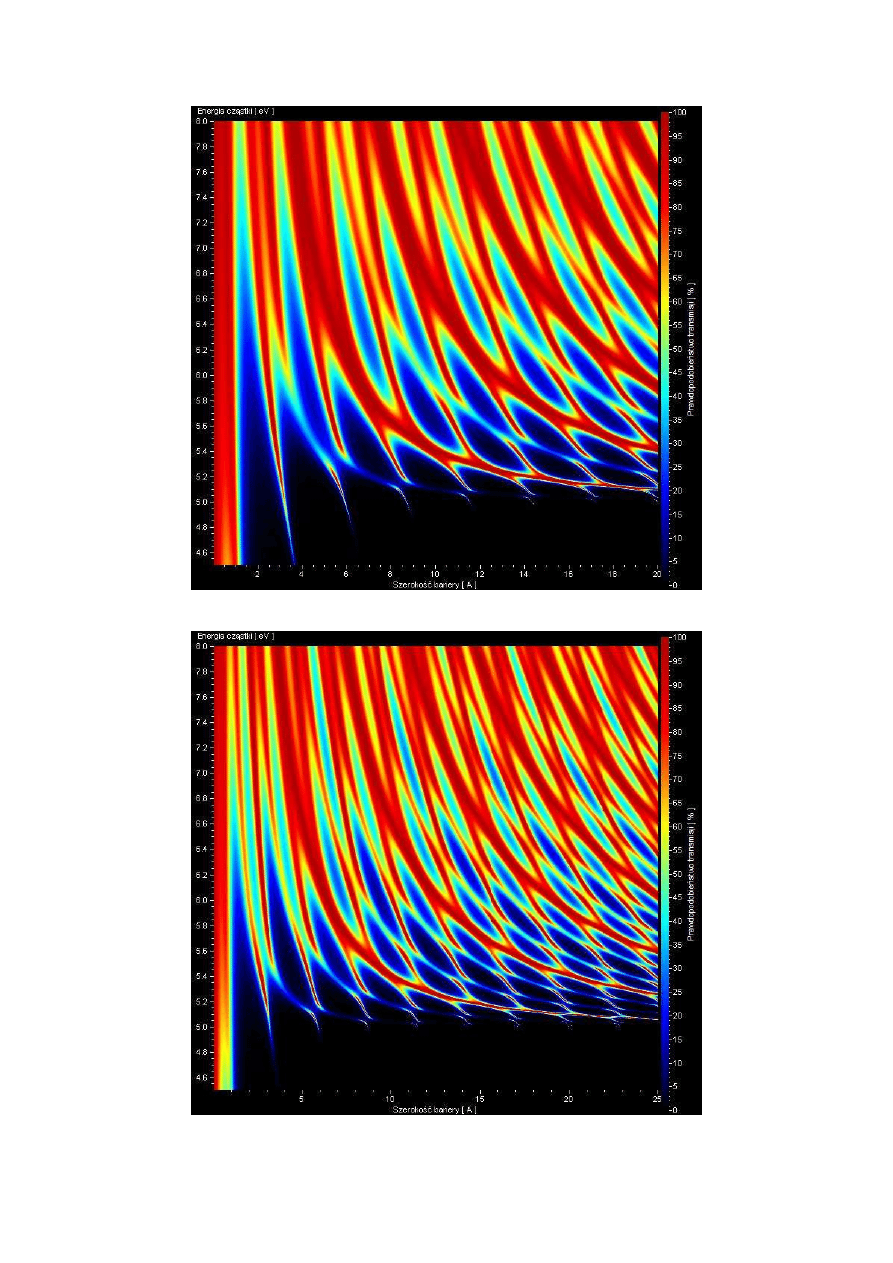
Ten podrozdział zawiera mapy transmisji przez układ nieidentycznych barier,

np. ostatni element jest znacznie szerszy (rys.6.7), lub wyższy (rys.6.10) od pierwszego.

Rys. 6.7 Niesymetryczna podwójna bariera

32

Rys. 6.8 Mapa transmisji przez barierę z rysunku 6.7, masa cząstki równa masie elektronu

Rys. 6.9 Niesymetryczna podwójna bariera – druga bariera trzy razy szersza od pierwszej

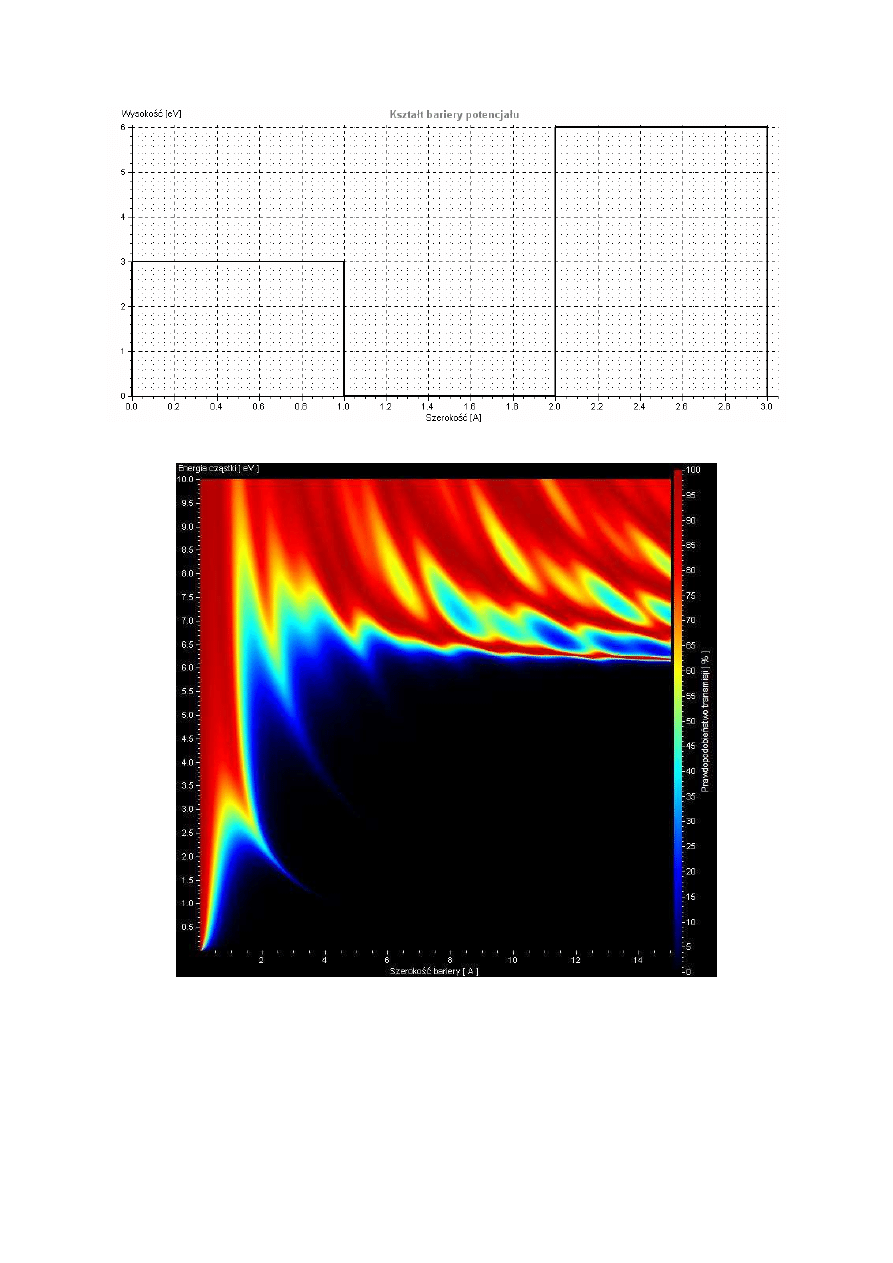
33

Rys. 6.10 Bariery o różnym potencjale oddzielone studnią

Rys. 6.11 Mapa transmisji przez barierę z rysunku 6.10

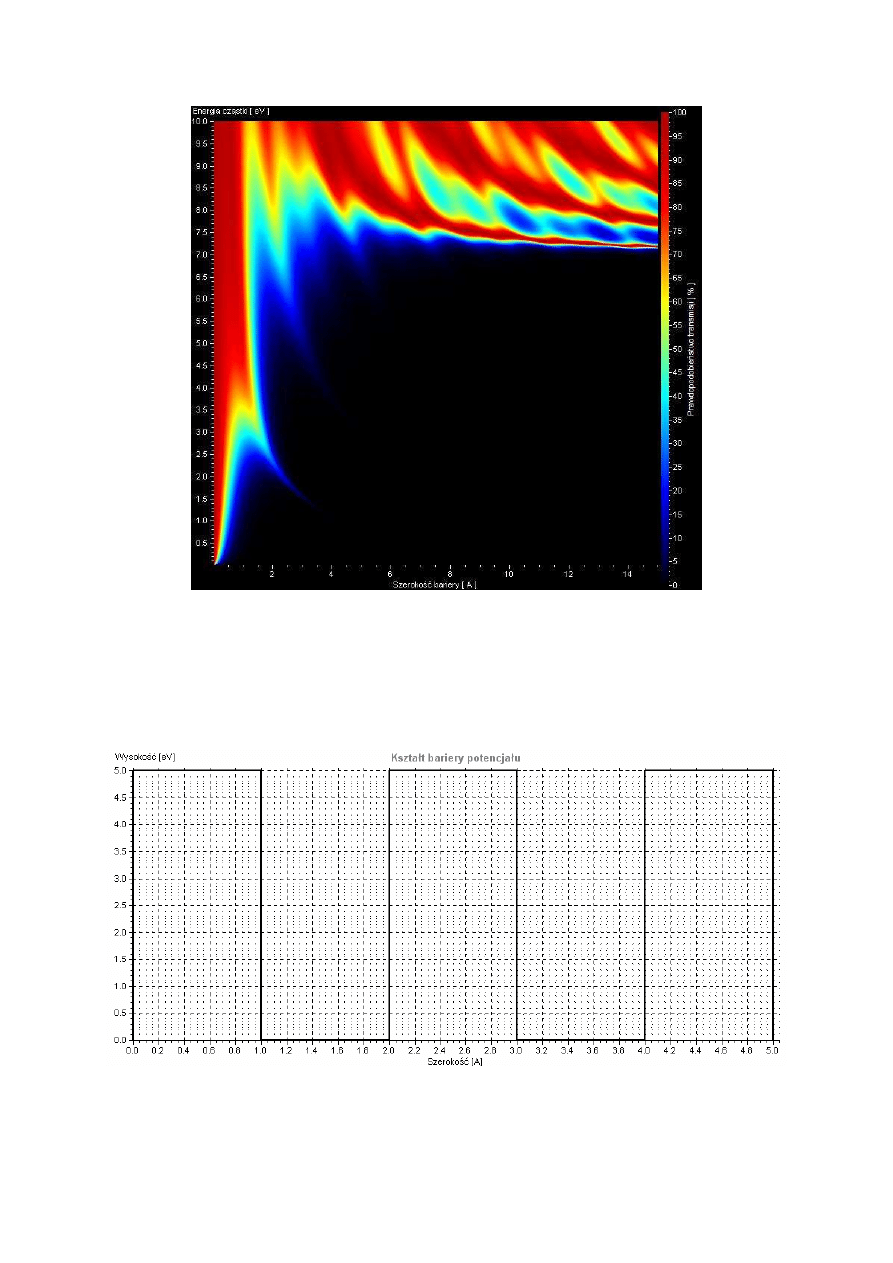
34

Rys. 6.12 Modyfikacja bariery z rys. 6.10 – druga bariera ma wysokość 7eV

6.4. Wielokrotne studnie potencjału

Rys. 6.13 Potrójna bariera

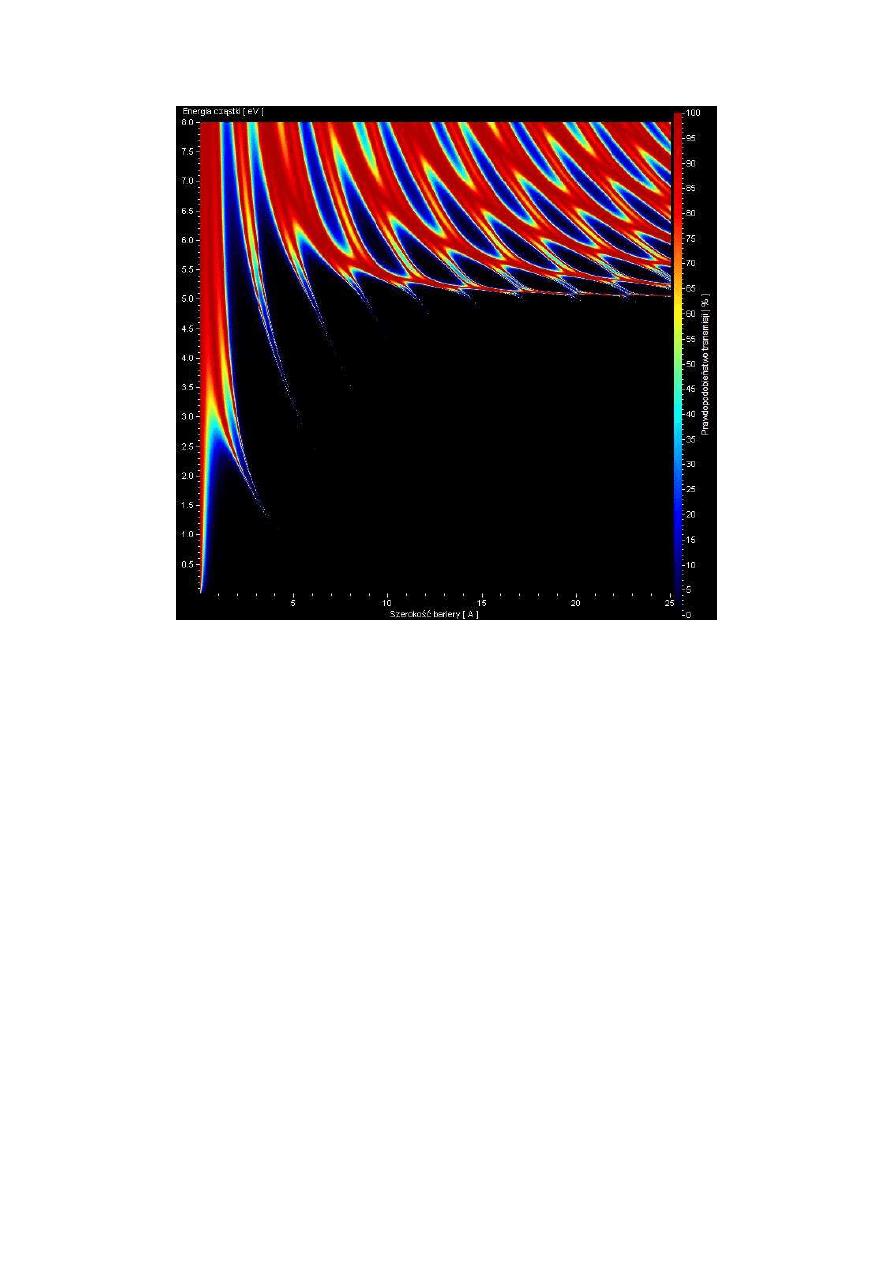
35

Rys. 6.14 Współczynnik transmisji przez barierę z rysunku 6.13

6.5. Tunelowanie cz

ą

stek o ró

ż

nych masach

Poniżej przedstawione mapy transmisji prezentują tunelowanie cząstek trzy razy

cięższych od elektronu przez wybrane bariery. Na rysunku 6.15 przedstawiliśmy mapę

transmisji przez pojedynczą barierę, a na rysunku 6.16 przez podwójną symetryczną barierę.

Rysunki 6.17 i 6.18 prezentują mapy transmisji przez podwójną barierę symetryczną

odpowiednio cząstek o masie 0,1 i 0,01 masy elektronu.

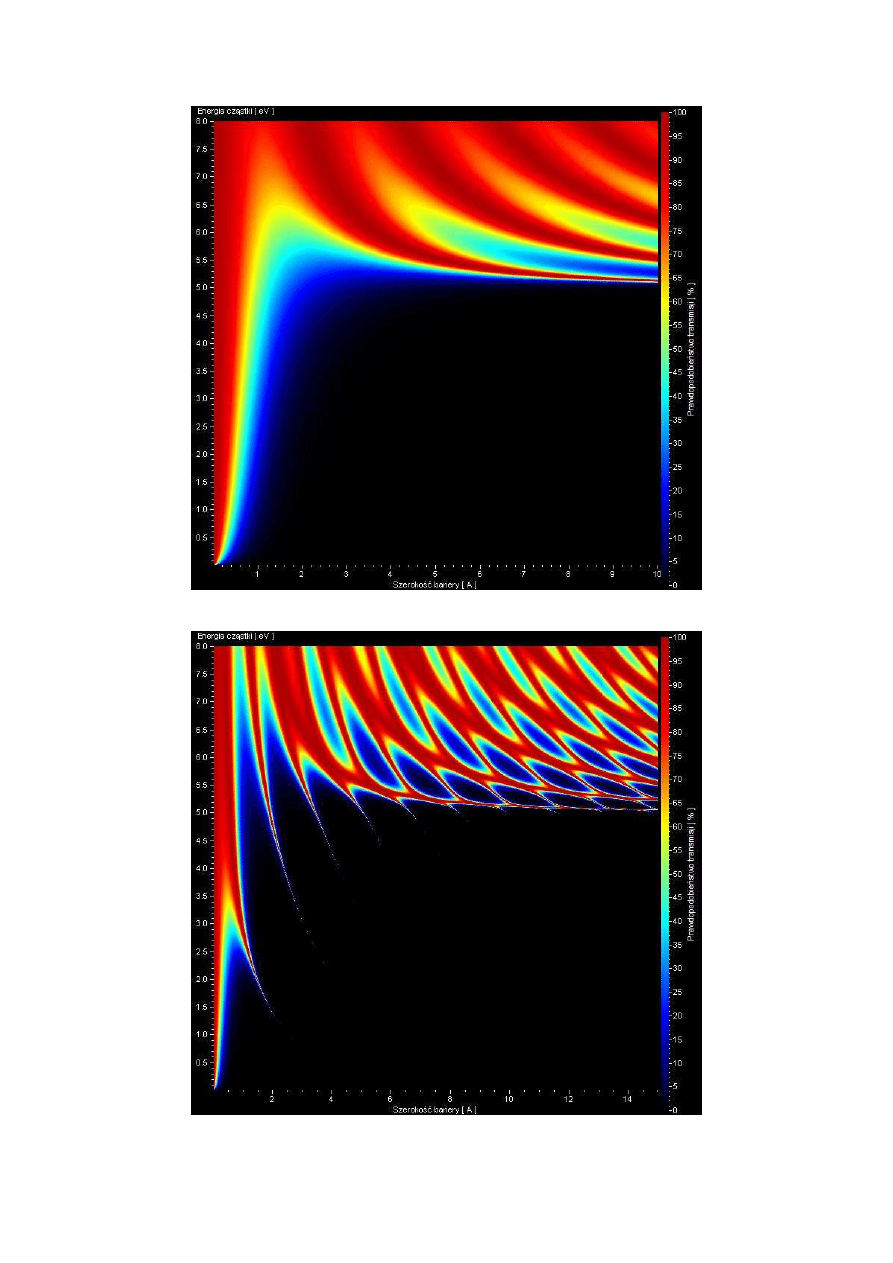
36

Rys. 6.15 Współczynnik transmisji przez pojedynczą barierę 5eV, masa cząstki: 3m

e

Rys. 6.16 Współczynnik transmisji przez podwójną barierę, masa cząstki: 3m

e

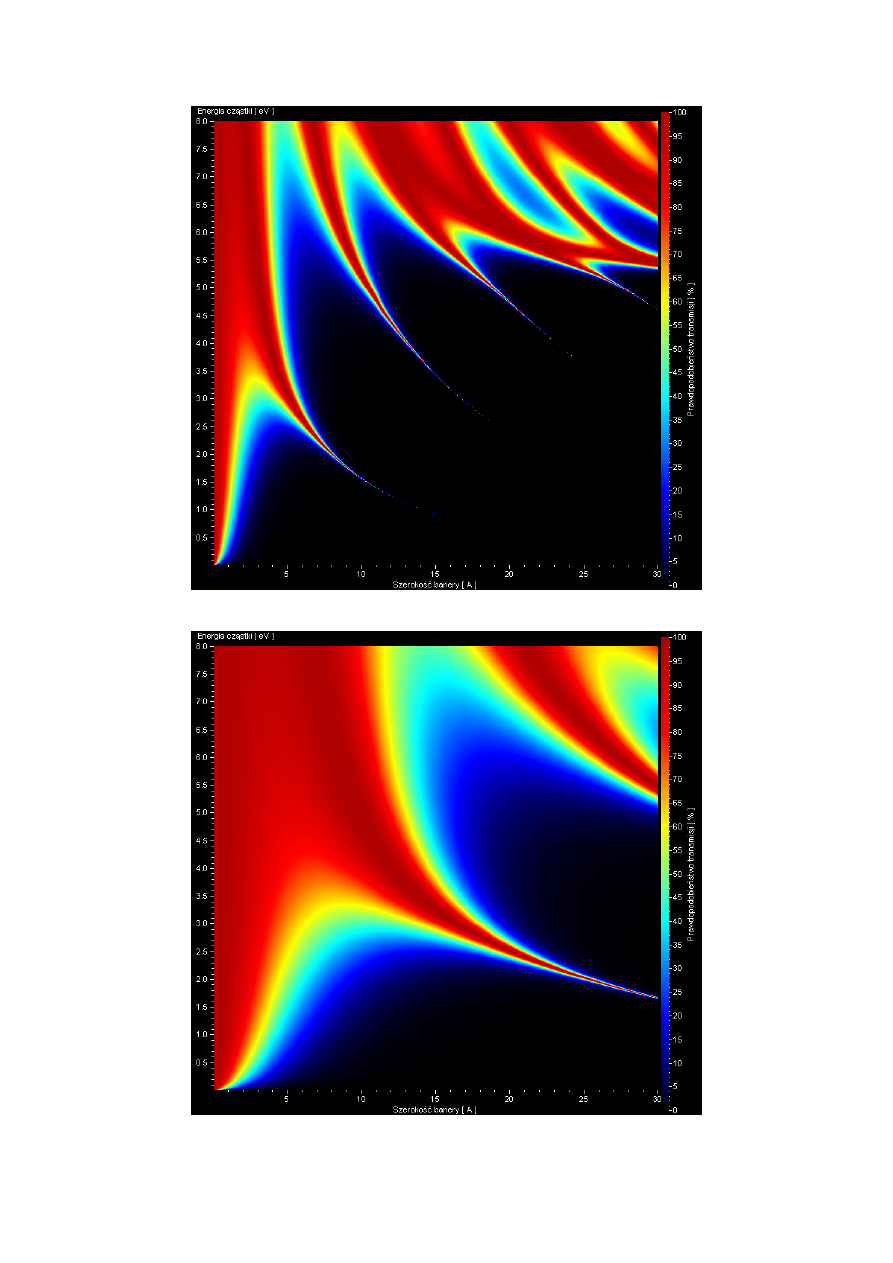
37

Rys. 6.17 Współczynnik transmisji przez podwójną barierę, masa cząstki: 0,1m

e

Rys. 6.18 Współczynnik transmisji przez podwójną barierę, masa cząstki: 0,01m

e

38

7. Wnioski

W niniejszej pracy przeanalizowano numerycznie wpływ parametrów prostokątnych

barier potencjalnych na prawdopodobieństwo transmisji i tunelowania T padających na nie

cząstek kwantowych. Nie zajmowaliśmy się przy tym bardzo interesującym zagadnieniem

wyznaczenia czasu tunelowania szeroko dyskutowanym m.in. w pracach [9 ÷ 12].

W celu obliczenia współczynnika transmisji T skorzystaliśmy z formalizmu macierzy

przejścia. Badanie bardziej skomplikowanych układów barier nieprostokątnych tą metodą

wymaga dużych mocy obliczeniowych. Dlatego skupiliśmy się w tej pracy jedynie na

najprostszych.

Wyniki

obliczeń

numerycznych

przedstawiono

za

pomocą

map

transmisji/tunelowania

1

. Na osi poziomej i pionowej mapy zostały odłożone odpowiednio

szerokość układu barier i energia padającej cząstki. Zastosowane kolory reprezentują wartości

współczynnika transmisji lub tunelowania. Kolorem czerwonym zaznaczone duże jego

wartości, a niebieskim i czarnym małe.

Poniżej przedstawiamy wnioski, które można sformułować na podstawie zawartych

w pracy wybranych wyników.

Analizując mapy transmisji przez pojedynczą barierę 6.2, 6,3 oraz 6.15 możemy

stwierdzić jak na T wpływa zmiana masy cząstki oraz parametrów bariery (wysokości i

szerokości). Zgodnie z oczekiwaniami dla bardzo wąskich barier T przyjmuje duży wartości

(bliskie 1) nawet dla cząstek o bardzo małej energii. Natomiast, co ciekawe, gdy energia

cząstki jest nawet dwa razy większa niż potencjał bariery obserwujemy znaczne oscylacje

wartości T, tj. naprzemienny wzrost i spadek współczynnika transmisji przy ustalonej

szerokości bariery. Jest to zgodne z wynikami analitycznymi [2-5] i spowodowane tym, że

bariera staje się częściowo przeźroczysta (T<1) dla padającej na nią cząstki, jeśli szerokość

bariery jest całkowitą wielokrotnością długości fali de Broglie’a stowarzyszonej z cząstką

(2.9). Efekt ten staje się wyraźniejszy przy wyższych barierach (porównaj rys. 6.2 i 6.3 oraz

6.15). Obserwowane oscylacje amplitudy współczynnika T (dla ustalonych wysokości barier)

zanikają wraz ze wzrostem energii cząstki, a rosną wraz z szerokością bariery.

1

Mapa reprezentuje wartości współczynnika transmisji cząstek o energii wyższej od wysokości bariery/barier

oraz wartości współczynnika tunelowania, jeśli energia cząsteczki jest mniejsza od wysokości bariery/barier.

39

Omówimy zmiany współczynnika transmisji obserwowane w przypadku tunelowania

cząstki przez układ dwóch identycznych prostokątnych barier potencjału oddzielonych

studnią (rysunki 6.5 i 6.6). Wnioski płynące z analizy pojedynczej prostokątnej bariery są

nadal aktualne, ale należy dodatkowo zauważyć pojawienie się stosunkowo wąskich pasm

tunelowania w obszarze energii podbarierowych. Ich występowanie jest związane

z istnieniem stanów metastabilnych

2

w obszarze studni kwantowej, które są rozwiązaniami

stacjonarnego równania Schrödingera dla studni kwantowej o skończonej wysokości. Energia

stanów kwantowych cząstki w nieskończenie głębokiej studni potencjalnej o szerokości a

wyraża się wzorem

,....

3

,

2

,

1

,

2

2

2

2

2

=

=

n

ma

n

E

n

h

π

.

Padająca cząstka o energii bliskiej energii stanu metastabilnego tuneluje dzięki zjawisku

rezonansu [2-5], co jest ponownie zgodne z wynikami analitycznymi (cząstka tuneluje przez

pierwszą barierę, odbija się od drugiej bariery i interferuje z „nadlatującymi” cząstkami, co

prowadzi do powstania fali stojącej). Dla danej szerokości i wysokości studni liczba

metastablinych stanów jest skończona. Wraz ze wzrostem szerokości studni rośnie ich liczba,

co prowadzi do większej liczby pasm rezonansowych na mapach tunelowania (patrz rys. 6.5,

6.6). Ten sam efekt (zwiększanie się liczby pasm transmisji) zachodzi przy zwiększaniu masy

cząstki dla ustalonej szerokości studni (porównaj rysunki 6.5, 6.16, 6.17 i 6.18). Dodatkowo,

szerokość pasm transmisji ulega istotnemu zmniejszeniu wraz ze wzrostem masy cząstki.

Odwrotna tendencja, potwierdzająca nasz wniosek, jest zauważalna na rys. 6.17-6.18, gdzie

przedstawiono mapy transmisji/tunelowania dla cząstek o mniejszych masach.

Jeżeli zakłócimy symetrię barier, np. poprzez zwiększenie szerokości jednej z nich

(rys. 6.7-6.9), to zaobserwujemy znaczne zmiany w mapach transmisji/tunelowania.

Współczynnik tunelowania osiąga duże wartości dla prawie ściśle określonych energii

padającej cząstki. Energie te ponownie odpowiadają energiom stanów metastabilnych cząstki

w obszarze studni kwantowej. Na rys. 6.8 i 6.9 współczynnik tunelowania w obszarze

podbarierowym jest praktycznie równy zeru za wyjątkiem bardzo wąskich obszarów energii

i szerokości barier, które zanikają na mapach wraz ze wzrostem szerokości zewnętrznych

barier. Jeśli energia cząstki jest zbliżona do wysokości barier lub większa, to obserwujemy

2

Używamy tutaj słowa metastabilne dla podkreślenia faktu, że cząstka zlokalizowana w obszarze studni

kwantowej (patrz rys. 6.4) ograniczonej z dwóch stron skończonymi barierami potencjalnymi ma skończony

czas życia ze względu na możliwość tunelowania przez wspomniane bariery.

40

duże wartości współczynników transmisji lub tunelowania. Dla energii cząstki większej od

wysokości bariery obserwujemy znaczne różnicowanie się współczynnika transmisji

w porównaniu z przypadkiem bariery symetrycznej. Niesymetryczność zewnętrznych barier

(ich szerokości nie są równe) w obszarze tuż nadbarierowym powoduje na mapach transmisji

zauważalny wzrost liczby wąskich obszarów wysokiej i niskiej transmisji. (porównaj rys. 6.5

i 6.8). Na rys. 6.8 widocznych jest znacznie więcej obszarów (określonych energią cząstki i

szerokością barier), w których współczynnik transmisji przyjmuje małe lub duże wartości.

Zaburzenie symetrii barier poprzez zróżnicowanie ich wysokości (rys. 6.10-6.12)

powoduje znikanie wielu pasm tunelowania rezonansowego (obserwowanych np. na mapach

z rys. 6.6), co jest konsekwencją zmniejszenia się liczby stanów metastabilnych w płytszej

studni kwantowej.

Jeśli wysokość jednej z barier jest dużo większa od wysokości drugiej, to mapa

transmisji odpowiada mapie transmisji przez pojedynczą barierę.

Godnym zauważenia jest również fakt, że wyniki obliczeń numerycznych nie zależą

od kolejności barier rozdzielonych studnią; użytkownik programu może samodzielnie o tym

się przekonać. Oznacza to, że współczynniki transmisji/ tunelowania badanych układów nie

zależą od tego z której strony padają cząstki.

Analiza wyników otrzymanych dla wielokrotnych studni potencjalnych (rys. 6.13-

6.14) wskazuje również na rezonansowy charakter tunelowania. Ze względu na to, że mapa

z rys. 6.14 odnosi się do układu zawierającego dwie symetryczne studnie kwantowe, to

widoczne są (zwłaszcza w obszarze odpowiadającym wąskim studniom, które reprezentuje

lewa część mapy) pasma tunelowania złożone z dwóch blisko siebie położonych poziomów

rezonansowych. Jest to przejaw istnienia metastabilnych poziomów energetycznych cząstki

kwantowej umieszczonej w badanym układzie. W badanym układzie poziomy energetyczne

tworzą pary poziomów blisko siebie położonych na skali energetycznej. Odległośc

energetyczna tych poziomów maleje wraz ze wzrostem szerokości barier lub studni

potencjalnych [1].

Jeżeli do układu dwóch studni dodamy następne, to otrzymamy dodatkowe pasma

rezonansowego tunelowania, w których liczba rezonansów będzie równa liczbie studni.

41

8. Podsumowanie

Główne osiągnięcia pracy to:

1.

Wyprowadzenie analitycznych formuł na macierze przejścia M

1

÷M

6

, których

jawne postacie przytoczono w rozdziale 4.

2.

Opracowanie środowiska programowego, wykorzystującego wyprowadzone

macierze

przejścia,

pozwalającego

użytkownikowi

na

badanie

jednowymiarowego

zjawiska

tunelowania

i

reprezentację

graficzną

współczynników transmisji i tunelowania w zależności od:

•

wysokości i szerokości barier potencjalnych,

•

kolejności barier w układzie kwantowym,

•

liczby studni kwantowych,

•

energii padającej cząstki kwantowej,

•

masy cząstki kwantowej.

Stworzone środowisko umożliwia samodzielne wykonywanie eksperymentów

komputerowych dotyczących czysto kwantowego zjawiska jakim jest tunelowanie.

Interesującą opcją jest możliwość numerycznego analizowania za jego pomocą zjawiska

tunelowania w wąskich przedziałach energii (takich wyników w pracy nie zamieszczono)

problemem Może ono służyć również jako narzędzie dydaktyczne wspomagające kursy fizyki

i mechaniki kwantowej.

Można zaproponować kilka sposobów rozwoju środowiska. Dotyczyłoby to m.in.

•

stworzenia użytkownikowi możliwości rysowania na ekranie monitora układu

barier o dowolnym kształcie, co pozwoliłoby analizować zjawisko transmisji i

tunelowania cząstek przez układ nieprostokątnych barier,

•

podglądu przekroju mapy transmisji dla określonej energii lub szerokości bariery.

Nie widzimy sposobu na zwiększenie szybkości działania środowiska innego niż

poprzez zmniejszenie dokładności obliczeń (wszystkie zmienne w zaprogramowanym

ś

rodowisku są przechowywane jako 10-bitowy typ extended) lub zmniejszenie gęstości siatki,

(obliczenia przeprowadzane są dla każdego piksela mapy).

42

9. Literatura

[1]

W. Salejda, notatki do kursu „Wstęp do fizyki kwantowej” Studia inżynierskie [152-

160], Wrocław 2003 r, W. Salejda, M. Tyc, M. Just, „Algebraiczne metody

rozwiązywania równania Schrödingera”, PWN 2002 r.

[2]

R. L. Liboff, „Wstęp do mechaniki kwantowej”, PWN 1987 r.; D. Griffiths,

„Introduction to Quantum Mechanics”, Prentice Hall 1995 .

[3]

R. Eisberg, R. Resnick, „Fizyka kwantowa atomów, cząsteczek, ciał stałych , jąder i

cząstek elementarnych“, Państwowe Wydawnictwa Naukowe 1983 r.

[4]

A. F. J. Levi, „Applied Quantum Mechanics”, Cambridge University Press 2003 r.

[5]

K.T. Hecht, „Quantum Mechanics”, Springer-Verlag New York, Inc. 2000 r.,

G. Bastard, „Wave mechanics applied to semiconductor heterostructures”, Halsed

Press 1988 r.

[6]

E. Wnuczak, „Fizyka, Działy Wybrane“, Politechnika Wrocławska 1995 r.

[7]

K.Yu. Bliokh, V.D. Freilikher, N.M. Makarov, „Scattering by one-dimensional

smooth potentials: between WKB and Born approximation“, Physica E 27 (2005)

262–269

[8]

K. N. Muchin, „Doświadczalna fizyka jądrowa”, Wydawnictwa Naukowo-

Techniczne, Warszawa 1978 r.

[9]

Stefano De Leo, Pietro P. Rotelli, „Tunnelling through two barriers”, Physics Letters

A 342 (2005) 294–298.

[10]

V. S. Olkhovsky, E. Recami, A. K. Zaichenko, „Resonant and non-resonant tunneling

through a double barrier“, Europhysics Letters, 70 (6), pp. 712–718 (2005)

[11]

Ashok V. Pimpale, „Quantum tunneling time and tunneling in time-dependent

potentials: A general formulation and some exactly solvable models”, Progress in

Quantum Electronics, 28 (2004) 345–355

[12]

N.L.Chuprikov, „From the paradoxes of the standard wave-packet analysis to the

definition of tunneling times for particles”, arXiv:quant-ph/0106129 2002 r.