Tematy zadań – arkusze maturalne 1-5.
1.
Zestaw 1 (egzamin przeprowadzony 7 stycznia 2003 r.)
Arkusz podstawowy
1)
Powierzchnia prostokątnej działki budowlanej równa się 1540 m
2
. Oblicz
wymiary tej działki wiedząc, że różnią się one o 9m.
2)
Na wspólne konto państwa Kowalskich wpływają pieniądze z ich dwóch pensji
miesięcznych, razem jest to kwota 3200 złotych. Na początku każdego miesiąca
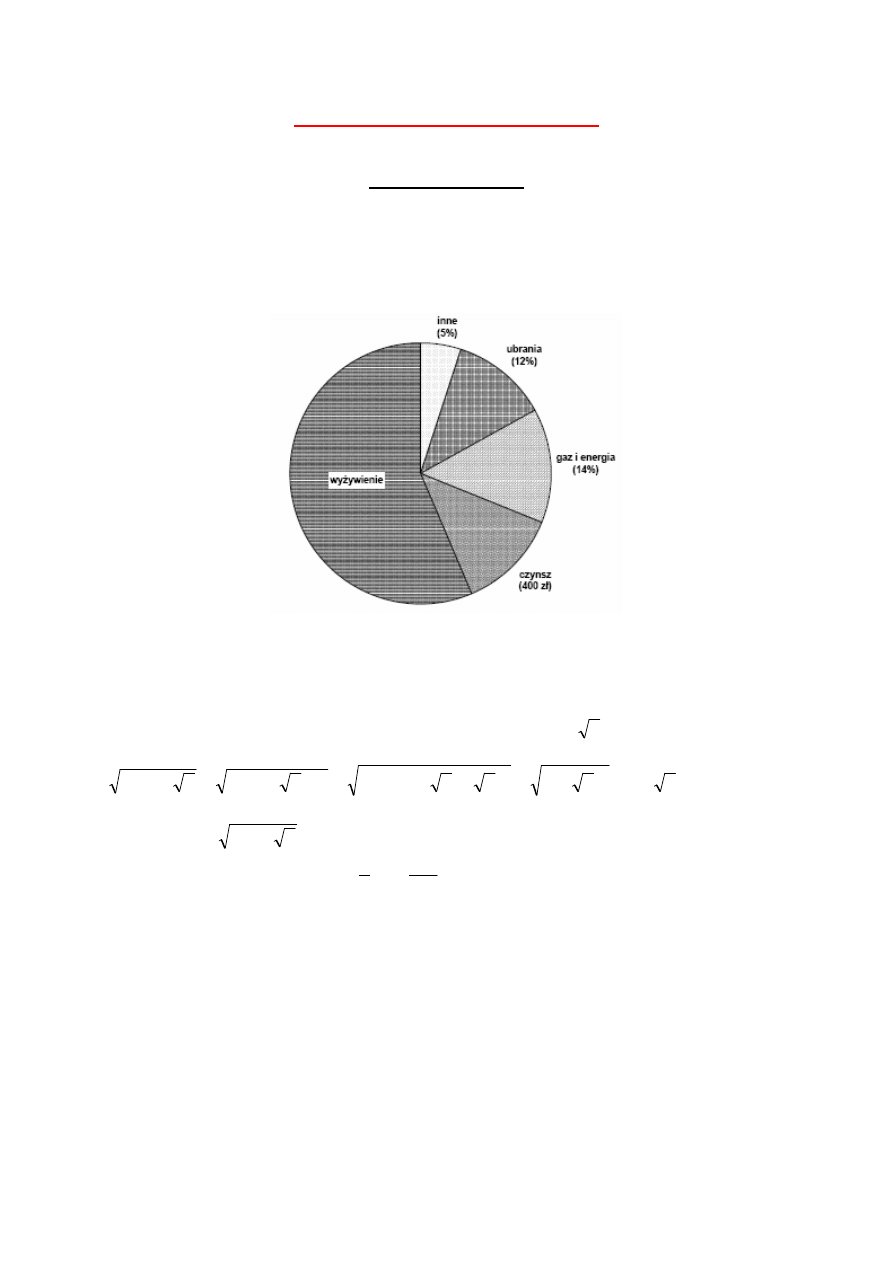
małżonkowie dzielą całość tej kwoty. Na diagramie kołowym przedstawiono
strukturę planowanych, przez państwa Kowalskich, miesięcznych wydatków.
Korzystając z tych danych:
a)
Oblicz, ile procent danej kwoty stanowią miesięczne wydatki państwa
Kowalskich na wyżywienie.
b)
Oblicz, ile pieniędzy wydają państwo Kowalscy w ciągu miesiąca łącznie, na
gaz i energię oraz czynsz
3)
Upraszczając pierwiastek kwadratowy z liczby
2
10
27
++++
, zapiszemy ją w postaci
kwadratu sumy dwóch liczb. Postępujemy następująco:
(((( )))) ((((
))))
2
5
2
5
2
2
5
2
5
2
2
10
25
2
10
27
2
2
2
++++
====
++++
====
++++
⋅⋅⋅⋅
⋅⋅⋅⋅
++++
====
++++
++++
====
++++
Przeanalizuj ten przykład, a następnie, stosując analogiczne postępowanie,
uprość
2
6
11
++++
.
4)
Równanie postaci
9
160
F
9
5
C
−−−−
⋅⋅⋅⋅
====
, ustala zależność między temperaturą,
wyrażoną w stopniach Celsjusza (C) oraz Fahrenheita (F).
a)
Oblicz, ile stopni w skali Fahrenheita, ma wrząca w temperaturze 100
0
C
woda.
b)
Wyznacz taką temperaturę, przy której liczba stopni w skali Celsjusza
jest równa liczbie stopni w skali Fahrenheita.
5)
Dany jest trójkąt, którego dwa boki mają długości 8 cm i 12 cm, kąt zawarty
między tymi bokami ma miarę 120
0
. Oblicz długość promienia okręgu opisanego
na tym trójkącie.
6)
Do pewnego przepisu z książki kucharskiej należy przygotować 0,25 litra płynu.
Mamy do wyboru trzy szklanki w kształcie walca, o wewnętrznych wymiarach:
pierwsza – o średnicy 6cm i wysokości 10cm, druga – o średnicy 5,8cm i

wysokości 9,5cm oraz trzecia – o średnicy 6cm i wysokości 9cm. Której szklanki
objętość jest najbliższa 0,25 litra? Odpowiedź uzasadnij.
7)
Funkcja
R
R
:
f
→
→
→
→
jest określona wzorem:
12
x
6
x
)
x
(
f
2
++++
−−−−
====
.
a)
Rozwiąż nierówność
0
19
)
x
(
f
>>>>
−−−−
.
b)
Uzasadnij, że obrazem wykresu funkcji f, w symetrii względem prostej o
równaniu x=6 nie jest parabola, określona równaniem
((((
))))
6
9
x
y
2
++++
−−−−
====
.
8)
Spośród wszystkich wierzchołków sześcianu wybieramy jednocześnie trzy
wierzchołki. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że
otrzymamy wierzchołki trójkąta równobocznego.
9)
Wykaż, że w trójkącie prostokątnym suma kwadratów sinusów miar wszystkich
jego kątów wewnętrznych równa się 2.
10)
Wszystkie liczby naturalne dwucyfrowe, podzielne przez 6 są kolejnymi
wyrazami pewnego ciągu arytmetycznego rosnącego.
a)
Zapisz wzór ogólny na n-ty wyraz tego ciągu arytmetycznego.
b)
Oblicz, ile wyrazów ma ten ciąg.
c)
Oblicz sumę piętnastu początkowych kolejnych wyrazów tego ciągu.
Arkusz rozszerzony
11)
Wyznacz najmniejszą i największą wartość funkcji
R
R
:
f
→
→
→
→
, określonej
wzorem:
)
x
5
)(
1
x
(
)
x
(
f
−−−−
−−−−
====
, w przedziale
7
,
0
.
12)
Dane jest równanie postaci
a
x
1
x
a
2
++++
====
−−−−
⋅⋅⋅⋅
, w którym niewiadomą jest x. Zbadaj
liczbę rozwiązań tego równania, w zależności od parametru a.
13)
Wyznacz te wartości parametrów a oraz b, przy których funkcja
R
R
:
g
→
→
→
→
,
określona wzorem
====
≠≠≠≠
−−−−
++++
====
2
x
dla
b
2
x
dla
2
x
a
x
)
x
(
g
2
jest ciągła w punkcie x=2.
14)
Suma n początkowych, kolejnych wyrazów ciągu
(((( ))))
n
a
, jest obliczana według
wzoru
((((
))))
++++
∈
∈
∈
∈
++++
====
N
n
,
n
3
n
S
2
n
. Wyznacz
n
a . Wykaż, że ciąg
(((( ))))
n
a
jest ciągiem
arytmetycznym.
15)
Dziesiąty wyraz pewnego ciągu geometrycznego równa się 10. Oblicz iloczyn
dziewiętnastu początkowych, kolejnych wyrazów tego ciągu.
16)
Rzucamy pięć razy symetryczną kostką sześcienną. Oblicz prawdopodobieństwo
zdarzenia, polegającego na tym, że „jedynka” wypadnie co najmniej cztery razy.
17)
W układzie współrzędnych są dane punkty:
)
2
,
9
(
A
−−−−
−−−−
oraz
)
2
,
4
(
B
. Wyznacz
współrzędne punktu C leżącego na osi OY, tak że kąt ACB jest kątem prostym.
18)
Wybierz dwie dowolne przekątne sześcianu i oblicz cosinus kąta między nimi.
Sporządź odpowiedni rysunek i zaznacz na nim kąt, którego cosinus obliczasz.
19)
Trapez równoramienny, o obwodzie równym 20cm, jest opisany na okręgu.
Wiedząc, że przekątna trapezu ma długość 41 cm, oblicz pole tego trapezu.
20)
Funkcja h jest określona wzorem
((((
))))
((((
))))
5
x
log
4
x
log
)
x
(
h
2
2
2
−−−−
−−−−
−−−−
====
. Wyznacz
wszystkie wartości parametru k, dla których równanie
0
k
log
)
x
(
h
2
====
−−−−
ma dwa
różne pierwiastki.
21)
Na kuli o promieniu R = 4 cm opisujemy stożki o promieniu r i wysokości H.
Spośród wszystkich takich stożków wyznacz ten, który ma najmniejszą objętość.
Oblicz tę objętość. Oblicz promień i wysokość znalezionego stożka.

2.
Zestaw 2 (egzamin przeprowadzony w maju 2002 r.)
Arkusz1 - poziom podstawowy
1)
Dana jest prosta l o równaniu
2
x
2
3
y
−−−−
====
oraz punkt
)
2
,
3
(
A
−−−−
−−−−
. Wykres
funkcji liniowej f jest prostopadły do prostej l , punkt A należy do wykresu
funkcji f. Wyznacz:
a)
wzór funkcji f,
b)
miejsce zerowe funkcji f
.
2)
Dany jest wektor
[[[[
]]]]
4
,
3
AB
−−−−
====
oraz punkt
)
2
,
1
(
A
−−−−
. Oblicz:
a)
współrzędne punktu B,
b)
współrzędne i długość wektora .
AB
2
v
⋅⋅⋅⋅
−−−−
====
3)
W klasie liczącej 30 uczniów, dziewięciu obejrzało film pt. „Nasz XXI wiek”.
Wychowawca klasy otrzymał 4 bilety i zamierza wylosować uczniów, których
zaprosi na projekcję tego filmu. Oblicz prawdopodobieństwo zdarzenia, że wśród
czterech wylosowanych z tej klasy uczniów nie ma ucznia, który już ten film
oglądał.
4)
W pewnej szkole średniej po pierwszym półroczu przeprowadzono test z
matematyki. Tabelka przedstawia zestawienie wyników testu:
a)
Sporządź diagram słupkowy przedstawiający zestawienie wyników testu.
b)
Oblicz średnią arytmetyczną uzyskanych ocen.
c)
Oblicz, ilu uczniów uzyskało ocenę wyższą od średniej arytmetycznej
ocen.
5)
Ania przeczytała książkę science-fiction w ciągu 13 dni, przy czym każdego dnia
czytała o taką samą liczbę stron więcej, niż w dniu poprzednim. Ile stron miała ta
książka, jeżeli wiadomo, że w trzecim dniu Ania przeczytała 28 stron a w
ostatnim 68?
6)
Jeżeli
1
x
,
3
x
,
2
x
3
2
1
−−−−
====
====
====
są
miejscami
zerowymi
wielomianu
d
cx
bx
ax
)
x
(
W
2
3
++++
++++
++++
====
, gdzie
0
a
≠≠≠≠
oraz
2
)
4
(
W
====
, to współczynnik a można
wyznaczyć postępując w następujący sposób: Wielomian W zapisujemy w postaci
iloczynowej:
)
1
x
)(
3
x
)(
2
x
(
a
)
x
(
W
++++
−−−−
−−−−
====
i wykorzystując warunek
2
)
4
(
W
====
otrzymujemy równanie:
)
1
4
)(
3
4
)(
2
4
(
a
2
++++
−−−−
−−−−
====
, stąd
5
1
a
====
.
Postępując analogicznie, wyznacz współczynnik a wielomianu
d
cx
bx
ax
)
x
(
W
2
3
++++
++++
++++
====
, wiedząc, że jego miejsca zerowe to:
2
x
,
1
x
,
2
x
3
2
1
====
====
−−−−
====
oraz
3
)
1
(
W
====
−−−−
.
7)
Planując czterotygodniowe wakacje, rodzina Kowalskich przeznaczyła pewną
kwotę na wyżywienie. W pierwszym tygodniu wydano 30%
zaplanowanej kwoty,
w drugim tygodniu o 60 złotych mniej niż w pierwszym, w trzecim połowę reszty
pieniędzy. Na czwarty tydzień zostało 270 złotych. Oblicz kwotę, którą rodzina
Kowalskich przeznaczyła na wyżywienie.
8)
Funkcja kwadratowa
3
bx
ax
)
x
(
f
2
−−−−
++++
====
, gdzie
0
b
>>>>
posiada dwa różne miejsca
zerowe, których iloczyn jest równy
)
3
(
−−−−
. Wiedząc, że funkcja ta przyjmuje
najmniejszą wartość równą
)
4
(
−−−−
, wyznacz:
a)
współczynniki a i b ,
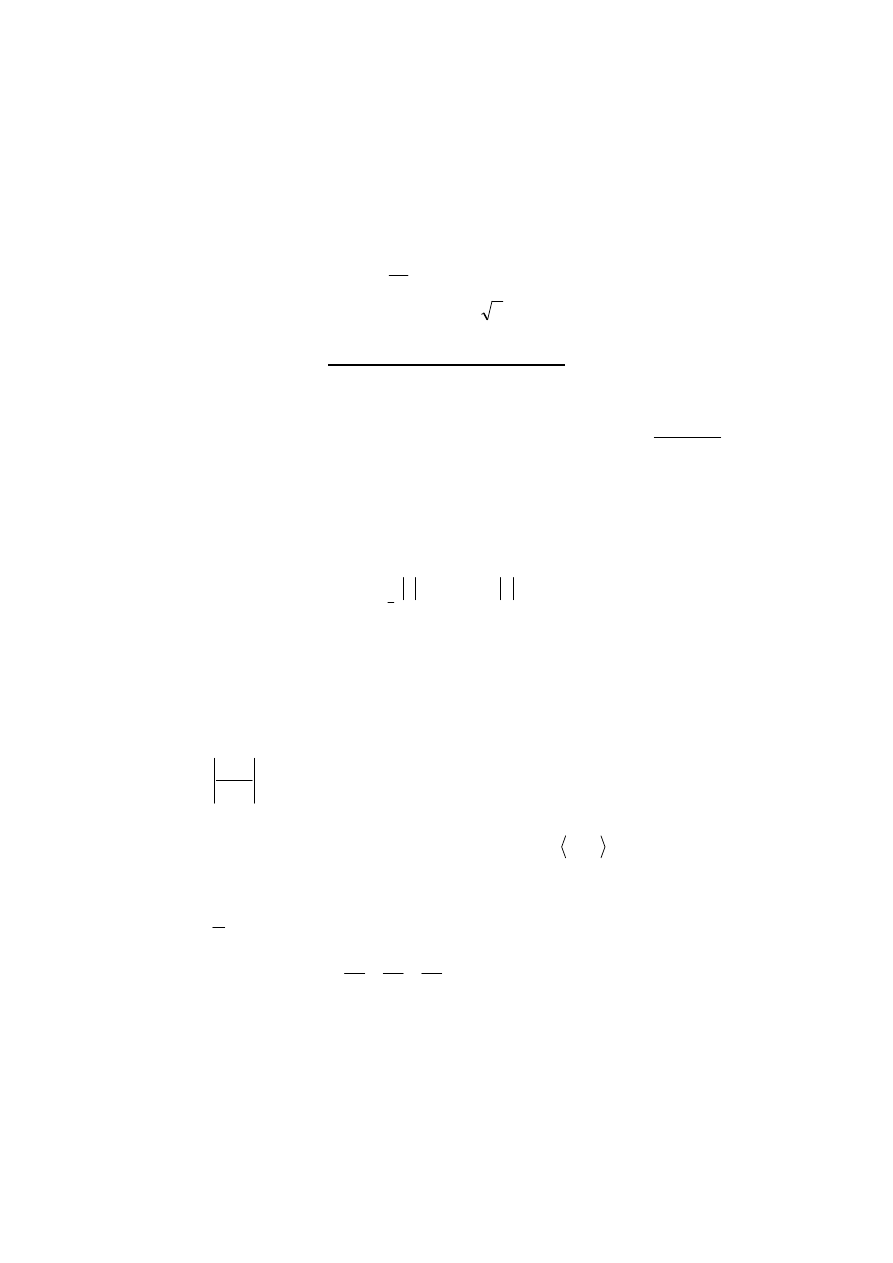
b)
miejsca zerowe funkcji f.
9)
Zaplanowano zalesić ugór w kształcie trójkąta równoramiennego, którego
długość najdłuższego boku, na planie w skali 1:1500, jest równa 12 cm i jeden z
kątów ma miarę 120
0
. W szkółce leśnej zamówiono sadzonki, w ilości
pozwalającej obsadzić obszar wielkości 40 arów. Oblicz, czy zamówiona ilość
sadzonek jest wystarczająca do zalesienia ugoru.
10)
Dane są dwie bryły: stożek, w którym długość promienia podstawy jest równa
4dm i wysokość ma długość
ππππ
18
dm
oraz ostrosłup prawidłowy czworokątny, w
którym krawędź podstawy ma długość
3
4
dm. Wiedząc, że objętości tych brył
są równe, wyznacz kąt nachylenia ściany bocznej ostrosłupa do jego podstawy.
Arkusz 2 - poziom rozszerzony
11)
Wyznacz wszystkie wartości parametru m, dla których równanie
0
m
x
)
1
m
(
3
mx
2
====
++++
++++
−−−−
nie ma rozwiązania w zbiorze liczb rzeczywistych.
12)
A i B są zdarzeniami losowymi i
0
)
B
(
P
>>>>
. Wykaż, że
((((
))))
(((( ))))
)
B
(
P
'
A
P
1
B
/
A
P
−−−−
≤≤≤≤
.
13)
Sprawdź,
że
przekształcenie
P
płaszczyzny
dane
wzorem
((((
))))
)
y
,
1
x
(
)
y
,
x
(
P
−−−−
++++
====
jest izometrią. Wyznacz równanie obrazu okręgu o
równaniu
0
x
2
y
x
2
2
====
−−−−
++++
w przekształceniu P.
14)
14)
14)
14)
Zaznacz na płaszczyźnie zbiór:
(((( ))))
((((
))))
>>>>
∧∧∧∧
−−−−
≥≥≥≥
−−−−
∧∧∧∧
∈
∈
∈
∈
∧∧∧∧
∈
∈
∈
∈
====
0
y
2
1
x
log
R
y
R
x
:
y
,
x
F
2
1
.
Napisz równania osi symetrii figury F.
15)
Objętość walca jest równa
3
cm
250
ππππ
. Przedstaw pole powierzchni całkowitej
tego walca jako funkcję długości promienia jego podstawy i określ dziedzinę tej
funkcji. Wyznacz długość promienia takiego walca, którego pole powierzchni
całkowitej jest najmniejsze.
16)
Naszkicuj w jednym układzie współrzędnych wykresy funkcji
1
x
2
)
x
(
f
++++
====
oraz
x
1
x
)
x
(
g
++++
====
. Na podstawie wykonanego rysunku określ liczbę ujemnych
rozwiązań równania
)
x
(
g
)
x
(
f
====
.
17)
Rozwiąż równanie:
x
cos
4
ctgx
x
2
sin
2
====
++++
dla
ππππ
∈
∈
∈
∈
2
,
0
x
. Ze zbioru rozwiązań
tego równania losujemy bez zwracania dwie liczby. Oblicz prawdopodobieństwo
zdarzenia, że co najmniej jedno z wylosowanych rozwiązań jest wielokrotnością
liczby
2
ππππ
.
18)
Rozwiąż nierówność
)
9
(
,
0
2
...
8
1
4
1
2
1
x
x
x
x
−−−−
>>>>
++++
++++
++++
, gdzie lewa strona tej
nierówności jest sumą nieskończonego ciągu geometrycznego.
19)
W trójkącie jeden z kątów ma miarę 120
0
. Długości boków tego trójkąta są
kolejnymi wyrazami ciągu arytmetycznego, którego suma wynosi 30. Wyznacz
stosunek długości promienia okręgu opisanego na tym trójkącie do długości
promienia okręgu wpisanego w ten trójkąt.

3.
Zestaw 3
Arkusz1 - poziom podstawowy
1)
Na prostej o równaniu
2
x
3
2
y
++++
====
znajdź taki punkt, by suma kwadratów
odległości od obu osi układu była najmniejsza.
2)
Dany jest trójkąt o bokach długości: 4cm, 6cm, 8cm. Dwusieczna największego
kąta wewnętrznego tego trójkąta dzieli przeciwległy bok na dwa odcinki. Oblicz
ich długości.
3)
Rozwiąż nierówność
0
12
x
5
x
2
2
>>>>
++++
−−−−
−−−−
. Wskaż liczby naturalne spełniające tę
nierówność.
4)
Kantor „Grosik” w dniu 1 lipca 2001 r. oferował swe usługi wg następującego
kursu walut:
Skup
Waluta
Sprzedaż
394
100 USD
402
169
100 DEM
174
547
100 GBP
557
51
100 FRF
52,50
217
100 CHF
223
Objaśnienie: USD – dolar amerykański, DEM – marka niemiecka, GBP – funt
angielski, FRF – frank francuski, CHF – frank szwajcarski.
a)
Jaka jest różnica cen sprzedaży i skupu 100 jednostek poszczególnych walut?
b)
Ile procent ceny skupu stanowi cena sprzedaży poszczególnych walut?
5)
Przed 10 laty ojciec był 4 razy starszy od syna. Za 10 lat obaj będą mieli razem
100 lat. Ile lat ma obecnie każdy z nich?
6)
Niech A oznacza zbiór wszystkich liczb całkowitych podzielnych przez 2, B –
zbiór wszystkich liczb całkowitych podzielnych przez 3. Opisz słownie lub
symbolicznie zbiory
B
A
∩
∩
∩
∩
oraz
B
A
∪
∪
∪
∪
, a następnie wyznacz zbiory:
))))
)
30
,
9
(
B
i
20
,
5
A
∩
∩
∩
∩
∩
∩
∩
∩
.
7)
Niech A oznacza zbiór wszystkich liczb całkowitych podzielnych przez 2, B –
zbiór wszystkich liczb całkowitych podzielnych przez 3. Opisz słownie lub
symbolicznie zbiory
B
A
∩
∩
∩
∩
oraz
B
A
∪
∪
∪
∪
, a następnie wyznacz zbiory:
))))
)
30
,
9
(
B
i
20
,
5
A
∩
∩
∩
∩
∩
∩
∩
∩
.
8)
Sporządź wykres funkcji danej wzorem:
>>>>
−−−−
≤≤≤≤
++++
====
0
x
dla
x
3
0
x
dla
x
2
x
y
2
9)
Sprawdź, czy podana równość jest tożsamością:
((((
))))
2
cos
sin
1
cos
sin
cos
1
sin
1
++++
αααα
αααα
====
αααα
++++
αααα
αααα
++++
αααα
10)
Zbiór Z jest zbiorem skończonym. Oblicz liczbę elementów tego zbioru wiedząc,
że posiada on 67 podzbiorów co najwyżej dwuelementowych.
11)
Ile waży stożek wykonany z miedzi, którego przekrój osiowy jest trójkątem o
bokach długości 10cm, 10cm, 12cm? (Ciężar właściwy miedzi wynosi
3
cm
G
9
,
8
).
Wynik podaj z dokładnością do 0,1 kG.
Arkusz 2 - poziom rozszerzony

12)
Funkcja f dana jest wzorem:
≤≤≤≤
>>>>
++++
====
3
x
dla
x
3
x
dla
a
x
)
x
(
f
3
. Czy istnieje a, dla
którego ta funkcja jest ciągła? Odpowiedź uzasadnij.
13)
Wykaż, stosując zasadę indukcji matematycznej, że suma kolejnych liczb
naturalnych od 1 do n jest równa
2
)
1
n
(
n
++++
14)
Zbadaj,
dla
jakich
wartości
rzeczywistych
parametru
m,
równanie
0
1
m
x
)
3
m
(
2
x
)
2
m
(
2
4
====
++++
++++
++++
−−−−
−−−−
ma cztery różne pierwiastki.
15)
Styczna do wykresu funkcji danej wzorem
1
x
5
x
4
x
2
)
x
(
f
2
3
−−−−
++++
−−−−
====
jest
równoległa do prostej o równaniu
x
3
y
====
. Wyznacz współrzędne punktu
styczności.
16)
Znajdź punkt symetryczny do punktu
)
6
,
2
(
A
====
względem prostej o równaniu
0
5
y
4
x
3
====
−−−−
++++
.
17)
Na paraboli
x
4
y
2
====
wyznacz punkt leżący najbliżej prostej opisanej równaniem
4
x
2
y
++++
====
.
18)
Dla jakich wartości
R
∈
∈
∈
∈
αααα
wielomian
αααα
−−−−
++++
−−−−
αααα
++++
====
2
sin
1
x
3
x
)
sin
2
(
x
2
)
x
(
W
2
3
jest podzielny przez
1
x
−−−−
?
19)
W jakiej odległości od środka należy przeciąć kulę o promieniu długości R, aby
stosunek pola przekroju do pola koła wielkiego kuli był równy
9
1
?
20)
Rozwiąż równanie:
5
n
1
n
1
n
2
1
n
n
3
19
4
5
2
11
3
7
lim
...
x
64
9
x
8
3
x
++++
−−−−
++++
++++
∞
∞
∞
∞
→
→
→
→
⋅⋅⋅⋅
−−−−
⋅⋅⋅⋅
⋅⋅⋅⋅
++++
⋅⋅⋅⋅
====
++++
++++
++++
, gdzie lewa strona
jest sumą zbieżnego szeregu geometrycznego.
4.
Zestaw 4
Arkusz1 - poziom podstawowy
1)
Są trzy siostry, z których najstarsza przychodzi do domu rodzinnego co 10 dni,
średnia co 6 dni, a najmłodsza – co 4 dni. Co ile dni wszystkie siostry spotykają
się w domu rodzinnym?
2)
Rozłóż na czynniki trójmian
6
x
7
x
3
y
2
−−−−
−−−−
====
.
3)
Operator telefonii miejscowej przedstawił abonamentom dwa warianty opłat:
•
Wariant I: abonament miesięczny wynosi 35zł, cena 1 min. rozmowy wynosi
22gr.
•
Wariant II: abonament miesięczny wynosi 23zł, cena 1 min. rozmowy wynosi
44gr.
a)
przy ilu minutach rozmów miesięcznie korzystniejszy jest wariant I ?
b)
w którym wariancie zapłacimy więcej i o ile zł, jeśli założymy, że w miesiącu
było 100 min. rozmów?
4)
Na okręgu o równaniu
0
12
y
8
x
12
y
x
2
2
====
−−−−
−−−−
++++
++++
opisano kwadrat. Jaka jest długość
boku tego kwadratu?
5)
Wyznacz
dziedzinę
i
miejsca
zerowe
funkcji
danej
wzorem:
3
x
4
x
3
x
x
3
x
)
x
(
f
2
2
3
++++
−−−−
++++
−−−−
−−−−
====
.

6)
Zbadaj dla jakich wartości rzeczywistych parametru m , funkcja f określona
wzorem
4
x
)
1
m
3
(
)
x
(
f
++++
−−−−
====
jest rosnąca w zbiorze R.
7)
Wyznacz
wartość
parametru
k,
aby
proste
o
równaniach
kx
y
i
x
2
1
y
,
4
y
====
====
====
ograniczały trójkąt o polu
2
j
60 .
8)
Oblicz sumę wszystkich dwucyfrowych liczb naturalnych.
9)
Promień okręgu opisanego na trójkącie rozwartokątnym ma długość równą
długości najdłuższego boku trójkąta. Oblicz miarę kąta rozwartego tego trójkąta.
10)
Z urny zawierającej 9 jednakowych kul ponumerowanych od 1 do 9 wylosowano
kolejno 3 kule bez zwracania. Oblicz prawdopodobieństwo tego, że numery
wszystkich wylosowanych kul są liczbami parzystymi.
11)
Stożek o promieniu podstawy r=12cm i kącie nachylenia tworzącej do podstawy
0
30
====
αααα
przecięto płaszczyzną zawierającą wysokość stożka.
a)
Oblicz pole otrzymanego przekroju.
b)
Oblicz miarę kąta rozwarcia stożka.
c)
Oblicz objętość i pole powierzchni stożka
Arkusz2 - poziom rozszerzony
12)
Nie korzystając z tablic ani kalkulatora oblicz:
0
0
75
cos
105
cos
⋅⋅⋅⋅
.
13)
Naszkicuj wykres funkcji określonej wzorem
(((( ))))
1
x
x
x
f
−−−−
++++
====
, gdzie
R
x
∈
∈
∈
∈
.
14)
Nie rozwiązując równania
0
900
x
200
x
2
====
++++
−−−−
wykaż, że wartość bezwzględna
różnicy jego pierwiastków jest nie mniejsza niż 20.
15)
Boki pewnego trójkąta zawierają się w prostych danych równaniami:
0
9
y
x
3
,
0
23
y
3
x
,
0
2
x
====
−−−−
−−−−
====
−−−−
++++
====
−−−−
.
a)
Do jakiego rodzaju trójkątów można zaliczyć ten trójkąt? Odpowiedź
uzasadnij.
b)
Oblicz pole koła opisanego na tym trójkącie.
16)
Rozwiąż równanie:
2
x
2
)
1
x
2
(
2
====
++++
−−−−
.
17)
Z dwóch stacji wyjechały ( po torach równoległych) jednocześnie naprzeciw
siebie dwa pociągi. Pierwszy jedzie z prędkością o 15km/h większą niż drugi.
Pociągi te spotkały się po 40 minutach jazdy. Gdyby drugi pociąg wyjechał o 9
minut wcześniej od pierwszego, to pociągi spotkałyby się w połowie drogi. Oblicz
odległość między stacjami.
18)
W trapez równoramienny o podstawach długości a i b można wpisać okrąg.
Udowodnij, że promień tego okręgu ma długość równą
ab
2
1
.
19)
Oblicz miarę kąta między wektorami:
]
11
;
7
;
8
[
b
],
7
;
8
;
2
[
a
====
−−−−
====
→
→
→
→
→
→
→
→
.
20)
Kocioł parowy o objętości V ma kształt walca zakończonego z jednej strony
półkulą (o czaszy na zewnątrz walca). Jakie wymiary powinien mieć kocioł, aby
na jego budowę zużyć jak najmniej blachy?
21)
Ile trzeba wykonać rzutów monetą, aby prawdopodobieństwo uzyskania
dokładnie cztery razy orła było takie samo, jak uzyskanie dokładnie sześć razy
reszki?
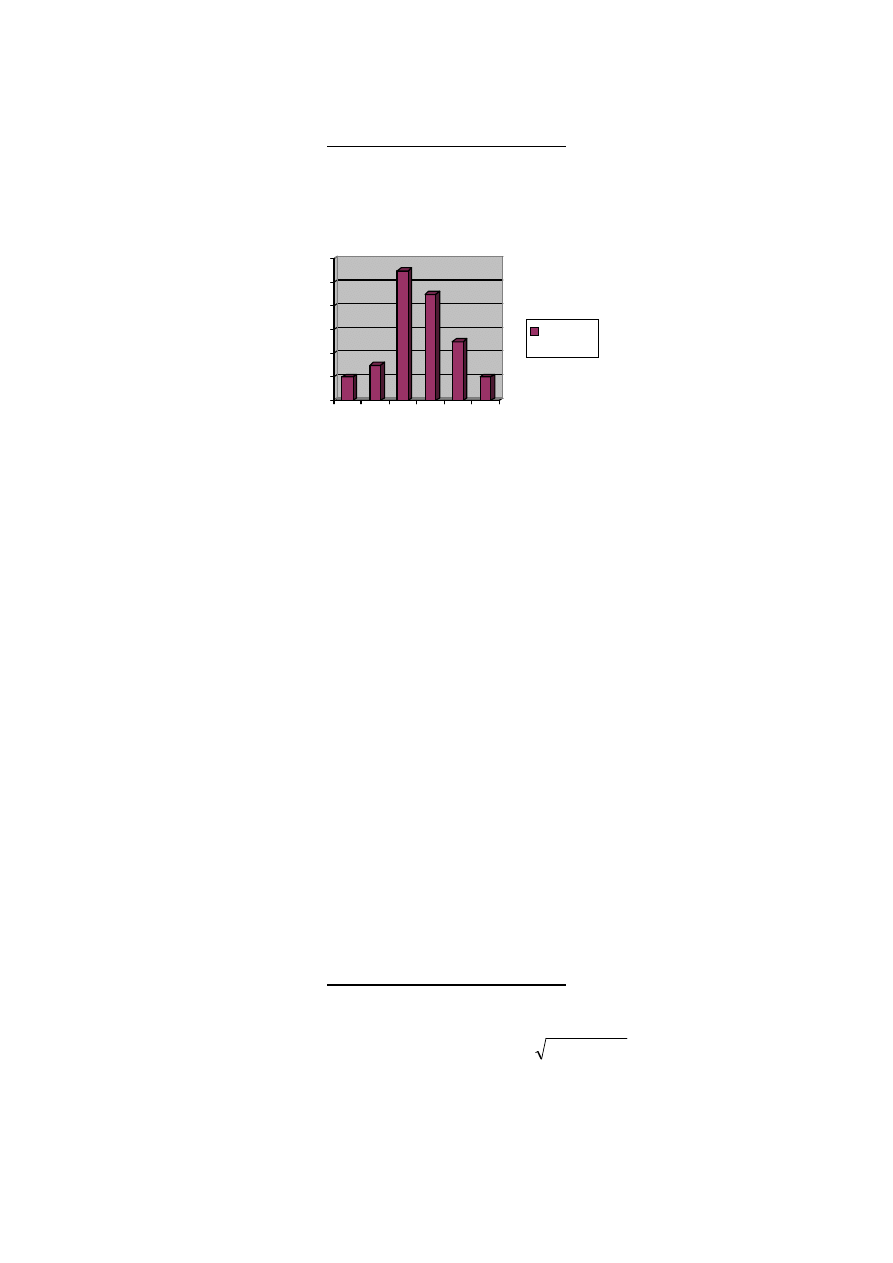
5.
Zestaw 5
Arkusz1 – poziom podstawowy
1)
Długości boków trójkąta są kolejnymi wyrazami ciągu arytmetycznego o różnicy
3. Oblicz długości tych boków, wiedząc, że trójkąt jest prostokątny.
2)
Na wykresie przedstawiono wyniki klasyfikacji rocznej z matematyki w klasie
liczącej 32 uczniów.
0
2
4
6
8
10
12
1
2
3
4
5
6
Liczba
uczniów
Oblicz średnią ocen z matematyki w tej klasie. Ilu uczniów uzyskało ocenę wyższą
od średniej? Jaki procent uczniów danej klasy stanowią uczniowie, którzy
uzyskali ocenę co najmniej bardzo dobrą? (Wynik podaj z dokładnością do 0,01).
3)
Wykresem funkcji liniowej jest prosta nachylona do osi OX pod kątem 135
0
,
przechodząca przez punkt P=(3,1). Wyznacz wzór tej funkcji.
4)
Znajdź wszystkie
>>>>
ππππ
∈<
∈<
∈<
∈<
,
0
x
takie, że
0
2
x
sin
x
cos
2
2
====
−−−−
−−−−
.
5)
Wyznacz współczynnik a wiedząc, że reszta z dzielenia wielomianu
2
x
ax
x
5
x
2
)
x
(
W
2
3
4
++++
−−−−
++++
−−−−
====
przez dwumian x+1 jest równa 12.
6)
Długości przekątnych rombu różnią się o 4. Pole tego rombu jest równe
2
cm
30
.
Oblicz długości przekątnych.
7)
Oblicz
pole
koła,
którego
brzegiem
jest
okrąg
o
równaniu
0
6
y
6
x
2
y
x
2
2
====
−−−−
++++
−−−−
++++
.
8)
Statek przepłynął 40km z prądem rzeki w 2 godziny, a 35km pod prąd w 2,5
godziny. Oblicz prędkość własną statku i prędkość prądu rzeki.
9)
Sześcian o krawędzi długości 1dm przecięto płaszczyzną, do której należą
dokładnie trzy jego wierzchołki. Oblicz pole otrzymanego przekroju.
10)
Student przyszedł na egzamin znając odpowiedzi na 40 spośród 50 pytań
podanych jako wymagania egzaminacyjne. Egzaminator zadał mu trzy pytania.
Oblicz prawdopodobieństwo zdarzenia , że student zna odpowiedź na dokładnie
dwa z tych pytań.
11)
Z pełnego naczynia stożkowego o wysokości 18cm i średnicy podstawy 24cm
przelano ciecz do pustego naczynia w kształcie walca o średnicy podstawy 10cm.
Jaka jest wysokość słupa cieczy w tym naczyniu? Wynik podaj z dokładnością do
1mm.
Arkusz 2 – poziom rozszerzony
12)
Dla
jakich
rzeczywistych
wartości
parametru
m,
nierówność:
0
1
m
8
x
)
2
m
(
x
2
>>>>
++++
++++
++++
++++
jest spełniona dla każdej liczby rzeczywistej x?
13)
Sporządź wykres funkcji danej wzorem
9
x
6
x
)
x
(
f
2
++++
++++
====
, a następnie określ
liczbę pierwiastków równania f(x)=a w zależności od wartości parametru
R
a
∈
∈
∈
∈
.
14)
Punkty A=(-2,-2), B=(2,1) i C=(3,5) są wierzchołkami równoległoboku ABCD.
Wyznacz współrzędne wierzchołka D oraz oblicz pole tego równoległoboku.

15)
Kopano studnię. Za pierwszy metr głębokości zapłacono 200zł, a za każdy
następny płacono o 20zł więcej niż za poprzedni. Łącznie za kopanie studni
zapłacono 14 700zł. Jaka jest głębokość studni?
16)
Oblicz wartość wyrażenia:
0
0
0
2
0
2
300
tg
150
ctg
72
sin
18
sin
++++
++++
.
17)
Udowodnij, że w trapezie opisanym na okręgu, trójkąty, których jednym bokiem
jest ramię trapezu, a wierzchołkami środek okręgu, są prostokątne.
18)
Na
płaszczyźnie
z
układem
współrzędnych
XOY
zaznacz
zbiór:
((((
))))
{{{{
}}}}
0
6
)
y
x
(
log
5
y
x
log
R
y
R
x
:
)
y
,
x
(
A
2
2
2
2
2
2
2
≤≤≤≤
++++
++++
−−−−
++++
∧∧∧∧
∈
∈
∈
∈
∧∧∧∧
∈
∈
∈
∈
====
. Oblicz pole i
długość brzegu figury A.
19)
Oblicz ile elementów ma zbiór, którego liczba elementów jest 60 razy mniejsza od
sumy dwuelementowych i trójelementowych kombinacji tego zbioru.
20)
Wyznacz asymptoty funkcji określonej wzorem:
2
x
x
y
2
−−−−
====
.
21)
Jakie wymiary powinna mieć metalowa otwarta puszka w kształcie
graniastosłupa prawidłowego czworokątnego o pojemności 100 litrów, aby na jej
wykonanie zużyć możliwie najmniej materiału? Wymiary podaj z dokładnością
do 1mm.
22)
Wycinek koła przy zwinięciu utworzył powierzchnię boczną stożka, którego kąt
rozwarcia jest prosty. Wyznacz miarę kąta środkowego tego wycinka.
Wyszukiwarka
Podobne podstrony:
2012 06 Technik informatyk arkusz zadaniaid 27644
arkusz 1 zadania id 68486 Nieznany (2)
2012 06 Technik informatyk arkusz zadania, E12 E13 E14, Technik Informatyk
2012 06 Technik informatyk arkusz zadania
Arkusze z zadaniami Chruścińskiej
arkusz 2 zadania id 68493 Nieznany (2)
arkusz z zadania info pr 10 04 Nieznany (2)
2012 06 Technik informatyk arkusz zadaniaid 27644
Zadania egzaminacyjne 2003, Nieorganiczna, chemia2, Arkusze powtórzeniowe, Pobieranie1, studia 1.2,
Zadania egzaminacyjneA 2005, Nieorganiczna, chemia2, Arkusze powtórzeniowe, Pobieranie1, studia 1.2,
Wyniki.I-KolokwiumB.2008, Nieorganiczna, chemia2, Arkusze powtórzeniowe, Pobieranie1, studia 1.2, za
Optyka zadania z arkuszy
Zadania dla maturzystów na dzień 28 marca 2010, matematyka, LICEUM, arkusze maturalne, Nowy folder (
więcej podobnych podstron