2013-05-28

1

1

Metody probabilistyczne

Dynamika zjawisk

2

Analiza dynamiki zjawisk

Problemy:



szereg czasowy, chronologiczny (momentów, okresów),



średni poziom zjawiska w czasie (średnia arytmetyczna, średnia
chronologiczna),



miary dynamiki (indeksy indywidualne, agregatowe),



średnie tempo zmian zjawiska w czasie,



wygładzanie szeregu czasowego (mechaniczne, analityczne),



analiza wahań okresowych (wskaźniki sezonowości),

2013-05-28

2

3

Szereg czasowy



Szereg czasowy { y

t

} -

uporządkowany ciąg wyników obserwacji

zjawiska w czasie.



Szeregi czasowe dzielimy na szeregi:



okresów (poziomy zjawiska w całych okresach, - strumienie: liczba
urodzin, liczba mieszkań oddanych w miesiącu, w roku)



momentów (poziomy zjawiska w ustalonych momentach okresów –
zasoby: liczba ludności na terenie województwa, stan zatrudnienia w
firmie)

Moment/okres t

1

2

3

4

5

6

7

Rok

2000

2001

2002

2003

2004

2005

2006

Liczba pojazdów

w UE-27 [tys.]

205 581 210 561

214 584

217 492

221 097

225 654

229 954

Liczba

wypadków

śmiertelnych na

drogach UE-27

56 412

54 314

53 331

50 355

47 262

45 296

42 953

„

Wypadki” - szereg okresów (łączna liczba

wypadków w każdym roku

„Pojazdy” - szereg momentów (w

każdym roku stan na 31.XII

4

Średni poziom zjawiska w czasie

Średni poziom zjawiska w czasie liczymy odmiennie w zależności od

rodzaju szeregu jako:



średnią arytmetyczną dla szeregu okresów



średnia chronologiczna dla szeregu momentów







n

t

t

y

n

y

1

1

1

2

1

2

1

1

2

1















n

y

y

y

y

y

n

n

ch



2013-05-28

3

5

Średni poziom zjawiska w czasie - przykład



„Wypadki” - szereg okresów (łączna liczba wypadków w każdym roku)



„Pojazdy” - szereg momentów (w każdym roku stan na 31.XII)

Moment/okres t

1

2

3

4

5

6

7

Rok

2000

2001

2002

2003

2004

2005

2006

Liczba pojazdów

w UE-27 [tys.]

205 581 210 561

214 584

217 492

221 097

225 654

229 954

Liczba

wypadków

śmiertelnych na

drogach UE-27

56 412

54 314

53 331

50 355

47 262

45 296

42 953

W latach 2000-2006

średnio w roku

zarejestrowanych było 399 332,2 tys. pojazdów

samochodowych

W latach 2000-2006

średnia roczna

liczba wypadków drogowych wyniosła

49 989,0 wypadków

0

49989

7

42953

45296

54314

56412

y

,















2

399332

1

7

229954

2

1

225654

210561

205581

2

1

y

ch

,

















6

Miary dynamiki



Przyrosty:



absolutne



jednopodstawowe



łańcuchowe



względne



jednopodstawowe



łańcuchowe



Indeksy dynamiki:



indywidualne



jednopodstawowe



łańcuchowe



agregatowe (zespołowe)



jednopodstawowe



łańcuchowe

2013-05-28

4

7

Miary dynamiki o podstawie stałej i zmennej

Miary dynamiki o podstawie stałej (jednopodstawowe)



Określają zmiany jakie następowały w kolejnych okresach
(momentach) t w odniesieniu do okresu (momentu) podstawowego
(bazowego) t*.



Ogólnie okresem (momentem) bazowym może być dowolny okres
(moment) k, tj. t*=k.



Dalej (dla wygody) przyjmiemy, że

okresem bazowym

będzie

pierwszy okres

, okres, tj. t*=1.

Miary dynamiki o podstawie ruchomej (łańcuchowe)



Określają one zmiany jakie następowały w kolejnych okresach
(momentach) t

w odniesieniu do okresu (momentu) bezpośrednio

poprzedzającego) tj. t*= t - 1.

8

Przyrosty absolutne



Określają one, o ile wzrósł (zmalał) poziom zjawiska w okresie
badanym (t

) w porównaniu z jego poziomem w okresie przyjętym za

podstawę porównania (t*).



Przyrosty absolutne są mianowane tak samo jak badana cecha.



jednopodstawowe (t*=1)



łańcuchowe (t*=t-1)

1

t

1

t

y

y







1

t

t

1

t

t

y

y











2013-05-28

5

9

Przyrosty absolutne -

przykład

dla okresu t=5:



Przyrost absolutny
jednopodstawowy



Przyrost absolutny łańcuchowy

Przyrosty absolutne

Moment

/okres t

Liczba

wypadków

Jednopods

tawowe

Łańcu
chowe

1

56412

-

-

2

54314

-2098

-2098

3

53331

-3081

-983

4

50355

-6057

-2976

5

47262

-9150

-3093

6

45296

-11116

-1966

7

42953

-13459

-2343

9150

56412

47262

y

y

1

5

1

5















2976

50355

47262

y

y

4

5

4

5















Przyrost absolutny

informuje, o ile jednostek wzrósł (znak plus) lub zmalał

(znak minus) poziom badanego zjawiska w okresie t w stosunku do poziomu z

okresu t* będącego podstawą porównania

10

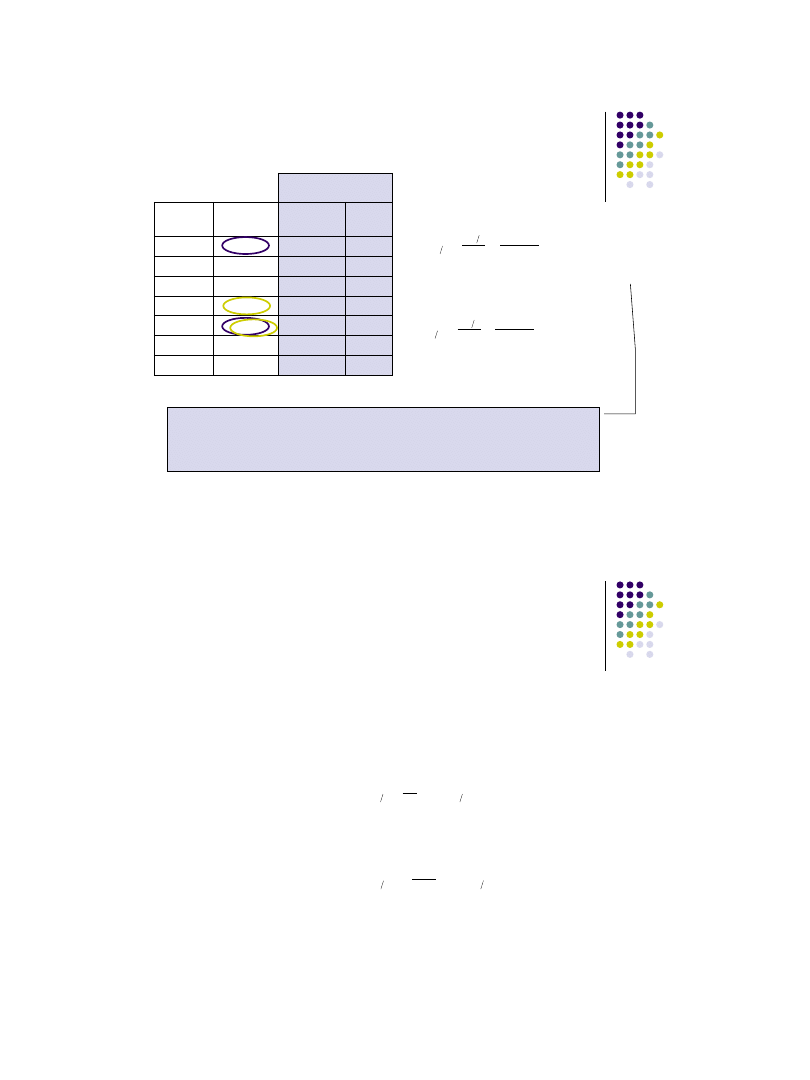
Przyrosty względne (wskaźniki tempa zmian)



Określają one stosunek przyrostu absolutnego w okresie badanym (t) do
jego poziomu w okresie przyjętym za podstawę porównania (t*).



Przyrosty względne są wielkościami niemianowanymi.



Wyrażamy je zawsze w ułamkach, ale interpretujemy w procentach.



jednopodstawowe (t*=1)



łańcuchowe (t*=t-1)

1

1

t

1

1

t

1

t

y

y

y

y

d









1

t

1

t

t

1

t

1

t

t

1

t

t

y

y

y

y

d



















2013-05-28

6

11

Przyrosty względne (wskaźniki tempa zmian) -

przykład

dla okresu t

=5 przyrost względny:



jednopodstawowy



łańcuchowy

Przyrosty względne

Moment/

okres t

Liczba

wypadków

Jednopod-

stawowe

Łańcu-

chowe

1

56412

-

-

2

54314

-0,037

-0,037

3

53331

-0,055

-0,018

4

50355

-0,107

-0,056

5

47262

-0,162

-0,061

6

45296

-0,197

-0,042

7

42953

-0,239

-0,052

162

0

56412

9150

y

d

1

1

5

1

5

,













061

0

50355

3093

y

d

4

4

5

4

5

,













Przyrost względny (wskaźnik tempa zmian) informuje:

o ile % wzrósł (znak plus) lub zmalał (znak minus) poziom badanego

zjawiska w okresie t w stosunku do poziomu z okresu t*

będącego podstawą porównania

12

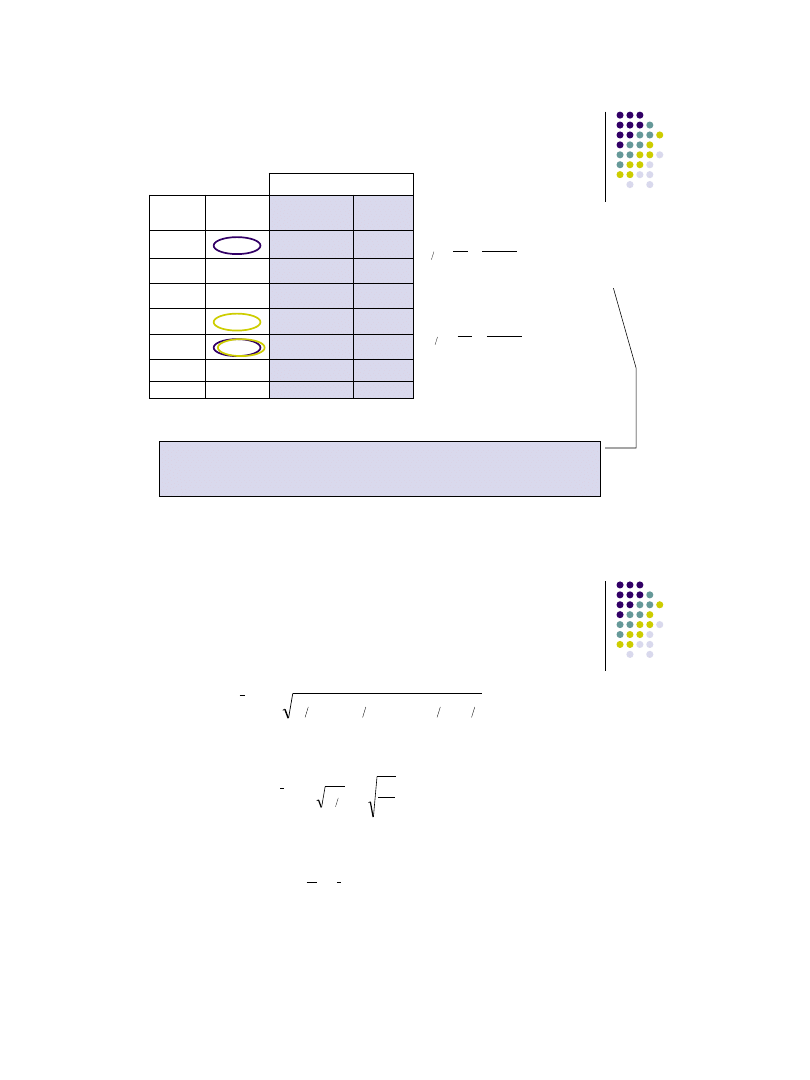
Indywidualne indeksy dynamiki



Określają one stosunek poziomu zjawiska w okresie badanym (t)
do jego poziomu w okresie przyjętym za podstawę porównania (t*).



Indeksy dynamiki

są wielkościami niemianowanymi.



Wyrażamy je zawsze w ułamkach, ale interpretujemy w procentach.



jednopodstawowe (t*=1)



łańcuchowe (t*= t - 1)

1

t

1

t

1

t

d

1

y

y

i







1

t

t

1

t

t

1

t

t

d

1

y

y

i













2013-05-28

7

13

Indywidualne indeksy dynamiki -

przykład

dla okresu indywidualny indeks

dynamiki:



jednopodstawowy



łańcuchowy

Indeksy indywidualne

Moment

/okres t

Liczba

wypadków

Jednopod-

stawowe

Łańcu-

chowe

1

56412

1,000

-

2

54314

0,963

0,963

3

53331

0,945

0,982

4

50355

0,893

0,944

5

47262

0,838

0,939

6

45296

0,803

0,958

7

42953

0,761

0,948

838

0

56412

47262

y

y

i

1

5

1

5

,







939

0

50355

47262

y

y

i

4

5

4

5

,







„Indeks dynamiki – 1” informuje o ile % wzrósł (znak plus)

lub zmalał (znak minus) poziom badanego zjawiska w okresie t

w stosunku do poziomu z okresu t

* będącego podstawą porównania

14

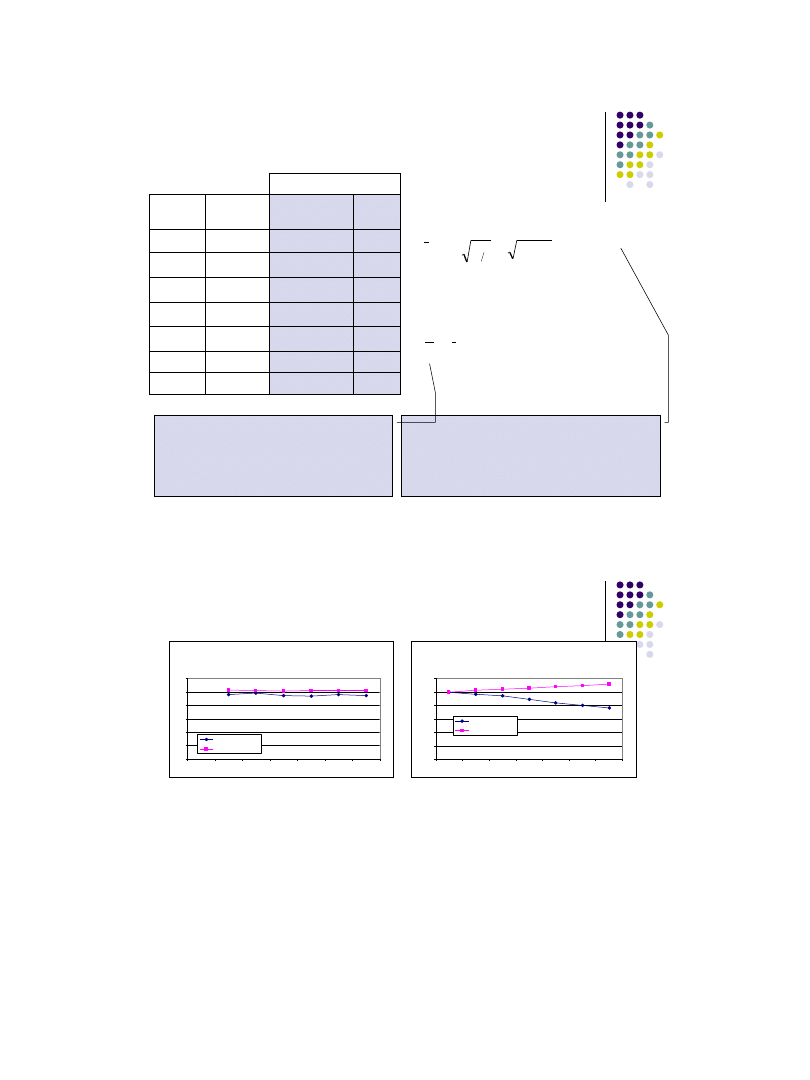
Średnie tempo zmian zjawiska w czasie



Średnie indeks zmian zjawiska w czasie wyznacza się jako
średnią geometryczną z indeksów łańcuchowych:



Jeżeli w liczeniu indeksów jednopodstawowych przyjmiemy okres
pierwszy jako bazowy (t

*=1), to wzór ten upraszcza się do:



Średniookresowe tempo zmian zjawiska w czasie wyznacza się
jako:

1

n

1

2

2

3

2

n

1

n

1

n

n

G

i

*

i

*

*

i

*

i

i













1

n

1

n

1

n

1

n

G

y

y

i

i









1

i

T

G

n





2013-05-28

8

15

Średnie tempo zmian zjawiska w czasie - przykład

Dla szeregu „Wypadki”



średni indeks zmian liczby
wypadków wynosi:



średniookresowe tempo zmian
liczby wypadków wynosi:

Indeksy indywidualne

Moment

/okres t

Liczba

wypadków

Jednopods-

tawowe

Łańcu-

chowe

1

56412

1,000

-

2

54314

0,963

0,963

3

53331

0,945

0,982

4

50355

0,893

0,944

5

47262

0,838

0,939

6

45296

0,803

0,958

7

42953

0,761

0,948

W ciągu badanych n okresów poziom

badanego zjawiska

rósł (znak plus) lub

malał (znak minus) średnio z okresu na

okres

o wyliczoną wartość-1 (%).

956

0

761

0

i

i

6

1

7

1

7

G

,

,









044

0

1

956

0

1

i

T

G

n

,

,













W ciągu 7 kolejnych lat (2000-2006) liczba

wypadków drogowych w UE-27 malała

(znak minus

) średnio z roku na rok o 4%

(malała średnio o 4% w stosunku do roku

poprzedniego).

16

Analiza dynamiki zjawisk na wykresach

Dynamika zjawiska

(zjawisk) może być wizualizowana za pomocą wykresów.



W celu uniknięcia pomyłek należy zwracać szczególną uwagę na dopiski w
tytule.



rok, miesiąc, itp. poprzedni = 1 (lub ... = 100) oznacza wykres dynamiki
opisanej indeksami

łańcuchowymi;



rok xxxx

= 1, miesiąc xx = 1, itp. (lub ... = 100) oznacza wykres dynamiki

opisanej indeksami

o stałej podstawie, którą jest okres podany w

dopisku.

Dynamika liczby pojazdów i wypadków w UE-27

w latach 2000-2006 (rok 2000 = 1)

0,000

0,200

0,400

0,600

0,800

1,000

1,200

2000

2001

2002

2003

2004

2005

2006

Liczba w ypadków

Liczba pojazdów

Dynamika liczby pojazdów i wypadków w UE-27

w latach 2000-2006 (rok poprzedni = 1)

0

0,2

0,4

0,6

0,8

1

1,2

2000

2001

2002

2003

2004

2005

2006

Liczba w ypadków

Liczba pojazdów

2013-05-28

9

17

Przyczyny zmian poziomu zjawiska w określonym czasie



główne – działają na zjawisko stale z niezmiennym nasileniem,
wytyczają kierunek zmian zjawiska w czasie – zw.

trendem

(tendencją rozwojową)

,



okresowe:



koniunkturalne

(cykliczne)

– są wynikiem zmian w otoczeniu

zjawiska (w gospodarce światowej), mają różny kierunek i
natężenie,



sezonowe

– działają regularnie krótkich rocznych cyklach wahań,

zależą od kalendarza, cyklu upraw,



przypadkowe, losowe

– wywołują nieregularne odchylenia

wielkości zjawiska od poziomu, jakiego oczekujemy na podstawie
działania innych czynników, ich wpływ jest nieprzewidywalny
zarówno co do siły jak i kierunku.

18

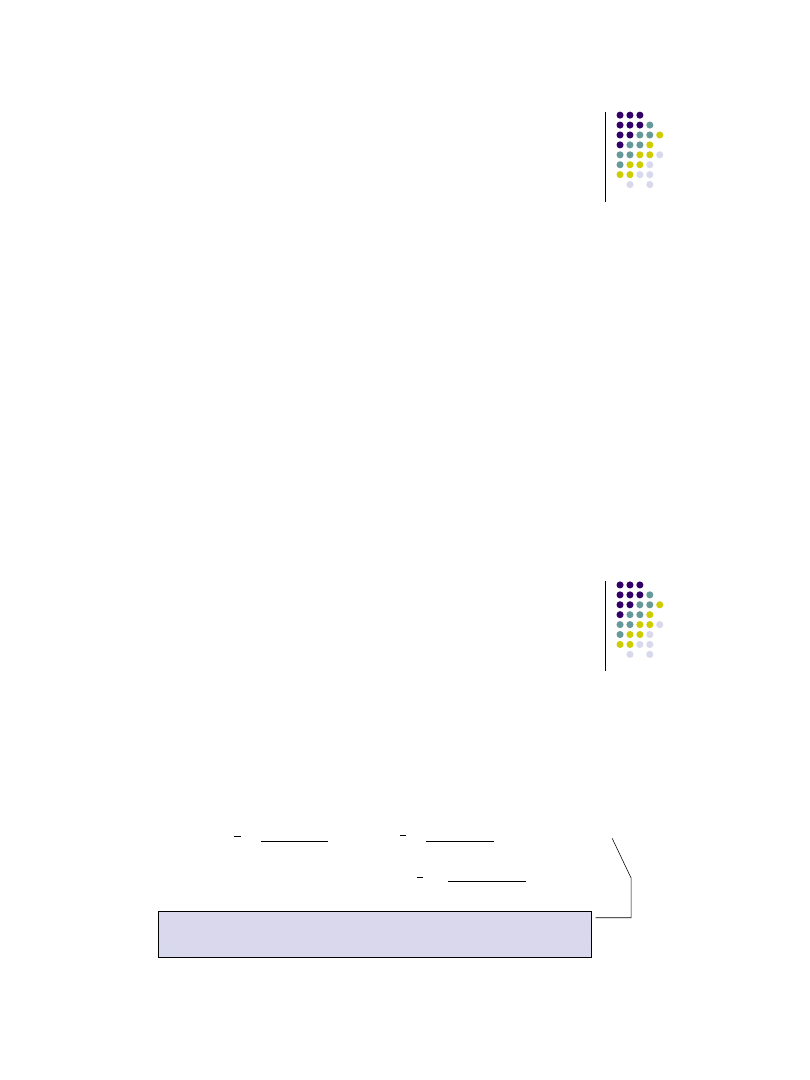
Dekompozycja szeregu czasowego

określenie sposobu nakładania się poszczególnych składowych:



addytywne - Y = T+S+P

zakłada się:



funkcja trendu jest liniowa (lub można ją do takiej sprowadzić),



składowe T, S, P są niezależne,



składowe są wyrażane jako wielkości absolutne (posiadające
miano),



multiplikatywne

– Y = T*S*P



trend jest wyrażany w takich jednostkach jak badane zjawisko,



składowe są wielkościami względnymi (wskaźnikami),



wahania sezonowe i przypadkowe są proporcjonalne do
wielkości trendu.

gdzie: T- trend, S

– wahania sezonowe, P- wahania przypadkowe.

2013-05-28

10

19

Wygładzanie szeregu czasowego

Wygładzanie jest to zabieg prowadzący do:



eliminacji wahań i



wyodrębnienia tendencji rozwojowej badanego zjawiska
(

tendencja rosnąca, malejąca bądź stabilizacja

).

Trend (tendencja rozwojowa)

– powolne, regularne, systematyczne

zmiany określonego zjawiska obserwowane w dostatecznie długim
przedziale czasowym i będące rezultatem działania przyczyn
głównych.

Szeregi czasowe wygładzamy stosując metody:



mechaniczną (wykorzystanie średnich ruchomych) oraz



analityczną (dopasowanie odpowiedniej funkcji do danych
szeregu czasowego).

20

Wygładzanie mechaniczne

(średnie ruchome k-okresowe)

Oznaczenia: kolejne wartości szeregu czasowego:

Średnie ruchome wyznaczamy różnie w zależności od ich długości (k).



Inaczej, gdy k jest nieparzyste, np. k = 3, 5, 7, itd.
Inaczej zaś gdy k jest parzyste, np. k = 2, 4, 6, itd.



Gdy k jest nieparzyste (np. k

=3), to średnie ruchome wyznacza się

następująco:

itd. aż do przedostatniego okresu

n

n

n

y

y

y

y

y

y

,

,

,

,

,

,

1

2

3

2

1







3

3

2

1

2

y

y

y

y







3

4

3

2

3

y

y

y

y







3

1

2

1

n

n

n

n

y

y

y

y













Przy k

=3 straci się jedną informację na początku i jedną na końcu szeregu

czasowego (1+1=2 straty).
Przy k

=5 straty wyniosą już 2+2=4, a przy k=7 wyniosą aż 3+3=6

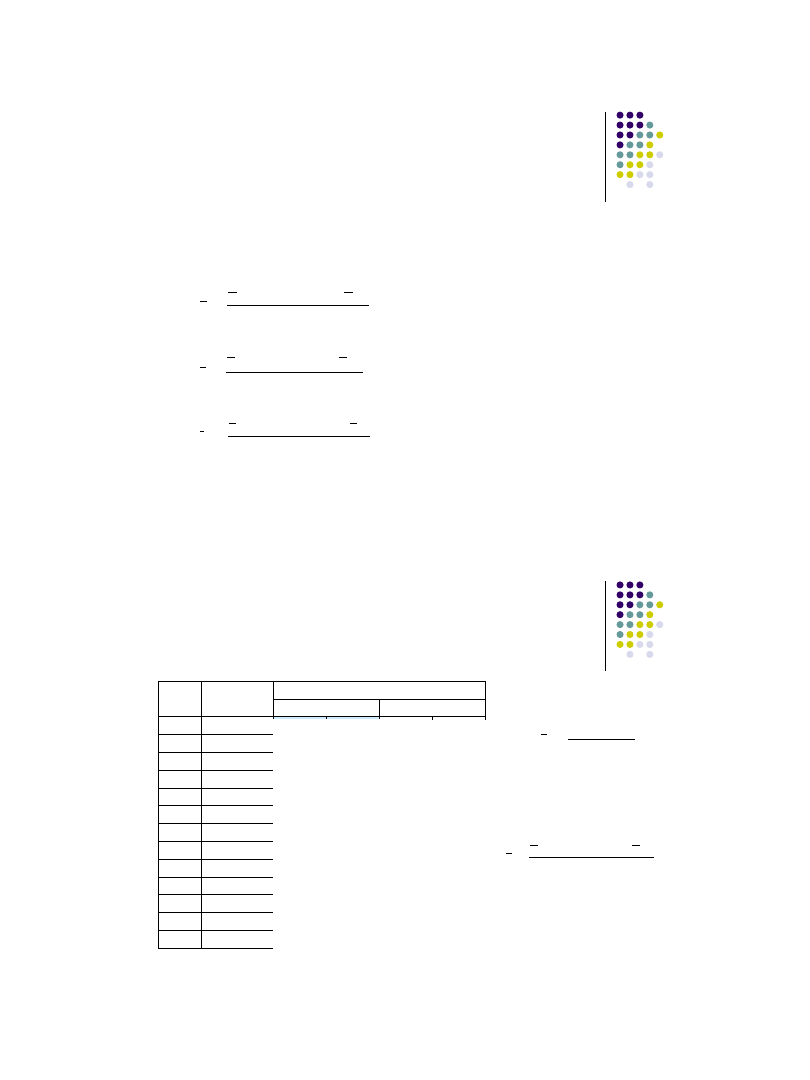
2013-05-28

11

21

Wygładzanie mechaniczne

(średnie ruchome k-okresowe)

Reguła: im dłuższa średnia ruchoma (im większe k), tym większe

straty na informacji, ale za to lepsze wygładzenie i możliwość
zaobserwowania tendencji rozwojowej badanego zjawiska.



Gdy k jest parzyste (np. k

=4), to średnie ruchome wyznacza się

następująco (tzw.

średnia scentrowana

):

4

2

1

2

1

5

4

3

2

1

3

y

y

y

y

y

y











4

2

1

2

1

6

5

4

3

2

4

y

y

y

y

y

y











4

2

1

2

1

1

2

3

4

2

n

n

n

n

n

n

y

y

y

y

y

y





















itd. aż do

22

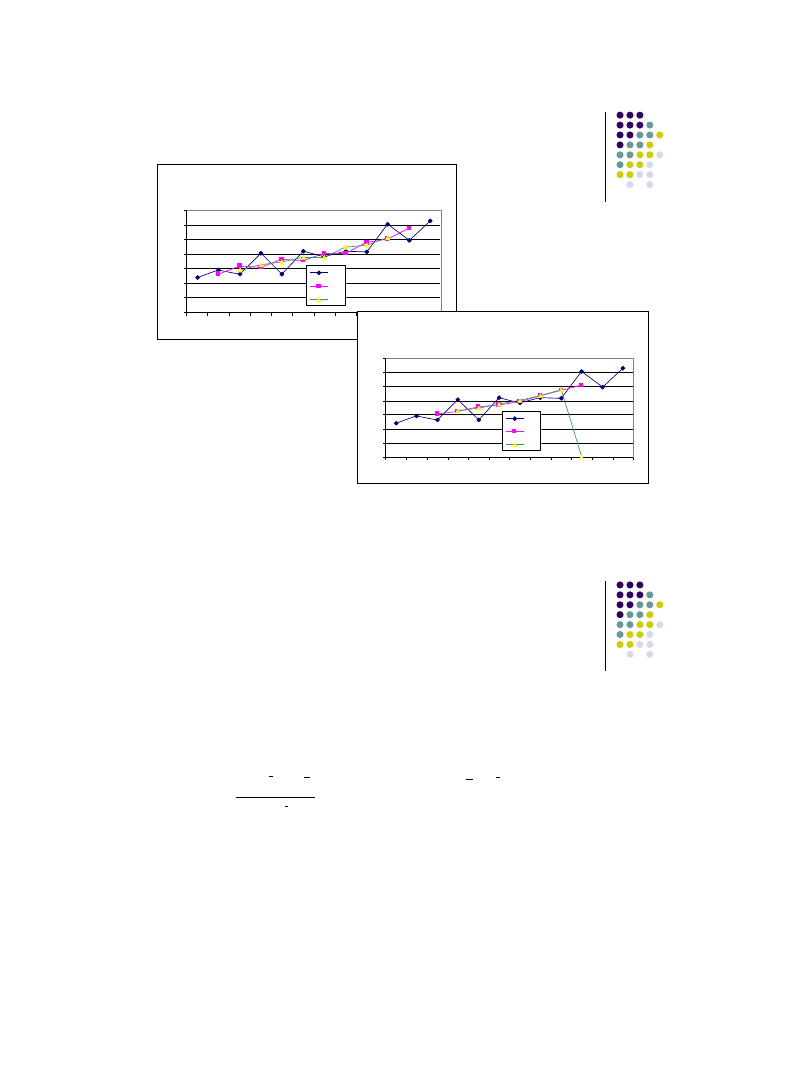
Średnie ruchome k-okresowe - przykład



Wielkość przewozów ( y

t

) firmy ABC [w tys. km] w ciągu 12 kolejnych

okresów (t) przedstawia poniższa tabela. W dwóch ostatnich kolumnach
pokazano średnie ruchome o różnej długości (k nieparzyste i parzyste).

okres

wielkość

przewozów

średnie ruchome

nieparzyste

parzyste

t

y

t

k=3

k=5

k=4

k=6

1

121

x

x

x

x

2

146

133

x

x

x

3

132

161

147

152

x

4

204

156

165

162

164

5

132

183

174

178

175

6

212

179

190

186

187

7

192

205

191

196

202

8

211

204

225

217

219

9

209

241

232

236

238

10

303

253

257

256

x

11

247

289

x

x

x

12

316

x

x

x

x

3

3

2

1

2

y

y

y

y







k - nieparzyste

k - parzyste

4

2

1

2

1

5

4

3

2

1

3

y

y

y

y

y

y











2013-05-28

12

23

Średnie ruchome k-okresowe - wykres

Wielkość przewozów firmy ABC

(wygładzanie k nieparzyste)

0

50

100

150

200

250

300

350

1

2

3

4

5

6

7

8

9

10

11

12

yt

k=3

k=5

Wielkość przewozów firmy ABC

(wygładzanie k parzyste)

0

50

100

150

200

250

300

350

1

2

3

4

5

6

7

8

9

10

11

12

yt

k=4

k=6

24

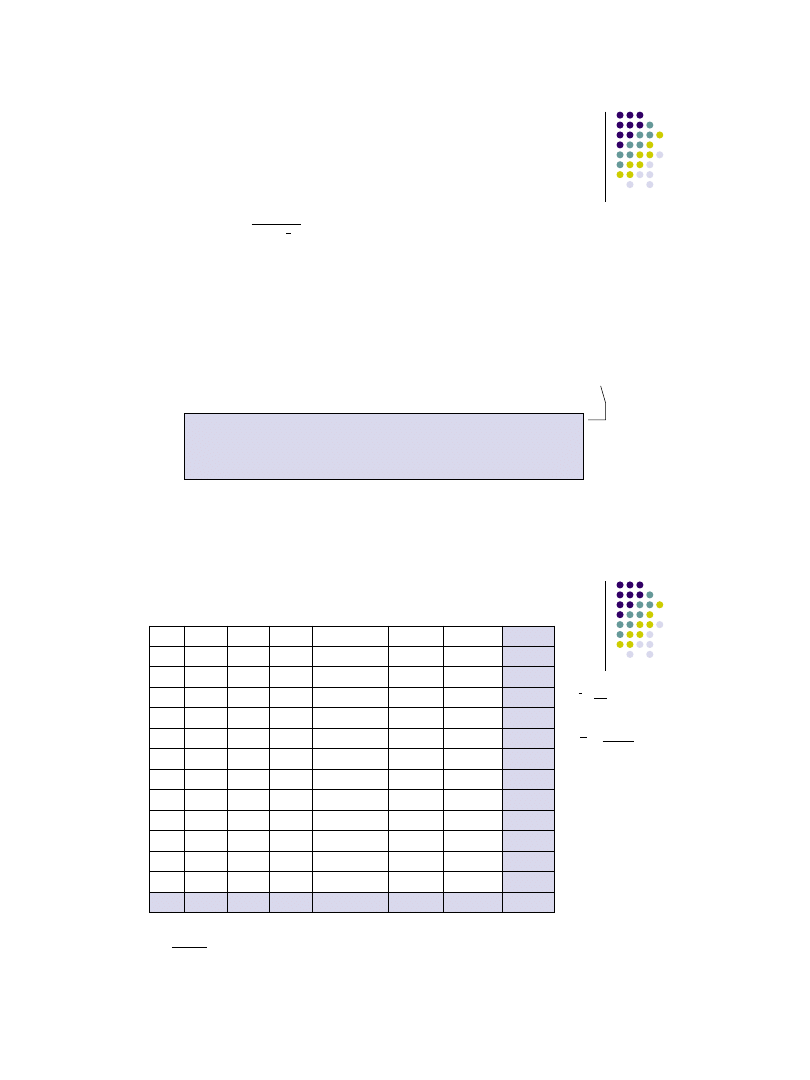
Wygładzanie analityczne (liniowa funkcja trendu)

Wygładzanie szeregu czasowego polega tutaj na oszacowaniu liniowej funkcji

trendu:



Nieznane parametry a i b wyliczamy na podstawie danych z szeregu
czasowego stosując następujące wzory:



a

– oznacza okresowe tempo wzrostu (a>0) lub ubytku (a<0) wielkości

badanego zjawiska



b

– oznacza stan zjawiska w okresie wyjściowym (tzn. dla t=0)

b

at

y

t





ˆ

 



 

















n

t

n

t

t

t

t

y

y

t

t

a

1

2

1

t

a

y

b





2013-05-28

13

25

Ocena dopasowania linii trendu



współczynnik zbieżności (φ

2

):

gdzie: 0 ≤ φ

2

≤ 1

Im φ

2

jest bliższy 0, tym dopasowanie jest lepsze

.



Popularniejszą miarą dopasowania jest współczynnik determinacji (R

2

):

gdzie

: 0 ≤ R

2

≤ 1

Tutaj im R

2

jest bliższy 1, tym dopasowanie jest lepsze.























n

t

t

n

t

t

t

y

y

y

y

1

2

1

2

2

ˆ



Popularna interpretacja R

2

:

liniowa funkcja trendu w (R

2



100)% opisuje kształtowanie się

badanego zjawiska.

2

2

1







R

26

Liniowa funkcja trendu -

przykład

t

y

t

t-t

śr

y

t

-y

śr

(t-t

śr

)*(y

t

-y

śr

)

(t-t

śr

)

2

(y

t

-y

śr

)

2

y

t

^

1

121

-5,5

-81

445,5

30,25

6561

116

2

146

-4,5

-56

252

20,25

3136

131

3

132

-3,5

-70

245

12,25

4900

147

4

204

-2,5

2

-5

6,25

4

163

5

132

-1,5

-70

105

2,25

4900

179

6

212

-0,5

10

-5

0,25

100

194

7

192

0,5

-10

-5

0,25

100

210

8

211

1,5

9

13,5

2,25

81

226

9

209

2,5

7

17,5

6,25

49

241

10

303

3,5

101

353,5

12,25

10201

257

11

247

4,5

45

202,5

20,25

2025

273

12

316

5,5

114

627

30,25

12996

288

78

2425

2246,5

143

4053

5

6

12

78

,





t

202

12

2425





y

7

15

143

5

2246

,

,





a

100

5

6

7

15

202









,

,

b

100

7

15

t

y

t





,

ˆ

2013-05-28

14

27

Liniowa funkcja trendu -

przykład

Wielkość przewozów firmy ABC (wygładzanie trendem)

y = 15,71x + 99,97

R

2

= 0,7833

0

50

100

150

200

250

300

350

0

2

4

6

8

10

12

yt

Liniow y (yt)

28

Liniowa funkcja trendu

– ocena dopasowania

t

y

t

y

t

^

(y

t

-y

t

^)

(y

t

-y

śr

)

(y

t

-y

t

^)

2

(y

t

-y

śr

)

2

1

121

116

5

-81

25

6561

2

146

131

15

-56

225

3136

3

132

147

-15

-70

225

4900

4

204

163

41

2

1681

4

5

132

179

-47

-70

2209

4900

6

212

194

18

10

324

100

7

192

210

-18

-10

324

100

8

211

226

-15

9

225

81

9

209

241

-32

7

1024

49

10

303

257

46

101

2116

10201

11

247

273

-26

45

676

2025

12

316

288

28

114

784

12996

suma

9838

45053

218

0

45053

9838

2

,







782

0

218

0

1

2

,

,







R

Liniowa funkcja trendu y

t

^ = 15,7 t + 100 wygładzająca wahania

przypadkowe opisuje wielkość przewozów firmy ABC w 78,2% (R

2

=0,782).

Wartość współczynnika determinacji R

2

zauważalnie odbiega od jedności.

Wniosek:
Obok wahań
przypadkowych
występują również
inne wahania, np.
wahania sezonowe
(cykliczne).























n

i

i

n

i

i

i

y

y

y

y

1

2

1

2

2

ˆ



2013-05-28

15

29

Analiza wahań okresowych



Aby wyodrębnić wahania sezonowe (cykliczne) w szeregu o n

okresach należy podzielić ten szereg na s cykli.



Podział musi być taki, aby w każdym cyklu występowała stała
liczba k faz cyklu

(długość cyklu sezonowego).



Działania mające na celu wyodrębnienie wahań sezonowych:



Wygładzić szereg czasowy { y

t

} analitycznie (lub mechanicznie

średnią ruchomą k-okresową). Na podstawie wyznaczonej funkcji

trendu obliczyć wartości teoretyczne { y

t

^ }.



Uwolnić szereg czasowy od trendu.



Gdy amplitudy wahań (różnice między wielkościami

rzeczywistymi zmiennej a teoretycznymi z funkcji trendu są:



w przybliżeniu takie same (wahania bezwzględnie stałe),



zmieniają się w tym samym stosunku (wahania względnie stałe).


.

k

mod

t

j

n

1,2,...,

t











t

j

t

t

P

S

yˆ

y

k

mod

t

j

n

1,2,...,

t







t

j

t

t

P

*

S

*

yˆ

y

30

Analiza wahań okresowych



W tym celu należy wyliczyć wielkości:



dla modelu addytywnego:



dla modelu multiplikatywnego:



Wielkości te zawierają wahania przypadkowe i sezonowe.



Pozbywanie się wahań przypadkowych w wielkościach w

t

.

W tym celu dla jednoimiennych okresów i (tj. okresów należących do

tej samej fazy) wyliczyć ich średnią arytmetyczną :



dla modelu addytywnego i multiplikatywnego:



dla każdej fazy i=1, 2, ... ,k. (k = 4 dla kwartałów, k= 12 dla

miesięcy).



Są to tzw. surowe wskaźniki sezonowości.

t

t

t

y

y

w



ˆ

/



t

t

t

y

y

w



ˆ





k

w

c

k

j

j

i

i









1

0

,

'

2013-05-28

16

31

Analiza wahań okresowych



Interpretacja:

(wskaźnik surowy – 1)



100% :

”O ile procent poziom zjawiska w danej fazie cyklu jest wyższy (znak plus)
lub niższy (znak minus) od poziomu jaki byłby osiągnięty, gdyby nie było
wahań cyklicznych, a rozwój następował zgodnie z trendem”.



Suma takich wskaźników w

t

dla wszystkich faz powinna być równa:



dla modelu addytywnego

– 0,



dla modelu multiplikatywnego - k.



Jeżeli tak nie jest, to należy surowe wskaźniki sezonowości skorygować
tzn. wyznaczyć wartość w

kor

:

a następnie:



dla modelu addytywnego -

wyznaczyć różnice:



dla modelu multiplikatywnego wyznaczyć iloraz:

kor

i

i

w

c

c

'



k

c

w

i

kor





'

kor

i

i

w

c

c





'

32

Prognoza na kolejny okres

τ



Dla modelu addytywnego:



Dla modelu multiplikatywnego:



Y

τ

– prognoza na moment τ



Ŷ

τ

- wstępna prognoza na podstawie modelu trendu,



j = τ mod k.

j

S

y

y

*

ˆ

*







j

S

y

y









ˆ

*

2013-05-28

17

33

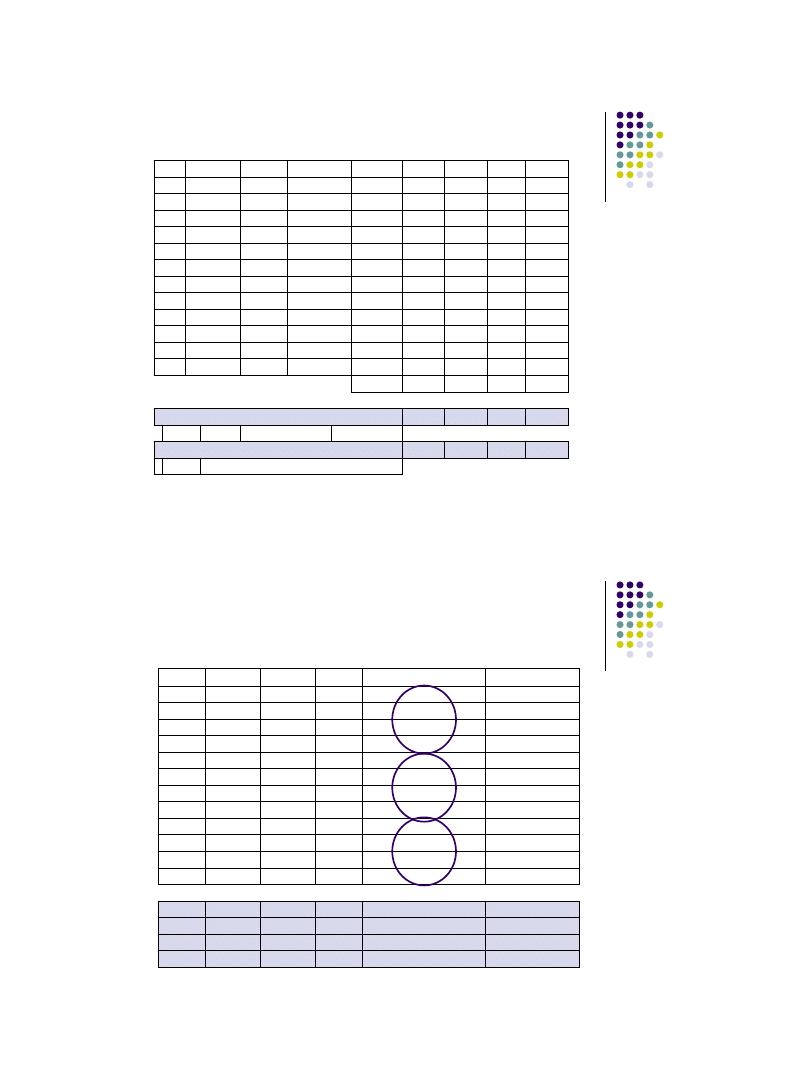
Analiza wahań okresowych - przykład

t

y

t

y

t

^

w

t

=y

t

/y

t

^

kwartał

I

II

III

IV

1

121

116

1,04

I

1,04

2

146

131

1,11

II

1,11

3

132

147

0,9

III

0,9

4

204

163

1,25

IV

1,25

5

132

179

0,74

I

0,74

6

212

194

1,09

II

1,09

7

192

210

0,91

III

0,91

8

211

226

0,93

IV

0,93

9

209

241

0,87

I

0,87

10

303

257

1,18

II

1,18

11

247

273

0,9

III

0,9

12

316

288

1,1

IV

1,1

∑w

it

2,65

3,38

2,71

3,28

Surowe wskaźniki sezonowości c

i

‘ = ∑w

it

/s 0,883

1,127 0,903 1,093

∑c

i

‘= 4,006

w

kor

=∑c

i

’ /4=

1,0015

Czyste wskaźniki sezonowości c

i

=c

i

’/w

kor

0,882

1,125 0,902 1,091

∑c

i

=

4,000

s=3
k=4

34

Prognozy dla kolejnych kwartałów - przykład



Jeżeli pomnożymy w każdym okresie teoretyczny poziom zjawiska przez
odpowiedni dla danego okresu wskaźnik sezonowości, to otrzymamy
teoretyczny

poziom zjawiska uwzględniający wahania sezonowe

t

y

t

y

t

^

kwartał wskaźniki sezonowości skorygowany y

t

^

1

121

116

I

0,882

102,3

2

146

131

II

1,125

147,4

3

132

147

III

0,902

132,5

4

204

163

IV

1,091

177,9

5

132

179

I

0,882

157,8

6

212

194

II

1,125

218,3

7

192

210

III

0,902

189,3

8

211

226

IV

1,091

246,6

9

209

241

I

0,882

212,5

10

303

257

II

1,125

289,2

11

247

273

III

0,902

246,1

12

316

288

IV

1,091

314,3

Prognoza dla kolejnych kwartałów

13

304

I

0,882

268,0

14

320

II

1,125

360,1

15

336

III

0,902

303,0

16

351

IV

1,091

383,1

2013-05-28

18

35

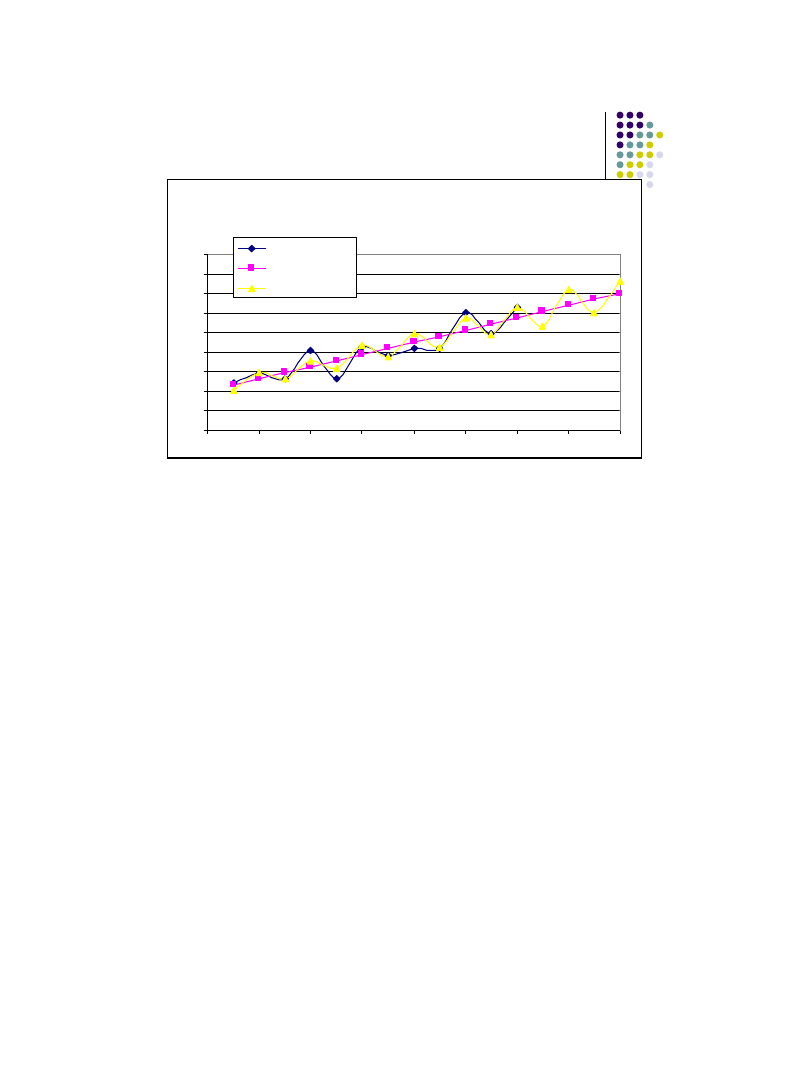
Prognozy dla kolejnych kwartałów - wykres

Wielkość przewozów firmy ABC (wygładzanie,

sezonowość, prognozy)

0

50

100

150

200

250

300

350

400

450

0

2

4

6

8

10

12

14

16

yt

trend

trend sezonow y