
Programowanie dynamiczne
Nadaje si˛e do rozwi ˛
azywania problemów, które mo˙zna
podzieli´c na podproblemy, ale ró˙zne podproblemy mog ˛
a
wymaga´c rozwi ˛
azania tych samych podpodproblemów.
(Metoda
dziel i zwyci˛e˙zaj
rozwi ˛
azuje wtedy te same
podpodproblemy wielokrotnie.)
Projektowanie algorytmu dynamicznego:
1. Scharakteryzowanie struktury optymalnego rozwi ˛
azania
2. Rekurencyjne zdefiniowanie kosztu optymalnego
rozwi ˛
azania
3. Obliczenie rozwi ˛
azania metod ˛
a
wst˛epuj ˛
ac ˛
a (
bottom-up
)
4. Konstruowanie optymalnego rozwi ˛
azania na podstawie
wyników wcze´sniejszych oblicze´n
M.Kik “AiSD 5” – p. 1

Mno˙zenie ci ˛agu macierzy
Dane:
ci ˛
ag
n
macierzy
A
1
,. . .
A
n
ró˙znych rozmiarów (takich,
˙ze mo˙zna wykona´c mno˙zenie
A
1
· A
2
. . .
·A
n
, t.j. macierz
A
i
ma wymiatry
p
i−1
× p
i
)
Wynik:
nawiasowanie minimalizuj ˛
ace ł ˛
aczny koszt mno˙ze ´n
Matrix-Multiply(A,B)
1 if
columns
[A] 6=
rows
[B]
then
2
error “niezgodne rozmiary”
3 else
3
for i ← 1 to
rows
[A]
do
4
for j ← 1 to
columns
[B]
do
5
C[i, j] ← 0
6
for k ← 1 to
columns
[A]
do
7
C[i, j] ← C[i, j] + A[i, k] · B[k, j]
8
returnc C
Czas:
Θ(p · q · r)
, gdzie
p × q
,
q × r
– wymiary macierzy
M.Kik “AiSD 5” – p. 2

liczba mo˙zliwych nawiasowa´n
P (n) =
(
1
dla
n = 1
P
n−1
k=1
P (k)P (n − k)
dla
n ≥ 2
P (n) = C(n − 1)
, gdzie
C(i)
–
i
-ta liczba Catalana.
C(n) =
1
n + 1
µ2n
n
¶
= Ω(4
n
/n
3
/2
)
Ro´snie wykładniczo ze wzgl˛edu na
n
.
M.Kik “AiSD 5” – p. 3

Struktura optymalnego nawiasowania
A
1
. . .
A
n
jest dzielony na (
A
1
. . .
A
k
) oraz (
A
k+1
. . .
A
n
),
dla pewnego
k
,
1 ≤ k < n
.
Umieszczenie nawiasów w
A
1
. . .
A
k
(odp.
A
k+1
. . .
A
n
)
jest
optymalnym nawiasowaniem
dla
A
1
. . .
A
k
(odp.
A
k+1
. . .
A
n
)
Rozwi ˛
azanie rekurencyjne:
m[i, j]
– optymalny koszt mno˙zenia podci ˛
agu
A
i
. . .
A
j
.
m[i, j] =
(
0
dla
i = j
min
i≤k<j
{m[i, k] + m[k + 1, j] + p
i−1
p
k
p
j
}
dla
i < j
UWAGA: liczba mo˙zliwych podproblemów wynosi:
¡
n
2
¢ + n = Θ(n
2
)
(dokładnie jeden podproblem dla ka˙zdej
pary
i
,
j
,
1 ≤ i ≤ j ≤ n
).
M.Kik “AiSD 5” – p. 4

Matrix-Chain-Order
Matrix-Chain-Order(p)
. p = hp
0
, ..., p
n
i
- wymiary
1 n ←
length
[p] − 1
2 for i ← 1 to n do
3
m[i, i] ← 0
4 for l ← 2 to n do
. l
- dł.
podci ˛
agu
5
for i ← 1 to n − l + 1 do
6
j ← i + l − 1
7
m[i, j] ← ∞
8
for k ← i to j − 1 do
9
q ← m[i, k] + m[k + 1, j] + p
i−1
p
k
p
j
10
if q < m[i, j] then
11
m[i, j] ← q
12
s[i, j] ← k
.
podział A
i
. . . A
j
13 return m i s
.
czas Θ(n
3
)
, pam.
Θ(n
2
)
M.Kik “AiSD 5” – p. 5

Wykonanie optymalnego mno˙zenia
s
– tablica wyznaczona przez
Matrix-Chain-Order
.
Mno˙zenie podci ˛
agu
A
i
. . .
A
j
.
Matrix-Chain-Multiply(A,s,i,j)
1 if j > i then
2
X ←
Matrix-Chain-Multiply(A,s,i,s[i, j])
3
Y ←
Matrix-Chain-Multiply(A,s,s[i, j] + 1,j)
4
return Matrix-Multipy(X,Y )
5 else return A
i
Wywołanie:
Matrix-Chain-Multiply(A,s,1,n)
M.Kik “AiSD 5” – p. 6

Recursive-Matrix-Chain
Recursive-Matrix-Chain(p,i,j)
1 if i = j
2
then return 0
3 m[i, j] ← ∞
4 for k ← i to j − 1 do
5
q ←
Recursive-Matrix-Chain(p,i,k)
+
Recursive-Matrix-Chain(p,k + 1,j)+p
i−1
p
k
p
j
6
if q < m[i, j]
7
then m[i, j] ← q
8 return m[i, j]
Czas:
T (n)
T (1) ≥ 1
T (n) ≥ 1 +
P
n−1
k=1
(T (k) + T (n − k) + 1)
dla
n > 1
(koszt wierszy 1-2 i 6-1
≥ 1
jednostka czasu)
M.Kik “AiSD 5” – p. 7

Oszacowanie T (n)
T (n) ≥ 1 +
P
n−1
k=1
(T (k) + T (n − k) + 1)
T (n) ≥ 2
P
n−1
i=1
T (i) + n
Inducja: Podstawa:
T (1) ≥ 2
0
= 1
. Zał. ind.: dla
i < n
,
T (i) ≥ 2
i−1
.
T (n) ≥ 2
P
n−1
i=1
2
i−1
+ n
= 2
P
n−2
i=0
2
i
+ n
= 2(2
n−1
− 1) + n
= (2
n
− 2) + n
≥ 2
n−1
T (n) = Ω(2
n
)
– czas wykładniczy (wielokrotnie
rozwi ˛
azywany ka˙zdy z
O(n
2
)
podproblemów).
M.Kik “AiSD 5” – p. 8

Spami˛etywanie
Dla ka˙zdego podproblemu zapami˛etujemy rozwi ˛
azanie i
zaznaczamy, ˙ze jest ju˙z rozwi ˛
azany. Przy nast˛epnym
napotkaniu tego samego podproblemu wykorzystujemy
wcze´sniej wyznaczone rozwi ˛
azanie. (Wtedy niektóre z
podproblemów rozwi ˛
azywanych w programowaniu metod ˛
a
wst˛epuj ˛
ac ˛
a mog ˛
a zosta´c pomini˛ete.)
Przykład dla ci ˛
agu macierzy:
Memoized-Matrix-Chain(p)
1 n ←
length
[p] − 1
2 for i ← 1 to n do
3
for j ← i to n do
4
m[i, j] ← ∞
5 return Lookup-Chain(p,1,n)
M.Kik “AiSD 5” – p. 9

Lookup-Chain
Lookup-Chain(p,i,j)
1 if m[i, j] < ∞
2
then return m[i, j]
3 if i = j then
4
m[i, j] ← 0
5 else
5
for k ← i to j − 1 do
6
q ←
Lookup-Chain(p,i,k)
+
Lookup-Chain(p,k + 1,j)+p
i−1
p
k
p
j
7
if q < m[i, j]
8
then m[i, j] ← q
9 return m[i, j]
Czas:
O(n
3
)
– ka˙zde z
Θ(n
2
)
pól
m[i, j]
jest
≤ 1
raz
wyznaczone w wierszach 4–8, co zajmuje
O(n)
(nie licz ˛
ac
czasu na wyznaczenie innych pól).
M.Kik “AiSD 5” – p. 10

Najdłu˙zszy Wspólny Podci ˛ag
Z = hz
1
. . . z
k
i
jest
podci ˛
agiem
ci ˛
agu
X = hx
1
. . . , x
m
i
, je´sli
istnieje rosn ˛
acy ci ˛
ag indeksów
hi
1
, . . . , i
k
i
, taki ˙ze dla
ka˙zdego
j = 1 . . . k
zachodzi
x
i
j
= z
j
.
Z
jest
wspólnym podci ˛
agiem
X
i
Y
je´sli jest podci ˛
agiem
X
oraz
jest podci ˛
agiem
Y
.
NWP
– najdłu˙zszy wspólny podci ˛
ag.
Prefix
X
i
= hx
1
. . . x
i
i
.
Tw. (O optymalnej podstrukturze NWP)
Niech
X = hx
1
. . . x
m
i
i
Y = hy
1
. . . y
n
i
. Niech
Z = hz
1
. . . z
k
i
– NWP
X
i
Y
.
1. Je´sli
x
m
= y
n
, to
z
k
= x
m
= y
n
i
Z
k−1
jest NWP
X
m−1
i
Y
n−1
2. Je´sli
x
m
6= y
n
i
z
k
6= x
m
, to
Z
jest NWP
X
m−1
i
Y
.
3. Je´sli
x
m
6= y
n
i
z
k
6= y
n
, to
Z
jest NWP
X
i
Y
n−1
.
M.Kik “AiSD 5” – p. 11

Najdłu˙zszy Wspólny Podci ˛ag
Z = hz
1
. . . z
k
i
jest
podci ˛
agiem
ci ˛
agu
X = hx
1
. . . , x
m
i
, je´sli
istnieje rosn ˛
acy ci ˛
ag indeksów
hi
1
, . . . , i
k
i
, taki ˙ze dla
ka˙zdego
j = 1 . . . k
zachodzi
x
i
j
= z
j
.
Z
jest
wspólnym podci ˛
agiem
X
i
Y
je´sli jest podci ˛
agiem
X
oraz
jest podci ˛
agiem
Y
.
NWP
– najdłu˙zszy wspólny podci ˛
ag.
Prefix
X
i
= hx
1
. . . x
i
i
.
Tw. (O optymalnej podstrukturze NWP)
Niech
X = hx
1
. . . x
m
i
i
Y = hy
1
. . . y
n
i
. Niech
Z = hz
1
. . . z
k
i
– NWP
X
i
Y
.
1. Je´sli
x
m
= y
n
, to
z
k
= x
m
= y
n
i
Z
k−1
jest NWP
X
m−1
i
Y
n−1
2. Je´sli
x
m
6= y
n
i
z
k
6= x
m
, to
Z
jest NWP
X
m−1
i
Y
.
3. Je´sli
x
m
6= y
n
i
z
k
6= y
n
, to
Z
jest NWP
X
i
Y
n−1
.
M.Kik “AiSD 5” – p. 11

Dowód Tw. o opt. podstrukturze NWP
D-d
1. Je´sli
z
k
6= x
m
to mo˙znaby doł ˛
aczy´c
x
m
= y
n
do
Z
uzyskuj ˛
ac dłu˙zszy wspólny podci ˛
ag
X
i
Y
.
2.
z
k
6= x
m
, czyli
Z
jest wspólnym podci ˛
agiem
X
m−1
i
Y
.
Gdyby istniał dłu˙zszy wspólny podci ˛
ag
W
ci ˛
agów
X
m−1
i
Y
, to
W
byłby te˙z wspólnym podci ˛
agiem
X
i
Y
dłu˙zszym ni˙z
Z
.
3. Analogicznie do poprzedniego przypadku.
¤
M.Kik “AiSD 5” – p. 12

Zale˙zno´s´c rekurencyjna i algorytm
c[i, j]
– długo´s´c NWP prefiksów
X
i
i
Y
j
.
c[i, j] =
0,
je´sli
i = 0
lub
j = 0
c[i − 1, j − 1] + 1
je´sli
i, j > 0
i
x
i
= y
j
max(c[i, j − 1], c[i − 1, j])
je´sli
i, j > 0
i
x
i
6= y
j
LCS-Length(X,Y )
1 m ←
length
[X]
2 n ←
length
[Y ]
3 for i ← 1 to m do
4
c[i, 0] = 0
5 for j ← 1 to n do
6
c[0, j] = 0
...
M.Kik “AiSD 5” – p. 13

LCS-Length (c.d.)
...
7 for i ← 1 to m do
8
for j ← 1 to n do
9
if x
i
= y
j
then
10
c[i, j] ← c[i − 1, j − 1] + 1
11
b[i, j] ← “ -
00
else
12
if c[i − 1, j] > c[i, j − 1] then
13
c[i, j] ← c[i − 1, j]
14
b[i, j] ← “ ↑
00
else
15
c[i, j] ← c[i, j − 1]
16
b[i, j] ← “ ←
00
17 return c i b
Czas:
Θ(nm)
, pami˛e´c:
Θ(nm)
.
M.Kik “AiSD 5” – p. 14

Print-LCS
Print-LCS(b, X,i,j)
1 if i = 0 or j = 0 then
2
return
3 if b[i, j] =
00
-
00
then
4
Print-LCS(b, X,i − 1,j − 1)
5
wypisz x
i
else
6 if b[i, j] =
00
↑
00
then
7
Print-LCS(b, X,i − 1,j)
8 else Print-LCS(b, X,i,j − 1)
Wywołanie:
Print-Lcs(b,X,
length
[X]
,
length
[Y ]
)
Czas:
O(m + n)
.
M.Kik “AiSD 5” – p. 15
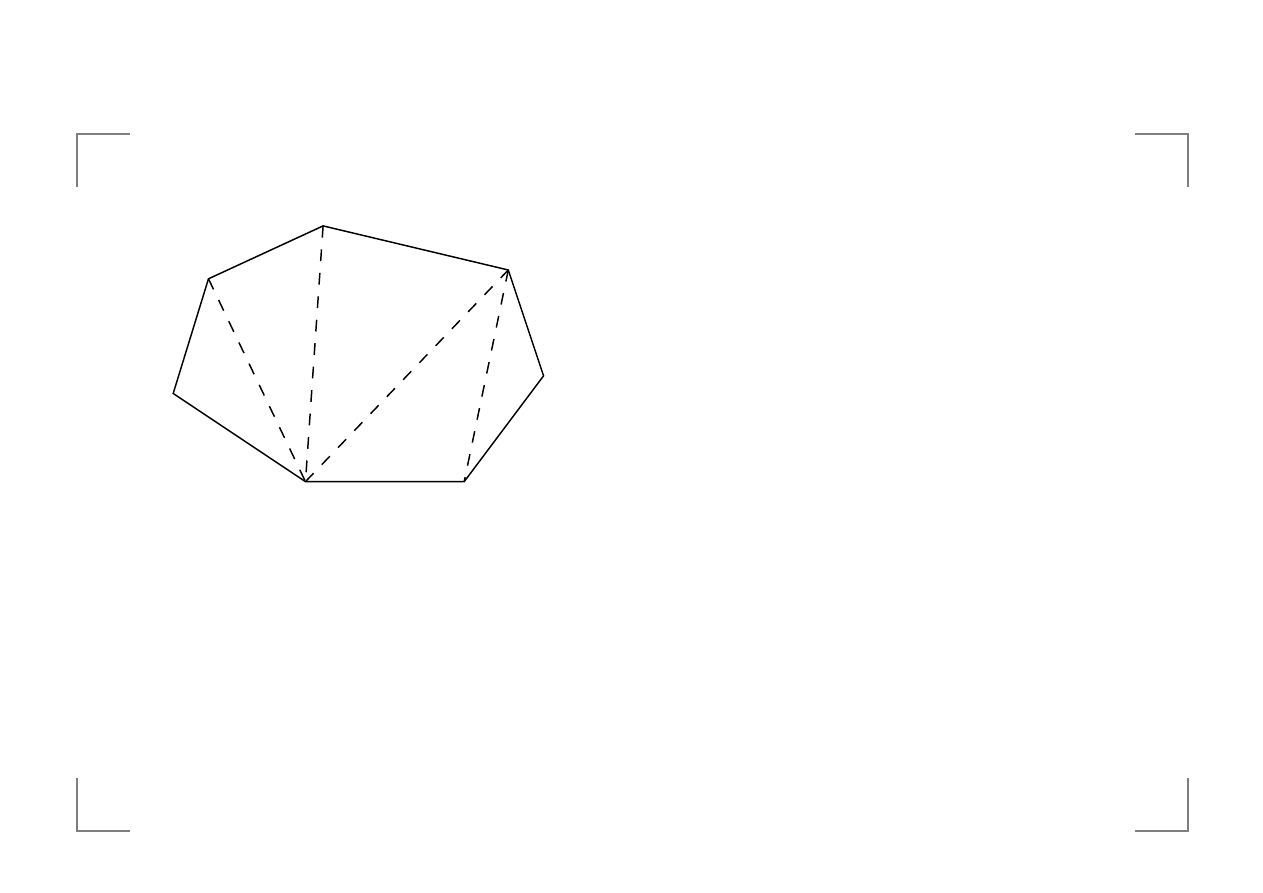
triangulacja wielok ˛ata wypukłego
v
0
v
1
v
2
v
3
v
4
v
5
v
6
Waga trójk ˛
ata:
w(4v
i
v
j
v
k
)
(n.p.
w(4v
i
v
j
v
k
) = |v
i
v
j
| + |v
j
v
k
| + |v
k
v
i
|
Koszt triangulacji = suma wag jej trójk ˛
atów.
M.Kik “AiSD 5” – p. 16
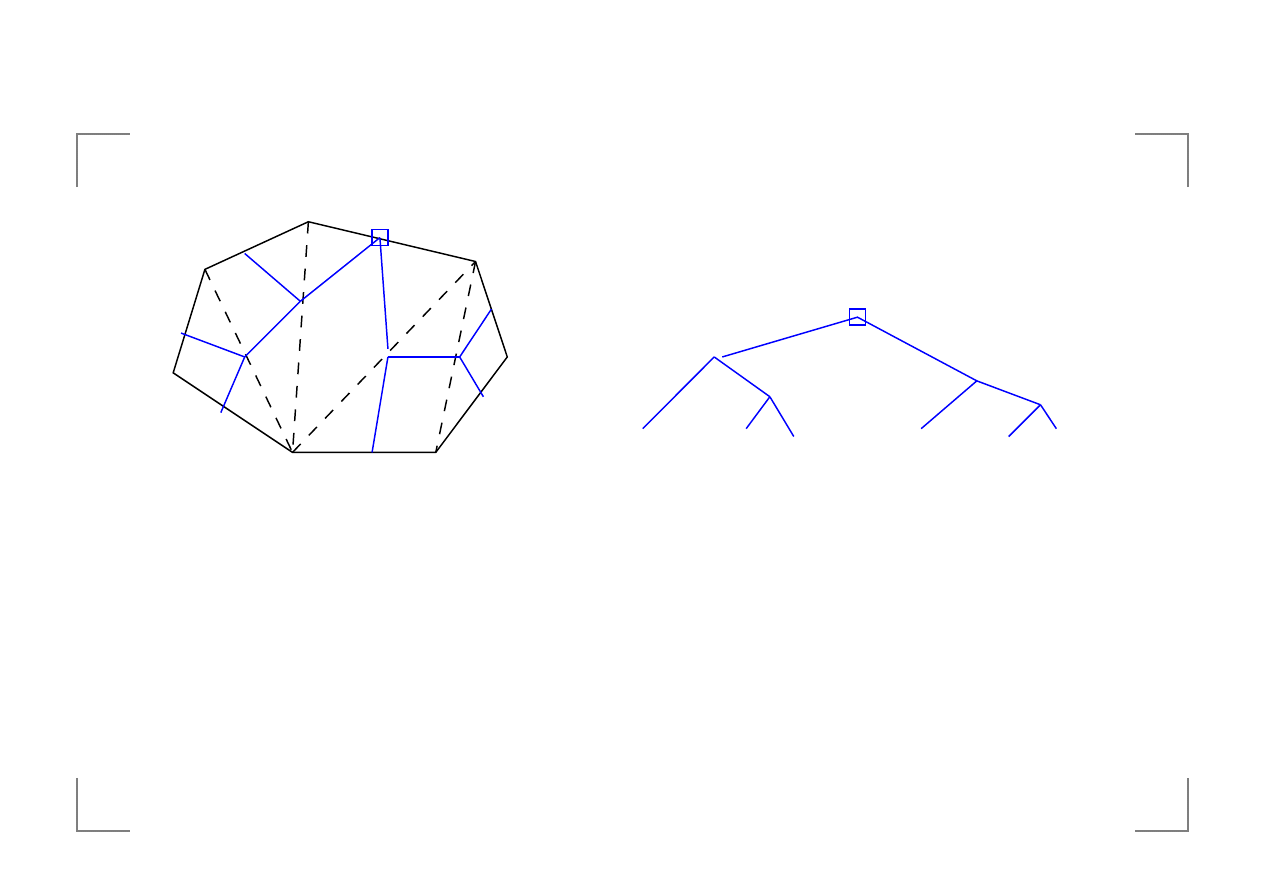
zwi ˛azek z problemem nawiasowania
A
1
A
6
A
1
A
2
A
3
A
5
A
4
(
)
(
)
(
(
))
(
)
v
0
v
1
v
2
v
3
v
4
v
5
v
6
A
6
A
5
A
4
A
3
A
2
Je´sli
A
i
ma wymiary
p
i−1
× p
i
, to problem nawiasowania
ci ˛
agu mno˙ze´n
A
1
. . . A
n
redukujemy do problemu
triangulacji przyjmuj ˛
ac:
w(4v
i
v
j
v
k
) = p
i
p
j
p
k
.
Algorytm
Matrix-Chain-Order
mo˙zna przerobi´c aby rozwi ˛
azywał
problem triangulacji: zamiast
p = hp
0
, . . . , p
n
i
– parametr
v = hv
0
, . . . , v
n
i
, oraz wiersz
9
zast˛epujemy:
9
q ← m[i, k] + m[k + 1, j] + w(4v
i
v
j
v
k
)
M.Kik “AiSD 5” – p. 17
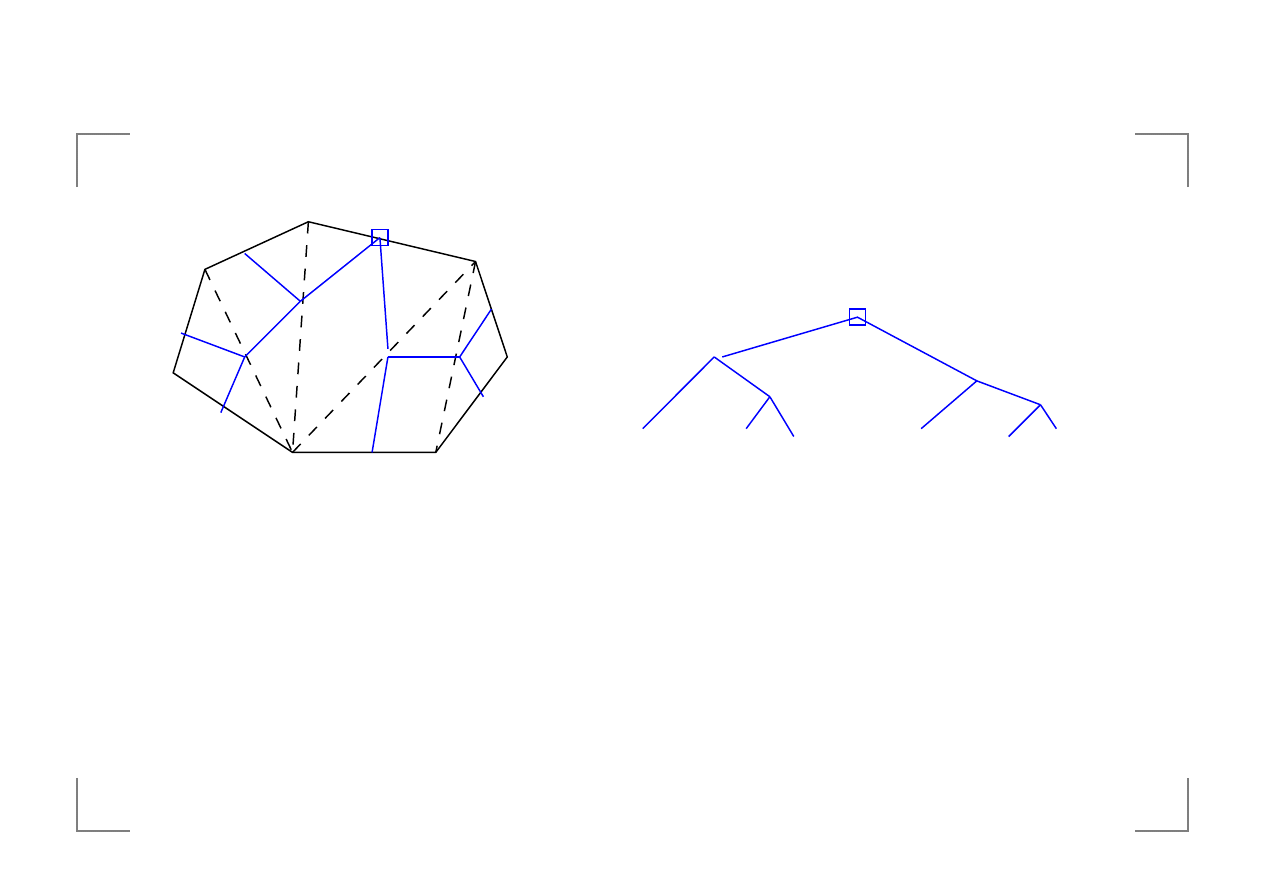
zwi ˛azek z problemem nawiasowania
A
1
A
6
A
1
A
2
A
3
A
5
A
4
(
)
(
)
(
(
))
(
)
v
0
v
1
v
2
v
3
v
4
v
5
v
6
A
6
A
5
A
4
A
3
A
2
Je´sli
A
i
ma wymiary
p
i−1
× p
i
, to problem nawiasowania
ci ˛
agu mno˙ze´n
A
1
. . . A
n
redukujemy do problemu
triangulacji przyjmuj ˛
ac:
w(4v
i
v
j
v
k
) = p
i
p
j
p
k
. Algorytm
Matrix-Chain-Order
mo˙zna przerobi´c aby rozwi ˛
azywał
problem triangulacji: zamiast
p = hp
0
, . . . , p
n
i
– parametr
v = hv
0
, . . . , v
n
i
, oraz wiersz
9
zast˛epujemy:
9
q ← m[i, k] + m[k + 1, j] + w(4v
i
v
j
v
k
)
M.Kik “AiSD 5” – p. 17

uzasadnienie
Niech
T
– optymalna triangulacja wielok ˛
ata wypukłego o
wierzchołkach
hv
0
. . . v
n
i
, zawieraj ˛
aca
4v
0
v
k
v
n
. Waga
T
=
suma
w(4v
0
v
k
v
n
)
oraz wag trangulacji dwu wielok ˛
atów
hv
0
. . . v
k
i
i
hv
k
. . . v
n
i
. Obie musz ˛
a by´c optymalne.
Równanie rekurencyjne:
Niech
t[i, j]
koszt optymalnej triangulacji
hv
i−1
. . . v
j
i
.
t[i, j] =
0
dla
i = j
min
i≤k≤j−1
{t[i, k] + t[k + 1, j]+
+w(4v
i−1
v
k
v
j
)}
dla
i < j
Poza funkcj ˛
a wagi – wzór identyczny ze wzorem na
m[i, j]
.
Wniosek.
Optymaln ˛
a triangulacj˛e mo˙zna wyznaczy´c w
czasie
Θ(n
3
)
i pami˛eci
Θ(n
2
)
.
M.Kik “AiSD 5” – p. 18
Document Outline
- Programowanie dynamiczne
- Mno¿enie ci±gu macierzy
- liczba mo¿liwych nawiasowañ
- Struktura optymalnego nawiasowania
- Matrix-Chain-Order
- Wykonanie optymalnego mno¿enia
- Recursive-Matrix-Chain
- Oszacowanie $T(n)$
- Spamiêtywanie
- Lookup-Chain
- Najd³u¿szy Wspólny Podci±g
- Dowód Tw. o opt. podstrukturze NWP
- Zale¿no¶æ rekurencyjna i algorytm
- LCS-Length (c.d.)
- Print-LCS
- triangulacja wielok±ta wypuk³ego
- zwi±zek z problemem nawiasowania
- uzasadnienie
Wyszukiwarka
Podobne podstrony:
aisd5-1
aisd5 1
aisd5
aisd5 2
więcej podobnych podstron