Wykład 27

Dyfrakcja Fresnela i Fraunhofera

Zjawisko dyfrakcji (ugięcia) światła odkrył Grimaldi (XVII w). Polega ono na uginaniu

się promieni świetlnych przechodzących w pobliżu przeszkody (np. brzeg szczeliny).

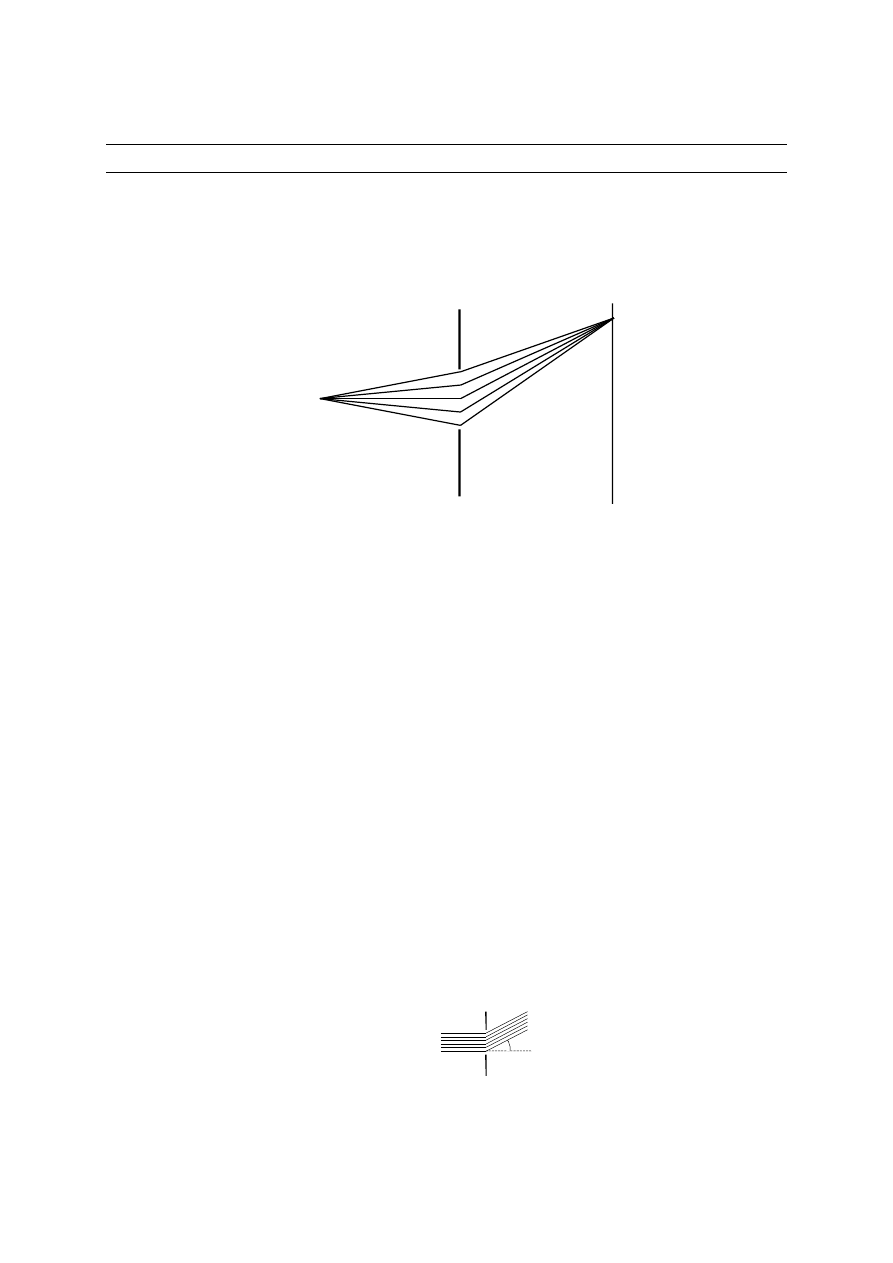
Wyjaśnienie dyfrakcji w oparciu o zasadę Huyghensa - Fresnela jest następująca.

S

B

C

P

a)

Fala ze źródła

S

pada na szczelinę

B

i przechodzące przez otwór pada na ekran

C

.

Natężenie w punkcie

P

można obliczyć dodając do siebie wszystkie wektory falowe E



pochodzące od wszystkich punktów szczeliny. Te zaburzenia falowe mają różne amplitudy i

fazy ponieważ: a) elementarne oscylatory Huyghensa (punkty w szczelinie) są w różnych

odległościach od punktu P; b) światło opuszcza te punkty pod różnymi kątami. Sytuacja gdy

fale opuszczające otwór nie są falami płaskimi pojawia się gdy źródło fal

S

i ekran

C

, na

którym powstaje obraz znajdują się w skończonej odległości od ekranu ze szczeliną

B

. Taki

przypadek nosi nazwę dyfrakcji Fresnela. Obliczenia natężeń światła są w tej sytuacji są

trudniejsze.

do bardzo
odległego
ekranu

z bardzo
odległęgo
źródła

b)

θ

B

348

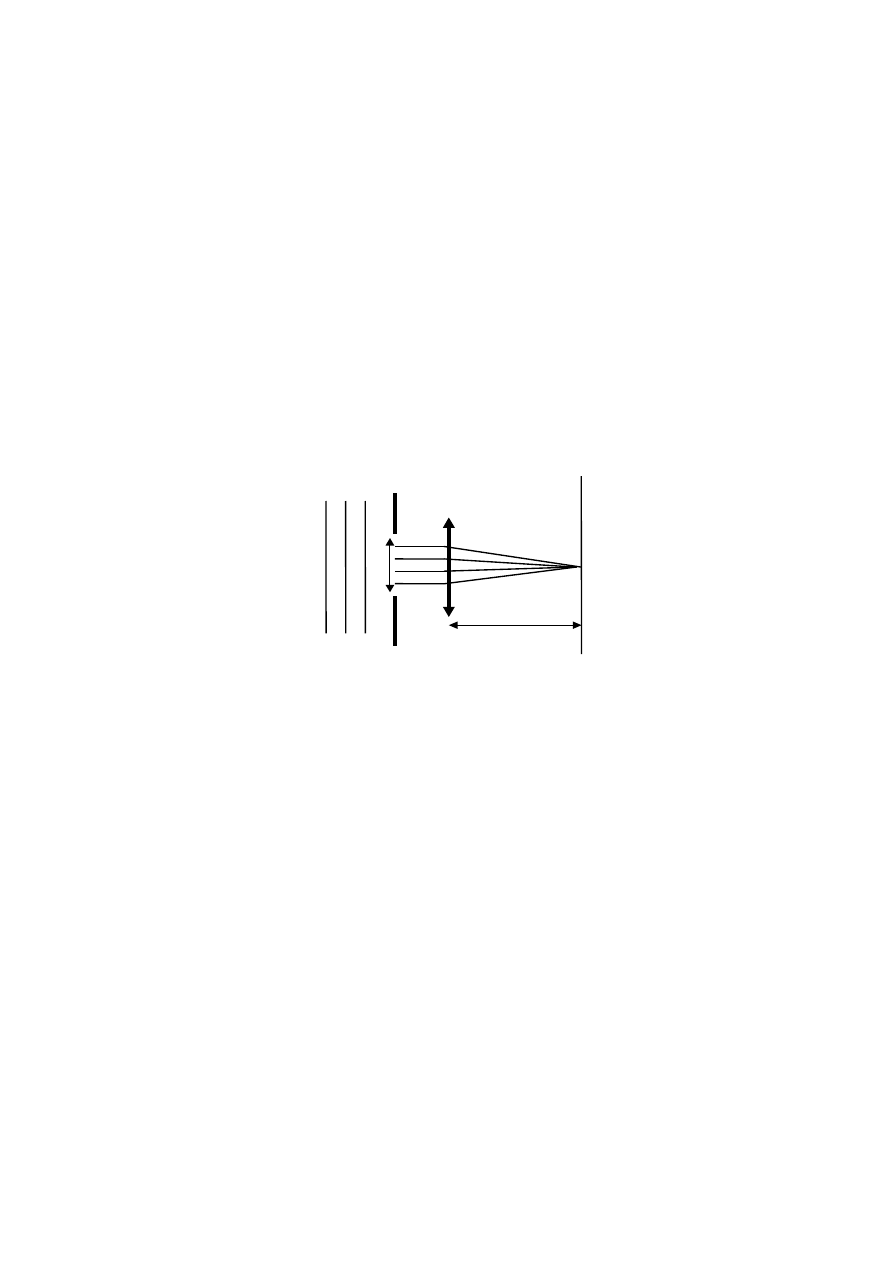
Całość upraszcza się, gdy źródło

S

i ekran

C

odsuniemy na bardzo duże odległości od

otworu uginającego. Ten graniczny przypadek nazywamy dyfrakcją Fraunhofera. Czoła fal

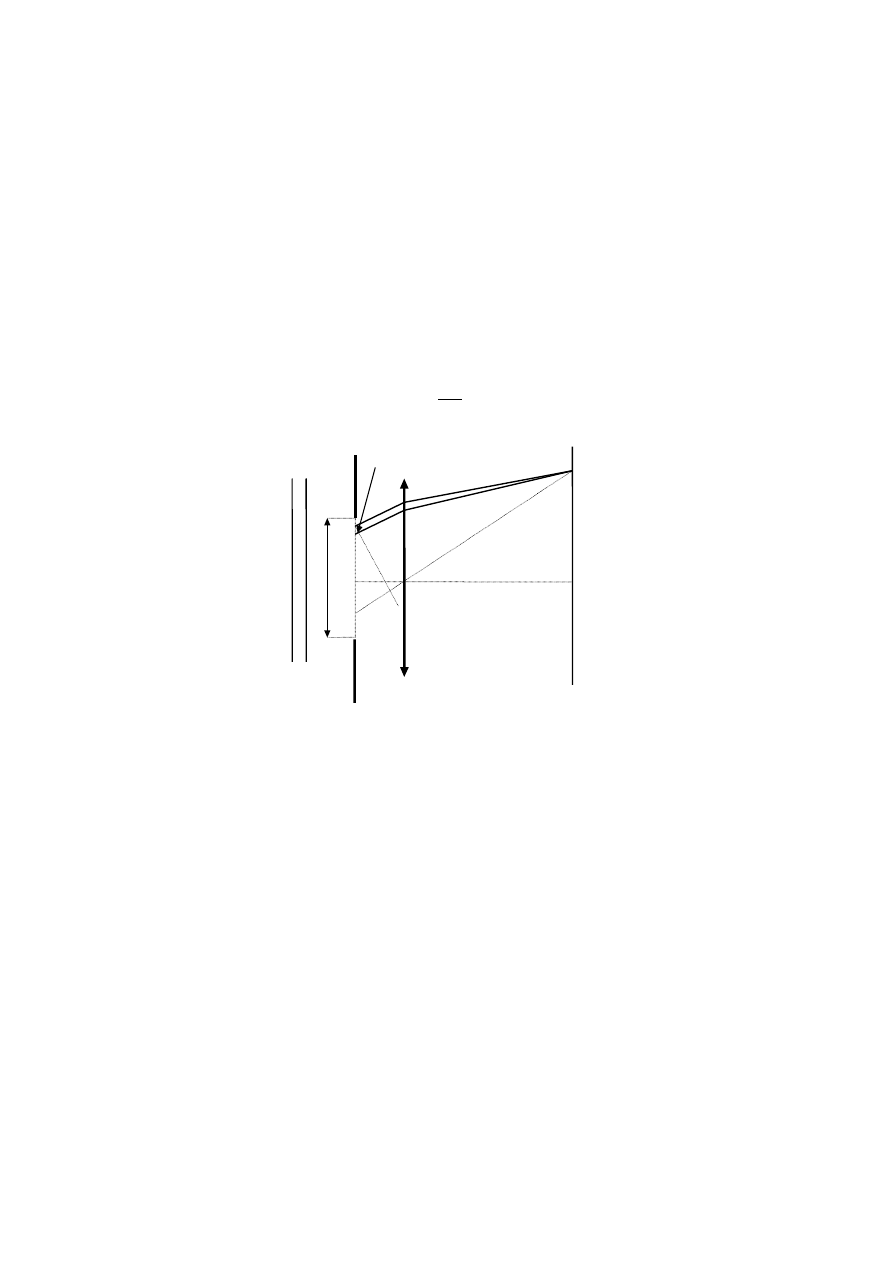
padających jak i ugiętych są płaszczyznami (promienie są równoległe) tak jak to widać na

rysunku (b). Wszystkie promienie oświetlające punkt

P

opuszczają otwór równolegle do linii

przerywanej (przechodzącej przez środek soczewki). Warunki dyfrakcji Fraunhofera były z

założenia spełnione w doświadczeniu Younga.

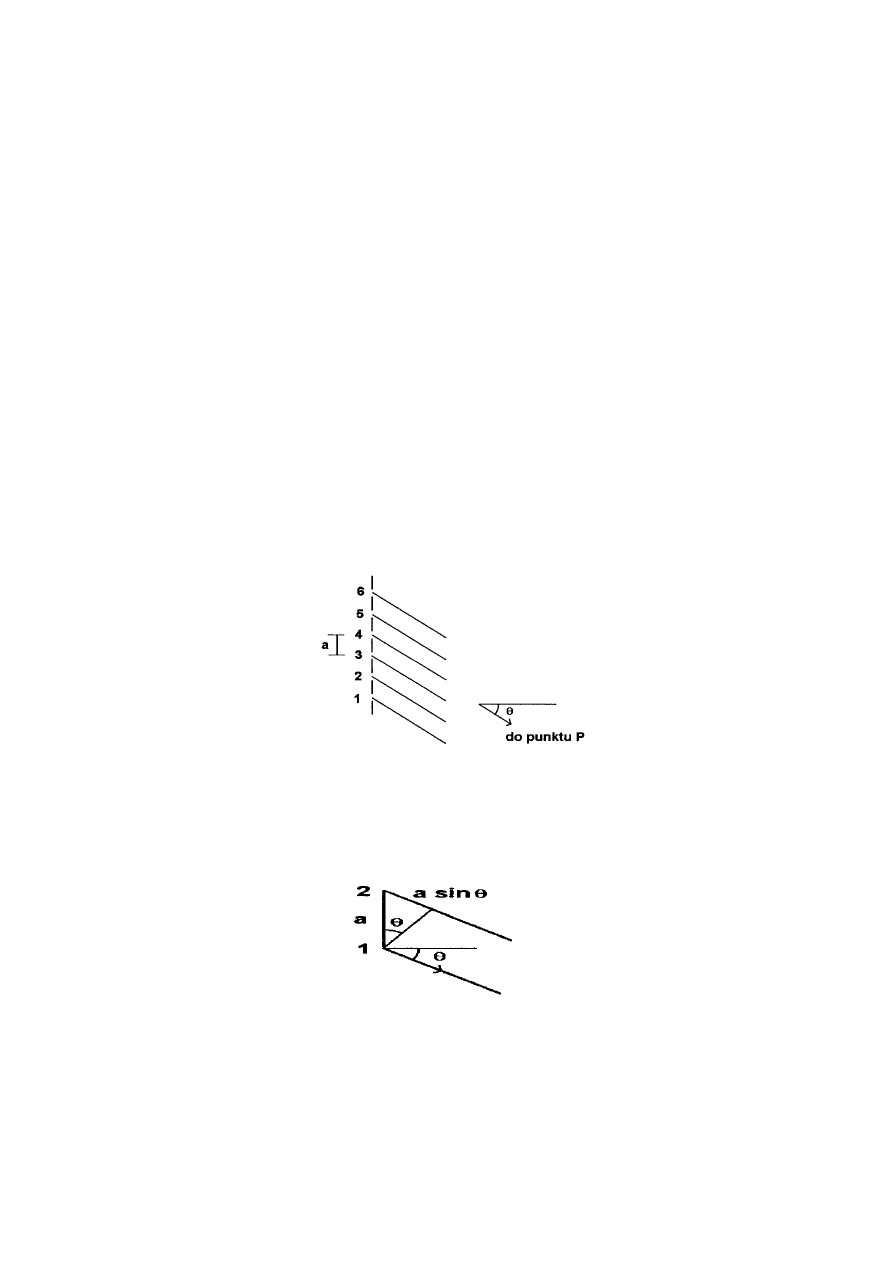
Dyfrakcja Fraunhofera na pojedynczej szczelinie

Rozważmy falę płaską padającą prostopadle na szczelinę o szerokości

a

. Rozpatrzmy

punkt środkowy

0

P ekranu. Równoległe promienie przebywają do tego punktu te same drogi

optyczne (różne geometryczne) tzn. promienie zawierają tę samą ilość długości fal (rozważane

soczewki są cienkie).

P

0

f

B

a

C

Ponieważ w szczelinie promienie są zgodne w fazie to po przebyciu takich samych dróg

optycznych nadal pozostają zgodne w fazie. Dlatego w środkowym punkcie

0

P będzie

maksimum.

Rozpatrzmy teraz inny punkt

1

P na ekranie (rysunek obok). Promienie docierające do

1

P wychodzą ze szczeliny pod kątem

θ

. Jeden promień ma początek u góry szczeliny, a drugi

w jej środku. (Promień

1

xP przechodzi przez środek soczewki więc nie jest odchylany).

Jeżeli wybierzemy punkt

1

P tak, żeby różnica dróg

/

bb wynosiła

2

/

λ

, to promienie

zgodne w fazie w szczelinie będą miały w punkcie

1

P fazy przeciwne i wygaszą się. Podobnie

każdy inny promień wychodzący z górnej połowy szczeliny będzie się wygaszał z

odpowiednim promieniem z dolnej połówki leżącym w odległości

2

/

a

poniżej. Punkt

1

P

349

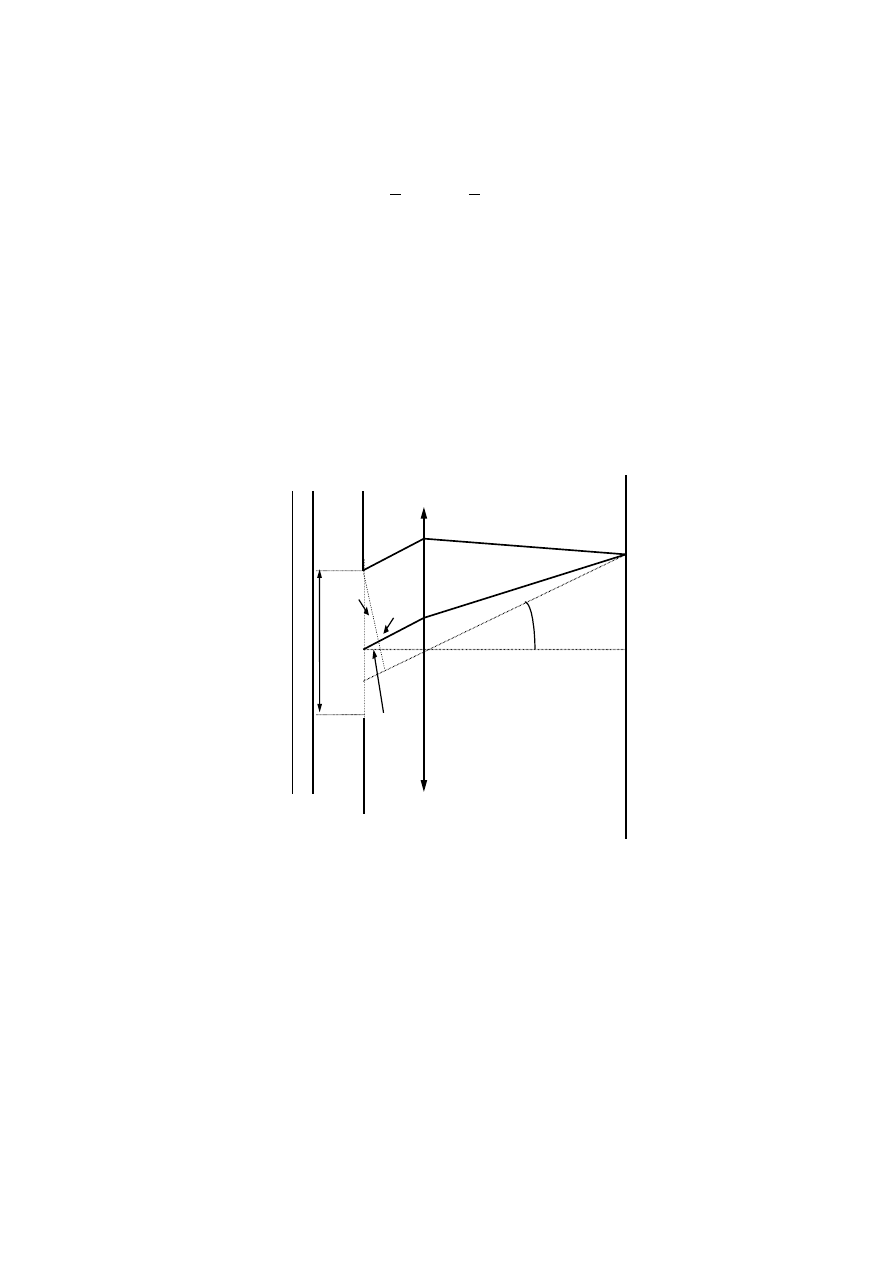
będzie miał natężenie zerowe (pierwsze minimum dyfrakcyjne). Warunek opisujący to

minimum ma następującą postać

λ

θ

2

1

sin

2

1

=

a

,

czyli

λ

θ

=

sin

a

.

Gdyby szerokość szczeliny była równa

λ

wtedy pierwsze minimum pojawiłoby się dla

θ

= 90

°

czyli środkowe maksimum wypełniłoby cały ekran. W miarę rozszerzania szczeliny

środkowe maksimum staje się węższe. Podobne rozważania możemy powtórzyć dla wielu

punktów szczeliny i otrzymamy ogólne wyrażenie dla minimów obrazu dyfrakcyjnego w

postaci

a

θ

θ

b

’

b

λ

/2

x

P

1

P

0

λ

θ

m

a

=

sin

,



,

3

,

2

,

1

=

m

(minimum) (27.1)

Mniej więcej w połowie między każdą para sąsiednich minimów występują oczywiście

maksima natężenia.

350

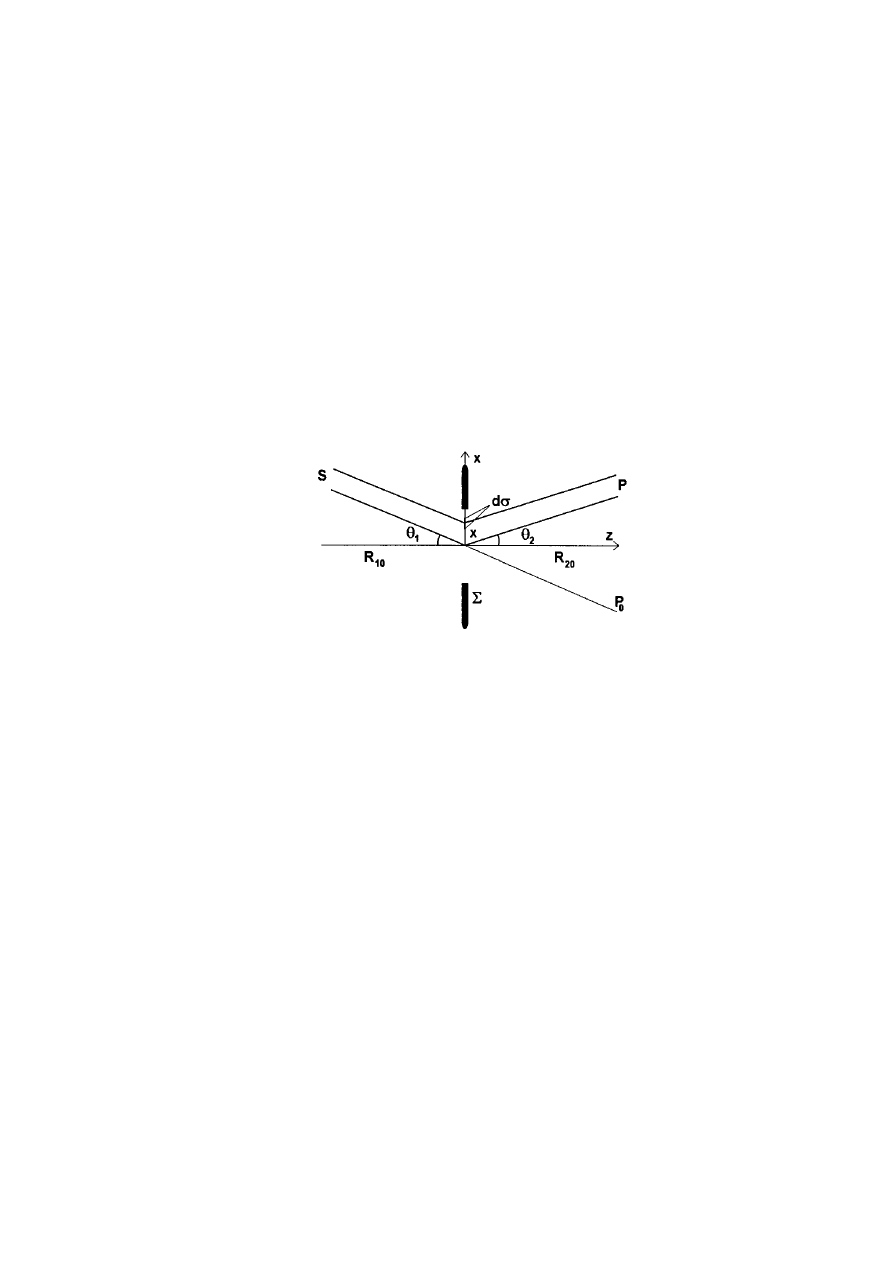
Całka dyfrakcyjna Fresnela-Kirchhoffa w przybliżeniu Fraunhofera

Sformułowanie podstaw koncepcyjnych potrzebnych do rozpatrywania zjawisk

dyfrakcji na pojedynczych otworach o różnych kształtach zawdzięczamy Huyghensowi,

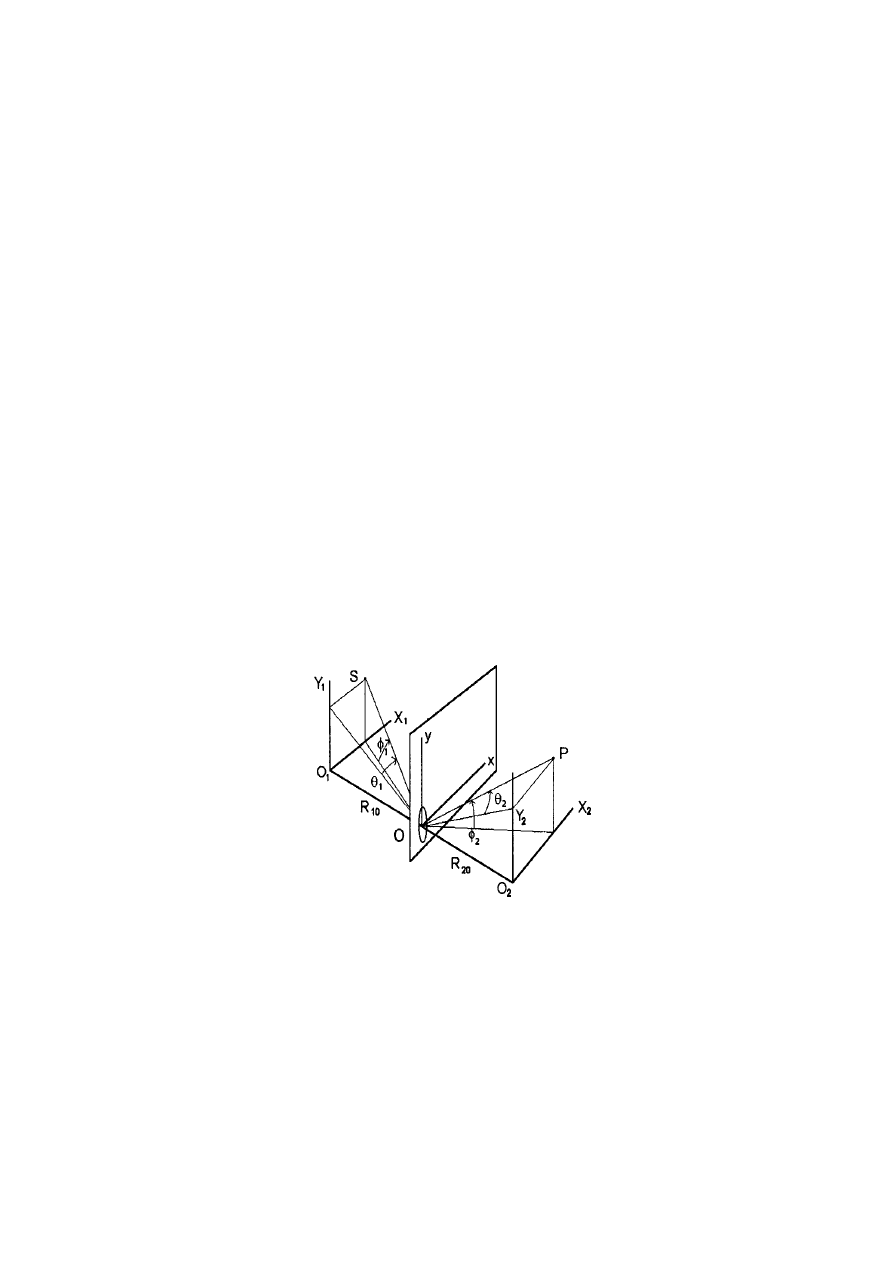
Fresnelowi i Kirchhoffowi. Rozważymy, dla uproszczenia, przypadek pojedynczego otworu o

dowolnym kształcie, pokazany na rysunku.

Fala świetlna dochodząca do punktu

P

będzie superpozycją wtórnych fal emitowanych

przez fikcyjne oscylatory Huyghensa rozłożone w otworze i wzbudzane przez falę pierwotną

emitowaną przez źródło

S

. Zakładamy, że spełniony jest warunek Fraunhofera, zatem dwa

promienie dochodzące z

S

do otworu są do siebie równoległe (czyli że fala wychodząca z

S

jest w przybliżeniu falą płaską).

Przyjmijmy, że monochromatyczna fala płaska dochodząca do otworu może być

opisana w środku otworu wzorem:

)]

(

exp[

)

0

(

10

0

t

kR

i

E

E

S

ω

−

⋅

=

. (27.2)

Do punktu

x

otworu, znajdującego się wyżej środka otworu, fala płaska dochodzi wcześniej i

ma zatem fazę (

t

kx

kR

ω

θ −

⋅

−

1

10

sin

):

)]

sin

(

exp[

)

,

(

1

10

0

0

t

kx

kR

i

E

t

x

E

ω

θ −

⋅

−

⋅

=

. (27.3)

Dla fali dochodzącej do punktu otworu o współrzędnych

)

,

( y

x

możemy zapisać

]

)

sin

sin

(

exp[

)

,

,

(

1

1

10

0

0

t

i

y

x

R

ik

E

t

y

x

E

ω

φ

θ

−

⋅

−

⋅

−

⋅

=

. (27.4)

Ze wzoru (27.4) wynika, że oscylatory Huyghensa rozłożone wzdłuż osi

x

i

y

w otworze

będą wzbudzane z różnymi fazami i, w związku z tym, wypromieniują fale wtórne, które także

351

będzie miały odpowiednio przesunięte fazy.

Za otworem wypromieniowana w kierunku określonym kątami (

2

2

,

θ

φ

) fala wynosi

]

)

sin

sin

sin

sin

(

exp[

)]

sin

sin

(

exp[

)

,

,

(

)

,

,

(

2

1

2

1

20

10

0

2

2

20

0

t

i

y

y

x

x

R

R

ik

E

y

x

R

ik

t

y

x

E

t

y

x

E

S

ω

φ

φ

θ

θ

φ

θ

−

⋅

−

⋅

−

⋅

−

⋅

−

+

⋅

=

=

⋅

−

⋅

−

⋅

=

, (27.5)

gdzie kąty

1

φ

i

2

φ

odgrywają podobną rolę jak kąty

1

θ

i

2

θ

; mianowicie ustalają położenia

kątowe źródła

S

i punktu obserwacyjnego

P

(patrz rysunek).

Wypromieniowane elementem powierzchni

dxdy

dS

=

otworu fali będą mieli

wypadkową amplitudę

dS

t

y

x

E

t

y

x

dE

S

S

⋅

=

)

,

,

(

)

,

,

(

. (27.6)

Całkowite pole fali świetlnej w punkcie

P

będzie dane całką

∫

∫

⋅

=

=

S

S

S

S

S

dS

t

y

x

E

t

y

x

dE

P

E

)

,

,

(

)

,

,

(

)

(

(27.7)

po całej powierzchni otworu, która jest często nazywana całką dyfrakcyjną (wzorem

dyfrakcyjnym) Fresnela-Kirchhoffa.

Wprowadźmy funkcję:

352







=

.

,

,

0

.

,

,

1

)

,

(

otwor

poza

y

x

dla

otworu

wewn

y

x

dla

y

x

T

, (27.8)

całkę dyfrakcyjną Fresnela- Kirchhoffa możemy zapisać w postaci

(

)

[

]

(

)

∫ ∫

∞

∞

−

∞

∞

−

+

+

+

−

−

+

⋅

=

dxdy

y

x

T

e

e

E

P

E

y

x

ik

t

R

R

k

i

S

)

,

(

)

(

)]

sin

(sin

sin

sin

[

0

2

1

2

1

20

10

φ

φ

θ

θ

ω

. (27.9)

Warto zwrócić uwagę na specjalny punkt

0

P , taki że

1

2

θ

θ

−

=

i

1

2

φ

φ

−

=

. Punkt

0

P będzie

leżał na prostej przechodzącej przez

S

i początek układu

O

, który znajduje się w płaszczyźnie

otworu. Dla punktu

0

P ze wzoru (27.9) mamy

(

)

[

]

∫ ∫

∞

∞

−

∞

∞

−

−

+

=

dxdy

y

x

T

e

E

P

E

t

R

R

k

i

S

)

,

(

)

(

20

10

0

0

ω

. (27.10)

Biorąc pod uwagę (27.10), wzór (27.9) możemy zapisać w postaci

)

(

)

(

)

(

0

P

G

P

E

P

E

S

S

S

⋅

=

, (27.11)

gdzie

.

Najbardziej interesuje nas natężenie światła w punkcie

P

, które, po uwzględnieniu

(27.11) na pole fali świetlnej wyrazi się następującym wzorem:

2

0

)

(

)

(

)

(

P

G

P

I

P

I

S

S

S

⋅

=

, (27.12)

gdzie

)

(

)

(

)

(

0

0

0

P

E

P

E

P

I

S

S

S

∗

=

.

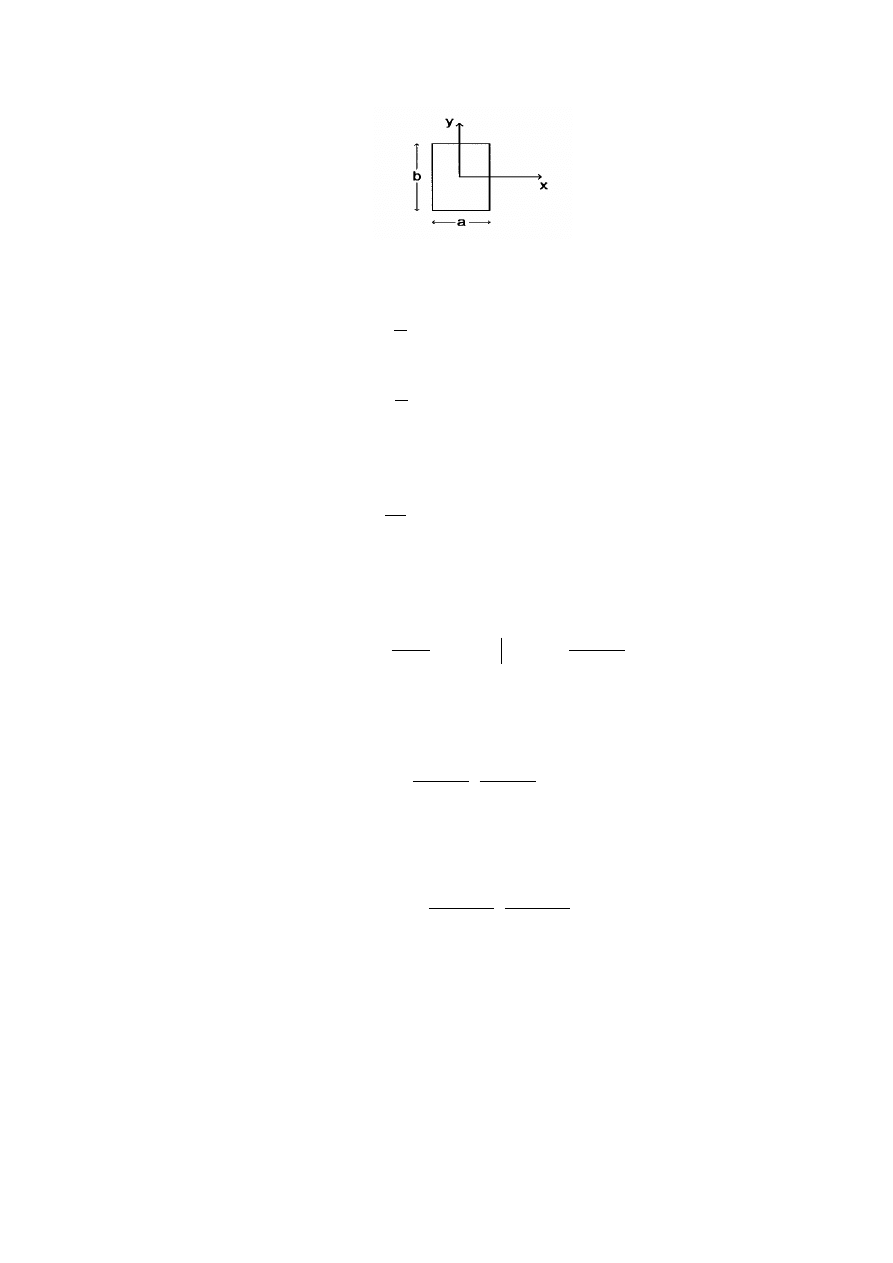
Dyfrakcja Fraunhofera na otworze prostokątnym

Jako przykład wyliczenia całki Fresnela-Kirchhoffa rozpatrzymy otwór prostokątny o

wymiarach

b

a

×

, pokazany na rysunku niżej. Oznaczmy:

353

∫ ∫

∫ ∫

∞

∞

−

∞

∞

−

∞

∞

−

∞

∞

−

+

+

+

−

⋅

⋅

=

dxdy

y

x

T

dxdy

e

y

x

T

P

G

y

x

ik

S

)

,

(

)

,

(

)

(

]

sin

(sin

)

sin

(sin

[

2

1

2

1

φ

φ

θ

θ

)

sin

(sin

2

1

θ

θ

λ

α

+

=

a

,

)

sin

(sin

2

1

φ

φ

λ

β

+

=

b

.

Wówczas podwójna całka

)

(P

G

S

przyjmuje postać:

dy

e

dx

e

ab

P

G

b

b

b

y

i

a

a

a

x

i

S

∫

∫

−

−

−

−

=

2

/

2

/

)

/

(

2

2

/

2

/

)

/

(

2

1

)

(

πβ

πα

. (27.13)

Każda z pojedynczych całek daje się łatwo scałkować; zrobimy to dla jednej z nich:

( )

πα

πα

πα

πα

πα

sin

2

2

/

2

/

)

/

(

2

2

/

2

/

)

/

(

2

⋅

=

−

=

−

−

−

−

∫

a

e

i

a

dx

e

a

a

a

x

i

a

a

a

x

i

.

Podobnie będzie z drugą całką, a zatem ostatecznie mamy:

( )

πβ

πβ

πα

πα

)

sin(

sin

)

(

⋅

=

P

G

S

.

Natężenie światła w punkcie obserwacji

P

będzie równe:

( )

2

2

2

2

0

)

(

)

(

sin

)

(

sin

)

(

)

(

πβ

πβ

πα

πα ⋅

⋅

=

P

I

P

I

S

S

. (27.14)

Jedna z dwóch funkcji typu

2

2

/

sin

x

x

występujących w powyższym wzorze jest pokazana na

rysunku. Wszystkie zera pokazanej funkcji odpowiadają zerom funkcji

x

sin

, a zatem ciemne

miejsca na ekranie odpowiadają wartości parametru

α

(dla drugiej funkcji będzie to parametr

β

) równej

,

2

,

1

±

±

itd.

354

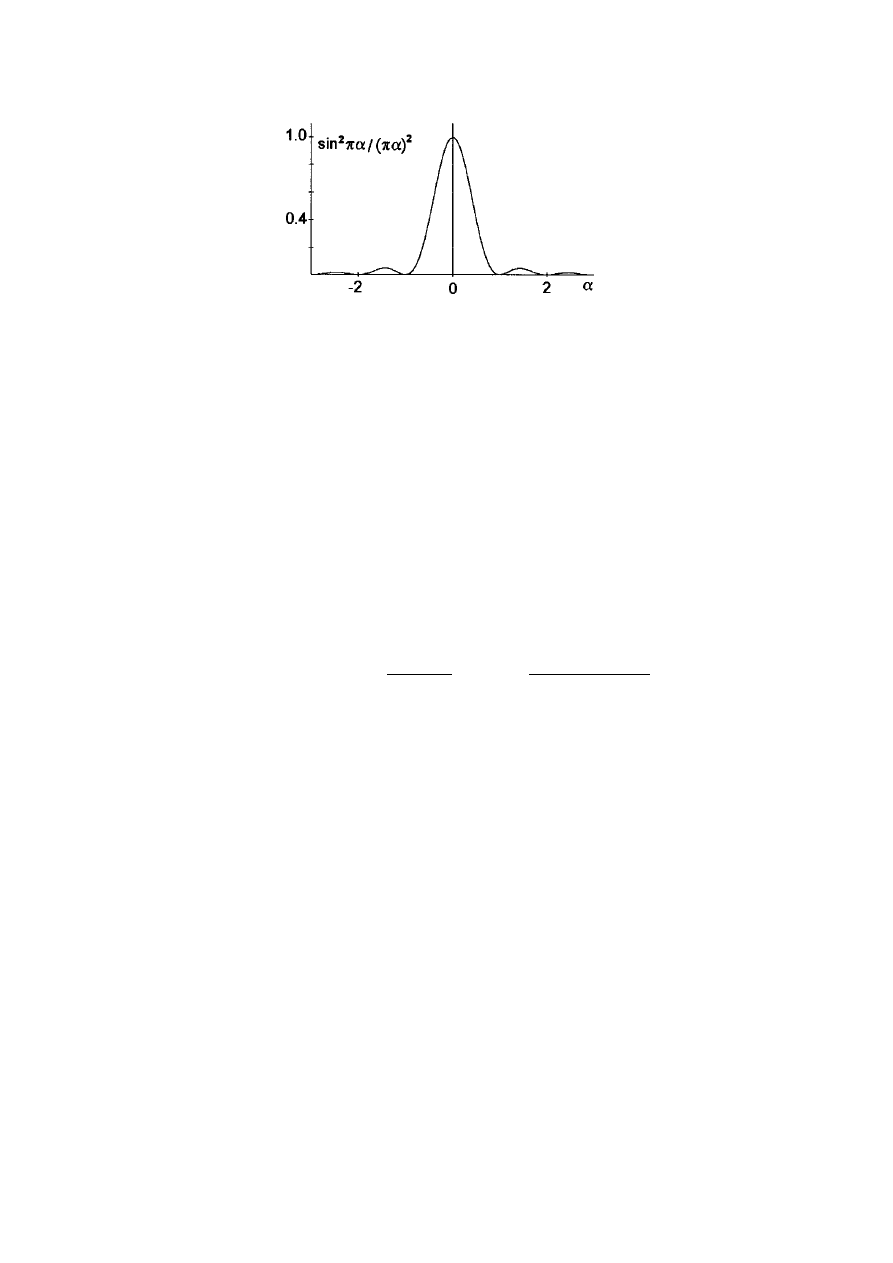
Maksymalną wartość funkcji

2

2

)

/(

sin

πα

πα

otrzymujemy w punkcie

0

=

α

. Natężenie w

każdym punkcie ekranu, zgodnie z (27.14) jest iloczynem dwóch takich funkcji, obraz nie

będzie się zatem składał z prążków, tylko z “plam” występujących w punktach przecięciach

“jasnych prążków” odpowiadających kolejnym maksimom obu omawianych funkcji.

Największe natężenia wystąpią zatem w tych “plamach” dla których oba parametry

α

i

β

będą równe zero (zobaczymy zatem charakterystyczny krzyż).

W przypadku wąskiej szczeliny (

a

b

<<

) ze wzoru (27.14) przy

0

→

β

otrzymujemy

( )

2

2

0

2

2

0

)

/

sin

(

)

/

sin

(

sin

)

(

)

(

sin

)

(

)

(

λ

θ

π

λ

θ

π

πα

πα

a

a

P

I

P

I

P

I

S

S

S

⋅

=

⋅

=

. (27.14)

Tu założyliśmy, że

0

1

=

θ

czyli czoło fali padającej jest równoległe do płaszczyzny xOy i

2

θ

θ ≡

.

Graficzna konstrukcja Fresnela

Wyliczenie całki dyfrakcyjnej Fresnela- Kirchhoffa nie zawsze jest tak łatwe.

Rozważmy inną graficzną metodę, zaproponowaną przez Fresnela. Ta metoda czasami daje

możliwość łatwo znaleźć dyfrakcyjny albo interferencyjny obraz. Metodę Fresnela zilustrujemy

najpierw rozważając doświadczenie Younga dotyczące interferencji fal pochodzących od

dwóch szczelin.

Aby wyliczyć wypadkowe natężenie światła w doświadczeniu Younga dodawaliśmy

dwa zaburzenia falowe postaci

t

E

E

ω

sin

0

1

⋅

=

,

)

sin(

0

2

ϕ

ω ∆

+

⋅

=

t

E

E

, które miały tę samą

częstość i amplitudę, a różniły się fazą o

ϕ

∆

.

355

E

2

E

1

E

1

E

0

E

0

E

0

ω

t

ω

t

ϕ

∆

Wynik uzyskany został algebraicznie na podstawie prostych wzorów

trygonometrycznych. Jednak metody analityczne stają się znacznie trudniejsze gdy dodajemy

więcej zaburzeń falowych (funkcji typu

x

x cos

,

sin

) i dlatego Fresnel wprowadził następującą

prostą metodę graficzną.

E

2

E

1

E

0

E

0

ω

t

ϕ

∆

E

θ

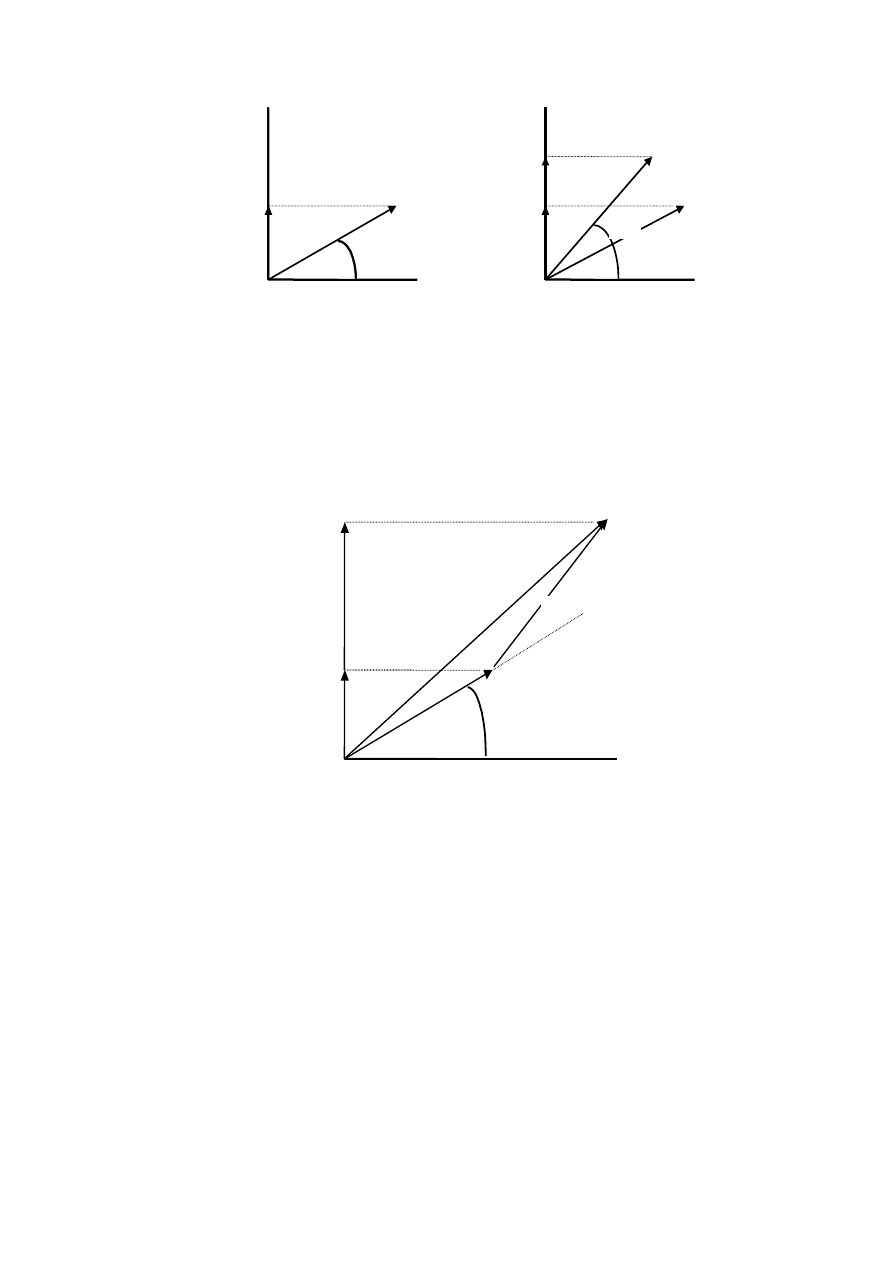
Harmoniczne (sinusoidalne albo cosinusoidalne) zaburzenie falowe może być

przedstawione graficznie jako obracający się z prędkością kątową

ω

wektor, którego długość

reprezentuje amplitudę

0

E . Taki wektor będziemy nazywać strzałką fazową (wskazem).

Zmienne w czasie zaburzenie falowe

t

E

E

ω

sin

0

1

⋅

=

w chwili t przedstawione jest wtedy

przez rzut tej „strzałki” na oś pionową (odpowiada to oczywiście pomnożeniu

0

E przez

t

ω

sin

). Drugie zaburzenie falowe

)

sin(

0

2

ϕ

ω ∆

+

⋅

=

t

E

E

, o tej samej amplitudzie

0

E , różni

się od

1

E fazą

ϕ

∆

. Znajdujemy je podobnie jako rzut „strzałki” na oś pionową. Teraz

356

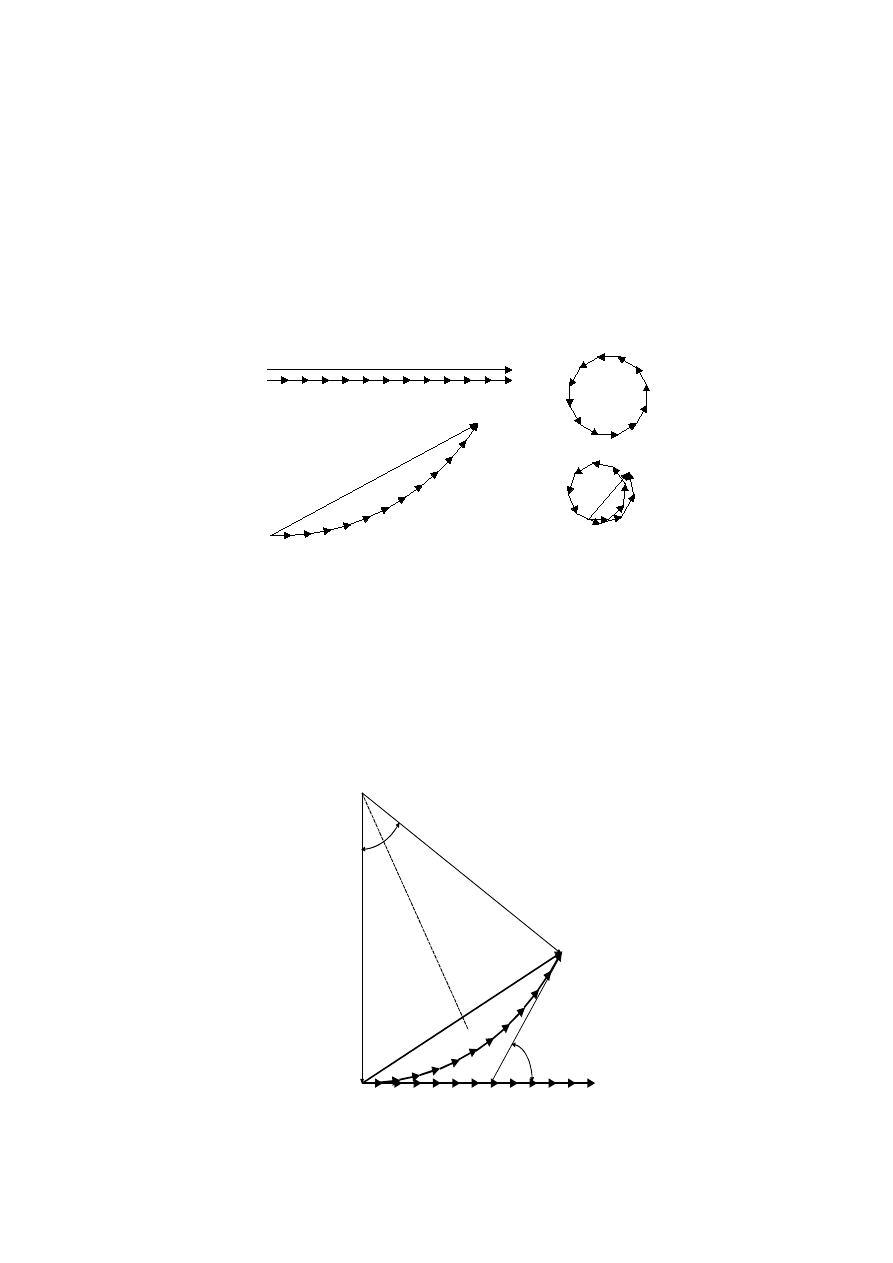
wystarczy dodać

1

E i

2

E żeby otrzymać wypadkowe zaburzenie. Widać to jeszcze lepiej gdy

umieści się początek jednej strzałki na końcu poprzedniej zachowując różnicę faz (rysunek

obok).

Jako przykład zastosowania metody graficznej Fresnela rozważmy dyfrakcję na wąskiej

szczelinie. Podzielmy szczelinę o szerokości

a

na

N

pasków o małej szerokości

x

∆

. Każdy

pasek jest źródłem fal kulistych Huyghensa, które wytwarzają na ekranie określone zaburzenie

falowe. Różnica dróg między sąsiednimi paskami wynosi

θ

sin

⋅

∆

≡

∆

x

r

stąd różnica faz

ϕ

∆

pomiędzy falami pochodzącymi z sąsiednich pasków wynosi

θ

ϕ

sin

⋅

∆

⋅

=

∆

⋅

=

∆

x

k

r

k

, czyli

θ

λ

π

ϕ

sin

2

x

∆

=

∆

. (27.15)

a

θ

θ

∆

x sin

θ

B

C

P

P

0

•

Zakładamy, że paski są tak wąskie, że wszystkie punkty na danym pasku mają tę samą

drogę optyczną do punktu

P

.

•

Dla małych kątów

θ

amplitudy

0

E

∆

zaburzeń falowych w punkcie

P

pochodzące od

różnych pasków przyjmujemy za jednakowe.

Zatem w puncie

P

dodaje się

N

pól elektrycznych o tej samej amplitudzie

0

E

∆

, tej samej

częstości i tej samej różnicy faz

φ

∆

między kolejnymi wektorami.

Na rysunku niżej przedstawione jest zaburzenie wypadkowe dla kilku różnych miejsc

na ekranie. Rys.(a) przedstawia warunki dla maksimum środkowego (

0

0

=

∆

ϕ

). Rys.(b) przed

357

stawia warunki dla kierunku nieco odmiennego od maksimum środkowego(

0

5

=

∆

ϕ

). Rys.(c)

przedstawia warunki dla pierwszego minimum (

0

30

=

∆

ϕ

). Rys.(d) przedstawia warunki

bliskie pierwszemu maksimum (poza środkowym) (

0

42

=

∆

ϕ

).

Zwróćmy uwagę, że długość łuku jest zawsze równa

M

E ale amplituda

θ

E jest różna.

Wektory na rysunku odpowiadają amplitudom (a nie natężeniom). Żeby otrzymać natężenia

trzeba je podnieść do kwadratu.

E

θ

=

E

M

E

θ

E

θ

E

θ

E

θ

= 0

a)

b)

c)

d)

Na rysunku niżej jest przedstawiona konstrukcja służąca do obliczenia natężenia światła

w przypadku dyfrakcji na jednej szczelinie. Sytuacja odpowiada tej pokazanej na poprzednim

rysunku (b).

R

R

E

m

E

m

E

θ

α

α

ϕ

ϕ

358

Jeżeli szczelinę podzielimy na nieskończenie wiele małych pasków o szerokości

dx

to

łuk strzałek będzie łukiem koła o promieniu

R

. Długość łuku wynosi

m

E czyli równa jest

amplitudzie w środku obrazu dyfrakcyjnego (linia prosta strzałek). Kąt

ϕ

w dolnej części

rysunku przedstawia różnicę fazy między skrajnymi wektorami w łuku tzn.

ϕ

jest różnicą faz

pomiędzy promieniami wychodzącymi z góry i dołu szczeliny. Jak widać z rysunku

R

E

/

)

2

/

(

)

2

/

sin(

θ

ϕ

=

, czyli

2

sin

2

ϕ

θ

⋅

=

R

E

(27.16)

W mierze łukowej

R

E

m

=

ϕ

. Podstawiając

ϕ

m

E

R

=

do równania (27.16) otrzymujemy

α

α

θ

sin

m

E

E

=

, (27.17)

gdzie

2

/

ϕ

α =

.

Przypomnijmy, że kąt

ϕ

jest różnicą faz dla promieni wychodzących z krańców

szczeliny. Ponieważ różnica dróg dla tych promieni wynosi (

θ

sin

⋅

a

), gdzie

a

- szerokość

szczeliny, posługując się znanym związkiem

różnica faz / 2

π

= różnica dróg /

λ

otrzymujemy

θ

λ

π

ϕ

sin

2 a

=

. Skąd

θ

λ

π

ϕ

α

sin

2

a

=

=

(27.18)

Biorąc pod uwagę wzory (27.17) i (27.18) znajdujemy następujący wzór na natężenie światła

dla dyfrakcji na pojedynczej szczelinie w kierunku określonym przez kąt

θ

:

( )

2

2

2

2

)

/

sin

(

)

/

sin

(

sin

)

(

sin

)

(

λ

θ

π

λ

θ

π

α

α

θ

a

a

I

I

P

I

m

m

⋅

=

⋅

=

. (27.19)

Jest to wynik całkowicie zgodny z uzyskanym poprzednio rozważaniem ilościowym (patrz

(27.14)).

359

Interferencja Fraunhofera na N jednakowych,

równoodległych otworach (szczelinach)

Na rysunku niżej jest pokazany układ, składający się z 6 otworów (szczelin)

oświetlonych wiązką światła padającego prostopadle do ekranu (wiązki padającej nie

pokazano). Ponieważ fala padająca dociera do wszystkich otworów w tej samej chwili czasu,

różnica dróg dla fal rozchodzących się z sąsiednich otworów w stronę punktu

P

leżącego

daleko na ekranie obserwacyjnym, pokazana na rysunku niżej dla otworów 1 i 2, będzie równa

(

θ

sin

⋅

a

). A zatem, jeżeli falę świetlną w punkcie

P

, pochodzącą od otworu 1, przedstawimy

w postaci:

)]

(

exp[

1

0

1

t

kr

i

E

E

ω

−

⋅

=





, (27.20)

to falę świetlną w punkcie

P

, pochodzącą od otworu 2 można zapisać w następujący sposób:

)]

sin

(

exp[

1

0

2

t

ka

kr

i

E

E

ω

θ −

⋅

+

⋅

=





. (27.21)

Zatem falę świetlną w punkcie

P

, pochodzącą od

n

-tego otworu można przedstawić w

następujący sposób:

360

)

sin

exp(

)]

sin

)

1

(

(

exp[

1

1

0

θ

ω

θ

⋅

=

−

⋅

−

⋅

+

⋅

=

−

ika

E

t

n

ka

kr

i

E

E

n

n







, (27.22)

a całkowitą, wypadkową falę świetlną w punkcie

P

od

N

otworów będzie reprezentować

następująca suma:

∑

∑

=

=

⋅

−

⋅

=

=

N

n

N

n

n

n

ika

E

E

P

E

1

1

1

]

sin

)

1

(

exp[

)

(

θ







. (27.23)

Korzystając ze wzoru

b

b

b

b

b

b

N

N

N

n

n

−

−

=

+

+

+

+

=

−

=

−

∑

1

1

1

1

2

1

1



.

wzór (27.23) możemy zapisać w postaci (tu

)

2

exp(

)

sin

exp(

δ

π

θ

⋅

≡

⋅

=

i

ika

b

;

λ

θ

δ

/

sin

⋅

=

a

):

=

⋅

−

⋅

=

∑

=

N

n

n

i

E

P

E

1

1

]

)

1

(

2

exp[

)

(

δ

π





(

)

( )

πδ

δ

π

δ

π

πδ

πδ

δ

π

δ

π

πδ

δ

π

πδ

δ

π

sin

sin

1

1

)

1

(

1

1

2

2

1

N

e

E

e

e

e

e

e

e

E

e

e

E

N

i

i

i

N

i

N

i

i

N

i

i

N

i

⋅

⋅

=

−

−

⋅

⋅

=

−

−

=

−

−

−







. (27.24)

Natężenie fali świetlnej w punkcie

P

będzie zatem równe:

(

)

2

1

2

2

1

1

2

)

(

)

(

sin

)

(

sin

)

(

)

(

F

P

I

N

E

E

P

E

P

I

⋅

≡

⋅

⋅

=

∝

∗

πδ

δ

π







, (27.25)

gdzie funkcja

)

(

1

P

I

opisuje rozkład natężenia światła (punkt

P

jest punktem bieżącym na

ekranie obserwacyjnym), a zatem będzie zawierać efekty dyfrakcyjne, natomiast drugi czynnik,

2

F , to czynnik interferencyjny, związany z nakładaniem się światła ugiętego na wszystkich

otworach.

Na rysunku (a) niżej są przedstawione dwie funkcje

)

(

sin

2

δ

π

N

i

)

(

sin

2

πδ

tworzące

czynnik interferencyjny dla układu 10 równoodległych i jednakowych otworów

rozmieszczonych na osi

Ox

. Na rysunku (b) przedstawiono ich iloraz. b), będzie także

okresowa z okresem zmiennej δ równym jeden. Dla

δ

całkowitych (

m

=

δ

;



,

2

,

1

,

0

±

±

=

m

itd.) wyrażenie

361

)

(

sin

)

(

sin

2

2

2

πδ

δ

π

N

F

=

, (27.26)

jest nieoznaczone (typu

0

/

0

). Przy

0

→

δ

ze wzoru (27.26) otrzymujemy:

(

)

( )

2

2

2

2

2

2

)

(

sin

)

(

sin

N

N

N

F

=

≈

=

πδ

δ

π

πδ

δ

π

. (27.27)

Łatwo wykazać, że dla innych

δ

całkowitych, ze względu na okresowość funkcji, wartości

2

F muszą być takie same i równe

2

N . Będą to wartości maksymalne, a odpowiadające im

prążki jasne będziemy nazywali prążkami głównymi. Inne lokalne maksima funkcji

2

F

odpowiadać będą maksimom funkcji

)

(

sin

2

δ

π

N

(a nie jej zerom, jak w przypadku maksimów

głównych), a ich wartości będą znacznie mniejsze. Będą one odpowiadały tak zwanym jasnym

prążkom bocznym albo wtórnym, a będzie ich, pomiędzy prążkami głównymi,

2

−

N

. Prążki

jasne rozdzielone są prążkami ciemnymi, których będzie, pomiędzy dwoma kolejnymi prążkami

głównymi,

1

−

N

.

Siatki dyfrakcyjne

Własności układu wielu równoległych i równoodległych szczelin zostały wykorzystane

w tzw siatkach dyfrakcyjnych, które umożliwiają jeden z najdokładniejszych pomiarów

(długości fali światła) rutynowo wykonywanych przez fizyków pracujących w wielu różnych

działach fizyki. Pierwsze siatki dyfrakcyjne zostały wykonane przez Fraunhofera już w 1820

roku. Podstawowy rodzaj siatki dyfrakcyjnej, to tzw. siatka odbiciowa pokazana na rysunku

362

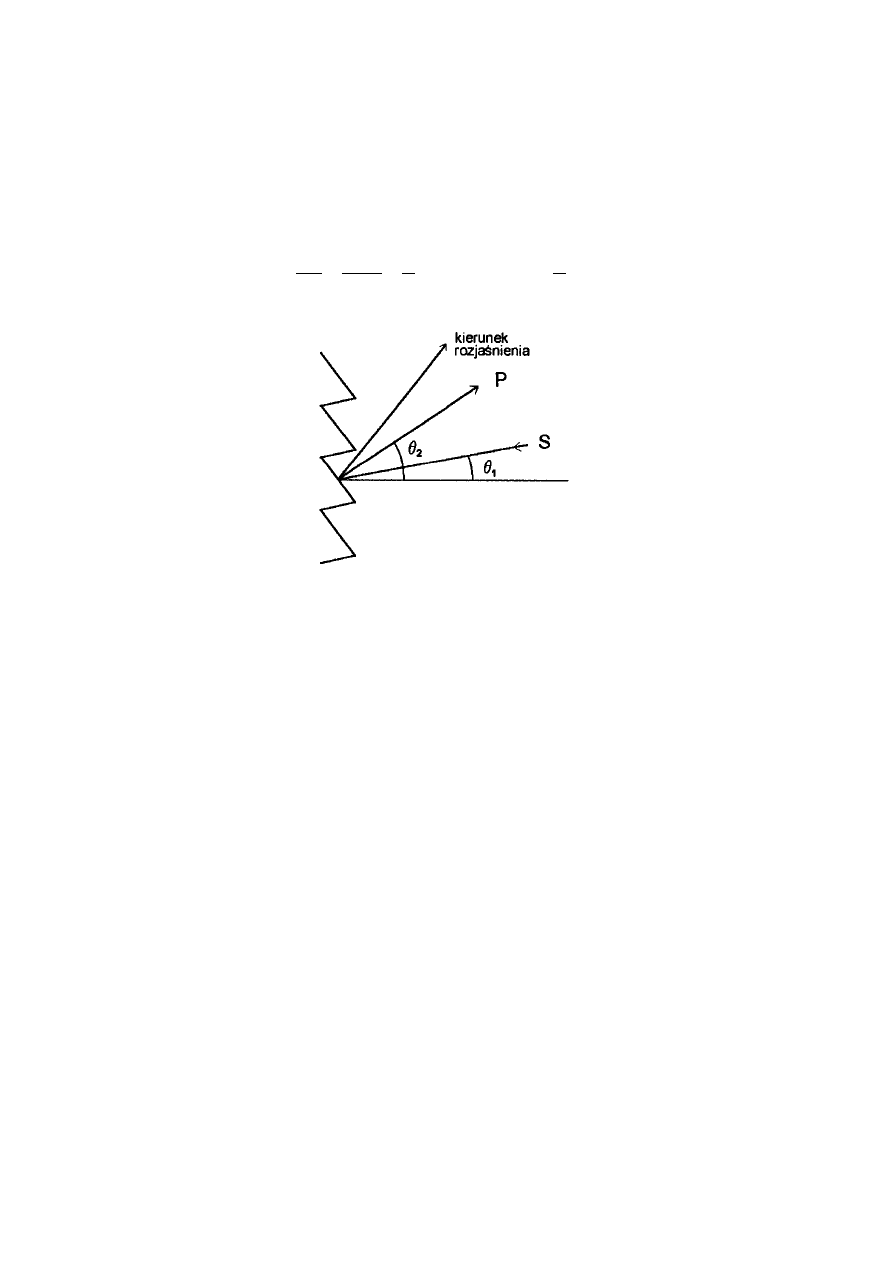
niżej. Ponieważ wiązka światła ze źródła

S

nie pada na siatkę prostopadle (tylko pod kątem

1

θ

) różnica faz dla fal ugiętych na sąsiednich otworach będzie składała się z dwóch podobnych

wyrazów. Zatem maksima główne siatki dyfrakcyjnej tego typu muszą spełniać następujący

warunek (patrz wzór (27.26)):

(

)

m

a

a

r

k

=

Φ

⋅

=

+

⋅

=

∆

⋅

=

∆

=

λ

θ

θ

λ

π

π

ϕ

δ

2

1

sin

sin

2

2

, (27.28)

gdzie

(

)

2

1

sin

sin

θ

θ +

=

Φ

i



,

2

,

1

,

0

±

±

=

m

. Dla ustalonego kąta padania

1

θ

, dla każdego

rzędu siatki

m

będziemy mieli wobec tego wzajemnie jednoznaczne przyporządkowanie

pomiędzy kątem

2

θ

i długością fali

λ

. A zatem pomiar długości fali można sprowadzić do

pomiaru położenia odpowiedniego prążka, który może być wykonany bardzo dokładnie. W

praktyce robi to się najczęściej nieco inaczej; przy ustalonych kierunkach do punktów

P

i

S

(których rolę grają szczeliny wyjściowa i wejściowa spektrometru), obracamy całą siatką i

mierzymy jej kąt obrotu. Przyrządy takie często nazywa się monochromatorami.

Kryterium Rayleigha

Bardzo ważną sprawą w przypadku przyrządów takich jakich monochromatory czy

spektrografy jest ich rozdzielczość spektralna, tzn zdolność rozróżnienia dwóch bliskich

długości fali. Rozważmy ten problem na przykładzie omawianej wyżej odbiciowej siatki

dyfrakcyjnej. Zgodnie z kryterium Rayleigha, dwa prążki główne, odpowiadające różnym

363

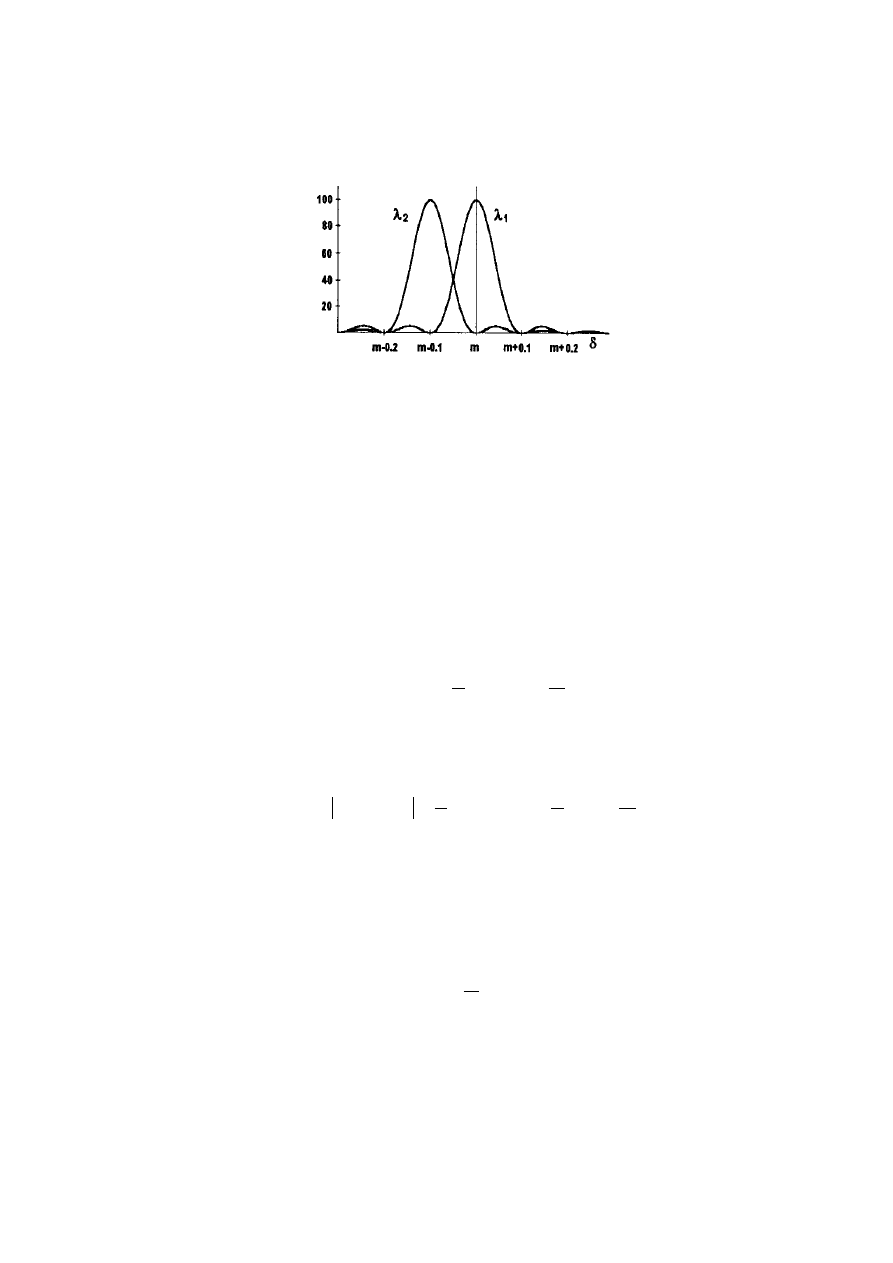
długościom fali

1

λ

i

2

λ

można rozróżnić, gdy maksimum pierwszego przypada nie bliżej niż

na pierwszy minimum drugiego.

Na rysunku pokazano rozkład natężeń dla którego, zgodnie z tzw kryterium Rayleigha,

można jeszcze rozróżnić dwie bliskie długości fali,

1

λ

i

2

λ

. Kryterium to jest oczywiście

trochę arbitralne, ale jest to w tej sytuacji nieuniknione. Pierwsze, najbliższe do głównego

maksimum (27.28), minima dla długości fali

λ

wypadają, zgodnie z (27.26), dla

N

m

/

1

±

=

δ

,

a zatem:

N

m

a

1

2

min

±

=

Φ

⋅

=

λ

δ

. (27.29)

Ze wzorów (27.28) i (27.29) znajdujemy

N

a

a

1

)

(

2

1

min

max

=

∆Φ

⋅

=

Φ

−

Φ

⋅

=

−

λ

λ

δ

δ

. (27.30)

Tu zgodnie z (27.28)

m

a

=

Φ

=

λ

δ

/

1

max

.

Z drugiej zaś strony, ze wzoru (27.28) otrzymujemy następujący ogólny związek

pomiędzy długością fali

λ

i wielkością

Φ

:

m

a /

Φ

=

λ

. Skąd

∆Φ

⋅

=

∆

m

a

λ

. (27.31)

Zestawiając razem wzory (27.30) i (27.31) otrzymujemy ostatecznie wyrażenie na najmniejszą

możliwą różnicę długości fali:

364

mN

aN

m

a

m

a

λ

λ

λ

=

⋅

=

∆Φ

⋅

=

∆

(27.32)

lub też, w innej, bardziej przyjętej postaci:

N

m

⋅

=

=

∆

R

λ

λ

, (27.33)

gdzie

R

nazywa się zdolnością rozdzielczą.

365