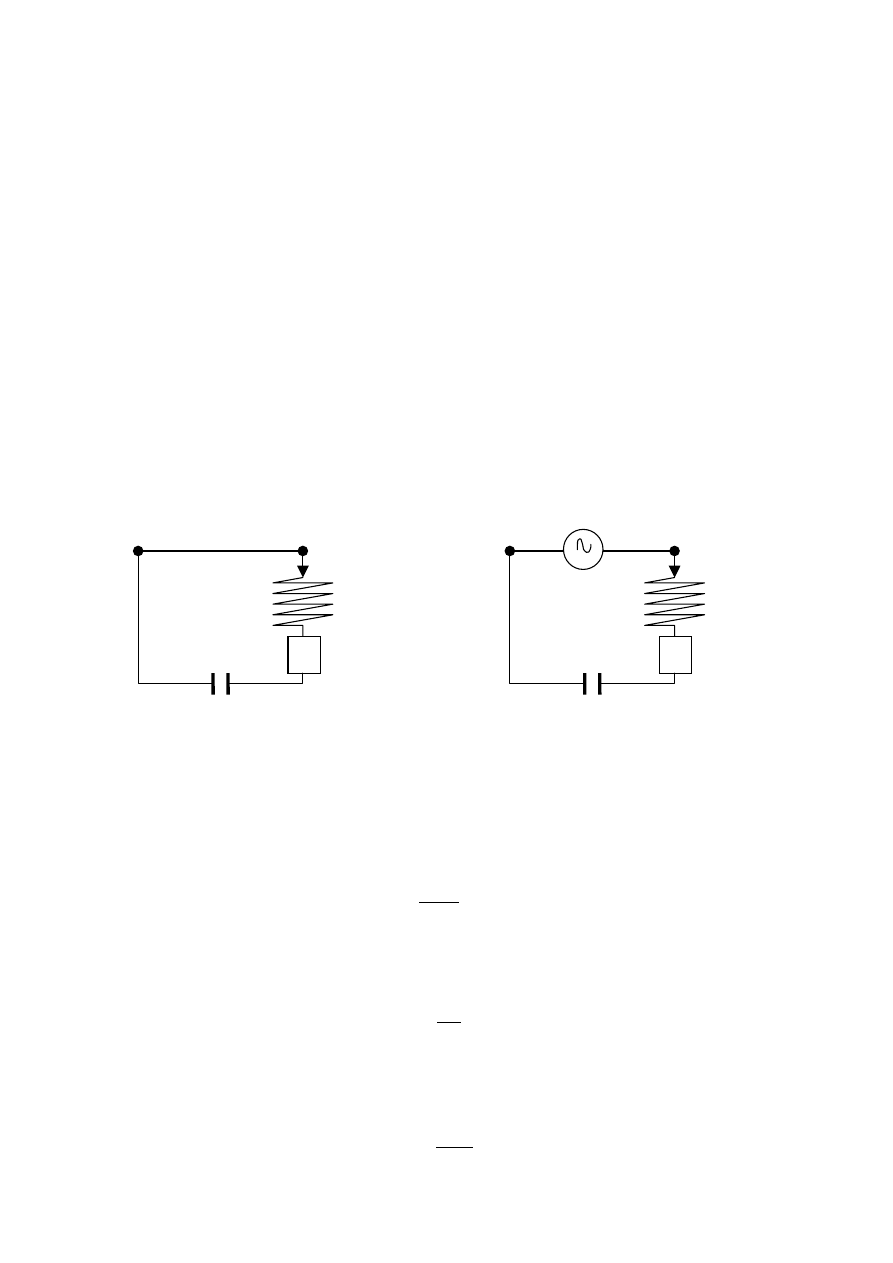
Ć w i c z e n i e 24
BADANIA REZONANSU
W OBWODACH ELEKTRYCZNYCH
24.1 Wstęp teoretyczny
Zjawisko rezonansu, które poniżej zostanie zdefiniowane, związane jest z „wymuszonymi drgania-
mi” układów drgających np. mechanicznych lub elektrycznych. Samo pojęcie drgań zostało opisane
w ćwiczeniach nr 4 i 5, gdzie badano drgania układów wytrąconych z równowagi i pozostawionych
samym sobie. W tych ćwiczeniach zdefiniowano pojęcia: okresu drgań, częstości drgań własnych,
drgania normalne, dudnienia. W ćwiczeniu 37 omówiono również drgania tłumione. Znajomość
tych pojęć jest niezbędna do zrozumienia efektu rezonansu. Pojęcie „wymuszenia drgań „ oznacza,
że obwód nie został wytrącony z równowagi i pozostawiony sam sobie, lecz przez cały czas działa
na niego siła. W rozważaniach na temat rezonansu będziemy badali, co się dzieje z układem, gdy
działa na niego siła harmoniczna np. F = F
0
cos(
ωt) oraz jak zachowanie układu zależy od częstości
siły wymuszającej. Ze względu na łatwość technicznej realizacji w ćwiczeniu badamy elektryczny
układ rezonansowy.
e(t)
i(t)
i(t)
L
L
C
R
C
R
a)
b)
Rys. 24.1. Układ rezonansowy RLC; a- bez wymuszenia, b – z wymuszeniem.
Drgania tłumione. Rozważmy układ bez wymuszenia. W pewnym momencie na kondensatorze C
został zgromadzony ładunek q, a prąd płynący w obwodzie jest równy zeru. Następuje rozładowa-
nie kondensatora, zaczyna płynąć prąd określony zależnością:
dt
t
dq
i
)
(
=
(24.1)
Energia zgromadzona w kondensatorze zależy od zgromadzonego w nim ładunku:
C
q
E
C
2
2
=
(24.2)
Wraz z rozładowaniem kondensatora energia ta maleje, wzrasta natomiast energia pola magnetycz-
nego gromadzona w cewce o indukcyjności L:
2
2
i
L
E
L
⋅
=
(24.3)
W rezultacie pole elektryczne maleje, pole magnetyczne wzrasta a energia zawarta w polu elek-
trycznym kondensatora zamienia się na energię pola magnetycznego cewki. W procesie tym przez
opornik R przepływa prąd i(t) wydzielając na nim ciepło Joule’a. Następuje więc zamiana części
energii na ciepło w ilości:
2
2
i
R
E
J
⋅
=
(24.4)
Jeden pełny cykl zaczynający się np. od chwili podłączenia do obwodu RLC naładowanego kon-
densatora zawiera rozładowanie kondensatora, naładowanie przeciwnym ładunkiem, ponowne roz-
ładowanie i naładowanie do pierwotnego stanu. Jeśli
0
≠
R
wtedy nastąpi strata energii cieplnej i
układ nie wróci do pierwotnego naładowania, ale cykl zamknie się w momencie uzyskania maksy-
malnej wartości ładunku na kondensatorze, ale mniejszej od początkowej. Dla R=0 układ jest bez-
stratny i istnieje pełna analogia opisu zjawiska do drgań swobodnego wahadła matematycznego.
Aby opisać zmiany prądu i(t) w obwodzie RLC skorzystamy z II prawa Kirchhoffa, które mówi, że
suma spadków napięć w oczku jest równa zeru.
Z prawa Ohma wiemy, że spadek napięcia na oporniku R jest równy:
R
t
i
t
U
R
⋅
= )
(
)
(
(24.5)
Napięcie na kondensatorze wyraża się zależnością:
∫
=
t
C
dt
t
i
C
t
U
0
)
(
1
)
(
(24.6)
Z prawa Faradaya wiemy, że w cewce pod wpływem zmiennego w czasie prądu indukuje się siła
elektromotoryczna:
dt
t
di
L
U
L
)
(
−
=
(24.7)
Dla obwodu z Rys. 24.1a korzystając z II prawa Kirchhoffa możemy napisać:
U
)
(
)
(
)
(
t
U
t
U
t
C
R
L
+
=
∫
+
=
−
t
dt
t
i
C
R
t
i
dt
t
di
L
0
)
(
1
)
(
)
(
(24.8)
Po uwzględnieniu zależności (24.1) równanie (24.8) przyjmie postać:
0
1
2
2
=
+
+
q
C
dt
dq
R
dt
q
d
L
(24.9)
Wprowadzając oznaczenia:
- współczynnik tłumienia
L
R
2
=
β
- częstotliwość drgań swobodnych zwaną częstością własną
LC
1
0
=
ω
uzyskuje się równanie różniczkowe analogiczne do równania drgań tłumionych:
0
2
2
0
2
2
=
+
+
q
dt
dq
dt
q
d
ω
β
(24.10)
Wielkością zmieniającą się w czasie jest ładunek zgromadzony na okładkach kondensatora. Roz-
wiązanie powyższego równania pokazuje charakter tych zmian:
)
cos(
)
(
0
ϕ
ω
β
+
=
−
t
e
q
t
q
t
(24.11)
gdzie:
2
2
0
β
ω
ω
−
=
- częstość (pulsacja) drgań tłumionych
Zauważmy, że wskutek działania tłumienia amplituda drgań maleje ekspotencjalnie (e
-
βt
) z upły-
wem czasu, zaś częstość drgań tłumionych jest mniejsza niż częstość drgań własnych.
Wielkością opisującą szybkość zmian amplitudy drgań tłumionych jest tzw. logarytmiczny dekre-
ment tłumienia - . Jest to logarytm naturalny stosunku amplitudy w chwili t oraz t+T ( T- okres
drgań).
Λ
T
e
q
e
q
T
t
t
β
β
β
=
=
Λ
+
−
−
)
(
0
0
ln
(24.12)
Zależności (24.11) i (24.12) mają sens, jeśli
ω
β
< . W przeciwnym razie ruch nie jest ruchem drga-
jącym lecz pełzającym (aperiodycznym). Charakteryzuje się ten ruch tym, że badany parametr nie
wykonuje drgań lecz zbliża się do położenia równowagi asymptotycznie. Szczególnym przypad-
kiem jest ruch pełzający krytyczny gdy
ω
β
= .
Drgania wymuszone.
Jeśli chcemy, aby mimo tłumienia utrzymać drgania harmoniczne niegasnące
powinniśmy wprowadzić odpowiednio zmienne wymuszenie w postaci źródła napięcia zmiennego
w czasie w sposób harmoniczny ( Rys.24.1 b):
)
cos(
)
(
0
t
U
t
e
Ω
=
(24.13)
gdzie - jest częstością wymuszenia.
Ω
Z II prawa Kirchhoffa możemy napisać:
)
cos(
1
0
2
2
t
U
q
C
dt
dq
R
dt
q
d
L
Ω
=
+
+
(24.14)
lub w formie:
)
cos(
1
0
2
2
t
L
U
q
LC
dt
dq
L
R
dt
q
d
Ω
=
+
+
(24.15)
Jest to równanie różniczkowe drgań wymuszonych. Rozwiązaniem są drgania harmoniczne o czę-
stości wymuszenia
Ω . Drgania wymuszone mogą być przesunięte w fazie względem wymuszenia o
kąt
φ
będący fazą początkową drgania wymuszonego. Ta faza jest różnicą fazy wychylenia (24.16)
i fazy wymuszenia (24.13). Amplituda tych drgań jest ściśle określona i jest zależna od częstości
wymuszenia oraz od amplitudy wymuszenia. Zatem rozwiązaniem jest:
)
cos(
)
(
φ
+
Ω
=
t
A
t
q
(24.16)
gdzie:
2
2
2
2
2
0
4
)
(
Ω
+
Ω
−
=
β
ω
L
U
A
(24.17)
Ω
−
Ω
−
=
2
2
0
2
ω
β
φ
arctg
(24.18)
Aby przekonać się, że funkcja przedstawiona w (24.16) jest rozwiązaniem równania (24.15) należy
zróżniczkować tą funkcję obliczając pierwszą i drugą pochodną i wstawić do równania (24.15).
Rezonans.
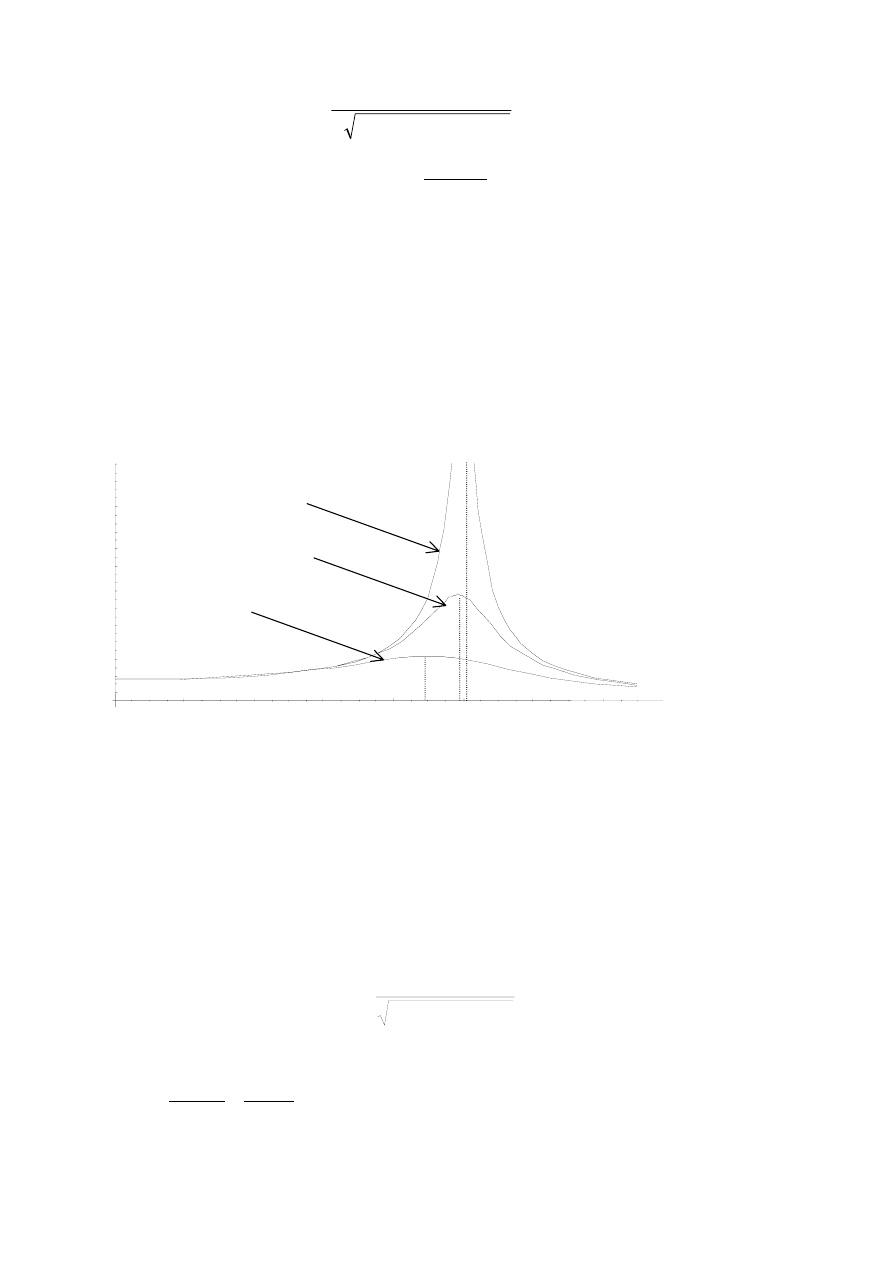
Jak wynika z analizy zależności (24.17) na amplitudę drgań wymuszonych, przy odpo-
wiednim dobraniu częstości wymuszenia nawet przy niewielkim wymuszeniu można uzyskać bar-
dzo dużą wartość. Takie zjawisko nazywamy rezonansem. Przeanalizujmy zależność amplitudy A
od częstości wymuszenia
Ω dla różnych wartości współczynnika tłumienia, przy czym
3
2
1
β
β
β
<
<
(rys. 24.2).
Rys. 24.2 Amplituda drgań wymuszonych w funkcji częstości
.
Wartość częstości wymuszenia przy której amplituda drgań osiąga maksimum (zaznaczono na wy-
kresie linią przerywaną) silnie zależy od współczynnika tłumienia
β. Im mniejsze jest β tym
ostrzejsza jest krzywa rezonansowa, a częstość rezonansu wzrasta.
Wykorzystując zależności (24.16)-(24.18) oraz (24.6), (24.7) (24.1) można napisać wyrażenia na
U
C
( oraz U
L
). W ćwiczeniu wykorzystuje się pomiar U
C
. Przyjmując, że układ rezonansowy ma
małe straty ( tzn. (
1
4
2
<<
β
) dla częstości bliskich rezonansu
2
2
2
4
0
)
2
( x
C
R
U
U
r
C
+
Ω
=
(24.19)
gdzie:
Ω
r
=2
πf
r
– częstość rezonansu ( dla danego
β),
r
r
r
r
f
f
f
x
−
=
Ω
Ω
−
Ω
=
jest względnym odchyleniem częstotliwości wymuszającej f od
częstotliwości rezonansowej f
r
.
20
40
60
80
100
120
140
1
2
3
4
5
A
β
1
β
2
β
3
Ω
Ω
r
Zauważmy, że dla
Ω = Ω
r
wartość x = 0, zatem:
Q
RC
U
U
U
U
r
L
C
=
Ω
=
=
2
0
0
1
(24.20)
Q jest jedną z najważniejszych wielkości charakteryzujących obwód rezonansowy, zwaną dobrocią
układu. Dla obwodu szeregowego mówi ona ilokrotnie w rezonansie wzrasta napięcie na elemen-
tach C oraz L. Zatem dla Q>>1 charakterystykę częstotliwościową w pobliżu rezonansu zapisujemy
w postaci:
2
2
0
)
2
(
1
1
x
Q
U
U
C
+
=
(24.21)
Zauważmy, że w rezonansie U
C
=QU
0
.
Wprowadza się również pojęcie pasma częstotliwości obwodu – B:
Q
Q
f
B
r
r
π
2
Ω
=
=
(24.22)
określone jako zakres częstotliwości, dla których zachodzi warunek:
Q
U
U
C
2
1
0
>
(24.23)
-0.4
-0.2
0.2
0.4
2
4
6
8
10
x
U
C
/U
0
Q
Q/
2
f
B
f
r
-B/2 f
r
+B/2
f
r
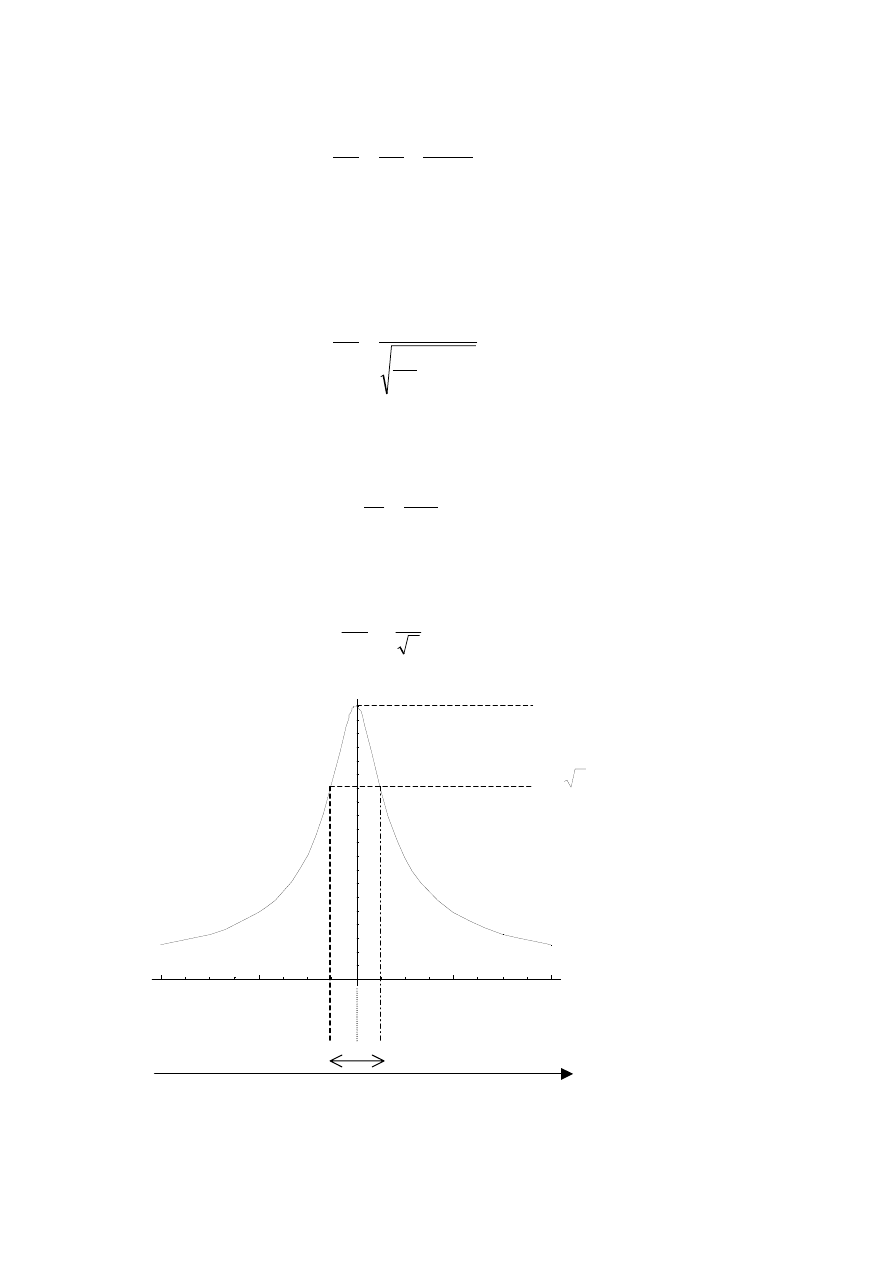
Rys. 24.3 Przykładowa krzywa rezonansowa.
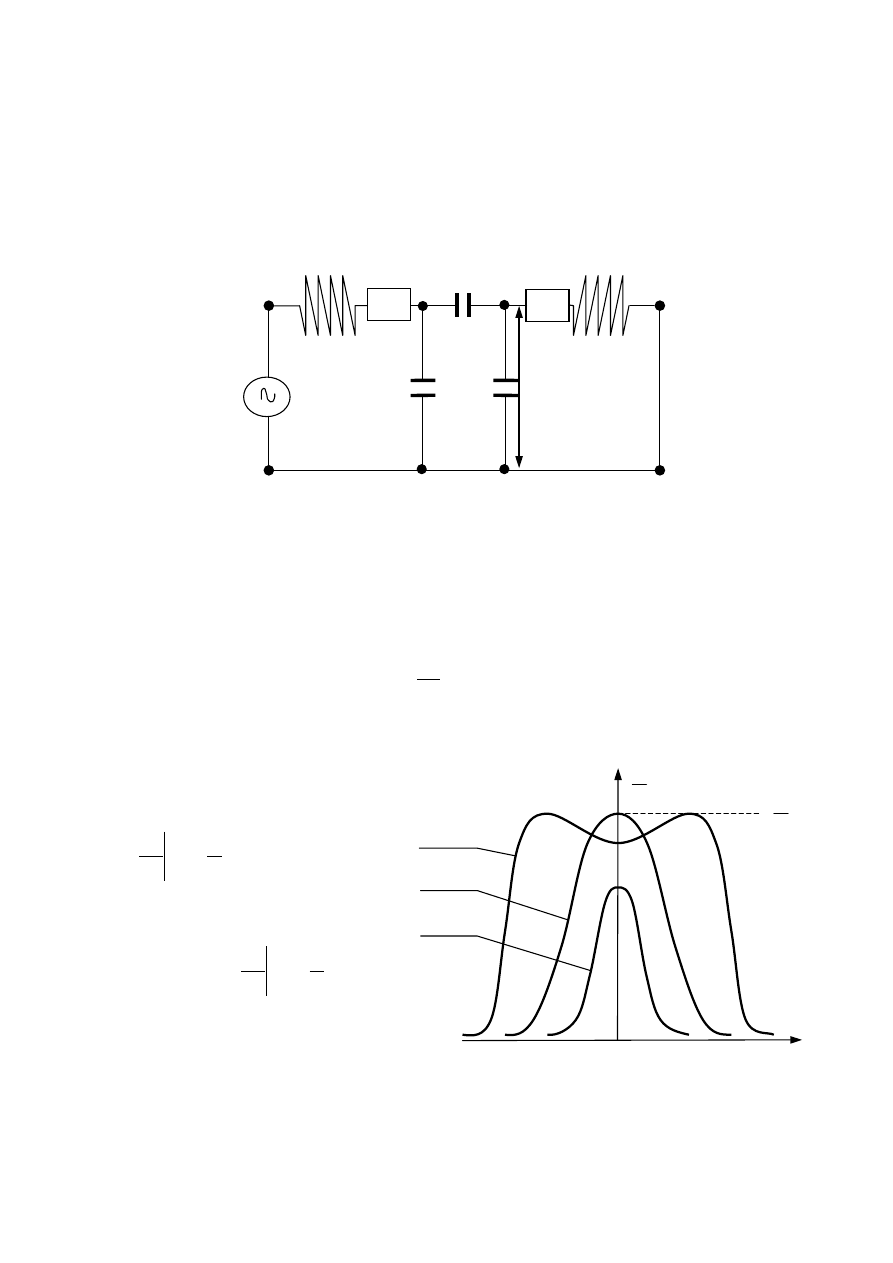
Jednym z podstawowych zastosowań obwodów rezonansowych jest ich wykorzystanie jako filtry.
Właściwości filtracyjne obwodu rezonansowego polegają na znacznym wzroście amplitudy napię-
cia wyjściowego dla częstotliwości napięcia podawanego na obwód leżących w paśmie częstotliwo-
ści B. Niestety, pojedynczy układ rezonansowy charakteryzuje się zbyt wolnym spadkiem napięcia
wyjściowego na krawędziach pasma B, co widać na Rys. 24.3. Znacznie lepsze charakterystyki w
tym względzie mają sprzężone obwody rezonansowe, w których drgania istniejące w jednym ob-
wodzie wpływają na zachowanie się drugiego obwodu. W zależności od rodzaju elementu sprzęga-
jącego wyróżniamy różne typy sprzężenia.
C
U
0
L
U
2
C
S
L
C
R
R
Rys. 24.4. Dwa układy rezonansowe sprzężone pojemnościowo.
W ćwiczeniu badamy układ dwóch obwodów rezonansowych sprzężonych pojemnościowo. Układ
ten przedstawiony jest na rysunku 24.4. Są to dwa układy rezonansowe, o tych samych elementach
skupionych R, L, C, sprzężone kondensatorem C
S
. W zależności od wielkości tzw. parametru
sprzężenia
χ zdefiniowanego:
C
C
s
=
χ
(24.24)
wyróżniamy następujące przypadki:
1) jeżeli
χ < 1/Q na wykresie krzywej
rezonansowej występuje jeden
punkt ekstremalny dla x = 0 – jest to
tzw. sprzężenie podkrytyczne
<
=
2
0
0
2
Q
U
U
x
0
χ < χ
k
χ = χ
k
χ > χ
k
Q
2
U
2
U
0
x
2) dla
χ = χ
k
= 1/Q – sprzężenie kry-
tyczne, mamy również jeden punkt
ekstremalny i
=
=
2
0
0
2
Q
U
U
x
3) dla
χ > 1/Q mamy trzy punkty eks-
tremalne – ten stan nazywamy
sprzężeniem nadkrytycznym.
Rys. 24.5. Krzywe rezonansowe dla
różnych wartości sprzężeń.
Wykres krzywych rezonansowych U
2
/U
0
dla trzech różnych sprzężeń przedstawia rys. 24.5.
24.2 Opis układu pomiarowego
Układ pomiarowy składa się z generatora napięcia sinusoidalnego o przestrajanej częstotliwości,
woltomierza z sondą oraz pudełka z obwodami rezonansowymi i trzema kondensatorami wymien-
nymi C
S
. Schemat układu wraz z danymi odnośnie układu znajduje się na stole pomiarowym.
24.3. Przebieg pomiarów
1. Podłączyć generator do pudełka z obwodami rezonansowymi za pomocą kabla koncentrycznego.
Zakres woltomierza ustawić na 10V. Sondę podłączyć do woltomierza, przy czym „masę” pod-
łączamy do zacisku pudełka z obwodami rezonansowymi.
2. Na podstawie danych parametrów obwodu obliczyć przybliżoną wartość f
r
. Ustawić tę częstotli-
wość na generatorze. Sondę woltomierza podłączyć do zacisku U
C
. Zmieniając stopniowo czę-
stotliwość na generatorze dobrać częstotliwość z dokładnością 10 Hz przy której U
C
osiąga mak-
symalną wartość. Tą częstotliwość przyjąć jako f
r
.
3. Wykonać pomiary U
C
dla częstotliwości na generatorze w zakresie od (f
r
-1) do (f
r
+1) kHz co
100 Hz.
4. Włączyć jeden z kondensatorów sprzęgających C
S
do gniazd pudełka. Sondę woltomierza połą-
czyć z zaciskiem U
2
.
5. Wykonać pomiary U
2
w zakresie częstotliwości na generatorze takich jak w punkcie 3.
6. Przeprowadzić pomiary U
2
dla pozostałych dwóch wartości pojemności C
S
.
24.4. Opracowanie wyników pomiarów.
1. Wykreślić zmierzoną zależność U
C
(f).
2. Wyznaczyć szerokość pasma B z szerokości krzywej rezonansowej na wysokości
2
max
C
U
(patrz Rys. 24.3).
3. Wyznaczyć dobroć układu Q i napięcie U
0
na podstawie wyrażenia 24.22 i 24.20.
4. Wykreślić wykres U
C
(x)/U
0
, gdzie x jest względnym odchyleniem od częstotliwości rezonanso-
wej. Porównać z krzywą otrzymaną z wyrażenia 24.21.
5. Wykreślić zależność U
2
(f) dla trzech wartości pojemności C
S
. Obliczyć parametr
χ i porównać
go z wartością 1/Q.
6. Przedstawić wnioski podsumowujące uzyskane wyniki.
L i t e r a t u r a
[1] Bartnicki S, Borys.W, Kostrzyński T; Fizyka ogólna – ćwiczenia laboratoryjne Cz II. Skrypt
WAT. Warszawa 1994r.
[2] Massalski J.M.: Fizyka dla inżynierów, cz.1, WNT, Warszawa 1973.