
1
Wykład 13
Obieg zamknięty z wodą i parą wodną jako
dwufazowym czynnikiem termodynamicznym
System dwufazowy woda – para wodna
Praca i ciepło w układach dwufazowych
Przykład; parowanie wody w 100°C
Cykl Carnota z wodą i parą wodną jako
dwufazową substancją roboczą
Przykład; cykl Carnota w układzie woda –
para wodna
2
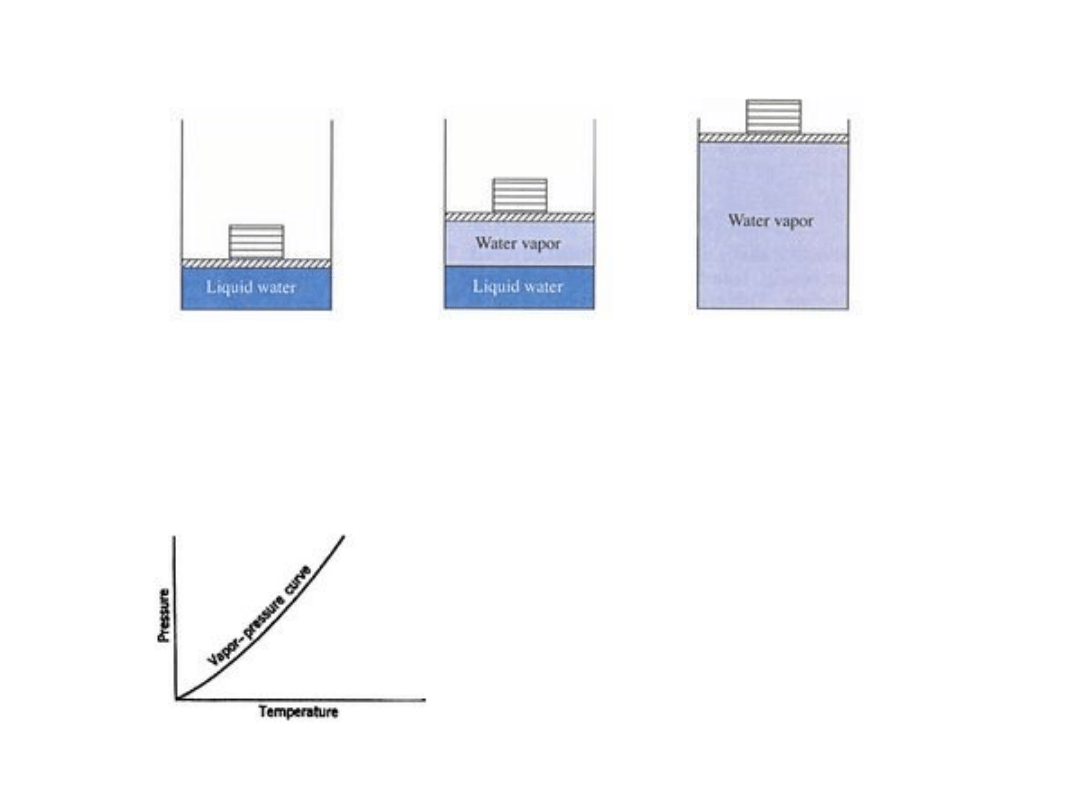
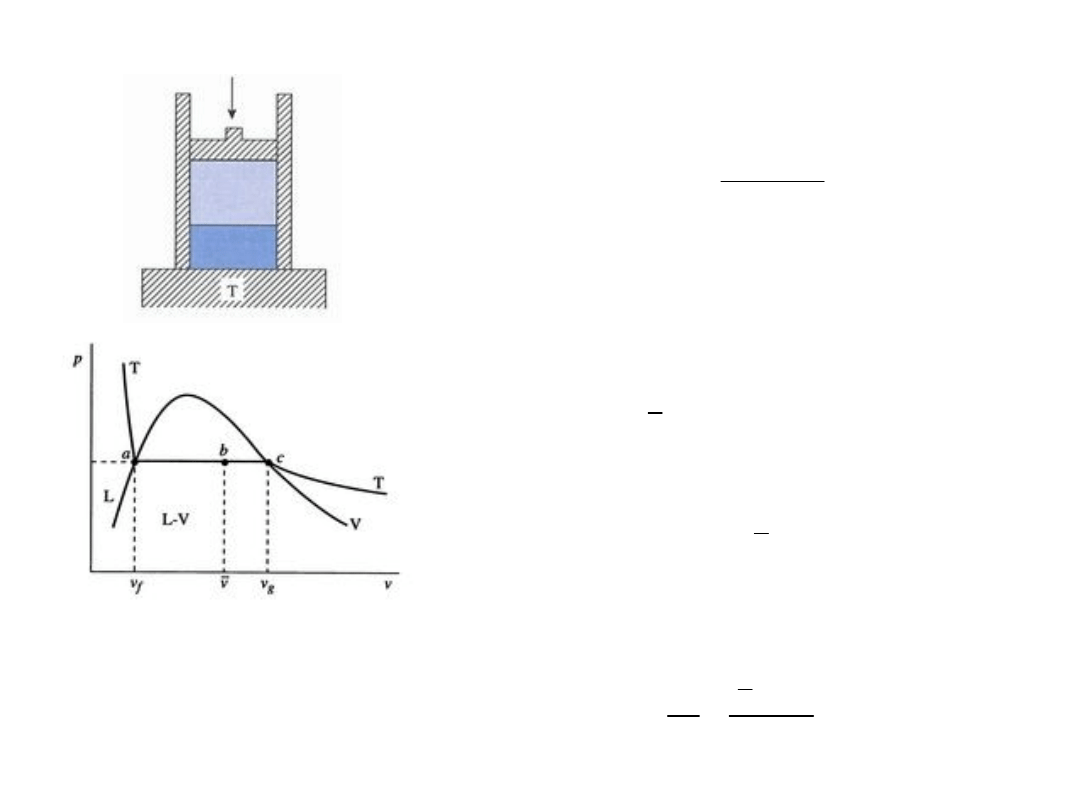
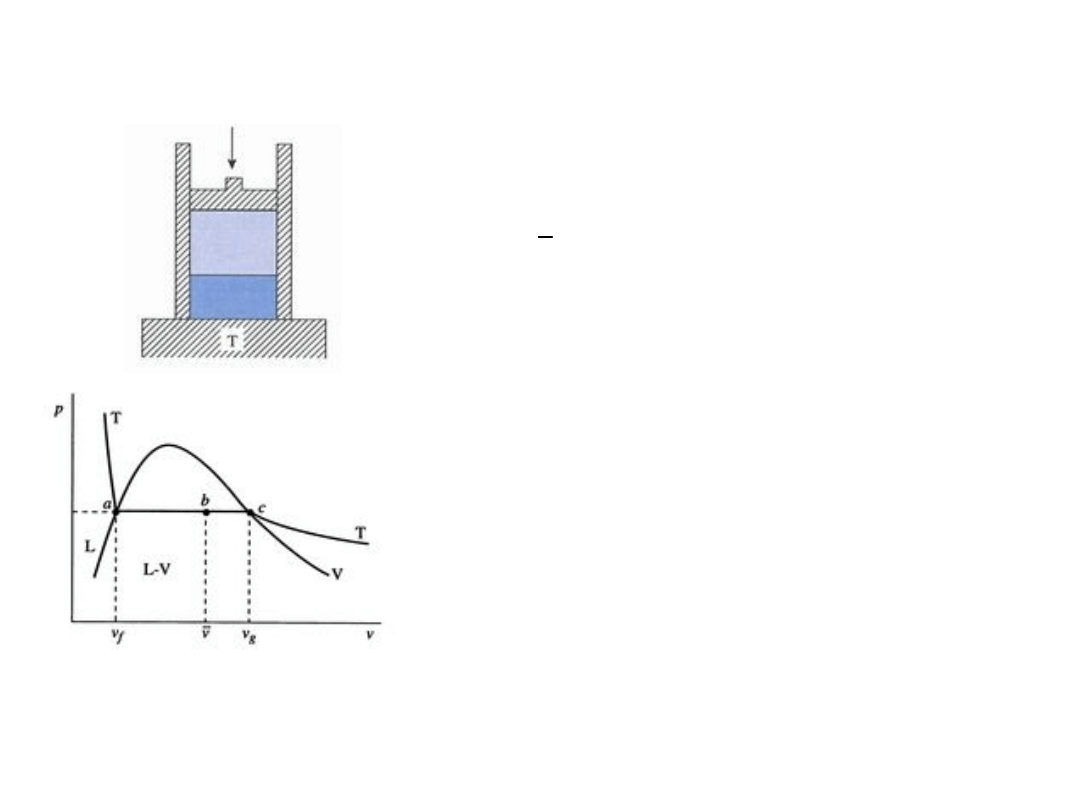
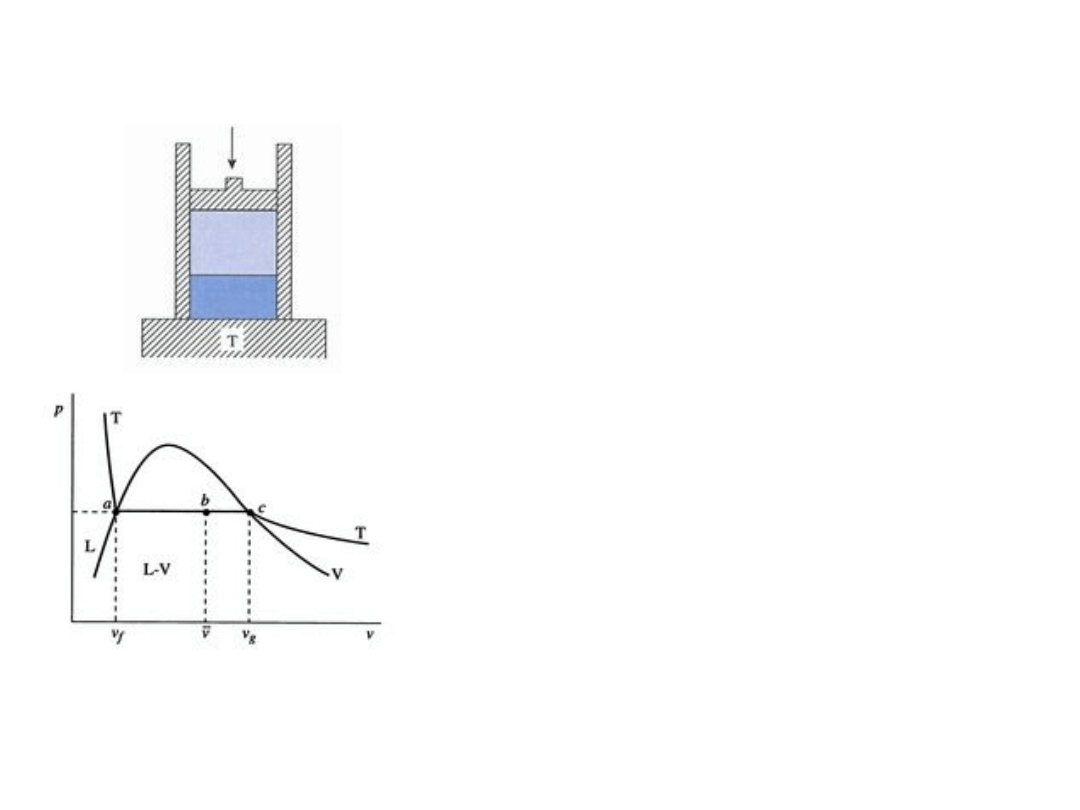
Zachowanie systemu dwufazowego woda – para
wodna
Układ woda – para wodna w kontakcie ze zbiornikiem ciepła o
stałej temperaturze T dopasowanej do ciśnienia p (obciążenie
tłoka). Zmiana ciśnienia wymaga dopasowania (zmiany)
temperatury, jak pokazano na rys. poniżej
©E. M. Greitzer, Z. S. Spakovszky, I. A. Waitz
http://web.mit.edu/16.unified/www/SPRING/propulsion/notes/notes.html
Zależność p – T dla układu woda –
para wodna
Dodatkowe ograniczenie dla
parametrów układu; przemiana ze
stałym ciśnieniem jest także
przemianą ze stałą temperaturą, czyli
przemiana izobaryczna jest także
przemianą izotermiczną
©E. M. Greitzer, Z. S. Spakovszky, I. A. Waitz
http://web.mit.edu/16.unified/www/SPRING/propulsion/notes/notes.html
3
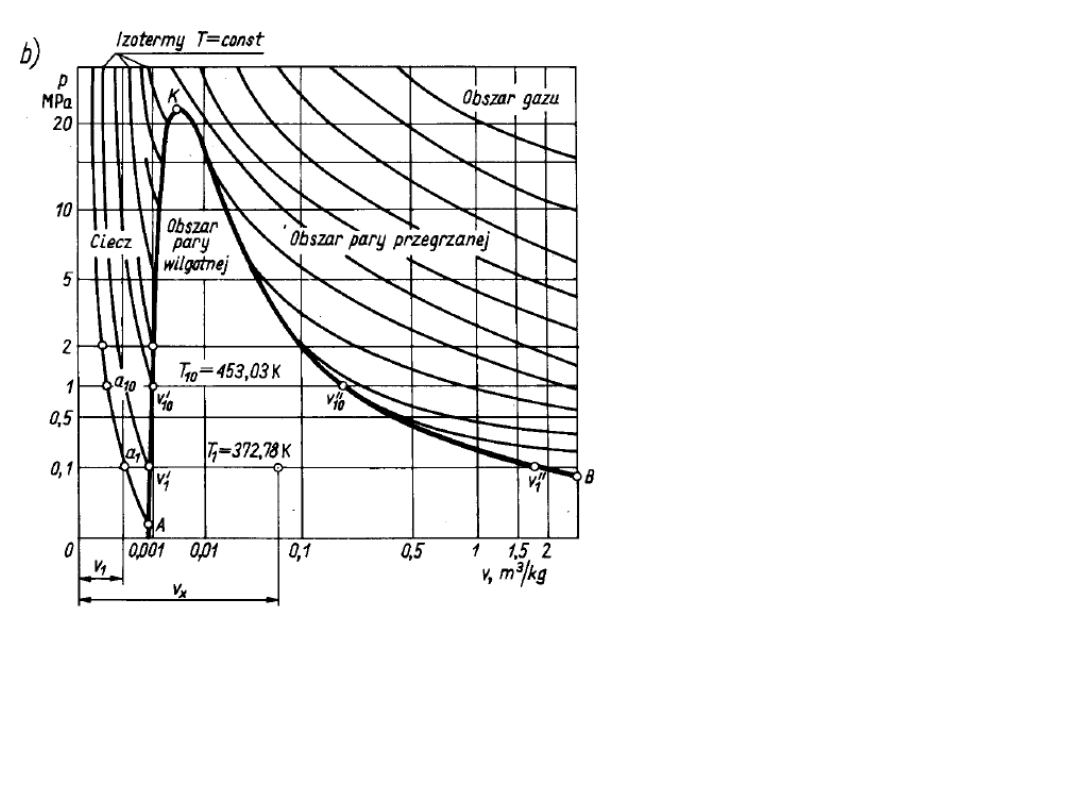
Diagram p – V dla układu
woda – para wodna
0,1 MPa
a
1
: woda chłodna 0,001
m
3
,
273,15 K
woda wrząca, para
wilgotna, para nasycona
sucha
v
1
’: woda wrząca
0,0010434 m
3
, 372,78 K,
para nasycona sucha
v
1
”: 1,946 m
3
1 MPa
a
10
: woda chłodna, 273 K
v
10
’: woda wrząca
0,0011274 m
3
, 453,03 K
v
10
’’: para nasycona
sucha
0,1943 m
3
gdyż:
Dla rosnących ciśnień, objętość właściwa cieczy chłodnej prawie
się nie zmienia, cieczy wrzącej powoli rośnie, pary nasyconej
suchej zmierza do objętości właściwej dla cieczy wrzącej; punkt
krytyczny p
k
= 22,115 MPa, T
k
= 647,27 K, v
k
= 3,147·10
-3
m
3
© Copyright by Wydawnictwa Szkolne
i Pedagogiczne S.A., Warszawa 1987
4
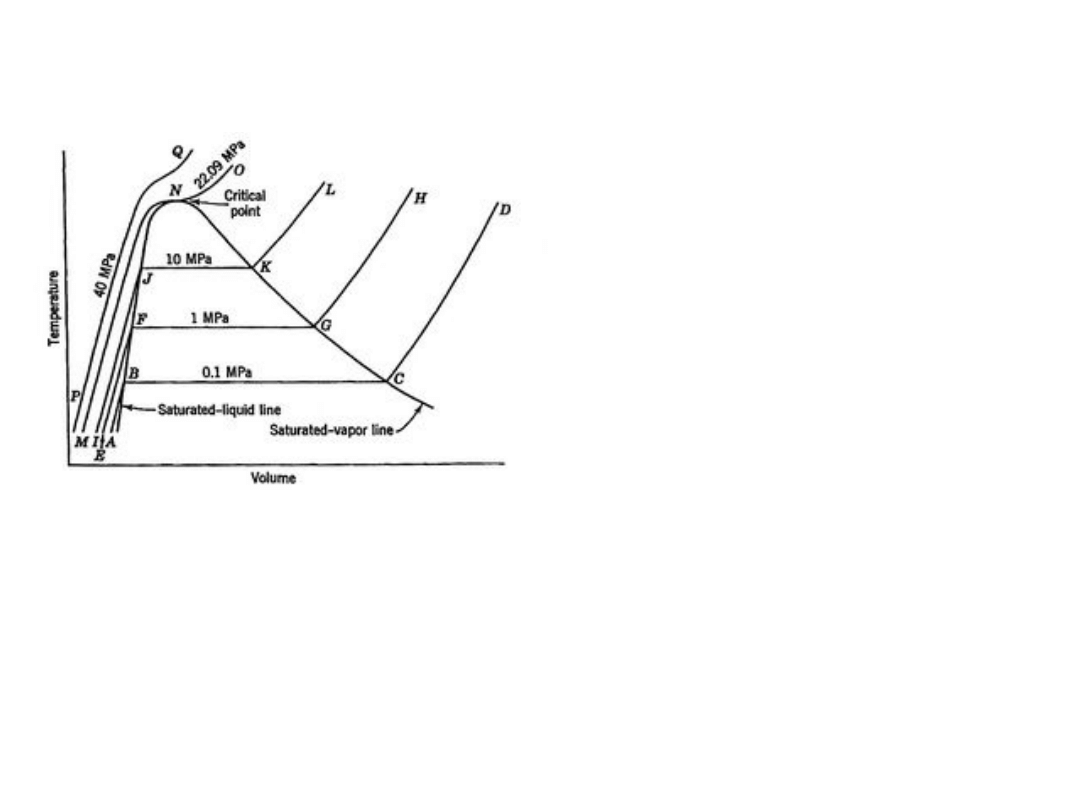
Diagram T – V dla układu woda
– para wodna w równowadze
termodynamicznej
W obszarze ciecz – para
izotermy są równocześnie
izobarami
Dla gazu doskonałego przy
stałym ciśnieniu:
T ~ V .
Proste o wspólnym początku w
(0,0)
Ciągłe przejście ciecz – gaz
powyżej temperatury krytycznej
©E. M. Greitzer, Z. S. Spakovszky, I.
A. Waitz
http://web.mit.edu/16.unified/www/SP
RING/ propulsion/notes/notes.html
5
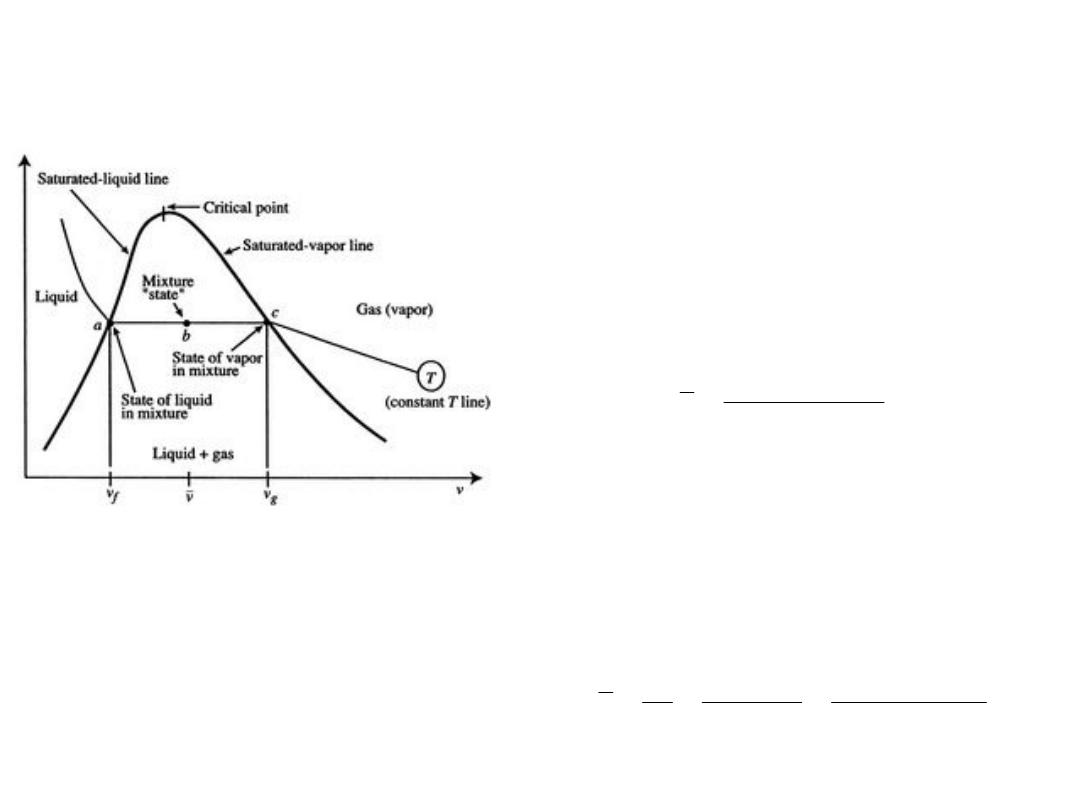
Diagram p – V dla układu woda –
para wodna (tzw. para wilgotna)
w równowadze termodynamicznej
v
f
≡ objętość właściwa fazy
ciekłej
na krzywej granicznej, w a
v
g
≡ objętość właściwa fazy lotnej
gazowej,
na krzywej granicznej, w c
W punkcie b, średnia objętość
właściwa:
©E. M. Greitzer, Z. S. Spakovszky, I.
A. Waitz
http://web.mit.edu/16.unified/www/SP
RING/ propulsion/notes/notes.html
g
f
g
g
f
f
m
m
v
m
v
m
v
gdyż:
g
g
g
f
f
f
v
m
V
v
m
V
a średnia objętość właściwa, przy
obecności obu faz:
g
f
g
g
v
f
g
f
g
f
m
m
v
m
v
m
m
m
V
V
M
V
v
Krzywa graniczna, punkt
krytyczny
Obszar cieczy, pary nasyconej
wilgotnej i pary przegrzanej
Krzywa parowania, krzywa
nasycenia (lewa i prawa)
Izotermy, izobary, izoterma
krytyczna
Stopień suchości pary, para
sucha nasycona i para wilgotna
6
Stopień suchości pary wilgotnej
(jakość układu para-ciecz) X:
©E. M. Greitzer, Z. S. Spakovszky, I.
A. Waitz
http://web.mit.edu/16.unified/www/SP
RING/ propulsion/notes/notes.html
.
m
m
m
X
g
f
g
Średnia objętość właściwa w
punkcie b może być wyrażona
przez X i objętości właściwe pary
i cieczy dla danej temperatury
(ciśnienia):
f
g
v
X
1
v
X
v
a z rysunku obok mamy:
f
g
f
v
v
ac
v
v
ab
oraz:
.
X
v
v
v
v
ac
ab
f
g
f
7
©E. M. Greitzer, Z. S. Spakovszky, I.
A. Waitz
http://web.mit.edu/16.unified/www/SP
RING/ propulsion/notes/notes.html
f
f
g
g
dm
v
dm
v
dV
const
m
m
m
f
g
Praca i ciepło w układach dwufazowych
Układ para – ciecz
Temperatura T, możliwość zmiany V.
Dla stałej masy m, ze zmianą V punkt b
będzie się przesuwał w prawo lub w
lewo, co odpowiada zmianie oraz
zmianie mas w obu fazach (przybywa
pary ubywa cieczy, lub na odwrót).
Mamy zatem:
v
a ponieważ masa m układu jest stała:
f
g
dm
dm
0
dm
mamy:
i możemy zdefiniować masę
przetworzoną z cieczy na parę:
f
g
fg
dm
dm
dm
8
©E. M. Greitzer, Z. S. Spakovszky, I.
A. Waitz
http://web.mit.edu/16.unified/www/SP
RING/ propulsion/notes/notes.html
fg
f
g
fg
f
fg
g
dm
v
v
dm
v
dm
v
dV
Zmiana objętości układu wyniesie
zatem:
.
u
X
1
Xu
u
f
g
przy czym:
.
dm
v
v
p
dV
p
fg
f
g
a wykonana praca (objętościowa):
fg
f
g
f
f
g
g
f
f
g
g
dm
u
u
dm
u
dm
u
dU
m
u
m
u
U
Energię wewnętrzną można wyrazić tak:
Jeśli wykorzystamy I zasadę
termodynamiki:
fg
f
g
fg
f
f
g
g
fg
f
g
fg
f
g
dm
h
h
dm
pv
u
pv
u
dm
v
v
p
dm
u
u
W
dU
Q
9
fg
f
g
fg
fg
f
g
h
h
h
m
Q
q
H
m
h
h
Q
Dla skończonej masy m
fg
przetransferowanej z cieczy do gazu,
otrzymamy:
gdzie h
fg
to entalpia właściwa dla zmiany stanu skupienia (ciepło
parowania).
Otrzymany wynik odpowiada przemianie bez zmiany ciśnienia, gdy
praca techniczna Vdp jest równa zero (p = const).
1
1
2
2
12
12
t
V
p
V
p
L
L
V
1
p
p
2
V
p
1
V
2
Praca techniczna i
objętościowa:
L
t12
L
12
Vdp
L
pdV
L
L
L
p
V
V
p
pV
t
t
1
1
2
2
12
t
12
V
p
V
p
L
L
pV
L
L
t

10
Przykład; parowanie wody w 100°C
1. Ile ciepła potrzeba dla odparowania jednostki masy
wody?
2. Jaka praca będzie wykonana?
3. Jaka będzie zmiana energii wewnętrznej?
W temperaturze 100°C ciśnienie pary wodnej wynosi
0,1013 MPa
Entalpia właściwa pary wodnej h
g
wynosi 2676 kJ/kg, a
wody 419 kJ/kg
Różnica entalpii właściwych pary wodnej i wody (ciepło
parowania) wynosi 2257 kJ/kg
Objętość właściwa pary wodnej w temperaturze 100°C
wynosi 1,6729 m
3
/kg, a wody 0,001044 m
3
/kg
Ciepło dostarczone do układu jest równe h
fg
= 2257 kJ/kg
Wykonana praca wynosi p(v
g
– v
f
) = 0,1013·10
6
Pa ·(1,6729 –
0,001044) m
3
/kg = 0,1013·1,6719 = 0,1694·10
6
J/kg
Zatem zmiana energii wewnętrznej wynosi 2257 -169,4 =
2088 kJ/kg.
Większość ciepła idzie na zmianę energii wewnętrznej a nie
na wykonanie pracy.
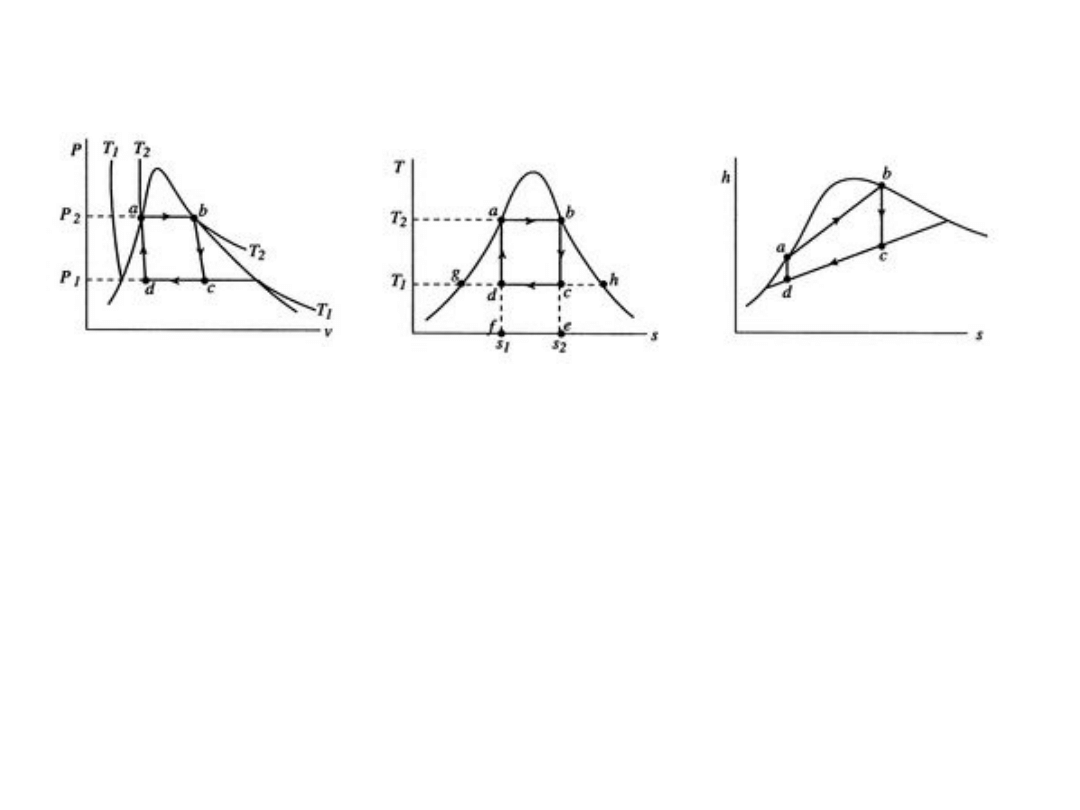
11
Cykl Carnota z wodą i parą wodną jako
dwufazową substancją roboczą
©E. M. Greitzer, Z. S. Spakovszky, I. A. Waitz
http://web.mit.edu/16.unified/www/SPRING/propulsion/notes/notes.html
diagram p – V diagram T – s
diagram h – s
1. Początek w a (ciecz nasycona), a – b izotermiczne rozprężanie
do pary suchej, ciepło właściwe pobrane q
H
ze źródła o
temperaturze wyższej T
2
, kocioł parowy
2. Odwracalne rozprężanie adiabatyczne b – c, turbina.
Temperatura spada do T
1
. Para wilgotna, X < 1.
3. Sprężanie izotermiczne c – d w temperaturze T
1
(niższej).
Układ oddaje ciepło właściwe q
L
do źródła T
1
, chłodnica –
skraplacz
4. Odwracalne sprężanie adiabatyczne, w którym para skrapla
się i układ powraca do a, sprężarka.
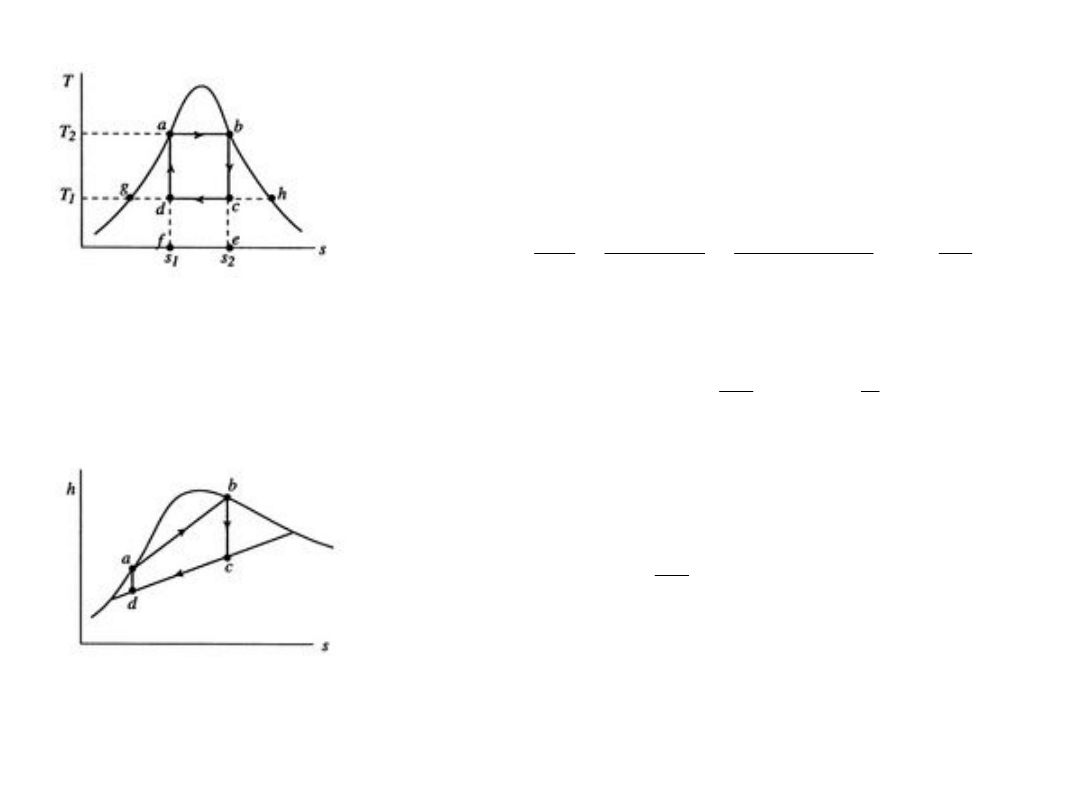
12
Przemiany izotermiczne; linie
horyzontalne
Przemiany adiabatyczne; linie
pionowe (ΔS = 0)
Powierzchnia pod krzywą; ciepło
pobrane lub oddane.
Sprawność wyniesie:
©E. M. Greitzer, Z. S. Spakovszky, I.
A. Waitz
http://web.mit.edu/16.unified/www/SP
RING/ propulsion/notes/notes.html
2
1
2
1
2
H
L
H
H
T
T
1
s
T
s
T
s
T
q
q
q
q
w
Z I i II zasady:
1
v
;
dp
dh
Tds
Dla odwracalnej przemiany
izobarycznej (para + ciecz):
T
ds
dh
dh
Tds
dq
Linie proste o stałym nachyleniu
równym T.
c
d
L
a
b
H
h
h
q
;
h
h
q
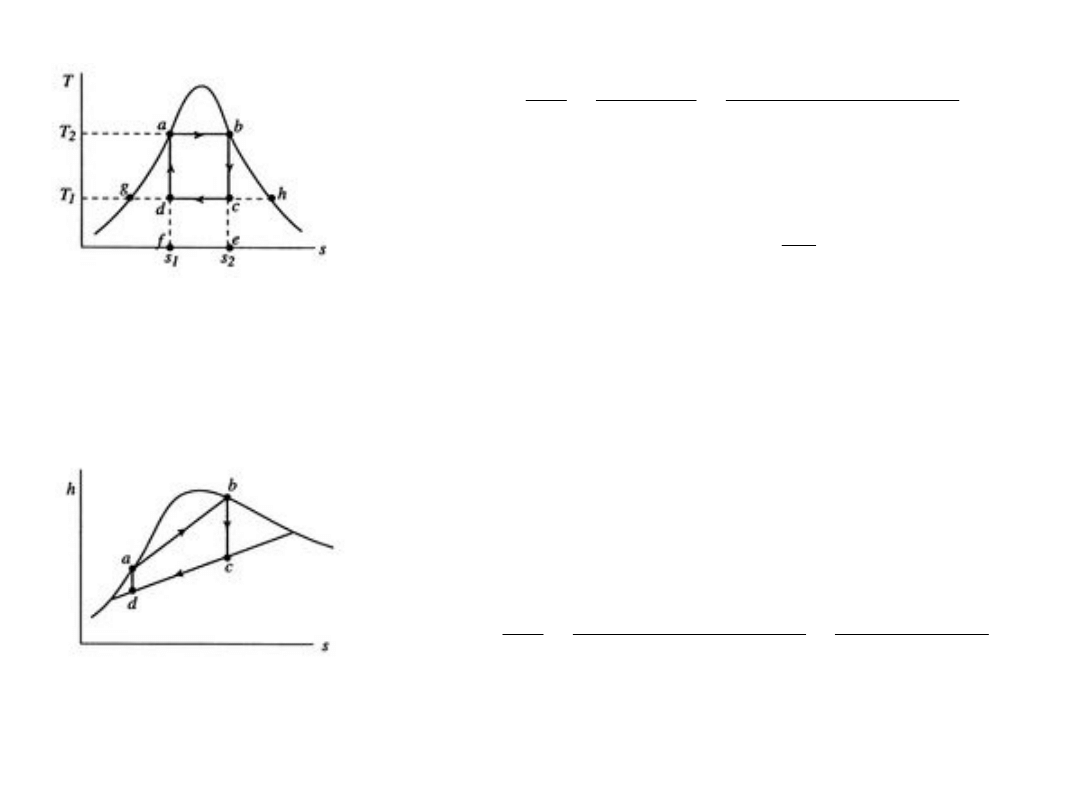
13
©E. M. Greitzer, Z. S. Spakovszky, I.
A. Waitz
http://web.mit.edu/16.unified/www/SP
RING/ propulsion/notes/notes.html
a
b
c
d
a
b
H
L
H
H
h
h
h
h
h
h
q
q
q
q
w
Z I i II zasady oraz definicji entalpii:
t
dL
dh
dq
dp
dh
Tds
Dla odwracalnej przemiany
adiabatycznej q = 0:
t
L
h
H
spr
turb
a
b
d
a
c
b
H
q
w
w
h
h
h
h
h
h
q
w
Zmieniając kolejność wyrazów
zapiszemy sprawność w następujący
sposób:

14
Przykład; cykl Carnota w układzie woda – para
wodna
Źródło ciepła – 300°C
Chłodnica – 20°C
Jaka jest i) sprawność i ii) stosunek pracy turbiny do
sprężarki przy założeniu, że wszystkie procesy są
odwracalne?
i) Dla cyklu odwracalnego sprawność:
489
,
0
573
293
1
ii) Dla cyklu odwracalnego praca turbiny i sprężarki.
Trzeba znaleźć zmiany entalpii właściwych pomiędzy
stanami b i c (dla turbiny) i a i d (dla sprężarki.
Znamy h, s i T dla stanów a i b. Ponieważ dla przemiany
adiabatycznej s się nie zmienia, znamy s i T dla stanów d
i c. Znamy dla stanów g i f dla temperatury T1 h i s,
możemy więc wyliczyć najpierw X, potem h dla stanów d i
c.

15
h
b
= h
g
(300°C) = 2749 kJ/kg
s
b
= s
g
(300) = 5,7045 kJ/kg·K
s
b
= s
c
Liczymy X (stopień suchości) dla stanu c:
f
c
g
c
c
s
X
1
s
X
s
c
f
c
g
c
f
c
c
T
s
T
s
T
s
s
X
Wiemy, że
s
c
= s
b
= 5,7045 kJ/kg·K
s
fh
= 8,3706 kJ/kg·K
s
f
= 0,2966 kJ/kg·K
Liczymy X (stopień suchości) dla stanu c:
646
,
0
3706
,
8
2966
,
0
7045
,
5
X
c
Entalpia w stanie c wyraża się wzorem:
f
c
g
c
c
h
X
1
h
X
h
Podstawiając wartości:
kg
kJ
4
,
1669
kg
kJ
96
,
83
354
,
0
kg
kJ
1
,
2538
646
,
0
h
c
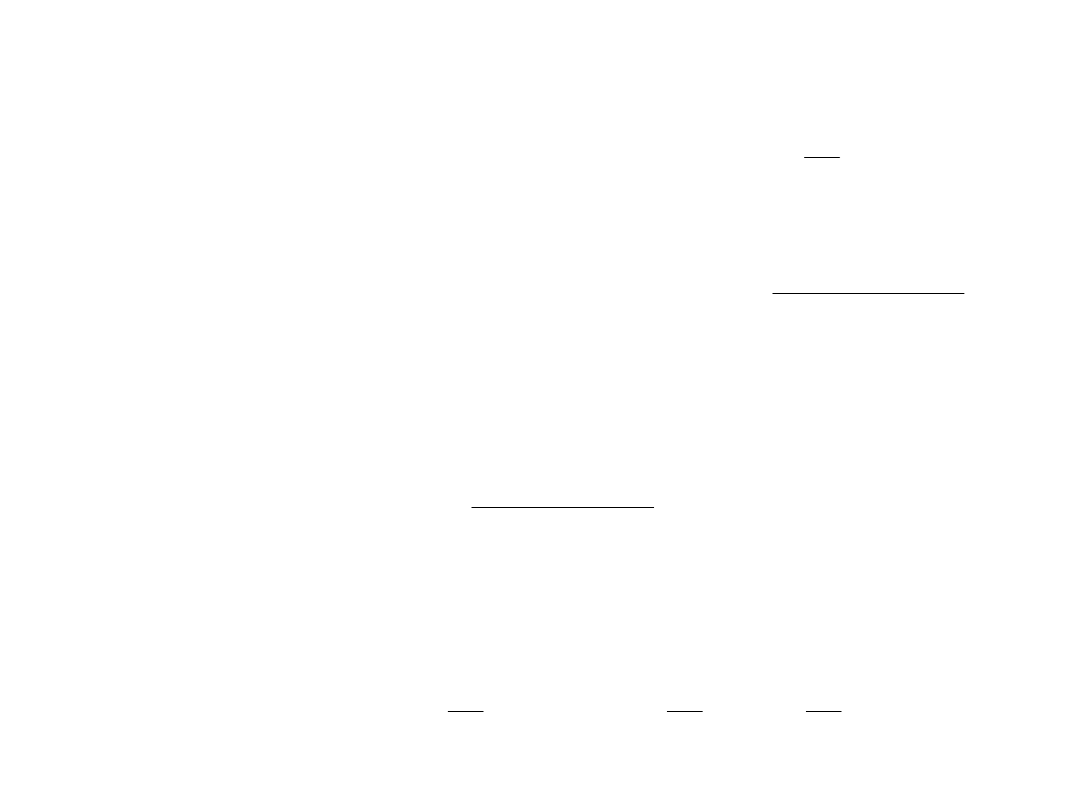
16
Praca właściwa turbiny to różnica entalpii:
kg
kJ
6
,
1079
4
,
1669
2749
h
h
w
c
b
turb
d
f
d
g
d
f
d
d
T
s
T
s
T
s
s
X
Podobnie liczymy stopień suchości dla stanu d:
353
,
0
3706
,
8
2966
,
0
253
,
3
X
d
Wykorzystując odpowiednie równości oraz s
d
= s
a
=
s
f
(300) znajdujemy:
f
d
g
d
d
h
X
1
h
X
h
Entalpia dla stanu d wyniesie:
kg
kJ
8
,
950
kg
kJ
96
,
83
647
,
0
kg
kJ
1
,
2538
353
,
0
h
d

17
Praca właściwa sprężarki to różnica entalpii:
kg
kJ
3
,
393
8
,
950
1344
h
h
w
d
a
spr
74
,
2
3
,
393
6
,
1079
w
w
spr
turb
Stosunek pracy turbiny do pracy sprężarki:
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
Wyszukiwarka
Podobne podstrony:
prezentacja dysf[1] para
Krzywa opytu w modelu chamberlena
3 1 Krzywa podazy AS ppt
Krzywa doświadczeń
12a Równowaga ciecz para w układach dwuskładnikowych (a)id 14224 ppt
KRZYWA MOZLIWOŚCI PRODUKCYJNYCH
całująca się para
Ćwiczenie K Konduktywno¶ ć
krzywa Phillipsa
parowanie, Ochrona Środowiska, meteorologia
KRZYWA PHILLIPSA, ● STUDIA EKONOMICZNO-MENEDŻERSKIE (SGH i UW), ekonomia matematyczna
Micha- G-owi˝ski o intertekstualno¶ci, STUDIA, poetyka i teoria literatury
VI PARA – UCZEŃ XVIII, 7.AKADEMIA, 7.AKADEMIA, AKADEMIA.KATYŃ, AKADEMIA2
ćw aktywacja grupa para wodna 2
AlemĂŁo urgente! Para brasileiros 10
Ciepło parowania
krzywa wydatku
1analiza dokladno¶
Alemão urgente! Para brasileiros 15 Complementação
więcej podobnych podstron