Triangularyzacja

dowolnego wielokąta

}.

,

,

{

},

,

,

,

{

},

,

,

,

{

},

,

,

;

,

,

,

;

,

,

,

{

13

12

11

3

10

9

8

7

2

6

2

1

1

13

12

11

10

9

8

7

6

2

1

P

P

P

S

P

P

P

P

S

P

P

P

S

P

P

P

P

P

P

P

P

P

P

W













Dane o wielokącie:
LS – liczba składowych,
LPS1 – liczba punktów pierwszej składowej (głównej),
LPS2 - liczba punktów drugiej składowej,
…,
LP_LS – liczba punktów ostatniej składowej.

Wprowadźmy następujące oznaczenia:

- zbiór węzłów wewnętrznych,
 - zbiór węzłów brzegowych,

Triangularyzacja

dowolnego wielokąta c.d.

T

N

i

i

T

T

1

}

{





- zbiór trójkątów,

T

N

- liczba trójkątów,

•Def. Zbiór trójkątów T nazywamy triangularyzacją obszaru , jeśli:

,

)

(

_

_

1

i

N

i

T

i

T





 

,

,

,

1

,

)

(













j

i

T

T

T

j

i

N

j

i

ii





(iii) Wszystkie wierzchołki są ze zbioru ,

.

.

,

1

)

(

k

T

T

wierzch

jest

Q

że

taki

N

k

k

Q

iv

















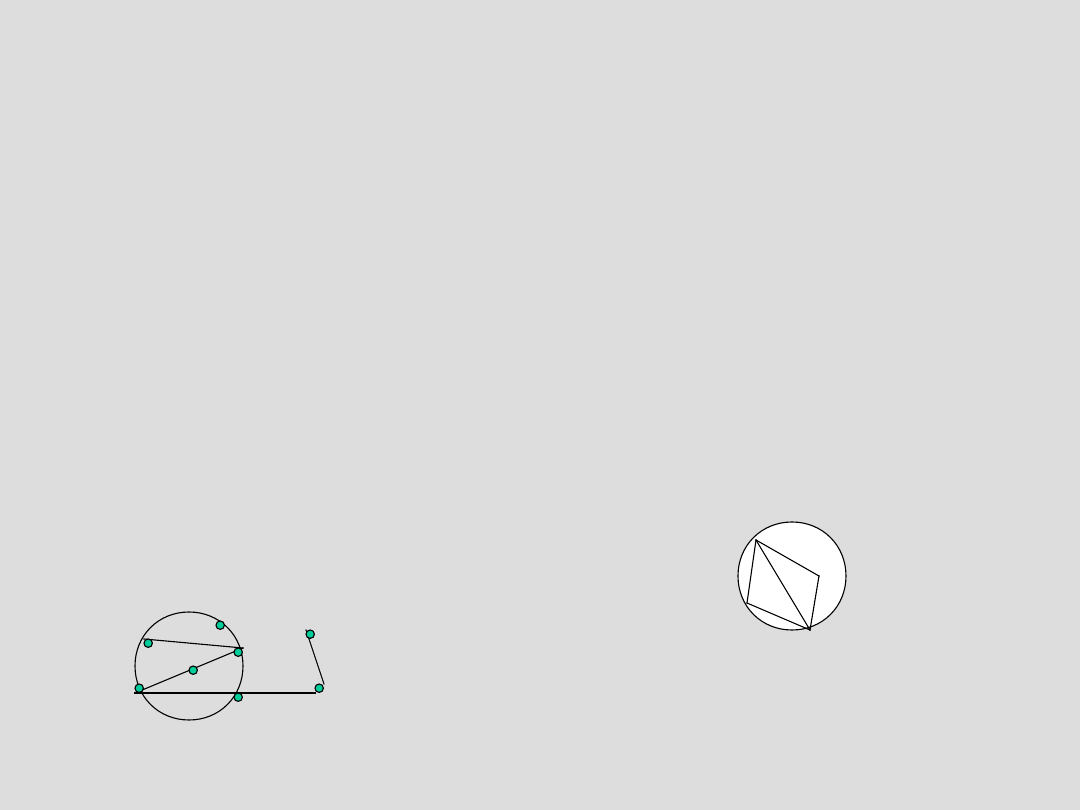
Triangularyzacja

dowolnego wielokąta c.d.

Uwaga: Triangulacją wielokąta wypukłego  jest triangularyzacja

układu punktów .

Def. Triangularyzację dowolnego obszaru płaskiego  nazywamy

triangularyzacją Delaunay’a, jeśli koło opisane na każdym trójkącie
tej triangularyacji nie zawiera innego punktu z , który mógłby

tworzyć z jakąkolwiek parą wierzchołków tego trójkąta trójkąt
zawarty w .

Triangularyzacja

dowolnego wielokąta c.d.

ALGORYTM

D – parametr gęstości siatki

1. Generowanie punktów brzegowych z gęstością D,
2. Generowanie punktów wewnętrznych z gęstością D,
3. Wygładzanie otrzymanej siatki.

Generowanie punktów brzegowych

A B L=|AB|

Generowanie punktów na

brzegu

.

,

,

1

,

0

,

,

1

,

,

1

'

'

m

i

AB

m

i

A

X

D

D

L

L

D

D

m

L

D

D

L

m

i



































Generowanie punktów

wewnętrznych

.

;

,

,

1

,

0

),

(

,

.

2

.

,

,

,

.

1

min

max

min

max

min

1

max

1

min

1

max

1

min















































D

y

y

m

m

i

y

y

m

i

y

h

h

y

poziomych

linii

nie

Poprowadze

i

y

i

x

i

y

i

y

e

Wyznaczani

i

i

N

i

N

i

N

i

N

i

y

x

y

y

P

P

P

P



Generowanie punktów

wewnętrznych c.d.

3. Dla i=0,1,…,m znalezienie przecięć prostej
z każdym segmentem brzegu

i

y

y 

).

,

)

)(

(

(

),

(

0

)

)(

(

lub

0

)

)(

(

),

,

(

),

,

(

)

y

y

y

x

x

y

y

x

Q

y

y

y

y

y

y

y

y

y

y

y

y

y

x

B

y

x

A

a

A

B

A

B

A

A

b

A

B

A

B

A

B

B

A

A



































b) Uporządkowanie otrzymanego zbioru punktów rosnąco
względem pierwszej zmiennej

},

,

,

1

),

,

(

{

l

j

y

x

Q

Q

Q

j

Q

j

i









(l musi być liczbą parzystą)

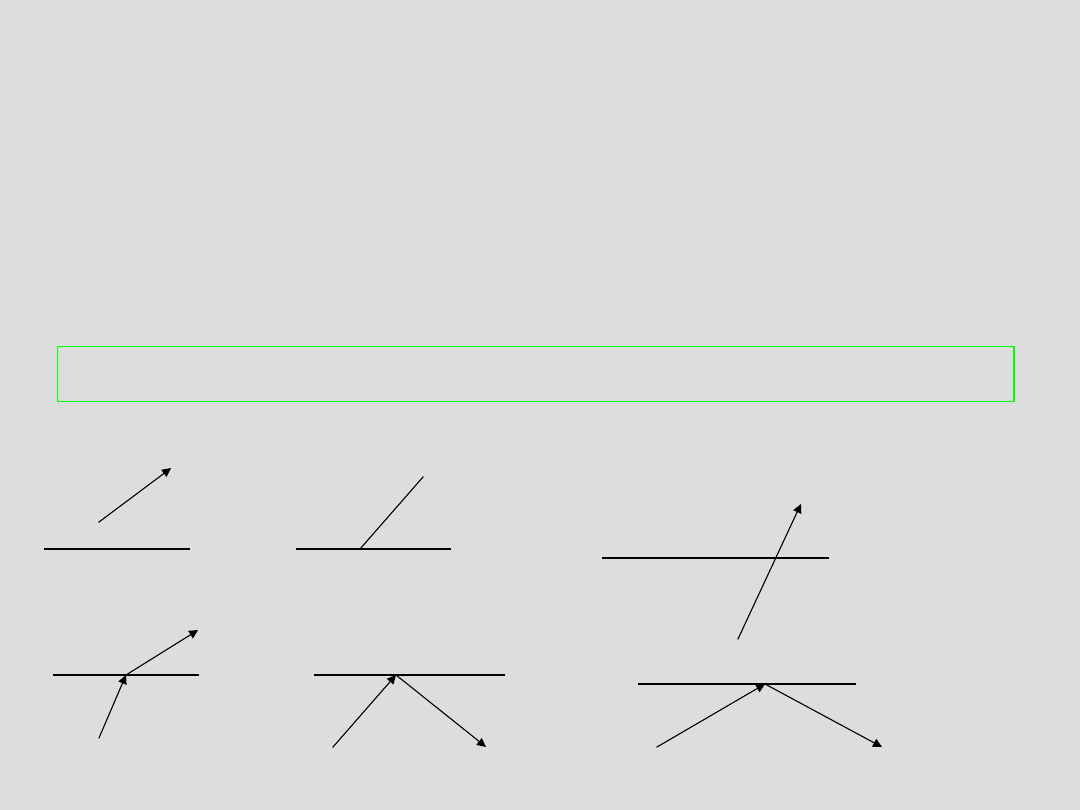
Generowanie punktów

wewnętrznych c.d.

c) Generowanie punktów na odcinkach wyznaczonych przez
kolejne pary pary uporządkowanych punktów ze zbioru Q.

Typy przecięć prostej poziomej z odcinkami brzegu

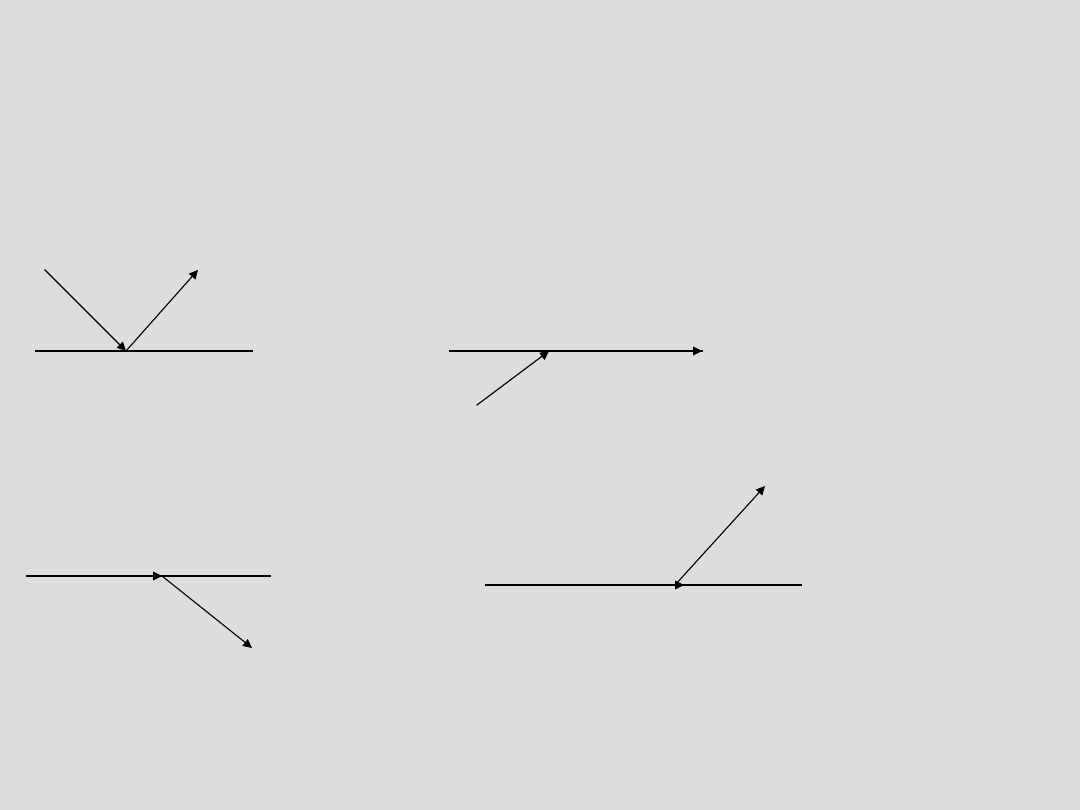
Generowanie punktów

wewnętrznych c.d.

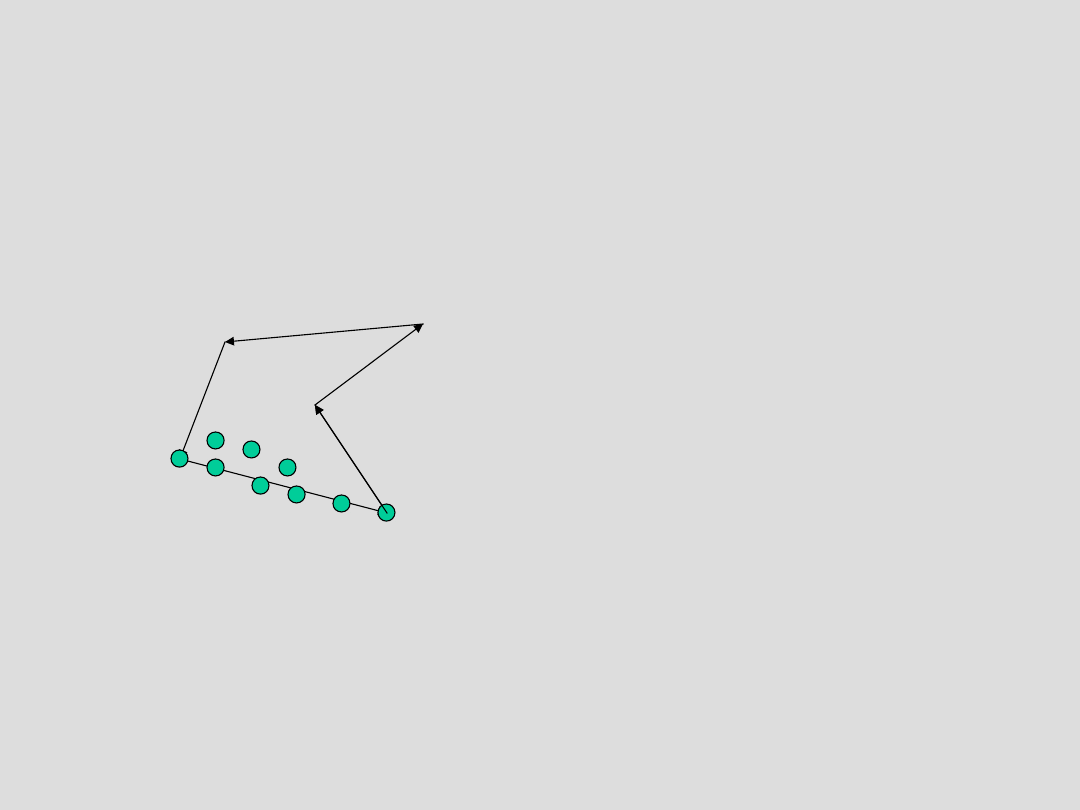
Triangularyzacja

Delaunay’a

}

,

,

,

,

{

0

1

2

2

1

1

0

0

A

A

A

A

A

A

A

A

S

N

N

N









i

D

N

S



-część nieDelaynay’owska
frontu

i

D

S

-część Delaynay’owska
frontu

.

,

i

D

i

D

N

i

i

D

i

D

N

S

S

S

S

S















Na początku:

.

,

0

0

0









D

D

N

S

S

S

Triangularyzacja

Delaunay’a

- zbiór punktów z  ograniczonych frontem

oraz leżących na foncie

i



A B

P

P

C

i

r

AB

:

{







-leży po lewej stronie

odcinka AB oraz należy do

wnętrza okręgu o promieniu
r>0 i przechodzącym przez
A, B}

Wprowadźmy następującą relację w

r

AB

C

ABQ

ABQ

r

AB

K

K

P

Q

P

C

Q

P

_

_

.

,











- jest kołem przechodzącym przez A,B,Q.

Relacja zwrotna, symetryczna i spójna



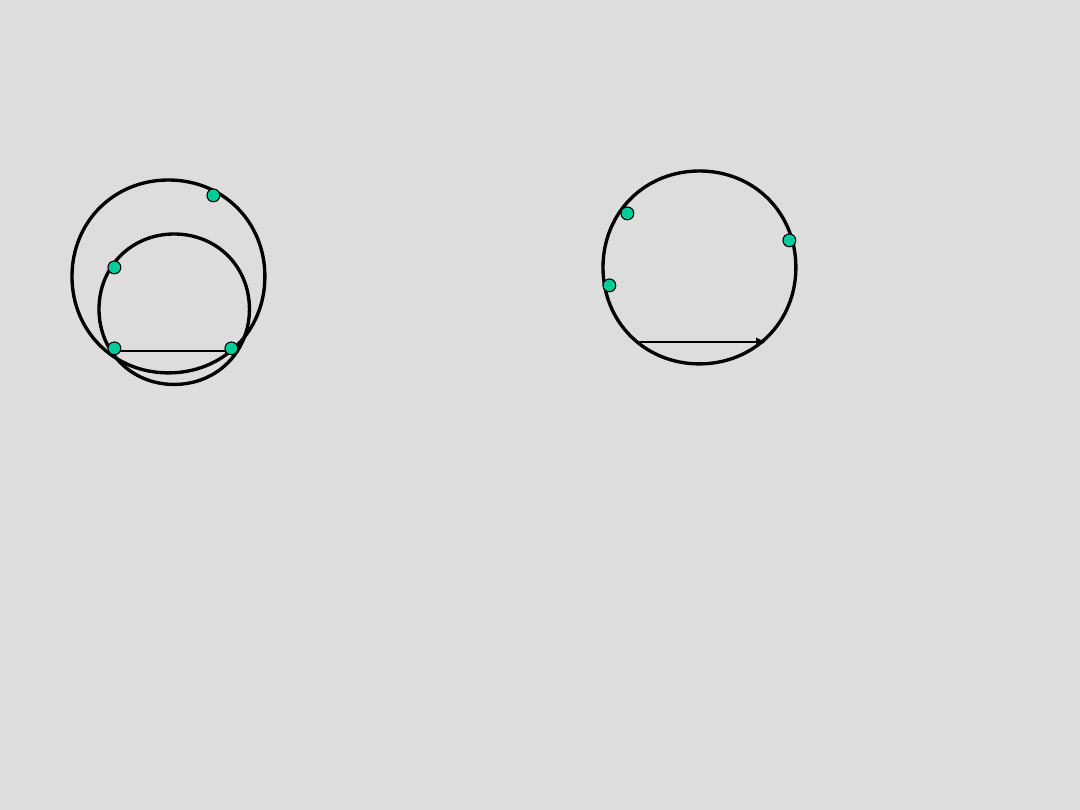
Triangularyzacja

Delaunay’a c.d.

A

P

Q

B

P

Q

R

Zwrotność:

ABP

K

P

P

P

_







Przechodniość:

.

,

R

P

R

Q

Q

P









Nie jest relacją antysymetryczną:

)

,

(

R

P

R

Q

Q

P











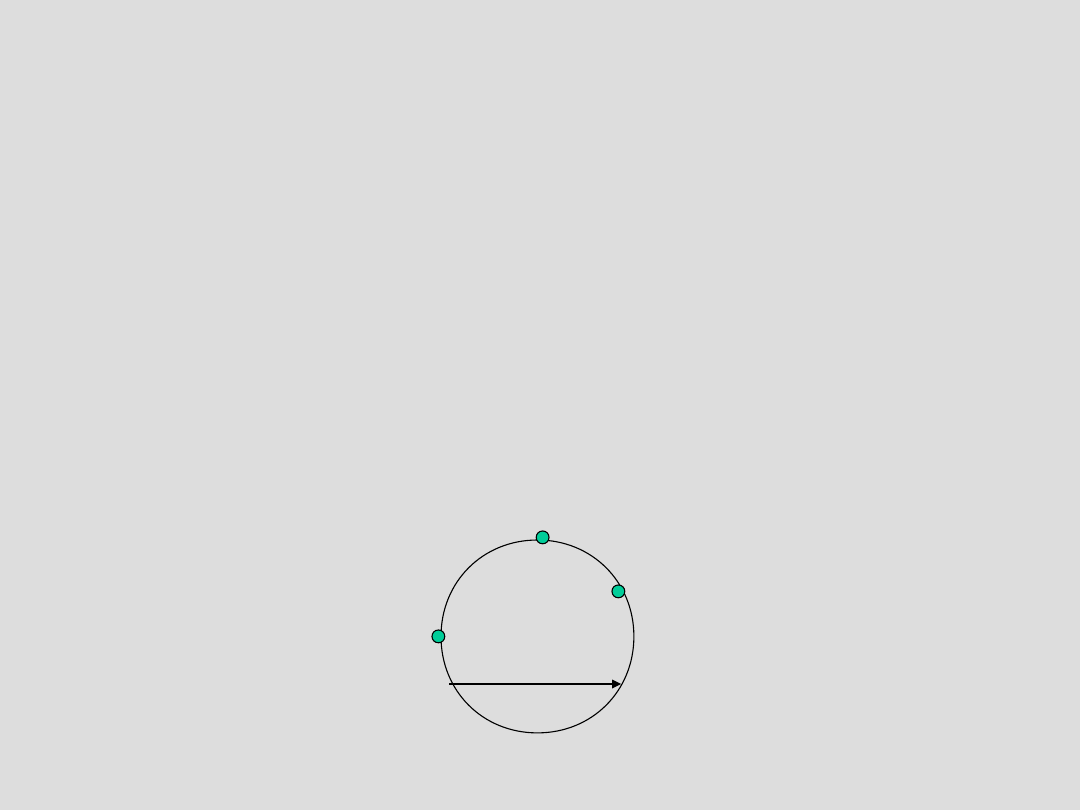
Triangularyzacja

Delaunay’a c.d.

W wprowadzamy relację:

]

[

,

,

_

_

ABP

ABQ

r

AB

K

Q

K

P

Q

P

C

Q

P















r

AB

C

Tw. Relacja  jest relacją równoważnościową.

Przechodniość:

P

Q

R

Triangularyzacja

Delaunay’a c.d.

.

.

.

]

[

]

[

]

[

,

,

,

_

_

_

_

_

_

_

_

_

d

n

c

R

P

K

R

K

P

K

K

K

K

R

K

Q

K

Q

K

P

R

Q

Q

P

C

R

Q

P

ABP

ABR

ABR

ABQ

ABP

ABQ

ABR

ABP

ABQ

r

AB













































Wprowadzamy zbiór klas abstrakcji:

}

:

]

{[

/

r

AB

r

AB

C

P

P

C









/

r

AB

C

W wprowadzamy relację:

Triangularyzacja

Delaunay’a c.d.

.

]

[

]

[

Q

P

Q

P

df









Tw. Relacja jest relacją porządku.





Dowód:
Łatwo sprawdzić, że relacja ta nie zależy od wyboru reprezentanta.
Zwrotność oraz przechodniość są konsekwencjami odpowiednic
własności dla .



Uwaga:

ABP

ABP

r

AB

C

C

Q

C

Q

P

},

:

{

]

[







- okrąg przechodzący przez punkty A, B, Q.

Relacja jest antysymetryczna.





Triangularyzacja

Delaunay’a c.d.

W celu efektywnego sprawdzania relacji wprowadzony został
lokalny układ współrzędnych.





A

B

u

v

P

Q

).

(

2

1

],

,

[

],

,

[

||

||

_

B

A

O

v

AB

AB

u





















Tw.



Q

P 

Współrzędna wektora (v) środka jest mniejsza
Od współrzędnej (v) środka

ABP

K

.

ABQ

K

Jeśli P zostanie wyselekcjonowany należy sprawdzić jeszcze
następujące warunki:

Triangularyzacja

Delaunay’a c.d.

}.

},

,

{

},

{

,

{

},

},

,

{

},

{

,

{

PB

P

B

B

S

PB

PA

P

A

A

S

PA

D

N

D

N

















Algorytm modyfikacji frontu:

}

{

}

{

\

)

(

.

2

},

{

\

.

1

1

1

1

PA

S

S

ELSE

PA

S

S

THEN

S

PA

IF

AB

S

S

S

S

i

D

i

D

i

D

i

D

i

D

i

i

i

i



















Triangularyzacja

Delaunay’a c.d.

.

}

{

}

{

\

)

(

.

3

1

1

ENDIF

BP

S

S

ELSE

BP

S

S

THEN

S

BP

IF

i

D

N

i

D

N

i

D

N

i

D

N

i

D

N























Algorytm Triangularyzacji

S

S

D

N





0

.

1

,

.

2

0





D

S

Wykonaj punkty a) do e) dla i=0,1,2,.. dopóki

:





i

S

THEN

S

IF

a

i

D

N

)

(

)







THEN

S

IF

i

D

)

(





Znajdź najmniejszy odcinek frontu

i

D

N

S

AB





ELSE

Znajdź najmniejszy odcinek frontu

i

D

S

AB

ELSE

Zakończ triangularyzację

.

ENDIF

Algorytm triangularyzacji

c.d.

b) Wyznacz zbiór kandydatów

AB

r

dla

C

r

AB



c) Znajdź jako najmniejszy element w zbiorze

r

AB

C



]

[

*

P

THEN

akcept

jest

P

IF

d

.)

(

)

*

dodaj trójkąt do listy trójkątów oraz modyfikuj

części frontu

wykorzystując algorytm modyfikacji frontu

ELSE

i

D

N

i

D

S

S



,

ENDIF

ENDIF

D

r

r

ELSE

THEN

C

IF

P

C

C

e

r

AB

r

AB

r

AB











)

(

}

{

\

)

*

idź do punktu 2d

gdzie D jest gęstością siatki

Algorytm triangularyzacji

c.d.

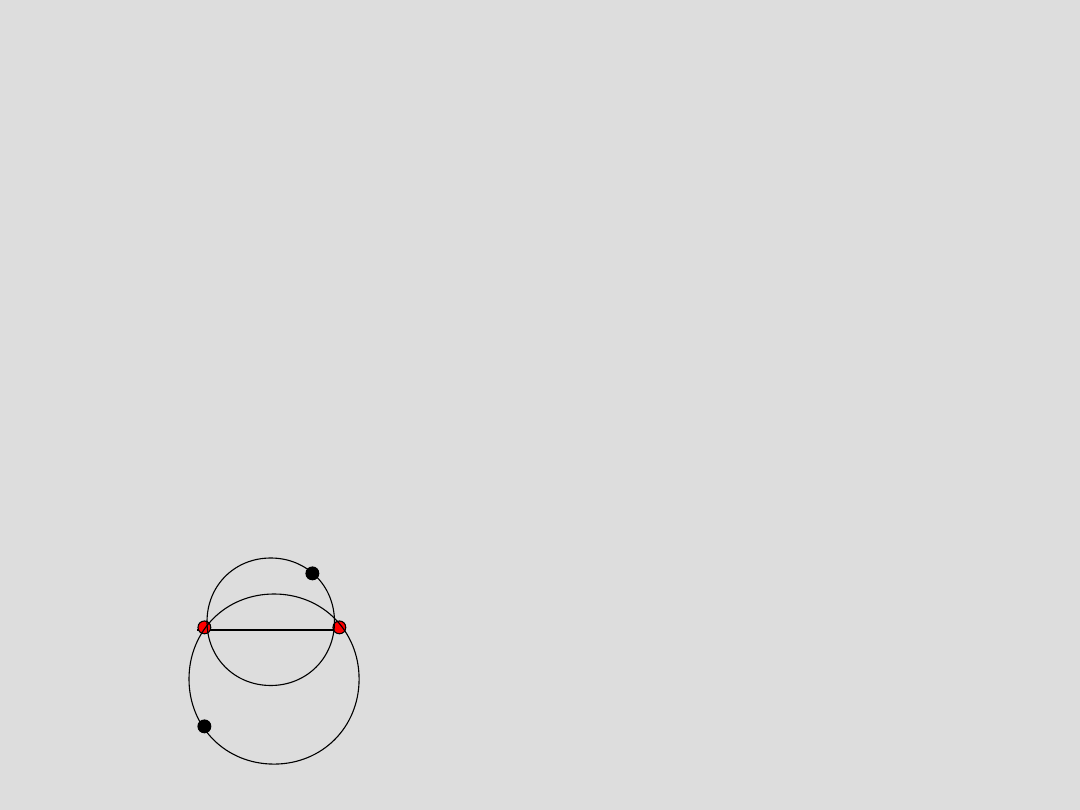
Tw. Załóżmy, że dane są dwa trójkąty T=ABC oraz S=ABD

mają wspólny bok AB i pozostałe dwa wierzchołki tych

trójkątów pozostają po przeciwnych stronach odcinka AB,

wówczas wierzchołek C trójkąta T nie należy do koła opisanego

na trójkącie S, to wierzchołek D tego trójkąta nie należy do koła

opisanego na trójkącie ABC.

A

D

C

B

Algorytm triangularyzacji

c.d.

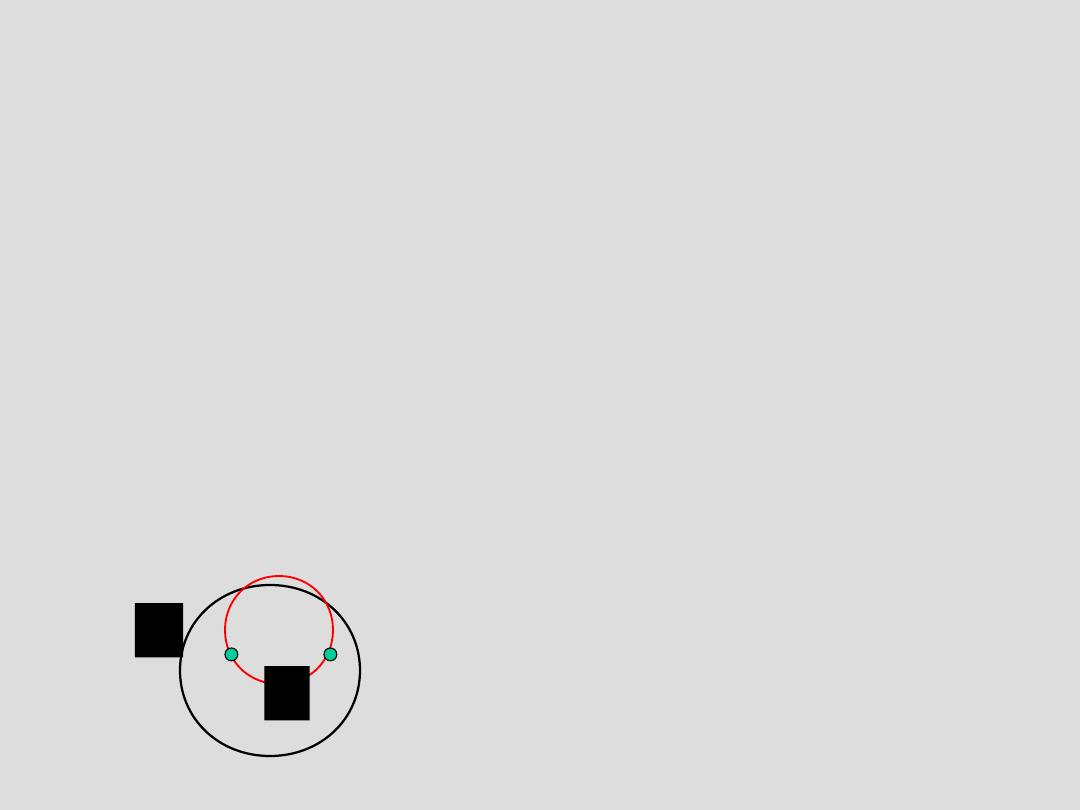
Tw. Z) Dany jest okrąg K oraz dwa punkty A, B należące do niego

lub jego wnętrza. Niech L będzie dowolnym okręgiem

przechodzącym przez A, B.

T) Co najmniej jeden z odcinków koła L wyznaczonych przez

cięciwę przechodzącą przez A, B zawiera się w kole określonym

przez okrąg K.

A

B

K

L

Algorytm triangularyzacji

c.d.

Twierdzenie

Powyższy algorytm łączący metodę postępującego frontu wraz

z opisanym sposobem budowy trójkąta nad wybranym elementem

prowadzi do triangularyacji Delaunaya obszaru płaskiego.

Dowód tego twierdzenia wynika z poprzedniego twierdzenia

oraz ze sposobu modyfikowania frontu. Indukcyjny ze względu

ciąg kolejne frontów.

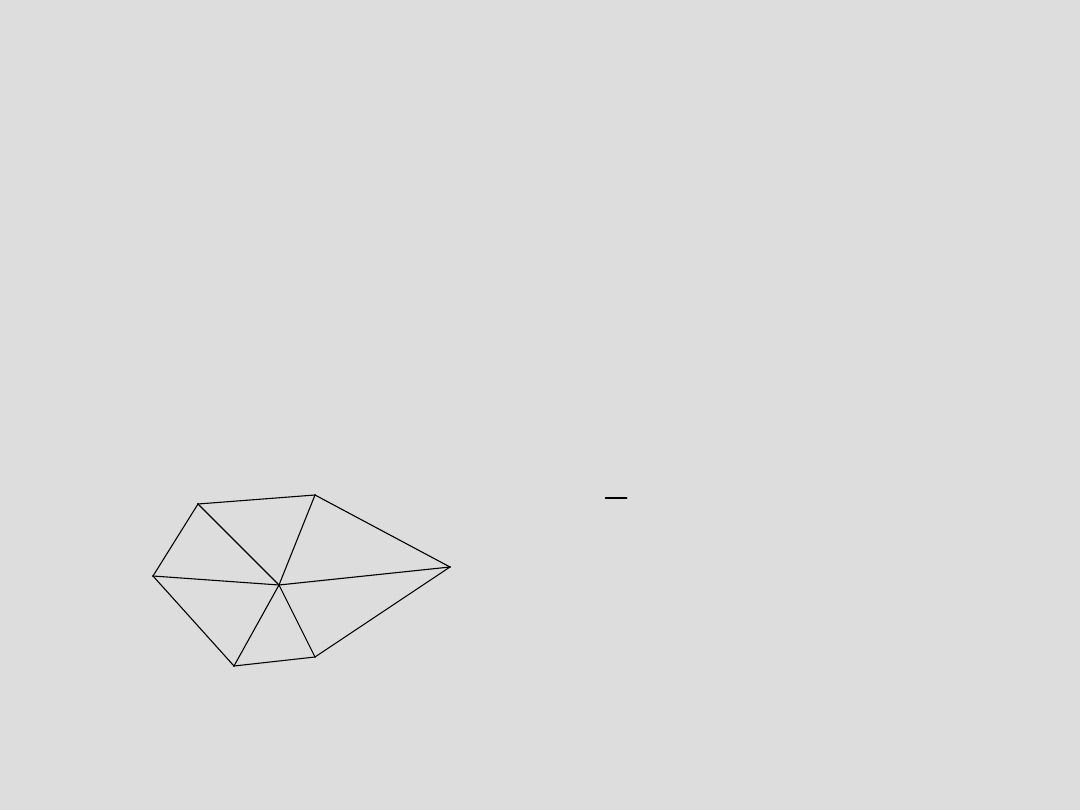
Wygładzanie

Po procesie triangularyacji w celu polepszenia jakości siatki stosowana

jest procedura tak zwanego wygładzania. Jedną z najbardziej

popularnych jest procedura wygładzania Laplace’a. Proces ten polega

na zastępowaniu punktów wewnętrznych środkami ciężkości trójkątów

schodzących się w tym punkcie.

m

P

l

P

k

P

j

P

i

P

n

P

)

(

6

1

'

n

m

l

k

j

i

P

P

P

P

P

P

P













Wygładzanie

Wprowadźmy oznaczenia:

}

,

,

1

,

{

T

i

N

i

T









- zbiór trójkątów pokrywających obszar

}

,

:

{

},

,

{

_

_

T

Q

T

P

Q

Q

P

T

P

T

P

P

P





































- zbiór punktów wewnętrznych



- zbiór punktów brzegowych

Przy powyższych oznaczeniach proces wygładania może

być interpretowany jako metoda Gaussa-Seidela

Wygładzanie c.d.

.

,

,

),

(

1























P

P

P

P

Q

N

P

P

Q

P

Gdzie jest liczbą

elementów zbioru

P

N

P



.

]

,

,

,

,

;

0

,

,

0

[

,

]

,

,

,

,

;

,

,

,

,

[

},

,

,

1

),

,

{(

},

,

,

1

),

,

{(

'

'

'

1

'

1

'

'

'

1

'

1

1

1

'

'

T

T

N

N

i

i

i

i

y

x

y

x

Y

y

x

y

x

y

x

y

x

X

N

i

y

x

N

i

y

x

Niech













































W postaci macierzowej:

.

,

,

,

,































N

N

N

N

N

N

I

O

A

Y

X

I

O

A