Eigenvectors and

eigenvalues

Lecture 11

EIGENVALUES AND EIGENVECTORS

In the following we shall deal only with linear
transformations T of space V into space V ,

T : V  V.

Note

The transformation matrix A

T

is a square matrix.

One can ask:
Under a linear transformation T, is there a direction
along which there is no rotation, just pure stretching?

One wants a direction x for which:
A

T

x = cx, where c

 R.

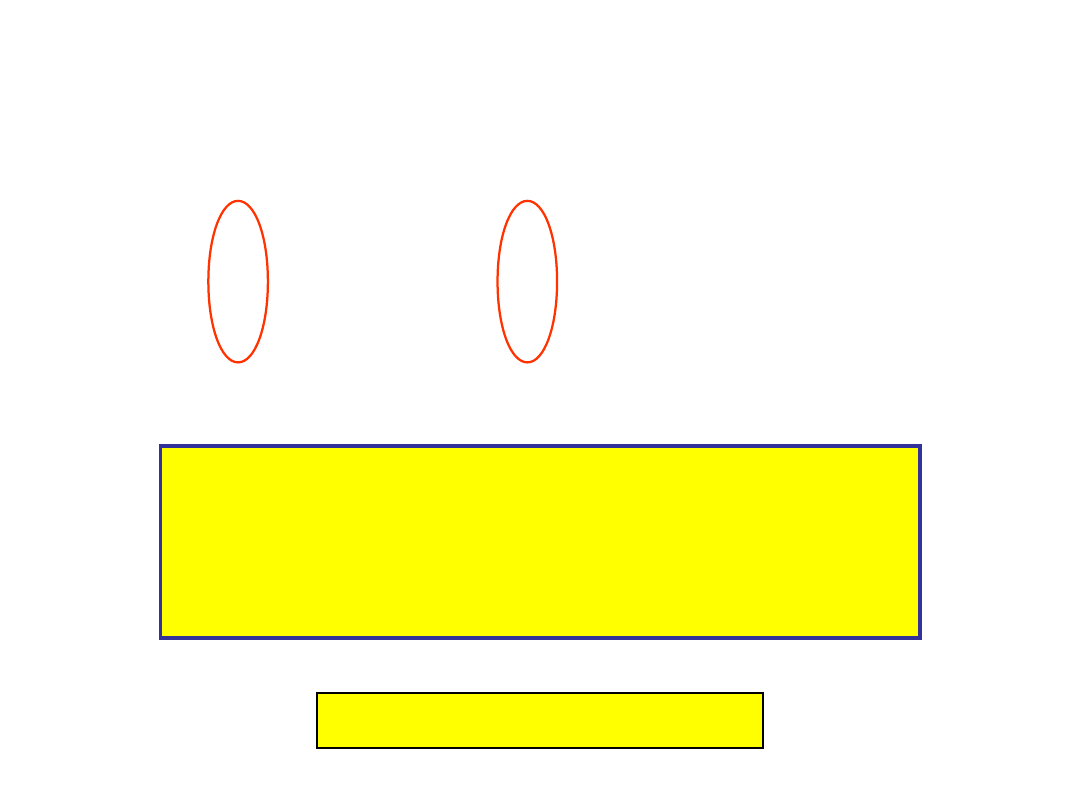
In this shear transformation of the Mona Lisa, the picture was deformed
in such a way that its central vertical axis (red vector) was not modified,
but the diagonal vector (blue) has changed direction. Hence the red
vector is an eigenvector of the transformation and the blue vector is
not. Since the red vector was neither stretched nor compressed, its
eigenvalue is 1.
All vectors along the same vertical line are also eigenvectors, with the
same eigenvalue. They form the eigenspace for this eigenvalue.

Definition
The vector x

is called the eigenvector and

λ

the

corresponding eigenvalue of a linear transformation T : V→
V if the equation

x

)

x

(

T





is true.

Let us consider V = R

n

. Then,

1. The eigenvector of the linear transformation is
an eigenvector of the transformation matrix.

2. The eigenvalue of the linear transformation is
the eigenvalue of the transformation matrix.

3

3

R

R

:

T







).

z

x

,

z

y

x

,

z

y

x

(

)

z

,

y

,

x

(

T

2

7

3

2

2













Example 1
Let us consider a linear transformation defined as follows:

,

We seek eigenvalues and eigenvectors of this transformation.

We guess that (but that is no way to find eigenvalues!!!)

T((1, 1, 1)) = (5, 5, 5) = 5(1, 1, 1).

Thus we can conclude that 5 is the eigenvalue and (1, 1, 1) is the eigenvector.

Example 2
Let T : V  V be a homothety with coefficient , that is

 

.

x

x

T

V)

x

(









Then every vector x V (x  0) is an eigenvector of this transformation and

 is the eigenvalue.

Example 3

Let T: R

2

 R

2

be a rotation by angle /2, i.e.





).

x

,

y

(

)

y

,

x

(

T





This transformation does not have any direction along which there
is no rotation, just pure streching, which means that the
transformation does not have any eigenvalues or eigenvectors.

FACT

Linear combinations of eigenvectors are also eigenvectors

.

HOW DO WE FIND EIGENVALUES

AND EIGENVECTORS.

Let us consider a linear transformation T: R

n

 R

n

.

A – transformation matrix of T:

,

a

...

a

...

...

...

a

...

a

A

nn

n

n























1

1

11

 vector of unknowns x = ( x

1

, ....., x

n

) in matrix form:

,

x

...

x

x

n























1

 vector of constants y = (y

1

, ....., y

n

) is the image of x in matrix form:

.

y

...

y

y

n























1

How to determine eigenvectors and eigenvalues.

We have to solve a matrix equation:

Ax =   x ,





0







x

I

A

.

...

x

...

x

x

a

...

a

a

...

...

...

...

a

...

a

a

a

...

a

a

n

nn

n

n

n

n























































































0

0

0

2

1

2

1

2

22

21

1

12

11

or

A non-zero solution of ( A - I ) x = 0, exists if the matrix ( A

- I ) is singular i.e. if its determinant Det [A - I ] is 0.

The dimension of the kernel (A -  I) is the dimension of the corresponding space

of eigenvectors.- the geometric multiplicity

0

2

1

2

22

21

1

12

11







































nn

n

n

n

n

a

...

a

a

...

...

...

...

a

...

a

a

a

...

a

a

det

is called

the characteristic equation of A,

and the polynomial det (A - I) the characteristic polynomial.

Equation:

Definition

The roots of the characteristic equation are the eigenvalues of matrix A.

Definition

.

A

T



















5

3

3

5











.

0

8

2

10

9

10

25

9

5

5

3

3

5

2

2

2





















































Example
Find the eigenvalues and eigenvectors of T:R

2

-> R

2

represented by the transformation matrix:

1. From the characteristic equation:

We obtain the eigenvalues: 

1

= 2, 

2

= 8.

SOLUTION





.

x

I

A

0





















































0

0

2

5

3

3

2

5

y

x

.

y

x











































0

0

3

3

3

3

















,

y

x

y

x

0

3

3

0

3

3

 

1

1

1

,

x 

Eigenvectors corresponding to eigenvectors.

For 

1

= 2:

or

So we have to solve the system

one of solutions is the eigenvector:

.

or the space S

1

={(t,t): t  R } = Lin{(1,1)} of eigenvectors corresponding to

eigenvalue 

1

= 2.

2. For each eigenvalue we solve the following equation (find the kernel of )

I

A 





















,

y

x

y

x

0

3

3

0

3

3





1

1

2



 ,

x

For 

1

= 8:

gives for example an eigenvector:

or the space S

2

= { (t, -t): t R} = Lin{ (1,-1) } of

eigenvectors corresponding to eigenvalue 

2

= 8.

Note that in this example the eigenvectors corressponding to
diferent eigenvalues are linearily independent

.



Theorem
Let T: V  V be a linear transformation of an n–

dimensional space V. If T has n distinct eigenvalues

λ

1

, λ

2

, ..., λ

n

then the corresponding eigenvectors

x

1

, x

2

, ..., x

n

are linearly independent and constitute

a basis of V.

,

n



































0

0

1

where 

i

are the eigenvalues.

The transformation matrix of T relative to the basis of eigenvectors has the form:

This means that if we write the eigenvectors as columns in the
transition matrix P (- from the unit basis to the eigenvector basis)

,

0

0

P

a

a

a

a

P

n

1

nn

1

n

n

1

11

1





























































































































































nn

1

n

n

n

2

21

2

n

1

11

1

nn

1

n

n

1

11

x

...

x

x

,

,

x

...

x

x

,

x

...

x

x

x

x

x

x

P













So





matrix

diagonal

P

A

P

1





Find the eigenvalues and eigenvectors of the transformation f represented by the
matrix A

f

relative to the unit basis:

.

A

f















2

0

5

2









2

2

2

0

2

2

0

5

2























1. The characteristic equation is :

we obtain one double eigenvalue



1

= 

2

= 2.

Example.

2. To find the eigenvectors we solve equation ( A - I ) x =0

Thus for 

1

= 

2

= 2:











































0

0

2

2

0

5

2

2

y

x

.

y

x







































0

0

0

0

5

0











0

0

0

5y

 

0

,

1

1



x

.

So, one of the eigenvectors is

,

dim Ker(A - I ) = 1

We didn't obtain two independent eigenvectors:
- we can't write the matrix P,
- we can't write the transformation matrix of f in diagonal form.

Theorem

The matrix A is equvalent to a diagonal
one if
the eigenvectors of A constitute a
basis for R

n

Example























2

2

1

1

3

1

1

2

2

A

1. The characteristic equation is (λ -5)(λ -1)

2

= 0, so

the eigenvalues

are

λ

1

= 5, λ

2

= λ

3

= 1.

2. The

eigenvector

associated with λ

1

= 5 is

v

1

= (1,1,1)

There are

two independent eigenvectors

asociated with the multiple root λ

2

= λ

3

= 1

v

2

= (2,-1,0) and v

3

=(1,0,-1)

IN THIS CASE THE EIGENVALUES CONSTITUTE A BASIS FOR R

n.

Theorem
The eigenvalues of a

real symmetric

matrix are all

real.

Theorem
If λ

i

is an eigenvalue of multiplicity r of a

real

symmetric

matrix,

then
there are r linearly independent eigenvectors.
associated with λ

i

,