1

1

Modele ARMA w

Modele ARMA w

prognozowaniu

prognozowaniu

2

2

Podstawowe pojęcia modeli

Podstawowe pojęcia modeli

ARMA

ARMA



stacjonarność

stacjonarność



biały szum

biały szum



funkcja autokorelacji ACF

funkcja autokorelacji ACF



funkcja częściowej

funkcja częściowej

autokorelacji PACF

autokorelacji PACF

3

3

Stacjonarny szereg

Stacjonarny szereg

czasowy

czasowy

Szereg czasowy nazywamy stacjonarnym,

Szereg czasowy nazywamy stacjonarnym,

jeśli spełnione są trzy warunki:

jeśli spełnione są trzy warunki:



wartość oczekiwana EY (t)

wartość oczekiwana EY (t)

jest stała

jest stała

(nie zmienia się wraz ze zmianą chwili

(nie zmienia się wraz ze zmianą chwili

czasowej t)

czasowej t)



wariancja

wariancja

Var (Y(t)) jest stała

Var (Y(t)) jest stała



autokorelacja

autokorelacja

zależy tylko od różnicy |

zależy tylko od różnicy |

t-s|

t-s|

4

4



Jeśli spełniony warunek (1) to

Jeśli spełniony warunek (1) to

szereg czasowy

szereg czasowy

nie ma trendu

nie ma trendu



Warunek (2) oznacza

Warunek (2) oznacza

brak

brak

sezonowości

sezonowości



Jeśli na zależność między

Jeśli na zależność między

obserwacjami ma wpływ tylko

obserwacjami ma wpływ tylko

odległość pomiędzy nimi to

odległość pomiędzy nimi to

wtedy warunek (3) jest spełniony

wtedy warunek (3) jest spełniony

5

5

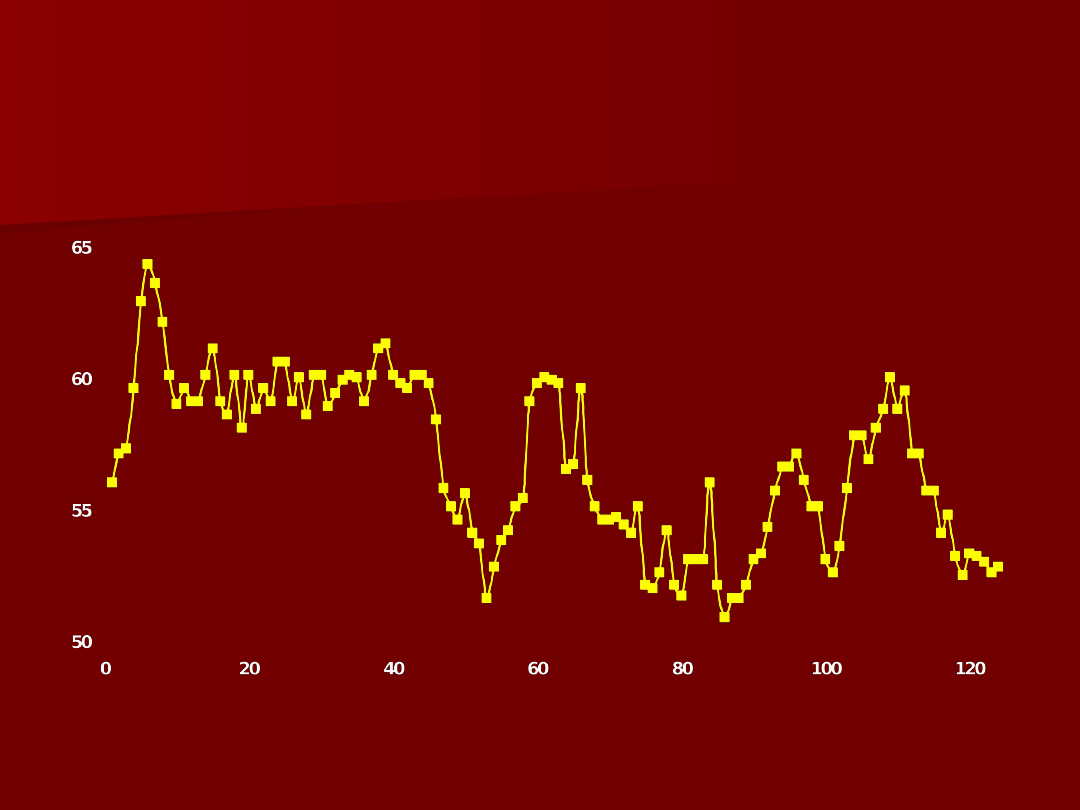
Wartość akcji banku PeKaO

Wartość akcji banku PeKaO

S.A. w roku 2001

S.A. w roku 2001

6

6

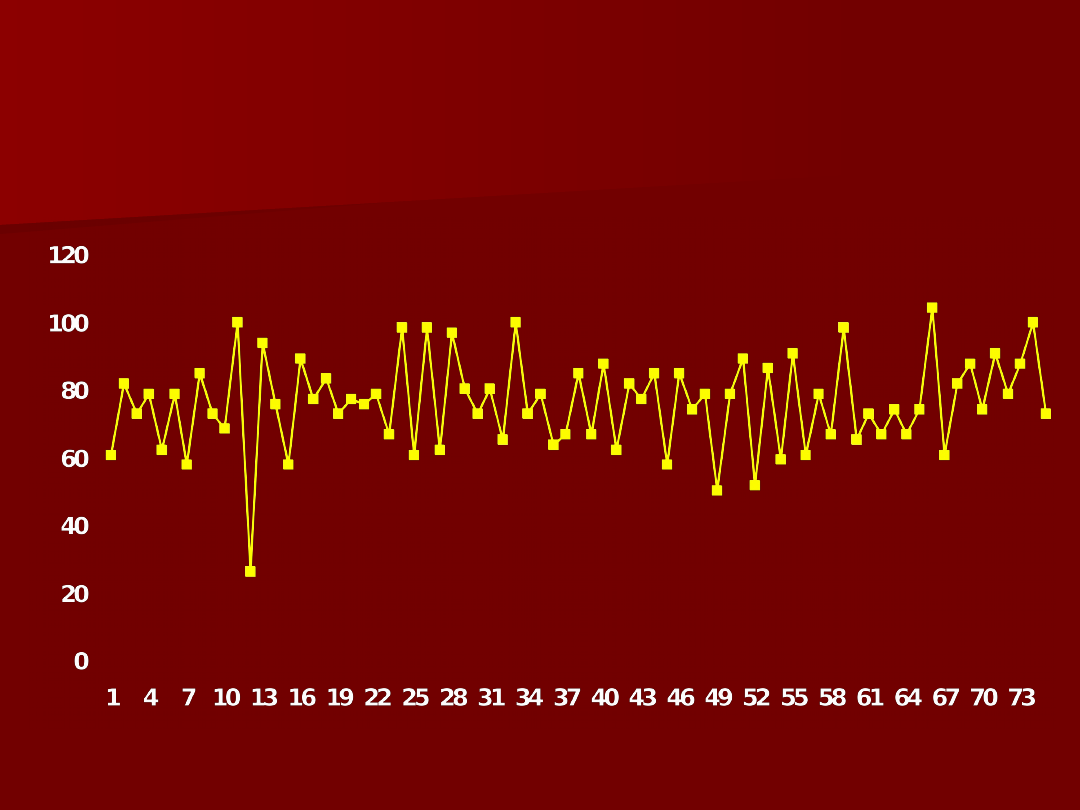
Wielkość sprzedaż kompanii

Wielkość sprzedaż kompanii

Atron

Atron

7

7

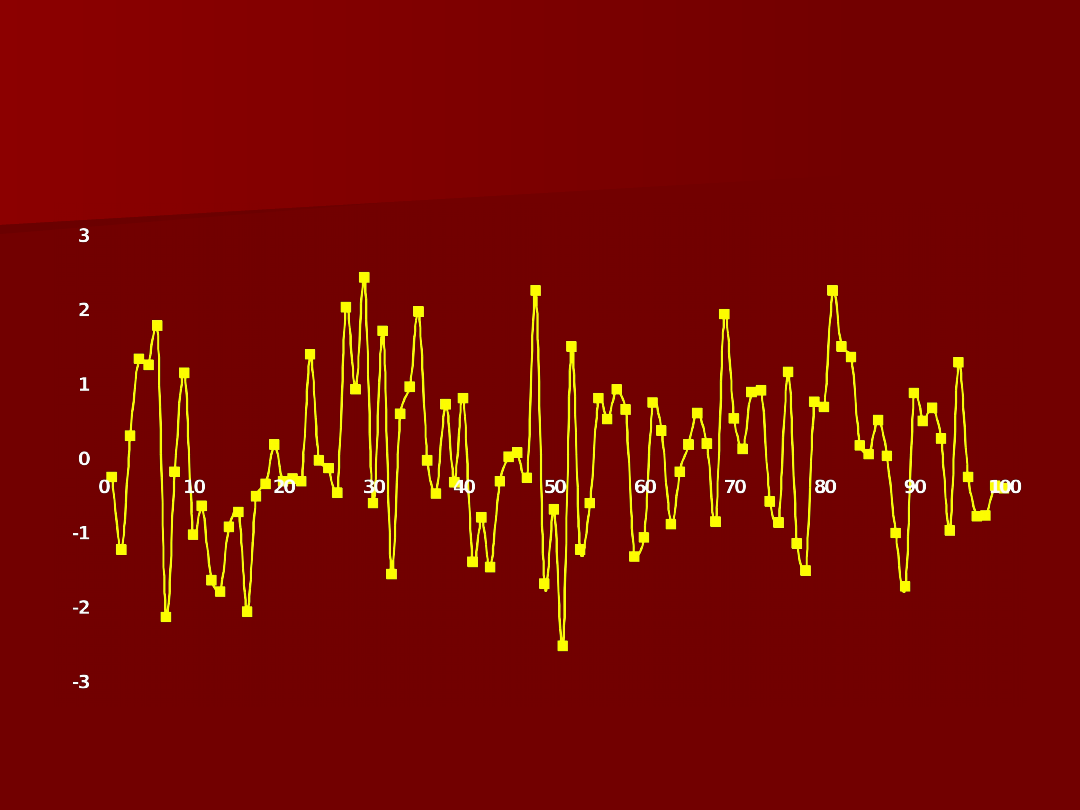
Biały szum

Biały szum

Szereg czasowy nazywa się

Szereg czasowy nazywa się

białym

białym

szumem

szumem

, gdy

, gdy

Y

Y

t

t

= c +

= c +

ε

ε

t

t

gdzie

gdzie

c – to pewna stała

c – to pewna stała

ε

ε

t

t

– to ciąg niezależnych zmiennych

– to ciąg niezależnych zmiennych

losowych o średniej zero i stałej

losowych o średniej zero i stałej

wariancji

wariancji

8

8

Biały szum

Biały szum

9

9

Funkcja autokorelacji

Funkcja autokorelacji

ACF

ACF





















T

t

t

T

k

t

k

t

t

Y

Y

Y

Y

Y

Y

k

ACF

1

2

1

)

(

)

)(

(

)

(

10

10

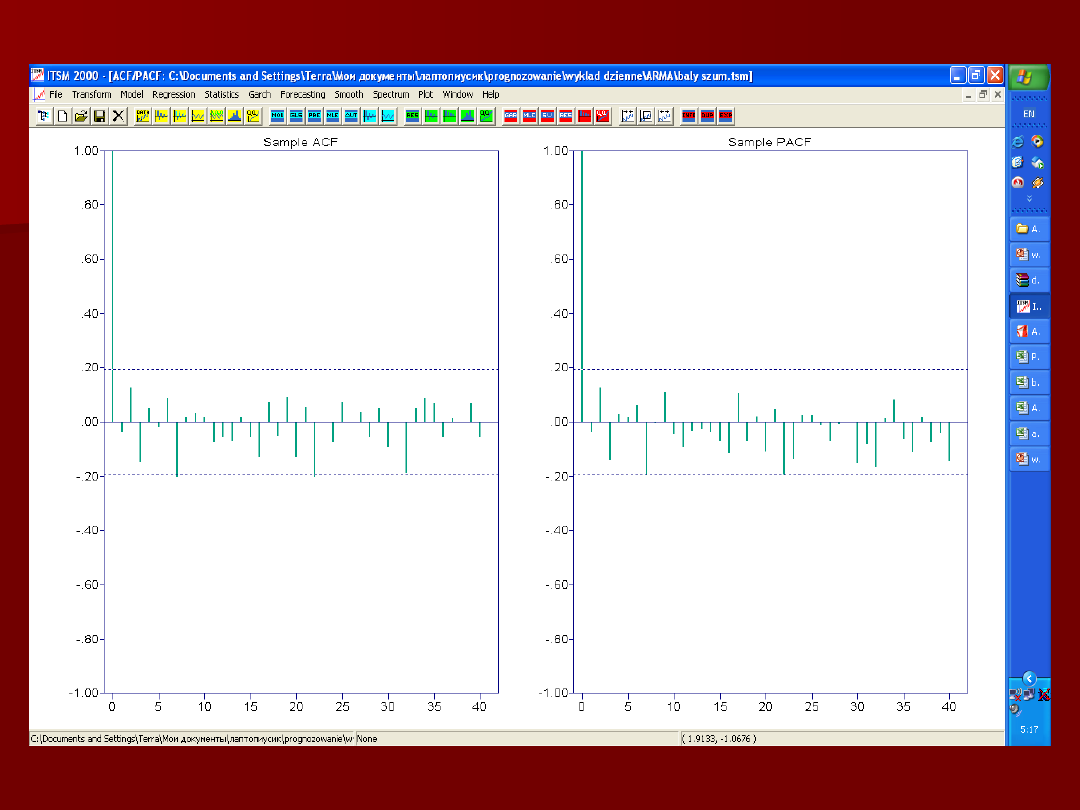
Jeśli szereg czasowy jest białym

Jeśli szereg czasowy jest białym

szumem, to dla każdego k > 0

szumem, to dla każdego k > 0

jego funkcja ACF (k) z

jego funkcja ACF (k) z

prawdopodobieństwem 95%

prawdopodobieństwem 95%

mieście się w przedziale

mieście się w przedziale

[ -1,96 /

[ -1,96 /

√n ; 1,96 / √n ]

√n ; 1,96 / √n ]

n – ilość obserwacji

n – ilość obserwacji

Wartość ACF (0) jest dla dowolnego

Wartość ACF (0) jest dla dowolnego

szeregu czasowego równa 1

szeregu czasowego równa 1

11

11

12

12

Funkcja częściowej

Funkcja częściowej

autokorelacji PACF (k)

autokorelacji PACF (k)

Y

Y

t

t

= b

= b

0

0

+ b

+ b

1

1

Y

Y

t-1

t-1

+ b

+ b

2

2

Y

Y

t-2

t-2

+ … + b

+ … + b

k

k

Y

Y

t-k

t-k

ε

ε

t

t

W modelu, szereg czasowy Y

W modelu, szereg czasowy Y

t

t

występuje

występuje

zarówno jako zmienna zależna i jako

zarówno jako zmienna zależna i jako

zmienna niezależna.

zmienna niezależna.

Taki model nazwiemy modelem

Taki model nazwiemy modelem

autoregresji rzędu k

autoregresji rzędu k

w skrócie AR (k)

w skrócie AR (k)

13

13

Wartość PACF (k) jest równa

Wartość PACF (k) jest równa

współczynnikowi b

współczynnikowi b

k

k

w tym modelu.

w tym modelu.

Mierzy ona zależność pomiędzy

Mierzy ona zależność pomiędzy

zmiennymi Y

zmiennymi Y

t

t

a Y

a Y

t-k

t-k

bez

bez

uwzględniania kroków pośrednich

uwzględniania kroków pośrednich

(„zależność bezpośrednia”)

(„zależność bezpośrednia”)

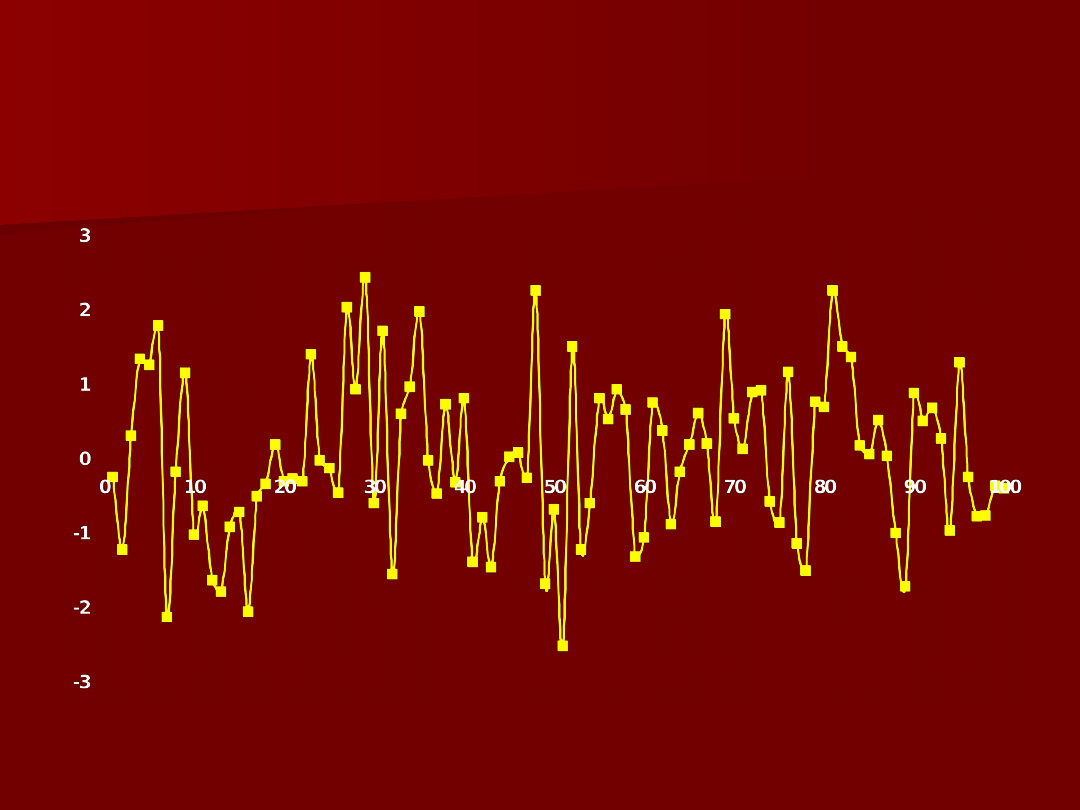
14

14

Biały szum

Biały szum

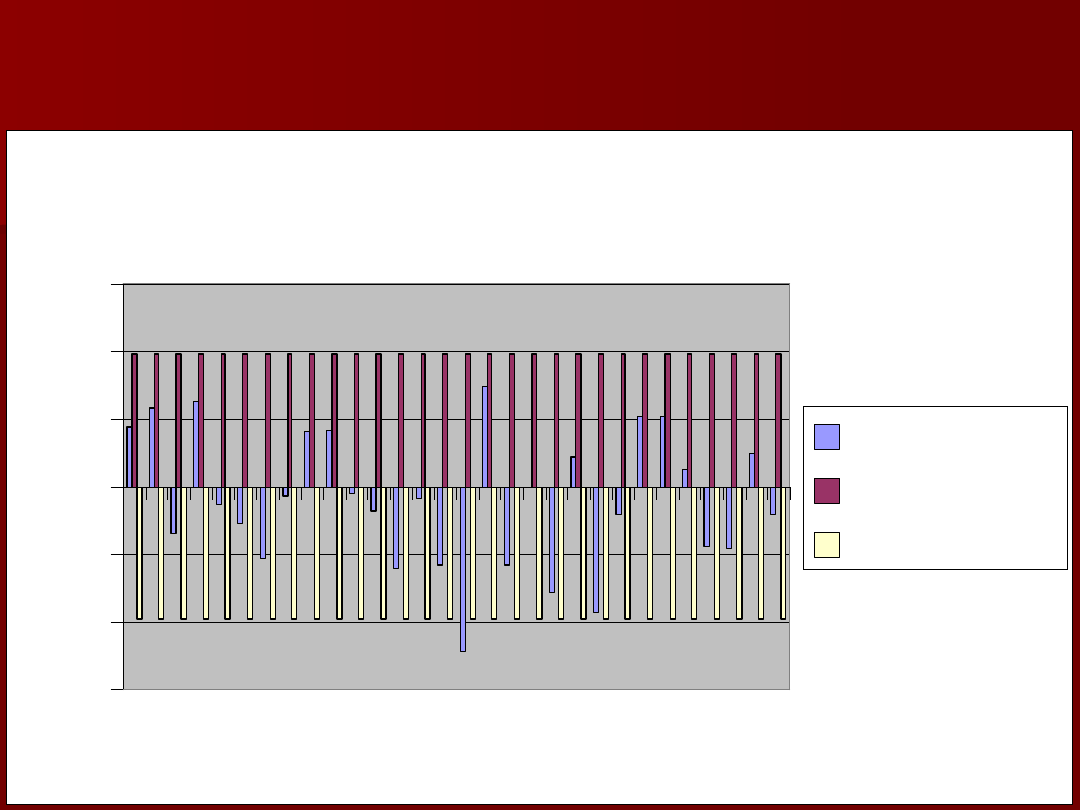
15

15

PACF

-0,3

-0,2

-0,1

0

0,1

0,2

0,3

1 4 7 10 13 16 19 22 25 28

lag

PACF
1,96/sqrt(n)
-1,96/sqrt(n)

16

16

Dla białego szumu funkcja PACF (k)

Dla białego szumu funkcja PACF (k)

(podobnie jak ACF (k)) mieście się

(podobnie jak ACF (k)) mieście się

w przedziale

w przedziale

[ -1,96 /

[ -1,96 /

√n ; 1,96 / √n ]

√n ; 1,96 / √n ]

n – ilość obserwacji

n – ilość obserwacji

Wartość PACF (0) jest dla dowolnego

Wartość PACF (0) jest dla dowolnego

szeregu czasowego równa 1

szeregu czasowego równa 1

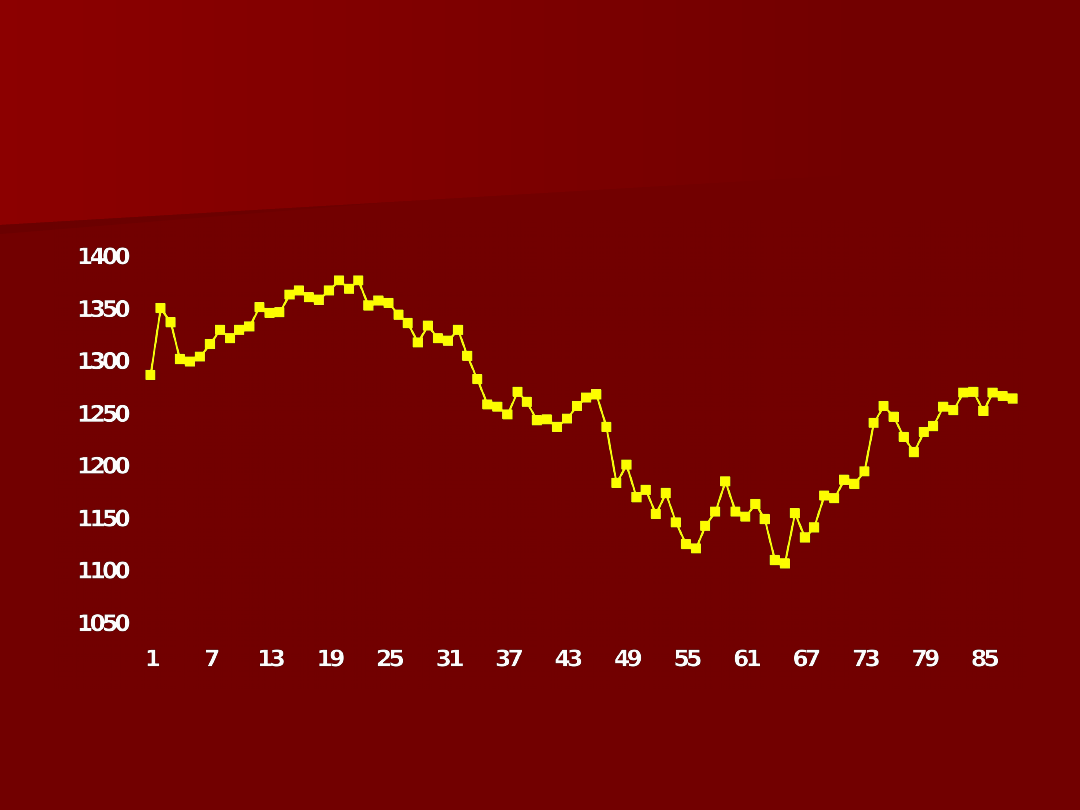
17

17

Wartości indeksu Standard

Wartości indeksu Standard

and Poor 500

and Poor 500

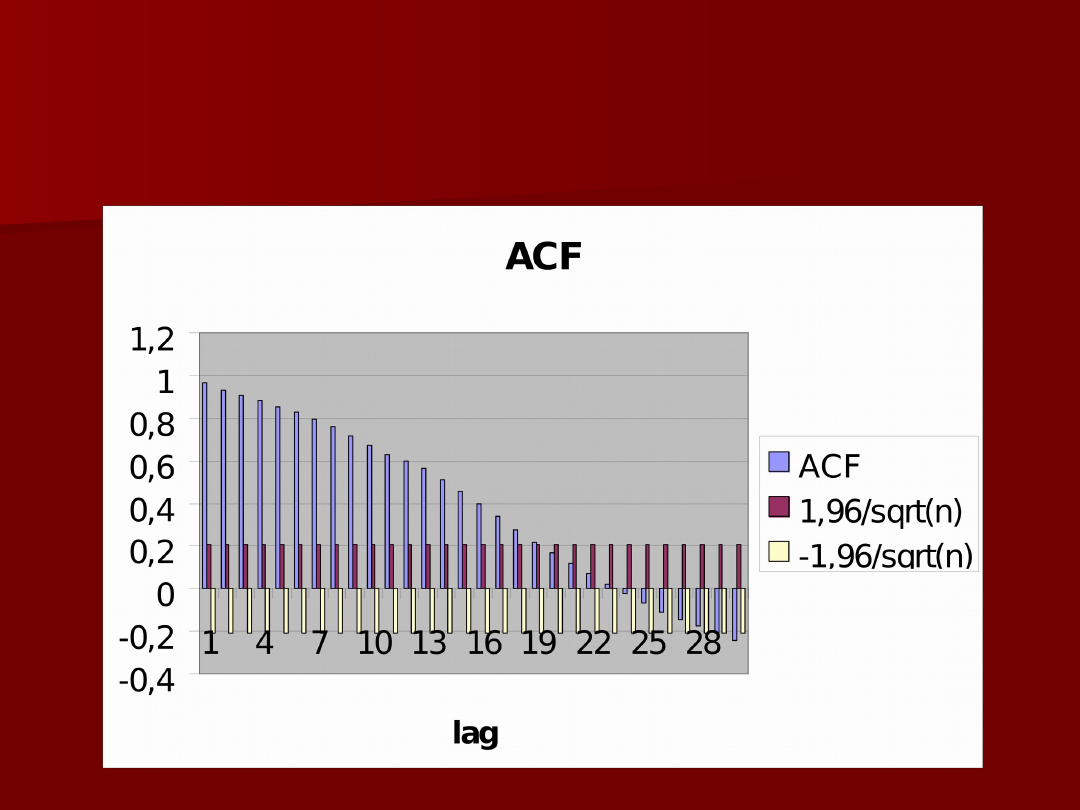
18

18

Funkcja ACF (k) dla indeksu

Funkcja ACF (k) dla indeksu

S&P 500

S&P 500

19

19

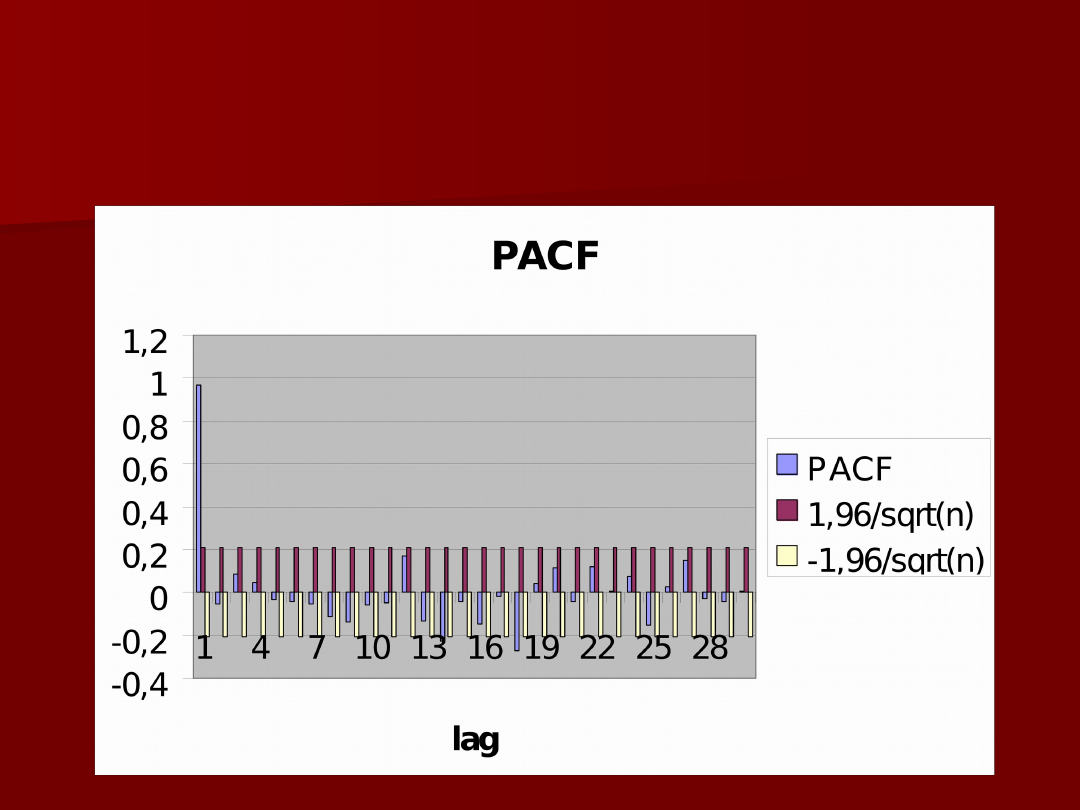
Funkcja PACF (k) dla

Funkcja PACF (k) dla

indeksu S&P 500

indeksu S&P 500

20

20

Różnicujemy szereg czasowy

Różnicujemy szereg czasowy

Obliczmy wartości kolejnych różnic

Obliczmy wartości kolejnych różnic

Y

Y

t

t

d

d

= Y

= Y

t

t

– Y

– Y

t-1

t-1

21

21

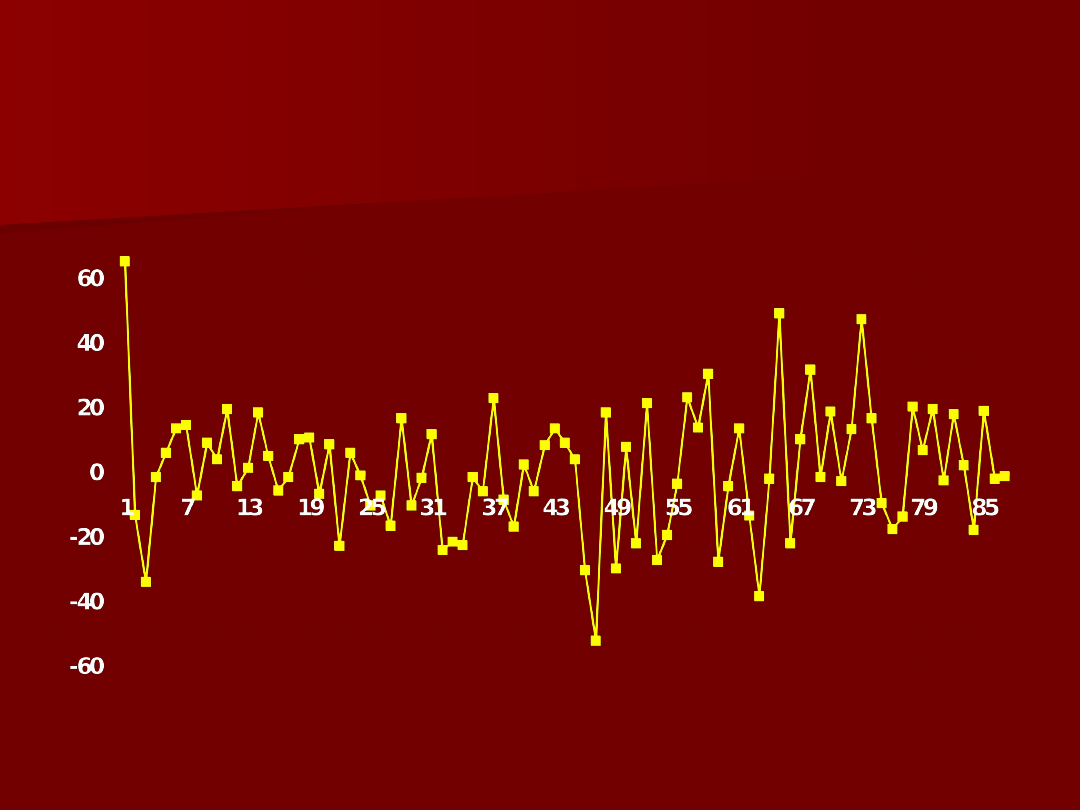
Indeks S&P 500 po

Indeks S&P 500 po

różnicowaniu

różnicowaniu

22

22

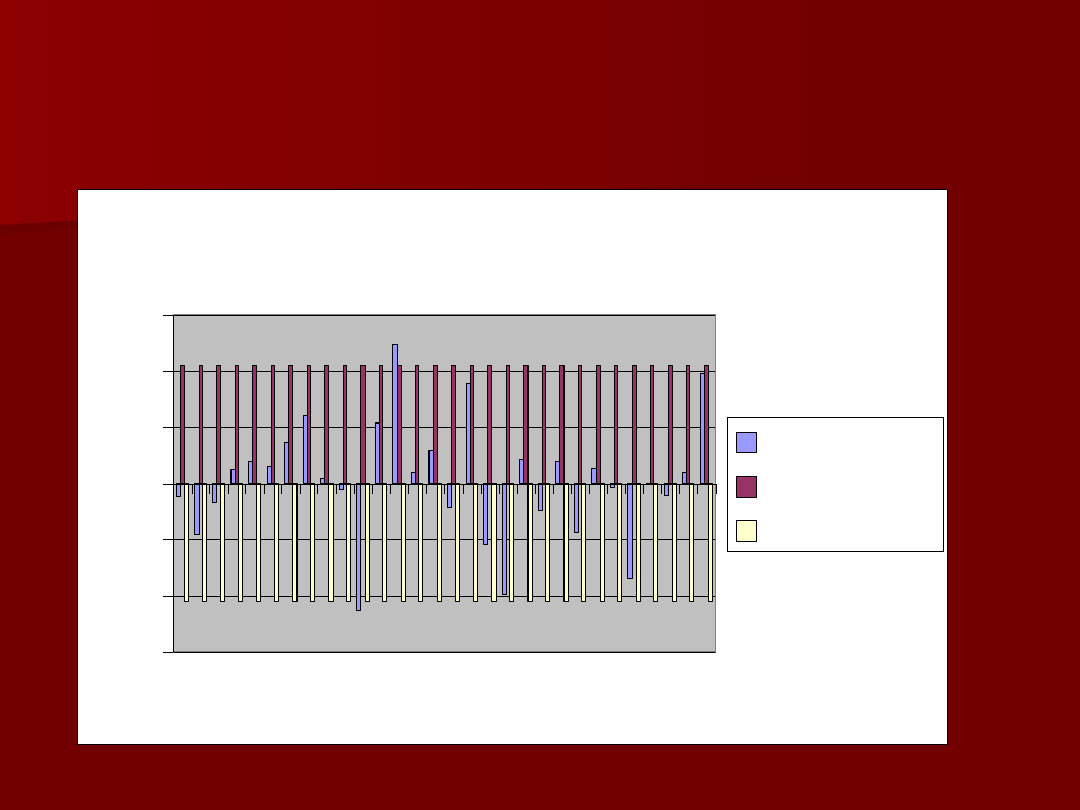
Funkcja ACF (k) dla

Funkcja ACF (k) dla

różnicowanego indeksu S&P

różnicowanego indeksu S&P

500

500

ACF

-0,3

-0,2

-0,1

0

0,1

0,2

0,3

1 4 7 10 13 16 19 22 25 28

lag

ACF
1,96/sqrt(n)
-1,96/sqrt(n)

23

23

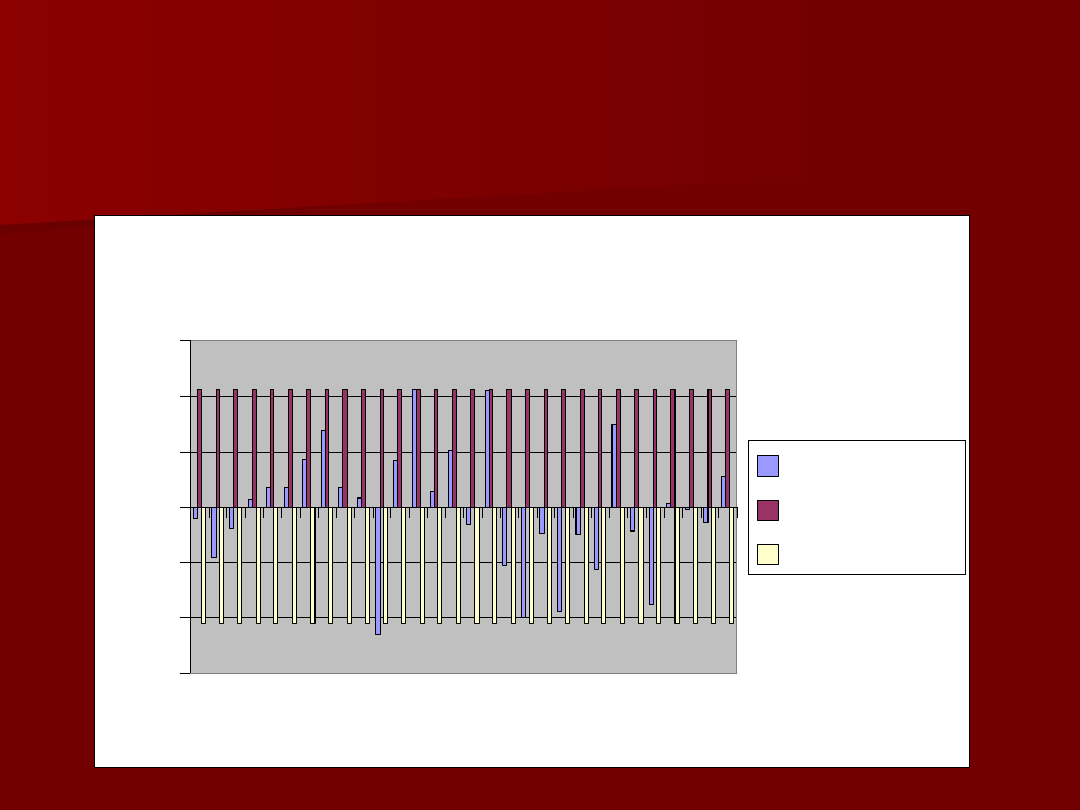
Funkcja PACF (k) dla

Funkcja PACF (k) dla

różnicowanego indeksu S&P

różnicowanego indeksu S&P

500

500

PACF

-0,3

-0,2

-0,1

0

0,1

0,2

0,3

1 4 7 10 13 16 19 22 25 28

lag

PACF
1,96/sqrt(n)
-1,96/sqrt(n)

24

24

Wykres wartości indeksu S&P 500

Wykres wartości indeksu S&P 500

charakteryzuje się wyraźną linią trendu.

charakteryzuje się wyraźną linią trendu.

Trend ten usunięto z danych za pomocą

Trend ten usunięto z danych za pomocą

operacji różnicowania.

operacji różnicowania.

Różnicowanie to spowodowało, iż funkcje

Różnicowanie to spowodowało, iż funkcje

ACF (k) i PACF (k) dla szeregu Y

ACF (k) i PACF (k) dla szeregu Y

t

t

d

d

mieszczą się (z nielicznymi wyjątkami) w

mieszczą się (z nielicznymi wyjątkami) w

przedziale ufności dla białego szumu.

przedziale ufności dla białego szumu.

Taki szereg nazywamy

Taki szereg nazywamy

błądzeniem

błądzeniem

losowym

losowym

25

25

Błądzenie losowe

Błądzenie losowe

Szereg, który w wyniku różnicowania

Szereg, który w wyniku różnicowania

jest białym szumem nazywamy

jest białym szumem nazywamy

błądzeniem losowym

błądzeniem losowym

Jeśli Y

Jeśli Y

t

t

jest błądzeniem losowym, to:

jest błądzeniem losowym, to:

Y

Y

t

t

= Y

= Y

t-1

t-1

+

+

ε

ε

t

t

ε

ε

t

t

– to ciąg niezależnych losowych o

– to ciąg niezależnych losowych o

średniej zero i stałej wariancji

średniej zero i stałej wariancji

26

26

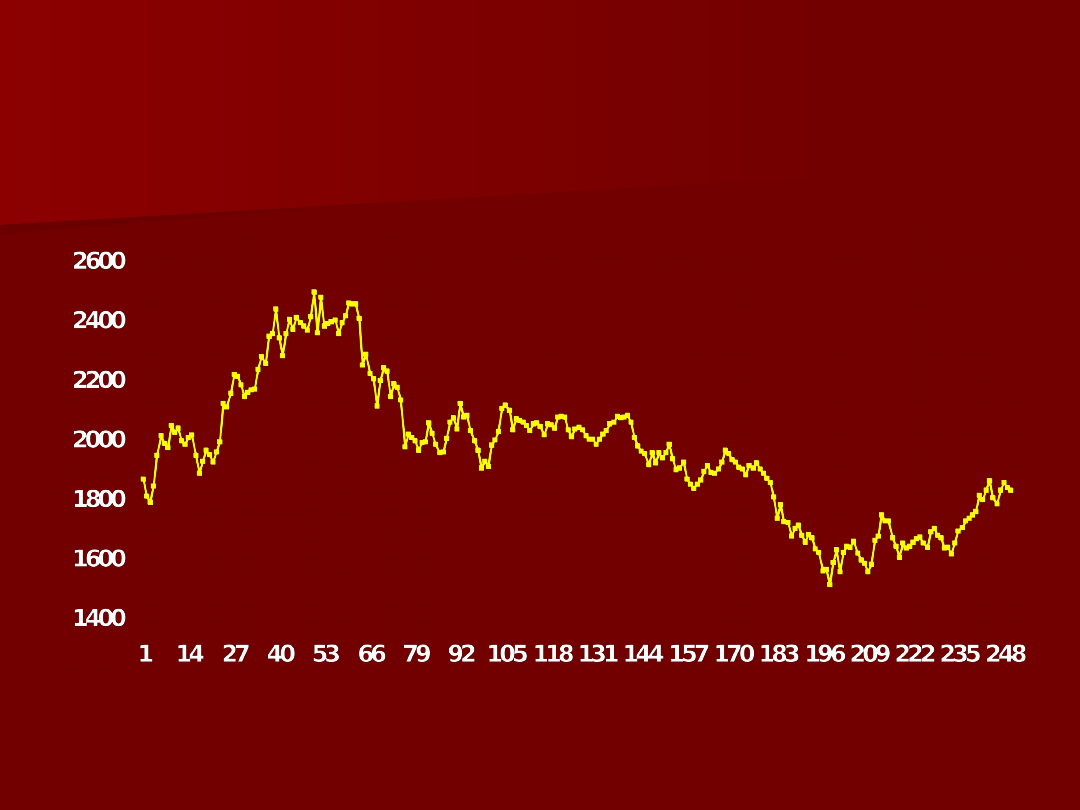
Wartość indeksu WIG 20

Wartość indeksu WIG 20