algorytmy

algorytmy

i

i

złożoność

złożoność

wykład 3

ZŁOŻONOŚĆ OBLICZENIOWA

Dokonując oceny różnych algorytmów rozwiązujących dane
zagadnienia chcemy wiedzieć, jaka jest ich złożoność
obliczeniowa, czyli inaczej, jaka ilość zasobów komputerowych
potrzebna jest do ich wykonania.

Za podstawowe zasoby komputerowe uważa się:

− czas działania algorytmu

− ilość zajmowanej pamięci.

Czy stwierdzenie:

Mój program (algorytm) jest szybki, bo rozwiązał zadanie w
55 sekund !

może posłużyć za obiektywną ocenę jego sprawności ?

Dodatkowo powinniśmy bowiem wiedzieć:

− na jakim komputerze program był wykonywany

− jaki miał procesor (częstotliwość zegara)

− co działo się w pamięci komputera podczas jego wykonywania

− jakiego kompilatora użyto do napisania programu, itp.

Ocena sprawności algorytmu przy pomocy kryteriów sprzętowych
nie jest oceną

obiektywną!

miara uniwersalna, która ma decydujący wpływ na czas
wykonywania
określonego algorytmu

Parametrem tym jest rozmiar danych wejściowych algorytmu.

Pojęcie to ma różne znaczenie dla różnych zagadnień, np.:

− w sortowaniu ciągu n-elementowego jest to ilość elementów tego ciągu, czyli n.

− dla zadań grafowych jest to liczba krawędzi rozpatrywanego grafu

− przy wyznaczaniu wartości wielomianu - stopień tego wielomianu

− dla operacji na macierzach - wymiary macierzy

− dla wyliczenia wartości funkcji n! -wartość danej n.

Dla złożoności pamięciowej jednostką jest słowo pamięci.

Dla złożoności czasowej problem jest bardziej złożony, ponieważ
jednostka ta powinna być własnością samego tylko algorytmu jako
metody rozwiązania problemu, a nie powinna zależeć od komputera,
języka programowania, kodowania , itp.
W tym celu wyróżnia się w klasie algorytmów charakterystyczne dla
niego operacje - nazywane są one operacjami dominującymi.

Przykłady operacji dominujących:

# w algorytmach sortowania
− porównanie dwóch elementów w ciągu wejściowym
− przestawienie dwóch elementów w ciągu

# w algorytmach numerycznych, np. obliczania wartości wielomianu
− operacje arytmetyczne: +, -, /, *

# w algorytmach przeglądanie drzewa binarnego
− przejście do wiązania pomiędzy dwoma węzłami w drzewie.

Za jednostkę złożoności czasowej przyjmuje się wykonanie jednej
operacji dominującej.

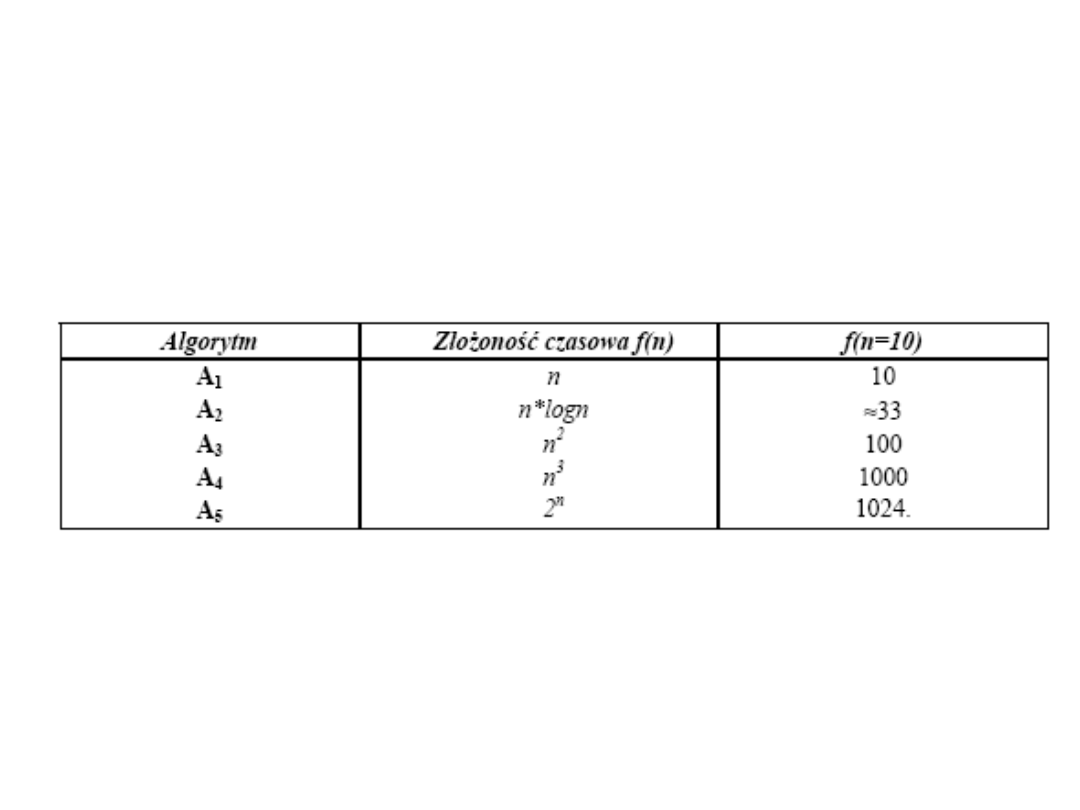
Czy postęp w szybkości obliczeń komputerów zmniejsza znaczenie
efektywności algorytmów?

Rozważmy pięć algorytmów A1, A2,..., A5, rozwiązujących ten sam problem
i mających następujące złożoności czasowe:

gdzie n - rozmiar danych wejściowych.

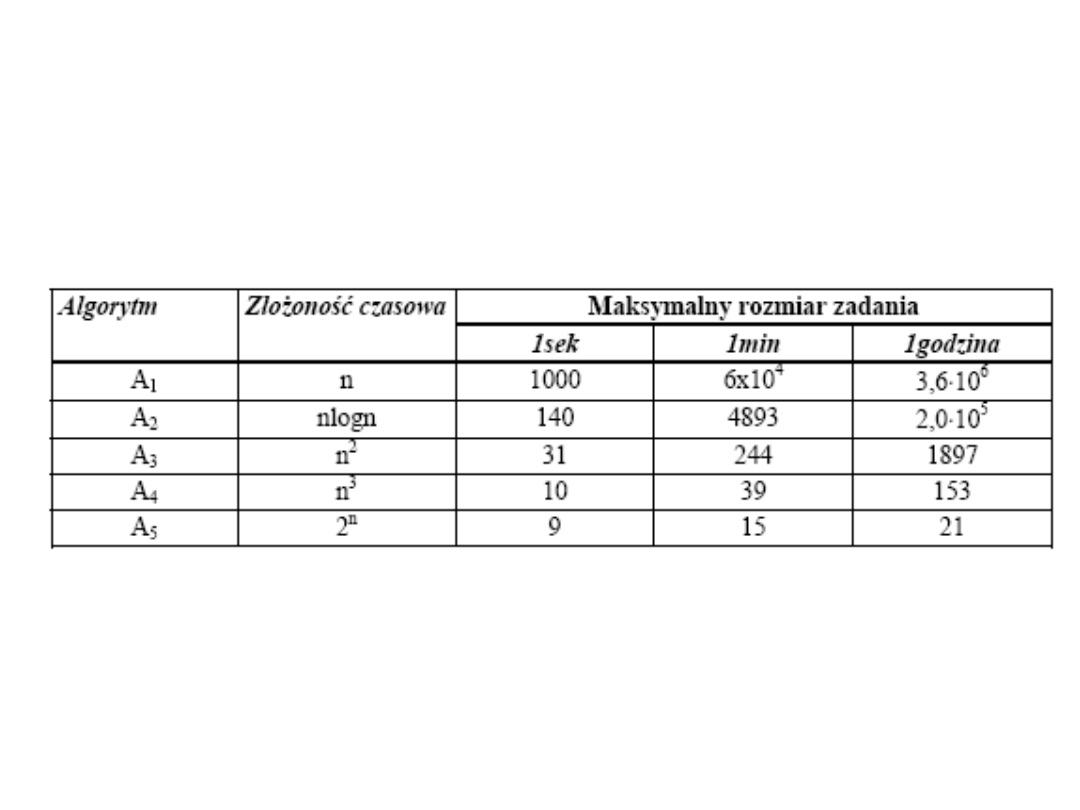
Zakładając, że jednostką czasu jest jedna milisekunda, pokażemy,
jakiego maksymalnego rzędu zadania mogą rozwiązać te algorytmy
odpowiednio w: 1 sekundzie, 1 minucie, 1 godzinie.

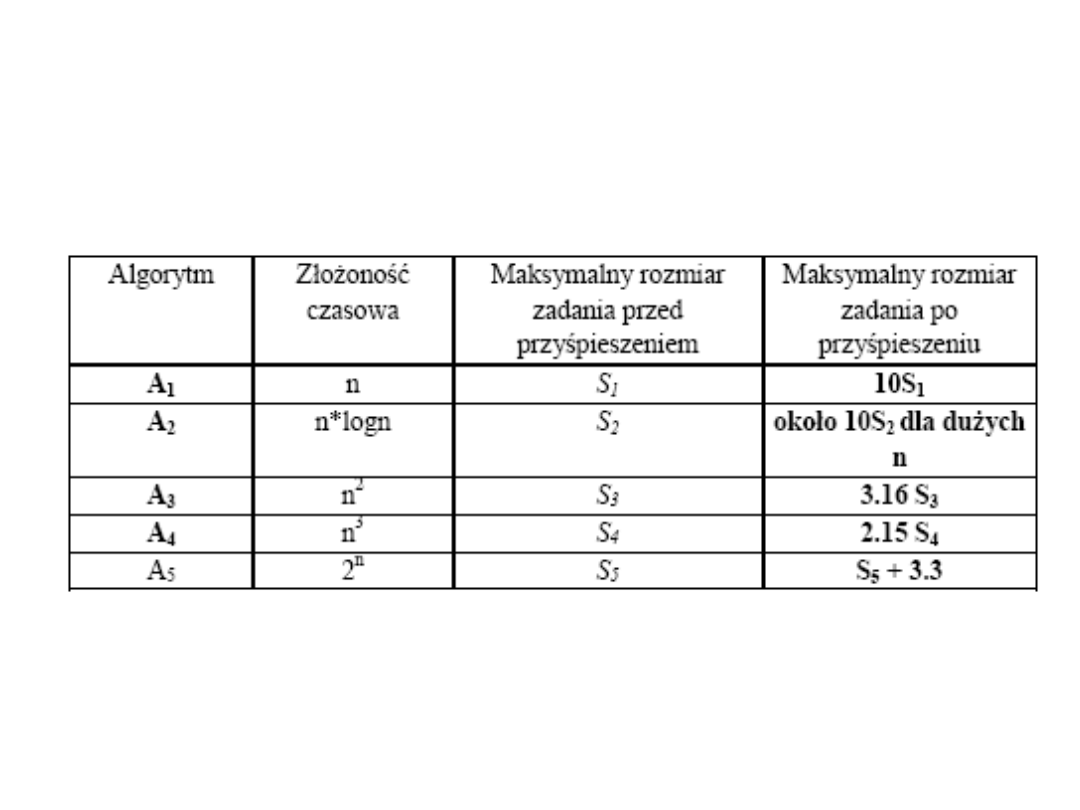
Przypuśćmy, że nowa generacja komputerów jest 10-krotnie szybsza.
Pokażemy, jaki jest wzrost rozmiaru zadań, które mogą być rozwiązane
dzięki wzrostowi szybkości komputerów:

WNIOSEK: Bardziej opłacalne jest konstruowanie szybszych algorytmów.

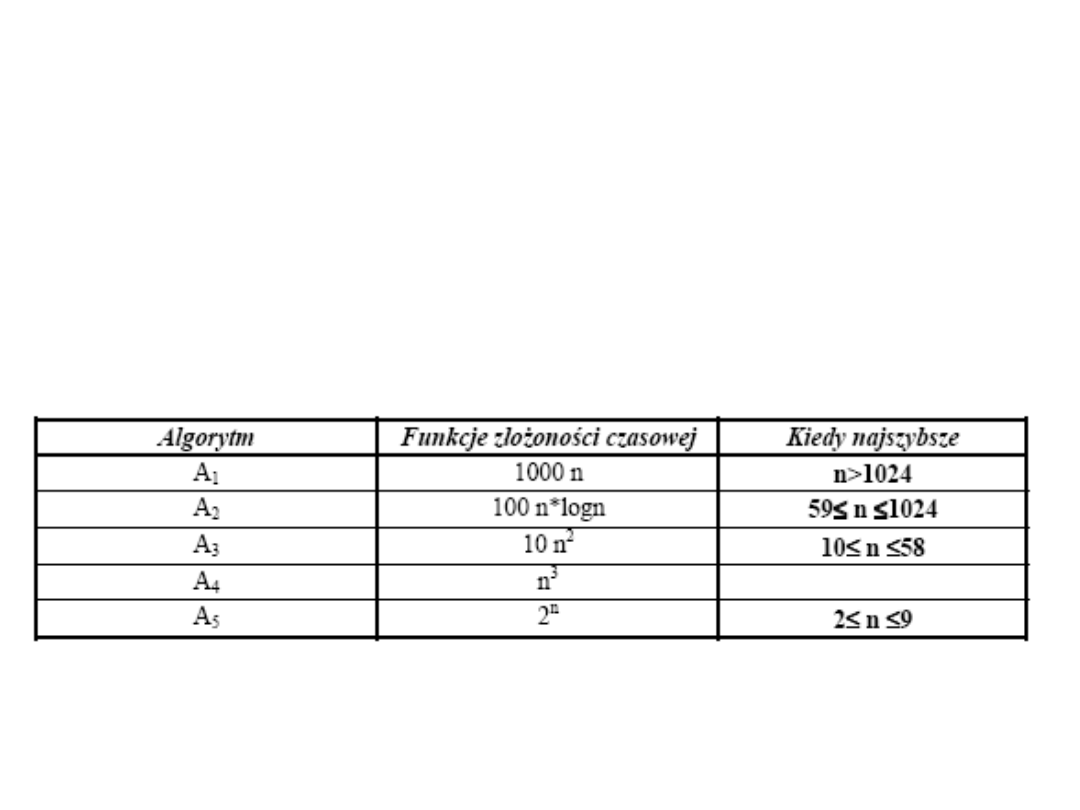
Rozpatrywane wyżej funkcje złożoności czasowej są tzw. złożonościami
asymptotycznymi, tzn. nie uwzględniają stałej proporcjonalności. Może się,
więc zdarzyć, że analizując faktyczne funkcje złożoności czasowej, algorytm
asymptotycznie gorszy jest szybszy dla małych zadań niż algorytm
asymptotycznie lepszy.

Dla ilustracji przypuśćmy, że rozważane algorytmy A1, ..., A5 mają następujące
faktyczne funkcje złożoności czasowej:

Wyznaczając złożoność czasową algorytmu (jest to funkcja rozmiaru danych n)
rozróżniamy jej dwie postacie:
1) złożoność pesymistyczna
− ilość operacji dominujących potrzebnych przy trafieniu na „najgorsze” dane
wejściowe rozmiaru n
2) złożoność oczekiwana
− ilość operacji dominujących potrzebnych przy „typowych” danych wejściowych
rozmiaru n.

Formalne definicje tych pojęć:

Przez pesymistyczną złożoność czasową algorytmu rozumie
się funkcję:

gdzie:

sup

- kres górny zbioru

D

n

- zbiór wszystkich możliwych zestawów danych

wejściowych rozmiaru n

t(d)

- liczba operacji dominujących dla zestawu

danych

wejściowych d

}

:

)

(

sup{

)

(

n

D

d

d

t

n

W





Przez oczekiwaną złożoność czasową algorytmu rozumie się funkcję:

gdzie:

p

nk

- rozkład prawdopodobieństwa zmiennej losowej X

n

,

tzn. prawdopodobieństwo,

że dla danych rozmiaru n algorytm

wykona k operacji dominujących (k ≥0),

X

n

- zmienna losowa, której wartością jest t(d), dla d D

n

czyli jest to wartość oczekiwana ave(X

n

) zmiennej losowej X

n

.









0

)

(

k

nk

p

k

n

A

W celu stwierdzenia, na ile funkcje W(n) i A(n) są reprezentatywne dla
wszystkich
danych wejściowych rozmiaru n, rozważa się dwie wrażliwości algorytmu:

miarę wrażliwości pesymistycznej:

miarę wrażliwości oczekiwanej:

gdzie dev(X

n

) jest standardowym odchyleniem zmiennej losowej X

n

, tzn.

var(X

n

) oznacza wariancję zmiennej losowej X

n

.

n

D

d

d

d

t

d

t

n









2

1

2

1

,

:

)

(

)

(

sup{

)

(

)

(

dev

)

(

n

X

n 



nk

k

n

n

n

n

p

X

k

X

X

X













2

0

))

(

ave

(

)

var(

)

var(

)

(

dev

Jak należy interpretować wartości wrażliwości ∆(n) i δ(n):

Im większe wartości ∆(n) i δ(n), tym algorytm jest bardziej wrażliwy na dane
wejściowe i tym bardziej jego zachowanie w wypadku rzeczywistych danych
może odbiegać od zachowania opisanego funkcjami W(n) i A(n).

przykład - algorytm przeszukiwania

sekwencyjnego ciągu

Problem: Dla podanego n-elementowego ciągu liczb naturalnych oraz liczby x
sprawdzić, czy liczba x jest elementem tego ciągu.

Dane wejściowe:
n, (n≥0) liczba naturalna
L[1..n+1] tablica z elementami ciągu (a

1

, ..., a

n

) na miejscach od 1do n ,

x poszukiwany element.

Dane wyjściowe (wynik):
zmienna logiczna p taka, że

p= prawda gdy element x należy do ciągu
p= fałsz, gdy element x nie należy do ciągu

przykład - algorytm przeszukiwania

sekwencyjnego ciągu cd.

Zapis algorytmu w pseudokodzie:

początek
j := 1;
L[n+1] := x;
dopóki L[j] # x wykonuj j:= j+1;
p := j ≤n
koniec;

przykład - algorytm przeszukiwania

sekwencyjnego ciągu cd.

Realizacja algorytmu (zestaw danych 1)
Dla: n = 4; ciągu (1,4,2,8), x = 4 mamy:
L[1]=1, L[2]=4, L[3]=2, L[4]=8
j=1 , L[5]=4
1 # 4, TAK j=1+1=2

( L[1]#4 )

4 # 4, NIE

( L[2)#4 )

p=2 ≤4 (prawda)

przykład - algorytm przeszukiwania

sekwencyjnego ciągu cd.

Realizacja algorytmu (zestaw danych 2)
Dla: n = 4; ciągu (1,4,2,8), x = 5 mamy
L[1]=1, L[2]=4, L[3]=2, L[4]=8
j=1 L[5]=5
1#5, TAK j=1+1=2 (L[1]#5 )
4#5, TAK j=2+1=3 (L[2]#5 )
2#5, TAK j=3+1=4 (L[3]#5 )
8#5, TAK j=4+1=5 (L[4]#5 )
5#5, NIE (L[5]#5 )
p=5 ≤4 (falsz)

przykład - algorytm przeszukiwania

sekwencyjnego ciągu cd.

Analiza złożoności algorytmu:

Rozmiar danych wejściowych :

n

Operacje dominujące :

porównania L[j])#a

Pesymistyczna złożoność czasowa :

W(n)=n+1

Pesymistyczna wrażliwość czasowa:

∆(n)=n

bo najwięcej porównań n+1

bo najmniej porównań 1

stąd ∆(n)=(n+1)-1=n

przykład - algorytm przeszukiwania

sekwencyjnego ciągu cd.

Jaka jest więc oczekiwana złożoność czasowa ?
Niech prawdopodobieństwo znalezienia elementu x na każdym z n możliwych
miejsc jest takie samo, oraz element x należy do ciągu (a

1

,.... a

n

), tzn.

Wówczas

n

1,2,

k

dla

1







n

p

nk

2

1

2

)

1

(

1

1

1

)

(

1

1

1































n

n

n

n

k

n

n

k

p

k

n

A

n

k

n

k

n

k

nk

przykład - algorytm przeszukiwania

sekwencyjnego ciągu cd.

Do obliczenia oczekiwanej wrażliwości czasowej należy znaleźć wcześniejsze
wariancje zmiennej losowej X

n





2

2

2

2

1

2

1

2

12

1

12

1

3

3

2

4

12

1

2

1

6

)

1

2

)(

1

(

2

1

2

)

1

(

2

)

1

(

2

6

)

1

2

)(

1

(

1

1

)

2

1

(

))

(

ave

(

)

var(

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

k

p

X

k

X

n

k

nk

n

k

n

n





























 



































 







































przykład - algorytm przeszukiwania

sekwencyjnego ciągu cd.

i teraz

 

 

n

n

X

X

dev

n

n

n

25

,

0

12

1

var

)

(

2











Wniosek:
Funkcja wrażliwości i funkcja złożoności są liniowe, a więc mocno wrażliwe
na układ danych wejściowych.

Faktyczna złożoność czasowa algorytmu w chwili jego użycia różni się od

wyliczonej teoretycznie, pewnym współczynnikiem proporcjonalności lub pewnymi
elementami stałymi. Ponieważ analiza złożoności interesuje się głównie zależnością
efektywności algorytmu (czasu działania) od rozmiaru problemu w sytuacji, gdy ten
ostatni wzrasta nieograniczenie, nie jest istotna dokładna formuła tej zależności, lecz
jej zachowanie asymptotyczne. Pomijamy w niej stałe elementy i inne, pozostawiając
jedynie najbardziej znaczące składniki formuły, czyli te, które decydują o zachowaniu
się formuły, gdy rozmiar n dąży do nieskończoności.

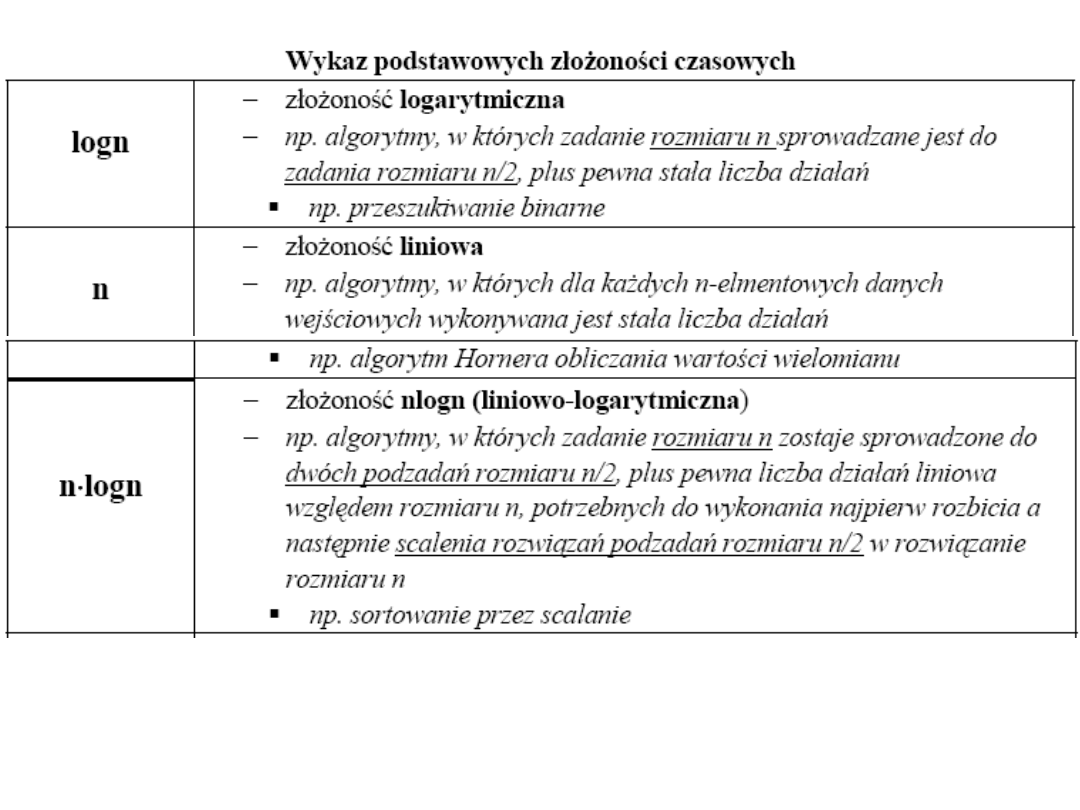
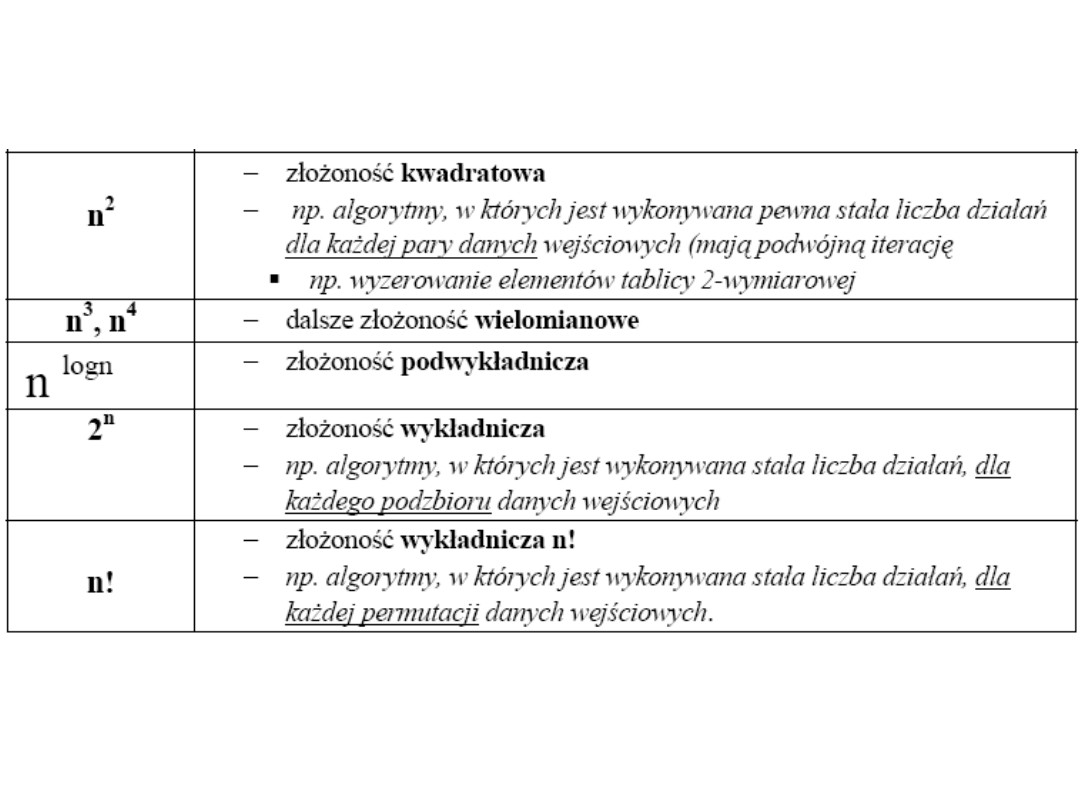
Reasumując, istotną częścią informacji, która jest zawarta w funkcji złożoności

czasowej W(n) jest jej rząd wielkości, czyli jej zachowania asymptotyczne,
gdy n dąży do nieskończoności. Poniżej omówione będą pewne pojęcia związane
z tym zagadnieniem.

Niech f, g, h : N→R

+

{0},

gdzie: N - zbiór liczb naturalnych

R

+

- zbiór liczb rzeczywistych dodatnich

NOTACJA O

NOTACJA O

Mówimy, że funkcja f jest co najwyżej rzędu funkcji g, co zapisujemy jako

f(n)= O (g (n))

jeżeli istnieje stała rzeczywista c>0 i stała naturalna n

0

takie, że

f(n) ≤ c g(n), dla każdego n ≥n

0

Np. Dla (n) = n

2

+2n mamy, że n

2

+2n=O(n

2

), bo istnieje stała c=3>0 i stała

naturalna n

o

=1 takie, że

n

2

+2n ≤ 3⋅ n

2

= 3g(n) dla każdego n ≥ 1⋅ i g(n)= n

2

Czyli f(n) = n

2

+2n jest co najwyżej rzędu O(n

2

)

NOTACJA Ω

NOTACJA Ω

Mówimy, że funkcja f jest co najmniej rzędu funkcji g, co zapisujemy jako

f(n) = Ω(g(n))

jeżeli istnieje stała c>0 i stała naturalna n

0

, takie, że

c ⋅g(n) ≤ f(n) dla każdego n ≥ n

0

Inaczej mówiąc: g(n) = O(f(n))

NOTACJA Θ

NOTACJA Θ
Mówimy, że funkcja f jest dokładnie rzędu funkcji g, co zapisujemy jako

f(n) = Θ(g(n))

jeżeli istnieja stałe c

1

>0, c

2

>0 oraz stała naturalna n

o

, takie, że

c

1

⋅g(n) ≤ f(n) ≤ c

2

⋅g(n) dla każdego n ≥ n

o

Czyli inaczej f(n) = O(g(n)) i f(n) = Ω(g(n)).

Np. Dla funkcji f(n) = 1/2 n

2 -

3n mamy, że f(n)= 1/2 n2 - 3n = Θ(n

2

)

ponieważ istnieją stałe c

1

>0, c

2

>0 i n

o

, dla których

c

1

n

2

≤ 1/2 n

2 -

3n ≤ c

2

n

2

dla każdego n ≥ n

o

Można bowiem sprawdzić, że dla c

1

= 1/14, c

2

= 1/2, n

0

=7 zachodzi nierówność

7.

n

dla

2

1

3

2

1

14

1

2

2

2









n

n

n

n

Do porównania rzędów wielkości dwóch danych funkcji f(n) i g(n) można
wykorzystać obliczenia następującej granicy:

Jeżeli
E=+∞, to

g(n) = O(f(n)) ale NIE f(n)=O(g(n))

E=c>0,

to

f(n) = Θ(g(n))

E=0,

to

f(n) = O(g(n)) ale NIE g(n)=O(f(n)).

)

(

)

(

lim

n

g

n

f

E

n 





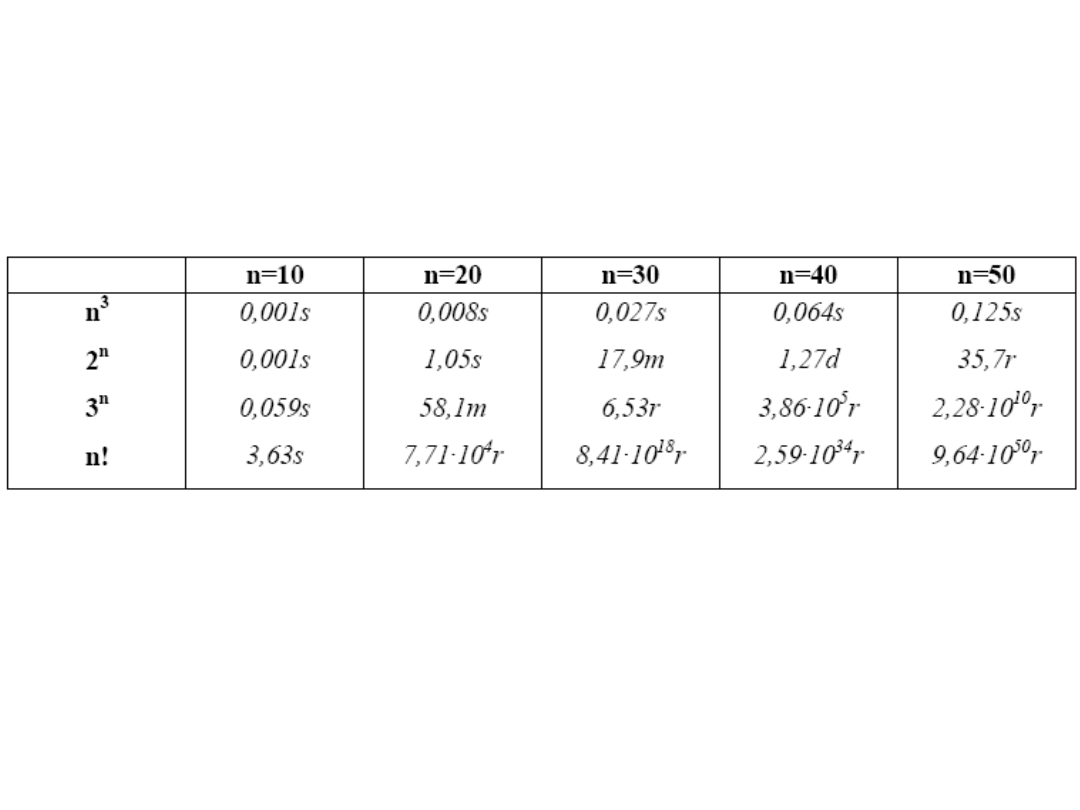
Przyjmijmy, że komputer, na którym wykonujemy te algorytmy może wykonać
1 milion operacji na 1 sek.

dla n!=24! czas jest większy niż obecny wiek wszechświata.