Dr Galina

Cariowa

•

M. Morris Mano

, Charles R. Kime – Podstawy

projektowania układów logicznych i

komputerów, Wydawnictwa Naukowo-

Techniczne,

•

Giovanni De Micheli

- Synteza i optymalizacja

układów

cyfrowych, Wydawnictwa Naukowo-Techniczne,

•

Majewski Władysław

- Układy logiczne,

Podręczniki

akademickie EiT,

•

Jan Pienkos

, Janusz Turczyński - Układy scalone

TTL w

systemach cyfrowych, Wydawnictwa Komunikacji i

Łączności,

•

Wilkinson Barry

- Układy cyfrowe,

•

Grocki Wojciech

- Układy cyfrowe,

•

Tyszer Jerzy

, Mrugalski Grzegorz-Technika

cyfrowa. Zbiór zadań z

rozwiązaniami, Wydawnictwa BCT.

LITERATURA

:

George Boole.

(1815 -1864)

W

1854

r.

opublikował

książkę

wprowadzając

ą

matematyczn

ą teorię logiki.

Algebra Boole’a

Początkowo algebra Boole’a

służyła do analizy zdań

logicznych i procesów

myślowych.

Obecnie algebra boolowska

jest stosowana do opisu

połączeń bramek cyfrowych

oraz do

analizy i projektowania

binarnych układów cyfrowych.

Algebra Boole’a

Układy cyfrowe

są

elementami sprzętu
elektronicznego, które
przetwarzają informację
binarną.

Układy cyfrowe

są implementowane

przy użyciu tranzystorów połączonych

ze sobą wewnątrz układów scalonych.

Algebra

Boole’a

Algebra Boole’a jest algebrą

związaną ze

zmiennymi binarnymi

, które mogą

przyjmować dwie dyskretne wartości,

0

i

1

, oraz matematycznymi

funkcjami logicznymi,

które

operują na tych zmiennych.

Logika dwuwartościowa

.

Trzy podstawowe operacje logiczne

związane ze zmiennymi binarnymi to

AND

,

OR

oraz

NOT

.

AND

.

Na przykład

, Z=XY lub

.

Ta operacja jest przedstawiana za

pomocą kropki lub brakiem
operatora

.

Alternatywnym symbolem dla symbolu

”kropka” jest symbol .



Y

X

Z





1. Operacja

AND

– mnożenie logiczne,

koniunkcja

Logika dwuwartościowa

Interpretacja

logiczna

AND

:

Z=1 wtedy i

tylko wtedy,

gdy X=1 i Y=1,

w przeciwnym

razie Z=0.

Poniższe

równania

definiują

operację logiczną

AND:

1

1

1

0

0

1

0

1

0

0

0

0

















Logika dwuwartościowa

Ta operacja przedstawiana jest

symbolem dodawania :

Z=X+Y

.

Alternatywnym symbolem dla

symbolu +, oznaczającego

OR

,

jest symbol .



2.

Operacja

OR

– dodawanie logiczne,

dysjunkcja

Logika dwuwartościowa

Interpretacja

logiczna OR

:

Z=1

, jeżeli X=1

lub Y=1, lub

obie

zmienne

X=1 i

Y=1.

Z=0

wtedy i

tylko

wtedy,

gdy

X=0 i

Y=0.

Poniższe

równania

definiują

operację

logiczną

OR

:

0+0=0

0+1=1

1+0=1

1+1=

1

W arytmetyce
binarnej 1+1=

10

.

Logika dwuwartościowa

Tę operację symbolizuje

kreska nad zmienną:

.

X

Z 

Oznacza to, że jeżeli X=1, to

Z=0,

ale jeśli X=0,

to Z=1.

3. Operacja

NOT

–

negacja

,

dopełnienie

.

Logika dwuwartościowa

Tablica prawdy

(ang.truth table)

dla danej operacji jest tablicą

kombinacji wartości binarnych

przedstawiająca zależność

między wartościami

przyjmowanymi przez zmienne a

wartościami stanowiącymi

wynik tej operacji.

Bramki logiczne

Bramki logiczne

Nazwy zakresów napięć

wyjściowych

i

wejściowych

:

WYSOKI STAN LOGICZNY

(

H

) i

NISKI

(

L

)

PRAWDA

(

T

) i

FAŁSZ

(

F

)

1

i

0

Zakładamy, że

PRAWDA

i 1 są związane z

wysokimi napięciami,

H,

a

FAŁSZ i 0

– z

niskimi,

L

.

Rodzaje

bramek

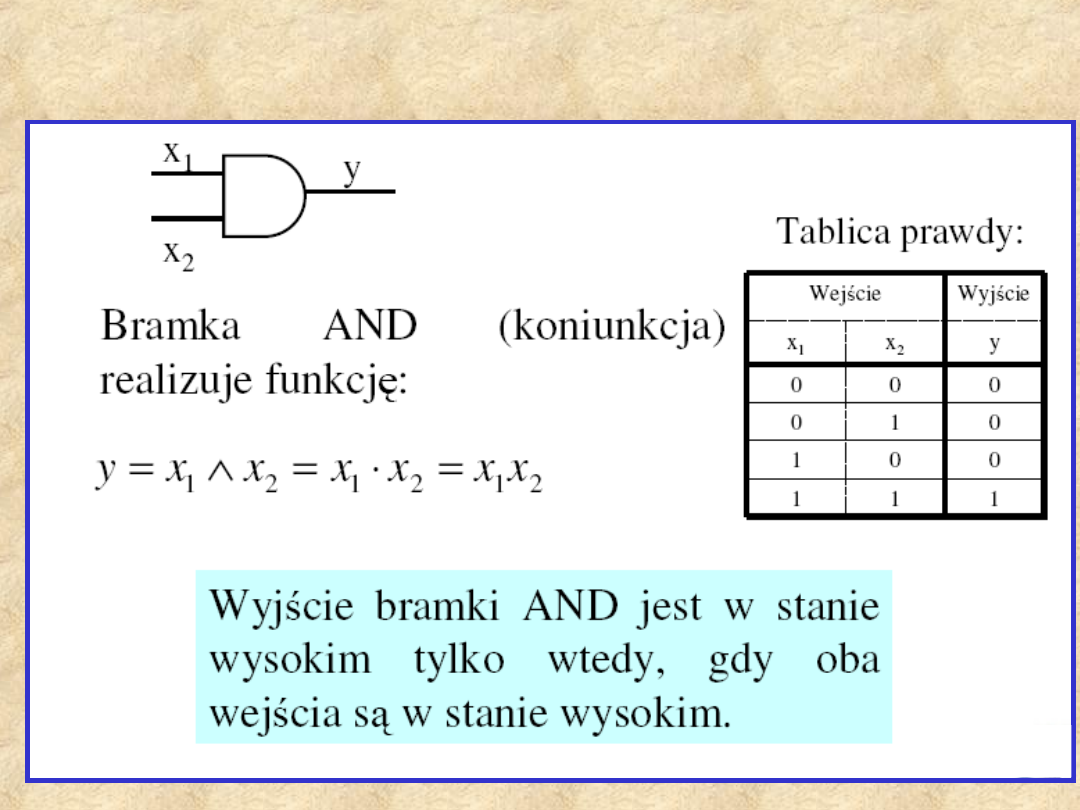
Bramka AND

Bramka OR

y=x

1

+

x

2

(dysjunkcj

a)

Bramka NOT

(negacja,

dopełnienie)

Kółeczko na wyjściu

symbolu wskazuje na

inwersję

Bramka

NAND

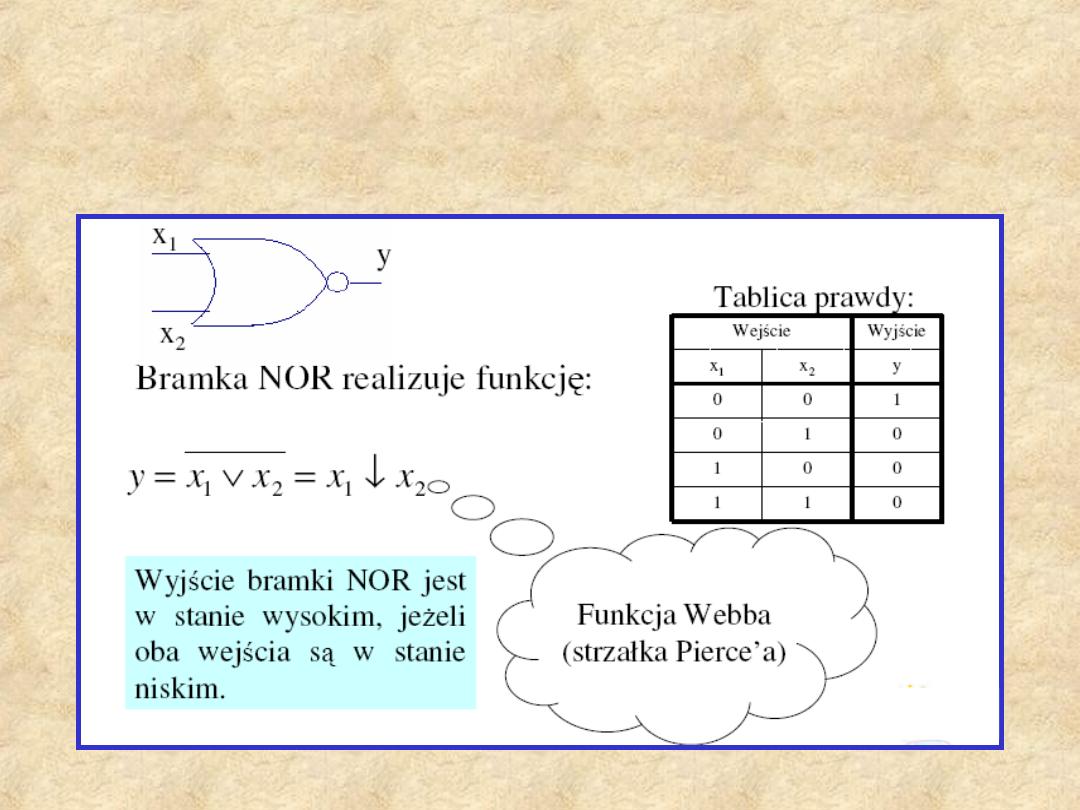
Bramka NOR

Bramka XOR (ExOR,

Albo)

nierównoważność

)

)(

(

2

1

2

1

2

1

x

x

x

x

x

x









2

)

Bramka ExNOR

)

)(

(

2

1

2

1

2

1

x

x

x

x

x

x

y











Algebra

Boole’a

Wyrażenie boolowskie

jest to

wyrażenie algebraiczne utworzone z

użyciem zmiennych binarnych, stałych 0 i

1, symboli operacji logicznych i

nawiasów.

Projektowanie układów logicznych jest

oparte na przekształceniu

wyrażeń

boolowskich

.

Algebra Boole’a

1) za pomocą

równania boolowskiego

,

które składa się ze zmiennej binarnej,

poprzedzającej znak równości i wyrażenia

boolowskiego. Na przykład:

F=1, jeśli X=1 lub Y=0 i Z=1.

Dwie części wyrażenia,

X

oraz ,

nazywamy

wyrazami

(ang. term)

wyrażenia F,

a zmienne X, Y, Z -

literalami.

Z

Y

X

Z

Y

X

F





)

,

,

(

Z

Y

Funkcja boolowska

może być opisana na dwa

sposoby:

Algebra Boole’a

2) Funkcja boolowska może być przedstawiona

za pomocą tablicy prawdy.

Tablica prawdy

funkcji zawiera spis

wszystkich kombinacji 0 i 1 , które

mogą być przypisane zmiennym

binarnym, oraz spis wartości funkcji

dla każdej kombinacji binarnej.

Liczba wierszy tablicy prawdy wynosi

, gdzie n jest liczbą zmiennych

funkcji.

n

2

Algebra

Boole’a

X Y Z

F

0 0 0

0

0 0 1

1

0 1 0

0

0 1 1

0

1 0 0

1

1 0 1

1

1 1 0

1

1 1 1

1

Kombinacje

binarne tablicy

prawdy stanowią

n-bitowe liczby

binarne

,

odpowiadające

liczeniu w

systemie

dziesiętnym od 0

do

1

2 

n

Tablica prawdy
funkcji

Z

Y

X

Z

Y

X

F





)

,

,

(

• Istnieje tylko jeden sposób

przedstawienia funkcji boolowskiej za

pomocą tablicy prawdy.

• Gdy funkcja jest przedstawiona w postaci

równania boolowskiego, można ją wyrazić

na wiele sposobów, ponieważ można

przekształcać wyrażenia boolowskie

zgodnie z

prawami algebry Boole’a.

Prawa Algebry Boole’a

Prawo
przemienności

yx

xy

x

y

y

x









Prawa Algebry

Boole’a

Kolejność, w jakiej

zmienne są zapisane, nie

wpływa na wynik

(operacji OR i AND) .

Prawa Algebry Boole’a

z

y

x

z

y

x











)

(

)

(

Prawo

łączności

z

xy

yz

x

)

(

)

(



Wynik operacji stosowanej do trzech

zmiennych nie zależy od kolejności

pobierania zmiennych,

nawiasy mogą

być usunięty.

Prawo rozdzielności

)

)(

(

)

(

)

(

)

(

)

(

z

x

y

x

yz

x

xz

xy

z

y

x















Prawa Algebry

Boole’a

Drugie prawo rozdzielności jest

dualne względem zwykłego

(pierwszego) prawa

rozdzielności.

Prawa Algebry Boole’a

Wyrażenie

dualne

do danego

wyrażenia algebraicznego uzyskamy,

zamieniając ze sobą operacje AND i

OR oraz zastępując jedynki zerami i

zera jedynkami.

Wyrażenie dualne nie jest

równe oryginalnemu

wyrażeniu

.

Prawa Algebry Boole’a

Prawa De Morgana

(dla dwóch

zmiennych)

y

x

y

x







y

x

y

x







Prawa De Morgana

(

dla wielu

zmiennych

)

n

n

x

x

x

x

x

x















...

...

2

1

2

1

n

n

x

x

x

x

x

x















...

...

2

1

2

1

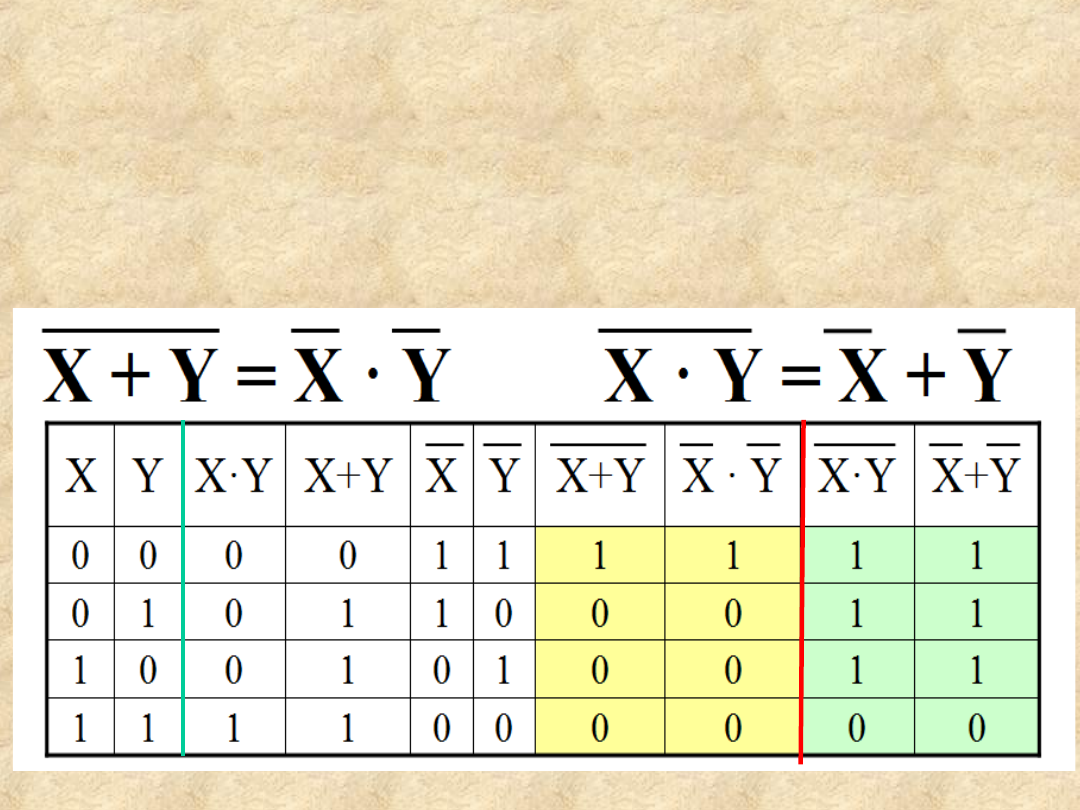
Weryfikacja twierdzenia

De Morgana

Prawa idempotentności

x

xx

x

x

x







Prawa

sprzeczności

1

0









x

x

x

x

Prawa Algebry

Boole’a

Prawa Algebry Boole’a

Prawo podwójnej negacji

x

x 

Dwukrotne dopełnienie przywraca

zmienną do jej pierwotnej wartości.

Pierwsze prawo identyczności

0

0

)

(

1

1









x

ie

pochlanian

x

Drugie

prawo identyczności

x

x

x

x









1

0

Stałe 0

Stała

1

Prawa Algebry

Boole’a

Prawa Algebry Boole’a

Twierdzenie o

zgodności

(

ang.

consensus theorem)

z

x

xy

yz

z

x

xy









Dowód

twierdzenia:











yz

x

xyz

z

x

xy











yz

x

z

x

xyz

xy











)

1

(

)

1

(

y

z

x

z

xy

z

x

xy

















)

(

x

x

yz

z

x

xy

yz

z

x

xy

Prawa Algebry Boole’a

Każdą zmienną w tożsamości

można zastąpić wyrażeniem

boolowskim, a tożsamość dalej

jest spełniona.

Przykład

.

Mamy wyrażenie

(A+B)(A+CD).

Przyjmiemy X=A, Y=B, Z=CD.

Na mocy drugiego prawa

rozdzielności

mamy:

(A+B)

(A+CD)=A+BCD

.

Zastosowanie algebry Boole’a.

Przekształcenie wyrażeń

boolowskich

Udowodnij, że lewa strona jest równa

prawej.

z

y

x

y

x

z

x

y











P

L

P

z

y

x

z

x

y

z

x

y

z

x

x

x

y

z

x

x

y

z

x

x

y

z

x

x

y

z

x

y

y

x

y

z

x

y

x

y

y

x

z

x

y

L



























































































)

(

1

)

)(

(

)

(

1

)

(

)

)(

(

)

(

prawo

przemienności

drugie prawo

rozdzielności

prawo

sprzeczności

prawo

sprzeczności

prawo

przemienności

Zastosowanie algebry

Boole’a

drugie prawo

rozdzielności

Zastosowanie algebry

Boole’a

Udowodnij, że lewa strona jest równa prawej

ab

b

a

a



 )

(

L

=

P

ab

aba

b

ab

aba

b

a

a

a

a

a

b

a

b

a

a

b

a

b

a

a

b

a

b

a

a

b

a

a



















































0

0

0

)

)(

(

)

(

)

(

L=

P

b

a

b

a

b

a







Prawo De

Morgana

Prawo De

Morgana

a

aa

o

a

a





Zastosowanie algebry

Boole’a

Znajdowanie

dopełnień:

- przez zamianę jedynek na zera i zer

na

jedynki w kolumnie tablicy

prawdy

opisującej wartości

funkcji;

-

algebraicznie

, stosując prawa De

Morgana;

- na podstawie

wyrażeń dualnych

.

Zastosowanie algebry

Boole’a

Znaleźć

dopełnienie

funkcji

.z

y

x

z

y

x

F











z

y

x

z

y

x

F







z

y

x

z

y

x

)

)(

(

z

y

x

z

y

x











prawo De

Morgana

prawo De

Morgana

Zastosowanie algebry

Boole’a

Znaleźć

dopełnienie

funkcji

.

z

y

x

z

y

x

F





)

(

)

(

z

y

x

z

y

x

F





Bierzemy w nawiasy

wyrazy pierwotnej

funkcji

)

)(

(

z

y

x

z

y

x









Zapisujemy wyrażenie

dualne do funkcji F

F

z

y

x

z

y

x











)

)(

(

Negujemy każdy

literał

Standardowe

postacie wyrażeń

boolowskich

Formuły standardowe zawierają ;

wyrazy iloczynowe

(np., )

oraz

wyrazy sumacyjne

(np.,

)

z

y

x

z

y

x





Iloczyn

, w którym wszystkie zmienne

występują dokładnie jeden raz,

zarówno w postaci prostej, jak i

zanegowanej, nazywa się

mintermem

.

Standardowe

postacie wyrażeń

boolowskich

Minterm

– przedstawia sobą

dokładnie

jedną

kombinację zmiennych

binarnych w tablicy prawdy;

– ma wartość

1

dla tej

kombinacji i

0 dla wszystkich

pozostałych

kombinacji.

Własności mintermów

1. Dla n zmiennych istnieje

dokładnie różnych

mintermów.

n

2

2. Dowolna funkcja boolowska może

być wyrażona w postaci sumy

logicznej mintermów.

3. Dopełnienie funkcji zawiera te

mintermy, których nie zawiera

pierwotna funkcja.
4. Funkcja, która zawiera wszystkie

mintermów, jest równa

logicznej 1.

n

2

Mintermy trzech

zmiennych

x y z

Wyraz

iloczyno

wy

Symbol

minter

mu

m

0

m

1

m

2

m

3

m

4

m

5

m

6

m

7

0

0

0

m

0

1 0 0 0 0 0 0 0

0

0

1

m

1

0 1 0 0 0 0 0 0

0

1

0

m

2

0 0 1 0 0 0 0 0

0

1

1

m

3

0 0 0 1 0 0 0 0

1

0

0

m

4

0 0 0 0 1 0 0 0

1

0

1

m

5

0 0 0 0 0 1 0 0

1

1

0

m

6

0 0 0 0 0 0 1 0

1 1

1

m

7

0 0 0 0 0 0 0 1

z

y

x

z

y

x

z

y

x

yz

x

z

y

x

z

y

x

z

xy

xyz

Standardowe postacie

wyrażeń boolowskich

Funkcja boolowska może być

przedstawiona algebraicznie na podstawie

tablicy prawdy przez utworzenie

sumy

logicznej wszystkich mintermów

, dla

których funkcja daje wartość 1.

Takie wyrażenie nosi nazwę

sumy

mintermów

.

Suma mintermów stanowi

standardową postać

wyrażenia

logicznego.

Standardowe postacie

wyrażeń boolowskich

Wyraz sumacyjny

, który zawiera

wszystkie zmienne w postaci prostej bądź

zanegowanej nazywany jest

makstermem.

Maksterm

– przedstawia sobą dokładnie

jedną

kombinację zmiennych

binarnych w

tablicy prawdy;

– ma wartość

0

dla tej kombinacji i

1

dla wszystkich

pozostałych kombinacji.

Makstermy trzech

zmiennych

x y z

Wyraz
sumacyj

ny

Symbol
makster

mu

M

0

M

1

M

2

M

3

M

4

M

5

M

6

M

7

0 0 0 x+y+

z

M

0

0 1 1

1

1

1

1

1

0 0 1

M

1

1 0 1

1

1

1

1

1

0 1 0

M

2

1 1 0

1

1

1

1

1

0 1 1

M

3

1 1 1

0

1

1

1

1

1 0 0

M

4

1 1 1

1

0

1

1

1

1 0 1

M

5

1 1 1

1

1

0

1

1

1 1 0

M

6

1 1 1

1

1

1

0

1

1 1 1

M

7

1 1 1

1

1

1

1

0

z

y

x 



z

y

x





z

y

x 



z

y

x 



z

y

x





z

y

x





z

y

x 



Standardowe postacie

wyrażeń boolowskich

Funkcja boolowska może być przedstawiona

algebraicznie na podstawie tablicy prawdy

przez utworzenie

iloczynu logicznego

wszystkich makstermów

, dla których

funkcja daje wartość 0.

Takie wyrażenie nosi nazwę

iloczynu

sum.

Iloczyn makstermów stanowi

standardową postać

wyrażenia

logicznego.

Sposoby zapisu funkcji

logicznych

• Zapis

algebraiczny

• Tablica prawdy
• Wektor prawdy
• Postać DCF
• Postać CCF
• Postać FDCF
• Postać FCCF

Zapis algebraiczny

z

z

y

xy

z

y

x

f









)

(

)

,

,

(

Funkcja boolowska jest opisana za

pomocą

równania boolowskiego

składającego ze zmiennej binarnej,

która poprzedza znak równości i

wyrażenie boolowskie.

Opcjonalnie

, po identyfikatorze

funkcji następuje, ujęta w nawiasy,

lista zmiennych, rozdzielonych

przecinkami.

Przykła

d.

.

Tablica prawdy

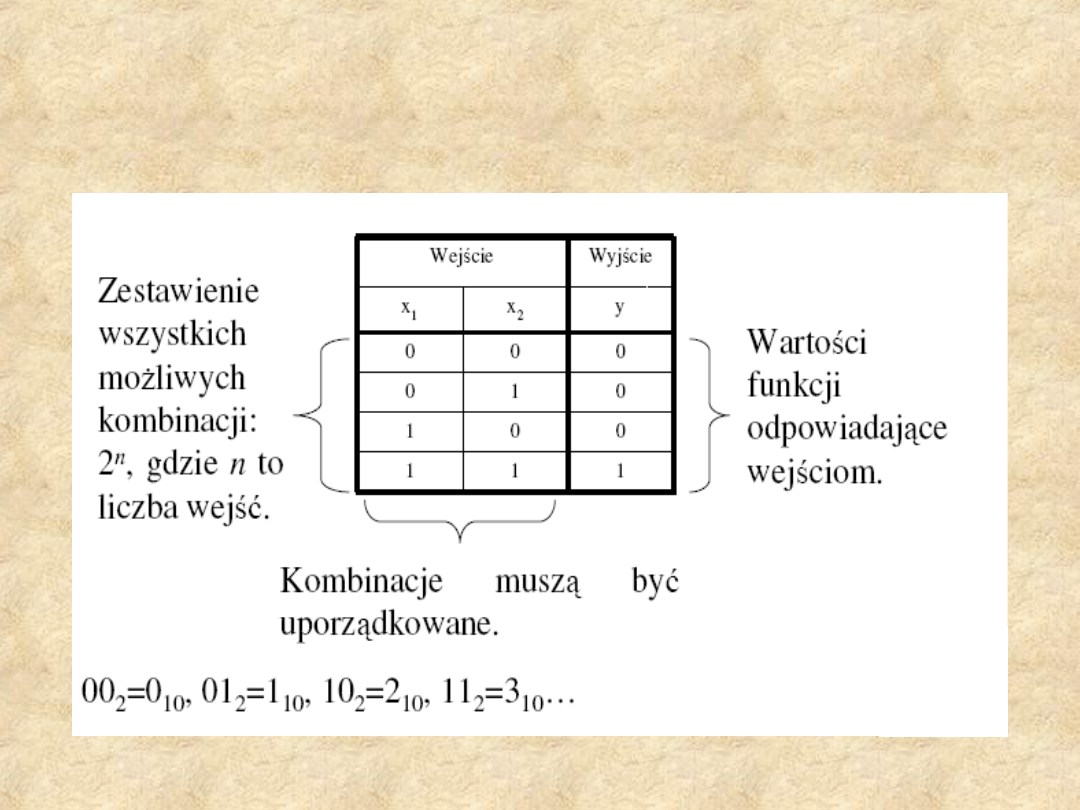
Tablica prawdy

(ang.Truth Table) to

zestawienie w kolejnych wierszach

tablicy wszystkich możliwych kombinacji

wartości logicznych argumentów funkcji

zdaniowej i dokładnie należących od

nich wartości logicznych tejże funkcji.

Kombinacje te muszą być

uporządkowane tak, aby tworzyły

kolejne liczby naturalne zapisane w

systemie dwójkowym.

Tablica prawdy bramki

AND

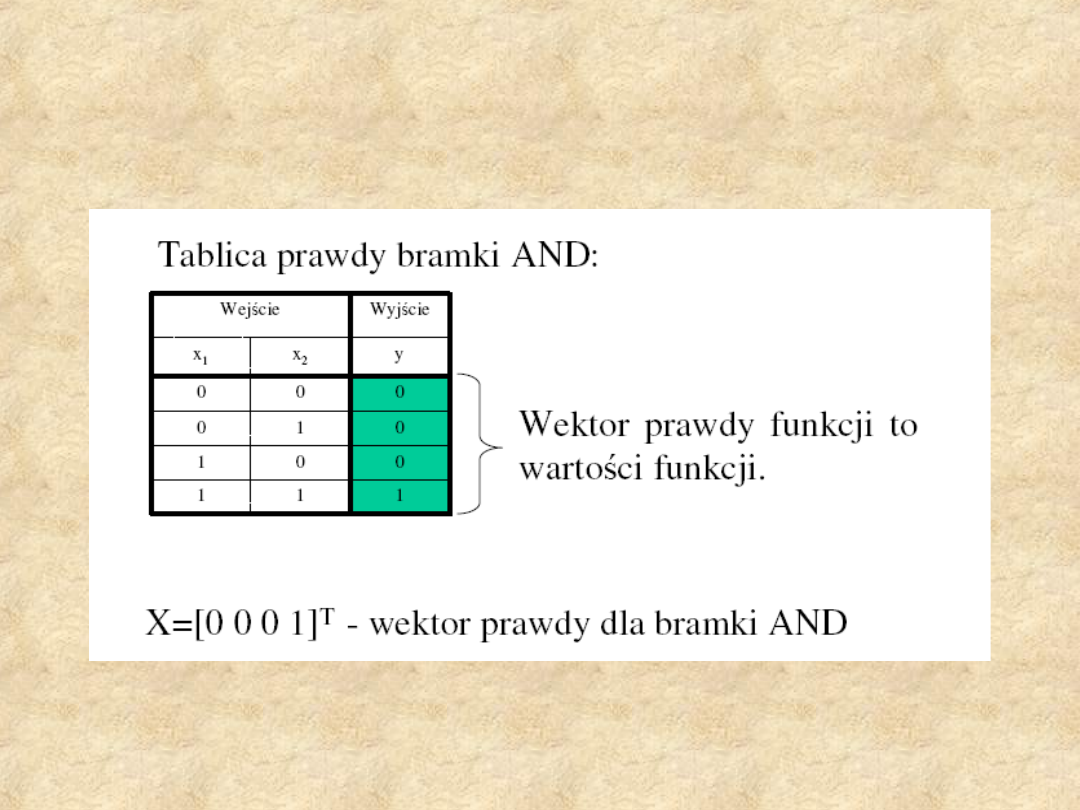
Wektor

prawdy

Standardowe postaci

funkcji boolowskich

1.

Postać DCF

(

postać dysjunkcyjna

normalna

)-

to jest dysjunkcja koniunkcji normalnych, na

przykład:

1

3

2

1

3

2

1

)

,

,

(

x

x

x

x

x

x

x

f





2.

Postać CCF

(

postać koniunkcyjna

normalna

) - to jest koniunkcja dysjunkcji

elementarnych,

na

przykład:

)

)(

)(

(

)

,

,

(

3

2

3

2

1

2

1

3

2

1

x

x

x

x

x

x

x

x

x

x

g











Standardowe postaci

funkcji boolowskich

To postać dysjunkcyjna, której składnikami są mintermy

(ang. minterm – to iloczyn wszystkich zmiennych danej

funkcji, przy czym zmienne te mogą występować jako

proste lub zanegowane) - jest to tzw.

konstytuenta „1”.

3.

Postać FDCF (SOP)

Full Disjunktive

Canonical Form

(Sum of

Products)

)

(

)

(

)

(

)

(

)

111

,

110

,

100

,

010

(

)

7

,

6

,

4

,

2

(

)

(

3

2

1

3

2

1

3

2

1

3

2

1

2

10

x

x

x

x

x

x

x

x

x

x

x

x

X

f



















Standardowe postaci

funkcji boolowskich

To postać koniunkcyjna, której składnikami są makstermy

(ang.

maksterm

– to suma wszystkich zmiennych danej

funkcji, przy czym zmienne te mogą występować jako

proste lub zanegowane) - jest to tzw.

konstytuenta „0”.











2

10

)

101

,

011

,

001

,

000

(

)

5

,

3

,

1

,

0

(

)

(x

f

4.

Postać FCCF (POS)

Full Conjunctive

Canonical Form

(Product of

Sum)

)

)(

)(

)(

(

3

2

1

3

2

1

3

2

1

3

2

1

x

x

x

x

x

x

x

x

x

x

x

x



















Uzyskiwanie postaci FDCF i

FCCF

1. Przekształcenia

algebraiczne

1. Przekształcenia

algebraiczne (c.d.)

Przykład. Przedstawić funkcję

w postaci FDCF.

c

b

a

c

b

a

h





)

,

,

(













c

b

a

a

c

c

b

b

a

c

b

a

h

)

(

)

)(

(

)

,

,

(















c

b

a

c

ab

c

b

a

c

b

a

c

ab

abc

.

c

b

a

c

b

a

c

b

a

c

ab

abc















)

7

,

6

,

5

,

4

,

2

(

)

,

,

(

FDCF

c

b

a

h

1.Przekształcenia

algebraiczne

1. Przekształcenia

algebraiczne

Przykład. Przedstawić funkcję

w postaci FCCF.

c

b

a

c

b

a

h





)

,

,

(









)

)(

(

)

,

,

(

c

a

b

a

c

b

a

h













)

)(

(

c

b

b

a

c

c

b

a





















)

)(

)(

)(

(

c

b

a

c

b

a

c

b

a

c

b

a

)

)(

)(

(

c

b

a

c

b

a

c

b

a



















)

3

,

1

,

0

(

)

,

,

(

FCCF

c

b

a

h

postać

CCF

2

. Algorytm tworzenia

FDCF

na podstawie tablicy

prawdy

• Z tablicy

wybrać zestawy zmiennych, dla

których funkcja równa się

1

;

• Dla tych zestawów stworzyć

konstytuenty

jedynki

, zawierające zmienną z inwersją, jeśli

przybiera ona w zbiorze wartość 0 i bez

inwersji, jeśli przybiera ona postać 1;

• Zbudować

dysjunkcię

uzyskanych

konstytuent 1.

2.

Algorytm tworzenia FCCF

na podstawie tablicy

prawdy

• Z tablicy

wybrać zestawy zmiennych, dla

których funkcja równa się

0

;

• Dla tych zestawów stworzyć

konstytuenty

zera

, zawierające zmienną z inwersją, jeśli

przybiera ona w zbiorze wartość 1 i bez

inwersji, jeśli przybiera ona postać 0;

• Zbudować

koniunkcję

uzyskanych

konstytuent 0.

Tworzenie funkcji w postaci

FDCF na podstawie tablicy

prawdy

Przykład

.

Tworzenie funkcji w postaci

FCCF na podstawie tablicy

prawdy

Maksterm

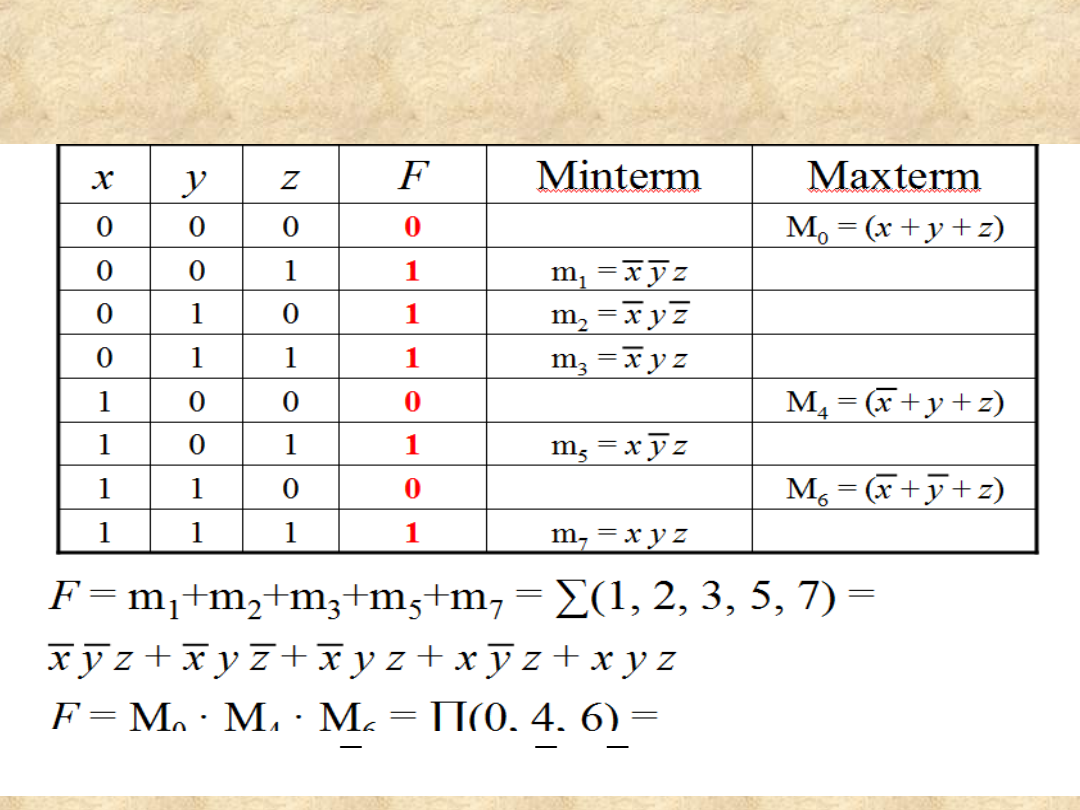
Tworzenie funkcji w postaci

FDCF i FCCF na podstawie

tablicy prawdy

)

)(

)(

(

z

y

x

z

y

x

z

y

x















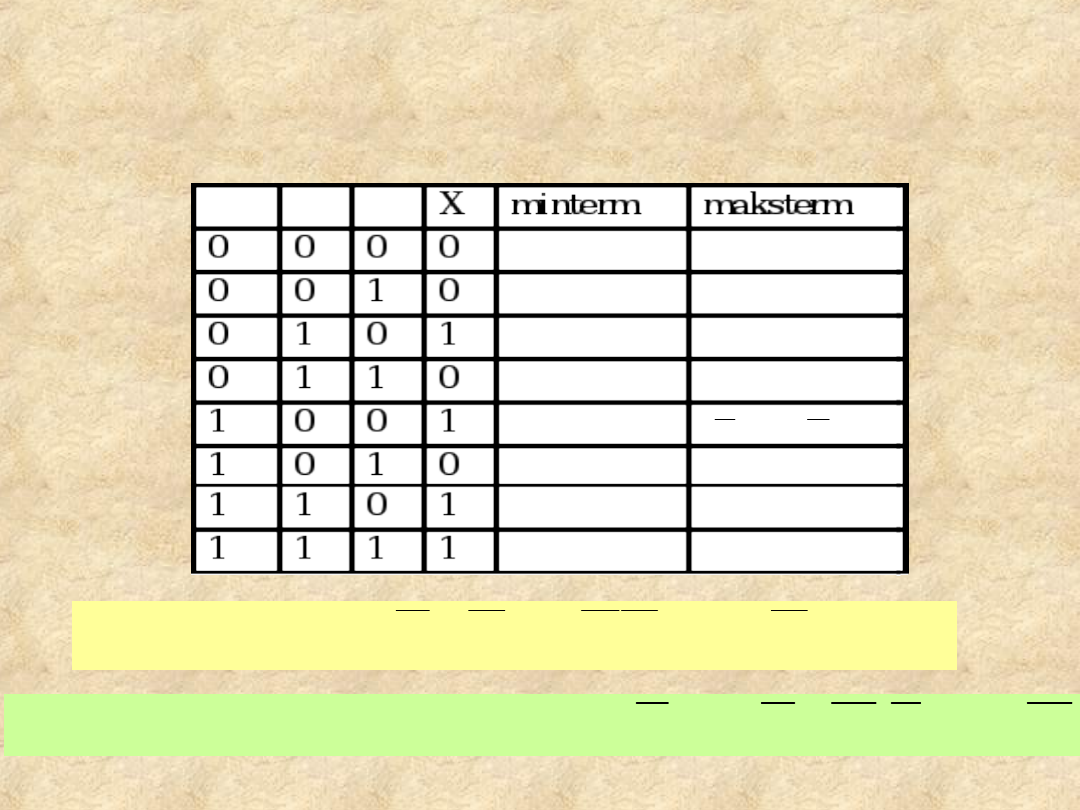
Tworzenie funkcji w postaci

FDCF i FCCF na podstawie

tablicy prawdy

3

2

1

3

2

1

3

2

1

3

2

1

3

2

1

)

,

,

(

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

f

FDCF









)

(

)

)(

)(

(

)

,

,

(

3

2

1

3

2

1

3

2

1

3

2

1

3

2

1

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

f

FCCF



















3

2

1

x

x

x





Dziękuję za uwagę

Dziękuję za uwagę

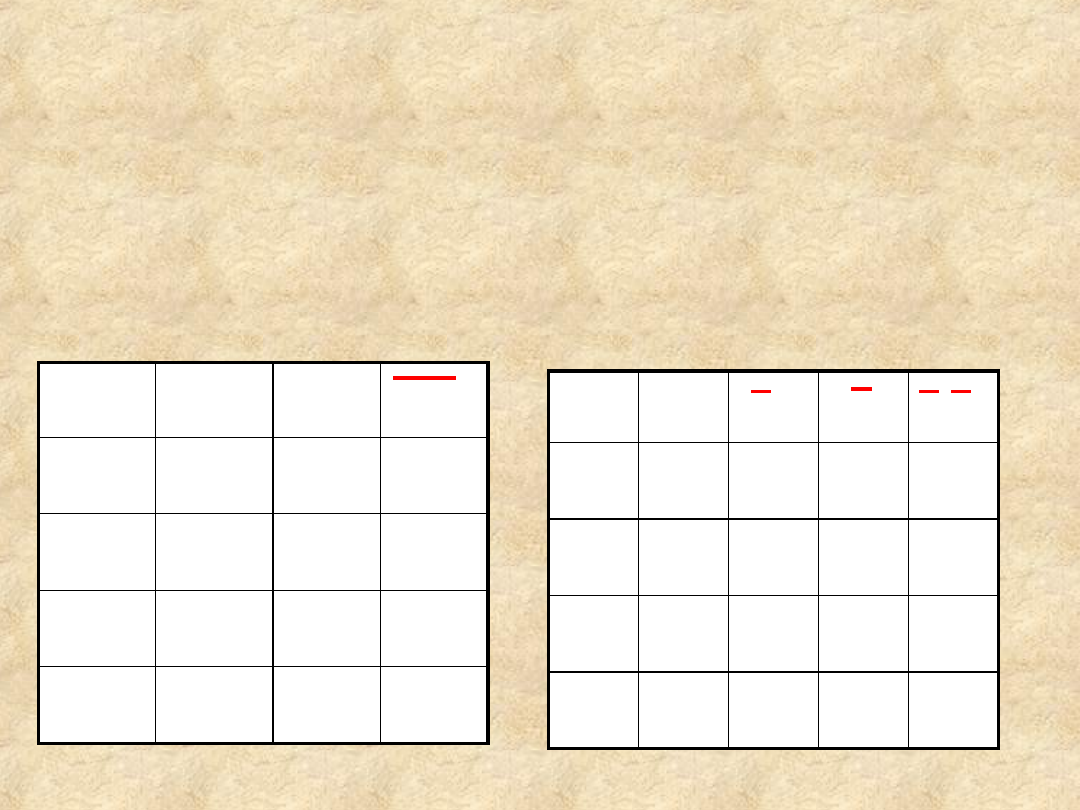
Prawa Algebry Boole’a

Tablice prawdy

do

weryfikacji

twierdzenia

De

Morgana

0

1

1

1

0

1

0

1

0

1

1

0

1

0

0

0

x+
y

x+
y

y

x

0

0

0

1

1

0

1

0

0

1

0

0

1

1

0

1

1

1

0

0

x
y

y

x

y

x