12 grudnia 2
001

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

1

Wykład 11

Wykład 11

Elementy Kombinatoryki

Elementy Kombinatoryki

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

2

Problem

Problem

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

3

Funkcje

Funkcje

Problem Dane są dwa zbiory X i Y skończone, X=
{x

1

,...,x

n

}, Y={y

1

,...,y

m

}. Ile jest funkcji

całkowitych f : X  Y?

Pudełko nr.
1

Pudełko nr.
2

Pudełko nr.
3

Pudełko nr.
4

Pudełko nr.
5

n=7, m=
5

X: a, b, c, d, e, f,
g

Y:

a

b c

d e

f

g

Jeśli |X|=n i |Y|=m, to |{f: X Y}|

= m

n

.

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

4

Przykład 1

Przykład 1

Na ile sposobów można wylosować pięć kart (ze
zwracaniem) z talii zawierającej 52 karty ?

Inaczej mówiąc : ile jest 5elementowych
ciągów, w których każdy element to jedna
52 kart?

Odp.: 52

5

lub

Ile jest funkcji ze zbioru {1,2,3,4,5} w
zbiór 52 elementowy?

lub

Na ile sposobów można włożyć liczby
1,2,3,4,5 do 52 pudełek?

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

5

Przykład 2

Przykład 2

Na ile sposobów można pokolorować graf o n
wierzchołkach, jeśli dysponujemy k kolorami?

Inaczej: Ile jest różnych funkcji całkowitych
postaci Kolor : Wierzchołki 

Zbiór_kolorów

Wierzchołk
i
pomalowan
e na żółto

Wierzchołki
pomalowan
e na
niebiesko

Wierzchołk
i
pomalowan
e na
czerwono

ODP.: k

n

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

6

Przykład 3

Przykład 3

Ile różnych liczb można zapisać w n
elementowym rejestrze bitowym?

Ile jest n elementowych ciągów, których
wyrazami jest zero lub jeden?

Ile jest różnych funkcji ze zbioru n
elementowego i o wartościach w
zbiorze{0,1}?

Odpowiedź : 2

n

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

7

Funkcje różnowartościowe

Funkcje różnowartościowe

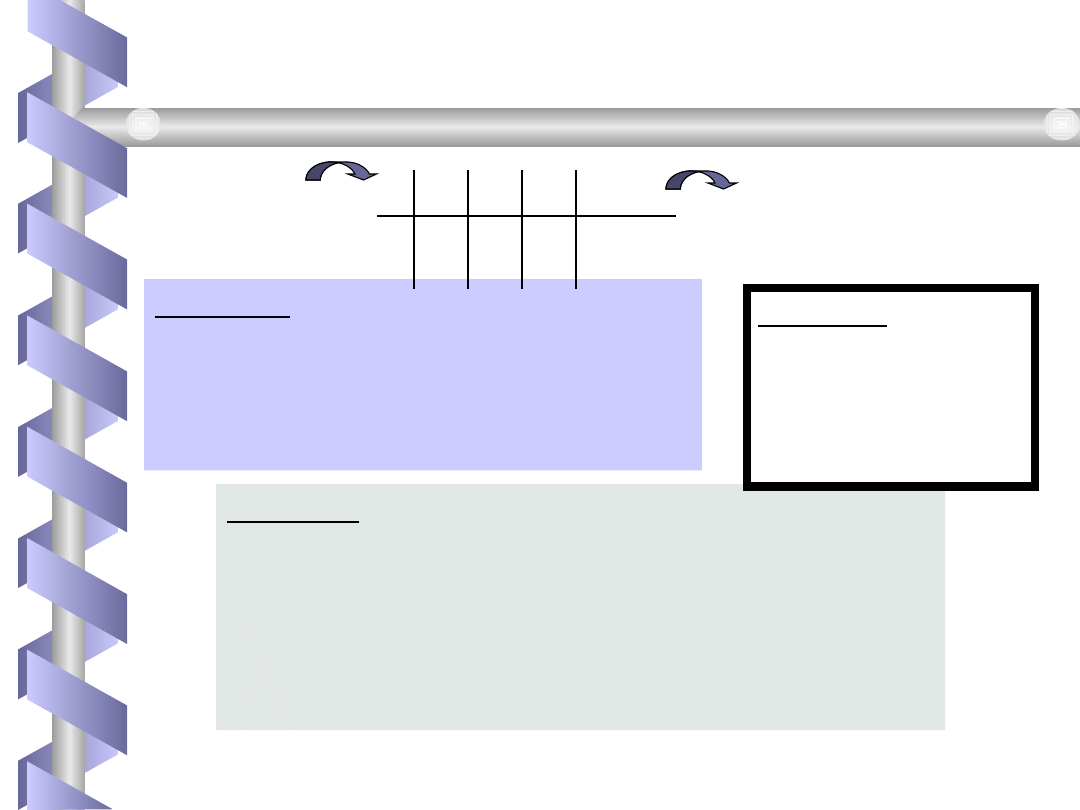
A co, jeśli wymagamy aby każde pudełko
zawierało co najwyżej jeden obiekt?

Pytanie Ile jest funkcji
całkowitych
różnowartościowych f : X 

Y ?

Oczywiście pierwszy element możemy włożyć
do dowolnego pudełka.

Y:

Jeśli x

1

włożyliśmy do pudełka y

1

, to

x

1

nie możemy tam włożyć już innych
elementów!

Czyli x

2

możemy włożyć tylko do

jednego z pozostałych pudełek.

Odpowiedź:

m

*

(m-1)

*

(m-

2) ...

*

(m-n+1)

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

8

Wariacje

Wariacje

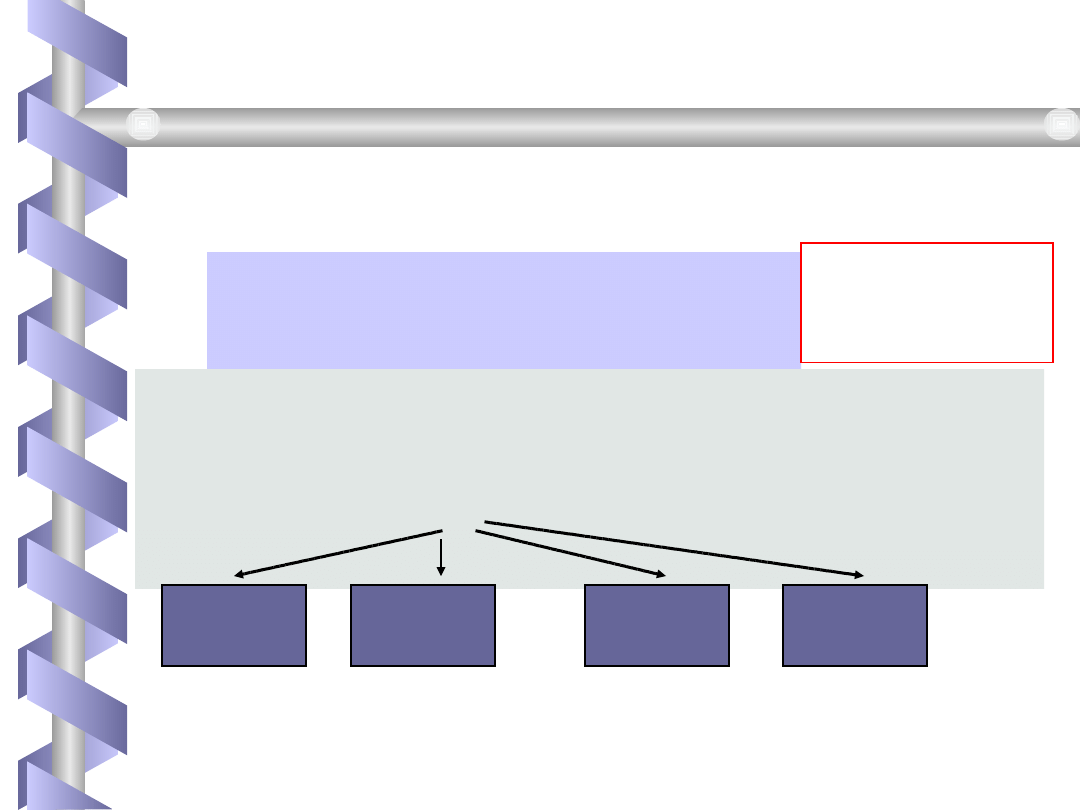
Definicja Ciąg n różnych
elementów ze zbioru m
elementowego nazywa się
wariacją n wyrazową ze zbioru m-
elementowego bez powtórzeń.

f : X  Y

1 2 3 ... n

y

i1

y

i2

y

i3

... y

in

< y

i1

, y

i2

,

y

i3

, ... ,

y

in

>

Przykład Niech A={1,2,3,4}. Wszystkie trzy-
wyrazowe wariacje ze zbioru A to:

1,2,3 1,2,4 1,3,2 1,3,4 1,4,2 1,4,3
2,1,3 2,1,4 2,3,1 2,3,4 2,4,1 2,4,3
3,1,2 3,1,4 3,2,1 3,2,4 3,4,1 3,4,2
4,1,2 4,1,3 4,2,1 4,2,3 4,3,1 4,3,2

Wniosek Liczba
tych wariacji
wynosi
m(m-1)...(m-
n+1).

1-
1

Różne elementy
zbioru Y

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

9

Przykład

Przykład

Jaka jest liczba możliwych słów 5cio literowych,
jeśli litery w słowie nie mogą się powtarzać i
dysponujemy alfabetem 24 literowym?

Ile można utworzyć ciągów 5
elementowych, bez powtórzeń, jeśli
elementami ciągu są litery z
24elementowego zbioru?

Ile jest różnowartościowych funkcji
odwzorowujących zbiór {1,2,3,4,5} w 24-ro
literowy alfabet?

Ile jest wariacji 5-
wyrazowych ze zbioru
24elementowego?

ODP.:
24*
23*22*21*20

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

10

Rozmieszczenia

Rozmieszczenia

uporządkowane

uporządkowane

Rozważmy sytuację, w której rozmieszczamy n obiektów w
m pudełkach, ale pudełka zawierają teraz ciągi, a nie
zbiory elementów.

Ile jest różnych możliwych
rozmieszczeń
uporządkowanych n obiektów w m
pudełkach?

1szy element na m sposobów, 2gi elememet na (m+1)
sposobów.

i-ty element można umieścić w pudełku k o i

k

-elementach

na i

k

+1- sposobów. Czyli razem, ity element wkładamy na

m+i-1 sposobów.

a, b

c

Pudełko 1

Pudełko 2

Pudełko
3 ....

Pudełko m

d

i

1

i

2

i

3

i

m

Odp.:
m(m+1)...
(m+n-1)

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

11

Przykład

Przykład

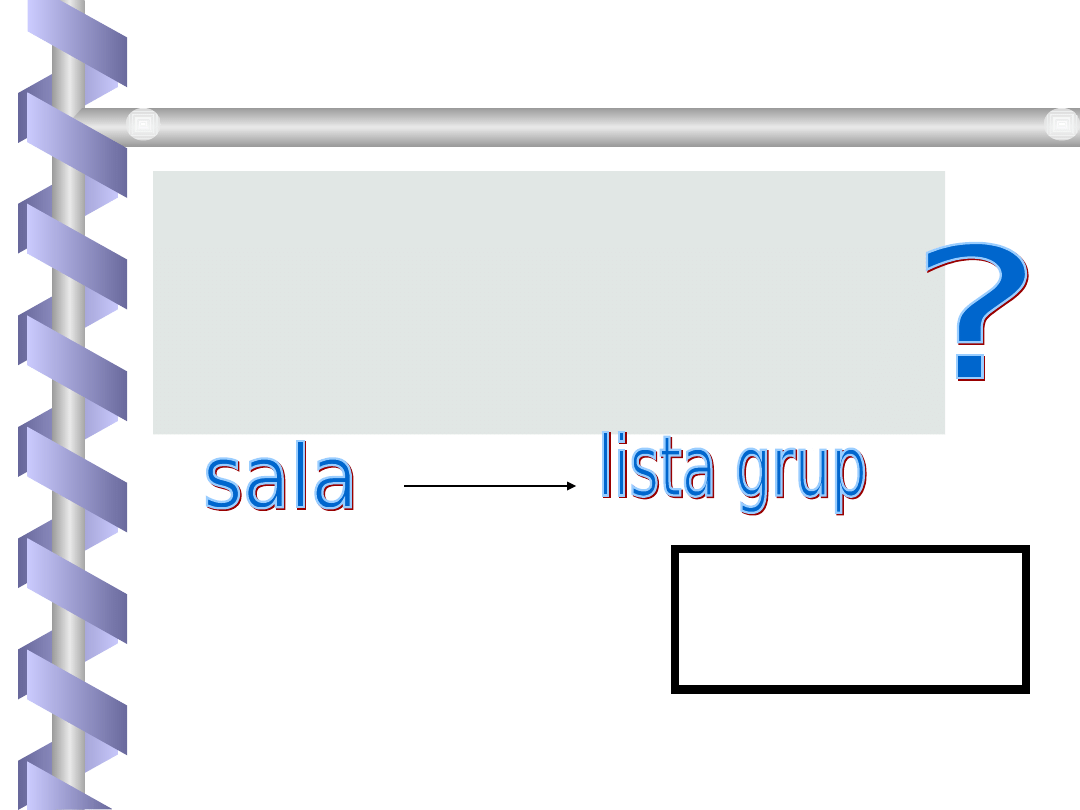
Przypuśćmy, że zajmujemy się układaniem
rozkładu zajęć. Jedno z zadań z tym związanych to
przypisanie zajęć(grup) do sal. Oczywiście o tej
samej godzinie nie możemy umieścić w tej samej
sali różnych zajęć. Przypuśćmy, że dysponujemy 7
salami i mamy 40 rożnych zajęć. Ile różnych
rozkładów zajęć można utworzyć?

Czyli: Ile jest różnych
rozmieszczeń uporządkowanych
40 obiektów w siedmiu
pudełkach?

Odp.:
7

*

8

*

9

*

...

*

(7+40-

1)

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

12

Permutacje

Permutacje

Definicja n wyrazowe
wariacje ze zbioru n
elementowego nazywamy
permutacjami.
Inaczej: permutacje to
funkcje całkowite,
różnowartościowe ze
zbioru X w zbiór X.

Liczba permutacji P(n)
zbioru n elementowego
wynosi
n*(n-1)...*2 *1, tzn. n!

Dowód tw. przez indukcje ze względu na n.

Krok 1. Liczba permutacji w zb. 1-elementowym wynosi
1. P(1)=1!=1
Założenie Ind.: P(k)=k! dla pewnego k >0.

Teza: P(k+1)= (k+1)!

Dowód. Element (k+1)szy umieszczamy na wszystkich
możliwych pozycjach (tzn. k+1 pozycjach ) we wszystkich
k-elementowych permutacjach. Zatem P(k+1)= P(k) *
(k+1)= (k+1)!

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

13

Oszacowanie

Oszacowanie

1. n!  n

n

Dzięki wzorowi Stirlinga mamy :

n! = (2n) (n/e)

n

(1+ (1/n))

2. n! = O(n

n

)

3. lg n! = (n lg n)

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

14

Przykład

Przykład

Rozważmy permutacje zbioru
{1,2,3,4}.

1,2,3,4
1,2,4,3
1,3,2,4
1,3,4,2
1,4,2,3
1,4,3,2
2,1,3,4
2,1,4,3
2,3,1,4
2,3,4,1 itd

1,2,3,4
2,1,3,4
1,3,2,4
3,1,2,4
2,3,1,4
3,2,1,4
1,2,4,3
2,1,4,3
1,4,2,3
4,1,2,3itd

*

1,2,3,4
2,1,3,4
2,3,1,4
2,3,4,1
3,2,4,1
3,2,1,4
3,1,2,4
1,3,2,4
1,3,4,2
3,1,4,2itd

*

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

15

Interpretacja

Interpretacja

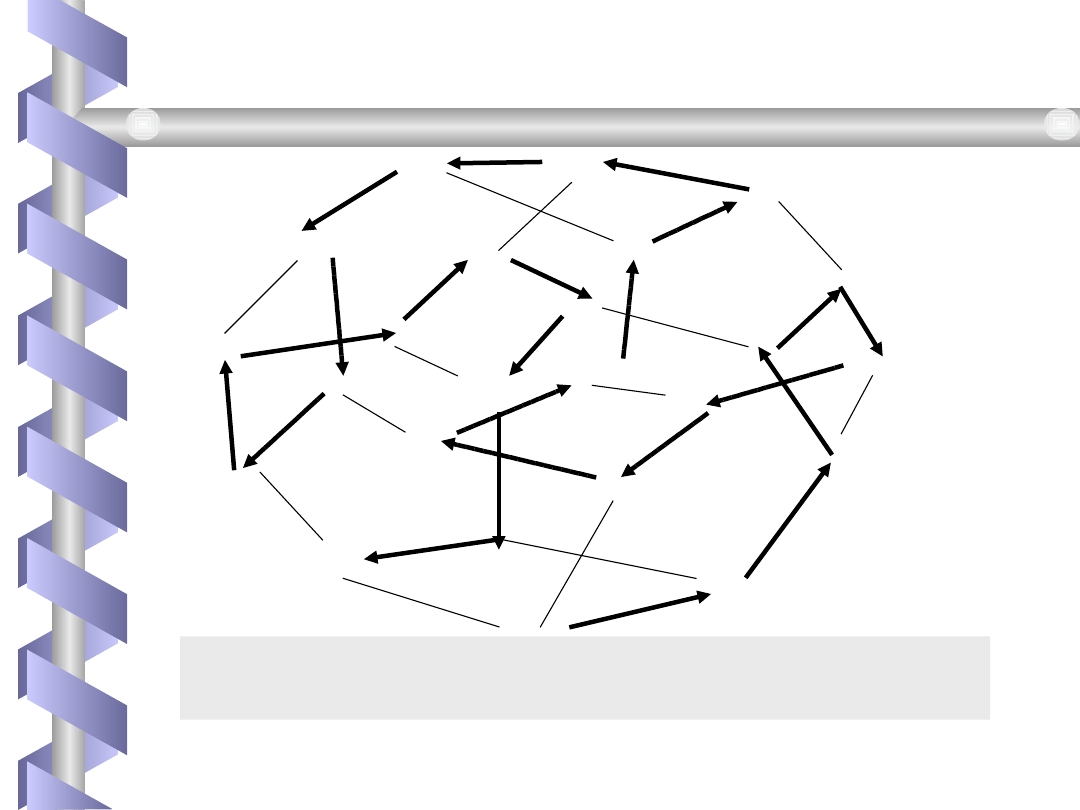
Ten ciąg permutacji odpowiada drodze Hamiltona
w grafie.

1234

1243

1423

4123

4132

4312

4321

3421

3241

3214

2314

2134

2143

1324

3124

2341

2413

2431

4231

4213

1432

3412

1342

3142

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

16

Generowanie permutacji

Generowanie permutacji

Generowanie wszystkich permutacji przez
minimalną liczbę transpozycji sąsiednich
elementów.

Procedure ANTYLEX(m)
begin
if m=1 then wypisz_permutację
P(1:n)
else
for i :=1 to m do
ANTYLEX(m-1);
if i<m then
zamień(P(i), P(m));
odwróć(m-1);
fi;
od;
fi
end;

Początkowo

P(i)=i dla
i=1...n

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

17

Symbol dwumianowy

Symbol dwumianowy

Liczbę wszystkich podzbiorów k-
elementowych zbioru n-elementowego
oznaczamy przez (n nad k) i nazywamy
symbolem dwumianowym Newtona.

Jeśli X ma n elementów, to liczba
wszystkich podzbiorów zbioru X wynosi
2

n

.

Kombinacje

bez powtórzeń

Lemat (n nad k)=0 gdy
k>n

(n nad k)= n!/ (k! (n-k)!)

Ciągów różnowartościowych długości k w zbiorze n
elem. jest

n (n-1)... (n-k+1)

Ale ciągów o różniących się kolejnością elementów jest
k! Stąd

(n nad k)= n (n-1)... (n-k+1)/k!

(

x+y)

n

= (n nad i) x

i

y

n-i







n

i

i 0

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

18

Trójkąt Pascala

Trójkąt Pascala

(n nad i) : i=0...n}

= 2

n

(n nad k) = (n nad n-
k)

(n nad k) = (n-1 nad k ) + (n-1 nad
k-1)

1 1

1 2 1
1 3 3 1
1 4 6 4
1
1 5 10 10 5
1

12 grudnia 200
1

Matematyka Dyskretna, Elementy Kombinatoryki G.Mir
kowska, PJWSTK

19

Przykłady

Przykłady

1. Ile jest ciągów zero-jedynkowych o długości n,
w których 1 występuje dokładnie k razy?

Uwaga Ciąg ( 0 1 0 1 1 1 0 0 0)
można traktować jako funkcję
charakterystyczną zbioru.

Zatem odpowiedź : (n
nad k)

2.

Niech będzie graf pełny G (bez pętli) o

n wierzchołkach. Ile taki graf ma
krawędzi m?

Uwaga Każda krawędź wyznacza 2
elementowy podzbiór i każdy 2 elementowy
podzbiór zbioru wierzchołków wyznacza
krawędź.

Zatem odpowiedź : (n
nad 2)