Zmienne losowe

Zmienna losowa

Definicja Niech będzie przestrzenią zdarzeń

elementarnych. Każdą funkcję określoną na zbiorze  i

o wartościach w zbiorze liczb rzeczywistych nazywać
będziemy zmienną losową.

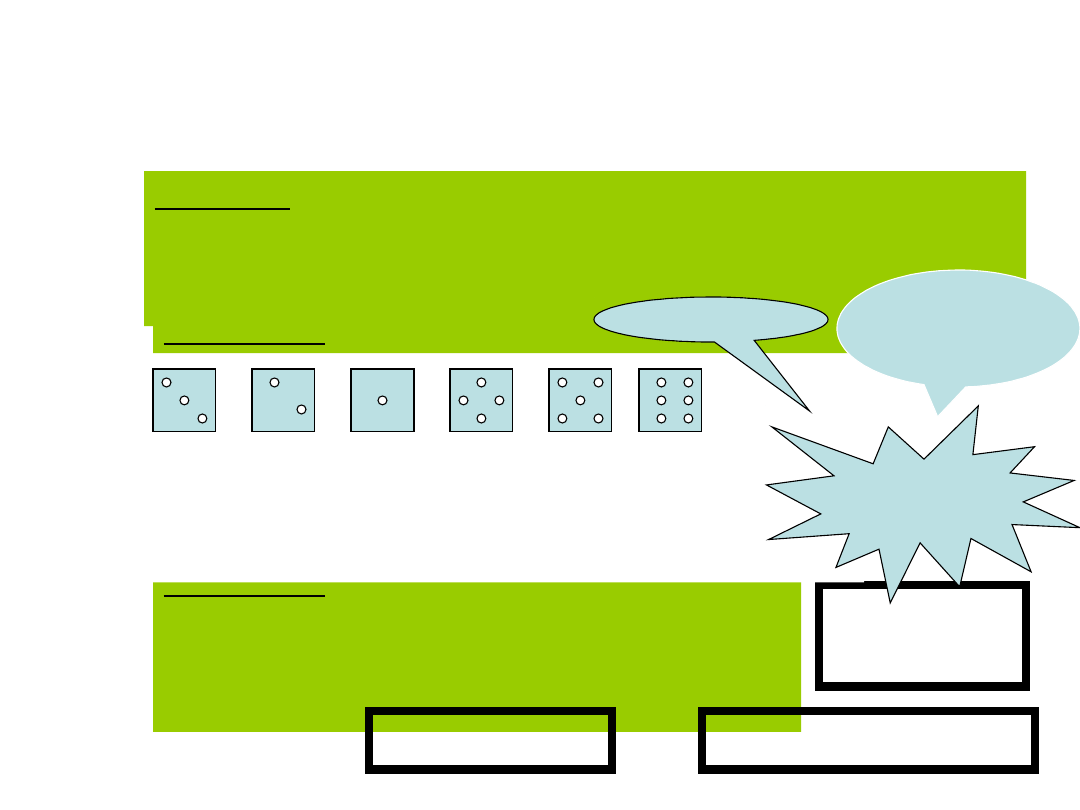
Przykład 1 Rzut jedną kostką.

3 2 1 4 5
6

X(

ω

i

) = i

Przykład 2 Rzut dwoma kostkami.

Zdarzenia elementarne ω ij = (i,j) , gdzie

i, j =1,2,3,4,5,6

X(

ω

ij

) =

i+j

Y(ω

i

) = 1 gdy i parzyste Y(ω

i

) =0 gdy i

nieparzyste

Y(

ω

ij

) = i/j

Nazwa zmiennejWartość zmiennej

dla zdarzenia wi

Z(

ω

ij

) = max(i,j)

Zmienne

dyskretne

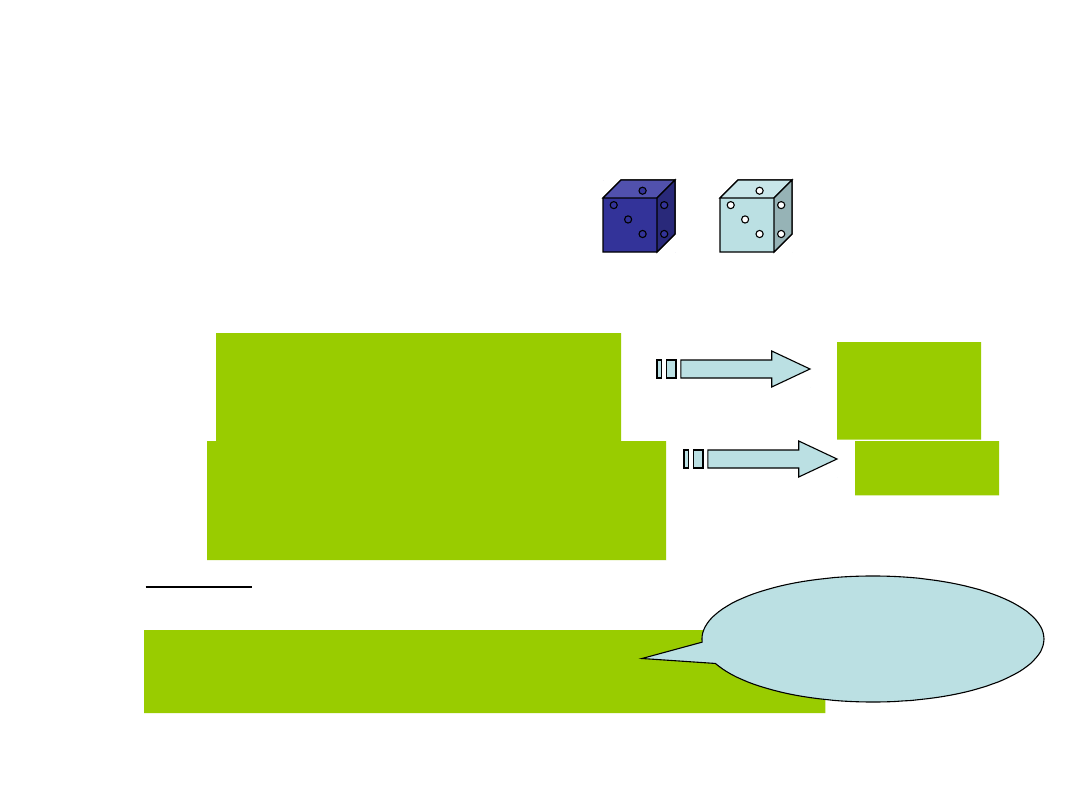
Przykład

Rozważmy
doświadczenie z rzutem
dwoma kostkami do gry.

Definiujemy zmienne losowe X , Y i Z : X(i,j)= i , Y(i,j) =
j, Z(i,j)=i+j

Zdarzenie A= „liczba
oczek na kostce 1 jest
nie większa niż 3”

X 

3

Zdarzenie B = „liczba oczek
na drugiej kostce wynosi co
najmniej 5

Y 5

Uwaga P(A) = 1/2 = P(X  3) P(B) =1/3 =P(Y 5)

Dla dowolnych k i l mamy
P(X=k i Y=l) = 1/36 = P(X=k) * P(X=l)

tzn. X i Y są zmiennymi

niezależnymi

Rozkład prawdopodobieństwa

Niech X będzie zmienną losową określoną w
przestrzeni .

Definicja Funkcję f

X

określoną na zbiorze R i o

wartościach
w zbiorze [0,1] taką, że

f

X

(x) = P(X=x) dla x R

nazywamy rozkładem prawdopodobieństwa zmiennej
losowej X

f

X

(x)

=

1/6 dla
x=1,2,3,4,5,6

0 dla
pozostałych x

f

Z

(x)

=

1/36 dla x=2 i x=
12
2/36 dla x=3 i
x=11
3/36 dla x=4 i
x=10
4/36 dla x=5 i
x=9
5/36 dla x=6 i
x=8 6/36 dla x=7
0 dla
pozostałych x

Przykład Rozważmy zmienne X, Y, Z
rozpatrywane
w przykładzie z rzutem dwoma kostkami do
gry.

Przykład

Rzucamy n-krotnie monetą . Niech

X

i

(w i-tym rzucie wypadł orzeł) = 1

X

i

(w i-tym rzucie wypadła reszka) = 0

Orzeł

Reszka

Mamy P( X

i

= 1)= 1/2

Niech S

n

= X

1

+ X

2

+...+ X

n

Liczba orłów w n rzutach monetą

P(S

n

= k) = (n nad k)/ 2

n

k orłów

w n rzutach monetą

Rozkłady prawdopodobieństwa zmiennych są
następujące:

f

Xi

(x)

=

1/2 dla x=0,1

0 dla pozostałych
x































N

x

dla

0

dla

2

)

(

N

x

x

n

x

f

n

sn

Niezależność zmiennych

losowych

Definicja Powiemy, że dwie zmienne losowe X i Y są
niezależne jeżeli dla dowolnych przedziałów I, J w
zbiorze liczb rzeczywistych
P (XI i Y J) = P(XI) * P(Y J)

Przykład
X

K

(data) - liczba stłuczek samochodowych w Krakowie

X

W

(data) - liczba stłuczek samochodowych w Warszawie

Ilość stłuczek w Warszawie nie powinna mieć wpływu na
liczbę stłuczek w Krakowie. Intuicyjnie te zmienne są
niezależne.

W przypadku zmiennych dyskretnych : niezależność
wyraża się warunkiem:

P(X=x i Y= y) = P(X=x) * P(Y=y) dla
dowolnych x,y  R.

Definicję tę można

uogólnić na dowolny

ciąg zmiennych

losowych

Dystrybuanta

Definicja Niech X będzie zmienną losową określoną na
dowolnej przestrzeni zdarzeń losowych .

Dystrybuantą zmiennej X nazywamy funkcję F : R 

[0,1] taką, że

F

X

(x) = P(X < x) dla x  R

W przypadku zmiennej losowej
dyskretnej mamy F

X

(x) =



y  x

f

X

(y)

Dystrybuanta akumuluje

wartości rozkładu

prawdopodobieństwa

Przykład

Dystrybuanta
zmiennej losowej X w
rzucie jedną kostką
do gry:

1
5/6
4/6
3/6

1 2 3 4 5 6 7 8

Przykłady

Przykład Zliczanie liczby orłów w n rzutach monetą.

Dystrybuanta każdej ze zmiennych X

i

jest określona:

F

X

(y) = 0 gdy y  0 F

X

(y) = 1/2 gdy 0<y  1 F

X

(y)=1 dla y > 1

Dystrybuanta zmiennej S ma postać

F(y) =



x  y

(n/x) / 2

n

Przykład Wybieramy losowo liczbę z przedziału [0,1).
 = [0,1). Niech U będzie zmienną losową taką że dla

x [0,1), U(x)=x.

Zmienna

jednostajna

P( U[a,b))= b-a b>a i b,a

[0,1)

To nie jest

dyskretna zmienna

losowa

Dystrybuanta F

U

(y) = P(U

 y)

0 gdy y<0
y gdy 0

y<1
1 gdy y 1

F

U

(y)

=

Wartość oczekiwana

Definicja  - skończona przestrzeń zdarzeń

elementarnych, X zmienna losowa określona w .

Wartością oczekiwaną zmiennej X nazywamy liczbę

E(X) =



w

X(w)* P({w}).

Jeśli wszystkie zdarzenia elementarne są
jednakowo prawdopodobne, to P({w}) =
1/card() czyli

)

(

)

(

)

(











card

X

X

E





Przykład Rzucamy jedną kostką do gry. Liczba
wyrzuconych oczek X jest zmienną losową o
wartościach 1,2,3,4,5,6 i ma rozkład jednostajny
P(X=i)=1/6.

Zatem E(X)= (1+2+...6)/6 = 3.5

Wartość oczekiwana zmiennej

dyskretnej

Niech X będzie zmienną losową dyskretną określoną w
pewnej przestrzeni zdarzeń elementarnych

}

,...,

2

,

1

:

{

n

i

x

i







)

(

1

i

n

i

i

x

X

P

x

EX









i

i

i

X

p

x

X

P

x

f







)

(

)

(

i

n

i

i

i

X

n

i

i

p

x

x

f

x

EX













1

1

)

(

Przykład

Zmienna losowa przypisująca losowi wygraną ma
rozkład prawdopodobieństwa f :
f(x

1

)=P(X=x

1

) = n

1

/n , f(x

2

)=P(X=x

2

) = n

2

/n ...

f(x

k

)=P(X=x

k

) = n

k

/n

Wartość oczekiwana zmiennej X , EX= 

i=1...k

(x

i

*n

i

/n)= 

i=1...k

(x

i

*n

i

)/n

1 los = EX zł

Zysk = n *EX

Suma
wygranych =


i=1...k

x

i

*n

i

W pewnej loterii sprzedaje się n losów, z których n

1

wygrywa sumę x

1

zł., n

2

- wygrywa x

2

zł., ...n

k

losów

wygrywa x

k

zł.

Loterię nazywamy sprawiedliwą, jeśli suma
wygranych jest równa ilości pieniędzy uzyskanych
ze sprzedaży biletów.

Jaka powinna być cena jednego losu, żeby loteria była
sprawiedliwa?

Przykład

5 biletów po 1,20zł 4 bilety po 2,40 zł

1,20

2,40

4,80

6 biletów po 4,80
zł

W tramwaju zgasło światło i pasażer skasował losowo
wyciągnięty bilet. Jaka jest wartość oczekiwana jego
opłaty za przejazd?

Rozkład prawdopodobieństwa f

X

:

f(1,20)= 5/15 f(2,40)= 4/15
f(4,80)= 6/15

bilet

Cena
tego
biletu

X

EX = 1,20 *5/15 + 2,40* 4/15+ 4,80 * 6/15 =
2,96

Własności wartości oczekiwanej

- przestrzeń zdarzeń, w której określone są zmienne

losowe X i Y.

Twierdzenie 1

E(cX) = c E(X)
E(X + Y) = E(X) + E(Y)
E(a) = a
E(X – E(X)) = 0

Twierdzenie 2

Jeśli X i Y są
niezależnymi
zmiennymi losowymi,
to
E(X * Y) = E(X) * E(Y).

Dowód Tw. 2:
E(X*Y) = 

w 

Y(w) *X(w) * P({w}) = 

xX(),y Y()

x*y P(X=x i Y=y)

=



xX(),y Y()

x*y P(X = x ) * P ( y = y ) =



xX()

x* P(X=x) *(

yY()

y * P(Y=y) ) = E(X) * E(Y).

Wariancja

Definicja

: D

2

X = E((X-EX)

2

)

Rozważmy dwie zmienne o rozkładach {(100,1/2),
(100,1/2)}, {(2,1/3), (-1,2/3)} Mamy EX = EY = 0.
Chociaż zmienne bardzo się
różnią, to wartości oczekiwane są takie same.

Nowy parametr, który
charakteryzuje rozrzut
wartości zmiennej losowej.

Niech X ma rozkład prawdopodobieństwa {(x

i

,p

i

)}

i=1,...n.
Oznaczmy EX= m. Wtedy D

2

X = ((x

1

- m)

2

*p

1

+...+ (x

n

–

m)

2

*p

n.

Co to znaczy, że
D

2

X jest małą

liczbą?

Twierdzenie D

2

X = E(X

2

) – (EX)

2

Prawdopodobieństwo
zdarzenia, że X przyjmuje
wartość dużo różniącą się
od m jest małe.

Przykład

Rozważmy zmienną losową o rozkładzie zero-
jedynkowym

Wtedy EX = p
oraz D

2

X = E((X- EX)

2

) = (1-p)

2

p +(0-p)

2

(1-p) =

p(1-p)



p

prawdop

z

p

prawdop

z

X

.

1

.

1

0





Definicja Liczbę
nazywamy odchyleniem standardowym
zmiennej X. dyspersja

X

D

2





Własności wariancji

Wniosek

Jeżeli zmienne X i Y są

niezależne, to

D

2

(X-Y) =

D

2

(X+Y).

Twierdzenie
D

2

(c) = 0

D

2

(cX) = c

2

D

2

(X)

D

2

(X + Y) = D

2

(X) + D

2

(Y) o ile X i Y są niezależne

Dowód
D

2

(X+Y) = E((X+Y - E(X+Y))

2

)= E((X-EX + Y-EY)

2

)=

E((X-EX)

2

+2(X-EX)(Y-EY) + (Y-EY)

2

)=

E ((X-EX)

2

) + E(2(X-EX)(Y-EY)) + E((Y-EY)

2

) =D

2

(X) +

D

2

(Y).

Ponieważ X i Y są
niezależne więc również (X-
c) i (Y-c) są zmiennymi
niezależnymi.

E(2(X-EX)(Y-EY))= 0

Przykład: Ryby

Dla ustalenia liczby ryb w jeziorze odławiamy pewną
liczbę ryb, np. 1000sztuk. Złapane ryby znakujemy i
wpuszczamy je do jeziora. Po upływie pewnego czasu
dokonujemy odłowu uzyskując np.: 1200 ryb, wśród
których było 25 znakowanych.

)

(

)

)(

(

N

n

C

c

B

b

N

P 

N liczba ryb = liczba kul w urnie
B ryby znakowane = kule białe
C ryby nie znakowane = kule czarne
n ryby odłowione = liczba losowań
zależnych
b wyłowione znakowane =wylosowane
białe
c wyłowione nie znakowane =
wylosowane czarne

Prawdopodobieństwo wylosowania b kul
białych i c kul czarnych w n losowaniach

Cd. ryby

Aby na podstawie tych danych empirycznych
oszacować liczbę ryb w jeziorze zastosujemy zasadę
największej wiarygodności, polegającej na wyznaczeniu
takiej liczby N, aby prawdopodobieństwo P

N

miało

wartość największą.

P

N

/P

N-1

>1 dla N<B*n/b

P

N

/P

N-1

<1 dla N> B*n/b

b

n

B

N

N

Bn

BN

nN

N

P

P

B

N

b

n

B

b

N

n

N

n

B

N

b

n

B

b

N

N































(

)

)(

(

)

(

*

)

(

)

)(

(

2

1

1

1

P

N

osiąga

największą wartość
dla N = [B* n/b]