1

Wykład 4

Sortowanie

2

Sortowanie - zadanie

Definicja (dla liczb):

wejście: ciąg n liczb A = (a

1

, a

2

, …, a

n

)

wyjście: permutacja (a

1

,…, a’

n

) taka, że a’

1

≤ … ≤ a’

n

Po co sortować?

– Podstawowy problem dla algorytmiki
– Wiele algorytmów wykorzystuje sortowanie jako procedurę

pomocniczą

– Pozwala pokazać wiele technik
– Dobrze zbadane (czas)

3

Sortowanie – taksonomia

 Wewnętrzne i zewnętrzne

– Zależnie od miejsca przechowywania zbioru: (RAM czy dysk)

 Sortowanie tablic i sortowanie list łączonych

– zależnie od struktury danych (pliku);
– różny sposób dostępu (bezpośredni dla tablicy, sekwencyjny dla listy).

 „W miejscu” lub nie

– Nie wymaga dodatkowej pamięci

 Stabilne i niestabilne

– Kolejność elementów o tych samych wartościach klucza nie zmienia

się. Inaczej kolejne sortowanie dla złożonych obiektów nie psuje
efektów poprzedniego sortowania.

 Bezpośrednie i pośrednie

– zależnie od tego przemieszczamy całe obiekty, czy tylko wskaźniki

(indeksy) do nich

4

Zestawienie czasów działania

 Przez wybór:

O(N

2

) zawsze

 Bąbelkowe:

O(N

2

) najgorszy przypadek; O(N)

najlepszy przyp.

 Wstawianie:

O(N

2

) średnio; O(N) najlepszy przypadek

 Shellsort: O(N

4/3

)

 Heapsort: O(NlogN) zawsze
 Mergesort: O(NlogN) zawsze
 Quicksort: O(NlogN) średnio; O(N

2

) najgorszy przypadek

 Zliczanie: O(N) zawsze
 Radix sort: O(N) zawsze

 zewnętrzne:

O(b logb)) dla pliku o b „stronach”.

5

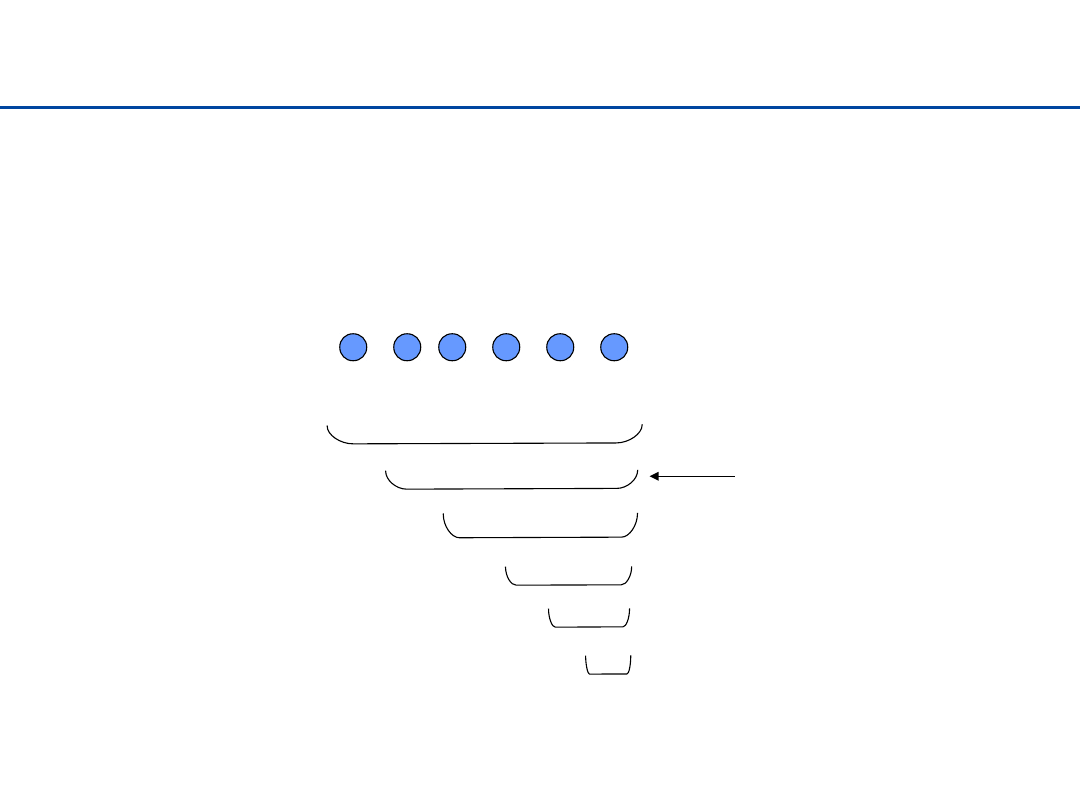
Sortowanie przez wybór – pomysł

 Znajdujemy najmniejszy element ciągu i zamieniamy go

z pierwszym elementem. Powtarzamy to dla podciągu
bez pierwszego elementu, itd.

Znajdź minimum i zamień
z pierwszym elementem

X

X

6

Sortowanie przez wybór – pseudokod

Selection_Sort(int A)
1 for i ← 1 to length[A]
2 do min ← i;
3

for j ← i+1 to length[A]

4 do if A[j] < A[min] then min ← j;
5 Exchange A[min] ↔ A[i]

7

ciąg: EASYQUESTION - rozmiar 12 znaków

#porównań #zamian

EASYQUESTION

A

ESYQUESTION

11

1

AE

SYQUESTION

10

1

AEE

YQUSSTION

9

1

AEEI

QUSSTYON

8

1

AEEIN

USSTYOQ

7

1

AEEINO

SSTYUQ

6

1

AEEINOQ

STYUS

5

1

AEEINOQS

TYUS

4

1

AEEINOQSS

YUT

3

1

AEEINOQSST

UY

2

1

AEEINOQSSTU

Y

1

1

Razem

66 11

1

2

3

4

5

6

7

8

9
1
0
1
1

Sortowanie przez wybór – przykład

iteracj
a

8

Sortowanie przez wybór – czas działania

 Zależność od danych wejściowych:

– Ilość przebiegów: nie (zawsze N-1)
– Ilość porównań: nie
– Ilość zamian: nie

 O(N

2

) zawsze (bez znaczenia jaki jest układ elementów w

danych – ważna tylko ilość)

9

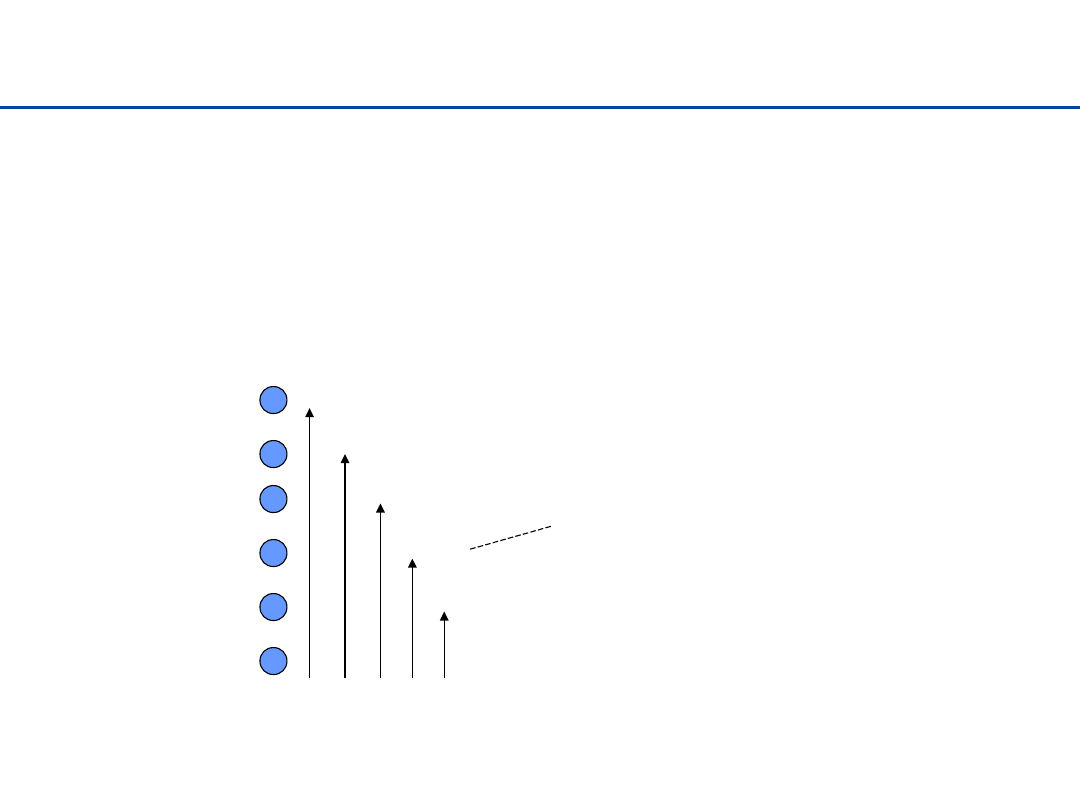
Sortowanie bąbelkowe (przez zamianę)

 Przechodzimy przez ciąg od jego końca, porównując sąsiadujące

elementy i ewentualnie zamieniając je miejscami. Powtarzamy te
procedurę aż do uporządkowania całego ciągu.

– Po pierwszym przejściu element minimalny znajduje się na początku – a[0],

po drugim na drugim miejscu znajduje się drugi co do wielkości – a[1], po itd.

Porównanie do
wypływających bąbelków –
stąd nazwa

.

10

Sortowanie bąbelkowe – pseudokod

BUBBLE_SORT(A)
1 for i ← 1 to length[A]
2 do for j ← length[A] downto i + 1
3 do if A[j] < A[j - 1]
4 then exchange A[j] ↔ A[j -

1]

11

Ciąg: EASYQUESTION, (12 znaków)

porównań

zamian

EASYQUESTION

(najgorszy przyp)

A

EESYQUISTNO

11 (11) 8 (11)

AE

EISYQUNSTO

10 (10) 6 (10)

AEE

INSYQUOST

9 (9) 6 (9)

AEEI

NOSYQUST

8 (8) 4 (8)

AEEIN

OQSYSUT

7 (7) 3 (7)

AEEINO

QSSYTU

6 (6) 2 (6)

AEEINOQ

SSTYU

5 (5) 1 (5)

AEEINOQS

STUY

4 (4) 1 (4)

AEEINOQS

STUY

3 (3)

0

(3)

(2) (2)

(1)

(1)

razem 63 (66)

31 (66)

iteracja

1
2
3
4
5
6
7
8
9

Sortowanie bąbelkowe – przykład

12

Sortowanie bąbelkowe – czas wykonania

 Zależność od danych wejściowych:

– Ilość potrzebnych przejść: tak

– Ilość porównań w jednym przejściu: nie

– Ilość zamian: tak

 Najgorszy przypadek: O(N

2

)

– Dane odwrotnie posortowane, np.: JIHGFEDCBA.

– N-1 przejść

– (N-1)N/2 porównań i (N-1)N/2 zamian

 Najlepszy przypadek: O(N)

– Jeśli elementy są już posortowane, np.: ABCDEFGHIJ.

– Tylko jedno przejście. Stąd mamy N-1 porównań i 0 zamian.

13

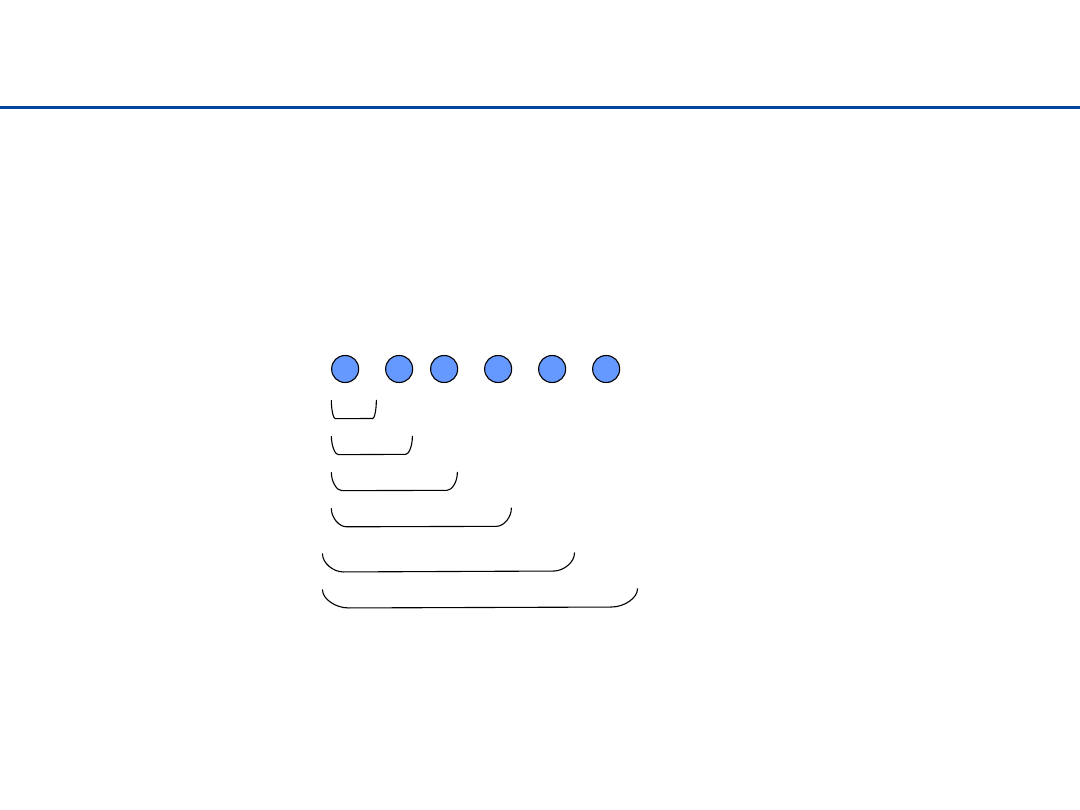
Sortowanie przez wstawianie – pomysł

 Dla każdego elementu ciągu (od lewej do prawej),

wstawiamy go we właściwe miejsce ciągu elementów
poprzedzających go (już posortowanych).

14

Sortowanie przez wstawianie – pseudokod

INSERTION_SORT(A)
1 for j ← 2 to length[A]
2 do key ← A[j]
3 i ← j-1
4 while i>0 and A[i]>key
5 do A[i+1] ← A[i]
6 i ← i-1
7 A[i+1] ← key

15

Ciąg: EASYQUESTION, (12 znaków)

porównań

zamian

(najgorszy przyp.)

E

ASYQUESTION

A

E

SYQUESTION

1 (1)

1 (1)

AE

S

YQUESTION

1 (2)

0 (2)

AES

Y

QUESTION

1 (3)

0 (3)

AE

Q

SY

UESTION

3 (4)

2 (4)

AEQS

U

Y

ESTION

2 (5)

1 (5)

AE

E

QSUY

STION

5 (6)

4 (6)

AEEQS

S

UY

TION

3 (7)

2 (7)

AEEQSS

T

UY

ION

3 (8)

2 (8)

AEE

I

QSSTUY

ON

7 (9)

6 (9)

AEEI

O

QSSTUY

N

7 (10)

6 (10)

AEEI

N

OQSSTUY

8 (11)

7 (11)

razem

41 (66) 31 (66)

iteracja

1
2
3
4
5
6
7
8
9
10
11

Sortowanie przez wstawianie – przykład

16

Sortowanie przez wstawianie – czas
działania

 Zależność od danych wejściowych:

– Ilość iteracji: nie (zawsze N-1)
– Ilość porównań: tak
– Ilość zamian: tak

 Najgorszy przypadek: O(N

2

)

– Elementy odwrotnie posortowane np.: JIHGFEDCBA.
– (N-1)N/2 porównań i (N-1)N/2 zamian.

 Najlepszy przypadek: O(N)

– Elementy już posortowane np.: ABCDEFGHIJ.
– Jedno porównanie i 0 zamian w każdej iteracji. Razem, N-1

porównań i brak zamian.

17

Shellsort – pomysł

 Modyfikacja (rozszerzona wersja) sortowania przez

wstawianie

 Dążymy do zmniejszenia ilości zamian – albo ciągi

krótkie, albo lepsze („bliższe” posortowania).

 Shellsort wykonuje sortowanie podciągów:

– Wybieramy ciąg liczb (zwany ciągiem przyrostów) h

t

, …

,

h

2

, h

1

;

– h

1

=1; h

t

> … > h

2

>h

1

;

– Sortujemy ciągi elementów odległych o h

t

, h

t-1

, h

t-2

,…,h

1

.

18

Shellsort – kod w C

void shellsort (int[ ] a, int n)

{

int i, j, k, h, v;

int[ ] cols = {1391376, 463792, 198768, 86961, 33936, 13776, 4592,

1968, 861, 336, 112, 48, 21, 7, 3, 1}

for (k=0; k<16; k++)

{

h=cols[k];

for (i=h; i<n; i++)

{

v=a[i];

j=i;

while (j>=h && a[j-h]>v)

{

a[j]=a[j-

h];

j=j-h;

}

a[j]=v;

}

}

}

19

Shellsort – przykład

ciąg: EASYQUESTION (12 znaków)
ciąg przyrostów 4, 1.

porównań zamian

EASYQUESTION

E

ASY

Q

UES

T

ION

2

0

E

A

SY

Q

I

ES

T

U

ON

3

1

E

A

E

Y

Q

I

O

S

T

U

S

N

3

2

E

A

E

N

Q

I

O

S

T

U

S

Y

3

3

Razem w tej fazie

11

6

faza 1: przyrost = 4

20

Shellsort – przykład

porównań zamian

EAENQIOSTUSY

AE

ENQIOSTUSY

1

1

AEE

NQIOSTUSY

1

0

AEEN

QIOSTUSY

1

0

AEENQ

IOSTUSY

1

0

AEEINQ

OSTUSY

3

2

AEEINOQ

STUSY

2

1

AEEINOQS

TUSY

1

0

AEEINOQST

USY

1

0

AEEINOQSTU

SY

1

0

AEEINOQSSTU

Y

3

2

AEEINOQSSTUY

1

0

Razem w tej fazie

16

6

faza 2: przyrost= 1

21

Shellsort – przykład

 Razem 27 porównań i 12 zamian.
 Dla sortowania przez wstawiania odpowiednio 41 i

31 !!!

– Polepszenie dostajemy przez wstępne posortowanie,

krótkich podciągów

 Zwykle stosuje się ciągi przyrostów o więcej niż 2

elementach.

22

Shellsort – czas działania

 Nie ma możliwości przeprowadzenie dokładnej analizy dla

przypadki ogólnego (wyniki są oparte o badania
empiryczne).

 Wybór ciągu przyrostów ma zasadniczy wpływ na czas

sortowania.

– Dla ciągu podanego przez Shell’a: O(N

2

)

• I

max

= Floor(N/2), I

k

= Floor(I

k+1

/2).

• np N=64:1, 2, 4, 8, 16, 32

– Dla ciągu podanego przez Knuth’a: O(N

3/2

)

• I

1

=1, I

k+1

= 1+3*I

k

.

• 1, 4, 13, 40, 121, 364, …

23

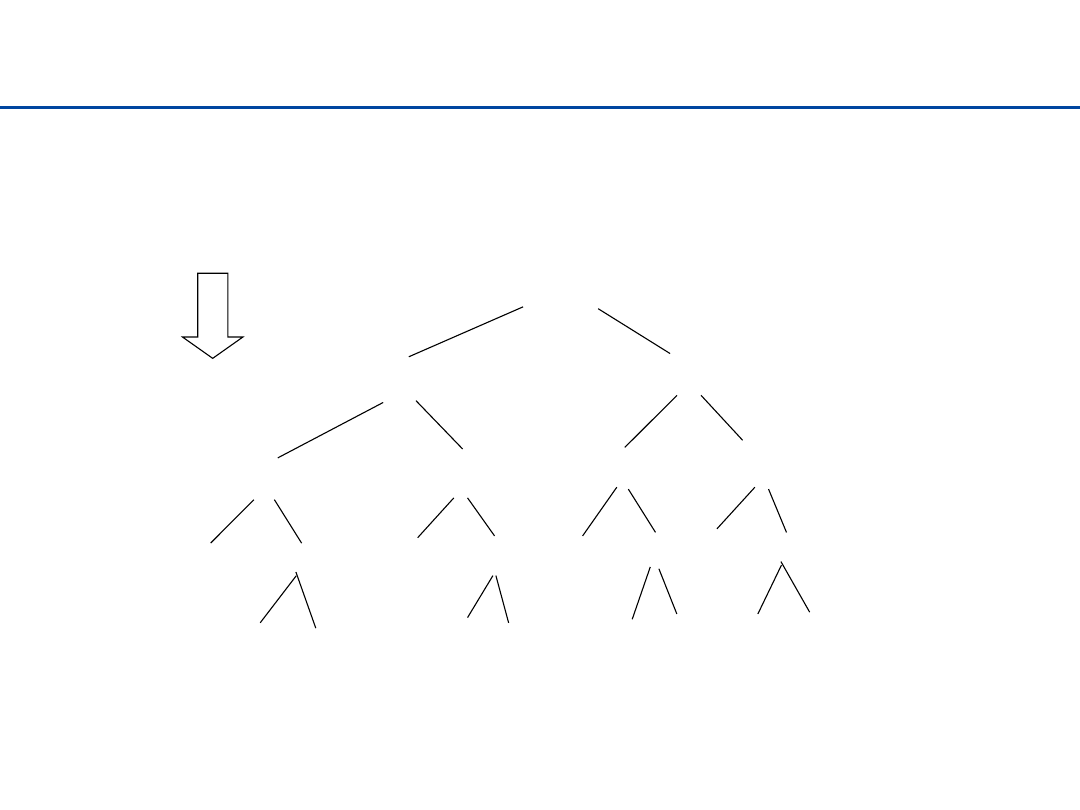
Mergesort – pomysł

 Dzielimy ciąg na podciągi, sortujemy te podciągi, a

następnie łączymy zachowując porządek.

– Przykład algorytmu typu „dziel i zwyciężaj”.
– Potrzeba dodatkowego miejsca dla tych podciągów – nie

jest to sortowanie „w miejscu”.

• Można realizować ten proces „w miejscu”, ale rośnie

stopień komplikacji.

24

Mergesort – przykład

ciąg: EASYQUESTION (12 znaków)

EASYQUESTION

EASYQU

ESTION

EAS

YQU

EST

ION

E

AS

Y

QU

E ST I ON

A S

Q U

S T

O N

podział

25

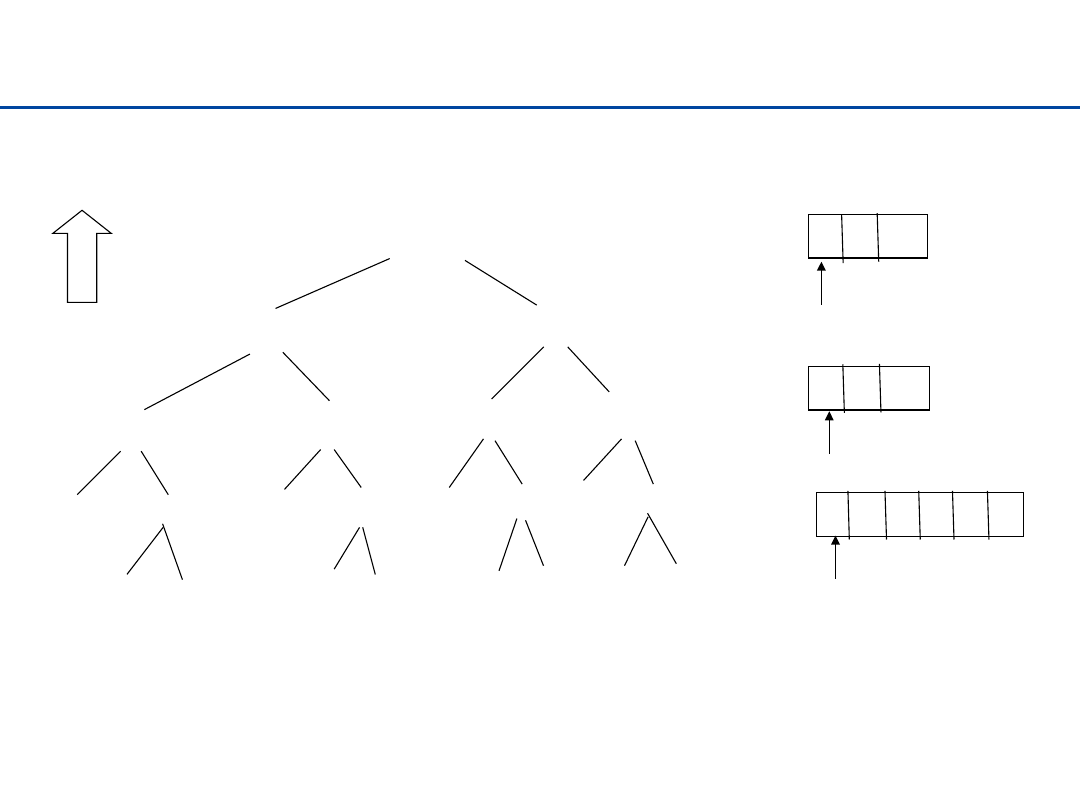
Mergesort – przykład

AEEINOQSSTUY

AEQSUY

EINOST

AES

QUY

EST

INO

E

AS

Y

QU

E

ST

I

NO

A S

Q U

S T

O N

łaczenie

A E S

Q U Y

C1

C2

C3

26

Mergesort - pseudokod

MERGE-SORT(A, p, r)

1 if p < r

2

then q ← ⌊(p + r)/2⌋

3

MERGE-SORT(A, p, q)

4

MERGE-SORT(A, q + 1, r)

5

MERGE(A, p, q, r)

27

Mergesort - pseudokod

MERGE(A, p, q, r)
1 n1 ← q - p + 1
2 n2 ← r - q
3 create arrays L[1 ..n1 + 1] and R[1 ..n2 +

1]

4 for i ← 1 to n1
5 do L[i] ← A[p + i - 1]
6 for j ← 1 to n2
7 do R[j] ← A[q + j]
8 L[n1 + 1] ← ∞
9 R[n2 + 1] ← ∞
10 i ← 1
11 j ← 1
12 for k ← p to r
13 do if L[i] ≤ R[j]
14

then A[k] ← L[i]

15

i ← i + 1

16 else A[k] ← R[j]
17 j ← j + 1

28

Sortowanie w czasie

liniowym

29

Przegląd

 Czy możliwe jest sortowanie w czasie lepszym niż dla

metod porównujących elementy (poprzednio – najlepsze
algorytmy dawały czas O(NlogN))?

 Algorytmy o liniowym czasie działania:

– Przez zliczanie (Counting-Sort)
– Radix-Sort
– Kubełkowe (Bucket-sort)

 Potrzeba dodatkowych założeń!

30

Sortowanie o czasie liniowym

 Możliwe przy dodatkowych informacjach (założeniach) o

danych wejściowych.

 Przykłady takich założeń:

– Dane są liczbami całkowitymi z przedziału [0..k] i k = O(n).
– Dane są liczbami wymiernymi z przedziału [0,1) o rozkładzie

jednostajnym na tym przedziale

 Trzy algorytmy:

– Counting-Sort
– Radix-Sort
– Bucket-Sort

31

Zliczanie (Counting sort)

wejście: n liczb całkowitych z przedziału [0..k], dla k = O(n).

pomysł: dla każdego elementu wejścia x określamy jego

pozycje (rank): ilość elementów mniejszych od x.

jeśli znamy pozycję elementu – umieszczamy go na r+1

miejscu ciągu

przykład: jeśli wiemy, że w ciągu jest 6 elementów mniejszych

od 17, to 17 znajdzie się na 7 miejscu w ciągu wynikowym.

powtórzenia: jeśli mamy kilka równych elementów

umieszczamy je kolejno poczynając od indeksu pozycja

32

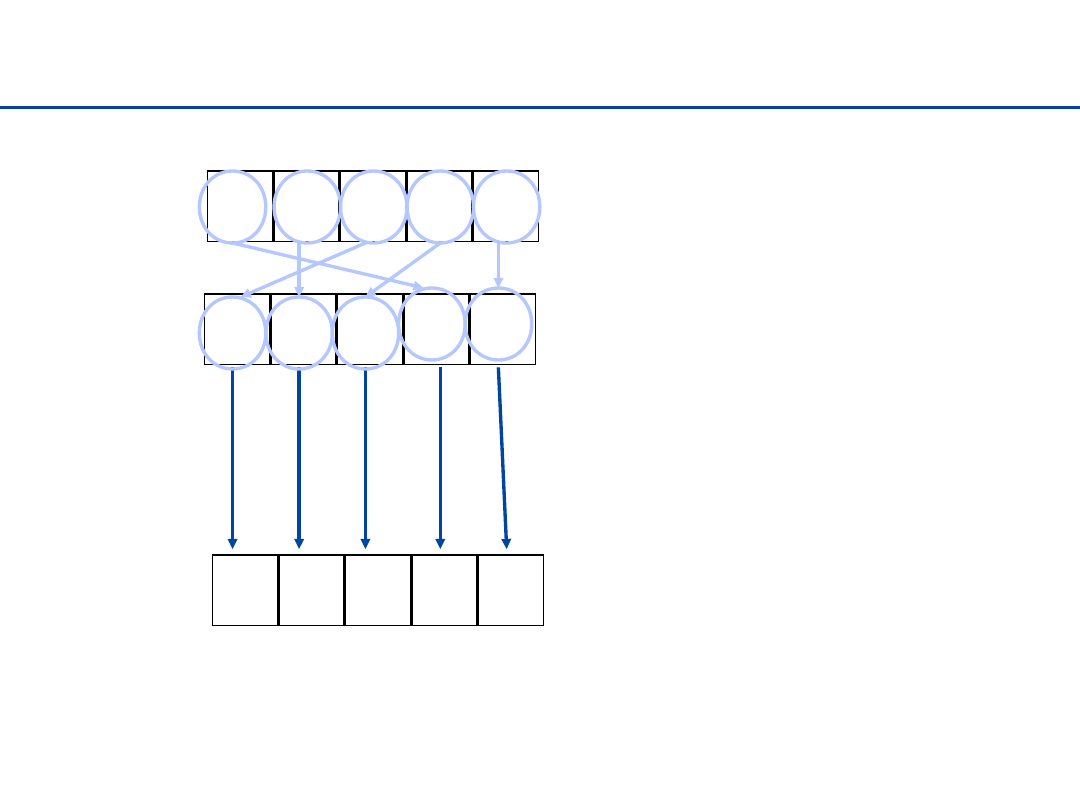
Zliczanie (Counting sort)

1

3

2

4 5

Jeśli nie ma powtórzeń i n = k,
Rank[A[i]] = A[i] i B[Rank[A[i]]
 A[i]

Dla każdego A[i], liczymy

elementy ≤ od niego. Daje to

rank (pozycję) elementu

4

1

2

5

A =

B =

Rank =

4

3

5

2

1

3

33

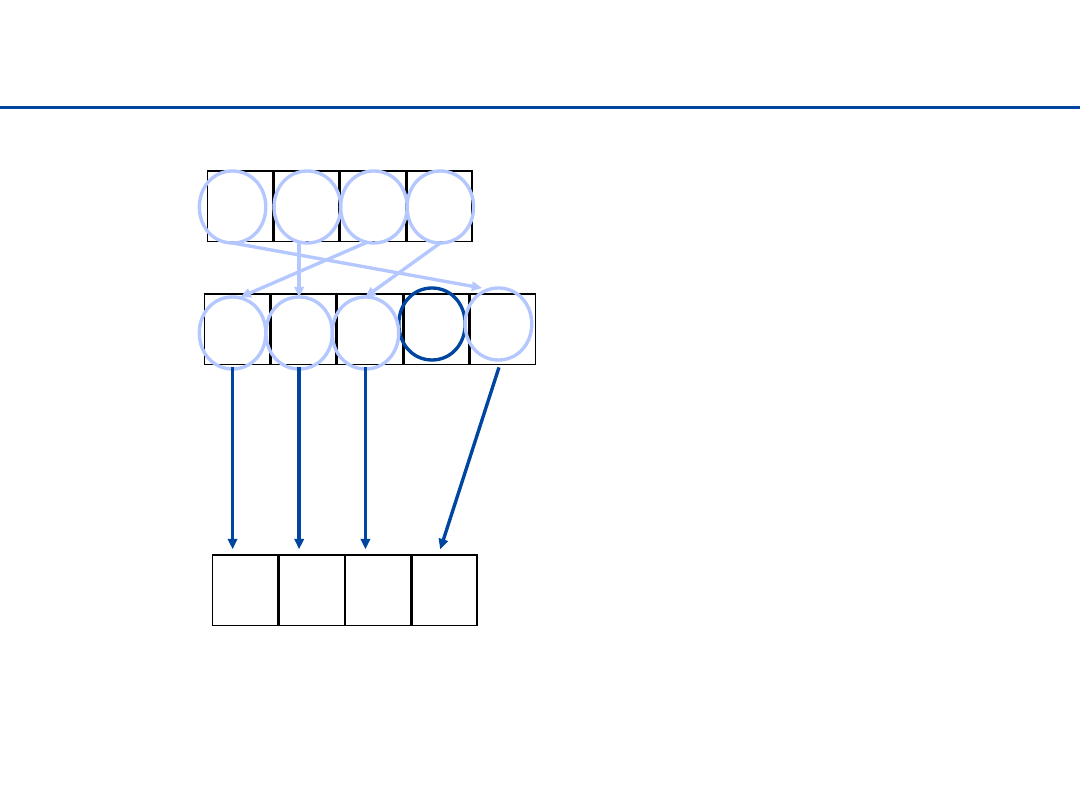
Zliczanie (Counting sort)

5

1

2

3

A =

3

2

4

Rank =

Jeśli nie ma powtórzeń i n <
k

,

Niektóre komórki tablicy
rank pozostają
niewykorzystane, ale
algorytm działa.

B =

5

2

1

1

3

34

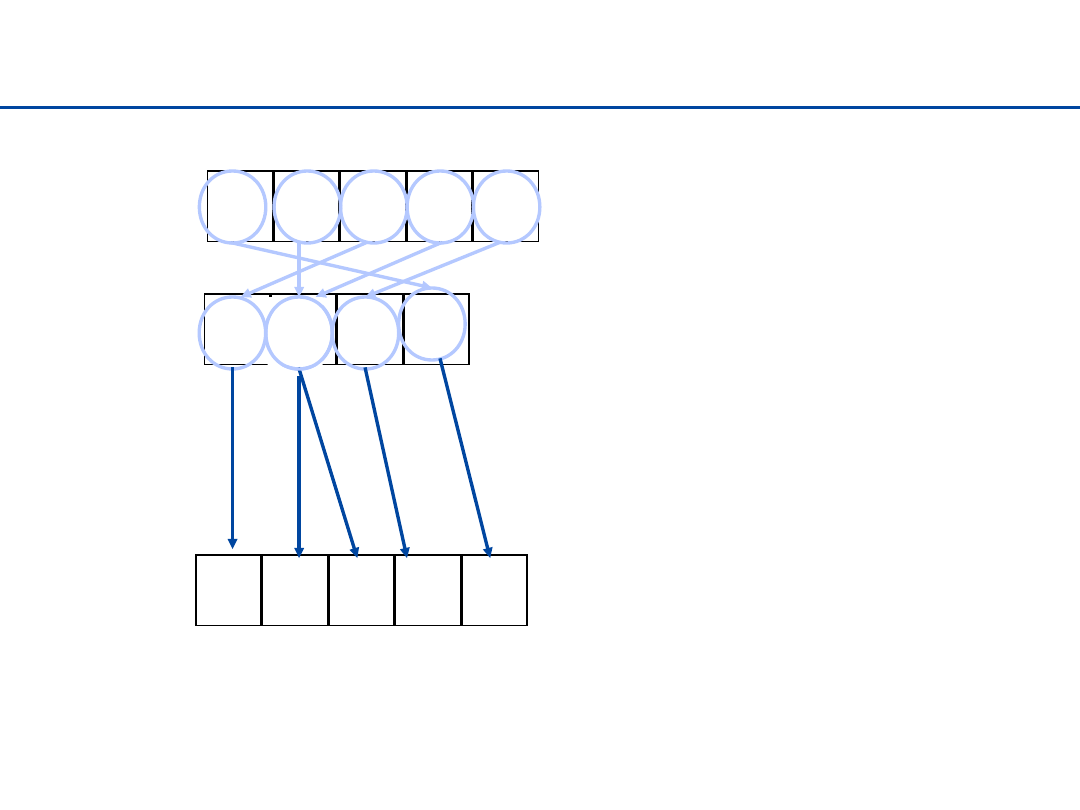
Zliczanie (Counting sort)

4

1

2

2

A =

1

4

3

5

Rank =

Jeśli n > k i mamy
powtórzenia,

umieszczamy na wyjściu
powtarzające się elementy
w takiej kolejności, w jakiej
występowały w oryginalnym
ciągu (stabilność)

B =

3

3 4

2

1

2

2

35

Zliczanie (Counting sort)

Counting-Sort(A, B, k)
1.

for i  0 to k

2.

do C[i]  0

3.

for j  1 to length[A]

4.

do C[A[j]]  C[A[j]] +1

5.

/* C zawiera ilości elementów równych i

6.

for i  1 to k

7.

do C[i]  C[i] + C[i –1]

8.

/* C zawiera ilości elementów ≤ i

9.

for j  length[A] downto 1

10.

do B[C[A[j]]]  A[j]

11.

C[A[j]]  C[A[j]] – 1

A[1..n] – tablica wejściowa
B [1..n] – tablica wyjściowa
C [0..k] – pomocnicza tablica (do zliczania)

36

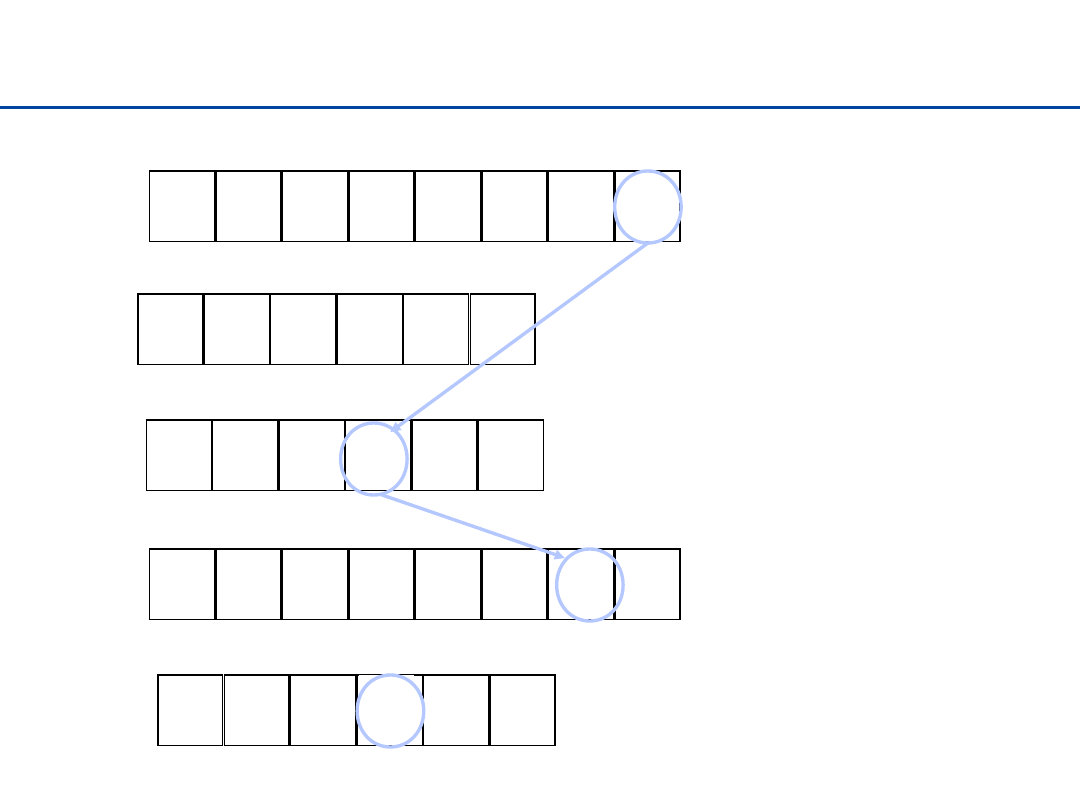
Sortowanie przez zliczanie – przykład (1)

n = 8
k = 6

B[C[A[j]]]  A[j]

C[A[j]]  C[A[j]] – 1

po p. 11

C[A[j]]  C[A[j]] +1

po p.4

C =

0 1 2 3 4 5

2

2

0

3 0 1

2

3

5

0 2 3 0 3

A =

1 2 3 4 5 6 7 8

2

4

2

7 7 8

C =

0 1 2 3 4 5

C[i]  C[i] + C[i –1]

po p. 7

2

4

2

7 8

C =

0 1 2 3 4 5

7

1 2 3 4 5 6 7 8

B =

3

6

37

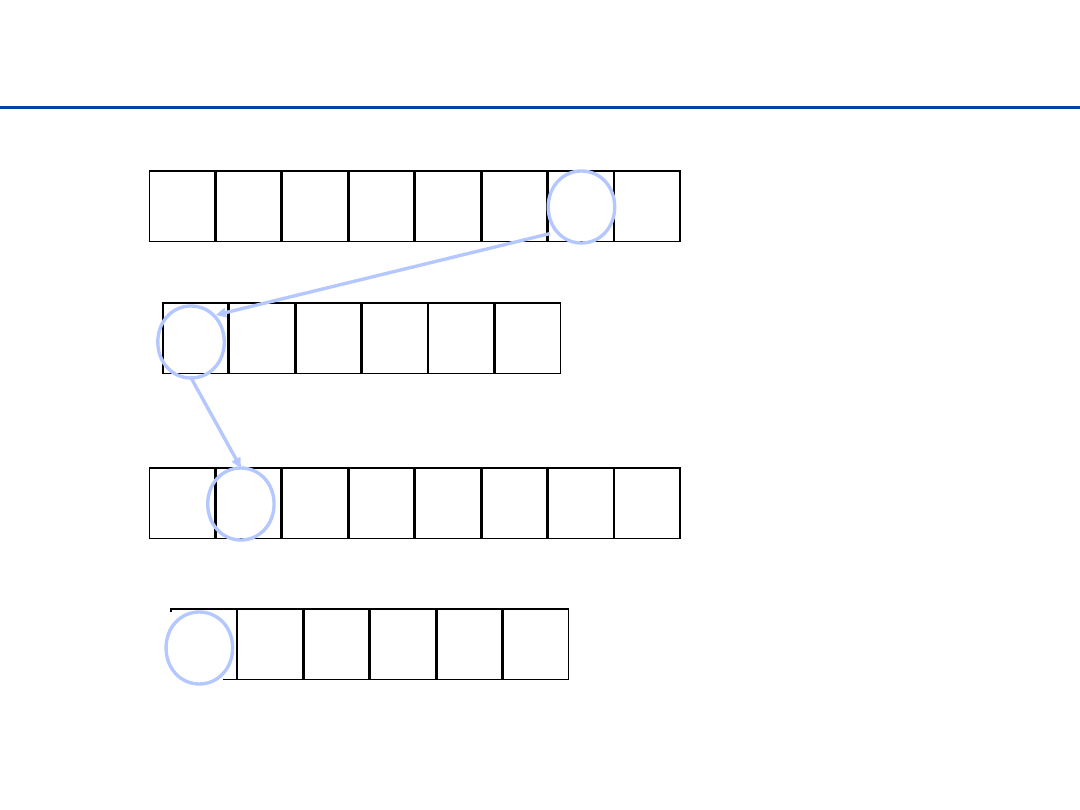
Sortowanie przez zliczanie – przykład (2)

0

3

B =

2

4

2

6 7 8

C =

0 1 2 3 4 5

1 2 3 4 5 6 7 8

2

3

5

0 2 3 0 3

A =

1 2 3 4 5 6 7 8

2

4

2

6 7 8

C =

0 1 2 3 4 5

1

38

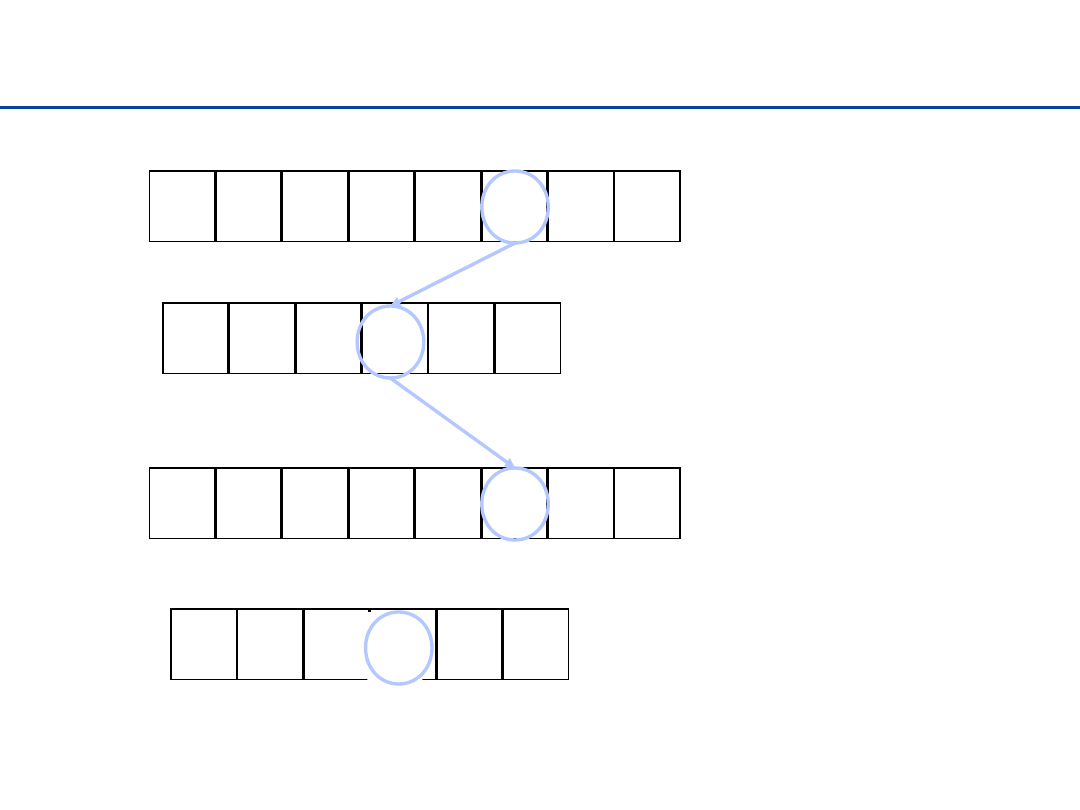
Sortowanie przez zliczanie – przykład (3)

0

3

B =

1

4

2

6 7 8

C =

0 1 2 3 4 5

1 2 3 4 5 6 7 8

2

3

5

0 2 3 0 3

A =

1 2 3 4 5 6 7 8

2

4

2

6 7 8

C =

0 1 2 3 4 5

3

5

39

Counting sort – czas działania

 Pętla for w p.1-2 zajmuje czas Θ(k)
 Pętla for w p.3-4 zajmuje czas Θ(n)
 Pętla for w p.6-7 zajmuje czas Θ(k)
 Pętla for w p.9-11 zajmuje czas Θ(n)
 Stąd dostajemy łączny czas Θ(n+k)
 Ponieważ k = O(n), T(n) = Θ(n)  algorytm jest

optymalny!!

 Konieczne jest założenie k = O(n). Jeśli k >> n to

potrzeba to potrzeba dużej ilości pamięci.

 Nie jest to sortowanie „w miejscu”.

40

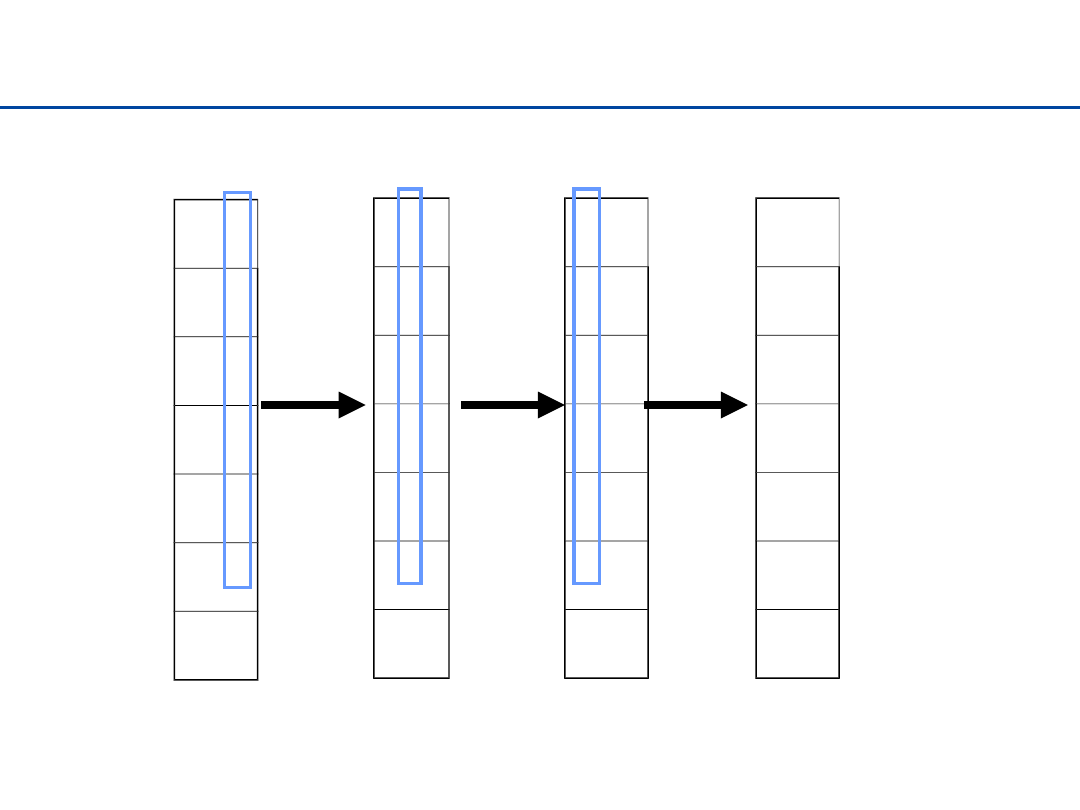
Radix sort – sortowanie pozycyjne

wejście: n liczb całkowitych, d-cyfrowych, łańcuchów o d-

pozycjach

pomysł: zajmować się tylko jedną z cyfr (sortować

względem kolejnych pozycji – cyfr/znaków). Zaczynamy
od najmniej znaczącej cyfry/znaku, potem kolejne pozycje
(cyfry/znaki), aż do najbardziej znaczącej. Musimy
stosować metodą stabilną. Ponieważ zbiór możliwych
wartości jest mały (cyfry – 0-9, znaki ‘a’-’z’) możemy
zastosować metodę zliczania, o czasie O(n)

Po zakończeniu ciąg będzie posortowany!!

41

Radix sort – przykład

7 2

0

3 2

9
4 3

6
8 3

9
3 5

5
4 5

7
6 5

7

3 2

9

4 5

7
6 5

7
8 3

9
4 3

6
7 2

0
3 5

5

7 2

0

3 5

5
4 3

6
4 5

7
6 5

7
3 2

9
8 3

9

3 2

9

3 5

5
4 3

6
4 5

7
6 5

7
7 2

0
8 3

9

42

Radix-Sort – pseudokod

Radix-Sort(A, d)
1. for i  1 to d
2. do zastosuj stabilną metodę sortowania do cyfry d dla

tablicy A

uwagi:
•

złożoność: T(n) = Θ(d(n+k))  Θ(n) dla stałego d i k = O(1)

•

wartości cyfr/znaków są z zakresu [0..k –1] dla k = O(1)

•

Metoda stosowana dla poszczególnych pozycji musi być
stabilna!

43

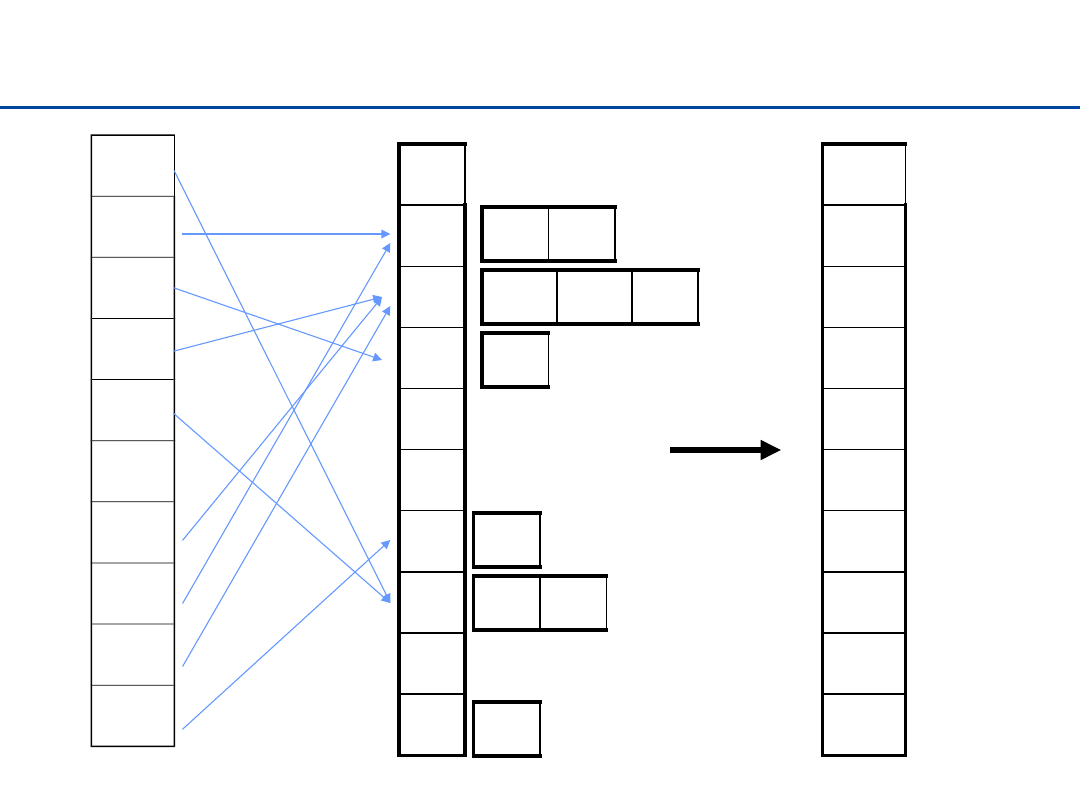
Sortowanie kubełkowe – Bucket sort

wejście: n liczb rzeczywistych z przedziału [0..1) ważne jest,

aby były równomiernie rozłożone (każda wartość równie
prawdopodobna)

pomysł: dzielimy przedział [0..1) na n podprzedziałów

(„kubełków”):0, 1/n, 2/n. … (n–1)/n. Elementy do
odpowiednich kubełków, a

i

: 1/i ≤ a

i

≤ 1/(i+1). Ponieważ

rozkład jest równomierny to w żadnym z przedziałów nie
powinno znaleźć się zbyt wiele wartości. Jeśli wkładamy je
do kubełków zachowując porządek (np. przez wstawianie –
Insertion-Sort), dostaniemy posortowany ciąg.

44

Bucket sort – przykład

.78

.17

.39

.26

.72

.94

. 21

.12

.23

.68

7

6

8

9

5

4

3

2

1

0

.17

.12

.26

.23

.21

.39

.68

.78

.72

.94

.68

.72

.78

.94

.39

.26

.23

.21

.17

.12

45

Bucket-Sort

Bucket-Sort(A)
1.

n  length(A)

2.

for i  0 to n

3.

do wstaw A[i] do listy B[floor(nA[i])]

4.

for i  0 to n –1

5.

do Insertion-Sort(B[i])

6.

Połącz listy B[0], B[1], … B[n –1]

A[i] tablica wejściowa
B[0], B[1], … B[n –1] lista „kubełków”

46

Bucket-Sort – złożoność czasowa

 Wszystkie instrukcje z wyjątkiem 5 (Insertion-Sort) wymagają

czasu O(n), w przypadku pesymistycznym.

 W przypadku pesymistycznym, O(n) liczb trafi do jednego

„kubełka” czyli ich sortowanie zajmie czas O(n

2

).

 Jednak w średnim przypadku stała ilość elementów wpada do

jednego przedziału – stąd czas średni wyniesie O(n).