Wykład
5

Zasady zmienności w dynamice

punktu

materialnego

Wykład 5

Zasady pędu, energii kinetycznej i krętu są
związane z II prawem dynamiki NEWTONA.

Pęd PM1

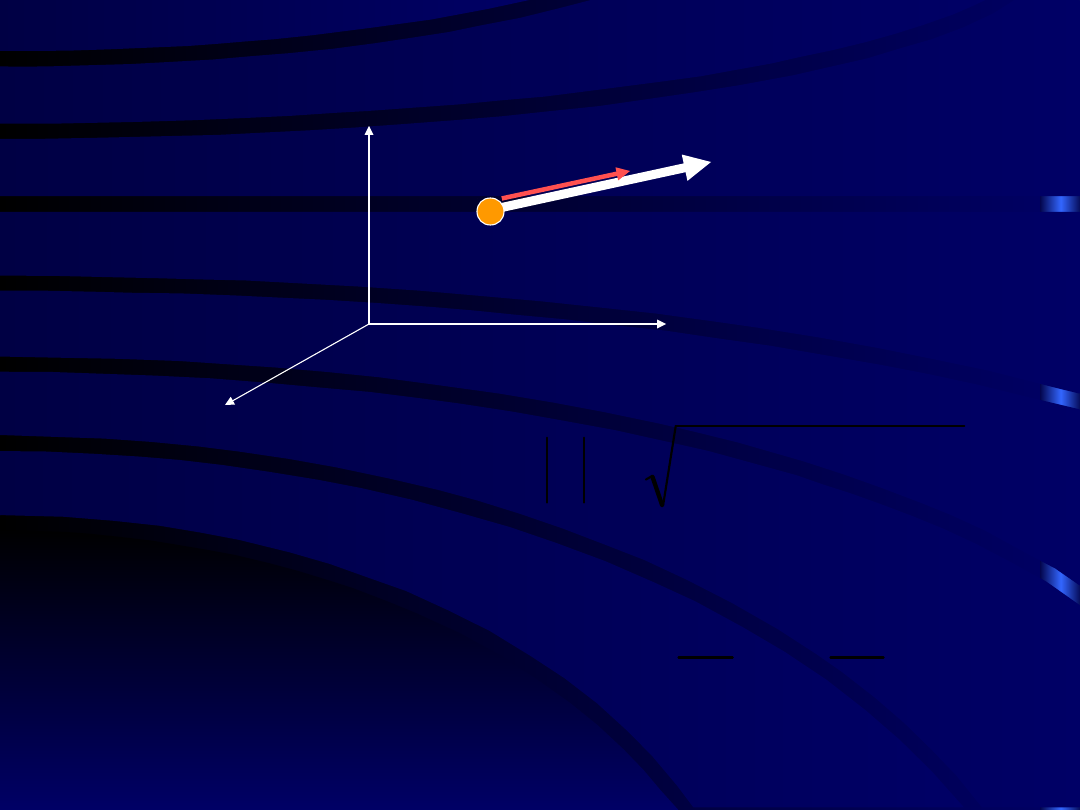
5.1 Pęd punktu

materialnego

(ilość ruchu PM)

v

m

p









z

z

y

y

x

x

e

p

e

p

e

p

p





















p



y

z

O

x

Moduł wektora pędu:

);

p

p

p

(

p

p

2
z

2
y

2

x











Jednostka pędu:

]

s

N

[

]

s

m

kg

[

]

p

[







Pęd

PM2

v



m

Zasada pędu
PM1

F

a

m

p

const

m

dla

),

v

m

(

dt

d

p























Różniczkowa zasada zmiany wektora
pędu:

Pochodna po czasie wektora pędu PM
jest równa wektorowi siły działającej na
ten punkt.









i

i

i

)

R

F

(

F

:

gdzie









 F

p

Związek wektora pędu PM z siłą działającą
na ten punkt i z II prawem dynamiki Newtona

Różniczkową zasadę zmiany pędu możemy również przedstawić:

;

Q

p

p

dt

F

p

d

dt

F

p

d

1

2

t

t

t

t

2

1

2

1

























 













2

1

t

t

dt

F

Q





-impuls siły lub popęd (t

1

t

2

)

Q

)

v

v

(

m

Q

p

p

1

2

1

2





















lub

Całkowa zasada zmiany pędu:

Zmiana wektora pędu w skończonym przedziale czasu (t

2

-t

1

)

jest równa impulsowi wektora siły w tym przedziale.

Zasada pędu
PM2

W szczególności,
jeśli

:

0

F



;

const

p

p

0

p

p

const

p

0

p

2

1

1

2





























lub

Zasada zachowania pędu punktu materialnego:

Jeżeli wypadkowy wektor sił działających na PM
jest równy zeru to wektor pędu jest stały.

Uwaga:

w praktyce może mieć miejsce sytuacja, np.:

0

F

,

0

F

,

0

F

z

y

x







wówcz
as

;

const

p

,

const

p

const

v

m

p

z

y

x

x











ale

Zasada pędu PM3

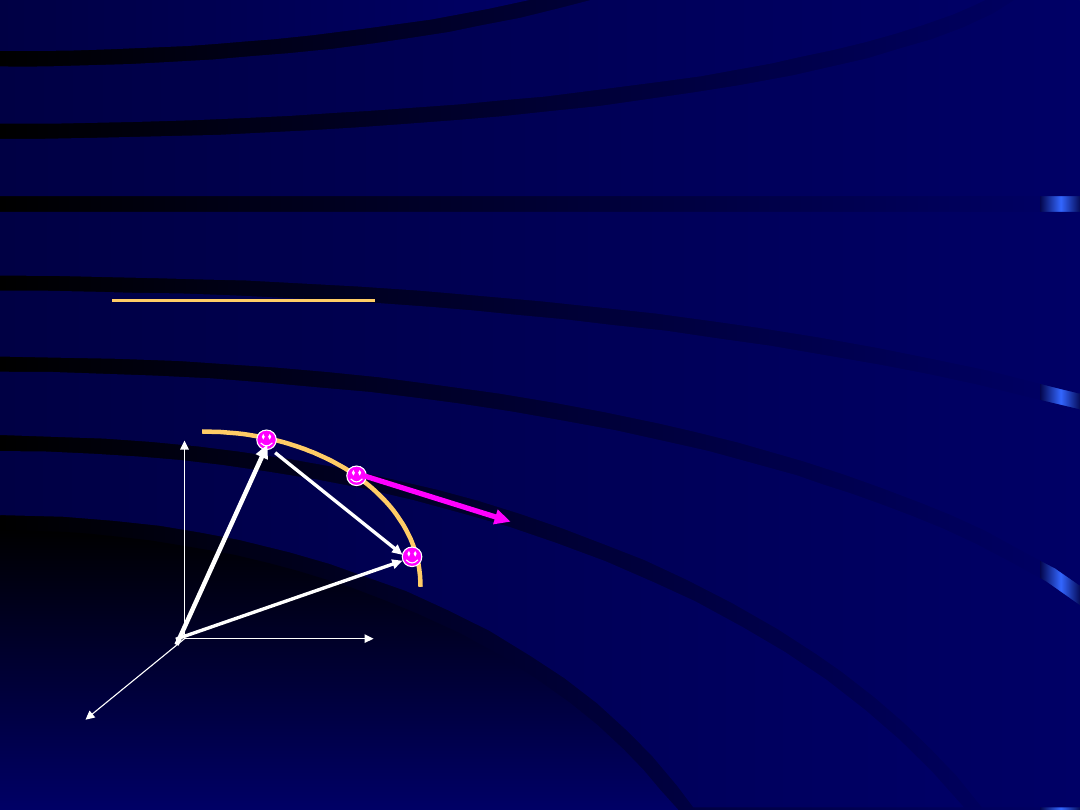
5.2 Praca i moc siły, energia kinetyczna PM

A

1

A

2

A

F



0

x

z

y

1

r

2

r

r



1

2

r

r

r













)

A

A

(

łuk

s

2

1





]

F

,

F

,

F

[

F

z

y

x



Praca siły
1

Praca siły

Praca
siły 2

|;

ds

|

|

r

d

|

,

ds

s

,

r

d

r

:

A

A

1

2



















1[N]1[m]=1[J]



















2

1

2

1

A

A

A

A

z

y

x

dz

F

dy

F

dx

F

r

d

F

L





:

A

A

drodze

na

F

sił

aca

Pr

2

1



[Nm]

Moc siły

Moc siły

dt

)

z

F

y

F

x

F

(

dz

F

dy

F

dx

F

dL

z

y

x

z

y

x



















Pracę wykonaną przez siłę w ciągu jednostki
czasu nazywamy

mocą tej siły

.

Moc oznaczamy przez

N

]

W

[

cos

v

F

v

F

dt

dL

N



















Energia kinetyczna i zasada równoważności pracy
i energii kinetycznej















 





2

1

2

1

A

A

v

v

;

r

d

F

v

d

v

m

dt

v

)

F

dt

v

d

m

(

dt)

v

r

(d





















L

E

E

lub

L

mv

2

1

mv

2

1

1

2

2

1

2
2









Energia kinetyczna p.m.:

2

mv

2

1

E

Zasada równoważności:

Zmiana energii kinetycznej PM w skończonym
przedziale czasu jest
równa sumie prac, które wykonały w tym samym
czasie wszystkie siły działające na ten punkt.

Energia
kinetyczna

Zasada zachowania energii mechanicznej PM

Zasada zachowania jest szczególnym przypadkiem zasady
równoważności pracy i energii kinetycznej PM

•Załóżmy, że w pewnym obszarze przestrzeni  działa pole sił:

)

z

,

y

,

x

(

F

F







•Jeśli w każdym punkcie przestrzeni 

to takie pole nazywamy

jednorodnym.

const

)

z

,

y

,

x

(

F





V=V(x,y,z) - jest potencjałem pola sił lub energią potencjalną PM

Zas. zachow.
E

M

PM1

•Jeśli:

z

V

F

,

y

V

F

,

x

V

F

.

,

V

d

gra

F

z

y

x





























tzn





to takie pole nazywamy

potencjalnym.

•Wtedy pracę L w potencjalnym polu sił przedstawimy:

































2

1

2

1

A

A

2

1

A

A

V

V

dV

)

dz

z

V

dy

y

V

dx

x

V

(

L

Wniosek:

Praca w potencjalnym polu sił nie zależy
od drogi lecz tylko od położenia
początkowego i końcowego.

Zasada zachowania energii mechanicznej PM:

Po podstawieniu powyższego wzoru na pracę L do prawej strony wzoru
wyrażającego zasadę równoważności pracy i energii kinetycznej otrzymamy:

const

V

E

V

E

2

2

1

1









E

m

= E + V

-nazywamy energią mechaniczną

Zas. zachow. E

M

PM2

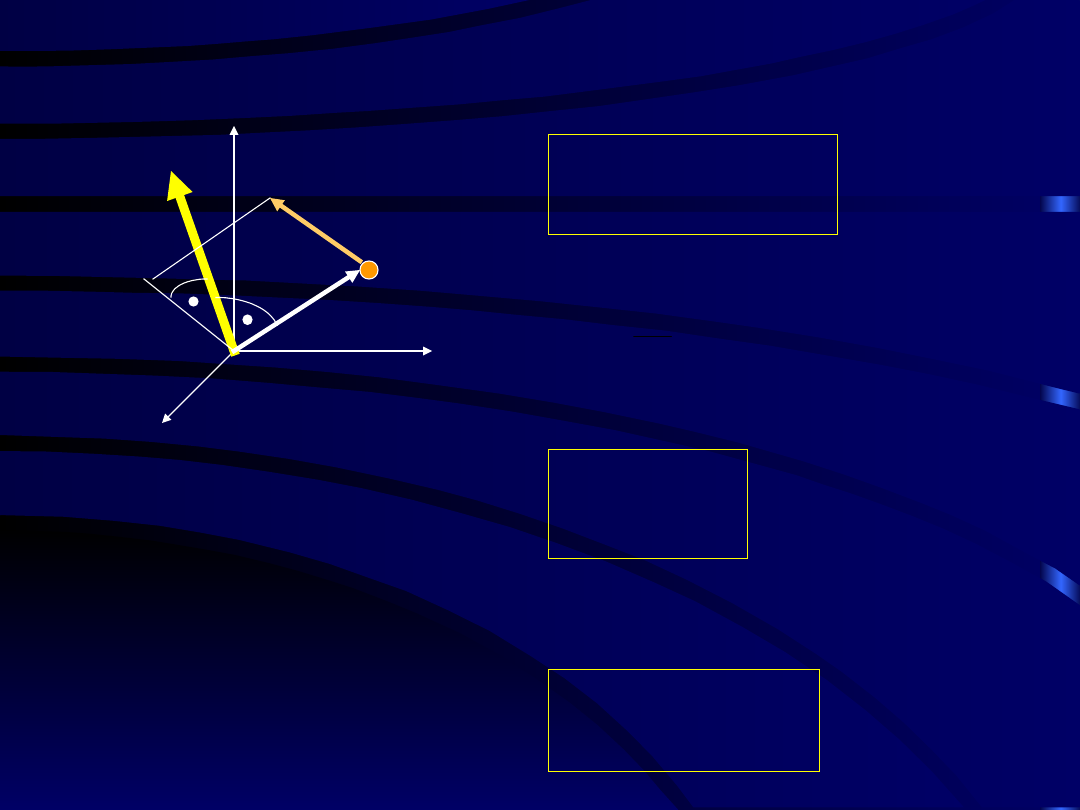
5.3 Kręt (moment pędu) punktu
materialnego

0

x

y

z

0

k



r

A

v

m

v

m

r

k

0











0

0

M

F

r

)

v

m

r

(

dt

d

k























Zasada zmiany krętu p.m.:

0

0

M

k



 

Zasada zachowania krętu p.m.:

Jeśli

0

M

0





dla t0 to mamy

const

k

0





Kręt i zasada krętu
PM

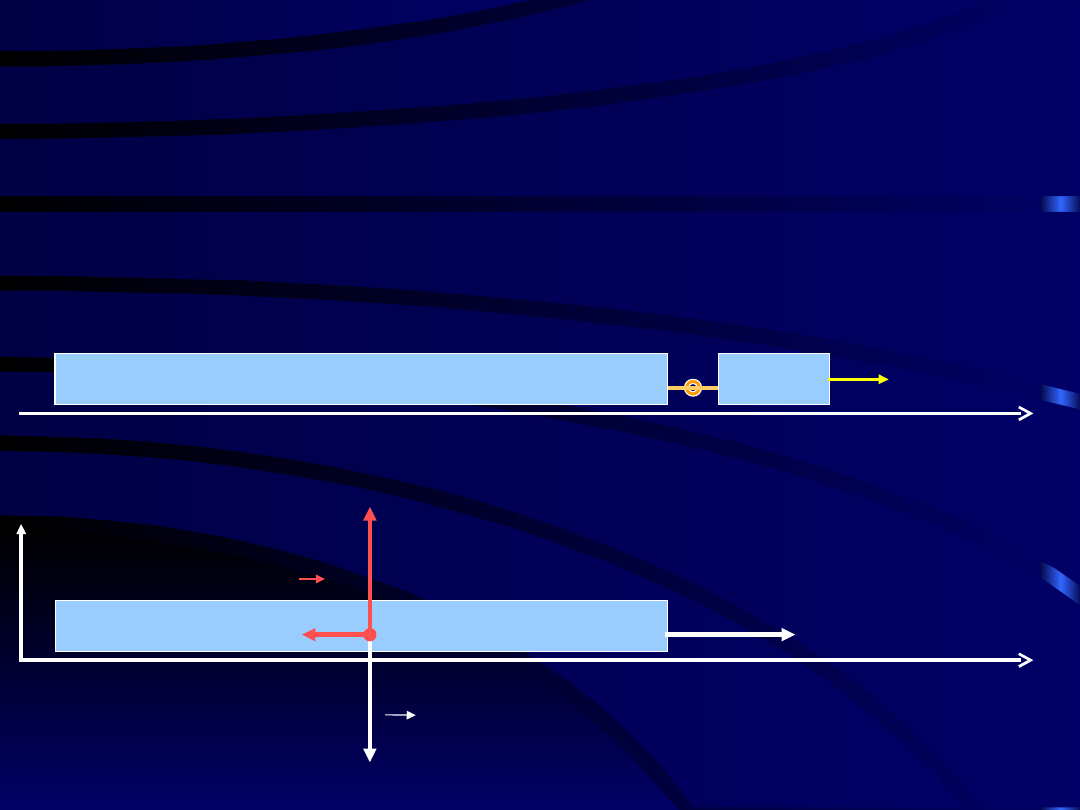
Przykład 1.

W celu zmierzenia ciężaru zestawu wagonów wstawiono między lokomotywą
a pierwszym wagonem dynamometr. W ciągu czasu t

1

=2[min] dynamometr

wskazywał średnio siłę F=100,8[T]. W tym czasie pociąg ze stanu spoczynku
nabrał prędkości v

1

=57,6[km/h]. Współczynnik tarcia



=0,02. Obliczyć ciężar

zestawu wagonów.

Przykład
1/1

N



x

F



G

T

y

Przykład
1/2













1

0

t

t

dt

)

N

G

T

F

(

Q











Q

)

v

v

(

m

lub

Q

p

p

0

1

0

1





















Rozwiązanie:
Z zasady zmiany pędu w postaci całkowej mamy:

W postaci skalarnej na oś x (t

o

=0, m=G/g):

;

gt

v

Fgt

G

t

)

G

F

(

v

g

G

1

1

1

1

1















Obliczenia: t

1

= 120[s], v=16[m/s], F=100,8[T];

G=3000,7[T]

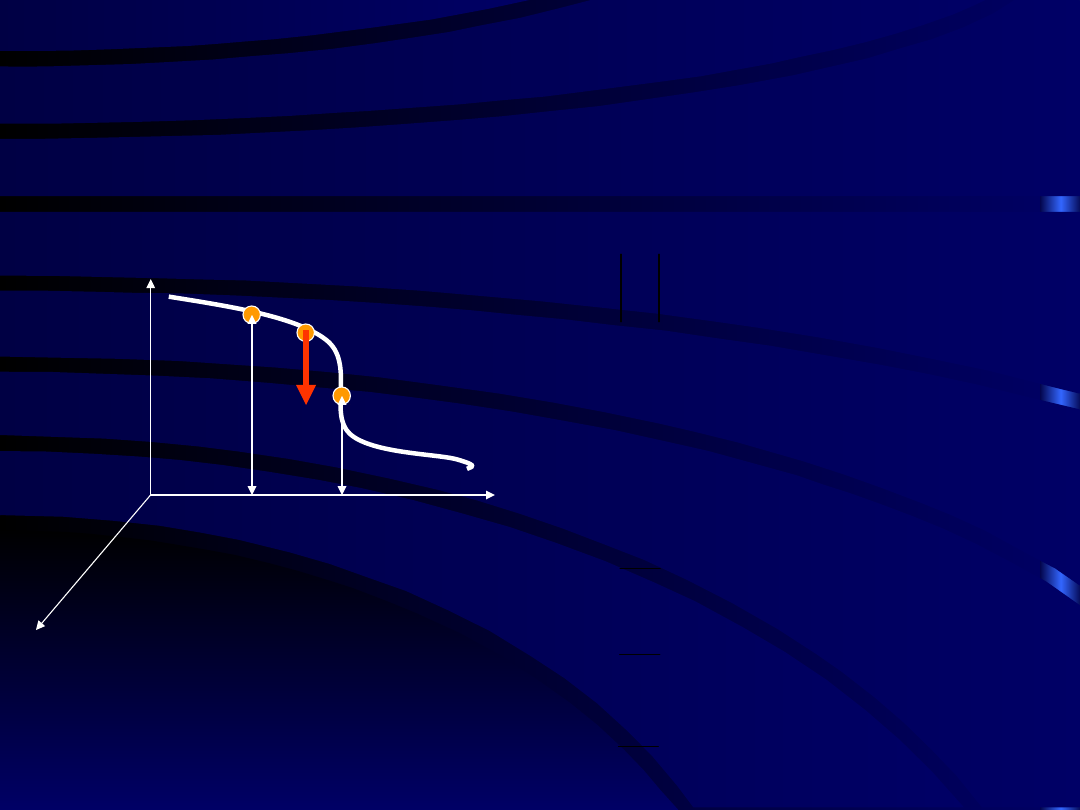
Przykład 2.

Obliczyć pracę punktu materialnego w polu grawitacyjnym w
pobliżu Ziemi między położeniami A

0

i A

1

. Wyznaczyć energię

potencjalną punktu materialnego.

x

y

z

O

A

0

A

1

z

0

z

1

Q



]

mg

,

0

,

0

[

Q

;

mg

Q

























1

0

1

0

z

z

1

0

A

A

z

)

z

z

(

mg

mgdz

dz

Q

L

);

z

(

V

C

mgz

V

mg

z

V

Q

,

C

)

y

(

V

0

y

V

Q

,

C

)

x

(

V

0

x

V

Q

3

z

2

y

1

x

















































Przykład
2

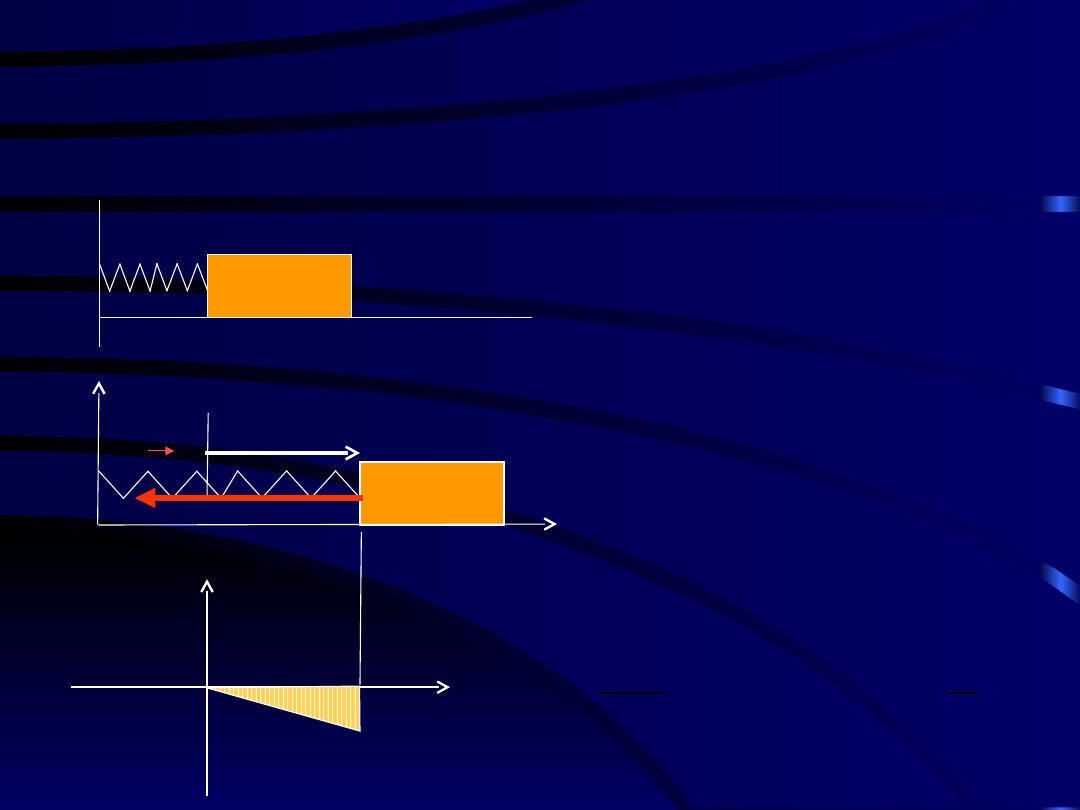
Przykład 3.

Obliczyć energię potencjalną siły sprężystej w
sprężynie o sztywności k.

O

kx

)

x

(

S

]

0

S

,

0

S

,

kx

S

[

S

z

y

x

















2

x

kx

2

1

V

,

S

dx

dV









-kx

S

x

x

Przykład
3

O

x

S

y

x

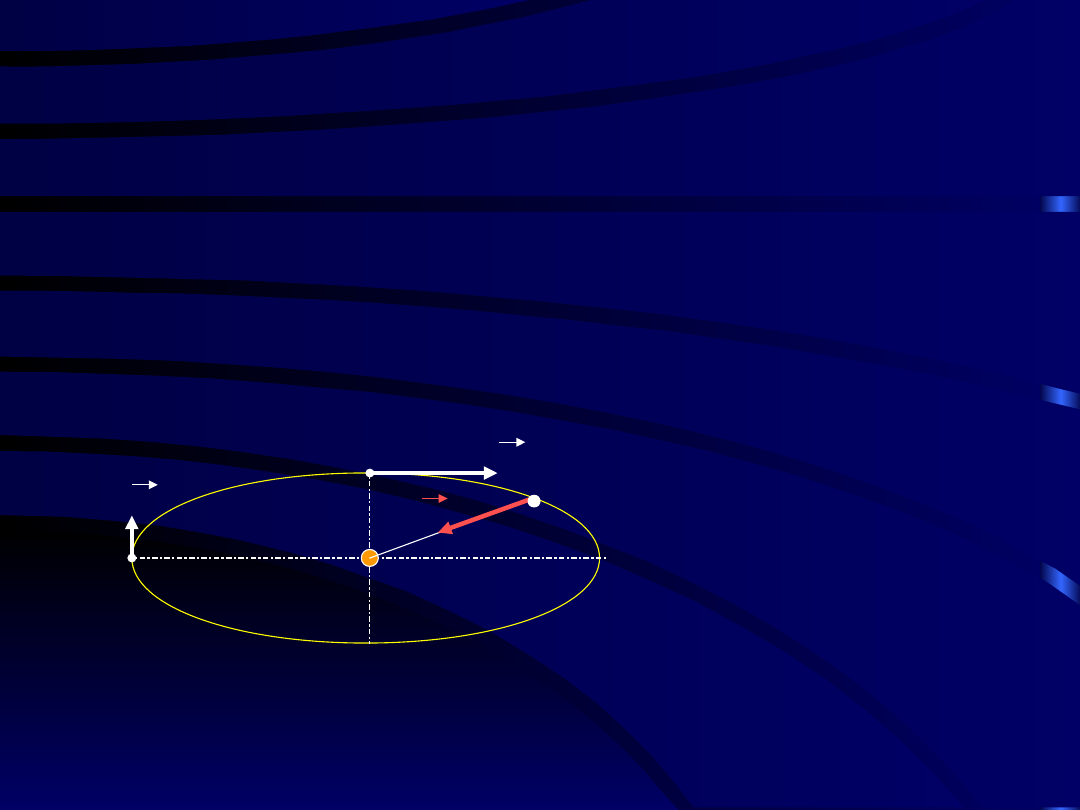
Przykład
4

Przykład 4.
Punkt

M

porusza się dokoła nieruchomego środka pod działaniem

siły przyciągającej do tego środka. Znaleźć prędkość

v

2

w punkcie

toru najbardziej oddalonym od środka, jeżeli prędkość punktu
w miejscu najbliższym środka wynosi

v

1

=3[m/s],

a promień

r

2

jest

5

razy większy od

r

1

.

M

1

M

2

M

v

1

v

2

F

r

1

r

2

0

Momenty
bezwładności

5.4. Podstawy teorii
momentów bezwładności

Środek masy i środek ciężkości UPM i CS

Założenia:

•Weźmy pod uwagę układ n punktów materialnych o
masach m

i

(i=1,...,n)

•Położenie tych punktów w stosunku do punktu
odniesienia O określone jest wektorami r

i

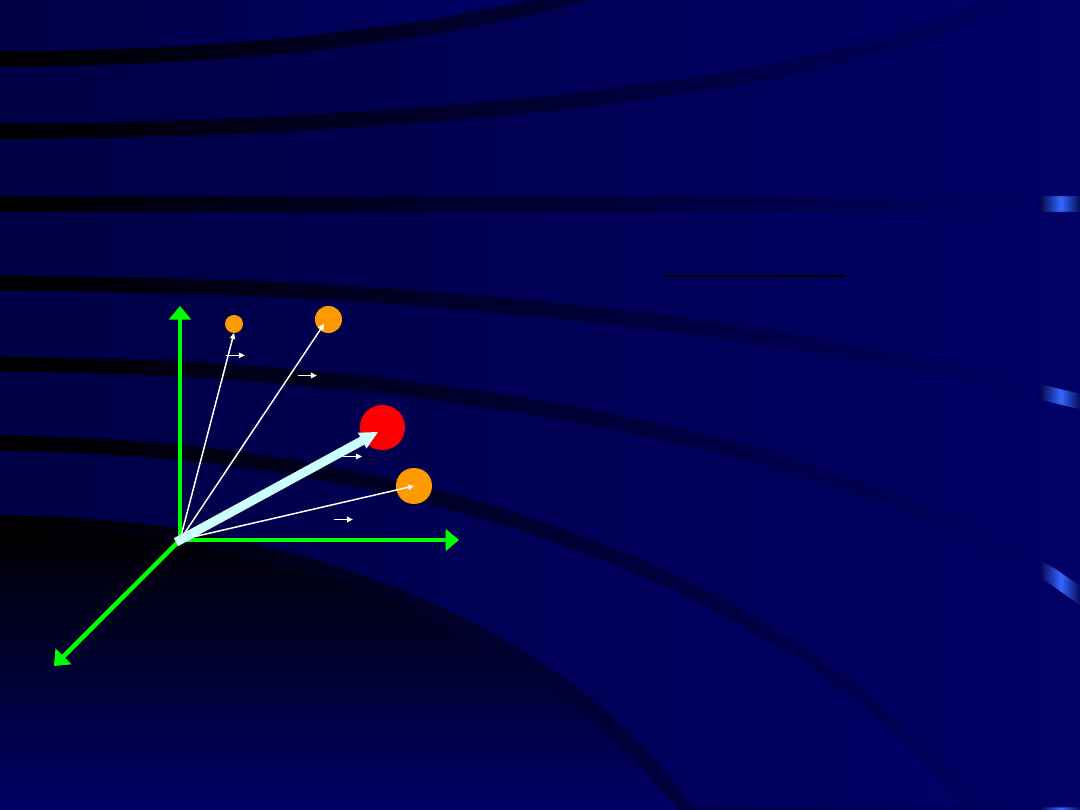
• Wprowadźmy umownie punkt C, którego
położenie
określone jest związkiem:

Punkt C nazywamy

środkiem masy

UPM.

m

1

m

2

m

n

x

y

z

O

r

1

r

2

r

n











n

i

i

n

i

i

i

c

m

r

m

r

1

1





C

r

C

masa punktu C:







n

i

i

m

m

1

Środek masy UPM1

Środek masy UPM2

];

z

,

y

,

x

[

r

c

c

c

c





;

m

z

m

z

;

m

y

m

y

;

m

x

m

x

n

i

i

i

c

n

i

i

i

c

n

i

i

i

c



















1

1

1

Pojęcie

środka masy

ma charakter ogólny i może być

zastosowane do dowolnego UPM, niezależnie od tego
czy układ jest sztywny czy nie, czy jest w ruchu czy w
spoczynku oraz czy znajduje się w polu sił.

Środek masy UPM w układzie Oxyz

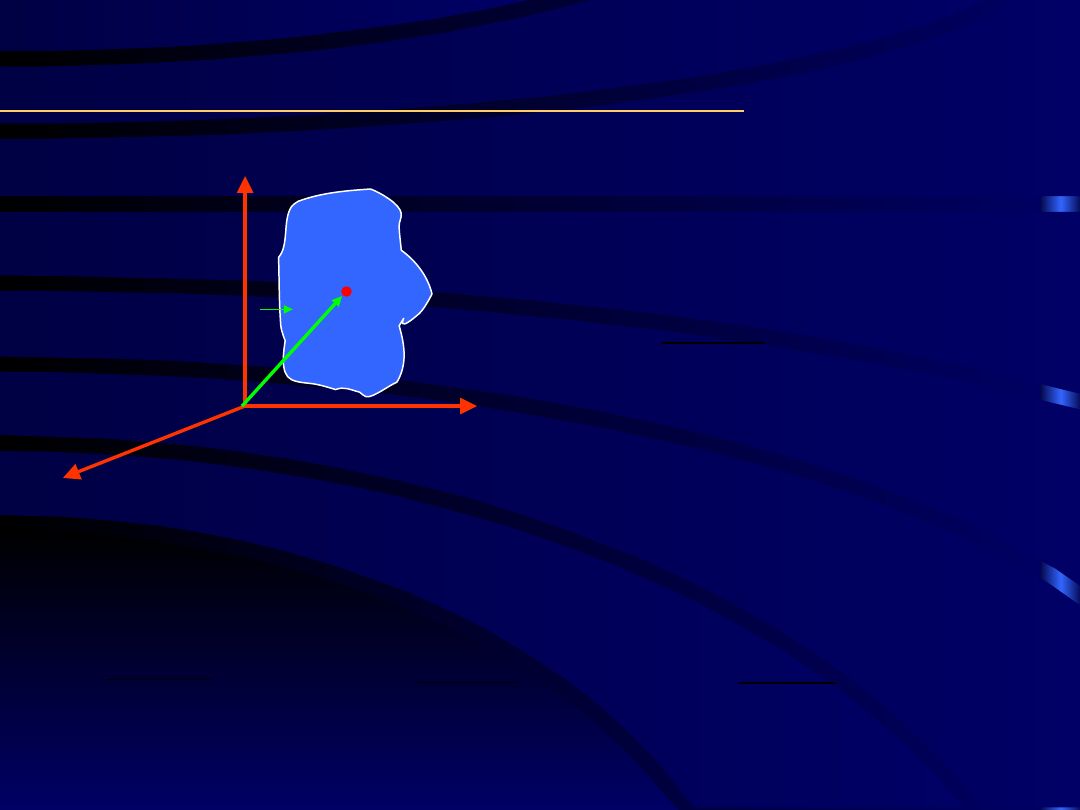
Środek masy CS1

O

x

y

z

m

dm

r

r

m

c









;

m

xdm

x

m

c





;

m

ydm

y

m

c





;

m

zdm

z

m

c





Środek masy ciała sztywnego ciągłego

C

r

c

Gęstość
CS2

const.





V

m

V



Gęstość CS
jednorodnego:

Gęstość CS dwuwymiarowego:
(powłoki, cienkie płyty)











2

m

kg

dA

dm

A













m

kg

dL

dm

L



Gęstość CS jednowymiarowego:
(pręty, liny, belki) :











3

m

kg

dV

dm

V



Gęstość CS dowolnego:

Gęstość CS ciągłego

Na obiekty znajdujące się w polu przyciągania Ziemi, działają

siły ciążenia. Siły te zastępujemy wypadkową siłą ciężkości.

Przy założeniu, że rozmiary obiektu są małe w porównaniu do

rozmiarów Ziemi można siły ciężkości uznać za równoległe i

wyznaczyć środek równoległych sił ciężkości. Punkt taki

nazywamy środkiem ciężkości obiektu (UPM lub CS).

Ciężar właściwy CS:

dV

dQ





Środek
ciężkości

Środek ciężkości

g

m

Q

Q

r

Q

r

i

i

n

i

i

n

i

i

i

c













:

gdzie

,

1

1





Środek ciężkości
UPM:

Wzory na środek masy CS upraszczają się gdy
mamy do czynienia z ciałem jednorodnym tzn.
takim,

w

którym

masa

jest

rozłożona

równomiernie w całej jego objętości.

Środek masy CS
jednorodnego

;

V

xdV

x

V

c





;

V

ydV

y

V

c





;

V

zdV

z

V

c





Środek masy CS jednorodnego

• Ze wzorów na środek masy wynika, że
jego
położenie w jednorodnym CS zależy tylko
od
jego geometrii.

Podsumowani
e

Podsumowanie

Ogólne własności jednorodnego CS:

• Jeżeli ciało ma płaszczyznę symetrii to środek
masy leży na tej płaszczyźnie.
• Jeżeli ciało ma oś symetrii to środek masy leży na
tej osi.
• Jeżeli ciało ma środek symetrii to środek masy
leży w tym środku.

Momenty
statyczne

Momentem statycznym

UPM względem płaszczyzny

nazywamy sumę iloczynów mas każdego punktu przez
ich odległości od tej płaszczyzny.

5.5 Momenty statyczne











V

xy

i

n

i

i

xy

zdm

S

z

m

S

:

c.s.

Dla

:

u.p.m.

Dla

1

Np. względem płaszczyzny 0xy:

;

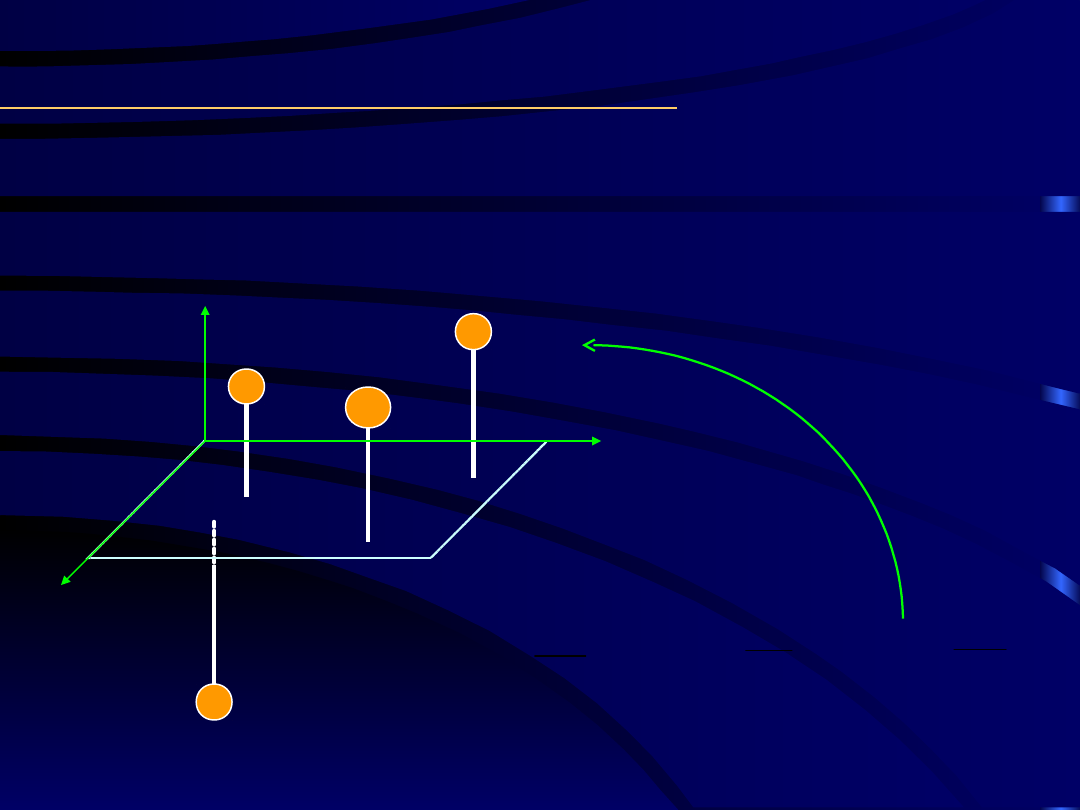
m

S

x

yz

c



;

m

S

y

xz

c



;

m

S

z

xy

c



m

1

z

1

m

2

z

2

m

n

z

n

m

3

z

3

Współrzędne środka masy można określić za
pomocą momentów statycznych względem
płaszczyzn układu Oxyz:

Momenty stat. a środek
masy

Momenty statyczne a środek masy

x

z

y

0

m

1

A

1

m

2

A

2

m

i-1

A

i-1

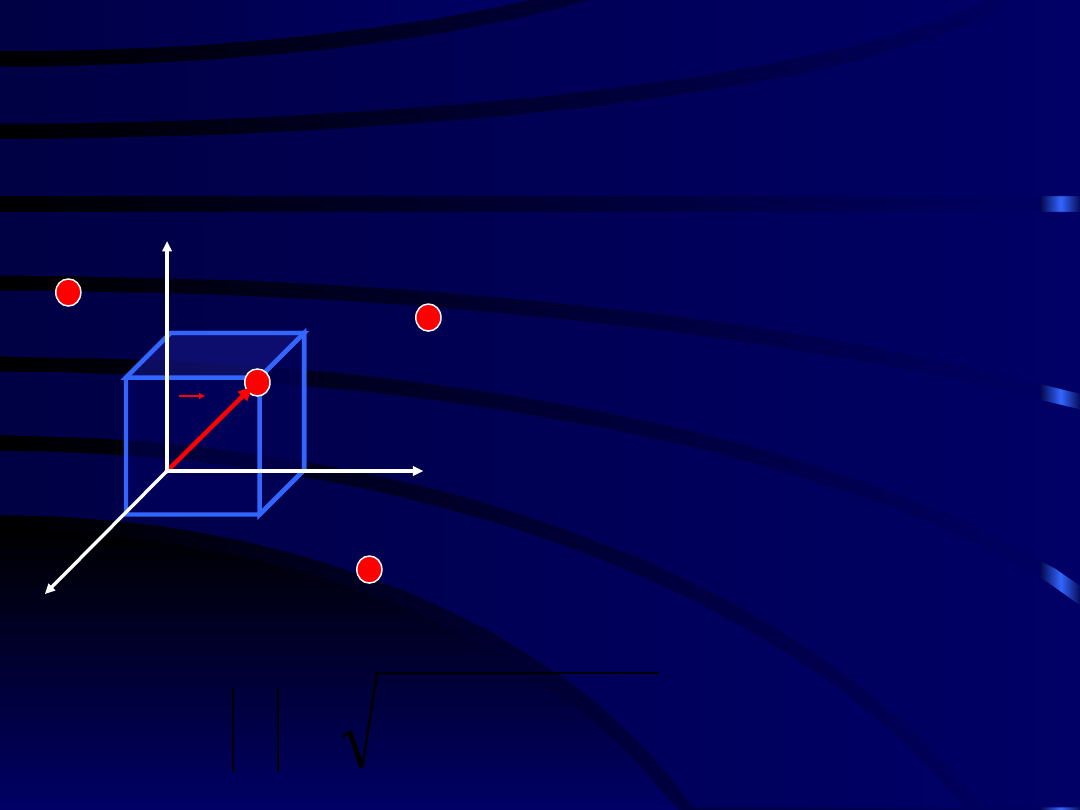
Momenty
bezwładności

z

i

y

i

x

i

m

i

r

i

A

i

A

i

[ x

i

, y

i

, z

i

]

n

1,2,...,

i

; 









2

2

2

i

i

i

i

i

z

y

x

r

r 

x

y

z

0

10.3 Momenty bezwładności

Momenty bezwł. wzgl.
płaszczyzn

Momenty bezwładności względem
płaszczyzn Oxyz

;

m

x

I

m

y

I

m

z

I

i

i

i

yz

i

i

i

xz

i

i

i

xy













2

2

2

;

;

Dla UPM:

;

dm

x

I

;

dm

y

I

dm

z

I

m

yz

m

xz

m

xy













2

2

2

;

Dla CS:

Momenty bezwł. wzgl.
osi

Momenty bezwładności względem osi 0xyz

;

m

)

y

x

(

I

m

)

z

x

(

I

m

)

z

y

(

I

i

i

2
i

2
i

z

i

i

2
i

2
i

y

i

i

2
i

2
i

x



















;

;

Dla UPM:



















m

z

m

y

m

x

;

dm

)

y

x

(

I

dm

)

z

x

(

I

dm

)

z

y

(

I

2

2

2

2

2

2

;

;

Dla CS:

Moment bezwł. wzgl.
bieguna

Moment bezwładności względem bieguna 0













i

i

i

i

i

i

i

i

m

r

m

)

z

y

x

(

I

2

2

2

2

0

Dla UPM:













m

m

dm

r

dm

)

z

y

x

(

I

2

2

2

2

0

Dla CS:

Wzajemne
zależności

0

0



I

,

I

,

I

,

I

,

I

,

I

,

I

z

y

x

yz

xz

xy

yz

xz

z

yz

xy

y

xz

xy

x

I

I

I

,

I

I

I

,

I

I

I













)

I

I

I

(

I

I

I

I

I

z

y

x

yz

xz

xy













2

1

0

0

lub

Ważne zależności

Momenty
dewiacyjne

zy

yz

zx

xz

yx

xy

D

D

,

D

D

,

D

D







Momenty dewiacyjne (mieszane) w układzie Oxyz

0





yz

xz

xy

D

,

D

,

D













i

i

i

i

i

i

yz

i

i

i

xz

i

i

i

xy

m

z

y

D

,

m

z

x

D

,

m

y

x

D

Dla UPM:.:













m

yz

m

xz

m

xy

yzdm

D

,

xzdm

D

,

xydm

D

Dla CS:

Macierz
bezwładności

I =

































z

zy

zx

yz

y

yx

xz

xy

x

I

D

D

D

I

D

D

D

I

I
-

opisuje własności bezwładnościowe CS lub UPM.

Macierz bezwładności (tensor
bezwładności)

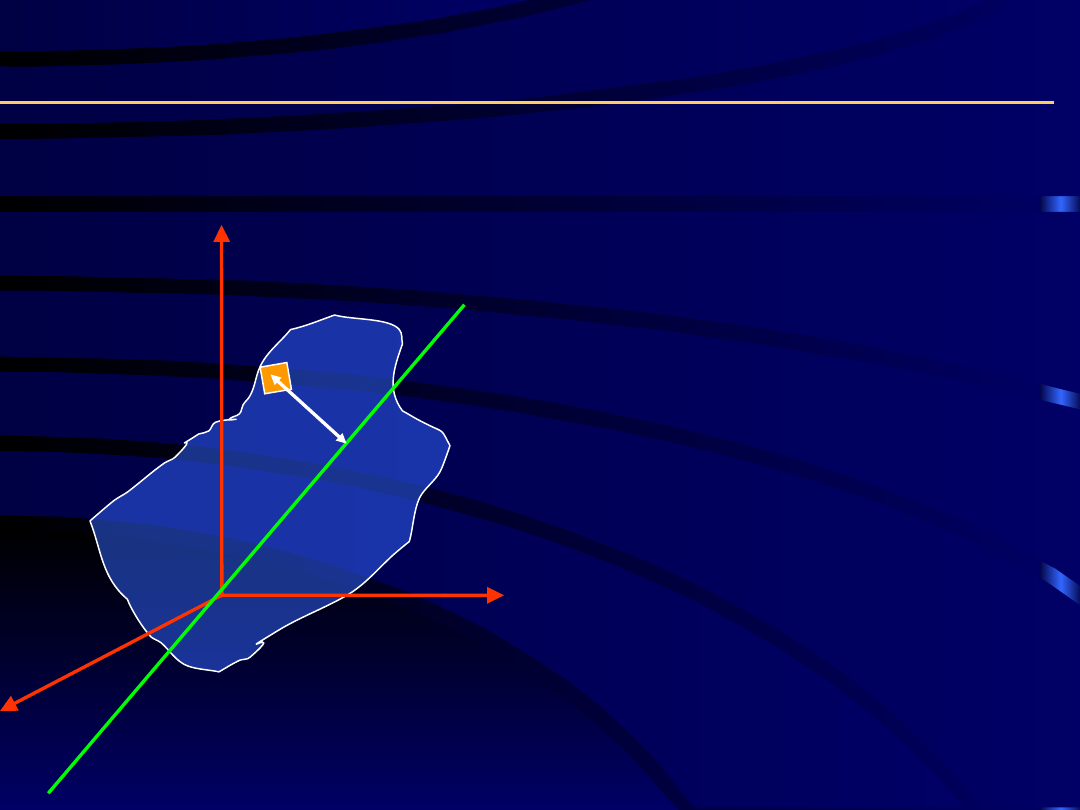
x

y

z

0

Moment bezwł.
względem l

l

l

l

l

– dowolna prosta

przechodząca
przez początek układu 0

dm

h









m

l

l

dm

h

I

dm

h

dI

2

2

)

z

,

l

(

),

y

,

l

(

),

x

,

l

(



















Moment bezwładności względem dowolnej osi l

Moment bezwł. względem l
c.d.

;

cos

cos

D

cos

cos

D

cos

cos

D

cos

I

cos

I

cos

I

I

yz

xz

xy

z

y

x

l



















2

2

2

2

2

2

















Po przekształceniach moment bezwładności
względem osi

l

l

wynosi

wynosi

:

:

Osie główne centralne

Jeżeli tak zorientujemy w przestrzeni osie układu

Cxyz

,

że

D

xy

=D

xz

=D

yz

=0

,

to takie osie nazywamy

głównymi

centralnymi.

Układ takich osi oznaczamy:

C123

.

Osie główne centralne i momenty bezwładności
względem nich

Lokując początek układu współrzędnych w środku
masy ciała mamy

centralny

układ osi Cxyz.

Główne centralne momenty
bezwładności

Momenty bezwładności względem

osi głównych centralnych

oznaczamy odpowiednio:

I

1

, I

2

, I

3

i nazywamy

głównymi centralnymi momentami bezwładności

c.s.







2

3

2

2

2

1

cos

I

cos

I

cos

I

I

l







Moment bezwładności względem dowolnej osi

l

, wyrażony

w układzie

głównym centralnym C123

ma postać:

Twierdzenie
Steinera

Twierdzenie Steinera

Moment bezwładności CS względem dowolnej osi

l

1

jest równy sumie momentu bezwładności

względem osi do niej równoległej

l

przechodzącej

przez środek masy tego ciała oraz iloczynu masy
ciała i kwadratu odległości między tymi osiami.

l

l

1

d

C

m

Momenty bezwładności względem osi równoległych

2

1

d

m

I

I

l

l





